DOI:
10.1039/D4SC02463J
(Edge Article)
Chem. Sci., 2024,
15, 11507-11514
Local electric field in nanocavities dictates the vibrational relaxation dynamics of interfacial molecules†
Received
15th April 2024
, Accepted 16th June 2024
First published on 25th June 2024
Abstract
Plasmonic nanocavities enable the generation of strong light–matter coupling and exhibit great potential in plasmon-mediated chemical reactions (PMCRs). Although an electric field generated by nanocavities (En) has recently been reported, its effect on the vibrational energy relaxation (VER) of the molecules in the nanocavities has not been explored. In this study, we reveal the impact of an electric field sensed by molecules (para-substituted thiophenol derivatives) in a nanocavity (Ef) on VER processes by employing advanced time-resolved femtosecond sum frequency generation vibrational spectroscopy (SFG-VS) supplemented by electrochemical measurements. The magnitude of En is almost identical (1.0 ± 0.2 V nm−1) beyond the experimental deviation while Ef varies from 0.3 V nm−1 to 1.7 V nm−1 depending on the substituent. An exponential correlation between Ef and the complete recovery time of the ground vibrational C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C state (T2) of the phenyl ring is observed. Substances with a smaller T2 are strongly correlated with the reported macroscopic chemical reactivity. This finding may aid in enriching the current understanding of PMCRs and highlights the possibility of regulating vibrational energy flow into desired reaction coordinates by using a local electric field.
C state (T2) of the phenyl ring is observed. Substances with a smaller T2 are strongly correlated with the reported macroscopic chemical reactivity. This finding may aid in enriching the current understanding of PMCRs and highlights the possibility of regulating vibrational energy flow into desired reaction coordinates by using a local electric field.
Introduction
Plasmonic nanocavities allow the localization and concentration of light into subnanoscale volumes and enable the generation of strong light–matter coupling.1–3 This exceptional ability provides a novel platform for access to biosensing, quantum chemistry and materials science.4–7 In particular, plasmonic nanocavities have been demonstrated to exhibit promising applications in mediating chemical reactions.8–10 In theory, vibrational energy relaxation (VER) is fundamentally important for chemical reaction dynamics owing to its intrinsic connection with energy dissipation at reaction active sites and chromophores, as well as its ability to govern reaction coordinates.11–15 Although plasmon-mediated chemical reactions (PMCRs) have achieved important milestones,16,17 the underlying effects of plasmons on the VER processes of interfacial molecules have largely not been explored.
Currently, several mechanisms for PMCRs have been proposed, including electromagnetic fields,18 hot electrons (holes) and heat generated by excited plasmons,19–21 and static electric fields.22–24 In the last mechanism, the nanocavity can generate a direct current (DC) electric field (En) to mediate chemical reactions.25–29 Here, En is an electrostatic field resulting from the photoexcitation of metal nanoparticles which is sustained over the full course of chemical turnover, rather than the instantaneous electric field resulting from the electromagnetic field concentration provided by plasmon resonance.26 Although a chemical potential contributed by plasmonic excitation was recently shown,23,29,30 direct probing of the DC electric field and its influence on molecules in the nanocavity is rather challenging.25,26,30 As a result, insight into the effect of plasmonic excitation on interfacial VER processes is poorly understood. In this study, we used self-assembled monolayers (SAMs) of para-substituted thiophenol derivatives on gold films and in plasmonic nanocavities as models and revealed the impact of the electric field sensed by the molecules in the nanocavity (Ef) on the VER processes. We determined the magnitudes of En and Ef by investigating the bandwidth of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode (νC
C stretching mode (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) of the phenyl ring via femtosecond sum frequency generation vibrational spectroscopy (SFG-VS) supplemented by electrochemical measurements. Here, the probed molecules are located in nanocavities based on a nanoparticle-on-mirror (NPoM) approach (Fig. 1a) (labeled as NPoM-SAMs).31,32 The selected aromatic thiols are well known to form good SAMs on metal surfaces and are widely adopted in photocatalysis and biomedicine.33–37 The feasibility and superiority of using the C
C) of the phenyl ring via femtosecond sum frequency generation vibrational spectroscopy (SFG-VS) supplemented by electrochemical measurements. Here, the probed molecules are located in nanocavities based on a nanoparticle-on-mirror (NPoM) approach (Fig. 1a) (labeled as NPoM-SAMs).31,32 The selected aromatic thiols are well known to form good SAMs on metal surfaces and are widely adopted in photocatalysis and biomedicine.33–37 The feasibility and superiority of using the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode of the phenyl ring as a probe have been confirmed by surface-enhanced Raman spectroscopy (SERS).38,39En is approximately 1.0 ± 0.2 V nm−1, and Ef varies from 0.3 V nm−1 to 1.7 V nm−1. An exponential correlation between Ef and the complete recovery time of the ground vibrational C
C stretching mode of the phenyl ring as a probe have been confirmed by surface-enhanced Raman spectroscopy (SERS).38,39En is approximately 1.0 ± 0.2 V nm−1, and Ef varies from 0.3 V nm−1 to 1.7 V nm−1. An exponential correlation between Ef and the complete recovery time of the ground vibrational C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C state (T2) was observed. A substance with a smaller T2 shows a strong correlation with the macroscopic chemical reactivity and plasmon-molecule interactions reported for PMCRs.40,41 This work highlights the possibility of regulating vibrational energy flow into desired reaction coordinates using the local electric field in which the molecules are sensed in nanocavities. In addition, it is well known that local electric field strengths on the order of 1 V nm−1 are not only responsible for the vibrational Stark effect in both single-molecule systems42 and condensed phases,43 but can also selectively promote, drive, and control chemical reactions44 such as proton transfer45 and catalytic processes,46–49 for example, the catalytic synthesis of ammonia from nitrogen and water microdroplets.50,51 Therefore, the findings in this work may aid in enriching the current understanding of these processes including vibrational dynamics and catalytic processes.
C state (T2) was observed. A substance with a smaller T2 shows a strong correlation with the macroscopic chemical reactivity and plasmon-molecule interactions reported for PMCRs.40,41 This work highlights the possibility of regulating vibrational energy flow into desired reaction coordinates using the local electric field in which the molecules are sensed in nanocavities. In addition, it is well known that local electric field strengths on the order of 1 V nm−1 are not only responsible for the vibrational Stark effect in both single-molecule systems42 and condensed phases,43 but can also selectively promote, drive, and control chemical reactions44 such as proton transfer45 and catalytic processes,46–49 for example, the catalytic synthesis of ammonia from nitrogen and water microdroplets.50,51 Therefore, the findings in this work may aid in enriching the current understanding of these processes including vibrational dynamics and catalytic processes.
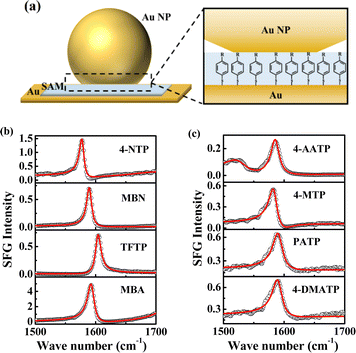 |
| | Fig. 1 (a) Picture depicting the SAMs assembled in NPoMs, R = NO2/CN/CF3/COOH/NHCOCH3/OCH3/NH2/N(CH3)2. The abbreviations for the corresponding substances are 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP. (b) The SE-SFG spectra of 4-NTP, MBN, TFTP and MBA in the frequency range of 1500–1700 cm−1. (c) The SE-SFG spectra of 4-AATP, 4-MTP, PATP and 4-DMATP in the frequency range of 1500–1700 cm−1. | |
Results and discussion
The ultrafast vibrational dynamics of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) C stretching mode of NPoM-SAMs
C stretching mode of NPoM-SAMs
We first measured the spectra and ultrafast vibrational dynamics of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of NPoM-SAMs using femtosecond time-resolved IR pump-SFG probe measurements. Fig. 1b and c show the ppp spectra of the NPoM-SAMs in the frequency range of 1500–1700 cm−1. All the peaks indicate a positive phase. The spectra in the frequency range of 1200–1800 cm−1 are displayed in Fig. S1.† All the samples had a νC
C mode of NPoM-SAMs using femtosecond time-resolved IR pump-SFG probe measurements. Fig. 1b and c show the ppp spectra of the NPoM-SAMs in the frequency range of 1500–1700 cm−1. All the peaks indicate a positive phase. The spectra in the frequency range of 1200–1800 cm−1 are displayed in Fig. S1.† All the samples had a νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C frequency of 1585 (±15) cm−1. Compared to those of the samples on the gold film without NPoMs (labeled as Au-SAMs) (Fig. S2†), the resonance signals of the molecules on the NPoM-SAMs are amplified with an enhancement factor >103. Fig. 2a and b depict the decay in the effective SFG peak strength (χ(2)) of the νC
C frequency of 1585 (±15) cm−1. Compared to those of the samples on the gold film without NPoMs (labeled as Au-SAMs) (Fig. S2†), the resonance signals of the molecules on the NPoM-SAMs are amplified with an enhancement factor >103. Fig. 2a and b depict the decay in the effective SFG peak strength (χ(2)) of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of thiophenol derivatives. In theory, SFG probes the surface population density of a vibrational state.52,53 The excitation of νC
C mode of thiophenol derivatives. In theory, SFG probes the surface population density of a vibrational state.52,53 The excitation of νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C from the ground state (ν0) to its first vibrational state (ν1) can reduce the SFG intensity. In general, the efficiency of vibrational excitation at the interface is very low. Currently, vibrational dynamics of only a few groups, such as OH and amide modes, have been reported.52,54–56 In the absence of nanocavities, the bleaching value is too small to be detected (Fig. S3†). However, in the presence of nanocavities, clear bleaching following excitation at 1580 cm−1 at t = 0 was observed (Fig. 2a and b) due to plasmon-enhanced vibrational excitation.57,58 Following this bleaching, the ν1 state relaxes to an intermediate state, and the SFG intensity gradually recovers. The vibrational dynamics of the νC
C from the ground state (ν0) to its first vibrational state (ν1) can reduce the SFG intensity. In general, the efficiency of vibrational excitation at the interface is very low. Currently, vibrational dynamics of only a few groups, such as OH and amide modes, have been reported.52,54–56 In the absence of nanocavities, the bleaching value is too small to be detected (Fig. S3†). However, in the presence of nanocavities, clear bleaching following excitation at 1580 cm−1 at t = 0 was observed (Fig. 2a and b) due to plasmon-enhanced vibrational excitation.57,58 Following this bleaching, the ν1 state relaxes to an intermediate state, and the SFG intensity gradually recovers. The vibrational dynamics of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode exhibit biexponential decays with a fast component (T1) and a slow component (T2). These two components were attributed to the fast population transfer between different C
C mode exhibit biexponential decays with a fast component (T1) and a slow component (T2). These two components were attributed to the fast population transfer between different C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C modes (T1) and the slow complete recovery of the ground vibrational state (T2), respectively. T2 is dominated by a combination of intramolecular vibrational relaxation (IVR) and nonadiabatic relaxation which contributes to the excitation of electron–hole pairs (EHPs) in gold substrates and gold nanoparticles.59,60 EHPs have been proven to be the primary energy transfer channel on metal surfaces.61,62 The T1 values of the different thiophenol derivatives are essentially identical at approximately 1 ps, which is consistent with the time required for rapid energy equilibrium among the delocalized νC
C modes (T1) and the slow complete recovery of the ground vibrational state (T2), respectively. T2 is dominated by a combination of intramolecular vibrational relaxation (IVR) and nonadiabatic relaxation which contributes to the excitation of electron–hole pairs (EHPs) in gold substrates and gold nanoparticles.59,60 EHPs have been proven to be the primary energy transfer channel on metal surfaces.61,62 The T1 values of the different thiophenol derivatives are essentially identical at approximately 1 ps, which is consistent with the time required for rapid energy equilibrium among the delocalized νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C modes.63 In contrast, significant differences in T2 values were observed across the samples (Table S1†). Specifically, the T2 values are 21.4 (±1.3), 20.0 (±0.4), 17.3 (±0.5), 15.2 (±0.3), 13.8 (±0.4), 12.7 (±0.5), 9.7 (±0.7) and 10.4 (±1.4) ps for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. The difference in T2 may arise from various factors, such as intermolecular interactions, molecular orientation, and the electric field.64–66 The studied SAMs exhibit very similar orientations with respect to the metal surface, thus ruling out orientation as the main reason for the difference in T2.64 The effect of intermolecular interactions on T2 can also be ruled out. Earlier reports suggested that the value of T2 is strongly dependent on the π–π interactions between molecules, with stronger intermolecular interactions promoting faster molecular energy dissipation.64 However, the observed results contradict this hypothesis. For instance, 4-NTP, which was expected to have a faster T2 due to its strong π–π interaction, actually exhibited a longer T2 (21.4 (±1.3) ps). Similarly, the presence of a –CF3 group theoretically weakens π–π interactions and may result in an increase in the T2 of the phenyl ring. However, these speculations in terms of intermolecular interactions contrast with our findings. Therefore, the electric field is most likely a significant factor in regulating vibrational relaxation dynamics. To verify this conjecture, we measured the magnitudes of En and Ef based on the DC Stark effect on the bandwidth of the νC
C modes.63 In contrast, significant differences in T2 values were observed across the samples (Table S1†). Specifically, the T2 values are 21.4 (±1.3), 20.0 (±0.4), 17.3 (±0.5), 15.2 (±0.3), 13.8 (±0.4), 12.7 (±0.5), 9.7 (±0.7) and 10.4 (±1.4) ps for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. The difference in T2 may arise from various factors, such as intermolecular interactions, molecular orientation, and the electric field.64–66 The studied SAMs exhibit very similar orientations with respect to the metal surface, thus ruling out orientation as the main reason for the difference in T2.64 The effect of intermolecular interactions on T2 can also be ruled out. Earlier reports suggested that the value of T2 is strongly dependent on the π–π interactions between molecules, with stronger intermolecular interactions promoting faster molecular energy dissipation.64 However, the observed results contradict this hypothesis. For instance, 4-NTP, which was expected to have a faster T2 due to its strong π–π interaction, actually exhibited a longer T2 (21.4 (±1.3) ps). Similarly, the presence of a –CF3 group theoretically weakens π–π interactions and may result in an increase in the T2 of the phenyl ring. However, these speculations in terms of intermolecular interactions contrast with our findings. Therefore, the electric field is most likely a significant factor in regulating vibrational relaxation dynamics. To verify this conjecture, we measured the magnitudes of En and Ef based on the DC Stark effect on the bandwidth of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of the phenyl ring by combining SFG-VS and electrochemical measurements.
C mode of the phenyl ring by combining SFG-VS and electrochemical measurements.
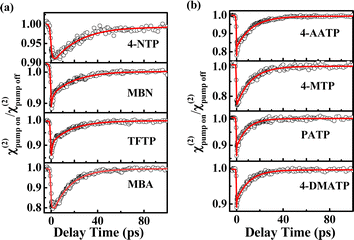 |
| | Fig. 2 (a) χ(2) decay of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of the phenyl rings of 4-NTP, MBN, TFTP and MBA. (b) χ(2) decay of the νC C mode of the phenyl rings of 4-NTP, MBN, TFTP and MBA. (b) χ(2) decay of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of the phenyl rings of 4-AATP, 4-MTP, PATP and 4-DMATP. C mode of the phenyl rings of 4-AATP, 4-MTP, PATP and 4-DMATP. | |
Determination of the magnitudes of the electric field En and Ef
In principle, Ef in nanocavities consists of two components, the molecular internal electric field (Ei) and En (eqn (1)). In the absence of nanocavities, Ef = Ei. It has been reported that Ei is linearly related to the Hammett constant (σ) of the para-substituted group on the chemical moiety.67–69 For simplicity of analysis, the magnitude of Ei in this work is the relative magnitude compared to that at σ = 0. Earlier studies indicated that the electric field can generate a vibrational Stark effect, yielding a linear correlation between the electric field and the frequency (ω)70–73 or peak area (intensity)74 of a vibrational mode. In addition to ω and peak area, the bandwidth also displays a linear dependence on the electric field and provides another molecular-level descriptor for evaluating the electric field (see eqn (2)–(4)).67,75 To determine the magnitude of En, we utilized an external electric potential (V) to increase the molecular bandwidth of the films in the absence of a nanocavity (Fig. 3a). When this bandwidth broadening of the “Au-SAMs + applied potential (V)” case equals the bandwidth broadening caused by the nanocavity, the value of the external electric potential can be used to determine the magnitude of the corresponding En using eqn (1)–(4). Specifically, by probing the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bandwidth change of each Au-SAM at different applied potentials (ΔΓp) using SFG-VS supplemented by electrochemical measurements, the dependence of ΔΓp on V can be determined by using eqn (2). The Ei and En of each sample can be deduced using eqn (3) and (4), respectively.
C bandwidth change of each Au-SAM at different applied potentials (ΔΓp) using SFG-VS supplemented by electrochemical measurements, the dependence of ΔΓp on V can be determined by using eqn (2). The Ei and En of each sample can be deduced using eqn (3) and (4), respectively.| | 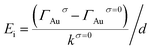 | (3) |
| |  | (4) |
where kσ is defined as the Stark bandwidth broadening rate, ΓAuσ is the bandwidth of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of thiophenol derivatives in the absence of nanocavities at zero applied electric potential, ΓNPoMσ is the corresponding bandwidth of the samples in the presence of nanocavities, and d is the spacer thickness of SAMs in the nanocavity. The subscript p represents the change induced by V, and the superscript σ corresponds to the Hammett constant. According to eqn (1)–(4), determining the values of En and Ef requires knowledge of ΓAuσ, ΓNPoMσ, and kσ.
C mode of thiophenol derivatives in the absence of nanocavities at zero applied electric potential, ΓNPoMσ is the corresponding bandwidth of the samples in the presence of nanocavities, and d is the spacer thickness of SAMs in the nanocavity. The subscript p represents the change induced by V, and the superscript σ corresponds to the Hammett constant. According to eqn (1)–(4), determining the values of En and Ef requires knowledge of ΓAuσ, ΓNPoMσ, and kσ.
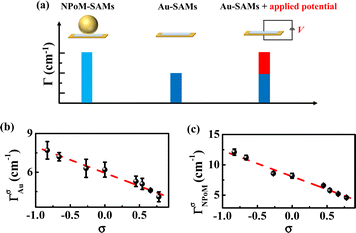 |
| | Fig. 3 (a) Schematic diagram for obtaining the magnitude of En based on the application of an external electric potential (V) to Au-SAMs. (b) ΓAuσ of Au-SAMs plotted against σ, and (c) ΓNPoMσ of NPoM-SAMs plotted against σ. | |
To determine the values of ΓAuσ and ΓNPoMσ, we fit the ppp spectra of the Au-SAMs and NPoM-SAMs (Fig. 1b, c and S2†) using a standard procedure (eqn (S1)†). The fitting parameters are shown in Tables S2 and S3.† The average ΓAuσ values were determined to be 4.1 (±0.4), 4.6 (±0.1), 5.1 (±0.4), 5.3 (±0.4), 6.2 (±0.5), 6.3 (±0.7), 7.2 (±0.3) and 7.7 (±0.6) cm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. The average ΓNPoMσ values were determined to be 4.6 (±0.2), 5.2 (±0.1), 5.8 (±0.2), 6.6 (±0.1), 8.2 (±0.6), 8.6 (±0.2), 11.2 (±0.3), and 12.1 (±0.5) cm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. The error bars represent more than 5 repeated experimental results (Tables S4 and S5†). The Hammett constants of the substituent groups in 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP are 0.78, 0.66, 0.54, 0.45, 0, −0.27, −0.66, and −0.83, respectively.76 A good linear correlation between the bandwidth and Hammett constant is observed (ΓAuσ = −2.0 × σ + 5.9 and ΓNPoMσ = −4.3 × σ + 8.1) (Fig. 3b and c), indicating that the bandwidth can provide an effective descriptor for evaluating the electric field. Indeed, recent investigations on the carbonyl group of acetophenones have also demonstrated the linear dependence of the bandwidth on the Hammett constant77 and potential.67 Compared to those of ΓAuσ, the plot of ΓNPoMσ against the Hammett constant has a greater slope and intercept (Fig. 3b and c), revealing that the introduction of nanocavities leads to peak broadening. Accordingly, the changes in bandwidth (ΔΓn = ΓNPoMσ − ΓAuσ) in the absence and presence of nanocavities are 0.5 (±0.3), 0.6 (±0.1), 0.7 (±0.3), 1.3 (±0.4), 2.0 (±0.3), 2.3 (±0.7), 4.0 (±0.1), and 4.4 (±0.3) cm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. Theoretically, peak broadening can be caused by several factors, e.g., pressure,78 temperature,79 and the electric field.24,75,80,81 The effects of pressure and temperature can be excluded because the contributions caused by pressure and temperature are expected to be similar for different substituted groups with the same fluences of input laser pulses, which is opposite to what we have observed.
The value of kσ can be determined by measuring the dependence of the bandwidth of the Au-SAMs (eqn (2)) on the potential via electrochemical testing experiments. Fig. 4a displays the potential-dependent SFG spectra of νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C of MBN. The data for other Au-SAMs are provided in Fig. S4a.†Fig. 4b and S4b† depict the dependence of ΔΓp on V. As the potential increases, ΔΓp for MBN, 4-NTP, TFTP, MBA, 4-AATP, and 4-MTP linearly decreases (Fig. 4b and S4b†), while those for PATP and 4-DMATP linearly increase (Fig. S4b†). The values of kσ are determined to be −0.5 (±0.1), −0.6 (±0.1), −0.9 (±0.1), −1.4 (±0.1), −2.0 (±0.1), −1.9 (±0.2), 4.0 (±0.4), and 4.4 (±0.9) cm−1 V−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively (Table S6†). Based on the linear relationship between kσ and σ shown in Fig. S5,†kσ=0 is deduced to be 2.2 cm−1 V−1. With the assumption of d ∼1 nm,32,82,83Ei is determined to be −0.7, −0.6, −0.5, −0.4, 0, 0.2, 0.6, and 0.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP, and 4-DMATP, respectively. Note that an electron withdrawing group (EWG) is equivalent to applying a negative electric field, while an electron donating group (EDG) represents the application of a positive electric field. This distinction arises from the fact that an upward electric field is defined as positive. When the substituent is an EWG, it induces an upward movement of the charge of the phenyl ring, equivalent to imposing a downward (negative) electric field.68 In contrast, an EDG corresponds to a positive electric field. Using eqn (4), En is deduced to be 1.0, 1.0, 0.8, 0.9, 1.0, 1.2, 1.0, and 1.0 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP, and 4-DMATP, respectively. The magnitude of En for all the studied samples is almost identical (1.0 ± 0.2 V nm−1) beyond the experimental deviation. The magnitude of En can be further confirmed by the results determined using Stark shift (shown in the ESI†), which is an acknowledged tool for quantifying electric fields.73,84 As a result, the Ef values of the different substituents were deduced to be 0.3, 0.4, 0.5, 0.6, 1.0, 1.2, 1.6 and 1.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively (Fig. 4d). The consistency of the electric field obtained through the peak shift and peak bandwidth provides robust support for the effectiveness of employing the bandwidth as a metric for electric field measurements.
C of MBN. The data for other Au-SAMs are provided in Fig. S4a.†Fig. 4b and S4b† depict the dependence of ΔΓp on V. As the potential increases, ΔΓp for MBN, 4-NTP, TFTP, MBA, 4-AATP, and 4-MTP linearly decreases (Fig. 4b and S4b†), while those for PATP and 4-DMATP linearly increase (Fig. S4b†). The values of kσ are determined to be −0.5 (±0.1), −0.6 (±0.1), −0.9 (±0.1), −1.4 (±0.1), −2.0 (±0.1), −1.9 (±0.2), 4.0 (±0.4), and 4.4 (±0.9) cm−1 V−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively (Table S6†). Based on the linear relationship between kσ and σ shown in Fig. S5,†kσ=0 is deduced to be 2.2 cm−1 V−1. With the assumption of d ∼1 nm,32,82,83Ei is determined to be −0.7, −0.6, −0.5, −0.4, 0, 0.2, 0.6, and 0.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP, and 4-DMATP, respectively. Note that an electron withdrawing group (EWG) is equivalent to applying a negative electric field, while an electron donating group (EDG) represents the application of a positive electric field. This distinction arises from the fact that an upward electric field is defined as positive. When the substituent is an EWG, it induces an upward movement of the charge of the phenyl ring, equivalent to imposing a downward (negative) electric field.68 In contrast, an EDG corresponds to a positive electric field. Using eqn (4), En is deduced to be 1.0, 1.0, 0.8, 0.9, 1.0, 1.2, 1.0, and 1.0 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP, and 4-DMATP, respectively. The magnitude of En for all the studied samples is almost identical (1.0 ± 0.2 V nm−1) beyond the experimental deviation. The magnitude of En can be further confirmed by the results determined using Stark shift (shown in the ESI†), which is an acknowledged tool for quantifying electric fields.73,84 As a result, the Ef values of the different substituents were deduced to be 0.3, 0.4, 0.5, 0.6, 1.0, 1.2, 1.6 and 1.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively (Fig. 4d). The consistency of the electric field obtained through the peak shift and peak bandwidth provides robust support for the effectiveness of employing the bandwidth as a metric for electric field measurements.
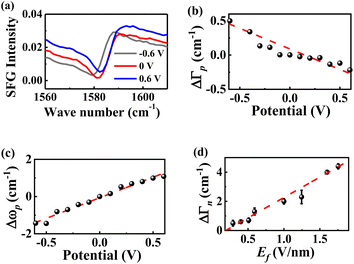 |
| | Fig. 4 (a) Potential-dependent SFG spectra of MBN between 0.6 V and −0.6 V vs. Ag/AgCl. ΔΓp (b) and Δωp (c) of νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C of MBN as a function of the electric potential. (d) The ΔΓn values of thiophenol derivatives plotted against Ef. C of MBN as a function of the electric potential. (d) The ΔΓn values of thiophenol derivatives plotted against Ef. | |
The correlation between Ef and relaxation time T2
We can now establish a correlation between Ef and T2 (Fig. 5a). Evidently, T2 exhibits an exponential dependence on Ef. A larger Ef corresponds to faster vibrational relaxation dynamics, while a smaller Ef corresponds to longer vibrational relaxation lifetimes. This correlation was further supported by the results obtained by applying a potential directly to 4-AATP (Fig. 5b). T2 is 10.8 ps and 15.6 ps for Ef = 1.5 and 0.5 V nm−1, respectively. Ef is related to the molecule–metal coupling. A larger Ef facilitates more efficient metal-molecule electron transfer and leads to faster transfer of molecular vibrational energy to the metal substrate, resulting in a shorter T2. Accordingly, a substance with a smaller T2 is expected to exhibit stronger reactivity because of its enhanced coupling to the metal. Indeed, this has been supported by some recent reports associated with PMCRs. For example, the H2 production rate of 4-MTP in plasmon-mediated hydrogenolysis reactions was approximately 60 times greater than that of 4-NTP.40 The plasmon-mediated methyl dehydrogenation occurrence rate of 4-methylbenzenethiol (4-MBT) exhibited a more than twofold increase at +0.5 V compared to that at −0.5 V.41
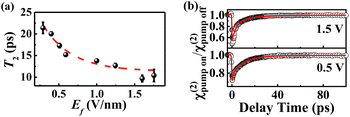 |
| | Fig. 5 (a) Ef plotted against the T2 of thiophenol derivatives. (b) The ppp χ(2) decay of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C of 4-AATP at different potentials. C of 4-AATP at different potentials. | |
Conclusion
In this study, we utilized femtosecond broadband SFG to investigate the electric field sensed by the molecules in a nanocavity (Ef) and its impact on the ultrafast dynamics of para-substituted thiophenol molecules confined within nanocavities. We demonstrate that the magnitude of the electric field generated in the nanocavity (En) and Ef can be determined by investigating the bandwidth of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode of the phenyl ring by combining SFG-VS and electrochemical measurements. En is approximately 1.0 ± 0.2 V nm−1. Ef is determined to be 0.3, 0.4, 0.5, 0.6, 1.0, 1.2, 1.6 and 1.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. An exponential correlation between Ef and the complete recovery time of the ground vibrational C
C stretching mode of the phenyl ring by combining SFG-VS and electrochemical measurements. En is approximately 1.0 ± 0.2 V nm−1. Ef is determined to be 0.3, 0.4, 0.5, 0.6, 1.0, 1.2, 1.6 and 1.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. An exponential correlation between Ef and the complete recovery time of the ground vibrational C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C state (T2) is observed. By extending this correlation to the reported macroscopic chemical reactivity (kCR), a profound connection between a higher kCR and a smaller T2 is found. This finding highlights the possibility of regulating vibrational energy flow into a desired reaction coordinate by introducing rationally designed molecular functionalities within spatially confined nanoscale environments. A molecular-level perspective on the relationship between kCR, Ef and T2 may aid in enriching the current understanding of PMCRs.
C state (T2) is observed. By extending this correlation to the reported macroscopic chemical reactivity (kCR), a profound connection between a higher kCR and a smaller T2 is found. This finding highlights the possibility of regulating vibrational energy flow into a desired reaction coordinate by introducing rationally designed molecular functionalities within spatially confined nanoscale environments. A molecular-level perspective on the relationship between kCR, Ef and T2 may aid in enriching the current understanding of PMCRs.
Methods
Materials and sample preparation
4-(Trifluoromethyl)-thiophenol (TFTP, with a purity >98%), 4-acetamidothiophenol (4-AATP, with a purity >95%) and 4-methoxythiophenol (4-MTP, with a purity >98%) were purchased from Shanghai Macklin Biochemical Technology Co., Ltd. 4-Nitrothiophenol (4-NTP, with a purity >95%) and p-aminothiophenol (PATP, with a purity >98%) were obtained from Aladdin. 4-Mercaptobenzonitrile (MBN, with a purity >97%) was obtained from Shanghai Haohong Scientific Co., Ltd. P-mercaptobenzoic acid (MBA, with a purity >90%) was purchased from Shanghai Acmec Biochemical Co., Ltd. 4-Dimethylamino-thiophenol (4-DMATP, with a purity >98%) was purchased from Shanghai Canspec S&T Co., Ltd. Ethanol and n-hexane were purchased from Sinopharm Chemical Reagent Co., Ltd. Ultrapure deionized (DI) water was purified by using a Milli-Q reference system. All the chemicals were used as received.
The substituents in 4-NTP, MBN, TFTP and MBA are EWGs –NO2, –CN, –CF3 and –COOH, respectively, while 4-AATP, 4-MTP, PATP and 4-DMATP are substituted with the EDGs –NHCOCH3, –OCH3, –NH2 and –N(CH3)2, respectively. The specific sample preparation method is described in the ESI.†
SFG-VS experiments
All SFG experiments were carried out using a femtosecond time-resolved SFG-VS system. Detailed information about the instrument parameters was provided in our previous studies.52,54 For a IR pump- SFG probe time-resolved SFG instrument, the pulse energies of the pump IR and probe IR pulses were ∼12 μJ and 11 μJ at ∼1580 cm−1, respectively. The pulse energy of vis was 0.4 μJ. The specific spectral fitting procedures and data analysis have been presented in our publications56,85 and are included in the ESI† for reference.
Electrochemical measurements
Electrochemical measurements were performed using a CHI660e workstation. The working electrode was a Au-SAM sample with a wire in contact with the Au film, the reference electrode was Ag/AgCl (in 3 M KCl), and the counter electrode was a Pt wire electrode. The electrolyte was a 0.3 M KCl solution. All potentials in the paper were relative to Ag/AgCl/3 M KCl, and a schematic diagram of the device is shown in Fig. S6.†In situ SFG measurements of Au-SAMs were performed over a potential range of −0.6 to 0.6 V to prevent desorption of thiol groups with a potential interval of 0.1 V. Fig. S7† illustrates the cyclic voltammetry curve with MBN as a typical example.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Author contributions
X. X. Zheng: conceptualization, investigation, formal analysis, visualization, writing – original draft preparation, writing – reviewing and editing; Q. B. Pei: investigation, writing – reviewing and editing; J. J. Tan: software, funding acquisition, project administration, data curation, writing – reviewing and editing; S. Y. Bai: writing – reviewing and editing; Y. Luo: conceptualization, funding acquisition, manuscript drafting; S. J. Ye: conceptualization, funding acquisition, supervision, data analysis, manuscript drafting, writing – reviewing and editing.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (92250306, 21925302, and 22273094), the Innovation Program for Quantum Science and Technology (2021ZD0303303), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB0450202), and the Anhui Initiative in Quantum Information Technologies (AHY090000).
References
- J. Sun, H. Hu, Y. Xu, Y. Li and H. Xu, Revealing the Photothermal Behavior of Plasmonic Gap Modes: Toward Thermostable Nanocavities, Laser Photonics Rev., 2022, 16, 2100564 CrossRef CAS.
- V. A. Milichko, D. A. Zuev, D. G. Baranov, G. P. Zograf, K. Volodina, A. A. Krasilin, I. S. Mukhin, P. A. Dmitriev, V. V. Vinogradov, S. V. Makarov and P. A. Belov, Metal-Dielectric Nanocavity for Real-Time Tracing Molecular Events with Temperature Feedback, Laser Photonics Rev., 2018, 12, 1700227 CrossRef.
- C.-Y. Li, S. Duan, B.-Y. Wen, S.-B. Li, M. Kathiresan, L.-Q. Xie, S. Chen, J. R. Anema, B.-W. Mao, Y. Luo, Z.-Q. Tian and J.-F. Li, Observation of Inhomogeneous Plasmonic Field Distribution in a Nanocavity, Nat. Nanotechnol., 2020, 15, 922–926 CrossRef CAS PubMed.
- G. Huang, K. Liu, G. Shi, Q. Guo, X. Li, Z. Liu, W. Ma and T. Wang, Elevating Surface-Enhanced Infrared Absorption with Quantum Mechanical Effects of Plasmonic Nanocavities, Nano Lett., 2022, 22, 6083–6090 CrossRef CAS PubMed.
- E. Kokin, H. J. An, D. Koo, S. Han, K. Whang, T. Kang, I. Choi and L. P. Lee, Quantum Electrodynamic Behavior of Chlorophyll in a Plasmonic Nanocavity, Nano Lett., 2022, 22, 9861–9868 CrossRef CAS PubMed.
- A. Xomalis, R. Chikkaraddy, E. Oksenberg, I. Shlesinger, J. Huang, E. C. Garnett, A. F. Koenderink and J. J. Baumberg, Controlling Optically Driven Atomic Migration Using Crystal-Facet Control in Plasmonic Nanocavities, ACS Nano, 2020, 14, 10562–10568 CrossRef CAS PubMed.
- A. Naldoni, V. M. Shalaev and M. L. Brongersma, Applying Plasmonics to a Sustainable Future, Science, 2017, 356, 908–909 CrossRef CAS PubMed.
- B. S. Hoener, S. R. Kirchner, T. S. Heiderscheit, S. S. E. Collins, W.-S. Chang, S. Link and C. F. Landes, Plasmonic Sensing and Control of Single-Nanoparticle Electrochemistry, Chem, 2018, 4, 1560–1585 CAS.
- D. W. Kim and J.-W. Jang, Plasmonic Nanocavity as a Spectroscopic Probe for Molecules, Matter, 2022, 5, 3102–3104 CrossRef CAS.
- E. Oksenberg, I. Shlesinger, A. Xomalis, A. Baldi, J. J. Baumberg, A. F. Koenderink and E. C. Garnett, Energy-Resolved Plasmonic Chemistry in Individual Nanoreactors, Nat. Nanotechnol., 2021, 16, 1378–1385 CrossRef CAS PubMed.
- J. Owrutsky, D. Raftery and R. Hochstrasser, Vibrational Relaxation Dynamics in Solutions, Annu. Rev. Phys. Chem., 1994, 45, 519–555 CrossRef CAS PubMed.
- F. F. Crim, Chemical Dynamics of Vibrationally Excited Molecules: Controlling Reactions in Gases and on Surfaces, Proc. Natl. Acad. Sci. U.S.A., 2008, 105, 12654–12661 CrossRef CAS PubMed.
- J. F. Cahoon, K. R. Sawyer, J. P. Schlegel and C. B. Harris, Determining Transition-State Geometries in Liquids Using 2D-IR, Science, 2008, 319, 1820–1823 CrossRef CAS PubMed.
- L. Chuntonov, Using Mirrors to Control Molecular Dynamics, Science, 2022, 378, 712 CrossRef CAS PubMed.
- R. Yin and B. Jiang, Mechanical Vibrational Relaxation of No Scattering from Metal and Insulator Surfaces: When and Why They Are Different, Phys. Rev. Lett., 2021, 126, 156101 CrossRef CAS PubMed.
- C. Zhan, J. Yi, S. Hu, X.-G. Zhang, D.-Y. Wu and Z.-Q. Tian, Plasmon-Mediated Chemical Reactions, Nat. Rev. Dis. Primers, 2023, 3, 12 CrossRef CAS.
- E. Cortés, R. Grzeschik, S. A. Maier and S. Schlücker, Experimental Characterization Techniques for Plasmon-Assisted Chemistry, Nat. Rev. Chem, 2022, 6, 259–274 CrossRef PubMed.
- Z. Liu, W. Hou, P. Pavaskar, M. Aykol and S. B. Cronin, Plasmon Resonant Enhancement of Photocatalytic Water Splitting Under Visible Illumination, Nano Lett., 2011, 11, 1111–1116 CrossRef CAS PubMed.
- E. L. Keller and R. R. Frontiera, Ultrafast Nanoscale Raman Thermometry Proves Heating Is Not a Primary Mechanism for Plasmon-Driven Photocatalysis, ACS Nano, 2018, 12, 5848–5855 CrossRef CAS PubMed.
- E. Kazuma, J. Jung, H. Ueba, M. Trenary and Y. Kim, Real-Space and Real-Time Observation of a Plasmon-Induced Chemical Reaction of a Single Molecule, Science, 2018, 360, 521–526 CrossRef CAS PubMed.
- A. A. Golubev, B. N. Khlebtsov, R. D. Rodriguez, Y. Chen and D. R. T. Zahn, Plasmonic Heating Plays a Dominant Role in the Plasmon-Induced Photocatalytic Reduction of 4-Nitrobenzenethiol, J. Phys. Chem. C, 2018, 122, 5657–5663 CrossRef CAS.
- D. R. Ward, F. Hüser, F. Pauly, J. C. Cuevas and D. Natelson, Optical Rectification and Field Enhancement in a Plasmonic Nanogap, Nat. Nanotechnol., 2010, 5, 732–736 CrossRef CAS PubMed.
- D. Kos, D. R. Assumpcao, C. Guo and J. J. Baumberg, Quantum Tunneling Induced Optical Rectification and Plasmon-Enhanced Photocurrent in Nanocavity Molecular Junctions, ACS Nano, 2021, 15, 14535–14543 CrossRef CAS PubMed.
- H. Wang, K. Yao, J. A. Parkhill and Z. D. Schultz, Detection of Electron Tunneling across Plasmonic Nanoparticle–Film Junctions Using Nitrile Vibrations, Phys. Chem. Chem. Phys., 2017, 19, 5786–5796 RSC.
- S. Yu and P. K. Jain, The Chemical Potential of Plasmonic Excitations, Angew. Chem., Int. Ed., 2020, 59, 2085–2088 CrossRef CAS PubMed.
- A. J. Wilson and P. K. Jain, Light-Induced Voltages in Catalysis by Plasmonic Nanostructures, Acc. Chem. Res., 2020, 53, 1773–1781 CrossRef CAS PubMed.
- D. A. Nelson and Z. D. Schultz, Influence of Optically Rectified Electric Fields on the Plasmonic Photocatalysis of 4-Nitrothiophenol and 4-Aminothiophenol to 4,4-Dimercaptoazobenzene, J. Phys. Chem. C, 2018, 122, 8581–8588 CrossRef CAS.
- D. A. Nelson and Z. D. Schultz, The Impact of Optically Rectified Fields on Plasmonic Electrocatalysis, Faraday Discuss., 2019, 214, 465–477 RSC.
- D. A. Nelson and Z. D. Schultz, Impact of Plasmon-Induced Optically Rectified Electric Fields on Second Harmonic Generation, J. Phys. Chem. C, 2019, 123, 20639–20648 CrossRef CAS.
- M. T. Sheldon, J. van de Groep, A. M. Brown, A. Polman and H. A. Atwater, Plasmoelectric Potentials in Metal Nanostructures, Science, 2014, 346, 828–831 CrossRef CAS PubMed.
- A. Ahmed, K. Banjac, S. S. Verlekar, F. P. Cometto, M. Lingenfelder and C. Galland, Structural Order of the Molecular Adlayer Impacts the Stability of Nanoparticle-on-Mirror Plasmonic Cavities, ACS Photonics, 2021, 8, 1863–1872 CrossRef CAS PubMed.
- J. J. Baumberg, J. Aizpurua, M. H. Mikkelsen and D. R. Smith, Extreme Nanophotonics from Ultrathin Metallic Gaps, Nat. Mater., 2019, 18, 668–678 CrossRef CAS PubMed.
- N. S. Mueller, R. Arul, L. A. Jakob, M. O. Blunt, T. Földes, E. Rosta and J. J. Baumberg, Collective Mid-Infrared Vibrations in Surface-Enhanced Raman Scattering, Nano Lett., 2022, 22, 7254–7260 CrossRef CAS PubMed.
- F. M. M. Aldosari, Characterization of Labeled Gold Nanoparticles for Surface-Enhanced Raman Scattering, Molecules, 2022, 27, 892 CrossRef CAS PubMed.
- R. D. Norton, H. T. Phan, S. N. Gibbons and A. J. Haes, Quantitative Surface-Enhanced Spectroscopy, Annu. Rev. Phys. Chem., 2022, 73, 141–162 CrossRef CAS PubMed.
- L. Dong, X. Yang, C. Zhang, B. Cerjan, L. Zhou, M. L. Tseng, Y. Zhang, A. Alabastri, P. Nordlander and N. J. Halas, Nanogapped Au Antennas for Ultrasensitive Surface-Enhanced Infrared Absorption Spectroscopy, Nano Lett., 2017, 17, 5768–5774 CrossRef CAS PubMed.
- K. Chen and H. Wang, Plasmon-Driven Photocatalytic Molecular Transformations on Metallic Nanostructure Surfaces: Mechanistic Insights Gained from Plasmon-Enhanced Raman Spectroscopy, Mol. Syst. Des. Eng., 2021, 6, 250–280 RSC.
- S. Hati, X. Yang, P. Gupta, B. B. Muhoberac, J. Pu, J. Zhang and R. Sardar, Hybrid Metal-Ligand Interfacial Dipole Engineering of Functional Plasmonic Nanostructures for Extraordinary Responses of Optoelectronic Properties, ACS Nano, 2023, 17, 17499–17515 CrossRef CAS PubMed.
- B. C. Pein, N.-H. Seong and D. D. Dlott, Vibrational Energy Relaxation of Liquid Aryl-Halides X-C6H5 (X = F, Cl, Br, I), J. Phys. Chem. A, 2010, 114, 10500–10507 CrossRef CAS PubMed.
- G. Joshi, R. Kashyap, K. Patrikar, A. Mondal and S. Khatua, Ligand-Mediated Electron Transport Channels Enhance Photocatalytic Activity of Plasmonic Nanoparticles, Nanoscale, 2023, 15, 16552–16560 RSC.
- J. Zhou, J. Guo, G. Ghimire, A. M. Mebel, S. Chang and J. He, Plasmon-Mediated Dehydrogenation of the Aromatic Methyl Group and Benzyl Radical Formation, Chem. Sci., 2023, 14, 13951–13961 RSC.
- V. Mollica Nardo, G. Cassone, R. C. Ponterio, F. Saija, J. Sponer, M. Tommasini and S. Trusso, Electric-Field-Induced Effects on the Dipole Moment and Vibrational Modes of the Centrosymmetric Indigo Molecule, J. Phys. Chem. A, 2020, 124, 10856–10869 CrossRef CAS PubMed.
- G. Cassone, J. Sponer, S. Trusso and F. Saija, Ab Initio Spectroscopy of Water under Electric Fields, Phys. Chem. Chem. Phys., 2019, 21, 21205–21212 RSC.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Electrostatic Catalysis of a Diels–Alder Reaction, Nature, 2016, 531, 88–91 CrossRef PubMed.
- G. Cassone, Nuclear Quantum Effects Largely Influence Molecular Dissociation and Proton Transfer in Liquid Water under an Electric Field, J. Phys. Chem. Lett., 2020, 11, 8983–8988 CrossRef CAS PubMed.
- F. Che, J. T. Gray, S. Ha, N. Kruse, S. L. Scott and J.-S. McEwen, Elucidating the Roles of Electric Fields in Catalysis: A Perspective, ACS Catal., 2018, 8, 5153–5174 CrossRef CAS.
- S. Shaik, D. Mandal and R. Ramanan, Oriented Electric Fields as Future Smart Reagents in Chemistry, Nat. Chem., 2016, 8, 1091–1098 CrossRef CAS PubMed.
- G. Cassone, J. Sponer and F. Saija, Ab Initio Molecular Dynamics Studies of the Electric-Field-Induced Catalytic Effects on Liquids, Top. Catal., 2022, 65, 40–58 CrossRef CAS.
- G. Cassone, F. Pietrucci, F. Saija, F. Guyot and A. M. Saitta, One-Step Electric-Field Driven Methane and Formaldehyde Synthesis from Liquid Methanol, Chem. Sci., 2017, 8, 2329–2336 RSC.
- X. Song, C. Basheer and R. N. Zare, Making Ammonia from Nitrogen and Water Microdroplets, Proc. Natl. Acad. Sci. U.S.A., 2023, 120, e2301206120 CrossRef CAS PubMed.
- G. Cassone, F. Saija, J. Sponer and S. Shaik, The Reactivity-Enhancing Role of Water Clusters in Ammonia Aqueous Solutions, J. Phys. Chem. Lett., 2023, 14, 7808–7813 CrossRef CAS PubMed.
- J. J. Tan, B. X. Zhang, Y. Luo and S. J. Ye, Ultrafast Vibrational Dynamics of Membrane-Bound Peptides at the Lipid Bilayer/Water Interface, Angew. Chem., Int. Ed., 2017, 56, 12977–12981 CrossRef CAS PubMed.
-
Y. R. Shen, The Principles of Nonlinear Optics, Wiley-Interscience, New York, NY, USA, United States, 1984 Search PubMed.
- J. J. Tan, J. H. Zhang, C. Z. Li, Y. Luo and S. J. Ye, Ultrafast Energy Relaxation Dynamics of Amide I Vibrations Coupled with Protein-Bound Water Molecules, Nat. Commun., 2019, 10, 1010 CrossRef PubMed.
- S. Nihonyanagi, S. Yamaguchi and T. Tahara, Ultrafast Dynamics at Water Interfaces Studied by Vibrational Sum Frequency Generation Spectroscopy, Chem. Rev., 2017, 117, 10665–10693 CrossRef CAS PubMed.
- J. J. Tan, Z. J. Ni and S. J. Ye, Protein-Water Coupling Tunes the Anharmonicity of Amide I Modes in the Interfacial Membrane-Bound Proteins, J. Chem. Phys., 2022, 156, 105103 CrossRef CAS PubMed.
- I. Morichika, K. Murata, A. Sakurai, K. Ishii and S. Ashihara, Molecular Ground-State Dissociation in the Condensed Phase Employing Plasmonic Field Enhancement of Chirped Mid-Infrared Pulses, Nat. Commun., 2019, 10, 3893 CrossRef PubMed.
- J. P. Kraack and P. Hamm, Vibrational Ladder-Climbing in Surface-Enhanced, Ultrafast Infrared Spectroscopy, Phys. Chem. Chem. Phys., 2016, 18, 16088–16093 RSC.
- C. Anfuso, A. M. Ricks, W. Rodríguez-Córdoba and T. Lian, Ultrafast Vibrational Relaxation Dynamics of a Rhenium Bipyridyl CO2-Reduction Catalyst at a Au Electrode Surface Probed by Time-Resolved Vibrational Sum Frequency Generation Spectroscopy, J. Phys. Chem. C, 2012, 116, 26377–26384 CrossRef CAS.
- A. Ge, B. Rudshteyn, J. Zhu, R. J. Maurer, V. S. Batista and T. Lian, Electron-Hole-Pair-Induced Vibrational Energy Relaxation of Rhenium Catalysts on Gold Surfaces, J. Phys. Chem. Lett., 2018, 9, 406–412 CrossRef CAS PubMed.
- M. Askerka, R. J. Maurer, V. S. Batista and J. C. Tully, Role of Tensorial Electronic Friction in Energy Transfer at Metal Surfaces, Phys. Rev. Lett., 2016, 116, 217601 CrossRef PubMed.
- H. Arnolds and M. Bonn, Ultrafast Surface Vibrational Dynamics, Surf. Sci. Rep., 2010, 65, 45–66 CrossRef CAS.
- X. He, P. Yu, J. Zhao and J. Wang, Efficient Vibrational Energy Transfer through Covalent Bond in Indigo Carmine Revealed by Nonlinear IR Spectroscopy, J. Phys. Chem. B, 2017, 121, 9411–9421 CrossRef CAS PubMed.
- Z. Yu and R. R. Frontiera, Intermolecular Forces Dictate Vibrational Energy Transfer in Plasmonic-Molecule Systems, ACS Nano, 2022, 16, 847–854 CrossRef CAS PubMed.
- C. Matranga and P. Guyot-Sionnest, Vibrational Relaxation of Cyanide at the Metal/Electrolyte Interface, J. Chem. Phys., 2000, 112, 7615–7621 CrossRef CAS.
- M. E. Schmidt and P. Guyot-Sionnest, Electrochemical Tuning of the Lifetime of the Co Stretching Vibration for Co/Pt(111), J. Chem. Phys., 1996, 104, 2438–2445 CrossRef CAS.
- S. D. Fried, L.-P. Wang, S. G. Boxer, P. Ren and V. S. Pande, Calculations of the Electric Fields in Liquid Solutions, J. Phys. Chem. B, 2013, 117, 16236–16248 CrossRef CAS PubMed.
- S. Sarkar, J. G. Patrow, M. J. Voegtle, A. K. Pennathur and J. M. Dawlaty, Electrodes as Polarizing Functional Groups: Correlation between Hammett Parameters and Electrochemical Polarization, J. Phys. Chem. C, 2019, 123, 4926–4937 CrossRef CAS.
- J. Heo, H. Ahn, J. Won, J. G. Son, H. K. Shon, T. G. Lee, S. W. Han and M.-H. Baik, Electro-Inductive Effect: Electrodes as Functional Groups with Tunable Electronic Properties, Science, 2020, 370, 214–219 CrossRef CAS PubMed.
- S. Chen, Y.-H. Xiao, M. Qin, G. Zhou, R. Dong, R. Devasenathipathy, D.-Y. Wu and L. Yang, Quantification of the Real Plasmonic Field Transverse Distribution in a Nanocavity Using the Vibrational Stark Effect, J. Phys. Chem. Lett., 2023, 14, 1708–1713 CrossRef CAS PubMed.
- D. T. Kwasnieski, H. Wang and Z. D. Schultz, Alkyl-Nitrile Adlayers as Probes of Plasmonically Induced Electric Fields, Chem. Sci., 2015, 6, 4484–4494 RSC.
- D. Wright, S. Sangtarash, N. S. Mueller, Q. Lin, H. Sadeghi and J. J. Baumberg, Vibrational Stark Effects: Ionic Influence on Local Fields, J. Phys. Chem. Lett., 2022, 13, 4905–4911 CrossRef CAS PubMed.
- D. Bhattacharyya, P. E. Videla, M. Cattaneo, V. S. Batista, T. Lian and C. P. Kubiak, Vibrational Stark Shift Spectroscopy of Catalysts under the Influence of Electric Fields at Electrode-Solution Interfaces, Chem. Sci., 2021, 12, 10131–10149 RSC.
- J. B. Weaver, J. Kozuch, J. M. Kirsh and S. G. Boxer, Nitrile Infrared Intensities Characterize Electric Fields and Hydrogen Bonding in Protic, Aprotic, and Protein Environments, J. Am. Chem. Soc., 2022, 144, 7562–7567 CrossRef CAS PubMed.
- J. Lee, N. Tallarida, X. Chen, L. Jensen and V. A. Apkarian, Microscopy with a Single-Molecule Scanning Electrometer, Sci. Adv., 2018, 4, eaat5472 CrossRef PubMed.
- C. Hansch, A. Leo and R. W. Taft, A Survey of Hammett Substituent Constants and Resonance and Field Parameters, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- R. N. Jones, W. F. Forbes and W. A. Mueller, The Infrared Carbonyl Stretching Bands of Ring Substituted Acetophenones, Can. J. Chem., 1957, 35, 504–514 CrossRef CAS.
- P. A. Madden and R. M. Lynden-Bell, Theory of Vibrational Linewidths, Chem. Phys. Lett., 1976, 38, 163–165 CrossRef CAS.
- Z. Getahun, C.-Y. Huang, T. Wang, B. De León, W. F. DeGrado and F. Gai, Using Nitrile-Derivatized Amino Acids as Infrared Probes of Local Environment, J. Am. Chem. Soc., 2003, 125, 405–411 CrossRef CAS PubMed.
- S. Shin, H. Kang, D. Cho, J. Y. Lee and H. Kang, Effect of Electric Field on Condensed-Phase Molecular Systems. II. Stark Effect on the Hydroxyl Stretch Vibration of Ice, J. Phys. Chem. C, 2015, 119, 15596–15603 CrossRef CAS.
- D. R. Martin and D. V. Matyushov, Why Are Vibrational Lines Narrow in Proteins, J. Phys. Chem. Lett., 2020, 11, 5932–5937 CrossRef CAS PubMed.
- H.-L. Wang, E.-M. You, R. Panneerselvam, S.-Y. Ding and Z.-Q. Tian, Advances of Surface-Enhanced Raman and IR Spectroscopies: From Nano/Microstructures to Macro-Optical Design, Light: Sci. Appl., 2021, 10, 161 CrossRef CAS PubMed.
- D. Wright, Q. Lin, D. Berta, T. Földes, A. Wagner, J. Griffiths, C. Readman, E. Rosta, E. Reisner and J. J. Baumberg, Mechanistic Study of an Immobilized Molecular Electrocatalyst by in Situ Gap-Plasmon-Assisted Spectro-Electrochemistry, Nat. Catal., 2021, 4, 157–163 CrossRef CAS.
- J. M. Marr and Z. D. Schultz, Imaging Electric Fields in SERS and TERS Using the Vibrational Stark Effect, J. Phys. Chem. Lett., 2013, 4, 3268–3272 CrossRef CAS PubMed.
- Q. B. Pei, X. X. Zheng, J. J. Tan, Y. Luo and S. J. Ye, Probing the Local Near-Field Intensity of Plasmonic Nanoparticles in the Mid-infrared Spectral Region, J. Phys. Chem. Lett., 2024, 15, 5390–5396 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Quanbing
Pei
a,
Junjun
Tan
*b,
Shiyu
Bai
a,
Yi
Luo
a,
Quanbing
Pei
a,
Junjun
Tan
*b,
Shiyu
Bai
a,
Yi
Luo
 *ab and
Shuji
Ye
*ab and
Shuji
Ye
 *ab
*ab
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C state (T2) of the phenyl ring is observed. Substances with a smaller T2 are strongly correlated with the reported macroscopic chemical reactivity. This finding may aid in enriching the current understanding of PMCRs and highlights the possibility of regulating vibrational energy flow into desired reaction coordinates by using a local electric field.
C state (T2) of the phenyl ring is observed. Substances with a smaller T2 are strongly correlated with the reported macroscopic chemical reactivity. This finding may aid in enriching the current understanding of PMCRs and highlights the possibility of regulating vibrational energy flow into desired reaction coordinates by using a local electric field.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode (νC
C stretching mode (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) of the phenyl ring via femtosecond sum frequency generation vibrational spectroscopy (SFG-VS) supplemented by electrochemical measurements. Here, the probed molecules are located in nanocavities based on a nanoparticle-on-mirror (NPoM) approach (Fig. 1a) (labeled as NPoM-SAMs).31,32 The selected aromatic thiols are well known to form good SAMs on metal surfaces and are widely adopted in photocatalysis and biomedicine.33–37 The feasibility and superiority of using the C
C) of the phenyl ring via femtosecond sum frequency generation vibrational spectroscopy (SFG-VS) supplemented by electrochemical measurements. Here, the probed molecules are located in nanocavities based on a nanoparticle-on-mirror (NPoM) approach (Fig. 1a) (labeled as NPoM-SAMs).31,32 The selected aromatic thiols are well known to form good SAMs on metal surfaces and are widely adopted in photocatalysis and biomedicine.33–37 The feasibility and superiority of using the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode of the phenyl ring as a probe have been confirmed by surface-enhanced Raman spectroscopy (SERS).38,39En is approximately 1.0 ± 0.2 V nm−1, and Ef varies from 0.3 V nm−1 to 1.7 V nm−1. An exponential correlation between Ef and the complete recovery time of the ground vibrational C
C stretching mode of the phenyl ring as a probe have been confirmed by surface-enhanced Raman spectroscopy (SERS).38,39En is approximately 1.0 ± 0.2 V nm−1, and Ef varies from 0.3 V nm−1 to 1.7 V nm−1. An exponential correlation between Ef and the complete recovery time of the ground vibrational C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C state (T2) was observed. A substance with a smaller T2 shows a strong correlation with the macroscopic chemical reactivity and plasmon-molecule interactions reported for PMCRs.40,41 This work highlights the possibility of regulating vibrational energy flow into desired reaction coordinates using the local electric field in which the molecules are sensed in nanocavities. In addition, it is well known that local electric field strengths on the order of 1 V nm−1 are not only responsible for the vibrational Stark effect in both single-molecule systems42 and condensed phases,43 but can also selectively promote, drive, and control chemical reactions44 such as proton transfer45 and catalytic processes,46–49 for example, the catalytic synthesis of ammonia from nitrogen and water microdroplets.50,51 Therefore, the findings in this work may aid in enriching the current understanding of these processes including vibrational dynamics and catalytic processes.
C state (T2) was observed. A substance with a smaller T2 shows a strong correlation with the macroscopic chemical reactivity and plasmon-molecule interactions reported for PMCRs.40,41 This work highlights the possibility of regulating vibrational energy flow into desired reaction coordinates using the local electric field in which the molecules are sensed in nanocavities. In addition, it is well known that local electric field strengths on the order of 1 V nm−1 are not only responsible for the vibrational Stark effect in both single-molecule systems42 and condensed phases,43 but can also selectively promote, drive, and control chemical reactions44 such as proton transfer45 and catalytic processes,46–49 for example, the catalytic synthesis of ammonia from nitrogen and water microdroplets.50,51 Therefore, the findings in this work may aid in enriching the current understanding of these processes including vibrational dynamics and catalytic processes.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) C stretching mode of NPoM-SAMs
C stretching mode of NPoM-SAMs![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of NPoM-SAMs using femtosecond time-resolved IR pump-SFG probe measurements. Fig. 1b and c show the ppp spectra of the NPoM-SAMs in the frequency range of 1500–1700 cm−1. All the peaks indicate a positive phase. The spectra in the frequency range of 1200–1800 cm−1 are displayed in Fig. S1.† All the samples had a νC
C mode of NPoM-SAMs using femtosecond time-resolved IR pump-SFG probe measurements. Fig. 1b and c show the ppp spectra of the NPoM-SAMs in the frequency range of 1500–1700 cm−1. All the peaks indicate a positive phase. The spectra in the frequency range of 1200–1800 cm−1 are displayed in Fig. S1.† All the samples had a νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C frequency of 1585 (±15) cm−1. Compared to those of the samples on the gold film without NPoMs (labeled as Au-SAMs) (Fig. S2†), the resonance signals of the molecules on the NPoM-SAMs are amplified with an enhancement factor >103. Fig. 2a and b depict the decay in the effective SFG peak strength (χ(2)) of the νC
C frequency of 1585 (±15) cm−1. Compared to those of the samples on the gold film without NPoMs (labeled as Au-SAMs) (Fig. S2†), the resonance signals of the molecules on the NPoM-SAMs are amplified with an enhancement factor >103. Fig. 2a and b depict the decay in the effective SFG peak strength (χ(2)) of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of thiophenol derivatives. In theory, SFG probes the surface population density of a vibrational state.52,53 The excitation of νC
C mode of thiophenol derivatives. In theory, SFG probes the surface population density of a vibrational state.52,53 The excitation of νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C from the ground state (ν0) to its first vibrational state (ν1) can reduce the SFG intensity. In general, the efficiency of vibrational excitation at the interface is very low. Currently, vibrational dynamics of only a few groups, such as OH and amide modes, have been reported.52,54–56 In the absence of nanocavities, the bleaching value is too small to be detected (Fig. S3†). However, in the presence of nanocavities, clear bleaching following excitation at 1580 cm−1 at t = 0 was observed (Fig. 2a and b) due to plasmon-enhanced vibrational excitation.57,58 Following this bleaching, the ν1 state relaxes to an intermediate state, and the SFG intensity gradually recovers. The vibrational dynamics of the νC
C from the ground state (ν0) to its first vibrational state (ν1) can reduce the SFG intensity. In general, the efficiency of vibrational excitation at the interface is very low. Currently, vibrational dynamics of only a few groups, such as OH and amide modes, have been reported.52,54–56 In the absence of nanocavities, the bleaching value is too small to be detected (Fig. S3†). However, in the presence of nanocavities, clear bleaching following excitation at 1580 cm−1 at t = 0 was observed (Fig. 2a and b) due to plasmon-enhanced vibrational excitation.57,58 Following this bleaching, the ν1 state relaxes to an intermediate state, and the SFG intensity gradually recovers. The vibrational dynamics of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode exhibit biexponential decays with a fast component (T1) and a slow component (T2). These two components were attributed to the fast population transfer between different C
C mode exhibit biexponential decays with a fast component (T1) and a slow component (T2). These two components were attributed to the fast population transfer between different C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C modes (T1) and the slow complete recovery of the ground vibrational state (T2), respectively. T2 is dominated by a combination of intramolecular vibrational relaxation (IVR) and nonadiabatic relaxation which contributes to the excitation of electron–hole pairs (EHPs) in gold substrates and gold nanoparticles.59,60 EHPs have been proven to be the primary energy transfer channel on metal surfaces.61,62 The T1 values of the different thiophenol derivatives are essentially identical at approximately 1 ps, which is consistent with the time required for rapid energy equilibrium among the delocalized νC
C modes (T1) and the slow complete recovery of the ground vibrational state (T2), respectively. T2 is dominated by a combination of intramolecular vibrational relaxation (IVR) and nonadiabatic relaxation which contributes to the excitation of electron–hole pairs (EHPs) in gold substrates and gold nanoparticles.59,60 EHPs have been proven to be the primary energy transfer channel on metal surfaces.61,62 The T1 values of the different thiophenol derivatives are essentially identical at approximately 1 ps, which is consistent with the time required for rapid energy equilibrium among the delocalized νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C modes.63 In contrast, significant differences in T2 values were observed across the samples (Table S1†). Specifically, the T2 values are 21.4 (±1.3), 20.0 (±0.4), 17.3 (±0.5), 15.2 (±0.3), 13.8 (±0.4), 12.7 (±0.5), 9.7 (±0.7) and 10.4 (±1.4) ps for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. The difference in T2 may arise from various factors, such as intermolecular interactions, molecular orientation, and the electric field.64–66 The studied SAMs exhibit very similar orientations with respect to the metal surface, thus ruling out orientation as the main reason for the difference in T2.64 The effect of intermolecular interactions on T2 can also be ruled out. Earlier reports suggested that the value of T2 is strongly dependent on the π–π interactions between molecules, with stronger intermolecular interactions promoting faster molecular energy dissipation.64 However, the observed results contradict this hypothesis. For instance, 4-NTP, which was expected to have a faster T2 due to its strong π–π interaction, actually exhibited a longer T2 (21.4 (±1.3) ps). Similarly, the presence of a –CF3 group theoretically weakens π–π interactions and may result in an increase in the T2 of the phenyl ring. However, these speculations in terms of intermolecular interactions contrast with our findings. Therefore, the electric field is most likely a significant factor in regulating vibrational relaxation dynamics. To verify this conjecture, we measured the magnitudes of En and Ef based on the DC Stark effect on the bandwidth of the νC
C modes.63 In contrast, significant differences in T2 values were observed across the samples (Table S1†). Specifically, the T2 values are 21.4 (±1.3), 20.0 (±0.4), 17.3 (±0.5), 15.2 (±0.3), 13.8 (±0.4), 12.7 (±0.5), 9.7 (±0.7) and 10.4 (±1.4) ps for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. The difference in T2 may arise from various factors, such as intermolecular interactions, molecular orientation, and the electric field.64–66 The studied SAMs exhibit very similar orientations with respect to the metal surface, thus ruling out orientation as the main reason for the difference in T2.64 The effect of intermolecular interactions on T2 can also be ruled out. Earlier reports suggested that the value of T2 is strongly dependent on the π–π interactions between molecules, with stronger intermolecular interactions promoting faster molecular energy dissipation.64 However, the observed results contradict this hypothesis. For instance, 4-NTP, which was expected to have a faster T2 due to its strong π–π interaction, actually exhibited a longer T2 (21.4 (±1.3) ps). Similarly, the presence of a –CF3 group theoretically weakens π–π interactions and may result in an increase in the T2 of the phenyl ring. However, these speculations in terms of intermolecular interactions contrast with our findings. Therefore, the electric field is most likely a significant factor in regulating vibrational relaxation dynamics. To verify this conjecture, we measured the magnitudes of En and Ef based on the DC Stark effect on the bandwidth of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of the phenyl ring by combining SFG-VS and electrochemical measurements.
C mode of the phenyl ring by combining SFG-VS and electrochemical measurements.

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of the phenyl rings of 4-NTP, MBN, TFTP and MBA. (b) χ(2) decay of the νC
C mode of the phenyl rings of 4-NTP, MBN, TFTP and MBA. (b) χ(2) decay of the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of the phenyl rings of 4-AATP, 4-MTP, PATP and 4-DMATP.
C mode of the phenyl rings of 4-AATP, 4-MTP, PATP and 4-DMATP.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bandwidth change of each Au-SAM at different applied potentials (ΔΓp) using SFG-VS supplemented by electrochemical measurements, the dependence of ΔΓp on V can be determined by using eqn (2). The Ei and En of each sample can be deduced using eqn (3) and (4), respectively.
C bandwidth change of each Au-SAM at different applied potentials (ΔΓp) using SFG-VS supplemented by electrochemical measurements, the dependence of ΔΓp on V can be determined by using eqn (2). The Ei and En of each sample can be deduced using eqn (3) and (4), respectively.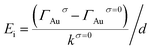

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode of thiophenol derivatives in the absence of nanocavities at zero applied electric potential, ΓNPoMσ is the corresponding bandwidth of the samples in the presence of nanocavities, and d is the spacer thickness of SAMs in the nanocavity. The subscript p represents the change induced by V, and the superscript σ corresponds to the Hammett constant. According to eqn (1)–(4), determining the values of En and Ef requires knowledge of ΓAuσ, ΓNPoMσ, and kσ.
C mode of thiophenol derivatives in the absence of nanocavities at zero applied electric potential, ΓNPoMσ is the corresponding bandwidth of the samples in the presence of nanocavities, and d is the spacer thickness of SAMs in the nanocavity. The subscript p represents the change induced by V, and the superscript σ corresponds to the Hammett constant. According to eqn (1)–(4), determining the values of En and Ef requires knowledge of ΓAuσ, ΓNPoMσ, and kσ.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C of MBN. The data for other Au-SAMs are provided in Fig. S4a.†Fig. 4b and S4b† depict the dependence of ΔΓp on V. As the potential increases, ΔΓp for MBN, 4-NTP, TFTP, MBA, 4-AATP, and 4-MTP linearly decreases (Fig. 4b and S4b†), while those for PATP and 4-DMATP linearly increase (Fig. S4b†). The values of kσ are determined to be −0.5 (±0.1), −0.6 (±0.1), −0.9 (±0.1), −1.4 (±0.1), −2.0 (±0.1), −1.9 (±0.2), 4.0 (±0.4), and 4.4 (±0.9) cm−1 V−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively (Table S6†). Based on the linear relationship between kσ and σ shown in Fig. S5,†kσ=0 is deduced to be 2.2 cm−1 V−1. With the assumption of d ∼1 nm,32,82,83Ei is determined to be −0.7, −0.6, −0.5, −0.4, 0, 0.2, 0.6, and 0.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP, and 4-DMATP, respectively. Note that an electron withdrawing group (EWG) is equivalent to applying a negative electric field, while an electron donating group (EDG) represents the application of a positive electric field. This distinction arises from the fact that an upward electric field is defined as positive. When the substituent is an EWG, it induces an upward movement of the charge of the phenyl ring, equivalent to imposing a downward (negative) electric field.68 In contrast, an EDG corresponds to a positive electric field. Using eqn (4), En is deduced to be 1.0, 1.0, 0.8, 0.9, 1.0, 1.2, 1.0, and 1.0 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP, and 4-DMATP, respectively. The magnitude of En for all the studied samples is almost identical (1.0 ± 0.2 V nm−1) beyond the experimental deviation. The magnitude of En can be further confirmed by the results determined using Stark shift (shown in the ESI†), which is an acknowledged tool for quantifying electric fields.73,84 As a result, the Ef values of the different substituents were deduced to be 0.3, 0.4, 0.5, 0.6, 1.0, 1.2, 1.6 and 1.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively (Fig. 4d). The consistency of the electric field obtained through the peak shift and peak bandwidth provides robust support for the effectiveness of employing the bandwidth as a metric for electric field measurements.
C of MBN. The data for other Au-SAMs are provided in Fig. S4a.†Fig. 4b and S4b† depict the dependence of ΔΓp on V. As the potential increases, ΔΓp for MBN, 4-NTP, TFTP, MBA, 4-AATP, and 4-MTP linearly decreases (Fig. 4b and S4b†), while those for PATP and 4-DMATP linearly increase (Fig. S4b†). The values of kσ are determined to be −0.5 (±0.1), −0.6 (±0.1), −0.9 (±0.1), −1.4 (±0.1), −2.0 (±0.1), −1.9 (±0.2), 4.0 (±0.4), and 4.4 (±0.9) cm−1 V−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively (Table S6†). Based on the linear relationship between kσ and σ shown in Fig. S5,†kσ=0 is deduced to be 2.2 cm−1 V−1. With the assumption of d ∼1 nm,32,82,83Ei is determined to be −0.7, −0.6, −0.5, −0.4, 0, 0.2, 0.6, and 0.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP, and 4-DMATP, respectively. Note that an electron withdrawing group (EWG) is equivalent to applying a negative electric field, while an electron donating group (EDG) represents the application of a positive electric field. This distinction arises from the fact that an upward electric field is defined as positive. When the substituent is an EWG, it induces an upward movement of the charge of the phenyl ring, equivalent to imposing a downward (negative) electric field.68 In contrast, an EDG corresponds to a positive electric field. Using eqn (4), En is deduced to be 1.0, 1.0, 0.8, 0.9, 1.0, 1.2, 1.0, and 1.0 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP, and 4-DMATP, respectively. The magnitude of En for all the studied samples is almost identical (1.0 ± 0.2 V nm−1) beyond the experimental deviation. The magnitude of En can be further confirmed by the results determined using Stark shift (shown in the ESI†), which is an acknowledged tool for quantifying electric fields.73,84 As a result, the Ef values of the different substituents were deduced to be 0.3, 0.4, 0.5, 0.6, 1.0, 1.2, 1.6 and 1.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively (Fig. 4d). The consistency of the electric field obtained through the peak shift and peak bandwidth provides robust support for the effectiveness of employing the bandwidth as a metric for electric field measurements.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C of 4-AATP at different potentials.
C of 4-AATP at different potentials.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode of the phenyl ring by combining SFG-VS and electrochemical measurements. En is approximately 1.0 ± 0.2 V nm−1. Ef is determined to be 0.3, 0.4, 0.5, 0.6, 1.0, 1.2, 1.6 and 1.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. An exponential correlation between Ef and the complete recovery time of the ground vibrational C
C stretching mode of the phenyl ring by combining SFG-VS and electrochemical measurements. En is approximately 1.0 ± 0.2 V nm−1. Ef is determined to be 0.3, 0.4, 0.5, 0.6, 1.0, 1.2, 1.6 and 1.7 V nm−1 for 4-NTP, MBN, TFTP, MBA, 4-AATP, 4-MTP, PATP and 4-DMATP, respectively. An exponential correlation between Ef and the complete recovery time of the ground vibrational C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C state (T2) is observed. By extending this correlation to the reported macroscopic chemical reactivity (kCR), a profound connection between a higher kCR and a smaller T2 is found. This finding highlights the possibility of regulating vibrational energy flow into a desired reaction coordinate by introducing rationally designed molecular functionalities within spatially confined nanoscale environments. A molecular-level perspective on the relationship between kCR, Ef and T2 may aid in enriching the current understanding of PMCRs.
C state (T2) is observed. By extending this correlation to the reported macroscopic chemical reactivity (kCR), a profound connection between a higher kCR and a smaller T2 is found. This finding highlights the possibility of regulating vibrational energy flow into a desired reaction coordinate by introducing rationally designed molecular functionalities within spatially confined nanoscale environments. A molecular-level perspective on the relationship between kCR, Ef and T2 may aid in enriching the current understanding of PMCRs.



