Open Access Article
Open Access ArticleMixed-ligand, radical, gold bis(dithiolene) complexes: from single-component conductors to controllable NIR-II absorbers†
Haia
Kharraz
a,
Pere
Alemany
 b,
Enric
Canadell
b,
Enric
Canadell
 *cd,
Yann
Le Gal
a,
Thierry
Roisnel
a,
Hengbo
Cui
e,
Kee Hoon
Kim
e,
Marc
Fourmigué
*cd,
Yann
Le Gal
a,
Thierry
Roisnel
a,
Hengbo
Cui
e,
Kee Hoon
Kim
e,
Marc
Fourmigué
 *a and
Dominique
Lorcy
*a and
Dominique
Lorcy
 *a
*a
aUnivRennes, CNRS, ISCR (Institut des Sciences Chimiques de Rennes), 35042 Rennes, France. E-mail: marc.fourmigue@univ-rennes.fr; dominique.lorcy@univ-rennes.fr
bDepartament de Ciència de Materials i Química Física and Institut de QuímicaTeòrica i Computacional (IQTCUB), Universitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, Spain
cInstitut de Ciencia de Materials de Barcelona, ICMAB-CSIC, Campus de la UAB, 08193 Bellaterra, Spain. E-mail: canadell@icmab.es
dRoyal Academy of Sciences and Arts of Barcelona, Chemistry Section, La Rambla 115, 08002 Barcelona, Spain
eInstitute of Applied Physics, Department of Physics and Astronomy, Seoul National University, Seoul 08826, Korea
First published on 21st June 2024
Abstract
Neutral radical bis(dithiolene) gold complexes [Au(dt)2]˙ are known to exhibit a strong absorption in the 1400–2000 nm NIR absorption range. Here, we demonstrate that the NIR signature of mixed-ligand bis(dithiolene) gold complexes [Au(dtA)(dtD)]˙ associating two different dithiolene, dtA and dtD, is found at higher energy, out of the range of the homoleptic analogs [Au(dtA)2]˙ and [Au(dtD)2]˙, in the looked-after NIR-II 1000–1400 nm absorption range. An efficient synthetic approach towards precursor mixed-ligand monoanionic gold bis(dithiolene) complexes [Au(dtA)(dtD)]−1 is reported. Using this strategy, no symmetrical complexes are formed and, upon electrocrystallization, no scrambling was observed in solution, allowing for the isolation of radical gold bis(dithiolene) complex such as [Au(bdt)(Et-thiazdt)]˙ (bdt: benzene-1,2-dithiolate; Et-thiazdt: N-ethyl-thiazoline-2-thione-3,4-dithiolate), which behaves as a single-component conductor. It is shown from theoretical calculations that the spin polarization induced by electron repulsions leads to a strong localization of the spin–orbitals, and provides a sound basis to understand, (i) the different ligand-based oxidation potentials, (ii) the NIR optical absorption at notably higher energies and (iii) the larger potential difference of the two redox processes than in the parent symmetric complexes. The solid-state properties of the radical complex [Au(bdt)(Et-thiazdt)]˙ are the consequence of a strongly 1D electronic structure with weakly dimerized chains and electronic localization favoring a semiconducting behavior, stable under pressures up to 18.2 GPa. Altogether, the versatility of the preparation method of [Au(dtA)(dtD)]−1 salts opens the route for a wide library of different mixed-ligand radical complexes [Au(dtA)(dtD)]˙ with simultaneously an adaptable absorption in the NIR-II range and the rich structural chemistry of single-component conductors.
Introduction
Near Infra-Red (NIR) light spanning from 780 to 2500 nm carries important information for multiple applications in telecommunications (1300–1600 nm), for biological imaging (NIR-I tissue-transparent windows NIR-I 650−950 nm, NIR-II 1000–1350 nm, NIR-III 1550–1850 nm) and solar cells (800–2000 nm).1 Near-infrared absorbing materials can roughly be divided into two groups:2 inorganic materials such as metal oxides and semiconductor nanocrystals; and molecular materials including metal complexes, ionic dyes, π-conjugated and charge-transfer chromophores. The latter group is known for example (i) in laser printers as a charge-generation material,3 or as photodetectors,4 (ii) in dye-sensitized solar cells for recovery of the sunlight fraction (55%) which lies in the NIR,5 (iii) for the photothermoelectric effect, toward solar energy harvesting and photodetection.6 Most of the molecular compounds developed so far for these numerous applications absorb in the NIR-I region, between 650 and 950 nm. Among them, neutral nickel bis(dithiolene) complexes [Ni(dt)2]0 (Scheme 1a) absorb in a wide range of NIR absorption maxima tunable between 700 and 1100 nm, depending on the dithiolene substituents. Their efficient photothermal properties have been used for photothermal therapy,7 photoacoustic imaging,8 or seawater desalinization.9 They are also known as single-component semi-conductors.10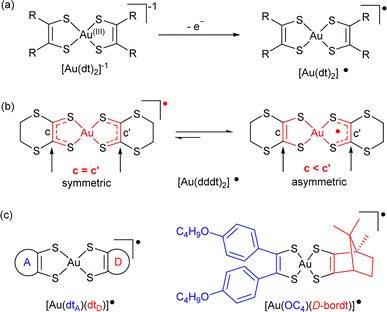 | ||
| Scheme 1 Radical gold dithiolene complexes: (a) generation, (b) symmetric vs. asymmetric character of the homoleptic complex [Au(dddt)2]˙, (c) mixed-ligand bis(dithiolene) complexes. | ||
However, most of these attractive applications are limited by the absorption in the NIR-I region while absorption in the NIR-II/NIR-III regions would be highly desirable. NIR-II absorbing materials are in high demand for capturing low energy radiation in photoconversion devices and in sensing applications where visible or thermal imaging cameras are ineffective. Unfortunately, it is challenging to achieve NIR-II absorption above 1000 nm in a small molecular structure. Gold bis(dithiolene) complexes offer in that respect a rich playground. Indeed 1e− oxidation of the Au(III) d8 closed-shell square-planar anionic complexes [Au(dt)2]−1 affords the neutral radical species [Au(dt)2]˙ (Scheme 1a). Their specific electronic structure (see below) gives them remarkable properties, such as (i) a strong delocalization of the spin density on the two dt ligands favoring face-to-face stacking to give single-component conductors,11,12 some with metallic behavior,13 and (ii) an intense absorption band in the NIR-III (1400–2000 nm) region, of interest for photothermal applications.14 Moreover, at variance with the isoelectronic, monoanionic nickel complexes with equal delocalization of the radical on the two dithiolene moieties, homoleptic radical gold complexes were found in some instances with two notably different ligand's geometry if one considers the intramolecular metallacycle's bond distances.15 Indeed, in these complexes, the lengthening of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond and concurrent shortening of the C–S bonds is systematically associated with a higher oxidation degree of the non-innocent dithiolene ligand. A differentiation between the two metallacycles in homoleptic complexes is therefore the signature of a charge localization, only observed up to now in a few gold complexes such as [Au(dddt)2]˙ and methylated analogs (Scheme 1b).15
C bond and concurrent shortening of the C–S bonds is systematically associated with a higher oxidation degree of the non-innocent dithiolene ligand. A differentiation between the two metallacycles in homoleptic complexes is therefore the signature of a charge localization, only observed up to now in a few gold complexes such as [Au(dddt)2]˙ and methylated analogs (Scheme 1b).15
One elegant way to further address these issues would consist in analyzing these evolutions within purposely designed mixed-ligand gold bis(dithiolene) complexes where two different dithiolene ligands, noted dtA and dtD in the following (A and D for acceptor/electron poor and donor/electron rich dithiolene respectively) are associated in [Au(dtA)(dtD)]˙ radical complexes (Scheme 1c). Such species were unknow until some of us disclosed in 2021 the isolation and full characterization of one single example, namely [Au(OC4)(D-bordt)]˙ (OC4 = 1,2-bis(4-butoxyphenyl)ethylene-dithiolate, bordt = bornylene-1,2-dithiolate) (Scheme 1c),16 where the D-bordt dithiolene ligand with alkyl substituents is a more electron-rich dithiolene (dtD) than the phenyl-substituted dtA OC4 ligand, as deduced from the comparison of the electrochemical potentials of the corresponding symmetric complexes. The remarkable features of [Au(OC4)(D-bordt)]˙ were: (i) the localization of the spin density on the most electron rich D-bordt ligand, (ii) the limited interactions between radicals in the solid state due to strong steric constraints, (iii) the NIR absorption band characteristic of gold bis(dithiolene) complexes observed at higher energy than in the two symmetric complexes, opening an attractive route to fill the NIR-II region with such mixed-ligand gold complexes.
Such compounds raise therefore many questions related to (i) the (de)localization of the radical species, (ii) its consequences on their single-component character in the solid state, (iii) the evolution of their NIR absorption wavelengths, by comparison with the homoleptic analogs [Au(dtA)2]˙ and [Au(dtD)2]˙ where it is usually found in the NIR-III 1400–2000 nm range. This single [Au(OC4)(D-bordt)]˙ example was calling for amplification, but its preparation method (scrambling of symmetric neutral complexes in solution) was strictly limited to soluble complexes, limiting de facto its extension to the desired variety of mixed-ligand complexes.
In the following, we describe our investigations toward a more general approach to the synthesis of such mixed-ligand Au(III) [Au(dtA)(dtD)]−1 complexes in their monoanionic form, and report and analyze the spectroscopic (NIR absorption) and conducting properties of derived radical complexes [Au(dtA)(dtD)]˙ obtained upon 1e− oxidation. We also confirm and explain why their NIR signature falls out of the range of the homoleptic analogs [Au(dtA)2]˙ and [Au(dtD)2]˙, opening an elegant way to tune at will this NIR absorption, filling the gap between the NIR-I and NIR-III absorption ranges of respectively neutral nickel and gold symmetric bis(dithiolene) complexes [Ni(dt)2]0 and [Au(dt)2]˙.
Results and discussion
Syntheses and molecular structures
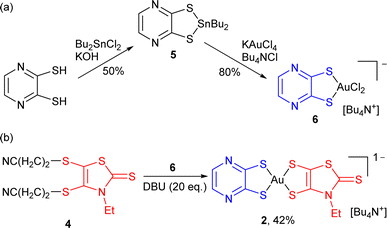
Square-planar bis(dithiolene) complexes with two different dithiolene ligands were explored already in 1967, essentially in the Ni/Pd/Pt triad.17 Their preparation was based on scrambling reactions in solution between two monoanionic complexes [Ni(dtA)2]−1 and [Ni(dtD)2]−1 to give the mixed-ligand complex [Ni(dtA)(dtD)]−1 in low yields (10–15%). When available with an electron-rich dithiolene ligand (dtD), a 2e− oxidized neutral (and soluble) complex [Ni(dtD)2]0 was also reacted with a dianionic [Ni(dtA)2]2− complex to afford the monoanionic mixed-ligand complex [Ni(dtA)(dtD)]−1, also in low yields. Direct syntheses through the mixing of two different dithiolate salts with NiCl2 afforded even lower yields (1–5%).18 On the other hand, scrambling reactions between two symmetric, 2e− oxidized neutral soluble complexes [Ni(dtA)2]0 and [Ni(dtD)2]0 were reported by Kato et al. to afford the mixed-ligand neutral complexes [Ni(dtA)(dtD)]0 in yields up to 66%.19 In the Pd and Pt series, neutral mixed-ligand complexes were also intensively investigated by Deplano et al. for their second-order nonlinear optical activity.20 Their preparation involved the 2e− oxidized form of the electron-rich dithiolene ligand, i.e. the α-dithione. Its PdCl2/PtCl2 complex was directly reacted with the electron-poor dithiolate dtA2− to give [Pd/Pt(dtA)(dtD)]0 by chloride displacement in good yields.Looking now for mixed-ligand gold complexes, as mentioned above, only one example, [Au(OC4)(D-bordt)]˙ (Scheme 1c) was isolated in 33% yield, from a scrambling reaction between the two soluble neutral radical complexes [Au(OC4)2]˙ and [Au(D-bordt)2]˙.16 However, this route cannot be easily exemplified since many neutral complexes interesting for their single component conductor character are highly insoluble. We therefore attempted scrambling reactions between two monoanionic (and soluble) gold complexes [Au(Et-thiazdt)2]−1 and [Au(dmit)2]−1. Albeit spectro- and electrochemical monitoring of the reaction mixture showed the apparition of the desired mixed-ligand complex [Au(dmit)(Et-thiazdt)]−1, we were not able to isolate it in a pure form. We therefore turned our attention to a recently reported method used to prepare bimetallic Au(III) complexes illustrated in Scheme 2a.21 It is based on the chloride displacement of the mono-dithiolene gold complex [(bdt)AuCl2]−3 by a tetrathiolate generated in situ.
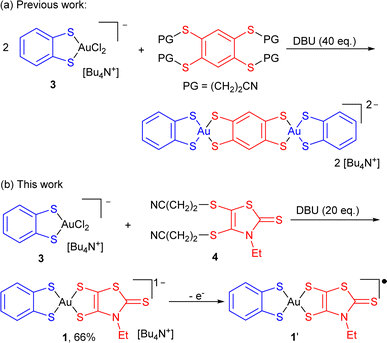 | ||
| Scheme 2 Synthetic paths to mixed-ligand bis-dithiolene complexes, and preparation of [nBu4N][Au(bdt)(Et-thiazdt)] 1. | ||
This route was adapted here for the preparation of monometallic, mixed-ligand complexes such as [nBu4N][Au(bdt)(Et-thiazdt)] 1 (Scheme 2b), starting from the [nBu4N][Au(bdt)Cl2] gold complex 3,21 and the cyanoethyl protected Et-thiazdt 4 dithiolate ligand,22 in the presence of DBU (1,8-diazabicyclo[5.4.0]undec-7-ene) to generate in situ the Et-thiazdt2− dithiolate which further reacts with 3 through chloride displacement to form the complex 1, isolated in a pure form, free of symmetrical complexes, in 66% yield.
This pathway was further extended, moving from the reported mono-dithiolene [Au(bdt)Cl2]− precursor complex 3 to another dithiolene with a stronger electron-withdrawing character, namely pyrazine-2,3-dithiolate, abbreviated as pzdt in the following (Scheme 3). The corresponding mono-dithiolene gold complex [nBu4N][Au(pzdt)Cl2] 6 was prepared in two steps from pyrazine-2,3-dithiol as detailed in Scheme 3a, also confirmed by its X-ray crystal structure, with the Au(III) in a square-planar environment (Fig. S1†).
The reaction of [nBu4N][Au(pzdt)Cl2] 6 with the cyanoethyl-protected Et-thiazdt dithiolate ligand 4, in the presence of DBU (Scheme 3b), also afforded the corresponding mixed-ligand bis-dithiolene complex [Bu4N][Au(pzdt)(Et-thiazdt)] 2, demonstrating the efficiency and generality of this method to prepare mixed-ligand gold complexes. Considering the variety of available dithiolene ligands, an extremely large library of mixed-ligand complexes can be now easily envisioned.
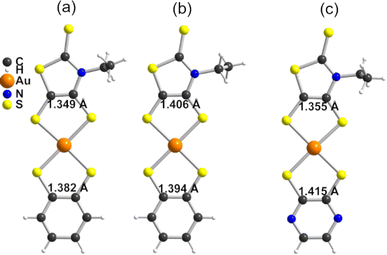
The molecular structure of the two novel anionic complexes 1 (Fig. 1a) and 2 (Fig. 1c) was confirmed by single crystal X-ray diffraction. Bond distances within the AuS2C2 metallacycles are an excellent indicator of the oxidation state (or charge transfer degree) in such bis(dithiolene) complexes. Deviation from the dithiolate form toward a more oxidized form is characterized by a shortening of the C–S bonds and a concomitant lengthening of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. Therefore such bond distances in 1 have been compared in Table 1 with those of the symmetric complexes [Au(bdt)2]−1 and [Au(Et-thiazdt)2]−1. The structure of [Bu4N][Au(bdt)2] has been determined here for that purpose.25 As shown in Table 1 (columns 2, 4, 6), the averaged bond distances within the two different metallacycles in 1 are comparable to those observed in the homoleptic anionic complexes [Au(bdt)2]−1 and [Au(Et-thiazdt)2]−1, indicating the absence of any internal charge transfer, in the monoanionic, closed-shell form. The same conclusions hold for 2, when compared with [Au(pzdt)2]−1 and [Au(Et-thiazdt)2]−1 (Table S1†).
C bond. Therefore such bond distances in 1 have been compared in Table 1 with those of the symmetric complexes [Au(bdt)2]−1 and [Au(Et-thiazdt)2]−1. The structure of [Bu4N][Au(bdt)2] has been determined here for that purpose.25 As shown in Table 1 (columns 2, 4, 6), the averaged bond distances within the two different metallacycles in 1 are comparable to those observed in the homoleptic anionic complexes [Au(bdt)2]−1 and [Au(Et-thiazdt)2]−1, indicating the absence of any internal charge transfer, in the monoanionic, closed-shell form. The same conclusions hold for 2, when compared with [Au(pzdt)2]−1 and [Au(Et-thiazdt)2]−1 (Table S1†).
| [Au(bdt)2]−1,˙ | 1 | 1′ | [Au(Et-thiazdt)2]−1,˙ | |||
|---|---|---|---|---|---|---|
| Anion | Radicala | Anion | Radical | Anionb | Radicalb | |
| a From ref. 24. b From ref. 13a. | ||||||
| a | 2.305(1) | 2.298(11) | 2.300(2) | 2.290(3) | ||
| c | 1.761(4) | 1.734(9) | 1.765(7) | 1.755(4) | ||
| e | 1.393(5) | 1.406(9) | 1.382(11) | 1.394(5) | ||
| A | 2.338(2) | 2.332(3) | 2.329(2) | 2.319(2) | ||
| B | 2.317(2) | 2.331(2) | 2.332(2) | 2.320(1) | ||
| C | 1.765(7) | 1.712(4) | 1.760(6) | 1.721(6) | ||
| D | 1.707(9) | 1.683(4) | 1.744(6) | 1.714(6) | ||
| E | 1.349(12) | 1.406(5) | 1.332(8) | 1.372(8) | ||
As mentioned above, neutral [Au(dtA)(dtD)]˙ radical complexes are of interest, in the one hand, as single-component conductors and, in the other hand as strong NIR absorbers. Electrocrystallization experiments were performed with the two anionic complexes 1 and 2 to isolate, possibly in a single crystalline form, the 1e−-oxidized, neutral radical forms. High quality single crystals were isolated only from 1 upon electrocrystallization in CH3CN with Et4NPF6 as electrolyte, while amorphous powders were obtained from 2 (Fig. S2†). Single crystal X-ray structure resolution confirmed that oxidation of 1 afforded the desired neutral radical, mixed ligand complex [Au(bdt)(Et-thiazdt)]˙, hereafter noted as 1′. Our ability to isolate 1′ also demonstrates that the mixed-ligand anionic complex [Au(bdt)(Et-thiazdt)]−1 in 1 is stable in solution and does not disproportionate over the long electrocrystallization time. 1′ crystallizes in the triclinic system, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , with one molecule in general position (Fig. 1b). The intramolecular bond distances within the two AuS2C2 metallacycles in 1′ are shown in Table 1, together with those observed in the anionic precursor 1 and in the reference symmetric neutral complexes [Au(bdt)2]˙ and [Au(Et-thiazdt)2]˙. On the one hand, it appears that the shortening of the C–S bonds (C, D) and lengthening of the C
, with one molecule in general position (Fig. 1b). The intramolecular bond distances within the two AuS2C2 metallacycles in 1′ are shown in Table 1, together with those observed in the anionic precursor 1 and in the reference symmetric neutral complexes [Au(bdt)2]˙ and [Au(Et-thiazdt)2]˙. On the one hand, it appears that the shortening of the C–S bonds (C, D) and lengthening of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond (E) in the thiazdt moiety in 1′, expected from the comparison with anionic 1, are also notably stronger than in the symmetric [Au(Et-thiazdt)2]˙. On the other hand, the shortening of the C–S bonds (c) and lengthening of the C
C bond (E) in the thiazdt moiety in 1′, expected from the comparison with anionic 1, are also notably stronger than in the symmetric [Au(Et-thiazdt)2]˙. On the other hand, the shortening of the C–S bonds (c) and lengthening of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond (e) in the bdt moiety in 1′ are notably smaller than in the symmetric [Au(bdt)2]˙. In other words, based on these bond distances, the oxidation of 1 into 1′ appears to be essentially localized on the most-electron rich dtD thiazdt dithiolene ligand, while the bdt moiety (dtA) is almost unaffected, with bond distances comparable to those of the anionic [Au(bdt)2]−1 complex.
C bond (e) in the bdt moiety in 1′ are notably smaller than in the symmetric [Au(bdt)2]˙. In other words, based on these bond distances, the oxidation of 1 into 1′ appears to be essentially localized on the most-electron rich dtD thiazdt dithiolene ligand, while the bdt moiety (dtA) is almost unaffected, with bond distances comparable to those of the anionic [Au(bdt)2]−1 complex.
Electrochemical and spectroscopic properties
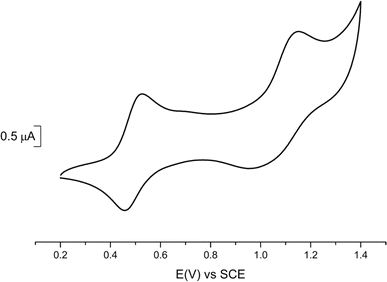
Cyclic voltammetry experiments (Table 2) were performed on 1 (Fig. 2) and 2 (Fig. S3†) and compared with data reported for the symmetric complexes [Au(bdt)2]−1, [Au(Et-thiazdt)2]−1 (Fig. S4†) and [Au(pzdt)2]−1 (Fig. S3†). All complexes exhibit at E1/2(−1/0) a reversible oxidation wave to the neutral radical species, followed at higher potentials, and only with the most electron-rich complexes, by a second process at E1/2(0/+1). An irreversible reduction wave centered on the gold atom is systematically found in reduction, in a −0.85/−1.2 V range.| Complex | E 1/2 (−1/0) | E 1/2 (0/+1) | ΔE |
|---|---|---|---|
| [Au(bdt)2]−1 | +0.66 | +0.99 | 0.33 |
| 1 | +0.485 | +1.06 | 0.575 |
| [Au(Et-thiazdt)2]−1 | +0.55 | +0.68 | 0.13 |
| 2 | +0.55 | — | — |
| [Au(pzdt)2]−1 | +1.10 | — | — |
| [Au(D-bordt)2]˙ | −0.05 | +0.61 | 0.66 |
| [Au(OC4)(D-bordt)]˙ | +0.03 | +0.72 | 0.69 |
| [Au(OC4)2]˙ | +0.25 | +0.75 | 0.50 |
We note that the first oxidation potential of 1 is not found in-between those of the symmetric compounds [Au(bdt)2]−1 (+0.66 V) and [Au(Et-thiazdt)2]−1 (+0.55 V) but is shifted to even lower oxidation potential (+0.485 V). Besides, the first oxidation potential of 2 compares with that of the most-electron-rich symmetric complex [Au(Et-thiazdt)2]−1. Both experiments indicate that the redox potential of the −1/0 oxidation process is essentially controlled by the most electron-rich dithiolene, confirming the outcome of the structural studies reported above which demonstrated that in the oxidized complex 1′, the most electron-rich Et-thiazdt ligand was essentially the only one affected by oxidation. In the same vein, we note that the potential difference between the two redox processes, −1/0 and 0/+1, is much larger in 1 that in the two symmetric complexes, indicating that the second oxidation process (0/+1) is now controlled by the most electron-poor dithiolene.
Spectroelectrochemical experiments give the absorption bands evolution upon oxidation of the monoanionic complexes into the neutral radical species and results are gathered in Table 3. As shown in Fig. 3, incremental oxidation of 1 into 1′ leads to the apparition of a NIR absorption band centered at 1200 nm, while a similar NIR band is observed in the corresponding symmetric neutral radical complexes at notably lower energies, 1390 nm for [Au(bdt)2]˙ and 2070 nm for [Au(Et-thiazdt)2]˙ (Fig. S5†). Similarly, the NIR absorption band observed upon incremental oxidation of 2 into 2′ is found at 950 nm (Fig. S6†). Note that the high oxidation potential of the symmetric [Au(pzdt)2]−1 (+1.10 V vs. SCE) and the insolubility of its oxidation product hindered the observation of the NIR absorption band of the elusive [Au(pzdt)2]˙ species. This hypsochromic shift of the NIR absorption of mixed-ligand complexes relative to the two symmetric analogs, already noted but to a weaker extent in [Au(OC4)(D-bordt)]˙ (Table 3), is thus unambiguously confirmed here. It offers a very useful way to cover a broader range of absorption wavelengths in the NIR region when using such dithiolene complexes for their photothermal properties and its origin will be now discussed based on theoretical investigations of the electronic structures of these complexes.
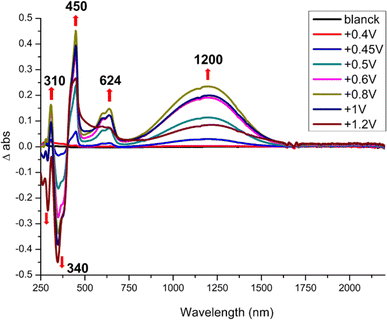 | ||
| Fig. 3 Differential UV-vis-NIR absorption spectra upon incremental oxidation of 1 into 1′, performed in CH2Cl2 with 0.2 M Bu4NPF6. Potentials in V vs. SCE. | ||
Electronic localization in asymmetric Au bis(dithiolene) complexes
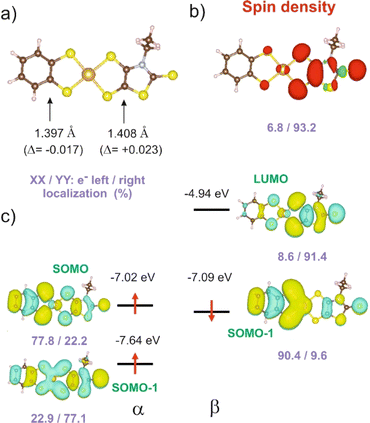
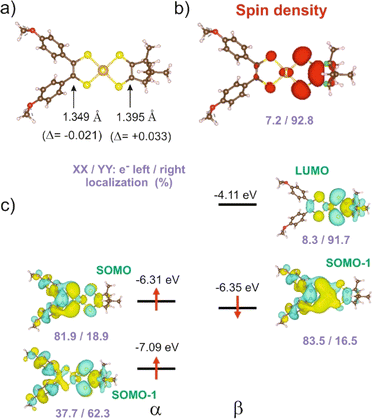
In order to give a rationale for the experimental results reported above, we performed DFT and TD-DFT calculations to examine the degree of electronic localization in such asymmetric gold bis(dithiolene) complexes and their consequences on their peculiar electrochemical, optical and solid-state properties. It is already known15 that even if the two dithiolene ligands are chemically equivalent, the electronic distribution, and most notably the unpaired electron, can be unevenly localized on the two ligands of these gold complexes. Here we will analyze this question by looking in detail at the newly described [Au(bdt)(Et-thiazdt)]˙ complex 1′, together with the reported complex [Au(OC4)(D-bordt)]˙ (Scheme 1c) for comparison purposes.16 Because of the potential problems when studying mixed-valence systems with DFT, we have used the hybrid BLYP35 functional as advised by Kaupp and coworkers.28 Previous work on gold bis(dithiolene) complexes with two identical ligands showed that this functional copes very well the symmetric vs. asymmetric nature of their electronic distribution.15 It is also known that the metal d orbitals have a very small participation in the SOMO (singly occupied molecular orbital) of Au bis(dithiolene) complexes15,16,29 so that the two ligands are almost uncoupled as far as the SOMO is concerned. As we discuss below, this feature may have an unexpected effect on the electronic structure.The DFT-optimized C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths for 1′ (Fig. 4a) clearly reflect the asymmetry. In agreement with the experimental results (see above), the longer C
C bond lengths for 1′ (Fig. 4a) clearly reflect the asymmetry. In agreement with the experimental results (see above), the longer C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is associated with the Et-thiazdt one (i.e. the electron-rich dtD dithiolene) and the shorter one with the bdt side (i.e. the electron-poor dtA dithiolene). The calculated C
C bond is associated with the Et-thiazdt one (i.e. the electron-rich dtD dithiolene) and the shorter one with the bdt side (i.e. the electron-poor dtA dithiolene). The calculated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths (1.408 and 1.397 Å) are in excellent agreement with the experimental ones (1.406 and 1.394 Å). Moreover, the most important result is that, according to our calculations, the bond length has increased by 0.023 Å on the Et-thiazdt donor side but has decreased by 0.017 Å on the bdt acceptor side when we compare with the C
C bond lengths (1.408 and 1.397 Å) are in excellent agreement with the experimental ones (1.406 and 1.394 Å). Moreover, the most important result is that, according to our calculations, the bond length has increased by 0.023 Å on the Et-thiazdt donor side but has decreased by 0.017 Å on the bdt acceptor side when we compare with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C values on the respective symmetric neutral complexes. The opposite trends are observed for the C–S bonds within the metallacycles. Since the HOMOs of both ligands are bonding with respect to the C
C values on the respective symmetric neutral complexes. The opposite trends are observed for the C–S bonds within the metallacycles. Since the HOMOs of both ligands are bonding with respect to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond (and antibonding with respect to the C–S bonds), these bond length changes are consistent with an oxidation of the anionic complex concentrated on the dtD Et-thiazdt side. Considering that in the neutral asymmetric compound 1′, the SOMO−1 is doubly filled and the SOMO is singly filled, we reach the conclusion that the SOMO−1 of the asymmetric ligand should be more concentrated on the bdt acceptor side while the SOMO should be more concentrated in the donor Et-thiazdt side. Apparently, this conclusion is corroborated by the fact that the calculated spin density (Fig. 4b), which in principle should also reflect the localization of the electron in the SOMO, is more localized in the Et-thiazdt donor side.
C bond (and antibonding with respect to the C–S bonds), these bond length changes are consistent with an oxidation of the anionic complex concentrated on the dtD Et-thiazdt side. Considering that in the neutral asymmetric compound 1′, the SOMO−1 is doubly filled and the SOMO is singly filled, we reach the conclusion that the SOMO−1 of the asymmetric ligand should be more concentrated on the bdt acceptor side while the SOMO should be more concentrated in the donor Et-thiazdt side. Apparently, this conclusion is corroborated by the fact that the calculated spin density (Fig. 4b), which in principle should also reflect the localization of the electron in the SOMO, is more localized in the Et-thiazdt donor side.
Note that all along our analysis, the asymmetry of the spin density of a complex, or the charge density associated with a given spin–orbital, will be quantified by integration of the magnitude in the left or right side of the complex (i.e. we define a plane perpendicular to the main axis of the complex passing through the Au atom which separates the two zones). For 1′, we find a strong localization of the spin density (93.2 vs. 6.8%) on the Et-thiazdt side as expected from the previous reasoning.
However, as shown in Fig. 4c, the calculated SOMO is at odds with the previous analysis since it is strongly localized on the bdt acceptor side (77.8 vs. 22.2%). This is very puzzling: why does the same calculation that correctly describes the asymmetry in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond length changes and the distribution of the spin density lead to a wrong answer concerning the localization of the SOMO? In fact, this is not a peculiarity of this complex and we have found it in the other mixed-ligand gold bis(dithiolene) complexes (see below). In addition, calculations with the B3LYP functional led also to the same qualitative results. Based on these observations we conclude that the results of Fig. 4 are not conflicting but more likely point out a flaw in the previous intuitive explanation which is based on a restricted or spin unpolarized calculation, where we use the same orbital to describe both the spin up (α) and spin down (β) electrons occupying the SOMO−1 orbital, neglecting possible spin polarization effects due to the presence of an unpaired electron in the molecule.
C bond length changes and the distribution of the spin density lead to a wrong answer concerning the localization of the SOMO? In fact, this is not a peculiarity of this complex and we have found it in the other mixed-ligand gold bis(dithiolene) complexes (see below). In addition, calculations with the B3LYP functional led also to the same qualitative results. Based on these observations we conclude that the results of Fig. 4 are not conflicting but more likely point out a flaw in the previous intuitive explanation which is based on a restricted or spin unpolarized calculation, where we use the same orbital to describe both the spin up (α) and spin down (β) electrons occupying the SOMO−1 orbital, neglecting possible spin polarization effects due to the presence of an unpaired electron in the molecule.
We remind that the Au orbitals have a small participation into the SOMO. Thus, as far as we deal with the properties of the SOMO and SOMO−1, we should consider the complex as made from two almost independent ligand-localized orbitals with a weak mixing. To understand the nature of the spin density in this type of radicals, it is mandatory to consider spin polarization effects in the SOMO, SOMO−1 and LUMO, which are all ligand based π type orbitals built from the same orbitals, the HOMOs of the two ligands. The SOMO, which is filled, let's say with α spin electron, is according to our calculations (Fig. 4c) mostly localized on the dtA acceptor side (77.8 vs. 22.2%). Electrons with the same spin tend to avoid each other more than electrons with opposite spin in order to reduce the electron–electron repulsion. Consequently, the α electron of the SOMO−1 will try to concentrate on the dtD side of the complex while the β electron of the SOMO−1 will tend to locate on the dtA acceptor side. Such electron distribution should reduce as much as possible the electronic repulsion between the three electrons in the SOMO and SOMO−1. Note that, since we are using an unrestricted or spin polarized calculation to deal with the open shell nature of the complex, the energies of the two spin–orbitals corresponding to the SOMO−1 in a restricted calculation appear with quite different energies due to the different electron–electron repulsion felt by α/β electrons with the unpaired α electron occupying the SOMO. These simple expectations concur with the results in Fig. 4c that are indicative of a quite clear localization of the SOMO and the SOMO−1 electrons. Since the spin density is the difference between spin α and spin β electron densities, the contributions of the α SOMO spin and the β SOMO−1 spin, largely cancel and in fact, the resulting total spin density reflects mainly the asymmetry in the α SOMO−1 spin–orbital and not that of the SOMO as expected when spin polarization effects are neglected. In contrast, the influence of the occupation of the α and β SOMO−1 spin–orbitals on the structure largely compensate and the asymmetry in C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths is governed by the asymmetry of the α SOMO spin–orbital with a heavier weight of the C
C bond lengths is governed by the asymmetry of the α SOMO spin–orbital with a heavier weight of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond on the acceptor side which is consequently shorter than in the corresponding symmetric complex. We finally conclude that all the results of Fig. 4 are mutually consistent. The main location of the SOMO and the shortened C
C bond on the acceptor side which is consequently shorter than in the corresponding symmetric complex. We finally conclude that all the results of Fig. 4 are mutually consistent. The main location of the SOMO and the shortened C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond length, with respect to the symmetrical neutral radical complexes is associated with the more acceptor side of the complex (here bdt) while the spin density localizes on the donor side (here Et-thiazdt).
C bond length, with respect to the symmetrical neutral radical complexes is associated with the more acceptor side of the complex (here bdt) while the spin density localizes on the donor side (here Et-thiazdt).
Note that the results in Fig. 4c also provide a rationale for the observations of the electrochemical results reported above for 1′ (Table 2). Two reversible redox processes were observed. Comparison of the oxidation potentials of the asymmetric and the two symmetric complexes led to the conclusion that the oxidation from the monoanionic asymmetric complex 1 affects preferentially the more electron-rich Et-thiazdt ligand side and the second oxidation is more concentrated in the less electron-rich bdt ligand side. This is in qualitative agreement with the preferential localization of the lowest empty β spin–orbital (LUMO) and α SOMO spin–orbitals in Fig. 4c that are located on the electron-rich Et-thiazdt and electron-poor bdt sides, respectively.
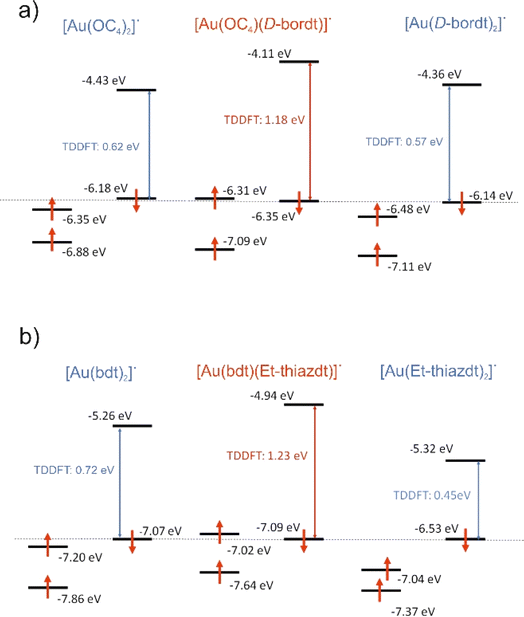
We carried out a similar theoretical study for the only other reported [Au(OC4)(D-bordt)]˙ complex.16 The DFT optimized C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths for this complex (Fig. 5a) clearly reflect the asymmetry. In agreement with the experimental results, the longer C
C bond lengths for this complex (Fig. 5a) clearly reflect the asymmetry. In agreement with the experimental results, the longer C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is associated with the dtDD-bordt side. When comparing the optimized C
C bond is associated with the dtDD-bordt side. When comparing the optimized C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distance in the asymmetric [Au(OC4)(D-bordt)]˙ and the symmetric [Au(OC4)2]˙ and [Au(D-bordt)2]˙ complexes, we find that the C
C distance in the asymmetric [Au(OC4)(D-bordt)]˙ and the symmetric [Au(OC4)2]˙ and [Au(D-bordt)2]˙ complexes, we find that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond length has decreased by 0.021 Å on the OC4 side, and has increased by 0.033 Å on the more electron-rich D-bordt side (these are average values since both, experimentally and theoretically the symmetric complexes already exhibit some degree of structural asymmetry). The difference in bond lengths is even larger than in 1′ (see above). The shortened C
C bond length has decreased by 0.021 Å on the OC4 side, and has increased by 0.033 Å on the more electron-rich D-bordt side (these are average values since both, experimentally and theoretically the symmetric complexes already exhibit some degree of structural asymmetry). The difference in bond lengths is even larger than in 1′ (see above). The shortened C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond length and the main location of the SOMO are associated with the OC4 acceptor side whereas the spin density reflects the opposite localization, on the dtDD-bordt side. The analysis of all the results in Fig. 5 follows perfectly the above discussion for 1′. We also report in the ESI Material (Fig. S7 and Table S2)† similar results for the other asymmetric complex mentioned here, [Au(pzdt)(Et-thiazdt)]˙ 2′, where the stronger electron accepting ability of the pzdt ligand with respect to the bdt one leads to an enhancement of the asymmetry in the electron distribution.
C bond length and the main location of the SOMO are associated with the OC4 acceptor side whereas the spin density reflects the opposite localization, on the dtDD-bordt side. The analysis of all the results in Fig. 5 follows perfectly the above discussion for 1′. We also report in the ESI Material (Fig. S7 and Table S2)† similar results for the other asymmetric complex mentioned here, [Au(pzdt)(Et-thiazdt)]˙ 2′, where the stronger electron accepting ability of the pzdt ligand with respect to the bdt one leads to an enhancement of the asymmetry in the electron distribution.
Evolution of the NIR absorption energy in mixed-ligand complexes
An interesting and unexpected experimental result for both [Au(bdt)(Et-thiazdt)]˙ 1′ and [Au(OC4)(D-bordt)]˙ complexes is the occurrence of a strong optical absorption in the NIR which does not occur at energies in-between those of the two symmetrical complexes but at a notably higher energy. We have carried out time-dependent DFT (TDDFT) calculations to analyze this puzzling observation. The calculated values for the first significant low energy transition of the asymmetric complexes [Au(bdt)(Et-thiazdt)]˙ 1′ and [Au(OC4)(D-bordt)]˙ together with the associated symmetric ones are shown in Fig. 6. This transition is ascribed to a SOMO−1 → LUMO transition. To facilitate the discussion, the β SOMO−1 levels of all complexes have been arbitrarily aligned in this figure. In both cases, the asymmetric complex is calculated to exhibit indeed a transition at higher energy than those of the symmetric complexes, as experimentally found.As already shown in Fig. 4 and 5, the LUMO is a spin–orbital mostly located in the electron-rich dtD donor side of the complex whereas the β SOMO−1 is mostly located in the dtA electron-poor side. Thus, the optical excitation in such mixed-ligand complexes is associated with a remarkable change in the location of the excited electron within the complex that is predicted to lead to a change of the localization of the spin density in these compounds upon excitation, a feature that should deserve further attention. If we compare the energy of the LUMO of the [Au(OC4)(D-bordt)]˙ complex and that of the symmetric complex with the two donor ligands [Au(D-bordt)2]˙ (see Fig. 6a left), it is clear that the localization on the donor side raises the energy of the LUMO (Δ = +0.25 eV). In contrast, comparing the energy of the β SOMO−1 of [Au(OC4)(D-bordt)]˙ and that of the symmetric complex with the two acceptor ligands [Au(OC4)2]˙ (see Fig. 6a right), it is clear that the localization on the acceptor side lowers the energy of the β SOMO−1 (Δ = −0.13 eV). As a consequence, the optical absorption is associated with a larger energy difference than those of the two symmetric complexes. Analysis of the results for [Au(bdt)(Et-thiazdt)]˙ (Fig. 6b) are also consistent with the previous discussion. Localization in the donor side raises the energy of the LUMO (Δ = +0.38 eV) and slightly decreases the energy of the β SOMO−1 (Δ = −0.02 eV). The small decrease due to the acceptor ligand is expected since the bdt ligand possesses a substantial electronic delocalization which, as previously noticed, opposes localization and keeps the β SOMO−1 of the very delocalized symmetric complex quite low in energy. Thus, the common trend at the origin of the NIR optical absorption shift to higher energies for the three complexes [Au(OC4)(D-bordt)]˙, [Au(bdt)(Et-thiazdt)]˙ 1′ and [Au(pzdt)(Et-thiazdt)]˙ 2′ (Table S2†) is the substantial destabilization of the LUMO with respect to that of the symmetric complex with the dtD ligand.
Note in Fig. 4c and 5c that the α SOMO and β SOMO−1 for each complex, [Au(bdt)(Et-thiazdt]˙ 1′ or [Au(OC4)(D-bordt)]˙, occur at very similar energies. They are also very similar in nature; in fact, they are the α and β versions of the same dtA centered orbital. This feature, that can seem paradoxical at first sight, is a consequence of the spin polarization mechanism occurring in these two-ligand complexes because of the very small participation of the central metal atom. Such feature, together with the above-mentioned destabilization of the LUMO under localization, suggests that the occurrence of the NIR optical absorption at higher energy in the asymmetric complex must be accompanied with a larger electrochemical potential difference between the two reversible redox processes, as observed experimentally (Cf.Table 2).
Of course, more complexes must be analyzed before concluding about the generality of the effects described above. We have also carried out two series of model calculations on (i) a series of [Au(R,Redt)(edt)]˙ complexes (Scheme 4a) where, by changing the nature of the two R substituents (R![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) F, CN) on of the two sides, one plays the role of donor whereas the other plays the role of acceptor and (ii) [Au(edt)2]˙ complexes where the C
F, CN) on of the two sides, one plays the role of donor whereas the other plays the role of acceptor and (ii) [Au(edt)2]˙ complexes where the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths at the two sides have been shortened/lengthened to simulate the same effect (Scheme 4b). In all cases (Fig. S8, S9, Tables S3 and S4†), the spin density is mostly associated with the dtD longer C
C bond lengths at the two sides have been shortened/lengthened to simulate the same effect (Scheme 4b). In all cases (Fig. S8, S9, Tables S3 and S4†), the spin density is mostly associated with the dtD longer C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C side whereas the SOMO is polarized in the opposite way and the β SOMO−1 → LUMO transition occurs at larger energies than those of the corresponding symmetric complexes. We thus believe that the scenario described in this section is appropriate for such mixed-ligand gold bis(dithiolene) complexes: the spin polarization induced by electron repulsions has a strong control of their structural and physical properties, a common feature of such asymmetric Au bis(dithiolene) complexes. The very substantial localization of the spin–orbitals is consistent with the structural differences between mixed-ligand and symmetric complexes and provides a sound basis to understand (i) the different ligand-based oxidation potentials, (ii) the NIR optical absorption at notably higher energies and (iii) the larger potential difference of the two redox processes in the mixed-ligand than in the symmetrical complexes.
C side whereas the SOMO is polarized in the opposite way and the β SOMO−1 → LUMO transition occurs at larger energies than those of the corresponding symmetric complexes. We thus believe that the scenario described in this section is appropriate for such mixed-ligand gold bis(dithiolene) complexes: the spin polarization induced by electron repulsions has a strong control of their structural and physical properties, a common feature of such asymmetric Au bis(dithiolene) complexes. The very substantial localization of the spin–orbitals is consistent with the structural differences between mixed-ligand and symmetric complexes and provides a sound basis to understand (i) the different ligand-based oxidation potentials, (ii) the NIR optical absorption at notably higher energies and (iii) the larger potential difference of the two redox processes in the mixed-ligand than in the symmetrical complexes.
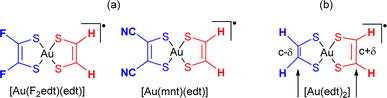 | ||
Scheme 4 Model complexes theoretically investigated with (a) [Au(R,Redt)(edt)]˙ (R![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) F, CN) complexes, (b) [Au(edt)2]˙ complexes with constrained C F, CN) complexes, (b) [Au(edt)2]˙ complexes with constrained C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds. C bonds. | ||
The neutral radical complex: solid-state properties
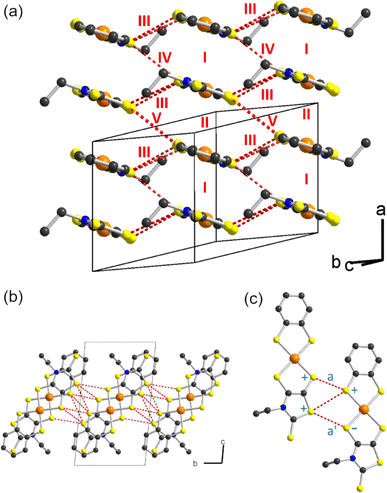
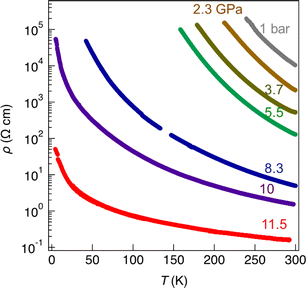
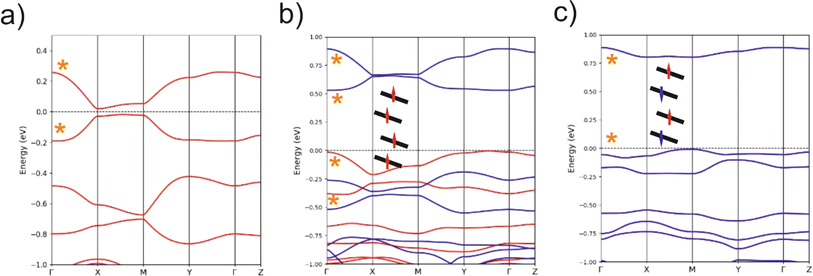
As mentioned above, radical gold complexes able to stack in the solid state provide an extended family of single-component conductors, some of them possibly becoming metallic under pressure. The successful isolation of the neutral, radical [Au(bdt)(Et-thiazdt)]˙ 1′ complex allows us to investigate in details its structural and conducting properties. As shown in Fig. 7a, radical complexes in 1′ are organized into ab layers containing parallel stacks of head-to-tail molecules, running along the a-direction. The stacks are quasi uniform with an alternation of plane-to-plane distances of 3.57 and 3.53 Å. Within the stacks, a longitudinal slip is observed between neighboring complexes (Fig. 7b). Transport measurements were performed on single crystals by the four-points technique at pressures between 1 bar and 18 GPa, with use of a Diamond Anvil Cell (DAC). The RT resistivity of 1′ amounts to 104 Ω cm, i.e. σRT = 1 × 10−4 S cm−1. As shown in Fig. 8, the compound is a semiconductor with an activation energy of 303 meV. Application of pressure strongly decreases the resistivity and the activation energy down to ρRT (11.5 GPa) = 0.15 Ω cm [σRT (11.5 GPa) = 6.6 S cm−1) and Eact (11.5 GPa) = 26 meV. Above 11.5 GPa, a slight increase of both the resistivity and the activation energy is observed, up to 18.1 GPa, with ρRT (18.1 GPa) = 16.7 Ω cm [σRT (18.1 GPa) = 0.06 S cm−1) and Eact (18.1 GPa) = 57 meV (Fig. S10†). This regime change is most probably associated to a structural phase transition.The electronic structure is governed by the intermolecular SOMO⋯SOMO interactions and thus it is important to know their relative strength to understand the semiconducting behavior of this single-component conductor. As shown in Fig. 7a, there are five different types of intermolecular interactions: two are intra-chain (I and II) and three are inter-chain (III–V). The simplest way to have a hint of the relative strength of the SOMO⋯SOMO interactions is by evaluating the so-called intermolecular interaction energies (β).30 The calculated βSOMO⋯SOMO interaction energies for this system are 0.4137 (I), 0.3920 (II), 0.0041 (III), 0.0002 (IV) and 0.0131 (V) eV. The two intra-chain interactions are very similar and substantial despite the non-occurrence of short S⋯S contacts. Although there are two short Au⋯S contacts, they are not responsible for these substantial intra-chain interactions. The interaction is due to the occurrence of four S⋯C contacts per intra-chain interaction associated with strong σ orbital interactions. Note that even if the two interactions (I and II) are crystallographically different, from the electronic viewpoint, the chains are practically uniform. Thus, we anticipate a relatively large band dispersion along the chain's direction in the solid. In contrast, interactions along the transverse b direction are very small. The main reason is that they are of the usually weak lateral π-type. In addition, for pseudo-symmetry reasons, some of the S⋯S contacts of some interactions almost cancel: see for instance in Fig. 7c that because of the signs of the S pz in the SOMO, the electronic effect of two of the short contacts (a and a′) of interaction III practically cancel. In short, 1′ should exhibit a very strong one-dimensional (1D) character.
Based on the previous analysis, the more likely electronic states for the solid should be strongly 1D and can be either delocalized within the chain, or localized with ferromagnetic (FM) or antiferromagnetic (AF) interactions. The calculated DFT band structures for the three possibilities are shown in Fig. 9a–c. That for a delocalized state with paired spins is shown in Fig. 9a. As expected from the previous analysis, the dispersion along the inter-chain b-direction is very small (see X−M and Γ−Y). The dispersion along the inter-layer direction (Γ−Z) is also very small because of the absence of S⋯S contacts. The band structure along the chain direction is that expected for an almost uniform chain with two molecules in the repeat unit, with a small band gap at X. The global dispersion of the SOMO bands is of the same order as that calculated for the related [Au(Me-thiazdt)2]˙ metallic solid,13d witnessing the occurrence of strong intra-chain interactions. Since the inter-chain interactions are very weak, a band gap separates the two SOMO bands all along the Brillouin zone and the system should be a small band gap semiconductor, as experimentally observed. Thus, in principle the chains of 1′ could be considered as the result of a weak Peierls distortion of a hypothetical metallic state.
Gold bis(dithiolene) complexes with uniform chains and a half-filled band (i.e. the situation here if it were not for the very small band gap) tend to exhibit electronic localization. It is thus compulsory to calculate other possible electronic states with electron localization. The calculated band structure of a localized state with ferromagnetic interactions (FM) is shown in Fig. 9b. The spin-up (red) and spin-down (blue) SOMO bands (i.e. those marked with an asterisk) have almost the same shape as in the non-localized state (Fig. 9a). They are almost rigidly shifted by a very large energy of ∼1 eV leading to a ∼0.5 eV band gap (Note the different energy scale in parts (a) and (b)/(c) of Fig. 9). Since there are two electrons to fill the SOMO bands, only the two spin-up (red) bands are filled leading to a ferromagnetic semiconductor. The very large shift due to the electronic repulsions (U) suggests a large stabilization with respect to the non-localized state. In agreement with this expectation, this FM state is calculated to be 127.8 meV per formula unit more stable than the delocalized state.
The band structure of a localized state with antiferromagnetic interactions (AF) is shown in Fig. 9c. Every band in this figure is really a pair of identical bands located on two equivalent parts of the lattice, one associated with spin-up and the other with spin-down. Again, a very large band gap of approximately 0.75 eV opens as a result of the localization with antiferromagnetic interactions along the chain. This AF state is found to be 14.7 meV per formula unit more stable than the FM state. As schematically shown in the inset of Fig. 9c, the spin up and spin-down identical bands of the AF state corresponds to the occurrence of a set of electrons with spin-up/spin-down in two independent sets of [Au(bdt)(Et-thiazdt)]˙, thus leading to a very small direct and indirect interaction and consequently, to very flat bands. Note that both FM and AF have been calculated using the crystallographic unit cell so that ferromagnetic interactions along the b transverse direction are forced. When antiferromagnetic interactions along b are introduced, it is found that the FM state is destabilized by 0.2 meV and the AF by 0.5 meV. Thus, the AF state is the ground state. However, note that, as expected, the transverse interactions are very weak and most likely there will not be a magnetic order in the transverse direction. We thus conclude that [Au(bdt)(Et-thiazdt)]˙ should be described as a set of antiferromagnetic chains with semiconducting behavior.
Finally, let us consider the possible role of pressure in the transport properties. As shown in Fig. 9a, the small gap at the X point could be effectively ignored by the system if the inter-chain interactions were not so weak and the two SOMO subbands could overlap in parts of the Brillouin zone. Thus, one could think that pressure could strengthen the inter-chain interactions and stabilize a metallic state. However, since the electronic interaction (III) through lateral contacts practically cancel, the increase of inter-chain interactions will be only modest. Even if some band overlap could be induced, the very large stabilization calculated for the localized states suggests that a localized state would still be the ground state. The reason for this stability is that a half-filled 1D chain with non-negligible electronic repulsions has a strong tendency to adopt a Mott insulating ground state.31 The way to stabilize a metallic state is by changing the SOMO band filling in a non-negligible way so that the band cannot be considered as half-filled anymore. This is exactly what is behind the metallic state of the related [Au(Me-thiazdt)2] complex.13d In that case, the SOMO−1 leads to a wide band that overlaps with the empty part of the SOMO band. Thus, some electron transfer is induced between the two bands and none of them is half-filled. However, as shown here in Fig. 9a, the two bands below the SOMO ones (i.e. the two SOMO−1 bands) are well separated and there is no chance that pressure can induce the abovementioned overlap, as indeed experimentally observed, up to pressures of 18 GPa (Fig. 8 and S9†). A more promising approach in that respect would be trying the Se for S replacement and/or use of the less bulky methyl substituent with Me-thiazdt ligand which would increase the inter- and intra-chain interactions. Also, replacing the bdt with a more sulfur-rich dithiolene ligand (dmit, dddt) could also increase these lateral interactions. Such chemical modifications are underway.
Conclusions
In conclusion, we have reported here an efficient synthetic approach towards original mixed-ligand monoanionic gold bis(dithiolene) complexes [Au(dtA)(dtD)]˙. Using this strategy, no symmetrical complexes are formed and, upon electrocrystallization, no scrambling was observed, allowing for the isolation of an original, neutral mixed-ligand radical gold bis(dithiolene) complex. Considering the variety of available dithiolene ligands, an extremely large library of such mixed-ligand complexes can now be easily envisioned. We also explain why their NIR signature falls out of the range of the homoleptic analogs [Au(dtA)2]˙ and [Au(dtD)2]˙, opening an elegant way to tune this NIR absorption in the 1000–1400 nm range, filling the gap between the NIR-I and NIR-III absorption ranges of respectively neutral [Ni(dt)2]0 and [Au(dt)2]˙ homoleptic bis(dithiolene) complexes. Furthermore, it is shown that the spin polarization induced by electron repulsions leads to a strong localization of the spin–orbitals, and provides a sound basis to understand, (i) the different ligand-based oxidation potentials, (ii) the NIR optical absorption at notably higher energies and (iii) the larger potential difference of the two redox processes than in the parent symmetric complexes. The solid-state properties of the radical complex [Au(bdt)(Et-thiazdt)]˙ are the consequence of a strongly 1D electronic structure with weakly dimerized chains and electronic localization favoring a semiconducting behavior, stable under pressures up to 18.2 GPa. The versatility of the preparation method opens the route for a wide library of different mixed-ligand radical complexes with simultaneously an adaptable absorption in the NIR-II range and a rich structural chemistry of single-component conductors.Experimental
All experimental information (synthesis and crystal growth, characterization data, X-ray crystallography, transport measurements and theoretical calculations) are in the ESI.†Data availability
The data supporting this article have been included as part of the ESI.† Crystallographic data has been deposited at the CCDC under CCDC numbers 2348567–2348571 for respectively compounds 6, 1, 1′, 2 and [Bu4N][Au(bdt)2] and can be obtained directly from https://www.ccdc.cam.ac.uk/products/csd/request/request.php4.Author contributions
H. K. and Y. L. conducted all synthesis and electrochemical experiments. T. R. conducted X-ray diffraction studies. H. C. and K. H. K. performed the transport measurements under pressure. E. C. and P. A. conducted all theoretical calculations and co-wrote the manuscript. M. F. and D. L. conceptualized and supervised the project, and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from ANR (France) through contract no ANR-23-CE07-0032-01 is acknowledged, as well as PhD grant (to H. K.) from Rennes University. The work at SNU was supported by the NRF through the Quantum Computing Research Infrastructure Construction Program (2022M3K2A1083855) and by the Ministry of Education through the core center Program (2021R1A6C101B418). The work in Spain was supported by MICIU through Grants PID2022-139776NB-C61 and PID2021-128217NB-I00 and by Generalitat de Catalunya (2021SGR01519 and 2021SGR00286). E. C. acknowledges the support of the Spanish MICIU through the Severo Ochoa FUNFUTURE (CEX2019-000917-S) Excellence Centre distinction and P. A. from the Maria de Maeztu Units of Excellence Program (CEX-2021-001202-M).References
- T. M. Liu, J. Conde, T. Lipiński, A. Bednarkiewicz and C. C. Huang, Revisiting the classification of NIR-absorbing/emitting nanomaterials for in vivo bioapplications, NPG Asia Mater., 2016, 8, e295 CrossRef CAS.
- G. Qian and Z. Y. Wang, Near-Infrared Organic Compounds and Emerging Applications, Chem.–Asian J., 2010, 5, 1006–1020 CrossRef CAS PubMed.
- D. S. Weiss and M. Abkowitz, Organic Photoconductors, in Springer Handbook of Electronic and Photonic Materials, ed Kasap, S. and Capper, P., Springer Handbooks. Springer, Cham, 2017 Search PubMed.
- S. Dalgleish, M. M. Matsushita, L. Hu, B. Li, H. Yoshikawa and K. Awaga, Utilizing Photocurrent Transients for Dithiolene-Based Photodetection: Stepwise Improvements at Communications Relevant Wavelengths, J. Am. Chem. Soc., 2012, 134, 12742–12750 CrossRef CAS PubMed.
- F. Grifoni, M. Bonomo, W. Naim, N. Barbero, T. Alnasser, I. Dzeba, M. Giordano, A. Tsaturyan, M. Urbani, T. Torres, C. Barolo and F. Sauvage, Toward Sustainable, Colorless, and Transparent Photovoltaics: State of the Art and Perspectives for the Development of Selective Near-Infrared Dye-Sensitized Solar Cells, Adv. Energy Mater., 2021, 11, 2101598 CrossRef CAS.
- D. Kraemer, B. Poudel, H.-P. Feng, J. C. Caylor, B. Yu, X. Yan, Y. Ma, X. Wang, D. Wang, A. Muto, K. McEnaney, M. Chiesa, Z. Ren and G. Chen, High-Performance Flat-Panel Solar Thermoelectric Generators with High Thermal Concentration, Nat. Mater., 2011, 10, 532–538 CrossRef CAS PubMed.
- (a) K. Mebrouk, F. Chotard, C. Le Goff-Gaillard, Y. Arlot-Bonnemains, M. Fourmigué and F. Camerel, Water-soluble nickel-bis(dithiolene) complexes as photothermal agents, Chem. Commun., 2015, 51, 5268–5270 RSC; (b) K. Mebrouk, T. Vives, S. Cammas-Marion, T. Benvegnu, C. Le Goff-Gaillard, Y. Arlot-Bonnemains, M. Fourmigué and F. Camerel, Fine and Clean Photothermally Controlled NIR Drug Delivery from Biocompatible Nickel-bis(dithiolene)-Containing Liposomes, ChemMedChem, 2017, 12, 1753–1758 CrossRef CAS PubMed; (c) M. Ciancone, K. Mebrouk, N. Bellec, C. Le Goff-Gaillard, Y. Arlot-Bonnemains, T. Benvegnu, M. Fourmigué, F. Camerel and S. Cammas-Marion, Biocompatible nanoparticles containing hydrophobic nickel-bis(dithiolene) complexes for NIR-mediated doxorubicin release and photothermal therapy, J. Mater. Chem. B, 2018, 6, 1744–1753 RSC; (d) M. Ciancone, N. Bellec, S. Cammas-Marion, A. Dolet, D. Vray, F. Varray, C. Le Goff-Gaillard, X. Le Goff, Y. Arlot-Bonnemains and F. Camerel, Liposomes Containing Nickel–Bis(dithiolene) Complexes for Photothermal Theranostics, Langmuir, 2019, 35, 15121–15130 CrossRef CAS PubMed.
- H. Liu, X. Wang, Y. Huang, H. Li, C. Peng, H. Yang, J. Li, H. Hong, Z. Lei, X. Zhang and Z. Li, Biocompatible Croconaine Aggregates with Strong 1.2–1.3 μm Absorption for NIR-IIa Photoacoustic Imaging in Vivo, ACS Appl. Mater. Interfaces, 2019, 11, 30511–30517 CrossRef CAS PubMed.
- Y.-C. Yang, J.-S. Lin and J.-S. Ni, Neutral d8 metal complexes with intervalence charge-transfer transition trigger an effective NIR-II photothermal conversion for solar-driven desalination, J. Mater. Chem. A, 2023, 11, 26164–26172 RSC.
- H. Hachem, H. Cui, T. Tsumuraya, R. Kato, O. Jeannin, M. Fourmigué and D. Lorcy, Single-component conductors based on closed-shell Ni and Pt bis(dithiolene) complexes: metallization under high pressure, J. Mater. Chem. C, 2020, 8, 11581–11592 RSC.
- (a) N. C. Schiødt, T. Bjørnholm, K. Bechgaard, J. J. Neumeier, C. Allgeier, C. S. Jacobsen and N. Thorup, Structural, electrical, magnetic, and optical properties of bis-benzene-1,2-dithiolato-Au(IV) crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 1773–1778 CrossRef PubMed; (b) D. Belo, H. Alves, E. B. Lopes, M. T. Duarte, V. Gama, R. T. Henriques, M. Almeida, A. Pérez-Benítez, C. Rovira and J. Veciana, Gold Complexes with Dithiothiophene Ligands: A Metal Based on a Neutral Molecule, Chem.–Eur. J., 2001, 7, 511–519 CrossRef CAS PubMed; (c) O. J. Dautel, M. Fourmigué, E. Canadell and P. Auban-Senzier, Fluorine Segregation Controls the Solid-State Organization and Electronic Properties of Ni and Au Dithiolene Complexes: Stabilization of a Conducting Single-Component Gold Dithiolene Complex, Adv. Funct. Mater., 2002, 12, 693–698 CrossRef CAS.
- (a) M. F. G. Velho, R. A. L. Silva, G. Brotas, E. B. Lopes, I. C. Santos, A. Charas, D. Belo and M. Almeida, Conducting neutral gold bisdithiolene complex [Au(dspdt)2], Dalton Trans., 2020, 49, 13737–13743 RSC; (b) A. I. S. Neves, I. C. Santos, J. T. Coutinho, L. C. J. Pereira, R. T. Henriques, E. B. Lopes, H. Alves, M. Almeida and D. Belo, 5-Methylthiophene-2,3-dithiolene Transition Metal Complexes, Eur. J. Inorg. Chem., 2014, 3989–3999 CrossRef CAS.
- (a) N. Tenn, N. Bellec, O. Jeannin, L. Piekara-Sady, P. Auban-Senzier, J. Íñiguez, E. Canadell and D. Lorcy, A Single-Component Molecular Metal Based on a Thiazole Dithiolate Gold Complex, J. Am. Chem. Soc., 2009, 131, 16961–16967 CrossRef CAS PubMed; (b) A. Filatre-Furcate, T. Roisnel, M. Fourmigué, N. Bellec, P. Auban-Senzier and D. Lorcy, Subtle Steric Differences Impact the Structural and Conducting Properties of Radical Gold Bis(dithiolene) Complexe, Chem.–Eur. J., 2017, 23, 16004–16013 CrossRef CAS PubMed; (c) G. Yzambart, N. Bellec, G. Nasser, O. Jeannin, M. Fourmigué, P. Auban-Senzier, J. Íñiguez, E. Canadell and D. Lorcy, Anisotropic Chemical Pressure Effects in Single-Component Molecular Metals Based on Radical Dithiolene and Diselenolene Gold Complexes, J. Am. Chem. Soc., 2012, 134, 17138–17148 CrossRef CAS PubMed; (d) Y. Le Gal, T. Roisnel, P. Auban-Senzier, N. Bellec, J. Íñiguez, E. Canadell and D. Lorcy, Stable Metallic State of a Neutral-Radical Single-Component Conductor at Ambient Pressure, J. Am. Chem. Soc., 2018, 140, 6998–7004 CrossRef CAS PubMed.
- J. B. Pluta, R. Guechaichia, A. Vacher, N. Bellec, S. Cammas-Marion and F. Camerel, Investigations of the Photothermal Properties of a Series of Molecular Gold-bis(dithiolene) Complexes Absorbing in the NIR-III Region, Chem.–Eur. J., 2023, 29, e202301789 CrossRef CAS PubMed.
- D. G. Branzea, F. Pop, P. Auban-Senzier, R. Clérac, P. Alemany, E. Canadell and N. Avarvari, Localization versus Delocalization in Chiral Single Component Conductors of Gold Bis(dithiolene) Complexes, J. Am. Chem. Soc., 2016, 138, 6838–6851 CrossRef CAS PubMed.
- R. Perochon, F. Barrière, O. Jeannin, L. Piekara-Sady and M. Fourmigué, A radical mixed-ligand gold bis(dithiolene) complex, Chem. Commun., 2021, 57, 1615–1618 RSC.
- A. Davison, J. A. McCleverty, E. T. Shawl and E. J. Wharton, Ligand-Exchange Reactions of Bis(cis-1,2-disubstituted ethylene-1,2-dithiolata) nickel Complexes, J. Am. Chem. Soc., 1967, 89, 830–832 CrossRef CAS.
- (a) G. C. Papavassiliou, G. C. Anyfantis, B. R. Steele, A. Terzis, C. R. Raptopoulou, G. Tatakis, G. Chaidogiannos, N. Glezos, Y. Weng, H. Yoshino and K. Murata, Some New Nickel 1,2-Dichalcogenolene Complexes as Single-Component Semiconductors, Z. Naturforsch., 2007, 62B, 679–684 CrossRef; (b) G. C. Papavassiliou, G. C. Anyfantis, A. Terzis, V. Psycharis, P. Kyritsis and P. Paraskevopoulou, Some Unsymmetrical Metal 1,2-Dithiolenes Based on Palladium, Platinum and Gold, Z. Naturforsch., 2008, 63B, 1377–1382 CrossRef.
- (a) Y. Kashimura, Y. Okano, J.-I. Yamaura and R. Kato, Synthesis, Structures, and Physical Properties of Molecular Conductors Based on Unsymmetrical Metal-dithiolene Complexes, Synth. Met., 1999, 103, 2123–2124 CrossRef CAS; (b) E. Watanabe, M. Fujiwara, J.-I. Yamaura and R. Kato, Synthesis and properties of novel donor-type metal-dithiolene complexes based on 5,6-dihydro-1,4-dioxine-2,3-dithiole (edo) ligand, J. Mater. Chem., 2001, 11, 2131–2141 RSC.
- (a) D. Espa, L. Pilia, L. Marchio, M.-L. Mercuri, A. Serpe, A. Barsella, A. Fort, S. J. Dalgleish, N. Robertson and P. Deplano, Redox-Switchable Chromophores Based on Metal (Ni, Pd, Pt) Mixed-Ligand Dithiolene Complexes Showing Molecular Second-Order Nonlinear-Optical Activity, Inorg. Chem., 2011, 50, 2058–2060 CrossRef CAS PubMed; (b) L. Pilia, D. Espa, A. Barsella, A. Fort, C. Makedonas, L. Marchio, M. -L Mercuri, A. Serpe, C. Mitsopoulou and P. Deplano, Combined Experimental and Theoretical Study on Redox-Active d8 Metal Dithione−Dithiolato Complexes Showing Showing Molecular Second-Order Nonlinear-Optical Activity, Inorg. Chem., 2011, 50, 10015–10027 CrossRef CAS PubMed; (c) D. Espa, L. Pilia, L. Marchio, F. Artizzu, A. Serpe, M.-L. Mercuri, D. Simao, M. Almeida, M. Pizzoti, F. Tessore and P. Deplano, Mixed-ligand Pt(II) dithione-dithiolato complexes: influence of the dicyanobenzodithiolato ligand on the second-order NLO properties, Dalton Trans., 2012, 41, 3485–3493 RSC; (d) F. Bigoli, P. Cassoux, P. Deplano, M.-L. Mercuri, M. A. Pellinghelli, G. Pintus, A. Serpe and E. F. Trogu, Synthesis, structure and properties of new unsymmetrical nickel dithiolene complexes useful as near-infrared dyes, Dalton Trans., 2000, 4639–4644 RSC; (e) P. Deplano, L. Pilia, D. Espa, M.-L. Mercuri and A. Serpe, Square-planar d8 metal mixed-ligand dithiolene complexes as second order nonlinear optical chromophores: Structure/property relationship, Coord. Chem. Rev., 2010, 254, 1434–1447 CrossRef CAS.
- M. Murata, S. Kaji, H. Nishimura, A. Wakamiya and Y. Murata, Efficient Synthesis on One- and Two-Dimensional Multimetallic Gold-Bis(dithiolene) Complexes, Eur. J. Inorg. Chem., 2016, 3228–3232 CrossRef CAS.
- Y. Le Gal, D. Ameline, N. Bellec, A. Vacher, T. Roisnel, V. Dorcet, O. Jeannin and D. Lorcy, Efficient routes towards a series of 5,5'-bithiazolidinylidenes as π-electron acceptors, Org. Biomol. Chem., 2015, 13, 8479–8486 RSC.
- Estimated standard deviations (esd) of mean value given in parentheses was calculated from the n experimental esd (σi) by the following equation σ = [(1/n)Σ(σi2)]1/2..
- G. Rindorf, N. Thorup, T. Bjornholm and K. Bechgaard, Structure of bis(benzene-1,2-dithiolato)gold(IV), Acta Crystallogr. C, 1990, 46, 1437–1439 CrossRef.
- R. J. Staples, J. P. Jr Fackler, R. M. Davila and T. E. Albreit, Crystal structure of bis(triphenylphosphoranylidene)ammonium bis(1,2-benzenedithiolato)aurate(III), [(C6H5)3PNP(C6H5)3][Au(S2C6H4)2], Z. Kristallogr., 1995, 210, 383–384 CAS.
- R. Perochon, L. Piekara-Sady, W. Jurga, R. Clérac and M. Fourmigué, Dalton Trans., 2009, 3052–3061 RSC.
- R. Perochon, C. Poriel, O. Jeannin, L. Piekara-Sady and M. Fourmigué, Eur. J. Inorg. Chem., 2009, 5413–5421 CrossRef CAS.
- (a) M. Kaupp, M. Renz, M. Parthey, M. Stolte, F. Würthner and C. Lambert, Computational and spectroscopic studies of organic mixed-valence compounds: where is the charge?, Phys. Chem. Chem. Phys., 2011, 13, 16973–16986 RSC; (b) M. Parthey and M. Kaupp, Quantum-chemical insights into mixed-valence systems: within and beyond the Robin–Day scheme, Chem. Soc. Rev., 2014, 43, 5067–5088 RSC.
- S. Kolkatam, K. Ray, J. Pap, E. Will, W. E. Geiger, R. J. LeSuer, P. H. Rieger, T. Weyhermüller, F. Neese and K. Wieghart, Molecular and Electronic Structure of Square-Planar Gold Complexes Containing Two 1,2-Di(4-tert-butylphenyl)ethylene-1,2-dithiolato Ligands: [Au(2L)2]1+/0/1-/2-. A Combined Experimental and Computational Study, Inorg. Chem., 2007, 46, 1100–1111 CrossRef PubMed.
- M.-H. Whangbo, J. M. Williams, P. C. W. Leung, M. A. Beno, T. J. Emge and H. H. Wang, Role of the Intermolecular Interactions in the Two-Dimensional Ambient-Pressure Organic Superconductors β-(ET)2I3 and β-(ET)2IBr2, Inorg. Chem., 1985, 24, 3500–3502 CrossRef CAS.
- E. H. Lieb and F. Y. Wu, Absence of Mott Transition in an Exact Solution of the Short-Range, One-Band Model in One Dimension, Phys. Rev. Lett., 1968, 20, 1445–1448 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental and characterization data; X-ray crystallographic information; additional details of computational structure simulations, Fig S1–S10 and Tables S1–S5. CCDC 2348567–2348571. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc03238a |
| This journal is © The Royal Society of Chemistry 2024 |