Open Access Article
Open Access ArticleDiversity-driven, efficient exploration of a MOF design space to optimize MOF properties†
Tsung-Wei
Liu‡
a,
Quan
Nguyen‡
b,
Adji Bousso
Dieng
 *c and
Diego A.
Gómez-Gualdrón
*c and
Diego A.
Gómez-Gualdrón
 *a
*a
aDepartment of Chemical and Biological Engineering, Colorado School of Mines, 1601 Illinois St, Golden, CO 80401, USA. E-mail: dgomezgualdron@mines.edu
bDepartment of Computer Science and Engineering, Washington University in St. Louis, 1 Brookings Dr, St. Louis, MO 63130, USA
cVertaix, Department of Computer Science, Princeton University, 35 Olden St, Princeton, NJ 08540, USA. E-mail: adji@princeton.edu
First published on 16th October 2024
Abstract
Metal–organic frameworks (MOFs) promise to engender technology-enabling properties for numerous applications. However, one significant challenge in MOF development is their overwhelmingly large design space, which is intractable to fully explore even computationally. To find diverse optimal MOF designs without exploring the full design space, we develop Vendi Bayesian optimization (VBO), a new algorithm that combines traditional Bayesian optimization with the Vendi score, a recently introduced interpretable diversity measure. Both Bayesian optimization and the Vendi score require a kernel similarity function, we therefore also introduce a novel similarity function in the space of MOFs that accounts for both chemical and structural features. This new similarity metric enables VBO to find optimal MOFs with properties that may depend on both chemistry and structure. We statistically assessed VBO by its ability to optimize three NH3-adsorption dependent performance metrics that depend, to different degrees, on MOF chemistry and structure. With ten simulated campaigns done for each metric, VBO consistently outperformed random search to find high-performing designs within a 1000-MOF subset for (i) NH3 storage, (ii) NH3 removal from membrane plasma reactors, and (iii) NH3 capture from air. Then, with one campaign dedicated to finding optimal MOFs for NH3 storage in a “hybrid” ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-MOF database, we identify twelve extant and eight hypothesized MOF designs with potentially record-breaking working capacity ΔNNH3 between 300 K and 400 K at 1 bar. Specifically, the best MOF designs are predicted to (i) achieve ΔNNH3 values between 23.6 and 29.3 mmol g−1, potentially surpassing those that MOFs previously experimentally tested for NH3 adsorption would have at the proposed operation conditions, (ii) be thermally stable at the operation conditions and (iii) require only ca. 10% of the energy content in NH3 to release the stored molecule from the MOF. Finally, the analysis of the generated simulation data during the search indicates that a pore size of around 10 Å, a heat of adsorption around 33 kJ mol−1, and the presence of Ca could be part of MOF design rules that could help optimize NH3 working capacity at the proposed operation conditions.
000-MOF database, we identify twelve extant and eight hypothesized MOF designs with potentially record-breaking working capacity ΔNNH3 between 300 K and 400 K at 1 bar. Specifically, the best MOF designs are predicted to (i) achieve ΔNNH3 values between 23.6 and 29.3 mmol g−1, potentially surpassing those that MOFs previously experimentally tested for NH3 adsorption would have at the proposed operation conditions, (ii) be thermally stable at the operation conditions and (iii) require only ca. 10% of the energy content in NH3 to release the stored molecule from the MOF. Finally, the analysis of the generated simulation data during the search indicates that a pore size of around 10 Å, a heat of adsorption around 33 kJ mol−1, and the presence of Ca could be part of MOF design rules that could help optimize NH3 working capacity at the proposed operation conditions.
1. Introduction
Metal–organic frameworks (MOFs) are a class of porous materials that could be bestowed with properties that could enable technological breakthroughs in energy, environment, and other fields.1–4 The idea is that judicious selection of MOF constituent nodes and linkers could yield whichever architecture and/or chemistry is required to engender the necessary material property or behavior to enable the breakthrough.5 However, one persisting challenge in MOF development has been that the combinatorics of constituent building blocks creates an overwhelmingly large material “design space,”6–8 To expedite the navigation of the MOF design space, for longer than a decade, MOF development has been aided by high throughput computation instead of solely relying on experiments.9–11High throughput computation in MOFs has usually relied on exhaustively predicting key performance-relevant properties in all MOFs in a database—usually using molecular simulation.12,13 Some notable databases have been created out of experimentally reported MOF structures (i.e. extant MOFs)14 curated from the Cambridge Structure Database, or hypothesized MOF structures outputted by crystal creation codes (i.e. MOF prototypes).6,15–17 Notable databases of extant MOFs have been created by Chung et al.14 (∼20k MOFs) and by Moghadam et al.18 (∼70k MOFs). On the other hand, notable databases of hypothesized MOFs include those created by Wilmer et al.15 (∼137k MOFs), Colón et al.19 (∼13k MOFs), Boyd et al.20 (∼280k MOFs), among others. Note, however, that the size of these databases is very small compared to the vastness of the MOF design space, which some estimate to span at least one trillion MOFs.21
Indeed, current computational capabilities only allow evaluation of a small number of MOFs relative to the MOF design space size. For instance, the work by Simon et al.13 only managed to predict methane adsorption in ∼650k materials, even though methane adsorption is one of the fastest properties to predict by simulation.22 Calculation of other properties have proven even more limiting. For instance, prediction of charge distribution through density functional theory (DFT) by Nazarian et al.23 was limited to ∼3k structures. Prediction of band gaps via DFT by Rosen et al.24 was limited to ∼20k structures. Prediction of thermal conductivity by Islamov et al.9via molecular dynamics was limited to ∼10k structures. Predictions of hexane isomer mixture adsorption by Chung et al.25 was limited to ∼500 structures. Moreover, in the case of adsorption applications, computational limits may be even more restrictive since screening for such properties for a given application may require considering different conditions in temperature, pressure, and composition (in the case of mixtures).
One can argue that the discovery of technology-enabling MOFs have been hampered by the inability to explore the MOF design space at large. One way that researchers have attempted to expand the number of MOFs considered in a given study is through hierarchical screening. But the latter first requires the calculation of an inexpensive descriptor which (hopefully) points to (smaller) regions of the MOF design space where the property of interest may have desirable values.25–27 Therefore, hierarchical screening presents caveats such as: (i) requiring extensive “domain knowledge” to identify an effective, inexpensive “descriptor”28 (ii) still being unlikely that the descriptor can be calculated on the MOF design space at large, (iii) due to a probably imperfect correlation, still being possible that the descriptor calculation may overlook regions of design space where the property of interest could have desirable values.
Hence, there is growing interest in methods that allow exploring the MOF design space efficiently, while still relying solely on direct property calculations. For instance, genetic algorithms (GAs) have been explored to evolve an initial small subset of MOFs into new subsets of MOFs with optimized values of the property of interest (e.g., pre-combustion CO2 capture properties,29 or CH4 storage properties21). However, it is understood that GAs tend to require a larger number of evaluations and are slower than other sophisticated search/optimization methods. GAs thus may become rapidly intractable as property calculation becomes more computationally expensive. In contrast, Bayesian optimization is known to be a more sample-efficient method,30 and hence is finding success in tasks such as screening molecules with high power conversion efficiency for clean energy,31 optimizing reactions for molecular synthesis,32 and finding low-energy molecular conformers,33 among others.34–36
The potential benefits of Bayesian methods to optimize porous materials have been suggested by work by Simon and coworkers.37 Working with the data from previously screened ∼70k covalent-organic frameworks (COFs), these authors showed that Bayesian optimization could find ca. 50% of the top-100 adsorbents for methane storage only exploring ca. 1% of the COFs. However, the approach used by these authors may not generalize well to searches aiming to optimize other material properties. For instance, their representation of the adsorbent consisted of a 12-component vector of five common (global) textural properties and simple counts of seven specific chemical elements. Such simple representation likely leverages that methane adsorption is primarily a (relatively) smooth function of textural properties. However, it may not be suitable when the property of interest also depends strongly on material chemistry.
On the other hand, traditional Bayesian optimization is designed to find one single optimal solution, which may turn out to correspond to a MOF design that may not be experimentally synthesizable or stable, or for which the performance prediction may have turned out to be unreliable. The task of optimizing a MOF performance metric while ensuring other properties (e.g., synthesizability and stability) also have desirable values can be framed as a multi-objective optimization problem. Such formulation, however, assumes that all relevant metrics are known a priori and can be evaluated in similar manners.26,38 Multi-objective optimization cannot be realized, however, if some objectives can only be evaluated after screening is completed, or if we cannot anticipate all possible factors that should be accounted for during the search (i.e., prediction reliability for each particular MOF). We thus take a different approach: finding multiple MOFs, different from one another, with desirable predicted values for the primary property of interest.
Specifically, in this work, we build a general and efficient framework for searching and finding several optimal MOF designs that are distinct from each other. Our framework is designed to be amenable to performance metrics that depend strongly on either MOF chemistry or textural properties, or both. More specifically, we combine the traditional tools of Bayesian optimization with the Vendi score—a statistical measure of diversity developed by Friedman and Dieng39—to find a diverse set of promising MOF designs, each yielding a sufficiently high value for the metric of interest, instead of committing to a single optimal MOF that may not be synthesizable or stable. This comes in the form of promoting more exploration in the behavior of our optimization algorithm, selecting MOFs that are diverse from those already inspected. We name this framework Vendi Bayesian optimization (VBO).
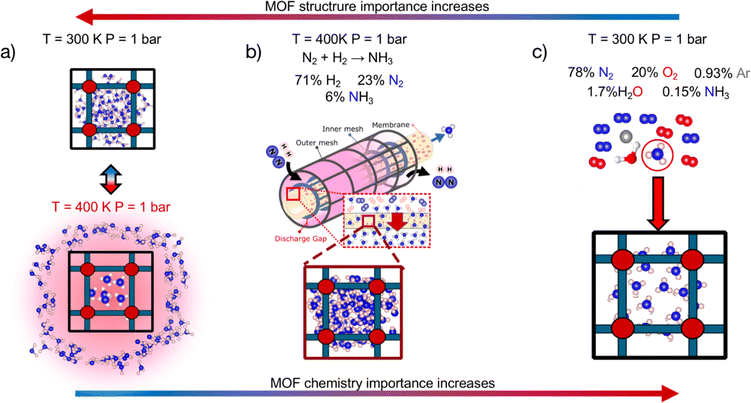
We first statistically test the efficacy of combining a chemistry- and structure-aware MOF representation with VBO, using a randomly drawn subset of ∼1000 MOFs as a testbed. We conducted these tests on the optimization of three performance metrics depending on the adsorption of NH3. We chose metrics involving this molecule because NH3 is important for our society as a precursor to fertilizers,40 and could gain further prominence in the near future as an energy vector.41 From an application perspective, the three chosen metrics are relevant to rank MOFs for their potential to help make the synthesis of NH3 sustainable and carbon-free,42 and NH3 storage and transportation easy, energy-efficient and safe.43–45 From a methods perspective, the three chosen metrics pose different challenges to our developed search method. Namely, the polarity of ammonia46 and the different adsorption conditions associated with each application (Fig. 1) make the different metrics balance differently their dependence on MOF chemistry and textural properties (vide infra). On the other hand, each metric present different (mathematical) complexity on their relation to adsorption loadings.
Upon statistical testing of VBO efficacy, we finish this work with a real search campaign on a ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-MOF hybrid database (i.e., containing extant and hypothesized structures) to find MOFs with outstanding predicted NH3 storage performance. We chose this application for the real search due to the growing interest of experimentalist chemists in the use of MOFs for NH3 storage as reflected by the growing number of NH3 adsorption measurements at 1 bar and 300 K (i.e., ambient conditions) reported in recent years. For instance, Moribe et al. reported 10.5 mmolNH3 gMOF−1 in Ga-PMOF,47 Guo et al. 12.8 mmolNH3 gMOF−1 in MIL-160,48 Kim et al. 23.9 mmolNH3 gMOF−1 in Mg-MOF-74 (ref. 49) and 23.5 mmolNH3 gMOF−1 in Ni_acryl_TMA,50 and Shi et al. 33.9 mmolNH3 gMOF−1 in LiCl-MIL-53,51 among others.52,53 But despite growing interest, not much has been done to leverage search algorithms to identify promising MOFs for NH3 storage. Thus, here we show how our developed VBO, a novel search algorithm for MOFs, can be used to fill such knowledge gaps. Furthermore, our analysis of the MOFs explored by our VBO provides new design rules to guide experimentalists developing MOFs for NH3 storage.
000-MOF hybrid database (i.e., containing extant and hypothesized structures) to find MOFs with outstanding predicted NH3 storage performance. We chose this application for the real search due to the growing interest of experimentalist chemists in the use of MOFs for NH3 storage as reflected by the growing number of NH3 adsorption measurements at 1 bar and 300 K (i.e., ambient conditions) reported in recent years. For instance, Moribe et al. reported 10.5 mmolNH3 gMOF−1 in Ga-PMOF,47 Guo et al. 12.8 mmolNH3 gMOF−1 in MIL-160,48 Kim et al. 23.9 mmolNH3 gMOF−1 in Mg-MOF-74 (ref. 49) and 23.5 mmolNH3 gMOF−1 in Ni_acryl_TMA,50 and Shi et al. 33.9 mmolNH3 gMOF−1 in LiCl-MIL-53,51 among others.52,53 But despite growing interest, not much has been done to leverage search algorithms to identify promising MOFs for NH3 storage. Thus, here we show how our developed VBO, a novel search algorithm for MOFs, can be used to fill such knowledge gaps. Furthermore, our analysis of the MOFs explored by our VBO provides new design rules to guide experimentalists developing MOFs for NH3 storage.
2. Simulation methods
2.1. MOF database
About 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures from the 2019 CoRE MOF database14 and about 3000 structures created earlier using ToBaCCo-3.0 (ref. 6) were used as a starting point to ultimately create a hybrid database of ∼10
000 structures from the 2019 CoRE MOF database14 and about 3000 structures created earlier using ToBaCCo-3.0 (ref. 6) were used as a starting point to ultimately create a hybrid database of ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures. These MOF sources are complementary. CoRE MOFs are extant structures with high, but non-systematic, chemical and structural diversity that tend to feature small pores.54 ToBaCCo MOFs are hypothesized structures with systematic, but medium, chemical and structural diversity that feature medium to large pores.54 All MOFs underwent characterization of their void fraction, surface area, and pore size distribution using zeo++. A probe radius of 1.3 Å was used by zeo++ to determine the accessibility of pores through the percolation algorithm.55 Then a probe of same size was used to determine the characteristic of the accessible pores. Note that the radius of 1.3 Å is adopted to match the kinetic radius of NH3.56 Failures during characterization calculations and assignment of charges to MOF atoms (see Section 2.2) ultimately reduced the total number of structures available for this work to around 10
000 structures. These MOF sources are complementary. CoRE MOFs are extant structures with high, but non-systematic, chemical and structural diversity that tend to feature small pores.54 ToBaCCo MOFs are hypothesized structures with systematic, but medium, chemical and structural diversity that feature medium to large pores.54 All MOFs underwent characterization of their void fraction, surface area, and pore size distribution using zeo++. A probe radius of 1.3 Å was used by zeo++ to determine the accessibility of pores through the percolation algorithm.55 Then a probe of same size was used to determine the characteristic of the accessible pores. Note that the radius of 1.3 Å is adopted to match the kinetic radius of NH3.56 Failures during characterization calculations and assignment of charges to MOF atoms (see Section 2.2) ultimately reduced the total number of structures available for this work to around 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
2.2. Monte Carlo simulations
Monte Carlo simulations were done using RASPA-2.0.57,58 Grand canonical Monte Carlo (GCMC) was used to predict adsorption loadings. Temperature and partial pressures of adsorbates in the gas phase were kept constant at the values relevant for the adsorption conditions of interest. Each simulation consisted of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 equilibration cycles, followed by 10
000 equilibration cycles, followed by 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 production cycles. Each cycle consisted of as many Monte Carlo moves as molecules there are in the simulation box, but never less than 20. Moves corresponded to insertion/deletion, translation, and rotation (and swap for mixture cases). The Widom insertion method,59 with at least 10
000 production cycles. Each cycle consisted of as many Monte Carlo moves as molecules there are in the simulation box, but never less than 20. Moves corresponded to insertion/deletion, translation, and rotation (and swap for mixture cases). The Widom insertion method,59 with at least 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 insertion moves, was used to calculate Henry's constants at the temperature of interest. Molecular interactions were modeled using the Lennard-Jones (LJ) and Coulomb potential. A cutoff of 12.8 Å was used for the LJ potential, and 12.0 Å for the Coulomb potential, after which distance Ewald summation was used.60,61 LJ parameters and charges for NH3 and N2 molecules were assigned according to the TraPPE force field62,63 for H2O according to the TIP4P model,64–66 whereas for H2 were obtained from the work by Darkrim and Levesque, including Feyman–Hibbs corrections.67,68 LJ parameters for MOF atoms were assigned according to the Dreiding force field,69 or universal force field70 if parameters from Dreiding were unavailable. LJ parameters for cross-interactions were obtained using Lorentz–Berthelot mixing rules. Note that the above LJ parameter selection have been used by Snurr and coworkers, and several others, to model NH3 adsorption in MOFs.71–75 Charges for MOF atoms were assigned based on the best method available for each MOF subset. Thus, charges in ToBaCCo MOFs were assigned in earlier work using the MBBB method,76 whereas for atoms in CoRE MOFs, charges were assigned using PACMOF.77 MBBB is based on DFT calculations on MOF building blocks, which are directly inherited by the MOF, when constructed by ToBaCCo. PACMOF, on the other hand, is a machine learning model that was trained by Snurr and coworkers, from DFT calculations on complete MOF unit cells, to predict charges in MOF atoms, with an accuracy of 0.02e in mean absolute error (R2 = 0.99). Moreover, the higher accuracy of PACMOF over other fast charge assignments was recently shown by Liu and Luan.78 Example comparison between simulated adsorption isotherms using the methods herein against experimental ones are shown in Fig. S2.†
000 insertion moves, was used to calculate Henry's constants at the temperature of interest. Molecular interactions were modeled using the Lennard-Jones (LJ) and Coulomb potential. A cutoff of 12.8 Å was used for the LJ potential, and 12.0 Å for the Coulomb potential, after which distance Ewald summation was used.60,61 LJ parameters and charges for NH3 and N2 molecules were assigned according to the TraPPE force field62,63 for H2O according to the TIP4P model,64–66 whereas for H2 were obtained from the work by Darkrim and Levesque, including Feyman–Hibbs corrections.67,68 LJ parameters for MOF atoms were assigned according to the Dreiding force field,69 or universal force field70 if parameters from Dreiding were unavailable. LJ parameters for cross-interactions were obtained using Lorentz–Berthelot mixing rules. Note that the above LJ parameter selection have been used by Snurr and coworkers, and several others, to model NH3 adsorption in MOFs.71–75 Charges for MOF atoms were assigned based on the best method available for each MOF subset. Thus, charges in ToBaCCo MOFs were assigned in earlier work using the MBBB method,76 whereas for atoms in CoRE MOFs, charges were assigned using PACMOF.77 MBBB is based on DFT calculations on MOF building blocks, which are directly inherited by the MOF, when constructed by ToBaCCo. PACMOF, on the other hand, is a machine learning model that was trained by Snurr and coworkers, from DFT calculations on complete MOF unit cells, to predict charges in MOF atoms, with an accuracy of 0.02e in mean absolute error (R2 = 0.99). Moreover, the higher accuracy of PACMOF over other fast charge assignments was recently shown by Liu and Luan.78 Example comparison between simulated adsorption isotherms using the methods herein against experimental ones are shown in Fig. S2.†
2.3. Assessed performance metrics
| ΔNNH3 = NNH3ads − NNH3des | (1) |
Due to its technical simplicity, here we consider the release of ammonia to be done simply by heating the adsorbent to 400 K at 1 bar (Fig. 1a). Note that as having enough space in the MOF pore is paramount to this application, ΔNNH3 is expected to be strongly influenced by MOF textural features such as pore size, void fraction and so forth.
| αNH3 = (NNH3/yNH3)/((∑Ni)/(∑yi)) | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 H2
1 H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2 feed ratio and a conversion of 10%, here yNH3, yN2 and yH2 are assumed to be 0.06, 0.23, 0.71, respectively. Seeking to account for both adsorption and selectivity, here we use MATS as a performance metric where:
N2 feed ratio and a conversion of 10%, here yNH3, yN2 and yH2 are assumed to be 0.06, 0.23, 0.71, respectively. Seeking to account for both adsorption and selectivity, here we use MATS as a performance metric where:| MATS = αNH3 × NNH3 | (3) |
Note that selectivity, αNH, is a reflection of the attraction of the MOF to NH3 relative to N2 and H2, and hence is expected to be strongly influenced by chemistry. On the other hand, the adsorption capacity NNH3 at non-dilute conditions is expected to also be influenced by MOF pore space. Thus, the complete metric MATS is expected to be influenced by both MOF chemistry and textural features. Also note that diffusion selectivity is an important aspect of choosing a material for a membrane. This selectivity could be incorporated into the performance metric (or could be considered in a subsequent screening step). However, for the purpose of testing the VBO framework, we decided to focus on the adsorption aspects of the membrane.
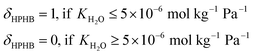 | (4) |
| MATSTH = MATS × δHPHB | (5) |
3. Diversity-driven MOF optimization
3.1. Workflow overview
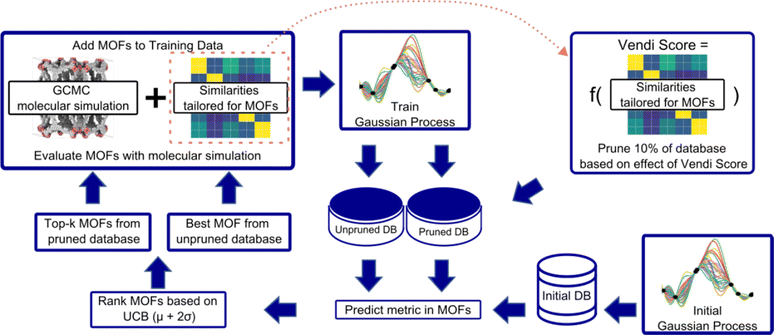
An overview of our diversity-driven MOF optimization/search framework is presented in Fig. 2. To start a MOF (design) optimization campaign, we randomly draw two MOFs and calculate their performance metrics using molecular simulations. These two datapoints are then used to train a Gaussian Process (GP) regression model88 whose kernel is designed to account for both chemistry and physics (see Section 3.2). The GP is trained to predict the performance metric and provide the uncertainty associated with the prediction. This fitted GP is then used to predict the performance of all MOFs in the hybrid database. From these predictions, our Vendi Bayesian Optimization (VBO) algorithm selects the next most promising MOF candidates for which to calculate the performance metric using molecular simulations.The first candidate that VBO selects is the one corresponding to the most “optimistic” performance prediction made by the trained GP. The remaining candidates are selected only after we prune 10% of the database. The pruning is done by taking out of the database 10% of the MOFs that, if added to the set of MOFs previously chosen by VBO and assessed via molecular simulations, would yield the lowest diversity change of that set. In our workflow, diversity of a MOF set is calculated using the Vendi score (see Section 3.3). The lower the Vendi score, the lower the diversity of the set. Thus, the MOFs removed from the database are those that would yield the lowest Vendi score if added to the set of MOFs that have been selected by our VBO algorithm.
Given that for each MOF the GP predicts a distribution of possible performance metric values, our VBO algorithm uses the upper confidence bound (UCB) criterion to assess the “potential” of a MOF. Specifically, the UCB is the mean value (μ) of the distribution of predictions for the MOF plus two times the standard deviation (σ). Ideally, upon evaluation with molecular simulation, some of the MOF selected by our VBO algorithm should have a higher value of the performance metric than the MOFs previously evaluated in this same manner. Regardless, upon completion of the evaluation with molecular simulation for MOFs that had been selected by the VBO algorithm, a new GP model is trained leveraging the newly generated data, and selection of new candidates is done again using the same procedure as described above. This procedure is repeated until either a preset target number of iterations is achieved or the highest value of the performance metric in the MOFs evaluated with molecular simulation no longer improves.
3.2. MOF representation
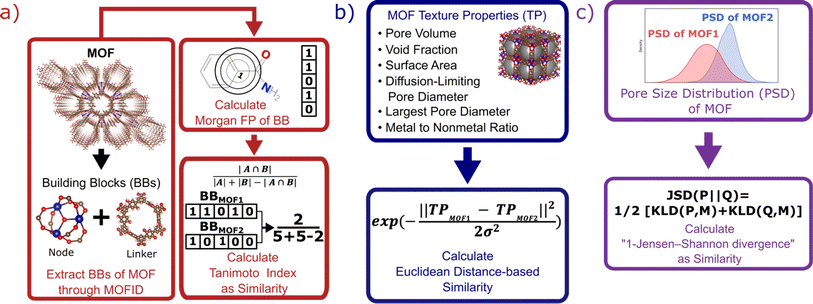
Each MOF is chemically characterized by the Morgan fingerprints89 of its constituent building blocks (nodes and linkers), which are extracted from each MOF using MOFid.7 MOFid provides the SMILES strings90 of the building blocks, which are used as input for RDKit to provide the fingerprints. Here, each fingerprint is a vector whose components describe the atom groups of the corresponding node or linker. Each MOF is also structurally characterized by its detailed pore size distribution and global textural properties usually used in the MOF field. Namely, specific pore volume, void fraction, specific surface area, largest and diffusion-limiting pore diameters, and metal-to-nonmetal content ratio. We design a specific similarity kernel for MOFs. This new kernel is the one we use for the GP and the calculation of the Vendi score in our VBO framework. More specifically, if we denote two different MOFs by x1 and x2, then the similarity between these MOFs is given by a specialized kernel function K that is an average of four different kernels, where each kernel Ki specializes in one particular aspect of MOFs and is weighted by a factor wi. Namely, the kernel similarity between two MOFs x1 and x2 is defined as:| K(x1, x2) = w1Knode(x1, x2) + w2Klinker(x1, x2) + w3Kglobal(x1, x2) + w4KPSD(x1, x2) | (6) |
K node and Klinker are each a kernel function computing the Tanimoto similarity91 between the Morgan fingerprints of either two nodes or two linkers, respectively (Fig. 3a). The Tanimoto similarities between Morgan fingerprints have been found to capture important differences in molecule chemistry, and has been shown effective at guiding machine learning models for search purposes in other areas.92 As a MOF could have more than one type of node or linker, we consider all possible pairwise comparisons and use the average value of Knode or Klinker. On the other hand, Kglobal operates on the global textural properties, and is defined to be the exponential of the Euclidean distance between the two vectors containing the (normalized) values of the above properties for the two MOFs being compared (Fig. 3b). This is analogous to what Simon and coworkers did for COFs.93 Finally, KPSD is a new kernel proposed by us, which computes the difference between the pore size distributions (PSDs) of the two MOFs being compared. We do this by using the Jensen–Shannon divergence (JSD).94 Given two PSDs P and Q, this function returns:
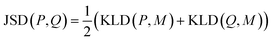 | (7) |
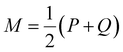 is a mixture distribution of the original two P and Q and:
is a mixture distribution of the original two P and Q and: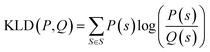 | (8) |
3.3. Vendi score
The Vendi score (VS) is key to encourage our optimization framework to find many diverse solutions, hence avoiding commitment to a single MOF design “solution” that might be infeasible to produce and test experimentally. The VS is a function whose input is the n × n similarity matrix K representing data points in a set of size n. The VS is calculated as the exponential of the Shannon entropy of the normalized eigenvalues of K, denoted by λi, as follows: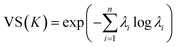 | (9) |
Friedman and Dieng39 showed that the VS is a mathematically well-defined diversity metric and quantifies the effective number of unique elements in a set.39 Here, the elements of the similarity matrix are calculated using eqn (6), meaning that the GP model and the VS use the same underlying mathematical object. To keep the output of the kernel function consistent across calculations of the VS, we set the weights wi in eqn (6) to all be equal to 0.25. However, note that the weights in eqn (6) take different values when training the GP model, where they are optimized for prediction.
3.4. Vendi Bayesian optimization (VBO) framework
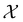 , where
, where 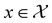 , and if f is a “black-box” function that returns the scalar value of the property or performance metric of interest (i.e.,
, and if f is a “black-box” function that returns the scalar value of the property or performance metric of interest (i.e., 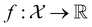 ), then we aim to find the MOF x* that maximizes the value of the performance metric. More formally, we find x* such that:
), then we aim to find the MOF x* that maximizes the value of the performance metric. More formally, we find x* such that: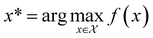 | (10) |
The above makes f an objective function that models the mapping between a given MOF and its performance metric. Here f is approximated by a GP that iteratively improves its “understanding” of f based on evaluations of f for specific MOFs x. Here, evaluating f(x) means running molecular simulations to calculate the relevant performance metric for a given MOF x. However, our VBO framework is also amenable to experimental work, where performance metrics are measured via experiments instead of molecular simulations. In each case, our VBO framework enables finding the optimal MOF x* in as few evaluations as possible, to overcome time and/or cost constraints associated with simulations or experiments.
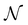 such that:
such that: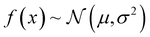 | (11) |
| α(x) = μ + 2σ. | (12) |
This simple expression elegantly captures the balance between exploration of MOFs we are uncertain about (with high σ), and exploitation of MOFs predicted to yield high performance (with high μ). In addition to its interpretability, Taw and Neaton96 demonstrated good optimization performance of the above acquisition function to optimize methane uptake capacity of MOFs. At each iteration of Bayesian optimization, we find the MOF that maximizes the UCB score to evaluate f(x) with. We repeat this process until our evaluation budget is depleted, each time updating the GP and the UCB score with the newly observed MOFs.
| ΔVS = VS(S ∪ {x}) − VS(S) | (13) |
If x is different from the data points in S, querying x will add more diversity to our data set, as reflected by a large ΔVS. If, on the other hand, x is similar to the points in S, ΔVS will be small. At each iteration, we compute ΔVS for each of the remaining candidate MOFs, and remove the MOFs that yield the lowest ΔVS until the remaining pool of candidates is reduced by ten percent. We thus reduce the effective search space at each iteration, removing candidates that are too similar to those already acquired.
This modification of traditional Bayesian optimization aims at building a diverse set of high-performance MOFs. While this increase level of exploration does not guarantee improved optimization performance, we do not necessarily sacrifice the top MOF either. As the diversity-aware pruning step is reset at each iteration, if we have found a region in our search space that contains very good candidates, our acquisition function allows us to come back to this region (i.e., zeroing in on the top MOF) once other promising regions have been explored. We can also think of this strategy as searching over multiple promising regions at the same time.
4. Results and discussion
4.1. Expressiveness of the MOF-specific kernel
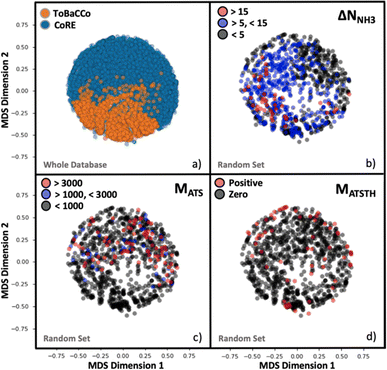
Although the representation of a MOF is inherently multidimensional, the plots in Fig. 4 maps MOFs onto a reduced two-dimensional space, by applying multidimensional scaling (MDS)97 to the covariance matrix of the MOFs, which was calculated using the kernel defined earlier by eqn (6). MDS conveys the similarity-dependent original distances between MOFs in multidimensional space, so that in Fig. 4 similar MOFs appear close to each other. From Fig. 4a, the complementary of CoRE MOFs (blue points) and our ToBaCCo MOFs (orange points) is apparent as the groups separate into individual regions. The usual differences between extant CoRE MOFs and hypothesized MOFs such as our ToBaCCo MOF have been pointed out previously in work by others such as Kulik and coworkers.54 For instance, CoRE MOFs tend to feature smaller pores and a more diverse selection of metals. ToBaCCo MOFs exhibit a systematic variation in textural properties, focusing on metals Cr, Zr, Mn, Co, Cu, and Zn. Therefore, the observed segregation in Fig. 4a indicates that our kernel captures meaningful similarities/differences between MOFs.Analogously, we present reduced dimensionality plots but only for a random subset of 1000 MOFs uniformly extracted from the ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hybrid database, and for which the performance metrics pertinent to NH3 storage, removal during plasma-assisted synthesis, and capture from air (ΔNNH3, MATS and MATSTH, respectively) were calculated using molecular simulation. Upon coloring the points based on the value of each performance metric in the corresponding MOF, it is apparent that segregation also tends to occur on the basis of performance (Fig. 4b–d). For instance, Fig. 4b shows MOFs with ΔNNH3 < 5 mmol g−1 locating in an outer ring, MOFs with 5 mmol g−1 < ΔNNH3 < 15 mmol g−1 locating in the inner region, and MOFs with ΔNNH3 > 15 mmol g−1 locating in a lower-right cluster. Such segregation indicates how well our measure of similarity (i.e., our kernel) is conducive to learning.
000 hybrid database, and for which the performance metrics pertinent to NH3 storage, removal during plasma-assisted synthesis, and capture from air (ΔNNH3, MATS and MATSTH, respectively) were calculated using molecular simulation. Upon coloring the points based on the value of each performance metric in the corresponding MOF, it is apparent that segregation also tends to occur on the basis of performance (Fig. 4b–d). For instance, Fig. 4b shows MOFs with ΔNNH3 < 5 mmol g−1 locating in an outer ring, MOFs with 5 mmol g−1 < ΔNNH3 < 15 mmol g−1 locating in the inner region, and MOFs with ΔNNH3 > 15 mmol g−1 locating in a lower-right cluster. Such segregation indicates how well our measure of similarity (i.e., our kernel) is conducive to learning.
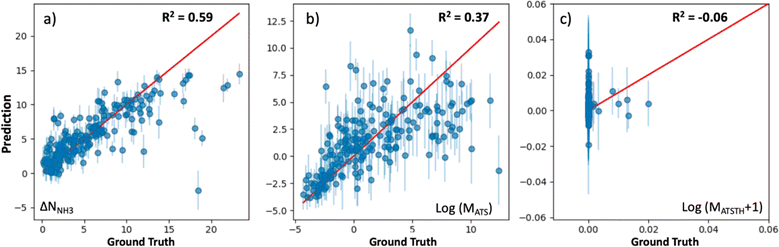
The extent at which our kernel facilitates learning is illustrated in Fig. 5, which shows parity plots comparing the prediction of the performance metrics NNH3, MATS and MATSTH by corresponding GP models trained on molecular simulation data of the 1000 random MOF subset. The GPs trained to predict ΔNNH3 and MATS (Fig. 5a and b) present relatively similar correlations between their predictions and the actual values (i.e., ground truth) of the corresponding performance metrics. Namely, R2 values of 0.59 and 0.37 for ΔNNH3 and MATS, respectively. On the other hand, the GP trained for the MATSTH case seems to face higher difficulty in learning to predict the performance metric, which is reflected by an R2 value of −0.06 (Fig. 5c). Such difficulty is partly due to the exceptional roughness of MATSTH as a function of MOF chemistry/structure—which partly motivated the selection of this metric for our testing. The roughness of MATSTH stems from the rather binary character of the metric, which is either zero or positive based on whether the MOF is deemed hydrophobic or not based on the threshold value of KH2O, resulting in discrete changes to MATSTH that are difficult to capture by machine learning models. Yet, as we will demonstrate shortly, our VBO framework remains effective at optimizing these metrics, including, perhaps surprisingly, MATSTH.
At this point, let us note that the optimized weights (wi) for the GP models (Table S3†) confirm our hypotheses of what MOF aspects control performance for each application. For instance, the chemical similarity kernel Knode weighs 0.97 in the model that predicts MATSTH but only weighs 0.02 in the model that predicts ΔNNH3. By contrast, KPSD weighs 0.37 in the model that predicts ΔNNH3, but only weighs 0.01 in the model that predicts MATSTH. On the other hand, all kernels weigh rather similarly in the model that predicts MATS.
4.2. Statistical testing of VBO efficacy
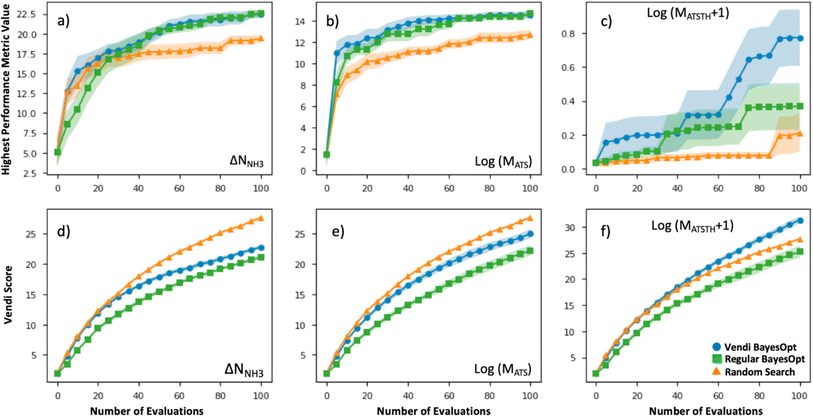
The efficacy of VBO was statistically assessed by simulating our workflow (Fig. 2) ten times on the subset of randomly selected 1000 MOFs, to iteratively optimize MOF design for the ΔNNH3, MATS and MATSTH metrics. During each run, two MOFs were randomly selected to be the initial training set, and 100 MOFs were evaluated in 20 batches of five MOFs each iteration (i.e., when 10% of the MOF subset was evaluated, the run stopped). Each time our VBO workflow was run, an analogous run without the Vendi score-based pruning (i.e., a regular Bayes optimization run) was done in parallel for comparison, as well as random search consisting of the evaluation of 100 randomly selected MOFs within the subset. The lines in Fig. 6 present the average progress of the VBO (blue), Bayesian optimization (green) and random search (orange) runs, whereas the corresponding shaded areas represent the corresponding standard errors.As evidenced by Fig. 6, although the uncertainty region for VBO and Bayesian optimization tend to overlap, on average VBO did equal or better than Bayesian optimization, when assessed based on the highest value for the metric encountered by the end of 100 evaluations. Notably, VBO outperformed Bayesian optimization for the evaluation of the MATSTH metric for NH3 capture from air. On the other hand, both VBO and Bayesian optimization clearly do better on average than random search when compared by the abovementioned criterion. Furthermore, the uncertainty regions for the latter two methods and random search barely overlap, suggesting that in a worst-case scenario VBO and Bayesian optimization would do at least as well as a best-case scenario random search that explores ten percent of the available design space.
But the most significant difference between VBO and Bayesian optimization is the more diverse exploration of the design space by VBO. This fact is evidenced by the consistently higher Vendi score among evaluated MOFs as VBO progresses compared to Bayesian optimization. As expected, random search tends to result in the highest diversity among evaluated MOFs as the search progresses. But it is surprising that for the optimization of MATSTH our VBO ended up on average with a higher diversity of evaluated MOFs than random search. Ultimately, the average behavior of the Vendi score in VBO versus Bayesian optimization is indicative that VBO is bound to create a more diverse pool of promising MOFs for a given application.
4.3. Full database search for MOFs for NH3 storage
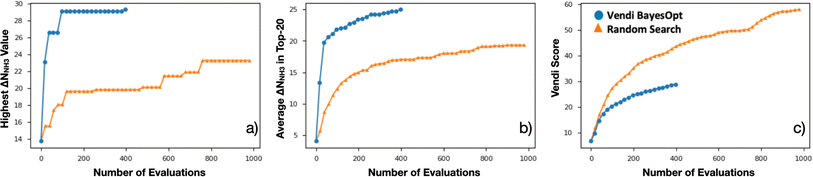
Encouraged by the statistical efficacy of our VBO framework, we decided to perform a full VBO run on the complete hybrid database (i.e., ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs) to optimize ΔNNH3. Specifically, to find MOFs with potential for NH3 storage, considering storage at 1 bar with storage/release through a 300 K to 400 K thermal swing. Fig. 7a presents the progress of the performed VBO run of 20 iterations (each iteration corresponds to a batch of 20 MOFs), comparing it against a random search (technically consisting of the previously randomly selected 1000 MOFs on which VBO was previously tested in Section 4.2). Evidently, VBO greatly outperforms random search, with the former identifying MOFs with ΔNNH3 values approaching as high as 30 mmolNH3 gMOF−1, whereas the latter did not identify MOFs with ΔNNH3 values higher than ∼23 mmolNH3 gMOF−1.
000 MOFs) to optimize ΔNNH3. Specifically, to find MOFs with potential for NH3 storage, considering storage at 1 bar with storage/release through a 300 K to 400 K thermal swing. Fig. 7a presents the progress of the performed VBO run of 20 iterations (each iteration corresponds to a batch of 20 MOFs), comparing it against a random search (technically consisting of the previously randomly selected 1000 MOFs on which VBO was previously tested in Section 4.2). Evidently, VBO greatly outperforms random search, with the former identifying MOFs with ΔNNH3 values approaching as high as 30 mmolNH3 gMOF−1, whereas the latter did not identify MOFs with ΔNNH3 values higher than ∼23 mmolNH3 gMOF−1.
Notably, the outperformance of VBO relative to random search occurred despite VBO terminating early at ca. 400 evaluations. This early termination was made because the highest ΔNNH3 value within the evaluated MOFs did not change significantly after around 80 evaluations. However, note that one should not be tempted to consider subsequent MOF evaluations after the 80th evaluation point as wasteful, as these evaluations enabled to strengthen the pool of promising MOF designs for NH3 storage. A fact that is evidenced by the steady improvement in the average ΔNNH3 for the “top-20” evaluated MOFs from the 80th to the 400th evaluation (Fig. 7b). Importantly, this improvement in average ΔNNH3 was accomplished while steadily improving the diversity of the evaluated MOF as indicated by the steady improvement in the Vendi score within the same range of evaluations (Fig. 7c). The latter creates confidence that the pool of promising MOFs to be suggested for future synthesis and experimental testing to be more diverse than provided by other methods.
4.4. Data-driven MOF design rules
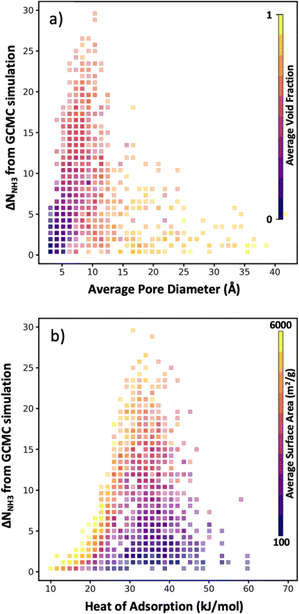
As noted earlier, a benefit of computational MOF screening is the emergence of structure–performance relationships, which are useful to establish design rules that experimentalists could leverage to conceive adsorbent designs of their own (not even necessarily for MOFs). Importantly, the emergence of these relationships allows extracting value from computational screenings independently of the success in synthesizing and testing the specific MOF designs recommended by the screening. However, the nature of the emerging relationships is empirical, and thus depend on a sufficiently large number of observations being made to create clear trends. Conveniently, here, while the number of evaluated MOFs is lower than in other screening studies that relied on exhaustive search, the bias of our selection method towards “good” MOFs allow us to still define well the “interesting” region of the relationship relevant to optimize the performance metric of interest.For instance, although in Fig. 8a there is a dearth of data for MOFs with average pore diameter (APD) larger than 14 Å, it is apparent that the optimal average pore diameter and for NH3 storage at the conditions herein proposed is 10 Å. Note that the scarcity of data for MOFs with APD larger than 14 Å is due to reluctance by the VBO algorithm to pick MOFs in that range of APD, probably due to rapidly learning that APDs larger than 14 Å tend not to optimize ΔNNH3. An APD of 10 Å seems to compromise confinement effects (i.e., overlap of interaction potentials) to enhance NH3 attraction to the pore walls and having sufficient space to accommodate NH3 molecules. To be sure, an APD of 10 Å should be interpreted as necessary, and not as a sufficient condition to optimize ΔNNH3, as evidenced by the wide range of ΔNNH3 values that can be observed for that APD value. The color coding in Fig. 8a suggests that such variability in ΔNNH3 at APD equal to 10 Å is partly explained by variations in MOF void fraction—with MOFs with void fraction around 0.7 tending to appear at the top. In other words, given two MOFs with APD equal to 10 Å, the one with higher void fraction probably corresponds to a higher ΔNNH3, again partly due to the implication that higher void fraction allows more space to accommodate NH3 molecules.
On the other hand, note that while attraction of NH3 to the pore walls (as reflected by the heat of adsorption Qst) is desired, too strong an attraction is detrimental to ΔNNH3 as it prevents the adsorbed NH3 molecules to be easily released. From our collected data, it seems that a Qst of 33 kJ mol−1 is optimal for ammonia storage at the conditions herein proposed (Fig. 8b). Analogous to our APD analysis, a Qst of 33 kJ mol−1 should be taken only as a necessary but not sufficient condition to optimize ΔNNH3. Indeed, there is a wide range of ΔNNH3 values at Qst equal 33 kJ mol−1. The color coding in Fig. 8b partly explains this variability on the basis of surface area variations—with MOFs with surface area around 4000 m2 g−1 tending to appear at the top, as they provide a larger number of sites with optimal interaction strength. Note that inspecting Fig. S6,† it seems that a Qst value around 33 kJ mol−1 enables recovering up to 95% of the NH3 molecules adsorbed at the storage conditions.
We acknowledge, however, that a design rule centered around Qst is somewhat abstract as this quantity does not depend only on MOF chemistry, but also on MOF structure. In an attempt to provide some chemistry-based MOF design rules for NH3 storage, we decided to explore trends in elemental composition among outstanding MOFs. Specifically, for each element in the periodic table, we calculated its average percent content in the top-14 MOFs evaluated with molecular simulation and compared this value with the corresponding average percent content in all ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs in the database (Fig. S7†). Then we used a t-test to assess the statistical significance of observed differences.
000 MOFs in the database (Fig. S7†). Then we used a t-test to assess the statistical significance of observed differences.
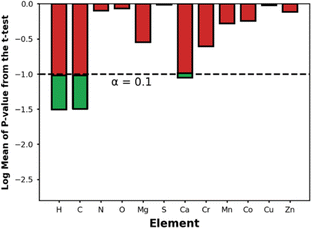
Fig. 9 shows the p-values for the t-test for the elements present in the top-14 MOFs. Using a p-value threshold of 0.1, it seems that C, H, and Ca are elements that are, with statistical significance, more abundant within the top-14 MOFs for NH3 storage than in MOFs at large. Using our understanding of MOF structure, we rationalize that the higher abundance of C, H is probably just a reflection of the optimal APD for ammonia storage being larger than the median APD in the database—i.e., larger pores imply longer linkers, hence more C and H content. On the other hand, we could not find an alternative explanation for the higher abundance of Ca within the outstanding MOFs, suggesting a primarily chemical effect—after all, CaCl2 is a popular ammonia adsorbent.98 To be sure, though, due to the role other MOF features play on ΔNNH3, the presence of Ca alone, as we will see below, does not guarantee the maximization of ΔNNH3.
4.5. Promising MOF designs
Contingent on adsorption simulation accuracy, now we proceed to present some promising MOF designs identified by our VBO run. The top-20 MOFs are listed in Table S4,† while the top-6 MOFs are presented in Fig. 10. Three of these MOFs correspond to hypothesized designs (top row), and the remaining three correspond to extant designs that have been realized synthetically (bottom row). The free energy of the hypothesized designs in Fig. 10 was calculated using the Frenkel–Ladd method as discussed in earlier work,99 resulting in free energies below 4.4 kJ mol−1 per atom, which per discussion in ref. 100 suggests high synthesizability likelihood. The MOFs in Fig. 10 present ΔNNH3 values in the 26.6–29.3 mmolNH3 gMOF−1. Consistent with observed structure–performance relationships (Section 4.4), these MOFs exhibit APDs around 10 Å, void fractions around 0.7 and surface areas around 3900 m2 g−1. As for metals, note that although Ca was more abundant in the top-14 MOFs than in the whole database, the six best MOF designs featured Cr, Cu, Mn, Zn, and Co instead. Probably, because the textural properties of Ca MOFs were not “ideal.” This situation underscores the importance of optimizing a MOF design both structurally and chemically.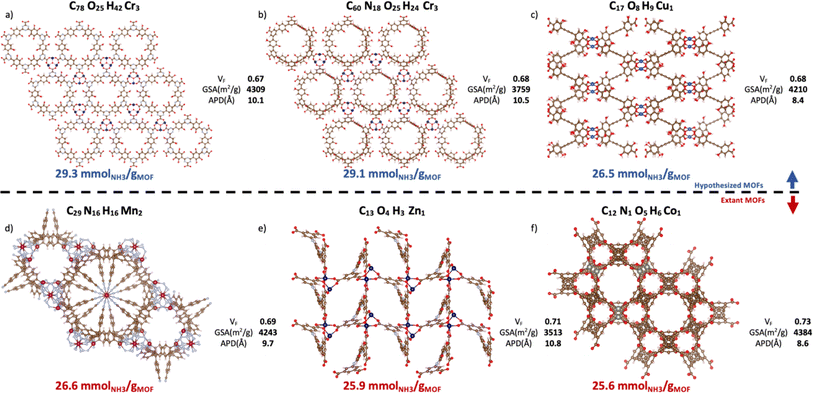 | ||
| Fig. 10 Top-6 MOFs ranked by ΔNNH3 value. Hypothesized (a–c) and extant MOFs (d–f) are in the top and bottom rows, respectively. VF, GSA, and APD represent, respectively, the void fraction, gravimetric surface areas, and average pore diameter from pore size distribution. The CSD refcode and corresponding publication can be found in Table S5† with (a) n = 1, (b) n = 2, (c) n = 4, (d) n = 3, (e) n = 5, (f) n = 6, where n is the MOF ranking. The three hypothesized MOFs are potentially synthesizable per the free energy criterion by Anderson and Gómez-Gualdrón (Table S6†).100 Ca MOFs appear in the top-14 but not in top-6 presumably due to suboptimal textural properties. | ||
To put the predicted ΔNNH3 for MOFs in Fig. 10 in the context of other MOFs experimentally tested in the literature, first let us reiterate that while NH3 adsorption in MOFs have been consistently evaluated considering 300 K and 1 bar as the storage condition, such consistency has not existed for the release condition. Thus, a direct comparison is not possible. However, note that, with the exception of LiCL-MIL-53, the highest reported NH3 loading at 300 K and 1 bar is 23.9 mmolNH3 gMOF−1, so that even assuming total recovery at the release conditions, the predicted ΔNNH3 for the MOFs in Fig. 10 is still higher. As for LiCl-MIL-53, its measured 33.9 mmolNH3 gMOF−1 loading at 300 K and 1 bar is accompanied by a reported Qst around 78 kJ mol−1.51 Based on the relationship between heat of adsorption and percent NH3 recovered (Fig. S6†) emerged in the study herein, a best case scenario for this Qst (i.e., 50% recovery) would yield a ΔNNH3 around 16.9 mmolNH3 gMOF−1 for this MOF, which again is below the predicted ΔNNH3 for the MOFs in Fig. 10.
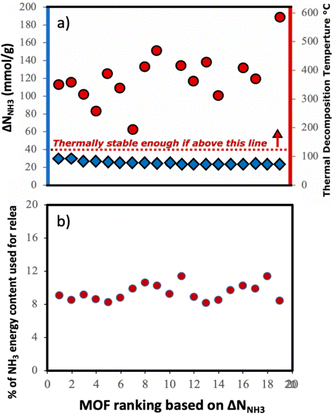
Although here we focused on optimizing the MOF design to maximize ΔNNH3, other factors also play a role when using a MOF for a given application. Considering that we propose a thermal swing to release NH3, it is important to assess the thermal stability of the MOFs to encourage experimental testing. Accordingly, in Fig. 11a, we show the thermal decomposition temperature Td of each of the top-20 MOFs (ΔNNH3 ranging from 23 to 30 mmolNH3 gMOF−1), as predicted by an ANN model developed by Nandy et al.,101 as available in the MOFsimplify website.102 This model makes the prediction based on the revised autocorrelation (RAC) descriptors of the MOFs, and was trained using reported thermogravimetric analysis (TGA) data for 3131 MOFs, with a mean absolute error (MAE) of 47 K. Considering this MAE and that the lowest predicted Td was 466 K (which is 66 K higher than the upper temperature for the thermal swing), it seems that the suggested MOF designs are likely to withstand the proposed operation conditions.
Finally, to inform considerations about energy efficiency and economic viability, we estimated the energy required to release each kilogram of stored NH3 with the proposed thermal swing, ΔQrelease, using:
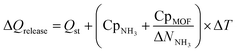 | (14) |
Assuming that the energy stored in NH3 corresponds to that of the H2 that is released from NH3via cracking, the energy content of NH3 is 22.5 MJ kgNH3−1.105 The latter implies that with the proposed MOF designs a penalty between 8% and 12% of the NH3 energy content would be used to release the stored NH3. For context, an analogous calculation can be done to estimate energy penalty for liquid NH3 storage, which can be estimated based on the latent heat of condensation for NH3 (1.4 MJ kgNH3−1)106 and the energy to cool down NH3 from 300 K down to 240 K. The above results in an estimated penalty of 7% of the NH3 energy content. Considering that adsorptive NH3 storage at ambient conditions can bypass other technological requirements such as insulation, toxicity, corrosion, or issues such as boil-off,43,45 among others, the operation conditions proposed herein for adsorptive NH3 storage (and materials to achieve so) seem to merit reasonable consideration.
5. Conclusions
In this work, we developed a novel framework for efficiently finding a diverse set of optimal MOFs for applications involving ammonia adsorption. Our framework, called Vendi Bayesian Optimization (VBO), seamlessly combines traditional Bayesian optimization with the Vendi score, a diversity measure rooted in ecology and quantum mechanics. VBO is also made possible by the introduction of a novel similarity function in the space of MOFs that accounts for both chemistry and structure. We used this similarity function both for the GP used by Bayesian optimization and to compute the Vendi score. Our framework enabled the efficient discovery of several optimal MOFs that are distinct from one another, and that perform better than MOFs previously studied experimentally for NH3 storage. Our analysis of the results of VBO highlights new design rules that MOF experimentalists can leverage to design optimal MOFs for the above application. We believe VBO introduces new useful capabilities for the efficient exploration of the combinatorially large MOF design space for the discovery of MOFs with desired properties. Importantly, our VBO framework is amenable to applications beyond ammonia adsorption. We leave the exploration of these applications as future work.Data availability
Data for this article, including the code are available at vertaix/VBO at https://github.com/vertaix/VBO. Data sources are available at https://wustl.box.com/s/3jkz8ksu9l3d1hqikir4olainke9wc5t and Jupyter notebooks to reproduce our figures are available at https://github.com/vertaix/VBO/tree/main/notebooks/Recreate%20figures.Author contributions
D. A. G.-G. and A. B. D. designed, supervised and acquired funding for the project. T.-W. L. and Q. N. conducted the work under D. A. G.-G. and A. B. D. supervision. T.-W. L. primarily focused on materials selection and characterization, data acquisition via molecular simulation, and analysis of simulation data in the context of target applications. Q. N. primarily focused on building the machine learning model and designing the search algorithm. D. A. G.-G. led the manuscript writing. All authors participated in discussions and intellectually contributed during the progress of the project. All authors edited and contributed to the editing of the manuscript and agreed on its final version.Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. A. G.-G. and A. B.-D. acknowledge funding from the National Science Foundation through grant OAC-2118201 (HDR: Institute for Data-Driven Dynamic Design). A. B. D. acknowledges Schmidt Sciences for the AI2050 Early Career Fellowship. Molecular simulations were possible thanks to the Mio supercomputer cluster at the Colorado School of Mines.References
- D. A. Gomez-Gualdron, O. V. Gutov, V. Krungleviciute, B. Borah, J. E. Mondloch, J. T. Hupp, T. Yildirim, O. K. Farha and R. Q. Snurr, Computational design of metal–organic frameworks based on stable zirconium building units for storage and delivery of methane, Chem. Mater., 2014, 26, 5632–5639 CrossRef CAS.
- J. Zheng, J. Tian, D. Wu, M. Gu, W. Xu, C. Wang, F. Gao, M. H. Engelhard, J.-G. Zhang and J. Liu, et al., Lewis acid-base interactions between polysulfides and metal organic framework in lithium sulfur batteries, Nano Lett., 2014, 14, 2345–2352 CrossRef CAS PubMed.
- D. A. Gómez-Gualdrón, Y. J. Colón, X. Zhang, T. C. Wang, Y.-S. Chen, J. T. Hupp, T. Yildirim, O. K. Farha, J. Zhang and R. Q. Snurr, Evaluating topologically diverse metal–organic frameworks for cryo-adsorbed hydrogen storage, Energy Environ. Sci., 2016, 9, 3279–3289 RSC.
- X. Zhao, S. Liu, Z. Tang, H. Niu, Y. Cai, W. Meng, F. Wu and J. P. Giesy, Synthesis of magnetic metal-organic framework (MOF) for efficient removal of organic dyes from water, Sci. Rep., 2015, 5, 11849 CrossRef PubMed.
- A. Kirchon, L. Feng, H. F. Drake, E. A. Joseph and H.-C. Zhou, From fundamentals to applications: a toolbox for robust and multifunctional MOF materials, Chem. Soc. Rev., 2018, 47, 8611–8638 RSC.
- R. Anderson and D. A. Gómez-Gualdrón, Increasing topological diversity during computational “synthesis” of porous crystals: how and why, CrystEngComm, 2019, 21, 1653–1665 RSC.
- B. J. Bucior, A. S. Rosen, M. Haranczyk, Z. Yao, M. E. Ziebel, O. K. Farha, J. T. Hupp, J. I. Siepmann, A. Aspuru-Guzik and R. Q. Snurr, Identification schemes for metal–organic frameworks to enable rapid search and cheminformatics analysis, Cryst. Growth Des., 2019, 19, 6682–6697 CrossRef CAS.
- M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, The Reticular Chemistry Structure Resource (RCSR) database of, and symbols for, crystal nets, Acc. Chem. Res., 2008, 41, 1782–1789 CrossRef PubMed.
- M. Islamov, H. Babaei, R. Anderson, K. B. Sezginel, J. R. Long, A. J. H. McGaughey, D. A. Gomez-Gualdron and C. E. Wilmer, High-throughput screening of hypothetical metal-organic frameworks for thermal conductivity, npj Comput. Mater., 2023, 9, 11 CrossRef CAS.
- Y. J. Colón and R. Q. Snurr, High-throughput computational screening of metal-organic frameworks, Chem. Soc. Rev., 2014, 43, 5735–5749 RSC.
- A. Ahmed, S. Seth, J. Purewal, A. G. Wong-Foy, M. Veenstra, A. J. Matzger and D. J. Siegel, Exceptional hydrogen storage achieved by screening nearly half a million metal-organic frameworks, Nat. Commun., 2019, 10, 1568 CrossRef PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- C. M. Simon, J. Kim, D. A. Gomez-Gualdron, J. S. Camp, Y. G. Chung, R. L. Martin, R. Mercado, M. W. Deem, D. Gunter and M. Haranczyk, et al., The materials genome in action: identifying the performance limits for methane storage, Energy Environ. Sci., 2015, 8, 1190–1199 RSC.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling and J. S. Camp, et al., Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal–Organic Framework Database: CoRE MOF 2019, J. Chem. Eng. Data, 2019, 64, 5985–5998 CrossRef CAS.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Large-scale screening of hypothetical metal-organic frameworks, Nat. Chem., 2011, 4, 83–89 CrossRef PubMed.
- M. A. Addicoat, D. E. Coupry and T. Heine, AuToGraFS: automatic topological generator for framework structures, J. Phys. Chem. A, 2014, 118, 9607–9614 CrossRef CAS PubMed.
- S. Bureekaew and R. Schmid, Hypothetical 3D-periodic covalent organic frameworks: exploring the possibilities by a first principles derived force field, CrystEngComm, 2013, 15, 1551 RSC.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Development of a cambridge structural database subset: A collection of metal–organic frameworks for past, present, and future, Chem. Mater., 2017, 29, 2618–2625 CrossRef CAS.
- Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Topologically Guided, Automated Construction of Metal–Organic Frameworks and Their Evaluation for Energy-Related Applications, Cryst. Growth Des., 2017, 17, 5801–5810 CrossRef.
- J. Burner, J. Luo, A. White, A. Mirmiran, O. Kwon, P. G. Boyd, S. Maley, M. Gibaldi, S. Simrod and V. Ogden, et al., ARC–MOF: A Diverse Database of Metal-Organic Frameworks with DFT-Derived Partial Atomic Charges and Descriptors for Machine Learning, Chem. Mater., 2023, 35, 900–916 CrossRef CAS.
- S. Lee, B. Kim, H. Cho, H. Lee, S. Y. Lee, E. S. Cho and J. Kim, Computational Screening of Trillions of Metal-Organic Frameworks for High-Performance Methane Storage, ACS Appl. Mater. Interfaces, 2021, 13, 23647–23654 CrossRef CAS PubMed.
- B. Borah, H. Zhang and R. Q. Snurr, Diffusion of methane and other alkanes in metal-organic frameworks for natural gas storage, Chem. Eng. Sci., 2015, 124, 135–143 CrossRef CAS.
- D. Nazarian, J. S. Camp and D. S. Sholl, A Comprehensive Set of High-Quality Point Charges for Simulations of Metal–Organic Frameworks, Chem. Mater., 2016, 28, 785–793 CrossRef CAS.
- A. S. Rosen, S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein and R. Q. Snurr, Machine learning the quantum-chemical properties of metal–organic frameworks for accelerated materials discovery, Matter, 2021, 4, 1578–1597 CrossRef CAS.
- Y. G. Chung, P. Bai, M. Haranczyk, K. T. Leperi, P. Li, H. Zhang, T. C. Wang, T. Duerinck, F. You and J. T. Hupp, et al., Computational screening of nanoporous materials for hexane and heptane isomer separation, Chem. Mater., 2017, 29, 6315–6328 CrossRef CAS.
- P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff, R. Bounds, A. Gładysiak, P. Schouwink, S. M. Moosavi and M. M. Maroto-Valer, et al., Data-driven design of metal-organic frameworks for wet flue gas CO2 capture, Nature, 2019, 576, 253–256 CrossRef CAS PubMed.
- P. Bai, M. Y. Jeon, L. Ren, C. Knight, M. W. Deem, M. Tsapatsis and J. I. Siepmann, Discovery of optimal zeolites for challenging separations and chemical transformations using predictive materials modeling, Nat. Commun., 2015, 6, 5912 CrossRef CAS PubMed.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, The high-throughput highway to computational materials design, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- Y. G. Chung, D. A. Gómez-Gualdrón, P. Li, K. T. Leperi, P. Deria, H. Zhang, N. A. Vermeulen, J. F. Stoddart, F. You and J. T. Hupp, et al., In silico discovery of metal-organic frameworks for precombustion CO2 capture using a genetic algorithm, Sci. Adv., 2016, 2, e1600909 CrossRef PubMed.
- R. Turner, D. Eriksson, M. McCourt, J. Kiili, E. Laaksonen, Z. Xu and I. Guyon, Bayesian optimization is superior to random search for machine learning hyperparameter tuning: Analysis of the black-box optimization challenge, arXiv, 2021, preprint, arXiv:2104.10201, DOI:10.48550/arXiv.2104.10201.
- J. M. Hernández-Lobato, J. Requeima, E. O. Pyzer-Knapp and A. Aspuru-Guzik, Parallel and Distributed Thompson Sampling for Large-scale Accelerated Exploration of Chemical Space, arXiv, 2017, arXiv:1706.01825, DOI:10.48550/arXiv.1706.01825.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Bayesian reaction optimization as a tool for chemical synthesis, Nature, 2021, 590, 89–96 CrossRef CAS PubMed.
- L. Fang, E. Makkonen, M. Todorović, P. Rinke and X. Chen, Efficient Amino Acid Conformer Search with Bayesian Optimization, J. Chem. Theory Comput., 2021, 17, 1955–1966 CrossRef CAS PubMed.
- D. E. Graff, E. I. Shakhnovich and C. W. Coley, Accelerating high-throughput virtual screening through molecular pool-based active learning, Chem. Sci., 2021, 12, 7866–7881 RSC.
- W. Gao and C. W. Coley, The synthesizability of molecules proposed by generative models, J. Chem. Inf. Model., 2020, 60, 5714–5723 CrossRef CAS PubMed.
- R.-R. Griffiths and J. M. Hernández-Lobato, Constrained Bayesian optimization for automatic chemical design using variational autoencoders, Chem. Sci., 2020, 11, 577–586 RSC.
- N. Gantzler, A. Deshwal, J. R. Doppa and C. M. Simon, Multi-fidelity Bayesian optimization of covalent organic frameworks for xenon/krypton separations, Digital Discovery, 2023, 2, 1937–1956 RSC.
- M. Wang, W. Kong, R. Marten, X.-C. He, D. Chen, J. Pfeifer, A. Heitto, J. Kontkanen, L. Dada and A. Kürten, et al., Rapid growth of new atmospheric particles by nitric acid and ammonia condensation, Nature, 2020, 581, 184–189 CrossRef CAS PubMed.
- D. Friedman and A. B. Dieng, The Vendi Score: A Diversity Evaluation Metric for Machine Learning, arXiv, 2022, preprint, arXiv:2210.02410, DOI:10.48550/arXiv.2210.02410.
- J. Lim, C. A. Fernández, S. W. Lee and M. C. Hatzell, Ammonia and nitric acid demands for fertilizer use in 2050, ACS Energy Lett., 2021, 6, 3676–3685 CrossRef CAS.
- M. H. Hasan, T. M. I. Mahlia, M. Mofijur, I. M. Rizwanul Fattah, F. Handayani, H. C. Ong and A. S. Silitonga, A comprehensive review on the recent development of ammonia as a renewable energy carrier, Energies, 2021, 14, 3732 CrossRef CAS.
- C. Smith, A. K. Hill and L. Torrente-Murciano, Current and future role of Haber–Bosch ammonia in a carbon-free energy landscape, Energy Environ. Sci., 2020, 13, 331–344 RSC.
- B. Kanjilal, A. Masoumi, N. Sharifi and I. Noshadi, Ammonia harms and diseases: ammonia corrosion hazards on human body systems (liver, muscles, kidney, brain), in Progresses in ammonia: science, technology and membranes, Elsevier, 2024, pp. 307–324 Search PubMed.
- S. Giddey, S. P. S. Badwal, C. Munnings and M. Dolan, Ammonia as a renewable energy transportation media, ACS Sustain. Chem. Eng., 2017, 5, 10231–10239 CrossRef CAS.
- M. Al-Breiki and Y. Bicer, Technical assessment of liquefied natural gas, ammonia and methanol for overseas energy transport based on energy and exergy analyses, Int. J. Hydrogen Energy, 2020, 45, 34927–34937 CrossRef CAS.
- L. F. Herrera, D. D. Do and G. R. Birkett, Comparative simulation study of nitrogen and ammonia adsorption on graphitized and nongraphitized carbon blacks, J. Colloid Interface Sci., 2008, 320, 415–422 CrossRef CAS PubMed.
- S. Moribe, Z. Chen, S. Alayoglu, Z. H. Syed, T. Islamoglu and O. K. Farha, Ammonia Capture within Isoreticular Metal–Organic Frameworks with Rod Secondary Building Units, ACS Mater. Lett., 2019, 1, 476–480 CrossRef CAS.
- L. Guo, J. Hurd, M. He, W. Lu, J. Li, D. Crawshaw, M. Fan, S. Sapchenko, Y. Chen and X. Zeng, et al., Efficient capture and storage of ammonia in robust aluminium-based metal-organic frameworks, Commun. Chem., 2023, 6, 55 CrossRef CAS PubMed.
- D. W. Kim, D. W. Kang, M. Kang, J.-H. Lee, J. H. Choe, Y. S. Chae, D. S. Choi, H. Yun and C. S. Hong, High Ammonia Uptake of a Metal-Organic Framework Adsorbent in a Wide Pressure Range, Angew. Chem., Int. Ed., 2020, 59, 22531–22536 CrossRef CAS PubMed.
- D. W. Kim, D. W. Kang, M. Kang, D. S. Choi, H. Yun, S. Y. Kim, S. M. Lee, J.-H. Lee and C. S. Hong, High Gravimetric and Volumetric Ammonia Capacities in Robust Metal-Organic Frameworks Prepared via Double Postsynthetic Modification, J. Am. Chem. Soc., 2022, 144, 9672–9683 CrossRef CAS PubMed.
- Y. Shi, Z. Wang, Z. Li, H. Wang, D. Xiong, J. Qiu, X. Tian, G. Feng and J. Wang, Anchoring LiCl in the Nanopores of Metal-Organic Frameworks for Ultra-High Uptake and Selective Separation of Ammonia, Angew. Chem., Int. Ed., 2022, 61, e202212032 CrossRef CAS PubMed.
- X. Han, W. Lu, Y. Chen, I. da Silva, J. Li, L. Lin, W. Li, A. M. Sheveleva, H. G. W. Godfrey and Z. Lu, et al., High Ammonia Adsorption in MFM-300 Materials: Dynamics and Charge Transfer in Host-Guest Binding, J. Am. Chem. Soc., 2021, 143, 3153–3161 CrossRef CAS PubMed.
- L. Luo, Y. Liu, Z. Wu, J. Liu, X. Cao, J. Lin, R. Ling, X. Luo and C. Wang, Macromolecular-metal complexes induced by Co(II) with polymer and flexible ligands for ammonia uptake compared with MOFs, Chem. Eng. J., 2022, 448, 137626 CrossRef CAS.
- S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun., 2020, 11, 4068 CrossRef CAS PubMed.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- Q. Wei, J. M. Lucero, J. M. Crawford, J. D. Way, C. A. Wolden and M. A. Carreon, Ammonia separation from N2 and H2 over LTA zeolitic imidazolate framework membranes, J. Membr. Sci., 2021, 623, 119078 CrossRef CAS.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, RASPA: molecular simulation software for adsorption and diffusion in flexible nanoporous materials, Mol. Simul., 2016, 42, 81–101 CrossRef CAS.
- D. Dubbeldam, A. Torres-Knoop and K. S. Walton, On the inner workings of Monte Carlo codes, Mol. Simul., 2013, 39, 1253–1292 CrossRef CAS.
- B. Widom, Some topics in the theory of fluids, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- Infinite crystals, accurate and efficient calculation.
- N. Karasawa and W. A. Goddard, Acceleration of convergence for lattice sums, J. Phys. Chem., 1989, 93, 7320–7327 CrossRef CAS.
- B. Chen and J. I. Siepmann, Transferable Potentials for Phase Equilibria. 3. Explicit-Hydrogen Description of Normal Alkanes, J. Phys. Chem. B, 1999, 103, 5370–5379 CrossRef CAS.
- L. Zhang and J. I. Siepmann, Development of the trappe force field for ammonia, Collect. Czech. Chem. Commun., 2010, 75, 577–591 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- M. A. González and J. L. F. Abascal, The shear viscosity of rigid water models, J. Chem. Phys., 2010, 132, 096101 CrossRef PubMed.
- J. L. Aragones and C. Vega, Plastic crystal phases of simple water models, J. Chem. Phys., 2009, 130, 244504 CrossRef CAS PubMed.
- B. Guillot and Y. Guissani, Quantum effects in simulated water by the Feynman–Hibbs approach, J. Chem. Phys., 1998, 108, 10162–10174 CrossRef CAS.
- F. Darkrim and D. Levesque, Monte Carlo simulations of hydrogen adsorption in single-walled carbon nanotubes, J. Chem. Phys., 1998, 109, 4981–4984 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, DREIDING: a generic force field for molecular simulations, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- P. Z. Moghadam, P. Ghosh and R. Q. Snurr, Understanding the effects of preadsorbed perfluoroalkanes on the adsorption of water and ammonia in mofs, J. Phys. Chem. C, 2015, 119, 3163–3170 CrossRef CAS.
- F. L. Oliveira, C. Cleeton, R. Neumann Barros Ferreira, B. Luan, A. H. Farmahini, L. Sarkisov and M. Steiner, CRAFTED: An exploratory database of simulated adsorption isotherms of metal-organic frameworks, Sci. Data, 2023, 10, 230 CrossRef CAS PubMed.
- P. Ghosh, K. C. Kim and R. Q. Snurr, Modeling water and ammonia adsorption in hydrophobic metal–organic frameworks: single components and mixtures, J. Phys. Chem. C, 2014, 118, 1102–1110 CrossRef CAS.
- D. Dokur and S. Keskin, Effects of force field selection on the computational ranking of mofs for CO2 separations, Ind. Eng. Chem. Res., 2018, 57, 2298–2309 CrossRef CAS PubMed.
- R. Anderson, A. Biong and D. A. Gómez-Gualdrón, Adsorption isotherm predictions for multiple molecules in MOFs using the same deep learning model, J. Chem. Theory Comput., 2020, 16, 1271–1283 CrossRef CAS PubMed.
- E. Argueta, J. Shaji, A. Gopalan, P. Liao, R. Q. Snurr and D. A. Gómez-Gualdrón, Molecular Building Block-Based Electronic Charges for High-Throughput Screening of Metal-Organic Frameworks for Adsorption Applications, J. Chem. Theory Comput., 2018, 14, 365–376 CrossRef CAS PubMed.
- S. Kancharlapalli, A. Gopalan, M. Haranczyk and R. Q. Snurr, Fast and Accurate Machine Learning Strategy for Calculating Partial Atomic Charges in Metal-Organic Frameworks, J. Chem. Theory Comput., 2021, 17, 3052–3064 CrossRef CAS PubMed.
- S. Liu and B. Luan, Benchmarking various types of partial atomic charges for classical all-atom simulations of metal-organic frameworks, Nanoscale, 2022, 14, 9466–9473 RSC.
- M. Aziz, A. T. Wijayanta and A. B. D. Nandiyanto, Ammonia as effective hydrogen storage: A review on production, storage and utilization, Energies, 2020, 13, 3062 CrossRef CAS.
- Q. Wang, J. Guo and P. Chen, Recent progress towards mild-condition ammonia synthesis, J. Energy Chem., 2019, 36, 25–36 CrossRef.
- G.-F. Han, F. Li, Z.-W. Chen, C. Coppex, S.-J. Kim, H.-J. Noh, Z. Fu, Y. Lu, C. V. Singh and S. Siahrostami, et al., Mechanochemistry for ammonia synthesis under mild conditions, Nat. Nanotechnol., 2021, 16, 325–330 CrossRef CAS PubMed.
- Y. Guan, H. Wen, K. Cui, Q. Wang, W. Gao, Y. Cai, Z. Cheng, Q. Pei, Z. Li and H. Cao, et al., Light-driven ammonia synthesis under mild conditions using lithium hydride, Nat. Chem., 2024, 16, 373–379 CrossRef CAS PubMed.
- K. van't Veer, Y. Engelmann, F. Reniers and A. Bogaerts, Plasma-Catalytic Ammonia Synthesis in a DBD Plasma: Role of Microdischarges and Their Afterglows, J. Phys. Chem. C, 2020, 124, 22871–22883 CrossRef.
- Y. Wang, W. Yang, S. Xu, S. Zhao, G. Chen, A. Weidenkaff, C. Hardacre, X. Fan, J. Huang and X. Tu, Shielding Protection by Mesoporous Catalysts for Improving Plasma-Catalytic Ambient Ammonia Synthesis, J. Am. Chem. Soc., 2022, 144, 12020–12031 CrossRef CAS PubMed.
- N. V. Namboothiri and A. R. Soman, Consequence assessment of anhydrous ammonia release using CFD-probit analysis, Process Saf. Prog., 2018, 37, 525–534 CrossRef CAS.
- P. Z. Moghadam, D. Fairen-Jimenez and R. Q. Snurr, Efficient identification of hydrophobic MOFs: application in the capture of toxic industrial chemicals, J. Mater. Chem. A, 2016, 4, 529–536 RSC.
- H. Zhang and R. Q. Snurr, Computational Study of Water Adsorption in the Hydrophobic Metal–Organic Framework ZIF-8: Adsorption Mechanism and Acceleration of the Simulations, J. Phys. Chem. C, 2017, 121, 24000–24010 CrossRef CAS.
- C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning, The MIT Press, 2005 Search PubMed.
- D. Rogers and M. Hahn, Extended-connectivity fingerprints, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- D. Weininger, SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules, J. Chem. Inf. Model., 1988, 28, 31–36 CrossRef CAS.
- P. Willett, J. M. Barnard and G. M. Downs, Chemical Similarity Searching, J. Chem. Inf. Comput. Sci., 1998, 38, 983–996 CrossRef CAS.
- F. Mukadum, Q. Nguyen, D. M. Adrion, G. Appleby, R. Chen, H. Dang, R. Chang, R. Garnett and S. A. Lopez, Efficient Discovery of Visible Light-Activated Azoarene Photoswitches with Long Half-Lives Using Active Search, J. Chem. Inf. Model., 2021, 61, 5524–5534 CrossRef CAS PubMed.
- N. Gantzler, A. Deshwal, J. R. Doppa and C. Simon, Multi-fidelity Bayesian Optimization of Covalent Organic Frameworks for Xenon/Krypton Separations, Digital Discovery, 2023, 2, 1937–1956 RSC.
- J. Lin, Divergence measures based on the Shannon entropy, IEEE Trans. Inf. Theory, 1991, 37, 145–151 CrossRef.
- P. Auer, Using confidence bounds for exploitation-exploration trade-offs, J. Mach. Learn. Res., 2002, 3, 397–422 Search PubMed.
- E. Taw and J. B. Neaton, Accelerated discovery of ch4 uptake capacity metal–organic frameworks using bayesian optimization, Adv. Theory Simul., 2022, 5, 2100515 CrossRef CAS.
- M. A. A. Cox and T. F. Cox, Multidimensional Scaling, in Handbook of data visualization, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008, pp. 315–347 Search PubMed.
- X. Tian, J. Qiu, Z. Wang, Y. Chen, Z. Li, H. Wang, Y. Zhao and J. Wang, A record ammonia adsorption by calcium chloride confined in covalent organic frameworks, Chem. Commun., 2022, 58, 1151–1154 RSC.
- R. Freitas, M. Asta and M. de Koning, Nonequilibrium free-energy calculation of solids using LAMMPS, Comput. Mater. Sci., 2016, 112, 333–341 CrossRef CAS.
- R. Anderson and D. A. Gómez-Gualdrón, Large-Scale Free Energy Calculations on a Computational Metal–Organic Frameworks Database: Toward Synthetic Likelihood Predictions, Chem. Mater., 2020, 32, 8106–8119 CrossRef CAS.
- A. Nandy, C. Duan and H. J. Kulik, Using Machine Learning and Data Mining to Leverage Community Knowledge for the Engineering of Stable Metal-Organic Frameworks, J. Am. Chem. Soc., 2021, 143, 17535–17547 CrossRef CAS PubMed.
- A. Nandy, G. Terrones, N. Arunachalam, C. Duan, D. W. Kastner and H. J. Kulik, MOFSimplify, machine learning models with extracted stability data of three thousand metal-organic frameworks, Sci. Data, 2022, 9, 74 CrossRef CAS PubMed.
- Y. Zou, L. Li, Y. Li, S. Chen, X. Xie, X. Jin, X. Wang, C. Ma, G. Fan and W. Wang, Restoring Cardiac Functions after Myocardial Infarction-Ischemia/Reperfusion via an Exosome Anchoring Conductive Hydrogel, ACS Appl. Mater. Interfaces, 2021, 13, 56892–56908 CrossRef CAS PubMed.
- F. A. Kloutse, R. Zacharia, D. Cossement and R. Chahine, Specific heat capacities of MOF-5, Cu-BTC, Fe-BTC, MOF-177 and MIL-53 (Al) over wide temperature ranges: Measurements and application of empirical group contribution method, Microporous Mesoporous Mater., 2015, 217, 1–5 CrossRef CAS.
- J. S. Cardoso, V. Silva, R. C. Rocha, M. J. Hall, M. Costa and D. Eusébio, Ammonia as an energy vector: Current and future prospects for low-carbon fuel applications in internal combustion engines, J. Cleaner Prod., 2021, 296, 126562 CrossRef CAS.
- D. Erdemir and I. Dincer, A perspective on the use of ammonia as a clean fuel: Challenges and solutions, Int. J. Energy Res., 2021, 45, 4827–4834 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Force field details, details on surrogate model selection, additional details on VBO campaigns, additional structure–property relationships, additional details about promising MOF designs for NH3 storage. See DOI: https://doi.org/10.1039/d4sc03609c |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |