Engineering MOF/carbon nitride heterojunctions for effective dual photocatalytic CO₂ conversion and oxygen evolution reactions

Abstract

Photocatalysis appears as one of the most promising avenues to shift towards sustainable sources of energy, owing to its ability to transform solar light into chemical energy, e.g. production of chemical fuels via oxygen evolution (OER) and CO₂ reduction (CO₂RR) reactions. Ti metal–organic frameworks (MOFs) and graphitic carbon nitride derivatives, i.e. poly-heptazine imides (PHI) are appealing CO₂RR and OER photo-catalysts respectively. Engineering of an innovative Z-scheme heterojunction by assembling a Ti-MOF and PHI offers an unparalleled opportunity to mimick an artificial photosynthesis device for dual CO₂RR/OER catalysis. Along this path, understanding of the photophysical processes controlling the MOF/PHI interfacial charge recombination is vital to fine tune the electronic and chemical features of the two components and devise the optimum heterojunction. To address this challenge, we developed a modelling approach integrating force field Molecular Dynamics (MD), Time-Dependent Density Functional Theory (TD-DFT) and Non-Equilibrium Green Function DFT (NEGF-DFT) tools with the aim of systematically exploring the structuring, the opto-electronic and transport properties of MOF/PHI heterojunctions. We revealed that the nature of the MOF/PHI interactions, the interfacial charge transfer directionality and the absorption energy windows of the resulting heterojunctions can be fine tuned by incorporating Cu species in the MOF and/or doping PHI with mono- or divalent cations. Interestingly, we demonstrated that the interfacial charge transfer can be further boosted by engineering MOF/PHI device junctions and application of negative bias. Overall, our generalizable computational methodology unravelled that the performance of CO₂RR/OER photoreactors can be optimized by chemical and electronic tuning of the components but also by device design based on reliable structure–property rules, paving the way towards practical exploitation.

---

Introduction

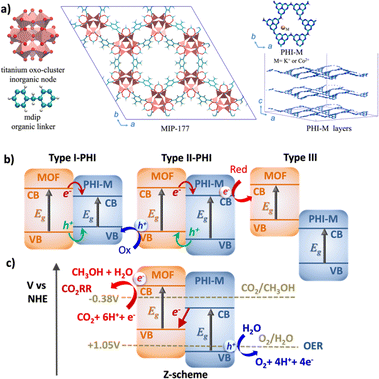
Photocatalysis, with its remarkable capability to efficiently harness and convert solar light into chemical energy, stands out as one the most relevant technologies for the usage of environmentally and friendly energy carrier.^1,2 Oxygen evolution reaction (OER)^3,4 and CO₂ reduction reaction (CO₂RR)^5,6 are among the most appealing catalytic processes since they involve the production of H₂ and CH₃OH respectively, representing an important source of green fuels meanwhile mitigating the environmental negative impact of the greenhouse gas CO₂. Graphitic carbon nitride (g-C₃N₄) materials have emerged over the last decade as prominent OER catalysts owing to their strong absorption in the visible (VIS) region, easy processability, long-lived photogenerated states, and high stability upon operating conditions.^7–9 In particular, the highly condensed g-C₃N₄ known as 2D layered poly-heptazine imides (PHI) materials (Fig. 1a) can host different doping metal ions in their porosities to tune their photophysical properties.^10–12 Besides its promising OER electrocatalysis performance,¹³ our recent computational study supported by experimental testing revealed PHI–Co²⁺ as an excellent OER photocatalyst, which was attributed to a favorable OER thermodynamics and to a red-shifted absorption in the VIS region.¹⁴ On the other hand, metal–organic frameworks (MOFs) have been recently envisaged as promising CO₂RR photocatalysts.^15–17 The high chemical and pore size/shape tunability of this family of hybrid materials offers a unique opportunity to design host porous frameworks with high CO₂ affinity. Moreover, their potentially large porosity can not only enable effective transport of reactants/products but also host Cu-based co-catalysts.¹⁸ Typically, the 3D Ti-MOF MIP-177 made of Ti₁₂O₁₅ clusters, formate ions, and 3,3′,5,5′-tetracarboxydiphenylmethane (mdip) ligands (Fig. 1a) was shown to exhibit high photoconductivity^19,20 and good catalytic activity for the dehydrogenation of formic acids.²¹ Further, its constitutive 1.1 nm-sized channel along the c-direction is large enough to host concomitantly Cu ions/complexes and CO₂ species. The incorporation of Cu single-atom catalysts in the MOF pores (Cu species@MOF) has been demonstrated as an effective strategy to enhance the stability, reaction product selectivity, and catalytic activity of this family of materials.^22–24 More specifically, recent Density Functional Theory (DFT) calculations revealed that the incorporation of Cu species in the pores of MIP-177, especially as Cu⁺ (Cu⁺@MOF) boosts the CO₂RR activity, as evidenced by its calculated low energy barriers for CO₂ conversion to CH₃OH.²⁵

Fig. 1 (a) Illustration of the MOF (MIP-177(Ti)) structure along the [001] direction and of the PHI–M layered structures. Representation of (b) the standard heterojunctions that can be envisaged by assembling MOF and PHI–M (M = metal ions), and (c) the innovative target Z-scheme MOF/PHI–M heterojunction for a simultaneous photocatalytic CO₂RR/OER process. Note that the labelling Type I-PHI and Type II-PHI denotes that the electron transfer directionality is pointing towards the PHI.

Notably, the CO₂ reduction mechanism implies many complex multi-electron redox steps with the intricate eight-electron/proton coupling steps towards the formation of CH₃OH, one of the most appealing energy vector, and therefore calls for an efficient charge generation and separation.²⁶ The construction of an innovative Z-scheme heterojunction by assembling CO₂RR MOF and OER PHI photocatalysts is envisioned as an innovative strategy to boost the solar CO₂ conversion into CH₃OH. Such an unprecedented MOF/PHI heterojunction is expected to ensure the transport of the electron produced at the lower antenna OER site (PHI) towards the hole of the higher antenna CO₂RR site (MOF) as well as a charge separation at the heterojunction interface to avoid a charge recombination of the photogenerated carriers.^27–29 Notably, the band alignment of the two associated photocatalysts ultimately governs the efficiency of this charge separation process and thus drives the functionality of the corresponding heterojunction, as illustrated in Fig. 1b.³⁰ For a Type-I heterojunction the charge flow of both holes and electrons is pointing towards the material with a lower gap, which acts as catalyst for both reduction and oxidation reactions. For a Type-II heterojunction, electrons or holes are transferred from one of the components to the other, thus contributing to a more efficient charge separation, whereas in the broken gap Type-III type of alignments no charge transfer (CT) takes place between the two components. Despite Type-II heterojunction is the most common architecture considered for photocatalytic processes, the need of an efficient charge transfer for both electrons and holes from one component to the other where the oxidation/reduction processes occur significantly reduces its efficiency. Indeed, when the donor valence band (VB) and the acceptor conductance band (CB) edges are close enough in energy, it is possible to promote the photogenerated electrons from the CB of the donor to the VB of the acceptor, thus forming the so-called Z-scheme architecture (Fig. 1c). This type of heterojunctions is of particular interest in the field of photocatalysis since it is expected to enhance the oxidation/reduction ability of the photogenerated electrons/holes, meanwhile avoiding the charge recombination due to the circuit close achieved by the donor-to-acceptor charge transfer (as represented by the central red arrow in Fig. 1b).^31–33 This process mimics the phenomena of photosynthesis where the electron transfer between photosystems involved in the process exhibits an identical Z-pathway as the one depicted in Fig. 1b.^34,35 The Z-scheme heterojunction thus ensures the selectivity of the charge transport of the electrons produced in both components.^36–38

MOF-based heterojunctions built by assembling MOFs with other co-catalysts, e.g. metal oxides, metal disulfides, or nanocarbon materials among others have been already exploited in the field of photocatalysis.^39–41 The unparalleled MOF/carbon nitride heterojunctions offer the opportunity to mitigate the intrinsic fast hole recombination of g-C₃N₄ derivatives by providing alternative electron transfer pathways,^42,43 thus paving the way to catalyze complex reactions such as H₂ production,⁴⁴ CO₂RR,⁴⁵ or pollutant degradation.⁴⁶ Besides the MOF/PHI systems we envisage here specifically for the target CO₂RR and OER applications, the development of an effective Z-scheme MOF-based heterojunctions has been only rarely considered in the field of photocatalysis so far,^47,48 mainly due to the lack of understanding of the charge transfer at the interface of the heterojunction, hardly achieved by conventional experimental techniques. Modelling can shed light on the photophysical processes governing the charge generation and separation within such a complex heterojunction. However, although, quantum calculations have been routinely applied to explore the electronic and catalytic properties of PHI^12,14,49,50 and a myriad of MOFs including our selected MOF MIP-177 (ref. 19, 21 and 51) individually, we are not aware of any theoretical studies on MOF/PHI heterojunctions.

This mostly comes from the complexity to construct a reliable atomistic MOF/PHI interface model of the corresponding heterojunction alongside its expected large size (>10k atoms) that still makes unfeasible the application of standard quantum methods to probe its electronic properties due to prohibitive computational costs. To address this challenge, we devised a numerical approach integrating force-field Molecular Dynamics (MD) and DFT/Time-dependent DFT (TD-DFT)/Non-Equilibrium Green Function Theory (NEGF)-DFT simulations to systematically explore the interfacial structuring and electronic charge transfer between the two components of the heterojunctions assembling the pristine and Cu⁺ loaded-MIP-177 (Cu⁺@MOF) with the pristine PHI–H and its metal-ions doped derivatives PHI–K⁺ and PHI–Co²⁺.This approach starts with the construction of large-scale atomistic interfacial models for the diverse MOF/PHI heterojunctions by assembling the MIP-177 [001] surface (c-oriented along the main channel) and PHI structures via force-field MD simulations in order to gain insight into the interactions between the two components and the interfacial structuring. DFT and TD-DFT methods are then applied on representative MOF/PHI heterojunction cluster models cut from these force field optimized MOF/PHI heterojunction models to determine their opto-electronic properties including their band alignment and their absorption characteristics. NEGF-DFT simulations further compute the charge transport within a device built by sandwiching the MOF/PHI interface cluster models between two Au electrodes to mimic the scenario of a photocatalytic cell.^52,53 It is worth mentioning that despite most of computational works dealing with modelling of MOF/graphitic carbon composites have been devoted to analyze the interactions between the two components and eventually adsorbed guest molecules by employing both large scale atomistic composite model^54,55 or cluster^56,57 models; this is the first time that a complete study of such MOF/carbon nitride interactions is reported at different scales including their implications in the opto-electronic and electronic transport properties. Besides delivering unprecedented insight into the interfacial structuring and the electronic transfer taking place in MOF/PHI heterojunctions, this innovative computational methodology evidenced the incorporation of Cu ions in the MOF pores and the doping of PHI by Co ions as a suitable strategy to enhance the heterojunction stability and light harvesting capacity, meanwhile offering the possibility to promote a Z-scheme electron transfer between components via the application of a negative bias.

Computational method

Construction of the MOF/PHI–M heterojunction models

MIP-177 surface slab models. The experimentally-determined crystal structure of MIP-177 (ref. 19) was first geometry optimized (atom positions and cell parameters fully relaxed) at the DFT level using the Vienna Ab initio Simulation Package (VASP, 5.4 version).⁵⁸ These calculations considered the generalized gradient approximation (GGA) Perdew–Burke–Ernzerhof (PBE) functional⁵⁹ and Grimme's DFT-D3 method⁶⁰ for the empirical dispersion (see ESI Section S1.1.1† for computational details).

The resulting DFT-optimized cell parameters were found to be in good agreement with the corresponding experimental data.¹⁹ A MOF surface model was cleaved from the DFT-optimized crystal structure along the crystallographic [001] plane to envisage the exposition of the hexagonal channel to PHI (M = H, K⁺ and Co²⁺). A length of ∼50 Å along the z-direction was considered to avoid surface to surface interactions while a vacuum of ∼20 Å was also added in this direction to prevent interactions between the slab and its periodic images. To achieve zero net dipole moment the surface was rebuilt accordingly. Since the surface termination state of the MOF is not known experimentally, herein, the slab models were terminated following the same strategy we employed previously for UiO-66(Zr)⁶¹ with the metal (Ti) exposed to the surface terminated by a OH⁻ groups while the remaining H⁺ atoms form a terminal formate group resulting from the cutting of the organic linker (see Fig. S1†). An additional MOF surface model was also constructed along the crystallographic [110] plane and used to rank the energy stability of these two possible surface models (see ESI Fig. S1 and S3†). Theoretically, different surface models can be created by cleaving the MOF along distinct crystallographic planes. Herein, we considered two MOF surfaces cleaved along the [001] and [110] crystallographic planes in such a way to offer an optimum exposure to the PHI along the hexagonal channel of 11 Å and the narrow pore of 3 Å respectively where the CO₂ molecules are expected to migrate in order to access the catalytic active sites present in the MOFs pores.

These MOF surface models were then DFT-geometry-optimized using the same level of theory and parameters than for the bulk MOF. The surface energy for the two slab models (E_surf) was further calculated using eqn (1):

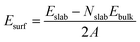where, E_slab and E_bulk are the energies of the slab and bulk crystal while N_slab is the number of atoms in the slab, and A is the total area of the slab.⁶² The [001] surface with an associated energy E_surf = 53.6 J m⁻², was found to be more energetically favourable than the [110] surface (E_surf = 74.2 J m⁻²) and was therefore selected to construct the heterojunctions formed with PHI–M.

The atomic partial charges for the MOF [001] slab surface model were calculated using the density derived electrostatic and chemical (DDEC6) method as implemented in the CHARGEMOL module.⁶³ The universal force-field (UFF) parameters⁶⁴ were selected to describe the inter-molecular interactions for the MOF slab model while the UFF parameters for the intra-molecular interactions were adjusted to reproduce the structural features of both DFT-optimized MOF crystal structure and DFT-optimized MOF surface slab model (see ESI Section S1.1.2† for computational details and parameters). The x- and y-dimensions of the resulting slab surface model were then expanded twice to achieve a dimension of 47.1 × 47.1 × 61.5 Å for further processing the construction of the MOF/PHI–M heterojunctions at the force field level.

PHI–M models. The periodic PHI–M (M = H, K⁺ and Co²⁺) structure models with a dimension of 21.4 × 12.4 × 17.5 Å made of 5 layers with interlayer spacing of 3.3 Å were first geometry optimized at the DFT level (see ESI† for details). Fig. S5† illustrates the DFT-optimized geometry of the three explored PHI–M. One observes that the metal-doping induces a substantial distortion of the PHI-layer compared to the well-ordered arrangement of PHI–H, this effect being more pronounced for PHI–K⁺ (see Section S1.1.3† for detailed analysis).

The atomic partial charges for PHI–M were equally calculated using the DDEC6 method.⁶⁵ For the description of the PHI–M at the force field level, the intra-molecular potential parameters of the liquid simulation-all atom (OPLS-AA),⁶⁶ force field were slightly adjusted to reproduce the DFT-optimized PHI–M structures. Note that the intermolecular potential parameters for the PHI structure were directly taken from OPLS,⁶⁶ while these terms for K⁺ and Co²⁺ cations were taken from UFF.⁶⁴ The corresponding overall parameters are listed in Table S9.†

The simulation box of these PHI–M structure models was reshaped in the x and y directions 47.1 × 47.1 × L_z (L_z = 35, 29.1, 30.1 Å for M = H, K⁺, and Co²⁺, respectively) to match the lattice parameters of the MOF slab model prior to construct the heterojunction MOF/PHI–M models.

MOF/PHI–M heterojunction models. The PHI–M structures were added on top of the MOF surface with an initial separating MOF/PHI–M distance of 5 Å. The non-bonded MOF/PHI–M surface interactions were described by the sum of coulombic and Lennard-Jones (LJ) van der Waals terms, while the system was treated as fully flexible with the intra-molecular parameters described above for each individual system. The LJ cross-interaction parameters were estimated using the Lorentz–Berthelot mixing rule.⁶⁷ These short-range interactions were truncated at a cutoff radius of 14 Å while the long-range electrostatic interactions were handled using the Ewald summation technique.⁶⁸ These MOF/PHI–M models undergo an equilibrium procedure comprised of a maximum of 10 000 steps of energy minimization, 1 ns of MD NPT simulations, and 1 ns of MD NVT simulation to obtain equilibrium configurations. The equilibrium configuration of the system can be verified by plotting the total energy of the system as a function of time (Fig. S7†). All the simulations were performed at 298 K using a Berendsen thermostat and a pressure coupling was applied anisotropic for the area in the x–y plane and z-dimension using a Parrinello–Rahman thermostat.

These MD simulations were performed using the GROMACS (version 5.1.4) simulation package.⁶⁹ Analysis of the MOF/PHI–M interactions as well as the PHI–M structuring was gained by averaging the data collected over the MD runs.

DFT and TD-DFT calculations on representative MOF/PHI–M heterojunction cluster models

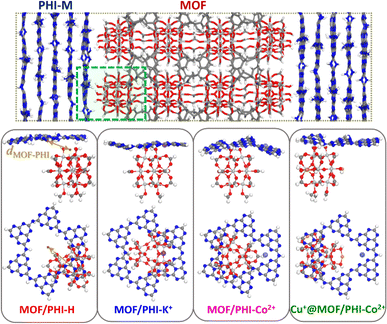
A representative heterojunction cluster model for the three MOF/PHI–M interfaces was cut from the corresponding force field MD-optimized heterojunction models. The MOF region comprises a Ti₁₂O₁₅ oxocluster with terminal Ti–OH functions in interaction with PHI–M while the lateral sides and bottom sides are terminated by formate moieties and methylidene groups to ensure the charge neutrality of the cluster model (see Fig. 3a). The PHI–M region is represented by a PHI ring hosting in the case of PHI–K⁺ and PHI–Co²⁺ one cation, whereas the initial connections between the PHI rings were saturated by H atoms. For the construction of the Cu⁺@MOF model, the MOF structure was loaded with Cu⁺ in such a way that two neighboring Ti atoms initially bounded to one formate group are coordinated by two OH groups and one Cu⁺ along the [001] direction following a scheme as the one adopted by R. J. Behm and coworkers to model Cu⁺ loaded UiO-66(Zr) materials.²² The overall shape of the MOF is unchanged and uniform Cu⁺ loading is obtained along the c-direction (Fig. S8†). The Cu⁺ species was incorporated in the MOF/PHI–Co²⁺ heterojunction cluster model following the same procedure to generate the Cu⁺@MOF/PHI–Co²⁺ heterojunction cluster model.

These heterojunction cluster models were geometry optimized at the DFT level using the procedure detailed in ESI (Section 1.2.1),† and they are illustrated in Fig. 3b. The electronic structure characterization of the heterojunction cluster models was further pursued by relying on a hybrid DFT-Hartree–Fock (HF) scheme. We first checked that the calculated opto-electronic properties (i.e. band edge energies, energy gaps and absorption features) of the isolated MOF and PHI–M cluster models were able to reproduce its corresponding bulk properties (see Table S11, Fig. S9 and S10†). Unrestricted calculations were performed for the PHI–Co²⁺-based heterojunction cluster models (MOF/PHI–Co and Cu⁺@MOF/PHI–Co) in their high spin configuration (S = 3/2) since it is more stable with respect to their low spin state (1.59 eV of difference between the ground state energies of the high vs. low spin configurations of the isolated PHI–Co²⁺ cluster), in line with the electron paramagnetic resonance (EPR) measurements previously reported for PHI–Co²⁺ compounds.¹³ Furthermore, the spin polarized calculations employed for the geometry optimizations of these clusters also converged in their high spin configurations.

Simplified TD-DFT (sTD-DFT) formalism implemented in the grimme-lab/stda set of tools^70,71 was applied to the MOF/PHI–M heterojunction cluster model (owing to its relatively large size and large number of states needed to cover the full UV-VIS-nIR spectrum) to assess their excited state properties. We carefully checked that the sTD-DFT approach leads to similar simulated absorption characteristic than that obtained by means of a full TD-DFT implementation (see Fig. S11, S12 and Table S12†).

NEGFT-DFT calculations on the device heterojunction models

For computing the transport properties across the device heterojunctions we relied on the same computational strategy we applied in our previous works to study relatively large junctions.^72–74 Within this approach, the geometry optimized heterojunction cluster models described above were sandwiched between gold electrodes represented by semi-infinite Au(111) wires (see a schematic representation of the device heterojunction in Fig. S14†) maintaining periodic conditions in all three directions. In this system, we considered 5 × 5 Au(111) slabs. The distance between neighboring Au(111) wires in the transport and transverse directions was maintained longer than 12 Å to avoid interactions with their corresponding images along these axes. The unit cell dimension of the device heterojunction model was geometry relaxed along the transport direction and kept fixed in the transverse directions. In these device heterojunction models, PHI–M interacts with the Au electrode via van der Waals contacts, while the termination of the bottom part of the device heterojunction cluster model (MOF side) is adjusted in a way to form Au–O covalent bond with the Au-electrode, as achieved by releasing its terminal methylidene moieties, thus allowing the neighboring O atoms to contact the Au surface (see Fig. S14†). Although few examples of oxygen-gold bonds have been described in the literature, the formation of O–Au bonds, which form self-assembled monolayers with properties similar to S–Au bonds, has recently been reported.⁷⁵ We systematically explored the impact of the number of Au–O bonds formed between Au and the MOF (from one to three contact points) for the MOF/PHI–K⁺ system, on the transmission and current–voltage (J–V) characteristics of the device heterojunction (see Section S1.3†). This systematic exploration enabled to define that the device junction characteristics involving two contact points between the MOF and Au converge with respect to the ones bearing three contacts (see Fig. S15 and 16† for more details). This guided the application of such two-contacted MOF-Au geometry for the other device MOF/PHI–M heterojunctions. All calculations were performed using the Keldysh non-equilibrium Green's function formalism combined with DFT (DFT-NEGF)^76–78 as implemented in the Quantum ATK package.⁷⁹ More theoretical details about the models employed to compute the transport properties along the device heterojunctions are provided in Section S1.3 of the ESI.†

Results and discussion

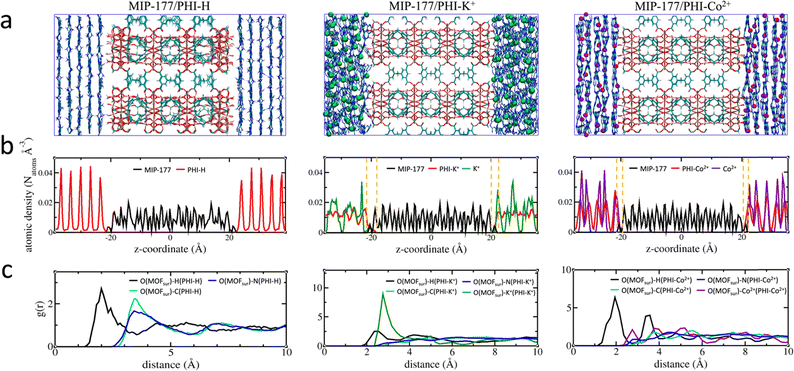
An illustration of the force field MD-constructed MOF/PHI–M heterojunction models is delivered in Fig. 2a alongside their density profile plotted along the direction normal to the MOF [001] surface (Fig. 2b), i.e. the z-axis. MOF is located at the center of the simulation box with the PHI–M on the left and right sides of MIP-177. The atomic density profile for PHI–H exhibits sharp peaks separated by about 3.3 Å supporting the well-ordered organization of its constitutive layer including the one in direct contact with the MOF surface. The behavior of PHI–K⁺ and PHI–Co²⁺ sharply differs with a much less-structured atomic density profile associated to the disordering of their layers driven by the presence of the cations in their pores, that is even more pronounced for PHI–K⁺. This trend remains the same than that observed for the DFT-optimized pristine PHI–M structures (Section S1.1.3 of the ESI†), in particular the MOF surface does not induce a higher degree of twisting of the PHI–M layers (see Table S10†). The atomic density of the three PHI–M systems further decays to zero at the proximity of the MOF surface. Interestingly, we can distinguish a zone (highlighted by dashed lines in Fig. 2b) where the MOF and both PHI–K⁺ and PHI–Co²⁺ atoms overlap. This is not the case for PHI–H. The overlap length is slightly longer for PHI–K⁺ (∼3.3 Å) compared to PHI–Co²⁺ (∼2.5 Å) demonstrating that the higher degree of structural disordering of PHI–K⁺ enables the PHI-backbone to more effectively pack at the MOF surface. The calculated MOF/PHI–M interaction energy calculated from the equilibrium MD simulations confirmed that the MOF/PHI–K⁺ and MOF/PHI–Co²⁺ heterojunctions are more stabilized than MOF/PHI–H (see Table S13†). The atomic density plots also show that both K⁺ and Co²⁺ can distribute close to the MOF surface thus contributing to the enhancement of the MOF/PHI interactions. Analysis of the radial distribution functions (RDF) plotted for the most representative MOF/PHI–M interacting atom pairs (Fig. 2c) confirmed that in addition to the interactions between the hydrogen atom of PHI–M and the oxygen atom of the OH groups present at the MOF surface, both cations establish strong interactions with the same oxygen atoms of MOF associated to an average separating distance of ∼2.8 Å.

Fig. 2 Force field MD simulations on the MOF/PHI–M heterojunctions (a) illustration of the atomistic models. Atom color codes: Ti (pink), O (red), C (cyan), H (white), N (blue), K⁺ (green), and Co²⁺ (magenta). (b) Atomic density profile plotted along the direction normal to the MOF surface. The overlapping region between MOF and PHI–M is delimited with a yellow dashed line. (c) Radial distribution function (RDF) plotted for the most representative MOF surface and PHI–M atoms.

Furthermore, since the RDF plots show MOF/PHI separating distances above 2 Å, van der Waals-type interactions dominate the heterojunction interface. These overall predictions therefore support that the metal-doping of PHI leads to a higher MOF surface/PHI affinity, a priori favorable for the electron transport between the two components.

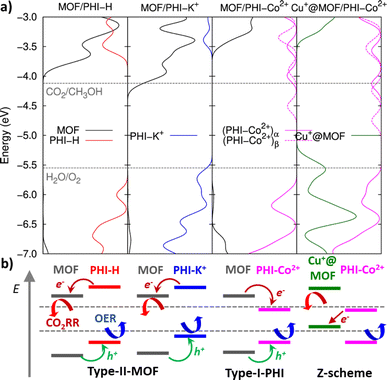
The DFT-optimized heterojunction cluster models shown in Fig. 3b, lead to a good qualitative description of the PHI structuring and nature of the MOF/PHI–M interactions evidenced above for the MOF/PHI–M heterojunction models, as evidenced by the radial distribution functions and interaction energies of the heterojunction cluster models reported in Fig. S17 and Table S14,† respectively. This observation supports the reliability of the cluster model to gain insight into the MOF/PHI–M heterojunction systems and discard the formation of any chemical bond between the two components at the interface which could be potentially neglected by the use of non-reactive force field MD simulations initially employed to construct the atomistic model of the heterojunction interface. The electronic coupling between MOF and PHI was thus found to be more pronounced for the metal doped PHI–M, as revealed by the DFT-derived charge density mixing plot for the corresponding MOF/PHI–M heterojunction cluster models (see Fig. S18†). We further performed Electrostatic Potential (ESP) charge population analysis to gain complementary information on the charge transfer at the MOF/PHI–M interfaces. The resulting ESP charges reported in Table S15† evidences that while a charge transfer occurs from PHI–H to MOF (0.06 e⁻), both the incorporation of Cu⁺ into the MOF and the metal loading of PHI leads to an opposite charge transfer (CT) directionality, i.e. from Cu⁺@MOF to PHI–M, which amounted up to 0.06 e⁻ in the case of the Cu⁺@MOF/PHI–Co²⁺ heterojunction cluster model (see Table S15†). To gain insight into the origin and consequences of the charge transfer in the MOF/PHI systems, their energetic alignments were investigated by plotting the projected density of states (PDOS) for both components and compared it with the redox CO₂/CH₃OH and H₂O/O₂ potentials (see Fig. 4).

Fig. 3 Schematic illustration of the heterojunction cluster model cleaved from the force field-based MOF/PHI–M composite heterojunction (top); and lateral and top views of the DFT-optimized MOF/PHI–M heterojunction cluster models (bottom panel).

Fig. 4 (a) Projected density of states (PDOS) along the MOF (right) and PHI (left part of the graphs) regions for all considered heterojunction cluster models, as obtained from Mulliken population analysis. Horizontal dashed lines represent the energies for the CO₂/CH₃OH and O₂/H₂O reaction potentials with respect to the vacuum level. Note that α and β stands for the spin up and down contributions, respectively, of the PHI–Co²⁺ based heterojunction cluster models; and (b) schematic representation of the respective types of interfacial energetic alignments obtained from the PDOS analysis.

MOF/PHI–H heterojunction cluster model displays a Type-II alignment where the PHI plays the role of light harvester transferring electrons to the MOF. Although this picture contradicts the target Z-pathway depicted in Fig. 1b, it is important to highlight the requirement of a large number of photogenerated electrons to achieve the complex multi-electron process required in CO₂RR. The VB of PHI–H and the CB of MOF lie 0.5 eV below and 0.3 eV above the CO₂/CH₃OH and O₂/H₂O potentials, respectively, thus exhibiting a suitable alignment to promote both CO₂RR and OER. Doping PHI with K⁺ leads to a destabilization of the VB edge of PHI due to the localization of holes around the metal ions, as it is observed in the frontier molecular orbitals (FMOs) depicted in Fig. S19.† As a result, the energy offset between the VB of PHI and the OER potential is reduced (up to 0.1 eV), as it can be observed in Fig. 4. A stabilization of the CB edge for PHI–Co²⁺ arises from the electron localization around the metal ions (see Fig. S19†) that translates into a Type-I alignment (see Fig. 1b) for the MOF/PHI–Co²⁺ heterojunction, where the PHI–Co²⁺ component acts as a charge reservoir. Notably, despite the reduction of the energy gaps should cause in principle an enhancement of the VIS region absorption, it becomes somehow detrimental for promoting CT separation within the heterojunction. Nonetheless, the incorporation of Cu⁺ in the MOF pore produces a significant destabilization of the VB edge of the MOF which turned the Cu⁺@MOF/PHI–Co²⁺ heterojunction energetics into a type of alignment very similar to the Z-scheme depicted in Fig. 1b since the VB and CB edges of Cu⁺@MOF and PHI–Co²⁺ respectively are close enough in energy (∼1.2 eV). It is noteworthy to mention that the destabilization of the MOF's states driven by the presence of the incorporated Cu⁺ is already observed for the Cu⁺@MOF/PHI–H heterojunction (see Fig. S20†). Overall, these calculations suggest that the conception of a Cu⁺@MOF/PHI–Co²⁺ heterojunction results in a low band gap in tandem with an architecture which mimics a Z-scheme similar to the one of artificial photosynthesis. Nevertheless, this energetic alignment scheme was obtained from a ground state perspective. We further investigated the optical properties of all considered MOF/PHI–M heterojunctions via TD-DFT calculations with the aim of analyzing the CT processes induced upon light irradiation. Fig. 5 displays their simulated UV-VIS absorption spectra alongside the identification of the most important contributions to the dominant excited states of the lowest energy absorption region.

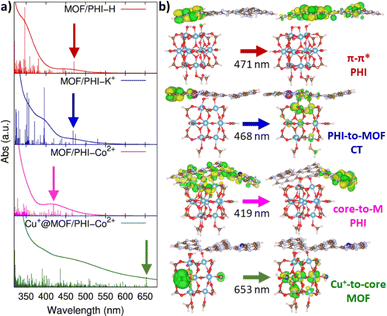Fig. 5 (a) Simulated absorption spectra for MOF/PHI–H, MOF/PHI–K⁺, MOF/PHI–Co²⁺ and Cu⁺@MOF/PHI–Co²⁺ heterojunction cluster models from the top to the bottom, vertical lines depict the intensity of the vertical excitations which convolute the absorption spectra; (b) iso-surface plots for the MOs conforming the main contributions to the vertical excitations pointed with arrows in the simulated spectra. All the information related with the main excited states conforming the simulated spectra and their corresponding orbital contributions are reported in Table S16 and Fig. S21,† respectively.

One observes that the MOF/PHI–H heterojunction cluster model exhibits its main absorption band centered at 350 nm which corresponds to the π–π* conjugated states of PHI–H thus confirming the light harvesting role played by PHI–H in the heterojunction; however, in spite of this, both the absorption of the MOF/PHI–H in the VIS region and the CT towards the MOF are still limited. PHI metal doping enhances the VIS and nIR light absorption by red-shifting the main PHI π–π* band and by the appearance of new absorption bands in the lowest energy region (see Fig. 5). Interestingly, K⁺ doping boosts the CT separation of the lowest energy states of the heterojunction (450–550 nm) due to the confinement of holes on the PHI cores surrounding the metal ions and the delocalization of electrons along the MOF surface. On the other hand, the lowest energy states (400–450 nm) of the MOF/PHI–Co²⁺ heterojunction are locally distributed in the PHI layer. In this case, the electrons tend to localize around the Co²⁺ states, thus reversing the desired flow of the CT which now operates towards the PHI. Strikingly, the largest impact in the absorption features of the heterojunction is intrinsically dictated by the incorporation of Cu⁺ in the MOF moiety, as it is clearly observed in the absorption spectra calculated for the Cu⁺@MOF/PHI–H heterojunction cluster model (see Fig. S22†). Notably, the incorporation of Cu⁺ in MIP-177 extends the energy window of the Cu⁺@MOF/PHI–Co²⁺ heterojunction to the VIS-nIR absorption region (λ > 600 nm). Indeed, these red photon absorption bands are formed by local MOF metal-to-core CT which, together with the blue VIS light local CT bands of the PHI–Co²⁺ layers, enables the Cu⁺@MOF/PHI–Co²⁺ heterojunction to display a panchromatic absorption covering the full UV-VIS region. However, these bands possess a local excitation character and therefore, no CT is expected to occur between MOF and PHI–M upon irradiation, thus leading to an uncomplete circuit of charges represented in Fig. 1b. This scenario would favor the recombination of the photogenerated charges. To address this limitation, we built a model device by sandwiching our heterojunction cluster models between two gold electrodes (see Fig. 6a) to explore their charge transport properties upon applying a voltage difference between the electrodes. This approach was inspired from a former work addressing the transport properties of MOF/fullerene based heterojunction devices.⁸⁰

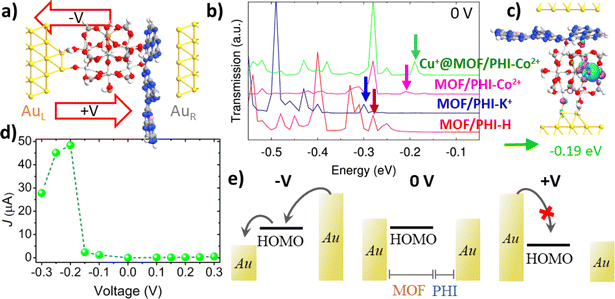Fig. 6 (a) Lateral view of the Au| Cu+@MOF/PHI–Co²⁺|Au based device heterojunction; (b) transmission spectra in the equilibrium for the MOF/PHI–H (red), MOF/PHI–K⁺ (blue), MOF/PHI–Co²⁺ (magenta), Cu⁺@MOF/PHI–Co²⁺ (green) device heterojunctions, and (c) transmission orbital shape corresponding to the signal appearing at −0.19 eV in the Cu⁺@MOF/PHI–Co²⁺ device heterojunction transmission spectrum; (d) current–voltage (J–V) curve for the Cu⁺@MOF/PHI–Co²⁺ device heterojunction; and (e) its respective scheme of the MOF's HOMO mediated transport of charges for negative (−V) and positive (+V) voltages. Note that for the sake of clarity only the α-spin contributions have reported here, while the transport properties for both spin components and the rest of the device heterojunctions are collected in Fig. S23 and S33.†

Fig. 6a shows a lateral view of the so-constructed Cu⁺@MOF/PHI–Co²⁺ heterojunction device model where the MOF is connected to the bottom Au electrode via two contacts associated with Au–O bond distances ranging from 1.9 Å to 2.2 Å (see Table S17†). The PHI layers are assembled via van der Waals interactions with the top electrode with the shortest contact distances with the C and N atoms of the PHI of 3.4–3.5 Å and 3.2–3.4 Å, respectively; which roughly correspond to the sum of the van der Waals radii for both Au–C (3.4 Å) and Au–N (3.2 Å). We have first explored all device heterojunctions in their equilibrium (no voltage applied). The computed transmission spectra of the MOF/PHI–M heterojunctions evidence that the occupied levels are the ones lying closer to the Fermi level, thus the transport across the device heterojunction is Highest Occupied Molecular Orbital (HOMO) mediated.

The corresponding PDOS shows that these occupied states are localized on the MOF region (see Fig. S23 and S24†), thus evidencing that the energetic alignment in the device is mainly driven by the coupling between these MOF states and the Au left electrode Fermi level, which is at the origin of the pinning effect.^81,82 This phenomenon is well-known to take place in metal–organic junctions built by employing covalent Au–S bonds.⁸³ The closest transmissions orbital to the Au Fermi level of the targeted Cu⁺@MOF/PHI–Co²⁺ is peaked with an energy offset about ε_h ∼ 0.19 eV (as indicated by the vertical arrows of the spectrum in Fig. 6b), whereas for the rest of the heterojunctions these energy offsets are slightly larger (ε_h ∼ 0.28 eV for MOF/PHI–H, ε_h ∼ 0.31 eV MOF/PHI–K⁺ and ε_h ∼ 0.22 eV for MOF/PHI–Co²⁺). The relatively close HOMO energies of Cu⁺@MOF/PHI–Co²⁺ with respect to the rest of the heterojunctions sharply contrast with the HOMO alignment observed in the heterojunction cluster models prior to their contact with the Au electrodes (see Fig. 4a), where the HOMO level of Cu⁺@MOF/PHI–Co²⁺ is about 1.5 eV up-shifted when compared to the other systems. Such energetic alignment independent on the intrinsic HOMO energies of the heterojunctions before the contacts has already been reported at both experimental and theoretical levels for molecular wires bearing different degrees of conjugation,^81,82 and/or electron donor–acceptor moieties,^83–85 and it is a clear signature of the Fermi level pinning.

Indeed, the relatively smaller HOMO offset of the PHI–Co²⁺ based device heterojunctions (MOF/PHI–Co²⁺ and Cu⁺@MOF/PHI–Co²⁺) with respect to the other systems (MOF/PHI–H, MOF/PHI–K⁺) can be ascribed to their stronger and weaker couplings with the left and right electrodes, respectively as it is derived from the charge density difference analysis at the device interfaces displayed in Fig. S25.† The corresponding transmission orbital of the peak present in the transmission spectrum of Cu+@MOF/PHI–Co²⁺ indicated by the green arrow in Fig. 6b is plotted in Fig. 6c. As already highlighted by the PDOS analysis, this transmission orbital is localized on the MOF moiety, with some extent of delocalization on the Au left electrode, which is a clear fingerprint of the coupling between MOF-Au states (see Fig. 6c). Similar shape features were observed for the rest of transmission orbitals belonging to the neighbor energy region to the Fermi level for all the studied device heterojunctions (see Fig. S26–S28†). We equally checked that all relevant transmission orbitals from the spectra correspond to the HOMO of the MOF, as they are represented in Fig. S26–S28.† As a result, in view of the similar energy and nature of their transmission orbitals, all device heterojunctions exhibit conductance values (G₀) within the same order of magnitude 10–100 μA (see Table S18†). We further proceeded to investigate the charge transport in the device heterojunction upon applying a voltage difference between the Au electrodes. To this end, we analyzed the evolution of the transmission spectra with the applied voltage for all the device heterojunctions (see Fig. S29–31†). Notably, when a positive voltage is applied, the HOMO offset with respect to the left electrode Fermi increases, thus leading to large charge injection barriers, and to a limited current crossing the device heterojunctions, as it can be evidenced in the current–voltage (J–V) curve of Cu⁺@MOF/PHI–Co²⁺ displayed in Fig. 6d. In contrast, the main HOMO levels appear in resonance with the voltage windows upon the application of a negative bias about −0.2 V for Cu⁺@MOF/PHI–Co²⁺; thus yielding to a substantial increase in the current of charges flowing in the PHI-to-MOF direction and to asymmetric J–V curves, as it is exemplified in the scheme depicted in Fig. 6e. The magnitude of the applied negative bias that is required to get the HOMO resonance for other systems is slightly larger (−0.28 V for MOF/PHI–H, −0.32 V for MOF/PHI–K⁺ and −0.22 V for MOF/PHI–Co²⁺) and therefore, identical asymmetric J–V curves were obtained for all device heterojunctions considered here (see Fig. S32†).

HOMO driven transport combined with asymmetric contacts (chemisorbed/physiosorbed) is often exploited to reach high rectification ratios (RR),^86,87 which for a given voltage (V) equal to RR = J(−V)/J(V) providing an estimation of the asymmetry of the charge transport. In this regard, Fig. S33† displays the RR values for all set of device heterojunctions and applied voltages considered here. As general trend, all device heterojunctions follow similar RR evolution with the applied voltage. This unambiguously demonstrates that the device characteristics of the heterojunction are mainly governed by the nature of the contacts with the electrodes. These findings highlight the importance to get a control of the surface terminations exposed to the Au contacts as a suitable strategy to monitor the device junction characteristics.

Conclusions

Herein we systematically explored the potential of MOF/PHI–M heterojunctions to act as effective CO₂RR/OER photoreactors. To this end, a computational strategy was deployed to construct reliable atomistic MOF/PHI–M heterojunction models and scrutinize the interactions and charge transfer between the two components. The enhancement of the MOF/PHI–M compatibility and stability was shown to be driven by cation doping the PHI layers at the origin of a larger electronic coupling between the components of the heterojunctions. We further demonstrated that either incorporating Cu⁺ into the MOF pore or doping PHI by mono-valent or divalent-cation is an effective route to engineer the Z-scheme required to promote dual CO₂RR and OER catalysis leading to a panchromatic absorption which extends the energy window up to the nIR region. Nonetheless, the localization of the photogenerated charges around Cu⁺ in MOF and cation sites in PHI–M was revealed detrimental for the charge transfer between the MOF and the PHI–M upon irradiation. This conclusion calls for experimental validation in future work using advanced time-resolved spectroscopies.^88,89 We further evidenced that the lack of charge transfer between the two components can be easily mitigated by the application of negative bias between the electrodes connected to the heterojunctions, due to the pinning of the MOF occupied states with the electrode Fermi level. Overall, our findings reveal that the performance and functionalities of MOF/PHI–M based photocatalytic reactors can be tuned via the combination of cation doping in PHI and cation incorporation in MOF device delivering key guidelines for the design of efficient photocatalytic cells. Interestingly, the theoretical scheme developed in this work can be further exploited to investigate the catalysis of other reactions of interest (i.e. HER) and/or any type of heterojunctions with applications of interest beyond the field of photocatalysis.

Data availability

Additional data can be found in the ESI.† Configurations files, gromacs inputs scripts can be obtained from GitHub repository (https://github.com/InderdipShere/MIP177_PHIM_composite).

Author contributions

V. D.-C. wrote the first draft. I. S., V. D.-C., and K. G.-T carried out the computational work corresponding to the MOF/PHI heterojunctions, heterojunction cluster models and device heterojunctions, respectively. G. M. designed and supervised the work and G. C. J. participated to the discussion of the results. All authors contributed to the revision of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the financial support provided by the METHASOL H2020-LC-SC3-RES-3-2020 (GA No. 101022649) and MOF2H2 (GA No. 101084131) projects. Authors also thank the financial support of ANID/CHILE under FONDECYT projects 1221072 (G. C.-J.). K. G.-T. is grateful for the support of VIPO (USACH) and ANID/Chile by Program/Doctorado Becas Nacionales 2021/21210404. The computational work was performed using HPC resources from GENCI-CINES (Grant A0160907613) and from the NLHPC (ECM-02) supercomputing infrastructure of the Universidad de Chile.

Notes and references

1. M. Melchionna and P. Fornasiero, ACS Catal., 2020, 10, 5493–5501.
2. Y.-J. Xu, Front. Catal., 2021, 1, 708319.
3. S. Lin, H. Huang, T. Ma and Y. Zhang, Adv. Sci., 2021, 8, 23–25.
4. J. Li, Nano-Micro Lett., 2022, 14, 112.
5. G. Y. Shinde, A. S. Mote and M. B. Gawande, Catalysts, 2022, 12, 94.
6. P. Ganji, R. K. Chowdari and B. Likozar, Energy Fuel., 2023, 37, 7577–7602.
7. X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 271–275.
8. W. J. Ong, L. L. Tan, Y. H. Ng, S. T. Yong and S. P. Chai, Chem. Rev., 2016, 116, 7159–7329.
9. P. Niu, J. Dai, X. Zhi, Z. Xia, S. Wang and L. Li, InfoMat, 2021, 3, 931–961.
10. A. Savateev, S. Pronkin, J. D. Epping, M. G. Willinger, C. Wolff, D. Neher, M. Antonietti and D. Dontsova, ChemCatChem, 2017, 9, 167–174.
11. A. Savateev, S. Pronkin, M. G. Willinger, M. Antonietti and D. Dontsova, Chem.–Asian J., 2017, 12, 1517–1522.
12. S. K. Sahoo, I. F. Teixeira, A. Naik, J. Heske, D. Cruz, M. Antonietti, A. Savateev and T. D. Kühne, J. Phys. Chem. C, 2021, 125, 13749–13758.
13. M. Y. Ye, S. Li, X. Zhao, N. V. Tarakina, C. Teutloff, W. Y. Chow, R. Bittl and A. Thomas, Adv. Mater., 2020, 32, 1903942.
14. S. Liu, V. Diez-Cabanes, D. Fan, L. Peng, Y. Fang, M. Antonietti and G. Maurin, ACS Catal., 2024, 14, 2562–2571.
15. A. Dhakshinamoorthy, Z. Li and H. Garcia, Chem. Soc. Rev., 2018, 47, 8134–8172.
16. J. D. Xiao and H. L. Jiang, Acc. Chem. Res., 2019, 52, 356–366.
17. X. Li and Q. L. Zhu, EnergyChem, 2020, 2, 100033.
18. Y. Zhang, J. Xu, L. Wang and B. Chen, Chem. Phys. Rev., 2022, 3, 041306.
19. S. Wang, T. Kitao, N. Guillou, M. Wahiduzzaman, C. Martineau-Corcos, F. Nouar, A. Tissot, L. Binet, N. Ramsahye, S. Devautour-Vinot, S. Kitagawa, S. Seki, Y. Tsutsui, V. Briois, N. Steunou, G. Maurin, T. Uemura and C. Serre, Nat. Commun., 2018, 9, 1–9.
20. S. Wang and C. Serre, ACS Sustain. Chem. Eng., 2019, 7, 11911–11927.
21. A. García-Baldoví, R. Del Angel, G. Mouchaham, S. Liu, D. Fan, G. Maurin, S. Navalón, C. Serre and H. Garcia, Energy Environ. Sci., 2023, 16, 167–177.
22. A. M. Abdel-Mageed, B. Rungtaweevoranit, M. Parlinska-Wojtan, X. Pei, O. M. Yaghi and R. Jürgen Behm, J. Am. Chem. Soc., 2019, 141, 5201–5210.
23. G. Wang, C. T. He, R. Huang, J. Mao, D. Wang and Y. Li, J. Am. Chem. Soc., 2020, 142, 19339–19345.
24. H. Issa Hamoud, P. Damacet, D. Fan, N. Assaad, O. I. Lebedev, A. Krystianiak, A. Gouda, O. Heintz, M. Daturi, G. Maurin, M. Hmadeh and M. El-Roz, J. Am. Chem. Soc., 2022, 144, 16433–16446.
25. S. Liu, V. Diez-Cabanes, D. Fan, P. Lyu and G. Maurin, in preparation.
26. S. Navarro-Jaén, M. Virginie, J. Bonin, M. Robert, R. Wojcieszak and A. Y. Khodakov, Nat. Rev. Chem, 2021, 5, 564–579.
27. H. Wang, L. Zhang, Z. Chen, J. Hu, S. Li, Z. Wang, J. Liu and X. Wang, Chem. Soc. Rev., 2014, 43, 5234–5244.
28. R. Marschall, Adv. Funct. Mater., 2014, 24, 2421–2440.
29. S. J. A. Moniz, S. A. Shevlin, D. J. Martin, Z. X. Guo and J. Tang, Energy Environ. Sci., 2015, 8, 731–759.
30. D. Cahen and A. Kahn, Adv. Mater., 2003, 15, 271–277.
31. J. Low, C. Jiang, B. Cheng, S. Wageh, A. A. Al-Ghamdi and J. Yu, Small Methods, 2017, 1, 1–21.
32. X. Li, C. Garlisi, Q. Guan, S. Anwer, K. Al-Ali, G. Palmisano and L. Zheng, Mater. Today, 2021, 47, 75–107.
33. J. Li, H. Yuan, W. Zhang, B. Jin, Q. Feng, J. Huang and Z. Jiao, Carbon Energy, 2022, 4, 294–331.
34. N. Nelson and A. Ben-Shem, Nat. Rev. Mol. Cell Biol., 2004, 5, 971–982.
35. J. Barber, Chem. Soc. Rev., 2009, 38, 185–196.
36. J. Fern, R. Greco, M. Navlani-Garc, W. Cao, Á. Berenguer-Murcia and D. Cazorla-Amor, Catalysts, 2022, 12, 1137.
37. J. Lin, W. Tian, H. Zhang, X. Duan, H. Sun, H. Wang, Y. Fang, Y. Huang and S. Wang, J. Hazard. Mater., 2022, 434, 128866.
38. S. Mazzanti, S. Cao, K. ten Brummelhuis, A. Völkel, J. Khamrai, D. I. Sharapa, S. Youk, T. Heil, N. V. Tarakina, V. Strauss, I. Ghosh, B. König, M. Oschatz, M. Antonietti and A. Savateev, Appl. Catal., B, 2021, 285, 119773.
39. Y. Qian, F. Zhang and H. Pang, Adv. Funct. Mater., 2021, 31, 1–34.
40. A. S. Belousov, D. G. Fukina and A. V. Koryagin, J. Chem. Technol. Biotechnol., 2022, 97, 2675–2693.
41. A. Dhakshinamoorthy, Z. Li, S. Yang and H. Garcia, Chem. Soc. Rev., 2024, 53, 3002–3035.
42. J. Fu, J. Yu, C. Jiang and B. Cheng, Adv. Energy Mater., 2018, 8, 1–31.
43. Y. Y. Han, X. L. Lu, S. F. Tang, X. P. Yin, Z. W. Wei and T. B. Lu, Adv. Energy Mater., 2018, 8, 1–8.
44. Z. Durmus and A. W. Maijenburg, Int. J. Hydrogen Energy, 2022, 47, 36784–36813.
45. J.-J. Jiang, F.-J. Zhang and Y.-R. Wang, New J. Chem., 2023, 47, 1599–1609.
46. S. K. Sharma, A. Kumar, G. Sharma, T. Wang, A. Iglesias-Juez and P. Dhiman, J. Mol. Liq., 2023, 382, 121890.
47. A. Chatterjee, L. Wang and P. Van Der Voort, Chem. Commun., 2023, 59, 3627–3654.
48. L. Yuan, P. Du, L. Yin, J. Yao, J. Wang and C. Liu, Nanoscale, 2024, 16, 5487–5503.
49. A. Savateev, N. V. Tarakina, V. Strauss, T. Hussain, K. ten Brummelhuis, J. M. Sánchez Vadillo, Y. Markushyna, S. Mazzanti, A. P. Tyutyunnik, R. Walczak, M. Oschatz, D. M. Guldi, A. Karton and M. Antonietti, Angew. Chem., Int. Ed., 2020, 59, 15061–15068.
50. X. Zhang, C. Yu, J. Guan, S. Jiang, Y. Wang, K. Deng, Z. Meng and R. Lu, Phys. Chem. Chem. Phys., 2020, 22, 9915–9922.
51. L. L. Lima, S. R. Tavares, C. V. Soares, G. Maurin and A. A. Leitão, Microporous Mesoporous Mater., 2023, 357, 112607.
52. F. Bian, X. G. Wu, S. S. Li, G. W. Qin, X. Y. Meng, Y. Wang and H. W. Yang, J. Mater. Sci. Technol., 2021, 92, 120–128.
53. J. Il Choi, C. Johnson, N. Fomina, A. Darvish, C. Lang, Y. S. Shin, H. S. Kim and S. S. Jang, J. Phys. Chem. C, 2023, 127, 2666–2674.
54. S. Bonakala, A. Lalitha, J. E. Shin, F. Moghadam, R. Semino, H. B. Park and G. Maurin, ACS Appl. Mater. Interfaces, 2018, 10, 33619–33629.
55. M. Muschi, A. Lalitha, S. Sene, D. Aureau, M. Fregnaux, I. Esteve, L. Rivier, N. Ramsahye, S. Devautour-Vinot, C. Sicard, N. Menguy, C. Serre, G. Maurin and N. Steunou, Angew. Chem., Int. Ed., 2020, 59, 10353–10358.
56. G. Xu, H. Zhang, J. Wei, H. X. Zhang, X. Wu, Y. Li, C. Li, J. Zhang and J. Ye, ACS Nano, 2018, 12, 5333–5340.
57. X. Zhou, L. zhang, H. Liu, Q. Yang, S. Zhu, H. Wu, T. Ohno, Y. Zhang, T. Wang, D. Su and C. Wang, J. Colloid Interface Sci., 2024, 658, 627–638.
58. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
59. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
60. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
61. R. Semino, J. C. Moreton, N. A. Ramsahye, S. M. Cohen and G. Maurin, Chem. Sci., 2018, 9, 315–324.
62. A. Patra, J. E. Bates, J. Sun and J. P. Perdew, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E9188–E9196.
63. N. G. Limas and T. A. Manz, RSC Adv., 2018, 8, 2678–2707.
64. A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
65. T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801.
66. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
67. C. L. Kong, J. Chem. Phys., 1973, 59, 2464–2467.
68. A. Y. Toukmaji and J. A. Board, Comput. Phys. Commun., 1996, 95, 73–92.
69. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. Van Der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
70. S. Grimme, J. Chem. Phys., 2013, 138, 244104.
71. C. Bannwarth and S. Grimme, Comput. Theor. Chem., 2014, 1040–1041, 45–53.
72. N. Montenegro-Pohlhammer, S. K. Kuppusamy, G. Cárdenas-Jirón, C. J. Calzado and M. Ruben, Dalton Trans., 2023, 52, 1229–1240.
73. M. I. Menéndez, N. Montenegro-Pohlhammer, R. Pino-Rios, R. Urzúa-Leiva, S. Morales-Lovera, M. Borges-Martínez, K. Granados-Tavera, R. López and G. Cárdenas-Jirón, J. Phys. Chem., 2023, 158, 164305–164320.
74. Y. Gu, Y. Hu, J. Huang, Q. Li and J. Yang, J. Phys. Chem. C, 2019, 123, 16366–16372.
75. B. Lawson, H. E. Skipper and M. Kamenetsk, Nanoscale, 2024, 16, 2022–2029.
76. J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 1–4.
77. J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 1–13.
78. M. Brandbyge, J. L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 1654011–16540117.
79. S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov, U. G. Vej-Hansen, M. E. Lee, S. T. Chill, F. Rasmussen, G. Penazzi, F. Corsetti, A. Ojanperä, K. Jensen, M. L. N. Palsgaard, U. Martinez, A. Blom, M. Brandbyge and K. Stokbro, J. Phys.: Condens.Matter, 2020, 32, 015901.
80. K. Granados-Tavera, N. Montenegro-Pohlhammer and G. Cárdenas-Jirón, Surf. Interfaces, 2023, 40, 103002–103012.
81. C. Van Dyck, V. Geskin and J. Cornil, Adv. Funct. Mater., 2014, 24, 6154–6165.
82. V. Diez-Cabanes, S. R. Gonzalez, S. Osella, D. Cornil, C. Van Dyck and J. Cornil, Adv. Theory Simul., 2018, 1, 1700020.
83. S. Rodriguez-Gonzalez, Z. Xie, O. Galangau, P. Selvanathan, L. Norel, C. Van Dyck, K. Costuas, C. D. Frisbie, S. Rigaut and J. Cornil, J. Phys. Chem. Lett., 2018, 9, 2394–2403.
84. G. Heimel, L. Romaner, J. L. Brédas and E. Zojer, Phys. Rev. Lett., 2006, 96, 2–5.
85. C. Van Dyck, V. Geskin, A. J. Kronemeijer, D. M. De Leeuw and J. Cornil, Phys. Chem. Chem. Phys., 2013, 15, 4392–4404.
86. C. A. Nijhuis, W. F. Reus and G. M. Whitesides, J. Am. Chem. Soc., 2010, 132, 18386–18401.
87. X. Chen, M. Roemer, L. Yuan, W. Du, D. Thompson, E. Del Barco and C. A. Nijhuis, Nat. Nanotechnol., 2017, 12, 797–803.
88. E. Pastor, M. Sachs, S. Selim, J. R. Durrant, A. A. Bakulin and A. Walsh, Nat. Rev. Mater., 2022, 7, 503–521.
89. D. Grinberg and Y. Paz, Curr. Opin. Green Sustainable Chem., 2023, 41, 100768.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc03630a

‡ These authors contributed equally to the work.

---