Open Access Article
Open Access ArticleCatalytic resonance theory: the catalytic mechanics of programmable ratchets†
Madeline A.
Murphy
ab,
Sallye R.
Gathmann
ab,
Rachel
Getman
ac,
Lars
Grabow
 ad,
Omar A.
Abdelrahman
ad and
Paul J.
Dauenhauer
ad,
Omar A.
Abdelrahman
ad and
Paul J.
Dauenhauer
 *ab
*ab
aCenter for Programmable Energy Catalysis, University of Minnesota, 421 Washington Ave. SE, Minneapolis, MN 55455, USA. E-mail: hauer@umn.edu
bDepartment of Chemical Engineering & Materials Science, University of Minnesota, 421 Washington Ave. SE, Minneapolis, MN 55455, USA
cWilliam G. Lowrie Department of Chemical and Biomolecular Engineering, The Ohio State University, Columbus, OH 43210, USA
dWilliam A. Brookshire Department of Chemical and Biomolecular Engineering, University of Houston, S222 Cullen College of Engineering Bldg 1, 4226 Martin Luther King Boulevard, Houston, TX 77204, USA
First published on 31st July 2024
Abstract
Catalytic reaction networks of multiple elementary steps operating under dynamic conditions via a programmed input oscillation are difficult to interpret and optimize due to reaction system complexity. To understand these dynamic systems, individual elementary catalytic reactions oscillating between catalyst states were evaluated to identify their three fundamental characteristics that define their ability to promote reactions away from equilibrium. First, elementary catalytic reactions exhibit directionality to promote reactions forward or backward from equilibrium as determined by a ratchet directionality metric comprised of the input oscillation duty cycle and the reaction rate constants. Second, catalytic ratchets are defined by the catalyst state of strong or weak binding that permits reactants to proceed through the transition state. Third, elementary catalytic ratchets exhibit a cutoff frequency which defines the transition in applied frequency for which the catalytic ratchet functions to promote chemistry away from equilibrium. All three ratchet characteristics are calculated from chemical reaction parameters including rate constants derived from linear scaling parameters, reaction conditions, and catalyst electronic state. The characteristics of the reaction network's constituent elementary catalytic reactions provided an interpretation of complex reaction networks and a method of predicting the behavior of dynamic surface chemistry on oscillating catalysts.
Introduction
The introduction of programmable catalysts with surfaces that change with time on the time scale of a catalytic turnover changes the strategy for molecular reaction control and chemical energy management.1,2 The ability to modulate catalytic transition states by modification of catalytic states is the opportunity provided by programmable catalysis to accelerate and control surface reactions. By using external perturbation of surfaces with light, charge, or strain to modulate a catalyst between physical or electronic states with time, molecules reacting on the surface experience a change in binding energy as the chemistry proceeds.3–6 Adsorbates release energy as the catalyst state shifts to stronger binding conditions and absorb energy as the catalyst state shifts to weaker binding conditions.7 However, each surface species responds differently to changes in catalyst state, such that variation in catalyst state changes the elementary heat of surface reaction and corresponding reaction transition states.2As depicted in Fig. 1a, one variation of a programmable catalyst is depicted for simple two state (green and blue) catalyst systems with a single elementary surface reaction. This endergonic reaction proceeds by the following steps: (i) reactant red molecule A(g) adsorbs to form A* in the weak-binding catalyst state (blue), (ii) the catalyst switches from the weak-binding to the strong-binding catalyst state (green) with energy output, (iii) in the strong-binding catalyst state, the red molecule A* readily traverses the transition state to form the purple molecule product B*, (iv) the catalyst state switches from strong-binding to weak-binding with significant energy input, and (v) the purple molecule desorbs from the surface in the weak-binding catalyst state to form the product B(g).
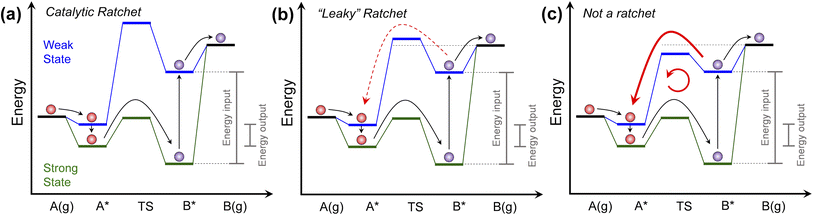 | ||
| Fig. 1 Programmable catalyst ratchet quality. (a) A programmable catalyst operating between two states blue and green, exhibits a high blue state transition energy, significantly decreasing the probability of purple product molecules reacting backwards in a ‘ratchet’ mechanism. (b) For programmable catalysts with blue state transition energies closer to the desorption energy of surface products, competition between desorption and backwards reaction over the transition state ‘leaks’ molecules back through the ratchet mechanism. (c) For programmable catalysts with low blue state transition energy relative to the purple molecule desorption energy, surface products primarily react backwards and move in an internal loop. Programmable catalytic ratchets are defined by the number of elementary steps (e.g., two-step) and the associated dynamic parameters of each elementary step, i (e.g., αi, βi, γi, δi – see Table 1 for parameter definitions). | ||
The programmable catalytic mechanism has two characteristics. As shown in Fig. 1a, the input energy associated with the external perturbation switching the catalyst from the strong-binding to the weak-binding catalyst state (green to the blue) is significantly greater than the energy output associated with switching the catalyst from the weak-binding to strong-binding (blue to the green) catalyst state. More importantly, when switching from strong to weak-binding states (green to blue), the purple product molecule has preferential kinetics for desorbing rather than reacting backwards to form the red reactant molecule. In the weak-binding state, the catalyst has a higher transition state energy than the purple molecule in the gas phase, forming what has been referred to as an ‘energy ratchet’.8,9 The net positive energy input has the role of promoting the reaction forward in a mechanism that has been shown to promote reactions past chemical equilibrium,2,10,11 raising the surface product energy using input work.
The core component of the programmable catalyst mechanism is the ‘energy ratchet’ which changes in both intermediate and transition state energies (Fig. 1a)1,12,13 as opposed to the ‘information ratchet’ which only changes in transition state barrier energies.14,15 For an energy ratchet oscillating between two or more states, the barrier for reaction progression changes allowing molecules to traverse a transition state in some catalyst states and limiting reverse traversal in other catalyst states. These energy ratchets can be driven by multiple possible physical mechanisms including chemical reaction (also called ‘catalysis-driven ratchets’), such that the catalyst changes state stochastically upon reaction (i.e., stochastic energy ratchets).16–18 Alternatively, energy ratchets that utilize external mechanisms such as charge, light, or strain will change in catalyst state via a pre-determined sequence (i.e., programmable energy ratchets) that provides the additional capability of temporal catalyst control.3,10,19,20 Energy ratchets can also be further categorized by whether they promote a reaction (i.e., catalytic ratchet)1,21,22 or molecular motion (i.e., pumping ratchet or molecular motor).23–25 With the addition of energy input or removal, the ratchet results in preferential change of molecules in a reaction away from equilibrium, as has been observed for many non-catalytic systems12,26–29 and catalytic systems.2,10
The quality of the ratchet, generally defined as the ability of the free energy profile to limit reaction to predominately one direction, therefore determines the energy efficiency of the programmable catalytic mechanism. As shown in Fig. 1, the performance of the catalytic ratchet for preferentially promoting molecules energetically uphill depends on at least two criteria. An effective catalytic ratchet (Fig. 1a) has a low forward (A* → B*) transition state barrier in the strong-binding (green) catalyst state while also having a high reverse (B* → A*) transition state in the weak-binding (blue) catalyst state (relative to the next elementary step of desorption, B* → B(g)). If the weak-binding state reverse transition state barrier is decreased and closer in energy to the B* desorption energy as depicted in Fig. 1b, then B* desorption competes with the reverse reaction (B* → A* in blue state) and the ratchet can be referred to as ‘leaky.’ For even lower weak-binding catalyst state transition state energies in Fig. 1c, the reverse reaction (B* → A* in blue state) is kinetically preferable to desorption, and the programmable catalyst becomes a reaction system that undesirably moves molecules in a loop converting work to heat. As shown in Fig. 1, the performance of the ratchet depends on the energies of the intermediates (A* and B*) and their interconnecting transition state.
In this work, programmable catalytic ratchets are evaluated at their component level of single elementary steps to understand the combinations of energy profiles leading to ratcheting behavior for varying programmable catalyst inputs such as frequency or duty cycle. Programmable catalytic ratchets are a mechanism that uses energy input to change catalyst states between different forward and reverse kinetics to drive surface reactions away from equilibrium. When decomposed to their fundamental design parameters, each mechanism can be varied within large parameter space such that identifying conditions of effective operation cannot currently be determined a priori, including the direction of the programmable ratchet (forward or reverse bias), the condition at which molecules traverse the ratchet (weak or strong catalyst binding state), and the temperatures and applied frequencies for which the ratchet becomes relevant to a catalytic reaction system. While characterization of stochastic energy ratchets has been extensively examined,11,12 this work will focus on the characteristics of programmable energy ratchets for catalysis. These fundamental descriptors of elementary catalytic ratchets will then serve to understand the more complicated behaviors of multi-step catalytic mechanisms that exist in important surface reactions for energy and chemical technologies.
Methods
Elementary ratchet calculations
The kinetic behavior of elementary catalytic ratchets was assessed for each catalyst state (blue or green) via the forward and reverse rate constants for surface species A* and B* (or any other intermediate surface species such as C* or D*). | (1) |
Evaluation of single catalytic elementary steps (C* to D*) considers only surface intermediates for which negligible desorption occurs (i.e., high desorption energy). Integration of eqn (1) and application of a site balance yields the surface coverage of C*, θC, on a surface at time, t, from initial surface coverage of C*, 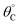 , as a function of the rate constants of that particular catalyst state, written in two forms.
, as a function of the rate constants of that particular catalyst state, written in two forms.
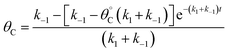 | (2a) |
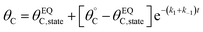 | (2b) |
Because the catalyst oscillates between two states (blue and green), the surface coverage was averaged over the time of each catalyst state by calculating the integral over the state period,
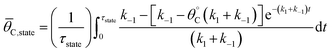 | (3) |
The average coverage of surface species C* was then determined for each catalyst state written in two forms.
 | (4a) |
 | (4b) |
To determine the average surface coverage in the limit cycle as it oscillates at temperature, T, and frequency, f, the average surface coverage was iteratively calculated for each state (blue then green) until the average surface coverage achieved a constant value to four decimal places. Derivations of eqn (1)–(4) are provided in the ESI.†
Reaction simulation
Reactions were modeled using Julia (version 9.0). Included in the model was the single elementary reaction of C* to form D*; C* and D* could desorb to form C(g) and D(g), which could also re-adsorb to form C* and D*. The overall reaction energy was defined as ΔGr. The surface reaction in the model was unimolecular and reversible,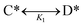 | (5) |
The catalyst was forced to change between catalyst binding states (weak and strong) leading to variation of the binding energy of each surface species, C* and D*. The catalyst states were described via the binding energy of species C* equal to the opposite of the heat of adsorption (−ΔHadsC = BEC), and the applied surface square wave oscillation was defined as having amplitude based on the change in binding energy of species C* (ΔBEC). The applied surface oscillation also had frequency, f, a shape (square), and a duty cycle, DB, defined as the fraction of the oscillation period that was in the blue weak-binding catalyst state.
After specifying the binding energy of C* in both catalyst states (strong and weak binding), the binding energy of D* and the activation energy (i.e., transition state energy) are defined relative to the binding energy of species C* using linear scaling relationships. The surface product, D*, is linearly scaled with C* via two parameters: gamma, γ, and delta, δ. The linear slope between the two binding energies is defined by γ, while δD–C represents the catalytic state in which two surface species have equivalent surface enthalpy.3,30
 | (6) |
| BEC = BED = δD–C | (7) |
The binding energy of D*, BED, is then determined from the binding energy of species C* viaeqn (8),
| BED = γD/CBEC + (1 − γD/C)δD–C | (8) |
The forward reaction of the unimolecular elementary step has an activation energy, Ea,1, that is determined by the Brønsted–Evans–Polanyi (BEP) relationship,31–33 which defines a linear relationship between the heat of surface reaction, ΔHR,1, and the activation energy, Ea,1.
| Ea,1 = α1ΔHR,1 + β1 | (9) |
To compute the forward rate constants, the pre-exponential factors were calculated using transition state theory, assuming a transmission coefficient of 1. These rate constants were computed at the set reaction temperature. The reverse reaction activation energy was be determined by the forward activation energy and the surface heat of reaction.
To model the adsorption and desorption of gas-phase molecules C and D, a CSTR reactor model was used. This reactor model was specified using the reactor volume (2.60 × 10−4 L), number of active catalytic sites (2.76 × 10−6 mol), and inlet mole fraction of C(g) (1.0 mol–C mol-total−1).34 A target conversion (e.g., XC = 1%) was set and an initial guess for the flowrate was provided to begin the simulation. The model was forward integrated using DifferentialEquations.jl35 with the RadauIIA5 solver36 until a steady-state solution (i.e., limit cycle) was reached.
The range of catalyst oscillation amplitudes viable for consideration extend to binding energy shifts of ∼1–2 eV (∼100 to 200 kJ mol−1). Experiments have demonstrated that adsorbates such as carbon monoxide can be varied in binding energy by ∼20 kJ mol−1 on hafnia-based catalytic condensers with capacitance of 200–300 nF cm−2.37,38 Recent experiments using catalytic condensers based on ion gel films have achieved capacitance as high as 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nF cm−2,39 providing the possibility that binding energy shifts could increase by at least an order of magnitude to hundreds of kilojoules per mole.
000 nF cm−2,39 providing the possibility that binding energy shifts could increase by at least an order of magnitude to hundreds of kilojoules per mole.
All simulations except the data of Fig. 11 used the method described in eqn (1)–(4) of iterative solving of eqn (1)–(4). The data of Fig. 11 was obtained by the simulation in Julia as described.
Results and discussion
Catalytic ratchets are a phenomenon that can occur with programmable surface reactions due to the dynamic variation of the catalytic surface with time. Conventional catalysts such as supported metals or metal oxides with static electronic state absent external perturbation will promote reactions only towards equilibrium; a generic reaction of R(g) to P(g) on a surface through intermediates R* and P* (and transition state, R–P‡) with zero ΔGrxn will proceed to equal gas-phase concentrations of each species. However, dynamic catalysts with forced-dynamic energy profiles (i.e., energy ratchets)1,8,40 that form ratchets can promote reactions away from equilibrium.2,34 Originally proposed by William P. Jencks in 1969, an oscillating enzyme catalyst was thought to promote a reaction either forwards or backwards.41 As the enzyme switches between two states of E and E′, the reaction energy profiles connecting the bound reactant and bound product change, resulting in distinct transition states for each enzyme state. This avoids violating the principle of microscopic reversibility, since the transition state is accessible in either reaction direction in either enzyme state, E or E′. More recently, kinetic simulations of an enzyme in an electric field oscillating between two states was shown to promote chemistry away from equilibrium, as predicted by Jencks.41–43Elementary catalytic ratchet
An energy ratchet in programmable heterogeneous catalysis also imparts directionality (forwards or backwards) to surface reactions.10,30 For the simplest case of gaseous A(g) reacting to gaseous B(g) through surface intermediates A* and B* with transition state AB‡ (Fig. 1), each of the state–state energy transitions are quantifiable and can be related to the ratchet performance. In more realistic reactions, the entire chemical surface mechanism is comprised of many elementary steps in series and parallel combinations in addition to the adsorption and desorption of chemical species (Fig. 2a).44,45 Each elementary reaction, i, exhibits reaction energy between intermediates as well as transition states all of which are defined for variation of catalyst state (e.g., weak- and strong-binding states) by the four linear scaling parameters of αi and βi for the transition state energy and γi and δi for the intermediate species energies (Table 1). Moreover, catalyst state oscillations are described by the change in energy of a single intermediate, ΔBEi, at varying frequencies, f. The breadth of parameters and resulting multi-state energy profiles for a single elementary reaction step currently results in sufficient complexity to prevent kinetic behavior by inspection, even when elementary steps exist independent of other elementary steps (e.g., other reactions or adsorption/desorption).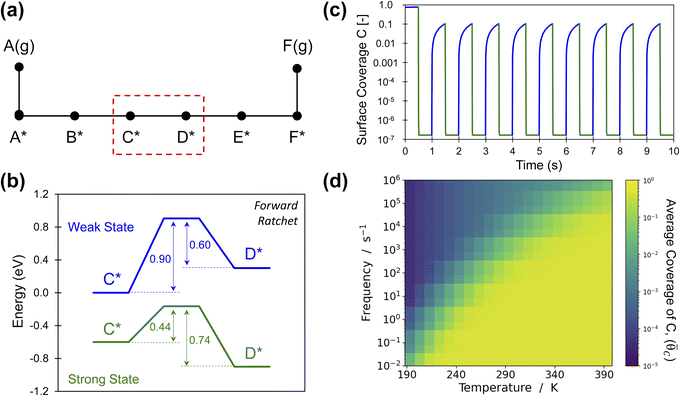 | ||
Fig. 2 Elementary programmable catalytic ratchet behavior. (a) A catalytic reaction is comprised of multiple elementary steps including adsorption, desorption, and reactions associated with bond-breaking and bond-making events. A single elementary reaction is considered for the conversion of C* to D* as part of a larger multistep reaction mechanism. (b) A single set of dynamic parameters describe the conversion of C* to D* for a catalyst that oscillates between a weak-binding catalyst state (blue) and a strong-binding catalyst state (green) with varying intermediate binding and transition state energies (α = 0.78, β = 0.67 eV, γD/C = 2.0, δC–D = 0.3, ΔBEC = 0.6 eV). (c) Starting from an initial surface coverage of θC = 0.75 and θD = 0.25, the surface coverages of C* and D* vary about seven orders of magnitude between catalyst states in blue and green at a temperature of 223 K and 1.0 Hz. (d) Oscillation of the elementary step between C* and D* exhibits an average surface coverage of C* (![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C) at the limit cycle that varies with temperature and applied oscillation frequency (10−2 < f < 106); the yellow region with average coverage of C) at the limit cycle that varies with temperature and applied oscillation frequency (10−2 < f < 106); the yellow region with average coverage of ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C ∼ 0.5 indicates the conditions whereby the ratchet does not function and the reaction equilibrates. Tabulated data available in Table S1 of the ESI.† C ∼ 0.5 indicates the conditions whereby the ratchet does not function and the reaction equilibrates. Tabulated data available in Table S1 of the ESI.† | ||
| Parameter | Units | Description |
|---|---|---|
| α | None | Brønsted–Evan–Polanyi (BEP) relationship slope, the proportionality constant between the heat of the surface reaction (C* ↔ D*) and the activation energy of the forward direction of the reaction |
| β | eV | BEP relationship constant offset. A constant defining the activation energy of the forward direction of the surface reaction (C* ↔ D*) in the case of the elementary reaction step being energetically neutral (heat of the surface reaction equals zero) |
| γ D/C | None | Linear scaling relationship parameter: the linear slope between driven changes in the binding energy of species D* to the corresponding change in the binding energy of species C* |
| δ C–D | eV | Linear scaling relationship parameter: an enthalpy corresponding to the catalytic state in which surface species C* and D* have equivalent surface enthalpies |
| θ i | None | Surface coverage of species i |
| θ i,eq | None | The equilibrium surface coverage of species i |
![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) i,hf
i,hf
|
None | The time-averaged surface coverage of species i at frequencies much larger than the corner frequency (f ≫ fc) |
![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) i
i
|
None | The time-averaged surface coverage of species i at any frequency or temperature |
| Temperature (T) | K | Temperature of the reactor and catalyst |
| BEi | eV | Binding energy of species i relative to the gase phase species i |
| ΔHr,C–D | eV | Heat of reaction between C(g) and D(g) |
| ΔBEi | eV | The amplitude of change in binding energy of species i resulting from an external oscillating perturbation |
| f | s−1 | The frequency of the oscillating perturbation applied to the catalyst surface |
| f c | s−1 | The corner or ‘cutoff’ frequency is defined as the boundary of the catalytic surface's frequency response, defined here as the frequency that results in a change in time-average surface coverage equal to half of the equilibrium value and the high frequency value, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) hf hf |
| D B | % | Duty cycle defined for the blue (B) catalyst state: for square waveforms, the duty cycle describes the percentage of time the catalyst exists in the blue state |
| λ | None | The elementary catalytic ratchet directionality metric. Values greater than unity indicate a ratchet that favors surface products (e.g., D*) versus surface reactants (e.g., C*), while values less than unity indicate a ratchet that favors surface reactants (e.g., C*) versus surface products (e.g., D*) |
Insight into the general behavior of elementary reaction step ratchets is obtained by considering a single case depicted in Fig. 2b. In this example, the catalyst oscillates between the weak binding state (blue) and the strong binding state (green); the depicted oscillation forcibly oscillates surface species C* (ΔBEC = 0.6 eV), with species D* and the transition state C–D‡ changing in energy as defined by the four linear scaling parameters (α = 0.78, β = 0.67 eV, γD/C = 2.0, δC–D = 0.3) selected to distinctly demonstrate elementary ratchet behavior. A key feature of this example is the difference in equilibrium between catalyst states; the weak-binding state (blue) overwhelmingly favors C*, while the strong-binding state (green) overwhelmingly favors state D*. As all reactions are first order, it is visually apparent that the fastest rate is k1 in the strong-binding state (green) with barrier of 0.44 eV, with the second fastest rate being k−1 in the weak-binding (blue) state with barrier of 0.60 eV.
A simulation of this elementary reaction ratchet is depicted in Fig. 2c at 223 K and a catalyst oscillation frequency of 1.0 Hz. Starting from a surface coverage of 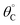 of 0.75 and
of 0.75 and 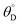 of 0.25, the initial weak-binding (blue) state (0 < t < 0.5 s) slowly increases the surface coverage of C*, after which the catalyst green state (0.5 < t < 1.0 s) rapidly converts C* to D* and achieves the surface equilibrium of θC,EQ ∼ 10−7 of the strong-binding catalyst state (green). Thereafter, the oscillation has achieved its final limit cycle. In the weak-binding catalyst state (blue), D* slowly reacts to C* increasing the surface coverage of C* (e.g., 1.0 < t < 1.5), after which the strong-binding catalyst state (green) rapidly returns the surface coverage of C* to low value (θC ∼ 10−7). An interesting observation is the time-averaged surface coverage and how it compares with the equilibrium coverage that would result in a non-oscillatory system. The time averaged surface coverage of C* for this elementary ratchet at these conditions (223 K, 1 Hz) is only
of 0.25, the initial weak-binding (blue) state (0 < t < 0.5 s) slowly increases the surface coverage of C*, after which the catalyst green state (0.5 < t < 1.0 s) rapidly converts C* to D* and achieves the surface equilibrium of θC,EQ ∼ 10−7 of the strong-binding catalyst state (green). Thereafter, the oscillation has achieved its final limit cycle. In the weak-binding catalyst state (blue), D* slowly reacts to C* increasing the surface coverage of C* (e.g., 1.0 < t < 1.5), after which the strong-binding catalyst state (green) rapidly returns the surface coverage of C* to low value (θC ∼ 10−7). An interesting observation is the time-averaged surface coverage and how it compares with the equilibrium coverage that would result in a non-oscillatory system. The time averaged surface coverage of C* for this elementary ratchet at these conditions (223 K, 1 Hz) is only ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C ∼ 0.05, which is far below the ratchet equilibrium surface coverage of
C ∼ 0.05, which is far below the ratchet equilibrium surface coverage of ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq = 0.5 (eqn (10)). This is a forward elementary catalytic ratchet that promotes the conversion of C* to D* beyond the equilibrium surface coverage.
C,eq = 0.5 (eqn (10)). This is a forward elementary catalytic ratchet that promotes the conversion of C* to D* beyond the equilibrium surface coverage.
The ratchet system of Fig. 2b was further simulated for a range of temperatures (193 < T < 393 K) and applied catalyst frequencies (10−2 < f < 106) to determine the time-averaged catalyst surface coverages at oscillatory steady state, which are presented as a logarithmic heat map (10−5 < ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C < 1) in Fig. 2d; the site balance of θC and θD sum to unity as the simulation assumes no open active sites for these unimolecular reactions and the net rate of formation of C* and D* from other surface pathways to be kinetically negligible. Inspection of the data indicates two general regions of behavior, indicating that an elementary step catalytic ratchet varies in performance with both applied temperature and frequency. At higher temperatures and lower applied catalyst oscillation frequencies, the average coverage of C* matches the equilibrium surface coverage of the catalytic ratchet,
C < 1) in Fig. 2d; the site balance of θC and θD sum to unity as the simulation assumes no open active sites for these unimolecular reactions and the net rate of formation of C* and D* from other surface pathways to be kinetically negligible. Inspection of the data indicates two general regions of behavior, indicating that an elementary step catalytic ratchet varies in performance with both applied temperature and frequency. At higher temperatures and lower applied catalyst oscillation frequencies, the average coverage of C* matches the equilibrium surface coverage of the catalytic ratchet, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq, defined as the averaged equilibrium coverage in each state of weak (W, θEQC,W) or strong (S, θEQC,W) binding,
C,eq, defined as the averaged equilibrium coverage in each state of weak (W, θEQC,W) or strong (S, θEQC,W) binding,
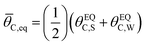 | (10a) |
 | (10b) |
The averaged equilibrium coverage can be calculated for any multi-state system with nj catalyst states. In the ratchet system of Fig. 2b, θEQC,S ∼ 0 while the θEQC,W ∼ 1, which results in an average equilibrium coverage of ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq ∼ 0.5, which is yellow in Fig. 2d. In these conditions that yield the average equilibrium coverage (low frequency, high temperature), the ratchet applies no directionality to the reaction and is dysfunctional. There is sufficient thermal energy and time for molecules to equilibrate in each catalytic state (weak-binding blue and strong-binding green), such that the catalytic ratchet has no impact on the average surface coverage. In the other general region of Fig. 2d (blue, top-left corner), average surface coverage of C* is less than 0.5, indicating that this particular catalytic ratchet has forward directionality that depletes the surface of C*. Increased ratchet performance, indicated by further deviation from the time-averaged equilibrium coverage, occurs at lower temperature and faster applied frequency, as indicated by lower time-averaged coverage of C*. It is apparent that determination of a ratchet kinetics and directionality requires identification of both temperature and oscillation frequency.
C,eq ∼ 0.5, which is yellow in Fig. 2d. In these conditions that yield the average equilibrium coverage (low frequency, high temperature), the ratchet applies no directionality to the reaction and is dysfunctional. There is sufficient thermal energy and time for molecules to equilibrate in each catalytic state (weak-binding blue and strong-binding green), such that the catalytic ratchet has no impact on the average surface coverage. In the other general region of Fig. 2d (blue, top-left corner), average surface coverage of C* is less than 0.5, indicating that this particular catalytic ratchet has forward directionality that depletes the surface of C*. Increased ratchet performance, indicated by further deviation from the time-averaged equilibrium coverage, occurs at lower temperature and faster applied frequency, as indicated by lower time-averaged coverage of C*. It is apparent that determination of a ratchet kinetics and directionality requires identification of both temperature and oscillation frequency.
Variations of elementary ratchets
Elementary catalytic surface reactions that oscillate between two or more states form ratchets of varying degrees of thermodynamic differences between reactants and products and accompanying kinetics. As depicted in Fig. 3a–c, ratchets of elementary reactions can promote reactions either forward or backwards away from equilibrium. Another characteristic of a catalytic ratchet is the equilibrium surface coverage of each catalyst state (e.g., θEQC,S) and the equilibrium surface coverage of the catalytic ratchet,![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq; two categories exist with either each state thermodynamically favoring opposite surface species (Fig. 2b and 3b) or both states thermodynamically favoring the same surface species (Fig. 3a and c).
C,eq; two categories exist with either each state thermodynamically favoring opposite surface species (Fig. 2b and 3b) or both states thermodynamically favoring the same surface species (Fig. 3a and c).
The operation of the elementary catalytic ratchets of Fig. 3 can be visualized on a line of surface coverage of surface species C*, θC. For Fig. 3a, both blue and green catalyst states thermodynamically and kinetically favor the formation of C*, such that the equilibrium coverages of each state (and the average of both states) is close to 100%. Fig. 3c depicts the opposite scenario, with both catalyst states favoring the formation of D*, and all equilibrium coverages of C* are close to zero. Alternatively, ratchets of catalyst states with opposite equilibrium surface coverages (e.g., Fig. 3b) exhibit surface coverages over a larger range. The ratchet range depicted in purple identifies the surface concentrations that the oscillating catalytic ratchet can promote, dependent on the system temperature and oscillation frequency, as demonstrated in Fig. 2d.
The elementary catalytic ratchet energy diagrams highlight the definition of a catalytic ratchet as a mechanism that uses energy input to change catalyst states resulting in different kinetics for the forward and reverse reactions to drive surface chemistry away from equilibrium. Energy input occurs via the changing of the catalyst and surface species from strong to weak binding (i.e., green state to blue state transitions). The difference in forward and reverse kinetics derives from the differences in transition state energy according to linear scaling relations as required for changes in surface reaction free energy with change in state. In the example of Fig. 2b, the catalyst in the strong-binding state (green) favors the forward reaction to form D*, while the next fastest surface rate constant in the weak-binding state (blue) favors the reverse direction. The other two elementary reactions (forward in the blue state and reverse in green state) are significantly slower with larger transition state barriers. The result is net acceleration of the forward reaction as the catalyst oscillates between states, despite the catalytic ratchet exhibiting an equilibrium coverage of ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq ∼ 0.5. The ratchet therefore promotes the reaction away from equilibrium, as shown in Fig. 2d. The three catalytic ratchets of Fig. 3 also show similar kinetic directionality, albeit with different adsorbate and transition state energies; all three systems exhibit an average surface coverage at equilibrium between the two state equilibria, with the forward and reverse bias ratchets promoting the reaction away from overall equilibrium towards surface coverages less than or greater than
C,eq ∼ 0.5. The ratchet therefore promotes the reaction away from equilibrium, as shown in Fig. 2d. The three catalytic ratchets of Fig. 3 also show similar kinetic directionality, albeit with different adsorbate and transition state energies; all three systems exhibit an average surface coverage at equilibrium between the two state equilibria, with the forward and reverse bias ratchets promoting the reaction away from overall equilibrium towards surface coverages less than or greater than ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq, respectively.
C,eq, respectively.
Elementary catalytic ratchet directionality metric
The directionality of an elementary catalytic ratchet can be determined from simulation (e.g., Fig. 2c and d); the limit cycle average surface coverage deviates higher or lower than equilibrium,![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq. However, each elementary catalytic ratchet can also be evaluated a priori via analysis of the constituent four kinetic rate coefficients (two for each catalyst state). For the range of possible parameters that define an elementary ratchet (α, β, γ, δ), one kinetic rate coefficient will be the fastest. For an elementary programmable ratchet that exhibits linear scaling behavior, the 2nd fastest rate coefficient exists in the opposite catalytic state relative to the fastest rate coefficient (i.e., if the fastest rate coefficient is in the blue state, the 2nd fastest will be in the green state). The ratchet behavior of this elementary step can therefore be characterized by these two fastest kinetic rate coefficients (with the other two slower rate coefficients contributing negligibly), which is defined as the ratchet directionality metric, λ, of the ratio of the sum of forward versus reverse rate coefficients weighted by the input oscillation duty cycle, DB, as derived in the ESI (eqn (S12)–(S14)).†
C,eq. However, each elementary catalytic ratchet can also be evaluated a priori via analysis of the constituent four kinetic rate coefficients (two for each catalyst state). For the range of possible parameters that define an elementary ratchet (α, β, γ, δ), one kinetic rate coefficient will be the fastest. For an elementary programmable ratchet that exhibits linear scaling behavior, the 2nd fastest rate coefficient exists in the opposite catalytic state relative to the fastest rate coefficient (i.e., if the fastest rate coefficient is in the blue state, the 2nd fastest will be in the green state). The ratchet behavior of this elementary step can therefore be characterized by these two fastest kinetic rate coefficients (with the other two slower rate coefficients contributing negligibly), which is defined as the ratchet directionality metric, λ, of the ratio of the sum of forward versus reverse rate coefficients weighted by the input oscillation duty cycle, DB, as derived in the ESI (eqn (S12)–(S14)).† | (11a) |
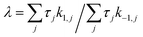 | (11b) |
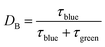
The ratchet directionality metric (eqn (11a)) can be written generally (eqn (11b)) for catalyst states j using the definition of the duty cycle. The duty cycle, DB, is defined as the fraction (0 ≤ DB ≤ 1) of an oscillation period (τ = 1/f) in a specific state, which in this case is the fraction of time of an oscillation period in the blue state.
 | (12) |
The efficacy of the ratchet directionality metric, λ, was evaluated by simulating multiple variations of dynamic parameters as depicted in Fig. 4 for DB of 0.5. For each parameter set, the sum of the forward rate constants weighted by the duty cycle were plotted versus the sum of the reverse rate coefficients weighted by the duty cycle, such that the parity line represents the boundary between forward and reverse elementary ratchets (i.e., λ = 1). Parameter sets that exhibited forward directionality (i.e., oscillatory steady state surface coverages of C* less than equilibrium, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq) via simulation are depicted in purple, while reverse bias ratchet parameter sets identified by simulation are depicted in orange. As shown, all forward bias ratchets (purple) exist in the forward region (λ > 1), while all reverse bias ratchets (orange) exist in the reverse region (λ < 1). Ratchets that exist near the parity line are close to flipping directional bias, indicating that more effective catalytic ratchets exist far from the parity line.
C,eq) via simulation are depicted in purple, while reverse bias ratchet parameter sets identified by simulation are depicted in orange. As shown, all forward bias ratchets (purple) exist in the forward region (λ > 1), while all reverse bias ratchets (orange) exist in the reverse region (λ < 1). Ratchets that exist near the parity line are close to flipping directional bias, indicating that more effective catalytic ratchets exist far from the parity line.
 | ||
| Fig. 4 Programmable elementary catalytic ratchet directionality metric, λ. Multiple combinations of dynamic scaling parameters (α, β, γ, δ, T, DB, and ΔBEA) were simulated to identify average surface coverage at oscillatory steady state to identify forward bias ratchets (purple) and reverse bias ratchets (orange). Ratchet directionality is predicted by the ratio of the sum of forward rate constants to the sum of reverse rate constants, weighted by the duty cycle as defined with the parameter, λ. Tabulated data available in Table S2-A and -B of the ESI.† | ||
Elementary ratchets
The simplicity of the ratchet directionality metric, λ, can also be tested by considering extreme ratchet parameter sets. In Fig. 5a, the strong-binding catalyst state (green) exhibits impartial equilibrium (ΔGgreen = 0), and the two fastest rate coefficients (k1,green and k−1,green) associated with the two lowest energy barriers (both 0.20 eV). When simulated at varying temperatures and applied frequencies, this elementary ratchet system operating at 50% duty cycle (τblue = τgreen) appears to violate the ratchet directionality metric with λ < 1 while exhibiting forward ratchet bias in simulations (Fig. S2 in ESI†). However, the ratchet of Fig. 5a exhibits nonviable linear scaling, making it unlikely to exist over viable oscillations in binding energy. The nonviability arises from the energetics in this system. Specifically, the smaller barrier of k−1,green (0.20 eV) relative to that of k−1,blue (0.25 eV), despite the reverse reaction of the blue catalyst state exhibiting negative reaction energy (ΔG−1,blue = −0.25 eV), would require a non-realistic transition state scaling parameter, α, less than zero. However, the similar yet viable ratchet of Fig. 5b is consistent with the ratchet directionality parameter; it is a backwards directionality ratchet with λ < 1 (Fig. S3 in the ESI†), which is possible since k−1,green < k−1,blue.Another elementary dynamic reaction exists when the two catalyst states are equal and opposite, as depicted in Fig. 5c. As shown, both catalyst states have fast kinetics with barriers of 0.25 eV and slow kinetics with barriers of 0.5 eV. For a duty cycle of DB = 0.5, this corresponds to a ratchet directionality metric of unity (λ = 1), and this particular ratchet does not promote the reaction away from equilibrium when simulated (Fig. S3 in the ESI†). Moreover, all elementary parameter sets that have exhibit equal and opposite kinetics between catalyst states will have λ of unity at equal state time constants (DB = 0.5) and will not behave as catalytic ratchets.
Weak and strong pass ratchets
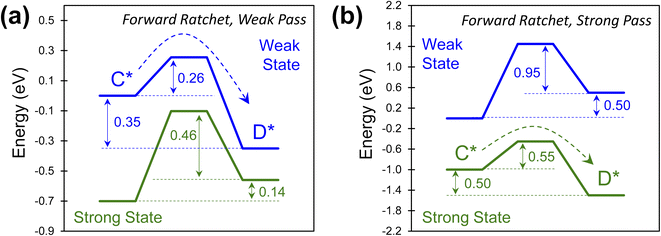
The combinations of energy barriers and rate constants lead to many possible catalytic ratchets which can be categorized by their enabling catalyst states (i.e., the strong or weak state that permits reactions to readily proceed through the transition state). If a ratchet has two (or more) catalytic states, then under functioning conditions such as viable temperature ranges (described later for viable cutoff frequencies) the ratchet will permit molecules to react through the transition state under one catalyst state and prohibit significant reaction in the other catalyst state(s).Ratchets can be further defined by the strength of adsorbate binding (strong or weak), leading to favorable catalytic reaction energetics as depicted in Fig. 6. In one type of ratchet, the strong binding catalyst state (green) exhibits large energy barriers (0.60 and 0.46 eV) for both the forward and the reverse reaction (Fig. 6a), while the weak binding state (blue) has a small forward barrier (0.26 eV) that allows C* to readily react to D* relative to all other rate constants. This is therefore a ‘weak pass’ forward ratchet (i.e., the fastest reaction occurs in the weak-binding state of the catalyst). In contrast, ratchets also exist as depicted in Fig. 6b, with large barriers in the weak-binding catalyst state (blue), while the strong binding state (green) has barriers readily traversable at accommodating temperatures (0.55 eV) in the forward direction, thus making this a ‘strong pass’ forward ratchet.
The type of ratchet, ‘strong pass’ or ‘weak pass,’ is identifiable by the catalyst state with the lowest reaction energy barrier. This characteristic, identifiable for individual ratchets in a multi-step series reaction, becomes important when considering the sequence of elementary steps. The order of ratchets determines if molecules can traverse multiple elementary steps at once; alternatively, a series of ratchets that switch between ‘strong pass’ and ‘weak pass’ characteristics would require multiple catalyst state changes to complete a catalytic reaction.
Elementary catalytic ratchet cutoff frequencies and temperatures
The elementary catalytic ratchet of Fig. 2 exhibits two general regions of behavior. At high temperature and low applied frequencies, the ratchet is disabled and the average surface coverage of C* in a C*–D* reversible surface reaction equals the equilibrium surface coverage of![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq ∼ 0.5 (yellow region in Fig. 2d). However, at lower temperatures and higher applied frequencies, the ratchet becomes functional and drives the reaction away from equilibrium, which for this particular ratchet is towards D* (and lower surface coverages of C*). The interface between the two ratchet behaviors exists with a sharp transition, indicative of on/off behavior of the ratchet, that varies both with applied frequency, duty cycle, and temperature.
C,eq ∼ 0.5 (yellow region in Fig. 2d). However, at lower temperatures and higher applied frequencies, the ratchet becomes functional and drives the reaction away from equilibrium, which for this particular ratchet is towards D* (and lower surface coverages of C*). The interface between the two ratchet behaviors exists with a sharp transition, indicative of on/off behavior of the ratchet, that varies both with applied frequency, duty cycle, and temperature.
The ratchet on/off transition can be predicted by modeling the ratchet as a frequency response filter as described in eqn (13). The time-averaged surface coverage of C*, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,Avg, depends on the equilibrium of the two catalytic states,
C,Avg, depends on the equilibrium of the two catalytic states, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq, defined in eqn (10). The surface coverage is modulated from equilibrium by the band pass equation with time constant 1/kII, where kII is the second fastest rate constant of the four in the two-state elementary catalytic ratchet. This is multiplied by the time associated with the state associated with the second fastest time constant, τII, divided by four, which is determined by the applied frequency, f, and the duty cycle, DB (i.e., the fraction of time in the oscillation period that exists in the blue state). This quantity in eqn (13) is multiplied by the difference between the equilibrium surface coverage and the inverse of λ plus one, a quantity that determines the surface coverage at high frequency (hf) ratchet function (derived in the ESI†).
C,eq, defined in eqn (10). The surface coverage is modulated from equilibrium by the band pass equation with time constant 1/kII, where kII is the second fastest rate constant of the four in the two-state elementary catalytic ratchet. This is multiplied by the time associated with the state associated with the second fastest time constant, τII, divided by four, which is determined by the applied frequency, f, and the duty cycle, DB (i.e., the fraction of time in the oscillation period that exists in the blue state). This quantity in eqn (13) is multiplied by the difference between the equilibrium surface coverage and the inverse of λ plus one, a quantity that determines the surface coverage at high frequency (hf) ratchet function (derived in the ESI†).
 | (13) |
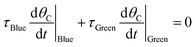 | (14a) |
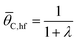 | (14b) |
The quantity, λ, is again the ratio of sum of forward rate constants to the sum of reverse rate constants weighted by the input program duty cycle, as written in eqn (11); it was derived in the ESI† beginning from eqn (14). By eqn (13), the deviation from equilibrium, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq, occurs when the oscillation frequency is sufficiently high and τII is sufficiently small. It is important to note that eqn (13) is a semi-empirical model, inspired by transfer functions commonly employed in the analysis of band pass filters/amplifiers. Error analysis of multiple model forms are presented in the ESI in Fig. S1,† where variations of transfer functions were considered. While many variations of transfer functions in eqn (13) approximate the average surface coverage of C* at oscillatory steady state conditions, all of the considered models were only effective at representing the data when using the second-fastest rate constant, kII, thereby indicating its importance in regulating ratchet kinetics.
C,eq, occurs when the oscillation frequency is sufficiently high and τII is sufficiently small. It is important to note that eqn (13) is a semi-empirical model, inspired by transfer functions commonly employed in the analysis of band pass filters/amplifiers. Error analysis of multiple model forms are presented in the ESI in Fig. S1,† where variations of transfer functions were considered. While many variations of transfer functions in eqn (13) approximate the average surface coverage of C* at oscillatory steady state conditions, all of the considered models were only effective at representing the data when using the second-fastest rate constant, kII, thereby indicating its importance in regulating ratchet kinetics.
The utility of the eqn (13) approximating the catalytic ratchet was evaluated by comparison with simulation, as shown in Fig. 7. The first ratchet in Fig. 7a is forward bias of the C*–D* surface reaction with equilibrium surface coverage of ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq ∼ 0.5; this is the same ratchet as evaluated in Fig. 2. As temperature increased, the applied frequency necessary to achieve time-averaged surface coverages less than equilibrium increased, resulting in average surface coverages at oscillatory steady state that are small fractions of a surface (0.0001 <
C,eq ∼ 0.5; this is the same ratchet as evaluated in Fig. 2. As temperature increased, the applied frequency necessary to achieve time-averaged surface coverages less than equilibrium increased, resulting in average surface coverages at oscillatory steady state that are small fractions of a surface (0.0001 < ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C < 0.01). Data points are the simulations, while the lines are eqn (13), using the kinetic parameters of each catalytic state; as shown, eqn (13) describes the equilibrium coverage at low applied frequency, the oscillatory steady state coverage of species i at high frequency,
C < 0.01). Data points are the simulations, while the lines are eqn (13), using the kinetic parameters of each catalytic state; as shown, eqn (13) describes the equilibrium coverage at low applied frequency, the oscillatory steady state coverage of species i at high frequency, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) i,hf = (1/(1 + λ)), and the transition between extreme coverage values.
i,hf = (1/(1 + λ)), and the transition between extreme coverage values.
 | ||
| Fig. 7 Programmable catalytic ratchets, oscillatory steady state coverage, and cutoff frequencies. Points are simulation, and lines are eqn (13). (a) A forward catalytic ratchet of C* reacting to D* at temperatures of 213–393 K decreases in surface coverage of C* with increasing applied frequency. α = 0.78, β = 0.67, γ = 2, δ = 0.3, ΔBEC = 0.6 eV. (b) A reverse ratchet of C* reacting to D* at temperatures of 213–293 K increases in surface coverage of C* with increasing applied frequency. α = 0.7, β = 0.5, γ = 1.2, δ = 0.5, ΔBEC = 0.2 eV. (c) A reverse ratchet of C* reacting to D* at temperatures of 193–273 K increases in surface coverage of C* with increasing applied frequency: α = 0.5, β = 0.5, γ = 2, δ = 0.3, ΔBEC = 0.5 eV. (d) Cutoff frequencies calculated from eqn (15) of the three ratchets determining their on/off states. All data is presented for duty cycles of DB = 0.5. Tabulated data available in Tables S3 of the ESI.† | ||
Another ratchet type of reverse bias depicted in Fig. 7b exhibits two catalytic states that both favor high surface coverage of C* with parameters: α = 0.7, β = 0.5, γ = 1.2, δ = 0.5, ΔBEC = 0.2 eV. With a high equilibrium C* surface coverage (0.95 < ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq < 0.99) at each temperature, the surface coverage further increases with increased applied frequency. This ratchet is also distinct due to the significant differences in equilibrium surface coverage,
C,eq < 0.99) at each temperature, the surface coverage further increases with increased applied frequency. This ratchet is also distinct due to the significant differences in equilibrium surface coverage, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq, which varies at each temperature. In comparison, the kinetic behavior of another reverse bias ratchet is depicted in Fig. 7c, which is the same ratchet as described in Fig. 3b. This catalytic ratchet has
C,eq, which varies at each temperature. In comparison, the kinetic behavior of another reverse bias ratchet is depicted in Fig. 7c, which is the same ratchet as described in Fig. 3b. This catalytic ratchet has ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq of ∼0.50, due to the opposing thermodynamics of the two catalyst states, while the time-averaged oscillatory steady state coverage of C* is
C,eq of ∼0.50, due to the opposing thermodynamics of the two catalyst states, while the time-averaged oscillatory steady state coverage of C* is ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C > 0.8 at high applied frequency. In all of these ratchets with different kinetic characteristics, eqn (13) describes the kinetic response of the simulation data.
C > 0.8 at high applied frequency. In all of these ratchets with different kinetic characteristics, eqn (13) describes the kinetic response of the simulation data.
For a catalytic ratchet oscillating at equal time in each state, the f ∼ 1/(2τII) corresponds to a duty cycle of DB of 50%. The cutoff frequency, fc, can be calculated from eqn (13) when the transfer function equals half of its value as described in eqn (15a),
 | (15a) |
The cutoff frequency can be calculated generally for any duty cycle viaeqn (15b).
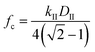 | (15b) |
The cutoff frequency, fc, where the ratchet becomes kinetically relevant (i.e., turns ‘on’) is readily calculable for each ratchet at each temperature using the second fastest rate constant, kII, and the duty cycle as defined for the catalyst state with the second fastest rate constant. The quantity, DII, is the duty cycle (0 < DII < 1.0) of the state which has the 2nd fastest rate coefficient; DII equals DB if kII is in the weak-binding blue state, or DII equals (1 − DB) if kII is in the strong-binding green state. For each of the three ratchets, the cutoff frequencies are depicted as a function of inverse temperature, indicating the transition between functioning and non-functioning catalytic ratchets dependent on the kinetics of each elementary step.
Negative scaling
The description of elementary catalytic ratchets to this point has focused on positive scaling (γD/C > 0), but some intermediates respond to catalyst stimuli via opposing changes in binding energy.34 As one adsorbate strengthens in binding energy, the other adsorbate weakens in binding energy; this corresponds to negative gamma scaling (γD/C < 0). As depicted in Fig. 8a, negative scaling elementary catalytic ratchets exhibit free energy profiles that change in opposite directions upon stimulation (α = 0.7, β = 0.7, γD/C = −2, δ = 0.1, ΔBEC = 0.2 eV). In this particular example, the fastest step and smallest barrier is the forward direction in the weak-binding catalyst state (blue), making this a forward ratchet, while the second fastest step and second highest barrier is the reverse direction in the strong-binding catalyst state (green).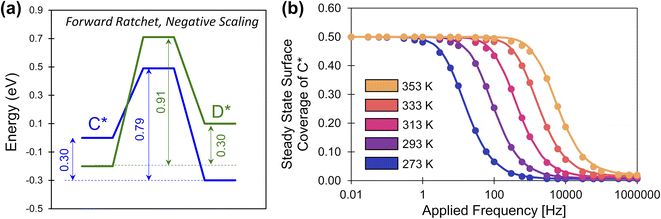 | ||
| Fig. 8 A negative-scaling programmable elementary catalytic ratchet. (a) An elementary ratchet with negative scaling (γ = −2) exhibits opposing changes in binding energy between reaction intermediates C* and D* (α = 0.7, β = 0.7, δ = 0.1, ΔBEC = 0.2 eV). (b) The elementary catalytic ratchet exhibits forward bias that decreases oscillatory steady state surface coverage of C* from its equilibrium value of 0.5 at increasing temperature; points are simulation, and lines are eqn (13). All data is presented for duty cycles of DB = 0.5. Tabulated data available in Table S4 of the ESI.† | ||
Simulation of the negative ratchet is depicted in Fig. 8b for five temperatures (273–353 K) over a range of 0.01 to 106 Hz. At low applied frequency, the average oscillatory steady state coverage of C* is 0.5, as expected for an elementary ratchet that exhibited significant changes in overall reaction energy in both states (0.30 and −0.30 eV). As applied frequency increased, the ratchet began to promote deviation of average surface coverage of C* to lower values (i.e., forward ratchet). The ratchet turned on (i.e., cutoff frequency) between ∼1 Hz at 273 K up to ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz at 373 K. Final oscillatory steady state surface coverages for each temperature matched the expected quantity at high frequency (
000 Hz at 373 K. Final oscillatory steady state surface coverages for each temperature matched the expected quantity at high frequency (![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,hf = 1/(1 + λ)). These simulated data were also predicted by eqn (13), indicating that positive and negative gamma scaling ratchets exhibit comparable and predictable behavior.
C,hf = 1/(1 + λ)). These simulated data were also predicted by eqn (13), indicating that positive and negative gamma scaling ratchets exhibit comparable and predictable behavior.
Ratchet duty cycle & mixed timescales
A catalyst surface input program has design options that include applied frequency, amplitude, and oscillation offset, but another option is the duty cycle setting (DB). The duty cycle, DB, is the fraction (0 ≤ DB ≤ 1) of an oscillation period in a specific state, which in this case is the fraction of time of an oscillation period in the blue state. Up to this point, the duty cycle has been fixed at DB of 50%. With varying DB corresponding to longer and shorter duration of each oscillation in each catalyst state, the chemistry has more or less time to approach equilibrium in each particular state, ultimately achieving different average surface coverage throughout the limit cycle.The implications of duty cycle were assessed in Fig. 9a by simulating the elementary catalytic ratchet of Fig. 2 (points are simulation, lines are eqn (13)) with varying duty cycle (0.0001 < DB < 0.999) and defined linear scaling parameters (α = 0.78, β = 0.67 eV, γ(D/C) = 2.0, δC–D = 0.3, ΔBEC = 0.6 eV). This forward ratchet at a duty cycle of 0.50 exhibited a cutoff frequency of fc ∼ 21 Hz and varied from the equilibrium surface coverage of ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq of ∼0.50 to the high frequency (f ≫ fc) coverage of
C,eq of ∼0.50 to the high frequency (f ≫ fc) coverage of ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,hf = 7.9 × 10−4. Variation of the duty cycle altered the surface coverage response by changing both the high frequency coverage
C,hf = 7.9 × 10−4. Variation of the duty cycle altered the surface coverage response by changing both the high frequency coverage ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,hf and cutoff frequency, fc. Lower duty cycles (DB < 0.5) exhibited lower cutoff frequencies (<10 Hz) and lower C* surface coverages at high frequency (
C,hf and cutoff frequency, fc. Lower duty cycles (DB < 0.5) exhibited lower cutoff frequencies (<10 Hz) and lower C* surface coverages at high frequency (![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,hf < 0.5), while higher duty cycles (DB > 0.5) exhibited higher cutoff frequencies (>10 Hz) and larger C* surface coverages at high frequency (
C,hf < 0.5), while higher duty cycles (DB > 0.5) exhibited higher cutoff frequencies (>10 Hz) and larger C* surface coverages at high frequency (![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,hf > 0.5). However, all considered duty cycles resulted in a ratchet with forward bias (λ > 1) that favored formation of D* relative to equilibrium,
C,hf > 0.5). However, all considered duty cycles resulted in a ratchet with forward bias (λ > 1) that favored formation of D* relative to equilibrium, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq.
C,eq.
 | ||
| Fig. 9 Variable duty cycle elementary catalytic ratchets. (a) An elementary reaction of C* to D* at 273 K with defined linear scaling dynamic parameters and binding energy shift exhibits variable average surface coverage of C* at oscillatory steady state with varying duty cycle, 0.0001 ≤ DB ≤ 0.999 (α = 0.78, β = 0.67 eV, γD/C = 2.0, δC–D = 0.3, ΔBEC = 0.6 eV). (b) An elementary reaction of C* to D* at 153 K with defined linear scaling dynamic parameters and binding energy shift exhibits varying average surface coverage of C* at oscillatory steady state with varying duty cycle, 0.0001 ≤ DB ≤ 0.9999 (α = 0.5, β = 0.375 eV, γD/C = 2.0, δC–D = 0.25, ΔBEC = 0.5 eV). This particular elementary catalytic ratchet shifts from a forward ratchet to a reverse ratchet below and above a duty cycle of 0.5, respectively. Tabulated data available in Table S5 of the ESI.† | ||
The impact of duty cycle on ratchet directionality is more significant in the simulation of Fig. 9b, which applies varying duty cycle to the elementary catalytic ratchet of Fig. 5c with defined linear scaling parameters (α = 0.5, β = 0.375 eV, γD/C = 2.0, δC–D = 0.25, ΔBEC = 0.5 eV). Simulations are represented by points, while the model of eqn (13) are lines. For a neutral duty cycle of DB = 0.5, this ratchet exhibited no directional bias to the reaction with all time-averaged surface coverages of C* at oscillatory steady state, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,Avg, equal to the
C,Avg, equal to the ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) C,eq of ∼0.50. However, variation of the duty cycle away from DB of 0.5 imposed directional bias on the catalytic ratchet; forward bias existed for this ratchet for duty cycles below 0.5, and reverse bias existed for this ratchet for duty cycles above 0.5. The switching of ratchet bias was predicted by the ratchet metric, λ, in eqn (11), where the reaction rate constants were modified by the duty cycle. However, the duty cycle only sufficiently influences the ratchet directionality metric, λ, when the fastest two rate constants are comparable in value or at extreme values of the duty cycle, DB.
C,eq of ∼0.50. However, variation of the duty cycle away from DB of 0.5 imposed directional bias on the catalytic ratchet; forward bias existed for this ratchet for duty cycles below 0.5, and reverse bias existed for this ratchet for duty cycles above 0.5. The switching of ratchet bias was predicted by the ratchet metric, λ, in eqn (11), where the reaction rate constants were modified by the duty cycle. However, the duty cycle only sufficiently influences the ratchet directionality metric, λ, when the fastest two rate constants are comparable in value or at extreme values of the duty cycle, DB.
Multi-step mechanisms and elementary ratchet symbols
The single elementary catalytic ratchet has no significance outside of a full catalytic reaction. Yet, the entire reaction network comprising a catalytic reaction can be described using a combination of multiple elementary steps. This approach of ‘detailed chemistry’ or ‘microkinetics’ has been the foundation of heterogeneous catalysis modeling for the past half century, with mean field kinetic models describing each elementary reaction describing complex reaction networks.46 Description of the kinetics of each elementary reaction is challenging due to the extent of required model characteristics; this challenge is further increased for kinetic reaction models that aim to describe programmable catalytic reactions on dynamic surfaces.The proposed benefit of understanding the dynamic behavior of each independent elementary step is that the combined reaction model with characteristics of the individual elementary step dynamics can be evaluated to understand its general behavior under varying temperature and applied frequency input programs. This interpretation assumes that the characteristics of individual ratchets described so far are relevant for understanding molecular behavior in more complex reaction networks. To consider this possibility, an example generic reaction network is depicted in Fig. 10a converting A(g) to E(g) through surface species A* to E* at temperature T1 and applied frequency, f. This example is not a real kinetic mechanism but instead a diagram to demonstrate the potential for interpreting reaction networks by their individual elementary ratchets. For the selected temperature, T1, the kinetic parameters of each elementary step, i, were calculated for each catalyst state (ki,g, k−i,g, kib, k−ib) and the three characteristics of each elementary catalytic ratchet can be calculated: (1) the ratchet directionality depicted as an arrow (→ or ←) was determined by calculating λ, (2) the cutoff frequency was calculated by eqn (15), and (3) the pass condition was identified as the strong- or weak-binding catalyst state (S or W) with the fastest rate constant. Each of these characteristics are listed next to the reaction network of Fig. 10a.
The reaction network is summarized on the frequency diagram of Fig. 10b, where each elementary reaction is depicted in the strong- or weak-pass column at the calculated cutoff frequency; each elementary ratchet directionality is shown as a forward or backwards arrow. These cutoff frequencies are then compared with the applied program frequency, f = 500 Hz, shown as a dashed line; all ratchets below 500 Hz are functional, while the single ratchet associated with C*–D* elementary reaction is dysfunctional at these conditions.
Without simulating this reaction network, it could be possible to anticipate the catalytic reaction progression under dynamic conditions (T1, f = 500 Hz). In the strong binding state of the catalyst, A(g) adsorbs to form A*, which then reacts to form B* and then F*. When the catalyst switches to the weak binding state, F* reacts to form G*. Switching back to the strong catalyst state, G* reacts to form C*. At this point C* has two other possible reaction paths; C* will likely not react to form B* in the strong binding catalyst state, since it would need to pass through a weak-pass elementary ratchet. Instead, C* will likely react to form D*; even though the C*–D* ratchet has reverse directionality, its cutoff frequency is higher than the applied frequency and the reaction can proceed in either catalyst state. While the catalyst is still in the strong binding state, D* will then react to form E*, which will then desorb to form E(g) product. The entire catalyst reaction requires a sequence of strong–weak–strong catalyst binding states for progression from A(g) to A* to E* to E(g).
It is unknown if the proposed interpretation of Fig. 10 would agree with a detailed simulation of the entire reaction network; will this overall approach of interpreting combined elementary ratchets by their three characteristics provide an a priori interpretation of complex networks of programmable catalytic reactions? Future work will simulate complex reaction networks and compare the flux of chemistry through different pathways and assess the viability of interpreting combinations of simple elementary catalytic ratchets.
A more simple three-reaction-step catalytic system was assessed via simulation in Fig. 11, which consisted of A(g) reacting to D(g) through the surface species A*, B*, C*, and D*. As shown in Fig. 11a, this exergonic reaction exhibits overall −2.5 eV in free energy change overwhelmingly favoring the formation of D(g) relative to A(g). This programmable reaction is depicted for an oscillation amplitude of ΔBEA of 1.8 eV, and all four surface intermediates and their transition states change in accordance with the linear scaling relationships and the parameters of Fig. 11b. It should be noted that the change in binding energies in the example of Fig. 11 (up to 3 eV) are significantly larger than have been experimentally demonstrated.
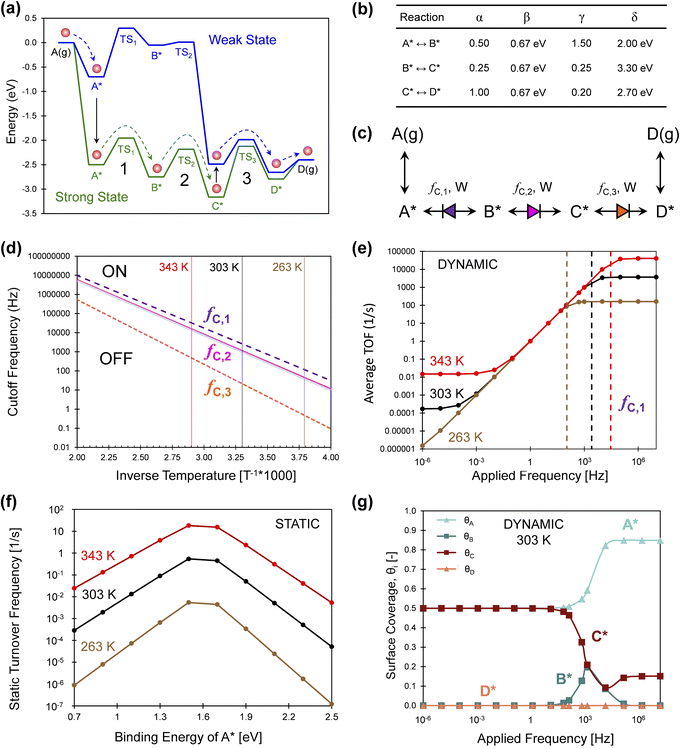 | ||
| Fig. 11 Series three-step catalytic escapement mechanism. (a) The reaction of A(g) to D(g) occurs on a catalytic surface through A*, B*, C*, and D* in two catalytic states that are strong (green) or weak (blue) binding. (b) The intermediate and transition state linear scaling parameters of the reaction from A* to D*. (c) All three surface reactions are weak-pass catalytic ratchets; their directionality was calculated by determining λ1, λ2, and λ3. (d) The cutoff frequencies of the three elementary catalytic ratchets, fc,i, was calculated as a function of reaction temperature. Three temperatures were considered of 263, 303, and 343 K. (e) Simulation of the three-step surface reaction determined the time-averaged turnover frequency at three temperatures over a frequency range of 10−6 to 107 Hz. Moderate applied frequencies exhibited turnover frequencies equal to the applied frequency. Maximum dynamic turnover frequency was achieved above the elementary reaction 1 cutoff frequency fc,1, depicted as vertical dashed lines for each temperature. (f) Static simulation of the three-step reaction at varying binding energy of A* results in Sabatier volcano peaks for three temperatures. (g) Surface coverages of A*, B*, C*, and D* on the dynamic three-step reaction for varying applied frequencies at 303 K. Tabulated data available in Fig. S6 of the ESI.† | ||
The exergonic reaction of Fig. 11 is particularly interesting as compared to the endergonic reaction of Fig. 1. The catalytic ratchet of Fig. 1 operates at specific amplitudes and frequencies to promote the unfavorable conversion of A(g) to B(g) using a net energy input to change catalyst states. In contrast, the series of catalytic ratchets in Fig. 11a serve the reverse purpose; the reaction pathway depicted by the red molecule follows a sequence of state changes and elementary reactions resulting in a net energy output (|ΔGA*,b→g| > |ΔGC*,g→b|) such that the reaction is generating work. In this manner, the series of catalytic elementary ratchet steps act as an ‘escapement,’ essentially metering out the reaction to proceed at the rate of applied frequency (similar to a mechanical watch). The total ‘net’ work will be negative (generating work) if the reaction proceeds through the A* blue-to-green transition as drawn; at sufficiently high temperatures and lower frequencies, the reaction could alternatively proceed in the blue state (weak binding) to B* and then react over TS2,b to C*, where it primarily releases heat. Selection of the applied frequency and reaction temperature will determine which path (work or heat generating) occurs.
The catalytic system of Fig. 11 was interpreted via the three characteristics of each catalytic elementary ratchet in Fig. 11c. All three elementary steps are weak-pass ratchets; ratchets 2 and 3 are forward directionality, and ratchet 1 is backward directionality. The cutoff frequencies of all three ratchets are calculated by eqn (15) and plotted as a function of inverse temperature in Fig. 11d. Reaction 3 always has the lowest cutoff frequency, while reactions 1 and 2 are similar higher frequencies.
The three-step reaction in Fig. 11a was simulated under dynamic conditions to determine the time-averaged turnover frequency (Fig. 11e) to form D(g) for varying temperature (263, 303, and 343 K) and varying applied frequency (10−6 to 107 Hz) at 1% conversion of A(g). These conditions were selected to demonstrate kinetics of relevance to a range of reasonable applied frequencies (up to ∼103 Hz). Simulations at all three temperatures exhibit three regions of catalytic behavior. At low applied frequencies, the programmable catalyst acts like two independent static catalysts averaged at a 50% duty cycle. At moderate applied frequencies, there exists parity between time-averaged TOF with the applied frequency; every turnover of the catalyst yields a catalytic turnover. At high frequency, the programmable catalyst achieves a maximum catalytic rate that is constant with applied frequency.
The observed dynamic catalytic behavior is consistent with prior examples and can be interpreted with the fundamental characteristics of elementary ratchets.1 For the three considered temperatures (263, 303, and 343 K), the static catalytic rates at 1% conversion of A(g) are depicted in Fig. 11f. This reaction yields a Sabatier volcano with varying binding energy of A*, such that the maximum static catalytic rate exists at BEA ∼ 1.6 eV. Moreover, oscillation of the binding energy of A* with time exhibits catalytic turnover frequencies in excess of the Sabatier peak by several orders of magnitude (compare Fig. 11e and f), as previously demonstrated.1
The transition between the parity region (equal applied frequency and TOF) and the maximum TOF at high applied frequency occurs at the cutoff frequency of the first elementary reaction. As marked with a vertical dashed line in Fig. 11e, the cutoff frequency of step 1 predicted by eqn (15) changes with temperature to demarcate the onset of the maximum time-averaged TOF. The overall rate limit imposed by step 1 is more apparent when observing the time-averaged surface coverage of all four surface species depicted in Fig. 11g. Below the step 1 cutoff frequency, fC,1, the time-averaged surface is comprised of equal fractions of A* and C*; this is consistent with the escapement mechanism, whereby the surface fills with A* in the weak state then fills with C* in the strong state. However, at the step 1 cutoff frequency, the surface coverage of C* decreases and A* increases as the rate of molecules traversing TS1 decreases. The only backwards ratchet in the mechanism becomes the overall rate limitation once it is turned on at frequencies above its cutoff frequency. B* is merely a short-lived intermediate in this mechanism.
The independent ratchet interpretation
The utility of interpreting independent catalytic elementary ratchets that are part of a larger reaction mechanism remains to be assessed. It is of course desirable to use the characteristics of each elementary ratchet (directionality, cutoff frequency, pass condition) to predict the catalytic behavior of a complex reaction network, as described in Fig. 10 and 11. A reaction network operating under programmed dynamics is an amalgamation of reaction frequencies; each forward (e.g., k1) or backwards (e.g., k−1) rate constant corresponds to a frequency. Assessing the cutoff frequency of each elementary reaction aids in identifying the relevant frequency for comparison with the applied frequency, which is shown in this work to be the cutoff frequency calculated from the second largest rate constant.Beyond simple model systems, it has already been shown that complex reaction networks of real chemistries exhibit complex behavior under dynamic programmable operation. For example, dynamic variation of surface strain of ruthenium catalyst surfaces in ammonia synthesis exhibited uncommon chemical behavior; the catalytic rate and extent of formation of ammonia was shown to change either above or below equilibrium with varying applied frequency.10 These behaviors could result from applied frequencies existing above or below different ratchet cutoff frequencies within the ammonia synthesis mechanism, changing the direction of reactions and yielding different catalytic rates. As these examples demonstrate, identification of the three key characteristics of elementary catalytic ratchets is just the beginning; future work is required to understand the impact of combinations of elementary ratchets in dynamic complex catalytic mechanisms.
Conclusions
Catalytic elementary reactions exhibiting ratchet-like behavior were evaluated to determine their fundamental behaviors under oscillating catalyst conditions to control chemistry and promote reactions away from equilibrium. Simulations evaluated oscillatory conditions that switched between two catalyst states of strong and weak binding of surface species to identify three characteristics that define elementary catalytic ratchets. First, promotion of surface chemistry in the forward or reverse direction away from equilibrium by elementary catalytic ratchets can be determined by a ratchet directionality metric based on the applied catalyst program duty cycle and the kinetic rate constants, which are based on the applied amplitude of surface energy oscillation. Second, each elementary catalytic ratchet oscillating between two catalyst states can be identified by one of its two states, strong or weak adsorbate binding, for which reactants traverse through the transition state. A third characteristic is the cutoff frequency of the elementary catalytic ratchet, which is the frequency which defines the transition of the ratchet between on and off conditions; applied frequencies above the cutoff frequency of a ratchet lead to promotion of reactions away from equilibrium, while applied frequencies below the cutoff frequency do not. These three characteristics of elementary ratchets are predictable by the kinetic rate constants of the catalytic ratchet and the characteristics of the applied oscillation to the catalyst surface; ratchet behavior was modeled for both time-averaged surface coverage of species and cutoff frequency behavior. It is proposed that future work can evaluate programmable complex reaction networks by assessing the three fundamental characteristics of elementary catalytic ratchets in each step of overall multi-step reaction networks.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
M. A. M., S. R. G., O. A. A. and P. J. D. conceived and designed the analysis. M. A. M., S. R. G., and P. J. D. performed the analysis and collected the data. M. A. M., S. R. G., R. G., L. G., O. A. A., and P. J. D. prepared figures, drafted the manuscript, and revised and edited all content.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported as part of the Center for Programmable Energy Catalysis, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences at the University of Minnesota under award #DE-SC0023464.References
- M. A. Ardagh, O. A. Abdelrahman and P. J. Dauenhauer, Principles of Dynamic Heterogeneous Catalysis: Surface Resonance and Turnover Frequency Response, ACS Catal., 2019, 9(8), 6929–6937, DOI:10.1021/acscatal.9b01606.
- M. A. Ardagh, T. Birol, Q. Zhang, O. A. Abdelrahman and P. J. Dauenhauer, Catalytic Resonance Theory: SuperVolcanoes, Catalytic Molecular Pumps, and Oscillatory Steady State, Catal.: Sci. Technol., 2019, 9(18), 5058–5076, 10.1039/c9cy01543d.
- M. Shetty, A. Walton, S. R. Gathmann, M. A. Ardagh, J. Gopeesingh, J. Resasco, T. Birol, Q. Zhang, M. Tsapatsis, D. G. Vlachos, P. Christopher, C. D. Frisbie, O. A. Abdelrahman and P. J. Dauenhauer, The Catalytic Mechanics of Dynamic Surfaces: Stimulating Methods for Promoting Catalytic Resonance, ACS Catal., 2020, 12666–12695, DOI:10.1021/acscatal.0c03336.
- T. M. Onn, S. R. Gathmann, Y. Wang, R. Patel, S. Guo, H. Chen, J. K. Soeherman, P. Christopher, G. Rojas, K. A. Mkhoyan, M. Neurock, O. A. Abdelrahman, C. D. Frisbie and P. J. Dauenhauer, Alumina Graphene Catalytic Condenser for Programmable Solid Acids, JACS Au, 2022, 2(5), 1123–1133, DOI:10.1021/jacsau.2c00114.
- J. Qi, J. Resasco, H. Robatjazi, I. B. Alvarez, O. Abdelrahman, P. Dauenhauer and P. Christopher, Dynamic Control of Elementary Step Energetics via Pulsed Illumination Enhances Photocatalysis on Metal Nanoparticles, ACS Energy Lett., 2020, 5(11), 3518–3525, DOI:10.1021/acsenergylett.0c01978.
- P. J. Dauenhauer, M. Shetty, M. A. Ardagh, Y. Pang and O. A. Abdelrahman, Electric-Field-Assisted Modulation of Surface Thermochemistry, ACS Catal., 2020, 10(21), 12867–12880, DOI:10.1021/acscatal.0c02124.
- O. A. Abdelrahman and P. J. Dauenhauer, Energy Flows in Static and Programmable Catalysts, ACS Energy Lett., 2023, 8(5), 2292–2299, DOI:10.1021/acsenergylett.3c00522.
- S. Borsley, J. M. Gallagher, D. A. Leigh and B. M. W. Roberts, Ratcheting Synthesis, Nat. Rev. Chem, 2024, 8, 8–29, DOI:10.1038/s41570-023-00558-y.
- S. Erbas-Cakmak, S. D. P. Fielden, U. Karaca, D. A. Leigh, C. T. McTernan, D. J. Tetlow and M. R. Wilson, Rotary and Linear Molecular Motors Driven by Pulses of a Chemical Fuel, Science, 2017, 358(6361), 340–343, DOI:10.1126/science.aao1377.
- G. R. Wittreich, S. Liu, P. J. Dauenhauer and D. G. Vlachos, Catalytic Resonance of Ammonia Synthesis by Simulated Dynamic Ruthenium Crystal Strain, Sci. Adv., 2022, 8(4), eabl6576, DOI:10.1126/sciadv.abl6576.
- R. D. Astumian, Kinetic Asymmetry and Directionality of Nonequilibrium Molecular Systems, Angew. Chem., 2024, 136(9), e202306569, DOI:10.1002/ange.202306569.
- S. Borsley, D. A. Leigh and M. W. Roberts, Molecular Ratchets and Kinetic Asymmetry: Giving Chemistry Direction, Angew. Chem., Int. Ed., 2024, 63(23), e202400495, DOI:10.1002/anie.202400495.
- P. M. Hoffmann, Life's Ratchet. How Molecular Machines Extract Order from Chaos., Basic Books, 2012, vol. 52, DOI:10.1002/anie.201304031.
- V. Serreli, C.-F. Lee, E. R. Kay and D. A. Leigh, A Molecular Information Ratchet, Nature, 2007, 445(7127), 523–527, DOI:10.1038/nature05452.
- M. Alvarez-Pérez, S. M. Goldup, D. A. Leigh and A. M. Z. Slawin, A Chemically-Driven Molecular Information Ratchet, J. Am. Chem. Soc., 2008, 130(6), 1836–1838, DOI:10.1021/ja7102394.
- S. Borsley, J. M. Gallagher, D. A. Leigh and B. M. W. Roberts, Ratcheting Synthesis, Nat. Rev. Chem, 2024, 8(1), 8–29, DOI:10.1038/s41570-023-00558-y.
- R. D. Astumian, Stochastically Pumped Adaptation and Directional Motion of Molecular Machines, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(38), 9405–9413, DOI:10.1073/pnas.1714498115.
- R. D. Astumian, Stochastic Conformational Pumping: A Mechanism for Free-Energy Transduction by Molecules, Annu. Rev. Biophys., 2011, 40, 289–313, DOI:10.1146/annurev-biophys-042910-155355.
- P. J. Dauenhauer, Up up down down Left Right Left Right B A Start for the Catalytic Hackers of Programmable Materials, Matter, 2023, 6(12), 4145–4157, DOI:10.1016/j.matt.2023.11.008.
- J. Qi, J. Resasco, H. Robatjazi, I. B. Alvarez, O. Abdelrahman, P. Dauenhauer and P. Christopher, Dynamic Control of Elementary Step Energetics via Pulsed Illumination Enhances Photocatalysis on Metal Nanoparticles, ACS Energy Lett., 2020, 3518–3525, DOI:10.1021/acsenergylett.0c01978.
- P. J. Dauenhauer, M. A. Ardagh, M. Shetty, A. Kuznetsov, Q. Zhang, P. Christopher, D. G. Vlachos and O. A. Abdelrahman, Catalytic Resonance Theory: Parallel Reaction Pathway Control, Chem. Sci., 2020, 11(13), 3501–3510, 10.1039/c9sc06140a.
- C. C. Tedesco, J. R. Kitchin and C. D. Laird, Cyclic Steady-State Simulation and Waveform Design for Dynamic/Programmable Catalysis, J. Phys. Chem. C, 2024, 128(22), 8993–9002, DOI:10.1021/acs.jpcc.4c01543.
- R. D. Astumian and I. Derényi, Fluctuation Driven Transport and Models of Molecular Motors and Pumps, Eur. Biophys. J., 1998, 27(5), 474–489, DOI:10.1007/s002490050158.
- Y. Qiu, Y. Feng, Q.-H. Guo, R. D. Astumian and J. F. Stoddart, Pumps through the Ages, Chem, 2020, 6(8), 1952–1977, DOI:10.1016/j.chempr.2020.07.009.
- C. Cheng, P. R. McGonigal, S. T. Schneebeli, H. Li, N. A. Vermeulen, C. Ke and J. F. Stoddart, An Artificial Molecular Pump, Nat. Nanotechnol., 2015, 10(6), 547–553, DOI:10.1038/nnano.2015.96.
- L. Zhang, H. Wu, X. Li, H. Chen, R. D. Astumian and J. F. Stoddart, Artificial Molecular Pumps, Nat. Rev. Methods Primers, 2024, 4(1), 1–21, DOI:10.1038/s43586-024-00291-w.
- Y. Feng, M. Ovalle, J. S. W. Seale, C. K. Lee, D. J. Kim, R. D. Astumian and J. F. Stoddart, Molecular Pumps and Motors, J. Am. Chem. Soc., 2021, 143(15), 5569–5591, DOI:10.1021/jacs.0c13388.
- R. D. Astumian, C. Pezzato, Y. Feng, Y. Qiu, P. R. McGonigal, C. Cheng and J. F. Stoddart, Non-Equilibrium Kinetics and Trajectory Thermodynamics of Synthetic Molecular Pumps, Mater. Chem. Front., 2020, 4(5), 1304–1314, 10.1039/D0QM00022A.
- R. D. Astumian, Nonequilibrium Steady States, Ratchets, and Kinetic Asymmetry, Matter, 2023, 6(8), 2533–2536, DOI:10.1016/j.matt.2023.07.007.
- M. A. Ardagh, T. Birol, Q. Zhang, O. A. Abdelrahman and P. J. Dauenhauer, Catalytic Resonance Theory: SuperVolcanoes, Catalytic Molecular Pumps, and Oscillatory Steady State, Catal.: Sci. Technol., 2019, 9(18), 5058–5076, 10.1039/c9cy01543d.
- J. E. Sutton and D. G. Vlachos, A Theoretical and Computational Analysis of Linear Free Energy Relations for the Estimation of Activation Energies, ACS Catal., 2012, 2(8), 1624–1634, DOI:10.1021/cs3003269.
- J. Greeley, Theoretical Heterogeneous Catalysis: Scaling Relationships and Computational Catalyst Design, Annu. Rev. Chem. Biomol. Eng., 2016, 7(1), 605–635, DOI:10.1146/annurev-chembioeng-080615-034413.
- Z.-J. Zhao, S. Liu, S. Zha, D. Cheng, F. Studt, G. Henkelman and J. Gong, Theory-Guided Design of Catalytic Materials Using Scaling Relationships and Reactivity Descriptors, Nat. Rev. Mater., 2019, 4(12), 792–804, DOI:10.1038/s41578-019-0152-x.
- S. R. Gathmann, M. A. Ardagh and P. J. Dauenhauer, Catalytic Resonance Theory: Negative Dynamic Surfaces for Programmable Catalysts, Chem Catal., 2022, 2(1), 140–163, DOI:10.1016/j.checat.2021.12.006.
- C. Rackauckas and Q. Nie, DifferentialEquations.Jl – A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia, J. Open Res. Software, 2017, 5(1) DOI:10.5334/jors.151.
- SciML, RadauIIA5 Solver, https://docs.sciml.ai/DiffEqDocs/stable/solvers/ode_solve/#SciMLBase.RadauIIA5.
- T. M. Onn, S. R. Gathmann, S. Guo, S. P. S. Solanki, A. Walton, B. J. Page, G. Rojas, M. Neurock, L. C. Grabow, K. A. Mkhoyan, O. A. Abdelrahman, C. D. Frisbie and P. J. Dauenhauer, Platinum Graphene Catalytic Condenser for Millisecond Programmable Metal Surfaces, J. Am. Chem. Soc., 2022, 144(48), 22113–22127, DOI:10.1021/jacs.2c09481.
- K.-R. Oh, T. M. Onn, A. Walton, M. L. Odlyzko, C. D. Frisbie and P. J. Dauenhauer, Fabrication of Large Area Metal-on-Carbon Catalytic Condensers for Programmable Catalysis, ACS Appl. Mater. Interfaces, 2024, 16(1), 684–694, DOI:10.1021/acsami.3c14623.
- T. M. Onn, K.-R. Oh, D. Z. Adrahtas, J. K. Soeherman, J. A. Hopkins, C. D. Frisbie and P. J. Dauenhauer, Flexible and Extensive Platinum Ion Gel Condensers for Programmable Catalysis, ACS Nano, 2024, 18(1), 983–995, DOI:10.1021/acsnano.3c09815.
- S. Amano, M. Esposito, E. Kreidt, D. A. Leigh, E. Penocchio and B. M. W. Roberts, Using Catalysis to Drive Chemistry Away from Equilibrium: Relating Kinetic Asymmetry, Power Strokes, and the Curtin-Hammett Principle in Brownian Ratchets, J. Am. Chem. Soc., 2022, 144(44), 20153–20164, DOI:10.1021/jacs.2c08723.
- W. P. Jencks, Catalysis in Chemistry and Enzymology, McGraw-Hill Book Co, New York, NY, 1969, vol. 47, DOI:10.1021/ed047pa860.2.
- R. D. Astumian, P. B. Chock, T. Y. Tsong and H. V. Westerhoff, Effects of Oscillations and Energy-Driven Fluctuations on the Dynamics of Enzyme Catalysis and Free-Energy Transduction, Phys. Rev. A, 1989, 39(12), 6416–6435, DOI:10.1103/PhysRevA.39.6416.
- B. Robertson and R. D. Astumian, Michaelis-Menten Equation for an Enzyme in an Oscillating Electric Field, Biophys. J., 1990, 58(4), 969–974, DOI:10.1016/S0006-3495(90)82441-3.
- K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Nørskov, Ammonia Synthesis from First-Principles Calculations, Science, 2005, 307(5709), 555–558, DOI:10.1126/science.1106435.
- L. C. Grabow and M. Mavrikakis, Mechanism of Methanol Synthesis on Cu through CO2 and CO Hydrogenation, ACS Catal., 2011, 1(4), 365–384, DOI:10.1021/cs200055d.
- J. A. Dumesic, L. M. Aparicio, J. E. Rekoske, A. A. Treviño and D. F. Rudd, The Microkinetics of Heterogeneous Catalysis, ACS Professional Reference Book, American Chemical Society, Washington, DC, 1993 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details including data tables of results presented in figures, derivation of the ratchet directionality metric, and comparison of average surface coverage models. See DOI: https://doi.org/10.1039/d4sc04069d |
| This journal is © The Royal Society of Chemistry 2024 |