Experimental and theoretical studies of the electronic transport of an extended curcuminoid in graphene nano-junctions

Abstract

Exploiting the potential of curcuminoids (CCMoids) as molecular platforms, a new 3.53 nm extended system (pyACCMoid, 2) has been designed in two steps by reacting a CCMoid with amino-terminal groups (NH₂-CCMoid, 1, of 1.79 nm length) with polycyclic aromatic hydrocarbon (PAH) aldehydes. CCMoid 2 contains pyrene units at both ends as anchoring groups to optimize its trapping in graphene nano-junctions created by feedback-controlled electro-burning. The measured I–V characteristics show gate-dependent behaviour at room temperature and 10 K, with increased conductance values compared to shorter CCMoids previously reported, and in agreement with DFT calculations. Our results show that the adjusted molecular design improves the conductance, as system 2 separates the conductive backbone from the anchor groups, which tend to adopt a planar configuration upon contact with the graphene electrodes. DFT calculations using Green functions of a set of different molecular conformations of 2 on graphene electrodes show a direct relationship between the units (e.g. pyrene, amide, etc.), in the molecule, through which electrons are injected and the conductance values; where the size of the spacing between the graphene electrodes contributes but is not the dominant factor, and thus, counter-intuitively the smallest spacing gives one of the lowest conductance values.

---

Introduction

Curcuminoids (CCMoids)¹ are molecular platforms,^2,3 that have been used to make an important contribution to biomedical science,^4,5 and are making their way into other areas of nanoscience, including molecular electronics. Examples of this is their exploration on surfaces, as luminescent molecules, using the UHV-STM technique⁶ or as efficient near-IR emitters,^7,8 owing to the impact of their conjugated configuration. In addition, some of us have shown that the combination of CCMoid skeletons with appropriate anchoring groups allows their use as nanowires suitable for single-molecule electronic transport studies.^9–11 The diarylheptanoid backbone efficiently mediates electron transport, and the terminal groups allow the binding to Au electrodes.¹² Using the mechanically controlled break junction technique,^13,14 we have established correspondences between the affinity of the terminal groups to Au and the conductance values and configurations of the molecules embedded between these electrodes.¹⁵ The effect of coordination has also been explored, finding the conditions under which certain CCMoids exhibit electronic switching behaviour.¹⁶

Modifications of the terminal groups also enable π–π coupling with graphene electrodes. In this topic, we have synthesized a family of CCMoids containing small polycyclic aromatic hydrocarbons (PAHs, anthracene units, Fig. 1a and b) as anchoring groups and varying the CCMoid chain dimensions, from 7 carbons (9ACCM, Fig. 1a) to 11C (9ALCCM, Fig. 1b), respectively. Such systems were studied on three-terminal hybrid devices, with graphene flakes as the source and drain electrodes and Si as a gate, respectively, separated by SiO₂ (insulator).^9–11 The motivation for such layout was given by the low atomic mobility of graphene at room temperature, its convenient work function suitable for matching the discrete energy levels of the molecules and the reduced shielding of the gate electrode potential.^12,17–19 For standard-sized molecules to form effective bridges between graphene-based electrodes, they must be separated by nanogaps of approximately 1–2 nm, and feedback-controlled electroburning is normally used to create them.⁹ Thus, 9ACCM and 9ALCCM (Fig. 1a and b) were embedded between few-layer graphene (FLG) electrodes.^9,10 Our studies showed that the longer the molecule (maintaining conjugation), the better the coupling with the FLG electrodes, finding for 9ALCCM the coexistence of vibrational excitations with Coulomb blocking physics at low temperature, a feature that was not observed for the former.¹⁰ The comparison also concluded that the enhanced coupling between the graphene flakes and the anthracene groups compensates for the final electronic transport of the molecules, yielding conductance values of the same order for the two systems (approximately 10⁻⁶G₀). The proposed route provided exciting results, but the methodology of adding double bonds to the CCMoid chain cannot be explored indefinitely, as it not only increases the molecular dimensions, but also the number of conformations which hinders the linear arrangement of the molecules.

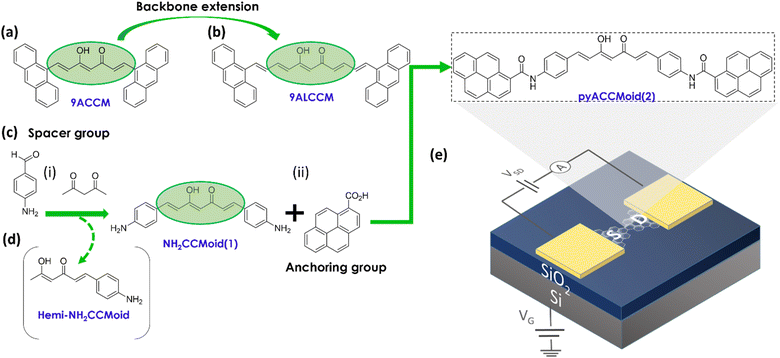Fig. 1 Chemical structures of (a) 9ACCM and (b) 9ALCCMoid emphasizing the increased backbone length, previously studied in graphene-hybrid molecular junctions.^9,10 (c) Synthetic pathway of (d) pyACCMoid (2): (i) inclusion of the spacer group through a Pabon's modified reaction and (ii) addition of the anchoring group by the formation of the amide bond. The pyrene groups stabilize the molecule in the junctions through π–π stacking to the electrodes. (e) Chemical structure of pyACCMoid integrated into a (f) three-terminal single-layer graphene (SLG) device where a doped silicon substrate is covered with 300 nm of thermal SiO₂ and used as a back-gate to modulate charge transport of the molecule trapped in graphene nano-gaps opened by feedback controlled electro-burning.

In this article we report a new derivative of the CCMoid family, with optimal dimensions and anchoring groups, which maintains a planar structure when incorporated between graphene electrodes and, as a consequence, produces a higher conductance compared to previous studies. First, we describe a synthetic approach to CCMoid elongation different from that mentioned above, using a standard CCMoid (NH₂CCMoid, 1, Fig. 1c) with terminal groups capable of further reacting with PAH units. This gives rise to a new CCMoid (pyACCMoid, 2, Fig. 1e), with the typical 7C skeleton but with extended aromatic arms. Here we have explored the amide bond, between the terminal amines of CCMoid 1 and the carboxylic groups of a pyrene derivative. Tests with an analogue of this CCMoid using an imine bond were abandoned because the system was unstable in solution over time (not shown). Also, pyrene is known to provide a reliable π–π molecule-graphene bond without compromising the solubility in organic solvents of the molecular systems.²⁰ One of the advantages of this procedure is that CCMoids (e.g.: 1) can be synthesized in a one-step reaction.¹⁸ Therefore, by carefully choosing the final elements, we can simplify the addition of functional groups of interest. The concept can be extrapolated to other reactive units, but this is beyond the scope of this work. Certainly, CCMoid 2 exhibits extended dimensions, while maintaining CCMoid conjugation and some flexibility, through the amine bond, enhancing its π–π interaction capability for better accommodation between single-layer graphene electrodes (Fig. 1f). Second, we show how our devices are now fabricated on commercially available substrates and how nanogaps are formed by electroburning on a single layer graphene²¹ with the advantage of being able to integrate most of the fabrication steps into standard semiconductor processing. We then present experimental studies of their single-electron transport properties that corroborate that the electronic behaviour benefits from the tailored molecular design. Third, we support the experimental results with DFT calculations and provide a deeper understanding of the findings by studying a set of possible configurations of the graphene/pyACCMoid/graphene system, analysing the relationship between the molecular groups at which the electron is injected and the conductance values achieved, discussing factors such as the spacing between graphene electrodes and the symmetric/asymmetric arrangement of the CCMoid.

Results and discussion

Synthesis and characterization of pyACCMoid (2)

The synthesis of CCMoids is a one-step process²² based on the use of acetylacetone, its coordination with boron derivatives and subsequent bilateral growth, through the process of condensation with an aldehyde. This approach can present variations mainly depending on the solubility and reactivity of the latest. In our case, the optimal synthesis of NH₂CCMoid (1, Fig. 1c) was achieved by performing the reaction in DMF and using an excess of freshly made 4-aminobenzaldehyde²² (30% yield). Interestingly, in the same process, the asymmetric system, the hemi-NH₂CCMoid (8% yield), was identified and isolated by filtration (Fig. 1d). Both CCMoids have been characterized by standard methods (Fig. S1–S11†) and their HOMO–LUMO energy gaps estimated by cyclic voltammetry (CV) in solution to obtain the values of the electrical bandgap E_{G_el}, and by UV-vis absorption spectroscopy in the solid-state (Fig. S3–S4, S9–S10†) for the optical bandgap E_{G_op}, with E_{G_el} and E_{G_op} values slightly above 2.0 eV for both.

As discussed above, NH₂CCMoid (1) has been reacted with PAH-based units having a terminal acidic group giving rise to a PAH-CCMoid using amide bonds: pyACCMoid (2) (Fig. 1e). Optimal conditions for the synthesis of 2 include the use of a microwave (MW) reactor.^23–25 Like 1, the new system has been characterized in a similar manner (Fig. S12–S17†) finding E_{G_el} and E_{G_op} values of 2.4 and 2.5 eV, correspondingly. The comparison of the HOMO–LUMO gaps estimated for systems 1 and 2 agrees well with what is expected for the more donor character of the amino group (in NH₂CCMoid, 1) versus the amide group (in pyACCMoid, 2) which is more acceptor, being the gap smaller for the former (Fig. S18†). The data agree with Density Functional Theory (DFT) calculations performed for the two systems (Fig. S19–S21†), summarised in Table S1,† and with additional theoretical studies on CCMoids.²⁶ Regarding the molecular size, the optimised theoretical structure shows dimensions between the most distant C atoms of 3.53 nm for 2, which is substantially longer compared and previously published systems (9Accm and 9ALCCM, Fig. 1a and b) with distances of 1.68 and 2.07 nm, respectively. Furthermore, it is interesting to emphasise the rotational nature of the amide bond,²⁷ which provides additional degrees of freedom to the CCMoid when accommodating between the graphene electrodes during the deposition process (see the DFT section and ESI†).

pyACCMoid (2) hybrid graphene nano-junctions in three-terminal devices: processing and measurements

For device fabrication, we used commercial substrates with single-layer chemical vapour deposited (CVD) graphene on SiO₂/Si (300 nm SiO₂). A scheme of the process is provided in the ESI (Fig. S22†). As a brief description, graphene is patterned in a bow-tie shape with a constriction of about 400 nm combining e-beam lithography and O₂ plasma etching. Then, the gold contacts are deposited by laser lithography, metal evaporation and lift-off. Graphene nano-junctions (GNJs) are then formed by using feedback-controlled electro-burning. This process relies on Joule heating which in the presence of atmospheric oxygen promotes the removal of carbon atoms progressively narrowing down the constriction.²¹ It is performed in air and at room temperature by ramping a voltage up to 10 V across the graphene constriction. In the electro-burning process, the output current from the voltage ramp is monitored by feedback software that sets the bias voltage rapidly to zero once the target resistance value across the junction is reached. The maximum voltage flowing through the junction is slowly increased until resistance values above 500 MΩ are achieved, preventing the formation of large gaps with the subsequent creation of split widths larger than a molecule at their closest points. The outcome of the process classified according to the measurement of the zero-bias resistance after electroburning is represented in Fig. S23.†

Opened constrictions are measured in vacuum and at room temperature by applying a bias voltage (V) and measuring the output current (I) and display the typical tunnel I–V characteristics (see inset of Fig. 2a and S24–S25†), indicating that the GNJs are in the order of a few nanometers. Their sizes can be estimated by using the Simmons model²⁸ with the tunnelling barrier height (determined by the work function of the electrodes), the width, and the area in the bias-voltage response window, as fit parameters (see ESI†). The overview of experiment statistics, based on the measurement of the zero-bias resistance after each step, i.e., electro-burning, molecule deposition, and cooling down, is detailed and discussed in the ESI (Fig. S23†). Before molecule deposition, the current measurement at fixed bias, as a function of the gate voltage applied at the Si bottom substrate, represented in Fig. 2b (referred to as a “gate-sweep” in the following) does not show any current modulation. The same is observed for the I–V characteristics measured as a function of gate voltage and shown in Fig. S25.† This and the nanometric size of the junctions imply that they can be used in the subsequent measurements. Molecules are deposited by dip coating the electro-burnt devices in a 0.1 mM solution of pyACCMoid (2), in THF for 1 hour, followed by rinsing with pure THF (an AFM picture of optimization of the surface functionalization is shown in ESI Fig. S26†). The solvent is chosen to dissolve the molecular compound without altering the graphene surface. Before starting the measurements, the samples are left in air for 30 min, and dried under vacuum for another 30 min more, to ensure complete solvent evaporation. We started the electrical characterization of the molecular devices at room temperature in vacuum (10⁻⁵ mbar) observing a resistance decrease of an order of magnitude, or higher, in about 12% of the devices incubated, suggesting the presence of molecules inside the GNJ (see Fig. S23† for the overview of the experiment statistics). We observed current variations in the order of a few picoamperes distinct from noise in the gate-sweep measurements shown in Fig. S27.† We note a resistance variation of about an order of magnitude in the I–V characteristics, measured as a function of bias and gate voltage and compiled in the stability diagram shown in Fig. S28.†

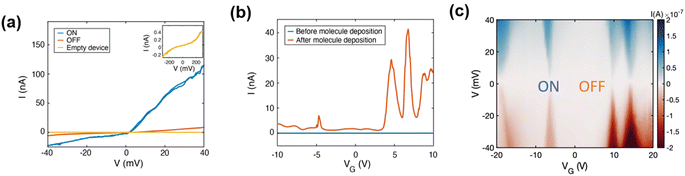Fig. 2 (a) Current vs. bias voltage (I–V) characteristic of devices through the different steps of the experiment: right after the electro-burning procedure (empty device, yellow curve) and after molecular deposition: in high current (ON) and blockaded regions (OFF) measured at 10 K. Empty devices display an order of magnitude lower current and non-linear increase at high voltage bias values, as depicted in the inset. (b) Current between the source and drain for a fixed bias voltage of 10 mV as a function of gate voltage (gate-sweep) before (blue, room temperature) and after (orange, 10 K) deposition of molecules. The low-temperature gate-sweep displays a clear current increase attributed to molecular resonances; the room-temperature gate-sweeps also exhibit features in the current shown in Fig. S27.† (c) Current as a function of source–drain bias and gate voltage (stability diagram) measured at 10 K. Alternating regions of high (ON) and low (OFF) current are visible giving rise to diamond-shaped areas (corresponding line cuts are shown in (a)).

At low temperatures (10 K), the conductance modulations in the gate sweeps become more defined, as seen in Fig. 2b (orange trace). This is also seen in the significant current enhancement measured in the “ON” state and represented in Fig. 2a showing an asymmetric current response to the voltage application which origin will be discussed in relation with results from theoretical modelling. We observed, as elsewhere reported, that cooling may cause some open GNJs to close, and the opposite, some closed GNJs to open, highlighting the presence of tensile stress building up in the graphene monolayer as the temperature changes. From over 39 junctions measured at low temperatures, 12 displayed resistances in the range expected for a molecule bridging electrode (hundreds of MΩ up to GΩ), among which two showed evidence of molecular signatures in the gate voltage range accessible (Fig. 2b and S29†). DFT calculations confirm such transport properties by comparing them with the energy of the charge state of the molecule.²⁹ The energies involved in the oxidation/reduction processes of molecule 2 show, also in agreement with the electrochemical data, a greater number of reduction processes (Fig. S29(c)†). The yield is close to values reported in the literature for devices fabricated with a similar procedure.²⁰ We observed variations of the current intensity measured in the gate-sweep between different devices (as highlighted for the two molecular junctions measured at low-temperature in Fig. S29 and S30†) as well as on repeated measurements on the same device, also seen in the slight shifting of the resonances between Fig. 2b and c causing a minor difference between the gate voltage at which they occur. These variations can be attributed to the different molecular conformations within the junction, as supported by the results of the DFT calculations showing the relevance of the spatial configuration of the molecule within the junction and will be further discussed in the theoretical section.

In GNJs, molecular species commonly present weak/intermediate coupling^9–11 to the source and drain graphene electrodes, resulting in charge transport dominated by single-electron transistor (SET) behaviour. In our case, the pyrene units are the main anchor to the graphene electrodes, leading to current suppression (Coulomb blockade) when the molecular energy level falls outside the bias voltage range. By applying a gate voltage, the molecular orbital levels align with the chemical potential of the electrodes causing resonant charge transport, as evidenced by current resonances in gate-sweeps (Fig. 2b, orange trace) and Coulomb Diamonds (CD) in the stability diagram characterized by current-blockaded regions (Fig. 2c, whitish areas) alternating with resonant transport regions (Fig. 2c, blue and red areas). Resonant peaks correspond to a change in the ground state of the molecule, indicating a transition of its electronic state at zero bias voltage. This point is referred to as the charge degeneracy point (CDP). A comparison of the stability diagrams of the previously published 9ACCM and 9ALCCM systems^9,10 with that of CCMoid 2 shows that the signal intensity has now increased, confirming charge transport enhancement of our new system.

The gate coupling, α, can be extracted from the slopes of the Coulomb diamonds, β and γ (as explained in the ESI and illustrated in Fig. S31†). We find α = 0.005 (0.5%) for the diamond around V_G = −25 V and α = 0.011 (1.1%) for that around V_G = −8 V. These values are in the lower range expected for graphene-based molecular junctions in three-terminal devices with 300 nm of SiO₂ as a gate dielectric.³⁰ We have also calculated the gate couplings for both diamonds of the second device (shown in Fig. S32†), reporting a large difference between the two accompanied by opposite source-drain coupling asymmetry. Both observations point to a different origin of the corresponding CDPs in this case, as discussed in the ESI.† For both molecular junctions, we find similar and large addition energy spacing (more than 400 meV). Large addition energies are usually observed in molecular junctions as opposed to a graphene island associated with a lower, and more variable, addition energy.³¹ It should be also stressed that in graphene-based molecular junctions, the gate field can affect the chemical potential of the electrodes giving rise to spectroscopic features associated with quantum interferences from the electrodes that are not intrinsic to the molecule^30,32 and limiting the possibility of measuring accurately the molecular resonances. This has been already observed^30,32 and here it is supported by the presence of lines not running parallel to the diamond edges (as displayed in the conductance map shown in Fig. S32(a)†).

Theoretical study of charge transport through pyACCMoid hybrid GNJs

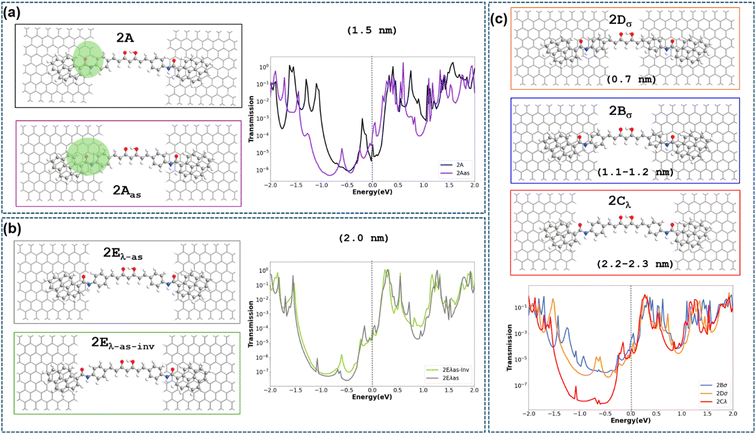
The transport properties of 2 deposited on a GNJ (Fig. 3a, 2A) have been first analysed by using Non-Equilibrium Green Function (NEGF)-DFT methods (ESI† Computational details). The calculated transmission curve (Fig. S19†) shows that the levels closest to the Fermi level are unoccupied transmission eigenfunctions (described in Fig. S19(b)† as TE1 and TE2, respectively). The comparison of their shape with the frontier orbitals of the isolated 2 (Fig. S20†) indicates that TE1 is essentially related to the LUMO orbital, while TE2 corresponds to LUMO+1 slightly mixed with the LUMO. The transport by electron carriers is also evidenced by the projected local density of states (Fig. S33†), which also shows a large HOMO–LUMO gap in the region corresponding to the CCMoid skeleton (not in contact with the electrodes) that is reduced in the two parts of pyACCMoid/graphene contact (Fig. 3a configuration “2A”) due to the presence of occupied energy levels near the Fermi level. The calculation of the conductance (at 0.1 V) for this configuration gives a value of 1.3 × 10⁻⁴G₀ that fits in the range of the experimental data. In addition, transmission pathways represented in Fig. S34† show that the transport is exclusively through the molecule.

Fig. 3 Seven configuration models: (a) 2A featuring the CCMoid symmetrically coupled to the electrodes with the backbone bridging a nano-gap of 1.5 nm 2A_as with an identical gap but asymmetric distribution of the CCMoid (anchoring on one side through the benzene-amide-pyrene moieties) along with the transmission spectrum (in log scale) corresponding to the two configurations; (b) 2E_λ-as and 2E_λas-inv showing asymmetric coupling of the CCMoid inside the nano-gap of 2 nm and its reverse, respectively accompanied by their transmission spectra. (c) 2B_σ and 2D_σ considering symmetric coupling with shorter nano-gaps; 2C_λ corresponding to symmetric coupling in the largest calculated nano-gap.

In addition, we considered a set of scenarios resulting from combining different gap sizes and arrangements of 2 in the gap. We analysed the configurations produced by the attachment of the different CCMoid moieties (diarylheptanoid chain/phenyl/amide/pyrene) to the graphene electrodes together with symmetric/asymmetric molecular arrangements with respect to the electrodes. Among all possibilities, we restricted our study to those shown in Fig. 3. For that, we took as reference the arrangement called 2A (described above), with the pyACCMoid disposed symmetrically between the electrodes spanning a gap of approximately 1.5 nm, with the amide-pyrene groups anchoring to the graphene electrodes. The additional configurations display shorter (σ) and longer (λ) gaps where CCMoid 2 appears to be attached to the graphene edges either symmetrically (Fig. 3, 2B_σ, 2C_λ and 2D_σ) or asymmetrically (Fig. 3, 2A_as, 2E_λ-as and 2E_λ-as-inv), respectively. Among the asymmetric cases (2E_λ-as), a reversed situation (2E_λ-as-inv) was also considered. For all of them, the size of the gap was estimated considering the first C/N/O atoms (from the CCMoid) that come into contact with each side of the electrodes. The calculations were carried out as for 2A, and Fig. 3 (centre) depicts the transmission spectra surrounded by the corresponding DFT optimised structures for all the different configurations.

The theoretical values of the conductance for the seven models in Fig. 3 have been calculated using the value of the transmission at the Fermi level (Table 1). Among the symmetric systems, 2Bσ, with a relatively short gap (1.1.–1.2 nm, smaller than 2A), shows the highest conductance value. However, according to the calculations, the size of the gap is not the main determinant of the conductance values. This is evident in the 2Dσ system, whose distance between the graphene electrodes is the shortest but provides the lowest conductance value. To understand the results obtained it is necessary to consider that transport in this type of device will involve the injection of electrons from the left electrode (source) to the molecule, as can be seen in the transmission pathway in Fig. S34.† By sorting the conductance data obtained by transmission in decreasing order and comparing them with which part of the molecule is in contact with the edge of the left electrode (see Table 1 and Fig. 3), it is clearly observed that the devices with the phenyl group in that position (2Bσ and 2A_as) are those with the highest conductance values (electron injection is more effective). Between these two values, the one with the smallest nanogap (2Bσ) also benefits from this fact, presenting the highest conductance value among them.

Table 1 Conductance values for the different graphene–pyACCMoid–graphene configurations ordered (from left to right) according to decreasing conductance values calculated from the transmission values at the Fermi level. Contact groups (pyrene/phenyl/amido/chain) of CCMoid 2 refer to those contacting the left electrode ends. Nanogap distances are collected from the models shown in Fig. 3

	2Bσ	2Aas	2Eλ-as-inv	2Cλ	2Dσ	2A	2Eλ-as
Conductance T Fermi level (10^−4G0)	2.8	1.2	0.80	0.49	0.32	0.23	0.16
Contact group of 2 with the left electrode (source)	Phenyl	Phenyl	Pyrene	Pyrene	Diarylheptanoid chain	Amide	Amide
Gap (nm)	1.1–1.2	1.5	2.0	2.2–2.3	0.7	1.5	2.0

---

The next two configurations in order of the highest conductance values are 2E_λ-as-inv and 2C_λ, which feature the longest nanogaps (2.0 nm and 2.2–2.3 nm, respectively) and the contact with the molecule is through the pyrene group. Comparison of these two cases again indicates how, in the presence of a similar contact between the molecule and electrode, the one presenting the smaller nanogap provides a higher conductance value (2E_λ-as-inv). The three lowest conductance values correspond to molecule–electrode contacts that do not occur through aromatic rings of the molecule. The most striking case is the system 2Dσ, which, despite having the smallest nanogap, has the lowest conductance value, contacting the edge of the source through the double bonds of the diarylheptanoid chain in 2. Finally, the two lowest values (2A and 2E_λ-as) occur when the contact is through the amide group of 2, and again there is a higher value for the case with a smaller nanogap (2A). These results demonstrate that the presence and arrangement of the aromatic rings, in the molecule–electrode contact area, is critical to obtain high conductance values and that, in cases with similar contacts, a smaller nanogap also improves transport.

Back to the calculated I–V plots (Fig. S35†), an interesting point is the presence of negative differential conductance (NDC) observed for the systems with the largest gaps, 2C_λ, 2E_λ-as and 2E_λ-as-inv, respectively. Experimental signatures of NDC can be spotted in the bottom part of Fig. S32(a),† however, it should also be pointed out that in experimental measurements NDC features could be due to various reasons. From a theoretical point of view, the NDC originates from the energetic disposition of the transmission peaks in the width-dependent bias windows and by the degree of localization of the transmission eigenfunctions. This behaviour is seen in Fig. S36† where the transmission of the most important peak (indicated with an asterisk) decreases its energy within the potential window when a voltage of 0.5 V instead of 0.4 V is applied. Likewise, the transmission function increases its location on the left side of the CCMoid at the higher voltage with respect to the lower one.

It is important to note that only when the molecule is symmetrically coupled to both electrodes, the transmission function is symmetrical with the applied voltage, for positive and negative energy values. In all the other cases, we see that when the molecule–electrode coupling is asymmetric, the enhancement of the transmission function is different for positive/negative energy values giving rise to the asymmetric current response seen in the theoretical I–V plots in Fig. S35† for the 2A_as and 2E_λ-as configurations. Given the limited knowledge of the experimental gap size, it is not trivial to find an exact connection between theoretical and experimental results. However, the appearance of asymmetry in the experimental I–V data suggests that the experimental conformation could be similar to one of the two theoretical configurations that give an asymmetric theoretical I–V response. Finally, we recall that the existence of different binding configurations is common in these experiments where there is no control over the landing of the molecule on the electrodes. Switching between different configurations could affect the reproducibility of the measurements over time and limit the accurate characterization of the molecular resonances.

Conclusions

We have synthesized, in an optimized number of steps, a new long CCMoid, pyACCMoid (2), which contains pyrene side groups connected via amide bonds to the π-conjugate CCMoid backbone, resulting in a total effective length for the molecule of 3.53 nm. Because of the amide bond, the extended arms confer rotational flexibility to the system favouring its accommodation between the heterogeneous edges of GNJs obtained by electro-burning. Studies of gate-dependent charge transport confirm the existence of pyACCMoid molecules coupled through π–π stacking to SLG electrodes. The large ON/OFF current ratio linked to the molecule CDP can be distinguished from quantum interference in the electrodes by a different capacitive coupling and asymmetry. In agreement with DFT calculations, we report higher conductance values compared to previously explored graphene–CCMoid molecular devices, due to improvements in molecular length and electrode interactions. Theoretical studies were performed considering a set of possible configurations of the graphene–pyACCMoid–graphene system showing that there is a direct correlation between the calculated conductance values and the groups of the CCMoid molecule through which the injection of electrons is performed at the left electrode (source). Mainly the presence of aromatic rings in this contact provides the highest conductance values. Moreover, in cases with similar molecule–electrode contacts, smaller nanogaps increase the transport. These results validate the chemical strategy explored in this work, based on the introduction of a spacer group between the conductive backbone and the anchor groups against the previously explored relying on the extension of the conjugate chain. Our methodology can be extrapolated to other PAH derivatives, where anticipation of possible solubility difficulties (by adding groups such as alkyl chains) can lead to more extended systems, such as nanoribbons, where the CCMoid backbone can provide coordination sites.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

T. C. L. and D. H.: investigation, molecular data collection, and data analysis – molecular synthesis and characterization; T. B. and R. Z.: conceptualization, investigation, device fabrication and characterization, electrical transport measurements and data analysis; R. P.: assistance in device preparation and analysis of physical data; R. Z., A. G. C., E. R., H. Z. and N. A. A.: conceptualization, investigation, data analysis, validation, supervision; all authors contributed to the writing and editing of the article. T. C. L. and T. B. contributed equally.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 R&D program (ERC-724981) and grant no. 863098 (SPRING). This work was also supported by the projects PID2019-108794GBI00, TED2021-129593B-I00 and PID2021-122464NB-I00 funded by MCIN/AEI/10.13039/501100011033 from the Ministerio de Ciencia e Innovación. R. P. acknowledges support from the Ramón y Cajal Fellowship (Ref. RyC2019-028474-I). E. R. thanks Generalitat de Catalunya for an ICREA Academia award and 2021-SGR-00286 grant, Spanish Ministry Science for a Maria de Maeztu excellence grant (CEX2021-001202-M), and BSC for computational resources. The CSIC authors acknowledge the financial support from the Spanish Ministry Science, through the “Severo Ochoa” Programme for Centres of Excellence (MATRANS42, CEX2023-001263-S).

Notes and references

1. D. Riba-López, R. Zaffino, D. Herrera, R. Matheu, F. Silvestri, J. Ferreira da Silva, E. C. Sañudo, M. Mas-Torrent, E. Barrena, R. Pfattner, E. Ruiz, A. González-Campo and N. Aliaga-Alcalde, Dielectric Behavior of Curcuminoid Polymorphs on Different Substrates by Direct Soft Vacuum Deposition, iScience, 2022, 25(12), 105686,  DOI:10.1016/j.isci.2022.105686.
2. D. Tejedor, S. López-Tosco, G. Méndez-Abt, L. Cotos and F. García- Tellado, Propargyl Vinyl Ethers and Tertiary Skipped Diynes: Two Pluripotent Molecular Platforms for Diversity-Oriented Synthesis, Acc. Chem. Res., 2016, 49(4), 703–713,  DOI:10.1021/acs.accounts.5b00545.
3. M. Valášek and M. Mayor, Spatial and Lateral Control of Functionality by Rigid Molecular Platforms, Chem.–Eur. J., 2017, 23(55), 13538–13548,  DOI:10.1002/chem.201703349.
4. T. Esatbeyoglu, P. Huebbe, I. M. A. Ernst, D. Chin, A. E. Wagner and G. Rimbach, Curcumin-from Molecule to Biological Function, Angew. Chem., Int. Ed., 2012, 51(22), 5308–5332,  DOI:10.1002/anie.201107724.
5. M. Shah, W. Murad, S. Mubin, O. Ullah, N. U. Rehman and M. H. Rahman, Multiple Health Benefits of Curcumin and Its Therapeutic Potential, Environ. Sci. Pollut. Res., 2022, 29(29), 43732–43744,  DOI:10.1007/s11356-022-20137-w.
6. T. Leoni, L. Nony, E. Zaborova, S. Clair, F. Fagès, F. Para, A. Ranguis, C. Becker and C. Loppacher, Stereoisomeric Selection upon Adsorption: A Structural and Optical Study of Curcuminoid Derivatives on Ultrathin Films of KCl on Au(111) and on Bulk KCl(001), Phys. Rev. B, 2021, 104(20), 205415,  DOI:10.1103/PhysRevB.104.205415.
7. K. R. Choi, D. H. Kim, Y. U. Lee, V. Placide, S. Huynh, D. Yao, G. Canard, E. Zaborova, F. Mathevet, L. Mager, B. Heinrich, J. C. Ribierre, J. W. Wu, F. Fages and A. D’Aléo, Effect of the Electron Donating Group on the Excited-State Electronic Nature and Epsilon- near-Zero Properties of Curcuminoid-Borondifluoride Dyes, RSC Adv., 2021, 11(60), 38247–38257,  10.1039/d1ra08025c.
8. V. Polishchuk, M. Stanko, A. Kulinich and M. Shandura, D–π–A–π–D Dyes with a 1,3,2-Dioxaborine Cycle in the Polymethine Chain: Efficient Long-Wavelength Fluorophores, Eur. J. Inorg. Chem., 2018, 2018(2), 240–246,  DOI:10.1002/ejoc.201701466.
9. F. Prins, A. Barreiro, J. W. Ruitenberg, J. S. Seldenthuis, N. Aliaga- Alcalde, L. M. K. Vandersypen and H. S. J. Van Der Zant, Room-Temperature Gating of Molecular Junctions Using Few-Layer Graphene Nanogap Electrodes, Nano Lett., 2011, 11(11), 4607–4611,  DOI:10.1021/nl202065x.
10. E. Burzurí, J. O. Island, R. Díaz-Torres, A. Fursina, A. González- Campo, O. Roubeau, S. J. Teat, N. Aliaga-Alcalde, E. Ruiz and H. S. J. Van Der Zant, Sequential Electron Transport and Vibrational Excitations in an Organic Molecule Coupled to Few-Layer Graphene Electrodes, ACS Nano, 2016, 10(2), 2521–2527,  DOI:10.1021/acsnano.5b07382.
11. J. O. Island, A. Holovchenko, M. Koole, P. F. A. Alkemade, M. Menelaou, N. Aliaga-Alcalde, E. Burzurí and H. S. J. Van Der Zant, Fabrication of Hybrid Molecular Devices Using Multi-Layer Graphene Break Junctions, J. Phys.: Condens.Matter, 2014, 26(47), 474205,  DOI:10.1088/0953-8984/26/47/474205.
12. X. Guo, J. P. Small, J. E. Klare, Y. Wang, M. S. Purewal, I. W. Tam, B. H. Hong, R. Caldwell, L. Huang, S. O'Brien, J. Yan, R. Breslow, S. J. Wind, J. Hone, P. Kim and C. Nuckolls, Covalently Bridging-Gaps in Single-Walled Carbon Nanotubes with Conducting Molecules, Science, 2006, 311(5759), 356–359,  DOI:10.1126/science.1120986.
13. F. H. Van Veen, L. Ornago, H. S. J. Van Der Zant and M. El Abbassi, Benchmark Study of Alkane Molecular Chains, J. Phys. Chem. C, 2022, 126(20), 8801–8806,  DOI:10.1021/acs.jpcc.1c09684.
14. C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. M. Woerde, R. Eelkema, F. C. Grozema and H. S. J. Van Der Zant, Signatures of Quantum Interference Effects on Charge Transport through a Single Benzene Ring, Angew. Chem., Int. Ed., 2013, 52(11), 3152–3155,  DOI:10.1002/anie.201207667.
15. A. Etcheverry-Berríos, R. Díaz-Torres, D. Jullian, I. Ponce, S. O. Vásquez, I. Olavarria, M. Perrin, R. Frisenda, H. S. J. van der Zant, D. Dulić, N. Aliaga-Alcalde and M. Soler, Multiscale approach to the study of the electronic properties of two thiophene curcuminoid molecules, Chem.–Eur. J., 2016, 22(36), 12808–12818,  DOI:10.1002/chem.201601187.
16. I. J. Olavarría-Contreras, A. Etcheverry-Berríos, W. Qian, C. Gutiérrez- Cerón, A. Campos-Olguín, E. C. Sañudo, D. Dulić, E. Ruiz, N. Aliaga-Alcalde, M. Soler and H. S. J. Van Der Zant, Electric-Field Induced Bistability in Single-Molecule Conductance Measurements for Boron Coordinated Curcuminoid Compounds, Chem. Sci., 2018, 9(34), 6988–6996,  10.1039/c8sc02337a.
17. A. K. Feldman, M. L. Steigerwald, X. Guo and C. Nuckolls, Molecular Electronic Devices Based on Single-Walled Carbon Nanotube Electrodes, Acc. Chem. Res., 2008, 41(12), 1731–1741,  DOI:10.1021/ar8000266.
18. S. Caneva, P. Gehring, V. M. García-Suárez, A. García-Fuente, D. Stefani, I. J. Olavarria-Contreras, J. Ferrer, C. Dekker and H. S. J. van der Zant, Mechanically Controlled Quantum Interference in Graphene Break Junctions, Nat. Nanotechnol., 2018, 13(12), 1126–1131,  DOI:10.1038/s41565-018-0258-0.
19. S. G. Sarwat, P. Gehring, G. Rodriguez Hernandez, J. H. Warner, G. A. D. Briggs, J. A. Mol and H. Bhaskaran, Scaling Limits of Graphene Nanoelectrodes, Nano Lett., 2017, 17(6), 3688–3693,  DOI:10.1021/acs.nanolett.7b00909.
20. B. Limburg, J. O. Thomas, G. Holloway, H. Sadeghi, S. Sangtarash, I. C. Y. Hou, J. Cremers, A. Narita, K. Müllen, C. J. Lambert, G. A. D. Briggs, J. A. Mol and H. L. Anderson, Anchor Groups for Graphene-Porphyrin Single-Molecule Transistors, Adv. Funct. Mater., 2018, 28(45), 1803629,  DOI:10.1002/adfm.201803629.
21. M. El Abbassi, L. Pósa, P. Makk, C. Nef, K. Thodkar, A. Halbritter and M. Calame, From Electroburning to Sublimation: Substrate and Environmental Effects in the Electrical Breakdown Process of Monolayer Graphene, Nanoscale, 2017, 9(44), 17312–17317,  10.1039/c7nr05348g.
22. H. J. J. Pabon, A Synthesis of Curcumin and Related Compounds, Recl. des Trav. Chim. des Pays-Bas, 1964, 83(4), 379–386,  DOI:10.1002/recl.19640830407.
23. M. Nüchter, B. Ondruschka, W. Bonrath and A. Gum, Microwave Assisted Synthesis – a Critical Technology Overview, Green Chem., 2004, 6(3), 128–141,  10.1039/b310502d.
24. D. Dallinger and C. O. Kappe, Microwave-Assisted Synthesis in Water as Solvent, Chem. Rev., 2007, 107(6), 2563–2591,  DOI:10.1021/cr0509410.
25. M. A. Tehfe, F. Dumur, E. Contal, B. Graff, F. Morlet-Savary, D. Gigmes, J. P. Fouassier and J. Lalevée, New Insights into Radical and Cationic Polymerizations upon Visible Light Exposure: Role of Novel Photoinitiator Systems Based on the Pyrene Chromophore, Polym. Chem., 2013, 4(5), 1625–1634,  10.1039/c2py20950k.
26. C. G. Vera-de la Garza, R. J. Martinez and F. Belmont-Bernal, Electronic Structure of Curcuminoids with Potential Medicinal Applications: A Theoretical Insight, Struct. Chem., 2023, 34(4), 1427–1438,  DOI:10.1007/s11224-022-02080-1.
27. S. Kubatkin, A. Danilov, M. Hjort, J. Cornil, J. L. Brédas, N. Stuhr- Hansen, P. Hedegård and T. Bjørnholm, Single-Electron Transistor of a Single Organic Molecule with Access to Several Redox States, Nature, 2003, 425(6959), 698–701,  DOI:10.1038/nature02010.
28. J. G. Simmons, Generalized Formula for the Electric Tunnel Effect between Similar Electrodes Separated by a Thin Insulating Film, J. Appl. Phys., 1963, 34(6), 1793–1803,  DOI:10.1063/1.1702682.
29. J. O. Thomas, J. K. Sowa, B. Limburg, X. Bian, E. Charalambos, J. L. Swett, S. Tewari, J. Baugh, G. C. Schatz, G. A. D. Briggs, L. A. Anderson and J. Mol, Charge Transport through extended molecular wires with strongly correlated electrons, Chem. Sci., 2021, 12, 11121,  10.1039/d1sc03050g.
30. J. M. Thijssen and H. S. J. Van Der Zant, Charge Transport and Single Electron Effects in Nanoscale Systems, Phys. Status Solidi B, 2008, 245(8), 1455–1470,  DOI:10.1002/pssb.200743470.
31. J. A. Mol, C. S. Lau, W. J. M. Lewis, H. Sadeghi, C. Roche, A. Cnossen, J. H. Warner, C. J. Lambert, H. L. Anderson and G. A. D. Briggs, Graphene-Porphyrin Single-Molecule Transistors, Nanoscale, 2015, 7(31), 13181–13185,  10.1039/c5nr03294f.
32. P. Gehring, J. K. Sowa, J. Cremers, Q. Wu, H. Sadeghi, Y. Sheng, J. H. Warner, C. J. Lambert, G. A. D. Briggs and J. A. Mol, Distinguishing Lead and Molecule States in Graphene-Based Single Electron Transistors, ACS Nano, 2017, 11(6), 5325–5331.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc04969a

‡ All the authors contributed equally.

---