Open Access Article
Open Access ArticleUltra-sensitive detection of PFASs using surface enhanced Raman scattering and machine learning: a promising approach for environmental analysis†
Joshua C.
Rothstein
a,
Jiaheng
Cui
 *b,
Yanjun
Yang
*b,
Yanjun
Yang
 a,
Xianyan
Chen
c and
Yiping
Zhao
a,
Xianyan
Chen
c and
Yiping
Zhao
 *a
*a
aDepartment of Physics and Astronomy, Franklin College of Arts and Sciences, The University of Georgia, Athens, GA 30602, USA. E-mail: zhaoy@uga.edu
bSchool of Electrical and Computer Engineering, College of Engineering, The University of Georgia, Athens, GA 30602, USA. E-mail: jiaheng.cui@uga.edu
cDepartment of Epidemiology & Biostatistics, College of Public Health, The University of Georgia, Athens, GA 30602, USA
First published on 2nd July 2024
Abstract
The contamination of per- and polyfluoroalkyl substances (PFAS) in drinking water presents a significant concern and requires a simple, portable detection method. This study aims to demonstrate the effectiveness of Raman and surface-enhanced Raman scattering (SERS) spectroscopies for identifying and quantifying various PFASs in water. Experimental Raman spectra of different PFASs reveal unique characteristic peaks that enable their classification. While direct SERS measurements from silver nanorod (AgNR) substrates may not exhibit distinct PFAS characteristic peaks, the presence of PFAS on SERS substrates induces noticeable spectral changes. By integration with machine learning (ML) techniques, these SERS spectra can be used to successfully differentiate and quantify PFOA in water, achieving a limit of detection (LOD) of 1 ppt. Modifying the AgNR substrates with cysteine and 6-mercapto-1-hexanol enhances the differentiation and quantification capabilities of SERS-ML. Despite alkanethiol molecules affecting spectral features, PFAS and PFOS concentrations produce observable spectral variations. A support vector machine model achieves 93% accuracy in differentiating PFOA, PFOS, and references, independent of concentration. A support vector regression model further establishes LODs of 1 ppt for PFOA and 4.28 ppt for PFOS. By removing spectra with concentrations lower than LODs, the classification accuracy is improved to 95%.
Introduction
The per- and polyfluoroalkyl substances (PFASs) are a diverse class of over 3000 chemicals in use since the 1950s in industrial and consumer products.1 They came under regulatory and scientific scrutiny in the last two decades due to high bioaccumulation and persistence in the environment, as well as toxicity. The most common analysis of PFASs in environmental samples is liquid chromatography with mass spectroscopy.2–4 This is a laboratory-based technique with low sensitivity and high cost. Recently, new emerging PFAS detection methods based on fluorescence spectroscopy, and the electrochemical method have been investigated.3,4 Though some new capabilities have been achieved in fluorescence detection, such as sub-ppt level of limit of detection (LOD),5 and the ability to differentiate perfluorooctanoic acid (PFOA) and perfluorooctanesulfonic acid (PFOS),6 many challenges remain, especially in terms of high sensitivity detection with desired LOD, the ability to detect and differentiate multiple PFAS species, and field applicability.Surface-enhanced-Raman scattering (SERS) spectroscopy is a very promising technology to address the challenges of PFAS detection. When the analyte molecules are attached to specially designed plasmonic nanostructures, their Raman signal amplitude can be enhanced 106 to 1010 times.7 Such a phenomenon has even been shown to achieve single-molecule detection.8 The vibrational spectroscopic features in SERS spectra can give molecular fingerprints for target molecules, allowing one to achieve high specificity without using fluorescent tags. Fang et al. used cationic dyes like ethyl violet and methyl blue to co-incubate with PFOA and PFOS from firefighting foams.9 Such a strategy allowed for greater loading of targeted fluorosurfactants on the graphene oxide (GO) mixed with colloidal silver nanoparticles (NPs), reaching an LOD for PFOA of 50 ppb (i.e., 5 × 104 ppt). Jet-printed silver NPs and graphene on Kapton as SERS substrates achieved an extremely low LOD of both PFOA and PFOS of 0.5 ppt.10 Park et al. fabricated silver nanograss substrates covered with self-assembled p-phenylenediamine nanoparticles to detect PFOA and obtained an LOD of 1.69 nM (0.53 ppt) in distilled water.11 Feng et al. synthesized Ag NP/Au@Ag core–shell nanorod SERS substrates, demonstrated their ability to detect PFOA, perfluorohexanoic acid (PFHxA), and potassium perfluorobutanesulfonate (PFBS), and achieved an LOD of 0.1 ppm (i.e., 1 × 105 ppt).12 All these studies show the great promise of using SERS for highly sensitive PFAS detection.
However, there are three challenges associated with SERS-based PFAS detection. First, high-enhancement SERS substrates are required to provide adequately strong signals for the desired limits of detection. Second, the affinity of PFAS molecules to the designed SERS substrates must be strong enough to demonstrate good SERS signals. Different substrates may have better or worse affinities with different analytes depending on their interactions. Finally, the SERS spectra from different PFAS molecules must be distinguishable. Many PFAS molecules have remarkably similar molecular structures, which can result in similar SERS or Raman spectra.
The solution to the first challenge is the creation of specific reproducible nanostructures to enhance plasmonic effects. We have shown that the silver nanorod (AgNR) arrays fabricated by oblique angle deposition can serve as excellent SERS substrates.13–16 The SERS enhancement factor can reach as high as ∼109; the SERS intensity variation from substrate to substrate and from deposition batch to batch is less than 10%.17 The substrates can be produced on a large scale. Many different devices, such as multiwell SERS substrate array for multiplexing detection, flow cells, and fiber sensors, have been developed for point-of-care applications.18–21 The AgNR substrates can be integrated with a portable Raman analyzer and a tablet and can be used in the field.22,23
For the second challenge, the ability of PFAS molecules to bond to the AgNR can be improved by taking advantage of their functional groups. The lipophobic/hydrophobic nature of the fluorocarbon tail and the different nature of the other functional groups of a PFAS molecule could interact differently on a charged surface. Functionalizing the AgNR surface to be positively or negatively charged may change the adsorption properties of the PFAS molecules, potentially improving sensitivity. In addition, in PFAS sorbent studies, it is well-known that different absorbent materials, such as carbonaceous materials and inorganic oxides (silica, alumina, hematite, etc.), have different PFAS absorption capabilities.4 The coating of these materials on AgNR substrates can also be used for improving the differentiation accuracy for PFASs.
Since many PFAS molecules have similar chemical bonds, except for the number of carbon atoms, it is expected that the SERS spectra of these PFAS molecules are highly similar. This is the source of the third challenge. Since the SERS spectra can be viewed as multi-variant data, the differentiation and quantification of targeted PFASs can benefit from modern machine learning algorithms (MLAs).24–26 Various classic MLAs, such as principal component analysis (PCA), partial least square discriminant analysis (PLS-DA), k-nearest neighbor (KNN), random forest (RF), etc., have been applied to SERS spectra for bacteria and virus identification, disease diagnosis, and forensic analysis.25–27 For example, Wu et al. demonstrated the use of PCA to visualize the cluster of 27 bacteria pathogens based on their SERS spectra,23 and Rebrošová et al. achieved 100% classification accuracy in distinguishing 16 types of staphylococcal species using PCA and SVM.28 Our recent studies demonstrate the capacity of SVM to effectively classify and quantify 11 different bacterial endotoxins29 and 13 different respiratory viruses.30 It is expected that these algorithms should also exhibit notable efficiency in distinguishing different PFASs based on their SERS spectra.
The goals of this work are to show that (1) the Raman spectra of different PFAS molecules, even with the same functional groups but different carbon chain numbers, are able to be used to differentiate the PFAS in solution; (2) the integration of SERS and machine learning (ML) can be used to differentiate and quantify various PFAS in water; (3) the use of thiol modified SERS substrates can improve the differentiation and quantification capabilities of the SERS-ML method. With the MCH-modified AgNR substrates and using an SVM, we achieved a 93% accuracy in differentiating PFOA, PFOS, and the reference, regardless of their concentrations. Furthermore, employing a support vector regression (SVR) model allowed us to determine LODs of 1 ppt for PFOA and 4.28 ppt for PFOS.
Experimental section
Materials
The silver and titanium used for deposition were purchased from Kurt J. Lesker. The AgNR substrates were prepared on Thermo Fisher Scientific glass microscope slides. MCH (6-mercapto-1-hexanol) and cysteine were all bought from Sigma-Aldrich. PFOS was purchased from ChemCruz at 97% purity. PFOA was acquired from Sigma-Aldritch at 95% purity. Perfluorodecanoic acid (PFDA) was obtained from Fisher Scientific. Perfluoronanoic acid (PFNA) was received from Cambridge Isotope Laboratories. Sylgard 184 Silicone Elastomer Base and Sylgard 184 Silicone Elastomer Curing Agent used to fabricate PDMS gel wells were purchased from Dow.AgNR substrate fabrication
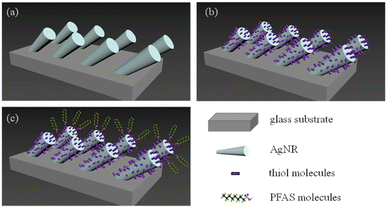
Glass microscope slides were cut into 0.5 inch × 0.5 inch square pieces. Followed by a standard cleaning procedure, AgNRs were deposited onto these glass slides in an electron beam deposition system using the OAD configuration; details can be found in.31,32 Before SERS measurements, the AgNR substrates were cleaned by argon plasma for 90 seconds. A polydimethylsiloxane (PDMS) gel layer containing 4 wells (2 × 2, with a well radius of 2 mm and a depth of 1 mm) was molded onto the cleaned AgNR substrates.33Fig. 1a illustrates the geometry of the AgNR array SERS substrate, and Fig. S1 in the ESI† is a representative electron micrograph of the fabricated SERS substrate.Raman measurement of PFAS
1 mg powder of four different PFASs (PFDA, PFNA, PFOS, and PFOA) was placed on the cleaned Si wafer for the Raman measurement. A confocal Raman microscope (Renishaw, InVia) with a 785 nm excitation laser was used for all the Raman and SERS measurements. The laser power was set to 171 mW at the sample position with a 20× objective lens and 10 s acquisition time.Direct SERS measurement of PFAS in methanol from AgNR substrates
Five different PFASs (hexafluoropropylene oxide dimer acid (HFPO-DA), PFDA, PFNA, PFOS, and PFOA) were diluted to 103 ppt in methanol. 2 μL of each sample was dropped onto AgNRs substrate and air-dried at 20 °C for the SERS measurement. The laser power was set to 0.855 mW at the sample position with a 20× objective lens and 10 s acquisition time. 120 SERS spectra were obtained for each sample. To explore the quantification capability of SERS, 100, 101, 103, 106, 107, and 108 ppt concentrations of PFOA in methanol were also prepared, and the corresponding SERS spectra were measured under the conditions mentioned above.SERS measurement from alkanethiol molecule modified AgNR substrates
As discussed in the introduction, to improve the affinity of PFAS molecules to AgNR substrate, it may be advantageous to put a self-assembled thiol molecule layer on the surface to change the surface charge as shown in Fig. 1b. It is envisioned that when PFAS molecules are dispensed on the thiol-modified surface, they will be aligned in a certain way according to electrostatic interaction, as shown in Fig. 1c. Here, we employed two thiol molecules: cysteine and MCH.20 μL of the 200 μM cysteine solution was pipetted into an AgNR well and incubated for 1 hour. After incubation, the wells were rinsed with DI water more than 3 times and then air-dried. Then, a droplet of 2 μL of 103 ppt PFOS, PFOA, PFNA, PFDA, and HFPO-DA in methanol was dispended in the cysteine-modified well. After drying for 1 minute, the corresponding SERS spectra were measured under the same conditions.
Based on the results shown in Fig. S2 in the ESI,† since the MCH concentration of 150 μM gave the most consistently high peak intensity, it was selected as the MCH functionalization concentration. 20 μL of the 150 μM was used to modify the AgNR well following the same procedure as cysteine modification. After MCH functionalization, the PFOA concentrations of 109, 108, 107, 106, 105, 104, 103, 102, 101, 100, and 10−1 ppt, and PFOS concentrations of 4.28 × 106, 4.28 × 105, 4.28 × 104, 4.28 × 103, 4.28 × 102, 4.28 × 101, 4.28 × 100, 4.28 × 10−1, and 4.28 × 10−2 ppt, diluted in DI water, respectively, were applied on MCH-modified AgNR-wells. To obtain better statistics, 20 μL solutions of each concentration were dispensed to 3 AgNR-wells on separated substrates and different well-locations. For PFOA in MCH, three different substrates were used to collect the spectra. From each substrate, 60 spectra were collected from a single well for each concentration. For PFOS in MCH, seven different substrates were used to collect the spectra. For concentrations of 4.28 × 105, 4.28 × 103, 4.28 × 101, 4.28 × 10−1 ppt, and the reference, 60 spectra were collected from a single well for each concentration. For concentrations of 4.28 × 106, 4.28 × 104, 4.28 × 102, 4.28, 4.28 × 10−2 ppt, a total of 60 spectra were collected from three wells from three different substrates (20 spectra per well). The data from the three wells were added to the dataset to reduce substrate-related variance in the model prediction. One of our recent publications indicates that the piece-to-piece difference between the substrates is within 10%.34 For all the above measurements, DI water-treated wells were used as a reference.
SERS spectra pre-treatment
Prior to analysis, all SERS spectra were processed by a standardized spectral preprocessing procedure, which included de-spiking, baseline removal, and area normalization. Unless otherwise specified, the baseline removal method employed in this study was WiRE by Renishaw, a widely used commercial baseline correction method based on polynomial fitting.Machine learning training
For data visualization, t-distributed stochastic neighbor embedding (t-SNE) was employed.35 The MLA, SVM, was used for spectral classification,36 while the SVR was utilized for spectral quantification.37 All implementation was coded in Python 3.8.6, using scikit-learn version 1.0.2.38 It is noted that the specific kernels and parameters were carefully selected and are detailed in the corresponding sections for clarity.Results and discussion
Raman spectra of selected PFAS compounds
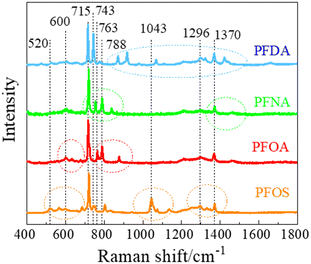
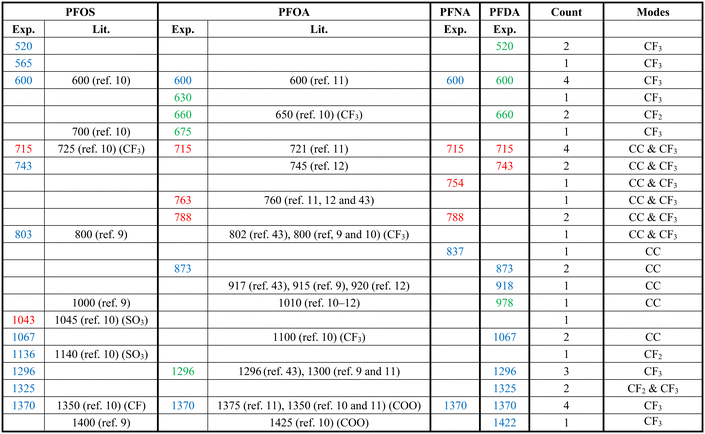
Fig. 2 shows the measured average Raman spectra of PFOS, PFOA, PFNA, and PFDA powders, and will be used as a reference for spectra comparison. Each spectrum exhibits multiple well-defined characteristic peaks, and the relevant peak details are summarized in Table 1. It is very hard to directly assign the vibrational modes of the experimental Raman spectra since there are very large discrepancies between the peak locations of experimental spectra and those calculated by density function theory,39 see Fig. S3 in the ESI.† However, there were existing assignments in the literature. In the case of PFOS and PFOA, which are the primary PFAS types discussed in this study, we have extracted peak information from existing literature, as indicated in the “Lit.” columns. The column labeled “Count” offers a summary of how frequently a given peak appears across all PFAS powders used in our experiments, offering insights into potential similarities. The final column provides our assignment of vibrational origins. Among these peaks, those at Δv = 600, 715, and 1370 cm−1 are consistently observed in all four compounds shown in Fig. 2. Additionally, Δv = 1296 cm−1 is shared by all PFASs except PFNA. PFOS and PFDA share peaks at Δv = 520, 743, 1067, and 1325 cm−1, whereas PFOA and PFNA share peaks at Δv = 788 cm−1, and PFOA and PFDA share peaks at Δv = 660 and 873 cm−1, respectively. Notably, PFOS exhibits unique peaks at Δv = 1043 and 1136 cm−1, PFOA at Δv = 630, 675, and 763 cm−1, PFNA at Δv = 754 and 837 cm−1, while PFDA at Δv = 427, 918, 978 and 1422 cm−1. These distinctive peaks, delineated by dashed circles in Fig. 2 for each PFAS compound, distinctly define the differences in the SERS spectra among these four compounds, and are expected to enable easy differentiation through MLAs.| a The “Exp.” column represents the results from Fig. 2, the “Lit.” columns refer to data from the literature, and the “Count” column shows the number of PFASs with the same peak observed in Fig. 2. The colors of peak positions indicate their relative intensity: red: strong; blue: medium; green: weak. |
|---|
|
Attributing specific vibrational modes to observed peaks is challenging due to the long-chain structure of PFAS compounds and the closely matched masses of carbon and fluorine atoms. According to ref. 10, peaks at Δv = 660, 715, 803, and 1100 cm−1 may correspond to vibrations of the CF3 group, while Δv = 1370 cm−1 could be attributed to CF or COO vibrations. Also, PFOS stands out in the table, as it possesses the only SO3 functional group, possibly accounting for the unique peaks at Δv = 1043 and 1136 cm−1.10 It is important to note that these assignments may not be accurate. The four most common peaks at Δv = 600, 715, 1370, and 1296 cm−1 are likely linked to vibrational modes of common structures present in all four PFASs we examined, unaffected by variations in molecular length and functional groups. Although the molecular structures of PFOA, PFNA, and PFDA are quite similar, featuring a COOH functional group, their distinctions arise from variations in carbon and fluorine counts. Specifically, PFOA comprises 8 carbons and 15 fluorines, PFNA contains 9 carbons and 17 fluorines, and PFDA consists of 10 carbons and 19 fluorines. As we anticipate, an increase in carbon atoms should minimally impact the normal vibrational modes of CF2 bonds and CF3 group, while the vibrational modes of C–C bonds could undergo splitting into multiple modes around their original normal modes. Based on some early experimental and theoretical Raman studies on C2F6 and C3F8, symmetric and asymmetric C–C stretchings were observed at Δv = 780 and 1008 cm−1.40–42 With the addition of more carbon atoms, it is reasonable to assume that C–C stretchings could span between 700–850 cm−1 and 900–1100 cm−1. Many of the observed peaks in Fig. 2 could be attributed to these wavenumber regions. In addition, according to those studies, CF3 vibrations fall within the 540–630, 720–800, 1200–1270, and 1350–1370 cm−1 wavenumber regions, while CF2 bonds exhibit modes at Δv = 340, 460, 660, 1150, and 1314 cm−1, respectively. Taking these insights into account, we have reevaluated the vibrational origins for each of the experimentally observed peaks, as indicated in the last column of Table 1.
SERS spectra of different PFASs from AgNR substrates
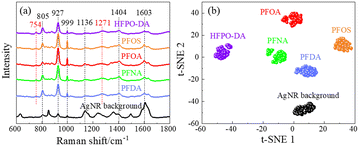
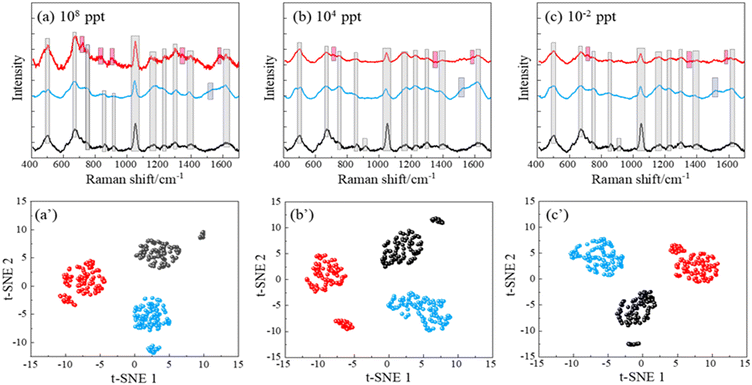
Fig. 3a shows the average SERS spectra of 103 ppt PFOS, PFOA, PFNA, PFDA, and HFPO-DA in methanol. Unlike the Raman spectra shown in Fig. 2, these spectra show broadened spectral features. A table listing peaks of these PFAS molecules can be found in Table S1 of the ESI.† The peaks seen in the Δv = 700–800 cm−1 range from Fig. 2 are no longer present. The dominating peaks now occur in the range of Δv = 800–900 cm−1. All the SERS spectra exhibit similar spectral features, especially sharp peaks at Δv = 805, 927, and 999 cm−1. Some other common peaks appear at Δv = 1136, 1401, and 1603 cm−1. Those peaks are all presented in the spectrum of the AgNR background. However, the relative peak intensity ratios are different for different PFASs, and there are some small variations in various wavenumber regions. In addition, at least two small peaks at Δv = 754 and 1271 cm−1 that do not belong to any peaks of the AgNR background appear in all the PFAS spectra. These peak locations are close to some of the peaks shown in Raman spectra (Δv = 743–763 and 1296 cm−1) shown in Table 1, which demonstrates the possibility of PFAS detection. The shift of the peaks in the SERS spectrum compared to the Raman spectrum could be due to two possible reasons: the breaking symmetry of some vibrational mode due to molecule adsorption on a surface in SERS, or due to charge transfer from the molecule to the adsorbed surface.44 The high similarity among the SERS spectra of all PFASs presented in Fig. 3a as well as the AgNR background spectrum is probably due to the low affinity of PFAS molecules to the AgNR substrate, but this needs to be further confirmed by other carefully designed experiments. We performed a cosine similarity test to further assess the similarity between the spectra in Fig. 3a. Cosine similarity is a measure of the similarity between two non-zero vectors, with values ranging from −1 to 1, where 1 indicates high similarity. Given two spectra Ia and Ib, the calculation of cosine similarity Sc(Ia, Ib) can be defined as Sc(Ia, Ib) = (Ia · Ib)/(‖Ia‖‖Ib‖), where the “·” operation represents the inner product of two vectors, and “‖I‖” represents the length of the vector I. The results, shown in Table S2,† indicate that there are moderate similarities between the PFAS spectra and the AgNR background, and the PFAS spectra are highly similar to each other (with values >0.9). This high similarity among PFAS spectra suggests that it is difficult to visually distinguish them. However, the values are not equal to 1, indicating that there are subtle differences between the spectra. These differences can be effectively captured and used for differentiation using mathematical techniques such as t-SNE.To investigate whether the SERS spectra can be used in differentiating different PFASs, the t-SNE analysis was implemented. t-SNE is a nonlinear dimensionality reduction technique well-suited for embedding high-dimensional data into a space of two or three dimensions, ideal for human interpretation and visualization. It is designed to identify hidden patterns, especially nonlinear local similarities, and can unveil distinctions within SERS spectra that may appear quite subtle to human observers.35 The t-SNE algorithm for SERS spectra observed in Fig. 3a was executed with a perplexity of 40, an iteration of 300, and initialized randomly. As shown in Fig. 3b, the SERS spectra from the same kind of PFAS molecules can form close, independent, and well-separated clusters with respect to each other, which demonstrates a clear differentiation capability of SERS. These results demonstrate that 1) the SERS spectra from PFASs with different numbers of carbon atoms but the same end functional groups (PFOA, PFNA, and PFDA) can be used to differentiate the PFAS species; 2) SERS spectra from PFASs with the same number of carbon atoms but different end functional group (PFOA and PFOS) can also be used to differentiate the PFAS species.
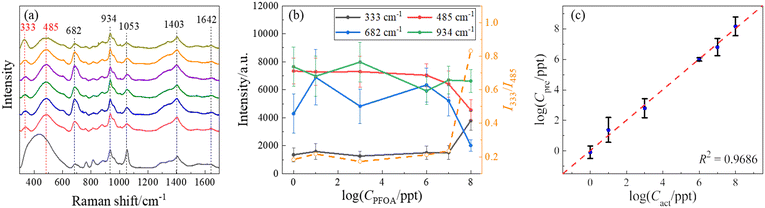
In order to demonstrate the quantification capability of SERS, the concentration-dependent SERS spectra of PFOA have been measured, and the representative average spectra are shown in Fig. 4a. These spectra are very similar except for some minute variations. A comparative analysis of peak locations relative to those in Fig. 2 and 3, as well as the reference, is listed in Table S3 of the ESI.† As shown in Fig. 4a and Table S3,† all spectra show common peaks at Δν = 682, 934, 1053, 1403, and 1642 cm−1, which are attributed to the background interference, while the peaks at Δν = 333 and 485 cm−1 are unique to the PFOA spectra. These two peaks show slight variations with the change in PFOA concentration. To quantify the PFOA concentration from SERS spectra, the traditional method is to establish a calibration curve, i.e., plotting the SERS intensities (IΔv) of characteristic peaks from the PFOA spectra as a function of known concentration (CPFOA). Similar to Table S2,† we calculated the cosine similarity for the spectra shown in Fig. 4a, comparing the reference spectrum with various concentrations of PFOA. The results are shown in Table S4.† The cosine similarity values still indicate moderate similarity between reference and PFOA spectra, and high similarity (but not 1) between the spectra at different concentrations. This again suggests that while it is difficult to visually distinguish them by human eyes, there are still subtle differences between the spectra that can be effectively captured using mathematical and machine learning techniques. These findings further justify the use of machine learning and support the robustness of our methodology. Fig. 4b presents some of the average peak intensities at Δv = 333, 485, 682, and 934 cm−1 and associated standard deviations versus the logarithm of CPFOA. It is noteworthy that the relationship between IΔv and CPFOA at Δν = 682, and 934 cm−1 exhibits significant variations. In contrast, I333 at Δv = 333 cm−1 remains relatively stable within the concentration range between 1 and 107 ppt, while increasing significantly at 108 ppt, which makes it difficult to be used as a concentration calibration curve for SERS-based detection. On the other hand, I485 shows an opposite trend, decreasing with increasing CPFOA. Since these two peaks are unique to PFOA spectra, the different CPFOA trends for these two vibrational modes indicate that there could be a possible orientation change of the adsorbed PFOA molecules on the AgNR surface during the increased CPFOA.45 Thus, the intensity ratio I333/I485 could be another way to establish a calibration curve. Fig. 4b also plots this ratio versus CPFOA (the open orange circles), and it does not appear to improve the quality of the calibration curve, i.e., at lower concentrations (CPFOA ≤ 107 ppt), the ratio I333/I485 also almost remains as a constant. The non-monotonic calibration curve can be explained by the following mathematical model described in a recent publication on SERS measurements.46 The intensity ISERS(Δv) at a specific wavenumber Δv can be expressed as:
| ISERS(Δv) = v(C)IvSERS(Δv) + m(C)ImSERS(Δv) + Inoise(Δv), |
Additionally, the large error bars in Fig. 4b indicate significant variations in the measurements. These variations can be attributed to two main factors. The first reason is the low affinity of PFAS molecules. PFAS molecules have a limited affinity to the SERS substrates, resulting in weak signals that are often overshadowed by noise. The limited affinity results in a lower signal-to-noise ratio (SNR), complicating the establishment of a stable calibration curve. This issue has been noted in recent studies. For example, Zhou et al. discussed the use of modified carbon fiber microelectrodes to enhance molecular affinity to plasmonic substrates through electrostatic interactions and electroenrichment.50 The results indicate that by regulating the potential, carotenoid molecules with a similar molecular structure can have higher SNR and be better quantified and identified by SERS. Another reason may be the attribution of background influences. The SERS substrates used in our study are modified by thiol molecules, which can generate a constant background signal. This background can interfere with the analyte signal, leading to variations in the observed intensities. Additionally, the choice of baseline removal technique affects the shape of the intensity versus concentration plot. For example, the black reference curve in Fig. 4a was obtained using a polynomial baseline removal technique called WiRE. The large peak at around Δv = 400 cm−1 is created by the polynomial-based nature and significantly contributes to the observed variances. Therefore, it is evident that alternative techniques may be necessary for accurate quantification of PFOA concentration.
To circumvent this problem, we can apply more complicated ML-based regression models to establish a calibration curve. ML techniques aim to overcome the difficulty of predicting CPFOA posed by this anomalous behavior and can be a more robust method for the determination of CPFOA. An SVR model was used to predict CPFOA based on the SERS spectra. In the SVR model, a radial basis function (RBF) kernel, with C = 100,  = 0.1, and a default γ value, was used. To ensure an unbiased evaluation and robust generalization of this model, stratified sampling was employed to split the spectral set into training and test sets. Unlike the typical 8
= 0.1, and a default γ value, was used. To ensure an unbiased evaluation and robust generalization of this model, stratified sampling was employed to split the spectral set into training and test sets. Unlike the typical 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 training-to-test ratio in ML tasks, a 1
1 training-to-test ratio in ML tasks, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio was chosen intentionally to demonstrate that accurate predictions of PFOA concentrations could be achieved with relatively limited data. To ensure the reliability of the result, the segmentation–training–prediction process was repeated ten times to account for the potential variation. Fig. 4c shows a log–log plot of the predicted concentration (Cpre) of PFOA versus the actual concentration (Cact) obtained from the optimized SVR model. The Cpre data are mainly distributed around the dashed line (Cpre = Cact), indicating that the concentrations of PFOAs predicted through SERS spectra closely approximate the actual concentrations on a qualitative level. The model's performance can be assessed quantitatively using the coefficient of determination R2, a statistical measure that quantifies the goodness-of-fit of a regression model.51 An R2 value approaching 1 typically indicates an excellent fit. The average R2 value resulting from 10 independent trials was 0.95 ± 0.01, while Fig. 4c shows the result from the best trial with an R2 of 0.97, highlighting the model's strong performance in PFOA concentration prediction. Remarkably, the prediction for a concentration Cact = 106 ppt (i.e., log(Cact) = 6) exhibited an average of 5.99 with a low standard deviation of 0.10. As illustrated in Fig. 4c, this data point almost converged to a single dot on the diagonal line, denoting an excellent fit. Regarding the behavior at low concentrations, the result of Cact = 1 ppt (i.e., log(Cact) = 0) is also close to the diagonal line. One-sample t-tests were performed to determine the limit of detection (LOD). These tests compare the mean of a single sample of data to a known value. In our case, the purpose of these tests was to determine whether the average predicted concentration at each tested level statistically equaled the actual concentration. One-sample t-tests were performed at all actual concentrations, starting from the lowest concentrations considered feasible for detection, i.e., 1 ppt for PFOA. The null hypothesis for each test was that the mean predicted concentration equaled the actual concentration, whereas the alternative hypothesis was that it did not. In the context of a one-sample t-test, when the p-value falls below the common significance threshold α, typically set at 0.05, it indicates that the predicted values significantly diverge from the true values.51 The LOD was determined by selecting the lowest concentration at which the p-value of the t-test was greater than or equal to 0.05. This implies that there was no significant evidence to reject the hypothesis that the predicted concentration equals the actual concentration. The observed p-value for 1 ppt is 0.53, which exceeds 0.05. As a result, it suggests that the predicted values are not significantly different from the true values, implying an LOD as low as 1 ppt.
1 ratio was chosen intentionally to demonstrate that accurate predictions of PFOA concentrations could be achieved with relatively limited data. To ensure the reliability of the result, the segmentation–training–prediction process was repeated ten times to account for the potential variation. Fig. 4c shows a log–log plot of the predicted concentration (Cpre) of PFOA versus the actual concentration (Cact) obtained from the optimized SVR model. The Cpre data are mainly distributed around the dashed line (Cpre = Cact), indicating that the concentrations of PFOAs predicted through SERS spectra closely approximate the actual concentrations on a qualitative level. The model's performance can be assessed quantitatively using the coefficient of determination R2, a statistical measure that quantifies the goodness-of-fit of a regression model.51 An R2 value approaching 1 typically indicates an excellent fit. The average R2 value resulting from 10 independent trials was 0.95 ± 0.01, while Fig. 4c shows the result from the best trial with an R2 of 0.97, highlighting the model's strong performance in PFOA concentration prediction. Remarkably, the prediction for a concentration Cact = 106 ppt (i.e., log(Cact) = 6) exhibited an average of 5.99 with a low standard deviation of 0.10. As illustrated in Fig. 4c, this data point almost converged to a single dot on the diagonal line, denoting an excellent fit. Regarding the behavior at low concentrations, the result of Cact = 1 ppt (i.e., log(Cact) = 0) is also close to the diagonal line. One-sample t-tests were performed to determine the limit of detection (LOD). These tests compare the mean of a single sample of data to a known value. In our case, the purpose of these tests was to determine whether the average predicted concentration at each tested level statistically equaled the actual concentration. One-sample t-tests were performed at all actual concentrations, starting from the lowest concentrations considered feasible for detection, i.e., 1 ppt for PFOA. The null hypothesis for each test was that the mean predicted concentration equaled the actual concentration, whereas the alternative hypothesis was that it did not. In the context of a one-sample t-test, when the p-value falls below the common significance threshold α, typically set at 0.05, it indicates that the predicted values significantly diverge from the true values.51 The LOD was determined by selecting the lowest concentration at which the p-value of the t-test was greater than or equal to 0.05. This implies that there was no significant evidence to reject the hypothesis that the predicted concentration equals the actual concentration. The observed p-value for 1 ppt is 0.53, which exceeds 0.05. As a result, it suggests that the predicted values are not significantly different from the true values, implying an LOD as low as 1 ppt.
SERS spectra of PFASs on cysteine-functionalized AgNR substrates
To better control the background SERS spectra and attempt to possibly change the affinity between the PFAS molecules to the AgNR substrates, we believe that a surface functionalization of the AgNR substrate is necessary. Alkanethiol molecules with different functional groups can be easily self-assembled on Ag surfaces. Once the AgNR substrates are immobilized with alkanethiol molecules, they will generate background SERS signals. Then, when PFAS molecules are adsorbed on these substrates, it is expected that the SERS signal will be changed. To illustrate this effect, we performed a preliminary study to functionalize the AgNR substrates with cysteine. Cysteine has a negatively charged carboxylate group and a positively charged amine group. Fig. 5a–c show the average SERS spectra of PFOA and PFOS of CPFOS and CPFOA = 108, 104, and 10−2 ppt on cysteine functionalized AgNR substrates, and their comparison to the SERS spectrum of the modified SERS substrate, respectively. In the SERS spectrum of the cysteine-modified AgNR, many peaks, such as Δv = 502, 672, 1050, 1164, 1304, 1399, and 1610 cm−1, appear, which are consistent with those reported in previous publications for Raman and SERS spectra of cysteine.52 With the addition of PFOA and PFOS solutions, these peaks also persist, but some peak intensities (such as Δv = 672, 1304, and 1399 cm−1 in PFOA 108 ppt spectrum (Fig. 5a) increase, while some (such as Δv = 1050 cm−1 in PFOA and Δv = 672, 1050, and 1399 cm−1 in PFOS 108 ppt spectrum, Fig. 5a) decrease. With the decrease in CPFOS and CPFOA, many intensities of the above-mentioned peaks increase, which demonstrates the higher interference effect of the cysteine at low analyte concentration. However, both the average spectra of PFOA and PFOS also show distinguished spectral features that are different from the cysteine spectrum. At a high concentration (CPFOS and CPFOA = 108 ppt), PFOA shows distinct peaks at Δv = 807, 904, and 1354 cm−1, and PFOS has a sharp peak at Δv = 973 and 1520 cm−1. For most of these peaks (except for Δv = 1520 cm−1), the peak intensities decrease with CPFOS and CPFOA, which is consistent with the analyte concentration change. A summary table of the center positions of the distinct peaks identified in the SERS spectra of PFOS and PFOA, and their presence in each spectrum shown in Fig. 5a–c is included in Table S5.†At lower concentrations (e.g., 10−2 ppt), the SERS spectra of PFOA and PFOS appear indistinguishable to the human eye. However, under a t-SNE analysis, the spectral signatures can still be distinctly differentiated, as evidenced in Fig. 5a′–c′. Each subplot corresponds to a different concentration, and intriguingly, three distinct clusters representing PFOS, PFOA, and cysteine-modified AgNR (reference) appear. This finding strongly demonstrates the ability to use a functionalized SERS substrate to enhance the specificity of PFAS identification across a broad range of concentrations. The use of advanced data analysis, such as the t-SNE algorithm, emphasizes its importance in revealing subtle spectral distinctions that are otherwise imperceptible to human observation.
To further demonstrate the ability of SERS spectra from functionalized AgNR substrates, all the spectra from Fig. 5a–c are combined together to construct an SVM model. For this analysis, we used a simple kernel – the linear kernel for SVM and maintained the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 training-to-test ratio. Surprisingly, even with this minimal setting, the SVM consistently achieved flawless results across all ten trials, attaining an average accuracy of 100%, as demonstrated by the confusion matrix shown in Fig. S4 of the ESI.†
1 training-to-test ratio. Surprisingly, even with this minimal setting, the SVM consistently achieved flawless results across all ten trials, attaining an average accuracy of 100%, as demonstrated by the confusion matrix shown in Fig. S4 of the ESI.†
These results indicate that when there are three concentrations in a spectral dataset, distinguishing between PFOA, PFOS, and reference based on SERS spectra from cysteine-modified AgNR substrates becomes an effortless task for the SVM. The exceptional performance of the SVM in differentiating the spectra implies that the inherent characteristics of the SERS spectra of PFOA, PFOS, and water on cysteine-modified AgNR substrates exhibit distinct patterns, enabling accurate classification with minimal data. Such a finding highlights the potential of using ML techniques to effectively discriminate between PFAS types, offering valuable insights for environmental monitoring and analysis.
SERS spectra of PFOS and PFOA on MCH-functionalized AgNR substrates
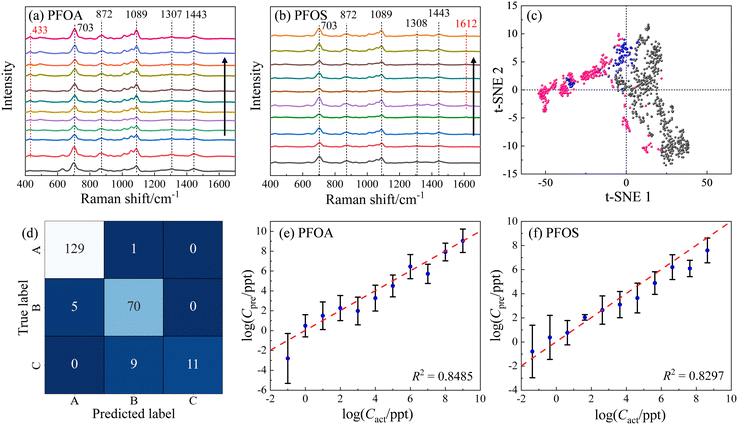
MCH (6-mercapto-1-hexanol) is a short-chain alkanethiol molecule with an end group of –OH. When the AgNR surface is functionalized with MCH, the surface will be negatively charged. Fig. 6a shows the resulting average spectra for different CPFOA on MCH–AgNR substrates, while Fig. 6b plots the spectra for PFOS. Visually discernible observations can readily identify several characteristics evident in Fig. 6a and b: 1) at most CPFOS, the SERS spectra are quite similar. In fact, the main spectral features are dominated by the MCH spectrum. Both the PFOS and PFOA spectra are characterized by the three signature MCH peaks: Δv = 703, 872, and 1089 cm−1. Fig. S5† presents the plots of the intensities of three distinct peaks against the logarithm of the concentrations for both PFOA and PFOS. It can be observed across all four subfigures that the relationship between peak intensities and concentration does not follow a monotonic trend, irrespective of the PFAS molecule type or the way baseline removal is employed. This inconsistency is attributed to variations in the enhancement factor, stemming primarily from batch-to-batch discrepancies. Such variations are the result of how spectra were acquired from different locations on the substrates and across multiple substrates, leading to the observed fluctuations. 2) Spectra of PFOA contain a unique peak in Fig. 6a at Δv = 433 cm−1, while those of PFOS display a unique peak at Δv = 1612 cm−1 in Fig. 6b, but only at CPFOS ≤ 4.28 × 102 ppt. This same peak also appears in Fig. 4 and 5, suggesting this unique peak is a part of the PFAS molecules and not the MCH. 3) With the increase of the PFOS concentration, the main features of MCH gradually diminish. These spectral similarities and differences can be used to classify and quantify PFOS in the solution.ML methods were used to classify and quantify the PFOS and PFOA spectra from MCH-modified AgNR substrates. To ensure a high-quality result for classification and quantification, we implement the Gaussian–Lorentzian function fitting (GLFF) to remove all the baselines in the spectra,53 through which the spectra can preserve the original signal but also minimize variations introduced by the intricate background. Fig. 6c presents a t-SNE plot based on the baseline removed and normalized SERS spectra. While the resulting t-SNE clusters could not be separated as distinctly as those observed in Fig. 3a and 5, a significant separation between the majority of PFOA (grey dots) and PFOS (pink dots) spectra is evident. Specifically, the 1st and 4th quadrants of the t-SNE plot predominantly contain PFOA data points, whereas the 2nd and 3rd quadrants predominantly contain PFOS data points. Notably, some PFOS data points appear within the 1st and 4th quadrants, and are close to the PFOA cluster, indicating challenges in achieving a complete differentiation between PFOA and PFOS even within a high-dimensional context. Moreover, it is noteworthy that the reference data (MCH, blue dots) form clusters in proximity to both PFOA and PFOS clusters. This proximity suggests the potential difficulty in effectively distinguishing the reference from the PFOA and PFOS compounds. These observations collectively emphasize the intricacies involved in accurately discerning between PFOA and PFOS spectra obtained from MCH-modified AgNR substrates, both in terms of their spectral patterns and their relationships with the reference data.
Subsequently, to demonstrate the capabilities of ML models, we partitioned the entire spectral dataset into distinct training, validation, and test subsets. Especially, regarding the PFOS spectral dataset and the accompanying reference spectra, data originating from three independent wells were collected. Consequently, we assigned the spectra from the first and second wells to the training and validation sets with a ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, while the spectra from the third well were exclusively assigned to the test set. For the PFOA spectral dataset and its corresponding reference data, measurements were obtained from a single well. To ensure an equitable division for training and validation, stratified sampling was applied with an 8
1, while the spectra from the third well were exclusively assigned to the test set. For the PFOA spectral dataset and its corresponding reference data, measurements were obtained from a single well. To ensure an equitable division for training and validation, stratified sampling was applied with an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Since these three groups exhibit more variations than the spectral dataset analyzed in the previous section, a more powerful SVM model with an RBF kernel with C = 100 and γ = ‘scale’ (indicating that γ is set automatically by the algorithm) was employed. Ten independent trials were conducted, resulting in an accuracy of 0.89 ± 0.02. The trial with the highest accuracy (0.93) is demonstrated by the confusion matrix shown in Fig. 6d. In this particular trial, the accuracy for PFOA is 0.99, with only one misclassification of a PFOA spectrum as PFOS; the accuracy for PFOS is 0.93, with 5 PFOS spectra being misclassified as PFOA. For the control group represented by MCH, the accuracy was notably lower at 0.55, with 9 as PFOS. These findings align with the results from t-SNE in Fig. 6c, corroborating the difficulty in effectively separating pure MCH from PFOA–MCH or PFOS–MCH mixtures.
1 ratio. Since these three groups exhibit more variations than the spectral dataset analyzed in the previous section, a more powerful SVM model with an RBF kernel with C = 100 and γ = ‘scale’ (indicating that γ is set automatically by the algorithm) was employed. Ten independent trials were conducted, resulting in an accuracy of 0.89 ± 0.02. The trial with the highest accuracy (0.93) is demonstrated by the confusion matrix shown in Fig. 6d. In this particular trial, the accuracy for PFOA is 0.99, with only one misclassification of a PFOA spectrum as PFOS; the accuracy for PFOS is 0.93, with 5 PFOS spectra being misclassified as PFOA. For the control group represented by MCH, the accuracy was notably lower at 0.55, with 9 as PFOS. These findings align with the results from t-SNE in Fig. 6c, corroborating the difficulty in effectively separating pure MCH from PFOA–MCH or PFOS–MCH mixtures.
To illustrate the quantification capability, two separate SVR models were built to quantify concentration-dependent PFOA and PFOS spectra. Both SVR models employed an RBF kernel, C = 1000, and γ = ‘scale’. For the PFOA model,  was set to be 0.001; while for PFOS,
was set to be 0.001; while for PFOS,  was adjusted to 0.1, suggesting the need for a larger error tolerance to enhance quantification results. Ten independent trials were performed for each SVR. The R2 values for PFOS and PFOA are 0.76 ± 0.04 and 0.82 ± 0.01, respectively, and the log–log plots of Cpreversus Cact of the best trials are plotted in Fig. 6e and f, respectively. These two plots showed the highest R2 values achieved in the analysis, which were 0.82 and 0.84 for PFOS and PFOA, respectively. Although the results for PFOS suggest that quantifying its concentration is more challenging, the model's prediction exhibits a notable alignment with the actual PFOS concentrations, i.e., most predicted concentrations closely follow the diagonal line, reinforcing the feasibility of this quantification approach. One-sample t-tests were employed to rigorously determine the LOD for both PFOA and PFOS. Similar to determining the LOD for Fig. 4, for each analyte tested, starting from the lowest feasible concentration, such as 0.1 ppt for PFOA or 4.28 × 10−2 ppt for PFOS, a one-sample t-test was conducted for the SVR model generated predicted concentrations against their respective actual concentration. We then identified the LOD by finding the lowest concentration at which the p-value of the t-test was greater than 0.05. By employing one-sample t-tests, the SVR model for PFOA achieved an LOD of 1 ppt, with a p-value of 0.37, while the LOD for PFOS was determined as 4.28 ppt, with a p-value of 0.10. With the prospect of incorporating more spectral data and refining the ML models, we believe that the quantification can be significantly improved.
was adjusted to 0.1, suggesting the need for a larger error tolerance to enhance quantification results. Ten independent trials were performed for each SVR. The R2 values for PFOS and PFOA are 0.76 ± 0.04 and 0.82 ± 0.01, respectively, and the log–log plots of Cpreversus Cact of the best trials are plotted in Fig. 6e and f, respectively. These two plots showed the highest R2 values achieved in the analysis, which were 0.82 and 0.84 for PFOS and PFOA, respectively. Although the results for PFOS suggest that quantifying its concentration is more challenging, the model's prediction exhibits a notable alignment with the actual PFOS concentrations, i.e., most predicted concentrations closely follow the diagonal line, reinforcing the feasibility of this quantification approach. One-sample t-tests were employed to rigorously determine the LOD for both PFOA and PFOS. Similar to determining the LOD for Fig. 4, for each analyte tested, starting from the lowest feasible concentration, such as 0.1 ppt for PFOA or 4.28 × 10−2 ppt for PFOS, a one-sample t-test was conducted for the SVR model generated predicted concentrations against their respective actual concentration. We then identified the LOD by finding the lowest concentration at which the p-value of the t-test was greater than 0.05. By employing one-sample t-tests, the SVR model for PFOA achieved an LOD of 1 ppt, with a p-value of 0.37, while the LOD for PFOS was determined as 4.28 ppt, with a p-value of 0.10. With the prospect of incorporating more spectral data and refining the ML models, we believe that the quantification can be significantly improved.
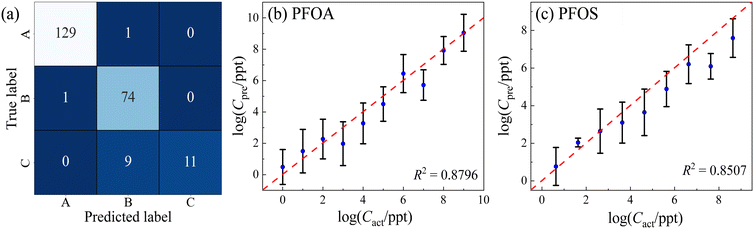
Taking into account the LOD for PFOA and PFOS, which are 1 and 4.28 ppt, respectively, the impact of low-concentration samples on both classification and regression models is noteworthy. As illustrated in Fig. 7a, by excluding concentrations below 1 ppt for PFOA and 4.28 ppt for PFOS, 3 of the 5 misclassified PFOS spectra were eliminated. All of them belonged to the lowest concentration tier of 4.28 × 10−2 ppt and were incorrectly identified as PFOA. When concentrations increased slightly to 4.28 × 10−1 ppt, the number of spectra misclassified as PFOA reduced to only 1. The elimination of these low-concentration samples resulted in the removal of 80% of the misclassifications from PFOS to PFOA. This led to a substantial improvement in the classification accuracy for PFOS, increasing it from 0.93 to 0.99, and lifting the overall model accuracy from 0.93 to 0.95. Contrastingly, the impact of removing low-concentration samples on regression models is modest. The R2 scores for PFOA and PFOS by the regression models would experience only marginal improvements, rising from 0.85 to 0.88 and from 0.83 to 0.85, as shown in Fig. 7b and c, respectively. The findings suggest that while classification models are notably sensitive to variations in low concentrations, regression models exhibit a higher level of robustness. Therefore, careful consideration of concentration ranges could be crucial in enhancing classification performance but may offer limited gains in the context of regression.
The stability of MCH-functionalized AgNR substrates
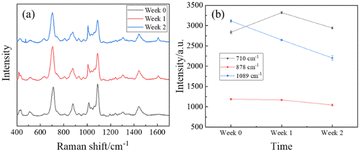
To demonstrate the stability of MCH modified AgNR substrates, a short time-dependent study was performed. Three AgNR substrates were immersed in 2 mL of 1 mM MCH for 1 hour before being dried with nitrogen. Each had 20 SERS spectra taken. 2 μL of 106 ppt PFOA in methanol was applied to one of the three substrates, and 20 SERS spectra were measured. After one week, 20 SERS spectra were measured from the two remaining substrates without PFOA. Then, the same volume and concentration of PFOA were applied to one of the two substrates, subsequently with 20 SERS spectra taken. After one more week, 20 SERS spectra were measured from the last substrate without PFOA. Then, another 20 SERS spectra were taken after PFOA was dispensed. The spectra for each substrate with PFOA had its baseline removed and were averaged to track 3 distinct peaks over the period of 2 weeks.Fig. 8a shows the spectrum comparison. The average spectra of the three measurements at different times have very similar spectral shapes with fluctuation in amplitude. However, the fluctuation in spectra amplitude was not significant. Fig. 8b plots the peak intensities at Δv = 710, 878, and 1089 cm−1, and these data do not have a consistent change over time. Additionally, the small error bars suggest that the outcomes derived from the MCH-modified AgNR substrates exhibit a high degree of stability over time.
Conclusions
In conclusion, our study demonstrates the effectiveness of utilizing both Raman and SERS spectra for the detection and differentiation of various PFAS. Raman spectra reveal distinct characteristic peaks specific to different PFAS molecules, allowing for a direct comparison with results from other literature. Meanwhile, while direct SERS spectra may not exhibit clearly distinguished PFAS characteristic peaks, the presence of PFAS on SERS substrates does induce noticeable spectral changes. By combining these spectral alterations with ML techniques, we have successfully differentiated and quantified the amounts of PFOA in water. Our approach, involving SERS and SVR, achieved an impressive LOD of 1 ppt, enabling highly sensitive PFAS detection. To further improve differentiation and quantification, we employed various alkanethiol molecules to modify the AgNR substrates, introducing different surface charge or wetting properties, expecting such a modification to alter the adsorption affinity of different PFAS molecules to the SERS substrates. Although the spectral features were dominated by the alkanethiol molecules, discernible changes due to the presence of different concentrations of PFAS and PFOS molecules were observed. Leveraging an SVM model, we achieved an average accuracy of 89% in differentiating PFOA, PFOS, and MCH, regardless of their concentrations. Once the spectra were accurately classified, further quantification was achieved through an SVR model, capable of predicting concentrations as low as 1 ppt for PFOA and 4.28 ppt for PFOS.Overall, our findings present a robust and efficient approach for PFAS detection, combining SERS and advanced MLAs. The high sensitivity and accuracy attained through this method hold great promise for addressing critical environmental and health concerns associated with PFAS contamination, opening avenues for the development of sensitive, reliable, and rapid detection systems to safeguard our water resources and communities. In particular, if a handheld Raman system is incorporated, this detection strategy can be portable and field-applicable.
However, our investigations do find several challenges in using SERS for PFAS detection. First, it is very hard to understand the spectral features. The obtained SERS spectra cannot be directly compared to Raman spectra.54 This deserves further investigation. Second, the PFAS molecules still have low affinity to any substrates presented in this work, which was suggested by the concentration-dependent SERS spectra. A better functionalization strategy shall be implemented to improve the affinity between PFAS molecules and SERS substrates. Third, it is a challenge to assign the Raman or SERS peak modes even though there are DFT calculations available. Finally, future research may explore the applicability of this approach to other contaminants and the potential for real-world implementation in environmental monitoring and water quality assessment. Experiments with real water samples containing PFAS are planned to provide a more comprehensive evaluation of our methodology. To address this, the collection of various water samples from different sources, including rivers, lakes, and household taps, under different conditions, has already been initiated. Currently, these samples are spiked and thus considered artificial. Furthermore, collaborations with agencies such as the EPA will be explored to obtain real samples with inherent PFAS contamination to strengthen the applicability and reliability of our detection method.
Author contributions
Joshua C. Rothstein: methodology, data curation, writing – original draft. Jiaheng Cui: formal analysis, writing – original draft. Yanjun Yang: methodology, data curation, writing – original draft. Xianyan Chen: supervision, writing – review & editing. Yiping Zhao: conceptualization, funding acquisition, supervision, project administration, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Joshua C. Rothstein, Yanjun Yang, and Yiping Zhao were partially supported by the National Science Foundation under the contract #ECCS-1808271. Jiaheng Cui, Xianyan Chen, and Yiping Zhao are funded by USDA NIFA Grant number 2023-67015-39237.References
- Z. Wang, J. C. DeWitt, C. P. Higgins and I. T. Cousins, Environ. Sci. Technol., 2017, 51, 2508–2518 CrossRef CAS PubMed.
- M. Al Amin, Z. Sobhani, Y. Liu, R. Dharmaraja, S. Chadalavada, R. Naidu, J. M. Chalker and C. Fang, Environ. Technol. Innovation, 2020, 19, 100879 CrossRef.
- H. Ryu, B. Li, S. De Guise, J. McCutcheon and Y. Lei, J. Hazard. Mater., 2021, 408, 124437 CrossRef CAS.
- Y. Wang, S. B. Darling and J. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 60789–60814 CrossRef CAS.
- Z. Jiao, J. Li, L. Mo, J. Liang and H. Fan, Microchim. Acta, 2018, 185, 473 CrossRef PubMed.
- Z. Cheng, L. Du, P. Zhu, Q. Chen and K. Tan, Spectrochim. Acta, Part A, 2018, 201, 281–287 CrossRef CAS.
- S. Schlücker, Angew. Chem., Int. Ed., 2014, 53, 4756–4795 CrossRef.
- K. Kneipp, H. Kneipp, I. Itzkan, R. R. Dasari and M. S. Feld, Chem. Rev., 1999, 99, 2957–2976 CrossRef CAS.
- C. Fang, M. Megharaj and R. Naidu, RSC Adv., 2016, 6, 11140–11145 RSC.
- C. McDonnell, F. M. Albarghouthi, R. Selhorst, N. Kelley-Loughnane, A. D. Franklin and R. Rao, ACS Omega, 2023, 8, 1597–1605 CrossRef CAS.
- H. Park, J. Park, W. Kim, W. Kim and J. Park, J. Hazard. Mater., 2023, 453, 131384 CrossRef CAS PubMed.
- Y. Feng, J. Dai, C. Wang, H. Zhou, J. Li, G. Ni, M. Zhang and Y. Huang, ACS Appl. Nano Mater., 2023, 6, 13974–13983 CrossRef CAS.
- C. L. Leverette, S. A. Jacobs, S. Shanmukh, S. B. Chaney, R. A. Dluhy and Y. P. Zhao, Appl. Spectrosc., 2006, 60, 906–913 CrossRef CAS PubMed.
- S. Shanmukh, L. Jones, J. Driskell, Y. Zhao, R. Dluhy and R. A. Tripp, Nano Lett., 2006, 6, 2630–2636 CrossRef CAS PubMed.
- Y. P. Zhao, S. B. Chaney, S. Shanmukh and R. A. Dluhy, J. Phys. Chem. B, 2006, 110, 3153–3157 CrossRef CAS.
- Y. Zhao, A. Kumar and Y. Yang, Chem. Soc. Rev., 2024, 53, 1004–1057 RSC.
- J. L. Abell, J. M. Garren and Y. Zhao, Appl. Spectrosc., 2011, 65, 734–740 CrossRef CAS.
- H. Chu, Y. Liu, Y. Huang and Y. Zhao, Opt. Express, 2007, 15, 12230–12239 CrossRef CAS PubMed.
- J. L. Abell, J. D. Driskell, R. A. Dluhy, R. A. Tripp and Y. P. Zhao, Biosens. Bioelectron., 2009, 24, 3663–3670 CrossRef CAS PubMed.
- Y. Zhu, R. A. Dluhy and Y. Zhao, Sens. Actuators, B, 2011, 157, 42–50 CrossRef CAS.
- J. P. Singh, H. Y. Chu, J. Abell, R. A. Tripp and Y. P. Zhao, Nanoscale, 2012, 4, 3410–3414 RSC.
- C. Y. Song, J. D. Driskell, R. A. Tripp, Y. P. Cui and Y. P. Zhao, The use of a handheld Raman system for virus detection, Proc. SPIE 8358, Chemical, Biological, Radiological, Nuclear, and Explosives (CBRNE) Sensing XIII, 4 May 2012, p. 83580I, DOI:10.1117/12.918758.
- X. M. Wu, C. Xu, R. A. Tripp, Y. W. Huang and Y. P. Zhao, Analyst, 2013, 138, 3005–3012 RSC.
- O. Adir, M. Poley, G. Chen, S. Froim, N. Krinsky, J. Shklover, J. Shainsky-Roitman, T. Lammers and A. Schroeder, Adv. Mater., 2020, 32, 1901989 CrossRef CAS.
- F. Lussier, V. Thibault, B. Charron, G. Q. Wallace and J.-F. Masson, TrAC, Trends Anal. Chem., 2020, 124, 115796 CrossRef CAS.
- N. M. Ralbovsky and I. K. Lednev, Chem. Soc. Rev., 2020, 49, 7428–7453 RSC.
- H. He, S. Yan, D. Lyu, M. Xu, R. Ye, P. Zheng, X. Lu, L. Wang and B. Ren, Anal. Chem., 2021, 93, 3653–3665 CrossRef CAS.
- K. Rebrošová, M. Šiler, O. Samek, F. Růžička, S. Bernatová, V. Holá, J. Ježek, P. Zemánek, J. Sokolová and P. Petráš, Sci. Rep., 2017, 7, 14846 CrossRef.
- Y. Yang, B. Xu, J. Haverstick, N. Ibtehaz, A. Muszyński, X. Chen, M. E. H. Chowdhury, S. M. Zughaier and Y. Zhao, Nanoscale, 2022, 14, 8806–8817 RSC.
- Y. J. Yang, B. B. Xu, J. Murray, J. Haverstick, X. Y. Chen, R. A. Tripp and Y. P. Zhao, Biosens. Bioelectron., 2022, 217, 114721 CrossRef CAS.
- S. B. Chaney, S. Shanmukh, R. A. Dluhy and Y. P. Zhao, Appl. Phys. Lett., 2005, 87, 031908 CrossRef.
- J. D. Driskell, S. Shanmukh, Y. Liu, S. B. Chaney, X. J. Tang, Y. P. Zhao and R. A. Dluhy, J. Phys. Chem. C, 2008, 112, 895–901 CrossRef CAS.
- J. L. Abell, J. D. Driskell, R. A. Dluhy, R. A. Tripp and Y. P. Zhao, Biosens. Bioelectron., 2009, 24, 3663–3670 CrossRef CAS.
- Y. P. Zhao, A. Kumar and Y. J. Yang, Chem. Soc. Rev., 2024, 53, 1004–1057 RSC.
- L. van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–297 Search PubMed.
- H. Drucker, C. J. Burges, L. Kaufman, A. Smola and V. Vapnik, Adv. Neural Inf. Process. Syst., 1996, 9, 155–161 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- Y. Chen, Y. Yang, J. Cui, H. Zhang and Y. Zhao, J. Hazard. Mater., 2024, 465, 133260 CrossRef CAS.
- W. F. Edgell, H. D. Mallory and D. G. Weiblen, J. Am. Chem. Soc., 1950, 72, 4856–4859 CrossRef CAS.
- R. A. Carney, E. A. Piotrowski, A. G. Meister, J. H. Braun and F. F. Cleveland, J. Mol. Spectrosc., 1961, 7, 209–222 CrossRef CAS.
- E. L. Pace, A. C. Plaush and H. V. Samuelson, Spectrochim. Acta, 1966, 22, 993–1006 CrossRef CAS.
- S. Bai, A. Hu, Y. Hu, Y. Ma, K. Obata and K. Sugioka, Nanomaterials, 2022, 12, 970 CrossRef CAS PubMed.
- J. Chowdhury, J. Sarkar, R. De, M. Ghosh and G. B. Talapatra, Chem. Phys., 2006, 330, 172–183 CrossRef CAS.
- W. M. Ingram, C. Q. Han, Q. J. Zhang and Y. P. Zhao, J. Phys. Chem. C, 2015, 119, 27639–27648 CrossRef CAS.
- Y. P. Zhao, Nanomaterials, 2023, 13, 2998 CrossRef CAS PubMed.
- H. T. Ngo, H.-N. Wang, A. M. Fales and T. Vo-Dinh, Anal. Chem., 2013, 85, 6378–6383 CrossRef CAS.
- H. Wang, X. Jiang, X. Wang, X. Wei, Y. Zhu, B. Sun, Y. Su, S. He and Y. He, Anal. Chem., 2014, 86, 7368–7376 CrossRef CAS.
- C. Y. Song, Y. J. Yang, B. Y. Yang, Y. Z. Sun, Y. P. Zhao and L. H. Wang, Nanoscale, 2016, 8, 17365–17373 RSC.
- H. Zhou and J. Kneipp, Anal. Chem., 2023, 95, 3363–3370 CrossRef CAS.
- J. A. Rice, Mathematical Statistics and Data Analysis, Cengage Learning/Brooks/Cole, Belmont, 3rd edn, 2007 Search PubMed.
- A. C. Sparavigna, ChemRxiv, 2023, preprint,10.26434/chemrxiv-2023-9swp9-v3, 10.26434/chemrxiv-22023-26439swp26439-v26433 Search PubMed.
- Y. Yang, B. Xu, J. Murray, J. Haverstick, X. Chen, R. A. Tripp and Y. Zhao, Biosens. Bioelectron., 2022, 217, 114721 CrossRef CAS.
- Y. L. Ju, O. Neumann, M. Bajomo, Y. P. Zhao, P. Nordlander, N. J. Halas and A. Patel, ACS Nano, 2023, 17, 21251–21261 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sd00052h |
| This journal is © The Royal Society of Chemistry 2024 |