Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hysteresis in phase volumes, compositions and interfacial roughness in model OPV-small-molecule/polymer thin-films†
A. M.
Higgins
 *a,
P.
Gutfreund
*a,
P.
Gutfreund
 b,
V.
Italia
c,
A.
Nelson
b,
V.
Italia
c,
A.
Nelson
 d,
J. T.
Cabral
d,
J. T.
Cabral
 e and
E. L.
Hynes
e and
E. L.
Hynes
 a
a
aSchool of Engineering and Applied Science, Swansea University, Fabian Way, Crymlyn Burrows, Swansea SA1 8EN, Wales, UK. E-mail: a.m.higgins@swansea.ac.uk
bInstitut Laue-Langevin, 71 avenue des Martyrs, 38000 Grenoble, France
cDepartment of Physics, Swansea University, Singleton Park, Swansea SA2 8PP, Wales, UK
dANSTO, Locked Bag 2001, Kirrawee DC, New South Wales 2232, Australia
eDepartment of Chemical Engineering, Imperial College London, London SW7 2AZ, UK
First published on 17th January 2024
Abstract
Domain morphology and composition, and the structure of interfaces between domains are key factors in the performance and stability of organic photovoltaics (OPVs) fabricated from polymer/small-molecule blends. In this study, we investigate the evolution of composition, phase-volume and interfacial roughness in model polymer/small-molecule bilayers, in response to thermal annealing. Polystyrene/fullerene mixing is studied as a function of annealing temperature, using in situ neutron reflectivity, in thin-film bilayer samples comprising pure component or mixed layers. Remarkably, we discover that thermal annealing at temperatures around or above the reported glass transition temperatures, Tg, of the components can result in extensive mass-transfer between layers, that has the superficial appearance of equilibration, but leaves the layer compositions, thicknesses, and/or the interfacial composition profile in a non-equilibrium state. This is not merely a case of slow kinetics near Tg, as subsequent heating to higher temperatures, followed by cooling, reveals pronounced hysteresis in these systems. This has important implications for the measurement of equilibrium compositions in polymer/small-molecule mixtures for OPV applications, and for device stability during operation.
Introduction
Mixing nanoparticles into polymer matrices can lead to a range of equilibrium and non-equilibrium phenomena with significant technological relevance, including the improvement of adhesive properties,1 control of optical and electronic properties,2 and stabilisation of thin-films.3,4 Fullerenes have been shown to be effective, at relatively low concentrations (around 1%), at stabilising thin-films,5 and have demonstrated the ability to form ordered structures6 (with exposure to light playing a significant role in controlling these processes7). However, the most widespread application of ‘fullerene nanocomposites’ is as the active layers of OPVs. Here, mixtures of conjugated polymers and fullerene derivatives are chosen so that they form a phase-separated donor/acceptor morphology when a common solvent is removed, resulting in functional ‘bulk heterojunction’ (BHJ) structures under appropriate solution and thermal processing conditions.8 The use of non-fullerene acceptors (NFAs) over the last five years or so has led to significant increases in OPV efficiency,9,10 yet device stability remains a significant challenge.9–12 The control of domain composition and morphology within BHJs is a key factor in maintaining device stability during operation. Microstructure is preserved by the arrest of domain coarsening,13 and the elimination of compositional changes within optimised BHJ domains14 is reported to be a requirement to avoid degradation.15–17 While BHJs in general consist of both crystalline and disordered phases, it has been recognised recently that the composition of mixed amorphous phases is of key importance for charge transport.18 Two strategies exist for suppressing composition changes within amorphous BHJ domains (discussed, for instance, by Qin et al.13), namely ‘thermodynamic stabilisation’ and ‘kinetic stabilisation’. In the former, domain compositions form co-existing phases at equilibrium, and in the latter non-equilibrium compositions are achieved by vitrification.15 Given the importance of designing OPV structure along the pathway to equilibrium, a number of experimental and (equilibrium) theoretical studies of polymer/small-molecule mixing have been reported; these include the examination of composition profiles within the thin-film geometries typical of OPVs, using model bilayers to probe mixing behaviour.18–26 Quantitative links between thermodynamic and kinetic properties, and performance18 and stability,26 in a range of fullerene and NFA systems, have been proposed.We have recently carried out a series of experimental investigations into the behaviour of model polymer/fullerene mixtures in thin-film geometries,27–30 employing narrow molecular-weight-distribution polystyrene (PS), and phenyl-C60-butyric acid methyl ester (PCBM) and bis-adduct phenyl-C60-butyric acid methyl ester (Bis-PCBM). PS/Bis-PCBM provides a relatively simple model system (a mixture of an amorphous polymer and an amorphous, low aspect-ratio small-molecule) which can be used as a benchmark for mixing behaviour in polymer/small-molecule OPV blends and comparison with equilibrium theories. In bilayer films heated well above the glass transition temperature, Tg, of the components, and subjected to thermal cycling, we generally observe behaviour consistent with equilibrium thermodynamics.30 However, non-equilibrium behaviour can also occur, resulting in a loss of reversibility upon thermal cycling.
In this paper, we explore different aspects of non-equilibrium behaviour in PS/Bis-PCBM bilayer films employing in situ annealing and neutron reflectivity (NR) as the primary tool for our investigation. Of particular relevance to our study is that, as well as probing layer compositions and thicknesses, NR holds an advantage over techniques such as ellipsometry22 and ion-beam methods,18,24 in being able to provide sub-nanometre resolution of the width of the interface (interfacial roughness) between adjacent layers.27 Our main finding is that isothermal annealing at temperatures of around 140 to 150 °C can produce temporal behaviour, involving extensive mass-transfer, that superficially has the appearance of equilibration, but where in fact the system parameters are trapped in a local minimum. We show that either the layer thickness and composition, or the interfacial roughness display non-reversible behaviour, and exhibit hysteresis when bilayer samples are heated further and then cooled.
Experimental methods
Sample preparation
PS (Agilent, UK) and Bis-PCBM (99.5% purity, Solenne, Netherlands) solutions were prepared by dissolving in toluene and chlorobenzene respectively. Two PS weight-average molecular weights (Mw) were used, below and above the entanglement Mw, namely 4.73, and 278.2 kg mol−1, with polydispersity indices (Mw/Mn, where Mn is the number-average molecular weight) of 1.04, and 1.05 respectively. Throughout the paper these are referred to as 5k and 300k. PS/Bis-PCBM blends were prepared by first mixing the PS and Bis-PCBM at a given mass ratio, and then adding chlorobenzene. The solutions were then left in the dark for several days. Single-side-polished silicon wafers (two-inch diameter, 2.5 mm thickness, from Siltronix, France) with a native oxide layer were sonicated in acetone and then isopropanol (15 min each). This was followed by rinsing in de-ionised water, and then by rotating the wafers on a spin-coater for one minute to remove the water. Bis-PCBM solutions were then spin-coated onto the silicon wafers, to produces highly uniform layers (see Fig. S9_1f, ESI†). Top layers (PS and PS/Bis-PCBM blends) were prepared by spin-coating solutions onto sheets of freshly cleaved mica (Goodfellow, UK) and then floating the layers onto the surface of a bath of de-ionised water. This floating layer was then deposited onto the silicon/Bis-PCBM to make a bilayer sample. This procedure gives a high degree of bilayer uniformity across a two-inch diameter sample. Further details relating to the floating methodology, and the quality of the resulting samples can be found in the ESI.† The samples were left to dry in the dark, before being placed under vacuum (at room temperature, in the dark) for 24 hours. Further details regarding solution concentrations and spin speeds are given in the ‘Sample preparation; further details’ section in the ESI.† Two batches of samples were fabricated; (i) batch A – fabricated and then measured on the reflectometer D17,31 at the Institut Laue-Langevin (ILL), Grenoble, France in 2021, and (ii) batch B – fabricated and then measured on D17 in 2019. The bulk of the results presented in this paper are from batch A; batch A contained seven samples (labelled A–G, containing 5k and 300k PS MWs), and batch B contained three samples (labelled α–γ, all with 300k PS MW).In situ neutron reflectivity (NR)
Samples were mounted onto the surface of a heater block within a vacuum chamber, and exposed to the neutron beam as they were thermally annealed in the dark. Experiments on batch A were performed using a turbo pump which achieved pressures of approximately 10−4 mbar during thermal annealing. Experiments on batch B were performed using a rotary pump, achieving pressures in the range 2 × 10−1 to 2 × 10−2 mbar. After the chamber was pumped down, the heater was set to either 80 °C (batch A) or around 120–130 °C (batch B), and a ‘full’ NR measurement was taken (with data acquired out to a momentum transfer, q, of around 0.2 Å−1). A full NR measurement consisted of acquisition using a white beam of neutrons in time-of-flight mode at incident angles of 0.8° and 3°. By using a relatively relaxed resolution, Δq/q, of around 2–4% at q = 0.008 Å−1 and around 8% at q = 0.15 Å−1, we were able to collect a full NR curve using a total of 10 minutes acquisition time (2 and 8 minutes acquisition for incident angles of 0.8° and 3° respectively).‡ The heater set-point temperature was then changed in a stepwise fashion. Extensive calibrations were performed both before and after each experiment on D17, to establish the offset between the heater set-point and the temperature at the surface of the silicon wafers. This included stabilisation measurements across the temperature range used in this study; full details can be found in Higgins et al.30 After waiting for a sufficient time for the sample surface temperature to stabilise (at least 6 minutes following a 10 °C increase or decrease in set-point temperature), a full NR measurement was taken. Throughout the main paper, unless stated otherwise, given temperatures are the sample surface temperatures, rather than the heater set-point temperatures.Data reduction and analysis
All NR data were reduced using Cosmos, within the ILL's data manipulation software, Lamp,32 following previously reported procedures30 detailed in ESI.† The error bars plotted in the NR curves represent standard deviations, calculated from the neutron counting statistics. Data analysis was performed using both unconstrained and constrained fits. In the unconstrained fits, NR curves were fitted within refnx33 using two uniform scattering length density (SLD) layers (refnx Slabs) with adjustable thickness and SLD. While, in general, asymmetric interface composition profiles can be found in a variety of equilibrium34 and non-equilibrium35–38 situations, we find that we are able to fit measurements well using an error function. In all fits the buried interface (between the two layers) is therefore quantified using an adjustable Gaussian roughness parameter,39,40 which is, in all cases, small compared to the two layer thicknesses. We illustrate the robustness of this approach by comparing fits using error function SLD profiles, to fits using free-form splines with different numbers of adjustable parameters. Fig. S10_1 (ESI†) shows very little difference between the interface SLD profiles using these different methodologies, and we therefore choose the simplest, error function, model. A brief description of how to interpret the interfacial roughness parameter extracted from specular NR measurements is given in the ESI.† An adjustable Gaussian roughness parameter is also used to parameterise the sample surface. A small adjustment in the overall normalisation was also allowed. Constrained fits in refnx had one fewer degree of freedom than the unconstrained fits, as the total scattering length per unit area of sample was held fixed for all measurements on a sample. For each sample, three sets of constrained fits were performed, each with a slightly different value for the total scattering length per unit area; these values were the mean, the maximum and the minimum values obtained from the unconstrained fits (these values typically differ by 2–3%; e.g. see Fig. S5_1d, ESI†). A fixed layer (SLD = 2.5 × 10−6 Å−2, thickness = 15 Å, roughness = 2 Å) representing the native oxide layer was included in the model between the adjustable layers and the semi-infinite silicon substrate. A fixed background of 10−7 was also included. The resolution from the data file (calculated in Cosmos from the instrumental settings) was used in all fits. For comparison purposes, a combination of Levenberg–Marquardt, differential evolution and Markov-chain-Monte-Carlo (MCMC) methods were used to fit the data.33 These all gave very similar fit parameters. The uncertainties of the MCMC fit parameters correspond to approximately one standard deviation.33Fourier transform infra-red spectroscopy (FTIR)
Prior to annealing, FTIR measurements were carried out on Bis-PCBM films to assess whether oxidation of the fullerene was likely to occur under our annealing protocols. Firstly, films of Bis-PCBM were made by drop-casting from chlorobenzene solution onto a silicon substrate. The films were then dried and measured using a PerkinElmer Spectrum Two spectrometer equipped with a diamond crystal for measuring in attenuated total reflection (ATR) mode. Annealing was then performed under more harsh conditions than used in the in situ NR experiments (at higher temperatures, for longer times and with lower vacuum). As found previously during our studies on PCBM,27 no evidence of characteristic fullerene oxidation41 was observed (see Higgins et al.30).Safety and hazards
Information relating to chemicals and materials, sample fabrication (including spin-coating) and neutron reflectivity measurements is given in the ESI.†Results and discussion
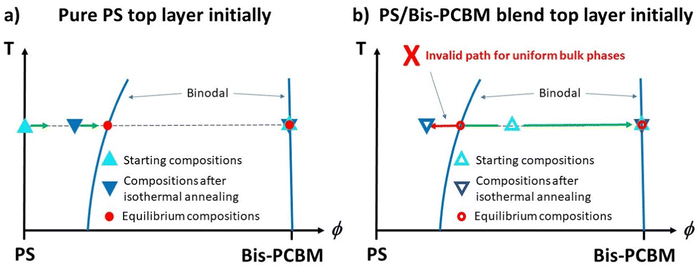
Bilayer samples were fabricated on silicon substrates, with pure Bis-PCBM layers deposited directly onto the silicon. Two different categories of top layers were then added; either a pure PS layer or a layer that was a blend of PS and Bis-PCBM. The main question posed in this study is represented schematically in Fig. 1(a–c); given that we have previously established that heating at sufficiently high temperatures causes bilayer composition profiles to evolve to equilibrium states (irrespective of the starting points in phase-space), does this occur upon annealing at lower temperatures (closer to the Tg of Bis-PCBM) that still confer sufficient molecular mobility to cause extensive mass-transfer between the layers? Typical annealing/NR measurement protocols are shown in Fig. 1(d–e). Samples were initially measured at 80 °C (a temperature at which there was no observable mixing between the two layers in the samples). Samples with blend top layers were then isothermally annealed for several hours at sample surface temperatures of either 139 or 148 °C (close to the reported Tg of the Bis-PCBM22), before being cycled through a range of different temperatures above and below the isothermal annealing temperature (from high-to-low-to-high temperature; Fig. 1d). One sample with a pure 300k PS top layer was annealed by gradually increasing the annealing temperature (Fig. 1e), while others were put through temperature cycling (from high-to-low-to-high temperature, as in the right-hand-side of Fig. 1d), but without an initial isothermal step at 139 or 148 °C. All samples were measured again after cooling to 80 °C. The behaviour of samples during temperature cycling, after first going to high temperature (173 °C) is as expected for systems at equilibrium; for a given MW, samples exhibit reversible behaviour with temperature, and converge to similar scattering length density (SLD) profiles (in terms of layer SLDs and interfacial roughnesses) from different starting points (from either pure PS top layers, or from blend top layers).30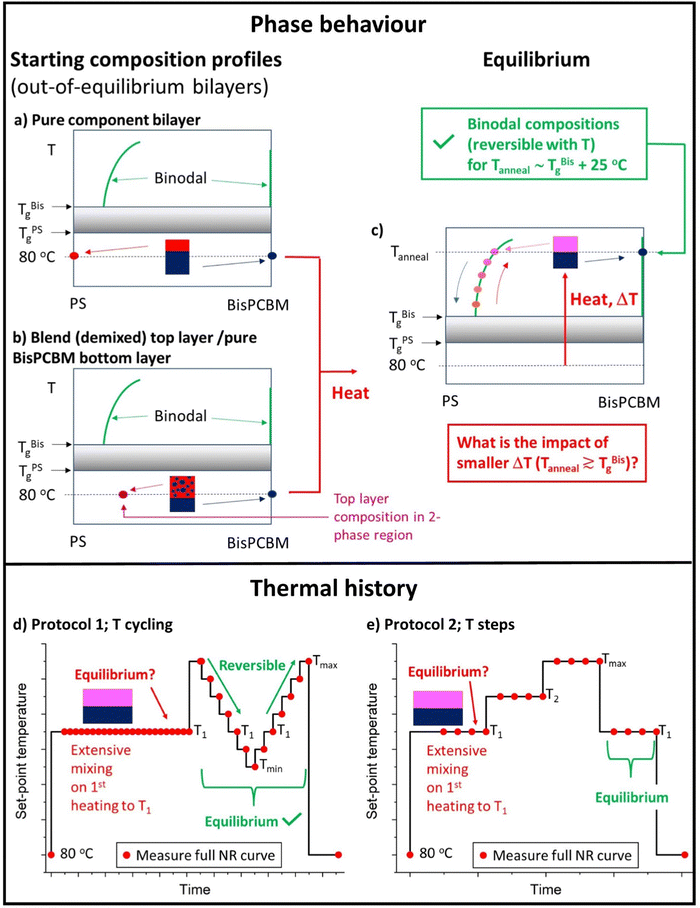 | ||
| Fig. 1 (a)–(c) Schematic PS/Bis-PCBM composition–temperature phase-diagrams representing the equilibration questions probed in this study, and (d) and (e) schematic diagrams showing the experimental programme – annealing protocols and neutron reflectivity (NR) measurements. Figure (a) and (b) show the starting points for the two different categories of bilayer samples (at 80 °C). (a) Represents a bilayer in which the bottom and top layers are initially pure Bis-PCBM and pure PS respectively and (b) represents a bilayer in which the bottom layer is pure Bis-PCBM, but the top layer is a PS/Bis-PCBM blend (with a composition that is in the 2-phase part of the phase-diagram). Figure (c) represents the behaviour when both categories of samples are heated well above the glass transition temperatures (Tg) of the components (TBisg and TPSg). Irrespective of the starting points, both categories of sample evolve to co-existing (binodal) compositions, which change reversibly with temperature.30 The key question of this study is what happens for annealing temperatures closer to the Tg of the Bis-PCBM? (d) A typical annealing protocol used for samples that initially had a top layer that consisted of a PS/Bis-PCBM blend (samples D, E and G). Isothermal annealing at T1 was followed by thermal cycling at temperatures above and below T1. T1 was either 139 °C or 148 °C. Tmax was either 173 °C or 181 °C. Tmin was either 114 °C or 123 °C. The thermal cycling protocol on the right-hand part of figure (d) was performed, without the preceding isothermal annealing, on some samples with initially pure PS top layers (samples B, C and F). (e) The annealing protocol used for sample A. Batch B samples (α–γ) were heated using a similar protocol to that shown in figure (e), but with a larger number of different temperatures and only one NR measurement at each temperature. | ||
Layer composition and interfacial roughness behaviour (unconstrained fits)
In this section we discuss the analysis that was performed on the NR data using unconstrained fits (the results of which are shown in Fig. 2–4), in which there were three adjustable parameters (thickness, SLD and roughness) in both the bottom and top layers, with no constraints on these parameters. Our main focus here is on a batch of seven PS/Bis-PCBM samples, made on a single batch of silicon substrates (batch A – samples A–G). Four of these samples initially had top layers that were pure PS and three had top layers that were initially PS/Bis-PCBM blends. A second small batch of samples (all with pure 300k PS top layers) was also investigated (batch B – samples α–γ). Details of all samples are given in Table 1. Fig. 2 shows the behaviour during isothermal annealing at 139 °C, of a bilayer sample with a top layer that was initially a 300k PS/Bis-PCBM blend (sample D). The blend ratio was such that this layer was initially in the two-phase part of the phase diagram.27,30 There is considerable, and rapid, change in the reflectivity curve on heating to 139 °C (Fig. 2b). As can be seen in the SLD profiles (Fig. 2c), this is as a result of transport of fullerene molecules from the top layer into the bottom layer; the bottom layer remains essentially pure Bis-PCBM, but thickens. Inspection of the NR and the SLD profiles in Fig. 2 shows that this change gradually slows down, with relatively little change in the bilayer after around two and a half hours annealing at 139 °C. This is quantified further by examining the change in the values of the fit parameters with time.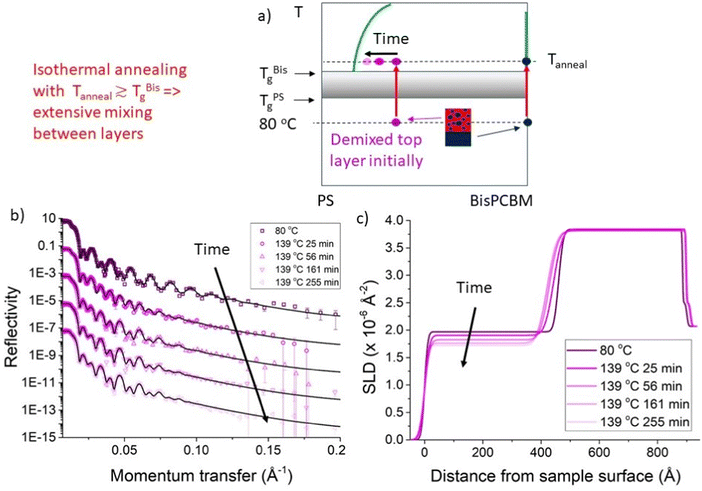 | ||
| Fig. 2 In situ bilayer annealing and neutron reflectivity (NR) measurements. (a) A schematic representation of the evolution in top layer composition during isothermal annealing, close to the Tg of Bis-PCBM, for a sample that initially had a top layer that was a 300k PS/Bis-PCBM blend. (b) NR data and (unconstrained) fits and (c) corresponding scattering length density (SLD) profiles, for a sample measured at 80 °C and at various different times after raising the temperature of the sample to 139 °C. The data shown in (b) and (c) are for a sample that initially had a 300k PS/Bis-PCBM blend top layer (Sample D). The times listed are at the end of each NR measurement. The NR curves in (b) are offset vertically for clarity. The NR curves and fits in (b) are reproduced without any vertical offsets in Fig. S2_1 (ESI†), over a restricted momentum transfer, q, range. Fig. S2_2 (ESI†) shows NR curves, fits and SLD profiles for a nominally duplicate sample, sample E, isothermally annealed at 148 °C. The 80 °C NR data, fit and SLD profile in (b) and (c) are reproduced from ref. 30, Fig. 2c). | ||
 | ||
| Fig. 3 Apparent equilibration of layer composition; measurements during isothermal annealing of batch A bilayers at sample surface temperatures of 139 °C or 148 °C, and measurements at 139 °C and 148 °C after equilibration at 173 °C. Figure (a) and (b) show data for 300k and 5k PS respectively. The left-hand sides of (a) and (b) (with light-yellow backgrounds) show the time dependence of the layer scattering length densities (SLDs), ρtop and ρbottom, during isothermal annealing at 139 °C or 148 °C, for samples A, D, E and G (the top layer of sample A is initially pure PS, and those of samples D, E and G are initially blends). The right-hand sides of (a) and (b) (with light-green backgrounds) show the SLD measured at 139 °C or 148 °C during thermal cycling, after equilibration at 173 °C, for all seven samples. The data points located in the regions with a white background represent measurements performed at 80 °C, before heating to higher temperatures. The time points correspond to the time at the end of each NR measurement. All parameters shown in this figure come from unconstrained fits. The lines are guides to the eye. Filled symbols represent samples that initially had pure PS top layers and open symbols represent samples that initially had PS/Bis-PCBM blend top layers. The initial layer SLDs (on a white background) are reproduced from ref. 30, Fig. 5a). The equilibrated data (with light-green backgrounds) are contained within the data in ref. 30, Fig. 7 and 8. | ||
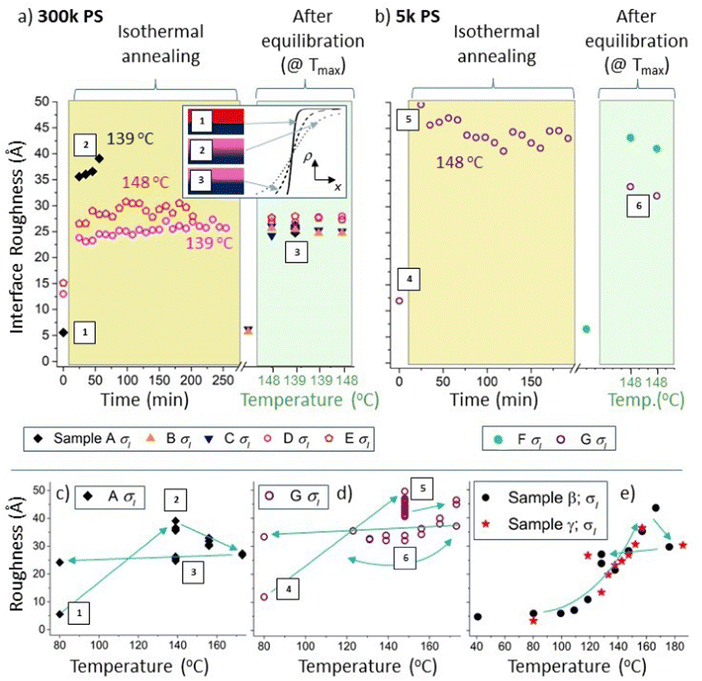 | ||
| Fig. 4 Interfacial roughness, σI, hysteresis in non-equilibrated samples. Figure (a) and (b) show σI data for 300k and 5k PS samples respectively. The left-hand sides of (a) and (b) (with light-yellow backgrounds) show the time dependence of σI during isothermal annealing at either 139 °C or 148 °C, for samples A, D, E and G. The right-hand sides of (a) and (b) (with light-green backgrounds) show σI measured at 139 °C or 148 °C during thermal cycling, after equilibration at 173 °C, for all seven batch A samples. The data points located in the regions with a white background represent measurements performed at 80 °C, before heating to higher temperatures. The inset in (a) shows a schematic diagram illustrating the hysteresis in σI in sample A. (c) σI for a 300k PS bilayer (top layer initially pure PS; sample A). (d) σI for a 5k PS bilayer (top layer initially a PS/Bis-PCBM blend; sample G). (e) σI for some members of a second batch of 300k PS bilayer samples (batch B; using a different batch of Si wafers and measured during a second experiment), initially all with pure PS top layers. In (a) and (b) each time point corresponds to the time at the end of each NR measurement. All parameters shown in this figure come from unconstrained fits. Accompanying layer thickness and scattering length density (SLD) parameters for sample A are shown in Fig. S4_1 (ESI†). The data in (c), (d) and (e) are reproduced in Fig. S4_2 (ESI†) along with additional details, including additional fits (using a Markov-chain-Monte-Carlo (MCMC) algorithm) and lines connecting the data points in chronological order. Surface roughness data is show in Fig. S4_2 (ESI†). Filled symbols represent samples that initially had pure PS top layers and open symbols represent samples that initially had PS/Bis-PCBM blend top layers. The labels 1, 2 and 3 are in chronological order and highlight the hysteresis in σI in sample A (representing the unannealed sample, the sample during isothermal annealing at 139 °C and the equilibrated sample at 139 °C respectively). Similarly, the labels 4, 5 and 6 are in chronological order and highlight the hysteresis in σI in sample G (this time at 148 °C). The equilibrated data (with a light-green background) in (b) are contained within the data in ref. 30, Fig. 7e and f. | ||
| Batch A (measured in 2021 on D17) | Initial top layer composition |
| Samples A, B and C | Pure 300k PS |
| Sample D and E | Bis-PCBM/300k PS blend (34 wt% Bis-PCBM) |
| Sample F | Pure 5k PS |
| Sample G | Bis-PCBM/5k PS blend (33 wt% Bis-PCBM) |
| Batch B (measured in 2019 on D17) | |
| Samples α, β and γ | Pure 300k PS |
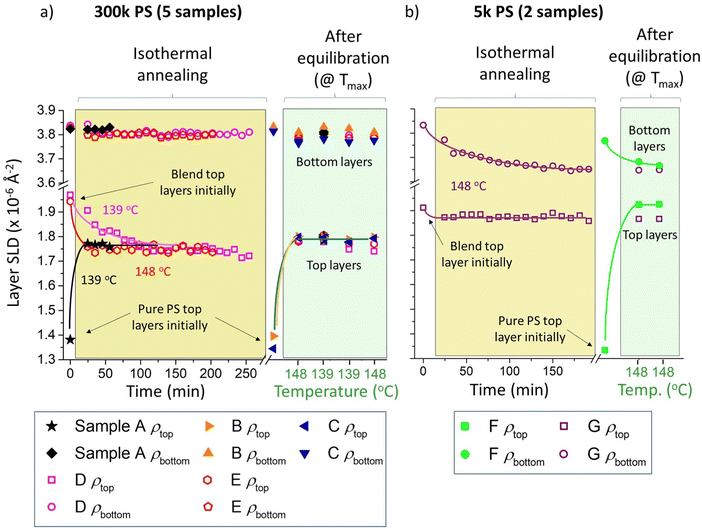
Fig. 3 shows SLD parameters extracted from bilayer fits to all seven batch A samples, in which the sample SLD profiles are parameterised by two layers (labelled ‘top’ and ‘bottom’) on a silicon substrate. In the model, both layers are parameterised by uniform SLDs (ρtop and ρbottom) and thicknesses (dtop and dbottom), plus two roughness parameters representing the sample surface roughness (σs) and the buried interfacial roughness between the top and bottom layers (σI). The SLD parameters in Fig. 3 are shown firstly as a function of time (during isothermal annealing – on a light-yellow background), and then temperature (during temperature cycling following equilibration – on a light-green background, showing only the data collected at the temperatures used for isothermal annealing). The left-hand side of Fig. 3a includes the evolution in layer SLD of two (nominally identical) samples, with top layers that were initially 300k PS/Bis-PCBM blends in the two-phase region of the phase diagram, at two different isothermal annealing temperatures (samples D and E). From examination of these data, it appears that, after a period of change, both of these samples are equilibrating, with this process occurring faster at the higher annealing temperature, as expected. Similar behaviour occurs for sample A (initially having a 300k PS top layer), and the layer SLDs of samples A, D and E at the end of the period of isothermal annealing are not markedly different to the layer SLDs of all five 300k PS samples measured at 139 or 148 °C after equilibration at higher temperature (samples A–E, shown in the right-hand side of Fig. 3a, which includes two samples, B and C, that underwent thermal cycling without an initial isothermal annealing stage). Similar apparent equilibration of the layer SLDs is seen for the 5k PS sample (sample G) in Fig. 3b. This time the SLD of the bottom layer changes significantly, as the fullerene-rich co-existing phase at equilibrium is not pure Bis-PCBM for low enough PS MW (the binodal branches are closer together for 5k PS/Bis-PCBM than 300k PS/Bis-PCBM, representing greater miscibility in the lower MW PS system30). There are, however, indications that samples D, E and G may not be properly equilibrated, if one looks at the layer thickness behaviour and the subtle details of the top layer SLD, versus time, for each individual sample (see Fig. S5_1 for sample D data, ESI†). This will be discussed in more detail in the section below, in relation to non-equilibrium behaviour in layer SLD and thickness, when we present the results of constrained fits on these samples.
First, we discuss clear non-equilibration and hysteresis in relation to the interfacial roughness. This occurs in samples that contain both 300k and 5k PS, and in samples where the top layer was initially either pure PS or a PS/Bis-PCBM blend. Using a similar format to Fig. 3, Fig. 4a and b plot the buried interface roughness, σI, as a function of time and then temperature. Fig. 4b plots σI for a sample with a top layer that was initially a 5k PS/Bis-PCBM blend (close to the boundary between the one-phase and two-phase regions of the phase diagram27,30 – sample G), and a sample with an initially pure 5k PS top layer (sample F). This shows that the interfacial roughness after extensive isothermal annealing of sample G (left-hand side of panel, with a light-yellow background) is significantly larger than that found in this sample after equilibration (right-hand side of panel, with a light-green background). Fig. 4d plots the interfacial roughness of sample G for the full set of measurements (isothermal annealing at 148 °C and temperature cycling after equilibration), as a function of temperature. What is significant about this plot is that the interfacial roughness values after isothermal annealing at 148 °C are separated from the values at this same temperature measured after equilibration. Strikingly, the interfacial roughness values following isothermal annealing are not intermediate between the starting point and the equilibrium values at 148 °C, meaning that this behaviour is not as a result of slow kinetics retarding the evolution of the system towards equilibrium.
Similar hysteresis behaviour is found in sample A, as shown in Fig. 4a and 4c. This is a sample that initially had a top layer that was pure 300k PS. This sample was annealed using the protocol shown in Fig. 1e; after the initial measurement at 80 °C, this consisted of annealing at four different temperatures (in chronological order – 139 °C, 156 °C, 173 °C and 139 °C again), with four consecutive NR measurements made at each temperature. The interfacial roughness at 139 °C on first heating is significantly higher than at 139 °C after equilibration. It is likely that this interfacial roughness consists of broadening of the interface due to molecular intermixing,39,40,42 rather than due to larger scale lateral roughness, such as occurs for capillary waves at a liquid–liquid interface.39,40 This is evidenced by the lack of any significant off-specular scattering43–45 from this sample (and the other 300k PS samples; see Fig. S4_3–S4_5 and accompanying text in the ESI† for further details). This behaviour is further corroborated by measurements on a second batch of samples (batch B – samples α–γ), fabricated on a different batch of silicon wafers and measured during a different NR experiment (see Fig. 4e and Fig. S4_2e, ESI†). We do not understand why these systems are displaying such hysteresis in the interfacial roughness, but the potential significance is clear, given the influence of molecular conformation,46 relative-positioning/orientation of molecules47,48 and roughness49–51 on the optoelectronic properties of interfaces, including those within BHJs.52 Before discussing interfacial roughness behaviour further, in the next section we present more detailed analysis of non-equilibrium behaviour involving the layer compositions and thicknesses. This involves performing fits with a single constraint on the top and bottom layer SLDs and thicknesses (details are given in the next section), enabling more careful examination of the temporal and thermal behaviour of individual samples.
Layer composition and thickness behaviour for 300k PS/Bis-PCBM blend top layers (constrained fits)
As briefly referred to in the previous section, in addition to the interfacial roughness hysteresis, the behaviour of the layer thicknesses and SLDs in samples D and E (both initially with 300k PS/Bis-PCBM blend top layers) indicate that these systems may also become stuck in non-equilibrium states after isothermal annealing. This is evidenced by plots of the layer thicknesses versus annealing temperature (Fig. S5_1a, ESI†) that show that thickness parameter values after isothermal annealing are well separated from the values obtained (reversibly) during subsequent temperature cycling. There is also an indication that there may be some hysteresis in the values of the top layer SLD (Fig. S5_1b, ESI†), although the variability in the SLD parameter values make it difficult to reach firm conclusions on this point from these unconstrained fits. However, for samples on a silicon substrate, where the thermal expansivity of the substrate is orders of magnitude lower than that of either layer above,53,54 the bilayer system would be expected to expand in the direction normal to the substrate only55 and therefore conserve mass per unit area of sample, and the total scattering length per unit area of sample (ρtopdtop + ρbottomdbottom), during heating. This is indeed close to the situation, even for the unconstrained fits for samples D and E (see Fig. S5_1d for sample D data, ESI†). Nonetheless, an improvement in the quality of the analysis regarding the layer SLDs, can be found by constraining the fits to conserve the total scattering length per unit area for an individual sample, across all measurements. In most cases this increases the value of the goodness-of-fit, χ2, parameter,56 but the increases are small (of order 10% typically), meaning that we still obtain very good fits to the data using bilayer models. The advantage of this procedure is that in disallowing small deviations from conservation of the sample constituents, we reduce the variability in the behaviour of the layer SLDs and preserve the layer thickness behaviour (which is rather strongly constrained anyway, even in the unconstrained fits, by the fringe spacing in the NR curves). Fig. 5 shows the results of the constrained fits for samples D and E (in which the total scattering length per unit area was fixed at the mean value obtained from the unconstrained fits for each sample). Fig. 5a and b show the layer thicknesses and layer SLDs respectively for sample E, which was annealed isothermally at 148 °C, before temperature cycling. In Fig. 5b there is a rapid and significant initial reduction in the SLD of the top layer on heating to 148 °C, which then remains relatively unchanged for over three hours during isothermal heating. A smaller initial reduction in the bottom layer SLD occurs (commensurate with the expected changes in a pure Bis-PCBM layer due to thermal expansion30), which is also followed by little change over the course of three hours isothermal heating. This is very similar to the plots of the layer SLDs for the unconstrained fits for this sample in Fig. 3a. The constrained fits come into their own when examining thermal cycling, which begins at just after 200 minutes for sample E. The symbols with filled black centres in Fig. 5b pick out the SLD measurements during temperature cycling that were performed at the isothermal annealing temperature of 148 °C. The bottom (close to pure Bis-PCBM) layer SLD, ρbottom, behaves in a way that is commensurate with reversible thermal expansion/contraction, as the temperature of this sample is cycled from 173 °C to 114 °C and then back to 181 °C, before final cooling to 80 °C (NB: this correspondence to thermal expansion of the bottom layer can only be understood in relation to ρbottom. As discussed in Higgins et al.,30dbottom actually reduces with temperature, due to changes in the equilibrium phases that result in mass-transfer of fullerene molecules into the top layer). It can be seen in Fig. 5b that ρbottom at 148 °C during thermal cycling is completely in-line with the measurements taken during isothermal annealing. The situation is, however, completely different regarding the top layer SLD, ρtop, in Fig. 5b, which changes significantly on heating to 173 °C at the start of thermal cycling, but then remains fairly constant (in comparison to ρbottom) as the temperature is cycled between 173 °C, 114 °C and 181 °C. Here, the (equilibrated) top layer SLDs at 148 °C during temperature cycling show a clearly increased value in comparison to the values at 148 °C during isothermal annealing. This plot is therefore indicative of a second type of hysteresis in which the system has evolved to a location in phase-space following isothermal annealing, that is not at equilibrium, and is also not intermediate (in terms of the top layer SLD parameter) between the starting point and equilibrium. Fig. 5a shows that the layer thickness behaviour is entirely consistent with this. In Fig. 5a the data are plotted as a function of temperature, rather than time, but it can be clearly seen that the layer thicknesses on isothermal annealing at 148 °C rapidly change to values (for both layers) that are not intermediate between the starting thicknesses and the thicknesses at equilibrium (the top and bottom thicknesses on isothermal annealing at 148 °C are completely separated from the reversible equilibrated layer thicknesses curves shown in Fig. 5a). Fig. 5c and d show similar plots to 5a and 5b, for a nominally identical sample (sample D) annealed at the lower temperature of 139 °C. This shows very similar behaviour to that at 148 °C, but with a longer timescale for the SLDs and thicknesses to reach steady values during isothermal annealing. In contrast to samples D and E, parameters for samples that were heated straight to 173 °C and then temperature cycled did not show such hysteresis (see Higgins et al.30 and Fig. S5_2, ESI†). The behaviour exhibited in Fig. 5a–d is depicted schematically in Fig. 6. Fig. 6b shows a liquid–liquid system, in which the top layer is initially within the two-phase part of the phase diagram, moving (on isothermal annealing) to a top layer composition that is within the single-phase region of the equilibrium phase diagram. Subsequent annealing at higher temperature allows the system to move out of this local free-energy minimum and equilibrate, with two phases (layers) at the binodal compositions. The key question is why does the system appear to undertake a trajectory that takes the top layer into the single phase region of phase space, through the binodal curve. For bulk systems with uniform phases, this would violate the second law of thermodynamics, and therefore we are left to conclude that our findings must be down to the system following a trajectory through phase-space that leads to a local minimum due to either (i) non-uniformity in the layer compositions that we are not sensitive to in our measurements or (ii) interfacial/thin-film effects (such as preferential segregation of some constituents to interfaces57,58). We anticipate that significant further work will be required to uncover the pathway that is actually taken. Given that hysteresis is also clearly observed (with-respect-to the interfacial width) in the (simpler) bilayers that start with a pure PS top layer, we propose that it would likely be most productive to perform further investigations starting with top layers within the single-phase part of the phase diagram). The data that we have on this so far (SLD data from sample A at 139 °C, during isothermal annealing and after equilibration – see Fig. S4_1 (ESI†), and represented schematically in Fig. 6a), does tentatively suggest that these kinds of samples may be trapped in a similar local minimum (in terms of the top layer compositions - see Fig. S4_1e, ESI†) to the bilayer samples that initially had blend top layers (samples D and E).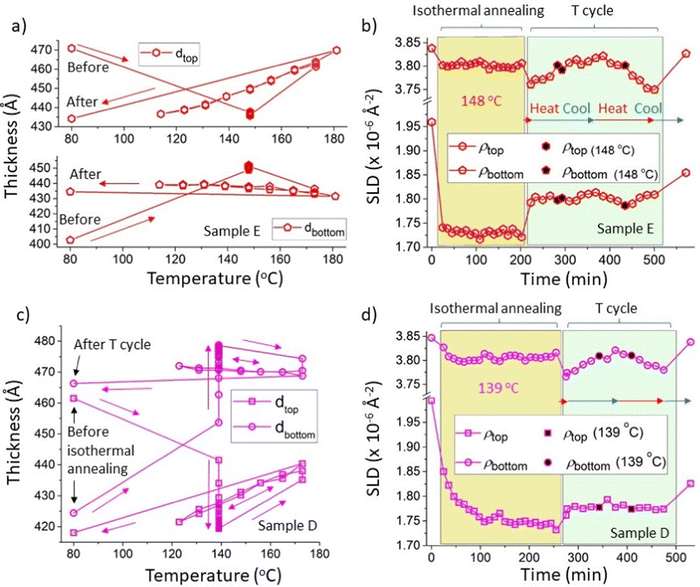 | ||
| Fig. 5 Constrained fits showing hysteresis in layer thickness and SLD (for initially 300k PS/Bis-PCBM blend top layer samples annealed at 139 and 148 °C). This shows constrained fits in which the scattering length density integrated across the depth of the sample (the total scattering length per unit area of sample) was held fixed (at the mean value obtained from the unconstrained fits) for all measurements on that particular sample. (a) and (b) Layer thicknesses versus temperature and layer SLDs versus time respectively, during isothermal annealing at 148 °C and temperature cycling of sample E (thermal cycling of sample E consisted firstly of heating to 173 °C, then cooling to 114 °C, then reheating to 181 °C and final cooling to 80 °C; see Table S1 in the ESI† for further details). (c) and (d) Layer thicknesses versus temperature and layer SLDs versus time respectively, during isothermal annealing at 139 °C and temperature cycling of sample D (thermal cycling of sample D consisted firstly of heating to 173 °C, then cooling to 123 °C, then reheating to 173 °C and final cooling to 80 °C; see Table S1 for further details, ESI†). The total scattering length per unit area of sample was fixed at 2468 Å−1 for sample E and 2553 Å−1 for sample D; very similar behaviour was found with the total scattering length per unit area of sample set to the minimum and maximum values obtained for the unconstrained fits (2439 Å−1 and 2492 Å −1 for sample E, and 2526 Å−1 and 2589 Å −1 for sample D). For both samples the symbols with filled black centres represent measurements taken during thermal cycling that are at the temperatures used for isothermal annealing for that particular sample. The horizontal red and blue arrows in (b) and (d) indicate times during which the samples were being heated and cooled respectively. | ||
One final point with regard to the two samples that initially had 300k PS/Bis-PCBM blend top layers (samples D and E), is that there is no evidence of any significant hysteresis in interfacial roughness (Fig. S5_3a and c, ESI†). This is in contrast to the samples with pure 300k PS top layers (A, β and γ) shown in Fig. 4, in which there are significantly broader interfaces on heating straight to temperatures in the range 140 to 150 °C than for equilibrated samples at these temperatures. This seems counterintuitive, as a pure PS top layer would appear to have a simpler path to equilibrium than the samples with top layers that were initially blends. In the former, both the starting point and equilibrium states consist of two uniform layers, whereas the latter begins with a composition in the two-phase part of the phase diagram (vitrified as a result of solvent evaporation during spin-coating). At present, we do not understand the origin of this difference, but emphasise its potential importance in relation to OPV devices during operation.
Kinetics and polymer MW (constrained fits)
In this section we further examine and compare the approach to equilibrium in 5k and 300k PS samples. The motivation is provided by the observation that Fig. 5b shows an approach to steady composition profiles during isothermal annealing at 148 °C for a 300k PS blend top layer sample (Sample E) that occurs relatively quickly (in significantly less than 50 min), whereas careful observation of the bottom layer SLD of a 5k PS blend (sample G) in Fig. 3b, shows a slight downwards drift occurring over a longer timescale, during isothermal annealing at the same temperature. In fact, even the SLDs of the 300k PS blend sample annealed at the lower temperature of 139 °C (sample D) shown in Fig. 5d reach steady values within a timescale over which the 5k PS blend sample (sample G) may still be slowly changing at 148 °C.To investigate these subtle changes further we therefore also analysed the 5k PS data from sample G using constrained fitting. The results of these fits are shown in Fig. 7. Fig. 7a–c confirm the observation of slow changes to the layer compositions and phase-volumes during isothermal annealing. Fig. 7c shows that the gradual reduction in the SLD of the bottom layer is confirmed, while the top layer SLD, after an initial reduction on heating to 148 °C, now also shows a gradual change (increase) over the same timeframe, that is not apparent in the unconstrained fits in Fig. 3b (for comparison, Fig. S7_1 (ESI†) overlays the layer SLDs for the constrained and unconstrained fits). These gradual SLD changes during isothermal annealing are accompanied by a gradual increase (Fig. 7b) in the bottom layer thickness, and a corresponding decrease (Fig. 7a) in the top layer thickness with time (the total thickness remaining approximately constant – see Fig. S7_2c, ESI†). The relatively slow speed at which these changes occur is likely due to the fact that neither co-existing phases is pure at equilibrium,30 meaning that for 5k PS both the fullerene and the polymer molecules now diffuse.
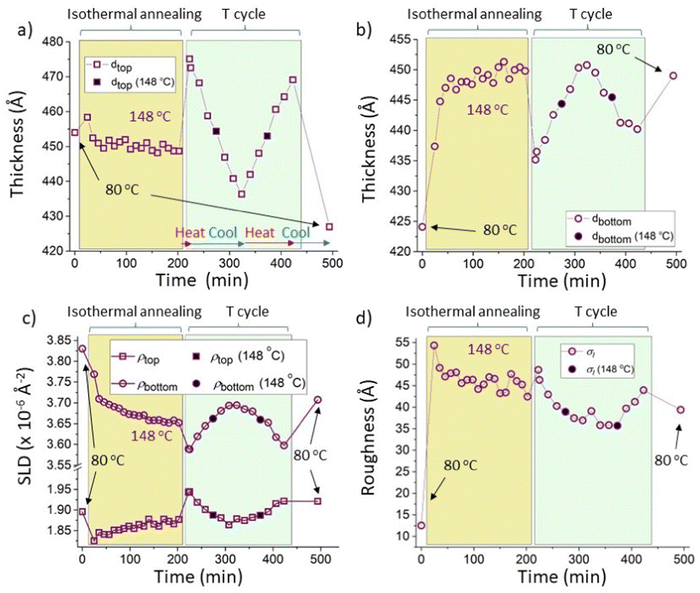 | ||
| Fig. 7 Constrained fits for a sample that initially had a 5k PS/Bis-PCBM blend top layer (sample G; isothermal annealing at 148 °C followed by thermal cycling). Thermal cycling of sample G consisted firstly of heating to 173 °C, then cooling to 123 °C, then reheating to 173 °C and final cooling to 80 °C; see Table S2 in the ESI† for further details (the temperatures used during the thermal cycling of this sample can also be seen in Fig. 4d). The fits had the scattering length density integrated across the depth of the sample (the total scattering length per unit area of sample) held fixed at the mean value obtained from the unconstrained fits (2485 Å−1), for all measurements; very similar behaviour was found with this set to the minimum and maximum values obtained for the unconstrained fits (2450 Å−1 and 2519 Å−1 respectively). (a) Top layer thickness. (b) Bottom layer thickness. (c) Top and bottom layer scattering length densities (SLDs). (d) Interfacial roughness, σI (σS data are shown, as a function of temperature, in Fig. S7_2d, ESI†). The symbols with filled black centres represent measurements taken during thermal cycling that are at the temperature used for isothermal annealing (148 °C). The horizontal red and blue arrows in (a) indicate times during which the samples were being heated and cooled respectively. | ||
Fig. 7a–d and Fig. S7_2 (ESI†) show that, following equilibration, the constrained fits preserve the reversible nature of the fit parameters as the temperature is cycled from 173 to 123 to 173 °C. Because of the slow kinetics, the differences between the layer SLDs in Fig. 7c during isothermal annealing at 148 °C and the equilibrated sample at 148 °C are not so easy to establish as for the 300k PS samples shown in Fig. 5. However, examination of Fig. 7a and b shows that the layer thicknesses are displaying similar behaviour to that shown for 300k PS in Fig. 5, in that the layer thicknesses during isothermal annealing are clearly not the same as those at equilibrium at the same temperature, and are also not intermediate between the starting thicknesses and the equilibrium values (Fig. S7_2a and 2b show the data from Fig. 7a and b, but plotted versus temperature, rather than time, ESI†).
In terms of the interfacial roughness, Fig. 7d shows (as for the unconstrained fits in Fig. 4b) that the equilibrated values at 148 °C (right-hand side of panel, during thermal cycling) are below those found during isothermal annealing. Fig. 7d does, however, show that there is slightly more of a drift downwards in the interfacial roughness during isothermal annealing at 148 °C, than shown in the unconstrained fits in Fig. 4b. It is therefore possible that over a longer time the interfacial roughness under annealing at 148 °C may continue to reduce and approach that at equilibrium at this temperature. What remains unclear however is why the interfacial roughness is higher during isothermal annealing than at equilibrium in the first place.
Annealed 5k PS samples exhibit lateral morphology on a length scale of a few tens of micrometres (see Fig. S9_1d and e, ESI†) which likely accounts for some off-specular scattering observed at low angles (see Fig. S4_5b, ESI†). By contrast, 300k PS samples show little evidence of off-specular scattering (ESI,† Fig. S4_3 and S4_5a) and real-space measurements do not reveal lateral inhomogeneities, except for occasional defects (which have no significant impact on the NR – see Fig. S9_1a–c, ESI†). We do not know the origin of this morphology. It could, perhaps, be dewetting of one of the layers following prolonged annealing, although this could only have begun in the latter stages of thermal cycling, as the degree of fit parameter reversibility during the main cooling/heating cycles in Fig. 7 is good. In principle, depending on the lengthscale and amplitude of the morphology, in comparison to the in-plane coherence length of the neutrons (of order tens of micrometres40,59,60) this could alter the fit parameters extracted for the 5k PS bilayers slightly. It is, however, unlikely that this would alter the overall findings (of significant hysteresis in layer thickness, SLD and interfacial roughness) from Fig. 7.
Although not central to our investigation, we briefly comment on the kinetics of the observed changes in Fig. 7 for 5k PS samples, in comparison to the 300k PS samples shown in Fig. 5. This comparison is complex due to the combination of two factors; firstly, the co-existing phases are of qualitatively different form for the two MWs; for 300k PS a mixed phase and an essentially pure fullerene phase co-exist,30 so only the fullerene diffuses between the layers, while the 5k PS/Bis-PCBM phase coexistence consists of two mixed layers, requiring the polymer to diffuse into the initially pure Bis-PCBM bottom layer; secondly, the polymer dynamics in these cases is different, with (MW-dependent) centre-of-mass diffusion and Rouse dynamics in the lower MW (unentangled) case, but additionally reptation at the higher MW (above the entanglement MW).61Fig. 7c shows that within around 30 minutes from the start of isothermal annealing of sample G at 148 °C, the SLDs of both layers has changed significantly (in comparison to the slower changes that occur over the next ∼170 minutes), but to (average) compositions that are within the single phase regions of the phase diagram (after 30 minutes the bottom layer SLD is higher than the circle symbols with filled black centres and the top layer SLD is lower than the square symbols with filled black centres in Fig. 7c). The reduction in the top layer SLD is commensurate with the thermal expansivity of PS between 80 and 148 °C,28,53 while the bottom layer SLD reduction by 30 minutes is significantly larger (by around a factor of two) than the level expected for pure Bis-PCBM thermal expansion30 (compare with the start of isothermal annealing in Fig. 5b and d). Therefore the changes in SLD within around 30 minutes are likely a combination of thermal expansion and PS diffusion into the bottom layer. Self-diffusion of 5k PS would occur across a distance of order 100 nm within a few minutes at 148 °C,62 but we do not have data on how this would change in an environment of Bis-PCBM; given the non-equilibrium mixing behaviour reported herein, this would require careful experiments to ascertain. The subsequent slower changes in the SLDs that occur during isothermal annealing from around 30 minutes onwards in Fig. 7c (at constant sample volume; see Fig. S7_2c, ESI†) are clearly due to the mutual diffusion of PS and fullerene.
We finally note that the phenomenon of interfacial roughness hysteresis (Fig. 7d), occurs in addition to compositional/phase volume hysteresis in sample G. In contrast the 300k PS samples only display interfacial roughness hysteresis in samples that initially had a pure PS top layer (Fig. 4c and e), but not in samples with PS/Bis-PCBM blend top layers initially.
Given that both the kinetics and the thermodynamics are different in the 5k and 300k PS systems, it is difficult to ascertain whether the 5k system is merely escaping from an intermediate state towards equilibrium faster than occurs for 300k PS (i.e. maybe the 300k PS could escape too, given time), or whether the different nature of the free-energy landscape for 5k PS means that there is a more easily escapable local minimum (or perhaps a valley) for 5k PS systems in comparison to 300k PS. It seems likely to us that to answer such questions first requires a fuller understanding of the nature of the equilibrium states themselves, including the incorporation of volume changes in the system. As discussed previously,30 this requires an approach beyond Flory–Huggins (such as an in-depth analysis within the framework of the locally-correlated-lattice theory developed and implemented by Lipson and co-workers55,63), and is beyond the scope of the current paper.
Conclusion
The key finding from our investigation is that thin-film polymer/fullerene systems can appear, by some measures, to equilibrate, but in fact reach non-equilibrium states that trap (or retard the structural evolution of) domain compositions, phase volumes and/or interfacial width. Given the importance of morphology, domain composition and interfacial structure in polymer/small-molecule OPVs,17,52,64 these findings are likely to be significant in terms of (i) fundamental understanding of mixing in OPVs, and (ii) understanding composition and morphology evolution during thermal cycling of devices (in operation). This includes the issue of carefully ascertaining that systems don’t end up in non-equilibrium states, by (if possible) examining thermal reversibility, before using mixing measurements to extract equilibrium properties. Morphological stability is recognised as a key consideration in OPV design,11 with recent studies by Ade and co-workers proposing that a crucial factor is the stabilisation of mixed polymer/small-molecule domains with compositions close to the percolation threshold of the small-molecules.15 While trapping in a local minimum would not necessarily give rise to additional issues during operation for ‘kinetically stabilised’ systems,13 which contain phases that are well away from equilibrium compositions anyway (requiring sufficient vitrification at operating temperatures within mixed, amorphous phases, to maintain optimised domain compositions), the situation is very different for ‘thermodynamically stabilised’ domains. Here, domain compositions are required to be at or close-to those of the co-existing equilibrium (binodal) compositions, and slow coarsening kinetics prevents significant morphological degradation (in terms of domain-size growth) within BHJs.13 Trapping within a local minimum during device fabrication in such cases would potentially undermine this stabilisation strategy, as, given sufficient molecular mobility (recently reported as being more likely in thermodynamically stabilised systems26), the system would be able to evolve in terms of both phase compositions and phase volumes, in addition to the (slow) coarsening of BHJ sizescale and connectivity.Data availability
Data can be downloaded using the DOIs for the two experiments: http://doi.ill.fr/10.5291/ILL-DATA.9-11-1903 and http://doi.ill.fr/10.5291/ILL-DATA.9-11-1983 after an embargo period of three years. Requests for data earlier than this should be emailed to the corresponding author.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank the ILL for the award of beam time (experiment numbers 9-11-1903 in 2019 and 9-11-1983 in 2021), and the staff of D17 for help during the experiments. We thank the IT group at ILL for establishing remote access to D17, which was used during experiment 9-11-1983. AH thanks Josh Barlow and Ben Harrison at Swansea University for use of their chemistry facilities to host the sample preparation activity, which was necessitated following a fire in Swansea which closed the usual chemistry laboratory for more than a year. EH acknowledges Swansea University for funding her studentship.References
- T. J. Wood, L. J. Ward and J. P. Badyal, Super-adhesive polymer-silica nanocomposite layers, ACS Appl. Mater. Interfaces, 2013, 5, 9678–9683, DOI:10.1021/am402731x.
- Z. Wang, M. R. Bockstaller and K. Matyjaszewski, Synthesis and Applications of ZnO/Polymer Nanohybrids, ACS Mater. Lett., 2021, 3, 599–621, DOI:10.1021/acsmaterialslett.1c00145.
- A. Das, A. B. Dey, G. Manna, M. K. Sanyal and R. Mukherjee, Nanoparticle-Mediated Stabilization of a Thin Polymer Bilayer, Macromolecules, 2022, 55, 1657–1668, DOI:10.1021/acs.macromol.2c00089.
- R. Mukherjee, et al., Stability and Dewetting of Metal Nanoparticle Filled Thin Polymer Films: Control of Instability Length Scale and Dynamics, ACS Nano, 2010, 7, 3709–3724 CrossRef PubMed.
- K. A. Barnes, et al., Suppression of Dewetting in Nanoparticle-Filled Polymer Films, Macromolecules, 2000, 33, 4177–4185 CrossRef CAS.
- H. C. Wong and J. T. Cabral, Spinodal clustering in thin films of nanoparticle-polymer mixtures, Phys. Rev. Lett., 2010, 105, 038301, DOI:10.1103/PhysRevLett.105.038301.
- H. C. Wong, A. M. Higgins, A. R. Wildes, J. F. Douglas and J. T. Cabral, Patterning polymer-fullerene nanocomposite thin films with light, Adv. Mater., 2013, 25, 985–991, DOI:10.1002/adma.201203541.
- A. Wadsworth, Z. Hamid, J. Kosco, N. Gasparini and I. McCulloch, The Bulk Heterojunction in Organic Photovoltaic, Photodetector, and Photocatalytic Applications, Adv. Mater., 2020, 32, e2001763, DOI:10.1002/adma.202001763.
- F. W. Zhao, et al., Emerging Approaches in Enhancing the Efficiency and Stability in Non-Fullerene Organic Solar Cells, Adv. Energy Mater., 2020, 10, 2002746, DOI:10.1002/aenm.202002746.
- A. Armin, et al., A History and Perspective of Non-Fullerene Electron Acceptors for Organic Solar Cells, Adv. Energy Mater., 2021, 11, 20003570, DOI:10.1002/aenm.202003570.
- W. Li, D. Liu and T. Wang, Stability Of Non-Fullerene Electron Acceptors and Their Photovoltaic Devices, Adv. Funct. Mater., 2021, 31, 2104552, DOI:10.1002/adfm.202104552.
- J. Luke, E. J. Yang, C. Labanti, S. Y. Park and J.-S. Kim, Key molecular perspectives for high stability in organic photovoltaics, Nat. Rev. Mater., 2023, 8, 839–852, DOI:10.1038/s41578-023-00606-5.
- Y. Qin, et al., The performance-stability conundrum of BTP-based organic solar cells, Joule, 2021, 5, 2129–2147, DOI:10.1016/j.joule.2021.06.006.
- Y. Liu, et al., Aggregation and morphology control enables multiple cases of high-efficiency polymer solar cells, Nat. Commun., 2014, 5, 5293, DOI:10.1038/ncomms6293.
- L. Ye, et al., Quenching to the Percolation Threshold in Organic Solar Cells, Joule, 2019, 3, 443–458, DOI:10.1016/j.joule.2018.11.006.
- N. Li, et al., Abnormal strong burn-in degradation of highly efficient polymer solar cells caused by spinodal donor-acceptor demixing, Nat. Commun., 2017, 8, 14541, DOI:10.1038/ncomms14541.
- M. Gao, Z. Liang, Y. Geng and L. Ye, Significance of thermodynamic interaction parameters in guiding the optimization of polymer:nonfullerene solar cells, Chem. Commun., 2020, 56, 12463–12478, 10.1039/d0cc04869k.
- L. Ye, et al., Quantitative relations between interaction parameter, miscibility and function in organic solar cells, Nat. Mater., 2018, 17, 253–260, DOI:10.1038/s41563-017-0005-1.
- D. Chen, A. Nakahara, D. Wei, D. Nordlund and T. P. Russell, P3HT/PCBM Bulk Heterojunction Organic Photovoltaics: Correlating Efficiency and Morphology, Nano Lett., 2011, 11, 561–567, DOI:10.1021/nl103482n.
- H. Chen, R. Hegde, J. Browning and M. D. Dadmun, The miscibility and depth profile of PCBM in P3HT: thermodynamic information to improve organic photovoltaics, Phys. Chem. Chem. Phys., 2012, 14, 5635–5641, 10.1039/c2cp40466d.
- B. A. Collins, et al., Molecular Miscibility of Polymer-Fullerene Blends, J. Phys. Chem. Lett., 2010, 1, 3160–3166, DOI:10.1021/jz101276h.
- D. Leman, et al., In Situ Characterization of Polymer–Fullerene Bilayer Stability, Macromolecules, 2015, 48, 383–392, DOI:10.1021/ma5021227.
- H. W. Ro, et al., Poly(3-hexylthiophene) and [6,6]-Phenyl-C61-butyric Acid Methyl Ester Mixing in Organic Solar Cells, Macromolecules, 2012, 45, 6587–6599, DOI:10.1021/ma3008527.
- N. D. Treat, et al., Interdiffusion of PCBM and P3HT Reveals Miscibility in a Photovoltaically Active Blend, Adv. Energy Mater., 2011, 1, 82–89, DOI:10.1002/aenm.201000023.
- Z. Peng, N. Balar, M. Ghasemi and H. Ade, Upper and Apparent Lower Critical Solution Temperature Branches in the Phase Diagram of Polymer:Small Molecule Semiconducting Systems, J. Phys. Chem. Lett., 2021, 12, 10845–10853, DOI:10.1021/acs.jpclett.1c02848.
- M. Ghasemi, et al., A molecular interaction-diffusion framework for predicting organic solar cell stability, Nat. Mater., 2021, 20, 525–532, DOI:10.1038/s41563-020-00872-6.
- E. L. Hynes, et al., Interfacial width and phase equilibrium in polymer-fullerene thin-films, Commun. Phys., 2019, 2, 112, DOI:10.1038/s42005-019-0211-z.
- E. L. Hynes, P. Gutfreund, A. J. Parnell and A. M. Higgins, Liquid-liquid equilibrium in polymer-fullerene mixtures; an in situ neutron reflectivity study, Soft Matter, 2020, 16, 3727–3739, 10.1039/c9sm02337b.
- D. Môn, et al., Bimodal crystallization at polymer-fullerene interfaces, Phys. Chem. Chem. Phys., 2015, 17, 2216–2227, 10.1039/c4cp04253k.
- A. M. Higgins, P. Gutfreund, V. Italia and E. L. Hynes, Equilibration and thermal reversibility in mixtures of model OPV small-molecules and polymers, J. Mater. Chem. C, 2023, 11, 2107–2119, 10.1039/d2tc04916c.
- T. Saerbeck, et al., Recent upgrades of the neutron reflectometer D17 at ILL, J. Appl. Cryst., 2018, 51, 249–256 CrossRef CAS.
- P. Gutfreund, et al., Towards generalized data reduction on a chopper-based time-of-flight neutron reflectometer, J. Appl. Cryst., 2018, 51, 606–615 CrossRef CAS.
- A. R. J. Nelson and S. W. Prescott, refnx: neutron and X-ray reflectometry analysis in Python, J. Appl. Crystallogr., 2019, 52, 193–200, DOI:10.1107/S1600576718017296.
- E. Helfand and A. M. Sapse, Theory of Unsymmetric Polymer-Polymer Interfaces, J. Chem. Phys., 1975, 62, 1327–1331, DOI:10.1063/1.430632.
- D. Kawaguchi, et al., Precise Analyses of Short-Time Relaxation at Asymmetric Polystyrene Interface in Terms of Molecular Weight by Time-Resolved Neutron Reflectivity Measurements, Macromolecules, 2011, 44, 9424–9433, DOI:10.1021/ma201717e.
- H. Zhang, K. Lamnawar and A. Maazouz, Rheological Modeling of the Mutual Diffusion and the Interphase Development for an Asymmetrical Bilayer Based on PMMA and PVDF Model Compatible Polymers, Macromolecules, 2012, 46, 276–299, DOI:10.1021/ma301620a.
- F. Brochard, J. Jouffroy and P. Levinson, Polymer-Polymer Diffusion in Melts, Macromolecules, 1983, 16, 1638–1641 CrossRef CAS.
- E. J. Kramer, P. Green and C. J. Palmstrom, Interdiffusion and marker movements in concentrated polymer-polymer diffusion couples, Polymer, 1984, 25, 473–480 CrossRef CAS.
- R. A. L. Jones and R. W. Richards, Polymers at Surfaces and Interfaces, Cambridge University Press, 1999 Search PubMed.
- M. Sferrazza, et al., Evidence for capillary waves at immiscible polymer/polymer interfaces, Phys. Rev. Lett., 1997, 78, 3693–3696, DOI:10.1103/PhysRevLett.78.3693.
- E. M. Speller, et al., Impact of Aggregation on the Photochemistry of Fullerene Films: Correlating Stability to Triplet Exciton Kinetics, ACS Appl. Mater. Interfaces, 2017, 9, 22739–22747, DOI:10.1021/acsami.7b03298.
- E. Helfand and Y. Tagami, Theory of Interface Between Immiscible Polymers, J. Chem. Phys., 1972, 56, 3592–3601, DOI:10.1063/1.1677735.
- D. James, et al., Measurement of molecular mixing at a conjugated polymer interface by specular and off-specular neutron scattering, Soft Matter, 2015, 11, 9393–9403, 10.1039/c5sm02008e.
- S. K. Sinha, E. B. Sirota, S. Garoff and H. B. Stanley, X-ray and Neutron-Scattering from Rough Surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 2297–2311, DOI:10.1103/PhysRevB.38.2297.
- A. Hafner, P. Gutfreund, B. P. Toperverg, M. Geoghegan and M. Sferrazza, 2D reflectometry for the investigation of polymer interfaces: off-specular neutron scattering, J. Phys. Condens. Matter., 2021, 33, 364002, DOI:10.1088/1361-648X/ac0282.
- D. P. McMahon, D. L. Cheung and A. Troisi, Why Holes and Electrons Separate So Well in Polymer/Fullerene Photovoltaic Cells, J. Phys. Chem. Lett., 2011, 2, 2737–2741, DOI:10.1021/jz201325g.
- Y. S. Huang, et al., Electronic structures of interfacial states formed at polymeric semiconductor heterojunctions, Nat. Mater., 2008, 7, 483–489, DOI:10.1038/nmat2182.
- P. Sreearunothai, et al., Influence of copolymer interface orientation on the optical emission of polymeric semiconductor heterojunctions, Phys. Rev. Lett., 2006, 96, 117403, DOI:10.1103/PhysRevLett.96.117403.
- A. M. Higgins, et al., The Impact of Interfacial Mixing on Förster Transfer at Conjugated Polymer Heterojunctions, Adv. Funct. Mater., 2009, 19, 157–163, DOI:10.1002/adfm.200800887.
- H. Yan, et al., Influence of Annealing and Interfacial Roughness on the Performance of Bilayer Donor/Acceptor Polymer Photovoltaic Devices, Adv. Funct. Mater., 2010, 20, 4329–4337, DOI:10.1002/adfm.201001292.
- B. P. Lyons, N. Clarke and C. Groves, The relative importance of domain size, domain purity and domain interfaces to the performance of bulk-heterojunction organic photovoltaics, Energy Environ. Sci., 2012, 5, 7657–7663, 10.1039/c2ee21327c.
- O. Alqahtani, et al., Evidence That Sharp Interfaces Suppress Recombination in Thick Organic Solar Cells, ACS Appl. Mater. Interfaces, 2021, 13, 56394–56403, DOI:10.1021/acsami.1c15570.
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Size-Dependent Depression of the Glass-Transition Temperature in Polymer-Films, Europhys. Lett., 1994, 27, 59–64, DOI:10.1209/0295-5075/27/1/011.
- C. A. Swenson, Recommended Values for the Thermal Expansivity of Silicon from 0 to 1000 K, J. Phys. Chem., 1983, 12, 179–182, DOI:10.1063/1.555681.
- R. P. White, et al., Thermodynamics of Model P alpha MSAN/dPMMA Blend: A Combined Study by SANS, Ellipsometry, and Locally Correlated Lattice (LCL) Theory, Macromolecules, 2020, 53, 7084–7095, DOI:10.1021/acs.macromol.0c00706.
- I. G. Hughes and T. P. Hase, Measurements and their Uncertainties, Oxford University Press, 2010 Search PubMed.
- D. Broseta, G. H. Fredrickson, E. Helfand and L. Leibler, Molecular-Weight and Polydispersity Effects at Polymer Polymer Interfaces, Macromolecules, 1990, 23, 132–139, DOI:10.1021/ma00203a023.
- P. Mahmoudi, W. S. R. Forrest, T. M. Beardsley and M. W. Matsen, Testing the Universality of Entropic Segregation at Polymer Surfaces, Macromolecules, 2018, 51, 1242–1247, DOI:10.1021/acs.macromol.7b02474.
- C. F. Majkrzak, et al., Determination of the effective transverse coherence of the neutron wave packet as employed in reflectivity investigations of condensed-matter structures. I. Measurements, Phys. Rev. A, 2014, 89, 033851, DOI:10.1103/PhysRevA.89.033851.
- R. M. Richardson, J. R. P. Webster and A. Zarbakhsh, Study of off-specular neutron reflectivity using a model system, J. Appl. Crystallogr., 1997, 30, 943–947, DOI:10.1107/s0021889897003440.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- Y. Pu, et al., Mobility of polymer chains confined at a free surface, Phys. Rev. Lett., 2001, 87, 206101, DOI:10.1103/PhysRevLett.87.206101.
- R. P. White, J. E. G. Lipson and J. S. Higgins, New Correlations in Polymer Blend Miscibility, Macromolecules, 2012, 45, 1076–1084, DOI:10.1021/ma202393f.
- S. Yoon, et al., Progress in morphology control from fullerene to nonfullerene acceptors for scalable high-performance organic photovoltaics, J. Mater. Chem. A, 2021, 9, 24729–24758, 10.1039/d1ta06861j.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01066j |
| ‡ Except for sample β in batch B, which had a reduced sample area. For this sample the beam footprint on the sample was reduced by a factor of two, and the acquisition time was increased to 4 and 16 minutes for angles 1 and 2 respectively. |
| This journal is © The Royal Society of Chemistry 2024 |