Open Access Article
Open Access ArticleCompetition among physical, chemical, and hybrid gelation mechanisms in biopolymers†
Ricky F.
López-Santiago
 a,
Jorge
Delgado
b and
Rolando
Castillo
a,
Jorge
Delgado
b and
Rolando
Castillo
 *a
*a
aInstituto de Física, Universidad Nacional Autónoma de México, P.O. Box 20-364, 01000, Mexico City, Mexico. E-mail: rolandoc@fisica.unam.mx
bDivisión de Ciencias e Ingenierías, Universidad de Guanajuato, Campus León, León, Guanajuato, Mexico
First published on 14th February 2024
Abstract
Depending on how they form their linkages, biopolymer gelatin gels are commonly classified as physical, chemical, or hybrid; in gelatin hybrid gels, the physical and chemical crosslinking mechanisms occur simultaneously. The viscoelastic behavior of gels following different gelation processes was determined around the gel point. Their gel fractal dimensions were obtained using the BST-scaling model from large amplitude oscillatory shear results. The fractal dimension of hybrid gels is between 1.46 and 1.60, depending on the dominant crosslinking process. The main features of the Lissajous–Bowditch curves were determined for maturated gels that follow different gelation processes, and it is possible to observe the dominant gelation mechanism. The gelation kinetics process is followed by measuring the mean squared displacement (MSD) of microspheres embedded in gelatin solutions using diffusion wave spectroscopy, which in turn allows evaluating G′(ω) and G′′(ω), the persistence length, and the mesh size as a function of time throughout the gelation process. The MSD, as a function of elapsed time from the start of the gelation process, follows a behavior that depends on the gelation processes. As time elapses after gelation starts, the persistence length of the unstructured, non-bonded flexible polymer sections decreases due to the formation of bonds. In the hybrid case, it is not a mixture of both processes; they are not independent when occurring simultaneously. The time evolution of the gel network's mesh size roughly follows an exponential decay.
1. Introduction
Gelatin is a biopolymer obtained by breaking down the collagen's triple-helix structure into single-strand through thermal treatment, and it has been used as a gelling ingredient in food, cosmetics, and pharmaceutical products, as well as in tissue scaffolds, and encapsulation in biomedical applications.1,2 A gel is an infinite polymeric network formed by molecules linked together, creating tridimensional branched structures similar to disordered lattices. According to the nature of linking, gels are commonly classified as chemical or physical gels. In physical gels, bonds are reversible when thermodynamic parameters such as pH, ionic strength, or temperature are modified. Physical junctions are constantly created and destroyed at very low rates, and the network seems to be permanently connected if the observation time is shorter than the bond's lifetime.3 In some gels, lattice formation is achieved by a conformational transition from single-strands to triple-helices of gelatin chains, as in the case of physical gelatin gels, which are formed by physical crosslinking when temperature decreases, and the coils randomly transform into partially renatured intermingled ordered triple helices mainly held together by hydrogen-bond junctions. If the temperature increases again, the triple helix conformations return to the coiled state, and the gel reversibly melts into a solution.4,5 On the other hand, chemical reactions are the route to form chemical gels, where permanent covalent bonds are created, and as a consequence, gelation is irreversible; many possible crosslinkers can be employed for chemical gelatin crosslinking, such as glutaraldehyde or transglutaminase.2,6–8 Furthermore, it is feasible to form hybrid gelatin gels by combining crosslinking processes, i.e., physical and chemical, producing the so-called physicochemical gels, which present some partial reversibility; however, they are not entirely thermoreversible. Fig. SI1 (ESI†) shows a cartoon of these gels according to crosslinking processes.Biopolymer gelatin is an excellent system for studying the competition among physical and chemical mechanisms in forming hybrid gels. One advantage is the well-known detailed self-assembly transition from single-strand to triple-helix chains and chemical gelation crosslinking mechanisms with glutaraldehyde. Depending on the sample preparation, temperature lowering, adding glutaraldehyde, or performing both simultaneously, physical, chemical, or hybrid gels can be obtained. This flexibility to form different gels from a single molecule makes gelatin ideal for studying critical and post-gel states in flexible biopolymers with different crosslinking mechanisms. Notwithstanding, achieving hybrid gels with two crosslinking mechanisms simultaneously operating is still quite challenging. Comprehension of the competition between physical and chemical mechanisms could probably be exploited to understand the evolution of the mechanical properties and mesoscopic scales of chemical gelatins formed with different chemical crosslinkers,9–11 as well as those using an enzymatic route,2,6 or in biopolymers undergoing natural gelation processes, where secondary structures are formed from single polymer molecules in a sol state, such as polysaccharides: alginate, pectin, and carrageenans.12 A subjacent issue would be determining whether these results can be applied to synthetic polymers under the appropriate thermodynamic conditions for obtaining different gels.
Different models were proposed to explain the formation and properties of gels.13–15 The gel transition can be described using the percolation model. Bonds are formed randomly with a probability p. When p < pc, only small clusters are formed; in contrast, if p > pc, an infinite cluster appears. Numerical analysis shows that in the neighborhood of pc, the size and mass of clusters broadly differ.16,17 A polymer at its gel point is commonly called a critical gel to distinguish it from the various materials named gels.3 A critical gel is far from equilibrium due to the diverging internal length scales, which causes very slow structural rearrangements. A large number of rheological experimental studies for a large variety of physical or chemical gelling materials in the regime of small amplitude oscillation shear (SAOS) indicate that the complex shear modulus, G*(ω) = G′(ω) + iG′′(ω), follows a power law in the angular frequency, ω,18,19i.e., 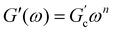 and
and 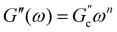 ; n is a critical exponent,
; n is a critical exponent, 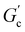 and
and 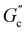 are constants, and the loss angle δ = arctan(G′′(ω)/G′(ω)) = nπ/2. These formulae are helpful for the gel point detection because G′(ω) and G′′(ω) must be parallel to each other, which causes tan
are constants, and the loss angle δ = arctan(G′′(ω)/G′(ω)) = nπ/2. These formulae are helpful for the gel point detection because G′(ω) and G′′(ω) must be parallel to each other, which causes tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ to be frequency independent. At the critical gel, the rich rheological diversity of a material converges to a universal dynamical state of less rheological complexity, exhibiting a simple self-similar relaxation behavior,
δ to be frequency independent. At the critical gel, the rich rheological diversity of a material converges to a universal dynamical state of less rheological complexity, exhibiting a simple self-similar relaxation behavior, 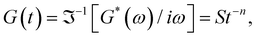 where G(t) is the real relaxation modulus, and S and n are two fitting material parameters characterizing the gel.18,19 J. Peyrelassee et al.20 studied the rheological properties of gelatin solutions below Tg. At the gel point, G′(ω) and G′′(ω) are proportional to ωn, and n is almost invariant at gelatin concentration (n ∼ 0.62). Zhi Yang et al.7 investigated the strain-hardening behavior of various gel networks of gelatin: a physical one, a chemically crosslinked one with glutaraldehyde as a crosslinker, and a hybrid gel made of a combination of the former two. In the last one, the chemical networks are made first, and then, the temperature is decreased to allow physical networks to form triple helices. Using small angle neutron scattering (SANS), these authors showed that physical gels form a relatively homogeneous network, whereas, in the chemically crosslinked gels, within the chemically crosslinked network, there are also some small crosslinked aggregates; these inhomogeneities prevent free stretching in these gels. However, it is unknown how the network is when the physical and chemical crosslinking mechanisms simultaneously occur.
where G(t) is the real relaxation modulus, and S and n are two fitting material parameters characterizing the gel.18,19 J. Peyrelassee et al.20 studied the rheological properties of gelatin solutions below Tg. At the gel point, G′(ω) and G′′(ω) are proportional to ωn, and n is almost invariant at gelatin concentration (n ∼ 0.62). Zhi Yang et al.7 investigated the strain-hardening behavior of various gel networks of gelatin: a physical one, a chemically crosslinked one with glutaraldehyde as a crosslinker, and a hybrid gel made of a combination of the former two. In the last one, the chemical networks are made first, and then, the temperature is decreased to allow physical networks to form triple helices. Using small angle neutron scattering (SANS), these authors showed that physical gels form a relatively homogeneous network, whereas, in the chemically crosslinked gels, within the chemically crosslinked network, there are also some small crosslinked aggregates; these inhomogeneities prevent free stretching in these gels. However, it is unknown how the network is when the physical and chemical crosslinking mechanisms simultaneously occur.
In addition to mechanical rheometry, micro-rheology has recently been used to measure the shear modulus to determine the gel point of different gels.21–23 The general principle behind micro-rheology is to minimize the mechanical probe that deforms the medium, which could be a colloidal microsphere. So, the material's properties can be extracted by tracing the motion of the thermally fluctuating probes in some way. The colloidal particle introduces the slightest possible perturbation in the structure and dynamics of delicate soft matter. Diffusing wave spectroscopy (DWS) microrheology allows the measurement of the mean square displacement of the tracers. The rheological material properties at high frequencies can be obtained from it, spanning micrometer and sub-micrometer scales through micro-rheology equations.24 Unlike rotatory mechanical rheometers, the material's strain could be virtually negligible during measurements due to the probes' small size. This feature is helpful in biopolymeric gels, in which even small imposed strains can cause structural reorganization and, consequently, a change in their viscoelastic properties.
The nature of linkages and their amount impact the network structure of a gel and, consequently, its deformation and elasticity properties, characterized by rheology, could drastically change from linear to nonlinear regimes. When the critical gel is achieved, the rich rheological diversity of a material converges into a universal dynamical state of less rheological complexity, exhibiting a simple self-similar relaxation behavior. As time elapses after gelation, the mesoscopic scales of the structure of the gel's network transform. So, the persistence length of the unstructured, non-bonded flexible polymer sections and the network's mesh size decrease due to the formation of linkages. These facts inspire the aims of this paper to study the critical gels, nonlinear rheological behavior, and gelation kinetics in gelatin solutions with different linking processes, i.e., physical, chemical, and hybrid (physicochemical). We want to answer some questions: Does the exponent of the frequency power law for the moduli or the fractal dimension of matured gels differ depending on the linking process?; can large amplitude oscillation shear (LAOS) measurements detect the different linking processes in these gels?; can the mean square displacement of tracer particles embedded in these gels detect the different gelation mechanisms?; can the complex shear modulus at high frequencies given by micro-rheology estimate the persistence and mesh size lengths during the gelation process and how they evolve for the different linking mechanisms?
2. Experimental section
2.1 Materials
Gelatin from porcine skin (type A, gel strength 300 Bloom, Mol. Wt. 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 Da, Sigma-Aldrich USA), glutaraldehyde solution (C5H8O2, 50 wt%, Sigma-Aldrich Germany), sodium azide (NaN3, purity > 99%, Sigma-Aldrich USA), and hydrochloric acid (HCl, Sigma-Aldrich USA). Solutions were prepared with ultrapure deionized water (Nanopure, USA). Chemical products were used as received. At low pH, glutaraldehyde molecules react through a hemiacetal bond with two hydroxyproline residues,25 which are linked to the gelatin chain through a covalent peptide bond. For describing the chemical and physicochemical gels, we will use the parameter R = [glutaraldehyde]/2[hydroxyproline] to indicate the molar quantity of glutaraldehyde, which will be interlinked with an equivalent molar number of hydroxyproline residues in the gelatin strand; the hydroxyproline concentration for gelatin type A is ∼13.5 wt%.25
500 Da, Sigma-Aldrich USA), glutaraldehyde solution (C5H8O2, 50 wt%, Sigma-Aldrich Germany), sodium azide (NaN3, purity > 99%, Sigma-Aldrich USA), and hydrochloric acid (HCl, Sigma-Aldrich USA). Solutions were prepared with ultrapure deionized water (Nanopure, USA). Chemical products were used as received. At low pH, glutaraldehyde molecules react through a hemiacetal bond with two hydroxyproline residues,25 which are linked to the gelatin chain through a covalent peptide bond. For describing the chemical and physicochemical gels, we will use the parameter R = [glutaraldehyde]/2[hydroxyproline] to indicate the molar quantity of glutaraldehyde, which will be interlinked with an equivalent molar number of hydroxyproline residues in the gelatin strand; the hydroxyproline concentration for gelatin type A is ∼13.5 wt%.25
2.2 Rheological measurements
All measurements for SAOS and LAOS were performed with a MCR-702 Twin Drive rheometer (Anton Paar, Austria) using a cone–plate geometry (2° cone angle, Diam. = 40 mm) and temperature control (±0.1 °C). A solvent trap was used to avoid water evaporation.2.3 Micro-rheology and diffusive wave spectroscopy (DWS)
The mean square displacement (MSD, 〈Δr2〉) of microspheres embedded in gelatin solutions is measured with DWS. The viscoelastic connection between MSDs and the complex module is described through the generalized Stokes–Einstein relationship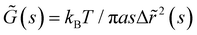 ,26,27 where the functions of s are Laplace transforms of G(t) and MSD, kB is Boltzmann's constant, T is the absolute temperature, and a is the sphere's radius. The experimental MSD curves were fitted using the Bellour model.28 For more details, see ref. 24, where our DWS setup is also described. Polystyrene microspheres (dia. 500 nm and 784 nm; Bangs Labs, USA) were added to the solutions (vol. fraction ∼0.025) at 35 °C, mixed, and placed in a rectangular optical glass cuvette (2 mm optical-path length, Sterna Cell, Inc.). Physical gels were quenched in a thermal bath to T ≤ Tg, serving as the starting point for the gelation process and the MSD measurements. The MSDs of probe microspheres were determined by collecting their scattered light from a speckle over a duration of 180–300 s, and the intensity auto-correlation functions were evaluated; measurements were taken over ∼8 h for different waiting times after gelation started. Scattered light collected for 180 s is enough to consider local thermodynamic equilibrium with good statistics. The protocols for measuring the MSD for chemical and physicochemical gels are similar. An aliquot of glutaraldehyde is added to the gelatin mixture after mixing the microspheres into the gelatin solutions; we considered this moment as the starting point of the gelation process for measuring the MSDs. Cuvettes were introduced into a thermal bath for chemical gels at T = 35 °C; for physicochemical gels, the thermal bath was set at T ≤ Tg to start the physical bonding simultaneously.
,26,27 where the functions of s are Laplace transforms of G(t) and MSD, kB is Boltzmann's constant, T is the absolute temperature, and a is the sphere's radius. The experimental MSD curves were fitted using the Bellour model.28 For more details, see ref. 24, where our DWS setup is also described. Polystyrene microspheres (dia. 500 nm and 784 nm; Bangs Labs, USA) were added to the solutions (vol. fraction ∼0.025) at 35 °C, mixed, and placed in a rectangular optical glass cuvette (2 mm optical-path length, Sterna Cell, Inc.). Physical gels were quenched in a thermal bath to T ≤ Tg, serving as the starting point for the gelation process and the MSD measurements. The MSDs of probe microspheres were determined by collecting their scattered light from a speckle over a duration of 180–300 s, and the intensity auto-correlation functions were evaluated; measurements were taken over ∼8 h for different waiting times after gelation started. Scattered light collected for 180 s is enough to consider local thermodynamic equilibrium with good statistics. The protocols for measuring the MSD for chemical and physicochemical gels are similar. An aliquot of glutaraldehyde is added to the gelatin mixture after mixing the microspheres into the gelatin solutions; we considered this moment as the starting point of the gelation process for measuring the MSDs. Cuvettes were introduced into a thermal bath for chemical gels at T = 35 °C; for physicochemical gels, the thermal bath was set at T ≤ Tg to start the physical bonding simultaneously.
From the MSD, the viscoelastic spectra can be evaluated up to high frequencies (ω ≈ 103–106 s−1), enabling the observation of stress relaxation through Rouse–Zimm and bending modes of the polymer chains. At these frequencies, G*(ω) exhibits a power-law behavior, |G*(ω)| ∼ ωμ, with μ ∼ 5/9 for Rouse–Zimm modes, which shifts to μ ∼ 3/4 where the internal bending modes of Kuhn segments dominate. The change occurs at the frequency ω0, corresponding to the shortest relaxation time in the Rouse–Zimm spectrum. From ω0 derived from that change in |G*(ω)|, the persistence length, lp, can be evaluated using the relationship ω0≈ kBT/8ηslp3, where ηs is the solvent viscosity.29 Additionally, it is possible to estimate the mesh size of the network, ξ; according to the flexible polymer theory, the relationship between the mesh size and de elastic modulus, G0, is ξ3 = (kBT/G0).17,30
3. Results and discussion
3.1 Gelation temperature for physical gels
T g for gelatin physical gels is determined according to the procedure described in the ESI† (see Fig. SI2). Fig. 1 presents Tg values vs. C, between 3 wt% and 16 wt%. Tg increases as the concentration increases, i.e., as more single chains are available, a higher temperature is needed for percolation. Within that concentration range, the average critical exponent is n ∼ 0.61 (see the inset in Fig. 1). Combining our data with those of Peyrelasse et al.,20 the power law behavior for gelatin critical physical gels is followed across a wide concentration range (3 wt% to 40 wt%). The inset in Fig. 1 also presents the stiffness factor as a function of gelatin concentration, which follows a power law, S = 0.016C1.68, as in polymers.31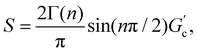 where Γ(n) is the gamma function.
where Γ(n) is the gamma function.
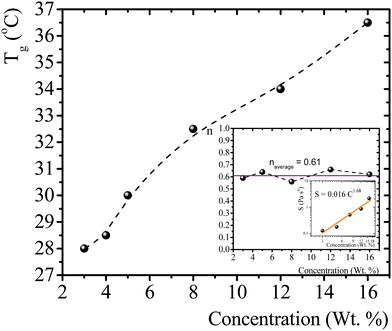 | ||
| Fig. 1 T g vs. gelatin concentration, the dotted line is a guide to the eye. Inset: n vs. C, and a log–log plot of S vs. C; the colored line is a linear fitting in the log–log plot (R2 = 0.95). | ||
3.2 Linear viscoelastic spectra of critical gels
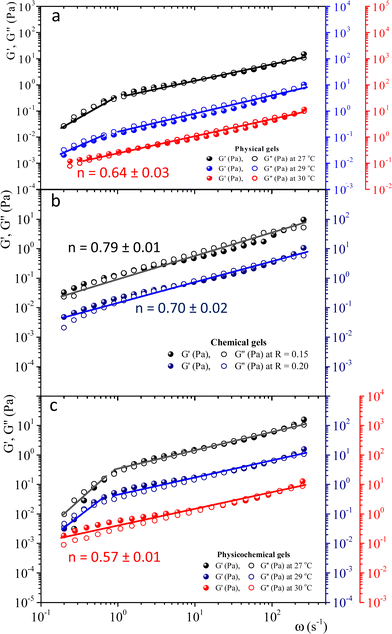
To study physical critical gels through mechanical rheology, we must choose a gelatin concentration where the gelation process is slow enough to allow for accurate measurements; but also, the gel must be strong enough to yield reliable stress measurements. For C = 5 wt%, the gelation time is ∼90 min at Tg = 30 °C. For higher concentrations, gelation time decreases, making it challenging to obtain precise measurements. For C = 3 wt% or below, gelation time increases; however, G′(ω) and G′'(ω) show instabilities, possibly because the formed network is weak and prone to breaking under the imposed strains. Therefore, we selected gelatin solutions with C = 5 wt% to reach the critical gel. Adding glutaraldehyde to gelatin solutions produces a chemical gel. Fig. SI3a (ESI†) shows the G′(t) and G′′(t) vs. time (ω = 0.5 s−1 and γ = 0.8%) for different R values at 35 °C. Gelation time where G′(t) ∼ G′′(t) decays as R increases (inset in Fig. SI3a, ESI†). For R < 0.15, gels are not formed because G′(t) always is below G′′(t), but for R = 0.15, the gelation time is ∼63 min. Therefore, we will use a relation of R = 0.15 to obtain the chemical and physicochemical critical gels, and only in a few experiments, R = 0.20.Fig. 2 presents the linear viscoelastic behavior for physical, chemical, and physicochemical critical gels, where G′(ω) and G′′(ω) are parallel across several orders of magnitude in frequency. As shown in Fig. 2, our measurements were delayed after gelation started until the system reached relatively close to the critical point, thereby avoiding the observation of a polymer solution in the initial stages of gelation. In some figure panels, we used different vertical scales (y-axis) to see all measurements in one figure, regardless of the quench extent. Fig. 2a shows G′(ω) and G′′(ω) for different temperature quenching scenarios from an initial T = 35 °C to a final Tf, (temperature quench with ΔTq = Tf − 35 °C). When the quench ends at Tg = 30 °C, G′(ω) and G′′(ω) are parallel for more than three orders of magnitude in frequency, i.e., the solution became a critical gel for C = 5 wt%; the exponent of the power law is n ∼ 0.64. In this figure, we also show a quench below Tg ∼ 30 °C, i.e., in a post-critical gel state below the critical point. Here, we found two regions in the plots. In the first region, ω < 1 s−1, the viscoelastic moduli have a slope >1, decreasing as the temperature quench decreases. In a second region, ω ≥ 1 s−1, the slope is ∼0.6. We suspect that the origin of two slopes of the viscoelastic moduli is related to the change of structure that occurs when the temperature is lowered from Tg. Points measured faster, ω ≥ 1 s−1, detect a different structure than those measured using longer times ω ≥ 1 s−1. As far as the temperature quench is close to Tg, the slope difference between these two regions is smaller until G′(ω) and G′′(ω) are parallel. Fig. 2b presents two critical chemical gels for R = 0.15 and R = 0.20, developed at 35 °C. These gels are established by covalent bonding.25 In both cases, G′(ω) and G′′(ω) are parallel along more than three orders of magnitude in ω; the exponents of their power laws are n = 0.79 and n = 0.70 for R = 0.15, and R = 0.20, respectively. In Fig. 2c, G′(ω) and G′′(ω) are plotted for physicochemical gels with R = 0.15; gelation started when glutaraldehyde is added at 35 °C, and a temperature quench to a temperature T is applied immediately (ΔTq = T − 35, °C), i.e., two gelation mechanisms run simultaneously. The critical gel is found at ΔTq = −5 °C, where moduli are parallel and follow a power law for more than three orders of magnitude in ω; n = 0.57. However, in a post-critical gel state for quenches ending at T < Tg, i.e., the gels inherit the behavior found in physical gels below the gelation temperature. They are parallel in a small range of ω (ω < 1 s−1) and follow a power law with a large exponent. After that, frequency moduli are parallel and have a power law close to that of the critical gel.
3.3 Fractal dimension and strain hardening of mature gels
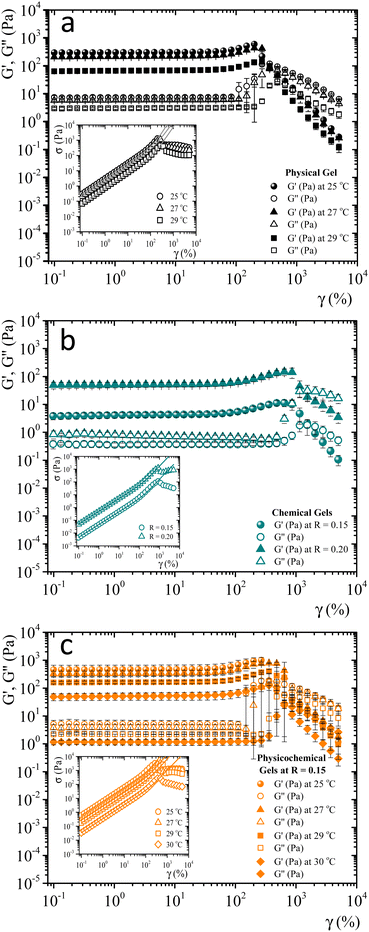
When gelatin gels are sheared, the observed stress is a nonlinear function of strain. We determined the strain-hardening behavior of matured gels using LAOS7,32,33 to look for differences between bonding mechanisms to form networks. As described by Yang et al.7 a matured gel is a gel where the viscoelastic moduli essentially do not vary with time. Fig. SI4 (ESI†) shows the viscoelastic moduli for a physical gel as a function of time at a fixed frequency and strain (ω = 0.5 s−1γ = 0.8%), obtained at 29 °C. Here, G′(t) > G′′(t) by around an order of magnitude; for t > 240 min, the viscoelastic moduli essentially do not change. For this gel, the gelation time is around ∼55 min at 29 °C, the largest gelation time of the studied systems. From a practical point of view, we will consider a gel aged four hours to be a matured one, whether physical, chemical, or physicochemical.Fig. 3 shows the viscoelastic moduli vs. shear strain (γ = 0.1–5000%) for a fixed frequency (ω = 1 s−1) for different matured gels. G′(γ) and G′′(γ) in matured gels exhibit similar trends, which could be described with three regions. In the first region, known as a linear viscoelastic region (LVR), G′(γ) and G′′(γ) are essentially independent of strain. In the second region, G′(γ) and G′′(γ) increase with a positive curvature strain, and a sudden overshoot produces a third region where G′(γ) and G′′(γ) decrease as the strain increases, suggesting a gelatin network failure where it starts to break. This failure can be easily seen in the σ vs. γ curves presented in the insets of Fig. 3. As γ increases, G′′(γ) > G′(γ), which is related to the flow of a broken gel. The overshoot in the viscoelastic moduli is typical strain-hardening behavior for physical and chemical gelatin gels,7,32 which physicochemical gels inherit.
Since accurate measurement of the nonlinearity could yield relevant information about the microstructure of the gel, we used the BST–scaling model34 to fit the nonlinear viscoelastic behavior of mature gels to determine the fractal structure of the polymers in terms of the fractal dimension, df. The shear stress in terms of the shear deformation given by Blatz et al.34 is:
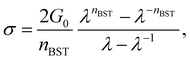 | (1) |
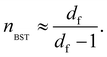 | (2) |
Table 1 presents all parameters for the BST – scaling model and breaking strains, γbreak, corresponding to strain where the shear stress is maximum. For γ > γbreak, the stress decreases due to the broken gel flow.
| G 0 (Pa) | n BST | d f | γ break (%) | |
|---|---|---|---|---|
| Matured physical gels | ||||
| T = 25 °C | 299.25 ± 5.08 | 3.36 ± 0.06 | 1.42 ± 0.01 | 200 |
| T = 27 °C | 210.60 ± 0.61 | 3.07 ± 0.004 | 1.48 ± 0.001 | 267 |
| T = 29 °C | 64.87 ± 11.45 | 3.18 ± 0.05 | 1.46 ± 0.001 | 297 ± 52 |
| Matured chemical gels | ||||
| R = 0.15 | 3.94 ± 0.99 | 2.62 ± 0.05 | 1.62 ± 0.02 | 861 |
| R = 0.20 | 55.07 ± 7.77 | 2.66 ± 0.04 | 1.60 ± 0.01 | 861 |
| Matured physicochemical gels | ||||
| T = 25 °C | 464.00 ± 196.04 | 3.19 ± 0.16 | 1.46 ± 0.03 | 267 |
| T = 27 °C | 327.34 ± 77.43 | 2.83 ± 0.08 | 1.55 ± 0.02 | 561 ± 115 |
| T = 29 °C | 174.94 ± 5.84 | 2.73 ± 0.02 | 1.58 ± 0.01 | 643 |
| T = 30 °C | 49.55 ± 12.20 | 2.74 ± 0.20 | 1.60 ± 0.04 | 480 |
According to the master curve of Holy-Duhamel et al.36 the concentration of the triple helices is proportional to 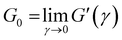 . From Table 1, for matured physical gels, G0 decreases as the temperature where it was maturated increases, and so does the triple helices concentration, which agrees with previous reports.5 However, γbreak slightly increases with temperature; a gel formed at 25 °C requires a lower strain to break the structure than a gel at 29 °C. One rupture mechanism is unzipping the triple helix junctions' zone;4,5,7 the triple helices formed from the gelatin solution are shorter5,37 when made at lower temperatures. On the other hand, G0 increases with the relative glutaraldehyde concentration, R, for matured chemical gels, but it is quite lower than in physical gels, and γbreak is larger than in physical gels. G0 for hybrid gels increases with respect to physical gels at the same temperature; approximately, they are ∼50% larger from 25 °C to 27 °C and ∼150% at 29 °C. In this case, γbreak is higher than in physical gels due to the covalent crosslinking plus the physical crosslinking; however, γbreak is minor compared to chemical gels. There is not a clear trend with the temperature. Yan et al.7 found a gel with C = 3 wt% of gelatin and 0.2 wt% of glutaraldehyde where the chemical networks were developed first, and after a temperature quench to allow physical networking, a so-called chemical-physical gel, the value of G0 is additive (G0 = Gphysical0 + Gchemical0). In our hybrid gels, the G0 value is not additive. However, in promoting both routes of gelation at the same time, as presented here, G0 increases more than in a chemical–physical gel, showing a technological advantage to promoting both gelation routes simultaneously.
. From Table 1, for matured physical gels, G0 decreases as the temperature where it was maturated increases, and so does the triple helices concentration, which agrees with previous reports.5 However, γbreak slightly increases with temperature; a gel formed at 25 °C requires a lower strain to break the structure than a gel at 29 °C. One rupture mechanism is unzipping the triple helix junctions' zone;4,5,7 the triple helices formed from the gelatin solution are shorter5,37 when made at lower temperatures. On the other hand, G0 increases with the relative glutaraldehyde concentration, R, for matured chemical gels, but it is quite lower than in physical gels, and γbreak is larger than in physical gels. G0 for hybrid gels increases with respect to physical gels at the same temperature; approximately, they are ∼50% larger from 25 °C to 27 °C and ∼150% at 29 °C. In this case, γbreak is higher than in physical gels due to the covalent crosslinking plus the physical crosslinking; however, γbreak is minor compared to chemical gels. There is not a clear trend with the temperature. Yan et al.7 found a gel with C = 3 wt% of gelatin and 0.2 wt% of glutaraldehyde where the chemical networks were developed first, and after a temperature quench to allow physical networking, a so-called chemical-physical gel, the value of G0 is additive (G0 = Gphysical0 + Gchemical0). In our hybrid gels, the G0 value is not additive. However, in promoting both routes of gelation at the same time, as presented here, G0 increases more than in a chemical–physical gel, showing a technological advantage to promoting both gelation routes simultaneously.
For physicochemical gels, it depends on what crosslinking process dominates; at low temperatures, it is the physical crosslinking, and at higher temperatures, it is the chemical one. Nevertheless, the advance in one of them could modify the performance of the other: for instance, once a chemical bond occurs, the orientation of a section of the polymer could hamper a triple helix formation process. To support these statements, it is necessary to consider: (a) In the case of physical gelation, Chen et al.38 gave an estimation of the temperature dependence of the sol–gel conversion rate constant. In the range of 30–19 °C, the rate of transformation increases as the temperature decreases, following the Arrhenius law, Ae−Ea/kBT, with Ea = −130 kJ mol−1. We estimated the conversion rate above Tg for chemical gelation using the data given in Fig. SI3b (ESI†), which also follows an Arrhenius equation with Ea = −92 kJ mol−1. Determining what process is going faster in the hybrid gel is more challenging as the temperature is ≤30 °C, because physical and chemical mechanisms work and interact simultaneously and cannot be separated to observe just one process alone. In both cases, the transformation rate increases as the temperature decreases. However, Ea is more negative in physical gels than in the chemical gel's Ea. Assuming that the Ea does not change too much below 30–31 °C, chemical bonding transformation is running slightly slower. (b) da Silva et al.39 studied the gelation evolution in gelatins using the fraction of triple helices (χ) by optical rotation and G′ at a fixed frequency (γ = 1%, G′ ∼ G0) for the case of the physical, chemical, and hybrid gels. The last two employ glutaraldehyde as a crosslinker at different temperatures below Tg. In physical gelation, the lower the temperature, the higher χ and G′. For a chemical gel, there are no triple helices above Tg, and G′ is several times lower than in the physical gel, and its time evolution during gelation is slower because as the crosslinker is consumed and the binding sites are occupied; the reaction will naturally slow down. For hybrid gels. The value of G′ increases as the temperature decreases, and they are larger than those of the physical gels at the same temperature. However, they reach saturation limits faster than in physical gels. χ are much lower than in physical gels at the same temperature, demonstrating that the formation of the chemical networks hinders the helical conformation change. There is a decoupling between χ and G′; not only triple-helix junctions contribute to G′. Increasing the temperature above Tg, the helix physical network is destroyed, leaving just the chemical scaffold with a G′ much lower than in the physical gel. We also measured G′ above Tg and observed the same result. In our experiments (see Fig. SI3c, ESI†), isothermal time sweep curves were developed for a gelatin solution under hybrid gelation (5 wt% and R = 0.15). The hybrid gel was formed at three different temperatures ≤Tg. Subsequently, the gel was melted to destroy the triple helices melted at 35 °C, allowing to show the remaining G′ due to the chemical scaffold. As the temperature of hybrid gel formation is lower than Tg, ΔG′ is larger, showing a greater quantity of triple helices than at temperatures closer to Tg. So, there is chemical bonding at low temperatures and a synergy between physical and chemical networks. The chemical networks obtained in the presence of the triple-helices present substantially higher G′ values than those obtained just by gelating the sol phase.
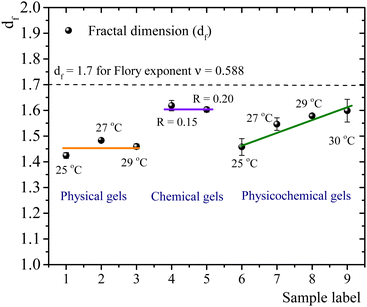
The self-similar network fractal dimensions,5,7,35,40,41 for the matured gels are displayed in Fig. 4. For physical gels, on average, df ∼ 1.45, which is similar to that obtained by Yang et al.7 using the LAOS for physical gelatin gels with C = 3 wt% at 20 °C (df = 1.40 ± 0.05), and by Pezron et al.42 using SANS with C = 5 wt% (df = 1.40 ± 0.02 for a scattering vector q = 0.20–1.66 nm−1). For chemical gels, we obtained df ∼ 1.61 (average from R = 0.15 and R = 0.2), which is lower than df = 1.48 ± 0.02 obtained by Yang et al.7 These authors associated their value with the existence of rod-like structures, swollen coils, and small crosslinking aggregates within their network due to their high crosslinker concentration (∼0.2 wt% of glutaraldehyde in C = 3 wt% of gelatin solution). In our case, the relative concentration of the crosslinker agent (∼0.1 wt% of glutaraldehyde in C = 5 wt%) is lower than in Yang et al.7 case. So, we expect that our network will have fewer crosslinking aggregates. The fractal dimension for chemical gels is close to df ≈ 1.7, corresponding to the Flory swelling exponent ν = 0.588 associated with isolated polymers in a good solvent;16,30 these results suggest that the chemical gel networks are swollen interlocking Gaussian chains. For physicochemical gels, where two gelation processes run simultaneously, initiated at 35 °C, immediately quenched and matured to 25 °C, df is similar to that obtained for physical gels quenched and matured to 25 °C. For physicochemical gels initiated at 35 °C, immediately quenched and matured to 30 °C, df is similar to the chemical gels at 35 °C. However, physicochemical gels for other intermediate quenching temperatures have df values between 1.46 and 1.60. In Fig. 4, it seems as if the fractal dimension of hybrid gels, formed at 25 °C, corresponds to a gel whose network is mainly formed by a physical mechanism. In the same way, when the physicochemical gel is formed at 30 °C, the network formation is apparently dominated by a chemical mechanism producing a df similar to that of a chemical gel; the physical gelation is perturbed by the chemical crosslinking as discussed above. However, df apparently detects a mean of chemical and physical processes for the gelation process occurring at intermediate temperatures quenches. This would explain the trend we observe for df with temperature in Fig. 4. We conclude that the differences in mechanisms to form the gel network can be slightly differentiated by the strain-hardening approach of matured gels, where the self-similarity of the network has a direct impact.
3.4 LAOS and Lissajous–Bowditch curves
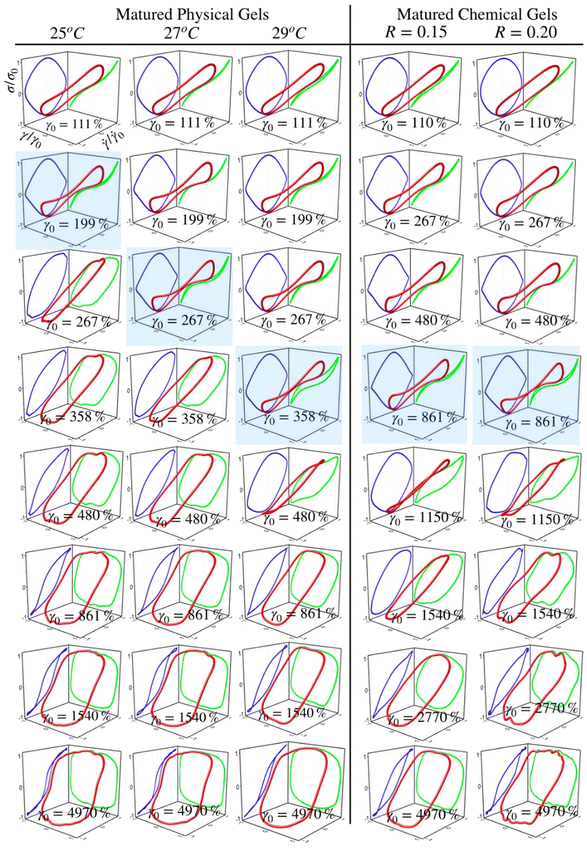
Fig. 5 and 6 present normalized 3D Lissajous–Bowditch (LB) curves (in red) and their projections for different matured gels in the elastic representation (σ/σ0vs. γ/γ0 in green) and viscous representation (σ/σ0vs.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /
/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 in blue). They are measured at ω = 1 s−1, and σ0, γ0, and
0 in blue). They are measured at ω = 1 s−1, and σ0, γ0, and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 are the maximum shear stress, shear strain, and shear rate in an oscillation cycle, respectively. Diagrams with a blue shadow indicate LB curves corresponding to an imposed strain deformation of γ0 = γbreak. LB curves for strain cycles in the LVR zone are not presented because they are independent of strain; in this region, the loci of σ/σ0vs. γ/γ0 and σ/σ0vs.
0 are the maximum shear stress, shear strain, and shear rate in an oscillation cycle, respectively. Diagrams with a blue shadow indicate LB curves corresponding to an imposed strain deformation of γ0 = γbreak. LB curves for strain cycles in the LVR zone are not presented because they are independent of strain; in this region, the loci of σ/σ0vs. γ/γ0 and σ/σ0vs. ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /
/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 is a diagonal line or a circle, respectively, which corresponds to solid-like behavior.33
0 is a diagonal line or a circle, respectively, which corresponds to solid-like behavior.33
For matured physical gels before γ ≤ γbreak, the nonlinear viscoelastic behavior is similar for temperatures 25 °C ≤ T ≤ 29 °C. For γ > γbreak, the LB curves are more similar for 25 °C and 27 °C. However, all of them differ for γ slightly larger than γbreak, although for 29 °C it is more notorious. Nevertheless, they all behave close to liquid-like when γ ≫ γbreak. In our LB curves, there are small oscillations (25 °C and 27 °C), which are not as strong as those observed by Goudoulas & Germann,32 probably because our gels are weak (G ≪ 3000 Pa). Their gelatine solutions have a G ≈ 3000 Pa (C = 3 wt%, matured for 30 min and 90 min after a large quench ending to Tf = 5 °C). Our LB curves are similar to recent simulation results for colloidal gels.43
For matured chemical gels at γ0 = 110%, we observe a small deviation from the linear viscoelastic behavior. In the σ/σ0vs. ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /
/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 plane, circles are slightly elongated, and as γ0 increases but without gel breaking (γ0 ≤ γbreak), the deviation of the linear viscoelastic behavior can be significant; circles become rhomboid-like. On the σ/σ0vs. γ/γ0, we found deformed lines, which as γ increases, they appear as lines with a shoulder. This behavior seems to be invariant with the chemical crosslinker concentration. However, as observed in their projections, when γ0 > γbreak, LB curves show significant changes. For γ0 = 1540%, the projections on both planes are analogous to deformed ellipses with similar areas, which corresponds to G′(γ) ∼ G′′(γ) of the strain sweep curves (see Fig. 3b). As strain is γ0 ≫ γbreak, the deformed ellipses change even more. In viscous representations, deformed ellipses are elongated, suggesting that the shear rate is close to being in phase with the stress, or equivalent, in an elastic representation, deformed ellipses change to distorted circles because the strain is close to being out of phase with stress; approaching to a liquid-like behavior. As maturation temperature increases, LB curves for matured physical and chemical gels behave similarly.
0 plane, circles are slightly elongated, and as γ0 increases but without gel breaking (γ0 ≤ γbreak), the deviation of the linear viscoelastic behavior can be significant; circles become rhomboid-like. On the σ/σ0vs. γ/γ0, we found deformed lines, which as γ increases, they appear as lines with a shoulder. This behavior seems to be invariant with the chemical crosslinker concentration. However, as observed in their projections, when γ0 > γbreak, LB curves show significant changes. For γ0 = 1540%, the projections on both planes are analogous to deformed ellipses with similar areas, which corresponds to G′(γ) ∼ G′′(γ) of the strain sweep curves (see Fig. 3b). As strain is γ0 ≫ γbreak, the deformed ellipses change even more. In viscous representations, deformed ellipses are elongated, suggesting that the shear rate is close to being in phase with the stress, or equivalent, in an elastic representation, deformed ellipses change to distorted circles because the strain is close to being out of phase with stress; approaching to a liquid-like behavior. As maturation temperature increases, LB curves for matured physical and chemical gels behave similarly.
LB curves for matured physicochemical gels with γ0 ≤ γbreak behave likewise when aged at 25 °C and 30 °C, although, at 27 °C, and 29 °C, they present slight differences. The deformed circles transform into deformed rhomboids, which increase as strain increases, quite visible in the viscous representation. On the elastic representation, the line becomes a shoulder. For γ0 > γbreak, LB curves for physicochemical gels matured at 30 °C are similar to those where the mechanism to form the network was chemical. On the contrary, LB curves for physicochemical gel matured at 25 °C are more similar to those for physical gel aged at 25 °C; here, the physical mechanism is dominant. Therefore, the features of LB curves and fractal dimension in hybrid gels depend on which gelation mechanism is dominant.
3.5 Kinetic of gelation using DWS – microrheology
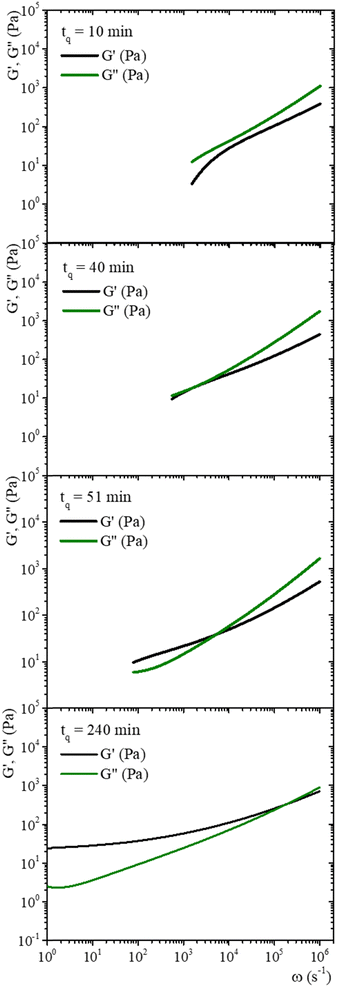
Fig. 7 shows MSD vs. t curves for gelatin solutions at different times after a temperature quench to produce a physical gel (T < Tg), after adding glutaraldehyde for chemical gels (T > Tg), and simultaneously after adding glutaraldehyde and quenching (T < Tg) for physicochemical gels. The elapsed time since the quench or glutaraldehyde addition will be named tq. For solutions that produce physical gels with C = 5 wt%, particles move in a simple liquid (sol state) at tq = 10 min after the quench started from 35 °C to 25 °C (see Fig. 7a). This behavior prevails for 20 min after the quench; at tq ∼ 75 min, a change onsets. The MSD vs. time curves bend to form a shoulder, up to t ∼ 0.02 s. The shoulder is more pronounced for tq > 75 min; their height decreases as tq increases. From a mesoscopic point of view, a shoulder in MSD vs. time curves is evidence of partial particle confinement. They explore all the available volume in the polymer network cage formed around it, limiting the displacement of the microsphere similar to those described by Sarmiento-Gomez et al.44 However, the cages formed by the polymer network slowly break and reform due to the physical nature of physical gel crosslinking. They are not permanent, allowing the particle to explore a larger space as time elapses; if particles were completely trapped, the curves would be flat horizontally.
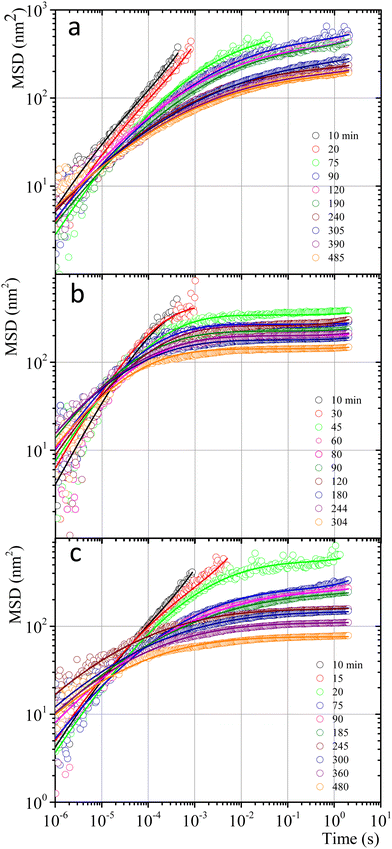 | ||
| Fig. 7 MSD vs. time for microspheres embedded in gelatin solutions. (a) Physical gel for C = 5 wt% (dia. 500 nm and vol. fraction 0.025) after a temperature quench to 25 °C. (b) Chemical gel for C = 3 wt% (dia. 799 nm and vol. fraction 0.025) after adding glutaraldehyde (R = 0.25). (c) Physicochemical gel formation for C = 5 wt% (dia. 500 nm and vol. fraction 0.025) after adding glutaraldehyde (R = 0.15) and simultaneously quenching to 25 °C. Open circles correspond to experimental MSD data, and continuous lines correspond to best fitting using the Bellour et al. model.28 | ||
Fig. 7b shows the MSD curves of colloidal particles embedded in gelatin solutions (C = 3 wt% with R = 0.25) which form a chemical gel. For tq ≤ 30 min, the MSD corresponds to simple diffusion at short times, MSD ∼ t, although when they reach 10−4 s, the MSD vs. t curves start to bend. For tq > 30 min, the MSD curves show a flat plateau, indicating that particles are confined. The flat shape of the plateau corresponds to particle movement in a polymer network cage that cannot relax due to the permanent chemical nature of the cross-linkings. It is not possible to see the evolution of the MSD curves for the gelation process in less soft chemical gels (C > 3 wt%) because the network completely traps them; correlation functions vs. time abruptly drop because particles are essentially fixed (not shown).
The MSDs for physicochemical gels have a mixed behavior between physical and chemical gels. At tq = 20 min, the MSD vs. time curve has bent to form a shoulder, and at tq > 20 min, the shoulder becomes increasingly horizontal, similar to the physical gel at the same temperature (25 °C). In the case where the final quench temperature T increases, the MSD vs. time curves become more horizontal as in a chemical gel, i.e., more confinement (see Fig. SI6a for T = 27 °C and Fig. SI6b for T = 30 °C, ESI†); covalent junctions hinder triple helix formation. Consequently, the chemical bonding contribution increases the network cages' rigidity. The MSD vs. t curves for microspheres embedded in hybrid gels show a slight dependence on gelation mechanisms that is more obvious at early times, which agrees with the contribution of both mechanisms running simultaneously, but at very long times, particles are finally trapped.
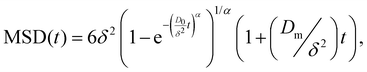 | (3) |
Fig. 8 shows the time evolution of viscoelastic spectra of a gelatin solution after a temperature quench from 35 °C to 25 °C to produce a physical gel, measured from tq = 10 min to tq ∼ 240 min, passing through the gel point. Fig. SI7 (ESI†) shows a similar gelation process to obtain chemical and physicochemical gels. All gels, 10 min after starting the gelation process, behave as in a sol state (G′′(ω) > G′(ω)), consistent with the simple diffusive dynamics of microspheres embedded in a liquid. As tq increases, the gel reaches the gel point where G′(ω) ∼ G′′(ω) ∼ ωn, in a range of frequencies from ω ∼ 102 to 104 s−1, which is similar to the data of Cardinaux et al.45 for C = 2 wt% at 20 °C. For large elapsed times after the quench, all gelatin solutions reach the gel state (G′(ω) > G′′(ω)), and the evolution of viscoelastic spectra is similar for all of them. The elapsed time for all solutions to reach the gel point after a quench was more extended in microrheology experiments than those developed in macroscopic rheometers because the number of cross-linkings needed by the network to percolate is larger in DWS cuvettes (∼2.3 mL) than in the rheometer geometry (∼1.2 mL); however, they have the same information, and viscoelastic spectra in the gel point are similar. It is not possible to discern which gelation process dominates in hybrid gels, which is consistent with our results of SAOS at gel points.
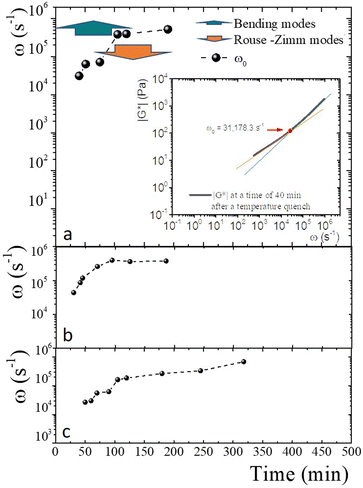
An advantage of measuring gelatine flexible polymer solutions' viscoelastic spectra at high frequencies is treating them like other biopolymers46,47 or living polymers.24,48–50 In a semidilute regimen concentration (>1 wt% for gelatin chains51), polymer chains can have different stress relaxation modes. As explained, stress relaxes at high frequencies first dominated by the Rouse–Zimm modes and at even higher frequencies by the internal bending modes of Kuhn segments. The frequency for the change, ω0, allows us to estimate the persistence length in the polymer network. The inset of Fig. 9a presents |G*| vs. ω for a gelatine solution quenched to 25 °C at tq = 40 min. It shows the frequencies where |G*(ω)| ∼ ω3/4, |G*(ω)| ∼ ω5/9, as well as ω0. Fig. 9a shows the frequencies where one of the relaxation modes dominates and ω0 for different tq up to 8 h after the gelation process started for producing a physical gel. In the same way, ω0 is presented in Fig. 9b for a chemical gel and in Fig. 9c, for a physicochemical gel with two gelation mechanisms running simultaneously. The place where Rouse–Zimm modes dominate is observed in all solutions below ω0, which increases as tq increases while bending modes dominate at even higher frequencies until we cannot measure them. For the hybrid process, quenched to 30 °C bending modes persist until 8 h after the gelation process started (not shown), displaying an important difference from the other gels. It is important to note that microspheres embedded in the gel measure bending modes for ω < 106 s−1, which is the limit of the DWS-microrheology technique.24,26
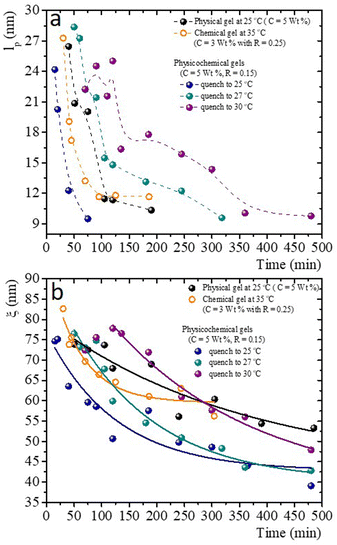
Fig. 10a presents the persistence length of polymer chains for gels with different gelation processes, i.e., the length at which polymer chains appear straight in the presence of thermal undulations given by lp = κ/kBT, where κ is the chain bending modulus. In physical gelation (C = 5 wt%), lp starts at ∼ 26 nm and decreases to lp ∼ 10 nm at tq ∼ 190 min. In chemical gelation (C = 3 wt% and R = 0.25), lp starts at ∼27 nm and decreases to ∼12 nm at tq ∼ 90 min; lp reaches a constant value at tq ∼ 200 min; apparently, this is the limiting of evolution for lp in a network formed by covalent crosslinking. For the hybrid case, where two mechanisms are evolving simultaneously, lp starts at ∼24–28 nm depending on the glutaraldehyde concentration, and it decreases to lp ∼ 10 nm at tq ∼ 360 min for the gel quenched to 30 °C. This lp is observed up to 8 h. The evolution of lp as a function of tq is slow despite two gelation mechanisms running simultaneously. For the physicochemical gel quenched to 25 °C, lp decreases to 10 nm at tq ∼ 75 min, comparable to the physical process, which seems to be the dominant mechanism when the solution is quenched to this temperature. However, it is unclear why the speed at which lp decreases to 10 nm is greater than in the other hybrid processes. For the hybrid process quenched to 27 °C, the evolution of lp has an intermediate behavior compared with the physical and hybrid process quenched to 30 °C. The crucial point for understanding Fig. 10a is what lp refers to in these biopolymer chains. As mentioned, the network is made of segments with triple chains, which must be semiflexible with a large lp as in other cases where lp ≥ ξ,30 and of unstructured non-bonded flexible polymer sections. It is important to mention that turbidity in our gelatin is quite low, so we ruled out the formation of semiflexible collagen fibrils.52 Then, our lp measurements capture the persistence length of the non-bonded flexible polymer sections where lp ≤ ξ. These polymer sections are relatively large when the gelation starts in all processes. As time elapses, the length of these polymer chains (Kuhn segments) appearing straight in the presence of thermal undulations decreases due to the formation of bonds. In this way, the curves for the gels undergoing physical and chemical processes seem similar. However, in the hybrid case, it is clear that these processes are not independent. As mentioned, covalent crosslinking hinders the formation of triple helices at T ≤ Tg; the lower the temperature quench, the faster decay of lp, where physical gelation dominates. In quenches to 25 °C, lp decays faster where the physical process dominates, and when the chemical process dominates, the decay is slower. At 27 °C, we observe that lp decays in an intermediate form between these two cases.
Fig. 10b presents the evolution of the gel network's volume mesh size, ξ, during the gelation process, which roughly follows an exponential decay. The general idea of mesh size is that a snapshot of a dense polymeric solution at a particular instant of time looks quite similar to an intricate network with a particular mesh size, independent of the presence of crosslinks. Consistent with what occurs in flexible polymers, in our measurements, ξ is much larger than lp. Roughly, the mesh size in a physical gel is larger than in a chemical gel, but at long times, the last one is larger than in hybrid gels, where the lower the quench temperature, the smaller the mesh size. As in the case of lp, for the hybrid gels, the decay of ξ as time elapses seems to have no relation with the pure physical or chemical processes, which seems to be another effect where the physical and chemical processes are not independent when running simultaneously.
4. Conclusions
Critical exponents for physical, chemical, and hybrid critical gels were determined. The features of LB curves and fractal dimensions in hybrid gels depend on the dominant gelation mechanism. Differences in forming the gel network were, to some extent, distinguished by the strain-hardening approach of matured gels, where the self-similarity of the network has a direct impact. Apparently, df results from a competition between physical and chemical gelation processes for physicochemical gels. For γ > γbreak, LB curves for physicochemical gels matured at 30 °C are similar to those where the mechanism to form the network was chemical. On the contrary, LB curves for physicochemical gel matured at 25 °C are more similar to those for physical gel aged at 25 °C; here, the physical mechanism is dominant. As gelation evolves, the MSD curves develop a shoulder in physical gels, which never becomes flat because the cage formed around microspheres can break and reform. Chemical gels completely trap microspheres due to the chemical nature of crosslinking, so the MSD vs. t curves form a plateau. The MSD vs. t curves for microspheres embedded in hybrid gels show a slight dependence on the gelation mechanism; at very long times, particles are trapped. At the gel point, it is impossible to discern which gelation process dominates with microrheology, in agreement with the SAOS results for critical gels.As time elapses after gelation starts, the persistence length of the unstructured, non-bonded flexible polymer sections decreases due to the formation of bonds. The curves for the gels undergoing physical and chemical processes seem similar. However, in the hybrid case, it is not a simple mixture of both processes since they are not independent. As far as we know, this is the first time that the evolution of scales of the mesoscopic structure has been observed after the critical gel has been reached with different mechanisms running simultaneously. The time evolution of the gel network's mesh size roughly follows an exponential decay. The lower the temperature quench, the smaller the mesh size. Understanding the behavior of ξ could be relevant for diffusing proteins or nanoparticles in biopolymer networks with applications in different fields. For ξ, as for lp, the decay as time elapses for hybrid gels seems to have no relation with the pure physical or chemical processes, which seems to be another effect where physical and chemical processes are not independent when running simultaneously.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support from SEP CONACYT (A1-S-15587), DGAPAUNAM (IN 106321), and a CONACYT scholarship for R. F. L.-S. We also thank C. Garza for the technical support.References
- J. Alipal, N. A. S. Mohd Pu’ad, T. C. Lee, N. H. M. Nayan, N. Sahari, H. Basri, M. I. Idris and H. Z. Abdullah, Mater. Today Proc., 2021, 42, 240–250 CrossRef.
- F. Bode, M. A. Da Silva, A. F. Drake, S. B. Ross-Murphy and C. A. Dreiss, Biomacromolecules, 2011, 12, 3741–3752 CrossRef CAS PubMed.
- H. H. Winter, Encyclopedia of Polymer Science and Technology, Wiley, 2016, pp. 1–15 Search PubMed.
- M. Djabourov, J. Leblond and P. Papon, J. Phys., 1988, 49, 319–332 CrossRef.
- L. Guo, R. H. Colby, C. P. Lusignan and A. M. Howe, Macromolecules, 2003, 36, 10009–10020 CrossRef CAS.
- S. Giraudier, D. Hellio, M. Djabourov and V. Larreta-Garde, Biomacromolecules, 2004, 5, 1662–1666 CrossRef PubMed.
- Z. Yang, Y. Hemar, L. Hilliou, E. P. Gilbert, D. J. McGillivray, M. A. K. Williams and S. Chaieb, Biomacromolecules, 2016, 17, 590–600 CrossRef PubMed.
- G. Dardelle, A. Subramaniam and V. Normand, Soft Matter, 2011, 7, 3315 RSC.
- M. T. Nickerson, J. Patel, D. V. Heyd, D. Rousseau and A. T. Paulson, Int. J. Biol. Macromol., 2006, 39, 298–302 CrossRef PubMed.
- G. Mugnaini, R. Gelli, L. Mori and M. Bonini, ACS Appl. Polym. Mater., 2023, 5, 9192–9202 CrossRef.
- D. Hellio and M. Djabourov, Macromol. Symp., 2006, 241, 23–27 CrossRef.
- M. Djabourov, K. Nishinari and S. B. Ross-Murphy, Physical Gels from Biological and Synthetic Polymers, Cambridge University Press, 2013 Search PubMed.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, Ithaca and London, 1953 Search PubMed.
- W. H. Stockmayer, J. Polym. Sci., 1952, 9, 69–71 CrossRef.
- R. M. Ziff, Kinetics of Aggregation and Gelation, Elsevier, North-Holland, Amsterdam, 1984 Search PubMed.
- D. Stauffer and A. Aharony, Introduction to Percolation Theory, Taylor & Francis, Abingdon, UK, 1985 Search PubMed.
- P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca and London, 1997 Search PubMed.
- K. Suman and Y. M. Joshi, J. Rheol., 2020, 64, 863–877 CrossRef CAS.
- F. Chambon and H. H. Winter, J. Rheol., 1987, 31, 683–697 CrossRef CAS.
- J. Peyrelasse, M. Lamarque, J. P. Habas and N. El Bounia, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 6126–6133 CrossRef CAS PubMed.
- W. Hong, G. Xu, X. Ou, W. Sun, T. Wang and Z. Tong, Soft Matter, 2018, 14, 3694–3703 RSC.
- L. G. Rizzi, J. Rheol., 2020, 64, 969–979 CrossRef CAS.
- T. H. Larsen and E. M. Furst, Phys. Rev. Lett., 2008, 100, 146001 CrossRef PubMed.
- A. Tavera-Vázquez, N. Rincón-Londoño, R. F. López-Santiago and R. Castillo, J. Phys.: Condens. Matter, 2022, 34, 034003 CrossRef PubMed.
- S. Farris, J. Song and Q. Huang, J. Agric. Food Chem., 2010, 58, 998–1003 CrossRef CAS PubMed.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 74, 1250–1253 CrossRef CAS PubMed.
- T. G. Mason, Rheol. Acta, 2000, 39, 371–378 CrossRef CAS.
- M. Bellour, M. Skouri, J.-P. Munch and P. Hébraud, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 8, 431–436 CrossRef CAS PubMed.
- N. Willenbacher, C. Oelschlaeger, M. Schopferer, P. Fischer, F. Cardinaux and F. Scheffold, Phys. Rev. Lett., 2007, 99, 068302 CrossRef CAS PubMed.
- M. Doi, S. F. Edwards and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, 1988, vol. 73 Search PubMed.
- J. C. Scanlan and H. H. Winter, Macromolecules, 1991, 24, 47–54 CrossRef CAS.
- T. B. Goudoulas and N. Germann, J. Colloid Interface Sci., 2019, 553, 746–757 CrossRef CAS PubMed.
- K. Hyun, M. Wilhelm, C. O. Klein, K. S. Cho, J. G. Nam, K. H. Ahn, S. J. Lee, R. H. Ewoldt and G. H. McKinley, Prog. Polym. Sci., 2011, 36, 1697–1753 CrossRef CAS.
- P. J. Blatz, S. C. Sharda and N. W. Tschoegl, Trans. Soc. Rheol., 1974, 18, 145–161 CAS.
- R. D. Groot, A. Bot and W. G. M. Agterof, J. Chem. Phys., 1996, 104, 9202–9219 CrossRef CAS.
- C. Joly-Duhamel, D. Hellio, A. Ajdari and M. Djabourov, Langmuir, 2002, 18, 7158–7166 CrossRef CAS.
- Y. Li, A. Asadi, M. R. Monroe and E. P. Douglas, Mater. Sci. Eng., C, 2009, 29, 1643–1649 CrossRef CAS.
- K. Chen and S. Vyazovkin, Macromol. Biosci., 2009, 9, 383–392 CrossRef CAS PubMed.
- M. A. da Silva, J. Kang, T. T. T. Bui, L. M. B. da Silva, J. Burn, J. L. Keddie and C. A. Dreiss, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 1850–1858 CrossRef CAS.
- S. Santinath Singh, V. K. Aswal and H. B. Bohidar, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 62 CrossRef CAS PubMed.
- W. Burchard, Physical networks: polymers and gels, Springer Science & Business Media, 1990 Search PubMed.
- I. Pezron, M. Djabourov and J. Leblond, Polymer, 1991, 32, 3201–3210 CrossRef CAS.
- G. J. Donley, M. Bantawa and E. Del Gado, J. Rheol., 2022, 66, 1287–1304 CrossRef CAS.
- E. Sarmiento-Gomez, I. Santamaría-Holek and R. Castillo, J. Phys. Chem. B, 2014, 118, 1146–1158 CrossRef CAS PubMed.
- F. Cardinaux, H. Bissig, P. Schurtenberger and F. Scheffold, Food Colloids, Royal Society of Chemistry, Cambridge, 2007, pp. 319–326 Search PubMed.
- B. Maciel, C. Oelschlaeger and N. Willenbacher, Colloid Polym. Sci., 2020, 298, 791–801 CrossRef CAS.
- G. H. Koenderink, M. Atakhorrami, F. C. MacKintosh and C. F. Schmidt, Phys. Rev. Lett., 2006, 96, 138307 CrossRef CAS PubMed.
- R. F. López-Santiago, J. Delgado and R. Castillo, J. Colloid Interface Sci., 2022, 626, 1015–1027 CrossRef PubMed.
- E. Sarmiento-Gomez, D. Lopez-Diaz and R. Castillo, J. Phys. Chem. B, 2010, 114, 12193–12202 CrossRef CAS PubMed.
- J. Galvan-Miyoshi, J. Delgado and R. Castillo, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 26, 369–377 CrossRef CAS PubMed.
- R. Granek, Langmuir, 1994, 10, 1627–1629 CrossRef CAS.
- J. Zhu and L. J. Kaufman, Biophys. J., 2014, 106, 1822–1831 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01682j |
| This journal is © The Royal Society of Chemistry 2024 |