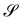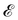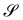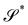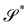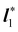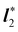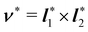DOI:
10.1039/D3SM01123B
(Paper)
Soft Matter, 2024,
20, 144-151
Pure measures of bending for soft plates
Received
25th August 2023
, Accepted 8th November 2023
First published on 14th November 2023
Abstract
This paper, originally motivated by a question raised by Wood and Hanna [Soft Matter, 2019, 15, 2411], shows that pure measures of bending for soft plates can be defined by introducing the class of bending-neutral deformations, which represent finite incremental changes in the plate's shape that do not induce any additional bending. This class of deformations is subject to a geometric compatibility condition, which is fully characterized. A tensorial pure measure of bending, which is invariant under bending-neutral deformations, is described in detail. As shown by an illustrative class of examples, the general notion of a pure measure of bending could be useful in formulating direct theories for soft plates, where stretching and bending energies are treated separately.
1 Introduction
It has been remarked that a pure measure of bending for extensible rods cannot be provided by the curvature of its centerline, as this can easily been shown to be affected by a superimposed dilation.1 Actually, within the nonlinear theory of extensible elastic rods, this issue has long be known, at least since the work of Antman2 and others who soon followed in his footsteps.3,4 It also has consequences on the choice of the appropriate form of the bending component of the strain energy, when in the direct approach one wishes to separate it neatly from the stretching component.
This was indeed the criterion advocated in ref. 2 for a planar extensible elastica: if ϑ denotes the centerline's deflection angle (relative to a fixed direction in the plane) of a naturally straight rod, the appropriate quadratic bending energy independent of stretching would be proportional to (∂xϑ)2, and not (∂sϑ)2, where x and s denote the arc-length coordinate in the reference and present configurations, respectively. As also remarked in ref. 2, a theory measuring the bending energy of an extensible rod by (∂sϑ)2, such as that proposed in ref. 5, would generally be more complicated.†
Other attempts to derive the balance equations for an extensible elastic rod have been based on Biot's nominal strain tensor8 as proposed in ref. 6 and 7 (also see ref. 9 and 10); they corroborated the approach purported in ref. 2. A similar corroboration was provided by ref. 11, which followed yet another avenue, designed according to the canons of modern continuum mechanics.
Similarly, for a plate whose planar midsurface S in the reference configuration gets deformed into the surface 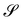 embedded in three-dimensional space, the invariants of the curvature tensor ∇sν, where ν is the outer unit normal to
embedded in three-dimensional space, the invariants of the curvature tensor ∇sν, where ν is the outer unit normal to 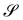 and ∇s denotes the surface gradient, cannot serve as pure measures of bending, as also neatly illustrated in ref. 12.
and ∇s denotes the surface gradient, cannot serve as pure measures of bending, as also neatly illustrated in ref. 12.
In analogy with the theory of stretchable rods, proposals for the bending energy of plates and shells (i.e., plates curved in their natural state) have been put forward that are not affected by one or another form of stretching. The approaches taken to achieve this goal are disparate, as are the conclusions reached; controversies abound, especially for shells, which I deliberately leave out of the scope of this paper.
In an alternative approach to geometric elasticity as formulated in ref. 13, a theory for deformable, geometrically incompatible sheets was derived in ref. 7 from a three-dimensional model phrased in terms of Biot's strain measures. The outcome differ from that in ref. 13, also in the rod-limit case, where the alternative energy is closer to Antman's. The theory of ref. 7 has been applied to a soft matter system in ref. 14; it effectively employs a measure of bending for plates that has a distant antecedent in ref. 15.
More recently, a dimension reduction method following the general lines proposed in ref. 16–19 was applied in ref. 20 to a three-dimensional isotropic quadratic strain energy formulated in terms of Biot's strain tensor to justify a model for shells.21 In particular, in the limiting case of plates, the one that concerns us here, two two-dimensional bending measures arose naturally from the method employed in ref. 20, one of these measures rmains invariant under arbitrary superimposed stretchings, and the other remains invariant only under superimposed dilations, both reducing to Antman's measure in the rod-limit.
The questions addressed in this paper will be of a pure kinematic nature. First, we need to identify a criterion of bending-neutrality for soft (highly deformable) plates: we must single out the incremental deformations that change the shape of 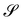 , but do not introduce any further bending. Thus, pure measures of bending will be defined as the ones invariant under bending-neutral deformations. I shall focus on one isotropic such measure, A, tensorial in character, alongside with its scalar invariants and contrast them with both similar and dissimilar measures from the literature. It will be shown that A reduces to Antman's measure for extensible rods.
, but do not introduce any further bending. Thus, pure measures of bending will be defined as the ones invariant under bending-neutral deformations. I shall focus on one isotropic such measure, A, tensorial in character, alongside with its scalar invariants and contrast them with both similar and dissimilar measures from the literature. It will be shown that A reduces to Antman's measure for extensible rods.
Identifying the pure measure of bending appropriate for a class of materials should prelude to a proposal for a direct theory of plates for which stretching and bending modes are kept separate from one another.
This paper is organized as follows. In Section 2, we define the class of bending-neutral deformations and present an isotropic measure of pure bending associated with them. Section 3 is devoted to the compatibility condition that a bending-neutral deformation must obey; we shall see that this class contains both pure tangential stretching deformations and planar drill rotations, characterized separately in ref. 22 and 23. Finally, in Section 4, we summarize the conclusions of this study and comment briefly about its possible extensions.
2 Bending-neutral deformations
Consider a surface S lying on the (x1,x2) plane of a Cartesian frame (e1, e2, e3), so that e3 is one of its unit normals. Let x denote the position vector in S and let y be the deformation that maps S onto 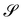 in three-dimensional Euclidean space
in three-dimensional Euclidean space ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) . We shall assume that y is at least of class C2 and we shall denote by ν the unit normal to
. We shall assume that y is at least of class C2 and we shall denote by ν the unit normal to 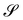 oriented coherently with the orientation of e3 (see Fig. 1).
oriented coherently with the orientation of e3 (see Fig. 1).
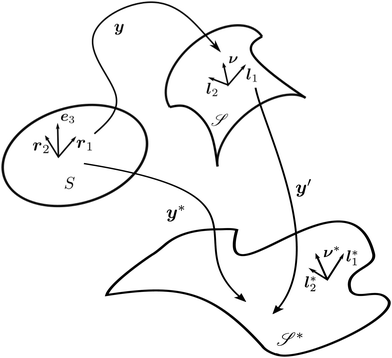 |
| | Fig. 1 A flat surface S in the (x1, x2) plane of a fixed Cartesian frame (e1, e2, e3) is deformed by the mapping y into a smooth surface 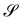 embedded in three-dimensional Euclidean space embedded in three-dimensional Euclidean space 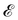 . The unit vectors (r1, r2) are the right principal directions of stretching in the reference configuration, while (l1, l2) are the left principal directions of stretching in the present configuration; e3 is the outer unit normal to S, while ν is the outer unit normal to . The unit vectors (r1, r2) are the right principal directions of stretching in the reference configuration, while (l1, l2) are the left principal directions of stretching in the present configuration; e3 is the outer unit normal to S, while ν is the outer unit normal to 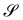 ; they are oriented so that e3 = r1 × r2 and ν = l1 × l2, respectively. Surface ; they are oriented so that e3 = r1 × r2 and ν = l1 × l2, respectively. Surface 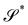 is obtained by combining y with the incremental deformation y′, so that y* = y′ ∘ y. The outer unit normal to is obtained by combining y with the incremental deformation y′, so that y* = y′ ∘ y. The outer unit normal to 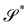 is ν* and the left principal directions of stretching associated with y* are is ν* and the left principal directions of stretching associated with y* are 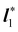 and and 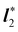 , with , with 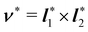 . . | |
Extending to the present geometric setting results well-known from three-dimensional kinematics (see, e.g., ch. 6 of ref. 24), the deformation gradient ∇y can be represented as
| | | ∇y = λ1l1⊗r1 + λ2l2⊗r2, | (1) |
where ∇ denotes the gradient in
x, the positive scalars
λ1 and
λ2 are the
principal stretches and the unit vectors
ri,
li are the corresponding
right and
left principal directions of stretching. While
r1(
x) and
r2(
x) exist on the (
x1,
x2) plane for all
x ∈
S,
l1(
x) and
l2(
x) exist on the tangent plane to
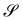
at
y(
x). The right and left Cauchy–Green tensors are correspondingly defined and represented by
| | | C := (∇y)T(∇y) = λ12r1⊗r1 + λ22r2⊗r2, | (2a) |
| | | B := (∇y)(∇y)T = λ12l1⊗l1 + λ22l2⊗l2. | (2b) |
I wish to introduce a bending-neutral deformation as an incremental (finite) deformation y′ that maps 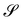 into a surface
into a surface 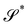 without further bending it. To make this notion precise, we first consider the composed deformation y* := y′ ∘ y, where y′ is a general, smooth (at least C2) mapping that changes
without further bending it. To make this notion precise, we first consider the composed deformation y* := y′ ∘ y, where y′ is a general, smooth (at least C2) mapping that changes 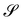 into
into 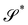 and is characterized by having
and is characterized by having
where
R′ belongs to the appropriate orthogonal group in three dimensions, SO(3), and
| | 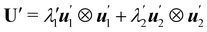 | (4) |
is a
stretching tensor with principal directions of stretching
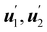
, tangent to
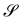
at
y(
x) and principal stretches
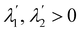
. The tensor
U′ is regarded as a (linear) mapping of the tangent plane to
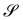
at
y(
x) into itself.
Eqn (3) is the form of polar decomposition fit to describe the deformation of material surfaces; it was established in ref. 25 within the general coordinate-free theory introduced in ref. 26, which will also be followed here (see also ref. 27). A tensor V′ that maps the tangent plane to 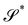 at y*(x) = y′(y(x)) into itself, can also be introduced via the following equation,
at y*(x) = y′(y(x)) into itself, can also be introduced via the following equation,
It follows from
(5) that
V′ possesses the same eigenvalues
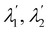
as
U′, while its eigenvectors are
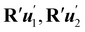
, which generally differ from the left principal directions of stretching
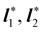
associated with
y* (and shown
Fig. 1). Using the chain rule,
| | 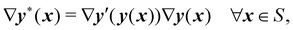 | (6) |
(3) and (5) imply that
| | 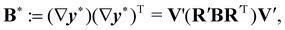 | (7) |
which shows that the eigenframes of
B* and
V′ coincide whenever
B and
U′ commute.
‡
It should also be noted that since y′ is defined on 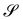 , its gradient ∇y′ featuring in (3) should be properly regarded as a surface gradient on
, its gradient ∇y′ featuring in (3) should be properly regarded as a surface gradient on 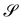 , ∇sy′, according to the definition given in ref. 26 (see also ref. 28).
, ∇sy′, according to the definition given in ref. 26 (see also ref. 28).
We say that y′ is a bending-neutral deformation if
where
R0 ∈ SO(3) is a
uniform rotation,
i.e., independent of position, and
Rν ∈ SO(
ν), where SO(
ν) is the group of rotations about the unit normal
ν. While
R0 is a global rigid motio
n,
Rν is a local
drill rotation. For
R′ as in
(8),
(3) represents an incremental deformation that entails local stretching of
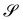
, described by
U′, possibly followed by a
twist distortion about
ν, described by
Rν, and an overall undistorting rotation
R0.
We shall discuss in Section 3 the compatibility condition that a bending-neutral deformation y′ must obey to exist, at least locally, on 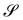 . Here, we only consider that this class of incremental deformations includes both pure stretching deformations, for which Rν is the identity, and pure drill rotations, for which U′ is the projection P(ν) := I − ν⊗ν on the plane orthogonal to ν.§ As shown in ref. 22 and 23, respectively, neither of these subclasses is empty.
. Here, we only consider that this class of incremental deformations includes both pure stretching deformations, for which Rν is the identity, and pure drill rotations, for which U′ is the projection P(ν) := I − ν⊗ν on the plane orthogonal to ν.§ As shown in ref. 22 and 23, respectively, neither of these subclasses is empty.
2.1 Pure measures of bending
We say that a deformation measure 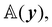 regarless of its nature (scalar or tensor), is a pure measure of bending if it obeys the following invariance condition,
regarless of its nature (scalar or tensor), is a pure measure of bending if it obeys the following invariance condition,| | 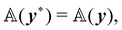 | (9) |
for all deformations y* := y′∘y, such that y′ is bending-neutral.¶
Since bending is intuitively associated with curvature, to flesh out this definition we first need to determine how ν*, the outer unit normal to 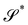 , is related to ν when y′ is a bending-neutral deformation (and then also how ∇ν* is related to ∇ν). To this end, we first recall that
, is related to ν when y′ is a bending-neutral deformation (and then also how ∇ν* is related to ∇ν). To this end, we first recall that
| | 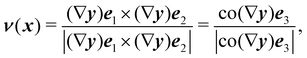 | (10) |
where co(·) denotes the cofactor of a tensor (according to the definition in Section 2.11 of ref.
24). Since for any two tensors,
L and
M, co(
LM) = co(
L)co(
M), by
(6) and (10), we have that
||| | 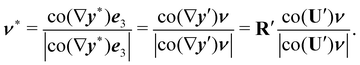 | (11) |
Now, if
y′ is a bending-neutral deformation, since from
(4)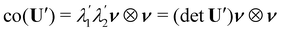
and
Rνν =
ν, we learn from
(11) and (8) that
Moreover, since ∇
R0 = 0, we see that
Thus, if we set
we readily see from
(13) that this is a pure (tensorial) measure of bending, as
| | 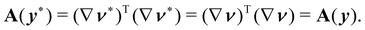 | (15) |
In the rest of the section, we shall focus on this measure. As defined in
(14),
A is a linear mapping of the plane hosting the reference configuration
S into itself, precisely as
C in
(2a). Similar to the latter tensor,
A is both symmetric and positive definite. According to our definition, its scalar invariants are pure measures of bending as well.
It is perhaps worth noting that the tensor Z(y) := (∇ν)(∇ν)T, similar in structure to B, which maps the plane tangent to 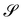 into itself, is not a pure measure of bending, although it has the same invariants as A: Z transforms as follows, Z(y*) = R0Z(y)RT0.
into itself, is not a pure measure of bending, although it has the same invariants as A: Z transforms as follows, Z(y*) = R0Z(y)RT0.
We denote by the curvature tensor of 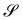 by ∇sν, for which we adopt a sign convention opposite to the one customary in differential geometry.** ∇sν is a symmetric tensor mapping the tangent plane to
by ∇sν, for which we adopt a sign convention opposite to the one customary in differential geometry.** ∇sν is a symmetric tensor mapping the tangent plane to  into itself; in its eigenframe, it is represented as
into itself; in its eigenframe, it is represented as
| | | ∇sν = κ1n1⊗n1 + κ2n2⊗n2, | (16) |
where
n1,
n2 are the principal directions of curvature of
and
κ1,
κ2 are the corresponding principal curvatures.
Using the chain rule,
| | | ∇ν(x) = ∇sν(y(x))∇y(x), | (17) |
and so it follows from
(14) that
A can also be written as
Here and in the following, for brevity, we drop the argument from
A(
y) and denote
A* :=
A(
y*).
An interesting interpretation for A and its invariance under bending-neutral deformations can be given starting from (18). This can indeed be seen as the referential representation for the third fundamental form of  (see, for example, p. 205 of ref. 32). Given two arbitrary vectors v1, v2 on S,
(see, for example, p. 205 of ref. 32). Given two arbitrary vectors v1, v2 on S,
| | 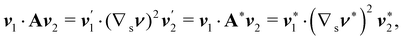 | (19) |
where
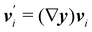
are vectors tangent to
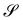
,
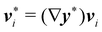
are vectors tangent to
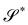
, and ∇
sν* is the curvature tensor of
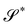
. Identity
(19) simply says that the third fundamental form is invariant under a bending-neutral deformation.
As pointed out in ref. 33, the tensorial deformation measure for shells considered in the works of Koiter,34 Sanders,31 and Budiansky30 can be given a coordinate-free expression, which in the case of plates reads simply as
This appears to be the referential representation of the second fundamental form of
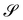
. Compared to
A,
K is not a pure measure of bending.
The linear invariant of A, trA (which is quadratic in the principal curvatures of 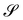 ), has already featured in the literature; it emerged as a strain energy density from a discretized model for membranes and plates35 and, more recently, also from a dimension reduction to plates.20 In the latter, the reduced strain energy density also involves the scalar invariants of the tensor
), has already featured in the literature; it emerged as a strain energy density from a discretized model for membranes and plates35 and, more recently, also from a dimension reduction to plates.20 In the latter, the reduced strain energy density also involves the scalar invariants of the tensor 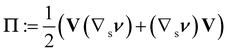 , where V is the stretching tensor of y in the present configuration, defined as the positive definite root of V2 = B. It is a simple exercise to show by example that neither Π nor its invariants are pure measures of bending according to the definition proposed in this paper.
, where V is the stretching tensor of y in the present configuration, defined as the positive definite root of V2 = B. It is a simple exercise to show by example that neither Π nor its invariants are pure measures of bending according to the definition proposed in this paper.
Finally, the shell model advanced in ref. 36 employs strains that reduce to the eigenvalues of A in the case of plates, under the further hypothesis that V and ∇sν commute, a hypothesis implicit in the symmetric class of deformations adopted in ref. 36.††
2.2 Impure measures of bending
It is interesting to link the invariants of A to other invariant, but impure measures of bending, namely, the mean curvature H and the Gaussian curvature K of 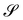 , defined as
, defined as| | 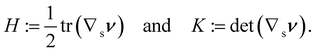 | (21) |
We begin by computing tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A. It readily follows from (18) that
A. It readily follows from (18) that
| | tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = tr(B(∇sν)2) = 2H A = tr(B(∇sν)2) = 2H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) tr(B∇sν) − K tr(B∇sν) − K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tr tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B, B, | (22) |
where the last equality follows from an identity proven in ref.
37 (see their
eqn (14)).
To obtain det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, we start from tr
A, we start from tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2, which by (18) also reads as
A2, which by (18) also reads as
| | tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 = (∇sν)2B·B(∇sν)2, A2 = (∇sν)2B·B(∇sν)2, | (23) |
where · denotes the inner product of tensors.
‡‡ Letting
B be represented as
| | | B = B11n1⊗n1 + B12(n1⊗n2 + n2⊗n1) + B22n2⊗n2 | (24) |
in the eigenframe of ∇
sν in
(16), we easily obtain from
(23) that
| | tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 = κ14B112 + κ24B222+ 2κ12κ22B122 = (tr A2 = κ14B112 + κ24B222+ 2κ12κ22B122 = (tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A)2 − 2K2det A)2 − 2K2det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B, B, | (25) |
which on applying the Cayley–Hamilton theorem to
A implies that
| | det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = K2det A = K2det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B = K2det B = K2det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C. C. | (26) |
Thus,
eqn (22) and (26) show how pure scalar measures of bending may result from combining measures of stretching and impure measures of bending.
In the special case of an isometry, for which C = I − e3⊗e3 and B = P(ν),
| | tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = κ12 + κ22 = 2C and det A = κ12 + κ22 = 2C and det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = (κ1κ2)2 = K2, A = (κ1κ2)2 = K2, | (27) |
where
C is the Casorati total curvature.
38
2.3 Pure rod-bending measure
To connect A to Antman's measure of pure bending for rods,2 we consider a class of deformations of S that produce a cylindrical surface, as shown in Fig. 2. More precisely, we take| | | y(x1,x2) = y1(x1)e1 + x2e2 + y3(x1)e3, | (28) |
where y1 and y3 are scalar functions of class C2. From (28) we easily arrive at| | 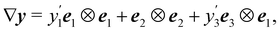 | (29) |
where a prime ′ denotes differentiation with respect to x1. Thus, by applying (10), we see that| | ν = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑe3 − sin ϑe3 − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑe1 ϑe1 | (30) |
With this choice of angle ϑ, the unit tangent t to the curve in space that sweeps 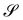 along the generatrix e2 is represented as
along the generatrix e2 is represented as| | 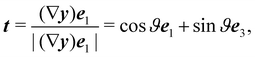 | (31) |
and it follows from (30) that| | 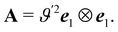 | (32) |
The only non-vanishing invariant of A is 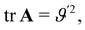 which, to within an elastic modulus, is precisely Antamn's bending energy for an extensible elastic rod.
which, to within an elastic modulus, is precisely Antamn's bending energy for an extensible elastic rod.
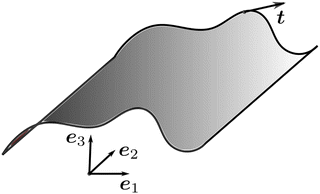 |
| | Fig. 2 Cylindrical surface produced by the deformation y described in (28). | |
2.4 An illustration: axisymmetric deformations
To illustrate the theory proposed in this paper, we consider now the general class of axisymmetric deformations of a disk of radius R. The geometric setting is shown in Fig. 3, where S is the undeformed disk and 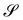 is an axisymmetric nightcap generated by the deformation y parametrized as
is an axisymmetric nightcap generated by the deformation y parametrized as| | | y(s,φ) = r(s)er + z(s)e3, | (33) |
where (s,φ), with 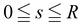 and
and 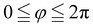 , are polar coordinates in the plane (x1,x2), so that x1 = s
, are polar coordinates in the plane (x1,x2), so that x1 = s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ and x2 = s
φ and x2 = s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, er is the radial unit vector and eφ the azimuthal unit vector, r(s) and z(s) are smooth functions representing radial and vertical components of the image under y of the generic point x = ser of S.
φ, er is the radial unit vector and eφ the azimuthal unit vector, r(s) and z(s) are smooth functions representing radial and vertical components of the image under y of the generic point x = ser of S.
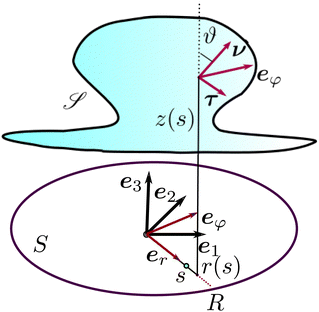 |
| | Fig. 3 Sketch of an axisymmetric nightcap obtained by deforming a flat disk S of radius R via the mapping y described using (33). The unit vector ν is the outward normal to obtained by deforming a flat disk S of radius R via the mapping y described using (33). The unit vector ν is the outward normal to  , while τ is the tangent unit vector along the meridians of , while τ is the tangent unit vector along the meridians of  , so that (τ, eφ, ν) is a mobile frame oriented like the fixed frame (e1,e2,e3). The angle ϑ, defined in (44), designates the relative inclination of the normals ν and e3, to , so that (τ, eφ, ν) is a mobile frame oriented like the fixed frame (e1,e2,e3). The angle ϑ, defined in (44), designates the relative inclination of the normals ν and e3, to  and S, respectively. and S, respectively. | |
Let x(t) = s(t)er(φ(t)) be a generic curve on S parameterized in t. Denoting by a superimposed dot differentiation with respect to t, we readily obtain that
| | 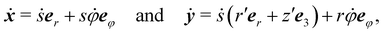 | (34) |
where a prime ′ denotes differentiation with respect to
s and
ẏ is the tangent to the curve
y(
t) resulting from composing
y with
x(
t). The deformation gradient ∇
y at a point
x0 must satisfy the identity
ẏ = (∇
y)
ẋ for every curve
x(
t) through
x0. The following formula is then an easy consequence of
(34),
| | 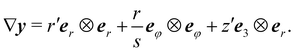 | (35) |
It follows from
(35) that
| | | C = (∇y)T(∇y) = λ12er⊗er + λ22e3⊗e3, | (36) |
where
| | 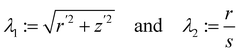 | (37) |
are the principal stretches of
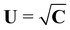
.
If the top of the nightcap in Fig. 3 is regular, that is, with a well defined tangent plane, symmetry requires the latter to be parallel to the (x1, x2) plane, and so ∇y must vanish there. From (35), this implies that both r′ and z′ must vanish at s = 0 and so does the limiting value of r/s, meaning that λ1(0) = λ2(0) = 0. This, in particular, says that the class of axisymmetric deformations y of S cannot accommodate the constraint of inextensibility, λ1λ2 ≡ 1, unless y is singular at the origin.
A simple computation yields
| | 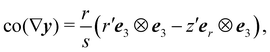 | (38) |
which using
(10) leads us to
| | 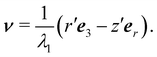 | (39) |
Defining by
τ :=
eφ ×
ν a tangent unit vector to
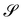
oriented along its meridians so that the mobile frame (
τ,
eφ,
ν) is oriented like (
e1,
e2,
e3), we can write
| | 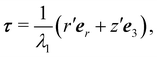 | (40) |
and
(35) becomes
| | | ∇y = λ1τ⊗er + λ2eφ⊗eφ. | (41) |
From the latter, we easily compute
| | | B = (∇y)(∇y)T = λ12τ⊗τ + λ22eφ⊗eφ | (42) |
and
| | 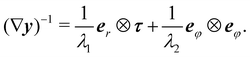 | (43) |
By introducing the angle
| | 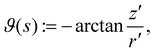 | (44) |
we give a more compact representation of
ν and
τ,
| | ν = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑe3 + sin ϑe3 + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑer, τ = cos ϑer, τ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑer − sin ϑer − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑe3. ϑe3. | (45) |
As a consequence of
(45) and (41), we can write
| | 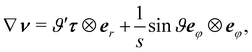 | (46) |
from which it follows that the pure measure of bending
A in
(14) acquires here the explicit representation
| | 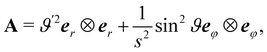 | (47) |
so that a quadratic pure bending invariant would be
| | 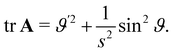 | (48) |
For a comparison, we also compute the quadratic invariants of the curvature tensor ∇sν. By (17), (43), and (46), we obtain that
| | 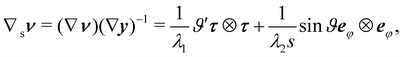 | (49) |
which, compared with
(16), yields
| | 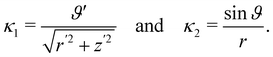 | (50) |
The quadratic impure bending measures would then read as
| | 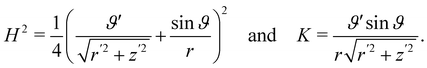 | (51) |
By combining together
(42),
(47), and the expression for
K in
(51), one easily sees that identity
(26) is indeed satisfied.
A simple direct theory of isotropic soft plates developed according to the principles purported in this paper would be based on the following strain energy density (per unit reference area),
| | 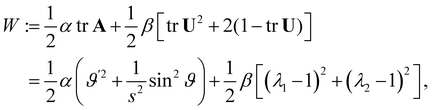 | (52) |
where
α and
β are positive elastic moduli. A similar (but not identical) expression for
W amenable to a formal Hamiltonian treatment was proposed for axisymmetric shells
39 (see also p. 642 of ref.
40). The strain energy functional resulting from
W is then
| | 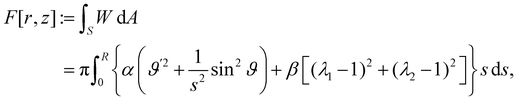 | (53) |
subject to appropriate boundary conditions on the edge of
S.
By contrast, a quadratic theory building on the impure measures in (51), would be based on an Helfrich-type functional,
| | 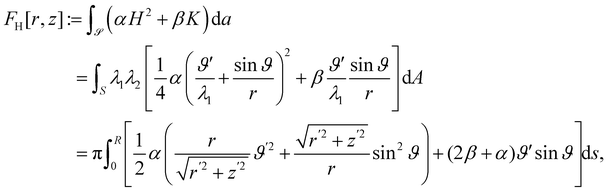 | (54) |
where the area element d
a on the present shape
has been related to the area element d
A =
sd
sd
φ on the reference shape
S through the equation d
a =
λ1λ2d
A.
Two features deserve notice in (54). First, as appropriate for a liquid membrane, FH is formulated as an integral on the present configuration 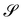 . Second, the Gaussian curvature K reveals itself as a null Lagrangian, as its contribution to the total strain energy depends only on the boundary value of ϑ,
. Second, the Gaussian curvature K reveals itself as a null Lagrangian, as its contribution to the total strain energy depends only on the boundary value of ϑ,
| | 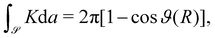 | (55) |
thus becoming an effective edge energy.
§§
3 Bending-neutrality compatibility
For y′ to be a bending-neutral deformation, neither U′ nor Rν can be arbitrary. They must be subject to a compatibility condition, which we shall discuss in some detail here along with its solutions. The special case where U′ = P(ν) has been considered and fully solved in ref. 23.
The condition of compatibility arises from the requirement that the curvature tensor ∇sν* of 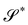 be symmetric, as it is expected to be.23 By writing (17) for ν* (and y*) instead of ν (and y), we have that
be symmetric, as it is expected to be.23 By writing (17) for ν* (and y*) instead of ν (and y), we have that
On the other hand, using
(12) and (13), we can also write
| | | ∇ν* = R0∇ν = R0(∇sν)(∇y), | (57) |
which, combined with
(56), leads us to
| | | ∇sν* = R0(∇sν)(U′)−1RTνRT0, | (58) |
once use is also made of
(6),
(3), and
(8). It follows from
(58) that ∇
sν* is symmetric if and only if (∇
sν)(
U′)
−1RTν is so. This latter condition will be written in the following equivalent way,
| | | ∇sν = Rν(U′)−1(∇sν)RνU′. | (59) |
Tensors on both sides of
(59) act on the local tangent plane of
. It is clear that every solution
U′ of
(59) is defined within a multiplicative surface dilation,
λ′
P(
ν), with arbitrary
λ′ > 0.
Two special classes of solutions of (59) deserve notice. They are better illustrated by using the classical Euler–Rodriguez formula to represent SO(ν) (see also ref. 50 for an updated account),
| | R(α) := I + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αW(ν) − (1 − cos αW(ν) − (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)P(ν), α ∈ [−π,π], α)P(ν), α ∈ [−π,π], | (60) |
where
W(
ν) is the skew-symmetric tensor associated with
ν, so that
W(
ν)
u =
ν ×
u, for all vectors
u.
First, if either Rν = R(0) = I or Rν = R(π) = −I + 2ν⊗ν, the latter acting as −I on the plane tangent to 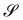 , then (59) reduces to the requirement that U′ commute with ∇sν, which just amounts to say that ∇sν and U′ must have the same eigenframe.22
, then (59) reduces to the requirement that U′ commute with ∇sν, which just amounts to say that ∇sν and U′ must have the same eigenframe.22
Second, for U′ = λ′P(ν), with λ′ > 0, (59) becomes
Taking the trace of both sides of
(61), and using both
(16) and (60), we arrive at
| | 2H(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2α) = 0, 2α) = 0, | (62) |
which for 2
H = tr(∇
sν) ≠ 0 reduces to either
α = 0 or
α = π, delivering again the first special solution of
(59) considered above. For
H = 0, which is the case of minimal surfaces,
(62) is identically satisfied and direct inspection of
(61) with the aid of
(60) shows that it is solved by all
Rν ∈ SO(
ν). For
λ′ = 1, this result was already proved in ref.
23.
¶¶
To find the general solution of (59), we represent U′ in (4) in the eigenframe of ∇sν in (16), by writing
| | 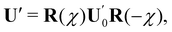 | (63) |
where
R(−
χ) =
R(
χ)
T,
| | 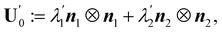 | (64) |
and
χ is the angle that
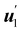
makes with
n1 (the same as the angle that
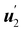
makes with
n2). By using these representation formulae and
(60), we finally obtain
(59) in the following expanded form,
| | 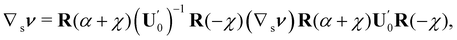 | (65) |
which, for given
κ1,
κ2, is meant to be an equation for
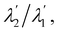 α
α, and
χ.
Actually, it is not difficult to show that (65) amounts to four scalar equations, whose solution is
| | 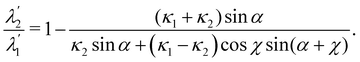 | (66) |
Requiring the ratio
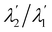
as delivered by
(66) to be positive, with little labour we arrive at the inequalities
where
αm(
χ) := min{
α1,
α2} and
αM(
χ) := max{
α1,
α2}, with
| | 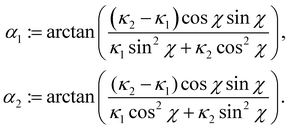 | (68) |
Thus, for a given
χ ∈ [−π,π] and
α ∈ [
αm,
αM],
U′ is determined using
(63) up to a surface dilation
λ′
P(
ν); in general, there exists a whole three-dimensional set of solutions to
(59), parameterized by (
χ,
α,
λ′). A singular case arises at umbilical points of
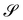
, where
κ1 =
κ2. There,
(66) would be incompatible for any
α∉ {0,π} since it requires
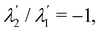
whereas, from
(68),
αm =
αM = 0, so that the standard solution
U′ =
λ′
P(
ν),
Rν =
I is recovered by continuity.
A particular two-dimensional family of solutions deserves attention. It is obtained from (66) by setting χ = 0, under the assumption that α ∉ {0,π} (an equivalent family would be obtained by setting 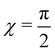 ). If
). If 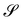 is a hyperbolic surface, that is, if K < 0, (66) readily gives
is a hyperbolic surface, that is, if K < 0, (66) readily gives
| | 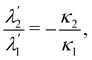 | (69) |
while
α is arbitrary. What makes this solution special is the curvature tensor of the surface
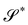
delivered by
y′. Letting
R0 =
I, with no prejudice to generality, we obtain from
(58) that
| | 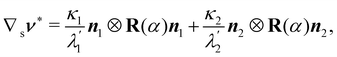 | (70) |
whence, also from
(69), it follows that
| | 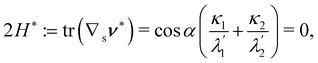 | (71a) |
| | 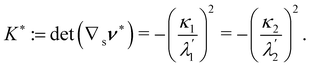 | (71b) |
In particular,
(71a) implies that
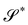
is a minimal surface.
Clearly, this conclusion relies on the very existence of 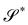 , which would be guaranteed, at least locally, if the surface tensor field defined on
, which would be guaranteed, at least locally, if the surface tensor field defined on 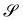 as
as
were a surface gradient. This is an integrability requirement that poses restrictions on both
λ′ and
α, which remain the only unknown scalar surface fields, once
(69) is enforced. The study of these restrictions goes beyond the scope of this paper and will be the subject of a future study, as will also be the integrability of
S for the general class of incremental deformations that obey
(66).
We have considered two distinct conditions that must be met for y′ to be a bending-neutral deformation, one compatibility condition and one integrability condition. Whenever 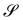 is such that either one or the other condition is not met, any incremental y′ will necessarily bring additional bending.
is such that either one or the other condition is not met, any incremental y′ will necessarily bring additional bending.
4 Conclusions
The primary objective of this paper is to answer a question posed by Wood and Hanna:1 “How do we wish to define a measure of bending, and by extension a bending energy and the concept of pure stretching deformation, for a thin structure”?
We (the patient reader and I) caracolled our way toward a possible answer through the notion of bending-neutral deformation, an incremental deformation that does not affect bending, but it is more than a pure stretching as it may include normal twisting.
Quite naturally, a pure measure of bending was then introduced as a deformation measure unaffected by bending-neutral deformations. An explicit, tensorial example of such a measure was given and contrasted against other measures known for plates.
Common wisdom suggests that plates (and shells, for that matter) are rather unresponsive to twists that induce local drill rotations.22 This observation may hold true for conventional, hard plates, but it may not apply to soft, polymeric plates, especially those with an activable internal structure, such as nematic elastomers (described in the landmark textbook by Warner and Terentjev54).
These latter material surfaces are anisotropic, as the nematic director field n on 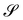 breaks the rotational symmetry about the normal ν. It might be interesting to find anisotropic pure measure of bending fit for these systems; they might be suggestive of direct theories where stretching and bending energy contents are kept separate, oblivious to whether they can be derived through dimension reduction of established three-dimensional strain energies or not.||||
breaks the rotational symmetry about the normal ν. It might be interesting to find anisotropic pure measure of bending fit for these systems; they might be suggestive of direct theories where stretching and bending energy contents are kept separate, oblivious to whether they can be derived through dimension reduction of established three-dimensional strain energies or not.||||
Whether the answer presented in this paper to the opening question is satisfactory or not is not for me to tell. In the second part of the paper, my interest shifts toward the legitimacy of bending-neutral deformations. They have been characterized by the fulfillment of a necessary kinematic compatibility condition, which generates a three-dimensional set of solutions. Of course, these only represent admissible bending-neutral deformations; which ones do actually exist for a given surface 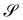 , is decided, at least locally, by the fulfillment of an integrability condition. The study of this condition and its solutions will be the subject of a future paper.
, is decided, at least locally, by the fulfillment of an integrability condition. The study of this condition and its solutions will be the subject of a future paper.
Conflicts of interest
There are no conflicts to declare.
References
- H. G. Wood and J. A. Hanna, Soft Matter, 2019, 15, 2411–2417 RSC.
- S. Antman, Quart. Appl. Math., 1968, 26, 35–47 CrossRef.
- E. Reissner, Z. Angew. Math. Phys., 1972, 23, 795–804 CrossRef.
- A. B. Whitman and C. N. DeSilva, J. Elast., 1974, 4, 265–280 CrossRef.
- I. Tadjbakhsh, Int. J. Eng. Sci., 1966, 4, 433–450 CrossRef.
- A. Magnusson, M. Ristinmaa and C. Ljung, Int. J. Sol. Struct., 2001, 38, 8441–8457 CrossRef.
- O. Oshri and H. Diamant, Phys. Rev. E, 2017, 95, 053003 CrossRef PubMed.
- M. A. Biot, Phil. Mag., 1939, 27, 468–489 Search PubMed.
- C. Truesdell, J. Rational Mech. Anal., 1952, 1, 125–300 Search PubMed.
-
M. A. Biot, Mechanics of Incremental Deformations, John Wiley & Sons, New York, 1965 Search PubMed.
- H. Irschik and J. Gerstmayr, Acta Mech., 2009, 206, 1–21 CrossRef.
- E. Vitral and J. A. Hanna, J. Elast., 2023, 153, 571–579 CrossRef.
- E. Efrati, E. Sharon and R. Kupferman, J. Mech. Phys. Solids, 2009, 57, 762–775 CrossRef.
- O. Oshri, S. Biswas and A. C. Balazs, Phys. Rev. E, 2019, 99, 033003 CrossRef CAS PubMed.
- S. N. Atluri, Comput. Struct., 1984, 18, 93–116 CrossRef.
- D. J. Steigmann, Int. J. Non-Linear Mech., 2007, 42, 233–240 CrossRef.
- D. J. Steigmann, Int. J. Eng. Sci., 2008, 46, 654–676 CrossRef.
- D. J. Steigmann, Int. J. Eng. Sci., 2012, 51, 216–232 CrossRef.
- D. J. Steigmann, J. Elast., 2013, 111, 91–107 CrossRef.
- E. Vitral and J. A. Hanna, J. Elast., 2023, 153, 581–598 CrossRef.
- E. Vitral and J. A. Hanna, Math. Mech. Solids, 2022, 27, 462–473 CrossRef.
- M. L. Szwabowicz, J. Elast., 2008, 92, 255–275 CrossRef.
- M. Mohammadi Saem, P. Lewintan and P. Neff, Proc. R. Soc. London, Ser. A, 2021, 477, 20210158 Search PubMed.
-
M. E. Gurtin, E. Fried and L. Anand, The Mechanics and Thermodynamics of Continua, Cambridge University Press, Cambridge, 2010 Search PubMed.
- C.-S. Man and H. Cohen, J. Elast., 1986, 16, 97–104 CrossRef.
- M. E. Gurtin and A. I. Murdoch, Arch. Rational Mech. Anal., 1975, 57, 291–323 CrossRef.
- W. Pietraszkiewicz, M. Szwabowicz and C. Vallée, Int. J. Non-Linear Mech., 2008, 43, 579–587 CrossRef.
- A. I. Murdoch, Glasgow Math. J., 1990, 32, 299–307 CrossRef.
-
C.-S. Man and H. Cohen, Proceedings of the Tenth Canadian Congress of Applied Mechanics, London, Ontario, Canada, 1985, pp. A81–A82 Search PubMed.
- B. Budiansky, J. Appl. Mech., 1968, 35, 393–401 CrossRef.
- J. L. Sanders, Quart. Appl. Math., 1963, 21, 21–36 CrossRef.
-
P. Grinfeld, Introduction to Tensor Analysis and the Calculus of Moving Surfaces, Springer, New York, 2013 Search PubMed.
- A. Acharya, Int. J. Sol. Struct., 2000, 37, 5517–5528 CrossRef.
-
W. T. Koiter, in Proc. IUTAM Symposium on the Theory of Thin Elastic Shells, ed. W. T. Koiter, Delft, North-Holland, Amsterdam, 1960, pp. 12–33 Search PubMed.
- H. S. Seung and D. R. Nelson, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 1005–1018 CrossRef PubMed.
- S. Knoche and J. Kierfeld, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 046608 CrossRef.
- O. Ozenda and E. G. Virga, J. Elast., 2021, 143, 359–384 CrossRef.
- F. Casorati, Acta Math., 1890, 14, 95–110 CrossRef.
- H. Cohen and F. Pastrone, Int. J. Non-Linear Mech., 1986, 21, 37–50 CrossRef.
-
P. Villaggio, Mathematical Models for elastic structures, Cambridge University Press, Cambridge, 1997 Search PubMed.
- D. H. Boal and M. Rao, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 3037–3045 CrossRef CAS PubMed.
- R. Capovilla, J. Guven and J. A. Santiago, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 021607 CrossRef CAS PubMed.
- Z. C. Tu, J. Chem. Phys., 2010, 132, 084111 CrossRef CAS PubMed.
- Z. Tu, J. Geom. Symmetry Phys., 2011, 24, 45–75 Search PubMed.
- Z. Tu and Z. Ou-Yang, Adv. Colloid Interface Sci., 2014, 208, 66–75 CrossRef CAS.
- X. Zhou, Int. J. Non-Linear Mech., 2018, 106, 25–28 CrossRef.
- B. Palmer and A. Pámpano, Proc. R. Soc. Edin. A, 2021, 151, 1225–1246 CrossRef.
- B. Palmer and A. Pámpano, J. Nonlinear Sci., 2021, 31, 23 CrossRef.
- B. Palmer and A. Pámpano, Calc. Var., 2022, 61, 79 CrossRef.
- B. Palais, R. Palais and S. Rodi, Am. Math. Mon., 2009, 116, 892–909 CrossRef.
- K. Abe and J. Erbacher, Math. Ann., 1975, 215, 197–201 CrossRef.
- D. A. Hoffman and R. Osserman, J. Diff. Geom., 1983, 18, 733–754 Search PubMed.
- J.-H. Eschenburg, B. Kruglikov, V. S. Matveev and R. Tribuzy, Differ. Geom. Appl., 2010, 28, 228–235 CrossRef.
-
M. Warner and E. M. Terentjev, Liquid Crystal Elastomers, Oxford University Press, New York, 2003, vol. 120 Search PubMed.
- O. Ozenda, A. M. Sonnet and E. G. Virga, Soft Matter, 2020, 16, 8877–8892 RSC.
- H. Singh and E. G. Virga, J. Elast., 2023, 153, 613–634 CrossRef PubMed.
- H. Singh and E. G. Virga, J. Elast., 2023, 154, 531–553 CrossRef.
- A. M. Sonnet and E. G. Virga, J. Elast., 2022 DOI:10.1007/s10659-022-09959-4.
Footnotes |
| † Indeed the major advantage of Antman's proposed constitutive law seems to be its simplicity, as witnessed by the neat analysis that ensued in ref. 2. |
‡ This follows easily from applying both sides of (7) to the eigenvectors 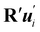 of V′. of V′. |
| § I represents the identity tensor in three space dimensions. |
¶ A different definition for a natural measure of bending was proposed in ref. 29 in the case of infinitesimal incremental deformations of 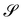 . . |
| || Use is also made here of the fact that co(R) = R, for any rotation R ∈ SO(3). |
** Here we follow ref. 30 and 31 in the desire to represent the curvature tensor of a sphere of radius R as 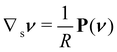 . . |
| †† This hypothesis, however, fails to make Π a pure measure of bending for plates. |
| ‡‡ For generic tensors L and M, L·M := tr(LTM). |
| §§ The interplay between FH and edge strain energies has been explored in a series of papers, some of which are recent.41–49 |
| ¶¶ As appropriately remarked,23 the same result had also been proved, albeit with different methods, in the differential geometry literature,51–53 but it was unknown to plates and shells practitioners. |
| |||| The role of bending energy in the theory for nematic elastomer plates is highlighted in the literature55 and applications have also been presented.56–58 |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
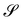 embedded in three-dimensional space, the invariants of the curvature tensor ∇sν, where ν is the outer unit normal to
embedded in three-dimensional space, the invariants of the curvature tensor ∇sν, where ν is the outer unit normal to 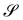 and ∇s denotes the surface gradient, cannot serve as pure measures of bending, as also neatly illustrated in ref. 12.
and ∇s denotes the surface gradient, cannot serve as pure measures of bending, as also neatly illustrated in ref. 12.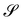 , but do not introduce any further bending. Thus, pure measures of bending will be defined as the ones invariant under bending-neutral deformations. I shall focus on one isotropic such measure, A, tensorial in character, alongside with its scalar invariants and contrast them with both similar and dissimilar measures from the literature. It will be shown that A reduces to Antman's measure for extensible rods.
, but do not introduce any further bending. Thus, pure measures of bending will be defined as the ones invariant under bending-neutral deformations. I shall focus on one isotropic such measure, A, tensorial in character, alongside with its scalar invariants and contrast them with both similar and dissimilar measures from the literature. It will be shown that A reduces to Antman's measure for extensible rods.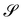 in three-dimensional Euclidean space
in three-dimensional Euclidean space ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) . We shall assume that y is at least of class C2 and we shall denote by ν the unit normal to
. We shall assume that y is at least of class C2 and we shall denote by ν the unit normal to  oriented coherently with the orientation of e3 (see Fig. 1).
oriented coherently with the orientation of e3 (see Fig. 1).
 at y(x). The right and left Cauchy–Green tensors are correspondingly defined and represented by
at y(x). The right and left Cauchy–Green tensors are correspondingly defined and represented by into a surface
into a surface  without further bending it. To make this notion precise, we first consider the composed deformation y* := y′ ∘ y, where y′ is a general, smooth (at least C2) mapping that changes
without further bending it. To make this notion precise, we first consider the composed deformation y* := y′ ∘ y, where y′ is a general, smooth (at least C2) mapping that changes 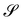 into
into 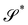 and is characterized by having
and is characterized by having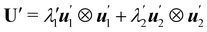
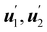 , tangent to
, tangent to 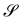 at y(x) and principal stretches
at y(x) and principal stretches 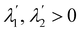 . The tensor U′ is regarded as a (linear) mapping of the tangent plane to
. The tensor U′ is regarded as a (linear) mapping of the tangent plane to 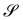 at y(x) into itself.
at y(x) into itself.
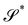 at y*(x) = y′(y(x)) into itself, can also be introduced via the following equation,
at y*(x) = y′(y(x)) into itself, can also be introduced via the following equation,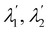 as U′, while its eigenvectors are
as U′, while its eigenvectors are 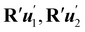 , which generally differ from the left principal directions of stretching
, which generally differ from the left principal directions of stretching 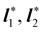 associated with y* (and shown Fig. 1). Using the chain rule,
associated with y* (and shown Fig. 1). Using the chain rule,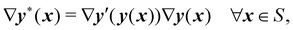
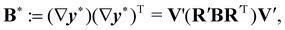
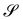 , its gradient ∇y′ featuring in (3) should be properly regarded as a surface gradient on
, its gradient ∇y′ featuring in (3) should be properly regarded as a surface gradient on 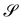 , ∇sy′, according to the definition given in ref. 26 (see also ref. 28).
, ∇sy′, according to the definition given in ref. 26 (see also ref. 28).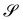 , described by U′, possibly followed by a twist distortion about ν, described by Rν, and an overall undistorting rotation R0.
, described by U′, possibly followed by a twist distortion about ν, described by Rν, and an overall undistorting rotation R0.
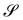 . Here, we only consider that this class of incremental deformations includes both pure stretching deformations, for which Rν is the identity, and pure drill rotations, for which U′ is the projection P(ν) := I − ν⊗ν on the plane orthogonal to ν.§ As shown in ref. 22 and 23, respectively, neither of these subclasses is empty.
. Here, we only consider that this class of incremental deformations includes both pure stretching deformations, for which Rν is the identity, and pure drill rotations, for which U′ is the projection P(ν) := I − ν⊗ν on the plane orthogonal to ν.§ As shown in ref. 22 and 23, respectively, neither of these subclasses is empty.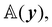 regarless of its nature (scalar or tensor), is a pure measure of bending if it obeys the following invariance condition,
regarless of its nature (scalar or tensor), is a pure measure of bending if it obeys the following invariance condition,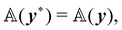
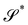 , is related to ν when y′ is a bending-neutral deformation (and then also how ∇ν* is related to ∇ν). To this end, we first recall that
, is related to ν when y′ is a bending-neutral deformation (and then also how ∇ν* is related to ∇ν). To this end, we first recall that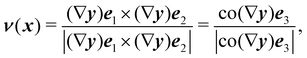
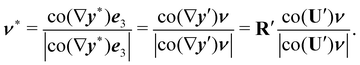
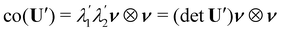 and Rνν = ν, we learn from (11) and (8) that
and Rνν = ν, we learn from (11) and (8) that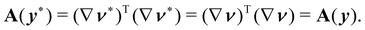
 into itself, is not a pure measure of bending, although it has the same invariants as A: Z transforms as follows, Z(y*) = R0Z(y)RT0.
into itself, is not a pure measure of bending, although it has the same invariants as A: Z transforms as follows, Z(y*) = R0Z(y)RT0. by ∇sν, for which we adopt a sign convention opposite to the one customary in differential geometry.** ∇sν is a symmetric tensor mapping the tangent plane to
by ∇sν, for which we adopt a sign convention opposite to the one customary in differential geometry.** ∇sν is a symmetric tensor mapping the tangent plane to  into itself; in its eigenframe, it is represented as
into itself; in its eigenframe, it is represented as and κ1, κ2 are the corresponding principal curvatures.
and κ1, κ2 are the corresponding principal curvatures.
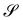 (see, for example, p. 205 of ref. 32). Given two arbitrary vectors v1, v2 on S,
(see, for example, p. 205 of ref. 32). Given two arbitrary vectors v1, v2 on S,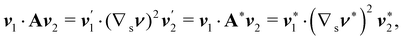
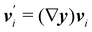 are vectors tangent to
are vectors tangent to 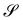 ,
, 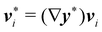 are vectors tangent to
are vectors tangent to 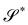 , and ∇sν* is the curvature tensor of
, and ∇sν* is the curvature tensor of 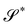 . Identity (19) simply says that the third fundamental form is invariant under a bending-neutral deformation.
. Identity (19) simply says that the third fundamental form is invariant under a bending-neutral deformation.
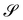 . Compared to A, K is not a pure measure of bending.
. Compared to A, K is not a pure measure of bending.
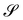 ), has already featured in the literature; it emerged as a strain energy density from a discretized model for membranes and plates35 and, more recently, also from a dimension reduction to plates.20 In the latter, the reduced strain energy density also involves the scalar invariants of the tensor
), has already featured in the literature; it emerged as a strain energy density from a discretized model for membranes and plates35 and, more recently, also from a dimension reduction to plates.20 In the latter, the reduced strain energy density also involves the scalar invariants of the tensor 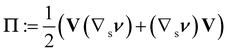 , where V is the stretching tensor of y in the present configuration, defined as the positive definite root of V2 = B. It is a simple exercise to show by example that neither Π nor its invariants are pure measures of bending according to the definition proposed in this paper.
, where V is the stretching tensor of y in the present configuration, defined as the positive definite root of V2 = B. It is a simple exercise to show by example that neither Π nor its invariants are pure measures of bending according to the definition proposed in this paper.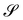 , defined as
, defined as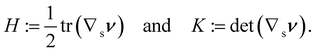
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A. It readily follows from (18) that
A. It readily follows from (18) that![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = tr(B(∇sν)2) = 2H
A = tr(B(∇sν)2) = 2H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) tr(B∇sν) − K
tr(B∇sν) − K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tr
tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B,
B,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, we start from tr
A, we start from tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2, which by (18) also reads as
A2, which by (18) also reads as![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 = (∇sν)2B·B(∇sν)2,
A2 = (∇sν)2B·B(∇sν)2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 = κ14B112 + κ24B222+ 2κ12κ22B122 = (tr
A2 = κ14B112 + κ24B222+ 2κ12κ22B122 = (tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A)2 − 2K2det
A)2 − 2K2det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B,
B,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = K2det
A = K2det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B = K2det
B = K2det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C.
C.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = κ12 + κ22 = 2C and det
A = κ12 + κ22 = 2C and det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = (κ1κ2)2 = K2,
A = (κ1κ2)2 = K2,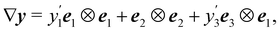
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑe3 − sin
ϑe3 − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑe1
ϑe1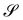 along the generatrix e2 is represented as
along the generatrix e2 is represented as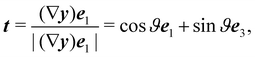
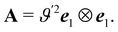
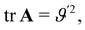 which, to within an elastic modulus, is precisely Antamn's bending energy for an extensible elastic rod.
which, to within an elastic modulus, is precisely Antamn's bending energy for an extensible elastic rod.

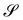 is an axisymmetric nightcap generated by the deformation y parametrized as
is an axisymmetric nightcap generated by the deformation y parametrized as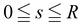 and
and 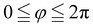 , are polar coordinates in the plane (x1,x2), so that x1 = s
, are polar coordinates in the plane (x1,x2), so that x1 = s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ and x2 = s
φ and x2 = s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, er is the radial unit vector and eφ the azimuthal unit vector, r(s) and z(s) are smooth functions representing radial and vertical components of the image under y of the generic point x = ser of S.
φ, er is the radial unit vector and eφ the azimuthal unit vector, r(s) and z(s) are smooth functions representing radial and vertical components of the image under y of the generic point x = ser of S.

 obtained by deforming a flat disk S of radius R via the mapping y described using (33). The unit vector ν is the outward normal to
obtained by deforming a flat disk S of radius R via the mapping y described using (33). The unit vector ν is the outward normal to  , while τ is the tangent unit vector along the meridians of
, while τ is the tangent unit vector along the meridians of  , so that (τ, eφ, ν) is a mobile frame oriented like the fixed frame (e1,e2,e3). The angle ϑ, defined in (44), designates the relative inclination of the normals ν and e3, to
, so that (τ, eφ, ν) is a mobile frame oriented like the fixed frame (e1,e2,e3). The angle ϑ, defined in (44), designates the relative inclination of the normals ν and e3, to  and S, respectively.
and S, respectively.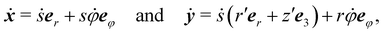
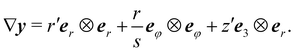
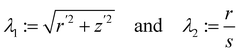
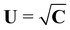 .
.
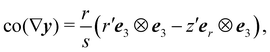
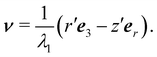
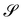 oriented along its meridians so that the mobile frame (τ, eφ, ν) is oriented like (e1, e2, e3), we can write
oriented along its meridians so that the mobile frame (τ, eφ, ν) is oriented like (e1, e2, e3), we can write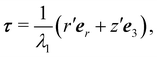
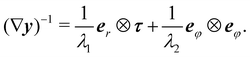
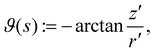
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑe3 + sin
ϑe3 + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑer, τ = cos
ϑer, τ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑer − sin
ϑer − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑe3.
ϑe3.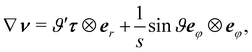
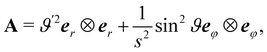
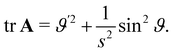
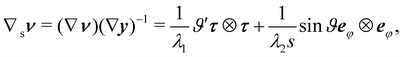
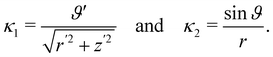
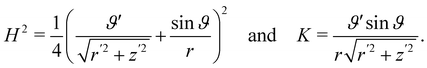
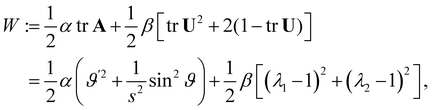
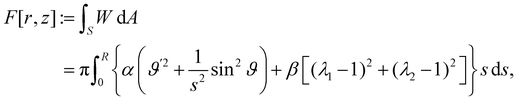
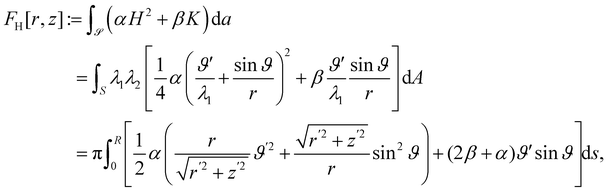
 has been related to the area element dA = sdsdφ on the reference shape S through the equation da = λ1λ2dA.
has been related to the area element dA = sdsdφ on the reference shape S through the equation da = λ1λ2dA.
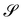 . Second, the Gaussian curvature K reveals itself as a null Lagrangian, as its contribution to the total strain energy depends only on the boundary value of ϑ,
. Second, the Gaussian curvature K reveals itself as a null Lagrangian, as its contribution to the total strain energy depends only on the boundary value of ϑ,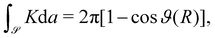
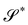 be symmetric, as it is expected to be.23 By writing (17) for ν* (and y*) instead of ν (and y), we have that
be symmetric, as it is expected to be.23 By writing (17) for ν* (and y*) instead of ν (and y), we have that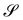 . It is clear that every solution U′ of (59) is defined within a multiplicative surface dilation, λ′P(ν), with arbitrary λ′ > 0.
. It is clear that every solution U′ of (59) is defined within a multiplicative surface dilation, λ′P(ν), with arbitrary λ′ > 0.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αW(ν) − (1 − cos
αW(ν) − (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)P(ν), α ∈ [−π,π],
α)P(ν), α ∈ [−π,π],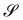 , then (59) reduces to the requirement that U′ commute with ∇sν, which just amounts to say that ∇sν and U′ must have the same eigenframe.22
, then (59) reduces to the requirement that U′ commute with ∇sν, which just amounts to say that ∇sν and U′ must have the same eigenframe.22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2α) = 0,
2α) = 0,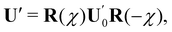
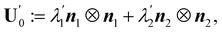
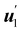 makes with n1 (the same as the angle that
makes with n1 (the same as the angle that 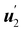 makes with n2). By using these representation formulae and (60), we finally obtain (59) in the following expanded form,
makes with n2). By using these representation formulae and (60), we finally obtain (59) in the following expanded form,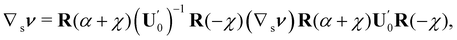
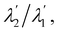 α, and χ.
α, and χ.
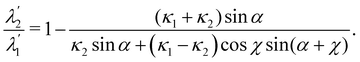
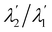 as delivered by (66) to be positive, with little labour we arrive at the inequalities
as delivered by (66) to be positive, with little labour we arrive at the inequalities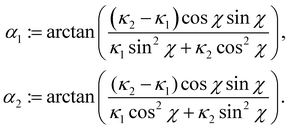
 , where κ1 = κ2. There, (66) would be incompatible for any α∉ {0,π} since it requires
, where κ1 = κ2. There, (66) would be incompatible for any α∉ {0,π} since it requires 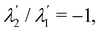 whereas, from (68), αm = αM = 0, so that the standard solution U′ = λ′P(ν), Rν = I is recovered by continuity.
whereas, from (68), αm = αM = 0, so that the standard solution U′ = λ′P(ν), Rν = I is recovered by continuity.
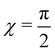 ). If
). If 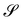 is a hyperbolic surface, that is, if K < 0, (66) readily gives
is a hyperbolic surface, that is, if K < 0, (66) readily gives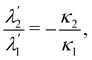
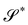 delivered by y′. Letting R0 = I, with no prejudice to generality, we obtain from (58) that
delivered by y′. Letting R0 = I, with no prejudice to generality, we obtain from (58) that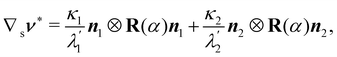
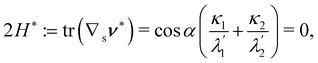
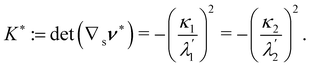
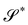 is a minimal surface.
is a minimal surface.
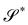 , which would be guaranteed, at least locally, if the surface tensor field defined on
, which would be guaranteed, at least locally, if the surface tensor field defined on 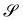 as
as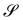 is such that either one or the other condition is not met, any incremental y′ will necessarily bring additional bending.
is such that either one or the other condition is not met, any incremental y′ will necessarily bring additional bending.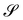 breaks the rotational symmetry about the normal ν. It might be interesting to find anisotropic pure measure of bending fit for these systems; they might be suggestive of direct theories where stretching and bending energy contents are kept separate, oblivious to whether they can be derived through dimension reduction of established three-dimensional strain energies or not.||||
breaks the rotational symmetry about the normal ν. It might be interesting to find anisotropic pure measure of bending fit for these systems; they might be suggestive of direct theories where stretching and bending energy contents are kept separate, oblivious to whether they can be derived through dimension reduction of established three-dimensional strain energies or not.||||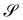 , is decided, at least locally, by the fulfillment of an integrability condition. The study of this condition and its solutions will be the subject of a future paper.
, is decided, at least locally, by the fulfillment of an integrability condition. The study of this condition and its solutions will be the subject of a future paper.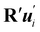 of V′.
of V′.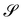 .
.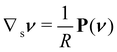 .
.