Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rheological effects on purely-elastic flow asymmetries in the cross-slot geometry†
Arisa
Yokokoji
 ,
Stylianos
Varchanis‡
,
Stylianos
Varchanis‡
 ,
Amy Q.
Shen
,
Amy Q.
Shen
 and
Simon J.
Haward
and
Simon J.
Haward
 *
*
Okinawa Institute of Science and Technology Graduate Univerisity, Onna-son, Okinawa 904-0495, Japan. E-mail: simon.haward@oist.jp
First published on 30th November 2023
Abstract
Viscoelastic flows in the cross-slot geometry can undergo a transition from a steady symmetric to a steady asymmetric flow state, ostensibly due to purely-elastic effects arising beyond a critical flow rate, or Weissenberg number Wi. However, some reports suggest that shear thinning of the fluid's viscosity may also play an important role in this transition. We employ a series of polymer solutions of varying rheological properties to investigate in detail how the interplay between fluid elasticity and shear thinning affects the onset and development of asymmetric flows in the cross-slot. Flow velocimetry is performed on each of the polymer solutions, and is used to assess the degree of flow asymmetry I in the cross-slot as a function of both Wi and a dimensionless parameter S quantifying the flow-rate-dependent extent of shear thinning. Typically, the flow field breaks symmetry as Wi is increased beyond a critical value, but the magnitude of I is found to also be dependent on S. For a few specific polymer solutions, the flow field recovers symmetry above a second, higher critical Wi as S becomes small. The experimental results are summarized in a flow state diagram in Wi–S space, showing the relationship between flow asymmetry and fluid rheology. Finally, to gain a deeper understanding of the effects of shear thinning, numerical simulations are performed using the linear simplified Phan–Thien–Tanner model. We demonstrate that the degree of both shear thinning and elasticity of the fluid, and their interplay, are important factors controlling elastic instabilities in the cross-slot geometry.
1 Introduction
Understanding the onset conditions of instabilities in viscoelastic flows is of ongoing academic interest and practical importance.1 Such instabilities can arise due to purely elastic forces, leading to symmetry breaking bifurcations, time-dependent flows and complex nonlinear dynamics even when inertia is negligible and an equivalent flow of a Newtonian fluid would remain perfectly steady and laminar.1 Similar to a Newtonian flow, in which instability can lead to turbulence as inertia increases, in a viscoelastic flow an initial instability can be a precursor for a self-sustaining chaotic state known as ‘elastic turbulence’, which arises as elastic forces increase.1,2 Elastic turbulence is implicated in the increased flow resistance and increased dispersion observed in viscoelastic porous media flows,3 and can also lead to drag reduced turbulent states,4 so is thus of great interest. While inertial forces are quantified by a Reynolds number Re = U![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /ν (where ν is the kinematic viscosity, and U and
/ν (where ν is the kinematic viscosity, and U and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are representative velocity and lengthscales, respectively), elastic forces are quantified by a Weissenberg number Wi = λU/
are representative velocity and lengthscales, respectively), elastic forces are quantified by a Weissenberg number Wi = λU/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (where λ is the relaxation time of the fluid). Elasticity is generally imparted to a fluid by the presence of dissolved long-chain polymers (like DNA, proteins, or synthetic polymers), which deform at Wi ≳ 0.5, modifying the stress in the bulk fluid. In a steady shearing flow, the rotational kinematics limit the deformation of the polymer and the typical response of the fluid is shear thinning; a progressive reduction in the shear viscosity as the shear rate is increased. In contrast, in irrotational elongational flows, a high degree of polymer chain deformation can be achieved via the coil–stretch transition5–7 and extra tensile stresses arising due to the entropic elasticity of the polymer lead to a nonlinear increase in the extensional viscosity.8,9
(where λ is the relaxation time of the fluid). Elasticity is generally imparted to a fluid by the presence of dissolved long-chain polymers (like DNA, proteins, or synthetic polymers), which deform at Wi ≳ 0.5, modifying the stress in the bulk fluid. In a steady shearing flow, the rotational kinematics limit the deformation of the polymer and the typical response of the fluid is shear thinning; a progressive reduction in the shear viscosity as the shear rate is increased. In contrast, in irrotational elongational flows, a high degree of polymer chain deformation can be achieved via the coil–stretch transition5–7 and extra tensile stresses arising due to the entropic elasticity of the polymer lead to a nonlinear increase in the extensional viscosity.8,9
A wide class of instabilities in viscoelastic flows are driven by the generation of elastic tensile stress along curving streamlines, as per the well-known ‘Pakdel–McKinley’ criterion,10–12 which predicts onset conditions for purely-elastic flow instabilities. As such, shear dominated viscoelastic flows with curving streamlines (e.g., in rotational rheometer fixtures13–16 or in curvilinear channels17–19) are subject to elastic instability and elastic turbulence. However, probably the most spectacular examples occur in flows with strong extensional kinematics (e.g., flow past a cylinder,20–22 or through channels with cross-sectional variations23–25) due to the large elastic tensile stresses that are induced in the fluid. Due to having a small characteristic lengthscale ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∼ 100 μm, microfluidic extensional flow devices are ideal for the study of elastic instabilities since they permit high Wi to be achieved for moderate to negligible Re. Of particular relevance to the present work are studies involving the microfluidic cross-slot geometry.26–31
∼ 100 μm, microfluidic extensional flow devices are ideal for the study of elastic instabilities since they permit high Wi to be achieved for moderate to negligible Re. Of particular relevance to the present work are studies involving the microfluidic cross-slot geometry.26–31
The cross-slot geometry consists of bisecting rectangular channels, forming two opposing inlets and two opposing outlets (see Fig. 1). Imposing equal volumetric flow rates through all four channels facilitates the creation of an irrotational planar elongational flow field around a free stagnation point at the center of the geometry. These conditions are ideal for extending the polymer chains in viscoelastic fluids for Wi ≳ 0.5, consequently leading to a strong elastic response.7,32 This, combined with highly curving streamlines around the stagnation point suggest the system should be prone to elastic instability.11,12,33 Gaining an improved understanding of the flow stability conditions in such a model system is highly relevant to understanding the dynamics of viscoelastic materials in general. Thus the cross-slot channel has been extensively used to study viscoelastic flow instabilities.26–38
Arratia et al.26 reported experimental results demonstrating two different elastic instabilities in the cross-slot geometry using a solution of flexible high molecular weight polyacrylamide with nearly constant shear viscosity. At low Wi < 4.5 the flow was steady and symmetric with the flow through each inlet dividing equally between each outlet. At the onset of the first flow instability (at critical Weissenberg number Wic = 4.5) the flow remained steady but transitioned to an asymmetric state in which the flow through each inlet selected a preferential (opposite) outlet channel. This instability was characterized as a supercritical pitchfork bifurcation, with the selection of outlet channel being random for each inlet. The second instability (at a higher critical value Wic2 = 12.5) was time-dependent with oscillation between the two possible asymmetric flow states. Time-dependent flows with characteristics of elastic turbulence have also been reported for viscoelastic fluids in a microfluidic cross-slot geometry.31 Arratia et al.26 also examined the flow of a dilute solution of a semi-rigid polymer (xanthan gum), which exhibits shear thinning but negligible elastic effects due to its low extensibility. Interestingly, they were unable to observe the same flow instability in the xanthan gum solution as they did in the case of the polyacrylamide solution, suggesting that the instability could be attributed to the elastic effect resulting from polymer chain stretching.
Subsequently, Poole et al.34 obtained the first numerical prediction of the steady flow asymmetry in the cross-slot geometry for Re = 0 using the upper-convected Maxwell (UCM) model, which exhibits a constant shear viscosity in steady flows, ostensibly confirming that the instability is caused solely by the elasticity of the fluid. The introduction of moderate inertia (Re up to 5) was shown to increase the value of Wic and to reduce the degree of flow asymmetry above Wic, but not to qualitatively change the nature of the supercritical bifurcation.
Further detailed numerical simulations were conducted by Rocha et al.36 using two different versions of the finitely-extensible nonlinear elastic dumbbell model (FENE-P and FENE-CR). The FENE-P model exhibits shear thinning, while the FENE-CR model is non-shear thinning in steady shear flows, otherwise the two models are similar. The extensibility, expressed through a parameter L, determines the fluid elasticity, while shear thinning is expressed through the solvent-to-total viscosity ratio β = ηs/(ηs + ηp), with ηs and ηp being the solvent and polymeric contributions to the viscosity, respectively. Unexpectedly, it was found that for equal values of L and low β = 0.1 in the two FENE models, the shear thinning in the FENE-P model destabilized the flow resulting in the onset of asymmetry at lower Wic than in the FENE-CR model. The authors expressed surprise at this result, remarking that shear thinning usually stabilized their numerical code allowing higher Weissenberg numbers to be reached.36 Shear thinning has also been shown to stabilize flows to elastic instability in both serpentine microchannels19 and in the Taylor–Couette geometry.39
Although it is clear that the elasticity of the fluid is essential in order for the steady flow asymmetry in the cross-slot device to occur, and indeed several studies (experimental and numerical) have indicated a broad consistency with the predictions of the Pakdel–McKinley criterion,33,36,40,41 there have been a number other studies indicating the influence of shear thinning (induced by the shear stress at the walls of the cross-slot channel). In a numerical study, Xi and Graham35 employed the FENE-P model, but with a high value of β = 0.95, which better represents a dilute, and very weakly shear thinning, polymer solution than the value of β = 0.1 employed in the simulations of Rocha et al.36 In contrast to the results of Rocha et al. for which the shear thinning in the FENE-P model resulted in a low Wic, by increasing the value of β in the FENE-P model, Xi and Graham did not observe the steady flow asymmetry in the cross-slot at all.35 Instead they found distinct time-dependent flow instabilities, localized along the outflowing symmetry axis, which they attributed to the feedback between the stress and flow fields around the stagnation point streamline. In addition, numerical simulations by Canossi et al.42 using the Oldroyd-B model in the cross-slot geometry found that steady asymmetric flow states were only supported for values of β ≲ 0.5. For higher values of β, the flow transitioned from steady and symmetric directly to a time-dependent state.
The difference between numerical results obtained with ostensibly non-shear thinning fluid models such as Oldroyd-B and FENE-CR with different values of β may be explained by their propensity to exhibit transient variations in viscosity when subjected to changes in the shear rate (in either the Eulerian or the Lagrangian reference frame).43 For low values of β, due to a synergy between the lag time for stress to respond to a change in the shear rate, and the act of normal stresses along curving streamlines, a decreased flow resistance occurs along streamlines that experience increasing shear rates (and increased flow resistance occurs along streamlines that experience decreasing shear rates). Such models should only be considered of spatio-temporally uniform viscosity in either steady simple shear flows or for high values of β → 1.43 We note that there is a change in shear rate along streamlines turning the corners of the cross-slot device and we suspect that flow resistance variations in these regions may be sufficient to promote the existence of a preferred flow path through the device in “non-shear thinning” models with sufficiently low β, and thus to support steady asymmetric flow states.
Experimentally, Haward et al.28,37 studied the flow of viscoelastic wormlike micellar solutions in the cross slot geometry. By varying the concentration of the micelle-forming surfactant in the solution, they varied the strength of the shear thinning (i.e., the power-law index n) and also the range of shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) over which the shear thinning was observed in the steady shear flow curve. Based on the nominal wall shear rate
over which the shear thinning was observed in the steady shear flow curve. Based on the nominal wall shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w in the channels of the cross-slot device, the occurrence of steady flow asymmetries correlated with the most strongly shear thinning region of the flow curve. At wall shear rates below the onset of shear thinning, the flow in the cross-slot device remained symmetric. At wall shear rates beyond the shear thinning region of the flow curve, the flow in the cross-slot device became time dependent.
w in the channels of the cross-slot device, the occurrence of steady flow asymmetries correlated with the most strongly shear thinning region of the flow curve. At wall shear rates below the onset of shear thinning, the flow in the cross-slot device remained symmetric. At wall shear rates beyond the shear thinning region of the flow curve, the flow in the cross-slot device became time dependent.
Furthermore, Sousa et al.30 examined the behaviour of a wide range of polymer solutions of different β in cross-slot devices of various dimensions. Across all of their experiments, they found that steady flow asymmetries only occurred in fluids with a low value of β ≲ 0.05. For higher values of β the steady flow asymmetry was not observed and instead the flow transitioned directly from steady and symmetric to a time-dependent state. These existing experimental and numerical studies28,30,35–37,42 suggest that both shear thinning and elasticity play a role in controlling flow asymmetry in the cross-slot geometry.
In this work, we seek to gain a deeper understanding of how shear thinning and elasticity interact to control the stability behaviour in the cross-slot device. Taking inspiration from a similar study examining viscoelastic instabilities around a microfluidic cylinder,20,44 we examine the flow behaviour of a range of viscoelastic fluids composed of hydrolyzed polyacrylamide. By varying the polymer and salt concentration in the aqueous solutions, the viscoelastic and shear thinning properties of the fluids are varied widely, enabling their effects to be effectively decoupled. Flow velocimetry is used to characterize the flow state in the cross-slot device as a function of the imposed Wi and as a function of a parameter S that quantifies the strength of shear thinning at a given applied shear rate. Interestingly, we find that a combination of strong shear thinning and viscoelasticity promotes the formation of steady asymmetric flow states in the cross-slot device, while weaker shear thinning results in time-dependent asymmetric states. For very weak shear thinning, we find that the flow field remains symmetric for all Wi. Perhaps most interestingly, for a few polymer concentrations that exhibit asymmetry over a range of Wi, we find that the flow can recover symmetry at sufficiently high flow rates such that S becomes small.
Our experimental results are compared qualitatively against creeping flow numerical simulations using the linear Phan–Thien–Tanner model, allowing parametric control of the shear thinning for constant extensional elastic properties of the fluids. Our results highlight how the interplay between elastic and shear thinning effects influence the transitions between flow states in the cross-slot device.
2 Experimental methods
2.1 Microfluidic device
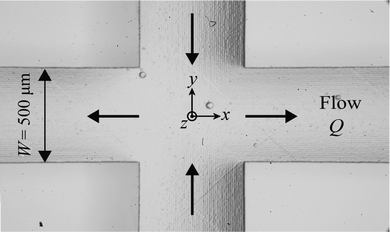
The microfluidic cross-slot device is fabricated by selective laser-induced etching in fused silica glass using a commercial LightFab three-dimensional (3D) printer (LightFab GmbH, Germany).45–47 An image of the same device used in the experiments is shown in Fig. 1 indicating the channel dimensions, the flow scheme, and the Cartesian coordinate system with the origin at the center of the geometry. The channels of the device each have a width of W = 500 μm, and a height of H = 2.0 mm (aspect ratio α = H/W = 4.0). The length of each of the four arms is 20 mm, allowing the flow to become fully developed within both the inlets and the outlets.2.2 Sample preparation and rheological characterization
The sample fluids are prepared by dissolving a high molecular weight hydrolyzed polyacrylamide (HPAA; Mw = 18 × 106 g mol−1; degree of substitution 0.30%; Polyscience Inc.) in deionized (DI) water. A stock solution at a polymer concentration of cp = 3000 parts-per-million (ppm, by weight) is first prepared by mixing the appropriate quantities of polymer powder and DI water on a laboratory roller for at least four days, and ensuring complete dissolution. Solutions with lower polymer concentration (down to 20 ppm) are subsequently prepared by dilution with additional DI water. To study the effects of salt addition, a cp = 3000 ppm HPAA solution is prepared by adding the polymer powder to a 0.5 mol L−1 sodium chloride (NaCl) solution, and again mixing on a laboratory roller for at least four days. Based on an earlier rheometric analysis of HPAA solutions in a similar range of concentration in the absence of NaCl, we expect the salt-free test fluids to be in the semidilute entangled concentration regime, at least for cp ≥ 60 ppm.20,48 Given the high cp of the solution with added NaCl, it is also expected to be semidilute and entangled.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≤ 500 s−1, a stainless steel double-gap geometry is used.
≤ 500 s−1, a stainless steel double-gap geometry is used.
Fig. 2(a) shows that all test fluids exhibit shear thinning behavior. All flow curves are well described by the Carreau–Yasuda model (solid lines in Fig. 2(a)):
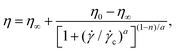 | (1) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c is the critical shear rate at the onset of shear thinning.49 The dimensionless parameter a controls the abruptness of the transition between the low shear rate viscosity plateau and the shear thinning region of the flow curve, and n is the power law index in the shear thinning region. Table 1 lists the parameters found by fitting eqn (1) to the experimental flow curves in Fig. 2(a). In the insert to Fig. 2(a) we plot the zero-shear-rate viscosity η0 from Table 1 as a function of the HPAA concentration for the salt-free polymer solutions. The data follow a power-law scaling with exponent 1.5, which is consistent with the prediction for salt-free polyelectrolyte solutions in the semidilute entangled regime,48 and also consistent with prior findings on HPAA solutions in a similar concentration range.20
c is the critical shear rate at the onset of shear thinning.49 The dimensionless parameter a controls the abruptness of the transition between the low shear rate viscosity plateau and the shear thinning region of the flow curve, and n is the power law index in the shear thinning region. Table 1 lists the parameters found by fitting eqn (1) to the experimental flow curves in Fig. 2(a). In the insert to Fig. 2(a) we plot the zero-shear-rate viscosity η0 from Table 1 as a function of the HPAA concentration for the salt-free polymer solutions. The data follow a power-law scaling with exponent 1.5, which is consistent with the prediction for salt-free polyelectrolyte solutions in the semidilute entangled regime,48 and also consistent with prior findings on HPAA solutions in a similar concentration range.20
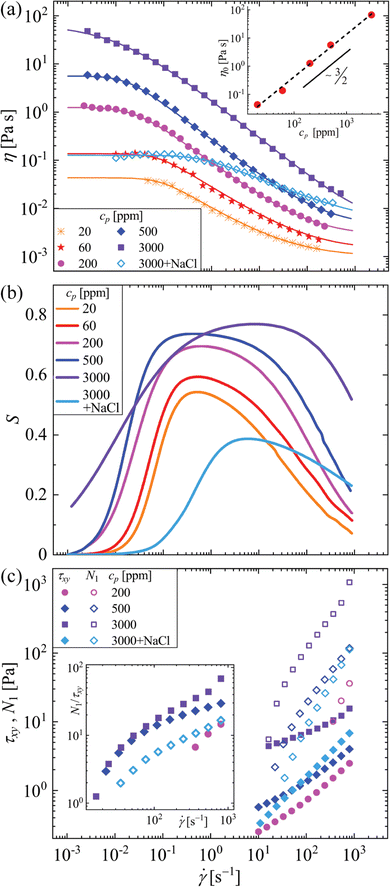 | ||
| Fig. 2 Rheological characterization of the aqueous HPAA test solutions in steady shear. (a) Flow curves measured for all sample solutions in a double-gap Couette geometry. Solid lines show the fits of the Carreau–Yasuda model. The insert shows the zero-shear-rate viscosity η0 as a function of the polymer concentration for salt-free solutions, where the dashed line is a power-law fit to the data with exponent 1.5. (b) The shear rate dependence of the shear thinning parameter S, which is calculated from the Carreau–Yasuda fits to the steady flow curves in part (a) based on eqn (3), see main text. (c) Shear stress τxy and first normal stress difference N1 measured (where possible) in a cone-and-plate geometry. The insert shows the shear rate dependence of τxy/N1. | ||
| c p [ppm] | η 0 [Pa s] | η ∞ [mPa s] |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c [s−1]
c [s−1] |
n | a | λ [ms] |
|---|---|---|---|---|---|---|
| 20 | 0.043 | 1.0 | 0.083 | 0.40 | 1.9 | 5 |
| 60 | 0.137 | 1.4 | 0.076 | 0.37 | 1.9 | 30 |
| 200 | 1.26 | 2.8 | 0.025 | 0.28 | 1.4 | 75 |
| 500 | 5.64 | 4.4 | 0.017 | 0.25 | 1.7 | 182 |
| 3000 | 65.8 | 4.5 | 0.011 | 0.21 | 0.62 | 716 |
| 3000 + NaCl | 0.127 | 4.0 | 0.670 | 0.56 | 1.4 | 182 |
To quantify the degree of shear thinning of each polymer solution, we introduce the shear thinning parameter S:
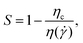 | (2) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the tangent viscosity (where τxy is the shear stress), and η(
is the tangent viscosity (where τxy is the shear stress), and η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is shear-rate-dependent viscosity.20,28 Thus, the shear thinning parameter can be readily found from the flow curve data (or the corresponding Carreau–Yasuda fit) according to:
) is shear-rate-dependent viscosity.20,28 Thus, the shear thinning parameter can be readily found from the flow curve data (or the corresponding Carreau–Yasuda fit) according to: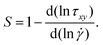 | (3) |
Fig. 2(b) plots S versus ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , with S being determined from eqn (3) using the Carreau–Yasuda fits to the experimental flow curves shown in Fig. 2(a). For all of the fluids at low shear rates, S is close to zero, corresponding to the zero-shear-rate plateau in the flow curve. At intermediate shear rates (
, with S being determined from eqn (3) using the Carreau–Yasuda fits to the experimental flow curves shown in Fig. 2(a). For all of the fluids at low shear rates, S is close to zero, corresponding to the zero-shear-rate plateau in the flow curve. At intermediate shear rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≈ 1 s−1), S reaches a maximum that corresponds to the highest slope in the flow curve. Finally, S decreases as the shear viscosity reaches towards the high-shear-rate plateau (i.e., for
≈ 1 s−1), S reaches a maximum that corresponds to the highest slope in the flow curve. Finally, S decreases as the shear viscosity reaches towards the high-shear-rate plateau (i.e., for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≳ 100 s−1). All of the curves in Fig. 2(b) display similar shapes, with S generally showing higher values over a wider range of shear rates as the HPAA concentration increases for salt-free solutions. The addition of salt to the polymer solution results in a lower zero-shear-rate viscosity and a lower degree of shear thinning (see open diamonds in Fig. 2(a)). When salt is added to the solution, it effectively screens the electrostatic interactions between polymer chain segments, reducing their repulsion. As a consequence, the segments are allowed to come closer to each other, leading to a more compact chain conformation. This reduced interaction between polymer chains contributes to the decrease in viscosity at low shear rates and reduces the shear thinning behavior of the solution.
≳ 100 s−1). All of the curves in Fig. 2(b) display similar shapes, with S generally showing higher values over a wider range of shear rates as the HPAA concentration increases for salt-free solutions. The addition of salt to the polymer solution results in a lower zero-shear-rate viscosity and a lower degree of shear thinning (see open diamonds in Fig. 2(a)). When salt is added to the solution, it effectively screens the electrostatic interactions between polymer chain segments, reducing their repulsion. As a consequence, the segments are allowed to come closer to each other, leading to a more compact chain conformation. This reduced interaction between polymer chains contributes to the decrease in viscosity at low shear rates and reduces the shear thinning behavior of the solution.
Where possible, we also employ a 50 mm diameter 1° cone-and-plate geometry to evaluate the first normal stress difference generated in the fluids as a function of the shear rate (see Fig. 2(c)). Note that this is only achievable for fluids of higher polymer concentration and over a limited (high) range of shear rates 10 ≤ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≤ 800 s−1, due to the negligible normal forces at lower concentrations and shear rates. For the fluids which permit a measurement, N1 increases monotonically over the accessible shear rate range in an approximately power law fashion.
≤ 800 s−1, due to the negligible normal forces at lower concentrations and shear rates. For the fluids which permit a measurement, N1 increases monotonically over the accessible shear rate range in an approximately power law fashion.
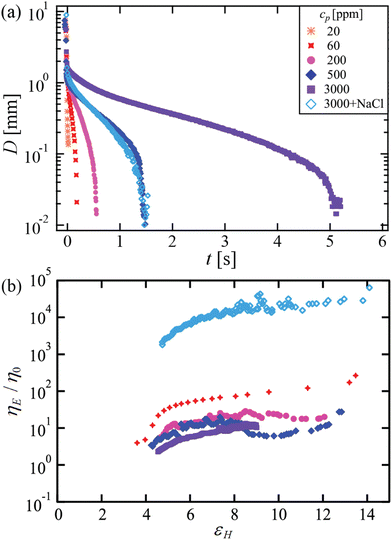
Within the elastocapillary thinning regime, the capillary thinning measurement can also be used to estimate the extensional viscosity ηE = −σ/(2dD(t)/dt) of the viscoelastic liquids, where σ = 72 mN m−1 is the surface tension of the fluids.50,51 In Fig. 3(b) we present the scaled extensional viscosity ηE/η0 as a function of the accumulated Hencky strain εH = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D0/D(t). All of the solutions show strain hardening behaviour, with values of 10 ≲ ηE/η0 ≲ 100, for the salt-free solutions. The polymer solution with added salt shows a significantly higher value of ηE/η0 ≈ 104 than the other polymer solutions. This can be understood by the contraction of polymer chains due to the electrostatic screening effect of the salt, which causes an increase in chain extensibility and a reduction in η0.
D0/D(t). All of the solutions show strain hardening behaviour, with values of 10 ≲ ηE/η0 ≲ 100, for the salt-free solutions. The polymer solution with added salt shows a significantly higher value of ηE/η0 ≈ 104 than the other polymer solutions. This can be understood by the contraction of polymer chains due to the electrostatic screening effect of the salt, which causes an increase in chain extensibility and a reduction in η0.
2.3 Dimensionless numbers
The sample solutions are driven through the cross-slot device at precisely controlled volumetric flow rates Q using four Nemesys low-pressure syringe pumps (Cetoni, GmbH). Two pumps inject fluid into the microchannel through the inflow arms, while two pumps withdraw fluid at the same rates from the outflow arms (see Fig. 1). The pumps are each fitted with Hamilton Gastight syringes of appropriate volumes such that the specified pulsation-free dosing rate is always exceeded even at the lowest imposed flow rates. Flexible silicone tubing is used for all connections between the microchannel and the syringes.To parameterize the various flow regimes and to understand how the degree of shear thinning and elasticity of the fluid depend on the imposed flow conditions, a few key dimensionless numbers are used.
The Reynolds number, Re, quantifies the relative strength of inertial to viscous forces and in the cross-slot device can be defined as:
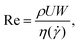 | (4) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is the shear rate-dependent viscosity calculated from the Carreau–Yasuda model, evaluated at a shear rate
) is the shear rate-dependent viscosity calculated from the Carreau–Yasuda model, evaluated at a shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) =
= ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w, where
w, where ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 6U/W is the nominal wall shear rate in the cross-slot channel arms. In most of our flow experiments in the cross-slot device, Re < 1 and can be safely neglected. For some of the more dilute and less viscous samples the Reynolds number can reach up to Re ≈ 5 at the highest imposed flow rates. Previous numerical simulations (e.g., those presented in ref. 34) have shown that such a level of inertia does not qualitatively affect the elastic flow phenomena in the cross-slot device, but does act to suppress elastic instability. We will use our own numerical simulations (described in Section 3, below) to confirm that the phenomena we report from our experiments are not caused by inertial effects.
w = 6U/W is the nominal wall shear rate in the cross-slot channel arms. In most of our flow experiments in the cross-slot device, Re < 1 and can be safely neglected. For some of the more dilute and less viscous samples the Reynolds number can reach up to Re ≈ 5 at the highest imposed flow rates. Previous numerical simulations (e.g., those presented in ref. 34) have shown that such a level of inertia does not qualitatively affect the elastic flow phenomena in the cross-slot device, but does act to suppress elastic instability. We will use our own numerical simulations (described in Section 3, below) to confirm that the phenomena we report from our experiments are not caused by inertial effects.
We define the Weissenberg number of our experiment, which describes the relative strength of elastic to viscous forces in the flow as:
Wi = λ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , , | (5) |
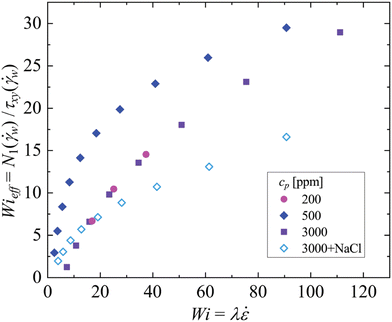
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1.87U/(W/2). This nominal value for the extension rate is based on consideration of the steady symmetric flow of a Newtonian fluid and represents the average extension rate between the center of the cross-slot geometry (i.e., the stagnation point, where the flow velocity would be zero) and the entrance to each outlet channel. The value of 1.87U in the numerator represents the streamwise flow velocity on the centerline of the outlet channel, and is estimated based on an infinite series analytical solution for fully-developed Poiseuille flow in a rectangular duct of aspect ratio α = 4.52 The Weissenberg number as defined here characterizes the strength of elastic effects near the stagnation point. Broadly, as Wi exceeds ≈0.5 nonlinear elastic effects are expected to become dominant.5,7,53 However, shear thinning in the fluid properties (Fig. 2(a)) will lead to a shear-rate-dependent relaxation time that reduces with increasing shear rate. This can be accounted for by considering a shear-rate-dependent effective Weissenberg number evaluated as Wieff(
= 1.87U/(W/2). This nominal value for the extension rate is based on consideration of the steady symmetric flow of a Newtonian fluid and represents the average extension rate between the center of the cross-slot geometry (i.e., the stagnation point, where the flow velocity would be zero) and the entrance to each outlet channel. The value of 1.87U in the numerator represents the streamwise flow velocity on the centerline of the outlet channel, and is estimated based on an infinite series analytical solution for fully-developed Poiseuille flow in a rectangular duct of aspect ratio α = 4.52 The Weissenberg number as defined here characterizes the strength of elastic effects near the stagnation point. Broadly, as Wi exceeds ≈0.5 nonlinear elastic effects are expected to become dominant.5,7,53 However, shear thinning in the fluid properties (Fig. 2(a)) will lead to a shear-rate-dependent relaxation time that reduces with increasing shear rate. This can be accounted for by considering a shear-rate-dependent effective Weissenberg number evaluated as Wieff(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = N1(
) = N1(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )/τxy(
)/τxy(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ). As can be seen from the insert in Fig. 2(c), for fluids where a measurement of N1 is available, this quantity increases monotonically with the shear rate. Furthermore, by evaluating Wieff at a shear rate
). As can be seen from the insert in Fig. 2(c), for fluids where a measurement of N1 is available, this quantity increases monotonically with the shear rate. Furthermore, by evaluating Wieff at a shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) =
= ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 6U/W[ = 6
w = 6U/W[ = 6![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) /(2 × 1.87)], we can see that for each fluid Wieff increases monotonically with Wi (Fig. 4).
/(2 × 1.87)], we can see that for each fluid Wieff increases monotonically with Wi (Fig. 4).
The strength of shear thinning effects in the cross-slot device is assessed using the shear thinning parameter S (eqn (3), Fig. 2(b)), which similar to both Re and Wieff, is evaluated at a shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) =
= ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 6U/W.
w = 6U/W.
2.4 Microparticle image velocimetry and experimental protocol
The flow states of the sample solutions in the cross-slot device are determined based on quantitative flow velocimetry performed using a volume illumination microparticle image velocimetry (μ-PIV) system (TSI Inc.). All test solutions are seeded with a low concentration (≈0.02 wt%) of red fluorescent polystyrene particles (Thermo Fisher Scientific Inc.) with 2 μm in diameter and with excitation and emission wavelengths of 530 nm and 607 nm, respectively. The z = 0 plane of the flow geometry (see Fig. 1) is brought into focus on an inverted microscope (Nikon Eclipse Ti) with a Nikon PlanFluor objective lens (5× magnification, numerical aperture NA = 0.15). These conditions result in a measurement depth of ≈125 μm,54 which is ≈H/16. In the experiment, particle fluorescence is induced by excitation with a dual pulsed Nd:YLF laser with a wavelength of 527 nm. The laser pulses are separated in time by a duration Δt. A high-speed imaging sensor (Phantom MIRO) operating in frame-straddling mode is able to capture pairs of particle images synchronized with the laser pulses.At each flow rate examined, the time Δt is set so that the average displacement of particles between the two images in each pair is ≈4 pixels. For most of the range of imposed Weissenberg numbers, the flow in the cross-slot is steady and hence the data can be time-averaged. Accordingly, 250 image pairs are processed using an ensemble-averaged cross-correlation PIV algorithm (TSI Insight 4G). In a few cases, the flow is observed to vary in time. In such instances, we perform both an ensemble-average cross correlation in order to obtain an overall picture of the flow field, and we also process image pairs individually for the purpose of generating movies. In either case, a recursive Nyquist criterion is employed to enhance the spatial resolution of the processing algorithm and obtain 2D velocity vectors u = (u,v) on a square grid of spacing 12.8 μm × 12.8 μm. Subsequent generation of contour plots and streamline traces is performed using the software Tecplot (Tecplot Inc., WA), and image analysis is performed using Matlab.
For each test fluid, the flow is driven through the cross-slot at a given Wi by imposing the appropriate value of Q in each of the four intersecting channels. The motion of tracer particles is observed in real time until the flow is deemed to have reached a steady state (where the waiting time is both fluid and flow rate dependent), before μ-PIV images are captured. The flow is then stopped while the captured images are processed into vector fields and briefly examined in order to assess whether the flow is steady or time-dependent, or if a longer waiting time is needed before image capture. Subsequently, the process is repeated at the next value of Wi by increasing the imposed Q, and so on until a complete sweep of Wi is achieved. Note that in order to perform such a sweep with a given syringe while maintaining the flow rate above the pulsation free limit throughout, a range of Wi spanning a factor ≈5000 is possible. In our experiments we explore a range spanning 0.02 ≲ Wi ≲ 100.
From the velocity fields measured by μ-PIV performed over a range of Wi, we assess the degree of flow asymmetry inside the cross-slot by using the following asymmetry parameter:
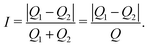 | (6) |
3 Theoretical approach
In the numerical simulations, we consider the 2D, steady, creeping flow of a polymer solution in a planar cross-slot, as illustrated in Fig. 1. The flow is described by the incompressible and isothermal Cauchy equations coupled with a constitutive equation, which accounts for the contribution of the non-Newtonian stresses. Neglecting inertia, the continuity and momentum equations are given as:| ∇·u = 0, | (7) |
∇·(−PI + τ + ηs![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a2.gif) ) = 0, ) = 0, | (8) |
The linear version of the simplified Phan–Thien–Tanner (l-PTT) model,56 under steady-state, is expressed as:
λ[u·∇τ − (∇u)T·τ − τ·∇u] + Yτ = ηp![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a2.gif) , , | (9) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a2.gif) is the deformation rate tensor, defined as:
is the deformation rate tensor, defined as:![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a2.gif) = ∇u + (∇u)T, = ∇u + (∇u)T, | (10) |
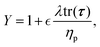 | (11) |
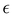 is a parameter that governs the rheological response of the fluid. The l-PTT model predicts shear thinning effects in steady simple shear, and a bounded extensional viscosity in steady extension. With increasing
is a parameter that governs the rheological response of the fluid. The l-PTT model predicts shear thinning effects in steady simple shear, and a bounded extensional viscosity in steady extension. With increasing 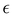 , the fluid becomes less strain hardening and the onset of shear thinning is translated to lower values of the shear rate. We also define the solvent-to-total viscosity ratio:
, the fluid becomes less strain hardening and the onset of shear thinning is translated to lower values of the shear rate. We also define the solvent-to-total viscosity ratio: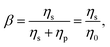 | (12) |
The usual no-slip and no-penetration boundary conditions (i.e., u = 0) are imposed on all walls of the channels. At the channel inlets, we impose fully-developed velocity and stress fields. At the channel outflows, we apply the open boundary condition (OBC).57 The Petrov–Galerkin stabilized finite element method for viscoelastic flows (PEGAFEM-V)58–60 is used to solve the governing equations. We solve directly for the steady-state solution, using a pseudo-arclength continuation algorithm for finite element simulations61 to track the solution branches in the parametric space. The flow variables, u, P, and τ, are interpolated by linear triangles in a structured mesh. Details about the numerical implementation and validation studies can be found in ref. 58–60.
4 Results and discussion
4.1 Experimental flow fields
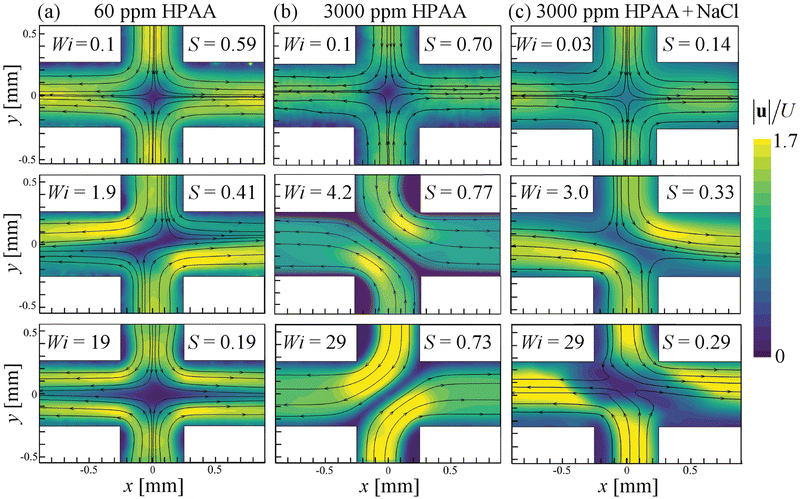
Representative flow fields measured for three of the tested HPAA solutions are shown for a range of Weissenberg numbers in Fig. 5, illustrating the various flow states that can be observed. Note that when the Weissenberg number is low (Wi ≲ 0.2), all of the fluids tested (regardless of the extent of shear thinning) display flow fields with a high degree of symmetry, and that appear in fact, quite Newtonian-like (as exemplified by the top row of images in Fig. 5). Apart from the lowest concentration HPAA solution tested (with cp = 20 ppm), for which the flow remains symmetric over the whole range of imposed Wi, all of the fluids display a transition to a state of steady flow asymmetry (as exemplified by the middle row of images in Fig. 5). At a rather low HPAA concentration cp = 60 ppm (Fig. 5(a)) at Wi = 1.9 and S = 0.41, the flow asymmetry is relatively mild. However, it is clear that most of the fluid that enters via the upper arm of the device selects the left arm by which to exit, while the majority of fluid that enters via the lower arm exits via the right arm. For the cp = 3000 ppm HPAA solution without salt (Fig. 5(b)) at Wi = 4.2 and S = 0.77, the asymmetry is intense, with essentially all of the fluid from the top inlet exiting to the right and all of the fluid from the bottom inlet exiting left. With the addition of salt to the cp = 3000 ppm HPAA solution (Fig. 5(c)) at a similar Wi = 3.0 but lower S = 0.33, the asymmetry is distinctly less intense than that observed for the same polymer concentration but without salt. Increasing the Weissenberg number further, each of the fluids responds rather differently (bottom row of images in Fig. 5). After passing through a state of time-dependence for 10 ≲ Wi ≲ 20 (see Movie M1, ESI†), remarkably the cp = 60 ppm solution recovers steadiness and symmetry of the flow field, see Fig. 5(a) at Wi = 19 and S = 0.19. However, this symmetric state is distinct from the low-Wi pseudo-Newtonian symmetric state described previously. At high Wi = 19 there is a clear band of low flow velocity located about the x-axis, which is not seen at low Wi = 0.1. This region of low flow velocity is considered to be due to the stretching of polymer chains that flow through the high velocity gradients near the stagnation point, and the resulting high elastic tensile stress that feeds back onto the flow field. For the cp = 3000 ppm HPAA solution (no salt), the state of strong and time-steady flow asymmetry is maintained up to high Wi (see Fig. 5(b) at Wi = 29 and S = 0.73). Different behaviour is observed for the cp = 3000 ppm HPAA solution with added salt, which undergoes a transition to a time-dependent asymmetric flow state as the Weissenberg number is increased (see Fig. 5(c) at Wi = 29 and S = 0.29, and the corresponding Movie M2, ESI†).We note that the recovery of steady symmetric flow at high Wi shown in Fig. 5(a) for the cp = 60 ppm (and also observed for the cp = 200 ppm solution), but with a signature in the flow field of strong elastic effects, is highly reminiscent of prior results on instabilities in similar fluids flowing around microfluidic cylinders.20 However, we are unaware of any previous report of an asymmetric to symmetric flow transition being reported for increasing Weissenberg numbers in the cross-slot geometry.
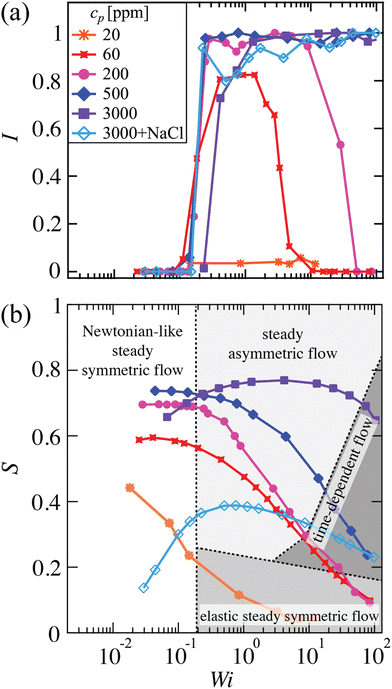
4.2 Flow asymmetry
The degree of flow asymmetry inside the cross-slot is quantified by using the asymmetry parameter I (eqn (6)), which is plotted as a function of Wi in Fig. 6(a). The lowest concentration polymer solution (cp = 20 ppm) shows negligible levels of asymmetry (I ≈ 0) over the whole range of accessible Weissenberg number. For a slightly higher polymer concentration (cp = 60 ppm) the asymmetry increases beyond a critical Weissenberg number Wic ≈ 0.2 up to a maximum value I ≈ 0.8. With further increase in Wi, I decreases before symmetry is regained at Wi ≈ 10. A similar trend is also observed for cp = 200 ppm, although in this case the maximum value of I ≈ 1 is higher than for cp = 60 ppm, and the flow remains asymmetric to higher Wi, with symmetry being fully recovered at Wi ≈ 50. At higher polymer concentrations (including cp = 3000 ppm with added salt) for Wi beyond the onset of asymmetry, significantly high values of asymmetry approaching I = 1 are reached and are maintained up to the highest Weissenberg numbers accessed. We point out that, at least for the cp = 200 ppm polymer solution, the recovery of symmetry cannot be attributed to any shear-induced reduction in the relaxation time, since Wieff evaluated at the channel wall increases monotonically with Wi over the range 20 ≲ Wi ≲ 40 through which the asymmetric to symmetric transition mostly occurs (see Fig. 4).Fig. 6(b) presents a flow state diagram showing the trajectories of all the HPAA solutions through Wi–S state space as the imposed flow rate through the cross-slot microchannel is varied. Newtonian-like steady symmetric, steady asymmetric, elastic steady symmetric, and time-dependent flow states are denoted by white, light-gray, medium-gray, and dark-gray backgrounds, respectively. We observe that for cases where the flow becomes asymmetric, symmetry can be recovered if the shear thinning parameter decreases to S ≲ 0.2. This observation suggests that the more concentrated polymer solutions do not recover symmetry in the range of Wi tested because the degree of shear thinning remains sufficiently high (i.e., S ≳ 0.2). The trends revealed by Fig. 6 are qualitatively similar to those observed in the case of HPAA solutions flowing around microfluidic cylinders.20,22
4.3 Numerical results
The experimental results presented in the previous section clearly suggest that shear thinning is closely related to the degree of flow asymmetry in the cross-slot. Stronger shear thinning promotes steady asymmetric states, time dependent flow states occur for high elasticity but weaker shear thinning, while asymmetric flows appear not to be supported for shear thinning parameters that are below S ≈ 0.2. However, we cannot ignore that inertia is present when flow resymmetrization takes place (the Reynolds number is up to Re ≈ 5 in those cases). Poole et al.34 have numerically demonstrated that inertia opposes elasticity in the cross-slot, suppressing the instability. Thus, one could argue that inertia drives the recovery of symmetry in the low concentration polymer samples. Furthermore, diluting the solution to decrease the degree of shear thinning unavoidably results in a simultaneous alteration in the degree of elasticity under extension. One could argue that weaker elastic effects lead to a reduced degree of flow asymmetry, in accordance with the observations by Rocha et al.36 A loss of elasticity could also occur due to polymer chain fracture at high extension rates. Numerical simulations with the two-species Vasquez–Cook–McKinley model representing wormlike micellar solutions have shown that such breakage can strongly suppress, or even eliminate, the flow asymmetry in the cross-slot device.62,63 Also in the experiments we are not able to fully account for normal stress effects through the evaluation of Wieff. Unfortunately, we cannot completely isolate the effects of shear thinning, elasticity, and normal stresses in a microfluidic experiment, and eventually inertia will always come into play as the flow rate is increased.By employing numerical simulations with the l-PTT model it is possible to examine the effect of varying shear thinning in the absence of inertia while maintaining constant extensional properties and avoiding the complication of possible breakage of polymer chains in the flow. Inertia can be simply ruled out by neglecting the velocity material derivative in the momentum equation (eqn (8)) and assuming creeping flow. Designing fluids with the same extensional but different shear rheology is more challenging. Our starting point is the paper by Shogin,64 where analytical solutions of the l-PTT model in homogeneous shear and extension are provided. After some calculations, one can prove that for any 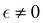 we have:
we have:
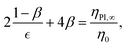 | (13) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) →∞) asymptotic value of the first planar extensional viscosity, ηPl = (τxx − τyy)/
→∞) asymptotic value of the first planar extensional viscosity, ηPl = (τxx − τyy)/![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) + 4ηs, as predicted by the l-PTT model. By setting ηPl,∞ equal to a constant and selecting different values for β, we can use eqn (13) to find the respective PTT parameters
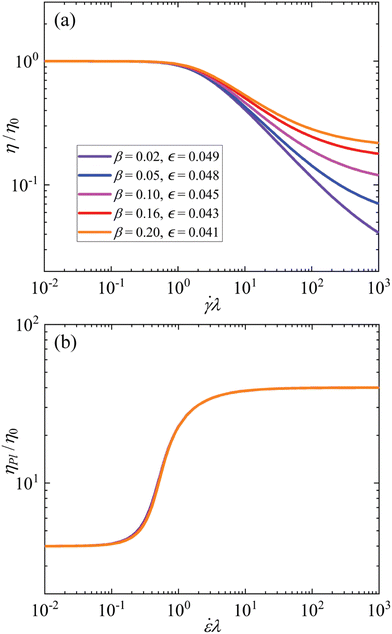
+ 4ηs, as predicted by the l-PTT model. By setting ηPl,∞ equal to a constant and selecting different values for β, we can use eqn (13) to find the respective PTT parameters 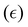 that generate fluids with almost the same steady extensional viscosities, but different steady shear viscosities. Based on the CaBER measurements for the series of fluids without added salt, we select a representative extensional viscosity of ηE ≈ 40η0 (see Fig. 3(b)). Assuming that the high extension rate viscosity plateau is the same in planar and uniaxial elongation, which is true for the l-PTT model,64 we set ηPl,∞/η0 = 40 and generate a set of five fluids with varying degrees of shear thinning, but nearly identical extension hardening, as can be seen in Fig. 7.
that generate fluids with almost the same steady extensional viscosities, but different steady shear viscosities. Based on the CaBER measurements for the series of fluids without added salt, we select a representative extensional viscosity of ηE ≈ 40η0 (see Fig. 3(b)). Assuming that the high extension rate viscosity plateau is the same in planar and uniaxial elongation, which is true for the l-PTT model,64 we set ηPl,∞/η0 = 40 and generate a set of five fluids with varying degrees of shear thinning, but nearly identical extension hardening, as can be seen in Fig. 7.
Note that by our chosen approach we are not attempting to obtain a quantitative match to the experimental data, but rather to use a simplified numerical model to gain a deeper insight into the physics underlying the observed flow instabilities. Due to the entangled nature of the experimental test fluids, they exhibit different relaxation times in shear (reptation time, 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c, Table 1) and extension (Rouse time λ, Table 1). Obtaining a quantitative match to their rheology would require using either a multi-mode approach65 or an appropriate model for entangled solutions (e.g., Rolie-Poly model66). However, either of these approaches would induce many additional material parameters, which would complicate the analysis of the physical mechanisms. Consequently, we stick to the simplicity of the l-PTT model and compromise with qualitative comparisons between the experiment and the model.
c, Table 1) and extension (Rouse time λ, Table 1). Obtaining a quantitative match to their rheology would require using either a multi-mode approach65 or an appropriate model for entangled solutions (e.g., Rolie-Poly model66). However, either of these approaches would induce many additional material parameters, which would complicate the analysis of the physical mechanisms. Consequently, we stick to the simplicity of the l-PTT model and compromise with qualitative comparisons between the experiment and the model.
In Fig. 8 we present the shear thinning parameter S and the effective Weissenberg number Wieff for the series of model fluids. Both S and Wieff are evaluated at a shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) =
= ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w and are plotted as a function of the Weissenberg number Wi = λ
w and are plotted as a function of the Weissenberg number Wi = λ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) near the stagnation point of the cross-slot geometry (as defined in eqn (5)). Note that here the extension rate in the cross-slot device is given by
near the stagnation point of the cross-slot geometry (as defined in eqn (5)). Note that here the extension rate in the cross-slot device is given by ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1.5U/(W/2) since the simulations are performed in 2D. The shear thinning parameter of the model fluids Fig. 8(a) is generally similar in form to that of the experimental test fluids (Fig. 2(b)). However, Wieff for the model fluids Fig. 8(a) shows a non-monotonicity that is not observed in the experiment (Fig. 4). The implications of this will be discussed further below.
= 1.5U/(W/2) since the simulations are performed in 2D. The shear thinning parameter of the model fluids Fig. 8(a) is generally similar in form to that of the experimental test fluids (Fig. 2(b)). However, Wieff for the model fluids Fig. 8(a) shows a non-monotonicity that is not observed in the experiment (Fig. 4). The implications of this will be discussed further below.
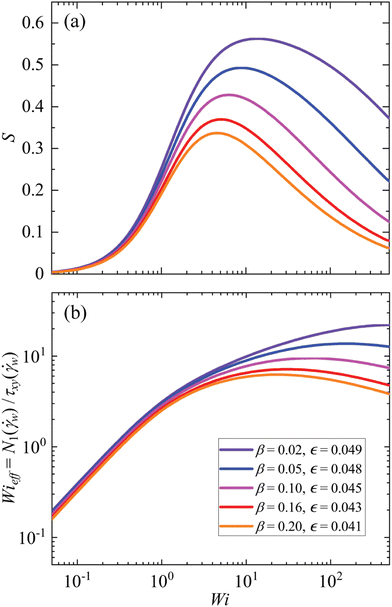
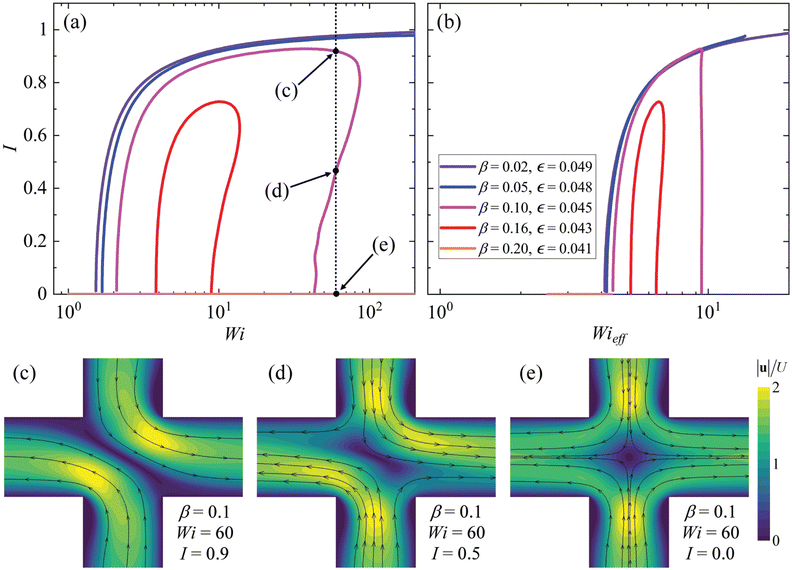
Fig. 9(a) presents the flow asymmetry parameter I versus Wi for the five different fluids with the same extensional response and decreasing degree of shear thinning in the range 0.02 ≤ β ≤ 0.2. For the most shear thinning fluids (β = 0.02 and β = 0.05), the flow becomes asymmetric via supercritical pitchfork bifurcations occurring between Wi = 1.5 and Wi = 1.8 and stays asymmetric up to the highest flow rate examined (Wi = 200). However, for the fluid with β = 0.1, the situation is strikingly different. As for the more shear thinning fluids, the flow loses symmetry via a supercritical bifurcation (here around Wi = 2.1), and a plateau in I is reached. However, the plateau only persists up to Wi = 80, before for higher Wi, I rapidly decreases and the flow becomes symmetric again via a subcritical pitchfork bifurcation. For further increases in Wi, no new asymmetric states are observed. The same trend is observed for the fluid with β = 0.16, which exhibits weaker shear thinning than β = 0.1 and for which asymmetric states exist only for a limited range of 4 ≲ Wi ≲ 9. Finally, for the least strongly shear thinning fluid with β = 0.2 asymmetric flow states are not observed at any Wi.
By comparing Fig. 8 and 9(a), we can see that the recovery of symmetry in fluids with β = 0.1 and β = 0.16 occurs for Weissenberg numbers (Wi≈80 and Wi ≈ 9, respectively) at which the shear thinning parameter for both fluids has reduced to S ≈ 0.3 and is decreasing. However, for the same values of Wi, the values of Wieff are both near their peak, but have not decreased appreciably. Indeed, for β = 0.16 and Wi = 0.9, Wieff is still increasing albeit gradually. Although both shear thinning and normal stresses contribute to reduced flow resistance, the earlier peak in the S curve suggests that shear thinning reduction contributes more to symmetry recovery than the reduction of Wieff. This is made more evident by plotting I as a function of Wieff in Fig. 9(b), the effect of which is only to distort and compresses each curve along the abscissa, but not to prevent the recovery of symmetry for either of the two particular fluids. We therefore attribute the recovery of symmetry in those two cases mostly to the reduction of shear thinning at higher values of Wi, as quantified by the parameter S shown in Fig. 8(a).
Although the rheology of the experimental test fluids and the model numerical fluids do not quantitatively match, we note a clear qualitative match between the simulations and the experiments. Flows with strongly shear thinning viscoelastic solutions become asymmetric and remain asymmetric up to very high flow rates or Wi. Moderately shear thinning solutions present asymmetric states only for a limited range of Wi, and for very weakly shear thinning solutions, the instability does not arise. Given that in the simulations we have excluded inertia and we have examined the response of fluids with varying shear thinning but the same steady extensional rheology, the present theoretical analysis validates that the asymmetric to symmetric transition is not related to either inertial or reduced elasticity effects, but is somehow related to shear thinning. One possible difference between the experimental and the numerical results relates to the criticality of the asymmetric to symmetric transition. In the simulations this is subcritical, but in the experiments it does not appear to be so. Although in the experiments we did not specifically test for hysteresis effects in the transitions, by the flow driving protocol we employed (Section 2.4) we would expect a subcritical transition to appear very abrupt as opposed to the quite gradual return to symmetry observed with increasing Wi in Fig. 6(a). Although inertia is clearly not required to drive this transition, it is possible that inertia affects the form of the transition (Reynolds numbers in the experiments are >1 where the asymmetric to symmetric transition is observed). It may be interesting in future to examine hysteresis effects and the possible influence of inertia on this transition in more detail.
Before we proceed to the analysis of the physical mechanisms underlying the observed flow transitions, it is worth taking a closer look at the velocity magnitude contours presented beneath the two plots in Fig. 9, for β = 0.1 and Wi = 60. As shown in the plot in Fig. 9(a), three solution branches coexist for Wi = 60; the upper solution branch (Fig. 9(c)), which is characterized by strongly asymmetric steady states, the middle branch (Fig. 9(d)), which incorporates asymmetric steady states, and the symmetric branch (Fig. 9(e)), which carries only symmetric solutions with I = 0. According to bifurcation analysis, the steady states on the upper branch are stable (can be observed in nature). The steady states on the symmetric branch are stable for all Wi values before the supercritical (Wi < 2.1 for β = 0.1) and after the subcritical (Wi > 42 for β = 0.1) pitchfork bifurcations, while they are unstable (cannot be observed in nature) for the range 2.1 < Wi < 42 (for β = 0.1). Finally, the steady states that lie on the middle branch are always unstable (cannot be observed in nature). The stable asymmetric steady state in Fig. 9(c), exhibits all of the flow characteristics observed in the strongly asymmetric states in the experiment (see Fig. 5), with the stagnation point being absent and almost all fluid coming from the upper (lower) inflow arm ending up in the right (left) outflow arm. The same match is observed in the case where symmetry is recovered, where we can distinguish a low-velocity elastic ‘strand’ region, extending from the stagnation point into the outflow arms, exactly as observed in the experimental μ-PIV data (see Fig. 5). One can also notice, both in the experiment (Fig. 5) and the simulations (Fig. 9(e)), that recirculation vortices exist upstream of both reentrant corners in cases where symmetry is recovered, accompanied by a velocity overshoot upstream of the stagnation point. We believe this is the first time (either experimentally or theoretically) that a transition from an asymmetric to a symmetric flow state has been reported as Wi is increased in the cross-slot device.
4.4 Proposed physical mechanism
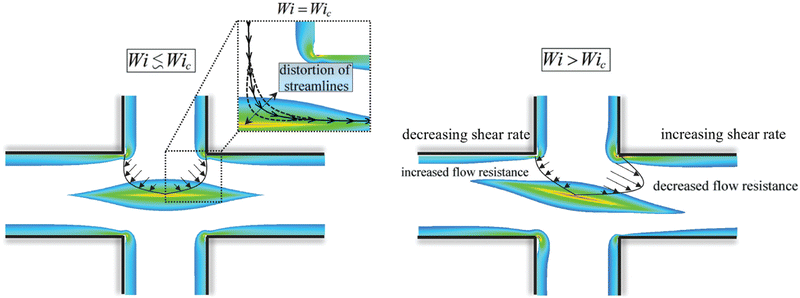
Based on present observations and knowledge gained from previous studies,11,21,22,26,28,29,34–37 we can propose a physical mechanism for the onset of steady flow asymmetry in the cross-slot. When the flow is symmetric for Wi < Wic, shear rates, hence also the shear-rate-dependent fluid viscosity, are equal on both sides of the stagnation point and the extensionally-thickened elastic strand of fluid (indicated by the colour contours around the stagnation point in Fig. 10) lies symmetrically about the outflow axis. At the onset of critical conditions (i.e., Wi = Wic), the accumulation of elastic tensile stress along the streamlines curving near the stagnation point (as per the Pakdel–McKinley criterion11,12,33,41) causes a disturbance that perturbs the elastic strand randomly to one side or the other. As outlined in Fig. 10, the deflection of the elastic wake to one side causes the shear rates across the two fluid paths to differ, which due to shear thinning results in an increased viscosity and flow resistance along one path and a decreased viscosity and flow resistance along the other. Thus, for a shear thinning viscoelastic fluid, an initial perturbation of the elastic strand about the stagnation point can be sustained by the positive feedback resulting from the shear thinning. If shear thinning remains significant as Wi is increased beyond Wic, steady and strongly asymmetric flow patterns like those in Fig. 5 and 9, can arise. Thus, the instability is triggered and maintained by a combination of elasticity and shear thinning. According to our physical mechanism, both elasticity and shear thinning are required for the steady flow asymmetry to manifest. The initial bifurcation is induced by elasticity, but shear thinning is responsible for keeping the flow steadily on one branch or the other once the bifurcation has occurred.The recovery of symmetry for some fluids as Wi is increased to high values is attributed to the simultaneous approach towards the high shear rate plateau of the steady shear flow curve. At a sufficiently high flow rate through the cross-slot, shear thinning effects will become negligible. As a result, a symmetric (but highly elastic) flow state can be reestablished.
Note that in the preceding outline of our proposed physical mechanism, we refer to “shear thinning” as being the cause of the flow resistance variation between the two diverging flow paths, as in most instances (i.e., for real viscoelastic fluids or for constitutive models that incorporate shear thinning) we expect shear thinning to provide the dominant effect. For non-shear thinning fluid models that exhibit steady asymmetric flow states (e.g., Oldroyd-B or FENE-CR with low values of β ≲ 0.536,42), the difference in flow resistance between the two flow paths is attributed to more subtle effects arising from a synergy between the lag time for stress to respond to a change in the shear rate, and the act of normal stresses along the curving streamlines passing around the corners of the cross-slot (as described in Section 1).43
It is worthwhile mentioning the similarity between the present results obtained in the cross-slot geometry and results presented recently showing flow asymmetries around cylinders in microchannels, which also exhibited the recovery of symmetry for high Wi and low S conditions.20–22 The similarity between the two flows may not be immediately obvious, but both involve mixed shear and extensional flows with a location where the flow divides into two paths causing a change in the shear rate, and a nearby stagnation point where high elastic stresses are generated at sufficient Wi. It may not then be surprising if both instabilities are governed by similar mechanisms involving the interaction between shear thinning and extension hardening effects. If this is indeed the case it would provide a plausible explanation for the results of Davoodi et al.,41 who found by numerical simulations that placing a cylinder in the centre of a cross-slot geometry did not prevent the instability from occurring but only shifted the onset conditions depending on the cylinder radius.
5 Conclusion
In this study, we have examined the flow of HPAA solutions with different degrees of shear thinning and elasticity in a cross-slot microchannel. Our primary objective was to establish a comprehensive understanding of the relationship between steady asymmetric flow states and the rheological properties of the test fluid. To achieve this, our analysis focused on two key rheological parameters: fluid elasticity, quantified by the Weissenberg number Wi, and the degree of shear thinning, expressed by the shear thinning parameter S. Previous studies predominantly attributed flow asymmetries in the cross-slot geometry to fluid elasticity alone. However, our findings challenge this notion, suggesting a coupling between the elasticity in the fluid induced by the extensional flow at the stagnation point, and shear thinning of the fluid due to the wall shear stress.Particularly compelling, we discovered that at high Weissenberg numbers, where fluid elasticity dominates but shear thinning becomes minimal, the flow can recover symmetry from an asymmetric state. This observation strongly suggests that shear thinning also plays a crucial role in the generation and maintenance of the asymmetric flow state. From numerical simulations it became evident that achieving the right balance between shear thinning and elasticity is vital for controlling the flow state within the cross-slot geometry.
Our combined experimental and numerical approaches provided the basis for a proposed physical mechanism underlying viscoelastic flow instabilities in the cross-slot device. Furthermore, they offered valuable insights providing a deeper understanding of these instabilities. The results obtained from this study contribute to the existing knowledge and shed light on the intricacies of flow behaviours in the cross-slot geometry.
Data availability statement
The data that support the findings of this study are available within the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the support of the Okinawa Institute of Science and Technology Graduate University (OIST) with subsidy funding from the Cabinet Office, Government of Japan, and also funding from the Japan Society for the Promotion of Science (JSPS, Grant No. 21K03884, 22K14184).Notes and references
- S. S. Datta, A. M. Ardekani, P. E. Arratia, A. N. Beris, I. Bischofberger, G. H. McKinley, J. G. Eggers, J. E. López-Aguilar, S. M. Fielding, A. Frishman, M. D. Graham, J. S. Guasto, S. J. Haward, A. Q. Shen, S. Hormozi, A. Morozov, R. J. Poole, V. Shankar, E. S. G. Shaqfeh, H. Stark, V. Steinberg, G. Subramanian and H. A. Stone, Phys. Rev. Fluids, 2022, 7, 080701 CrossRef.
- V. Steinberg, Annu. Rev. Fluid Mech., 2021, 53, 27–58 CrossRef.
- C. A. Browne and S. S. Datta, Sci. Adv., 2021, 7, eabj2619 CrossRef CAS PubMed.
- Y. Li and V. Steinberg, Sci. Rep., 2023, 13, 1064 CrossRef CAS PubMed.
- P. G. De Gennes, J. Chem. Phys., 1974, 60, 5030–5042 CrossRef CAS.
- A. Keller and J. A. Odell, Colloid Polym. Sci., 1985, 263, 181–201 CrossRef CAS.
- T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016–2021 CrossRef CAS PubMed.
- C. W. Macosko, Rheology: Principles, Measurements, and Applications, Wiley, 1996 Search PubMed.
- F. A. Morrison, Understanding Rheology, Oxford University Press, 2001 Search PubMed.
- G. H. McKinley, P. Pakdel and A. Öztekin, J. Non-Newtonian Fluid Mech., 1996, 67, 19–47 CrossRef CAS.
- P. Pakdel and G. H. McKinley, Phys. Rev. Lett., 1996, 77, 2459–2462 CrossRef CAS PubMed.
- A. Öztekin, B. Alakus and G. H. McKinley, J. Non-Newtonian Fluid Mech., 1997, 72, 1–29 CrossRef.
- S. J. Muller, R. G. Larson and E. S. G. Shaqfeh, Rheol. Acta, 1989, 28, 499–503 CrossRef CAS.
- G. H. McKinley, A. Öztekin, J. A. Byars and R. A. Brown, J. Fluid Mech., 1995, 285, 123–164 CrossRef CAS.
- A. Groisman and V. Steinberg, Nature, 2000, 405, 53–55 CrossRef CAS PubMed.
- S. J. Muller, Korea-Aust. Rheol. J., 2008, 20, 117–125 Search PubMed.
- A. Groisman and V. Steinberg, Nature, 2001, 410, 905–908 CrossRef CAS PubMed.
- J. Zilz, C. Schäfer, C. Wagner, R. J. Poole, M. A. Alves and A. Lindner, Lab Chip, 2014, 14, 351–358 RSC.
- L. Casanellas, M. A. Alves, R. J. Poole, S. Lerouge and A. Lindner, Soft Matter, 2016, 12, 6167–6175 RSC.
- S. J. Haward, C. C. Hopkins and A. Q. Shen, J. Non-Newtonian Fluid Mech., 2020, 278, 104250 CrossRef CAS.
- S. Varchanis, C. C. Hopkins, A. Q. Shen, J. Tsamopoulos and S. J. Haward, Phys. Fluids, 2020, 32, 053103 CrossRef CAS.
- S. J. Haward, C. C. Hopkins, S. Varchanis and A. Q. Shen, Lab Chip, 2021, 21, 4041–4059 RSC.
- L. E. Rodd, T. P. Scott, D. V. Boger, J. J. Cooper-White and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2005, 129, 1–22 CrossRef CAS.
- L. E. Rodd, J. J. Cooper-White, D. V. Boger and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2007, 143, 170–191 CrossRef CAS.
- E. M. Ekanem, S. Berg, S. De, A. Fadili, T. Bultreys, M. Rücker, J. Southwick, J. Crawshaw and P. F. Luckham, Phys. Rev. E, 2020, 101, 042605 CrossRef CAS PubMed.
- P. E. Arratia, C. C. Thomas, J. Diorio and J. P. Gollub, Phys. Rev. Lett., 2006, 96, 144502 CrossRef CAS PubMed.
- J. A. Pathak and S. D. Hudson, Macromolecules, 2006, 39, 8782–8792 CrossRef CAS.
- S. J. Haward and G. H. McKinley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 031502 CrossRef PubMed.
- S. J. Haward and G. H. McKinley, Phys. Fluids, 2013, 25, 083104 CrossRef.
- P. C. Sousa, F. T. Pinho, M. S. N. Oliveira and M. A. Alves, Soft Matter, 2015, 11, 8856–8862 RSC.
- P. C. Sousa, F. T. Pinho and M. A. Alves, Soft Matter, 2018, 14, 1344–1354 RSC.
- S. J. Haward, Biomicrofluidics, 2016, 10, 043401 CrossRef CAS PubMed.
- S. J. Haward, G. H. McKinley and A. Q. Shen, Sci. Rep., 2016, 6, 33029 CrossRef.
- R. J. Poole, M. A. Alves and P. J. Oliveira, Phys. Rev. Lett., 2007, 99, 164503 CrossRef CAS.
- L. Xi and M. D. Graham, J. Fluid Mech., 2009, 622, 145–165 CrossRef CAS.
- G. N. Rocha, R. J. Poole, M. A. Alves and P. J. Oliveira, J. Non-Newtonian Fluid Mech., 2009, 156, 58–69 CrossRef CAS.
- S. J. Haward, T. J. Ober, M. S. N. Oliveira, M. A. Alves and G. H. McKinley, Soft Matter, 2012, 8, 536–555 RSC.
- B. Qin, R. Ran, P. F. Salipante, S. D. Hudson and P. E. Arratia, Soft Matter, 2020, 16, 6969–6974 RSC.
- R. G. Larson, S. J. Muller and E. S. G. Shaqfeh, J. Non-Newtonian Fluid Mech., 1994, 51, 195–225 CrossRef CAS.
- F. A. Cruz, R. J. Poole, A. M. Afonso, F. T. Pinho, P. J. Oliveira and M. A. Alves, J. Non-Newtonian Fluid Mech., 2016, 227, 65–79 CrossRef CAS.
- M. Davoodi, A. F. Domingues and R. J. Poole, J. Fluid Mech., 2019, 881, 1123–1157 CrossRef CAS.
- D. O. Canossi, G. Mompean and S. Berti, Europhys. Lett., 2020, 129, 24002 CrossRef CAS.
- S. Varchanis, J. Tsamopoulos, A. Q. Shen and S. J. Haward, J. Non-Newtonian Fluid Mech., 2022, 300, 104698 CrossRef CAS.
- S. J. Haward, N. Kitajima, K. Toda-Peters, T. Takahashi and A. Q. Shen, Soft Matter, 2019, 15, 1927–1941 RSC.
- G. Meineke, M. Hermans, J. Klos, A. Lenenbach and R. Noll, Lab Chip, 2016, 16, 820–828 RSC.
- N. Burshtein, S. T. Chan, K. Toda-Peters, A. Q. Shen and S. J. Haward, Curr. Opin. Colloid Interface, 2019, 43, 1–14 CrossRef CAS.
- J. Gottmann, M. Hermans and J. Ortmann, Phys. Proc., 2012, 39, 534–541 CrossRef.
- A. V. Dobrynin, R. H. Colby and M. Rubinstein, Macromolecules, 1995, 28, 1859–1871 CrossRef CAS.
- K. Yasuda, J. Text. Eng., 2006, 52, 171–173 CrossRef.
- V. M. Entov and E. J. Hinch, J. Non-Newtonian Fluid Mech., 1997, 72, 31–54 CrossRef CAS.
- S. L. Anna and G. H. McKinley, J. Rheol., 2001, 45, 115–138 CrossRef CAS.
- R. K. Shah and A. L. London, Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data, Academic Press, New York, 1978 Search PubMed.
- R. G. Larson and J. J. Magda, Macromolecules, 1989, 22, 3004–3010 CrossRef CAS.
- C. D. Meinhart, S. T. Wereley and M. H. B. Gray, Meas. Sci. Technol., 2000, 11, 809–814 CrossRef CAS.
- C. C. Hopkins, S. J. Haward and A. Q. Shen, Phys. Rev. Lett., 2021, 126, 054501 CrossRef CAS PubMed.
- N. Phan-Thien and R. I. Tanner, J. Non-Newtonian Fluid Mech., 1977, 2, 353–365 CrossRef.
- T. C. Papanastasiou, N. Malamataris and K. Ellwood, Int. J. Numer. Meth. Fl., 1992, 14, 587–608 CrossRef CAS.
- S. Varchanis, A. Syrakos, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newtonian Fluid Mech., 2019, 267, 78–97 CrossRef CAS.
- S. Varchanis, A. Syrakos, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newtonian Fluid Mech., 2020, 284, 104365 CrossRef CAS.
- S. Varchanis and J. Tsamopoulos, Sci. Talks, 2022, 100053 CrossRef.
- S. Varchanis, Y. Dimakopoulos and J. Tsamopoulos, Phys. Rev. Fluids, 2017, 2, 124001 CrossRef.
- A. Kalb, L. A. Villasmil-Urdaneta and M. Cromer, Phys. Rev. Fluids, 2017, 2, 071301 CrossRef.
- A. Kalb, L. A. Villasmil-Urdaneta and M. Cromer, J. Non-Newtonian Fluid Mech., 2018, 262, 79–91 CrossRef CAS.
- D. Shogin, Phys. Fluids, 2021, 33, 123112 CrossRef CAS.
- S. Varchanis, Y. Dimakopoulos and J. Tsamopoulos, J. Rheol., 2018, 62, 25–47 CrossRef CAS.
- A. E. Likhtman and R. S. Graham, J. Non-Newtonian Fluid Mech., 2003, 114, 1–12 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Two example movies depicting time-dependent viscoelastic flows through the cross-slot geometry. See DOI: https://doi.org/10.1039/d3sm01209c |
| ‡ Present address: Center for Computational Biology, Flatiron Institute, New York, New York 10010, USA. |
| This journal is © The Royal Society of Chemistry 2024 |