Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Diffusion across particle-laden interfaces in Pickering droplets†
Yanyan
Liu
,
Mingjun
Xu
,
Luis M.
Portela
and
Valeria
Garbin
 *
*
Department of Chemical Engineering, Delft University of Technology, van der Maasweg 9, Delft 2629 HZ, The Netherlands. E-mail: v.garbin@tudelft.nl
First published on 4th December 2023
Abstract
Emulsions stabilized by nanoparticles, known as Pickering emulsions, exhibit remarkable stability, which enables applications ranging from encapsulation, to advanced materials, to chemical conversion. The layer of nanoparticles at the interface of Pickering droplets is a semi-permeable barrier between the two liquid phases, which can affect the rate of release of encapsulates, and the interfacial transfer of reactants and products in biphasic chemical conversion. A gap in our fundamental understanding of diffusion in multiphase systems with particle-laden interfaces currently limits the optimal development of these applications. To address this gap, we developed an experimental approach for in situ, real-time quantification of concentration fields in Pickering droplets in a Hele-Shaw geometry and investigated the effect of the layer of nanoparticles on diffusion of solute across a liquid–liquid interface. The experiments did not reveal a significant hindrance on the diffusion of solute across an interface densely covered by nanoparticles. We interpret this result using an unsteady diffusion model to predict the spatio-temporal evolution of the concentration of solute with a particle-laden interface. We find that the concentration field is only affected in the immediate vicinity of the layer of particles, where the area available for diffusion is affected by the particles. This defines a characteristic time scale for the problem, which is the time for diffusion across the layer of particles. The far-field concentration profile evolves towards that of a bare interface. This localized effect of the particle hindrance is not measurable in our experiments, which take place over a much longer time scale. Our model also predicts that the hindrance by particles can be more pronounced depending on the particle size and physicochemical properties of the liquids and can ultimately affect performance in applications.
Introduction
Pickering emulsions and foams, which are liquid–fluid dispersions stabilized by solid particles instead of molecular surfactants,1 find a wide range of applications in advanced materials,2,3 food science,4,5 and chemical conversion.6,7 Solid particles offer superior stability to emulsions compared to molecular surfactants.1 Depending on the particle radius, a, and the three-phase contact angle, θ, the energy cost of removing a particle from a liquid–fluid interface can be 102–106 times larger than for a molecular surfactant, resulting in long-term stability of foams and emulsions.8The layer of solid particles at the liquid–fluid interface in a Pickering system is partially permeable, a feature that enables controlled release,9 selective filtration3 and exchange of reactants and products in chemical conversion.6,7 Several studies have explored the macroscopic effect of particles on diffusion across interfaces in Pickering systems, for instance during drop dissolution,10,11 bubble dissolution,12–14 evaporation of liquid marbles,15–17 and compositional ripening.18,19 Most of these works report that the addition of particles hinders diffusion across the interface, but the effect has not been quantified because the experiments involved a change in interfacial area, which causes morphological changes of the monolayer (buckling or particle expulsion12,17). It is therefore difficult to isolate the effect of the particles on diffusion in controlled conditions. The same phenomena are also relevant to evaporation of aerosol droplets containing particles and surface active agents, such as respiratory droplets.20
Another challenge in quantifying the effect of interfacial particles on diffusive transport across a liquid–fluid interface lies in performing controlled measurements of concentration fields in multi-component, multiphase systems. Multicomponent systems exhibit rich phenomenology upon evolution of their composition21 that can be difficult to control, for instance nucleation and phase separation,22 compositional Marangoni effects23 and density changes.24 Experiments with pH indicators enable to monitor qualitatively the time evolution of composition in reactive surface nanodroplets,25 but space- and time-resolved measurements of the concentration field and its evolution in multicomponent droplets remains challenging.
Quantitative measurements of concentration fields have been achieved for a gas–liquid system, using calibrated fluorescence intensity measurements of diffusion of CO2 from a single, dissolving bubble in a Hele-Shaw geometry.26 The limitation of dissolving bubbles or drops is that the motion of the interface imparts a bulk flow, which complicates the analysis of diffusive transport23,26 and that, due to the gradual decrease in interfacial area, a layer of particles on the interface would change morphology over time.
In this paper, we design an experimental system to characterize the diffusive transport of a trace amount of fluorescent solute across the interface of a Pickering droplet, which results in a constant droplet volume and constant interfacial area throughout the experiment. We use a Hele-Shaw geometry for quantitative mapping of the quasi-2D concentration field of solute as a function of time. The results can be understood in terms of an unsteady diffusion model where the area through which diffusion occurs is determined by the arrangement of particles at the interface. By comparing the experimental results and model predictions with the case of a bare droplet, we reveal the spatio-temporal effect of particles on the diffusion of solute across the interface. These insights will ultimately pave the way towards better understanding and rational design of complex, multiphase systems for a variety of applications.
Materials and methods
Materials
1-Heptanol (synthesis quality), hexadecane (≥99%) and rhodamine B (RhB) were purchased from Merck Ltd. The fluorophore RhB, with excitation wavelength of 540 nm and emission wavelength of 625 nm, was selected after screening many fluorophores, because it is soluble in both water and heptanol and emits a strong fluorescent signal in both solvents. Potassium hydrogen phosphate (≥98%) and potassium dihydrogen phosphate (≥99%) were purchased from Brunschwig Chemie B.V. for the preparation of 20 mmol L−1 potassium phosphate buffer solution (pH = 7), which was used to prepare 0.1 mmol L−1 rhodamine B solutions. Partly hydrophobized fumed silica nanoparticles (HDK H15, Wacker Chemie) were kindly provided by IMCD group (The Netherlands). The primary spherical particles of radius a = 5–15 nm typically form non-spherical, porous aggregates of approximately 100 nm, as reported in the literature.27 The hydrophobic character of H15 nanoparticles originates from substitution of 50% of surface hydroxyl groups by dimethylsiloxy groups. Milli-Q water was used, if applicable, for the preparation of aqueous solutions. All chemicals were used as received.Partition coefficients, α = Cw/Co, were measured by equilibrating the concentration of RhB in the organic (Co) and aqueous phase (Cw) for 2 days and measuring the equilibrium concentrations with a UV-VIS spectrometer (Hach Lange DR5000). The partition coefficient of RhB for water/heptanol is α ≈ 1/88 and for water/hexadecane it is α ≈ 1. The diffusivity of RhB in water, Dw = 4.2 × 10−10 m2 s−1, was taken from literature.28 The diffusivity in the organic phase, Do, was computed via Einstein–Stokes's law using literature values for the viscosities29 of hexadecane and heptanol, resulting in Do = 1.2 × 10−10 m2 s−1 (hexadecane) and Do = 0.6 × 10−10 m2 s−1 (heptanol). All experiments were conducted at ambient temperature and pressure.
Fluorescent intensity calibration in Hele-Shaw geometry
Hele-Shaw cells were fabricated by gluing an imaging spacer (13 mm inner diameter, Grace bio-Labs, Secure-Seal™ series) of thickness h = 175 μm on a glass slide (Thermo Scientific) and sealing the top with a glass coverslip (VMR). A Hele-Shaw geometry was selected to obtain a quasi-2D concentration profile, i.e., independent of the vertical direction. The concentration of dye in the Hele-Shaw cell was then calibrated against fluorescent intensity, as the cell height was the same in all experiments. The fluorescent intensity calibration was performed for water and heptanol by a series of known RhB concentrations. The details are given in ESI† (Fig. S1).Preparation of Pickering emulsion and isolation of single droplet
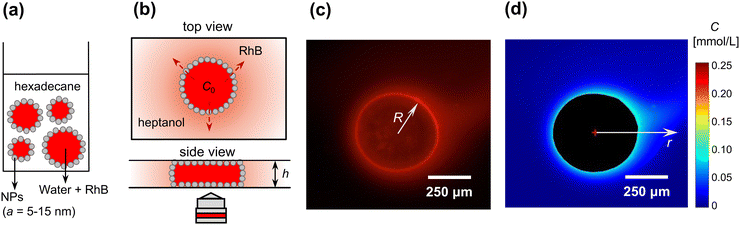
The experimental setup and method to quantify the diffusive transport of solute across the interface of a Pickering droplet with spatial and temporal resolution is shown in Fig. 1. First, a 1 wt% suspension of the silica nanoparticles was formed by dispersing the particles in hexadecane via ultrasonication (20 min). A Pickering emulsion was then prepared by shaking in a vortex mixer an aqueous solution of 1 mmol L−1 RhB with the suspension of nanoparticles in hexadecane, forming a water-in-oil emulsion (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v), as shown in the schematic of Fig. 1(a). The droplet sizes obtained were in the range 100–1000 μm, and the interface was densely covered by nanoparticles as confirmed by optical microscopy.
1 v/v), as shown in the schematic of Fig. 1(a). The droplet sizes obtained were in the range 100–1000 μm, and the interface was densely covered by nanoparticles as confirmed by optical microscopy.
The dye RhB possesses a hydrophobic part and a positively charged group; it is found to adsorb on the partially hydrophobic H15 silica nanoparticles, either because of hydrophobic–hydrophobic interactions, or because of electrostatic interaction with negatively charged silica. Direct measurement of RhB concentration inside the Pickering drops is therefore not possible, due to the layer of nanoparticles with adsorbed dye. Negatively charged dyes (fluorescein and its derivatives) were tested to prevent adsorption via electrostatic repulsion, but were found to either be insoluble, or to not emit a detectable fluorescent signal, in one of the solvents (see ESI†).
The emulsion was left to rest for 1 day, to allow the equilibration of the fluorescent dye between the two liquid phases (water/hexadecane, α ≈ 1) and on the particles. The extent of adsorption on the nanoparticles was then quantified in a control experiment by breaking the emulsion by centrifugation, recovering the aqueous phase and measuring the RhB concentration in water by fluorescent intensity; the concentration is found to be 0.1 mmol L−1, and the same concentration is expected in hexadecane due to equilibrium partitioning between equal volumes with α ≈ 1. Approximately 80% of the dye initially present is therefore adsorbed on the particles. The concentration of dye in the droplets is still sufficient to detect a fluorescence signal and map the concentration profiles during the diffusion experiment. The fluorescence intensity coming from the layer of nanoparticles does not saturate the camera or affect the concentration measurement in the outer phase.
To isolate a single Pickering droplet, a small volume of emulsion was first transferred onto a glass slide and diluted with pure hexadecane. The dilution with pure hexadecane causes the concentration of RhB in the Pickering droplets to slightly decrease due to partitioning; the concentration of RhB in a droplet after the dilution step can be calculated after the diffusion experiment has taken place, by measuring the total mass of RhB diffused from the droplet, and is estimated at C0 ≈ 0.09 mmol L−1.
A single Pickering droplet was then transferred to a Hele-Shaw cell filled with heptanol, in which RhB is 88 times more soluble than in hexadecane, to initiate diffusion from the droplet through the particle-laden interface. Manually placing the glass cover slip to flatten the Pickering droplet and seal the Hele-Shaw geometry typically caused a spurious flow, which affects the expected radial symmetry of the concentration profiles. Because imaging starts after 20–30 s, due to manual positioning of the sample on a microscope, while diffusion of solute from the droplet starts immediately upon placement in heptanol, the early stages of diffusion are not captured.
An important advantage of the choice of RhB as the solute is that because the volume fraction needed to detect a fluorescent signal and measure concentrations is less than 0.01%, the volume of the drop is essentially unchanged even after all the solute is transferred to the outer phase.
Experimental measurement of quasi-2D concentration field
Images were captured by a fluorescence microscope (Olympus BXFM upright microscope, 4× magnification) mounted with a digital camera (DCC1645C, Thorlabs, frame rate 0.1 fps), as shown in Fig. 1(b). Due to the confinement in the Hele-Shaw cell (h = 175 μm), the Pickering droplet was squeezed to a cylindrical ‘pancake’ with h < 2R, R being the radius of the squeezed droplet. All experiments presented in the following, for bare and Pickering droplets, were performed on such ‘pancake’ droplets. Fig. 1(c) shows a typical image of RhB diffusing outwards from a Pickering droplet, where the concentration outside the droplet can be quantified by the fluorescent intensity. We expect that some RhB also desorbs from the nanoparticles when the droplet is placed in heptanol, due to the higher solubility of RhB in heptanol compared to hexadecane. In control experiments we quantified the mass of RhB desorbing from the nanoparticles and confirmed that it is about 2 orders of magnitude lower than the mass diffusing from the bulk of the droplet [see Fig. S3 and details given in ESI†], hence it is not a significant source of uncertainty on the concentration measurements.Using the fluorescent intensity calibration, the concentration distribution was extracted pixel by pixel, as shown in Fig. 1(d). The concentration as a function of distance from the droplet center, C(r), with r > R, was then calculated by computing the angular average. As shown in Fig. 1(c) and (d), the concentration was not radially symmetric, because of the small convective flow induced while manually placing the coverslip. The standard deviation on the angular average quantifies this deviation from radial symmetry and is taken as the error on C(r), since the other measurement errors are much smaller.
Diffusion model
Because the experiments are designed to observe transfer of a trace amount of solute across an interface without changing the drop volume, the interface of the drop remains static and no bulk convective flow is generated, such that we can describe the evolution of the concentration field, C(r, t), by simply solving the unsteady diffusion equation,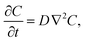 | (1) |
Diffusion of solute across a bare interface
To model the diffusion of a solute in the case of a bare interface, we assume that the drop in the Hele-Shaw geometry is a cylinder of radius R, and we solve eqn (1) in cylindrical coordinates to obtain C(r, t). The solute is initially present only in the droplet with uniform concentration C0, and it diffuses to the outer phase through the curved interface of the cylinder. In keeping with the experiments, the droplet phase (r < R) is water, where the diffusivity of solute is Dw, and the outer phase (r > R) is oil, where the diffusivity is Do.Equilibrium partitioning of the solute, governed by the partition coefficient α, is assumed to be instantaneously established at the water–oil interface, r = R:
| C|r=R− = αC|r=R+. | (2) |
Three-dimensional model of diffusion of solute across a particle-laden interface
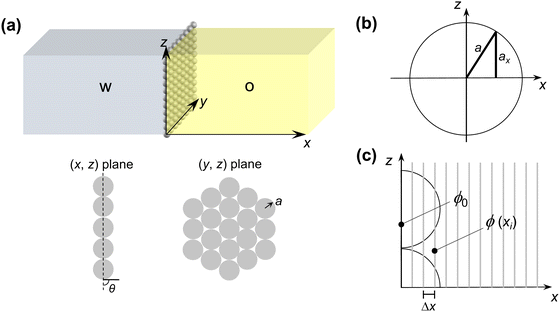
To model the diffusion of solute across a particle-laden interface, we consider for simplicity a planar interface between two semi-infinite domains. The assumption of a planar interface is justified by the large drop-to-particle size ratio in the experiments, R/a ∼ 103–104, where R is the drop radius and a is the particle radius. The assumption is also motivated by the fact that our goal here is to focus on the region close to the interface, to identify the effect of the particles.We assume that the particles form a monolayer at the interface, separating two semi-infinite, immiscible phases. Fig. 2(a) shows the schematic of the three-dimensional domain containing a liquid–liquid interface stabilized by solid particles, across which the solute is transferred from the water phase to the oil phase. The spherical particles, with three-phase contact angle θ = 90°, are arranged in a hexagonal configuration, covering a fraction of the total interfacial area 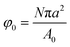 , where N/A0 is the number of particles per unit area.
, where N/A0 is the number of particles per unit area.
Eqn (1) is solved in Cartesian coordinates, with the x-axis normal to the interface. At the surface of the particles, a no-penetration boundary condition is imposed. The boundary conditions far from interface are C (x = L) = 0 and C (x = −L) = C0, with L = 500a. We checked that this domain size is sufficient for convergence of the concentration field. The concentration at the interface, x = 0, obeys instantaneous equilibrium partitioning, with partition coefficient α [see eqn (2)]. The boundary conditions in the y- and z-direction are periodic. The distance from the interface is normalized with the particle radius, a. The time t is made dimensionless by the characteristic time scale for diffusion of the solute over a distance equal to the particle radius a (based on the diffusion coefficient in the water phase, Dw):
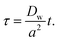 | (3) |
Quasi-1D model of diffusion of solute across a particle-laden interface
We propose a quasi-1D model to calculate average concentration profiles as a function of distance from a planar interface, C(x, t). In this model, we account for the effect of the particles as a decrease in the area available for diffusion. The diffusion equation for C(x, t) becomes: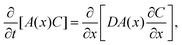 | (4) |
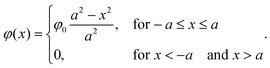 | (5) |
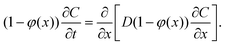 | (6) |
Results and discussion
Experimental concentration profiles for bare and Pickering droplets
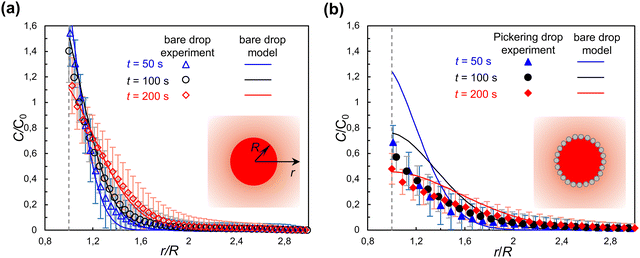
Fig. 3 shows the evolution of concentration profiles of solute RhB outside respectively a bare droplet and a Pickering droplet. The concentration is normalized by C0, the initial concentration inside the droplet. For a bare droplet, C0 is known. As explained in Methods, for a Pickering droplet C0 is calculated after the end of the experiment by measuring the total mass of RhB diffused from the drop.Fig. 3(a) shows that the experimental results of RhB diffusion from a bare droplet (R = 470 μm) agree well with the predictions of the bare interface model, which validates the assumptions of negligible dependence of the concentration on the vertical direction, and of no motion of the interface. As expected, because the water/heptanol partition coefficient causes the concentration at the interface to be higher in heptanol than in water, just outside the interface (r/R = 1), (vertical dashed line) it is C/C0 > 1. The error bars represent the standard deviation on the angular average from which C(r) is calculated; the convective flow induced by the placement of the cover glass after positioning the droplet significantly affects the precision of the measurement.
The validation of the bare drop experiments against the bare drop model will now enable us to directly compare the behavior of a bare droplet and a Pickering droplet of the same size. In experiments, it was not possible to obtain bare and Pickering droplets of the same size. However, the evolution of the concentration field depends on the drop size because the drop is a finite reservoir of solute. This is clearly seen in Fig. 3(a): the concentration just outside the interface, which is in equilibrium with the concentration inside the droplet via the partition coefficient, decreases over time as the drop is depleted of solute. Having confirmed that the bare drop model correctly predicts the evolution of the concentration field for a bare drop, we can calculate C(r, t) for a bare drop of the same size as a Pickering droplet, and compare them directly.
The experimental results for the concentration of RhB for a Pickering droplet are shown as solid symbols in Fig. 3(b), together with the prediction of the bare drop model for a bare droplet of the same size (solid lines), for comparison. With most of the water–oil interface covered by particles, we expected a significantly slower extraction of RhB to the outer phase for a Pickering droplet compared to a bare droplet. The experimental results show that at t = 50 s the concentration C/C0 for a Pickering droplet (R = 230 μm) is about half the value as for a bare droplet of the same size. With increasing time (t = 100 s and 200 s) the difference between the concentration profile for a Pickering and a bare droplet seems to gradually decrease. Additional experiments on different droplets (Fig. S4 in ESI†) show qualitatively similar behavior. The large uncertainties on C(r) and C0, due to the limitations of the experiments, do not allow us to draw a quantitative conclusion of the effect of nanoparticles on diffusion across a liquid–liquid interface. To gain further insights, we turn to the 3D and quasi-1D theoretical models of diffusion across a particle-laden interface.
Model predictions for diffusion across a particle-laden interface
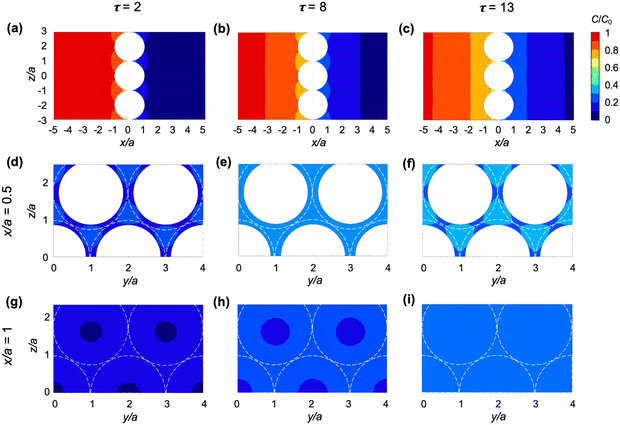
We first examine the predictions obtained from the 3D model of diffusion across a particle-laden interface, which gives access to the early times of the diffusion process, and to particle-scale details of the concentration field.We consider the spatio-temporal effect of particles on the diffusion of solute across a close-packed hexagonal monolayer of particles (ϕ0 ≈ 0.91) at the planar interface between two immiscible phases. To isolate the effect of the particles alone, in this simulation we set Dw = Do and α = 1, so that the liquid–liquid interface is fictitious. We do not aim to compare the results of this model directly with the experiments, both because of the large uncertainty in the concentration measurements, and because the particle size and surface coverage are not controlled precisely in the experiments.
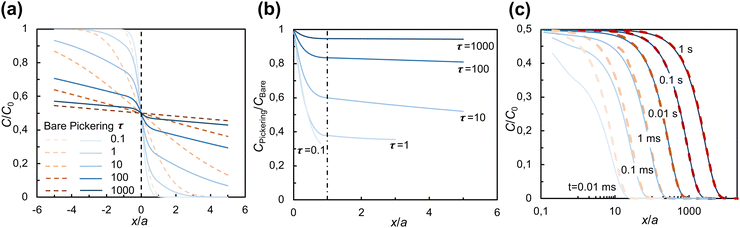
Fig. 4 shows the spatial effect of the particles on the iso-concentration contours for dimensionless times τ = 2, 8, and 13. The iso-concentration contours in the (x, z) plane [Fig. 4(a)–(c)] are affected by the particles only in the immediate vicinity of the interface (up to x/a ≈ 1) and become planar as diffusion progresses further (x/a > 1). Iso-concentration contours in the (y, z) plane are shown within the layer of particles (x/a = 0.5) and just outside the layer of particles (x/a = 1) in panels (d)–(f) and (g)–(i) of Fig. 4, respectively. As can be seen from both (x, z) and (y, z) cross-sections of the concentration field, the diffusion front advances faster in the center of the gaps between particles. This effect disappears at x/a ≈ 1 for τ = 13 [see Fig. 4(c) and (i)].
The quasi-1D model gives access to both early times and long times at little computational cost and, having been validated against the 3D model, can be used to examine the evolution of concentration profiles C(x, t) for comparison with our experiments. Fig. 5 shows the average solute concentration profiles C(x, t). As shown in Fig. 5(a), at the start of diffusion (τ = 0.1), the difference between the concentration across a Pickering interface (CPickering/C0, solid lines) and that across the bare interface (Cbare/C0, dashed lines) is minimal. From τ = 1 to 10, the difference becomes more significant. At later times (τ = 100 to 1000), the two sets of concentrations get closer with each other. At all times, in the solute-poor phase CPickering/C0 is lower than Cbare/C0, which highlights the hindrance to diffusion caused by the particles.
To isolate the effect of the particles more clearly, in Fig. 5(b), CPickering/C0 is compared with Cbare/C0 by plotting CPickering/Cbare. The spatial gradient of CPickering/Cbare is only significant in the region x/a < 1 and becomes substantially smaller outside this region, approaching zero in the far field, consistent with the qualitative behavior of the iso-concentration profiles in Fig. 4. Furthermore, CPickering/Cbare increases with time, approaching 1 when τ > 1000, indicating that the net effect of the particles on diffusion gradually decays with time.
In Fig. 5(c), we turn to dimensional times to compare the evolution of concentration profiles with our experimental observations. The dimensional time t is calculated for the particle size in our experiments, a = 15 nm (primary particle size of fumed silica). As can be seen, after t = 0.01 s, the concentration profiles for bare and Pickering interface start to overlap with each other. If we take as particle size a ≈ 100 nm (typical size of fumed silica aggregates), the dimensional time is approximately 100 times larger, with the concentration profile for a Pickering droplet converging to that of a bare droplet after t ≈ 1 s. After this time, the effect of the particles can no longer be observed. Given the assumption in the model of a monolayer of particles, while in experiment the particles may form multilayers or aggregated microstructures, this comparison is only qualitative. Nevertheless, it does explain why our experiments did not reveal a significant hindrance of the particles on diffusion across a Pickering interface and why the effect decreases with time (Fig. 3).
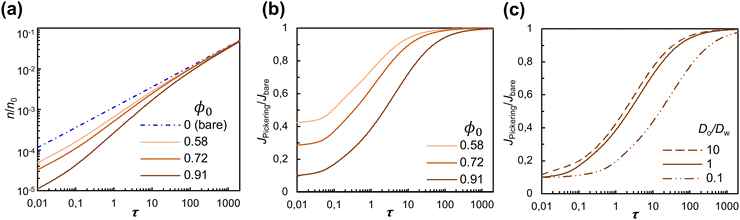
The quasi-1D model also enables us to examine the effects of surface coverage and of the physicochemical properties of the fluid phases without resorting to time-consuming 3D simulations. We compute the cumulative mass of solute transferred to the solute-poor phase, n(τ), from which we extract the diffusive flux at the interface, 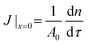 , where A0 is the total area of the interface, comprising both the particle-free area, A(x) = (1 − ϕ(x))A0, and the area occupied by particles. The quantities n(τ) and J|x=0 contain no information on the spatial concentration profile, rather, they are a global measure of the hindrance caused by particles on the diffusion process. In Fig. 6(a) the mass of solute n(τ) is compared for different surface coverages by particles, ϕ0 = 0.58, 0.72, 0.91, for a fictitious interface (Do = Dw and α = 1); n is normalized by n0, the total mass initially present in the solute-rich phase. At early times (τ < 0.1) the magnitude of n decreases linearly with the particle-free area, A(x) = (1 − ϕ0)A0. For later times (τ > 100), the magnitude of n and the diffusion rate dn/dτ of a Pickering interface are the same as for a bare interface, for all surface coverages considered.
, where A0 is the total area of the interface, comprising both the particle-free area, A(x) = (1 − ϕ(x))A0, and the area occupied by particles. The quantities n(τ) and J|x=0 contain no information on the spatial concentration profile, rather, they are a global measure of the hindrance caused by particles on the diffusion process. In Fig. 6(a) the mass of solute n(τ) is compared for different surface coverages by particles, ϕ0 = 0.58, 0.72, 0.91, for a fictitious interface (Do = Dw and α = 1); n is normalized by n0, the total mass initially present in the solute-rich phase. At early times (τ < 0.1) the magnitude of n decreases linearly with the particle-free area, A(x) = (1 − ϕ0)A0. For later times (τ > 100), the magnitude of n and the diffusion rate dn/dτ of a Pickering interface are the same as for a bare interface, for all surface coverages considered.
In Fig. 6(b) we plot JPickering/Jbare as a function of dimensionless time, τ, where JPickering is the flux at the interface for the cases with particles, and Jbare is for the case without particles. Note that the flux is calculated based on the total area A0 for all values of ϕ0 considered. Consistent with the results for n(τ), at early times the flux of solute for particle-laden interfaces is proportional to the particle-free area. It then gradually increases with time until it reaches the value for a bare interface (JPickering/Jbare = 1) for τ ≈ 100–1000. Indeed, as shown in Fig. 6(a), forτ ≈ 100–1000, dn/dτ approaches the value of a bare interface for all values of ϕ0.
Finally, we examine the effect of the diffusivity of the solute in the solute-poor phase (Do) and in the solute-rich phase (Dw). Fig. 6(c) shows the time evolution of JPickering/Jbare for a Pickering interface with ϕ0 = 0.91 and different values of Do/Dw. The solid line in Fig. 6(c) represents the reference case of a fictitious interface (Do/Dw = 1). For Do/Dw = 10, the curve is shifted to earlier times because the solute has higher diffusivity in the solute-poor phase than in the solute-rich phase, and for Do/Dw = 0.1 the curve is shifted to later times. The partition coefficient is found to have no effect on the time evolution of JPickering/Jbare (result not shown). Because the jump in equilibrium concentration at the interface between the two phases that α enforces [eqn (2)] is the same for a bare interface and for a particle-laden interface, the ratio JPickering/Jbare is independent of α. For the water–RhB–heptanol system in our experiments, the ratio of diffusivities is Do/Dw ≈ 0.1, in which case the time for the flux to reach the value of a bare interface is longer than for a fictitious interface. The results of Fig. 6(c) suggest that specific combinations of solvents and solute may accentuate the effect of the particle layer on diffusion.
Conclusions
We investigated the effect of a layer of nanoparticles on diffusive transport of a solute across a liquid–liquid interface. The diffusion of a fluorescent dye (rhodamine B) across the particle-laden interface of a single Pickering droplet was quantified experimentally in a Hele-Shaw geometry using calibrated fluorescence intensity. The experiments revealed a limited hindrance of the particle layer on diffusion, which we explained with the help of a simple diffusion model. A 3D model for the diffusion of solute across a particle-laden interface revealed that the spatio-temporal effect of particles is limited to a distance comparable to the particle radius, and a timescale for diffusion over that distance. This finding also helps to rationalize previous observations reported in the literature: for instance, the effect of particles was limited in hindering the diffusion of small molecules (e.g., O2) as measured by monitoring oxidation in Pickering emulsions.30 Furthermore, the effect of particle size on the characteristic time scale for diffusion is consistent with previous reports that the evaporation rate of water marbles is slower for drops coated by larger particles.16 Our experimental measurements of concentration fields were complicated by the physicochemical interactions of the fluorescent dye, which was also our solute, with the surface of the nanoparticles. In the future, to improve the precision of these experiments, decoupling the solute from the tracer should be beneficial. Furthermore, concentration measurements based on fluorescence lifetime, instead of fluorescence intensity, should help overcome possible artifacts coming from adsorption of dye on the nanoparticles. Methods to control the start of the diffusion process, such as a change in partition coefficient triggered by external fields, will be beneficial to improve the temporal range of the experiment.We also proposed and validated a quasi-1D model that accounts for the presence of the particles via an effective area available for diffusion. This model revealed that the time scale after which the effect of the particles becomes negligible also depends on the diffusivities of solutes in both liquids. Thus, by tuning the particle size and the properties of the solvents and solute, a more significant effect of the particles may be observed. These insights will contribute to controlling the performance of Pickering emulsions in encapsulation, controlled release, and chemical conversion, and to a better understanding of multicomponent droplet evaporation.
Author contributions
Y. L.: methodology, investigation, formal analysis, validation, writing–original draft; M. X.: methodology, software; L. M. P.: formal analysis, writing–review & editing; V.G.: conceptualization, supervision, writing–review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank B. P. Binks, D. Lohse and J. R. van Ommen for helpful discussions.Notes and references
- B. P. Binks, Curr. Opin. Colloid Interface Sci., 2002, 7, 21–41 CrossRef CAS.
- Y. Zhang, M. C. Allen, R. Zhao, D. D. Deheyn, S. H. Behrens and J. C. Meredith, Langmuir, 2015, 31, 2669–2676 CrossRef CAS PubMed.
- M. A. Khan, A. J. Sprockel, K. A. Macmillan, M. T. Alting, S. P. Kharal, S. Boakye-Ansah and M. F. Haase, Adv. Mater., 2022, 34, 2109547 CrossRef CAS PubMed.
- D. Z. Gunes, M. Murith, J. Godefroid, C. Pelloux, H. Deyber, O. Schafer and O. Breton, Langmuir, 2017, 33, 1563–1575 CrossRef CAS PubMed.
- A. Sarkar and E. Dickinson, Curr. Opin. Colloid Interface Sci., 2020, 49, 69–81 CrossRef CAS.
- S. Crossley, J. Faria, M. Shen and D. E. Resasco, Science, 2010, 327, 68–72 CrossRef CAS.
- A. M. B. Rodriguez and B. P. Binks, Soft Matter, 2020, 16, 10221–10243 RSC.
- A. Marefati and M. Rayner, J. Sci. Food Agric., 2020, 100, 2807–2811 CrossRef CAS PubMed.
- A. D. Dinsmore, M. F. Hsu, M. G. Nikolaides, M. Marquez, A. R. Bausch and D. A. Weitz, Science, 2002, 298, 1006–1009 CrossRef CAS.
- B. P. Binks, P. D. Fletcher, B. L. Holt, P. Beaussoubre and K. Wong, Langmuir, 2010, 26, 18024–18030 CrossRef CAS PubMed.
- H. Miyazaki and S. Inasawa, Soft Matter, 2017, 13, 8990–8998 RSC.
- V. Poulichet and V. Garbin, Langmuir, 2015, 31, 12035–12042 CrossRef CAS PubMed.
- K. Achakulwisut, C. Tam, A. Huerre, R. Sammouti, B. P. Binks and V. Garbin, Langmuir, 2017, 33, 3809–3817 CrossRef CAS PubMed.
- S. Saha, B. Saint-Michel, V. Leynes, B. P. Binks and V. Garbin, Rheol. Acta, 2020, 59, 255–266 CrossRef CAS.
- A. Tosun and H. Y. Erbil, Appl. Surf. Sci., 2009, 256, 1278–1283 CrossRef CAS.
- Y. Asaumi, M. Rey, K. Oyama, N. Vogel, T. Hirai, Y. Nakamura and S. Fujii, Langmuir, 2020, 36, 13274–13284 CrossRef CAS PubMed.
- A. Gallo, F. Tavares, R. Das and H. Mishra, Soft Matter, 2021, 17, 7628–7644 RSC.
- L. Sacca, A. Drelich, F. Gomez, I. Pezron and D. Clausse, J. Dispersion Sci. Technol., 2008, 29, 948–952 CrossRef CAS.
- B. P. Binks, P. D. Fletcher, B. L. Holt, O. Kuc, P. Beaussoubre and K. Wong, Phys. Chem. Chem. Phys., 2010, 12, 2219–2226 RSC.
- C. Seyfert, J. Rodríguez-Rodríguez, D. Lohse and A. Marin, Phys. Rev. Fluids, 2022, 7, 023603 CrossRef.
- D. Lohse and X. Zhang, Nat. Rev Phys., 2020, 2, 426–443 CrossRef.
- H. Tan, C. Diddens, P. Lv, J. G. M. Kuerten, X. Zhang and D. Lohse, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8642–8647 CrossRef CAS.
- R. A. Lopez de la Cruz, C. Diddens, X. Zhang and D. Lohse, J. Fluid Mech., 2021, 923, A16 CrossRef CAS.
- Ó. R. Enríquez, D. Robles, P. Peñas-López and J. Rodríguez-Rodríguez, Phys. Rev. Fluids, 2019, 4, 100502 CrossRef.
- Z. Wei, J. B. You, H. Zeng and X. Zhang, J. Phys. Chem. C, 2022, 126, 1326–1336 CrossRef CAS.
- P. Peñas-López, B. van Elburg, M. A. Parrales and J. Rodríguez-Rodríguez, Phys. Rev. Fluids, 2017, 2, 063602 CrossRef.
- M. Petzold, S. Röhl, L. Hohl, D. Stehl, M. Lehmann, R. von Klitzing and M. Kraume, Chem. Ing. Tech., 2017, 89, 1561–1573 CrossRef CAS.
- P. O. Gendron, F. Avaltroni and K. J. Wilkinson, J. Fluoresc., 2008, 18, 1093–1101 CrossRef CAS PubMed.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, New York, US, 95th edn, 2014 Search PubMed.
- A. Schröder, J. Sprakel, W. Boerkamp, K. Schroën and C. C. Berton-Carabin, Food Res. Int., 2019, 120, 352–363 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01262j |
| This journal is © The Royal Society of Chemistry 2024 |