Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Freezing-induced topological transition of double-emulsion†
Jochem G.
Meijer
 a,
Pallav
Kant
a,
Pallav
Kant
 b and
Detlef
Lohse
b and
Detlef
Lohse
 ac
ac
aPhysics of Fluids group, Max Planck Center Twente for Complex Fluid Dynamics, Department of Science and Technology, Mesa+ Institute and J. M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, Enschede 7500 AE, The Netherlands. E-mail: j.g.meijer@utwente.nl
bSchool of Engineering, University of Manchester, M13 9PL, UK
cMax Planck Institute for Dynamics and Self-Organization, Am Faßberg 17, Göttingen 37077, Germany. E-mail: d.lohse@utwente.nl
First published on 22nd February 2024
Abstract
Solidification of complex liquids is pertinent to numerous natural and industrial processes. Here, we examine the freezing of a W/O/W double-emulsion, i.e., water-in-oil compound droplets dispersed in water. We show that the solidification of such hierarchical emulsions can trigger a topological transition; for example, in our case, we observe the transition from the stable W/O/W state to a (frozen) O/W single-emulsion configuration. Strikingly, this transition is characterised by sudden expulsion of the inner water drop from the encapsulating oil droplet. We propose that this topological transition is triggered by the freezing of the encapsulating oil droplet from the outside in, putting tension on the inner water drop thus, destabilizing the W/O/W configuration. Using high-speed imaging we characterize the destabilization process. Interestingly, we find that below a critical size of the inner drop, Rin,crit ≈ 19 μm, the topological transition does not occur any more and the double-emulsion remains stable, in line with our interpretation.
1 Introduction
The characteristic physical feature common between the fabrication of functionalized ceramics,1–4 cryo-biology,5–7 frost-heaving in colder regions8–10 and ice cream making is the interaction between insoluble dispersed particles in a melt and a moving solidification front. Due to its relevance and impact in both natural phenomena and technological applications, this interaction has been extensively studied both experimentally and theoretically.1,2,5–8,11–13 The prominent focus of these investigations has been to determine the conditions under which dispersed particles are either engulfed or rejected by the advancing freezing front.11,12,14–16 This aspect holds particular importance in material science, as the distribution of dispersed particles profoundly influences the resulting micro-structure, thereby governing the functional properties of the solidified materials. Importantly, these collective efforts have revealed that the interaction between a particle and the moving solidification front is influenced by distinct physical processes operating across different length scales. This characteristic renders it a true multi-scale problem, with each decade of length scale presenting its own set of governing mechanisms and phenomena. For instance, at the particle level, the interaction is influenced by factors such as thermal conductivity mismatches between the particle and the melt, as well as density changes during the liquid–solid phase transition. At smaller scales, van der Waals interactions and the flow of lubricating films in premelted layers dictate the local dynamics.17 Furthermore, recent investigations involving “soft” particles, such as droplets or bubbles, have shown that the overall complexity is further amplified due to the mechanical deformation experienced by the particles during the interaction with the moving solidification front.18–20The current understanding of this subject primarily stems from studying the interaction between uniform particles and a moving solidification interface. However, in modern technological applications, such as cryobiology and material science, complex and multi-component particles are frequently encountered. Inspired by these applications, in this Letter, we extend the envelope of the current state of the art on this subject to the interaction between the solidification front and multi-component particles. Using a dilute W/O/W double-emulsion as a model system, we report unexpected behaviors that emerge during its solidification. We show that dispersed compound droplets in a double-emulsion can undergo a topological change upon engulfment in the solidifying bulk. This topological transition is triggered by the partial solidification of the dispersed compound droplet. Our findings are relevant for exerting better control over cryopreservation procedures of bio-specimen as well as the fabrication of advanced materials.
2 Experimental procedure
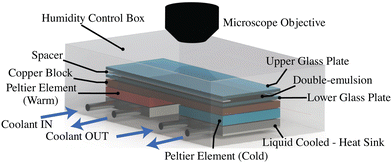
The W/O/W double-emulsions used in our current experiments are prepared using a microfluidic setup similar to the one described in ref. 23. In our adopted setup, we exploit the process of spontaneous liquid–liquid phase separation of a ternary mixture (water, ethanol and oil) to achieve double-emulsions, as discussed in detail in ref. 24 and 25. Note that here we use diethyl-phthalate (DEP) as an oil phase and Pluronic-F127 as surfactant to stabilise the emulsion. The oil has a freezing point close to that of water, i.e., Tm,DEP = −3 °C. Since the process of emulsion preparation is extremely sensitive to the initial composition of the ternary mixture, we use a DEP/ethanol/water mixture (0.74/0.05/0.21 vol.) with which we achieve a stable double-emulsion. As a consequence of the adopted methodology of the double-emulsion preparation, both the inner water drop and the encapsulating oil droplet contain traces of ethanol.The experimental assembly employed in current investigations is shown schematically in Fig. 1. In a typical experiment, the W/O/W double-emulsion is first injected into a horizontal Hele-Shaw cell of thickness 200 μm, resting on a copper block. A thermal gradient G ∼5 K mm−1 is then applied to this copper block using Peltier elements (spaced 3 mm apart), such that the continuous phase of the double-emulsion (water) begins to solidify uniformly from the cold end. Solidification is initiated by placing a small piece of ice at the cold end of the cell when its temperature falls below the melting point of water. It is important to note that, due to the extremely slow freezing rates employed in our experiments, clear ice is formed with a refractive index (1.31) similar to that of water (1.33). The solidification rate V of the bulk medium is controlled by the applied thermal gradient G. The engulfment of the dispersed compound droplets into the solidified bulk is recorded in top-view using a camera (Nikon D850 or Photron NOVA S16) connected to a long working distance lens (Thorlabs, MVL12X12Z plus 2X lens attachment). The sample is illuminated with diffused cold-LED to avoid localised heating. For further experimental details and the protocol for the double-emulsion preparation, we refer to the ESI.†
3 Results and discussion
The sequence of images in Fig. 2(a) highlights the events leading up to the sudden topological transition of a W/O/W double-emulsion when a dispersed water-in-oil compound droplet is engulfed into the solidifying bulk at a steady rate, V ≈ 0.5 μm s−1. The moment in time when the solidification front makes contact with the compound droplet is defined as t = 0. As shown in Fig. 2(a), while the solidification front passes over, the encapsulating oil droplet severely deforms into a pointy, tear-like shape. Recent findings20 have revealed that this deformation of the engulfed droplet is mediated by pressure variations in the nanometric thin liquid film, also referred to as premelted film,17 sandwiched between the dispersed droplet and the solidifying bulk. In contrast, during this engulfment process, the inner water drop clearly remains unaffected. However, very unexpectedly, a few minutes (∼16 min) after the dispersed compound droplet is completely engulfed in the solidified bulk (ice) and the solidification front is not in its vicinity, the inner water drop suddenly gets expelled outside the encapsulating oil droplet, altering the topology of the initially stable W/O/W double-emulsion. The expelled liquid gathers in the thin premelted film enveloping the oil droplet. Interestingly, the accumulation predominantly occurs at the warmer end, suggesting that the temperature gradient plays a role in this process. More importantly, as this topological transition occurs, the pointy, tear-like shape of the oil droplet relaxes to its original unperturbed (spherical) shape. Finally, we observe that the expelled liquid eventually begins to migrate towards the moving solidification front at a constant speed vdiff ∼ 2 μm s−1, see Fig. 2(c). This surprising migration of the liquid through the solidified bulk resembles a process akin to brine-pocket diffusion in sea ice that is driven by a delicate diffusive process of solute diffusion and its influence on the local phase equilibrium.26–28 It is worth noting that, as a result of the chosen fabrication method for the double-emulsions used in this study, the dispersed compound droplets contain traces of ethanol, which eventually acts as a solute, thus enabling a diffusive process that leads to the migration of the liquid pocket. For a detailed discussion of the physical mechanisms leading to the migration of the liquid pocket, we refer to the ESI.† In the following, we focus on the main finding of this paper: the sudden topological transition of the double-emulsion.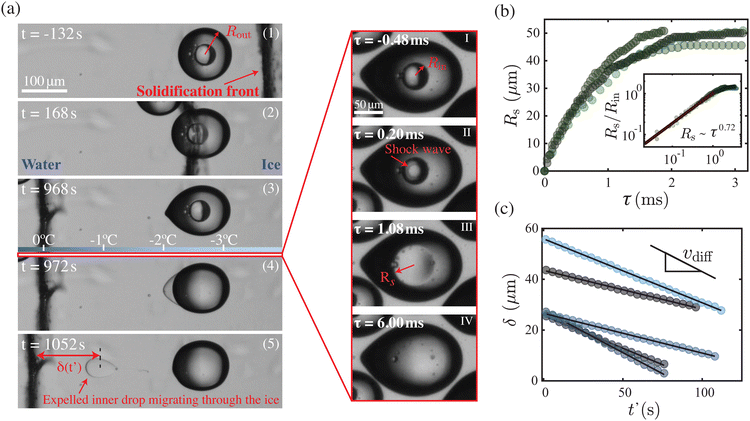 | ||
Fig. 2 (a) (1)–(5) Sequence of images capturing the engulfment of a water-in-oil compound droplet by a solidification front, advancing at rate V = 0.5 μm s−1 (Movie 1, ESI†). The moment in time the front makes first contact with the droplet is set to t = 0. The third panel shows a sketch of the expected temperature distribution in the ice at a certain moment in time set by the strength of the applied thermal gradient G. (I)–(IV) High-speed images were acquired at 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fps, showing the sudden topological transition (Movies 2 and 3, ESI†). At τ = 0 a shock wave appears at the center of the inner drop and an ethanol vapour cloud expands radially outward. (b) Radius Rs of the shock wave as a function of time for different transitions, indicated by different shades. The inset shows that at the early stages, when Rs/Rin < 1, it follows a power-law-like behaviour that is consistent with that of a diverging spherical shock wave.21,22 (c) Distance δ between the solidification front and the center of the expelled inner drop migrating through the ice. Note the ∼ 5 orders of magnitude difference in time scale in (c) as compared to (b). At t′ = 0 the expelled drop detaches from the oil. The migration velocity is determined by the velocity vdiff at which diffusion takes place within the expelled water–ethanol pocket. 000 fps, showing the sudden topological transition (Movies 2 and 3, ESI†). At τ = 0 a shock wave appears at the center of the inner drop and an ethanol vapour cloud expands radially outward. (b) Radius Rs of the shock wave as a function of time for different transitions, indicated by different shades. The inset shows that at the early stages, when Rs/Rin < 1, it follows a power-law-like behaviour that is consistent with that of a diverging spherical shock wave.21,22 (c) Distance δ between the solidification front and the center of the expelled inner drop migrating through the ice. Note the ∼ 5 orders of magnitude difference in time scale in (c) as compared to (b). At t′ = 0 the expelled drop detaches from the oil. The migration velocity is determined by the velocity vdiff at which diffusion takes place within the expelled water–ethanol pocket. | ||
Since the time scales associated with the topological change of engulfed compound droplets are much faster than the rate of solidification, we employ high-speed imaging to reveal the details of this apparently instantaneous event. As illustrated in the sequence of images in Fig. 2(a)(I)–(IV), the transition is triggered at the center of the inner drop, marked by the appearance of a radially expanding dark ring. Remarkably, this outward-moving dark ring is also accompanied by a localized increase in light intensity at its center, forming a discernible bright spot. Once the size of the bright spot exceeds the dimensions of the inner drop, it gradually fades (see ESI†), coinciding with the complete disappearance of the inner water drop. Following this event, the disappeared liquid collects outside the enveloping oil droplet within the premelted film in about 10–100 ms (not shown here). By tracking the temporal expansion of this dark ring, Rs(t), we obtain a power-law-like behaviour Rs ∼ τ0.72 at the early stages of its growth when Rs/Rin < 1, see inset Fig. 2(b). Such scaling behavior evokes similarities with an adiabatically expanding spherical shock wave, which entails a discontinuity in density, pressure, and temperature.21,22 Considering that the double-emulsions used in our current experiments contain traces of ethanol, we propose that all the above described features are triggered by its phase transition from liquid to vapor during the solidification of the surrounding oil droplet. Since ethanol is crucial for the stability of the double-emulsion, its sudden phase transition leads to the dissolution of the inner water drop, destabilizing the compound droplet. The process of dissolution, we argue, is optically screened-off by the vapour cloud (bright spot) itself and therefore not visible in Fig. 2(a)(I)–(IV). Note that the ethanol vapor allows greater transmission of light because of its reduced refractive index, which in turn rationalizes the appearance of a bright spot during the transition. Also, we will see later that the rate of dissolution indeed exceeds the rate at which the vapour cloud expands.
The hypothesized phase transition of ethanol during the solidification of the double-emulsion is rationalized as follows: following engulfment, as the solidification front steadily recedes away from the dispersed compound droplet, the local temperature in its vicinity progressively decreases in line with the applied thermal gradient (see sketch in Fig. 2(a)(3)). Upon reaching the freezing point of the oil (Tm,DEP = −3 °C), the outer oil droplet begins to solidify, causing shrinkage in its volume, since ρoil-solid >ρoil-melt. Nevertheless, this volumetric shrinkage is prevented due to the confinement by the solidified bulk water. As a result the pressure inside the encapsulating oil droplet plummets, imposing tension on the inner water drop and causing it to stretch. An approximate estimate of the pressure reduction experienced by the inner drop due to the solidification of the encapsulating oil droplet can be determined from the Gibbs–Duhem relation29
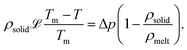 | (1) |
Here, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) is the latent heat of solidification, T is the temperature and Δp the corresponding pressure change which we want to evaluate. Estimating Δp from eqn (1) with typical values, Tm − T = 0.1 K and 1 − ρsolid/ρliquid = − 0.1, yields Δp ∼ − 1 MPa. Such a depression in pressure critically affects the local phase equilibrium of ethanol for which the saturated vapour pressure at T = − 3 °C is pv,eth ≈ 1.2 kPa. To verify our hypothesis, we performed additional experiments by replacing DEP with dibutyl-phthalate (DBP) as an oil phase, while keeping the procedure of the double-emulsion preparation the same (see ESI†). Since the freezing point of the DBP is much lower compared to DEP, Tm,DBP = − 35 °C, which cannot be achieved in our experimental setup, no abrupt topological transitions are observed. For further details related to these experiments, we refer to the ESI.†
is the latent heat of solidification, T is the temperature and Δp the corresponding pressure change which we want to evaluate. Estimating Δp from eqn (1) with typical values, Tm − T = 0.1 K and 1 − ρsolid/ρliquid = − 0.1, yields Δp ∼ − 1 MPa. Such a depression in pressure critically affects the local phase equilibrium of ethanol for which the saturated vapour pressure at T = − 3 °C is pv,eth ≈ 1.2 kPa. To verify our hypothesis, we performed additional experiments by replacing DEP with dibutyl-phthalate (DBP) as an oil phase, while keeping the procedure of the double-emulsion preparation the same (see ESI†). Since the freezing point of the DBP is much lower compared to DEP, Tm,DBP = − 35 °C, which cannot be achieved in our experimental setup, no abrupt topological transitions are observed. For further details related to these experiments, we refer to the ESI.†
Since the dissolution process of the inner water drop is screened-off by the ethanol vapor cloud (bright spot) appearing at the center, it is extremely difficult to directly measure related characteristic features. For this, we rely on experiments performed with metastable W/O/W emulsions. In these instances, especially for relatively large compound droplets with an inner drop size greater than Rin ≥ 30 μm, the dissolution process is directly measured without any hindrance from the ethanol vapour cloud, see Fig. 3(a). Note that the sudden dissolution of the inner drop in these barely stable compound droplets is triggered by disturbances in the ambient conditions. The sequence of images in Fig. 3(a) exemplifies one such case, where the inner drop dissolves while the compound droplet is getting engulfed in the solidifying bulk. The rate at which the inner drops dissolve, here directely measured, agrees well with the simplified Epstein–Plesset model,30,31
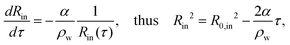 | (2) |
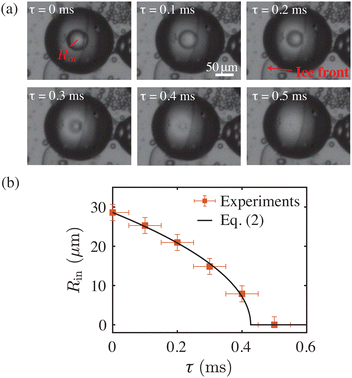 | ||
| Fig. 3 (a) Experimental snapshots showing the sudden dissolution of the inner drop, here triggered by the ice front passing over the compound droplet (Movie 4, ESI†). (b) Radius Rin of the inner water drop as function of time (boxes). The rate of shrinking for several of such cases follows the steady Epstein–Plesset model of dissolution (solid line, eqn (2)). | ||
Beyond the freezing driven liquid-to-vapor phase transition of the constituent liquid, another surprising feature of our system is that the topological transition of the double-emulsions is strongly dependent on the size of the inner drop. We find that below a critical size, Rin,crit ≈ 19 μm, the compound droplets remain stable, see Fig. 4. Note that due to the applied procedure of double-emulsion preparation Rout and Rin cannot be varied independently and their ratio, here Rout/Rout ≈ 3.3 (see Fig. 4(a)), is governed by the ethanol mass transfer rate during preparation 24,25. A second control parameter is the rate of freezing, characterised by the advancing velocity V. Due to experimental limitations we are not able to capture both the engulfment and sudden transition of each drop. To nevertheless still qualitatively address the rate at which freezing occurred, we couple the rate of engulfment V to the experienced drop deformation Γ once incorporated into the ice, as it has been established that both are inversely related.19,20 Here, a large deformation (larger Γ) is related to slower freezing (smaller V) and vice versa, where for the range of advancing velocities is approximately 0.2 μm s−1 ≲ V ≲ 2 μm s−1. In Fig. 4(b) we thus show that the critical size dependence remains unaffected by the extend of the experienced deformation Γ and hence by the rate of engulfment V.
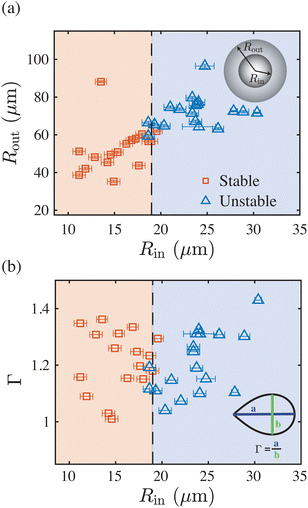 | ||
| Fig. 4 Parameter space showing the dependence of the topological transition on (a) the size of the compound droplet and (b) its aspect ratio Γ after encapsulation by the ice. The latter is directly related to the (adjustable) advancing velocity V of the solidification front, i.e., Γ – V−1 for pure oil drops in water.19,20 Below a critical inner drop size, Rin,crit ≈ 19 μm, the compound droplets remain stable. The rate of freezing does not affect this critical size. | ||
To examine this unexpected size dependence we consider that the pressure in the inner drop, pin(t), needs to fall below the vapour pressure of ethanol, pv,eth, at T = −3 °C, to trigger the topological transition. Due to the tension exerted by the partially solidifying oil on the inner drop a reduction in pressure is expected (ideally) as Δpin(t) = −KΔVin(t)/Vin, where K is the elastic bulk modulus of water and ΔVin(t)/Vin the relative change in volume over time. The initial pressure in the drop is given by the sum of ambient and Laplace pressure, resulting in the condition that the compound droplet remains stable if pin,ref + 2σ/Rin−KΔVin(t)/Vin > pv,eth, or, in terms of the inner drop size, if Rin < 2σ/(pv,eth + KΔVin(t)/Vin − pin,ref), where σ is the interfacial surface tension. Given the critical drop size, Rin,crit, observed experimentally (see Fig. 4) we conclude that the experienced change in volume over time, ΔVin(t)/Vin, stagnates and that therefore the amount of tension applied to the inner drop is limited. We suspect that, given the limitations of the experimental set-up and the bounded applied thermal gradient, sufficiently low temperatures could not be achieved and a thermal equilibrium is reached, causing only a small portion of the encapsulating oil to solidify.
4 Conclusion
In summary, in this Letter, we discussed that a dilute double-emulsion, i.e., water-in-oil compound droplets in water, can undergo the topological transition from its W/O/W state to an O/W state after being frozen. The sudden topological transition, we argue, is triggered by the partial solidification of the encapsulating oil, putting tension on the inner drop, causing the trace amounts of liquid ethanol inside to undergo a liquid-to-vapour phase transition. As the vapour cloud expands, ethanol is depleted, making the compound drop unstable, and the inner drop dissolves. The then expelled interior accumulates at the warmer end and migrates though the ice in the direction of motion of the advancing solidification front. The topological transition critically depends on the size of the inner drop and does not depend on the engulfment velocity V. We found that below Rin,crit ≈ 19 μm the topological transition does not occur and the double-emulsion remains stable. We rationalised that this size dependence originates from the limited amount of tension applied to the inner drop. Our findings on the individual compound droplets can be extrapolated to those in a more densely packed double-emulsion, where the same phenomena is observed (see ESI†).The surprising topological transition we found is relevant when freezing multi-component systems and in the context of the cryopreservation procedures of food emulsions and bio-specimen. In addition, our findings highlight the effect of phase changing liquid inclusions in a solidifying material and how this might alter their topology in unexpected ways.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Gert-Wim Bruggert and Martin Bos for the technical support and Duco van Buuren for performing preliminary experiments. Additionally, we thank Andrea Prosperetti and Vincent Bertin for stimulating discussions. The authors acknowledge the funding by Max Planck Center Twente and the Balzan Foundation.References
- S. Deville, E. Saiz, R. K. Nalla and A. P. Tomsia, Science, 2006, 311, 515–518 CrossRef CAS PubMed.
- S. Deville, E. Saiz and A. P. Tomsia, Acta Mater., 2007, 55, 1965–1974 CrossRef CAS.
- S. Deville, Adv. Eng. Mater., 2008, 10, 155–169 CrossRef CAS.
- S. Deville, Materials, 2010, 3, 1913–1927 CrossRef CAS.
- V. Bronstein, Y. Itkin and G. Ishkov, J. Cryst. Grow., 1981, 52, 345–349 CrossRef CAS.
- C. Körber, Q. Rev. Biophys., 1988, 21, 229–298 CrossRef PubMed.
- K. Muldrew, J. P. Acker, J. A. Elliott and L. E. McGann, Life in the frozen state, CRC Press, 2004, pp. 93–134 Search PubMed.
- A. W. Rempel, J. Glaciol., 2010, 56, 1122–1128 CrossRef.
- S. Peppin, A. Majumdar, R. Style and G. Sander, SIAM J. Appl. Math., 2011, 71, 1717–1732 CrossRef.
- S. S. Peppin and R. W. Style, Vadose Zone J., 2013, 12, 1 CrossRef.
- D. Shangguan, S. Ahuja and D. Stefanescu, Metall. Trans. A, 1992, 23, 669–680 CrossRef.
- A. Rempel and M. Worster, J. Cryst. Grow., 2001, 223, 420–432 CrossRef CAS.
- M. S. Park, A. A. Golovin and S. H. Davis, J. Fluid Mech., 2006, 560, 415–436 CrossRef.
- D. Dedovets, C. Monteux and S. Deville, Science, 2018, 360, 303–306 CrossRef CAS PubMed.
- S. Tyagi, H. Huynh, C. Monteux and S. Deville, Materialia, 2020, 12, 100802 CrossRef CAS.
- J. G. Meijer, V. Bertin and D. Lohse, arXiv, 2023, preprint, arXiv:2311.09477 DOI:10.48550/arXiv.2311.09477.
- J. S. Wettlaufer and M. G. Worster, Annu. Rev. Fluid Mech., 2006, 38, 427–452 CrossRef.
- S. Tyagi, C. Monteux and S. Deville, Sci. Rep., 2021, 11, 3513 CrossRef CAS PubMed.
- S. Tyagi, C. Monteux and S. Deville, Soft Matter, 2022, 18, 4178–4188 RSC.
- J. G. Meijer, P. Kant, D. van Buuren and D. Lohse, Phys. Rev. Lett., 2023, 130, 214002 CrossRef CAS PubMed.
- G. Guderley, Luftfahrtforschung, 1942, 19, 302 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics: Landau and Lifshitz: Course of Theoretical Physics, Elsevier, 2013, vol. 6 Search PubMed.
- B. Van Elburg, G. Collado-Lara, G.-W. Bruggert, T. Segers, M. Versluis and G. Lajoinie, Rev. Sci. Instrum., 2021, 92, 035110 CrossRef CAS PubMed.
- M. F. Haase and J. Brujic, Angew. Chem., 2014, 126, 11987–11991 CrossRef.
- P. G. Moerman, P. C. Hohenberg, E. Vanden-Eijnden and J. Brujic, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 3599–3604 CrossRef CAS PubMed.
- W. Whitman, Am. J. Sci., 1926, 5, 126–132 CrossRef.
- P. Hoekstra, T. E. Osterkamp and W. F. Weeks, J. Geophys. Res., 1965, 70, 5035–5041 CrossRef CAS.
- J. Harrison, J. Appl. Phys., 1965, 36, 3811–3815 CrossRef CAS.
- F. Reif, Statistical thermal physics, Mcgraw-Hill Kogakusha, 1965 Search PubMed.
- P. S. Epstein and M. S. Plesset, J. Chem. Phys., 1950, 18, 1505–1509 CrossRef CAS.
- P. B. Duncan and D. Needham, Langmuir, 2006, 22, 4190–4197 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01657a |
| This journal is © The Royal Society of Chemistry 2024 |