Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Motor crosslinking augments elasticity in active nematics†
Steven A.
Redford
 ab,
Jonathan
Colen
ab,
Jonathan
Colen
 cd,
Jordan L.
Shivers
cd,
Jordan L.
Shivers
 de,
Sasha
Zemsky
de,
Sasha
Zemsky
 fi,
Mehdi
Molaei
g,
Carlos
Floyd
fi,
Mehdi
Molaei
g,
Carlos
Floyd
 de,
Paul V.
Ruijgrok
f,
Vincenzo
Vitelli
cd,
Zev
Bryant
de,
Paul V.
Ruijgrok
f,
Vincenzo
Vitelli
cd,
Zev
Bryant
 fh,
Aaron R.
Dinner
fh,
Aaron R.
Dinner
 *bde and
Margaret L.
Gardel
*bde and
Margaret L.
Gardel
 *bcdg
*bcdg
aThe Graduate Program in Biophysical Sciences, University of Chicago, Chicago, IL 60637, USA
bInstitute for Biophysical Dynamics, University of Chicago, Chicago, IL 60637, USA. E-mail: dinner@uchicago.edu; gardel@uchicago.edu
cDepartment of Physics, University of Chicago, Chicago, IL 60637, USA
dJames Franck Institute, University of Chicago, Chicago, IL 60637, USA
eDepartment of Chemistry, University of Chicago, Chicago, IL 60637, USA
fDepartment of Bioengineering, Stanford University, Stanford, CA 94305, USA
gPritzker School of Molecular Engineering, The University of Chicago, Chicago, IL 60637, USA
hDepartment of Structural Biology, Stanford University School of Medicine, Stanford, CA 94305, USA
iProgram in Biophysics, Stanford University, Stanford, CA 94305, USA
First published on 2nd February 2024
Abstract
In active materials, uncoordinated internal stresses lead to emergent long-range flows. An understanding of how the behavior of active materials depends on mesoscopic (hydrodynamic) parameters is developing, but there remains a gap in knowledge concerning how hydrodynamic parameters depend on the properties of microscopic elements. In this work, we combine experiments and multiscale modeling to relate the structure and dynamics of active nematics composed of biopolymer filaments and molecular motors to their microscopic properties, in particular motor processivity, speed, and valency. We show that crosslinking of filaments by both motors and passive crosslinkers not only augments the contributions to nematic elasticity from excluded volume effects but dominates them. By altering motor kinetics we show that a competition between motor speed and crosslinking results in a nonmonotonic dependence of nematic flow on motor speed. By modulating passive filament crosslinking we show that energy transfer into nematic flow is in large part dictated by crosslinking. Thus motor proteins both generate activity and contribute to nematic elasticity. Our results provide new insights for rationally engineering active materials.
Introduction
Systems composed of active agents that locally break detailed balance can exhibit striking collective behaviors that are inaccessible to assemblies that couple to energy sources in a nondirected fashion (e.g., thermally).1,2 These behaviors include directed collective motion, enhanced information storage, giant number fluctuations, self-sorting, and motility-induced phase separation.3–6 A better understanding of active systems can suggest mechanisms in natural systems,7–9 enable control of nonequilibrium pattern formation, and guide the design of new materials.10–13 One of the most well-studied classes of active materials is active nematics (also known as active liquid crystals).13,14 In nematics, elongated components (mesogens) interact locally through excluded volume, yielding a material that exhibits long-ranged orientational order while maintaining translational fluidity.15,16 The tendency of the mesogens to align gives a nematic an effective elasticity that resists distortions and acts to align the field as a whole.2 This tendency to align is opposed by activity (i.e., mechanical work done on the individual elements of a system). Activity induces structural distortions and flow in the nematic field, leading to a dynamical steady state.There are various ways to characterize structure in an active nematic. These include the spacing of topological defects, the correlation length of the orientation of the mesogens (director field), and the correlation length of the velocity or vorticity.17–19 However, theory,17 simulation,18 and experiments20,21 suggest that these quantities all scale identically with activity—i.e., for a given set of conditions, active nematic dynamics are governed by a single length scale, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . This length scale arises from the balance of the elastic stress, K/
. This length scale arises from the balance of the elastic stress, K/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2, where K is the elastic constant, with the active stress scale, α, so that
2, where K is the elastic constant, with the active stress scale, α, so that 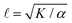 .18 While
.18 While ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) quantifies how much energy imparted by activity is stored in distortions to the nematic field, the average flow speed of the nematic captures how much energy is dissipated viscously. As such, by force balance, the average flow speed in a nematic is expected to scale as
quantifies how much energy imparted by activity is stored in distortions to the nematic field, the average flow speed of the nematic captures how much energy is dissipated viscously. As such, by force balance, the average flow speed in a nematic is expected to scale as 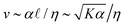 , where η is the solvent viscosity.18 Thus exerting control over K and α affords control over the steady-state dynamics and structure of an active nematic.
, where η is the solvent viscosity.18 Thus exerting control over K and α affords control over the steady-state dynamics and structure of an active nematic.
How exactly K and α relate to microscopic properties of the elements that make up active nematics is not well understood. In active nematics composed of cytoskeletal elements—semiflexible filaments, molecular motors, and crosslinkers—activity is generated when the molecular motors hydrolyze adenosine triphosphate (ATP) and slide pairs of filaments, giving rise to interfilament strain (Fig. 1(B)-(ii)), which generates extensile force dipoles within the nematic.3 Biochemical regulation affords control of microscale mesogen properties and active stresses allowing for explicit tuning of hydrodynamic properties on a microscopic scale. For example, in active nematics composed of actin filaments and myosin II motors, the elastic constant was shown to depend on filament length.14,20 In nematics composed of microtubules and kinesin, active stresses have been modulated by changing the concentration of ATP ([ATP]) available to motors. In this case, the impact of altering [ATP] was to affect the activity through motor stepping speed and not the elasticity.21 The motor employed in this and other studies of cytoskeletal active nematics (kinesin and myosin II filaments) have high processivities. That is, they almost never detach from filaments before reaching their ends.22,23 Because a motor must link a pair of filaments to generate extensile stress, one would expect that differences in filament binding propensities lead to differences in force transmission capabilities. Indeed, filament crosslinking was observed to impact local rigidity and force transmission in other cytoskeletal contexts.24 However, the roles of motor processivity and, more generally, crosslinking in active nematics have not been explored to the best of our knowledge.
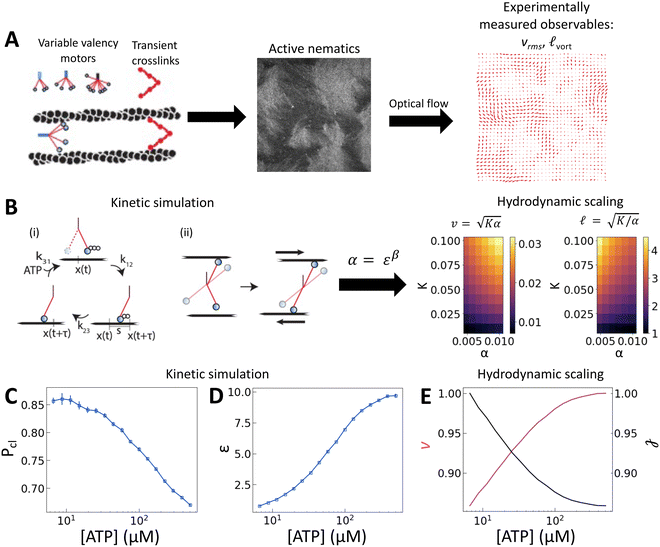 | ||
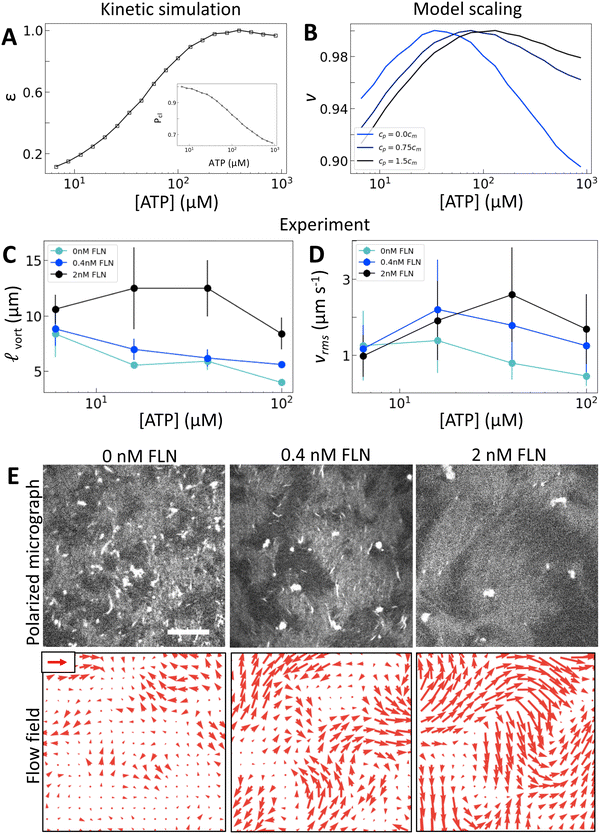
Fig. 1 [ATP] and activity can be related through a microscopic model. (A) Schematic of the experiments. We study synthetic motors with controlled numbers of myosin XI enzymatic heads that bind and slide actin filaments of length 2 μm at an oil–water interface. Due to the polarized binding of a dye to actin filaments, regions with filaments oriented vertically in the laboratory frame appear brighter than those oriented horizontally.14,20 The experimental images are analyzed by optical flow34 to estimate the horizontal and vertical components of the velocity at each pixel. From the velocity field, we calculate the average flow speed, vrms, and average vortex radius ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort as in ref. 35. (B) We simulate the catalytic cycle of myosin XI with three states: (1) unbound with ATP (top), (2) bound with ADP (right), and (3) bound while nucleotide free (left). (i) Rate constants are tuned based on prior measurements of speed and processivity on single filaments (Fig. S2, ESI†). (ii) We extend the simulation to two filaments as described in the text and compute the filament extension rate, ε, and the probability of crosslinking, Pcl, as described in the text. These quantities are used to compute the nematic speed and correlation length as vort as in ref. 35. (B) We simulate the catalytic cycle of myosin XI with three states: (1) unbound with ATP (top), (2) bound with ADP (right), and (3) bound while nucleotide free (left). (i) Rate constants are tuned based on prior measurements of speed and processivity on single filaments (Fig. S2, ESI†). (ii) We extend the simulation to two filaments as described in the text and compute the filament extension rate, ε, and the probability of crosslinking, Pcl, as described in the text. These quantities are used to compute the nematic speed and correlation length as 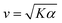 and and 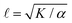 , respectively. (C) Pcl and (D) ε from two-filament simulations for a cluster with four heads. (E) Normalized v (magenta) and , respectively. (C) Pcl and (D) ε from two-filament simulations for a cluster with four heads. (E) Normalized v (magenta) and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (black) for activity derived from (D) assuming constant elasticity, K = 0.001. (black) for activity derived from (D) assuming constant elasticity, K = 0.001. | ||
To address this gap, here we utilize synthetic myosin motors that range in their propensities for binding filaments.25 We tune processivity through both [ATP] and motor oligomerization state (valency). We find that nematic speed depends nonmonotonically on [ATP], reflecting opposite trends in filament strain and crosslinking with [ATP]. We find that crosslinking modulates the elasticity, and we introduce a simple model that accounts for the observed trends. Consistent with the model, we show that the addition of the passive crosslinker filamin also modulates elasticity and in so doing alters the energetic balance in active flows. Our results reveal a previously unappreciated connection between activity and elasticity through motor proteins and show how these quantities can be tuned independently through molecular composition.
Results
To probe how the microscopic interactions between motors and filaments control nematic structure and dynamics, we pair in vitro experiments with multiscale modeling. Experimentally, we can alter processivity by changing the availability of ATP or motor valency. Specifically we employ synthetic myosin motors that consist of the enzymatic head from Chara myosin XI, which is linked via a flexible linker to an engineered multimerization domain.25 By utilizing different multimerization domains, either engineered GCN4 coiled coils26 or de novo two-helix hairpins,27 which form clusters of well-defined sizes, we are able to query clusters with identical enzymology but with three, four, or eight heads (Fig. 1(A) and Fig. S1, ESI†). In the high-ATP limit the Chara myosin XI head has a low duty ratio, meaning it spends less than half of its catalytic cycle bound to an actin filament.28–30 Because this duty ratio depends on [ATP], motor velocity and the distance a motor travels before dissociating (run length) on single filaments also depend strongly on [ATP]: at [ATP] = 10 μM, tetrameric clusters have single-filament velocities of 0.5 μm s−1 with run lengths of 4 μm, while at [ATP] = 500 μM, the velocity is 10 μm s−1, and the run length is 0.5 μm (Fig. S2, ESI†).25A microscopic model relates motor properties to hydrodynamic parameters
To understand how the activity depends on [ATP] in our system and in turn to make predictions for the nematic speed and correlation length through the relations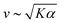 and
and 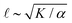 , we developed a microscopic model of motors with variable valencies. Because activity is generated via filament pair strain and not merely motor speed, this model focuses on the calculation of filament strain rate, ε, which we take as the total displacement of the filaments relative to each other divided by the total time in a simulation. We then use this quantity in the scaling relation α ∼ εβ, which was previously observed to hold for active nematics composed of microtubules and kinesin motors,21 given the known dependence on [ATP] of the speed of single kinesin motors walking on single filaments.22
, we developed a microscopic model of motors with variable valencies. Because activity is generated via filament pair strain and not merely motor speed, this model focuses on the calculation of filament strain rate, ε, which we take as the total displacement of the filaments relative to each other divided by the total time in a simulation. We then use this quantity in the scaling relation α ∼ εβ, which was previously observed to hold for active nematics composed of microtubules and kinesin motors,21 given the known dependence on [ATP] of the speed of single kinesin motors walking on single filaments.22
Building upon a previous approach,31 we coarsely approximate the catalytic cycle of each head using three states: (1) unbound from the filament with ATP, (2) bound to the filament in the post-powerstroke state with ADP, and (3) bound to the filament without a nucleotide (Fig. 1(B)). Transitions between these states are irreversible. An essential idea is that a head with ATP has low affinity for the filament. As a result, the transition from state 1 to state 2 requires ATP hydrolysis. Similarly, the head quickly releases the filament once it exchanges ADP for ATP, and the rate of the transition from state 3 to state 1 is linearly dependent on [ATP]. We simulate the cycle for each head independently. That is, if there are n heads in a simulation, we need to track 3n states. Because the heads are independent and rates are irreversible, there are only n allowed transitions at any time. To evolve the system forward, we perform the Gillespie algorithm over all possible transitions at a given time.32 This scheme allows us to simulate clusters of independent heads with any valency.
We assume that the joint between the lever arm and the multimerization domain is flexible and that the motor prefers to bind in its least strained position. Thus, when a head undergoes a transition from state 1 to state 2 and binds to a filament, we draw its position from the normal distribution N(x(t) + s/2,s/2). Here, x(t) is the position of the multimerization domain that couples independent heads together and s is the average step length of a motor. On each filament, we take x(t) to be a distance s/2 ahead of the rearmost bound head. Assuming fast diffusion relative to binding rates, when a motor can bind multiple filaments we choose between them randomly with equal probability. When a transition occurs, x(t) is reevaluated. We calculate the average velocity of a motor on a filament as the total distance a motor travels divided by the final time in the simulation. For pairs of filaments, strain is only recorded if motion occurs while the motor crosslinks the two filaments.2,33 We compute the filament strain rate, ε, by dividing the total strain by the final time in the simulation. We also compute the probability of crosslinking, Pcl, as the fraction of time that both filaments are bound simultaneously.
We scan the three rate constants (k12, k23, k31) to identify values that yield average single-filament speeds and run lengths (i.e., the length traveled between the first time a head is bound to the last time) that reproduce measured trends and approximately correspond to measured values from experiments with tetrameric clusters (Fig. S2, ESI†).25 Two filament results, ε and Pcl, for a tetrameric motor cluster are shown in Fig. 1(C) and (D). These simulations show that Pcl decreases while ε increases with [ATP].
As described above, we use the computed strain rate to estimate the activity by α ∼ εβ. This form is based on the suggestion by Lemma and co-workers that α scales with a power of motor velocity, which they showed to be consistent with their data and the known dependence of kinesin velocity on [ATP].21 Here we replace motor velocity with our calculated ε. To fit the data, we use β = 0.1, which means that the nematic activity grows relatively slowly with the motor activity (for comparison, values ranging from 0.31 to 1.54 are considered for the kinesin velocity scaling exponent in ref. 21). The low value of β may reflect detailed mechanics of the engineered myosin XI motor,25 which are not accounted for in the model used to calculate ε. Substituting the resulting α into 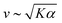 and
and 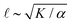 , we obtain an increase in v and a decrease in
, we obtain an increase in v and a decrease in ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) with [ATP], for fixed K (Fig. 1(E)).
with [ATP], for fixed K (Fig. 1(E)).
Nematic elasticity depends on the probability of crosslinking
To test our predictions, we use nematics composed of short (2 μm) actin filaments labelled with tetramethylrhodamine (TMR) and synthetic motors with Chara myosin XI enzymatic heads.25 We form nematics by crowding the actin filaments to a surfactant stabilized oil–water interface through depletion forces imposed by methyl-cellulose (Fig. 1(A)). Once the nematic is formed, we add 120 pM tetrameric motors to the sample to introduce activity. We image the sample with time-lapse fluorescence microscopy at a rate of 0.5 frames s−1 for 100 s. Because of the polarization of TMR dye along filaments and the polarization of our excitation laser, brighter (darker) patches represent filaments oriented vertically (horizontally) in the imaging plane.14,20 Given the video microscopy data, we estimate the nematic velocity at each pixel using optical flow,34 as described in Materials and methods.The results for one series of [ATP] are shown in Fig. 2 and Movie S1 (ESI†). As we expected, the length scale ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort, calculated using correlated displacement velocimetry, decreases as [ATP] increases (Fig. 2(A) and (C)).36 We use
vort, calculated using correlated displacement velocimetry, decreases as [ATP] increases (Fig. 2(A) and (C)).36 We use ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort to quantify length scale because it agrees well with the velocity correlation length but requires fewer assumptions to measure8,35 (Fig. S3, ESI†). While
vort to quantify length scale because it agrees well with the velocity correlation length but requires fewer assumptions to measure8,35 (Fig. S3, ESI†). While ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort decreases with [ATP], the root mean square flow velocity, vrms, exhibits a nonmonotonic dependence on [ATP], with a peak at 50 μM (Fig. 2(A), (B) and Fig. S4, ESI†). This behavior contrasts with the model prediction (Fig. 1(E)), suggesting that something is missing from the model.
vort decreases with [ATP], the root mean square flow velocity, vrms, exhibits a nonmonotonic dependence on [ATP], with a peak at 50 μM (Fig. 2(A), (B) and Fig. S4, ESI†). This behavior contrasts with the model prediction (Fig. 1(E)), suggesting that something is missing from the model.
 | ||
Fig. 2 Motor crosslinking modulates nematic elasticity. (A, top row) Polarized fluorescence micrographs of nematics (gray scale) driven by tetrameric motor clusters from ref. 25 with [ATP] of 6, 40 or 100 μM (concentration of motors is 120 pM). (A, bottom row) Velocity fields estimated from optical flow. Scale arrows are 3 μm s−1. (B) Average flow speed, vrms, for the experiments in (A) and similar ones with [ATP] of 16 μM. Error bars are standard deviations of speed over 100 s of steady-state activity. (C) Critical vorticity length scale, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort, measured as in ref. 35, for the same experiments as in (B). Error bars are standard deviations on 5 sets of 5 non-overlapping frames. (D) and (E) Normalized v and vort, measured as in ref. 35, for the same experiments as in (B). Error bars are standard deviations on 5 sets of 5 non-overlapping frames. (D) and (E) Normalized v and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for tetrameric motors calculated from the model scaling with various ratios of κ to K0. All calculations presented subsequently use κ = 10K0 and β = 0.1. for tetrameric motors calculated from the model scaling with various ratios of κ to K0. All calculations presented subsequently use κ = 10K0 and β = 0.1. | ||
Previous work established that the rheological37,38 and dynamical24,39–42 properties of cytoskeletal networks can be modulated by microscopic crosslinking. Specifically, theoretical work proposed that nematic elasticity should scale linearly with crosslinker concentration.43 Given this work and our observation that the probability of motor crosslinking is an ATP-dependent phenomenon (Fig. 1(C)), we reasoned that the elastic constant K should depend (linearly) on the effective concentration of crosslinkers, ce:
| K ∼ K0 + κce, | (1) |
 and
and 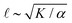 , we obtain nonmonotonic v and decreasing
, we obtain nonmonotonic v and decreasing ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) with increasing [ATP] (Fig. 2(D) and (E)). Physically, there is a competition between the tendency for increased [ATP] to increase motor speed, resulting in a higher strain rate, and to reduce motor binding, resulting in lower Pcl. In the case of kinesin, the latter tendency is negligible and thus was not necessary to consider in previous studies.21,22
with increasing [ATP] (Fig. 2(D) and (E)). Physically, there is a competition between the tendency for increased [ATP] to increase motor speed, resulting in a higher strain rate, and to reduce motor binding, resulting in lower Pcl. In the case of kinesin, the latter tendency is negligible and thus was not necessary to consider in previous studies.21,22
The peak in v becomes more pronounced as the second term in (1) becomes large compared with the first (Fig. 2(D)). To understand how a peak in v could arise from these scaling relationships, we differentiate  with respect to [ATP] and solve for the maximum by setting the resulting expression equal to zero. This yields
with respect to [ATP] and solve for the maximum by setting the resulting expression equal to zero. This yields
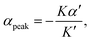 | (2) |
An alternative model supports the same physical interpretation
Note that the variations in the predicted v and![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) in Fig. 1 and 2 are smaller than in experiment. This may reflect simplifying assumptions in this model. On a hydrodynamic scale, we assume that turbulent scaling relations hold at all concentrations, even though we expect them to hold only above a critical [ATP]. Furthermore, our assumption that K is linear in Pcl is likely an oversimplification. Microscopically, we neglect complex coupling45 and correlated binding31 in our motor stepping model, both of which would reduce Pcl at high [ATP]. The model could be elaborated to adjust for these assumptions, but we do not pursue that here for simplicity.
in Fig. 1 and 2 are smaller than in experiment. This may reflect simplifying assumptions in this model. On a hydrodynamic scale, we assume that turbulent scaling relations hold at all concentrations, even though we expect them to hold only above a critical [ATP]. Furthermore, our assumption that K is linear in Pcl is likely an oversimplification. Microscopically, we neglect complex coupling45 and correlated binding31 in our motor stepping model, both of which would reduce Pcl at high [ATP]. The model could be elaborated to adjust for these assumptions, but we do not pursue that here for simplicity.
To test the robustness of our conclusions, we also consider an alternative model in which the motor velocity vm and motor crosslinking probability Pcl are assumed to follow simple Michaelis–Menten-like dependences on [ATP] (S1 and S2),21,46 such that increasing [ATP] results in an increasing motor velocity and decreasing motor crosslinking probability (Fig. S6A and B, ESI†). We then approximate the extension rate as ε ∼ vmPcl, which enables us to capture some of the missing microscopic physics phenomenologically. The remainder of the model is the same as previously: we assume that activity scales as α ∼ εβ and elasticity obeys (1). For reasonable values of the relevant parameters, we find that the predicted dependences of the characteristic velocity v and length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) on [ATP] closely resemble the experimentally observed trends over the relevant range of [ATP] (Fig. S6(C) and (D), ESI†). Moreover, we find that the qualitative trends (non-monotonicity in v and decreasing
on [ATP] closely resemble the experimentally observed trends over the relevant range of [ATP] (Fig. S6(C) and (D), ESI†). Moreover, we find that the qualitative trends (non-monotonicity in v and decreasing ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) within the relevant range of [ATP]) are fairly insensitive to the exponent β. These observations provide further support for the physical picture presented above, i.e., that the experimentally observed trends in v and
within the relevant range of [ATP]) are fairly insensitive to the exponent β. These observations provide further support for the physical picture presented above, i.e., that the experimentally observed trends in v and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are a consequence of the contribution of motors to both the activity and the nematic elasticity.
are a consequence of the contribution of motors to both the activity and the nematic elasticity.
Motor valency tunes nematic dynamics
We now consider how the motor valency (i.e., the number of heads in a cluster) affects the structure and dynamics of the active nematics. Simulations of motors on single filaments show that increasing the motor valency reduces the speed and increases the processivity, consistent with experimental measurements25 (Fig. S7, ESI†). These trends shift the dependence of ε on [ATP] in simulations of motors on two filaments such that higher [ATP] is required to reach the same relative extension rate (Fig. 3(A)). Higher valency also leads to a greater probability of crosslinking across all [ATP] and a smaller relative decrease in crosslinking across the range of [ATP] that we consider (Fig. 3(B)). These microscopic trends lead to a valency-dependent shift of the peak in v to higher [ATP] (Fig. 3(C), dotted line) and a decrease in the relative change in![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) between low and high [ATP] (Fig. 3(D)).
between low and high [ATP] (Fig. 3(D)).
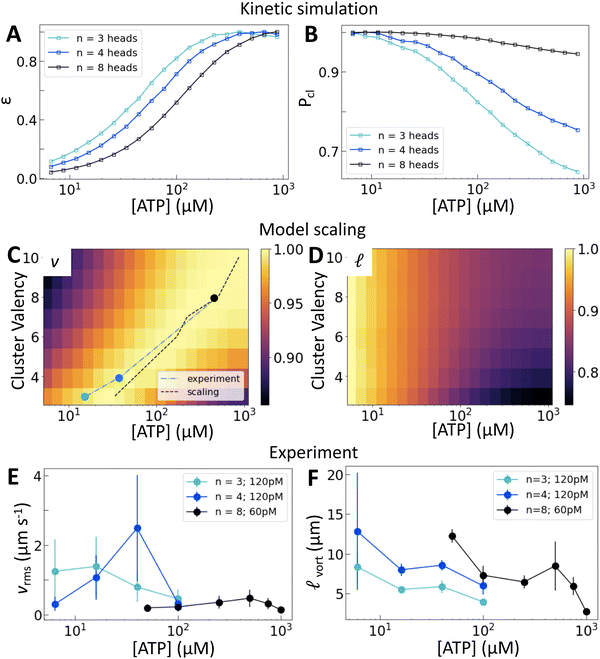 | ||
Fig. 3 Motor valency tunes nematic dynamics. (A) and (B) Normalized ε and Pcl calculated for clusters of variable valency. (C) and (D) Normalized v and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) from model scaling. The black dotted line in (C) traces the location of the peak in nematic speed predicted by the scaling model; symbols and blue line show the positions of peaks in (E). Brighter colors are higher values. A similar plot from multiple experimental replicates at various concentrations is shown in Fig. S12 (ESI†). (E) and (F) vrms and from model scaling. The black dotted line in (C) traces the location of the peak in nematic speed predicted by the scaling model; symbols and blue line show the positions of peaks in (E). Brighter colors are higher values. A similar plot from multiple experimental replicates at various concentrations is shown in Fig. S12 (ESI†). (E) and (F) vrms and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort for a range of [ATP] and cluster valencies. Error bars for speed are standard deviations over 100 s of steady-state activity. Error bars for length scale are standard deviations on five sets of five non-overlapping frames from a single experiment. Data from independent replicates are shown in Fig. S11 (ESI†). vort for a range of [ATP] and cluster valencies. Error bars for speed are standard deviations over 100 s of steady-state activity. Error bars for length scale are standard deviations on five sets of five non-overlapping frames from a single experiment. Data from independent replicates are shown in Fig. S11 (ESI†). | ||
Experimentally, we utilize the control afforded by the motor's multimerization domain to consider clusters with n = 3, 4, or 8 heads. We take into account the contributions of cluster valency and total number of motor heads by considering trimeric (Movie S2, ESI†) and tetrameric motor clusters at 120 pM and octameric (Movie S3, ESI†) motor clusters at 60 pM (Fig. 3(E)). This allows us to separate the contributions from cluster valency and the total head number in the system. We find that the peak in vrms is indeed dependent on cluster valency and shifts to higher [ATP] as valency increases (Fig. 3(E) and Fig. S8–S10, ESI†). This trend holds across multiple independent series (Fig. S11 and S12, ESI†). In fact, the shift that we find in experiment closely matches that predicted by our simulations (Fig. 3(C); the black dashed line traces the simulation peaks; the blue line traces the experimental peaks). Furthermore, as valency increases, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort at a given [ATP] increases (Fig. 3(F)). Thus we can access different ATP response regimes in these nematics by tuning motor valency. However, separating the contributions of Pcl and ε in these experiments is not possible as these quantities vary simultaneously as valency changes (Fig. 3(A) and (B)).
vort at a given [ATP] increases (Fig. 3(F)). Thus we can access different ATP response regimes in these nematics by tuning motor valency. However, separating the contributions of Pcl and ε in these experiments is not possible as these quantities vary simultaneously as valency changes (Fig. 3(A) and (B)).
Crosslinking modulates the efficiency of nematic energy transfer
To separate the effects of crosslinking and strain rate, we consider the effects of adding the passive crosslinker filamin (FLN). Here, we use active nematics driven by trimeric motors because they have the lowest baseline level of crosslinking. To incorporate the contribution from passive crosslinkers in the model, we simply add a contribution to the effective concentration of crosslinkers: ce = cmPcl + cp, where cp is the concentration of passive crosslinkers. Otherwise the model is the same (Fig. 4(A)). This model predicts that the addition of passive crosslinkers leads to a shift in the peak in v to higher [ATP] (Fig. 4(B)). We note that this shift is different from that in response to changing the valency in that it occurs for constant ε and Pcl. Experimentally, we find that adding crosslinker to these samples yields a dramatically longer length scale as is expected from increased K (Fig. 4(C) and (E)). Furthermore, we find that increased concentrations of passive crosslinker do indeed lead to a shift in the peak in vrms to higher [ATP] (Fig. 4(D) and (E)). These observations support our model, in which crosslinking linearly increases the elastic modulus. In turn, the shift in vrms can be understood in terms of (2). Previously we discussed the case of increasing κ, which increases K′, shifting αpeak to lower [ATP]. By contrast, adding passive crosslinkers leaves K′ unchanged while increasing overall K, shifting αpeak to higher [ATP].As noted before, this shift is accompanied by an increase in ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort and vrms (Fig. 4(C) and (D)). Thus for a given [ATP] the nematic features fewer defects but moves faster (Fig. 4(E)). These changes occur without a substantial change in ε, suggesting that shifts in K affect how the activity supplied by motors manifests in nematic dynamics. Indeed, lattice Boltzmann simulations show that in the high activity regime total energy in the nematic actually increases with K (Fig. S13, ESI†). This indicates a crucial role for filament crosslinking in determining the efficiency of energy transfer from motor stress into active nematic motion.
vort and vrms (Fig. 4(C) and (D)). Thus for a given [ATP] the nematic features fewer defects but moves faster (Fig. 4(E)). These changes occur without a substantial change in ε, suggesting that shifts in K affect how the activity supplied by motors manifests in nematic dynamics. Indeed, lattice Boltzmann simulations show that in the high activity regime total energy in the nematic actually increases with K (Fig. S13, ESI†). This indicates a crucial role for filament crosslinking in determining the efficiency of energy transfer from motor stress into active nematic motion.
Conclusions
In this work, we show that crosslinking has a profound effect on active nematic dynamics through elasticity. Previous work with high processivity motors focused on the motors’ role in activity despite clues to their role in elasticity from machine learning47 and experiments in the low [ATP] limit.21 Our investigation here of active nematics with low processivity motors reveals that reduced filament crosslinking at high [ATP] leads to reduced nematic elasticity and a nonmonotonic dependence of nematic speed on [ATP]. Indeed, we find that the contribution to elasticity from crosslinking dominates that from excluded volume interactions. We note that our results are consistent with results for nematics formed by microtubules and kinesin.21 Kinesin run length is independent of [ATP] across a broad range of [ATP] and only deviates at low [ATP], where rigor sets in.22 As such nematics formed by microtubules and kinesin should not exhibit significant changes in K except at low [ATP], consistent with previous observations.21Our results suggest that exquisite control over active nematics dynamics can be achieved through the choice of molecular composition. Increasing motor valency affects both the activity and the elasticity due to the effects on both the strain rate and filament crosslinking. Adding passive crosslinkers in principle allows one to tune just the elasticity. That both motors and crosslinkers affect elasticity has long been appreciated for actin gels.38,48 Transient crosslinkers have also been shown to tune viscoelastic properties in fluid actin droplets.49,50 Our results suggest that the degree to which motor proteins dictate elasticity can be tuned by their physical and biochemical properties. Consistent with this idea, it was recently observed that transitions between aster-like and vortex-like motifs as [ATP] varied in reconsituted actomyosin networks could be explained by changes in the likelihood of motors binding more than one filament.51 It is thus interesting to speculate that the fantastic diversity of naturally occurring motors and crosslinkers reflects in part evolutionary pressures to achieve different materials properties.
Our study is a step toward quantitatively linking hydrodynamic parameters of active materials to microscopic properties. How transferable such relations may be is an open question. For example, even though active nematics composed of bacteria can be described in the hydrodynamic limit with similar scaling laws, activity is generated by microscopic mechanisms that are distinct from the active nematics considered here.9 As a result, the characters of their force dipoles may also be distinct, despite both being extensile. While this suggests that it will be necessary to go beyond scaling relations to characterize active materials fully, it is also an opportunity for tailoring active materials with unique properties.
Materials and methods
Experimental procedures
Cloning and purification of motor constructs
The tetrameric motor construct CM11CD7462R ∼ 1R∼ TET is described in ref. 25. Motor constructs were assembled from gene fragments encoding the Chara corallina myosin XI motor domain (residues 1–746), Dictyostelium α-actinin (residues 266–502 for the lever arm and residues 266–388 for the flexible linker), a multimerization domain, and a C-terminal HaloTag and FLAG-tag (DYKDDDDK). The tetrameric motor construct contains the GCN4 leucine zipper variant p-LI as the multimerization domain, which forms a parallel tetrameric coiled-coil.26 In the trimeric construct, the multimerization domain was replaced with the GCN4 variant p-II, which forms a coiled-coil trimer rather than a tetramer,26 as previously described for similar constructs.25 To create the octameric construct, the tetramerization domain was replaced with a de novo two-helix hairpin that was designed to assemble into a water-soluble octameric pore (WSHC8 from ref. 27 PDB 6O35) and the HaloTag is N-terminal to the motor. Constructs were cloned into the insect expression vector pBiEx-1.For protein expression, plasmids were directly transfected into Sf9 cells as described previously.54 Purification was performed as described in ref. 54 and 55. Briefly, proteins were purified using anti-FLAG resin and labeled with Alexa Fluor 660 HaloTag Ligand (Promega). Proteins were eluted into storage buffer containing glycerol and then immediately flash-frozen in small aliquots and stored at −80 °C until use.
Assay conditions
All experiments within a series were performed on a single day to ensure that trends observed did not arise from uncontrolled variations in molecular activities and environmental conditions. Actin filaments were polymerized at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 labelling ratio and a concentration of 2 μM in a 50 μL polymerization mix. This mix contained 1X F-buffer [10 mM imidazole, 1 mM MgCl2, 50 mM KCl, 0.2 mM egtazic acid (EGTA), pH 7.5] with each of the concentrations of ATP studied. No additional MgCl2 was added with ATP. To minimize photobleaching, an oxygen scavenging system 4.5 mg mL−1 glucose, 2.7 mg mL−1 glucose oxidase (catalog no. 345486, Calbiochem, Billerica, MA), 17
10 labelling ratio and a concentration of 2 μM in a 50 μL polymerization mix. This mix contained 1X F-buffer [10 mM imidazole, 1 mM MgCl2, 50 mM KCl, 0.2 mM egtazic acid (EGTA), pH 7.5] with each of the concentrations of ATP studied. No additional MgCl2 was added with ATP. To minimize photobleaching, an oxygen scavenging system 4.5 mg mL−1 glucose, 2.7 mg mL−1 glucose oxidase (catalog no. 345486, Calbiochem, Billerica, MA), 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 units per mL catalase (catalog no. 02071, Sigma, St. Louis, MO) and 0.5 vol% β-mercaptaethanol was added. Actin filaments were crowded to the surface by including 0.3% w%400 cP methylcellulose in the polymerization mix. Capping protein was first thawed on ice, then diluted to 500 nM in 1X F-buffer, and added at a final concentration of 30 nM in the mix. This polymerization reaction was allowed to proceed for one hour on ice before it was added to the imaging chamber.
000 units per mL catalase (catalog no. 02071, Sigma, St. Louis, MO) and 0.5 vol% β-mercaptaethanol was added. Actin filaments were crowded to the surface by including 0.3% w%400 cP methylcellulose in the polymerization mix. Capping protein was first thawed on ice, then diluted to 500 nM in 1X F-buffer, and added at a final concentration of 30 nM in the mix. This polymerization reaction was allowed to proceed for one hour on ice before it was added to the imaging chamber.
The imaging chamber was created by first rinsing a small glass cloning cylinder (catalog no. 09-552-20, Corning Inc.) with ethanol and then attaching it to a silanated glass coverslip with two-part epoxy. To prevent the actin from sticking and maintain fluidity, the coverslip was coated with a thin layer of Novec 7500 Engineered Fluid (3M, St. Paul, MN) that included PFPE-PEG-PFPE surfactant (catalog no. 008, RAN Biotechnologies, Beverly, MA) at 2% w/v before the polymerization mix was added. The mixture was allowed to sit in the sample chamber for about 30 min before imaging to allow for the formation of the nematic.
The sample was imaged on an Eclipse-Ti inverted microscope (Nikon, Melville, NY) in confocal mode utilizing a spinning disk (CSU-X, Yokagawa Electric, Musashino, Tokyo, Japan) and a CMOS camera (Zyla-4.2 USB 3; Andor, Belfast, UK). Experiments were imaged at one frame every 2 s.
Data analysis
Flow fields were calculated between every two frames from time lapse images with optical flow using the Classic + NL-fast method.34,56 This method is based on the classic Horn-Schunck method which minimizes an objective function penalizing intensity differences between subsequent frames (the data term) as well as enforcing smoothness in the estimated field. Flow is estimated at various spatial scales iteratively to capture first global and then local motion. The optical flow code was obtained from https://cs.brown.edu/people/mjblack/code.html.Average flow speed v was calculated from the N vectors, ui, as v = Σ|ui|/N. The velocity correlation length quoted in Fig. S2 (ESI†) was calculated as the distance r at which the velocity autocorrelation function Cuu(r) = 〈ui(0)·uj(r)/|ui||uj|〉 reaches 1/e, where the average is over all pairs (i,j) and e is Euler's number.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort was calculated with the method of correlated displacement fields, as described in ref. 35. Briefly, the normalized cross correlation is measured in two dimensions between the vorticity field ν and the velocity field u. This procedure effectively measures the response of the nematic to a unit vortical perturbation at the origin. To extract a length scale from this response, the azimuthal average of the correlation field is taken. This average results in a one dimensional function with a single maximum.
vort was calculated with the method of correlated displacement fields, as described in ref. 35. Briefly, the normalized cross correlation is measured in two dimensions between the vorticity field ν and the velocity field u. This procedure effectively measures the response of the nematic to a unit vortical perturbation at the origin. To extract a length scale from this response, the azimuthal average of the correlation field is taken. This average results in a one dimensional function with a single maximum. ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort is the distance r at which this maximum occurs. This length scale has been shown in active nematics to be equal to the average radius of a vortex in the flow field.35 Error for this method was calculated by measuring
vort is the distance r at which this maximum occurs. This length scale has been shown in active nematics to be equal to the average radius of a vortex in the flow field.35 Error for this method was calculated by measuring ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) vort over 5 separate non-overlapping sets of frames from the 100 s of steady-state data considered in vrms. The code is available at https://github.com/Gardel-lab/ResponseFunction.
vort over 5 separate non-overlapping sets of frames from the 100 s of steady-state data considered in vrms. The code is available at https://github.com/Gardel-lab/ResponseFunction.
Motor stepping model
The code to run an analyze the myosin stepping model described in Results is available at https://github.com/Gardel-lab/myosin_stepping_model.Lattice Boltzmann simulations
Simulations of active nematic hydrodynamics were performed using a custom Julia implementation of the hybrid lattice Boltzmann algorithm.57,58 The simulated equations of motion are the same as those detailed in ref. 13 and 47. The simulation domain consists of 400 × 400 lattice points in two dimensions with periodic boundary conditions. The turbulent state was generated by initially perturbing the system and evolving for 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, and then data was collected every 50 steps for another 15
000 steps, and then data was collected every 50 steps for another 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. For each condition we ran 5 independent trials using different random seeds for the initial perturbation. We used the following parameters (in lattice units): a collision time τ = 1.5 (corresponding to viscosity η = 1/3), a flow-alignment parameter ξ = 0.7, a rotational diffusion constant Γ = 0.13, and polarization free energy coefficients of A0 = 0.1, U = 3.5, leading to an equilibrium nematic polarization magnitude of q = 0.62. The elastic constant K ∈ [0,0.1] and activity coefficient α ∈ [0,0.01] (where positive α corresponds to extensile activity) were varied to generate the results shown here.
000 steps. For each condition we ran 5 independent trials using different random seeds for the initial perturbation. We used the following parameters (in lattice units): a collision time τ = 1.5 (corresponding to viscosity η = 1/3), a flow-alignment parameter ξ = 0.7, a rotational diffusion constant Γ = 0.13, and polarization free energy coefficients of A0 = 0.1, U = 3.5, leading to an equilibrium nematic polarization magnitude of q = 0.62. The elastic constant K ∈ [0,0.1] and activity coefficient α ∈ [0,0.01] (where positive α corresponds to extensile activity) were varied to generate the results shown here.
Author contributions
SAR, MM, ZB, ARD, and MLG designed the research. SZ and PVR designed motor constructs and expressed motor proteins. SAR, ZB, and ARD designed the kinetic simulation. SAR performed the experiments and kinetic simulations. JC and JLS developed the hydrodynamic connection between simulations and scaling laws. CSF performed lattice Boltzmann simulations. All authors contributed to and approved the manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We thank Chunfu Xu for sharing the sequence of the octameric helical bundle construct before publication. SAR is grateful to Cristian Suarez and Rachel Kadzik for help purifying proteins and valuable discussions. This work was partially supported by the University of Chicago Materials Research Science and Engineering Center, which is funded by National Science Foundation under award number DMR-2011854. MLG and ZB acknowledge support from NSF award DMR-2215605 and NIH R01GM143792. ARD acknowledges support from NSF Award MCB-2201235. ZB acknowledges support from NIH R01GM114627. SAR was supported by the NIH under award T32 EB009412. Simulations were performed on computational resources provided by the University of Chicago Research Computing Center.References
- S. Ramaswamy, The Mechanics and Statistics of Active Matter, Annu. Rev. Condens. Matter Phys., 2010, 1(1), 323–345 CrossRef.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. Aditi Simha, Hydrodynamics of soft active matter, Rev. Mod. Phys., 2013, 85(3), 1143–1189 CrossRef CAS.
- T. Sanchez, S. J. DeCamp, M. Heymann and Z. Dogic, Spontaneous motion in hierarchically assembled active matter, Nature, 2012, 491(7424), 431–434 CrossRef CAS PubMed.
- C. del Junco, L. Tociu and S. Vaikuntanathan, Energy dissipation and fluctuations in a driven liquid, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(14), 3569–3574 CrossRef CAS PubMed.
- N. Kumar, R. Kumar Gupta, H. Soni, S. Ramaswamy and A. K. Sood, Trapping and sorting active particles: Motility-induced condensation and smectic defects, Phys. Rev. E, 2019, 99(3), 032605 CrossRef CAS PubMed.
- S. Ramaswamy, R. Aditi Simha and J. Toner, Active nematics on a substrate: Giant number fluctuations and long-time tails, Europhys. Lett., 2003, 62(2), 196 CrossRef CAS.
- A. Cavagna and I. Giardina, Bird Flocks as Condensed Matter, Annu. Rev. Condens. Matter Phys., 2014, 5(1), 183–207 CrossRef CAS.
- C. Dombrowski, L. Cisneros, S. Chatkaew, R. E. Goldstein and J. O. Kessler, Self-Concentration and Large-Scale Coherence in Bacterial Dynamics, Phys. Rev. Lett., 2004, 93(9), 098103 CrossRef PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Meso-scale turbulence in living fluids, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(36), 14308–14313 CrossRef CAS PubMed.
- P. Guillamat, J. Ignés-Mullol and F. Sagués, Control of active liquid crystals with a magnetic field, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(20), 5498–5502 CrossRef CAS PubMed.
- K.-T. Wu, J. B. Hishamunda, D. T. N. Chen, S. J. DeCamp, Y.-W. Chang, A. Fernández-Nieves, S. Fraden and Z. Dogic, Transition from turbulent to coherent flows in confined three-dimensional active fluids, Science, 2017, 355(6331), eaal1979 CrossRef PubMed.
- T. D. Ross, H. J. Lee, Z. Qu, R. A. Banks, R. Phillips and M. Thomson, Controlling organization and forces in active matter through optically defined boundaries, Nature, 2019, 572(7768), 224–229 CrossRef CAS PubMed.
- R. Zhang, S. A. Redford, P. V. Ruijgrok, N. Kumar, A. Mozaffari, S. Zemsky, A. R. Dinner, V. Vitelli, Z. Bryant, M. L. Gardel and J. J. de Pablo, Spatiotemporal control of liquid crystal structure and dynamics through activity patterning, Nat. Mater., 2021, 20(6), 875–882 CrossRef CAS PubMed.
- N. Kumar, R. Zhang, S. A. Redford, J. J. de Pablo and M. L. Gardel, Catapulting of topological defects through elasticity bands in active nematics, Soft Matter, 2022, 18(28), 5271–5281 RSC.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, 1993 Search PubMed.
- A. Doostmohammadi, T. N. Shendruk, K. Thijssen and J. M. Yeomans, Onset of meso-scale turbulence in active nematics, Nat. Commun., 2017, 8, 15326 CrossRef CAS PubMed.
- L. Giomi, Geometry and Topology of Turbulence in Active Nematics, Phys. Rev. X, 2015, 5(3), 031003 Search PubMed.
- E. J. Hemingway, P. Mishra, M. Cristina Marchetti and S. M. Fielding, Correlation lengths in hydrodynamic models of active nematics, Soft Matter, 2016, 12(38), 7943–7952 RSC.
- A. Doostmohammadi, J. Igné-Mullol, J. M. Yeomans and F. Sagués, Active nematics, Nat. Commun., 2018, 9(1), 3246 CrossRef PubMed.
- N. Kumar, R. Zhang, J. J. de Pablo and M. L. Gardel, Tunable structure and dynamics of active liquid crystals, Sci. Adv., 2018, 4(10), eaat7779 CrossRef CAS PubMed.
- L. M. Lemma, S. J. DeCamp, Z. You, L. Giomi and Z. Dogic, Statistical properties of autonomous flows in 2D active nematics, Soft Matter, 2019, 15(15), 3264–3272 RSC.
- S. Verbrugge, S. M. J. L. Van Den Wildenberg and E. J. G. Peterman, Novel Ways to Determine Kinesin-1's Run Length and Randomness Using Fluorescence Microscopy, Biophys. J., 2009, 97(8), 2287–2294 CrossRef CAS PubMed.
- M. J. Bloemink and M. A. Geeves, Shaking the myosin family tree: Biochemical kinetics defines four types of myosin motor, Semin. Cell Dev. Biol., 2011, 22(9), 961–967 CrossRef CAS PubMed.
- S. Stam, S. L. Freedman, S. Banerjee, K. L. Weirich, A. R. Dinner and M. L. Gardel, Filament rigidity and connectivity tune the deformation modes of active biopolymer networks, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(47), E10037 CrossRef CAS PubMed.
- T. D. Schindler, L. Chen, P. Lebel, M. Nakamura and Z. Bryant, Engineering myosins for long-range transport on actin filaments, Nat. Nanotechnol., 2014, 9(1), 33–38 CrossRef CAS PubMed.
- P. B. Harbury, T. Zhang, P. S. Kim and T. Alberd, A Switch Between Two-, Three-, and Four-stranded Coiled Coils in GCN4 Leucine Zipper Mutants, Science, 1993, 262(5138), 1401–1407 CrossRef CAS PubMed.
- C. Xu, P. Lu, T. M. G. El-Din, X. Y. Pei, M. C. Johnson, A. Uyeda, M. J. Bick, Q. Xu, D. Jiang, H. Bai, G. Reggiano, Y. Hsia, T. J. Brunette, J. Dou, D. Ma, E. M. Lynch, S. E. Boyken, P.-S. Huang, L. Stewart, F. DiMaio, J. M. Kollman, B. F. Luisi, T. Matsuura, W. A. Catterall and D. Baker, Computational design of transmembrane pores, Nature, 2020, 585(7823), 129–134 CrossRef CAS PubMed.
- K. Ito, M. Ikebe, T. Kashiyama, T. Mogami, T. Kon and K. Yamamoto, Kinetic mechanism of the fastest motor protein, Chara myosin, J. Biol. Chem., 2007, 282(27), 19534–19545 CrossRef CAS PubMed.
- H. Sumiyoshi, M. Ooguchi, A. Ooi, T. Okagaki and S. Higashi-Fujime, Insight into the mechanism of fast movement of myosin from Chara corallina, Cell Motility, 2007, 64(2), 131–142 CrossRef CAS PubMed.
- T. Haraguchi, M. Tamanaha, K. Suzuki, K. Yoshimura, T. Imi, M. Tominaga, H. Sakayama, T. Nishiyama, T. Murata and K. Ito, Discovery of ultrafast myosin, its amino acid sequence, and structural features, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(8), e2120962119 CrossRef CAS PubMed.
- A. Vilfan, Elastic Lever-Arm Model for Myosin V, Biophys. J., 2005, 88(6), 3792–3805 CrossRef CAS PubMed.
- D. T. Gillespie, Exact stochastic simulation of coupled chemical reactions, J. Phys. Chem., 1977, 81(25), 2340–2361 CrossRef CAS.
- T. Gao, R. Blackwell, M. A. Glaser, M. D. Betterton and M. J. Shelley, Multiscale Polar Theory of Microtubule and Motor-Protein Assemblies, Phys. Rev. Lett., 2015, 114(4), 048101 CrossRef PubMed.
- D. Sun, S. Roth and M. J. Black, Secrets of optical flow estimation and their principles. In 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pages 2432–2439, June 2010.
- M. Molaei, S. A. Redford, W.-H. Chou, D. Scheff, J. J. de Pablo, P. W. Oakes and M. L. Gardel, Measuring response functions of active materials from data, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(42), e2305283120 CrossRef CAS PubMed.
- M. Molaei, N. G. Chisholm, J. Deng, J. C. Crocker and K. J. Stebe, Interfacial Flow around Brownian Colloids, Phys. Rev. Lett., 2021, 126(22), 228003 CrossRef CAS PubMed.
- S. Syed, F. C. MacKintosh and J. L. Shivers, Structural Features and Nonlinear Rheology of Self-Assembled Networks of Cross-Linked Semiflexible Polymers, J. Phys. Chem. B, 2022, 126(50), 10741–10749 CrossRef CAS PubMed.
- M. L. Gardel, J. H. Shin, F. C. MacKintosh, L. Mahadevan, P. Matsudaira and D. A. Weitz, Elastic Behavior of Cross-Linked and Bundled Actin Networks, Science, 2004, 304(5675), 1301–1305 CrossRef CAS PubMed.
- J. M. Belmonte, M. Leptin and F. Nédélec, A theory that predicts behaviors of disordered cytoskeletal networks, Mol. Syst. Biol., 2017, 13(9), 941 CrossRef PubMed.
- P. J. Foster, S. Fürthauer, M. J. Shelley and D. J. Needleman, Active contraction of microtubule networks, eLife, 2015, 4, e10837 CrossRef PubMed.
- S. L. Freedman, G. M. Hocky, S. Banerjee and A. R. Dinner, Nonequilibrium phase diagrams for actomyosin networks, Soft Matter, 2018, 14(37), 7740–7747 RSC.
- M. Scholz, K. L. Weirich, M. L. Gardel and A. R. Dinner, Tuning molecular motor transport through cytoskeletal filament network organization, Soft Matter, 2020, 16(8), 2135–2140 RSC.
- A. Ahmadi, M. C. Marchetti and T. B. Liverpool, Hydrodynamics of isotropic and liquid crystalline active polymer solutions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74(6), 061913 CrossRef PubMed.
- R. Zhang, N. Kumar, J. L. Ross, M. L. Gardel and J. J. de Pablo, Interplay of structure, elasticity, and dynamics in actin-based nematic materials, Proc. Natl. Acad. Sci. U. S. A., 2017, 115(2), E124–E133 Search PubMed.
- E. Forgacs, S. Cartwright, T. Sakamoto, J. R. Sellers, J. E. T. Corrie, M. R. Webb and H. D. White, Kinetics of ADP dissociation from the trail and lead heads of actomyosin V following the power stroke, J. Biol. Chem., 2008, 283(2), 766–773 CrossRef CAS PubMed.
- S. Leibler and D. A. Huse, Porters versus rowers: A unified stochastic model of motor proteins, J. Cell Biol., 1993, 121(6), 1357–1368 CrossRef CAS PubMed.
- J. Colen, M. Han, R. Zhang, S. A. Redford, L. M. Lemma, L. Morgan, P. V. Ruijgrok, R. Adkins, Z. Bryant, Z. Dogic, M. L. Gardel, J. J. de Pablo and V. Vitelli, Machine learning active-nematic hydrodynamics, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(10), e2016708118 CrossRef CAS PubMed.
- S. Stam, J. Alberts, M. L. Gardel and E. Munro, Isoforms Confer Characteristic Force Generation and Mechanosensation by Myosin II Filaments, Biophys. J., 2015, 108(8), 1997–2006 CrossRef CAS PubMed.
- D. R. Scheff, K. L. Weirich, K. Dasbiswas, A. Patel, S. Vaikuntanathan and M. L. Gardel, Tuning shape and internal structure of protein droplets via biopolymer filaments, Soft Matter, 2020, 16(24), 5659–5668 RSC.
- K. L. Weirich, S. Banerjee, K. Dasbiswas, T. A. Witten, S. Vaikuntanathan and M. L. Gardel, Liquid behavior of cross-linked actin bundles, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(9), 2131–2136 CrossRef CAS PubMed.
- S. C. Al-Izzi, D. V. Köster and R. G. Morris, More ATP Does Not Equal More Contractility: Power And Remodelling In Reconstituted Actomyosin, arXiv, 2023, preprint, arXiv.2108.00764 DOI:10.48550/arXiv.2108.00764.
- J. A. Spudich and S. Watt, The Regulation of Rabbit Skeletal Muscle Contraction: I. Biochemical studies of the interaction of the tropomyosin-troponin complex with actin and the proteolytic fragments of myosin, J. Biol. Chem., 1971, 246, 4866–4871 CrossRef CAS PubMed.
- T. A. Burke, A. J. Harker, R. Dominguez and D. R. Kovar, The bacterial virulence factors VopL and VopF nucleate actin from the pointed end, J. Cell Biol., 2017, 216(5), 1267–1276 CrossRef CAS PubMed.
- J.-C. Liao, M. Williard Elting, S. L. Delp, J. A. Spudich and Z. Bryant, Engineered Myosin VI Motors Reveal Minimal Structural Determinants of Directionality and Processivity, J. Mol. Biol., 2009, 392(4), 862–867 CrossRef CAS PubMed.
- P. V. Ruijgrok, R. P. Ghosh, S. Zemsky, M. Nakamura, R. Gong, L. Ning, R. Chen, V. T. Vachharajani, A. E. Chu, N. Anand and others, Optical control of fast and processive engineered myosins in vitro and in living cells, Nat. Chem. Biol., 2021, 17(5), 540–548 CrossRef CAS PubMed.
- D. Sun, S. Roth and M. J. Black, A Quantitative Analysis of Current Practices in Optical Flow Estimation and the Principles Behind Them, Int. J. Comput. Vis., 2014, 106(2), 115–137 CrossRef.
- C. Floyd, S. Vaikuntanathan and A. R. Dinner, Simulating structured fluids with tensorial viscoelasticity, J. Chem. Phys., 2023, 158(5), 054906 CrossRef CAS PubMed.
- L. Nicola Carenza, G. Gonnella, A. Lamura, G. Negro and A. Tiribocchi, Lattice Boltzmann methods and active fluids, Eur. Phys. J. E: Soft Matter Biol. Phys., 2019, 42(6), 81 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01176c |
| This journal is © The Royal Society of Chemistry 2024 |