Open Access Article
Open Access ArticleThere and back again: bridging meso- and nano-scales to understand lipid vesicle patterning†
Julie
Cornet
a,
Nelly
Coulonges
ab,
Weria
Pezeshkian
 c,
Maël
Penissat-Mahaut
b,
Hermes
Desgrez-Dautet
d,
Siewert J.
Marrink
c,
Maël
Penissat-Mahaut
b,
Hermes
Desgrez-Dautet
d,
Siewert J.
Marrink
 e,
Nicolas
Destainville
*a,
Matthieu
Chavent
e,
Nicolas
Destainville
*a,
Matthieu
Chavent
 *bd and
Manoel
Manghi
*bd and
Manoel
Manghi
 *a
*a
aLaboratoire de Physique Théorique, Université de Toulouse, CNRS, UPS, France. E-mail: nicolas.destainville@univ-tlse3.fr; manoel.manghi@univ-tlse3.fr
bInstitut de Pharmacologie et Biologie Structurale, Université de Toulouse, CNRS, Université Toulouse III - Paul Sabatier, 31400, Toulouse, France. E-mail: matthieu.chavent@univ-tlse3.fr
cNiels Bohr International Academy, Niels Bohr Institute, University of Copenhagen, Blegdamsvej 17, 2100 Copenhagen, Denmark
dLaboratoire de Microbiologie et Génétique Moléculaires (LMGM), Centre de Biologie Intégrative (CBI), Université de Toulouse, CNRS, UPS, France
eGroningen Biomolecular Sciences and Biotechnology Institute, University of Groningen, Nijenborgh 7, 9747 AG Groningen, The Netherlands
First published on 22nd May 2024
Abstract
We describe a complete methodology to bridge the scales between nanoscale molecular dynamics and (micrometer) mesoscale Monte Carlo simulations in lipid membranes and vesicles undergoing phase separation, in which curving molecular species are furthermore embedded. To go from the molecular to the mesoscale, we notably appeal to physical renormalization arguments enabling us to rigorously infer the mesoscale interaction parameters from its molecular counterpart. We also explain how to deal with the physical timescales at stake at the mesoscale. Simulating the as-obtained mesoscale system enables us to equilibrate the long wavelengths of the vesicles of interest, up to the vesicle size. Conversely, we then backmap from the meso- to the nano-scale, which enables us to equilibrate in turn the short wavelengths down to the molecular length-scales. By applying our approach to the specific situation of patterning a vesicle membrane, we show that macroscopic membranes can thus be equilibrated at all length-scales in achievable computational time offering an original strategy to address the fundamental challenge of timescale in simulations of large bio-membrane systems.
1 Introduction
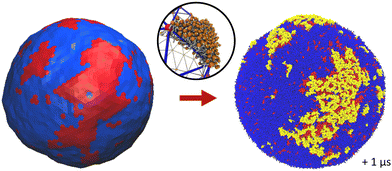
The physics of living systems is permanently confronted by the multiplicity of the length- and time-scales of interest: from the nanoscopic molecular scale where events occur below the nano-second timescale, to the micrometric cellular scale where microseconds or seconds are at stake. Different physical and numerical techniques have been developed to study these different scales, which are either quantum or classical, with explicit or implicit water, including stochastic or hydrodynamics techniques. But bridging these scales is still a difficult task as the methods employed for each scale may not use the same physical dynamics – e.g., molecular dynamics (MD) or Monte Carlo (MC) – nor the same integration scheme – e.g., Newtonian or Brownian dynamics. Thus, even though multi-scale workflows have been developed recently,1–3 these types of approaches have been limited in terms of the spatial/timing range they can span4 and they have generally been constrained to “one spatial direction”,5–8 from the nanoscale to the meso/micro-scale or the other way around. Here, thanks to recent advances in the field,9,10 we provide details of and rationalize a method to fully bridge, forward and backward, nano- and meso-scales in biomembranes (see Fig. 1).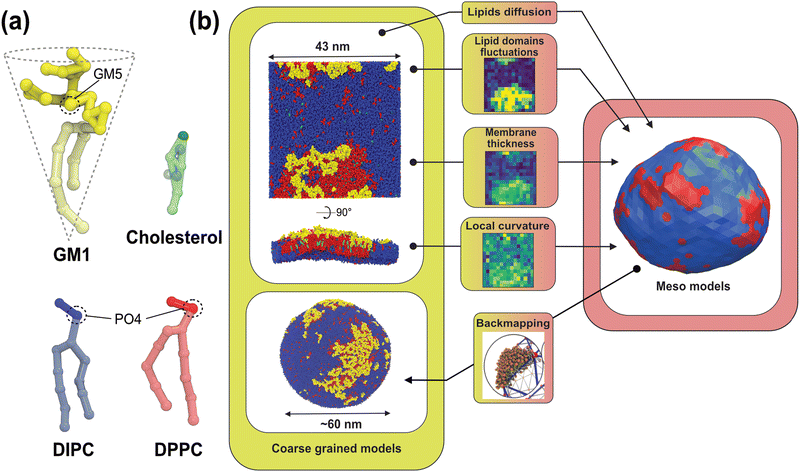 | ||
| Fig. 1 Principle of our multiscale modeling scheme for lipid membranes. (a) The lipid models used in the CG simulations. The GM1 model corresponds to the monosialotetrahexosylganglioside and cholesterol model,11 the DIPC model corresponds to 1,2-dilinoleoyl-sn-glycero-3-phosphocholine, and the DPPC model corresponds to 1,2-dipalmitoyl-sn-glycero-3-phosphocholine. The most hydrophilic parts of the lipids are represented in darker colors while the lighter colors depict the more hydrophobic parts of the models. The PO4 and GM5 beads used to define the membrane surface are outlined on the different lipids (see the methods section). (b) From the CG molecular dynamics simulations (upper-left panel), we infer the physical parameters required by the mesoscale Monte Carlo model (right panel) consisting of a bi-phasic tessellated vesicle. The extraction of these parameters is illustrated in the central panels. They are: (i) two dynamical parameters relating the time-scales of lipid diffusion in the membrane plane, and transverse membrane fluctuations; (ii) lipid domain boundary fluctuations from which is inferred the line tension between both lipid phases; (iii) the membrane thickness difference between phases, from which bending moduli ratio can be inferred, and (iv) the spontaneous curvature of the Lo phase induced by insertion of GM1 in the upper leaflet. Conversely, the Meso-to-CG backmapping at the full vesicle scale (lower-left) is illustrated in the lower-middle panel. | ||
We developed this approach in the specific context of lipidic biomembrane patterning. With the recent in vivo, in vitro, and in silico developments, it is now recognized that cell membrane components are not homogeneously distributed, but are organized into functional lipid and protein sub-micrometric domains.12–18 These nanodomains play fundamental roles in cell biology, especially as they serve as platforms or micro-reactors for many biological functions such as infections (viral or bacterial), cell adhesion, transport of solutes, or signaling. Thus, deciphering the formation and evolution of these domains is essential to fully understand these fundamental biological processes. Among the mechanisms proposed for their formation, the role of spontaneous curvature induced by different membrane constituents, with specific shapes, is the focus of particular attention.19
For example, the glycosphingolipid GM1 has a bulky head comprised of four monosaccharides resulting in this lipid having an overall conical shape17,20 (see Fig. 1a). Present predominantly in the outer cell membrane,21,22 this lipid can act as a membrane anchor for different toxins, bacteria and viruses23,24 and plays important roles in several neuronal processes and diseases, notably auto-immune ones.24,25 Although knowledge about its lateral organization remains an active field of research,22 the properties of GM1 are thought to be linked to its propensity to curve the membrane, ensuing from its conical shape.21,26,27 To test this hypothesis on well-defined model systems, giant unilamellar vesicles (GUVs) were used to better characterize in vitro the relationship between curvature generation and lipid domain formation.21,27–29 However, fully linking microscopy visualization, with an intrinsically limited resolution, to nanoscale partitioning of the lipids, is still a challenge.
On the one hand, MD simulations are suitable tools to understand how GM1 perturbs the lipid membrane organization at the molecular scale, notably by curving the bilayer,30 or by destabilizing lipid–lipid phase separation in multicomponent membranes.22 On the other hand, describing the effect of phase separation combined with intrinsic curvature at vesicular or cellular scales makes the use of a much larger degree of coarse-graining inevitable. Here, we illustrate how to bridge the theoretical gap between Coarse-Grained Molecular Dynamics (CG-MD) simulations and mesoscale (Meso for short) Monte Carlo simulations31,32 focusing on vesicular systems, as shown in Fig. 1. Using physically relevant concepts, we first show which data to extract at the nanoscale, obtained with CG-MD simulations, and how they can be used to parametrize the mesoscale Monte Carlo model. We then go from the nano- to meso-scale by integrating out microscopic degrees of freedom, a non-trivial task due to renormalization issues,33 that we fully take into account in this work. Then we show how this leads to meaningful results for the mesoscale model, allowing one to equilibrate membrane patterning at the scale of a whole vesicle, and how this model can predict experimental data at micrometric scales. Finally, we explain how to scale back to CG models to equilibrate the short length-scales, and decipher the overall organization of large lipid domains down to the nanoscale. We also discuss the feasibility of our approach and the limitations inherent to each model when one passes from one scale to another. This thorough approach to linking the scales combined with careful explanations of how to extract meaningful data will pave the way for further development of fully integrated multiscale workflows.
2 Methods
2.1 Coarse-grained (MARTINI) molecular dynamics simulations
We use the CHARMM-GUI MARTINI Maker34,35 to generate 43 × 43 nm2 lipid bilayer systems. The membrane patches are surrounded by about 4 nm of water on each side. Ions are added to neutralize the system. We study a mixture of C16:0 dipalmitoyl PC (DPPC), C18:2 dilinoleoyl PC (DLiPC), also named DIPC in the MARTINI force field, and cholesterol with a concentration ratio of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 and with varying concentrations of C(d18:1/18:0) N-stearoyl-D-erythro (GM1) in the upper leaflet (given in mol mol−1) (see Table 1).
12 and with varying concentrations of C(d18:1/18:0) N-stearoyl-D-erythro (GM1) in the upper leaflet (given in mol mol−1) (see Table 1).
| System | Particles | Duration |
|---|---|---|
| DPPC–DIPC–Chol | 167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 409 409 |
20 |
| DPPC–DIPC–Chol + 2.5% GM1 | 279![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
20 |
| DPPC–DIPC–Chol + 5% GM1 | 181![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 285 285 |
20 |
| DPPC–DIPC–Chol + 7.5% GM1 | 279![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 981 981 |
20 |
| DPPC–DIPC–Chol + 10% GM1 | 181![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756 756 |
20 |
| DPPC–DIPC–Chol + 15% GM1 | 207![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 647 647 |
20 |
| Vesicle | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 487![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 094 094 |
10 |
The CG-MD simulations are performed using the MARTINI v2.236 force field in the NPT ensemble and run with GROMACS 2016 software.37 The temperature is set to 310 K at which Lo and Ld phases coexist for these lipid mixtures. We use the velocity rescaling thermostat38 coupled to a semi-isotropic Parinello–Rahman barostat39 with a pressure of 1 bar. The standard time step of 20 fs is used for all simulations. All systems are equilibrated following equilibration steps as described in the Membrane Builder workflow.40 For production, all the planar systems are simulated for 20 μs to ensure convergence.
The analysis scripts are written in Python3 using MDAnalysis packages.41 In particular, we use the LeafletFinder tool that allows identifying upper and lower leaflets.
2.2 Mesoscale model
The mesoscale model used in the present work was developed and validated previously by one of our groups. We provide an overview of the model in this section, and the interested reader can refer to previously published work for further details.42,43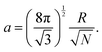 | (1) |
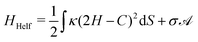 | (2) |
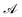 is the total vesicle area. 2H is the total curvature, i.e. the sum of the two principal curvatures, and C is the (local) spontaneous curvature imposed by the molecular species. We do not account for the Gaussian curvature in this model. Using the Laplace–Beltrami operator45 for the curvature term, the discrete elastic free energy reads
is the total vesicle area. 2H is the total curvature, i.e. the sum of the two principal curvatures, and C is the (local) spontaneous curvature imposed by the molecular species. We do not account for the Gaussian curvature in this model. Using the Laplace–Beltrami operator45 for the curvature term, the discrete elastic free energy reads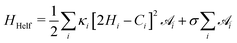 | (3) |
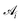 is the area associated with a vertex (
is the area associated with a vertex (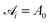 at the start). The total curvature 2Hi is obtained as the signed norm of the Laplace–Beltrami operator Ki
at the start). The total curvature 2Hi is obtained as the signed norm of the Laplace–Beltrami operator Ki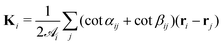 | (4) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = σR2/(kBT).
= σR2/(kBT).
The vesicle volume V is fixed close to the initial volume V0 by a hard quadratic constraint. Hence the following energy term is added to the Helfrich energy
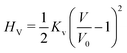 | (5) |
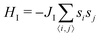 | (6) |
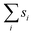 and thus at a fixed concentration
and thus at a fixed concentration 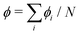 and temperature T. Varying the temperature between the different simulations of the Ising model amounts to varying the Ising coupling JI. In our simulations we chose to fix the temperature T and to tune the value of JI. Its exact critical value where the phase transition takes place is JI,c = (ln3/4)kBT ≃ kBT/3.64 on an infinite triangular lattice,47 which means that if JI < JI,c (resp. JI > JI,c), then the system is in the disordered (resp. ordered) phase.
and temperature T. Varying the temperature between the different simulations of the Ising model amounts to varying the Ising coupling JI. In our simulations we chose to fix the temperature T and to tune the value of JI. Its exact critical value where the phase transition takes place is JI,c = (ln3/4)kBT ≃ kBT/3.64 on an infinite triangular lattice,47 which means that if JI < JI,c (resp. JI > JI,c), then the system is in the disordered (resp. ordered) phase.
The local spontaneous curvature Ci = C(ϕi) used in eqn (3) depends on the local concentration ϕi and can take two values in the mesoscopic model, C0 = 2/R for the Ld phase and CvesicleLo+GM1 for the Lo + GM1 one (see below). Similarly, the local bending modulus κi = κ(ϕi) can take two values, κLd and κLo. In this work, for simplicity, κLo does not depend on the GM1 concentration in the simulations.
We used the mesoscale code developed in ref. 42 and 43 to simulate fluctuating vesicles. At each Monte Carlo step, two local movement attempts are applied to randomly chosen vertices: (1) a single vertex undergoes a small radial displacement δr according to the Metropolis rule, which locally modifies the elastic energy; (2) the compositions ϕi of two neighboring vertices are swapped, modifying the interaction energy as well as the elastic energy through the elastic parameters κ(ϕi) and C(ϕi) above. Since we consider a system with a conserved order parameter ϕ, we use the Kawasaki algorithm.48
Contrary to alternative models in the spirit of the Dynamic Triangulated Surface (DTS) one,1,33,49–52 edge flips are not allowed in the tessellated system and vertex moves are only radial, and consequently no constraint on edge lengths needs to be applied in the present model. In compensation, our model is valid in the vesicle quasi-spherical regime only. For more information refer to ref. 43 in which the whole simulation scheme is described and discussed in detail.
2.3 Extraction of line tension from domain boundary fluctuations
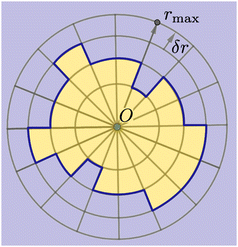
As shown in Fig. 2, we use a new discretization of the plane, in the form of a “dartboard” made of nc concentric circles, centered on the domain geometric barycenter and separated by δr = 2 nm, as well as na = 20 angular sectors. In each box of the as-obtained “dartboard”, we use the same majority rule as in the square mesh (see Section 3.1.2 below) so as to identify the boxes belonging to the Lo domain and those belonging to the Ld surrounding phase. Starting from the center and following the rays, we then identify the boundary where at least two successive Ld boxes (or the last circle) are encountered, so that small bubbles of the Ld phase are not considered as being part of the boundary. This defines a discrete version of the domain boundary r(θ).We then use eqn (3) from ref. 53 to directly link the power spectrum of the boundary fluctuations to the line tension λ of the mixture. However, we use a different convention for the Fourier coefficients:
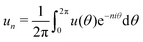 | (7) |
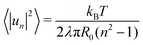 | (8) |
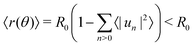 .53 In practice, however, R0 is close to 〈r(θ)〉 for the line tension values at play here and we identify both.
.53 In practice, however, R0 is close to 〈r(θ)〉 for the line tension values at play here and we identify both.
2.4 Relationship between the CG extracted parameters and the mesoscale model ones
In order to bridge the two modeling scales, the coarse-grained and mesoscale ones, we need to establish the link between the parameters that we measure in the CG-MD simulations with the input parameters of the mesoscale description. This can lead to technical difficulties, as outlined below.Due to renormalization issues,33 the Ising parameter depends on the coarse-graining level because it must account for the microscopic degrees of freedom integrated out in the coarse-graining process. We denote by
• a the simulation lattice spacing at the mesoscale, i.e. the average length-size of the elementary tessellation triangles, see eqn (1).
• l0 ∼ 1 nm the typical distance between lipids at the molecular scale,
• JI,0 the Ising interaction parameter at the molecular scale, of critical value JI,c. It is directly related to the Flory parameter χ of the binary mixture.54
We assume that the interaction network at the molecular scale can be assimilated to a triangular lattice, due to the symmetries of bidimensional liquids. Close to the critical point, one has
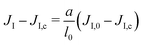 | (9) |
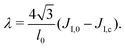 | (10) |
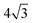 on a triangular lattice.55 Due to eqn (9), we thus also have
on a triangular lattice.55 Due to eqn (9), we thus also have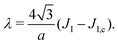 | (11) |
The analysis of bilayer simulations at the molecular level thus provides realistic membrane parameter values that can be injected into the mesoscale model. In this way, the simulations can then be tuned in order to tackle different biologically relevant systems at large length and time scales. Note that the bending moduli κ depend only logarithmically on the scale a,56 and we thus consider them as a constant for the sake of simplicity.
2.5 Backmapping from the mesoscale to the coarse-grained scale
The mesoscale model can be backmapped to CG resolution (Martini 2.2) based on the TS2CG approach of ref. 9. We follow the different steps presented in the TS2CG tutorial (https://cgmartini.nl/index.php/2021-martini-online-workshop/tutorials/558-9-ts2cg). Briefly, the last frame from the mesoscale model is saved in a dynamic triangulated surface (DTS) file format readable by the TS2CG program. In this file, both Lo and Ld domains were defined as well as the overall shape of the vesicle using labeled triangles. TS2CG inputs such as lipid concentrations and Area Per Lipid (APL) are extracted from the previous CG simulation of a planar system with 15% of GM1. These values are presented in Table 2.| Lipid type | Upper leaflet | Lower leaflet | APL |
|---|---|---|---|
| Ld domain | |||
| DPPC | 0.06 | 0.06 | 0.68 |
| DIPC | 0.91 | 0.91 | 0.77 |
| CHOL | 0.03 | 0.03 | 0.5 |
| Lo domain | |||
| DPPC | 0.40 | 0.68 | 0.68 |
| DIPC | 0.04 | 0.04 | 0.77 |
| CHOL | 0.28 | 0.28 | 0.5 |
| GM1 | 0.28 | 0 | 0.7 |
We perform 1000 steps of standard energy minimization and 5000 steps of molecular dynamics runs with lipid headgroup positions restrained to relax the lipid chains. We perform these steps without solvent particles using the Dry Martini force field.57 Next, the vesicle membrane is solvated by propagating an equilibrated Martini water box in the system and removing any water particle within a certain cutoff from the membrane particles as done previously.58
The solvated system is then equilibrated following several steps of equilibration as carried out for the planar systems (see above). For these steps, the constraints beads, called Wall, are present to keep the overall shape of the vesicle (see ref. 9 for more details). Then, we remove the wall beads and performed 10 μs of production using the same thermostat and barostat parameters as for the planar systems (see above) with isotropic pressure coupling.
In equilibrated vesicles, the two leaflets do not have the same area for geometrical reasons and thus have different molecule numbers. In experiments on vesicles, equilibration is a rather slow process ensured by thermally activated lipid flip-flops. Such flip-flops cannot occur at the rapid simulation timescale, so that one must take care of filling in each leaflet with the appropriate molecule number. This is guaranteed by TS2CG.
3 Results
3.1 Nanoscale analysis of lipid phase separation and GM1 partitioning
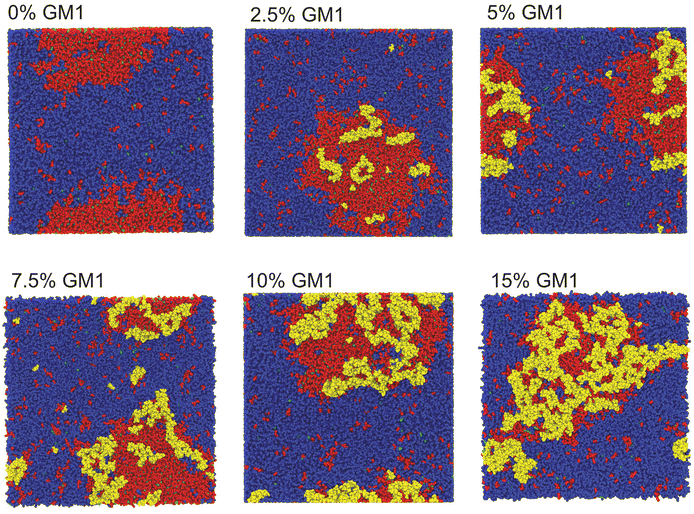
We have performed CG-MD simulations of 43 × 43 nm2 bilayers made of a DPPC–DIPC–Chol mixture with varying molar concentrations of GM1 molecules in the upper leaflet from 0% up to 15% (see the methods section). The duration of these simulations is set to 20 μs. The DPPC–DIPC–Chol mixture allows these systems to undergo phase separation where a phase enriched in DPPC and cholesterol molecules called the liquid-ordered (Lo) phase and another phase enriched in DIPC, the liquid-disordered phase (Ld) coexist,22,59–61 as displayed in Fig. 3.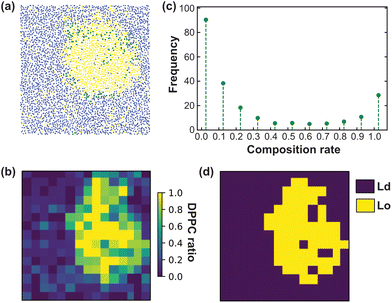 | ||
Fig. 5 Lo/Ld discretisation of the CG membrane model. (a) Illustration of the spatial distribution of the different lipid species for the last frame of the planar CG system (see Fig. 3). Each molecule position is identified by the position of one bead in the leaflet plane (see the text). DPPC is shown in yellow, DIPC in blue and GM1 in green. (b) Examples of analysis performed for a DPPC–DIPC–Chol (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12) mixture with 10% GM1 in the upper leaflet (using a different snapshot as compared to in (a)). The bilayer is divided into a 15× 15 mesh. (c) The composition distribution (fraction of DPPC in boxes of the bilayer, measured throughout the simulation time). (d) The composition repartition matrix in terms of DPPC ratio is binarized in Lo (yellow) and Ld (blue) boxes based on the composition distribution presented in c and according to the majority rule described in the text. 12) mixture with 10% GM1 in the upper leaflet (using a different snapshot as compared to in (a)). The bilayer is divided into a 15× 15 mesh. (c) The composition distribution (fraction of DPPC in boxes of the bilayer, measured throughout the simulation time). (d) The composition repartition matrix in terms of DPPC ratio is binarized in Lo (yellow) and Ld (blue) boxes based on the composition distribution presented in c and according to the majority rule described in the text. | ||
3.2 Calculation of parameters extracted from CG-MD simulations to accurately design the mesoscale model
Initial calculations allow us to calculate parameters extracted from CG simulations to be used as inputs for the mesoscale model (see the methods section). They are:1. The bending moduli of both phases (κLd and κLo).
2. The two dimensionless spontaneous curvatures of the Ld and Lo + GM1 phases, denoted by RC0 and RCvesicleLo+GM1.
3. The Ising parameter JI (related to the line tension between both phases).
4. The relative timescales associated with diffusion in the membrane plane on the one hand and transverse deformation modes on the other hand, if one is interested in dynamical properties.
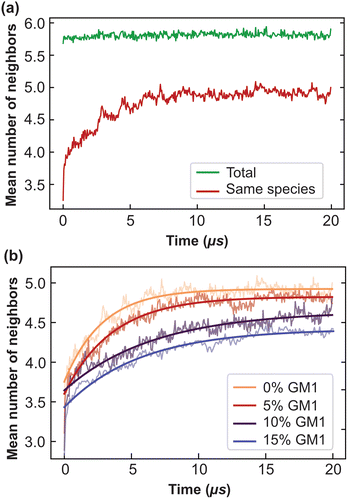
We explain below how to extract from CG simulations the values of these parameters, which are intrinsic to the molecular species at play (and their phase state through temperature). As the system needs at most around 8 μs to equilibrate (see Fig. 4b), the following measurements are performed after 8 μs, for a duration of 12 μs (unless stated otherwise) so that phase separation is essentially reached.
Two other parameters are important for membrane patterning:19,43,62
• The membrane surface tension σ
• The area fraction of each phase (ϕ is the fraction of the Lo + GM1 phase and 1 − ϕ the fraction of the Ld phase, both conserved through time)
These extrinsic parameters depend on the experimental conditions and are not extracted from the CG simulations.
Generically, ref. 63 has shown how the bending modulus κ of a bilayer made of a homogeneous lipid mixture can be inferred from the spectral density of the membrane thermal shape fluctuations in CG simulations using the Helfrich model for membranes. In our CG simulations, the surface tension was set to σ = 0, to make the determination of κ easier. However, the continuous Helfrich model ignores short-wavelength molecular scales where individual lipids jiggle out of the local membrane plane, forming some “protrusions”.64–66 Assuming that protrusions and Helfrich fluctuations are independent random variables, one obtains the spectral density of fluctuations in the Fourier space67
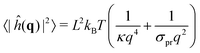 | (12) |
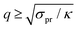 , i.e. at wavelengths 2π/q ≤ 4 nm when κ ∼ 10 kBT. Thus one must use large enough system sizes L to reliably measure κ, as well as long simulation times to reduce statistical errors.
, i.e. at wavelengths 2π/q ≤ 4 nm when κ ∼ 10 kBT. Thus one must use large enough system sizes L to reliably measure κ, as well as long simulation times to reduce statistical errors.
We performed these measurements on our own CG simulations of Ld and Lo membranes, by using the approach in ref. 63. Fitting with eqn (12), we estimated the values of κ for both systems, κLd = 13 kBT for the Ld phase, and κLo = 25 kBT for the Lo one (see the ESI,† Section B, for further details).
![[capital Delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10b.gif) , using the four nearest neighbors, applied on the height field:
, using the four nearest neighbors, applied on the height field: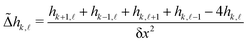 | (13) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the height of the membrane on the box of integer coordinates (k,
is the height of the membrane on the box of integer coordinates (k,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) on the 15 × 15 mesh defined above, endowed with periodic boundary conditions. Note that we choose to measure the curvature of the upper leaflet because we are primarily interested in the curvature generated by GM1 insertions in this leaflet.
) on the 15 × 15 mesh defined above, endowed with periodic boundary conditions. Note that we choose to measure the curvature of the upper leaflet because we are primarily interested in the curvature generated by GM1 insertions in this leaflet.
The Lo phase, where GM1 molecules are mainly inserted, as shown in Fig. 6, displays a higher curvature than the Ld one (Fig. 7a and b). This Lo domain curvature increases with the addition of GM1 molecules (Fig. 7c). We notice that for 0% of GM1, the Lo domain has a weak curvature. This upper leaflet weak curvature results from the difference in thickness in between the Lo and Ld domains and the fact that the leaflet position is identified through the positions of the PO4 and GM5 beads (see above).
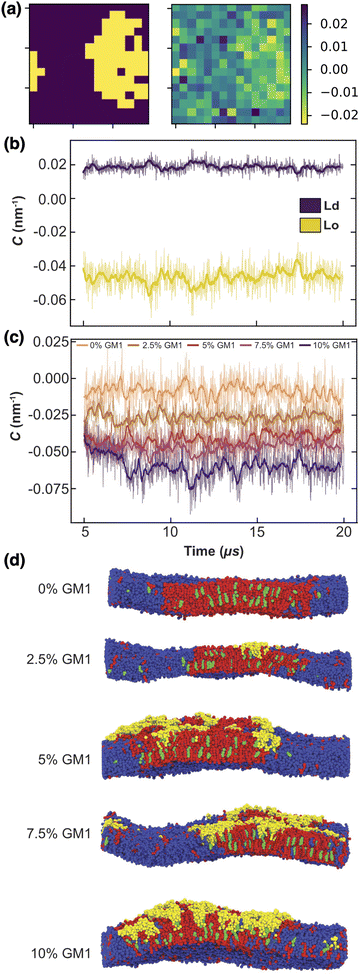 | ||
| Fig. 7 The local curvature imposed by GM1 molecules. (a) The local curvature (right, in nm−1) against the lipid phase (left). (b) The local curvature measurement through time, averaged for the Lo and Ld phase separately, in the upper leaflet for a DPPC–DIPC–Chol mixture with 7.5% GM1 in the upper leaflet. (c) Curvature of the Lo phase from 0 to 10% GM1 in the upper leaflet (by increments of 2.5) from orange to purple. This curvature is negative because of our sign convention in eqn (13). (d) Side views of the different systems at 20 μs. | ||
Note that because of the periodic boundary conditions, the total curvature averaged on the whole system mathematically vanishes when it is approximated by a Laplacian. Thus if the Lo phase is curved, the Ld phase must be curved as well in the opposite direction, so that the average curvature is zero (Fig. 7d).
To quantify how GM1 molecules affect upper leaflet curvature, we plot (the absolute value of) the difference in curvature CplanarLo+GM1 between the Lo domains enriched in GM1 and the small reference curvature (|C| ≃ 0.0087 nm−1) of the Lo domain without GM1 insertions (Fig. 8). The curvature values are averaged from 10 to 20 μs on the measurements shown in Fig. 7c to ensure that they are extracted from equilibrated domains. We find that CplanarLo+GM1 depends linearly on the GM1 fraction as
| CplanarLo+GM1 ≃ 0.5 ϕGM1 nm−1 | (14) |
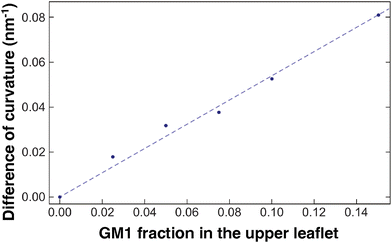 | ||
Fig. 8 The correlation between curvature and GM1 concentration. The difference in curvature CplanarLo+GM1 between the Lo domain with GM1 and the reference Lo domain without GM1 in planar geometry. The curvature values are averaged on the last 10 μs. The DPPC–DIPC–Chol (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12) mixture with a growing fraction of GM1 in the upper leaflet, and the linear fit given in eqn (14) (dashed line). 12) mixture with a growing fraction of GM1 in the upper leaflet, and the linear fit given in eqn (14) (dashed line). | ||
Below, we want to model non-planar systems (i.e. vesicles) with our mesoscale model. We denote using C0 the spontaneous curvature of the Ld phase. In the present case, C0 = 2/R is set by the vesicle average radius R in equilibrium, to accommodate the area difference between both leaflets.68 We recall that we also denote by CvesicleLo+GM1 the spontaneous curvature of the Lo + GM1 phase on a vesicle. On a vesicle, we can also assume that before insertion of GM1, the Lo phase has the same curvature C0 = 2/R, for the same reason as for the Ld phase, so that the GM1 curvature comes in addition to C0 as examined in detail in ref. 68. Thus CvesicleLo+GM1 = C0 + CplanarLo+GM1 where CplanarLo+GM1 is given in eqn (14). A more thorough discussion about this relationship is provided in the ESI,† Section A.
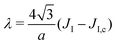 | (15) |
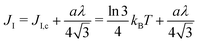 | (16) |
To measure the line tension λ at the boundary of Lo and Ld phases in a mixture devoid of GM1, we measure the fluctuations of the Lo domain boundary. We use the same method as the one applied to fluorescence microscopy images in ref. 53 or in mesoscale simulations.69 We use the polar discretization (detailed in the methods section) in order to identify the location r(θ) of the Lo + GM1 domain boundary, the origin of coordinates being the domain barycenter. We then apply the DPPC fraction threshold of 0.6 (Fig. 5c) to delineate the boundary between Lo and Ld domains and calculate the Fourier coefficients un of u(θ), defined by r(θ) = R0[1 + u(θ)], using a fast Fourier transform algorithm. Finally, we use eqn (8) to relate the power spectrum of the boundary fluctuations to the line tension of the domain boundary 〈|un|2〉 against 1/(n2 − 1). We fit only the first long wavelength modes to avoid discretization effects, as shown in Fig. 9. The fitted line tension is λ ≃ 3 pN for a DPPC–DIPC–Chol (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12) mixture devoid of GM1 at T = 310 K, of the same pN order of magnitude as the experimental values.19
12) mixture devoid of GM1 at T = 310 K, of the same pN order of magnitude as the experimental values.19
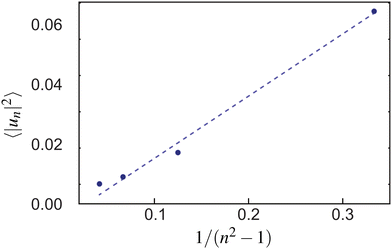 | ||
| Fig. 9 The power spectrum of the Lo–Ld boundary in a DPPC–DIPC–Chol mixture without GM1 from which the line tension λ is extracted through a fit with eqn (8) (dashed line). | ||
We also measured how λ depends on the GM1 concentrations, as shown in Table 3. In agreement with the CG simulations in ref. 21, λ decreases when the GM1 concentration increases above 5%, resulting in an increased width of the phase boundary, which appears less regular in Fig. 3. Indeed, the width of the phase boundary is set by the spatial correlation length ξ, itself inversely proportional to λ in the 2D Ising universality class47 where λξ = kBT.
| % GM1 | 0 | 2.5 | 5 | 7.5 | 10 | 15 |
| λ (pN) | 3.0 | 3.0 | 5.0 | 2.4 | 1.2 | 0.8 |
In the mesoscale model, the rate at which vertex-composition flips (Kawasaki dynamics, see the methods section) are attempted must be set by a relevant timescale δt at the length scale a, the average lattice spacing. This is related to the diffusion coefficient D of the minority species in the bulk of the majority phase at this scale, through the relationship a2 = 4Dδt. Here, we also show how D can be inferred from the measurement of the line tension λ in CG-MD simulations. However, the effective value of D also depends on the mesoscopic length scale a, as we discuss it now. Note that D cannot simply be set as the diffusion coefficient of molecules in the bilayer because a membrane patch at the mesoscale can be a collection of dozens of lipids, or even more. Its diffusive properties are the fruit of the collective behavior of its interacting elementary constituents, themselves in interaction with the surrounding fluid.
Domain boundary fluctuations are known to be a relevant probe of diffusion in phase-separated membranes.53,70,71 A notorious difference can already be noticed between our mesoscopic modeling on the one hand and MD simulations or experiments on the other hand. While hydrodynamic interactions are absent in the former due to the construction of our MC simulations, they are intrinsically present in the latter where the solvent is explicitly simulated (note however that accounting for hydrodynamic interactions in Monte Carlo simulations in general72 and in membrane modeling in particular is feasible in principle,73,74 at least as far as homogeneous membranes are concerned). This implies different scaling laws of the timescales as a function of the length scales.
Ref. 70 and 71 thoroughly address the role of hydrodynamic interactions in this context, in the frame of the Saffman–Delbruck theory. One can define a typical length, the Saffman–Delbruck length LSD = hηm/(2ηf), where ηm and ηf are the viscosities of the membrane and the fluid, respectively, and h is the membrane thickness. LSD is on the order of 100 nm to 10 μm in experimental systems. On length scales below LSD, 2D hydrodynamics inside the membrane dominates, while above it, 3D hydrodynamics in the surrounding solvent dominates. Considering a boundary fluctuation wavelength Λ, it follows that its relaxation time scales as τ(Λ) ∝ Λ2 if Λ ≫ LSD and τ(Λ) ∝ Λ if Λ ≪ LSD. In the ESI,† Section F, we properly define the relaxation times and we discuss these relationships. Below, we focus on (nanometric) values of Λ ≪ LSD at the molecular scale, so that
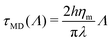 | (17) |
Our choice to set the value of D in mesoscale simulations consists in identifying the molecular and mesoscopic time scales at the smallest wavelength accessible in the mesoscale model, namely Λ = 2a.‡ This means that we assume here that hydrodynamic interactions are at play up to the length scale a only. Since hydrodynamics interactions are known to enhance dynamics75 it implies that the larger a, the faster the dynamics at large scales, thus the larger effective D, as we quantify it now.
In the mesoscale simulations where no hydrodynamic interactions are at play and where the order parameter is conserved, it can be demonstrated76 that the relaxation time at wavelength Λ is related to the diffusion coefficient D through
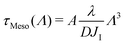 | (18) |
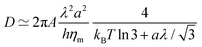 | (19) |
Given that dynamics are known to be significantly enhanced in MD simulations using the MARTINI force field77–79 (see also the ESI,† Section F), we prefer to use experimental values of ηm rather than numerically measured ones. In the present case, we estimate in the SI that hηm ≃ 4 × 10−10 Pa.m.s. For instance, for a vesicle of radius R = 30 nm as considered below, the average tessellation edge length is a = 2.25 nm for N = 2562 vertices. With the measured value λ ≈ 0.8 pN at 15% of GM1 in the upper leaflet, and T = 310 K, we get the numerical values D ≈ 3.6 μm2 s−1 and finally δt ≈ 0.35 μs. The value of D is lower than the lipid diffusion coefficients measured in real model membranes, e.g. vesicles,80 although they are on the same order of magnitude because with this value of R, the patches are small, and each vertex represents about 6 lipid molecules in each leaflet.
In the ESI,† Section G, the value of δt, associated with diffusion in the membrane plane, is compared to its transverse counterpart δtp, the physical timescale associated with (one-dimensional) radial MC moves. With the same model parameters as above, one obtains δtp = 90 ps, which is much shorter than δt. This means that if one were interested in studying realistic vesicle dynamics through kinetic Monte-Carlo simulations,48 one would need to execute a large number of vertex radial moves in-between two vertex-composition flips, on the order of δt/δtp ≈ 4000. This ratio depends on the value of the vesicle radius R through several parameters.
3.3 Mesoscale simulation
Relying on the numerical results at the coarse-grained scale and after the extraction of the key parameters, we perform the mesoscale Monte Carlo simulation of a tessellated vesicle made of two phases, one corresponding to the Ld phase, the other one, with a higher spontaneous curvature, accounting for the Lo phase curved by GM1 insertions. We simulate a vesicle with N = 2562 vertices. Since our objective is to come back later to the CG scale through backmapping, we shall focus here on a small unilamellar vesicle (SUV). Details of the mesoscale numerical scheme are given in ref. 42 and 43, and summarized in the methods section.As notably discussed in ref. 43, coarse-graining up to the mesoscale is a quantitative process which consists in pre-averaging the degrees of freedom at length-scales smaller than the lattice spacing a, the physical foundations of which are prescribed by the renormalization group theory.33,46 Consequently, one expects the mesoscale model to describe correctly the fluctuations of the real system at large scales, with the advantage that it will reach equilibrium much faster in terms of computational time, provided, as described just above, that microscopic details have been correctly integrated out in the mesoscale parameters. Note that in the same spirit, force fields used in all-atom or CG models have already integrated out electronic degrees of freedom, and are consequently already approximate.
As explained above, we use the following parameter values to simulate a vesicle of real radius R = 30 nm with the same Ld and Lo + GM1 phases as in the bilayer with 15% of GM1 in the upper leaflet studied above:
1. The bending moduli are set to κLo = 25 kBT and κLd = 13 kBT after calculation of the membrane fluctuation spectra in the CG model.
2. The spontaneous curvature of the Ld phase is equal to C0 = 2/R, the one of the average sphere. The spontaneous curvature of the Lo + GM1 phase is fixed to CvesicleLo+GM1 = C0 + CplanarLo+GM1 = 4.43/R, from measurements of CplanarLo+GM1 in CG simulations at 15% of GM1, as explained above.
3. The Ising parameter is set to JI = 0.336 kBT to match the measured line tension λ, through eqn (15). This value is above the critical one JI,c = (ln3/4)kBT ≃ 0.275 kBT on a triangular lattice.
4. The surface tension is arbitrary since it is an extrinsic parameter imposed by experimental conditions, and not a property of the membrane. In the simulations, its dimensionless value ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = σR2/(kBT) was set at 1100, which corresponds to σ = 5.3 × 10−3 J m−2 for a radius R = 30 nm. This value ensures it is the quasi-spherical vesicle regime, where our mesoscale model is fully valid.42
= σR2/(kBT) was set at 1100, which corresponds to σ = 5.3 × 10−3 J m−2 for a radius R = 30 nm. This value ensures it is the quasi-spherical vesicle regime, where our mesoscale model is fully valid.42
5. The area fraction ϕ of the Lo + GM1 phase is chosen equal to 20%, so that Lo domains are well-defined. Increasing this value would lead to more complex interdigitated, labyrinthine patterning.43
The system was run for a long time (1010 MC steps) to ascertain that thermodynamic equilibrium has been reached.43 A snapshot by the end of the simulation is displayed in Fig. 10.
With the parameters inferred from the CG model, the SUV displays nanodomains in equilibrium. As observed in previous work,43 the domains form rapidly after starting the simulation from a configuration where Ld and Lo vertices were randomly distributed. Then the domains fluctuate in size and shape, permanently exchanging Lo “monomers” with the surrounding phase. They can also coalesce or split. It must be emphasized that as compared to the CG simulations above where a single nanodomain, necessarily smaller than the simulated box size, was formed in few μs on the quasi-flat membrane due to phase separation, the full phase separation displaying a single, large Lo domain, is avoided on the curved SUV, by introducing a surface tension, σ. Hence, the nanodomain size is controlled by the typical length scale λ/σ, since larger curved domains have a too large surface free-energy.19 The nanodomains are not generically larger (in real size) than in the CG simulations, but they never coalesce in a single, large Lo region.
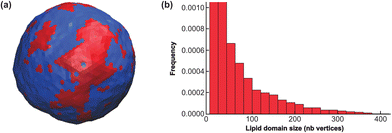
To quantify this vesicle meso-patterning, we computed the nanodomain size-distribution, as illustrated in Fig. 10. As compared to distributions generally observed on large GUVs below the critical temperature (see the ESI† or ref. 43 for examples), the distribution is not bimodal but monotonously decreasing. The main reason for this difference is that on a SUV, the ratio between the Lo domain curvature CvesicleLo+GM1 and the sphere one C0 is moderate as compared to a GUV. The mesoscale model thus predicts that nanodomains on SUVs can dynamically adopt a wide range of sizes, from very small to very large (with respect to the number of available Lo vertices) ones, that however never reach the maximum allowed size of 512.
3.4 Backmapping from the mesoscale model to the CG one
Backmapping from the mesoscale model to the CG system consists in decorating the elementary triangles of the mesoscale tessellation while respecting both the bilayer geometry and its local composition9 (see the methods section). The triangles are decorated with the same Ld and Lo + GM1 phases as in the bilayer with 15% of GM1 in the upper leaflet studied above with the help of CG simulations. The interior and exterior of the R = 30 nm-radius vesicle are filled with water (and ions) in order to constrain the vesicle interior volume as in the mesoscale simulation. Backmapping is exemplified in Fig. 11. We shall now verify that after backmapping from the mesoscale model to the CG one, CG simulations run from the so-obtained simulation output are stable through time, which will support the fact that the mesoscale parameters were correctly estimated. Whereas simulations at the mesoscale enable one to equilibrate the slow long wave-length fluctuations, above the lattice spacing a, at the price of ignoring the short wavelengths, CG simulations after backmapping enable one to equilibrate in turn these short, fast wavelengths, and finally to obtain a CG system equilibrated at all wavelengths, whereas equilibrating long wavelengths with the help of the sole CG model would be prohibitive in terms of computational cost.First, we have checked that at the molecular scale, backmapping reproduces faithfully lipid-tail ordering in both phases, by computing the usual acyl-chain order parameter in both systems with GM1 (see the ESI,† Section H).
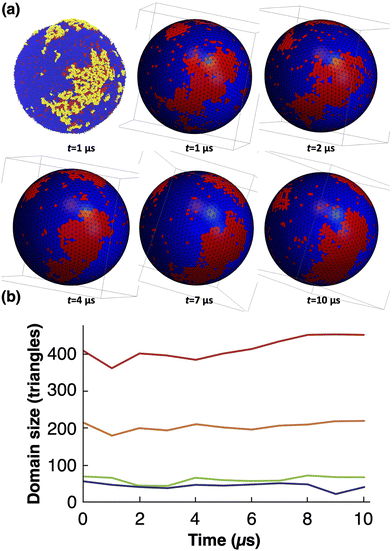
Then, in order to assess the supramolecular stability of the backmapped CG vesicle, notably in terms of its nano-patterning, we have tracked the largest nanodomains along a 10 μs-long CG simulation, as shown in Fig. 12a. In order to identify unambiguously the Lo nanodomains, we have radially projected the lipid coordinates onto a regularly tessellated sphere made of 5120 elementary triangles and attributed the Lo or Ld nature to each of them by using the same kind of majority rule as previously, as shown in Fig. 5. We have measured that the total number of Lo triangles remains remarkably stable through time, very close to the initial 20% fraction before backmapping (see Fig. S6 in the ESI†). Furthermore, nanodomains are identified as the connected components of the Lo phase. As expected, the size of the largest nanodomains fluctuates, as they regularly lose or gain lipids of the Lo phase, however their size does not evolve much with time (see Fig. 12b). This suggests that the nanopatterning ensuing from the mesoscale simulation remains qualitatively stable with time and validates our whole multiscale scheme.
4 Discussion
This work proposes a complete strategy to extract valuable parameters from coarse-grained simulations to design a mesoscale model of biphasic vesicles. Going from the molecular scale to mesoscopic scales can present intrinsic difficulties, that we have fully addressed here, appealing to important physics concepts such as the renormalization group theory. This concerns in particular the scale-dependent relationship between the line tension at the interface between both phases, which is measured in CG simulations through the fluctuation spectrum of the interface between both phases, and controlled by the Ising parameter JI in the mesoscale model. Once equilibrated, the mesoscopic system is back-mapped to the molecular scale through a well-defined procedure. This multiscale simulation scheme eventually allows one to obtain large systems equilibrated at all length scales, which could not be achieved solely at the CG scale due to the prohibitive simulation time it would require. In particular, modeling at the mesoscale enables equilibration of long length scales before equilibration of short ones after back-mapping to the molecular scale. Equilibrating long length scales enabled us to sample accurately the domain size distribution. Here we have tackled an SUV of modest size (diameter of 60 nm) as a proof of concept, but there is no obstacle in principle to tackle larger systems for which real equilibration times can become very large, on the order of hours for a GUV.27One aspect of equilibration that is not apprehended in this work is equilibration between both leaflets, through lipid flip-flops.68 Phospholipids flip-flops are rare events in CG molecular dynamics, with associated timescales on the order of hours, and they cannot be implemented in the mesoscale model that does not explicitly take leaflets into account. On timescales much shorter than the typical flip-flop time of interest here, the asymmetric distribution between leaflets is therefore considered to be metastable. At the mesoscale, this issue can in principle be solved by taking explicitly both leaflet compositions into account,44 with stochastic composition exchanges between leaflets. In this case, note that the membrane spontaneous curvature would directly depend on these compositions.
In the present context, and in relation to the experiments of ref. 27, our CG simulations gave us new insights into the effect of insertion of the glycolipid GM1 into the Lo phase. Since GM1 is only inserted in one leaflet, the ensuing asymmetry imposes a local spontaneous curvature to the membrane, proportional to the concentration of GM1 in the leaflet. In addition, GM1 makes the Ld/Lo interface widen, which is a visual manifestation of the decrease in the interface line tension λ. From a dynamical point of view, it also slows down the convergence to equilibrium. The two latter phenomena are intimately related since boundary fluctuation time-scales are inversely proportional to the line tension.76 Increasing the spontaneous curvature of the minority phase while decreasing the line tension are both favorable to the stabilization of mesophases, where phase separation is incomplete in equilibrium, as observed in the mesoscale simulations. Note that the spontaneous curvature values imposed by GM1 are comparable to the spontaneous curvatures locally imposed by the insertion of some transmembrane proteins, measured by experimental or numerical techniques to be on the order of few 0.01 nm−1.81–84 Thus the meso-patterning effect observed at relatively large concentrations of GM1 is also expected to occur on cell membranes where curving proteins are abundant.19
Here we have used the Martini 2.2 forcefield. Recently, a new version of this forcefield was released increasing the number of bead types and sizes85 refining diverse features especially related to the protein. This resulted in a recent reparametrization of carbohydrates86 but a CG model of GM1 lipid has not yet been released. It will be interesting, in the coming years, to extend our CG modelling to see how this new version affects the quantitative results. In the meantime, the Martini 2.2 version has already given reasonable results21,22 on GM lipids and curvature to validate our proof of concept.
To perform our Monte Carlo mesoscale simulations, we used a model that some of us developed and characterized in recent studies.42,43 A more common model used in numerical statistical mechanics of membranes is the dynamically triangulated surface/membrane (DTS/DTM) model.51,52 Designed in the early 1990s to study the crumpling phase transition of homogeneous fluid membranes,87,88 it has been extended and enriched in order to model membranes or vesicles closer to cell membranes, in particular by endowing it with multiphasic composition.1,49 In our model, the vertices of the tessellation experience only radial moves and there are no edge-flips, which are an important characteristic of the DTS model.
These features do not modify in depth the overall properties of the model, however using our own model presents at least two advantages in the present context. First, as far as the Ising model is concerned, it dwells on a triangular lattice (except for the 12 vertices that have only 5 neighbors, necessary to close the membrane, due to Euler's polyhedron formula), whereas in the DTS case, it would dwell on a disordered lattice, with vertices that can have in principle any number of neighbors larger than 3. The rigorous connection between the line tension and the Ising parameter JI relies on the knowledge of the critical parameter JI,c and of the prefactor 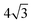 in eqn (15), whereas they are not exactly known on a disordered lattice. The same problem arises when it comes to diffusion and dynamical issues, as in eqn (19). Second, in the DTS model, edge lengths are constrained by an upper and a lower bound, in order to ensure membrane self-avoidance and to prevent some triangles from becoming very large to the detriment of the smallest ones. Because of entropic effects due to these constraints in the configuration space, an additional entropic term modifies the input surface tension σ in a way that is difficult to control because it depends in a non-trivial way on the total area of the vesicle. The quantification of this effect is out of the scope of this work and will be the object of a forthcoming publication. For these reasons, we did not opt for the DTS model in the present study where every mesoscale parameter must be well-controlled.
in eqn (15), whereas they are not exactly known on a disordered lattice. The same problem arises when it comes to diffusion and dynamical issues, as in eqn (19). Second, in the DTS model, edge lengths are constrained by an upper and a lower bound, in order to ensure membrane self-avoidance and to prevent some triangles from becoming very large to the detriment of the smallest ones. Because of entropic effects due to these constraints in the configuration space, an additional entropic term modifies the input surface tension σ in a way that is difficult to control because it depends in a non-trivial way on the total area of the vesicle. The quantification of this effect is out of the scope of this work and will be the object of a forthcoming publication. For these reasons, we did not opt for the DTS model in the present study where every mesoscale parameter must be well-controlled.
The membrane surface tension is one of the key parameters of the mesoscale model because the topology of the meso-pattern89 and even its stability depend on the surface tension value. A large enough value is required to destabilize the macrophase whereas a too large value would suppress membrane fluctuations and thus also lead to macrophase separation.19,43,62 When backmapping to CG simulations, the surface tension can easily be monitored in planar geometry by applying anisotropic pressure on the simulation box.77 However, controlling the surface tension is more challenging in vesicle geometry.90 Indeed, it depends on the quantity of water and ions encapsulated inside the vesicle, due to the Laplace law, through the difference in pressure across the membrane. In this work, we have not quantified the surface tension of the vesicle after backmapping, but simply filled the vesicle with the maximum quantity of water (plus ions), anticipating that since the overall interior volume was the same as in the mesoscale vesicle simulations, the surface tensions should be comparable. Since it is difficult to compute a priori the value of the surface tension, the most obvious way to control it is to proceed by trial and error, removing water and ions if the tension it too high and adding ones if it is too weak, for example by pushing the existing solvent away from the center of the vesicle through application of a radial force. This issue will be addressed in the near future.
In the era of exascale computing,91,92 it is tempting to design molecular systems to study from organelles9,93 to viruses93,94 or even an entire cell.95–97 Yet, the computing power necessary to simulate such large systems is still very huge and prevents one from reaching simulated timescales useful to decipher even simple phenomena such as the diffusion of large molecules93 without even mentioning relevant biological time scales of milliseconds or longer. Our approach may help in tackling this issue by equilibrating a simplified triangulated version of such huge systems using Monte Carlo simulations to then only refine the equilibrated system on nano- to micro-second timescales.
Author contributions
J. C. performed the simulations and analyzed the results. N. C. contributed to the analyses and M. P.-M. contributed to the CG simulations. M. C., W. P. and S. J. M. contributed to the simulations and result analyses. M. M., M. C. and N. D. designed and supervised the research. J. C., N. D., M. C. and M. M. wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. C. is supported by the CNRS-MITI grant “Modélisation du vivant” 2020 and by the ITMO Cancer of Aviesan “Mathematiques et Informatique”. This work was granted access to the HPC resources of CALMIP supercomputing center (under the allocation 2021-P21020) and TGCC Joliot-Curie supercomputer (under the GENCI allocation A0110712941). W. P. acknowledges funding from the Novo Nordisk Foundation (grant No. NNF18SA0035142) and Independent Research Fund Denmark (grant No. 10.46540/2064-00032B). M. M. and N. D. are affiliated with the Université Toulouse III-Paul Sabatier and the Centre National de la Recherche Scientifique (CNRS).References
- W. Pezeshkian, M. Konig, S. J. Marrink and J. H. Ipsen, Front. Mol. Biosci., 2019, 6, 59 CrossRef CAS PubMed
.
- H. I. Ingólfsson,
et al.
, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2113297119 CrossRef PubMed
.
- H. I. Ingólfsson, H. Bhatia, F. Aydin, T. Oppelstrup, C. A. López, L. G. Stanton, T. S. Carpenter, S. Wong, F. D. Natale, X. Zhang, J. Y. Moon, C. B. Stanley, J. R. Chavez, K. Nguyen, G. Dharuman, V. Burns, R. Shrestha, D. Goswami, G. Gulten, Q. N. Van, A. Ramanathan, B. V. Essen, N. W. Hengartner, A. G. Stephen, T. Turbyville, P.-T. Bremer, S. Gnanakaran, J. N. Glosli, F. C. Lightstone, D. V. Nissley and F. H. Streitz, J. Chem. Theory Comput., 2023, 19, 2658–2675 CrossRef PubMed
.
- O. N. Vickery and P. J. Stansfeld, J. Chem. Theory Comput., 2021, 17, 6472–6482 CrossRef CAS PubMed
.
- E. Lyman, H. Cui and G. A. Voth, Phys. Chem. Chem. Phys., 2011, 13, 10430–10436 RSC
.
- T. A. Wassenaar, K. Pluhackova, R. A. Böckmann, S. J. Marrink and D. P. Tieleman, J. Chem. Theory Comput., 2014, 10, 676–690 CrossRef CAS PubMed
.
- T. D. Newport, M. S. P. Sansom and P. J. Stansfeld, Nucleic Acids Res., 2018, 47, 1362–4962 Search PubMed
.
- Y. Peng, A. J. Pak, A. E. P. Durumeric, P. G. Sahrmann, S. Mani, J. Jin, T. D. Loose, J. Beiter and G. A. Voth, J. Phys. Chem. B, 2023, 127, 8537–8550 CrossRef CAS PubMed
.
- W. Pezeshkian, M. Konig, T. A. Wassenaar and S. J. Marrink, Nat. Commun., 2020, 11, 2296 CrossRef CAS PubMed
.
- W. Pezeshkian and S. J. Marrink, Curr. Opin. Cell Biol., 2021, 71, 103–111 CrossRef CAS PubMed
.
- M. N. Melo, H. I. Ingólfsson and S. Marrink, J. Chem. Phys., 2015, 143, 243152 CrossRef CAS PubMed
.
- S. A. Shelby, I. Castello-Serrano, K. C. Wisser, I. Levental and S. L. Veatch, Nat. Chem. Biol., 2023, 1–9 CAS
.
- S. L. Veatch, P. Cicuta, P. Sengupta, A. Honerkamp-Smith, D. Holowka and B. Baird, ACS Chem. Biol., 2008, 3, 287–293 CrossRef CAS PubMed
.
- T. Lang and S. Rizzoli, Physiology, 2010, 25, 116–124 CrossRef CAS PubMed
.
- H. I. Ingólfsson, M. N. Melo, F. J. V. Eerden, C. Arnarez, C. A. Lopez, T. A. Wassenaar, X. Periole, A. H. D. Vries, D. P. Tieleman and S. J. Marrink, J. Am. Chem. Soc., 2014, 136, 14554–14559 CrossRef PubMed
.
- E. Sezgin, I. Levental, S. Mayor and C. Eggeling, Nat. Rev. Mol. Cell Biol., 2017, 18, 361–374 CrossRef CAS PubMed
.
- M. Cebecauer, M. Amaro, P. Jurkiewicz, M. Sarmento, R. Sachl, L. Cwiklik and M. Hof, Chem. Rev., 2018, 118, 11259–11297 CrossRef CAS PubMed
.
- A. L. Duncan, R. A. Corey and M. S. P. Sansom, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 7803–7813 CrossRef CAS PubMed
.
- N. Destainville, M. Manghi and J. Cornet, Biomolecules, 2018, 8, 104 CrossRef PubMed
.
- D. Marsh, Chem. Phys. Lipids, 2010, 163, 667–677 CrossRef CAS PubMed
.
- R. Dasgupta, M. S. Miettinen, N. Fricke, R. Lipowsky and R. Dimova, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5756–5761 CrossRef CAS PubMed
.
- Y. Liu, J. Barnoud and S. J. Marrink, Biophys. J., 2019, 117, 1215–1223 CrossRef CAS PubMed
.
- H. Ewers, W. Romer, A. E. Smith, K. Bacia, S. Dmitrieff, W. Chai, R. Mancini, J. Kartenbeck, V. Chambon, L. Berland, A. Oppenheim, G. Schwarzmann, T. Feizi, P. Schwille, P. Sens, A. Helenius and L. Johannes, Nat. Cell Biol., 2010, 12, 11–18 CrossRef CAS PubMed
.
- M. Aureli, L. Mauri, M. G. Ciampa, A. Prinetti, G. Toffano, C. Secchieri and S. Sonnino, Mol. Neurobiol., 2016, 53, 1824–1842 CrossRef CAS PubMed
.
- C.-L. Schengrund, Trends Biochem. Sci., 2015, 40, 397–406 CrossRef CAS PubMed
.
- S. Sonnino, L. Cantù, M. Corti, D. Acquotti and B. Venerando, Chem. Phys. Lipids, 1994, 71, 21–45 CrossRef CAS PubMed
.
- S. F. Shimobayashi, M. Ichikawa and T. Taniguchi, EPL, 2016, 113, 56005 CrossRef
.
- R. Bao, L. Li, F. Qiu and Y. Yang, J. Phys. Chem. B, 2011, 115, 5923–5929 CrossRef CAS PubMed
.
- J. Steinkühler, P. Fonda, T. Bhatia, Z. Zhao, F. S. C. Leomil, R. Lipowsky and R. Dimova, Adv. Sci., 2021, 8, 2102109 CrossRef PubMed
.
- A. Sreekumari and R. Lipowsky, J. Chem. Phys., 2018, 149, 084901 CrossRef PubMed
.
- A. Duncan and W. Pezeshkian, Biophys. J., 2023, 122(11), 1883–1889 CrossRef CAS PubMed
.
- V. T. Ruhoff, P. M. Bendix and W. Pezeshkian, Emerging Top. Life Sci., 2023, 7, 81–93 CrossRef CAS PubMed
.
- J. J. Amazon and G. W. Feigenson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022702 CrossRef PubMed
.
- P. C. Hsu, B. M. H. Bruininks, D. Jefferies, P. C. T. D. Souza, J. Lee, D. S. Patel, S. J. Marrink, Y. Qi, S. Khalid and W. Im, J. Comput. Chem., 2017, 38, 2354–2363 CrossRef CAS PubMed
.
- Y. Qi, H. I. Ingólfsson, X. Cheng, J. Lee, S. J. Marrink and W. Im, J. Chem. Theory Comput., 2015, 11, 4486–4494 CrossRef CAS PubMed
.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Pall, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef
.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed
.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182 CrossRef CAS
.
- E. L. Wu, X. Cheng, S. Jo, H. Rui, K. C. Song, E. M. Dávila-Contreras, Y. Qi, J. Lee, V. Monje-Galvan, R. M. Venable, J. B. Klauda and W. Im, J. Comput. Chem., 2014, 35, 1997–2004 CrossRef CAS PubMed
.
- R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domanski, D. L. Dotson, S. Buchoux, I. M. Kenney and O. Beckstein, Proceedings of the 15th Python in Science Conference, 2016, pp. 98–105.
- G. Gueguen, N. Destainville and M. Manghi, Soft Matter, 2017, 13, 6100–6117 RSC
.
- J. Cornet, N. Destainville and M. Manghi, J. Chem. Phys., 2020, 152, 244705 CrossRef CAS PubMed
.
- G. Gueguen, N. Destainville and M. Manghi, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 76 CrossRef PubMed
.
-
M. Meyer, M. Desbrun, P. Schröder and A. H. Barr, Discrete differential-geometry operators for triangulated 2-manifolds, Springer Berlin Heidelberg, Berlin, Heidelberg, 2003, pp. 35–57 Search PubMed
.
-
P. M. Chaikin and T. C. Lubensky, Principles of condensed matter physics, Cambridge University Press, 1995 Search PubMed
.
-
R. Baxter, Exactly solved models in statistical mechanics, Academic Press, 1982 Search PubMed
.
-
M. E. J. Newman and G. T. Barkema, Monte Carlo Methods in Statistical Physics, Oxford University Press, Oxford, New York, 1999 Search PubMed
.
- J. Hu, T. Weikl and R. Lipowsky, Soft Matter, 2011, 7, 6092–6102 RSC
.
- S. Penic, A. Iglic, I. Bivas and M. Fosnaric, Soft Matter, 2015, 11, 5004–5009 RSC
.
- M. Siggel, S. Kehl, K. Reuter, J. Köfinger and G. Hummer, J. Chem. Phys., 2022, 157, 174801 CrossRef CAS PubMed
.
- W. Pezeshkian and J. H. Ipsen, Nat. Commun., 2024, 15, 548 CrossRef CAS PubMed
.
- C. Esposito, A. Tian, S. Melamed, C. Johnson, S.-Y. Tee and T. Baumgart, Biophys. J., 2007, 93, 3169–3181 CrossRef CAS PubMed
.
-
P. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed
.
- V. A. Shneidman and R. K. P. Zia, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 085410 CrossRef
.
-
S. Safran, Statistical thermodynamics of surfaces, interfaces, and membranes, CRC Press, 2003 Search PubMed
.
- C. Arnarez, J. J. Uusitalo, M. F. Masman, H. I. Ingólfsson, D. H. D. Jong, M. N. Melo, X. Periole, A. H. D. Vries and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 260–275 CrossRef CAS PubMed
.
- W. Pezeshkian, F. Grünewald, O. Narykov, S. Lu, V. Arkhipova, A. Solodovnikov, T. A. Wassenaar, S. J. Marrink and D. Korkin, Structure, 2023, 31, 492–503.e7 CrossRef CAS PubMed
.
- E. Jefferys, M. S. P. Sansom and P. W. Fowler, Faraday Discuss., 2014, 169, 209–223 RSC
.
- H. J. Risselada and S. J. Marrink, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17367–17372 CrossRef CAS PubMed
.
- G. A. Pantelopulos and J. E. Straub, Biophys. J., 2018, 115, 2167 CrossRef CAS PubMed
.
- S. Weitz and N. Destainville, Soft Matter, 2013, 9, 7804–7816 RSC
.
- P. W. Fowler, J. Hélie, A. Duncan, M. Chavent, H. Koldsø and M. S. P. Sansom, Soft Matter, 2016, 12, 7792–7803 RSC
.
- R. Goetz, G. Gompper and R. Lipowsky, Phys. Rev. Lett., 1999, 82, 221–224 CrossRef CAS
.
- A. Imparato, J. C. Shillcock and R. Lipowsky, Europhys. Lett., 2005, 69, 650–656 CrossRef CAS
.
- F. Schmid, Biophys. Rev. Lett., 2013, 08, 1–20 CrossRef CAS
.
- H. Shiba and H. Noguchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031926 CrossRef PubMed
.
- A. Hossein and M. Deserno, Biophys. J., 2020, 118, 624–642 CrossRef CAS PubMed
.
- J. Ehrig, E. P. Petrov and P. Schwille, New J. Phys., 2011, 13, 045019 CrossRef
.
- B. Camley, C. Esposito, T. Baumgart and F. Brown, Biophys. J., 2010, 99, L44–L46 CrossRef CAS PubMed
.
- B. Camley and F. Brown, Phys. Rev. Lett., 2010, 105, 148102 CrossRef PubMed
.
- K. Kikuchi, M. Yoshida, T. Maekawa and H. Watanabe, Chem. Phys. Lett., 1992, 196, 57–61 CrossRef CAS
.
- L. C.-L. Lin and F. Brown, Phys. Rev. Lett., 2007, 93, 256001 CrossRef PubMed
.
- E. Reister-Gottfried, S. Leitenberger and U. Seifert, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 011908 CrossRef PubMed
.
- M. Manghi, X. Schlagberger, Y.-W. Kim and R. Netz, Soft Matter, 2006, 2, 653–668 RSC
.
- N. Destainville and N. Coulonges, Phys. Rev. E, 2022, 105, 064115 CrossRef CAS PubMed
.
- GROMACS, GROMACS Reference Manual, 2016, https://manual.gromacs.org/, Online; accessed June 26, 2020.
- W. den Otter and S. Shkulipa, Biophys. J., 2007, 93, 423–433 CrossRef CAS PubMed
.
- M. Vögele, J. Köfinger and G. Hummer, J. Phys. Chem. B, 2019, 123, 5099–5106 CrossRef PubMed
.
- G. Lindblom and G. Oradd, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 234–244 CrossRef CAS PubMed
.
- S. Aimon, A. Callan-Jones, A. Berthaud, M. Pinot, G. Toombes and P. Bassereau, Dev. Cell, 2014, 28, 212–218 CrossRef CAS PubMed
.
- K. Rosholm, N. Leijnse, A. Mantsiou, V. Tkach, S. Pedersen, V. Wirth, L. Oddershede, K. Jensen, K. Martinez, N. Hatzakis, P. Bendix, A. Callan-Jones and D. Stamou, Nat. Chem. Biol., 2014, 13, 724–729 CrossRef PubMed
.
- C. Kluge, M. Pohnl and R. Bockmann, Biophys. J., 2022, 121, 671–683 CrossRef CAS PubMed
.
- H. Noguchi, N. Walani and M. Arroyo, arXiv, 2023, preprint, arXiv:2303.09142 DOI:10.48550/arXiv.2303.09142.
- P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, H. M. Khan, J. Domański, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. D. Vries and S. J. Marrink, Nat. Methods, 2021, 18, 382–388 CrossRef CAS PubMed
.
- F. Grünewald, M. H. Punt, E. E. Jefferys, P. A. Vainikka, M. König, V. Virtanen, T. A. Meyer, W. Pezeshkian, A. J. Gormley, M. Karonen, M. S. P. Sansom, P. C. T. Souza and S. J. Marrink, J. Chem. Theory Comput., 2022, 18, 7555–7569 CrossRef PubMed
.
- J. S. Ho and B. A. Straub, EPL, 1990, 12, 395 CrossRef
.
- D. M. Kroll and G. Gompper, Science, 1992, 255, 968 CrossRef CAS PubMed
.
- S. Komura, N. Shimokawa and D. Andelman, Langmuir, 2006, 22, 6771 CrossRef CAS PubMed
.
- O. H. S. Ollila, H. J. Risselada, M. Louhivuori, E. Lindahl, I. Vattulainen and S. J. Marrink, Phys. Rev. Lett., 2009, 102, 078101 CrossRef PubMed
.
- M. Wieczór, V. Genna, J. Aranda, R. M. Badia, J. L. Gelpí, V. Gapsys, B. L. Groot, E. Lindahl, M. Municoy, A. Hospital and M. Orozco, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, 13, e1622 Search PubMed
.
- C. Chang, V. L. Deringer, K. S. Katti, V. V. Speybroeck and C. M. Wolverton, Nat. Rev. Mater., 2023, 8, 309–313 CrossRef PubMed
.
- C. Gupta, D. Sarkar, D. P. Tieleman and A. Singharoy, Curr. Opin. Struct. Biol., 2022, 73, 102338 CrossRef CAS PubMed
.
- L. Casalino, C. Seitz, J. Lederhofer, Y. Tsybovsky, I. A. Wilson, M. Kanekiyo and R. E. Amaro, ACS Cent. Sci., 2022, 8, 1646–1663 CrossRef CAS PubMed
.
- J. V. Vermaas, C. G. Mayne, E. Shinn and E. Tajkhorshid, J. Chem. Inf. Model., 2021, 62, 602–617 CrossRef PubMed
.
- Z. Luthey-Schulten, Z. R. Thornburg and B. R. Gilbert, Curr. Opin. Struct. Biol., 2022, 75, 102392 CrossRef CAS PubMed
.
- J. A. Stevens, F. Grünewald, P. A. M. V. Tilburg, M. König, B. R. Gilbert, T. A. Brier, Z. R. Thornburg, Z. Luthey-Schulten and S. J. Marrink, Front. Chem., 2023, 11, 1106495 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary text and 6 figures. See DOI: https://doi.org/10.1039/d4sm00089g |
| ‡ Indeed, the circumference of a circular domain of radius R0 is discretized into NR ⋍ 2πR/a elementary edges of the sphere tesselation. The discrete Fourier transform of the boundary fluctuations is written with Fourier coefficients un associated with wavelengths 2πR/n (see the methods section), n running from −NR/2 + 1 to NR/2. Hence the smallest accessible wavelength is 2πR/(NR/2) = 2a. |
| This journal is © The Royal Society of Chemistry 2024 |