DOI:
10.1039/D4SM00408F
(Paper)
Soft Matter, 2024,
20, 5527-5537
Microrheology of active suspensions†
Received
7th April 2024
, Accepted 1st June 2024
First published on 11th June 2024
Abstract
We study the microrheology of active suspensions through direct hydrodynamic simulations using model pusher-like microswimmers. We demonstrate that the friction coefficient of a probe particle is notably reduced by hydrodynamic interactions (HIs) among a moving probe and the swimmers. When a swimmer approaches a probe from the rear (front) side, the repulsive HIs between them are weakened (intensified), which results in a slight front-rear asymmetry in swimmer orientation distribution around the probe, creating a significant additional net driving force acting on the probe from the rear side. The present drag-reduction mechanism qualitatively differs from that of the viscosity-reduction observed in sheared bulk systems and depends on probing details. This study provides insights into our fundamental knowledge of hydrodynamic effects in active suspensions and serves as a practical example illuminating distinctions between micro- and macrorheology measurements.
1 Introduction
In active suspensions, the intrinsic activity of swimming particles leads to distinctive collective behaviors and transport/rheological properties deviating from those observed in passive particle suspensions.1–3 A striking example is anomalous rheology.4–23 In particular, in suspensions of pusher-like microswimmers, such as E. coli, the viscosity significantly decreases,5–9 frequently establishing zero or negative viscosity states.7,9,12 The underlying mechanism behind such anomalous rheology involves weak orientational order along the extension axis of the externally applied flow field, which could be attributed to rotational diffusivities and/or hydrodynamic interactions (HIs).11,13,16,18,22 The active dipolar forces with the orientational order intensify the mean flow, reducing the resistive stress required to drive the external flow and consequently diminishing the viscosity.4 The anomalous viscosity reduction in active suspensions contrasts with the viscosity behavior of dilute suspensions of passive particles, which is well described by the Einstein viscosity formula.24
The local viscosity or viscoelastic properties of active suspensions are of great interest; probing rheological properties at the μm level can provide further insights into the underlying mechanisms and enable a more detailed characterization of the anomalous rheology. When probing smaller-scale rheological properties of complex fluids or soft materials, microrheology measurements are considered powerful tools (see recent reviews25–27 and the references therein). By tracking the motions of small probes suspended in fluids, typically at a μm scale, microrheology allows for measuring viscoelastic properties across a wider range of temporal scales than conventional macrorheology techniques. This finer resolution in both time and length scales may offer a more comprehensive understanding of the material's rheological properties. However, microrheology still faces several unresolved issues. One such issue is whether the observations made using microrheology accurately reflect the actual local rheological properties of the material in the absence of probes. The interactions among probes and suspended constituents or inner structures can significantly influence the motion of the probes and potentially alter the local rheological properties around the probe. Understanding and accounting for these effects are crucial for accurately interpreting microrheology measurements and relating them to a material's intrinsic viscoelastic properties.
Microrheological investigations on active suspensions have provided various intriguing results.28–40 A simulation study by Foffano et al.32,33 demonstrated that a probe particle can experience a negative viscosity in active nematics composed of contractile-puller-type swimmers. More recent numerical studies34–36,38 have predicted that the friction coefficient of a probe can be reduced in active Brownian particle baths without HIs, but not to a level smaller than that defined in the absence of active/passive Brownian particles, indicating that the measured viscosity is larger than the solvent viscosity. However, as described above, in bulk rheological experiments of extensile-pusher-type swimmers, it has been observed that the measured viscosity can be lower than the solvent viscosity and even approach zero. This raises a question of whether such a phenomenon can be replicated in microrheology measurements when HIs are taken into account. If so, this would prompt further investigation into whether the reduction of the friction coefficient of a probe shares a similar mechanism to the viscosity reduction observed in macrorheology.
2 Simulation methods
For the present purpose, we conduct direct hydrodynamic simulations using a model of active suspensions comprised of N rod-like dumbbell swimmers. Our model swimmer, shown in Fig. 1(a), is essentially the same as the one employed in our previous investigation of macrorheology simulations.22 In this model, each swimmer consists of a body and a flagellum: the body is treated as a rigid-body particle, while the flagellum is considered a massless “phantom” particle that simply follows the body's motions. This treatment maintains the relative position of the body and flagellum parts. For the α-th swimmer (α = 1, …, N), we assume that a force FA![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α acting on the (front) body is exerted by the (rear) flagellum and that the flagellum also exerts the force −FA
α acting on the (front) body is exerted by the (rear) flagellum and that the flagellum also exerts the force −FA![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α directly on the solvent fluid. Here,
α directly on the solvent fluid. Here, ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α is the direction of the α-th swimmer, and these forces compose a dipolar force of magnitude FA
α is the direction of the α-th swimmer, and these forces compose a dipolar force of magnitude FA![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, with
0, with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 being the characteristic swimmer's length [see Fig. 1(a)]. Such a force-prescribed particle model emulates rod-like pusher-type microorganisms such as E. coli, as initially proposed in the ref. 41 and 42 and employed in subsequent studies.16,18,22,43–46
0 being the characteristic swimmer's length [see Fig. 1(a)]. Such a force-prescribed particle model emulates rod-like pusher-type microorganisms such as E. coli, as initially proposed in the ref. 41 and 42 and employed in subsequent studies.16,18,22,43–46
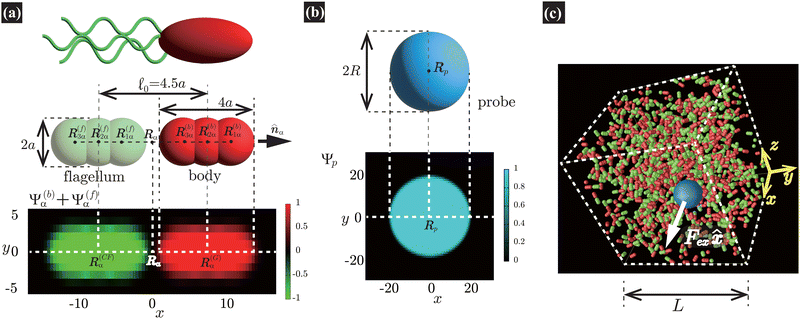 |
| | Fig. 1 (a) Our model swimmer comprises body and flagellum parts with symmetric shapes. Each part is constituted by a superposition of three spheres with radius a. We assume that a force FA![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α is exerted on the body, while −FA α is exerted on the body, while −FA![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α is directly exerted on the solvent through the flagellum part, with α is directly exerted on the solvent through the flagellum part, with ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α being the orientation of the α-th swimmer. These forces constitute a force dipole of magnitude FA α being the orientation of the α-th swimmer. These forces constitute a force dipole of magnitude FA![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, with 0, with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 being the characteristic swimmer's length, which for the present model is given as the separation distance between the body and flagellum centers. In this study, to incorporate the present model swimmer into the SPM, the body and flagellum parts are represented through field variables, Ψ(b)α(r) and Ψ(f)α(r), respectively. In the bottom panel, we plot Ψ(b)α(r) + Ψ(f)α(r) in the xy-plane, where both R(G)α = (2.25a,0,0) and R(CF)α = (−2.25a,0,0) are included. (b) In our microrheology simulation, a single probe particle with radius R is immersed in a fluid. The probe particle is also described by the field variable Ψp(r). In the bottom panel, we plot Ψp(r) representing the probe particle in the xy-plane, where the probe center is set to Rp = (0,0,0). In (a) and (b), the discretized mesh size h is the same as that used in practical simulations (h = 0.3125a and ξ = 0.5h). Here, ξ is the interface thickness controlling the degree of smoothness of Ψ(b)α(r), Ψ(f)α(r), and Ψp(r). (c) A single probe particle immersed in a fluid is dragged by a constant force Fex along the x-direction. The periodic boundary conditions are imposed in all directions with the linear dimension L. 0 being the characteristic swimmer's length, which for the present model is given as the separation distance between the body and flagellum centers. In this study, to incorporate the present model swimmer into the SPM, the body and flagellum parts are represented through field variables, Ψ(b)α(r) and Ψ(f)α(r), respectively. In the bottom panel, we plot Ψ(b)α(r) + Ψ(f)α(r) in the xy-plane, where both R(G)α = (2.25a,0,0) and R(CF)α = (−2.25a,0,0) are included. (b) In our microrheology simulation, a single probe particle with radius R is immersed in a fluid. The probe particle is also described by the field variable Ψp(r). In the bottom panel, we plot Ψp(r) representing the probe particle in the xy-plane, where the probe center is set to Rp = (0,0,0). In (a) and (b), the discretized mesh size h is the same as that used in practical simulations (h = 0.3125a and ξ = 0.5h). Here, ξ is the interface thickness controlling the degree of smoothness of Ψ(b)α(r), Ψ(f)α(r), and Ψp(r). (c) A single probe particle immersed in a fluid is dragged by a constant force Fex along the x-direction. The periodic boundary conditions are imposed in all directions with the linear dimension L. | |
As illustrated in Fig. 1(a), the body and flagellum parts are assumed to have the same shape and are each described by a superposition of three spheres with a common radius a. The spheres composing the body are located at the positions R(b)i,α = R(G)α + (2 − i)a![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α (i = 1, 2, 3), where R(G)α is the α-th swimmer's center-of-mass position. Similarly, the spheres composing the flagellum part are located at R(f)i,α = R(CF)α + (2 − i)a
α (i = 1, 2, 3), where R(G)α is the α-th swimmer's center-of-mass position. Similarly, the spheres composing the flagellum part are located at R(f)i,α = R(CF)α + (2 − i)a![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α (i = 1, 2, 3), where R(CF)α = R(G)α − 4.5a
α (i = 1, 2, 3), where R(CF)α = R(G)α − 4.5a![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α = R(G)α −
α = R(G)α − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0
0![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α is the position of the center of the flagellum. The shape of the present model swimmer shows the head–tail symmetry, and the mid-point is thus given by Rα = (R(G)α + R(CF)α)/2. Although arbitrary shapes of swimmers with an imposed head-tail asymmetry can be composed, we can obtain qualitatively the same results as long as these swimmers have rod-like forms with the prescribed force dipoles.
α is the position of the center of the flagellum. The shape of the present model swimmer shows the head–tail symmetry, and the mid-point is thus given by Rα = (R(G)α + R(CF)α)/2. Although arbitrary shapes of swimmers with an imposed head-tail asymmetry can be composed, we can obtain qualitatively the same results as long as these swimmers have rod-like forms with the prescribed force dipoles.
In our simulations, we use the smoothed profile method (SPM)47–49 to accommodate many-body hydrodynamic interactions (HIs) among the constituent swimmers. The SPM can accurately reproduce even the near-field HIs:49 in the present study, the ratio of the simulation mesh size to the particle size a is on the order of 0.1, determining the spatial resolution of HIs. With this setting, the SPM can quantitatively replicate the near-field HIs (lubrication interactions) to a satisfactory degree up to a closer distance as h/a ∼ 0.1 (or even less),49 where h represents the gap distance measured as the separation distance between the interfaces of adjacent particles. However, to fully reproduce the singular divergence of lubrication forces, which become crucial at much closer distances, finer resolutions are required. This situation is similar to other hybrid simulation methods.50–55 However, such singular lubrication interactions act only on particles with extremely smooth and rigid surfaces, where the degree of surface roughness is significantly smaller than the particle size. Thus, for modeling HIs among microswimmers or those between the probe particle and microswimmers, reproducing singular lubrication interactions is not necessary.
Here, we describe a detailed scheme to simulate the present model swimmer system, essentially the same as that used in a previous study.22 The body and flagellum parts of a swimmer are represented through the field variables Ψ(b)α(r) and Ψ(f)α(r), respectively:
| | 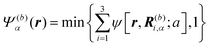 | (1) |
and
| | 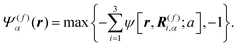 | (2) |
In this study, we adopt the following function to
ψ as
| | 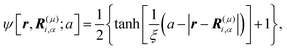 | (3) |
where
μ =
b,
f and
ξ is the interface thickness controlling the degree of smoothness. In
Fig. 1(a), we show the cross section of the model swimmer described by
Ψ(b)α(
r) and
Ψ(f)α(
r), including both
R(G)α and
R(CF)α in the same plane.
In our microrheology simulation, a single probe particle (radius R) is immersed in a fluid, which is dragged by a constant force Fex along the x-direction. Similarly to the swimmers, as shown in Fig. 1(b), the probe particle is also described by the field variable Ψp(r) as
where
Rp is the position of the probe sphere's center and
R is the probe radius.
The working equations for the velocity field ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v(r,t) are given as
v(r,t) are given as
| | 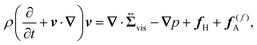 | (5) |
| | 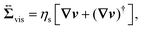 | (6) |
Eqn (5) is the usual Navier–Stokes equation.
24 Here,
ρ is the solvent mass density,
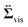
, given as
eqn (6), is the viscous stress tensor with
ηs being the solvent viscosity, and the hydrostatic pressure
p is determined by the incompressibility condition,
eqn (7). In addition,
fH is the body force required to satisfy the rigid-body condition for the swimmer's body and probe particle regions, and
f(f)A is the active force directly exerted by the flagellum part to the fluid:
| | 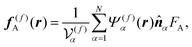 | (8) |
where
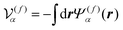
is the volume of the flagellum part. In addition, the volume of the body part is given as
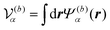
. In this study, because the shapes of the body and flagellum parts are assumed to be the same,
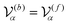
.
For the model swimmers, the equations of motion for the center-of-mass velocity V(G)α and the angular velocity with respect to the center-of-mass Ω(G)α are
| | 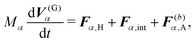 | (9) |
| | 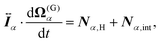 | (10) |
where
| | 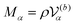 | (11) |
and
| | 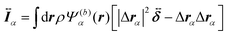 | (12) |
are the mass and the moment of inertia of the
α-th swimmer's body, respectively. Here,
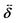
is the unit tensor and Δ
rα =
r −
R(G)α. In this study, the swimmer's density is assumed to be the same as the solvent density. In
eqn (9) and (10),
Fα,H and
Nα,H are the force and torque exerted on the
α-th swimmer due to HIs, respectively. The explicit forms of
Fα,H,
Nα,H, and the body force
fH are given in the ESI.
†Fα,int and
Nα,int are the force and torque acting on the
α-th swimmer's body, respectively, due to the particle–particle and particle–probe potential interactions:
| | 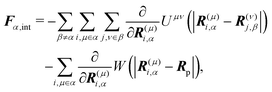 | (13) |
| | 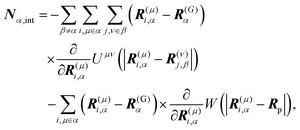 | (14) |
where
i,
j = 1, 2, 3 and
μ,
ν =
b,
f. Here,
Uμν is the interaction potential between two spheres in which each comprise the body or the flagellum part of different swimmers, and
W is the interaction potential between such a sphere and the probe sphere. The explicit forms of
Uμν and
W are provided below. The active force acting on the body part,
F(b)α,A, is given as
| | F(b)α,A = FA![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α. α. | (15) |
Eqn (8) and (15) prescribe a force dipole FA![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0
0![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α with
α with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0
0![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α = R(G)α − R(CF)α [see also eqn (34)].
α = R(G)α − R(CF)α [see also eqn (34)].
Similarly, for the probe particle, the equations of motion for the center-of-mass velocity Vp and the angular velocity with respect to the center-of-mass Ωp are
| | 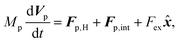 | (16) |
| | 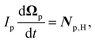 | (17) |
where
| | 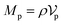 | (18) |
and
| | 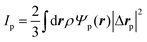 | (19) |
are the mass and the moment of inertia of the probe particle, respectively. Here, Δ
rp =
r −
Rp,
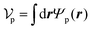
is the volume of the probe particle, and the probe particle density is also assumed to be the same as the solvent density. In
eqn (16),
Fp,int is the force due to the interaction with swimmers:
| | 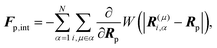 | (20) |
where
i = 1, 2, 3 and
μ =
b,
f.
We assume the following form of the interparticle potentials:
| | 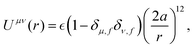 | (21) |
where
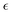
is a positive energy constant,
δμ,f is the Kronecker delta, and
μ,
ν =
b,
f. This form prevents the body part of a swimmer from overlapping on different swimmers but allows overlaps among the flagellum parts. The interaction potential
W between the probe particle and the particles constituting a swimmer is introduced to prevent the penetration of swimmers through the probe boundary. In this study,
W is assumed to be given as
| | 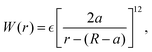 | (22) |
where we assume the same energy constant as that of
Uμν.
For a direct comparison between simulations with and without HIs, we have made equivalent simulations without HIs, using the same parameters for the interactions. Furthermore, in eqn (9), (10), (16), and (17), the hydrodynamic forces and torques are replaced as
| | 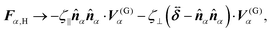 | (23) |
Here, the values of the friction coefficients ζ‖, ζ⊥, and ζR are numerically evaluated as those of an isolated swimmer with HIs; ζ‖ = 9.6πηsa, ζ⊥ = 10.9πηsa, and ζR = 38.7πηsa3. This approach draws parallels with the conventional frameworks used in Brownian or relaxation dynamics simulations of spherical particles, for which the friction coefficient is usually defined as 6πηa, with η and a representing the solvent viscosity and the sphere radius, respectively.
In our simulations, as illustrated in Fig. 1(c), periodic boundary conditions are imposed in all directions with the linear dimension L. The probe dynamics are influenced by periodic image probes and swimmers; as elucidated below, the probe dynamics are significantly influenced by HIs between the probe and its nearby surrounding swimmers. Therefore, while HIs with distant image swimmers (located farther than the nearest neighbors) will have a small quantitative contribution, they should not alter the qualitative aspects of the simulation results. We make the equations dimensionless by measuring space and time in units of h and t0, respectively. Here, h denotes the discretization mesh size used in solving eqn (5)–(7), and t0 = ρh2/ηs is the momentum diffusion time across the unit length. Accordingly, the scaled solvent viscosity is 1, and the units of velocity, stress, force, and energy are chosen to be h/t0 = ηs/(ρh), ρh2/t02 = ηs2/(ρh2), ρh4/t02 = ηs2/ρ, and ρh5/t02 = ηs2h/ρ, respectively. Note that ρh4/t02 = ηs2/ρ is the intrinsic force scale of a Newtonian fluid. In our simulations, we set 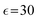 and FA = 20. The parameters determining the swimmer's shape are set to be a = 3.2,
and FA = 20. The parameters determining the swimmer's shape are set to be a = 3.2, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = |R(G)α − R(CF)α| = 4.5a and ξ = 0.5. In this study, the swimmer volume fraction is identified as that of the rigid body particles given by
0 = |R(G)α − R(CF)α| = 4.5a and ξ = 0.5. In this study, the swimmer volume fraction is identified as that of the rigid body particles given by 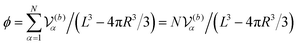 .
.
3 Results
3.1 Friction coefficients
Fig. 2(a), (c), and (d) present the scaled friction coefficient ζ/ζ0 for various conditions. In this study, the friction coefficient of the probe particle ζ is defined as| | 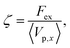 | (27) |
where Vp,x is the x-component of the probe velocity, 〈⋯〉 represents the time average in a steady state, and ζ0 is the bare friction coefficient experienced by the probe particle suspended in a pure solvent.
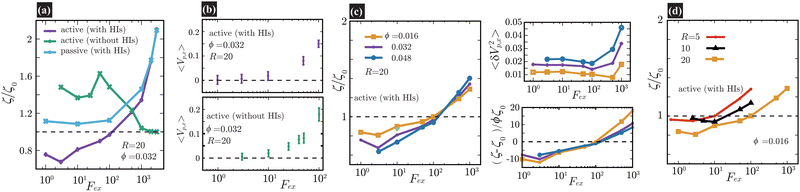 |
| | Fig. 2 In (a), (c), and (d), we present the friction coefficients ζ scaled by ζ0 against Fex. For the cases with HIs, ζ0 is the friction coefficient of the probe particle suspended in a pure solvent with Fex = 10. On the contrary, in the cases without HIs, ζ0 = 6πηsR as set in eqn (25). In (a), ζ/ζ0 is shown for three different conditions at a probe radius R = 20(= 6.25a) and ϕ = 0.032. With HIs, ζ is significantly smaller than ζ0 for Fex ≲ 102, contrasting with the behavior in the absence of HIs. We also present a passive case, where we use the same swimmer model but without the active force (FA = 0). Note that for Fex ≳ 103, ζ for active and passive systems almost converges, simply because the influence of the self-propulsion of swimmers is relatively diminished.34–36 In (b), we plot 〈Vp,x〉, with error bars, for Fex ≤ 102 both with and without HIs, shown in the upper and lower panels, respectively. In (c), ζ/ζ0 is shown for different ϕ at a probe radius R = 20(= 6.25a) with HIs. The main data are the results for L = 128, while the yellow-green closed circle represents the data for a larger system size L = 256 at R = 20, ϕ = 0.016, and Fex = 10, almost corresponding to the case of L = 128 at the same R and ϕ. The upper-right pannel displays 〈δVp,x2〉 with δVp,x = Vp,x − 〈Vp,x〉. For relatively small Fex, 〈δVp,x2〉 is nearly constant and smaller for lower ϕ. In the lower-right panel, the normalized friction coefficient, (ζ − ζ0)/(ζ0ϕ), is plotted. For 3 ≲ Fex ≲ 102, an almost linear dependence of ζ − ζ0 on ϕ is shown. In (d), ζ/ζ0versus Fex is shown for several different probe sizes (R = 5, 10, and 20) at ϕ = 0.016. At R = 5 and 10, within the examined range of Fex, the reduction of ζ is less pronounced than at R = 20. | |
In Fig. 2(a), ζ/ζ0 is shown for three different conditions for a probe with radius R = 20(= 6.25a) and a volume fraction ϕ = 0.032. When HIs are considered, ζ is significantly smaller than ζ0 for Fex ≲ 102. To provide further insights into the role of HIs, equivalent simulations without HIs are performed, employing identical parameters for the particle–particle interactions. Without HIs, ζ is always larger than ζ0, showing non-monotonic Fex dependence56 similar to that observed in earlier simulation study.34 The observed distinction strongly suggests that HIs play a significant role in the reduction of ζ in active suspensions. Additionally, we present a passive case, where we use the same swimmer model but without the active force (FA = 0). Notably, for Fex ≳ 103, the values of ζ for both active and passive systems with HIs tend to converge with a marked force thickening. This convergence is simply because the influence of the self-propulsion of swimmers is relatively diminished.34–36 In the ref. 57 and 58, the thickening of microviscosity due to hydrodynamic lubrication is explored in the context of active microrheology in passive suspensions, and it is found that the thickening becomes notable when the attainable gap distance h can be approximately less than 0.1 of the particle size. In our simulation, a similar degree of the resolution of HIs is achieved, which may explain the observed increase in ζ at larger Fex as reflecting this thickening effect.
Fig. 2(b) shows the average probe velocity 〈Vp,x〉 at a probe radius R = 20(= 6.25a) and ϕ = 0.032, both with and without HIs. For relatively smaller Fex, strong fluctuations in Vp,x are found, reflecting significant back-and-forth motions due to frequent collisions with surrounding swimmers. However, each data point is derived from simulations conducted over extended periods to ensure the accuracy of 〈Vp,x〉; especially for smaller Fex values like Fex = 3 and 10, the simulation ran for a period where the probe particle traveled several hundred times its own size. For further details on related topics, please refer to Fig. 3 and the associated discussion.
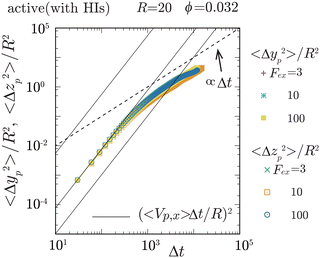 |
| | Fig. 3 The mean square displacement (MSD) of the probe particle, normalized by R2, in the transverse (y- and z-) directions, is plotted for Fex = 3, 10, and 102 at ϕ = 0.032 and R = 20. The solid lines represent (〈Vp,x〉Δt/R)2 with Δt being the elapsed time, for Fex = 3, 10, and 102, from lower to higher, respectively. The crossover from ballistic to diffusive motions is observed at around Δt ∼ 103. Notably, 〈Δyp2〉/R2 and 〈Δzp2〉/R2 roughly converge into a single curve, ensuring the axisymmetric behavior of the probe particle motions around the external force direction (x-direction). For Fex ≲ 10, there exists a period where 〈Vp,x〉Δt is less than the average diffusive displacement of the probe particle in the transverse directions, which is consistent with that the magnitude of fluctuations in Vp,x is larger than 〈Vp,x〉 for the same Fex range. | |
In Fig. 2(c), ζ/ζ0 is shown for different ϕ at a probe radius R = 20(= 6.25a) with HIs. The reduction in ζ is enhanced as the swimmer volume fraction ϕ increases at least within the range examined in our simulations (ϕ ≲ 0.05). The upper-right pannel displays 〈δVp,x2〉 with δVp,x = Vp,x − 〈Vp,x〉. For relatively small Fex, where the average probe velocity 〈Vp,x〉 is considerably smaller than the average speed of microswimmers, 〈δVp,x2〉 is nearly constant and smaller for lower ϕ. This feature suggests that the fluctuations in probe velocities are determined by the details of probe-swimmer collisions and their statistics. In the lower-right panel, the normalized friction coefficient, (ζ − ζ0)/(ζ0ϕ), is plotted. It indicates a linear dependence of ζ − ζ0 on ϕ for Fex ≲ 102 within the present range of ϕ. However, this linear relationship does not extend to higher Fex values. Furthermore, even for Fex ≲ 3, the expected scaling also breaks. The precise origin of these deviations – whether they arise from statistical inaccuracies or more intrinsic phenomena – remains to be elucidated.
In macrorheology simulations using the same rod-like model swimmer, HIs induce a weak alignment of swimmer orientations along the elongation axis of the applied flow field, resulting in the acceleration of the mean flow and a subsequent reduction in the viscosity.22 Accordingly, we can expect that the decrease in ζ in the present microrheology simulations also reflects a similar mechanism involving some ordering of swimming directions in the bulk region. However, as shown below, this is not the case.
Fig. 2(d) shows ζ/ζ0 against Fex for three different probe sizes. For the Fex ranges at R = 5 and 10, the magnitude of the induced velocity gradient in the bulk region (more than one swimmer size away from the probe surface) approximately corresponds to that observed for Fex ∼ 10–103 at R = 20, but the reduction in ζ is not as noticeable as for R = 20. Furthermore, in Fig. 2(c), the main data are the results for L = 128, while the yellow-green closed circle represents the data for a larger system size L = 256 at R = 20, ϕ = 0.016, and Fex = 10. Although we examine only a single case, a significant system-size dependence is hardly observed, which contrasts with the macrorheology case, where the viscosity reduction shows a strong system-size dependence.22 These findings suggest that the drag-reduction mechanism depends on the local probing details and thus qualitatively differs from that of the viscosity reduction observed through macrorheology measurements.
3.2 Local swimmer states around the probe particle
To elucidate the mechanism behind the reduction in ζ, let us explore the local swimmer states around the probe and their impact on the probe dynamics. Before proceeding, it is important to verify the symmetry around the x-axis, which corresponds to the direction of the applied external force. In Fig. 3, we plot the probe particle's mean square displacement (MSD) along the y- and z-directions for various values of Fex at ϕ = 0.032 and R = 20. The MSD in these transverse directions is proportional to Δt for larger Δt, where Δt represents the elapsed time, indicating clear diffusive behavior of the probe particle in these directions. Importantly, the diffusion coefficients in the y- and z-directions are nearly identical, and these diffusivities do not show a significant Fex dependence. Therefore, this observation ensures the axisymmetric behavior of the probe particle around the external force direction (x-direction) and indicates that the probe motion along and across the x-direction does not interfere significantly with each other. The same behavior was also observed for different ϕ (not shown here). In the following analysis, we assume that axial symmetry about the x-axis approximately holds. Note that, with increasing ϕ, collisions with swimmers occur more frequently, resulting in the enhanced probe diffusivity.
In Fig. 4(a)–(f), we show the contour plots of the number density of the swimmers 〈ρ(x,y)〉. At R = 20(≳ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0), as shown in Fig. 4(a), (b), (e), and (f), 〈ρ(x,y)〉 near the probe boundary is considerably larger than in the bulk region, irrespective of the presence of HIs. As indicated in the literature, both the steric59 and hydrodynamic60 effects cause the entrapment of microswimmers on the boundaries. A self-propulsive rod-like particle, upon colliding with the probe, cannot rebound immediately due to the steric/geometric constraints. Instead, it stays near the probe for a while, swimming along the surface. This behavior may result in a larger density near the probe surface. Note that HIs between the probe and the swimmers enhance the entrapment,60 but they are not significantly dominant in the present condition. At R = 5(≲
0), as shown in Fig. 4(a), (b), (e), and (f), 〈ρ(x,y)〉 near the probe boundary is considerably larger than in the bulk region, irrespective of the presence of HIs. As indicated in the literature, both the steric59 and hydrodynamic60 effects cause the entrapment of microswimmers on the boundaries. A self-propulsive rod-like particle, upon colliding with the probe, cannot rebound immediately due to the steric/geometric constraints. Instead, it stays near the probe for a while, swimming along the surface. This behavior may result in a larger density near the probe surface. Note that HIs between the probe and the swimmers enhance the entrapment,60 but they are not significantly dominant in the present condition. At R = 5(≲ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0), as shown in Fig. 4(c) and (d), the peak of 〈ρ(x,y)〉 near the boundary decreases, both with and without HIs, suggesting a weaker entrapment effect for smaller R. Also, as shown in Fig. 4(g) and (h), without HIs, the increase in 〈ρ(x,y)〉 is slightly more pronounced on the front than the rear, but such a behavior diminishes with HIs.
0), as shown in Fig. 4(c) and (d), the peak of 〈ρ(x,y)〉 near the boundary decreases, both with and without HIs, suggesting a weaker entrapment effect for smaller R. Also, as shown in Fig. 4(g) and (h), without HIs, the increase in 〈ρ(x,y)〉 is slightly more pronounced on the front than the rear, but such a behavior diminishes with HIs.
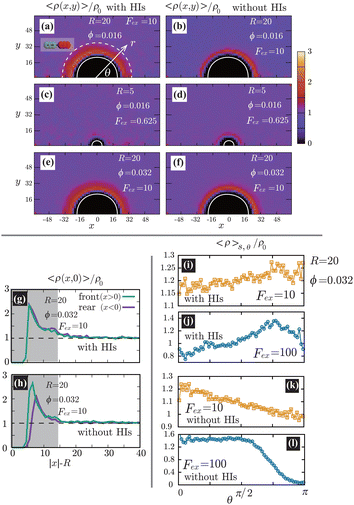 |
| | Fig. 4 (a)–(f) Contour plots of the scaled number density 〈ρ(x,y)〉/ρ0 for various conditions, where ρ0 is the average density defined as ρ0 = N/[L3 − 4πR3/3]. The left and right panels correspond to cases with and without HIs, respectively. The white semi-circular curves represent the boundary of the probe sphere. In (a), the swimmer is shown at the same scale as the probe to compare these sizes directly. We assume axial symmetry about the x-axis. At R = 20(≳ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0), as shown in (a), (b), (e), and (f), 〈ρ(x,y)〉 near the probe boundary is considerably larger than ρ0, irrespective of the presence of HIs. On the other hand, for R = 5(≲ 0), as shown in (a), (b), (e), and (f), 〈ρ(x,y)〉 near the probe boundary is considerably larger than ρ0, irrespective of the presence of HIs. On the other hand, for R = 5(≲ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0), as shown in (c) and (d), the peak of 〈ρ(x,y)〉 near the surface is less pronounced. In (g) and (h), 〈ρ(x,0)〉/ρ0 is shown at R = 20, ϕ = 0.032, and Fex = 10 with and without HIs, respectively. Here, the gray-colored regions indicate 0 ≤ |x| − R ≤ 0), as shown in (c) and (d), the peak of 〈ρ(x,y)〉 near the surface is less pronounced. In (g) and (h), 〈ρ(x,0)〉/ρ0 is shown at R = 20, ϕ = 0.032, and Fex = 10 with and without HIs, respectively. Here, the gray-colored regions indicate 0 ≤ |x| − R ≤ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. (i)–(l) The scaled density 〈ρ〉s,θ/ρ0 averaged over the range R < r < R + 0. (i)–(l) The scaled density 〈ρ〉s,θ/ρ0 averaged over the range R < r < R + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 at the polar angle θ for Fex = 10 and 100 with and without HIs. In (a), the dashed white semi-circular curve represents r = R + 0 at the polar angle θ for Fex = 10 and 100 with and without HIs. In (a), the dashed white semi-circular curve represents r = R + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. 0. | |
The distinction between with and without HIs is illustrated in Fig. 4(i)–(l), where we plot the density, averaged over the range R < r < R + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 and scaled by ρ0:
0 and scaled by ρ0:
| | 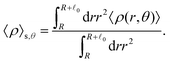 | (28) |
Here, 〈
ρ(
x,
y)〉 is reinterpreted as 〈
ρ(
r,
θ)〉 with
x =
r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ and
y =
r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ. As demonstrated, in the presence of HIs, the density at the rear is larger than at the front, whereas in their absence, the reverse is observed. This tendency becomes more pronounced with increasing
Fex.
Fig. 5 shows the orientation distribution of swimmers P(![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ; x, y) around the probe particle. It is defined as
; x, y) around the probe particle. It is defined as
| | 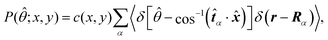 | (29) |
where
r = (
x,
y, 0),
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif)
is the unit vector along the
x-axis and
![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) α
α =
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ‖α
‖α/|
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ‖α
‖α| with
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ‖α
‖α denoting the projected swimming direction onto the
x–
y plane. The normalization factor
c(
x,
y) specific to the present visualization in
Fig. 5 is determined so that
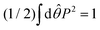
. The main text presents the results for two cases at
Fex = 10 and 100 with HIs. For cases without HIs, please refer to the ESI.
† In
Fig. 5, the panels (a)–(e) show
P(
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif)
;
x,
y) near the probe boundary. The tilt angle of the swimmers (measured with respect to the tangential direction of the probe surface) is larger when they face the probe than when they face the bulk, but this distinction is subtle in (c) and (d) for
Fex = 10. Additionally, more swimmers face the probe for
x < 0 than
x > 0. These characteristics are more evident at
Fex = 100 than at
Fex = 10.
 |
| | Fig. 5 The orientation distributions of swimmers P(![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ; x, y) averaged over a square region outlined by dashed lines at R = 20 and ϕ = 0.032 with HIs, with the block size being 2a = 0.32R(= 6.4). For the definition of P( ; x, y) averaged over a square region outlined by dashed lines at R = 20 and ϕ = 0.032 with HIs, with the block size being 2a = 0.32R(= 6.4). For the definition of P(![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ; x, y), please refer to the explanation presented in the main text. The probe-sphere's center is located at (x, y) = (0, 0). In (a)–(f), the left and right panels present the distributions at Fex = 10 and 100, respectively. The violet and dark-green lines correspond to P( ; x, y), please refer to the explanation presented in the main text. The probe-sphere's center is located at (x, y) = (0, 0). In (a)–(f), the left and right panels present the distributions at Fex = 10 and 100, respectively. The violet and dark-green lines correspond to P(![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ; x, y) (x < 0) and P(180° − ; x, y) (x < 0) and P(180° − ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ; x, y) (x > 0), respectively, calculated in the regions indicated by identical colored characters and normalized to make the total enclosed area equal 1. The dotted lines guide the normal and tangential directions along the probe sphere. ; x, y) (x > 0), respectively, calculated in the regions indicated by identical colored characters and normalized to make the total enclosed area equal 1. The dotted lines guide the normal and tangential directions along the probe sphere. | |
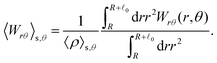
These observations are further illustrated in Fig. 6, where we plot various components of the following quantities:
| | 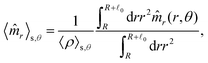 | (30) |
| | 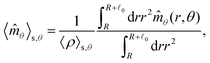 | (31) |
| | 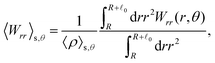 | (32) |
| |  | (33) |
Here,
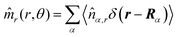
,
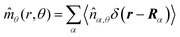
,
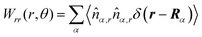
, and
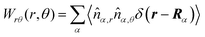
, where
r = (
x,
y, 0) with
x =
r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ and
y =
r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ. Here,
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) α,r
α,r and
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) α,θ
α,θ are
r- and
θ-components of the (unit vector) direction of the
α-th swimmer, respectively.
Eqn (30) and (31) represent
r- and
θ-components of the average orientation vector of the swimmers, respectively. On the other hand,
eqn (32) and (33) represent
rr- and
rθ-components of the average nematic order parameter, respectively. These quantities are averaged values per swimmer within the range
R <
r <
R +
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0
0 at the polar angle
θ. They are evaluated under conditions where
R = 20 and
ϕ = 0.032, with HIs, for
Fex = 10 and 100.
Fig. 6(a) and (b) demonstrate that the swimmers face the probe more likely than facing the bulk, and such a tendency is more enhanced at
Fex = 100 than
Fex = 10. As shown in
Fig. 6(c) and (d), at
Fex = 100, more swimmers move along the probe surface from the rear- to the front-sides, while at
Fex = 10, such a tendency is not obvious. Furthermore, we can find that the
rr-component of the nematic order is more enhanced in the rear than in the front, and this tendency is more enhanced at
Fex = 100 than at
Fex = 10. Such a front-rear asymmetry in 〈
Wrθ〉
s,θ is weaker than that in 〈
Wrr〉
s,θ. This difference is essential in the observed front-rear asymmetry in the active stress, as shown in
Fig. 7.
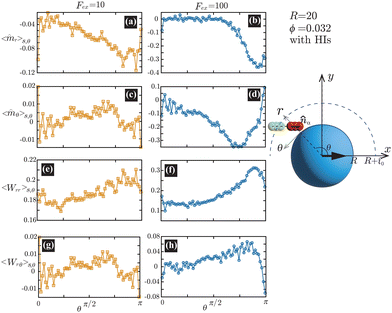 |
| | Fig. 6 (a) and (b) show 〈![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) r〉s,θ defined in eqn (30), while (c) and (d) represent 〈 r〉s,θ defined in eqn (30), while (c) and (d) represent 〈![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) θ〉s,θ defined in eqn (31). Here, 〈 θ〉s,θ defined in eqn (31). Here, 〈![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) r〉s,θ and 〈 r〉s,θ and 〈![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) θ〉s,θ represent r- and θ-components of the average orientation vector, respectively. (e) and (f) show 〈Wrr〉s,θ defined in eqn (32), while (g) and (h) represent 〈Wrθ〉s,θ defined in eqn (33). Here, 〈Wrr〉s,θ and 〈Wrθ〉s,θ represent rr- and rθ-components of the average nematic order parameter, respectively. These quantities are averaged values per swimmer within the range R < r < R + θ〉s,θ represent r- and θ-components of the average orientation vector, respectively. (e) and (f) show 〈Wrr〉s,θ defined in eqn (32), while (g) and (h) represent 〈Wrθ〉s,θ defined in eqn (33). Here, 〈Wrr〉s,θ and 〈Wrθ〉s,θ represent rr- and rθ-components of the average nematic order parameter, respectively. These quantities are averaged values per swimmer within the range R < r < R + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 at the polar angle θ. They are evaluated under conditions where R = 20 and ϕ = 0.032, with HIs, for Fex = 10 and 100. 0 at the polar angle θ. They are evaluated under conditions where R = 20 and ϕ = 0.032, with HIs, for Fex = 10 and 100. | |
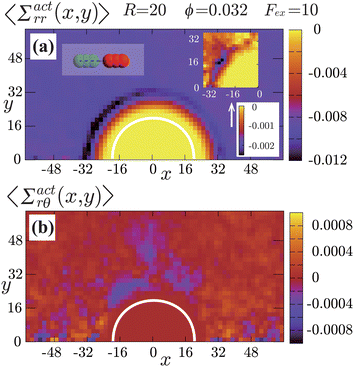 |
| | Fig. 7 Contour plots of the rr- and rθ-components of the active stresses, denoted as 〈Σactrr(x,y)〉 (a) and 〈Σactrθ(x,y)〉 (b), respectively, for Fex = 10 and ϕ = 0.032. The white semi-circular curves represent the boundary of the probe sphere. In (a), the swimmer is shown at the same scale as the probe to compare these sizes directly. In (a), the inset shows 〈Σactrr(x,y) − Σactrr(−x,y)〉, indicating apparent front-rear asymmetry in 〈Σactrr(x,y)〉. This asymmetry means that the swimmers exert more force from the rear. It is noteworthy to mention the following. If we make the active stress tensor 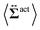 traceless, as is often done in the literature, 〈Σactrr〉 approaches zero with increasing distance from the probe. However, in our definition of the active stress eqn (34), we leave traceless, as is often done in the literature, 〈Σactrr〉 approaches zero with increasing distance from the probe. However, in our definition of the active stress eqn (34), we leave 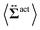 as as 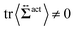 , resulting in a finite, though nearly constant 〈Σactrr〉 at distances away from the probe. In (b), 〈Σactrθ(x,y)〉 shows more significant fluctuations than 〈Σactrr(x,y)〉. , resulting in a finite, though nearly constant 〈Σactrr〉 at distances away from the probe. In (b), 〈Σactrθ(x,y)〉 shows more significant fluctuations than 〈Σactrr(x,y)〉. | |
Hydrodynamic interactions (HIs) cause swimmers to be repelled more significantly when approaching from the front than from the rear. When approaching from the front, HIs between the swimmer and probe tend to push them away from each other. On the other hand, when approaching from the rear, such a tendency is diminished, and for sufficiently large Fex, the swimmer can be pulled towards the probe depending on factors such as their relative velocity and angle of approach. In this situation, swimmers suffer from significant scatterings at the front side, while scatterings are comparatively weaker at the rear. This difference in scattering causes to the observed asymmetry between the front and rear in both the orientation and the nematic orders of the swimmers. Additional supporting simulations for this observation are provided in the ESI.†
3.3 Driving force exerted on the probe particle by swimmers
The observed local swimmers’ behavior significantly affects the probe motions. To illustrate this, we display the contour plots of the rr- and rθ-components of the active stresses, denoted as Σactrr(x,y) and Σactrθ(x,y), respectively, for Fex = 10 and ϕ = 0.032 in Fig. 7.
We here derive an expression for the local active stress tensor defined in a small subsystem denoted as K, with a volume VK and a representative position of (x,y,z). Referring to a similar procedure given in the previous studies,22,48 the active stress can be derived as
| | 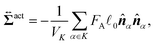 | (34) |
where
α ∈
K indicates that the position
Rα is within the region
K. Essentially, identical expressions of the local active stress were previously derived (see the ref.
61 and
62, for example). More detailed derivation of
eqn (34) is presented in the ESI.
†
By using the conversion formula to transform the tensor from Cartesian to polar coordinates, we obtain the following expressions
| | 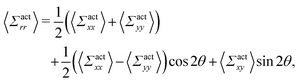 | (35) |
| | 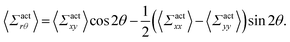 | (36) |
Here, we assume axial symmetry about the x-axis of the local swimmers' properties in steady states. In our calculations, we evaluate the active stress in a small region with a linear dimension of a, which is not large enough to define an instantaneous stress tensor. However, this does not pose any practical problem when investigating the average properties of the active stress in steady states.
The rr-component 〈Σactrr(x,y)〉 reflects the degree of the extent to which the swimmers face the probe sphere, either from the tail or the head. As shown in Fig. 7(a), around the probe, the magnitude of 〈Σactrr(x,y)〉 is slightly less pronounced at the front side than at the rear, reflecting the front-rear asymmetry in P(![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ; x, y). This behavior intuitively suggests that the swimmers exert more force on the probe from the rear than from the front, which is more clearly seen in the inset plotting 〈Σactrr(x,y) − Σactrr(−x,y)〉. On the other hand, as shown in Fig. 7(b), 〈Σactrθ(x,y)〉 exhibits a notable negative value around the regions indicated as (c)–(e) for x < 0 in Fig. 5. Note, however, that despite averaging over a period in which the probe particle moves several hundred times more than R, 〈Σactrθ(x,y)〉 still exhibits significant fluctuations.
; x, y). This behavior intuitively suggests that the swimmers exert more force on the probe from the rear than from the front, which is more clearly seen in the inset plotting 〈Σactrr(x,y) − Σactrr(−x,y)〉. On the other hand, as shown in Fig. 7(b), 〈Σactrθ(x,y)〉 exhibits a notable negative value around the regions indicated as (c)–(e) for x < 0 in Fig. 5. Note, however, that despite averaging over a period in which the probe particle moves several hundred times more than R, 〈Σactrθ(x,y)〉 still exhibits significant fluctuations.
Then, we phenomenologically argue the contribution from the active stress to the reduction of the probe friction as follows. Integrating the net stress tensor over an arbitrary closed surface encapsulating the region including the probe particle, denoted as Sp, gives the friction force acting on that region, which is equal to −Fex![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) balancing with the external force Fex
balancing with the external force Fex![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) :
:
| | 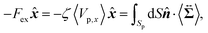 | (37) |
where
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif)
represents the unit vector that is normal to and pointing outward from the enclosing surface
Sp, and d
S denotes the surface area differential on
Sp. The net stress
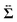
comes from two different sources; one is the stress acting through the solvent,
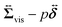
, and the other is the active stress
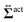
. First, let us adopt
Sp to the probe surface. In this case,
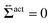
on
Sp because the swimmers do not exist due to steric repulsions. Therefore, the solvent solely accounts for the stress exerted on
Sp. As shown in
Fig. 2, the average probe speed 〈
Vp,x〉 =
Fex/
ζ can be increased compared with the case when moving in a pure solvent. This results in a smaller friction coefficient
ζ than
ζ0, meaning that the average velocity gradient at the probe surface is decreased to the same extent as the increase in 〈
Vp,x〉. We then ask: what causes such an increase in 〈
Vp,x〉? To further argue this question, we adopt
Sp to the surface slightly exterior to the probe surface, wrapping the peak of 〈
ρ(
x,
y)〉. In this case, the contribution from the active stress is estimated as
| | 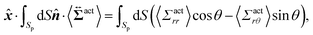 | (38) |
where cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ =
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif)
·
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif)
and we assume axial symmetry around the
x-axis and that the non-zero contribution from the active stress remains along the
x-axis after taking the time average in a steady state.
Eqn (38) represents the force exerted by the swimmers on the region surrounded by
Sp and, hereafter, is referred to as
Fact. As shown in
Fig. 7, the magnitude of 〈
Σactrθ(
x,
y)〉 is approximately 0.1 of 〈
Σactrr(
x,
y)〉 on
Sp, and
Fact mostly depends on 〈
Σactrr(
x,
y)〉. Noticing that 〈
Σactrr(
x,
y)〉 − 〈
Σactrr(−
x,
y)〉 ∼ −10
−3 for
x < 0 on
Sp, as indicated in the inset of
Fig. 7(a), and the area of
Sp is approximately 10
4,
Fact can be comparable with
Fex. This
Fact is positive and thus can be considered a negative friction force, effectively acting as a driving force. On the other hand, the force from the solvent viscous stress acting on the same surface may be approximated as −
ζ0〈
Vp,x〉, whose magnitude surpasses
Fex(=
ζ〈
Vp,x〉). The smaller friction coefficient
ζ than
ζ0 indicates that the average flow velocity becomes larger than those observed when moving in a pure solvent environment. Essentially, velocity gradients are larger in the regions slightly outside the probe, while those are smaller in the thin region directly adjacent to the probe surface. The active stress serves to connect these varying behaviors across the different regions. With these two contributions of the active and solvent stresses, we may approximately express the force balance in a steady state as: −
Fex = −
ζ〈
Vp,x〉 ∼ −
ζ0〈
Vp,x〉 +
Fact, which is further rewritten as: (
ζ0 −
ζ) ∼
Fact/〈
Vp,x〉.
The above argument explains the notable reduction in ζ for smaller Fex. However, as Fex increases, while the front-rear asymmetry in the active stress is enhanced, Fact may not linearly increase in Fex, resulting in less noticeable contributions to the reduction in ζ for larger Fex.
4 Concluding remarks
Let us evaluate the applicability of our results to realistic situations by considering a typical experimental setup of dilute E. coli suspensions with a volume fraction similar to our simulations (∼0.01). Here, we assume that the swimming speed of E. coli is vs ∼ 10 μm s−1, the magnitude of the active force is FA ∼ 1 pN, and the cell size is ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 ∼ 1 μm. In a typical condition of magnetic-bead microrheology, the force exerted on the probe is in the pN range, and magnetic colloidal particles have diameters ranging from 1 to 10 μm (= 2R). In our simulation conditions, where the drag reduction is observed, the force ratio is Fex/FA ≲ 3 and the size ratio is 2R/
0 ∼ 1 μm. In a typical condition of magnetic-bead microrheology, the force exerted on the probe is in the pN range, and magnetic colloidal particles have diameters ranging from 1 to 10 μm (= 2R). In our simulation conditions, where the drag reduction is observed, the force ratio is Fex/FA ≲ 3 and the size ratio is 2R/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 ∼ 3, and these can be met in real experiments.26 Therefore, we can expect that a substantial drag reduction occurs, if similar density and orientational distributions to those obtained in our simulations are realized in practical experiments.
0 ∼ 3, and these can be met in real experiments.26 Therefore, we can expect that a substantial drag reduction occurs, if similar density and orientational distributions to those obtained in our simulations are realized in practical experiments.
In summary, using a pusher-type swimmer model, the present study investigated the microrheology of active suspensions through direct hydrodynamic simulations. We revealed that, with HIs, the friction coefficient of the probe particle can be significantly smaller than when immersed in a pure solvent for relatively small drag forces. The local swimmer states near the probe boundary predominantly influence the observed drag reduction. That is, in active suspensions, microrheology measurements are strongly influenced by local probing details and thus can be qualitatively different from macrorheology measurements. Hydrodynamic interactions induce the front-rear asymmetry in the swimmer orientation distributions. This asymmetry further causes a force/stress imbalance, resulting in an additional driving force acting on the probe particle through solvent-mediated interactions (HIs). However, without HIs, the local states of swimmers outside the (short) range of the direct interaction potential do not contribute to the friction force. Our simulation studies illuminate the fundamental importance of HIs in active suspensions and suggest potential microfluidics applications. These issues will be further explored in subsequent studies.
Author contributions
Takahiro Kanazawa: investigation, formal analysis, visualization, writing – review and editing. Akira Furukawa: conceptualisation, methodology, software, supervision, funding acquisition, investigation, formal analysis, visualization, project administration, writing – original draft preparation, review, and editing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by KAKENHI (Grants No. 20H05619) from the Japan Society for the Promotion of Science (JSPS). We are also grateful for UROP (Undergraduate Research Opportunity Program) of the Institute of Industrial Science, the University of Tokyo.
Notes and references
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef
 .
.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS
 .
.
- C. Bechinger, R. Di Leonardo, H. Loẅen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef
 .
.
- Y. Hatwalne, S. Ramaswamy, M. Rao and R. A. Simha, Phys. Rev. Lett., 2004, 92, 118101 CrossRef PubMed
 .
.
- A. Sokolov and I. S. Aranson, Phys. Rev. Lett., 2009, 103, 148101 CrossRef PubMed
 .
.
- J. Gachelin, G. Miño, H. Berthet, A. Lindner, A. Rousselet and E. Clément, Phys. Rev. Lett., 2013, 110, 268103 CrossRef PubMed
 .
.
- H. M. López, J. Gachelin, C. Douarche, H. Auradou and E. Clément, Phys. Rev. Lett., 2015, 115, 028301 CrossRef
 .
.
- A. Liu, K. Zhang and X. Cheng, Rheol. Acta, 2019, 58, 439–451 CrossRef
 .
.
- V. A. Martinez, E. Clément, J. Arlt, C. Douarche, A. Dawson, J. Schwarz-Linek, A. K. Creppy, V. Škultéty, A. N. Morozov, H. Auradou and W. C. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 2326–2331 CrossRef CAS PubMed
 .
.
- S. Rafaï, L. Jibuti and P. Peyla, Phys. Rev. Lett., 2010, 104, 098102 CrossRef PubMed
 .
.
- D. Saintillan, Exp. Mech., 2010, 50, 1275–1281 CrossRef
 .
.
- M. C. Marchetti, Nature, 2015, 525, 37–39 CrossRef CAS PubMed
 .
.
- D. Saintillan, Annu. Rev. Fluid Mech., 2018, 50, 563–592 CrossRef
 .
.
- T. Ishikawa and T. J. Pedray, J. Fluid Mech., 2007, 588, 399–435 CrossRef
 .
.
- M. E. Cates, S. M. Fielding, D. Marenduzzo, E. Orlandini and J. M. Yeomans, Phys. Rev. Lett., 2008, 101, 068102 CrossRef CAS PubMed
 .
.
- B. M. Haines, A. Sokolov, I. S. Aranson, L. Berlyand and D. A. Karpeev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 041922 CrossRef PubMed
 .
.
- L. Giomi, T. B. Liverpool and M. C. Marchetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 051908 CrossRef PubMed
 .
.
- S. D. Ryan, B. M. Haines, L. Berlyand, F. Ziebert and I. S. Aranson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 050904(R) CrossRef PubMed
 .
.
- M. Moradi and A. Najafi, EPL, 2015, 109, 24001 CrossRef
 .
.
- T. M. Bechtel and A. S. Khair, Rheol. Acta, 2017, 56, 149–160 CrossRef CAS
 .
.
- S. C. Takatori and J. F. Brady, Phys. Rev. Lett., 2017, 118, 018003 CrossRef CAS PubMed
 .
.
- H. Hayano and A. Furukawa, Phys. Rev. Res., 2022, 4, 043091 CrossRef CAS
 .
.
- A. G. Bayram, F. Jan Schwarzendahl, H. Loẅen and L. Biancofiore, Soft Matter, 2023, 19, 4571–4578 RSC
 .
.
-
L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Pergamon Press, New York, 1959 Search PubMed
 .
.
- T. M. Squires and T. G. Mason, Annu. Rev. Fluid Mech., 2010, 42, 413–438 CrossRef
 .
.
-
E. M. Furst and T. M. Squires, Magnetic bead microrheology, Microrheology, Oxford University Press, New York, 2017, ch. 8 Search PubMed
 .
.
- R. N. Zia, Annu. Rev. Fluid Mech., 2018, 50, 371–405 CrossRef
 .
.
- X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017–3020 CrossRef CAS
 .
.
- D. T. N. Chen, A. W. Lau, L. A. Hough, M. F. Islam, M. Goulian, T. C. Lubensky and A. G. Yodh, Phys. Rev. Lett., 2007, 99, 148302 CrossRef CAS PubMed
 .
.
- K. C. Leptos, J. S. Guasto, J. P. Gollub, A. I. Pesci and R. E. Goldstein, Phys. Rev. Lett., 2009, 103, 198103 CrossRef PubMed
 .
.
- J. J. Molina, Y. Nakayama and R. Yamamoto, Soft Matter, 2013, 9, 4923–4936 RSC
 .
.
- G. Foffano, J. S. Lintuvuori, A. N. Morozov, K. Stratford, M. E. Cates and D. Marenduzzo, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 98 CAS
 .
.
- G. Foffano, J. S. Lintuvuori, K. Stratford, M. E. Cates and D. Marenduzzo, Phys. Rev. Lett., 2012, 109, 028103 CAS
 .
.
- E. W. Burkholder and J. F. Brady, J. Chem. Phys., 2019, 150, 184901 CrossRef PubMed
 .
.
- E. W. Burkholder and J. F. Brady, Soft Matter, 2020, 16, 1034–1046 CAS
 .
.
- Z. Peng and J. F. Brady, J. Rheol., 2002, 66, 955–972 CrossRef
 .
.
- M. Knežević and H. Stark, New J. Phys., 2020, 22, 113025 CrossRef
 .
.
- M. Knežević, L. E. A. Podgurski and H. Stark, Sci. Rep., 2021, 11, 22706 CrossRef PubMed
 .
.
- A. Loisy, J. Eggers and T. B. Liverpool, Phys. Rev. Lett., 2018, 121, 018001 CrossRef CAS PubMed
 .
.
- C. Reichhardt and C. J. O. Reichhardt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 032313 CrossRef CAS
 .
.
- J. P. Hernandez-Ortiz, C. G. Stoltz and M. D. Graham, Phys. Rev. Lett., 2005, 95, 204501 CrossRef PubMed
 .
.
- P. T. Underhill, J. P. Hernandez-Ortiz and M. D. Graham, Phys. Rev. Lett., 2008, 100, 248101 CrossRef PubMed
 .
.
- D. Saintillan and M. Shelley, Phys. Rev. Lett., 2007, 99, 058102 CrossRef PubMed
 .
.
- V. Gyrya, I. S. Aranson, L. V. Berlyand and D. Karpeev, Bull. Math. Biol., 2010, 72, 148–183 CrossRef PubMed
 .
.
- A. Decoene, S. Martin and B. Maury, Math. Modell. Nat. Phenom., 2011, 6, 98–129 CrossRef
 .
.
- A. Furukawa, D. Marenduzzo and M. E. Cates, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022303 CrossRef PubMed
 .
.
- Y. Nakayama and R. Yamamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 036707 CrossRef PubMed
 .
.
- J. J. Molina, K. Otomura, H. Shiba, H. Kobayashi, M. Sano and R. Yamamoto, J. Fluid Mech., 2016, 792, 590–619 CrossRef CAS
 .
.
- R. Yamamoto, J. J. Molina and Y. Nakayama, Soft Matter, 2021, 17, 4226–4253 RSC
 .
.
- A. J. C. Ladd, Phys. Rev. Lett., 1993, 70, 1339–1342 CrossRef CAS
 .
.
- M. E. Cates, K. Stratford, R. Adhikari, P. Stainsell, J.-C. Desplat, I. Pagonabarraga and A. J. Wagner, J. Phys.: Condens. Matter, 2004, 16, S3903 CrossRef CAS
 .
.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338–1341 CrossRef CAS PubMed
 .
.
- A. Furukawa, M. Tateno and H. Tanaka, Soft Matter, 2018, 14, 3738–3747 RSC
 .
.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef
 .
.
- S. Ji, R. Jiang, R. G. Winkler and G. Gompper, J. Chem. Phys., 2011, 135, 134116 CrossRef PubMed
 .
.
- We speculate on the origin of significant non-monotonic behavior in ζ for the case without HIs, which is shown in Fig. 2(a). For small enough Fex, the probe particle experiences collisions with the swimmers almost equally from both the front and the rear sides. However, as Fex increases, the swimmers colliding from the front side are scattered more significantly than those from the rear. That is, more swimmers face the probe at the rear than at the front. Consequently, the force exerted from the front becomes gradually weaker as Fex increases, which may cause the first thinning behavior exhibited in Fig. 2(a). Then, as Fex increases more, very few swimmers catch up with the probe from the rear, making the impact of the swimmer colliding from the front more dominant. Notably, the average velocities of the probe and the swimmer are comparable at around the peak of ζ. As a result, the resistance increases with increasing Fex, resulting in the force-thickening observed at intermediate values of Fex. As Fex is further increased, the active force becomes negligibly small compared to Fex, leading to a decrease in ζ, which is observed as the second thinning. Even with HIs, a slight non-monotonicity in ζ is also found at smaller Fex, to which a similar explanation may be applicable. A detailed investigation of these behaviors will be presented elsewhere.
- A. S. Khair and J. F. Brady, J. Fluid Mech., 2006, 557, 73–117 CrossRef
 .
.
- J. W. Swan and R. N. Zia, Phys. Fluids, 2013, 25, 083303 CrossRef
 .
.
- G. Li and J. X. Tang, Phys. Rev. Lett., 2009, 103, 078101 CrossRef
 .
.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef
 .
.
- R. A. Simha and S. Ramaswarmy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef PubMed
 .
.
- D. Saintillan and M. Shelley, Phys. Fluids, 2008, 20, 123304 CrossRef
 .
.
Footnote |
| † Electronic supplementary information (ESI) available: Explicit time-integration algorithm in the present simulations and supplementary simulation results. See DOI: https://doi.org/10.1039/d4sm00408f |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *b
*b
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α acting on the (front) body is exerted by the (rear) flagellum and that the flagellum also exerts the force −FA
α acting on the (front) body is exerted by the (rear) flagellum and that the flagellum also exerts the force −FA![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α directly on the solvent fluid. Here,
α directly on the solvent fluid. Here, ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α is the direction of the α-th swimmer, and these forces compose a dipolar force of magnitude FA
α is the direction of the α-th swimmer, and these forces compose a dipolar force of magnitude FA![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, with
0, with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 being the characteristic swimmer's length [see Fig. 1(a)]. Such a force-prescribed particle model emulates rod-like pusher-type microorganisms such as E. coli, as initially proposed in the ref. 41 and 42 and employed in subsequent studies.16,18,22,43–46
0 being the characteristic swimmer's length [see Fig. 1(a)]. Such a force-prescribed particle model emulates rod-like pusher-type microorganisms such as E. coli, as initially proposed in the ref. 41 and 42 and employed in subsequent studies.16,18,22,43–46
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α (i = 1, 2, 3), where R(G)α is the α-th swimmer's center-of-mass position. Similarly, the spheres composing the flagellum part are located at R(f)i,α = R(CF)α + (2 − i)a
α (i = 1, 2, 3), where R(G)α is the α-th swimmer's center-of-mass position. Similarly, the spheres composing the flagellum part are located at R(f)i,α = R(CF)α + (2 − i)a![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α (i = 1, 2, 3), where R(CF)α = R(G)α − 4.5a
α (i = 1, 2, 3), where R(CF)α = R(G)α − 4.5a![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α = R(G)α −
α = R(G)α − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0
0![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α is the position of the center of the flagellum. The shape of the present model swimmer shows the head–tail symmetry, and the mid-point is thus given by Rα = (R(G)α + R(CF)α)/2. Although arbitrary shapes of swimmers with an imposed head-tail asymmetry can be composed, we can obtain qualitatively the same results as long as these swimmers have rod-like forms with the prescribed force dipoles.
α is the position of the center of the flagellum. The shape of the present model swimmer shows the head–tail symmetry, and the mid-point is thus given by Rα = (R(G)α + R(CF)α)/2. Although arbitrary shapes of swimmers with an imposed head-tail asymmetry can be composed, we can obtain qualitatively the same results as long as these swimmers have rod-like forms with the prescribed force dipoles.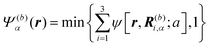
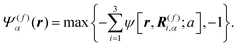
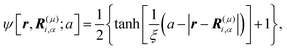
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v(r,t) are given as
v(r,t) are given as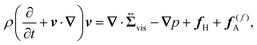
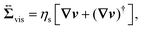
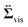 , given as eqn (6), is the viscous stress tensor with ηs being the solvent viscosity, and the hydrostatic pressure p is determined by the incompressibility condition, eqn (7). In addition, fH is the body force required to satisfy the rigid-body condition for the swimmer's body and probe particle regions, and f(f)A is the active force directly exerted by the flagellum part to the fluid:
, given as eqn (6), is the viscous stress tensor with ηs being the solvent viscosity, and the hydrostatic pressure p is determined by the incompressibility condition, eqn (7). In addition, fH is the body force required to satisfy the rigid-body condition for the swimmer's body and probe particle regions, and f(f)A is the active force directly exerted by the flagellum part to the fluid: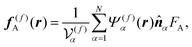
 is the volume of the flagellum part. In addition, the volume of the body part is given as
is the volume of the flagellum part. In addition, the volume of the body part is given as 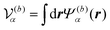 . In this study, because the shapes of the body and flagellum parts are assumed to be the same,
. In this study, because the shapes of the body and flagellum parts are assumed to be the same, 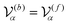 .
.
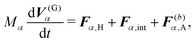
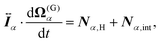
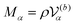
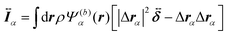
 is the unit tensor and Δrα = r − R(G)α. In this study, the swimmer's density is assumed to be the same as the solvent density. In eqn (9) and (10), Fα,H and Nα,H are the force and torque exerted on the α-th swimmer due to HIs, respectively. The explicit forms of Fα,H, Nα,H, and the body force fH are given in the ESI.†Fα,int and Nα,int are the force and torque acting on the α-th swimmer's body, respectively, due to the particle–particle and particle–probe potential interactions:
is the unit tensor and Δrα = r − R(G)α. In this study, the swimmer's density is assumed to be the same as the solvent density. In eqn (9) and (10), Fα,H and Nα,H are the force and torque exerted on the α-th swimmer due to HIs, respectively. The explicit forms of Fα,H, Nα,H, and the body force fH are given in the ESI.†Fα,int and Nα,int are the force and torque acting on the α-th swimmer's body, respectively, due to the particle–particle and particle–probe potential interactions: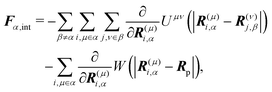
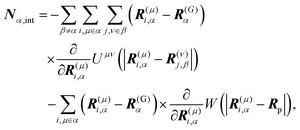
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α.
α.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0
0![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α with
α with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0
0![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) α = R(G)α − R(CF)α [see also eqn (34)].
α = R(G)α − R(CF)α [see also eqn (34)].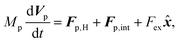
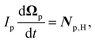
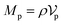
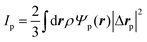
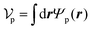 is the volume of the probe particle, and the probe particle density is also assumed to be the same as the solvent density. In eqn (16), Fp,int is the force due to the interaction with swimmers:
is the volume of the probe particle, and the probe particle density is also assumed to be the same as the solvent density. In eqn (16), Fp,int is the force due to the interaction with swimmers: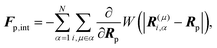
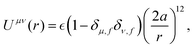
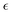 is a positive energy constant, δμ,f is the Kronecker delta, and μ, ν = b, f. This form prevents the body part of a swimmer from overlapping on different swimmers but allows overlaps among the flagellum parts. The interaction potential W between the probe particle and the particles constituting a swimmer is introduced to prevent the penetration of swimmers through the probe boundary. In this study, W is assumed to be given as
is a positive energy constant, δμ,f is the Kronecker delta, and μ, ν = b, f. This form prevents the body part of a swimmer from overlapping on different swimmers but allows overlaps among the flagellum parts. The interaction potential W between the probe particle and the particles constituting a swimmer is introduced to prevent the penetration of swimmers through the probe boundary. In this study, W is assumed to be given as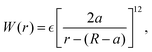
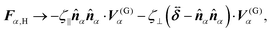
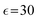 and FA = 20. The parameters determining the swimmer's shape are set to be a = 3.2,
and FA = 20. The parameters determining the swimmer's shape are set to be a = 3.2, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = |R(G)α − R(CF)α| = 4.5a and ξ = 0.5. In this study, the swimmer volume fraction is identified as that of the rigid body particles given by
0 = |R(G)α − R(CF)α| = 4.5a and ξ = 0.5. In this study, the swimmer volume fraction is identified as that of the rigid body particles given by 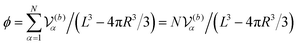 .
.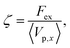

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0), as shown in Fig. 4(a), (b), (e), and (f), 〈ρ(x,y)〉 near the probe boundary is considerably larger than in the bulk region, irrespective of the presence of HIs. As indicated in the literature, both the steric59 and hydrodynamic60 effects cause the entrapment of microswimmers on the boundaries. A self-propulsive rod-like particle, upon colliding with the probe, cannot rebound immediately due to the steric/geometric constraints. Instead, it stays near the probe for a while, swimming along the surface. This behavior may result in a larger density near the probe surface. Note that HIs between the probe and the swimmers enhance the entrapment,60 but they are not significantly dominant in the present condition. At R = 5(≲
0), as shown in Fig. 4(a), (b), (e), and (f), 〈ρ(x,y)〉 near the probe boundary is considerably larger than in the bulk region, irrespective of the presence of HIs. As indicated in the literature, both the steric59 and hydrodynamic60 effects cause the entrapment of microswimmers on the boundaries. A self-propulsive rod-like particle, upon colliding with the probe, cannot rebound immediately due to the steric/geometric constraints. Instead, it stays near the probe for a while, swimming along the surface. This behavior may result in a larger density near the probe surface. Note that HIs between the probe and the swimmers enhance the entrapment,60 but they are not significantly dominant in the present condition. At R = 5(≲ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0), as shown in Fig. 4(c) and (d), the peak of 〈ρ(x,y)〉 near the boundary decreases, both with and without HIs, suggesting a weaker entrapment effect for smaller R. Also, as shown in Fig. 4(g) and (h), without HIs, the increase in 〈ρ(x,y)〉 is slightly more pronounced on the front than the rear, but such a behavior diminishes with HIs.
0), as shown in Fig. 4(c) and (d), the peak of 〈ρ(x,y)〉 near the boundary decreases, both with and without HIs, suggesting a weaker entrapment effect for smaller R. Also, as shown in Fig. 4(g) and (h), without HIs, the increase in 〈ρ(x,y)〉 is slightly more pronounced on the front than the rear, but such a behavior diminishes with HIs.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 and scaled by ρ0:
0 and scaled by ρ0: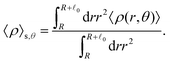
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and y = r
θ and y = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. As demonstrated, in the presence of HIs, the density at the rear is larger than at the front, whereas in their absence, the reverse is observed. This tendency becomes more pronounced with increasing Fex.
θ. As demonstrated, in the presence of HIs, the density at the rear is larger than at the front, whereas in their absence, the reverse is observed. This tendency becomes more pronounced with increasing Fex.
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ; x, y) around the probe particle. It is defined as
; x, y) around the probe particle. It is defined as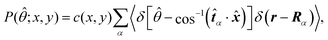
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) is the unit vector along the x-axis and
is the unit vector along the x-axis and ![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) α =
α = ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ‖α/|
‖α/|![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ‖α| with
‖α| with ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ‖α denoting the projected swimming direction onto the x–y plane. The normalization factor c(x, y) specific to the present visualization in Fig. 5 is determined so that
‖α denoting the projected swimming direction onto the x–y plane. The normalization factor c(x, y) specific to the present visualization in Fig. 5 is determined so that 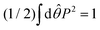 . The main text presents the results for two cases at Fex = 10 and 100 with HIs. For cases without HIs, please refer to the ESI.† In Fig. 5, the panels (a)–(e) show P(
. The main text presents the results for two cases at Fex = 10 and 100 with HIs. For cases without HIs, please refer to the ESI.† In Fig. 5, the panels (a)–(e) show P(![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ; x, y) near the probe boundary. The tilt angle of the swimmers (measured with respect to the tangential direction of the probe surface) is larger when they face the probe than when they face the bulk, but this distinction is subtle in (c) and (d) for Fex = 10. Additionally, more swimmers face the probe for x < 0 than x > 0. These characteristics are more evident at Fex = 100 than at Fex = 10.
; x, y) near the probe boundary. The tilt angle of the swimmers (measured with respect to the tangential direction of the probe surface) is larger when they face the probe than when they face the bulk, but this distinction is subtle in (c) and (d) for Fex = 10. Additionally, more swimmers face the probe for x < 0 than x > 0. These characteristics are more evident at Fex = 100 than at Fex = 10.
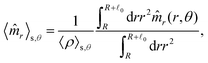
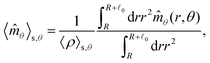
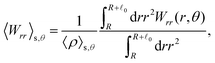

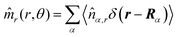 ,
, 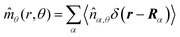 ,
, 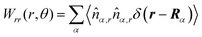 , and
, and 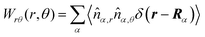 , where r = (x, y, 0) with x = r
, where r = (x, y, 0) with x = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and y = r
θ and y = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Here,
θ. Here, ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) α,r and
α,r and ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) α,θ are r- and θ-components of the (unit vector) direction of the α-th swimmer, respectively. Eqn (30) and (31) represent r- and θ-components of the average orientation vector of the swimmers, respectively. On the other hand, eqn (32) and (33) represent rr- and rθ-components of the average nematic order parameter, respectively. These quantities are averaged values per swimmer within the range R < r < R +
α,θ are r- and θ-components of the (unit vector) direction of the α-th swimmer, respectively. Eqn (30) and (31) represent r- and θ-components of the average orientation vector of the swimmers, respectively. On the other hand, eqn (32) and (33) represent rr- and rθ-components of the average nematic order parameter, respectively. These quantities are averaged values per swimmer within the range R < r < R + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 at the polar angle θ. They are evaluated under conditions where R = 20 and ϕ = 0.032, with HIs, for Fex = 10 and 100. Fig. 6(a) and (b) demonstrate that the swimmers face the probe more likely than facing the bulk, and such a tendency is more enhanced at Fex = 100 than Fex = 10. As shown in Fig. 6(c) and (d), at Fex = 100, more swimmers move along the probe surface from the rear- to the front-sides, while at Fex = 10, such a tendency is not obvious. Furthermore, we can find that the rr-component of the nematic order is more enhanced in the rear than in the front, and this tendency is more enhanced at Fex = 100 than at Fex = 10. Such a front-rear asymmetry in 〈Wrθ〉s,θ is weaker than that in 〈Wrr〉s,θ. This difference is essential in the observed front-rear asymmetry in the active stress, as shown in Fig. 7.
0 at the polar angle θ. They are evaluated under conditions where R = 20 and ϕ = 0.032, with HIs, for Fex = 10 and 100. Fig. 6(a) and (b) demonstrate that the swimmers face the probe more likely than facing the bulk, and such a tendency is more enhanced at Fex = 100 than Fex = 10. As shown in Fig. 6(c) and (d), at Fex = 100, more swimmers move along the probe surface from the rear- to the front-sides, while at Fex = 10, such a tendency is not obvious. Furthermore, we can find that the rr-component of the nematic order is more enhanced in the rear than in the front, and this tendency is more enhanced at Fex = 100 than at Fex = 10. Such a front-rear asymmetry in 〈Wrθ〉s,θ is weaker than that in 〈Wrr〉s,θ. This difference is essential in the observed front-rear asymmetry in the active stress, as shown in Fig. 7.

![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) r〉s,θ defined in eqn (30), while (c) and (d) represent 〈
r〉s,θ defined in eqn (30), while (c) and (d) represent 〈![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) θ〉s,θ defined in eqn (31). Here, 〈
θ〉s,θ defined in eqn (31). Here, 〈![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) r〉s,θ and 〈
r〉s,θ and 〈![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) θ〉s,θ represent r- and θ-components of the average orientation vector, respectively. (e) and (f) show 〈Wrr〉s,θ defined in eqn (32), while (g) and (h) represent 〈Wrθ〉s,θ defined in eqn (33). Here, 〈Wrr〉s,θ and 〈Wrθ〉s,θ represent rr- and rθ-components of the average nematic order parameter, respectively. These quantities are averaged values per swimmer within the range R < r < R +
θ〉s,θ represent r- and θ-components of the average orientation vector, respectively. (e) and (f) show 〈Wrr〉s,θ defined in eqn (32), while (g) and (h) represent 〈Wrθ〉s,θ defined in eqn (33). Here, 〈Wrr〉s,θ and 〈Wrθ〉s,θ represent rr- and rθ-components of the average nematic order parameter, respectively. These quantities are averaged values per swimmer within the range R < r < R + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 at the polar angle θ. They are evaluated under conditions where R = 20 and ϕ = 0.032, with HIs, for Fex = 10 and 100.
0 at the polar angle θ. They are evaluated under conditions where R = 20 and ϕ = 0.032, with HIs, for Fex = 10 and 100.
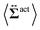 traceless, as is often done in the literature, 〈Σactrr〉 approaches zero with increasing distance from the probe. However, in our definition of the active stress eqn (34), we leave
traceless, as is often done in the literature, 〈Σactrr〉 approaches zero with increasing distance from the probe. However, in our definition of the active stress eqn (34), we leave 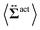 as
as 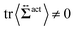 , resulting in a finite, though nearly constant 〈Σactrr〉 at distances away from the probe. In (b), 〈Σactrθ(x,y)〉 shows more significant fluctuations than 〈Σactrr(x,y)〉.
, resulting in a finite, though nearly constant 〈Σactrr〉 at distances away from the probe. In (b), 〈Σactrθ(x,y)〉 shows more significant fluctuations than 〈Σactrr(x,y)〉.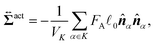
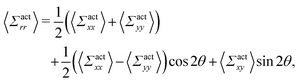
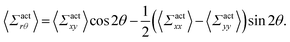
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ; x, y). This behavior intuitively suggests that the swimmers exert more force on the probe from the rear than from the front, which is more clearly seen in the inset plotting 〈Σactrr(x,y) − Σactrr(−x,y)〉. On the other hand, as shown in Fig. 7(b), 〈Σactrθ(x,y)〉 exhibits a notable negative value around the regions indicated as (c)–(e) for x < 0 in Fig. 5. Note, however, that despite averaging over a period in which the probe particle moves several hundred times more than R, 〈Σactrθ(x,y)〉 still exhibits significant fluctuations.
; x, y). This behavior intuitively suggests that the swimmers exert more force on the probe from the rear than from the front, which is more clearly seen in the inset plotting 〈Σactrr(x,y) − Σactrr(−x,y)〉. On the other hand, as shown in Fig. 7(b), 〈Σactrθ(x,y)〉 exhibits a notable negative value around the regions indicated as (c)–(e) for x < 0 in Fig. 5. Note, however, that despite averaging over a period in which the probe particle moves several hundred times more than R, 〈Σactrθ(x,y)〉 still exhibits significant fluctuations.![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) balancing with the external force Fex
balancing with the external force Fex![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) :
: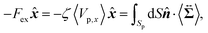
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) represents the unit vector that is normal to and pointing outward from the enclosing surface Sp, and dS denotes the surface area differential on Sp. The net stress
represents the unit vector that is normal to and pointing outward from the enclosing surface Sp, and dS denotes the surface area differential on Sp. The net stress  comes from two different sources; one is the stress acting through the solvent,
comes from two different sources; one is the stress acting through the solvent, 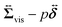 , and the other is the active stress
, and the other is the active stress 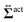 . First, let us adopt Sp to the probe surface. In this case,
. First, let us adopt Sp to the probe surface. In this case, 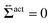 on Sp because the swimmers do not exist due to steric repulsions. Therefore, the solvent solely accounts for the stress exerted on Sp. As shown in Fig. 2, the average probe speed 〈Vp,x〉 = Fex/ζ can be increased compared with the case when moving in a pure solvent. This results in a smaller friction coefficient ζ than ζ0, meaning that the average velocity gradient at the probe surface is decreased to the same extent as the increase in 〈Vp,x〉. We then ask: what causes such an increase in 〈Vp,x〉? To further argue this question, we adopt Sp to the surface slightly exterior to the probe surface, wrapping the peak of 〈ρ(x,y)〉. In this case, the contribution from the active stress is estimated as
on Sp because the swimmers do not exist due to steric repulsions. Therefore, the solvent solely accounts for the stress exerted on Sp. As shown in Fig. 2, the average probe speed 〈Vp,x〉 = Fex/ζ can be increased compared with the case when moving in a pure solvent. This results in a smaller friction coefficient ζ than ζ0, meaning that the average velocity gradient at the probe surface is decreased to the same extent as the increase in 〈Vp,x〉. We then ask: what causes such an increase in 〈Vp,x〉? To further argue this question, we adopt Sp to the surface slightly exterior to the probe surface, wrapping the peak of 〈ρ(x,y)〉. In this case, the contribution from the active stress is estimated as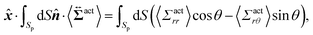
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ =
θ = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) ·
·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) and we assume axial symmetry around the x-axis and that the non-zero contribution from the active stress remains along the x-axis after taking the time average in a steady state. Eqn (38) represents the force exerted by the swimmers on the region surrounded by Sp and, hereafter, is referred to as Fact. As shown in Fig. 7, the magnitude of 〈Σactrθ(x,y)〉 is approximately 0.1 of 〈Σactrr(x,y)〉 on Sp, and Fact mostly depends on 〈Σactrr(x,y)〉. Noticing that 〈Σactrr(x,y)〉 − 〈Σactrr(−x,y)〉 ∼ −10−3 for x < 0 on Sp, as indicated in the inset of Fig. 7(a), and the area of Sp is approximately 104, Fact can be comparable with Fex. This Fact is positive and thus can be considered a negative friction force, effectively acting as a driving force. On the other hand, the force from the solvent viscous stress acting on the same surface may be approximated as −ζ0〈Vp,x〉, whose magnitude surpasses Fex(= ζ〈Vp,x〉). The smaller friction coefficient ζ than ζ0 indicates that the average flow velocity becomes larger than those observed when moving in a pure solvent environment. Essentially, velocity gradients are larger in the regions slightly outside the probe, while those are smaller in the thin region directly adjacent to the probe surface. The active stress serves to connect these varying behaviors across the different regions. With these two contributions of the active and solvent stresses, we may approximately express the force balance in a steady state as: −Fex = −ζ〈Vp,x〉 ∼ −ζ0〈Vp,x〉 + Fact, which is further rewritten as: (ζ0 − ζ) ∼ Fact/〈Vp,x〉.
and we assume axial symmetry around the x-axis and that the non-zero contribution from the active stress remains along the x-axis after taking the time average in a steady state. Eqn (38) represents the force exerted by the swimmers on the region surrounded by Sp and, hereafter, is referred to as Fact. As shown in Fig. 7, the magnitude of 〈Σactrθ(x,y)〉 is approximately 0.1 of 〈Σactrr(x,y)〉 on Sp, and Fact mostly depends on 〈Σactrr(x,y)〉. Noticing that 〈Σactrr(x,y)〉 − 〈Σactrr(−x,y)〉 ∼ −10−3 for x < 0 on Sp, as indicated in the inset of Fig. 7(a), and the area of Sp is approximately 104, Fact can be comparable with Fex. This Fact is positive and thus can be considered a negative friction force, effectively acting as a driving force. On the other hand, the force from the solvent viscous stress acting on the same surface may be approximated as −ζ0〈Vp,x〉, whose magnitude surpasses Fex(= ζ〈Vp,x〉). The smaller friction coefficient ζ than ζ0 indicates that the average flow velocity becomes larger than those observed when moving in a pure solvent environment. Essentially, velocity gradients are larger in the regions slightly outside the probe, while those are smaller in the thin region directly adjacent to the probe surface. The active stress serves to connect these varying behaviors across the different regions. With these two contributions of the active and solvent stresses, we may approximately express the force balance in a steady state as: −Fex = −ζ〈Vp,x〉 ∼ −ζ0〈Vp,x〉 + Fact, which is further rewritten as: (ζ0 − ζ) ∼ Fact/〈Vp,x〉.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 ∼ 1 μm. In a typical condition of magnetic-bead microrheology, the force exerted on the probe is in the pN range, and magnetic colloidal particles have diameters ranging from 1 to 10 μm (= 2R). In our simulation conditions, where the drag reduction is observed, the force ratio is Fex/FA ≲ 3 and the size ratio is 2R/
0 ∼ 1 μm. In a typical condition of magnetic-bead microrheology, the force exerted on the probe is in the pN range, and magnetic colloidal particles have diameters ranging from 1 to 10 μm (= 2R). In our simulation conditions, where the drag reduction is observed, the force ratio is Fex/FA ≲ 3 and the size ratio is 2R/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 ∼ 3, and these can be met in real experiments.26 Therefore, we can expect that a substantial drag reduction occurs, if similar density and orientational distributions to those obtained in our simulations are realized in practical experiments.
0 ∼ 3, and these can be met in real experiments.26 Therefore, we can expect that a substantial drag reduction occurs, if similar density and orientational distributions to those obtained in our simulations are realized in practical experiments.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.




