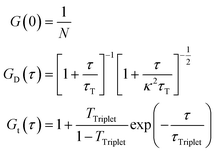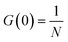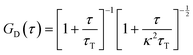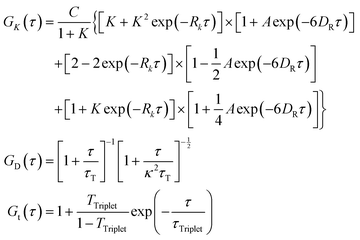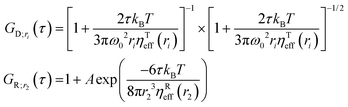DOI:
10.1039/D4SM00422A
(Paper)
Soft Matter, 2024,
20, 5810-5821
Rotational and translational diffusion of biomolecules in complex liquids and HeLa cells†
Received
11th April 2024
, Accepted 7th July 2024
First published on 11th July 2024
Abstract
Diffusive motion accompanies many physical and biological processes. The Stokes–Sutherland–Einstein relation for the translational diffusion coefficient, DT, agrees with experiments done in simple fluids but fails for complex fluids. Moreover, the interdependence between DT and rotational diffusion coefficient, DR, also deviates in complex fluids from the classical relation of DT/DR = 4r2/3 known in simple fluids. Makuch et al. Soft Matter, 2020, 16, 114–124 presented a generalization of the classical translational and rotational diffusion theory for complex fluids. In this work, we empirically verify this model based on simultaneous translational and rotational diffusion measurements. We use fluorescently stained cowpea chlorotic mottle virus (CCMV) particles as monodisperse probes and aqueous polyethylene glycol (PEG) solutions as a model complex fluid. The theory and experimental data obtained from fluorescence correlation spectroscopy (FCS) measurements agreed. Finally, we used the same model and analyzed the diffusion of Yo-Pro-1 stained large ribosomal subunits (LSU) in the cytoplasm and nucleus of living HeLa cells.
Introduction
Diffusive phenomena are ubiquitous in nature. They play a significant role in many chemical, physical, and biological processes. At the nanoscale, they are one of the primary means of transport and vital for understanding biochemical systems like living cells. At this scale, diffusion is understood as the motion of individual particles caused by thermal fluctuations. This process is called the Brownian motion. There are two types of diffusive motions – translational diffusion, which is related to the spatial displacement of a particle, and rotational diffusion, which is related to the change of the orientation of a particle in space. For simple liquids, e.g. water, it is characterized by the classical theory developed independently by Sutherland, Einstein, and Smoluchowski.1–3 However, the classical theory is insufficient for complex liquids such as polymer solutions. In this article we show an experimental verification of the recently developed model4 for the interdependence of the translational and rotational diffusion in complex liquids. In the literature, one may find many seemingly contradictory results. For example, Dauty et al.5 showed that the diffusion coefficient of nanospheres (hydrodynamic radius, r = 10 nm) or albumin (r = 4.5 nm) in ficol (polymer hydrodynamic radius, Rh ∼ 2.5 nm) or in glycerol (Rh < 1 nm) follows the Stokes–Sutherland–Einstein relation (SSE). In contrast, a small tracer, rhodamine of radius r ≲ Rh, exhibited substantial deviations from that relation. In another example, Wang et al.6 studied the translational and rotational diffusion of small proteins in the solutions of glycerol, polymers, and proteins. They noticed that in polymers, both translational and rotational diffusion coefficients were significantly lower than the one predicted from the SSE or Stokes–Einstein–Debye relation (SED) under the assumption that the viscosity in SSE or SED is equal to the viscosity of polymer solution (macroscopic viscosity). In protein solutions, the trends were counterintuitively opposite, which we relate to attractive/repulsive interactions of the tracer protein with charged proteins forming the liquid. There is still much room for studies on this topic, but we will not tackle this problem in this article. In the cytoplasm of living cells, the picture emerging from the literature is even more blurry. Bellotto et al.7 recently examined a broad range of proteins diffusing in E. coli cytoplasm and showed that their diffusion coefficient scales with the molecular weight of the protein as DT ∼ Mw−0.56; note that for the simple diffusion described by the Stokes–Sutherland–Einstein relation, we expect DT ∼ Mw−0.39 (Kalwarczyk et al.8). Moreover, Garner et al.9 showed that the diffusion coefficients of nanoparticles of r = 20 nm in the cytoplasm of E. coli exhibit broad heterogeneity, probably attributed to the heterogeneity of the cytoplasm structure. To fill some gaps and make the field less confusing, we empirically verify the recently developed model for the interdependence of translational and rotational diffusion in complex liquids.
Translational diffusion in simple and complex liquids
In simple fluids such as water, the translational diffusion is described by the classical SSE relation developed independently by Sutherland and Einstein from their works on Brownian motion:1,3| | 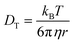 | (1) |
DT is a translational diffusion coefficient, η is a solvent viscosity, r is a probe's hydrodynamic radius, T is the temperature, and kB is the Boltzmann constant. However, this equation fails to describe diffusion in complex liquids. There, one has a hierarchical structure with multiple length scales, some larger than the diffusing particle's size. Many liquids of industrial and biological importance belong to this category. The deviation of translational diffusion in complex fluids from eqn (1) can be as high as many orders of magnitude. It has been studied extensively from the second part of the 20th century, both experimentally and theoretically.10–21 An extensive overview of these studies was presented in a paper by Hołyst et al.22 The length scale-dependent viscosity model of complex fluids (LSVM)22,23 resolved the abovementioned problem. According to this model, the effective viscosity ηeff(r) experienced by a diffusing particle depends on its size – r. The LSVM was developed for multiple complex systems, including polymer solutions and mixtures, micellar and colloidal solutions, the cytoplasm of mammalian, human and bacterial cell lines as well as living cell's nucleus. A thorough description of the LSVM was presented in a review article.24 Plots with examples of LSVMs used in this paper are shown in Fig. 1. The translational diffusion in complex liquids is given by applying the LSVM to eqn (1):| | 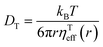 | (2) |
Here ηTeff(r) is the effective viscosity for translational diffusion.
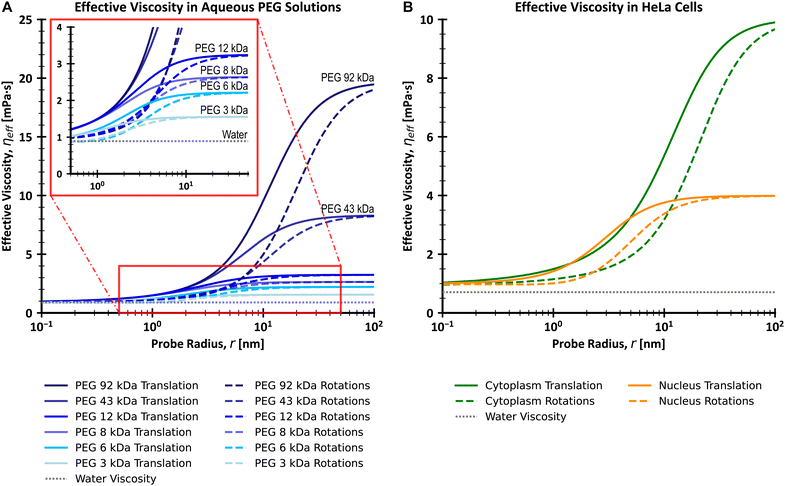 |
| | Fig. 1 Plots of effective viscosities for translational and rotational motion (A) for a series of PEG (poly(ethylene glycol)/poly(ethylene oxide)) aqueous solutions with varying molecular weights and (B) for cytoplasm and nucleus of living HeLa cells, with comparison to the viscosity of water. The insert on (A) shows a magnification of the viscosity curves for the range of 0.5–50 nm on the x-axis and 0–4 mPa s on the y-axis. Values were calculated using the LSVMs25–27 and a temperature of 25 °C (A) or 36 °C (B). All polymer solutions from (A) have a concentration equal to 0.1 g cm−3. The effective viscosity for translational and rotational motion experienced by the diffusing probe is similar to that of the solvent (water) for probes whose r ≪ Rh (here Rh is the hydrodynamic radius of the main crowder). On the other hand, large probes with r ≫ Rh experience macroscopic viscosity, while the exponential scaling of effective viscosity occurs for probes of similar size to Rh. Of note is that the range of values of r for which the scaling takes place is shifted towards larger values for rotational motion as compared to translational motion. | |
Rotational diffusion in simple and complex liquids
Similarly to the translational diffusion, the rotational diffusion in simple fluids is described by the Stokes–Einstein–Debye relation (SED):| | 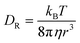 | (3) |
where DR is the rotational diffusion coefficient. This leads to the classical relation between diffusion coefficients based on eqn (1) and (3):| | 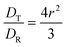 | (4) |
It needs to be stated that eqn (4) is correct only for particles whose shape is well approximated by a sphere. The rotational diffusion in complex liquids also shows deviations from eqn (3). Moreover, the deviations observed for rotational diffusion are different from those for translational diffusion.28–31 The description of rotational diffusion in complex fluids can also be done using the framework of the previously shown length scale-dependent viscosity model. However, for the given particle, the two types of diffusion occur on different length scales. Therefore, the rotational diffusion cannot be described by simply applying the ηTeff(r) relation to eqn (3) since all the mentioned LSVMs are semi-empirical models developed on the basis of studies of translational diffusion. The solution to this problem was given in the work by Makuch et al.4 In their work, they used a general framework with viscosity described by a function of the wave vector in reciprocal space and introduced a formulation that allows one to relate the rotational and translational diffusion coefficients:| | 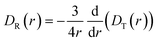 | (5) |
Combining eqn (2) with eqn (5) leads to a description of the rotational diffusion in complex fluids. If used for simple liquids in which the viscosity is independent of the length scale (ηeff(r) = const), eqn (5) reduces to the classical relation between diffusion coefficients – eqn (4). Introducing effective viscosity for rotationally diffusing probe – ηReff(r) allows us to rewrite eqn (5) as a relation of effective viscosities for rotational and translational motion:| | 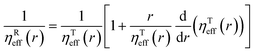 | (6) |
To develop the relation for the rotational diffusion coefficient in complex fluids, it is necessary to solve eqn (5) using system-specific LSVM. For example, in the case of aqueous polyethylene glycol solutions, a series of experimental studies resulted in a phenomenological equation for ηTeff(r):24| | 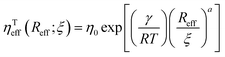 | (7) |
where γ is a system-dependent energy parameter. It is related to the magnitude of polymer–polymer, polymer–solvent, and polymer–probe interactions. According to our previous studies,32 in the studied system γ is temperature and concentration independent. However, it is expected to vary between different polymer/solvent systems and different probes in the case of probe diffusion.25a is a constant in the order of unity, η0 is the viscosity of the pure solvent. ξ is a correlation length corresponding to the mean distance between entanglement points in the polymer matrix of the system's main crowder. R is the gas constant. Reff is an effective radius, given by the equation:eqn (7) is a function of the probe's hydrodynamic radius (r) with the parameters: γ; ξ; Rh; a and η0 depending on the solvent, polymer, and polymer concentration used. From eqn (2) and (5)–(7), the relation for the rotational diffusion coefficient in aqueous polyethylene glycol solutions is given by eqn (9), and the relation for effective viscosity of rotational motion by eqn (10).| | 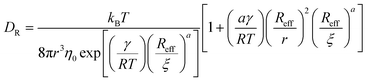 | (9) |
| | 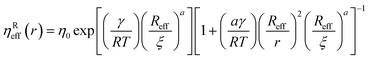 | (10) |
Both ηTeff(r) and ηReff(r) increase to macroscopic viscosity (ηmacro) for sufficiently large probes (when r ≫ Rh). Of note, since ηReff(r) is only a mathematical transformation of ηTeff(r), the corresponding length scales are the same for both models, namely Rh and ξ. Similarly to eqn (2) and (9), the relations for diffusion coefficients can be developed for other complex fluids with a known form of LSVM, including some naturally occurring complex liquids – cytosol and nucleosol of HeLa cells.26,27 In this paper, our purpose is to experimentally verify the model of the interdependence of the translational and rotational diffusion from the work of Makuch et al.4 as given by eqn (5) and (6). We apply fluorescence correlation spectroscopy (FCS) to simultaneously measure both rotational and translational diffusion in model (PEG aqueous solutions) and biological (HeLa cells cytoplasm and nucleus) complex fluids. We use cowpea chlorotic mottle virus (CCMV) particles as probes for studies in aqueous polymer solutions, and Yo-Pro-1 stained large ribosomal subunits for probing rotational diffusion in the cytoplasm and nucleus of living HeLa cells.
Materials and methods
Staining of the cowpea chlorotic mottle viruses
The CCMV viruses were obtained as a courtesy of Prof. Jeroen J. L. M. Cornelissen's group (University of Twente, Faculty of Science and Technology, Enschede, The Netherlands). Stock solutions of CCMV viruses (20 mg ml−1) in a virus buffer were transferred via spin desalting column (ZEBA Spin Desalting Columns, 7 K MWCO, 2 ml; Thermo Fisher Scientific) to phosphate buffer according to the vendor's manual using – MPW-260R (Med. Instruments) centrifuge at 1000 g for 2 minutes. The dyes of interest, Alexa Fluor™ 647 NHS Ester (Alexa647), (Molecular Probes®, Thermo Fisher Scientific) or SulfoCyanine5 bis-NHS ester (Sulfo-Cy5), (Lumiprobe), was dissolved in the anhydrous DMSO (≥99.9%, Sigma-Aldrich). The ratio of dye molecules to CCMV particles was dependent on the desired degree of labeling. For a single dye per CCMV molecule, we used 0.2 mol of dye per 1 mol of viruses. For multiply labeled CCMV, 200 mol of dye per 1 mol of viruses. CCMV viruses were incubated for about an hour with the dye molecules. After staining, the unreacted dye was neutralized by the addition of the TRIS buffer (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v ratio of TRIS buffer to used dye solution), and then the viruses were purified from the excess of unreacted dye using ZEBA spin desalting columns. During the procedure, the phosphate buffer in which the reaction was performed was exchanged with the virus buffer to maintain the viruses' stability. The complete protocol for staining the CCMV viruses was taken from the work by Comellas et al.33 Virus buffer was an aqueous solution of 0,1 mol l−1 sodium acetate (anhydrous, BioUltra, ≥99.0%, Sigma-Aldrich), 0.001 mol l−1 Ethylenediaminetetraacetic acid – EDTA (anhydrous, BioUltra, ≥99%, Sigma-Aldrich), 0.001 mol l−1 sodium azide (BioXtra, ≥99.8%, Sigma-Aldrich). At 25 °C (298.15 K), it has a viscosity equal to 0.89 mPa s (same as water) and a density of 1.002 g cm−3. Phosphate buffer with pH = 7.58 (di-sodium hydrogen phosphate dodecahydrate (POCH); sodium dihydrogen phosphate (POCH)), measured by pH meter HI 3220 (HANNA instruments). TRIS buffer was an aqueous solution of 1 mol l−1 tris(hydroxymethyl)aminomethane (ACS reagent, ≥99.8%, Sigma-Aldrich).
1 v/v ratio of TRIS buffer to used dye solution), and then the viruses were purified from the excess of unreacted dye using ZEBA spin desalting columns. During the procedure, the phosphate buffer in which the reaction was performed was exchanged with the virus buffer to maintain the viruses' stability. The complete protocol for staining the CCMV viruses was taken from the work by Comellas et al.33 Virus buffer was an aqueous solution of 0,1 mol l−1 sodium acetate (anhydrous, BioUltra, ≥99.0%, Sigma-Aldrich), 0.001 mol l−1 Ethylenediaminetetraacetic acid – EDTA (anhydrous, BioUltra, ≥99%, Sigma-Aldrich), 0.001 mol l−1 sodium azide (BioXtra, ≥99.8%, Sigma-Aldrich). At 25 °C (298.15 K), it has a viscosity equal to 0.89 mPa s (same as water) and a density of 1.002 g cm−3. Phosphate buffer with pH = 7.58 (di-sodium hydrogen phosphate dodecahydrate (POCH); sodium dihydrogen phosphate (POCH)), measured by pH meter HI 3220 (HANNA instruments). TRIS buffer was an aqueous solution of 1 mol l−1 tris(hydroxymethyl)aminomethane (ACS reagent, ≥99.8%, Sigma-Aldrich).
Preparation of PEG solutions
The samples for FCS measurements of diffusion of CCMV particles in polymer solutions were prepared as follows: firstly, we dissolved a given mass of polymer in virus buffer. We added both the polymer and the buffer to a glass flask and then stirred it with a magnetic stirrer for up to 3 hours until the polymer completely dissolved. Then, we mixed it with virus buffer solution of fluorescently labeled CCMV particles. The polymer concentration in a given sample was determined by measuring the mass of each added component (RADWAG AS 110/X scale). Of note, the concentrations of polymer solutions used in this paper are given in g cm−3 – grams of polymer per cubic centimeter of solvent. The polymers used to prepare the aqueous solutions were poly(ethylene glycol)/poly(ethylene oxide) with low PDI (Polymer Standards Service, Germany) and number average molecular weight: 5900 Da (6 kDa); 8400 Da (8 kDa); 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 Da (12 kDa) (values from macro viscosity measurements (Malvern Kinexus Pro rheometer), calculated according to publication34); 43
900 Da (12 kDa) (values from macro viscosity measurements (Malvern Kinexus Pro rheometer), calculated according to publication34); 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 Da (43 kDa); 91
100 Da (43 kDa); 91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 Da (92 kDa) – values from producer certificate based on GPC/SEC.
800 Da (92 kDa) – values from producer certificate based on GPC/SEC.
Cell culture and staining of ribosomes
HeLa cells (ATCC) were cultured as a monolayer at 37 °C, 5% CO2. The cell culture medium was based on Dulbecco's Modified Eagle's Medium (DMEM) with low glucose content (Institute of Immunology and Experimental Technology, Wrocław, Poland), supplemented with fetal bovine serum (FBS), L-glutamine 1% v/v (Sigma-Aldrich), and the antibiotics: streptomycin (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 U ml−1) (Merck) and penicillin (10 mg ml−1) 1% v/v (Sigma-Aldrich). For FCS experiments, cells were seeded into 8-well cover glass plates (Cellvis) and cultured overnight. Ribosomes were stained using Yo-Pro-1 dye (Invitrogen). Briefly, cells were incubated in 40 nM Yo-Pro-1 in PBS for 30 minutes before the measurement. FCS setup was calibrated using a solution of rhodamine 110 dissolved in 2.5%w/w glucose in PBS.35 Confocal volume was positioned in the cytoplasm or nucleus of the selected cell (approximately 2 μm above the glass surface). Cells were selected based on spindle-shaped morphology.
000 U ml−1) (Merck) and penicillin (10 mg ml−1) 1% v/v (Sigma-Aldrich). For FCS experiments, cells were seeded into 8-well cover glass plates (Cellvis) and cultured overnight. Ribosomes were stained using Yo-Pro-1 dye (Invitrogen). Briefly, cells were incubated in 40 nM Yo-Pro-1 in PBS for 30 minutes before the measurement. FCS setup was calibrated using a solution of rhodamine 110 dissolved in 2.5%w/w glucose in PBS.35 Confocal volume was positioned in the cytoplasm or nucleus of the selected cell (approximately 2 μm above the glass surface). Cells were selected based on spindle-shaped morphology.
Fluorescence correlation spectroscopy measurements
The FCS measurements were taken with a setup composed of Nikon Eclipse TE2000U confocal microscope (Nikon, Japan), Pico Harp 300 FCS (PicoQuant, Germany), picosecond pulse lasers – 488 nm with 5 ± 1 μW power for Yo-Pro-1 stained ribosomes, 636 nm with 15 ± 1 μW power for CCMV plant viruses (PicoQuant, Germany) and Single Photon Avalanche Diodes (MPD and PerkinElmer) as detectors. We used SymphoTime software (PicoQuant, Germany) to collect raw data and calculate FCS Autocorrelation curves. We then analyzed the FCS results using the authors' Python scripts.
Results and discussion
Simultaneous measurement of translational and rotational diffusion
We use fluorescence correlation spectroscopy (FCS) to study diffusive phenomena at the nanoscale. This technique was developed in the 1970s36,37 and is based on the measurement of fluorescence intensity fluctuations. The main application of FCS is the study of translational diffusion. In some circumstances, FCS can also be used to study rotational diffusion.38 The characteristic time scale of these processes is the limiting factor for applying FCS to study them. The relations between the characteristic times of rotational and translational diffusion and corresponding diffusion coefficients are given in eqn (11) and (12):| | 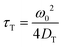 | (11) |
| | 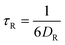 | (12) |
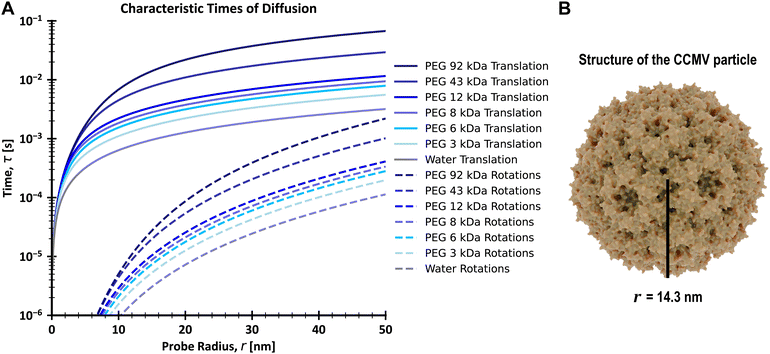
τT is the characteristic time of translational diffusion, τR is the characteristic time of rotational diffusion, and ω0 is the size of the confocal focus. As a result, based on eqn (1) and (3), the considered time scales depend on the probe size and the solution's viscosity. Typical FCS setup allows for measuring processes with time scales from 1 μs to 1 s (6 orders of magnitude) while keeping a good signal-to-noise ratio. This allows for the study of translational diffusion coefficient, inversely proportional to the probe's hydrodynamic radius, of objects as small as simple dyes in water and water-based complex liquids such as cellular cytoplasm. However, as rotational diffusion coefficient depends on the inverse of r3, it is much faster for small objects than translational diffusion. E.g. for a simple dye of hydrodynamic radius <1 nm in an aqueous solution, the rotational diffusion time is in the order of 1–10 ns. As a result, the hydrodynamic radius of the used probe must be at least ∼10 nm to measure rotational diffusion by FCS. Fig. 2A shows plots of the relations of characteristic diffusion times to the probe's size for water and water-based complex liquids. The minimal size requirement leads to the fact that only a few articles describing the use of FCS for the measurements of rotational diffusion were published,30,31,39–45 especially before the popularisation of synthetic nanoparticles of appropriate size. However, due to the methods of their synthesis, synthetic nanoparticles display polydispersity of sizes, which means that they do not have a well-defined size but rather a distribution of sizes.46–48 Said polydispersity causes issues with analyzing experimental data obtained when using fluorescent nanoparticles as probes for diffusion in complex liquids.35 This problem can be solved for translational diffusion by using the anomalous diffusion model for data analysis.35 However, it is much more problematic for rotational diffusion, which has a stronger dependency on the probe's size (eqn (3)). As a result, synthetic nanoparticles are unreliable for testing the new model of the interdependence of rotational and translational diffusion in complex liquids. The solution for the above-mentioned problem with polydispersity that we proposed in this article is the use of biological nanoparticles. Such nanoparticles have well-defined shapes and sizes and, after fluorescent staining, can be used for FCS measurements.
 |
| | Fig. 2 (A) Plots of characteristic times of rotational and translational diffusion in a series of PEG aqueous solutions with varying molecular weights as a function of the probe radius, with comparison to water. Values were calculated using the LSVM25eqn (6), (11) and (12), with all polymer solutions having a concentration equal to 0.1 g cm−3 and a temperature of 25 °C. The size of the confocal focus was set as 250 nm. As seen in the figure, a typical FCS setup cannot be used to study the rotational diffusion of probes smaller than 6 nm, even for polymer solutions, as according to the LSVM for rotational diffusion, such probes experience effective viscosity similar to water. (B) Shows a scheme of the structure and size of a CCMV particle. The size of CCMV was taken from the literature.49 | |
Diffusion of CCMV plant viruses in buffer
We prepared two types of fluorescent probes by staining the CCMV particles. Single stained probes with one dye molecule per virus particle and multiply stained probes prepared using excess dye. The single stained probes were prepared in two versions with either Alexa647 or Sulfo-Cy5 dye, while the multiply stained probes were prepared using only Sulfo-Cy5 (see Materials and methods). Then, we performed FCS measurements in the virus buffer at 25 °C of all the above-mentioned probes. We did it to test the feasibility of measuring the rotational diffusion with said probes and establish their parameters, such as hydrodynamic radius. For the single-stained probes, we expected to observe a good signal from rotational diffusion with τR ≈ 3 μs and translational diffusion with τT ≈ 0.6 ms (Fig. 2A). On the other hand, CCMV particles labeled with multiple dye molecules will have lower orientational anisotropy. That is why we expected that the measurements for multiply stained probes would result in FCS curves with a well-visible component from translational diffusion and a small or non-visible signal from rotational diffusion. Fig. 3A shows results from FCS measurements in the buffer for single Alexa647 stained probes. The experimental data from FCS measurements in the buffer for single Sulfo-Cy5 stained probes and multiple Sulfo-Cy5 stained probes are presented in ESI,† 2.1. The results obtained match the abovementioned predictions well. However, we also observed a third component on the registered auto-correlation curves (ACF) for single-stained probes, with characteristic times of ∼40 μs. We assume that the additional component comes from the fact that the dye attached to the surface of the virus particles has a certain freedom of movement and can assume multiple conformations.50 Alternatively, it may result from triplet state dynamics with unusually long relaxation times. The FCS autocorrelation function (ACF) for the translational motion in three dimensions and triplet state dynamics is described by a formula given in eqn (13):| | | G(τ) = G(0)GD(τ)Gt(τ) | (13) |
τ is the lag time. G(0) is the value of the autocorrelation function at τ equal to 0.
 |
| | Fig. 3 (A) FCS data obtained for single Alexa 647 stained CCMV particles in virus buffer (viscosity equal to water) at 25 °C with descriptions of parts of the ACF corresponding to the three observed dynamic processes. The experimental data was fitted with a model including translational diffusion and coupling of rotational diffusion with first-order dynamics, achieving a good fit. The residuals were calculated as a difference between experimental and theoretical values divided by errors of experimental values for each datapoint. (B) Scheme visualizing the three dynamic processes observed in FCS measurements of fluorescently stained CCMV particles. Gray spheres represent virus particles, red-yellow stars represent dye molecules, and a black line represents the dye–virus bond. For the purpose of visualization, the scheme does not conserve the relative sizes of the shown objects. | |
G
D(τ) is the autocorrelation function for translational motion in three dimensions. Gt(τ) is the autocorrelation function for triplet state dynamics. N is the average number of probes in focal volume and depends on sample concentration. κ is the aspect ratio of the focal volume and is obtained from calibration. τT is the characteristic time of translational diffusion. τTriplet is a triplet state lifetime and TTriplet is a fraction of molecules in the triplet state. Eqn (13) is known as the simple diffusion model. Combining eqn (13) with eqn (11) and (1) or eqn (2) allows us to express it with r and η or ηTeff(r) as parameters. The theoretical model for ACF with both translational and rotational diffusion is given by eqn (14):
| | | G(τ) = G(0)GD(τ)GR(τ) | (14) |
GR(τ) = 1 + A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−6DRτ) exp(−6DRτ) |
GR(
τ) is the autocorrelation function for rotational diffusion.
A is a constant for the rotational diffusion amplitude.
DR is the rotational diffusion coefficient. Combining
eqn (14) with
eqn (3) or
eqn (9) allows us to express it with
r and
η or
ηTeff(
r) and
ηReff(
r) as parameters. However, to analyze our experimental data, we needed a more complicated model that included the additional dye dynamics on the virus surface. That is why we developed a new model that includes translational diffusion, coupling of rotational diffusion with first-order reaction and triplet state dynamics (the model assumes a single dye attached to the surface of a nanosphere):
| | | G(τ) = GK(τ)GD(τ)Gt(τ) | (15) |
Here
GK(
τ) is the autocorrelation function for the coupling of rotational diffusion with first-order reaction.
C is a constant related to the concentration and fluorescence of measured probes and the volume of the confocal focus.
K is the equilibrium constant for the considered first-order reaction.
Rk is a sum of forward and backward rate constants for said reaction. The complete development of this model is presented in ESI,
† 1. In the case of
eqn (15),
A has a theoretical value of 1.096. Similarly to
eqn (13) and (14),
eqn (15) can be expressed with
r and
η or
ηTeff(
r) and
ηReff(
r) instead of
τT and
DR. As a result of using the new model (
eqn (15)) to analyze the FCS data from the diffusion of single Alexa 647 stained CCMV particles in virus buffer, we obtained a good fit of theoretical and experimental values (
Fig. 3A). We set
A,
K,
Rk, and
r as fitting parameters, with
η set as 0.89 mPa s and
κ and
ω0 taken from setup calibration. The values of
τTriplet and
TTriplet were taken from the analysis of multiple Sulfo-Cy5 stained probes. We did the same analysis for the FCS data from the diffusion of single Sulfo-Cy5 stained CCMV particles in the virus buffer, which also resulted in a good fit. To analyze the FCS data for multiple Sulfo-Cy5 stained CCMV particles in the buffer, we used a simple diffusion model (
eqn (13)) with
r,
τTriplet and
TTriplet as a fitting parameters and
η set as 0.89 mPa s and
κ and
ω0 taken from setup calibration. We did not observe the signal from the additional dye dynamics for the multiple stained probes. This results from the relative change of the total fluorescence of multiple stained nanoparticle being small from only one of the dyes undergoing reaction. And as the possible dye dynamics is a random process the chances of multiple dyes undergoing reaction simultaneously are very low. The FCS results for single and multiple Sulfo-Cy5 stained probes in buffer with fitted models are presented in ESI,
† 2.1. The resulting parameters for single Alexa 647 stained, single Sulfo-Cy5 stained, and multiple Sulfo-Cy5 stained CCMV particles are presented in
Table 1. Of note is that the hydrodynamic radius of all analyzed probes matches the value of the physical radius of CCMV particles found in literature – 14.3 nm.
49 An alternative analysis of the experimental data for single stained probes, with fitted triplet states dynamic instead of the coupling of rotational diffusion with first-order reaction, is presented in ESI,
† 2.2. We did not observe photobleaching of our sample as we used relatively low laser power and each probe spends only ∼ 1 ms in the confocal focus (see ESI,
† 2.6). We fitted
A since it was lower than the expected theoretical value of 1.096. We suspect that it is caused by the lower than theoretical orientational anisotropy of obtained probes resulting from limited freedom of movement of the dye on the CCMV particle's surface.
Table 1 The parameters of CCMV-derived probes from fitting experimental data obtained from measurements in the virus buffer at 25 °C. The values of τTriplet and TTriplet were fitted only for multiple Sulfo-Cy5 stained probes. For single stained probes we fixed these values from the analysis of multiple stained probes
|
|
Single Alexa647 stained |
Single sulfo-Cy5 stained |
Multiple sulfo-Cy5 stained |
|
r [nm] |
15.7 ± 0.6 |
14.5 ± 0.5 |
15.9 ± 0.3 |
|
A
|
0.54 ± 0.02 |
0.70 ± 0.05 |
— |
|
K
|
1.39 ± 0.02 |
1.42 ± 0.04 |
— |
|
R
k
[ms−1] |
24.4 ± 5.0 |
25.3 ± 6.0 |
— |
|
τ
Triplet [μs] |
10.0 (fixed) |
10.0 (fixed) |
10.0 ± 1.8 (fitted) |
|
T
Triplet
|
0.056 (fixed) |
0.056 (fixed) |
0.056 ± 0.002 (fitted) |
Diffusion of CCMV plant viruses in polymer solutions
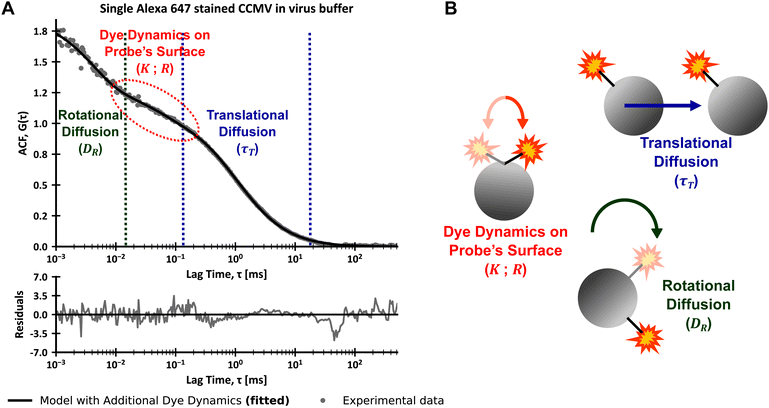
Finally, we performed FCS measurements of the single Alexa647 stained and single Sulfo-Cy5 stained CCMV particles in a range of PEG (polyethylene glycol) solutions with varying average molecular weights and concentrations.
Then, we compared the experimental data with theoretical curves obtained from eqn (15) and values of τT and DR calculated using eqn (2), (7)–(9) and (11). The parameters of the LSVM are presented in ESI,† 2.3. We used the values of A, K, Rk, τTriplet, TTriplet and r obtained from the analysis of FCS data from measurements in the virus buffer – Table 1 (we did not perform any data fitting, only normalized the ACF curves to exclude the influence of samples’ concentrations). The experimental results, with corresponding calculated theoretical curves, are presented in Fig. 4. Analysis of the experimental data and theoretical curves shows good agreement of the signal from rotational diffusion and calculated values for all results. In ESI,† 2.4, we show an alternative analysis of the experimental data that assumes triplet states dynamics with longer times instead of the coupling of rotational diffusion with first-order reaction. This alternative approach results in the same conclusions as mentioned above. The minor differences between theoretical and experimental data in the range of translational diffusion for samples with higher polymer concentrations (PEG 6 kDa 0.081 g cm−3 and 0.110 g cm−3) are caused by the aggregation of CCMV particles in mentioned samples. The aggregation is more substantial the higher the concentration of polymer and the higher its molecular weight (see additional results presented in ESI,† 2.5). That is why, to avoid this phenomenon, we have performed measurements in samples with low polymer concentrations.
 |
| | Fig. 4 FCS data for single Sulfo-Cy5 (A)–(F) and single Alexa647 (G)–(J) stained CCMV particles in solutions of PEG of various molecular weights in virus buffer at 25 °C and calculated theoretical curves, with plots of residues. (A) Data for 0.050 g cm−3 solution of PEG 6 kDa in virus buffer. (B) Data for 0.053 g cm−3 solution of PEG 8 kDa in virus buffer. (C) Data for 0.055 g cm−3 solution of PEG 12 kDa in virus buffer. (D) Data for 0.010 g cm−3 solution of PEG 43 kDa in virus buffer. (E) Data for 0.010 g cm−3 solution of PEG 92 kDa in virus buffer. (F) Data for 0.010 g cm−3 solution of PEG 196 kDa in virus buffer. (G) Data for 0.020 g cm−3 solution of PEG 6 kDa in virus buffer. (H) Data for 0.049 g cm−3 solution of PEG 6 kDa in virus buffer. (I) Data for 0.081 g cm−3 solution of PEG 6 kDa in virus buffer. (J) Data for 0.110 g cm−3 solution of PEG 6 kDa in virus buffer. Data presented as solid lines are not fits and were calculated according to eqn (2), (7)–(9), (11) and (15). The residuals were calculated as a difference between experimental and theoretical values divided by errors of experimental values for each datapoint. The above-given values of polymer molecular weights are the number average molecular weights. | |
Rotations of ribosomal subunits in HeLa cells
We used Yo-Pro-1 dye to stain large ribosomal subunits (LSU) in living HeLa cells due to its ability to intercalate double-stranded RNA domains (be inserted in between base pairs of the RNA). Then, we used FCS to measure the translational and rotational diffusion of Yo-Pro-1 stained probes in cytoplasm and nucleus in living HeLa cells at 36 °C. Yo-Pro-1 also stains tRNAs, so we expected an additional diffusing component in the obtained FCS data. However, tRNAs have hydrodynamic radii equal to 2 nm (see ESI,† 2.8) and their rotational diffusion is too fast to be detectable by our experimental setup. As such, we expect FCS results with three components – translational diffusion of LSU and tRNAs and rotational diffusion of LSU. The results obtained match the above-mentioned predictions well. Additional explanations on the staining of ribosomes with Yo-Pro-1 are given in ESI,† 2.7. We analyzed the experimental data by fitting it with a model given by eqn (16), which includes translational diffusion of LSU and tRNAs and rotational diffusion of LSU:| | 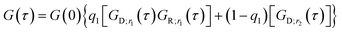 | (16) |
Here GD;r1(τ) and GD;r2(τ) are autocorrelation functions for translational diffusion of LSU and tRNAs, expressed with r1 and r2 as parameters. GR;r2(τ) is the autocorrelation function for rotational diffusion of LSU, expressed with r1 as a parameter. r1 is a hydrodynamic radius of large ribosomal subunits, and r2 is a hydrodynamic radius of tRNAs. q1 is a fraction of LSU. However, it is not directly related to the number of molecules since the molecular brightnesses of LSU and tRNAs are unequal. q1 can be interpreted as the portion of the total signal from translational diffusion that comes from LSU (on a 0–1 scale). The contribution of rotational diffusion to the autocorrelation curve is given by the constant A. Unlike with the experiments with CCMVs, we did not include additional dye dynamics in eqn (16) since Yo-Pro-1 intercalates (and thus has a limited freedom of movement) to both LSU and tRNA. Moreover, we did not observe any signal from triplet state dynamics. This can be explained by the lower excitation power in experiments in living cells and the different photophysics of Yo-Pro-1 from dyes used for CCMV staining. We used ηTeff(r) from publications on LSVMs for HeLa cytoplasm51 and nucleus.27 Then, we developed ηReff(r) using eqn (6) and corresponding ηTeff(r) for HeLa cytoplasm and nucleus (see Fig. 1B). The complete equations for ηTeff(r) and ηReff(r) with the values of used constants are given in ESI,† 2.9. Of note, the nucleus is much less crowded in the nanoscale than the cytoplasm (Fig. 1B), this was broadly described in the work of Bubak et al.27 We interpret these data as unobstructed diffusion in the interchromatin spaces (typically of 150 nm width), with relatively low number of bigger objects. We set r1, q1 and A as fitting parameters. The FCS results from living HeLa cells with fitted models are presented in Fig. 5, and the values of fitted parameters are given in Table 2. The agreement between the experimental data and fitted model is exceptionally high, both in the cytoplasm and nucleus, considering the complexity of human cells. Moreover, the obtained hydrodynamic radius of LSU matches between the cytoplasm and nucleus within the margin of error.
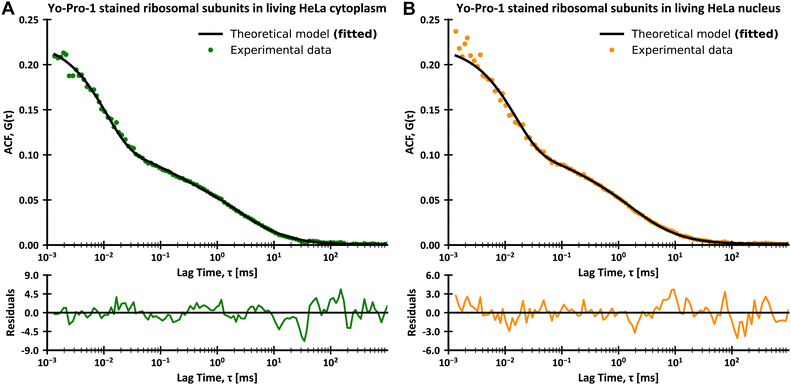 |
| | Fig. 5 FCS data for the diffusion of Yo-Pro-1 stained large ribosomal subunits and tRNAs in living HeLa cells at 36 °C, with plots of residues. (A) Data for the diffusion in the cytoplasm with fitted theoretical curve based on eqn (16). (B) Data for the diffusion in the nucleus with fitted theoretical curve based on eqn (16). The residuals were calculated as a difference between experimental and theoretical values divided by errors of experimental values for each datapoint. | |
Table 2 Parameters of ribosomal subunits obtained from FCS measurements in living HeLa cytoplasm and nucleus at 36 °C
|
|
Living HeLa cytoplasm |
Living HeLa nucleus |
| Radius of LSU, r1 [nm] |
15.5 ± 1.3 |
16.2 ± 0.7 |
| Fraction of LSU, q1 |
0.57 ± 0.09 |
0.66 ± 0.07 |
|
A
|
1.45 ± 0.35 |
1.55 ± 0.14 |
Conclusions
The purpose of this paper was the experimental verification of the relation for the interdependence of the rotational and translational diffusion in complex fluids developed by Makuch et al.4 – eqn (5). We applied fluorescence correlation spectroscopy (FCS) to simultaneously measure both rotational and translational diffusion in both model (PEG aqueous solutions) and biological (HeLa cells cytoplasm and nucleus) complex fluids with known LSVMs. As probes, we used fluorescently stained biological nanoparticles – cowpea chlorotic mottle viruses (r ≈ 15 nm) for PEG solutions and ribosomes (r ≈ 16 nm) for HeLa cells. We chose these probes due to their monodispersity and sufficiently large sizes for their rotational diffusion to occur at timescales in the range detectable by the FCS setup.
We have shown that the considered relation (eqn (5)) and following eqn (9) and (10) can be practically used to describe the rotational diffusion in all studied complex fluids. We then used this relation (eqn (5)) to determine the radius of large ribosomal subunits in living HeLa cells. Of note is an open challenge with the lack of description on how interactions affect diffusion – as a result, we did not know how the value of the γ parameter (from eqn (7)) depends on the used probes and had to perform translational diffusion measurements to determine the said value for probes used in this paper.
Author contributions
Jarosław Michalski methodology: validation, formal analysis, investigation, writing – original draft, visualization. Tomasz Kalwarczyk: conceptualization, methodology, formal analysis, investigation, resources, writing – original draft. Karina Kwapiszewska: methodology, investigation, writing – original Draft. Jörg Enderlein: methodology. Andrzej Poniewierski: methodology. Aneta Karpińska: investigation. Karolina Kucharska: investigation. Robert Hołyst: conceptualization, resources, writing – review & editing, supervision, funding acquisition.
Data availability
The data supporting this article have been included as part of the ESI.† The SI3 contains data shown on Figures, raw FCS curves which analysis resulted in values given in Tables and FCS setup calibration values.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Research funded by the Polish Science Fund within the framework of the Virtual Research Institute; grant WIB-1/2020-O11 – WIB_HERO. Aneta Karpinska was supported by the Foundation for Polish Science (FNP) through START scholarship. The TOC graphic was created with BioRender.com
Notes and references
- A. Einstein, Zur Theorie der Brownschen Bewegung, Ann Phys., 1906, 324(2), 371–381, DOI:10.1002/andp.19063240208.
- M. von Smoluchowski, Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen, Ann Phys., 1906, 326(14), 756–780, DOI:10.1002/andp.19063261405.
- W. Sutherland, LXXV. A dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin, London, Edinburgh Dublin Philos. Mag. J. Sci., 1905, 9(54), 781–785, DOI:10.1080/14786440509463331.
- K. Makuch, R. Hołyst, T. Kalwarczyk, P. Garstecki and J. F. Brady, Diffusion and flow in complex liquids, Soft Matter, 2020, 16(1), 114–124, 10.1039/C9SM01119F.
- E. Dauty and A. S. Verkman, Molecular crowding reduces to a similar extent the diffusion of small solutes and macromolecules: measurement by fluorescence correlation spectroscopy, J. Mol. Recognit., 2004, 17(5), 441–447, DOI:10.1002/jmr.709.
- Y. Wang, C. Li and G. J. Pielak, Effects of Proteins on Protein Diffusion, J. Am. Chem. Soc., 2010, 132(27), 9392–9397, DOI:10.1021/ja102296k.
- N. Bellotto, J. Agudo-Canalejo, R. Colin, R. Golestanian, G. Malengo and V. Sourjik, Dependence of diffusion in Escherichia coli cytoplasm on protein size, environmental conditions, and cell growth. Amir A, Barkai N, Mullineaux CW, eds, Elife, 2022, 11, e82654, DOI:10.7554/eLife.82654.
- T. Kalwarczyk, M. Tabaka and R. Holyst, Biologistics—Diffusion coefficients for complete proteome of Escherichia coli, Bioinformatics, 2012, 28(22), 2971–2978, DOI:10.1093/bioinformatics/bts537.
- R. M. Garner, A. T. Molines, J. A. Theriot and F. Chang, Vast heterogeneity in cytoplasmic diffusion rates revealed by nanorheology and Doppelgänger simulations, Biophys. J., 2023, 122(5), 767–783, DOI:10.1016/j.bpj.2023.01.040.
- M. Tokita, T. Miyoshi, K. Takegoshi and K. Hikichi, Probe diffusion in gels, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1996, 53(2), 1823–1827, DOI:10.1103/PhysRevE.53.1823.
- S. P. Radko and A. Chrambach, Mechanisms of retardation of rigid spherical particles with 3 to 1085 nm radius in capillary electrophoresis, using buffered polyacrylamide (molecular weight 5 × 106) solutions, Electrophoresis, 1996, 17(6), 1094–1102, DOI:10.1002/elps.1150170619.
- D. Langevin and F. Rondelez, Sedimentation of large colloidal particles through semidilute polymer solutions, Polymer, 1978, 19(8), 875–882, DOI:10.1016/0032-3861(78)90191-X.
- T. F. Kosar and R. J. Phillips, Measurement of protein diffusion in Dextran solutions by holographic interferometry, AIChE J., 1995, 41(3), 701–711, DOI:10.1002/aic.690410327.
- M. R. Wattenbarger, V. A. Bloomfield, Z. Bu and P. S. Russo, Tracer diffusion of proteins in DNA solutions, Macromolecules, 1992, 25(20), 5263–5265, DOI:10.1021/ma00046a024.
- G. D. J. Phillies, G. S. Ullmann, K. Ullmann and T. Lin, Phenomenological scaling laws for ‘“semidilute”’ macromolecule solutions from light scattering by optical probe particles, J. Chem. Phys., 1985, 82(11), 5242–5246, DOI:10.1063/1.448969.
- T. Odijk, Depletion Theory of Protein Transport in Semi-Dilute Polymer Solutions, Biophys. J., 2000, 79(5), 2314–2321, DOI:10.1016/S0006-3495(00)76477-0.
- T. C. Laurent, I. Björk, A. Pietruszkiewicz and H. Persson, On the interaction between polysaccharides and other macromolecules: II. The transport of globular particles through hyaluronic acid solutions, Biochim. Biophys. Acta, 1963, 78(2), 351–359, DOI:10.1016/0006-3002(63)91645-7.
- D. Rodbard and A. Chrambach, Estimation of molecular radius, free mobility, and valence using polyacrylamide gel electrophoresis, Anal. Biochem., 1971, 40(1), 95–134, DOI:10.1016/0003-2697(71)90086-8.
- A. Chrambach and D. Rodbard, Polyacrylamide Gel Electrophoresis, Science, 1971, 172(3982), 440–451, DOI:10.1126/science.172.3982.440.
- H. K. Schachman and W. F. Harrington, On viscosity measurement in the ultracentrifuge1, J. Am. Chem. Soc., 1952, 74(15), 3965–3966, DOI:10.1021/ja01135a533.
- S. P. Radko and A. Chrambach, Electrophoresis of proteins in semidilute polyethylene glycol solutions: Mechanism of retardation, Biopolymers, 1997, 42(2), 183–189, DOI:10.1002/(SICI)1097-0282(199708)42:2
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) 183::AID-BIP7
183::AID-BIP7![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) 3.0.CO;2-J.
3.0.CO;2-J.
- R. Holyst, A. Bielejewska and J. Szymański,
et al., Scaling form of viscosity at all length-scales in poly(ethylene glycol) solutions studied by fluorescence correlation spectroscopy and capillary electrophoresis, Phys. Chem. Chem. Phys., 2009, 11(40), 9025–9032, 10.1039/B908386C.
- J. Szymański, A. Patkowski, A. Wilk, P. Garstecki and R. Holyst, Diffusion and Viscosity in a Crowded Environment: from Nano- to Macroscale, J. Phys. Chem. B, 2006, 110(51), 25593–25597, DOI:10.1021/jp0666784.
- T. Kalwarczyk, K. Sozanski and A. Ochab-Marcinek,
et al., Motion of nanoprobes in complex liquids within the framework of the length-scale dependent viscosity model, Adv. Colloid Interface Sci., 2015, 223, 55–63, DOI:10.1016/j.cis.2015.06.007.
- A. Wisniewska, K. Sozanski, T. Kalwarczyk, K. Kedra-Krolik and R. Holyst, Scaling Equation for Viscosity of Polymer Mixtures in Solutions with Application to Diffusion of Molecular Probes, Macromolecules, 2017, 50(11), 4555–4561, DOI:10.1021/acs.macromol.7b00545.
- K. Kwapiszewska, K. Szczepański and T. Kalwarczyk,
et al., Nanoscale Viscosity of Cytoplasm Is Conserved in Human Cell Lines, J. Phys. Chem. Lett., 2020, 11(16), 6914–6920, DOI:10.1021/acs.jpclett.0c01748.
- G. Bubak, K. Kwapiszewska and T. Kalwarczyk,
et al., Quantifying Nanoscale Viscosity and Structures of Living Cells Nucleus from Mobility Measurements, J. Phys. Chem. Lett., 2021, 12(1), 294–301, DOI:10.1021/acs.jpclett.0c03052.
- J. Qing, A. Chen and N. Zhao, A new scaling for the rotational diffusion of molecular probes in polymer solutions, Phys. Chem. Chem. Phys., 2017, 19(48), 32687–32697, 10.1039/C7CP07047K.
- T. Skóra, F. Vaghefikia, J. Fitter and S. Kondrat, Macromolecular Crowding: How Shape and Interactions Affect Diffusion, J. Phys. Chem. B, 2020, 124(35), 7537–7543, DOI:10.1021/acs.jpcb.0c04846.
- J. Yamamoto, A. Matsui and F. Gan,
et al., Quantitative evaluation of macromolecular crowding environment based on translational and rotational diffusion using polarization dependent fluorescence correlation spectroscopy, Sci. Rep., 2021, 11(1), 10594, DOI:10.1038/s41598-021-89987-7.
- C. Li, Y. Wang and G. J. Pielak, Translational and Rotational Diffusion of a Small Globular Protein under Crowded Conditions, J. Phys. Chem. B, 2009, 113(40), 13390–13392, DOI:10.1021/jp907744m.
- K. Sozanski, A. Wisniewska, T. Kalwarczyk, A. Sznajder and R. Holyst, Motion of Molecular Probes and Viscosity Scaling in Polyelectrolyte Solutions at Physiological Ionic Strength, PLoS One, 2016, 11(8), e0161409, DOI:10.1371/journal.pone.0161409.
-
M. Comellas Aragones, The Cowpea Chlorotic Mottle Virus as a Building Block in Nanotechnology, 2010 Search PubMed.
- A. Agasty, A. Wisniewska, T. Kalwarczyk, K. Koynov and R. Holyst, Macroscopic Viscosity of Polymer Solutions from the Nanoscale Analysis, ACS Appl. Polym. Mater., 2021, 3(5), 2813–2822, DOI:10.1021/acsapm.1c00348.
- T. Kalwarczyk, K. Kwapiszewska and K. Szczepanski,
et al., Apparent Anomalous Diffusion in the Cytoplasm of Human Cells: The Effect of Probes’ Polydispersity, J. Phys. Chem. B, 2017, 121(42), 9831–9837, DOI:10.1021/acs.jpcb.7b07158.
- D. Magde, E. Elson and W. W. Webb, Thermodynamic Fluctuations in a Reacting System---Measurement by Fluorescence Correlation Spectroscopy, Phys. Rev. Lett., 1972, 29(11), 705–708, DOI:10.1103/PhysRevLett.29.705.
- D. Magde, E. L. Elson and W. W. Webb, Fluorescence correlation spectroscopy. II. An experimental realization, Biopolymers, 1974, 13(1), 29–61, DOI:10.1002/bip.1974.360130103.
- S. R. Aragón and R. Pecora, Fluorescence correlation spectroscopy and Brownian rotational diffusion, Biopolymers, 1975, 14(1), 119–137, DOI:10.1002/bip.1975.360140110.
- P. Kask, P. Piksarv, Ü. Mets, M. Pooga and E. Lippmaa, Fluorescence correlation spectroscopy in the nanosecond time range: rotational diffusion of bovine carbonic anhydrase B, Eur. Biophys. J., 1987, 14(4), 257–261, DOI:10.1007/BF00256359.
- P. Kask, P. Piksarv, M. Pooga, Ü. Mets and E. Lippmaa, Separation of the rotational contribution in fluorescence correlation experiments, Biophys. J., 1989, 55(2), 213–220, DOI:10.1016/S0006-3495(89)82796-1.
- A. Loman, I. Gregor, C. Stutz, M. Mund and J. Enderlein, Measuring rotational diffusion of macromolecules by fluorescence correlation spectroscopy, Photochem. Photobiol. Sci., 2010, 9(5), 627–636, 10.1039/B9PP00029A.
- C. M. Pieper and J. Enderlein, Fluorescence correlation spectroscopy as a tool for measuring the rotational diffusion of macromolecules, Chem. Phys. Lett., 2011, 516(1), 1–11, DOI:10.1016/j.cplett.2011.06.091.
- S. Alam and A. Mukhopadhyay, Translational Anisotropy and Rotational Diffusion of Gold Nanorods in Colloidal Sphere Solutions, Langmuir, 2015, 31(32), 8780–8785, DOI:10.1021/acs.langmuir.5b01682.
- M. Roos, M. Ott and M. Hofmann,
et al., Coupling and Decoupling of Rotational and Translational Diffusion of Proteins under Crowding Conditions, J. Am. Chem. Soc., 2016, 138(32), 10365–10372, DOI:10.1021/jacs.6b06615.
- M. Oura, J. Yamamoto, H. Ishikawa, S. Mikuni, R. Fukushima and M. Kinjo, Polarization-dependent fluorescence correlation spectroscopy for studying structural properties of proteins in living cell, Sci. Rep., 2016, 6(1), 31091, DOI:10.1038/srep31091.
- C. Neuchl and A. Mersmann, Fractionation of polydisperse dextran using ethanol, Chem. Eng. Sci., 1995, 50(6), 951–958, DOI:10.1016/0009-2509(94)00492-A.
- M. T. Gokmen and F. E. Du Prez, Porous polymer particles—A comprehensive guide to synthesis, characterization, functionalization and applications, Prog. Polym. Sci., 2012, 37(3), 365–405, DOI:10.1016/j.progpolymsci.2011.07.006.
- L. Rodriguez-Lorenzo, B. Rothen-Rutishauser, A. Petri-Fink and S. Balog, Nanoparticle Polydispersity Can Strongly Affect In Vitro Dose, Part. Part. Syst. Charact., 2015, 32(3), 321–333, DOI:10.1002/ppsc.201400079.
- J. A. Speir, S. Munshi, G. Wang, T. S. Baker and J. E. Johnson, Structures of the native and swollen forms of cowpea chlorotic mottle virus determined by X-ray crystallography and cryo-electron microscopy, Structure, 1995, 3(1), 63–78, DOI:10.1016/S0969-2126(01)00135-6.
- J. Widengren and P. Schwi
![[l with combining umlaut]](https://www.rsc.org/images/entities/char_006c_0308.gif) le, Characterization of photoinduced isomerization and back-isomerization of the cyanine dye cy5 by fluorescence correlation spectroscopy, J. Phys. Chem. A, 2000, 104(27), 6416–6428, DOI:10.1021/jp000059s.
le, Characterization of photoinduced isomerization and back-isomerization of the cyanine dye cy5 by fluorescence correlation spectroscopy, J. Phys. Chem. A, 2000, 104(27), 6416–6428, DOI:10.1021/jp000059s.
- K. Kwapiszewska, T. Kalwarczyk and B. Michalska,
et al., Determination of oligomerization state of Drp1 protein in living cells at nanomolar concentrations, Sci. Rep., 2019, 9(1), 5906, DOI:10.1038/s41598-019-42418-0.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Tomasz
Kalwarczyk
a,
Tomasz
Kalwarczyk
 a,
Karina
Kwapiszewska
a,
Karina
Kwapiszewska
 a,
Jörg
Enderlein
a,
Jörg
Enderlein
 b,
Andrzej
Poniewierski
a,
Aneta
Karpińska
b,
Andrzej
Poniewierski
a,
Aneta
Karpińska
 a,
Karolina
Kucharska
a,
Karolina
Kucharska
 a and
Robert
Hołyst
a and
Robert
Hołyst
 *a
*a
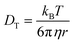
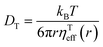

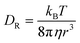
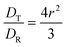
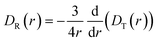
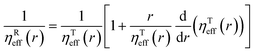
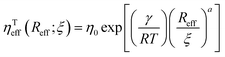
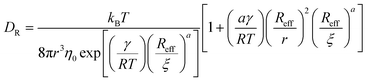
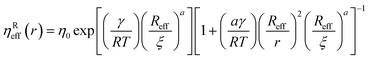
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v ratio of TRIS buffer to used dye solution), and then the viruses were purified from the excess of unreacted dye using ZEBA spin desalting columns. During the procedure, the phosphate buffer in which the reaction was performed was exchanged with the virus buffer to maintain the viruses' stability. The complete protocol for staining the CCMV viruses was taken from the work by Comellas et al.33 Virus buffer was an aqueous solution of 0,1 mol l−1 sodium acetate (anhydrous, BioUltra, ≥99.0%, Sigma-Aldrich), 0.001 mol l−1 Ethylenediaminetetraacetic acid – EDTA (anhydrous, BioUltra, ≥99%, Sigma-Aldrich), 0.001 mol l−1 sodium azide (BioXtra, ≥99.8%, Sigma-Aldrich). At 25 °C (298.15 K), it has a viscosity equal to 0.89 mPa s (same as water) and a density of 1.002 g cm−3. Phosphate buffer with pH = 7.58 (di-sodium hydrogen phosphate dodecahydrate (POCH); sodium dihydrogen phosphate (POCH)), measured by pH meter HI 3220 (HANNA instruments). TRIS buffer was an aqueous solution of 1 mol l−1 tris(hydroxymethyl)aminomethane (ACS reagent, ≥99.8%, Sigma-Aldrich).
1 v/v ratio of TRIS buffer to used dye solution), and then the viruses were purified from the excess of unreacted dye using ZEBA spin desalting columns. During the procedure, the phosphate buffer in which the reaction was performed was exchanged with the virus buffer to maintain the viruses' stability. The complete protocol for staining the CCMV viruses was taken from the work by Comellas et al.33 Virus buffer was an aqueous solution of 0,1 mol l−1 sodium acetate (anhydrous, BioUltra, ≥99.0%, Sigma-Aldrich), 0.001 mol l−1 Ethylenediaminetetraacetic acid – EDTA (anhydrous, BioUltra, ≥99%, Sigma-Aldrich), 0.001 mol l−1 sodium azide (BioXtra, ≥99.8%, Sigma-Aldrich). At 25 °C (298.15 K), it has a viscosity equal to 0.89 mPa s (same as water) and a density of 1.002 g cm−3. Phosphate buffer with pH = 7.58 (di-sodium hydrogen phosphate dodecahydrate (POCH); sodium dihydrogen phosphate (POCH)), measured by pH meter HI 3220 (HANNA instruments). TRIS buffer was an aqueous solution of 1 mol l−1 tris(hydroxymethyl)aminomethane (ACS reagent, ≥99.8%, Sigma-Aldrich).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 Da (12 kDa) (values from macro viscosity measurements (Malvern Kinexus Pro rheometer), calculated according to publication34); 43
900 Da (12 kDa) (values from macro viscosity measurements (Malvern Kinexus Pro rheometer), calculated according to publication34); 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 Da (43 kDa); 91
100 Da (43 kDa); 91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 Da (92 kDa) – values from producer certificate based on GPC/SEC.
800 Da (92 kDa) – values from producer certificate based on GPC/SEC.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 U ml−1) (Merck) and penicillin (10 mg ml−1) 1% v/v (Sigma-Aldrich). For FCS experiments, cells were seeded into 8-well cover glass plates (Cellvis) and cultured overnight. Ribosomes were stained using Yo-Pro-1 dye (Invitrogen). Briefly, cells were incubated in 40 nM Yo-Pro-1 in PBS for 30 minutes before the measurement. FCS setup was calibrated using a solution of rhodamine 110 dissolved in 2.5%w/w glucose in PBS.35 Confocal volume was positioned in the cytoplasm or nucleus of the selected cell (approximately 2 μm above the glass surface). Cells were selected based on spindle-shaped morphology.
000 U ml−1) (Merck) and penicillin (10 mg ml−1) 1% v/v (Sigma-Aldrich). For FCS experiments, cells were seeded into 8-well cover glass plates (Cellvis) and cultured overnight. Ribosomes were stained using Yo-Pro-1 dye (Invitrogen). Briefly, cells were incubated in 40 nM Yo-Pro-1 in PBS for 30 minutes before the measurement. FCS setup was calibrated using a solution of rhodamine 110 dissolved in 2.5%w/w glucose in PBS.35 Confocal volume was positioned in the cytoplasm or nucleus of the selected cell (approximately 2 μm above the glass surface). Cells were selected based on spindle-shaped morphology.
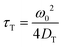
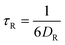

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−6DRτ)
exp(−6DRτ)
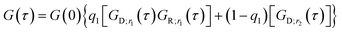

![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) 183::AID-BIP7
183::AID-BIP7![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) 3.0.CO;2-J.
3.0.CO;2-J.![[l with combining umlaut]](https://www.rsc.org/images/entities/char_006c_0308.gif) le, Characterization of photoinduced isomerization and back-isomerization of the cyanine dye cy5 by fluorescence correlation spectroscopy, J. Phys. Chem. A, 2000, 104(27), 6416–6428, DOI:10.1021/jp000059s.
le, Characterization of photoinduced isomerization and back-isomerization of the cyanine dye cy5 by fluorescence correlation spectroscopy, J. Phys. Chem. A, 2000, 104(27), 6416–6428, DOI:10.1021/jp000059s.