2D capsid formation within an oscillatory energy landscape: orderly self-assembly depends on the interplay between a dynamic potential and intrinsic relaxation times

Abstract

Multiple dissipative self-assembly protocols designed to create novel structures or to reduce kinetic traps have recently emerged. Specifically, temporal oscillations of particle interactions have been shown effective at both aims, but investigations thus far have focused on systems of simple colloids or their binary mixtures. In this work, we expand our understanding of the effect of temporally oscillating interactions to a two-dimensional coarse-grained viral capsid-like model that undergoes a self-limited assembly. This model includes multiple intrinsic relaxation times due to the internal structure of the capsid subunits and, under certain interaction regimes, proceeds via a two-step nucleation mechanism. We find that oscillations much faster than the local intrinsic relaxation times can be described via a time averaged inter-particle potential across a wide range of interaction strengths, while oscillations much slower than these relaxation times result in structures that adapt to the attraction strength of the current half-cycle. Interestingly, oscillation periods similar to these relaxation times shift the interaction window over which orderly assembly occurs by enabling error correction during the half-cycles with weaker attractions. Our results provide fundamental insights to non-equilibrium self-assembly on temporally variant energy landscapes.

---

1 Introduction

Self-assembly is the process by which a disordered system forms ordered patterns or nanostructures without external intervention due to the interactions that are encoded within the assembling components and their environment. The driving forces behind self-assembly can organize lipids into bilayers,¹ gather capsomers into viral capsids,^2–6 and arrange block copolymers into a wide range of microphase topologies.⁷

Several studies have worked to uncover governing principles that would enable the design of interparticle interactions that lead to well-ordered, self-assembled equilibrium states. As a result, we now know that the strength, placement, and specificity of the interactions between the assembling components,^8–13 their shapes,^8,9,12,14 and their concentrations^5,15 can all be tuned to stabilize a specific equilibrium target structure. However, the ability to reach these equilibrium assemblies is highly dependent upon the assembly kinetics.^5,16 Strengthening the interactions that lower the free energy of the target structure often increases the kinetic barriers to its formation, making it a challenge to design components that reliably self-assemble on a reasonable timescale.^10,16–18 Insightful work has been done to characterize the different dynamic pathways a system can take during self-assembly and the various types of kinetic traps that may emerge.^18,19 One recent article has even been able to optimize interactions that not only select a target equilibrium structure, but also simultaneously control specific kinetic features along its assembly pathway.²⁰

Alternatively, dissipative self-assembly processes can result in well-ordered structures by driving a system out of equilibrium and either creating new assembly routes towards equilibrium structures or forming non-equilibrium steady-states (NESSs).^21,22 These non-equilibrium self-assembly pathways couple an assembling system to an energy source, such as when particles are self-propelled with a constant directional force^13,23,24 or when assembly occurs within a shear flow.^25,26 Recently, large deviation theory has been successfully employed to optimize both interactions and external shear forces in order to target specific steady states.²⁵

The energy source in dissipative self-assembly may be temporally modulated through the change of an internal or external parameter, such as environmental changes that modify the interactions between assembling particles^27–29 or that change their interactions with an external field.^30–35 The self-assembly of many biological structures occurs within complex and ever-changing environments, and even certain naturally-forming non-biological materials appear to require time-variant environments to assemble – recent investigations have revealed that cycling between undersaturation and supersaturation may be necessary for the formation of naturally-occurring dolomite.^36,37

One way to optimize a time-dependent dissipative self-assembly pathway is to employ feedback control, in which the assembly process is monitored in real time and the driving forces are adjusted on the fly, based on that feedback, to guide the process towards a desired outcome. One such approach adjusted the inter-particle interactions during assembly simulations based on the ratio of correlation and response functions and the degree to which they indicated an optimal balance of local microscopic reversibility (to avoid kinetic traps) and overall global irreversibility (towards assembly).³⁸ More generally, it has been shown that high dimensional non-equilibrium time-dependent forces are able to guide an assembly towards a desired structure, however there is an unavoidable energetic cost to doing so.³⁹ Bevan and coworkers constructed an experimental system to demonstrate the feasibility of feedback control: the 2D assembly of charged colloids were monitored in real time via optical microscopy while being subjected to a tunable electric potential. Within this set-up, the electric potential was adjusted based on feedback from the structural order parameter in order to construct perfectly crystalline configurations.^40–42 Even so, it is clear that the need to monitor and adjust assembly conditions in real time would present significant difficulties to widely implementing feedback control approaches.

As an alternative to monitoring and adjusting each assembly process in real-time, information can be gathered from multiple simulations or experimental realizations of a dissipative assembly process and used to construct time-dependent protocols that are optimized for the ensemble of likely assembly pathways. One such approach employed evolutionary reinforcement learning to determine time-dependent temperature and chemical potential protocols for the efficient assembly of patchy disks into desired polymorphs.⁴³ Similarly, Markov state models have been constructed from simulations of colloidal oligomers and capsids in order to design optimal time-dependent interaction profiles for the finite-time folding and assembly of those systems.⁴⁴ However, significant data is required in order to optimize each time-dependent protocol, which will depend on the specifics of the system, and the implementation of these time-dependent protocols in real systems may prove challenging.

Oscillatory or cyclic changes to the environment in which assembly proceeds may provide a more experimentally accessible avenue to design new dissipative assembly pathways. A number of studies have shown that the cyclical exposure of oil droplets to an external magnetic field can facilitate local relaxation processes in the resulting aggregates, thereby enabling them to overcome kinetic barriers to equilibration.^30–35,45 In simulations of photosensitive nanoparticles, light-induced aggregation proceeded more rapidly after short pauses in the light irradiation.⁴⁶ Simulations by Risbud and Swan found that toggling inter-particle depletion interactions on and off at a timescale that allowed for sufficient particle diffusion relaxed kinetic traps and resulted in the more rapid formation of low-defect colloidal crystals.⁴⁷ Finally, joint experiment and simulation work showed that the cyclic toggling of an external electric field on a timescale close to the characteristic melting time could anneal defects in colloidal crystals.⁴⁸

Temporal environmental oscillations may also provide experimentally accessible ways to create and maintain long-lived non-equilibrium steady states (NESSs). Tagliazucchi and coworkers used simulations and theory to show that novel non-equilibrium steady state phases of binary pH-sensitive colloids can form when pH oscillations are faster than the colloid's characteristic diffusional timescale,^27,28 and a similar effect was observed with three dimensional close packed colloids.²⁹ Additional simulations have shown that oscillations in inter-particle interactions and external fields can result in ellipsoids adopting a non-equilibrium chiral smectic phase⁴⁹ and in the formation of non-equilibrium lamellar structures in homopolymer mixtures.⁵⁰

Prior work has focused on the assembly of extended NESS structures or the annealing of defects in extended colloidal crystals. In this work, however, we investigate the assembly of a self-limited capsid-like model with multiple inherent length scales and relaxation timescales that arise from the internal structure of the capsid building blocks. Specifically, we probe the impact of oscillatory time-dependent interactions on the assembly mechanisms over a range of oscillation timescales and amplitudes. In Section 2, we outline the coarse grained viral capsid-like model. In Section 3.1, we discuss assembly with static interactions. Then, in Section 3.2, we perform simulations with oscillatory interactions that are faster than, slower than, or similar to inherent relaxation timescales within the model to probe their influence on assembly. Finally, in Section 3.3, we vary oscillation amplitude to investigate how these temporal oscillations can act as an error correction technique. As summarized in Section 4, we find that the inherent timescales of the model system are critical in determining the effect of fast, intermediate, and slow oscillatory interactions on the resulting assembly process.

2 Modeling

Viral capsid models have proven essential in the theoretical and computational study of self-assembly, due in part to their organization into self-limiting ordered structures.^{5,15,19,51–58} Inspired by earlier studies on capsid assembly, in this work we investigate the assembly of two-dimensional, rigid triangular particles that assemble into capsid-like hexamers, as shown in Fig. 1a. The model was based upon a similar one in Mallory and Cacciuto's work on the role of self-propulsion in capsid-like colloidal assembly.¹³ The placement of attractive particles (green) on only two edges of the triangles causes these monomer units to assemble either into distinct hexamers or into extended snake-like structures (see Fig. 1a).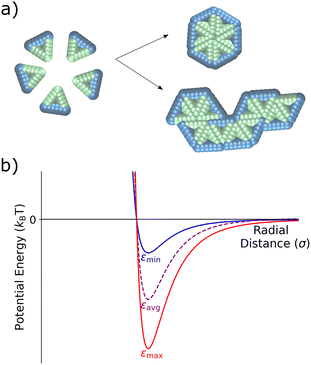

Fig. 1 Schematic of the coarse-grained capsid-like model and inter-particle potential. (a) Triangular particles with two type A edges (green) and one type B edge (blue) start in a random distribution within the simulation box. Type A – type A interactions are defined via a Lennard-Jones potential, while the type A – type B and type B – type B particles interact via a Weeks–Chandler–Andersen potential.⁵⁹ As the simulation proceeds, triangles can assemble into hexameric capsid-like structures or into larger snake-like aggregates. (b) The Lennard-Jones potential for the type A – type A interaction, showing the two different values of ε – ε_min and ε_max – with the time-averaged ε_avg shown in purple.

The triangular monomers are composed of fifteen partially overlapping circular subparticles that are rigidly held together, as shown in Fig. 1a. Each subparticle is assigned one of two different types, A or B, which determines its interparticle potential. The subparticles on two edges of the equilateral triangle are assigned type A (green) and interact via a Lennard-Jones (LJ) potential, the strength of which can be tuned by changing ε, the LJ well-depth. The subparticles on the third edge are assigned type B (blue) and interact via the Weeks–Chandler–Andersen (WCA) potential.⁵⁹ Thus, type B subparticles are purely repulsive, and interactions between type A and type B subparticles are also defined by the WCA potential. The placement of these differently-interacting subparticles introduces an overall anisotropic interaction between the individual triangular particles. Fig. 1b illustrates the attractive interactions between the type A subparticles of different triangular particles for various ε values. A more detailed descriptions of the particles and interactions can be found in the ESI.†

Oscillatory interactions are implemented by switching the ε value of the type A-type A interactions between ε_min and ε_max in a square wave pattern. We investigate the effect on capsid formation of variations in both the oscillation period and its amplitude (defined as the magnitude of the shift in each direction from the central, ε_avg-value). Variations in ε are considered here as a way to investigate the effects of a temporally-dependent interaction strength on assembly.

Simulations begin with a randomly distributed system of 150 triangular particles in a periodic box with no particle overlap. Langevin dynamics is utilized to evolve the system in time, which also provides a thermostat to maintain a constant temperature over the simulation and mimics the drag and random fluctuations associated with the dynamics of solvated particles. The system is first allowed to equilibrate with the type A interactions turned off and all subparticles interacting via the WCA potential, as this ensures that there is no particle overlap while establishing a random initial distribution of the triangles, both spatially and orientationally. After the equilibration period, the type A attractive interactions are turned on, and the system is progressed for 150 000τ, where τ is time in reduced units. See ESI† for additional details.

3 Results and discussion

3.1 Capsid assembly is non-monotonic with attraction strength

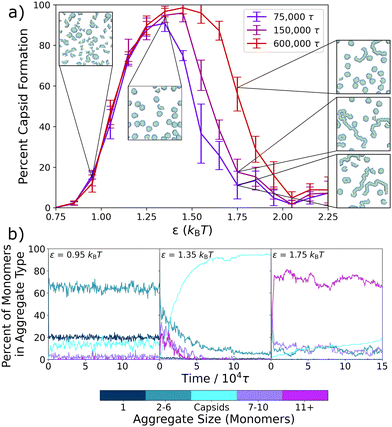
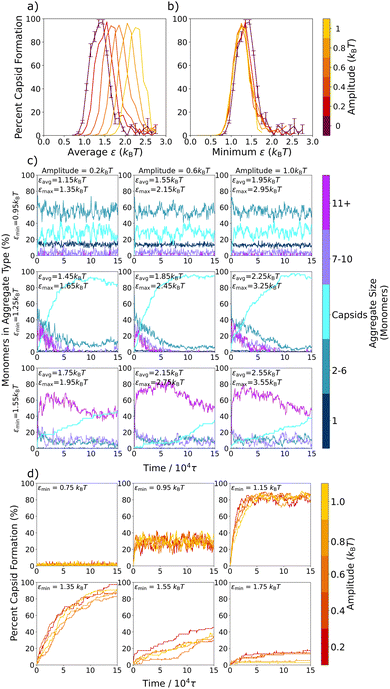
We first model the formation of the complete capsid-like hexamers within a series of static environments, each with fixed effective interactions, ranging from ε = 0.75k_BT to ε = 2.25k_BT. Fig. 2a shows the resulting capsid yields and sample configurations as a function of ε for three different simulation times, and Fig. 2b shows how the presence of differently-sized aggregates changes with ε and simulation time.

Fig. 2 Capsid yield and aggregate formation within the static system. (a) Capsid yield curves are plotted after three different simulation times vs. the attraction strength, ε. As simulation time increases, the capsid yield does not change on the left hand side of the curve. However, on the right hand side, capsid yield increases with longer simulation time. Inset are final snapshots of the system at ε = 0.95k_BT, ε = 1.35k_BT, and ε = 1.75k_BT. (b) The percentage of triangular monomers within each group of different sized aggregates is plotted over 150 000τ for three different ε values (ε = 0.95k_BT, ε = 1.35k_BT, and ε = 1.75k_BT). Aggregates of varying size are shown with the color bar, with the hexameric structure shown in cyan. Capsid yields and kinetic traces are averaged over five independent trajectories, and the error bars in (a) display the standard deviation.

In keeping with prior work on similar models of viral capsids,^{5,13,19,52,54,56} we observe in Fig. 2a that capsid assembly is non-monotonic with interaction strength. As ε increases from 0.75k_BT to 1.35k_BT, capsid yield also increases. However, above ε = 1.35k_BT, capsid yield decreases. This non-monotonic trend is due to a transition from thermodynamically equilibrated systems on the left-hand side of the curve to kinetically constrained systems on the right-hand side as interactions become too strong for full equilibration to occur within the simulation time. Sampling for various lengths of time verifies this transition from thermodynamic to kinetic products, as the left-hand side of the curve remains unchanged for sampling times ranging from 75 000τ to 600 000τ, while the right-hand side shifts to higher values as sampling times lengthen and the kinetically constrained structures have additional time to relax.

The inset snapshots in Fig. 2a provide further evidence of this transition. At low ε interaction strengths, such as shown for ε = 0.95k_BT, most triangles exist as free monomers or in small aggregates, and only a few complete capsids form. By ε = 1.35k_BT, the snapshot shows almost complete capsid formation. However, at ε = 1.75k_BT, well-formed capsids appear alongside larger, snake-like and kinetically trapped aggregates, with the number of snake-like aggregates decreasing and the number of capsids increasing as simulation times lengthen.

To better probe capsid assembly kinetics, in Fig. 2b we track the percent of the triangular monomers that are assembled into differently sized aggregates as a function of simulation time. At a weaker interaction strength of ε = 0.95k_BT, the system almost instantaneously assembles into small aggregates of 2–6 monomers (turquoise) in length, which slightly decreases over the first 1 × 10⁴τ of the simulation as a small number of capsids (cyan) assemble. At an intermediate attraction strength of ε = 1.35k_BT, a significant number of longer aggregates composed of 7–10 (purple) and 11+ (magenta) monomers rapidly form initially, but then decrease on the same timescale as capsid structures emerge. At a stronger attraction of ε = 1.75k_BT, where the capsid yield curve has crossed into the kinetic regime, most monomers rapidly assemble into the largest aggregates (magenta), which only slightly and gradually convert into capsids over the remainder of the simulation time. By 150 000τ, most monomers remain in these very large aggregates due to the difficulties in overcoming the high energetic barriers associated with strong inter-particle interactions.

Interestingly, at the intermediate and stronger attraction values, the assembly process in Fig. 2b follows a non-classical, two-step assembly pathway.^60,61 During non-classical assembly pathways, which have been seen in protein^11,62,63 and colloidal particle crystallization,^64–66 the system assembles into a condensed, disordered phase that has a lower free energy barrier to nucleation than the disassembled system, so that the final assembled structure grows from pre-formed aggregates.^63,65,66 This process is clearly in evidence at both ε = 1.35k_BT and ε = 1.75k_BT in Fig. 2b, where capsid counts increase as the initially assembled larger aggregates decrease. To probe exactly the ε values at which this changeover in assembly mechanism occurs, we expand Fig. 2b in Fig. S2 (ESI†) and plot the results for values ranging from ε = 0.75k_BT to ε = 2.15k_BT at 0.10k_BT intervals. Evidence for this two-step mechanism can be seen as early as ε = 1.25k_BT, and a clear cross-over is seen around ε = 1.45k_BT, where non-capsid monomers are present in smaller and larger aggregates in about equal numbers, with both types of aggregates decreasing as capsids form. At higher ε values, the two-step pathway dominates, with most monomers assembling rapidly into the larger, snake-like aggregates.

Having established the assembly behavior of the 2D model capsid system within a series of static environments, we now temporally vary the inter-monomer attractions by switching the strength of the Lennard-Jones potential between two values during assembly. We define the stronger attraction strength as ε_max and the weaker interaction strength as ε_min. The oscillation amplitude defines the distance of ε_max and ε_min from a central ε_avg value, where ε_avg = (ε_max + ε_min)/2 see Fig. 1. We also define the period of oscillation, τ_osc, as the time it takes to complete a full cycle, with half the cycle at ε_max and the other half at ε_min. In the rest of the paper, we investigate how these oscillatory interactions influence capsid formation across a variety of oscillation periods (Section 3.2) and oscillation amplitudes (Section 3.3).

3.2 Assembly depends on the oscillation frequency

First, we consider how different oscillation periods, τ_osc, affect the assembly process. During the ε_max half-cycle, triangular monomers are more strongly attractive and assemble together, while in the ε_min half-cycle, such structures may rearrange or be broken apart. The degree to which assembly and disassembly occurs depends upon the time spent in each half-cycle, and how that time compares to the time required for the system to equilibrate.

Previous studies investigating oscillations in inter-colloidal potentials compare τ_osc to a characteristic diffusional time-scale, t_d = σ²/D, where σ specifies the size of the assembling colloids and D is the diffusion coefficient.^27,47 Oscillation periods that are significantly shorter than the characteristic diffusional time-scale (τ_osc ≪ t_d) are considered to be at the fast oscillation limit, while at the slow oscillation limit (τ_osc » t_d), periods are long enough to allow the system to relax to different equilibrium structures during each oscillation half-cycle.^27,28,47

As can be seen in the structure shown in Fig. 1, more than one length-scale is needed to fully describe the assembling particles; the diameter of the circular subparticles is σ_LJ = 0.25σ, while the edge length of the triangular particles is 1σ. In addition, at the higher attraction strengths we probe, capsid formation proceeds via the initial formation of a condensed disordered phase (see Fig. 2a) and its subsequent relaxation. The multiple length-scales and assembly pathways within this model are expected to influence how capsid formation varies with oscillation frequency.

To better understand the interplay of the oscillation period and these inherent length-scales, we list in Table 1 a set of key distances that characterize important energetic and structural changes, ranging from the distance required to reduce the attractive interaction to a tenth of its maximum strength to the full edge length of a single triangular particle. To estimate how long it would take for the triangular particles to traverse these distances, we plot the mean squared displacement vs. time for a single triangular particle in Fig. S3a (ESI†). Since the relevant length scales span the ballistic and diffusive time regimes, we estimate the time it takes for the particle to move over these critical distances directly from the results in Fig. S3a (ESI†). Additionally, we plot in Fig. S3b (ESI†) the rotational autocorrelation function vs. time for a single triangular particle and calculate the mean rotational lifetime using an exponential decay fit. Below, we first consider oscillations at the fast limit, where the period is shorter than the timescales associated with these key distances (τ_osc ≪ {t_d}), and show that the assembly behavior in this regime can be described by the ε value averaged over a single oscillation period, ε_avg. Next, we investigate slow oscillations, where the period is longer than the timescales that correspond to the distances in Table 1 (τ_osc ≫ {t_d}), such that the system has time to at least partially equilibrate to the current ε value during each half period of the oscillation. Lastly, we simulate oscillations in the intermediate regime (τ_osc ≈ {t_d}) and show how the window of capsid assembly shifts with the oscillation period.

Table 1 Characteristic lengths and their corresponding relaxation times. Important length-scales within the model are provided along with the estimated time, t_d, that it takes for a single, isolated, triangular particle to move over that distance or to lose its rotational orientation, based on its mean squared displacement and its rotational autocorrelation function (see Fig. S3, ESI)

Characteristic distance	Distance (σ)	t d (τ)
a For the rotational relaxation, td describes the mean lifetime for the exponential decay from the rotational correlation function in Fig. S3b (ESI).
0.72σLJ (−ε → −0.1ε)	0.18	0.59
Diameter of subparticle	0.25	0.91
Edge of triangle	1.00	10.33
Rotational relaxation^a	—	7.10

---

The fast oscillation limit obtains the equilibrium yield curve for a well-depth of ε_avg. In prior work on colloidal assembly under an oscillatory potential, Szleifer and coworkers employed the Fokker–Planck equation while dividing up the oscillation period into a series of infinitesimally small time steps to show that, when the period of oscillation is much, much shorter than the inherent diffusional time-scale of the simulated colloidal particles, the oscillatory interaction potential can be described by a static effective inter-particle potential that is equal to the time-averaged potential over a single oscillation period.^27,28 In our system, where we oscillate the well-depth of the Lennard-Jones potential such that half of each oscillation period is at a strength of ε_max and half at a strength of ε_min, the time-averaged potential over a single period works out to be the LJ potential with a well depth of ε_avg = (ε_max + ε_min)/2 (see ESI† for details).

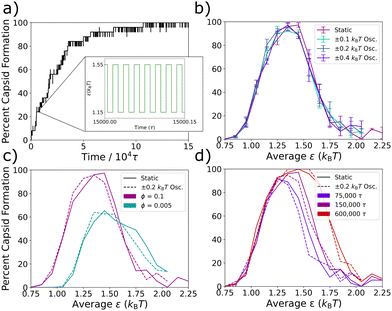
To test the behavior of our system at the fast oscillation limit, in Fig. 3 we compare the degree of capsid formation at static ε values to that at the corresponding ε_avg values for various oscillation amplitudes, monomer concentrations, and simulation times. An oscillation period of 0.02τ was chosen (see Fig. 3a), which is expected to yield fast limit behavior since it is much shorter than the calculated time-scales of interest in Table 1. In Fig. 3b, we confirm that this period reproduces the static non-monotonic yield curve across three different oscillation amplitudes. In Fig. 3c, we test the correspondence between the static and effective potentials across changes in particle density. The static yield curves (solid lines) at volume fractions of ϕ = 0.1 and ϕ = 0.005 differ, which is expected since a decreased volume fraction requires a stronger ε for capsid formation. However, at both densities, the oscillatory potential with a period of 0.02τ and an amplitude of 0.2k_BT (dashed lines) returns the corresponding static yield curve for ε_avg. Finally, in Fig. 3d, we investigate the timescales of relaxation at the fast oscillation limit as compared to those in the static system by comparing the oscillatory and static capsid yield curves after simulation times of 75 000τ, 150 000τ, and 600 000τ. We find that capsid formation at the fast oscillation limit increases with simulation time in precisely the same way as capsid formation does within the corresponding static potential. This result suggests that kinetic traps affect the system dynamics at the fast oscillation limit in the same way as in the static system, supporting the prior claim that even a system's non-equilibrium dynamics can be described by an appropriate time-averaged potential at the fast oscillation limit²⁸ and explaining the observation that in both Fig. 3b and c, the correspondence between the oscillatory and static curves is as good for the kinetically constrained right-hand side of the curve as it is for the thermodynamically equilibrated left-hand side. In summary, when the Lennard-Jones potential is oscillated at a very short period of 0.02τ, the system organizes in the same manner as with the non-oscillatory potential across a number of tested variations.

Fig. 3 Assembly at the fast oscillation limit. (a) A kinetic trace is shown from a single 150 000τ trajectory of the assembling capsids at an attraction strength of ε_avg = 1.35k_BT, an oscillation amplitude of 0.2k_BT, and an oscillation period of 0.02τ. Inset displays a zoomed in schematic of the oscillation waveform to compare the oscillation frequency to the timescale of capsid assembly. (b) Capsid yield curves at 150 000τ are plotted for three different amplitudes as well as the non-oscillatory system at a period of 0.02τ. (c) Capsid yield curves at 150 000τ are plotted for the oscillatory system at a period of 0.02τ and the static potential are shown at two different densities. (d) Capsid yield curves at three different simulation times are plotted for the static system (solid lines) and compared to the results for the system with interactions oscillated for a period of 0.02τ with an amplitude of 0.2k_BT (dashed lines). Percent capsid formation is averaged over three independent trajectories, and the average standard deviations for the capsid yield measurements were ±3.2% for the static systems and ±3.8% for the oscillatory systems.

Under slow oscillations, the system adapts to the ε value of each half-cycle. Next we look at the slow oscillation limit, where the period is longer than the displacement times {t_d} in Table 1, and the system has sufficient time within a single half-cycle to adapt itself substantially to the current ε value. Fig. 4 plots capsid yield as a function of simulation time for the static reference case (a) and three longer oscillation periods (b–d), for three different ε_avg values, all with an oscillation amplitude of 0.4k_BT.

Fig. 4 Capsid formation changes with each half-cycle. Capsid formations at different ε_avg values are shown at an oscillation amplitude of 0.4k_BT for three longer periods, as compared to the non-oscillatory capsid formation curves in (a). We show (b) τ_osc = 6250τ, (c) τ_osc = 12 500τ, and (d) τ_osc = 50 000τ. Each period has the waveform overlaid in gray to show the oscillation period. The kinetic traces are averaged over three independent trajectories.

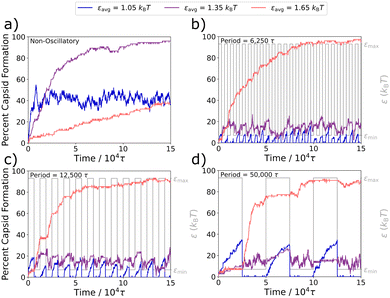
In the Fig. 4a static case, a weaker attraction strength of ε_avg = 1.05k_BT results in the capsid yield quickly plateauing to about 40%, a moderate attraction strength of ε_avg = 1.35k_BT results in nearly complete capsid assembly over a slightly longer time-scale, and a stronger interaction strength of ε_avg = 1.65k_BT results in kinetic trapping and slow capsid assembly.

In Fig. 4b–d, we plot capsid formation along with the oscillation profiles for periods of 6250τ, 12 500τ, and 50 000τ, where τ_osc ≫ {t_d}. For the weakest interaction strength of ε_avg = 1.05k_BT (in blue), at the given amplitude of 0.4k_BT, the simulation oscillates between a well-depth of ε_min = 0.65k_BT and ε_max = 1.45k_BT. For all three τ_osc periods, capsids rapidly assemble in the ε_max half-cycle and rapidly disassemble in the ε_min half-cycle, where interactions are too weak for the structures to remain intact. As with the weakest ε_avg value, simulations at the strongest ε_avg value investigated here of 1.65k_BT (in orange) also display significantly different assembly behaviors in each half-cycle. At these stronger attraction strengths, capsids no longer rapidly fall apart during the ε_min half-cycles, however the kinetically trapped snake-like structures can still relax to form additional capsids. As a result, significant capsid formation occurs during the ε_min half-cycles of ε_avg = 1.65k_BT. These capsids remain intact during the ε_max half-cycles, however the stronger attractive forces keeping the subparticles together also largely arrest the relaxation of kinetic traps and thus the formation of additional capsids. Behavior with the intermediate ε_avg of 1.35k_BT (in purple) is more complex. The system oscillates between ε_min = 0.95k_BT and ε_max = 1.75k_BT, both of which result in only modest capsid yields in the static system (see Fig. 2a), and we observe that same modest yield in all three longer oscillation periods in Fig. 4b–d, despite the fact that a high yield is obtained for ε = 1.35k_BT in the static case in Fig. 4a.

Overall, when considering oscillations that are slow compared to the characteristic displacement times in Table 1, we see that the system substantially adapts to each half-cycle, which can result in capsid yields that grow and shrink over each oscillation or in capsid yields that remain static during most ε_max half-cycles and then further increase during most ε_min half-cycle. It is important to note that even the very long oscillation periods investigated here are still shorter than the time needed to fully relax the kinetic traps of the system, which can take longer than 75 000τ even at ε = 1.45k_BT, just slightly above the capsid yield curve's peak (see Fig. 2a).

Intermediate oscillation periods causes yield curves to shift to stronger ε_avg-values. In order to probe how oscillatory interactions influence capsid assembly between the fast and slow oscillation limits, in Fig. 5 we plot the capsid yield curves across a range of oscillation periods at an amplitude of 0.4k_BT. Details of aggregate formation for three of these periods are shown for a range of ε_avg values in Fig. S4 (ESI†).

Fig. 5 Capsid yield curves for different periods of oscillation. (a) Capsid yield curves after 150 000τ are compared to the scaled ε_avg value (in units of k_BT^(obs)) for different oscillation periods at an amplitude of 0.4k_BT. The black, dashed line indicates 50% capsid formation on the left hand side of the yield curves. (b) The scaled ε_avg values that result in 50% capsid formation on the left hand side of the capsid yield curve are plotted vs. τ_osc. The dark gray bar indicates the non-oscillatory regime, the light gray bar plots the upper asymptotic limit of a sigmoidal fit, and the dotted line indicates the midpoint between the two. Points in (b) that are shown in (a) are represented by a closed circle, while additional periods not shown in (a) are denoted by an open circle. (c) The percentage of assembled capsids is plotted over 150 000τ for three different ε_avg values (ε_avg = 1.35k_BT, ε_avg = 1.55k_BT, ε_avg = 1.75k_BT) for six different oscillation periods and the static case are shown with the color bar. Capsid yield and kinetic growth curves are averaged over three independent trajectories, and the error bars on the static yield curve show its standard deviation.

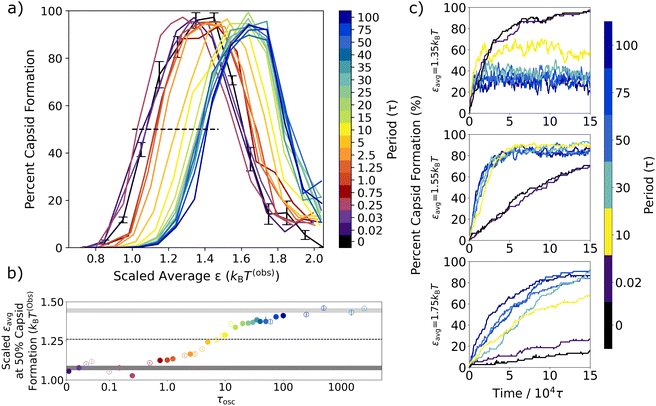
For all periods, capsid assembly remains non-monotonic with interaction strength, and the window of orderly assembly is approximately the same width for systems undergoing oscillatory interactions as for those with static interactions. However, as the period of oscillation increases in Fig. 5a, the capsid yield curves shift to higher ε_avg values, which is similar to results from simulations on colloidal crystal grown under toggled interactions.⁶⁷ Our results show that the window of orderly assembly can be expanded into interaction strengths that are typically infeasible due to their long relaxation times.

One technical complication arises as the oscillation period increases slightly from the fast oscillation limit period of 0.02τ. From about 0.03τ to about 5τ, where τ_osc is similar to the timescale of the thermostat relaxation, we find that the Langevin thermostat is not able to maintain the target temperature due to the rate of energy transfer as the interparticle potentials oscillate. To enable comparisons that include these oscillation frequencies, the ε_avg values in Fig. 5 were simply scaled by reporting ε values in units of k_BT^(obs), where T^(obs) is the actual observed temperature at each oscillation period. A plot of the observed temperatures vs. oscillation period is shown in Fig. S1 in the ESI.†

To quantify the capsid yield curve shift, in Fig. 5b we plot the appropriately scaled ε_avg value that results in 50% capsid formation on the left hand side of the yield curves in Fig. 5a (i.e., where it intersects the black dashed line) vs. the oscillation period, τ_osc. The ε value that results in 50% capsid formation in the static system is indicated by the dark gray bar, while the corresponding ε_avg value for the long oscillation periods is indicated by the light grey bar.

The result for the fast oscillation limit (τ_osc = 0.02τ) overlaps with the non-oscillatory dark gray bar, as previously observed in Fig. 3. For oscillation periods between 0.02τ and about 0.5τ, the scaled ε_avg values are clustered around the dark gray bar and there is no sustained shift away from the static ε value. After 0.5τ, however, the scaled ε_avg value at 50% capsid formation steadily increases with oscillation period, crosses the dotted line that indicates the halfway point between the fast and slow oscillation limits at a period of about τ_osc = 7τ, and then plateaus at the slow oscillation value (light grey bar).

To make sense of the shift with oscillation period in Fig. 5, we return to the inherent length-scales of our model and their corresponding local relaxation time-scales, as described in Table 1. After aggregates nucleate, there are three important local relaxation processes that facilitate the second stage of the hexagonal capsid formation from either smaller or larger aggregates: (1) the diffusion of subparticles away from one another; (2) the sliding of triangular particle edges along one another; and (3) the rotation of a triangular particle away from or towards another. All three of these movements are more likely to occur during the ε_min half-cycle when attractions are weaker. Table 1 provides estimates for the timescales of these local relaxation processes, based on simulations of a single triangular particle (see Fig. S3, ESI†). First, the diffusion of one subparticle out of the LJ attractive well of a neighboring subparticle is characterized by the length-scale of the LJ attraction. The distance a subparticle must move for the attractive interaction to be reduced to a tenth of its full strength is 0.18σ, which is estimated to take approximately 0.6τ. Second, the edge length of a single triangular particle is 1.0σ, and the corresponding diffusion time for that distance is 10.3τ. Third, the mean lifetime for the rotational degree of freedom is estimated to be 7.1τ, based on the rotational correlation function calculated in Fig. S3 (ESI†). These intrinsic local relaxation timescales aid our interpretation of the shift in the capsid yield curves with oscillation period in Fig. 5.

At a period of τ_osc = 0.5τ, where the steady shift towards higher ε_avg values starts, there is just enough time during each ε_min half-period for a subparticle to move away from a neighbor so that their attractive LJ interaction is reduced by two thirds. At a period of about 1.2τ, the ε_min half-cycle is just slightly longer than the time it takes for a subparticle's LJ interaction to be reduced to a tenth of its maximum strength, on average. That is, particles that were originally interacting are likely to diffuse far enough from their original configurations so that they no longer experience a significant attraction to their original neighbors.

The black dashed line indicates the half-way mark between the fast and slow oscillation behaviors, which happens at an oscillation period of about τ_osc = 7τ. From Table 1, we see that several local relaxation processes that are helpful in the formation of capsids are achievable within an ε_min half-period of 3.5τ. Within this half-cycle, particles can diffuse far enough from their original configurations so that they no longer experience a significant attraction to their original neighbors, even shifting the full diameter of a subparticle. If a particle located in an aggregate can shift a subparticle away from their original configuration, this could lower the energetic barrier for the triangle to diffuse from an aggregate structure.

After a period of 20τ, we observe the start of a plateau in the scaled ε_avg values that corresponds to 50% capsid formation. Interestingly, a period of 20τ corresponds to a half-cycle of 10τ, which is about the time needed for a triangular particle to diffuse 1σ, or the distance of one full edge of the triangle. This edge length is an important distance in disrupting longer aggregates, since a particle in the middle of a snake-like aggregate would need to diffuse about 1σ to leave the aggregate and thereby break up a longer aggregate. In addition, this length is central to the motions of a trimer of particles that enable full capsid formation from a half-capsid structure on the end of a snake-like aggregate, as can be seen in Fig. 1. Given the mean rotational lifetime of approximately 7τ, it is clear that by an oscillation period of 20τ, triangular particles can fully diffuse from aggregate structures and rotate to better align with other particles to facilitate capsid formation during the ε_min half-cycles.

To probe the effect of oscillations on capsid assembly kinetics, in Fig. 5c we track the percent capsid formation as a function of simulation time for several oscillation periods and ε_avg values. As expected from prior theoretical work,²⁸ the kinetics under the static potential and at the fast oscillation limit are indistinguishable for all ε_avg values. In contrast, intermediate oscillation periods result in faster capsid assembly rates relative to the static potential case for all ε_avg values. This increase in assembly rates has been previously observed in other oscillatory protocols.^48,65 We find it is most dramatic at the higher ε_avg values (Fig. 5c, bottom two panels) since, at intermediate periods, the oscillations shift the capsid yield curve into the interaction regime where static assembly slows due to kinetic trapping. However, this increased rate holds even in the case of ε_avg = 1.35k_BT, where the oscillatory cases with intermediate periods (10τ and longer) plateau more rapidly than the static case – even though they plateau at lower capsid yields.

A closer look at the ε_avg = 1.35k_BT case (Fig. 5c, top panel) provides helpful insight as to why the capsid yield curve shifts to the right as the oscillation period increases but does not broaden. The oscillation amplitude in Fig. 5 is 0.4k_BT, so the ε_avg = 1.35k_BT case oscillates between an ε_min value of 0.95k_BT and an ε_max value of 1.75k_BT. At the fast oscillation limit, the capsid yield after 150 000τ should be equal to that of the static yield at ε = 1.35k_BT (96%), which we observe. At the slow oscillation limit, we expect the yield to switch back and forth between the capsid yields expected for the ε_min and ε_max values, which are 12% and 14%, respectively. In the intermediate oscillation regime, we see that the system forms a non-equilibrium steady state where the steady-state capsid yield depends on the oscillation period. As the period increases, the capsid yield will eventually transition away from the fast oscillation limit value of 96% to the slow oscillation limit values of 12% (an equilibrium value) and 14% (a kinetically-determined value, which will depend on the initial configuration and the relaxation time). At that slow oscillation limit, it will no longer be in a steady-state, and the number of capsids will shift depending on the oscillation half-cycle. Overall, the observed yield curve on the left-hand side shifts to the right with increased oscillation period. On the right-hand side of the shifted curves, when ε_min becomes too strong, the weaker half-cycle can no longer facilitate error correction, which results in the oscillatory capsid yield curves reproducing the static yield curve's non-monotonic behavior.

3.3 Shift in capsid yield with amplitude provides evidence for the critical role of error correction

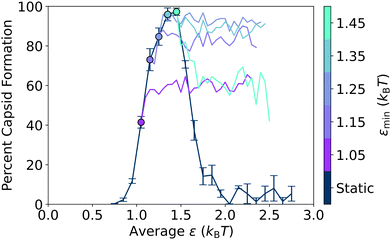
Previously, Risbud and Swan⁴⁷ and others^30–35,45 observed that oscillating attractions could result in local relaxation, since the system was able to relax kinetic barriers via diffusion when the attractions were turned off. In our model, the formation of capsid-like structures is also limited by kinetic traps at stronger attractions, as demonstrated in Fig. 2a by the increase in capsid yield with longer simulation times. In addition, at these higher ε values, the initial formation of snake-like structures that can convert into capsid-like hexamers makes it clear that error correction – the ability of sub-optimally assembled particles to rearrange themselves into a more favorable structure – plays an important role in the total capsid yield, both in the static and oscillatory interaction cases. Indeed, in Fig. 4b–d, at the slow oscillation limit with an amplitude of 0.4k_BT, we directly observed the effect of error correction on the capsid formation process during the lower ε_min half-cycles for the case where ε_avg = 1.65k_BT. Capsid yields almost always remained static in the ε_max half-cycles, but ratcheted up to higher levels in the ε_min half-cycles. In this section, we further probe how the ε_min half-cycles affect error correction within this model system by varying the oscillation amplitude. As the amplitude increases, ε_avg stays the same, but attractions oscillate between a weaker ε_min and stronger ε_max. Results are shown in Fig. 6 for an intermediate oscillation period of 100τ, which is long enough for most local relaxation processes to occur – see Table 1 and the almost-completed shift towards the long-time oscillation value at 100τ in Fig. 5b.

Fig. 6 Capsid yield and aggregate formation for different oscillation amplitudes. Capsid yield curves are plotted in (a) vs. ε_avg and in (b) vs. ε_min for five different oscillation amplitudes with an oscillation period of 100τ and the static potential case. The formation of different sized aggregates is plotted vs. time in (c) for three different amplitudes at a period of 100τ. Although they have different ε_avg values, ε_min = 0.95k_BT for all amplitudes in row 1, ε_min = 1.25k_BT for all amplitudes in row 2, and ε_min = 1.55k_BT for all amplitudes in row 3. (d) The capsid growth curves are plotted over 150 000τ for six different ε_min values at five different oscillation amplitudes (shown with the color bar). Capsid yield curves and monomer counts in the different aggregate types are averaged over three independent trajectories. In the static case in (a) and (b), the error bars represent the standard deviation.

In Fig. 6a, we show a series of capsid yield curves at different oscillation amplitudes plotted vs. ε_avg. As amplitude increases, yield curves shift to the right to higher ε_avg values – values where orderly assembly is not observed in the static system. However, when we plot these same yield curves vs. ε_min instead of ε_avg in Fig. 6b, the curves for all amplitudes collapse into one curve, which is very close to the capsid yield curve for the static potential. This collapse of the yield curves indicates that, at oscillation periods sufficiently longer than the local intrinsic relaxation processes in the system, the main determinant of capsid yield in the oscillatory system is simply the value of ε_min. Indeed, this full shift from the yields observed at ε_avg to those observed at ε_min as the oscillation periods lengthen can be clearly seen in Fig. 5a.

To further probe this shift to the ε_min value fully determining the yield at oscillation times longer than the local relaxation processes, in Fig. 6c we show the percent of the triangular monomers in each aggregate size as a function of time for a series of simulations with varying amplitudes and ε_min values. From the top row to the bottom row, ε_min increases, while within each row, ε_min is held fixed while the amplitude increases from left to right. Notably, we find that the kinetic assembly traces for a given ε_min value are essentially the same across the three amplitudes. In Fig. 6d we overlay the kinetic traces for full capsid assembly over more amplitudes and ε_min values. Regardless of oscillation amplitude, the capsid yield curves collapse onto one another for each ε_min value, demonstrating that ε_min largely determines capsid assembly even as ε_avg changes. Similar kinetic curve collapses have been observed in experiments of polarizable colloids exposed to toggled magnetic fields³² and simulations of nanoparticles with toggled potentials.⁶⁷ This universal ε_min dependence shows that, as long as oscillation periods are longer than the local intrinsic relaxation processes and ε_max is above the threshold for kinetic trap formation, the strength of ε_min is what determines the degree to which kinetically trapped aggregates are able to relax into fully formed capsids.

Building on this insight, in Fig. 7, we plot capsid yield curves for static and oscillatory protocols where ε_min is fixed at different attraction strengths, ε_max is varied, and the results are plotted vs. ε_avg. On the left-hand size, there is a slight increase in the yield as the ε_avg value increases from the corresponding static case (indicated by the dot). In contrast, on the right-hand side, there is a drop off in the yield as ε_avg increases from the static case. In both cases, the yield appears to plateau at some point as ε_avg increases further. Essentially, further increases in attraction strength past some value of ε_max do not change the resulting yield, which then depends only on the error correction enabled by the ε_min value, as shown in Fig. 6. As a result, fixing ε_min to a value just below the peak of the static capsid yield curve removes the non-monotonicity of the static yield curve.

Fig. 7 Capsid yield for oscillation protocols where ε_min is held constant. Capsid yields are plotted at an oscillation period of 100τ for five fixed ε_min conditions while ε_max is varied, and the results are plotted vs. ε_avg. The static yield curve is shown for comparison, and the static result corresponding to each ε_min series is indicated with the solid colored dot. All capsid yields plotted have been averaged over three independent trajectories. The error bars show the standard deviations on the static curve.

4 Conclusion

In this work, we investigate how temporal oscillations influence the dissipative self-assembly of anisotropic 2D triangular particles that assemble into self-limited capsid-like structures. At stronger attractions, the formation of these hexamers occurs through a non-classical, two-step nucleation pathway and is prone to kinetic trapping, resulting in a non-monotonic dependence of capsid yield on attraction strength in both the static and oscillatory cases.

Temporal oscillations in inter-particle attractions offer experimentally accessible dissipative self-assembly protocols for a wide range of materials. Such oscillations may be implemented by changes in temperature, external applied fields, light irradiation, pH changes, or other mechanisms, and in our study we implement them by changing the strength of the attractions in time by switching between two LJ well-depths. As in previous studies, we find that tuning the oscillations enables orderly assembly across a broader range of time-averaged interactions, as can be seen in the envelope of capsid yield curves in Fig. 5 and the full region of ε_avg that they span, which provides routes to substantive capsid yields at any of these time-averaged interaction strengths. In addition, we generally observe faster capsid formation under oscillatory conditions, providing a route to more rapidly produce self-limited assembled structures.^33,48,67

In keeping with prior work,^47,48 our results highlight the correspondence between the different oscillation timescales and the particle motions that govern local relaxation processes – in the case of our more complex anisotropic particles, these include both translations and rotations. At the limit of oscillations that are very fast compared to these intrinsic time-scales, assembly proceeds as if the system were subject to the static attraction that is the time-averaged strength over a single oscillation period, defined by the averaged LJ well-depth, ε_avg. At the slow oscillation limit, the system evolves according to the attractive forces at play within the current half-cycle. In between these extremes, the assembly yield curve shifts from one determined by ε_avg to one determined by ε_min, the attraction strength during the weaker attraction half-cycles, since it is the error correction made possible at those times that determines the degree to which kinetic traps can be overcome.

These findings provide insights that could aid in the design of time-dependent assembly protocols for novel materials. Advanced materials may be composed of more complex, hierarchically ordered components with multiple intrinsic lengths, and thus multiple relaxation time-scales. Even without closed feedback loops or detailed simulations of the specific system of interest, we show that designing protocols with interactions that oscillate over times similar to the intrinsic relaxation times of that material may provide efficient assembly routes. Estimating the translational and rotational timescales that corresponds to important energetic and structural length scales within the assembling system will serve as a starting point for creating oscillation protocols that can relax kinetically trapped structures. In addition, the choice of an oscillation amplitude may be guided by evaluating the interaction regimes where moderate assembly occurs under static conditions, as we find that error correction within a system can be enhanced by periodically switching to attraction strengths that promote a moderate yield and are therefore weak enough to allow critical relaxation processes to proceed.

Author contributions

Jessica K. Niblo: conceptualization, investigation, methodology, data curation, software, formal analysis, visualization, writing – original draft. Jacob R. Swartley: methodology, writing – reviewing. Zhongmin Zhang: methodology, writing – reviewing. Kateri H. DuBay: conceptualization, methodology, supervision, formal analysis, writing – original draft.

Data availability

The data presented in this study, along with submission and analysis scripts, are openly available on GitHub at https://github.com/dubayresearchgroup/2024_VCO_1.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This material is based upon work supported by a startup grant from the University of Virginia. The authors also acknowledge Research Computing at the University of Virginia (https://rc.virginia.edu) for providing computational resources and technical support that have contributed to the results reported within this publication.

Notes and references

1. N.-J. Cho, L. Y. Hwang, J. J. R. Solandt and C. W. Frank, Materials, 2013, 6, 3294–3308.
2. A. Zlotnick, J. Mol. Biol., 1994, 241, 59–67.
3. A. Zlotnick, R. Aldrich, J. M. Johnson, P. Ceres and M. J. Young, Virology, 2000, 277, 450–456.
4. S. D. Hicks and C. L. Henley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 031912.
5. M. F. Hagan and D. Chandler, Biophys. J., 2006, 91, 42–54.
6. C. Sigl, E. M. Willner, W. Engelen, J. A. Kretzmann, K. Sachenbacher, A. Liedl, F. Kolbe, F. Wilsch, S. A. Aghvami, U. Protzer, M. F. Hagan, S. Fraden and H. Dietz, Nat. Mater., 2021, 20, 1281–1289.
7. N. A. Lynd, A. J. Meuler and M. A. Hillmyer, Prog. Polym. Sci., 2008, 33, 875–893.
8. Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413.
9. S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562.
10. S. Hormoz and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5193–5198.
11. T. K. Haxton and S. Whitelam, Soft Matter, 2012, 8, 3558.
12. M. Grünwald and P. L. Geissler, ACS Nano, 2014, 8, 5891–5897.
13. S. A. Mallory and A. Cacciuto, Phys. Rev. E, 2016, 94, 022607.
14. P. F. Damasceno, M. Engel and S. C. Glotzer, Science, 2012, 337, 453–457.
15. M. F. Hagan and O. M. Elrad, Biophys. J., 2010, 98, 1065–1074.
16. J. Grant, R. L. Jack and S. Whitelam, J. Chem. Phys., 2011, 135, 214505.
17. A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150–168.
18. S. Whitelam and R. L. Jack, Annu. Rev. Phys. Chem., 2015, 66, 143–163.
19. M. F. Hagan, O. M. Elrad and R. L. Jack, J. Chem. Phys., 2011, 135, 104115.
20. C. P. Goodrich, E. M. King, S. S. Schoenholz, E. D. Cubuk and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024083118.
21. G. M. Whitesides and M. Boncheva, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4769–4774.
22. M. Fialkowski, K. J. M. Bishop, R. Klajn, S. K. Smoukov, C. J. Campbell and B. A. Grzybowski, J. Phys. Chem. B, 2006, 110, 2482–2496.
23. S. E. Ilse, C. Holm and J. de Graaf, J. Chem. Phys., 2016, 145, 134904.
24. H. Löwen, Europhys. Lett., 2018, 121, 58001.
25. A. Das and D. T. Limmer, J. Chem. Phys., 2021, 154, 014107.
26. A. Das and D. T. Limmer, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2217242120.
27. M. Tagliazucchi, E. A. Weiss and I. Szleifer, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 9751–9756.
28. M. Tagliazucchi and I. Szleifer, Faraday Discuss., 2016, 186, 399–418.
29. C. Long, Q.-l Lei, C.-l Ren and Y.-q Ma, J. Phys. Chem. B, 2018, 122, 3196–3201.
30. J. H. E. Promislow and A. P. Gast, Langmuir, 1996, 12, 4095–4102.
31. J. H. E. Promislow and A. P. Gast, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 642–651.
32. J. W. Swan, P. A. Vasquez, P. A. Whitson, E. M. Fincke, K. Wakata, S. H. Magnus, F. De Winne, M. R. Barratt, J. H. Agui, R. D. Green, N. R. Hall, D. Y. Bohman, C. T. Bunnell, A. P. Gast and E. M. Furst, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16023–16028.
33. J. W. Swan, J. L. Bauer, Y. Liu and E. M. Furst, Soft Matter, 2014, 10, 1102–1109.
34. J. L. Bauer, Y. Liu, M. J. Kurian, J. W. Swan and E. M. Furst, J. Chem. Phys., 2015, 143, 074901.
35. H. Kim, M. Sau and E. M. Furst, Langmuir, 2020, 36, 9926–9934.
36. J. M. García-Ruiz, Science, 2023, 382, 883–884.
37. J. Kim, Y. Kimura, B. Puchala, T. Yamazaki, U. Becker and W. Sun, Science, 2023, 382, 915–920.
38. D. Klotsa and R. L. Jack, J. Chem. Phys., 2013, 138, 094502.
39. S. Chennakesavalu and G. M. Rotskoff, J. Chem. Phys., 2021, 155, 194114.
40. J. J. Juárez and M. A. Bevan, Adv. Funct. Mater., 2012, 22, 3833–3839.
41. Y. Xue, D. J. Beltran-Villegas, X. Tang, M. A. Bevan and M. A. Grover, IEEE Trans. Control Syst. Technol., 2014, 22, 1956–1963.
42. X. Tang, B. Rupp, Y. Yang, T. D. Edwards, M. A. Grover and M. A. Bevan, ACS Nano, 2016, 10, 6791–6798.
43. S. Whitelam and I. Tamblyn, Phys. Rev. E, 2020, 101, 052604.
44. A. Trubiano and M. F. Hagan, J. Chem. Phys., 2022, 157, 244901.
45. J. Martín-Roca, M. Horcajo-Fernández, C. Valeriani, F. Gámez and F. Martínez-Pedrero, Nanomaterials, 2023, 13, 397.
46. P. K. Jha, V. Kuzovkov, B. A. Grzybowski and M. Olvera de la Cruz, Soft Matter, 2012, 8, 227–234.
47. S. R. Risbud and J. W. Swan, Soft Matter, 2015, 11, 3232–3240.
48. P.-K. Kao, B. J. VanSaders, S. C. Glotzer and M. J. Solomon, Sci. Rep., 2021, 11, 11042.
49. Z.-Q. Chen, Y.-W. Sun, Y.-L. Zhu, Z.-W. Li and Z.-Y. Sun, Soft Matter, 2022, 18, 2569–2576.
50. L. Pigard and M. Müller, Phys. Rev. Lett., 2019, 122, 237801.
51. R. L. Jack, M. F. Hagan and D. Chandler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 021119.
52. H. D. Nguyen, V. S. Reddy and C. L. Brooks, Nano Lett., 2007, 7, 338–344.
53. D. C. Rapaport, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051905.
54. D. C. Rapaport, Phys. Rev. Lett., 2008, 101, 186101.
55. V. Krishna, G. S. Ayton and G. A. Voth, Biophys. J., 2010, 98, 18–26.
56. J. D. Perlmutter and M. F. Hagan, Annu. Rev. Phys. Chem., 2015, 66, 217–239.
57. A. J. Pak, J. M. A. Grime, A. Yu and G. A. Voth, J. Am. Chem. Soc., 2019, 141, 10214–10224.
58. M. F. Hagan and G. M. Grason, Rev. Mod. Phys., 2021, 93, 025008.
59. J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247.
60. D. Kashchiev, P. G. Vekilov and A. B. Kolomeisky, J. Chem. Phys., 2005, 122, 244706.
61. J. J. De Yoreo, P. U. P. A. Gilbert, N. A. J. M. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Cölfen and P. M. Dove, Science, 2015, 349, aaa6760.
62. J. Dogan, S. Gianni and P. Jemth, Phys. Chem. Chem. Phys., 2014, 16, 6323–6331.
63. C. J. Wilson, A. S. Bommarius, J. A. Champion, Y. O. Chernoff, D. G. Lynn, A. K. Paravastu, C. Liang, M.-C. Hsieh and J. M. Heemstra, Chem. Rev., 2018, 118, 11519–11574.
64. Z. M. Sherman and J. W. Swan, ACS Nano, 2016, 10, 5260–5271.
65. Z. M. Sherman and J. W. Swan, ACS Nano, 2019, 13, 764–771.
66. J. R. Savage and A. D. Dinsmore, Phys. Rev. Lett., 2009, 102, 198302.
67. Z. M. Sherman, H. Rosenthal and J. W. Swan, Langmuir, 2018, 34, 1029–1041.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00455h

---