Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stable polydisperse free-standing porous films made by mechanical deformation†
Hsiao-Ping
Hsu
 and
Kurt
Kremer
and
Kurt
Kremer
 *
*
Max-Planck-Institut für Polymerforschung, Ackermannweg 10, Mainz, 55128, Germany. E-mail: hsu@mpip-mainz.mpg.de; kremer@mpip-mainz.mpg.de
First published on 2nd August 2024
Abstract
Using molecular dynamics simulations, we show that the methodology of making thin stable nanoporous monodisperse films by biaxial mechanical expansion and subsequent cooling into the glassy state, also works for polydisperse films. To test this, a bidisperse polymer system of an equal number of very long (≈72 entanglements) and short (≤4 entanglements) chains with a polydispersity index of 1.80 is considered. The void formation and the development of the local morphology upon expansion, relaxation, and cooling are investigated. As for the monodisperse case, long chains in thin porous polydisperse films extend over several pores, stabilizing the whole morphology. The short chains do not fill up the pores but tend to aggregate inside the polymer matrix and to avoid surface areas and reduce conformational constraints imposed by the surrounding, a scenario very similar to strain-induced segregation between the strained long and relaxed short chains.
I. Introduction
Porous polymer membranes are of high scientific and technological interest because of their potential applications in many fields such as water filtration, fuel cells or in pharmaceutical and biotechnology industries. This wide field of potential applications makes robust and simple preparation procedures very desirable.1,2 Typically the preparation of (nano)porous films takes advantage of incompatibility of components. Thus, a variety of block copolymers3 have been employed for designing nanostructured porous materials by changing block volume fractions, molecular weights, thermodynamic interactions between chemically different blocks (incompatibility), and solvent qualities.4–9 A collection of recently developed synthesis methods of generating micro-, meso-, and macro-porous materials with different properties is summarized in ref. 10. There exist also several reviews describing specific application driven requirements such as specific large absorption areas, high surface to volume ratios,5,8,11 and prospective developments.12 However, most methods of making porous polymer membranes are rather complex and often need very elaborate precision chemistry, and require processes controlled in detail.In our recent work,13–15 we have demonstrated by simulation and by experiment that stable well controlled nanoporous films can be made just by mechanical deformation of highly entangled monodisperse polymer films and a subsequent quench of this nonequilibrium material into the glassy state. We have shown that the long chains extend over several bridges between pores. The relaxation is significantly slowed down by chain entanglements, which display a high density at regions of merging bridges between pores. This stabilizes the pores and prevents further growth and coalescence. In our previous study we have found typical pore diameters dp ≈ 5–10dT, dT being the reputation tube diameter. For the simulation part we considered a melt of chains of length N = 2000 ≈ 71Ne, Ne = 28 being the entanglement length while for experiment we used polystyrene (PS) of 1000 kDa ≈ 60Me with a polydispersity index of MW/MN = 1.03. Thus in both cases there were either no short chains or their volume fraction was negligible. Of course if one thinks of a broader application of such a process, which is just based on mechanical deformation of a pure polymer system without any additives or stabilizing chemical reactions, the demand of such a high monodispersity could be detrimental. Thus we investigate the influence of short chains on the properties of the mechanically deformed polymer films by studying a system containing an equal number of long and short chains. We show that the same process can be successfully applied to such polydisperse highly entangled polymer films. The short chains aggregate in the center of the polymer bridges, which form the pore walls and avoid contact with the surface. By that the average pore size is somewhat larger due to a slightly increased effective entanglement length, but the qualitative picture remains unchanged.
The outline of the paper is as follows: we first describe the system and investigate the morphological properties of polydisperse film subject to biaxial expansion in Section II. Then the developments of porous structures of thin expanded films upon subsequent relaxation in Section III and cooling in Section IV are analyzed. Finally, Section V contains our conclusions.
II. Morphology of polydisperse films upon biaxial deformation
We consider a thick polymer film containing an equal number of chains of two lengths, N1 = 1900 and N2 = 100, respectively, which leads to a polydispersity index of MW/MN = 1.8. This system was prepared by starting from the fully equilibrated free-standing monodisperse polymer film containing 1000 weakly semiflexible chains of N = 2000 monomers of a simulation model based on a modification of the standard bead-spring model,16–19 which is well suited to study systems with free surfaces and the glass transition, at bulk melt (monomer number) density14,20ρ0 = 0.85σ−3. To prepare the bidisperse films a short piece of length N2 = 100 was cut off at the end of each chain of N = 2000. This film of now 2000 chains was equilibrated for about 3τR,N=N2, τR,N being the Rouse time of chains of size N, a time long enough for the short chains to move their own diameter. Alternatively, equilibrated polydisperse films can also be prepared via a soft-sphere approach and hierarchical backmapping.20,21 By this we arrived at eqilibrated films of effective thickness h ≈ 130σ ≈ 4.4R(0)g(N = N1) and two lateral dimensions with periodic boundary conditions, Lw = Lx = Ly ≈ 134σ. For comparison, R(0)g(N = N1 = 1900) ≈ 29.3σ and R(0)g(N = N2 = 100) ≈ 6.7σ are the root-mean square radii of gyration for bulk chains22 of size N, while we here have Rg(N1 = 1900) ≈ 28.5σ and Rg(N2 = 100) ≈ 6.7σ, showing that chain in thick films are very similar to those in bulk.14,20This free standing film is subject to a simple “biaxial expansion” deformation. It is stretched into two lateral dimensions, i.e., equal-biaxial strain23–25 with periodic boundary conditions up to a maximum expansion of λ × λ ≈ 4 × 4 at T = 1.0ε/kB, while the thickness of the film is free to adjust, cf. Fig. S1 of ESI† (ref. 26). We follow the same protocol as in our previous work.13,14 In our earlier work we compared fast and slow deformation and found no significant differences in the results. Thus, we here apply the fast deformation rate, as shown in Fig. S1 and S2 (ESI†). The deformation rate is set that we can expect subchains of length of up to 0.6Ne ≈ 17 can equilibrate during the expansion, while the conformations of longer strands will be affected. Details are given in the appendix.
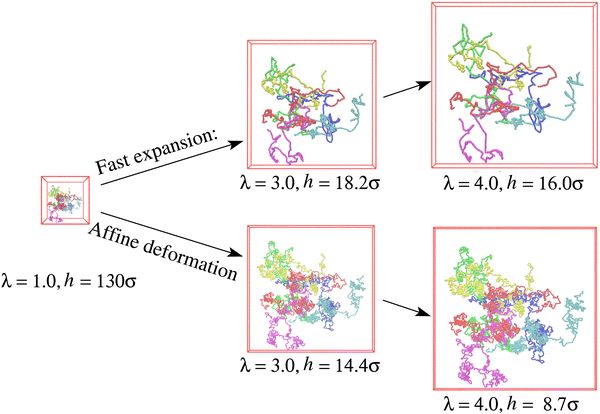
Snapshots of free-standing polydisperse polymer films for λ ≈ 1.0, 3.0, and 4.0 produced with an effective average strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) τe ≈ 2.61 (see Fig. S2b, ESI†) are shown in Fig. 1. To demonstrate the conformational changes of long chains in the film, six randomly selected chains of N1 = 1900 are marked in different colors. Obviously, the overall shape of long chains follows an affine deformation while short chains do not (shown in Fig. S3 of ESI†). The overall morphologies are quite similar as they were observed for a monodisperse polymer films subject to a similar expansion rate
τe ≈ 2.61 (see Fig. S2b, ESI†) are shown in Fig. 1. To demonstrate the conformational changes of long chains in the film, six randomly selected chains of N1 = 1900 are marked in different colors. Obviously, the overall shape of long chains follows an affine deformation while short chains do not (shown in Fig. S3 of ESI†). The overall morphologies are quite similar as they were observed for a monodisperse polymer films subject to a similar expansion rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) τR,N=2000 ≈ 14
τR,N=2000 ≈ 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 710, i.e.,
710, i.e., ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) τe ≈ 2.88, also allowing for relaxation of subchains up to about 0.6Ne (see ref. 14).
τe ≈ 2.88, also allowing for relaxation of subchains up to about 0.6Ne (see ref. 14).
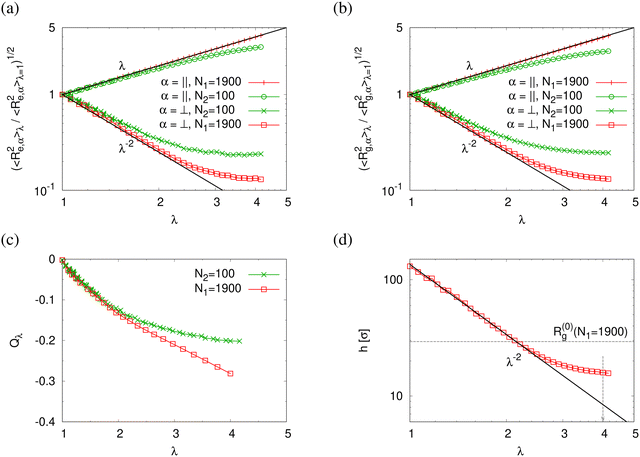
Normalized strain-dependent chain extensions are shown in Fig. 2a and b. Affinely, the deformation follows λ for the parallel components and λ−2 for the perpendicular, respectively. For N1 = 1900 the in-plane expansion is affine all the way up to λ ≈ 4.0, while deviations for N2 = 100 develop around λ ≈ 2.6. In the perpendicular direction, long chains deform affinely (λ−2) only up to λ ≈ 2.4 in agreement with the adjustment of the film thickness, cf.Fig. 2d, while short chains deform nonaffinely almost from the very beginning. These global conformational changes also lead to characteristic changes in the bond orientational order parameter Qλ. Choosing the z-axis as a reference, 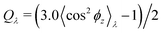 where ϕz is the angle between any bond vector and the z-axis. For an isotropic distribution of bond directions Qλ = 0, while Qλ = −1/2, if all bonds would lie in the xy plane. The strain-dependent orientational order parameter Qλ of bond vectors along chains of N1 = 1900 shows that bond vectors in the extended films tend to lie randomly along the direction parallel to the interfaces. For short chains of N2 = 100, Qλ approaches a plateau value for λ > 3.5. The effective film thickness h determined from the monomer density profile (see Fig. S4a of ESI†) follows affine deformation up to λ ≈ 2.6 then approaches a plateau value approximately for λ ≥ 3 in the thin film regime, Fig. 2d.
where ϕz is the angle between any bond vector and the z-axis. For an isotropic distribution of bond directions Qλ = 0, while Qλ = −1/2, if all bonds would lie in the xy plane. The strain-dependent orientational order parameter Qλ of bond vectors along chains of N1 = 1900 shows that bond vectors in the extended films tend to lie randomly along the direction parallel to the interfaces. For short chains of N2 = 100, Qλ approaches a plateau value for λ > 3.5. The effective film thickness h determined from the monomer density profile (see Fig. S4a of ESI†) follows affine deformation up to λ ≈ 2.6 then approaches a plateau value approximately for λ ≥ 3 in the thin film regime, Fig. 2d.
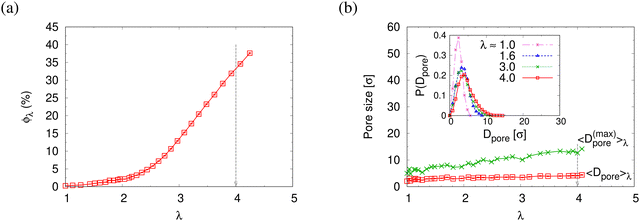
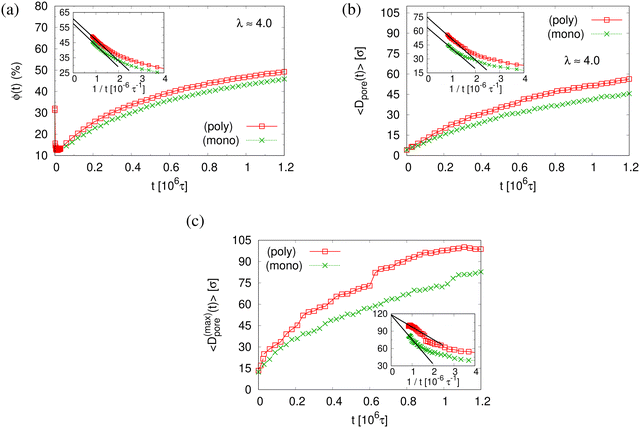
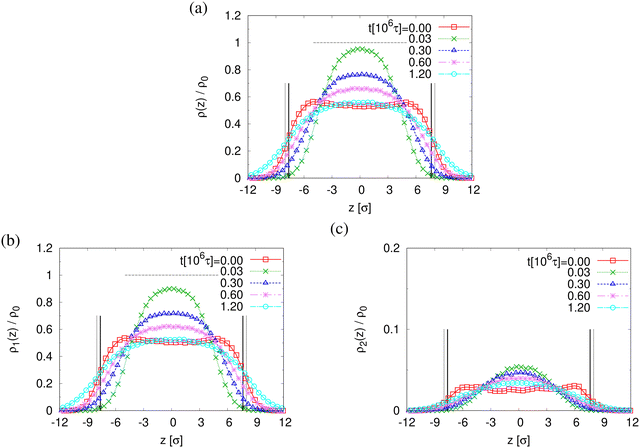
The reduction of the normalized monomer density profile for λ > 2.3 shown in Fig. S4a (ESI†) indicates the onset of porosity ϕ (see Fig. 3a). Considering monomers in long and short chains separately, Fig. S4b and c show that ρ1(z) and ρ2(z) follow the same behavior as ρ(z). Here the porosity ϕ and pore size distribution P(Dpore) of pore diameter Dpore in expanded films is estimated following the definition given by Gubbins et al.,27–30 where ϕ and P(Dpore) depend on the accessible volume of a hard spherical test particle of size 1.0σ. I.e. the test particles explore all regions in the film, where the nearest monomer is at least a distance of 1σ away. This is a purely geometrical measure, as no interaction between test particles and monomers is considered. The porosity ϕ is then given by the percentage of void volume Vvoid compared to the total effective volume Vfilm = hLxLy of the films.14 Results of the strain-dependent porosity ϕλ, average pore size 〈Dpore〉λ, maximum pore size 〈D(max)pore〉λ, and probability distribution of pore size P(Dpore) are shown in Fig. 3. The porosity ϕ increases monotonically with the increase of strain λ. No significant change in 〈Dpore〉 while 〈D(max)pore〉 increases with the increase of strain λ slightly. P(Dpore) has a unimodal-like distribution and the distribution becomes broader with the increase of λ. Again this is very similar to the results of monodisperse films.
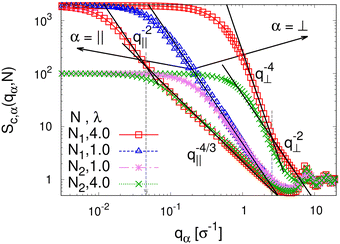
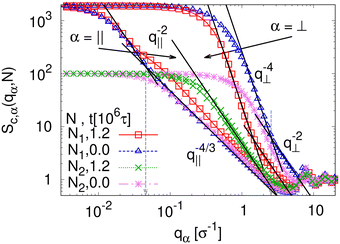
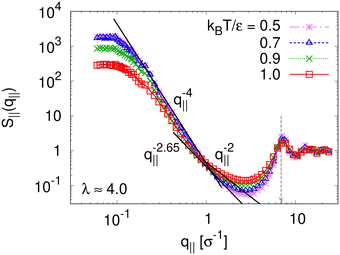
To detect the anisotropy of the chain structure and to compare short and long chains the strain-dependent two components of single chain structure factor Sc,‖(q‖,N) and Sc,⊥(q⊥,N) are shown in Fig. 4. Initially, at λ = 1 both, Sc,‖(q‖,N) and Sc,⊥(q⊥,N) ∼ q⊥−2 follow the Gunier law decay Sc,α(qα,N) = N(1 − qα2Rg,α2(N)/3) for small qα as expected for ideal bulk chains. As the strain λ increases, Sc,⊥(q⊥,N) increases while Sc,‖(q‖,N) decreases which are consistent with the change in 〈Rg,⊥2(N)〉λ and 〈Rg,‖2(N)〉λ shown in Fig. 2b, respectively. In the thin film regime (λ ≥ 3.0), chains are highly stretched in the expansion plane. As for the monodisperse case chains Sc,‖(q‖,N) ∼ q‖−4/3 in an intermediate q‖ range. We relate this 2-d self-avoiding walks like structure to the pore structure in the film, as argued below. Again there is no difference between short and long chains in this regime. As for the monodisperse case the pores seem to introduce an effective excluded volume on shorter and intermediate length scales. Only on large length scales, q‖ ≤ 0.045σ−1 the ideal chain behavior Sc,‖(q‖,N) ∼ q‖−2 is recovered for N = N1 = 1900. In contrast, Sc,⊥(q⊥,N) ∼ q⊥−2, on short length scales (q⊥ > 2σ−1). On large length scales, a sharp interface described by a Porod law like scaling Sc,⊥(q⊥,N) ∼ q⊥−4 is observed for λ ≥ 3.0. However, the short chains seem to be a bit compressed in the perpendicular direction on shorter length scales.
We also calculate the two components of the collective scattering function of the films, S‖(q‖) and S⊥(q⊥), respectively (see Fig. S5 of ESI†). The intensity of S‖(q‖) increases with λ on large and intermediate length scales while on short length scales (q‖ > 2σ−1), it remains unchanged, showing that the local monomer packing is still conserved. The conserved peak at 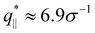 shows that the inter-monomer packing distance of
shows that the inter-monomer packing distance of 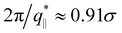 still remains the same. On large and intermediate length scales, S‖(q‖) ∼ q‖−2 is observed at λ ≥ 3.0. The sharp local minima at nq = hq⊥/(2π), nq = 1, 2,… in the curves of S⊥(q⊥) confirm that the film thickness estimate h shown in Fig. 2d is consistent with the estimate from S⊥(q⊥). Even the q⊥−4 envelope for λ = 4 is reasonably well displayed, which is an indication of a rather uniform film thickness. Altogether, the data are almost indistinguishable from the monodisperse case. There is, however one interesting difference for λ = 1.0. The low q‖ regime indicates a slightly smaller compressibility or spatial density inhomogeneity for the polydisperse film compared to the monodisperse one. This indicates that short chain additions seem to level out fluctuations more effectively.
still remains the same. On large and intermediate length scales, S‖(q‖) ∼ q‖−2 is observed at λ ≥ 3.0. The sharp local minima at nq = hq⊥/(2π), nq = 1, 2,… in the curves of S⊥(q⊥) confirm that the film thickness estimate h shown in Fig. 2d is consistent with the estimate from S⊥(q⊥). Even the q⊥−4 envelope for λ = 4 is reasonably well displayed, which is an indication of a rather uniform film thickness. Altogether, the data are almost indistinguishable from the monodisperse case. There is, however one interesting difference for λ = 1.0. The low q‖ regime indicates a slightly smaller compressibility or spatial density inhomogeneity for the polydisperse film compared to the monodisperse one. This indicates that short chain additions seem to level out fluctuations more effectively.
III. Relaxation of expanded polydisperse film at T = 1.0ε/kB
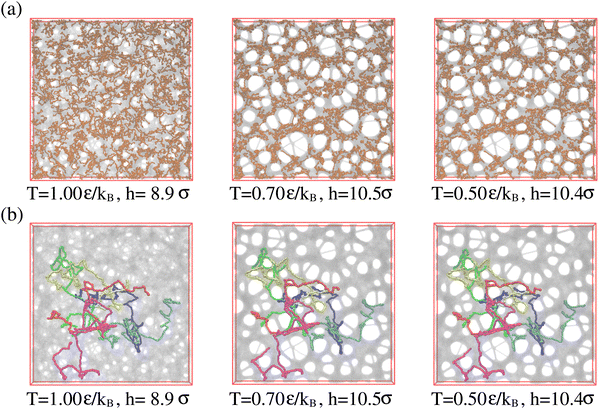
So far we have studied the initial structure of the expanded films and found that the differences between mono- and polydisperse films are only marginal and that the dominance of the very long chains to determine the film properties remains unchanged. We now turn to the relaxation of the expanded film at the process temperature, kept at λ ≈ 4.0. Our previous study on monodisperse films at λ ≈ 4.0 has shown a strong retardation of conformational relaxation. This eventually stabilized nanoscopic pores, which then slowly grew under fixed strain. The overall pore diameter was limited by entanglement constraints. The central question here is, whether and how the shorter chains influence the stability and growth of pores. It should be kept in mind that T = 1.0ε/kB ≈ 1.5T(0)g, T(0)g ≈ 0.67ε/kB being the glass transition temperature of a bulk polymer melt.31,32 To investigate the influence of polydispersity we follow the same relaxation protocol as in ref. 13 and 14 and observe the relaxation of the films by MD simulations in the NVT ensemble over a time of up to t = 1.2 × 106τ. Fig. 5 shows the morphological changes of expanded polydisperse polymer film, see Fig. S6 in the ESI,† for more details. We observe the same nucleation and slowed coarsening of the hole structures as for the monodisperse case with, however, somewhat larger holes. There is one important difference between a typical nucleation and the growth mechanism in our present system. Small pores, which disappear by shrinking and not by merging with other pores, since the long polymers extend over several holes merging is prevented. Fig. 5 already points to three important features. The first, just as for the monodisperse films, long chains extend over several pores, stabilizing the whole morphology. Second, the short chains seem to tend to aggregate inside the polymer matrix and avoid the surface regions. This is even better seen, when we look at thin slices of the film. Slices of thickness 3σ are shown in Fig. S7 in the ESI.† And third, this aggregation scenario is very similar to strain-induced segregation between the strained long and relaxed short chains is observed due to the reduction of conformational constrains of short chains imposed by the surrounding.Times covered range up to t = 1.2 × 106 ≈ 530τe, corresponding to the Rouse time of subchains of length of Ns ≈ 644. Similarly, as observed for monodisperse films upon fast expansion and in contrast to slow expansion, initially no well defined pore structure is seen. After a short time well defined pores nucleate. The pore sizes increase accompanied by some drop in the number of pores. The growth of the pores slows down significantly after about half of the relaxation time, which corresponds to the Rouse time of subchains of about 16Ne. Pore sizes in the fast expanded monodisperse film appear only weakly smaller than in the polydisperse film. This relaxation retardation is also demonstrated by the six marked chains whose conformations only marginally change, obviously due to the topological constraints these highly entangled chains encounter.33–35 Moreover, in all cases the shape of pores tends to become spherical to minimize surface tension.
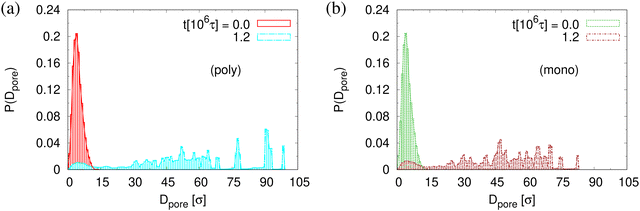
The small difference in pore size and porosity is confirmed by the direct measurement of the porosity ϕ(t), the pore size Dpore(t), and the maximum pore size D(max)pore(t) which all increase upon time (see Fig. 6). For both films the average pore sizes and maximum pore sizes continue to grow only very slowly with increasing time. The average pore diameter at t = 1.2 × 106τ corresponds to about 46σ ≈ 9dT for monodisperse film. Here we observe 56σ for the polydisperse film. Assuming that this size is directly determined by the tube diameter, we estimate the shift in dT upon cutting off the short chains, since they have ample time to relax completely in the course of the relaxation. With N1 = 1900 for the polydisperse system the packing length p = N1/(ρ1R2(N1)) is increased by a factor of 1/0.95, ρ1 being the density of just the long chains. Taking the relation between plateau modulus and p and Ne, respectively, one would expect a shift of dT of about 5%, which is relatively close to the shift in the pore diameter.36 Assuming a linear extrapolation to 1/t→0, ϕ(t) ≈ 61% and 〈D(max)pore(t)〉 ≈ 120σ converge within error to the same values for both cases while 〈Dpore(t)〉 is larger for expanded polydiseperse film, 〈Dpore(t)〉 ≈ 75σ ≈ 14dT, and 64σ ≈ 13dT for the monodisperse film, respectively. Again this shift is roughly within the expected range. A more detailed theoretical account, however, is needed to make this argument more quantitative. The probability distributions of pore size Dpore, P(Dpore) are shown in Fig. 7. At t = 0τ, P(Dpore) has a unimodal distribution for both cases, and it becomes a much broader multimodal distribution at t = 1.2 × 106τ. For polydisperse film, results of P(Dpore) show that the probability of finding larger pore size Dpore increases while it decreases for small pore sizes, as illustrated in Fig. 5, similar as for the expanded monodisperse film upon fast expansion.
The finding that the system relaxation slows down significantly also is supported by the reduction of restoring forces per unit area, σB(t), shown in Fig. 8. We observe a dramatic reduction in net restoring stress σB(t) = |Pzz(t) − (Pxx(t) + Pyy(t))/2| after a very short initial time of about (0.2–0.3) × 106τ. At the same time Pzz(t) remains at 0.0ε/σ3. Furthermore, after that the time-dependent stress is almost indistinguishable between these two cases, again in accord with the visual inspections of the membranes. The results of h(t) in Fig. 8b show that the initial reduction of film thickness for both cases follows the same curve. This reverse behavior for the films upon fast expansion also appears in the change of monomer density profile ρ(z) (see Fig. 9). Eventually the expanded polydisperse film upon relaxation remains somewhat thicker in agreement with the apparently slightly larger porosity and thus larger pores.
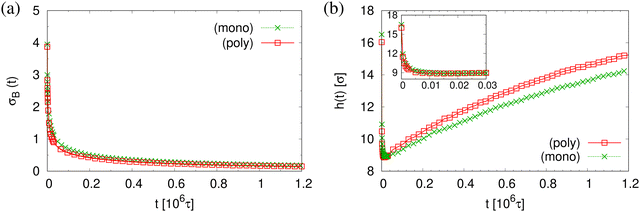 | ||
| Fig. 8 Net stress σB(t) (a), and film thickness h(t) (b), plotted versus relaxation time t for polydisperse and monodisperse porous films at λ ≈ 4.0. | ||
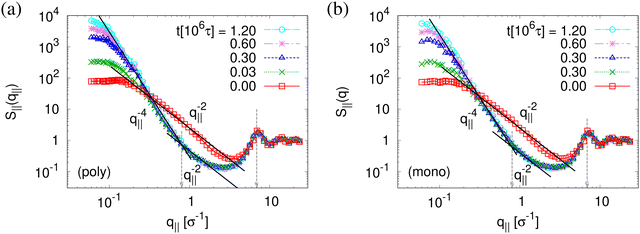
The above described scenario is well supported by the in expansion plane collective structure factor S‖(q‖) in Fig. 10 at several relaxation times t. The region around the amorphous halo at 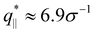 remains unchanged upon relaxation for all times. Thus the local bead packing is not affected by our processes. With the increase of time, the signature of sharp pore surfaces, Porod scaling S‖(q‖) ∼ q‖−4, is stabilized and extended a little further to larger length scales, as expected by the slow increase of porosity37ϕ(t) (see Fig. 6). For both cases, the initially fuzzy interfaces sharpen and already after short relaxation time the same scaling is observed. The initially large q‖−2 regime narrows down to a small region. In all cases, S‖(q‖) reaches a shallow maximum/plateau at low q‖, roughly corresponding to distances around 100σ, corresponding to 2–3 average pore diameters and reminding of a semidilute 2-d liquid of hard disks (i.e. the pores). It should be noted that the late time data are almost indistinguishable from the same data obtained from films, which were expanded in a much slower process, see ref. 14.
remains unchanged upon relaxation for all times. Thus the local bead packing is not affected by our processes. With the increase of time, the signature of sharp pore surfaces, Porod scaling S‖(q‖) ∼ q‖−4, is stabilized and extended a little further to larger length scales, as expected by the slow increase of porosity37ϕ(t) (see Fig. 6). For both cases, the initially fuzzy interfaces sharpen and already after short relaxation time the same scaling is observed. The initially large q‖−2 regime narrows down to a small region. In all cases, S‖(q‖) reaches a shallow maximum/plateau at low q‖, roughly corresponding to distances around 100σ, corresponding to 2–3 average pore diameters and reminding of a semidilute 2-d liquid of hard disks (i.e. the pores). It should be noted that the late time data are almost indistinguishable from the same data obtained from films, which were expanded in a much slower process, see ref. 14.
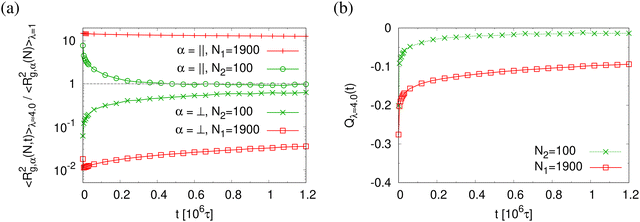
This comes along with the restricted conformational relaxation of the individual chains, as characterized by their linear dimensions and structure factor. The time-dependent two components of 〈Rg,α2(N,t)〉 parallel (α = ‖) and perpendicular (α = ⊥), and the bond orientational order parameter Qλ(t) are shown in Fig. 11. For long chains (N = N1) 〈Rg,‖2(N,t)〉 only decreases marginally during initial relaxation and then remains almost unchanged throughout the whole relaxation time. 〈Rg,⊥2(N,t)〉 increases slightly with time t after a very short time initial decrease, but then gets stuck at a value compatible with the thickness of the thin film. Note that marginal relaxation indicates that the chain retraction inside the tube as predicted by the Doi-Edwards and GLaMM tube models38,39 here is strongly retarded. For short chains (N = N2), chain retraction is not observed since chains are only weakly entangled.34 〈Rg,‖2(N,t)〉 decreases while 〈Rg,⊥2(N,t)〉 increases during initial relaxation and eventually move towards the equilibrium value. Especially 〈Rg,‖2(N,t)〉 reaches the unperturbed bulk value. Similarly the bond orientational order parameter Q(t) displays a significant relaxation delay towards the isotropic phase for long chains while an isotropic distribution of bond directions is found for short chains. The two components of the single chain structure factor, Sc,‖(q‖,N) and Sc,⊥(q⊥,N), only change slightly with time t for N = N1 while for N = N2, Sc,‖(q‖,N) ≈ Sc,⊥(q⊥,N) ∼ q⊥,‖−2 at t = 1.2 × 106 ≈ 42τR,N1, cf.Fig. 12, as expected for ideal chains. The instantaneously observed crossover for N = N1 from a two dimensional self-avoiding walk like structure (Sc,‖(q‖,N) ∼ q‖−4/3) to ideal random walk like structure (Sc,‖(q‖,N) ∼ q‖−2) at low q‖ is even shifted to lower q‖ and hardly visible anymore. However, the perpendicular component still displays a pronounced Porod power law (Sc,⊥(q⊥,N) ∼ q⊥−4) indicating the sharp surface.
IV. Stabilization by cooling
Above we have shown, that the conformational and morphological relaxation of the expanded films is significantly retarded. The same and ultimate stabilization can be achieved by cooling the systems down towards the glass transition temperature Tg.32,40 For this we follow a stepwise cooling protocol with the fixed cooling rate Γ = 8.3 × 10−7ε/(kBτ) = ΔT/Δt (ΔT = 0.025ε/kB, Δt = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ) by NVT MD simulations with Langevin thermostat, just as also applied for the monodisperse case.13,14 We apply this to the polydisperse film of film thickness h ≈ 16.0σ at λ ≈ 4.0, right after deformation. For this cooling rate chains of length O(100) can full relax around and weakly below T = 1.0ε/kB. Thus the short chains of N2 = 100 can equilibrate completely while for N1 = 1900 only subchains of similar lengths can relax. Fig. 13 illustrates this. Similar structures are observed for the thin monodisperse polymer film upon fast expansion.14 However, the pore sizes are slightly larger in the polydisperse system. The clustering of the short chain indicates some strain-induced segregation between the strained long chains and relaxed short chains. At the same time short chains seem to avoid the surfaces. However, this does not affect the suitability of the resulting porous polydisperse film, since long chains extend over several pore envelopes.
000τ) by NVT MD simulations with Langevin thermostat, just as also applied for the monodisperse case.13,14 We apply this to the polydisperse film of film thickness h ≈ 16.0σ at λ ≈ 4.0, right after deformation. For this cooling rate chains of length O(100) can full relax around and weakly below T = 1.0ε/kB. Thus the short chains of N2 = 100 can equilibrate completely while for N1 = 1900 only subchains of similar lengths can relax. Fig. 13 illustrates this. Similar structures are observed for the thin monodisperse polymer film upon fast expansion.14 However, the pore sizes are slightly larger in the polydisperse system. The clustering of the short chain indicates some strain-induced segregation between the strained long chains and relaxed short chains. At the same time short chains seem to avoid the surfaces. However, this does not affect the suitability of the resulting porous polydisperse film, since long chains extend over several pore envelopes.
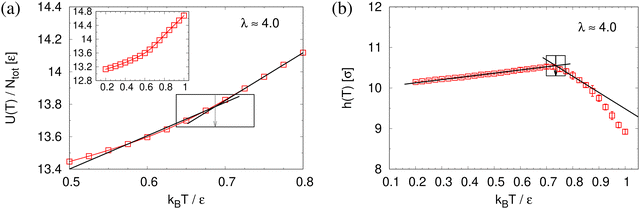
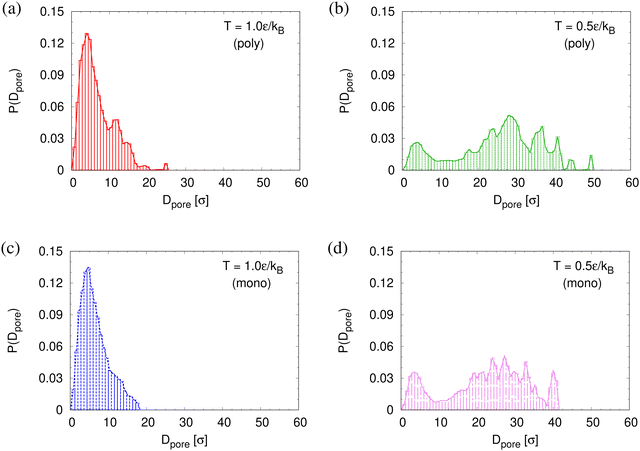
To determine the apparent glass transition temperature Tg we resort to the total potential energy U(T) shown in Fig. 14, which gives TUg = 0.69(5)ε/kB. A good measure of the density shift upon cooling is difficult due to the pore structure. Another estimate of Tg from the change in film thickness h(T) based from the monomer density profile (see Fig. S8, ESI†) gives Thg = 0.74(4)ε/kB, respectively. The latter value is a bit too high, compared to independent studies of thin films.32 However, there is no influence of polydispersity on Tg. The glass transition is around 0.70ε/kB as found for thin monodisperse nanoporous films at ref. 14λ ≈ 4.0. The porous structures characterized by porosity ϕ(T) and by pore size Dpore(T) are presented in Fig. 15. As T decreases ϕ(T) is increasing, approaching a plateau value in a temperature region, where also the monomer density profile ρ(z) converges. Both 〈Dpore(T)〉 and 〈D(max)pore(T)〉 behave similar as ϕ. They all first increase with the decrease of T for T > Tg, and then tend to reach a plateau approximately around Tg. The resulting porosity ϕ ≈ 33%, 〈Dpore〉 ≈ 25σ, and 〈D(max)pore〉 ≈ 50σ for T < Tg are slightly larger than the expanded monodisperse polymer film upon fast expansion (ϕ ≈ 29%, 〈Dpore〉 ≈ 22σ, 〈Dmax〉 ≈ 42σ). The pore size distribution P(Dpore) presented in Fig. 16 at T = 1.0ε/kB is no longer a unimodal-like distribution after short chains are relaxed. At T = 0.5ε/kB, the multmodal distribution is slightly broader comparing to the expanded monodisperse film upon fast expansion.
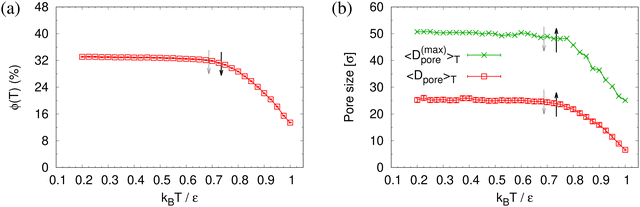 | ||
| Fig. 15 Porosity ϕ(T) (a), mean pore size 〈Dpore〉T and mean maximum pore size 〈D(max)pore〉T (b), plotted as a function of temperature T for expanded thin polydisperse films at λ ≈ 4.0. Estimates of Tg from h(T) and U(T) are indicated by solid black and dotted gray arrows, respectively, cf.Fig. 14. | ||
The observed very strong similarity to the properties of monodisperse films also hold for the collective in-plane scattering function, S‖(q‖) as shown in Fig. 17. With the decrease of T, S‖(q‖) increases on large length scale, and levels off in a broad maximum/shoulder below q ≈ 0.2σ−1 related to the average pore size. More locally, surfaces become flat and sharp for T < Tg, i.e., S‖(q‖) ∼ q‖−4. The changes in local wall structure of pores and microscopic monomer packing also remains unchanged compared to the monodisperse example.
V. Conclusions
In summary, we have extended the concept of employing entanglements to create and stabilize nanoporous polymer films13,14 to polydisperse melts. By choosing a bidisperse system of an equal number of very long (N1 = 1900) and short (N2 = 100) chains, i.e. MW/MN = 1.8, the system contains short chains which can fully equilibrate throughout the film expansion process while the long chains cannot relax, leading to essentially conserved entanglements and by this to a stabilization of the pores. As in our first study, no additional chemical processing or stabilization beyond quenching the system into the glassy state is needed. Despite the addition of short chains even well above Tg the relaxation of the expanded film is significantly slowing down, making the whole process rather robust. The glass transition temperature itself for films at strain of λ ≈ 4.0 remains within our error bars at the bulk value. The temperature dependence of the film thickness, which displays a kink at a slightly higher temperature, points to additional stabilization mechanisms, which await a more detailed investigation. As in our previous study the pore properties are determined by the entanglement structure of the underlying polymer melt. However, the polydispersity leads to slightly larger pores of an extrapolated 〈Dpore〉 ≈ 14dT, which is within the expected regime, considering faster relaxation and reduced entanglement density due to the shorter chains. Importantly, the short chains do not diffuse to the surfaces of the pores and thus do not fill up smaller pores. They stay within the bulk of the polymer matrix and by that can assume equilibrium conformations. The pores themselves act like an excluded volume interaction on the conformation of the chains winding around them, which is seen in the intermediate exponent in the scattering function. Altogether this study demonstrates that stable nanoporous polymer films can be made by mechanical deformation also for polydisperse systems as long as there are enough long chains which extend over several pores and by that stabilize the overall structure.Author contributions
H.-P. H. designed research, performed the molecular dynamics simulations, analyzed the data, and wrote the paper. K. K. designed research, analyzed the data and wrote the paper.Data availability
Data for this article are available on https://github.com/dehphsu/Publication_data/tree/b0d0357891fb1a7b0696163018f787479d28dac6/SM_2024.Conflicts of interest
There are no conflicts to declare.Appendix
The components of pressure tensor along the two lateral dimensions are the same during the expansion process as shown in Fig. S2 (ESI†). Technically, the film is first instantaneously stretched by a factor of 1.02 along the x-direction, and then along the y-direction. This deformation step is chosen to be small enough, not to induce any numerical instabilities. After each deformation step along one direction the lateral dimensions are fixed and the system is allowed to relax for (0.02τe/C), resulting in an effective strain rate![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = C/τe. C is the measure of the strain rate relative to the entanglement time τe = τ0Ne2 with the characteristic relaxation time22τ0 ≈ 2.89τ and the entanglement length22,41Ne ≈ 28. We initially use C = 6.27, i.e. the strain rate is much faster compared to the Rouse relaxation of the overall chains while subchains of chain lengths up to about
= C/τe. C is the measure of the strain rate relative to the entanglement time τe = τ0Ne2 with the characteristic relaxation time22τ0 ≈ 2.89τ and the entanglement length22,41Ne ≈ 28. We initially use C = 6.27, i.e. the strain rate is much faster compared to the Rouse relaxation of the overall chains while subchains of chain lengths up to about 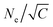 are expected to be able to relax during deformation. Moreover, after each expansion step the film thickness relaxes and the instant pressure Pzz, quickly approaches zero as shown in Fig. S2 (ESI†). This latter relaxation required even a slowing down of the expansion leading to an effective C ≈ 2.61 based on the total time (2393.13τ) for deformation and thus leading to 0.6Ne ≈ 17, see ESI,† of ref. 14 for the detailed simulation protocol, and Fig. S2 (ESI†). This protocol is repeated until the desired expansion is reached. In our simulation, the expanded polydisperse polymer film finally is in the thin film regime (h ≈ 16.0σ < R(0)g(N1 = 1900)) with Pzz ≈ 0.0ε/σ3.
are expected to be able to relax during deformation. Moreover, after each expansion step the film thickness relaxes and the instant pressure Pzz, quickly approaches zero as shown in Fig. S2 (ESI†). This latter relaxation required even a slowing down of the expansion leading to an effective C ≈ 2.61 based on the total time (2393.13τ) for deformation and thus leading to 0.6Ne ≈ 17, see ESI,† of ref. 14 for the detailed simulation protocol, and Fig. S2 (ESI†). This protocol is repeated until the desired expansion is reached. In our simulation, the expanded polydisperse polymer film finally is in the thin film regime (h ≈ 16.0σ < R(0)g(N1 = 1900)) with Pzz ≈ 0.0ε/σ3.
Acknowledgements
We thank M. Mezger, M. K. Singh and T. Stuehn for helpful discussions, and Martin Girard for a critical reading of the manuscript. We thank M. K. Singh also for making the reference experimental samples and their characterization. This work has been supported by European Research Council under the European Union's Seventh Framework Programme (FP7/2007–2013)/ERC Grant Agreement no. 340906-MOLPROCOMP. We also gratefully acknowledge the computing time granted by the John von Neumann Institute for Computing (NIC) and provided on the supercomputer JUWELS at Jülich Supercomputing Centre (JSC), and the Max Planck Computing and Data Facility (MPCDF).Open Access funding provided by the Max Planck Society.
References
- H. Lin and Y. Ding, J. Polym. Sci., 2020, 58, 2433–2434 CrossRef CAS.
- V. Abetz, T. Brinkmann and M. Sözbilir, Chem. Teach. Int., 2021, 3, 141–154 CrossRef.
- F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38 CrossRef CAS.
- V. Abetz, Macromol. Rapid Commun., 2015, 36, 10–22 CrossRef CAS PubMed.
- V. Abetz, K. Kremer, M. Mueller and G. Reiter, Macromol. Chem. Phys., 2019, 220, 1800334 CrossRef.
- K. Sankhala, J. Koll and V. Abetz, Membranes, 2020, 10, 83 CrossRef CAS PubMed.
- J. Bang, S. H. Kim, E. Drockenmuller, M. J. Misner, T. P. Russell and C. J. Hawker, J. Am. Chem. Soc., 2006, 128, 7622–7629 CrossRef CAS PubMed.
- K. Ariga, M. Nishikawa, T. Mori, J. Takeya, L. K. Shrestha and J. P. Hill, Sci. Technol. Adv. Mater., 2019, 20, 51–95 CrossRef CAS PubMed.
- M. A. Hillmyer, Block Copolymers II. Advances in Polymer Science, Springer-Verlag, Berlin, 2005, vol. 190, pp. 137–181 Search PubMed.
- D. Zhao and T. Zhao, ACS Cent. Sci., 2023, 9, 1499–1503 CrossRef CAS PubMed.
- R. W. Baker, Ind. Eng. Chem. Res., 2002, 41, 1393–1411 CrossRef CAS.
- T. D. Bennett, F.-X. Coudert, S. L. James and A. I. Cooper, Nat. Mater., 2021, 20, 1179–1187 CrossRef CAS PubMed.
- H.-P. Hsu, M. K. Singh, Y. Cang, H. Thérien-Aubin, M. Mezger, R. Berger, I. Lieberwirth, G. Fytas and K. Kremer, Adv. Sci., 2023, 10, 2207472 CrossRef CAS PubMed.
- H.-P. Hsu and K. Kremer, Macromolecules, 2024, 57, 2998–3012 CrossRef CAS PubMed.
- K. Kremer, H.-P. Hsu, M. Singh and G. Fytas, Free standing dry and stable nanoporous polymer films made through mechanical deformation, European patent Application No. EP23386025, 2023 Search PubMed.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057 CrossRef CAS.
- R. Faller, A. Kolb and F. Müller-Plathe, Phys. Chem. Chem. Phys., 1999, 1, 2071 RSC.
- M. Kröger, Comput. Phys. Commun., 1999, 118, 278–298 CrossRef.
- H.-P. Hsu and K. Kremer, J. Chem. Phys., 2019, 150, 159902 CrossRef PubMed.
- H.-P. Hsu and K. Kremer, J. Chem. Phys., 2020, 153, 144902 CrossRef PubMed.
- G. Zhang, L. A. Moreira, T. Stuehn, K. C. Daoulas and K. Kremer, ACS Macro Lett., 2014, 3, 198 CrossRef CAS PubMed.
- H.-P. Hsu and K. Kremer, J. Chem. Phys., 2016, 144, 154907 CrossRef PubMed.
- M. H. Wagner, P. Ehrecke, P. Hachmann and J. Meissner, J. Rheol., 1998, 42, 621–638 CrossRef CAS.
- P. Hachmann and J. Meissner, J. Rheol., 2003, 47, 989–1010 CrossRef CAS.
- K.-H. Nitta, T. Sawada, S. Yoshida and T. Kawamura, Polymer, 2015, 74, 30–37 CrossRef CAS.
- See ESI†.
- L. D. Gelb and E. Gubbins, Langmuir, 1999, 15, 305–308 CrossRef CAS.
- K. T. Thomson and K. E. Gubbins, Langmuir, 2000, 16, 5761–5773 CrossRef CAS.
- J. Pikunic, C. Clinard, N. Cohaut, K. E. Gubbins, J.-M. Guet, R. J.-M. Pellenq, I. Rannou and J.-N. Rouzaud, Langmuir, 2003, 19, 8565–8582 CrossRef CAS.
- S. Bhattacharya and K. E. Gubbins, Langmuir, 2006, 22, 7726–7731 CrossRef CAS PubMed.
- M. K. Singh, M. Hu, Y. Cang, H.-P. Hsu, H. Therien-Aubin, K. Koynov, G. Fytas, K. Landfester and K. Kremer, Macromolecules, 2020, 53, 7312–7321 CrossRef CAS PubMed.
- H.-P. Hsu and K. Kremer, J. Chem. Phys., 2023, 159, 071104 CrossRef CAS PubMed.
- H.-P. Hsu and K. Kremer, ACS Macro Lett., 2018, 7, 107–111 CrossRef CAS PubMed.
- H.-P. Hsu and K. Kremer, Phys. Rev. Lett., 2018, 121, 167801 CrossRef PubMed.
- H.-P. Hsu and K. Kremer, Macromolecules, 2019, 52, 6756–6772 CrossRef CAS PubMed.
- R. Everaers, S. K. Sukumaran, G. S. Grest, C. Svaneborg, A. Sivasubramanian and K. Kremer, Science, 2004, 303, 823 CrossRef CAS PubMed.
- E. Huang, M. F. Toney, W. Volksen, D. Mecerreyes, P. Brock, H.-C. Kim, C. J. Hawker, J. L. Hedrick, V. Y. Lee, T. Magbitang, R. D. Miller and L. B. Lurio, Appl. Phys. Lett., 2002, 81, 2232 CrossRef CAS.
- M. Doi and S. Edwards, The theory of polymer dynamics, Oxford University Press, New York, 1986 Search PubMed.
- R. S. Graham, A. E. Likhtman, T. C. B. McLeish and S. T. Milner, J. Rheol., 2003, 47, 1171–1200 CrossRef CAS.
- H.-P. Hsu and K. Kremer, J. Chem. Phys., 2019, 150, 091101 CrossRef PubMed.
- L. A. Moreira, G. Zhang, F. Müller, T. Stuehn and K. Kremer, Macromol. Theory Simul., 2015, 24, 419 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00569d |
| This journal is © The Royal Society of Chemistry 2024 |