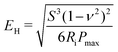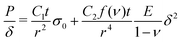Open Access Article
Open Access ArticleExplaining the spread in measurement of PDMS elastic properties: influence of test method and curing protocol†
Hannah
Varner
 a and
Tal
Cohen
a and
Tal
Cohen
 *ab
*ab
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
bDepartment of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: talco@mit.edu
First published on 6th September 2024
Abstract
Accuracy in the measurement of mechanical properties is essential for precision engineering and for the interrogation of composition–property relationships. Conventional methods of mechanical testing, such as uniaxial tension, compression, and nanoindentation, provide highly repeatable and reliable results for stiff materials, for which they were originally developed. However, when applied to the characterization of soft and biological materials, the same cannot be said, and the spread of reported properties of similar materials is vast. Polydimethylsiloxane (PDMS), commonly obtained from Dow as SYLGARD 184, is a ubiquitous such material, which has been integral to the rapid development of biocompatible microfluidic devices and flexible electronics in recent decades. However, reported shear moduli of this material range over 2 orders of magnitude for similar chemical compositions. Taking advantage of the increased mechanical scrutiny afforded to SYLGARD 184 in recent years, we combine both published and new experimental data obtained using 9 mechanical test methods. A statistical analysis then elucidates the significant bias induced by the test method itself, and distinguishes this bias from the influence of curing protocols on the mechanical properties. The goal of this work is thus two-fold: (i) it provides a quantitative understanding of the different factors that influence reported properties of this particular material, and (ii) it serves as a cautionary tale. As researchers in the field of mechanics strive to quantify the properties of increasingly complex soft and biological materials, converging on a standardized measurement of PDMS is a necessary first step.
1 Introduction
Modern engineering of material systems relies on the testing and quantification of a material's mechanical response. The tension, compression, indentation and impact testing methods that most engineers first encounter are all standard for metal samples but may not be appropriate for soft materials, which are significantly more challenging to test. Nonetheless, the use of soft materials is becoming increasingly prevalent in engineering, as researchers try to better understand and interface with the human body, and develop smaller and more compliant material structures and devices. Comparing measurements from a range of techniques, several studies1–3 report wide discrepancies in measured stiffness of soft biological materials. It is notable that despite well documented variations in biological tissue, these discrepancies are often attributed primarily to the testing method and not to material variations.Even commercially available synthetic materials are hard to test. One example is polydimethylsiloxane (PDMS) where reported elastic moduli range by 2 orders of magnitude for similar compositions, as shown herein. PDMS is a two-part material system and the stiffness of the resulting silicone polymer can be easily tuned to suit the needs of an application. PDMS will cure at room temperature, or can have the curing accelerated with an oven cure. It is widely used in microfluidics,4–6 medical devices, and electronics.7–9 In engineering mechanics, it is a common surrogate material for method development in the measurement of elastic, adhesion, and fracture response,10–14 and as a component in the development of tough materials that can undergo large deformations before failure.15–21 The flexibility of composition and cure is particularly useful in the context of biological research where PDMS has been proposed as a scaffold for cell growth,22–25 as a biological membrane mimic in microfluidics,26 and in biohybrid devices.27–29 Given its widespread use in biology, numerous authors have worked to modify the adhesion, wetablity, absorptivity, dielectric properties, and mechanical characteristics of PDMS, with comprehensive reviews provided by Wolf et al.,30 Zhou et al.,31 Abbasi et al.,32 Teixeira et al.33 and Murphy et al.34 However, far less attention has been paid to systematically understanding and measuring the bulk properties of PDMS (or, often, the commercially branded product Dow SYLGARD 18435). The same fabrication flexibility and wide availability that makes commercial SYLGARD 184 applicable across a range of fields also highlights a critical problem of mechanical reproducibility.
The primary goal of this work is to elucidate the bias induced by the testing method in determining the elastic response of soft materials. To this end, we choose SYLGARD 184 as a test case, taking advantage of the breadth of available data in the literature spanning a range of test methods, and combined with new volume controlled cavity expansion (VCCE) data, reported here. The secondary goal of this work is, thus, the interrogation of SYLGARD 184 mechanical properties. While frequent users of SYLGARD 184 often expect minor inconsistencies in the mechanical properties due to changes from the manufacturer‡, we hypothesize instate that measurement discrepancies can be mainly attributed to bias imparted by: (1) different mechanical testing methods, and (2) wide variation in the cure conditions used for similar mixing ratios.
“Round Robin” studies have been used to compare test methodologies and increase the “reliability and repeatability” of measurements in ceramics,39,40 composites,41 adhesives,42 concrete,43 steel,44 and many other materials and industries. In their versailles advanced materials and standards report, Kubler et al.39 articulate their motivation for conducting the study to determine if the Single-edge-V-Notched beam method for measuring fracture toughness is “user-friendly, reliable and… comparable to other recognised methods.” A similar effort in the context of PDMS elasticity characterization is, in the view of the authors, overdue. To this end, we embark on this study in an effort to understand the magnitude of the problem at hand. We present the scale of variability observed across literature and in our own data, and hope to motivate the community to converge on more consistent preparation, and testing methodologies to improve repeatability for PDMS and across the field of soft material mechanics.
This paper is organized as follows: we begin by describing how studies were chosen for inclusion in this meta-analysis (Section 2.1) and provide a brief description of the mechanical testing methods used across the included studies (Section 2.2). We then present the results of our analysis (Section 3) and include new data for moduli obtained via VCCE (detailed in Section 2 of the ESI,† Table T1). Finally, we conclude with remarks and cautions on stiffnesses reported in literature for PDMS (Section 4).
2 Methods
2.1 Data gathering
Articles surveyed for this review were found through key word searches and references lists of included articles. Keywords included “elasticity” or “modulus” or “stiffness” and “PDMS” or “polydimethylsiloxane” or “SYLGARD 184”, as well as related derivatives and searches were performed across Google Scholar and Web of Science from January–August 2023. Studies included in the results presented here were those with defined (a) mix ratios for curing agent and base, (b) cure time, and (c) cure temperature. We restrict this study to Dow's SYLGARD 184. Hence, studies that used other commercial formulations such as GE RTV PDMS silicones were excluded (such as by Liu et al.45 and some results reported by Schneider et al.46). Note that one of the most commonly cited studies on PDMS moduli (see Fig. F1 in ESI†), Lötters7 has not been included as the authors used ABCR PS851 PDMS.All included studies are summarized in Table T2 of Section S3 (ESI†). Studies with parameters listed as “variable” intentionally survey a large range of values and are therefore not listed in the table (though included where appropriate in corresponding figures). New data collected by the authors and included in Table T2 (ESI†), is described in Section S2 (ESI†) with fabrication and measurement detailed in T1 (ESI†).
Dow recommends a mixing ratio of 10 parts base to 1 part curing agent (crosslinker) on a weight to weight basis; we will abbreviate this as 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or more generally wB
1 or more generally wB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wC. Where the mix ratio was instead reported as a percent, we have converted to the X parts base:1 part curing agent format. All stiffnesses are reported here as shear modulus, μ. Where authors initially reported the stiffness as an elastic or Young's modulus, E, incompressibility is assumed with a Poisson's ratio ν = 0.547 and μ = E/(2(1 + ν)) = 3E. For studies investigating viscoelastic material parameters or high strain rate responses, the quasistatic modulus is reported in the summary charts and where only an instantaneous modulus is reported, we denote it as μ0. For studies reporting a cure at room temperature, 25 °C was used in plotting and comparison tables.
wC. Where the mix ratio was instead reported as a percent, we have converted to the X parts base:1 part curing agent format. All stiffnesses are reported here as shear modulus, μ. Where authors initially reported the stiffness as an elastic or Young's modulus, E, incompressibility is assumed with a Poisson's ratio ν = 0.547 and μ = E/(2(1 + ν)) = 3E. For studies investigating viscoelastic material parameters or high strain rate responses, the quasistatic modulus is reported in the summary charts and where only an instantaneous modulus is reported, we denote it as μ0. For studies reporting a cure at room temperature, 25 °C was used in plotting and comparison tables.
2.2. Test methodologies
Authors have used a diverse range of test methods to establish the stiffness of PDMS depending on the curing agent ratio in question and goal of the study. The fundamental assumptions and geometries of the different methods are discussed below and depicted in Fig. 1.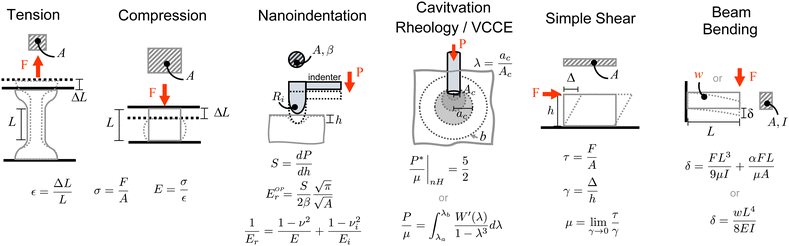 | ||
| Fig. 1 Common types of testing used to determine shear or elastic modulus, μ and E for PDMS. Variable definitions are included in the text. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base to curing agent ratio.
1 base to curing agent ratio.
for a spherical indenter with radius of curvature Ri and ν is assumed to be 0.5 for PDMS. Multiple authors acknowledge the significance of adhesion in nanoindentation measurements and employ the Johnson, Kendall, Roberts (JKR) model instead of Hertzian contact,14,58,61 or in addition to it.62,63 However, authors disagreed whether the Hertzian contact model returned a higher moduli than the JKR model58 or a lower moduli.14
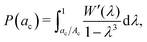 | (1) |
Li et al.66 use similar assumptions in a cylindrical geometry, finding a very good match between analytical and experimental results.
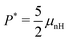 .
.
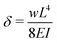 with I describing the second moment of area. By contrast, Du et al.72 considered a point load at the tip of a low aspect ratio beam and added a Timoshenko term
with I describing the second moment of area. By contrast, Du et al.72 considered a point load at the tip of a low aspect ratio beam and added a Timoshenko term 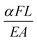 with the shear coefficient α.
with the shear coefficient α.
using geometric coefficients C1,C2 and f(ν) and residual stress σ0, and again assuming ν = 0.5.
2.3. Correlation analysis
Compiled data is visualized to observe trends and the monotonicity of relationships is quantified using Spearman rank74 correlation coefficient, ρ. The Spearman correlation presents the null hypothesis that there is no correlation between an input (predictor) variable and the output, and returns −1 ≤ ρ ≤ 1 indicating whether a monotonic correlation exists, and whether it is negative or positive, respectively. A significance p < 0.05 indicates confidence in rejecting the null hypothesis of the data originating from an uncorrelated dataset (more precisely, from a dataset that is less well correlated than indicated by the magnitude of ρ). Spearman correlation is used given the non-normal distribution of all predictor variables, and the desire to not impose a linear relationship between the inputs and stiffness.75 Further discussion of the statistical distribution of the predictor variables is given in Section 4 of the ESI.†The correlation is executed via MATLAB 2023 and is applied between preparation conditions (cure temperature, time) and within subgroups of individual test methods in order to isolate where monotonicity might hold internal to a test method, but not within the entire population. While ρ provides indication of how monotonic the relation between two inputs is (0.3 ≤ |ρ| < 0.6: fair, 0.6 ≤ |ρ| < 0.8: moderate, 0.8 ≤ |ρ| < 1: very strong, |ρ| = 1: perfect76), it does not indicate the magnitude or linearity of an effect.
3 Results & discussion
3.1 Wide modulus variability and dominance of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 ratio
1 ratio
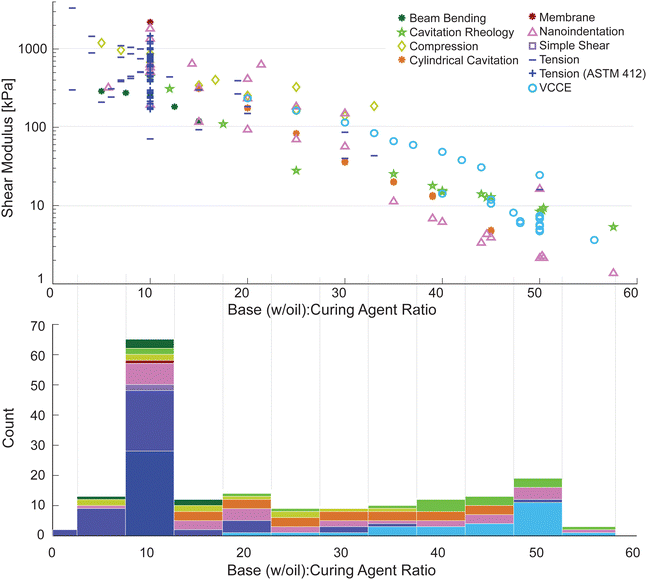
Despite reportedly identical mix ratios, the measured shear moduli vary by two orders of magnitude between different studies as shown in Fig. 2. We observe that this is due to three main factors: (1) different test methods producing ranging results, (2) variation in specified cure schedule, and (3) the inclusion of non-reactive oils in the base mixture that are sometimes added to manipulate the viscoelasticity of the cured silicone. The histogram in Fig. 2 shows a count of how many experimental results exist by test method across a range of curing agent ratios and highlights how different test methods tend to be used for different stiffness of materials. While combining all the data is useful to inspire caution when using literature reported “stiffness” for SYLGARD 184, diving further into the data is necessary to try and identify the sources of the variability and the key parameters driving the reported ranges.
Table 1 presents the Spearman correlation between shear modulus and key process parameters: curing agent ratio, cure temperature, and cure time. Correlations are calculated for all tests and cure ratios combined using the number of data points Ntests listed in Table 1, then separately for select testing methods with data from multiple authors (and conditions) for Ntests > 10. The second section of the table presents only tests performed at the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (that recommended on the product technical data sheet (TDS)35), followed by those excluding this ratio.
1 ratio (that recommended on the product technical data sheet (TDS)35), followed by those excluding this ratio.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 wB
1 wB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wC in order to remove the disproportionate number of tests recorded at this ratio from biasing the results. Blanks in the table indicate cases where conditions are the same for all trials within the row
wC in order to remove the disproportionate number of tests recorded at this ratio from biasing the results. Blanks in the table indicate cases where conditions are the same for all trials within the row
| Test type | N datasets | N tests | Curing agent ratio | Cure temperature | Cure time | |||
|---|---|---|---|---|---|---|---|---|
| ρ | p | ρ | p | ρ | p | |||
| All tests | 36 | 178 | −0.88 | 0.00 | 0.32 | 0.00 | −0.29 | 0.00 |
| Cavitation rheology | 3 | 16 | −0.98 | 0.00 | ||||
| Compression | 2 | 11 | −0.94 | 0.00 | 0.52 | 0.10 | −0.52 | 0.10 |
| Nanoindentation | 9 | 30 | −0.90 | 0.00 | 0.72 | 0.00 | −0.37 | 0.05 |
| Tension | 12 | 66 | −0.44 | 0.00 | 0.43 | 0.00 | −0.16 | 0.20 |
| VCCE | 4 | 25 | −0.92 | 0.00 | −0.85 | 0.00 | 0.85 | 0.00 |
All tests 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
27 | 53 | 0.30 | 0.03 | −0.37 | 0.01 | ||
| Tension | 12 | 38 | 0.26 | 0.12 | −0.46 | 0.00 | ||
All tests excluding 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
24 | 122 | −0.92 | 0.00 | 0.24 | 0.01 | −0.13 | 0.14 |
| Nanoindentation | 6 | 23 | −0.91 | 0.00 | 0.61 | 0.00 | −0.05 | 0.82 |
| Tension | 6 | 28 | −0.63 | 0.00 | 0.62 | 0.00 | 0.33 | 0.09 |
Tension testing results tend to be less correlated than other test methods. All comparisons between stiffness and curing agent ratio indicate very strong correlations with an exceptionally low p-value, as expected from the reaction chemistry described in ESI.5.† However, for those tests performed using tension testing, the correlation is only fair to moderate. Examining cure temperature, when all curing agent ratios are considered, the correlation with cure temperature is higher within tension testing than across other methods. However, at the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio where one would expect the dependency to be most cleanly expressed given the elimination of one variable entirely, this trend does not hold and the data fail the correlation with p = 0.12. Cure time is weakly correlated when examining all tests combined. However, within individual test methods correlation routinely fails the null hypothesis and predicts a weaker or inverted correlation when evaluated with tension testing. Across all test methods and within tension testing, additional data are required to conclude that there is monotonic correlation.
1 ratio where one would expect the dependency to be most cleanly expressed given the elimination of one variable entirely, this trend does not hold and the data fail the correlation with p = 0.12. Cure time is weakly correlated when examining all tests combined. However, within individual test methods correlation routinely fails the null hypothesis and predicts a weaker or inverted correlation when evaluated with tension testing. Across all test methods and within tension testing, additional data are required to conclude that there is monotonic correlation.
Note that in the TDS, Dow reports a tensile modulus of 6.7 MPa for a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mix ratio.35 Though not included in Fig. 2 or Table 1 given incomplete information on test method and cure conditions, this is significantly above all results compiled here.
1 mix ratio.35 Though not included in Fig. 2 or Table 1 given incomplete information on test method and cure conditions, this is significantly above all results compiled here.
3.2. False equivalencies arise due to test method
Mix ratio and cure temperature are expected to consistently effect stiffness regardless of the test method. Indeed, examining Table 1, correlations of stiffness with curing agent ratio and temperature are observed within a given test method. However, when all methods are combined this correlation is weaker. This provides evidence of test method bias.We hypothesize that the variation imparted by test method is driven by a number of factors including, but not limited to: material rate dependence, such that different methods measure the instantaneous vs. relaxed modulus, the additional models required to separate stiffness from adhesion effects in contact measurements, and sample preparation and fixturing imparting imperfections in boundary conditions and defect nucleation.
In an effort to isolate the influence of cure schedule from that of the test method, Fig. 3 compares stiffness for samples cured 120 minutes at 85–100 °C across multiple authors. Particularly for the lower wB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wC ratio samples, the measured stiffness varies by hundreds of kilopascals between testing methods. Tension testing inconsistently reports moduli both higher and lower than nanoindentation, and is not used for softer samples. While the general softening trend with higher base ratios can provide a rough qualitative understanding of polymer composition's influence on stiffness, there is minimal overlap in test methods that are used between soft samples and stiff samples, leaving open the question that the trends are due to the test methodology.
wC ratio samples, the measured stiffness varies by hundreds of kilopascals between testing methods. Tension testing inconsistently reports moduli both higher and lower than nanoindentation, and is not used for softer samples. While the general softening trend with higher base ratios can provide a rough qualitative understanding of polymer composition's influence on stiffness, there is minimal overlap in test methods that are used between soft samples and stiff samples, leaving open the question that the trends are due to the test methodology.
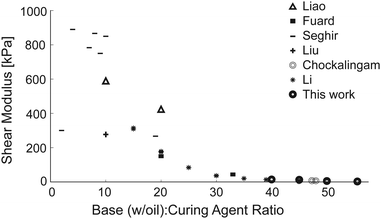 | ||
| Fig. 3 Test method imparts variability even when a similar cure schedule is used: 120 minutes at between 85 and 100 °C. Test type indicated by marker shape matching those used in Fig. 2. | ||
Restricting the wB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wC ratio to a more narrow range and examining three cavity-expansion based methods, encourages caution about biases that may be more pervasive in the dataset. Fig. 4 compares the μ0 of Yang et al.69 measured through CR and assuming a neo-Hookean material model, to results obtained via VCCE for comparable mix ratios (oil containing samples are excluded). The VCCE results from Raayai-Ardakani et al.11,64 are also μ0, while those of Chockalingam et al.65 and this work are μ.
wC ratio to a more narrow range and examining three cavity-expansion based methods, encourages caution about biases that may be more pervasive in the dataset. Fig. 4 compares the μ0 of Yang et al.69 measured through CR and assuming a neo-Hookean material model, to results obtained via VCCE for comparable mix ratios (oil containing samples are excluded). The VCCE results from Raayai-Ardakani et al.11,64 are also μ0, while those of Chockalingam et al.65 and this work are μ.
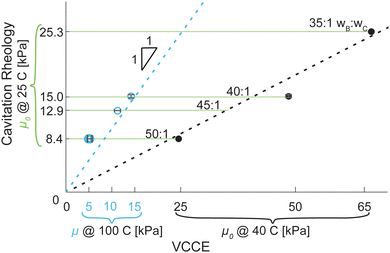 | ||
Fig. 4 VCCE results of11,64 for μ0 (filled marker), as well as μ from Chockalingam65 and this work (unfilled cyan circle, cyan axis labels) compared to CR results for μ0 by Yang et al.69 Horizontal green lines specify the measured μ0 from cavitation rheology for comparable mix ratios (wB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wC as noted on plot) measured with VCCE. Dashed lines are visual aids depicting both a 1 wC as noted on plot) measured with VCCE. Dashed lines are visual aids depicting both a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correlation for μ 1 correlation for μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μ0 and lack of correlation for μ0 μ0 and lack of correlation for μ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μ0. μ0. | ||
As expected from a solid mechanics perspective, μ < μ0 when measured with VCCE with instantaneous moduli more than double the quasistatic moduli for comparable wB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wC ratio. However, in these datasets, all samples used to measure μ were cured hotter and for less time than all samples to measure μ0. This results in the inversion of ρ in Table 1 for both cure temperature and time when considering VCCE independently. This inversion is another indication that the comparison of measured stiffness between different test methods and/or cure protocols can be misleading.
wC ratio. However, in these datasets, all samples used to measure μ were cured hotter and for less time than all samples to measure μ0. This results in the inversion of ρ in Table 1 for both cure temperature and time when considering VCCE independently. This inversion is another indication that the comparison of measured stiffness between different test methods and/or cure protocols can be misleading.
Furthermore, it can be seen on Fig. 4 that μ0 does not correlate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 between CR and VCCE. The observed deviation between Raayai-Ardakani and Yang et al. can therefore be attributed to the 6 day room temperature cure of Yang et al. producing softer samples than the 3 days at 40 °C cure schedule used by Raayai-Ardakani. By contrast, the unexpected 1
1 between CR and VCCE. The observed deviation between Raayai-Ardakani and Yang et al. can therefore be attributed to the 6 day room temperature cure of Yang et al. producing softer samples than the 3 days at 40 °C cure schedule used by Raayai-Ardakani. By contrast, the unexpected 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correlation between μ0 by CR and μ by VCCE (blue line on Fig. 4) is likely attributed to the discrepancy between the room temperature cure schedule used by Yang et al.69 and the 100 °C 2 h schedule used by Chocaklingam et al.65 and this work.
1 correlation between μ0 by CR and μ by VCCE (blue line on Fig. 4) is likely attributed to the discrepancy between the room temperature cure schedule used by Yang et al.69 and the 100 °C 2 h schedule used by Chocaklingam et al.65 and this work.
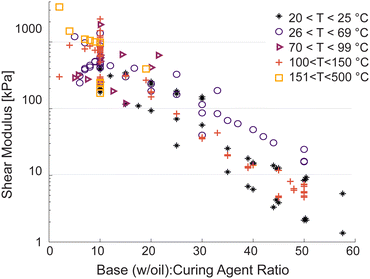
3.3. Hotter cures result in stiffer material
An increase in cure temperature is more directly correlated to a monotonic increase measured stiffness (fair correlations considering the full data set) than is an increase cure time (weak – fair correlations). Fig. 5 shows that cure temperatures evaluated are not uniformly distributed amongst the base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) curing agent ratios, with larger ratios being more often cured at room temperature and never over 150 °C compared to the stiffer, low ratio, samples. This likely compounds the effect of higher mix ratio samples appearing softer due to both lower temperature and less curing agent.
curing agent ratios, with larger ratios being more often cured at room temperature and never over 150 °C compared to the stiffer, low ratio, samples. This likely compounds the effect of higher mix ratio samples appearing softer due to both lower temperature and less curing agent.
Table 1 also shows the counterintuitive result that longer cure times correlate with softer samples, however this is likely due to the significantly longer times used with room temperature curing. While stiffness does not follow a linear trend with all predictor variables (as is clear from Fig. 3) a basic regression performed on the complete data set provides insights into the relative importance of temperature, time, and curing agent ratio. Utilizing MATLAB 2023b to fit a linear regression model, cure temperature is connected to stiffness as 2.71 kPa °C−1 (standard error SE of 0.74 kPa °C−1) while cure time is effected as 0.004 kPa min−1 cure (SE 0.006 kPa min−1 and a p > 0.05, thus failing the assumption of a linear correlation). Curing agent ratio is most strongly linked to stiffness as −15.5 kPa/1 wB+oil (SE 1.7 kPa/1 wB+oil). Contour plots depicting the interplay between all three predictors can be seen in Section S6 of the ESI.† With the strength of the correlation between temperature and stiffness, the tendency of lower temperature curing to produce softer samples overshadows the effect of longer cure times producing stiffer samples.
In an effort to reduce the variability imparted by different test methods, Table 1 is subdivided by test types and further to isolate 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio samples. Across nanoindentation and tension testing, the correlation between cure temperature and stiffness increases to moderate – strong when test methods are considered independently, and is even stronger when 10
1 ratio samples. Across nanoindentation and tension testing, the correlation between cure temperature and stiffness increases to moderate – strong when test methods are considered independently, and is even stronger when 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio samples are excluded (confirming that the number of tests performed only at this ratio may be biasing the overall trends in results).
1 ratio samples are excluded (confirming that the number of tests performed only at this ratio may be biasing the overall trends in results).
There is, however, a limit at which higher temperatures will no longer produce stiffer samples and instead will degrade the polymer. Liu et al.51 set out to study the effect of heating on PDMS mechanical properties and also observe that stiffness increase between 100 and 150 °C, but decreases for 200 °C and 300 °C samples.¶
3.4. Nonreactive oils act as part of the wB in stiffness trends
Oil-based thinners have been proposed as a method to decouple the viscoelastic and elastic responses of PDMS without effecting the stiffness.56,69 An unspecified “thinner” was used by Schneider et al.46 while Moučka et al.56 use 194 cSt silicone oil and Chockalingam et al.,65 Yang et al.69 and the new results presented in this work use 350 cSt silicone oil added to the base.
Fig. 6 shows that the correlation of shear modulus to mix compositions is stronger when the added oil is included in the wB than when it is not. The correlation for Yang et al. increased to |ρ| = 0.96 from |ρ| = 0.47 and |ρ| = 0.85 from |ρ| = 0.74 combining Chockalingam et al. and this work. Across both sets of data, increasing wB+oil![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wC reduces the observed shear modulus (μ or μ0) by a similar amount (0.768 vs. 0.766 kPa per added wB+oil with a linear fit to the data in this region). While all authors report changes to the viscoelastic time constants when including nonreactive oils, the trend in softening with increasing wB+oil for soft PDMS is shown to be consistent (a) regardless as to whether the ratio is altered with base or oil, and (b) in both instantaneous and quasistatic modulus.
wC reduces the observed shear modulus (μ or μ0) by a similar amount (0.768 vs. 0.766 kPa per added wB+oil with a linear fit to the data in this region). While all authors report changes to the viscoelastic time constants when including nonreactive oils, the trend in softening with increasing wB+oil for soft PDMS is shown to be consistent (a) regardless as to whether the ratio is altered with base or oil, and (b) in both instantaneous and quasistatic modulus.
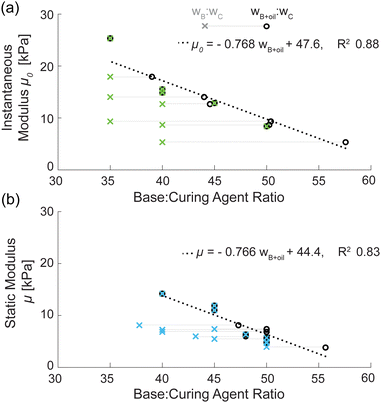 | ||
Fig. 6 If wB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wC is considered without taking oil into account (crosses), the correlation of ratio with stiffness is not as strong as when wB+oil wC is considered without taking oil into account (crosses), the correlation of ratio with stiffness is not as strong as when wB+oil![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wC is considered (circles) and the R2 of a linear fit drops from 0.88 to 0.21 for CR and 0.83 to 0.31 for VCCE. (a) shows μ0 from Yang et al.69 against an abscissa calculated both with and without oil included in wB; (b) depicts μ from Chockalingam et al.65 and this work. wC is considered (circles) and the R2 of a linear fit drops from 0.88 to 0.21 for CR and 0.83 to 0.31 for VCCE. (a) shows μ0 from Yang et al.69 against an abscissa calculated both with and without oil included in wB; (b) depicts μ from Chockalingam et al.65 and this work. | ||
3.5. Reaction chemistry offers hypotheses for variation
A number of the studies point out changes in mechanical properties of SYLGARD 184 within days to weeks after completing cure.60,65 Cheng et al. showed nearly a doubling in stiffness with 18 vs. 3 days of storage at room temperature after an initial cure. In their work with pure PDMS, Esteves et al. propose that secondary reactions occur as PDMS polymerizes.77 They observed that consumption of Si–H groups in the cross linker cannot be fully explained by hydrosylation (the conventionally understood pathway of PDMS cross linking) thus requiring that additional pathways are present. These additional pathways would be effected by ambient oxygen and moisture, pointing to relative humidity during fabrication as an additional parameter to consider in fabrication and storage of PDMS.Recent work by Bardelli et al.78 points to cure temperature as a factor in changing the molecular weight between crosslinks Mc in PDMS. As described in ESI.5,†Mc is directly connected to the stiffness of a polymer. Bardelli et al. observe nearly a doubling of μ between a 4 hour cure at 65 °C compared to 150 °C (with Mc decreasing from 2050 to 1050 g mol−1). Additionally, if lower temperature cures allow for more secondary reactions to take place, this could explain the resulting solid being softer.
4. Conclusions
The choice of mechanical testing method can have a significant influence of the measured stiffness of soft materials. Using commercially available PDMS (SYLGARD 184) as a test case, we examine this bias by combining new experimental data and that surveyed from 33 published papers, spanning 9 different testing methods. Statistical analysis reveals that bias imparted by test method is compounded by inconsistent curing approaches. The current methods of both testing and reporting are thus far from providing reproducible results for the mechanical properties of SYLGARD 184 and, by extension, for other soft and biological materials. A number of steps must be taken to better observe the properties that so many authors to date have claimed to measure.Test method has been implicated previously as returning variable measurements within identical soft material samples, and PDMS is no exception. Tension tests on PDMS reported the widest variation of stiffness, with nanoindentation also providing widely variable results. Though these are both common testing techniques, we recommend caution in the use of both methods. At low mixing ratios PDMS is brittle54 and tension testing is highly sensitive to surface imperfections on the sample, while at higher wB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wC ratios, the soft modulus means that results are influenced by the clamping conditions, without a guarantee that it is possible to set up a successful test at all. The variability of nanoindentation is likely due to the uncertain nature of the adhesion between the sample and indenter tip, which was the focus of many of the authors referenced here. Using such a method that relies on consistent surface adhesion, in a material where surface treatments are applied to widely varying degrees, will continue to produce imprecise results.
wC ratios, the soft modulus means that results are influenced by the clamping conditions, without a guarantee that it is possible to set up a successful test at all. The variability of nanoindentation is likely due to the uncertain nature of the adhesion between the sample and indenter tip, which was the focus of many of the authors referenced here. Using such a method that relies on consistent surface adhesion, in a material where surface treatments are applied to widely varying degrees, will continue to produce imprecise results.
The limitations of testing make it challenging to characterize the composition–property relationship of SYLGARD 184. This difficulty is further accentuated by the inconsistency of fabrication conditions and reporting of curing protocols. At present, cure schedules ranged widely between researchers with very little overlap if the authors were not currently or historically from the same research group. Of utmost importance is fully reporting the cure schedule and preparation method, as well as timing between cure and test. Unifying how PDMS is cured to obtain well characterized responses could help to enhance data comparisons and reliability. Hence, we would propose three temperatures for PDMS where control of mechanical properties is desired: a 25 °C room temperature, a “moderate” 60 °C at or below the glass transition temperature of plastics commonly used in additive manufacturing, and a “hot” 100 °C for rapid curing. Curing times may vary depending on sample geometry.
Each researcher has unique needs and capabilities for their research, and not each mechanical testing method is possible for a given sample. As soft materials research continues to expand into more complex and biological systems that present additional challenges for reproducible measurements, building agreement around common synthetic soft materials is worthwhile for the community. By noting the current discrepancies in literature on PDMS and by advocating that work going forward place a greater emphasis on consistency and comparison to the full body of literature (not selected works that happen to align with ones results), we anticipate better agreement in measured mechanical properties is easily attainable and hope that this manuscript motivates this as a community goal.
Author contributions
Hannah Varner: writing – original draft, writing – review & editing, conceptualization, investigation, data curation, methodology, formal analysis, visualization. Tal Cohen: conceptualization, writing – review & editing, resources, supervision.Data availability
All of the data for this paper is provided in the main text and the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the partial support of our work through Office of Naval Research grant N000142312530, and the support from the National Science Foundation under award number CMMI-1942016. H. V. acknowledges the support of the Department of Defense through the National Defense Science & Engineering Graduate Fellowship Program (2020–2023 Fellowship Class). Funding agencies were not involved in study design; in the collection, analysis and interpretation of data; in the writing of the report; or in the decision to submit the article for publication.References
- Y. Ji, A. Dagro, G. Dorgant, D. Starr and J. Wilkerson, Exp. Mech., 2022, 62, 799–812 CrossRef.
- F. Malone, E. McCarthy, P. Delassus, P. Fahy, J. Kennedy, A. Fagan and L. Morris, Cardiovasc. Eng. Technol., 2018, 9, 489–502 CrossRef CAS PubMed.
- H. Varner, G. P. Sugerman, M. K. Rausch and T. Cohen, J. Mech. Behav. Biomed. Mater., 2023, 143, 105901 CrossRef CAS PubMed.
- J. C. McDonald and G. M. Whitesides, Acc. Chem. Res., 2002, 35, 491–499 CrossRef CAS PubMed.
- Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184 CrossRef CAS.
- K. Raj and S. Chakraborty, J. Appl. Polym. Sci., 2020, 137, 48958 CrossRef.
- J. C. Lötters, W. Olthuis, P. H. Veltink and P. Bergveld, J. Micromech. Microeng., 1997, 7, 145 CrossRef.
- J. Wu, R. Wang, H. Yu, G. Li, K. Xu, N. C. Tien, R. C. Roberts and D. Li, Lab Chip, 2015, 15, 690–695 RSC.
- W.-Y. Wu, X. Zhong, W. Wang, Q. Miao and J.-J. Zhu, Electrochem. Commun., 2010, 12, 1600–1604 CrossRef CAS.
- B. Zhang and S. B. Hutchens, Soft Matter, 2021, 17, 6728–6741 RSC.
- S. Raayai-Ardakani and T. Cohen, Extreme Mech. Lett., 2019, 31, 100536 CrossRef.
- M. Kothari, Z. Lemon, C. Roth and T. Cohen, Soft Matter, 2020, 16, 9838–9843 RSC.
- H. Patel, C. Yang, H. Lee and A. A. Pelegri, ASME Int. Mech. Eng. Congr. Exp., 2019, V009T11A031 Search PubMed.
- X. Peng, J. Huang, H. Deng, C. Xiong and J. Fang, Meas. Sci. Technol., 2011, 22, 027003 CrossRef.
- Z. Wang, C. Xiang, X. Yao, P. Le Floch, J. Mendez and Z. Suo, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 5967–5972 CrossRef CAS PubMed.
- H.-C. Jung, J.-H. Moon, D.-H. Baek, J.-H. Lee, Y.-Y. Choi, J.-S. Hong and S.-H. Lee, IEEE Trans. Biomed. Eng., 2012, 59, 1472–1479 Search PubMed.
- R. Ariati, F. Sales, A. Souza, R. A. Lima and J. Ribeiro, Polymers, 2021, 13, 4258 CrossRef CAS PubMed.
- X. Niu, S. Peng, L. Liu, W. Wen and P. Sheng, Adv. Mater. Deerf Beach Weinheim, 2007, 19, 2682 CrossRef CAS.
- D. Chen, F. Chen, X. Hu, H. Zhang, X. Yin and Y. Zhou, Compos. Sci. Technol., 2015, 117, 307–314 CrossRef CAS.
- P. Kowol, S. Bargmann, P. Görrn and J. Wilmers, Extreme Mech. Lett., 2022, 54, 101724 CrossRef.
- Q. Jiao, M. Shi, T. Yin, Z. Suo and J. J. Vlassak, Extreme Mech. Lett., 2021, 48, 101433 CrossRef.
- X. Q. Brown, K. Ookawa and J. Y. Wong, Biomaterials, 2005, 26, 3123–3129 CrossRef CAS PubMed.
- J. Kim, J. Park, S. Yang, J. Baek, B. Kim, S. H. Lee, E.-S. Yoon, K. Chun and S. Park, Lab Chip, 2007, 7, 1504–1508 RSC.
- Y. Tanaka, K. Sato, T. Shimizu, M. Yamato, T. Okano and T. Kitamori, Lab Chip, 2007, 7, 207–212 RSC.
- D. Fuard, T. Tzvetkova-Chevolleau, S. Decossas, P. Tracqui and P. Schiavone, Microelectron. Eng., 2008, 85, 1289–1293 CrossRef CAS.
- D. Huh, B. D. Matthews, A. Mammoto, M. Montoya-Zavala, H. Y. Hsin and D. E. Ingber, Science, 2010, 328, 1662–1668 CrossRef CAS PubMed.
- A. W. Feinberg, A. Feigel, S. S. Shevkoplyas, S. Sheehy, G. M. Whitesides and K. K. Parker, Science, 2007, 317, 1366–1370 CrossRef CAS PubMed.
- J. C. Nawroth, H. Lee, A. W. Feinberg, C. M. Ripplinger, M. L. McCain, A. Grosberg, J. O. Dabiri and K. K. Parker, Nat. Biotechnol., 2012, 30, 792–797 CrossRef CAS PubMed.
- J. Chen, J. Zheng, Q. Gao, J. Zhang, J. Zhang, O. M. Omisore, L. Wang and H. Li, Appl. Sci., 2018, 8, 345 CrossRef.
- M. P. Wolf, G. B. Salieb-Beugelaar and P. Hunziker, Prog. Polym. Sci., 2018, 83, 97–134 CrossRef CAS.
- J. Zhou, A. V. Ellis and N. H. Voelcker, Electrophoresis, 2010, 31, 2–16 CrossRef CAS PubMed.
- F. Abbasi, H. Mirzadeh and A.-A. Katbab, Polym. Int., 2001, 50, 1279–1287 CrossRef CAS.
- I. Teixeira, I. Castro, V. Carvalho, C. Rodrigues, A. Souza, R. Lima, S. Teixeira and J. Ribeiro, AIMS Mater. Sci., 2021, 8, 952–973 CAS.
- E. C. Murphy, J. H. Dumont, C. H. Park, G. Kestell, K.-S. Lee and A. Labouriau, J. Appl. Polym. Sci., 2020, 137, 48530 CrossRef CAS.
- Dow, SYLGARD 184 Silicone Elastomer, 2024.
- V. Heinrichs, S. Dieluweit, J. Stellbrink, W. Pyckhout-Hintzen, N. Hersch, D. Richter and R. Merkel, PLoS One, 2018, 13, e0195180 CrossRef PubMed.
- R. N. Palchesko, L. Zhang, Y. Sun and A. W. Feinberg, PLoS One, 2012, 7, e51499 CrossRef CAS PubMed.
- J. Schweitzer, S. Merad, G. Schrodj, F. Bally-Le Gall and L. Vonna, J. Chem. Educ., 2019, 96, 1472–1478 CrossRef CAS.
- J. Kübler, Proceedings of the 21st Annual Conference on Composites, Advanced Ceramics, Materials, and Structures’ B: Ceramic Engineering and Science Proceedings, 1997, pp. 155-162.
- G. D. Quinn, R. J. Gettings and J. J. Kübler, Proceedings of the 18th Annual Conference on Composites and Advanced Ceramic Materials’ B: Ceramic Engineering and Science Proceedings, 1994, pp. 846–855.
- P. Davies, H. Kausch, J. Williams, A. Kinloch, M. Charalambides, A. Pavan, D. Moore, R. Prediger, I. Robinson and N. Burgoyne, et al. , Compos. Sci. Technol., 1992, 43, 129–136 CrossRef CAS.
- B. Blackman, A. Kinloch, M. Paraschi and W. Teo, Int. J. Adhes. Adhes., 2003, 23, 293–305 CrossRef CAS.
- J. Van Mier, S. Shah, M. Arnaud, J. Balayssac, A. Bascoul, S. Choi, D. Dasenbrock, G. Ferrara, C. French and M. Gobbi, et al. , Mater. Struct., 1997, 30, 195–209 CrossRef.
- A. Ruiz-Moreno, P. Hähner, L. Kurpaska, J. Jagielski, P. Spätig, M. Trebala, S.-P. Hannula, S. Merino, G. de Diego and H. Namburi, et al. , Nanomaterials, 2020, 10, 130 CrossRef CAS PubMed.
- C. Liu, Y. Qiu and K. Lian, Microfluidics, BioMEMS, and Medical Microsystems III, 2005, pp. 179–185 Search PubMed.
- F. Schneider, T. Fellner, J. Wilde and U. Wallrabe, J. Micromech. Microeng., 2008, 18, 065008 CrossRef.
- D. Armani, C. Liu and N. Aluru, Technical Digest. IEEE International MEMS 99 Conference. Twelfth IEEE International Conference on Micro Electro Mechanical Systems (Cat. No. 99CH36291), 1999, pp. 222–227.
- K. Upadhyay, D. Spearot and G. Subhash, Int. J. Impact Eng., 2021, 156, 103949 CrossRef.
- K. Khanafer, A. Duprey, M. Schlicht and R. Berguer, Biomed. Microdev., 2009, 11, 503–508 CrossRef CAS PubMed.
- T. K. Kim, J. K. Kim and O. C. Jeong, Microelectron. Eng., 2011, 88, 1982–1985 CrossRef CAS.
- M. Liu, J. Sun and Q. Chen, Sens. Actuators, A, 2009, 151, 42–45 CrossRef CAS.
- I. D. Johnston, D. K. McCluskey, C. K. Tan and M. C. Tracey, J. Micromech. Microeng., 2014, 24, 035017 CrossRef CAS.
- K. Mills, X. Zhu, S. Takayama and M. Thouless, J. Mater. Res., 2008, 23, 37–48 CrossRef CAS PubMed.
- R. Seghir and S. Arscott, Sens. Actuators, A, 2015, 230, 33–39 CrossRef CAS.
- ASTM, Standard Test Methods for Vulcanized Rubber and Thermoplastic Elastomers Tension, Astm standard, 2021 Search PubMed.
- R. Moučka, M. Sedlačk, J. Osička and V. Pata, Sci. Rep., 2021, 11, 19090 CrossRef PubMed.
- A. Mata, A. J. Fleischman and S. Roy, Biomed. Microdev., 2005, 7, 281–293 CrossRef CAS PubMed.
- F. Carrillo, S. Gupta, M. Balooch, S. J. Marshall, G. W. Marshall, L. Pruitt and C. M. Puttlitz, J. Mater. Res., 2005, 20, 2820–2830 CrossRef CAS.
- Z. Wang, A. A. Volinsky and N. D. Gallant, J. Appl. Polym. Sci., 2014, 131, 41050 CrossRef.
- C. Cheng, PhD thesis, The University of Texas at Dallas, 2011.
- Y. Cao, D. Yang and W. Soboyejoy, J. Mater. Res., 2005, 20, 2004–2011 CrossRef CAS.
- S. Gupta, F. Carrillo, C. Li, L. Pruitt and C. Puttlitz, Mater. Lett., 2007, 61, 448–451 CrossRef CAS.
- Q. Liao, J. Huang, T. Zhu, C. Xiong and J. Fang, Mech. Mater., 2010, 42, 1043–1047 CrossRef.
- S. Raayai-Ardakani, Z. Chen, D. R. Earl and T. Cohen, Soft Matter, 2019, 15, 381–392 RSC.
- S. Chockalingam, C. Roth, T. Henzel and T. Cohen, J. Mech. Phys. Solids, 2021, 146, 104172 CrossRef CAS.
- J. Li, Z. Xie, H. Varner, S. Chockalingam and T. Cohen, arXiv, 2024, preprint, arXiv:2408.12920 [cond-mat.mtrl-sci] Search PubMed.
- M. P. Milner and S. B. Hutchens, Mech. Mater., 2021, 154, 103741 CrossRef.
- M. P. Milner, PhD thesis, University of Illinois at Urbana-Champaign, 2020.
- S. Yang, D. Bahk, J. Kim, A. Kataruka, A. C. Dunn and S. B. Hutchens, Int. J. Fract., 2019, 219, 89–99 CrossRef.
- K. Upadhyay, A. Bhattacharyya, G. Subhash and D. Spearot, Exp. Mech., 2019, 59, 733–747 CrossRef.
- L. Nunes, Mater. Sci. Eng. A, 2011, 528, 1799–1804 CrossRef.
- P. Du, I.-K. Lin, H. Lu and X. Zhang, J. Micromech. Microeng., 2010, 20, 095016 CrossRef.
- A. L. Thangawng, R. S. Ruoff, M. A. Swartz and M. R. Glucksberg, Biomed. Microdev., 2007, 9, 587–595 CrossRef CAS PubMed.
- C. Spearman, in Studies in individual differences: The search for intelligence, ed. J. J. J. D. G. Paterson, Appleton-Century-Crofts, 1961, pp. 45–58 Search PubMed.
- B. S. Everitt and A. Skrondal, The Cambridge dictionary of statistics, Cambridge University Press, 2010 Search PubMed.
- H. Akoglu, Turkish J. Emerg. Med., 2018, 18, 91–93 CrossRef PubMed.
- A. Esteves, J. Brokken-Zijp, J. Laven, H. Huinink, N. Reuvers, M. Van and G. De With, Polymer, 2009, 50, 3955–3966 CrossRef CAS.
- T. Bardelli, C. Marano and F. Briatico Vangosa, et al. , Express Polym. Lett., 2022, 16, 924–932 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of original data published here for the first time, summary of all articles included across the meta-analysis, including interconnection mapping of citations. Additional details of regression analysis. See DOI: https://doi.org/10.1039/d4sm00573b |
| ‡ The exact composition of SYLGARD 184 is proprietary. Reading the product literature and safety data sheets provides the following insights.30,36–38 The base contains a majority dimethylvinyl-terminated dimethyl siloxane (>60%), with a significant portion of silica fillers (30–60% dimethylvinylated and trimethylated silica), as well as 1–5% tetra(trimethylsiloxy) silane and small amounts of ethylbenzene, xylene and a platinum catalyst (<1% each). The curing agent is a majority the cross linking agent dimethyl methylhydrogen siloxane (40–70%), additional methylated silica and siloxanes, and 1–5% the inhibitor tetramethyl tetravinyl cyclotetrasiloxane. |
| § This result can be obtained directly from eqn (1) at the limit λ → ∞, with a neo-Hookean form of W(λ), as shown in ref. 64. |
| ¶ The data displayed here from Liu et al.51 have been down selected to only the 100 °C and 200 °C data, though 150 °C and 300 °C cure temperatures were also evaluated in the original work. |
| This journal is © The Royal Society of Chemistry 2024 |