Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interfacial rheology of lanthanide binding peptide surfactants at the air–water interface†
Stephen A. Crane a,
Felipe Jiménez-Ángeles
a,
Felipe Jiménez-Ángeles b,
Yiming Wang
b,
Yiming Wang a,
Luis E. Ortuno Macias
a,
Luis E. Ortuno Macias cd,
Jason G. Marmorstein
cd,
Jason G. Marmorstein e,
Jiayi Deng
e,
Jiayi Deng a,
Mehdi Molaei
a,
Mehdi Molaei a,
E. James Petersson
a,
E. James Petersson e,
Ravi Radhakrishnan
e,
Ravi Radhakrishnan af,
Cesar de la Fuente-Nunez
af,
Cesar de la Fuente-Nunez afgh,
Monica Olvera de la Cruz
afgh,
Monica Olvera de la Cruz b,
Raymond S. Tu
b,
Raymond S. Tu c,
Charles Maldarelli
c,
Charles Maldarelli cd,
Ivan J. Dmochowski
cd,
Ivan J. Dmochowski e and
Kathleen J. Stebe
e and
Kathleen J. Stebe *a
*a
aDepartment of Chemical and Biomolecular Engineering, University of Pennsylvania, Philadelphia, PA 19104, USA. E-mail: kstebe@seas.upenn.edu
bDepartment of Materials Science and Engineering, Northwestern University, Evanston, IL 60208, USA
cDepartment of Chemical Engineering, The City College of New York, New York, NY 10031, USA
dLevich Institute, The City College of New York, New York, NY 10031, USA
eDepartment of Chemistry, University of Pennsylvania, Philadelphia, PA 19104, USA
fDepartment of Bioengineering, University of Pennsylvania, Philadelphia, PA 19104, USA
gMachine Biology Group, Departments of Psychiatry and Microbiology, Institute for Biomedical Informatics, Institute for Translational Medicine and Therapeutics, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA 19104, USA
hPenn Insitute for Computational Science, University of Pennsylvania, Philadelphia, PA 19104, USA
First published on 6th August 2024
Abstract
Peptide surfactants (PEPS) are studied to capture and retain rare earth elements (REEs) at air–water interfaces to enable REE separations. Peptide sequences, designed to selectively bind REEs, depend crucially on the position of ligands within their binding loop domain. These ligands form a coordination sphere that wraps and retains the cation. We study variants of lanthanide binding tags (LBTs) designed to complex strongly with Tb3+. The peptide LBT5− (with net charge −5) is known to bind Tb3+ and adsorb with more REE cations than peptide molecules, suggesting that undesired non-specific coulombic interactions occur. Rheological characterization of interfaces of LBT5− and Tb3+ solutions reveal the formation of an interfacial gel. To probe whether this gelation reflects chelation among intact adsorbed LBT5−:Tb3+ complexes or destruction of the binding loop, we study a variant, LBT3−, designed to form net neutral LBT3−:Tb3+ complexes. Solutions of LBT3− and Tb3+ form purely viscous layers in the presence of excess Tb3+, indicating that each peptide binds a single REE in an intact coordination sphere. We introduce the variant RR-LBT3− with net charge −3 and anionic ligands outside of the coordination sphere. We find that such exposed ligands promote interfacial gelation. Thus, a nuanced requirement for interfacial selectivity of PEPS is proposed: that anionic ligands outside of the coordination sphere must be avoided to prevent the non-selective recruitment of REE cations. This view is supported by simulation, including interfacial molecular dynamics simulations, and interfacial metadynamics simulations of the free energy landscape of the binding loop conformational space.
1 Introduction
We are developing peptide surfactants (PEPS) that bind rare earth elements (REEs) and adsorb at fluid interfaces for exploitation in REE recovery and purification using foam fractionation methods. The REEs, which comprise the lanthanides (Lns), yttrium (Y), and scandium (Sc), are considered critical elements. These elements are commonly categorized as light REEs (which include Sc, and the elements La through Gd) and heavy REEs (which include Y, and the elements Tb through Lu). Despite their name, REEs are not rare, but have crustal abundance similar to that of copper and lead, with light REEs being more abundant than heavy ones. REEs have unique properties crucial to many modern technologies including lasers, catalysts, turbines and electric vehicles.1–3Typically, REEs are found in minerals as mixtures with low concentrations, presenting a separation challenge. This separation challenge is most notable for the Ln cations, which are present predominantly in a +3-oxidation state and have ionic radii that differ by approximately 0.2 Å between La3+ (the lightest Ln3+) and Lu3+ (the heaviest Ln3+). This modest decrease in cation radius, the so-called lanthanide contraction, causes differences in the lanthanides’ coordination with surrounding water molecules. This contraction is also exploited to generate selectivity among extractants used in liquid–liquid extraction (LLE), the most common method for Ln separation and purification. In LLE, extractant molecules (e.g. phosphoric acids, carboxylic acids, or amines) are placed in an organic phase (typically kerosene) which is layered atop an aqueous phase that contains mixtures of REE cations. The extractants form complexes with Ln3+ at the aqueous-organic phase interface and subsequently partition into the organic phase. The complexation of the extractants and Ln3+ is weakly selective, allowing REEs to be separated and purified from REE mixtures.4–6 However, neighboring REEs typically have separation factors close to 1, so many stages of LLE are required, which presents an environmental burden on regions engaged in large-scale REE separations.6 The difficulty of these separations has inspired research on new, green alternative approaches.
In an interesting recent advance, peptides derived from EF-hand domains of calcium binding proteins have been immobilized on solid supports and used to capture REEs.7–9 EF hands are evolutionarily conserved, multi-ligand domains that are known to envelop a single ion in a binding loop. An important advantage of this approach is that REE-binding peptides based on EF-hands are relatively small biomolecules that are easy to modify and synthesize for high throughput screening.10 Our work is complementary to this approach. In our envisioned process, rather than immobilizing REE-binding peptides, we aim to form selective PEPS-REE complexes in aqueous solution and to collect them at air–water interfaces in a foam recovery process. Briefly, the envisioned process would involve PEPS selectively binding to one Ln3+ cation in bulk and adsorbing to the interface of bubbles sparged through the solution. The resulting foam could then be acidified, to protonate PEPS and release the bound cations. The protonated PEPS could then be removed from the cation enriched solution in a second foaming process, thereby allowing the recycling of PEPS. This approach exploits the enhanced and tunable selectivity of REE binding loop extractants and eliminates the organic phase of LLE which would lead to a more efficient and green process.
We develop PEPS based on lanthanide binding tags (LBTs), peptides containing a binding loop sequence of amino acids known to form a 3-dimensional coordination sphere of several (6–8) ligands, primarily carboxylates and carbonyls, around the bound REE. The LBTs have been chemically evolved from calcium binding EF hands within calcium binding proteins.10–12 Because of the similarity in size of Ca2+ and the REE cations, these loops coordinate to REEs with even higher affinity, attributable, in part, to their higher charge density. LBTs have been optimized by screening methods to coordinate with high affinity to particular lanthanides (e.g. terbium and europium).
We have previously studied PEPS with sequences LBT5− and LBT3−, shown in Fig. 1a; the net charge on these sequences in the unbound state is given in their superscript. LBT3− is a variant of LBT5− in which the charge of the native peptide is altered by replacing anionic ligands outside of the coordination sphere, specifically by amidating the C-terminus and exchanging an aspartic acid in the 11th position with asparagine (D11N). Fig. 1b shows a molecular dynamics (MD) simulation snapshot of LBT5− which has formed a binding loop; its backbone envelops the Ln3+ and has its coordinating amino acid side chains facing inwardly, cradling the ion. Careful inspection of this figure shows that LBT5− also has two free ligands which face outside of the coordination sphere (highlighted in yellow). We refer to these anionic ligands as non-binding loop ligands, or ligands outside the coordination sphere, which likely play a role in chelating excess ions. To assess the importance of these ligands, we also probe the surface rheological response of the PEPS with sequence RR-LBT3− which has two positive arginine residues inserted before the tyrosine at the N-terminus of the LBT5− sequence.
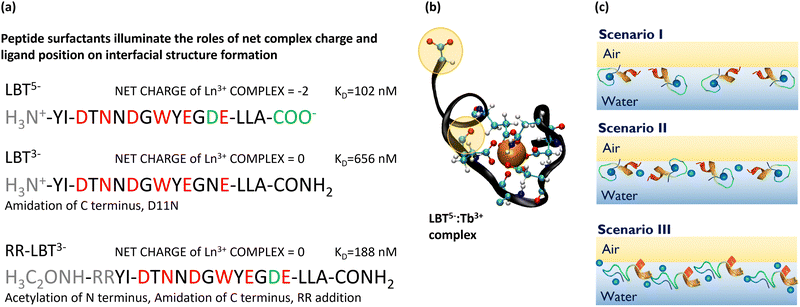 | ||
| Fig. 1 PEPS sequences, structure, and hypothesized self-assembly at the air–water interface. (a) PEPS sequences with positively charged components in gray, binding loop residues in red, and non-binding loop ligands in green. The net charge upon complexation with Tb3+ is given along with the KD in nM for PEPS:Tb3+ complexes. The KD for LBT5− and LBT3− were measured in previous work.13 The KD for RR-LBT3− was measured for this paper, see Fig. S1 (ESI†) for details. (b) An MD snapshot of the binding loop with all binding loop ligands and non-binding loop ligands shown. (c) Hypothesized PEPS morphologies at the air–aqueous interface. Depiction of PEPS acting as selective monomers with binding loop intact (scenario I), PEPS forming multimers with intact binding loops but chelation from ligands outside the coordination sphere which reduces selectivity (scenario II), and PEPS that denature in the air–aqueous interface resulting in complete loss of the selective binding and many PEPS:Tb3+:PEPS interactions (scenario III). | ||
Relevant to the current study, for both LBT5− and LBT3−, in prior work, we have quantified the binding affinity in bulk, and characterized air–aqueous interfaces of PEPS and Tb3+ solutions using pendant drop tensiometry, X-ray fluorescence near total reflection (XFNTR) and X-ray reflectivity. These data show that PEPS and Tb3+ bind in the bulk and adsorb to form a monolayer at the interface. In particular, the ELLA residues at the C-terminus of the LBT sequence form an α-helix that adsorbs to the air–water interface. For LBT5− in the presence of Tb3+ at greater than equimolar concentrations, the ratio of Tb3+ cations to peptide present in the interface is 1.66, whereas for LBT3− the ratio of Tb3+ cations to adsorbed peptide is 1.0.13 These prior results show that excess REE cation adsorption can be mitigated by managing electrostatic charge in the PEPS-REE complexes and suggest that the binding loop is intact in the interface.
In this study, we use interfacial rheology to further probe the integrity of the LBT binding loop and, by probing judiciously selected peptide variants, show that electrostatic interactions and associated restructuring of the interfacial layer depend subtly on the location and role of ligands in the peptide sequence. We study surface rheology at fixed PEPS concentration in the presence of Tb3+ at concentrations varying from equimolar solutions to superequimolar solutions, and in the absence of Tb3+. Our aim is to understand how PEPS structures relate to the ability to bind REE cations and recruit them to fluid interfaces without non-selective interactions or loss of the binding loop structure. One can imagine three scenarios for PEPS at air–aqueous interfaces, as shown schematically in Fig. 1c. In scenario I, PEPS adsorb with their binding loop intact, which minimizes non-specific binding. The rheology of such interfaces is expected to be purely viscous because interactions between adsorbed PEPS:REE complexes should arise from relatively weak hydrophobic interactions. Scenario II shows PEPS that adsorb with their binding loops intact but with additional, non-selectively bound Tb3+ ions chelated by PEPS non-coordinating ligands to form a multimeric structure. This introduces non-selective binding outside of the binding loop that would compromise the selectivity of the separation. We hypothesize that the non-binding loop ligands that face outwards play a role in this multimeric structure formation. The rheology of surfaces laden with PEPS in scenario II would show a viscous to viscoelastic transition in the presence of excess Ln3+ cations. Lastly, in scenario III, PEPS denature in the interfacial layer, an undesired situation. These PEPS would lose all selectivity and their rheology would be highly elastic, as the binding ligands of adsorbed, disordered PEPS would be accessible for crosslinking via multi-site coordination with Ln3+.
Interfacial shear rheology is characterized via single particle microrheology and correlated displacement velocimetry (CDV). Experimental results are corroborated by MD simulations of PEPS structural dynamics at the interface. These results allow us to infer that the binding loop is intact, albeit perturbed, in the fluid interface. Further, by probing system response in the presence of non-REE cations (e.g. Ca2+ and Al3+), and by study of PEPS variants designed to yield neutral PEPS-REE complexes, we propose a nuanced view of the roles of excess charge and binding ligands on the selectivity of PEPS in the interface. Our results suggest that anionic ligands located outside of the binding pocket participate in non-selective binding, whereas those within the binding loop do not.
2 Materials and methods
2.1 Sample preparation
Stock solutions of lyophilized peptides purchased from Genscript (>95% purity) were prepared in MES buffer solution. Buffer was prepared by dissolving 50 mM MES (2-(N-morpholino)ethanesulfonic acid) (Acros Organics 99%), and 100 mM NaCl, (Fisher Chemicals >99%), in deionized water from a Milli-Q system with resistivity of 18.2 MΩ cm. The peptide concentration of each stock solution was quantified by UV-Vis spectroscopy by measuring absorbance at 280 nm and using Beer's law with the extinction coefficient ε = 8480 cm−1 M−1.14 Solutions of Tb3+ cations were prepared at concentrations of 5 mM from TbCl3·6H2O (Sigma Aldrich 99.9%) dissolved in Milli-Q water that was slightly acidified with HCl. The same procedure was followed to prepare 5 mM stock solutions of CaCl2 (Fisher Chemicals ≥96%), and AlCl3 (Sigma Aldrich 99.99%), respectively. Polystyrene particles suspended in solution with no surface functionalization and average diameter of 2a = 1.0 μm were purchased from Polysciences. The particles were washed and centrifuged before undergoing solvent exchange with ethanol. The particles in ethanol suspensions were dried into a powder following a protocol from Bangs Laboratories, Inc. (Tech Note 203A). To ensure that particle type did not impact the results, additional control experiments were performed with both negatively charged, carboxylated particles, and positively charged, aminated particles. Experiments conducted with these particles produce similar results to the neutral particles that were used to gather the data presented in this work.2.2 Particle tracking
Particle tracking experiments were conducted in a custom-made vessel constructed by affixing a 14 mm ID ring, with a lower half made of aluminum and upper half made of Teflon, to a no. 1 coverslip using Corning vacuum grease to allow for imaging on an inverted microscope.15,16 Care is taken to ensure a good seal without introducing grease to the sample. Prior to affixing to the ring, the coverslip is treated with O2 plasma, making the glass surface more hydrophilic, which aids in forming a flat air–aqueous interface. Appropriate dilutions of Tb3+ stock solutions are made in buffer and placed in the vessel, in which they spread to form a planar interface. Colloidal particles are introduced to the interface via an aerosolization method to avoid the use of spreading solvents. In this method, clusters of dried particles are rubbed between two clean microscope slides to form a thin layer of individual particles. The dried particles are aerosolized using a blast of compressed gas and allowed to settle under gravity onto the interface.17 The peptide solution is gently added by injection beneath the interface after the particles to fill the sample chamber to the aluminum–Teflon seam, with a total sample volume of 120 μL. The Teflon seam pins the air–liquid interface, which has an area of Asurface = 1.54 cm2. Unless otherwise noted, all particle-tracking experiments were conducted on solutions of 65 μM PEPS with varying molar concentrations of Tb3+ ranging from 0 μM to 260 μM, i.e. spanning a molar ratio of Tb3+ to PEPS from 0.0 to 4.0. Samples are allowed to equilibrate for 30 min before particle tracking begins. Particle tracking is carried out using an inverted microscope in brightfield with a 40× air objective (NA 0.55). For each condition studied, three videos of 5000 frames captured at 26 frames per second are recorded at three distinct positions at the interface using a CMOS camera (Point Grey). The images are analyzed using a Python implementation of the algorithm by Crocker et al. to track each particle's position.18,19 Collective drift of all particles is removed.Two methods are used to characterize surface shear rheology. For purely viscous interfaces, we determine the surface viscosity ηs, which we report in non-dimensional form in terms of the Boussinesq number,
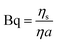 | (1) |
For viscoelastic interfaces, we determine the interfacial storage and loss moduli, G′ and G′′, respectively. We report the storage modulus in terms of Ĝ, a non-dimensional number defined in terms as a ratio of characteristic interfacial elastic to bulk viscous effects,
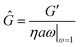 | (2) |
| 〈Δr2(τ)〉 = 〈[r(t + τ) − r(t)]2〉 | (3) |
To infer local surface rheology or to probe the heterogeneity of response on the interface, the MSD of individual colloidal particles can be tracked. Alternatively, to infer average surface rheological response of the interface, the ensemble averaged mean square displacements (EMSD) can be analyzed. In either case, the MSD (or EMSD) vs. τ is fitted with a power-law model,
| 〈Δr2(τ)〉 = Aτn | (4) |
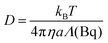 | (5) |
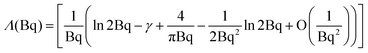 | (6) |
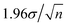 .24 Typically n ∼ 102 for our measurements, so the 95% confidence interval is smaller than the σ error bars. This implies that if any Bq are separated by their σ we can claim that the mean Bq are significantly different with a minimum of 95% confidence.
.24 Typically n ∼ 102 for our measurements, so the 95% confidence interval is smaller than the σ error bars. This implies that if any Bq are separated by their σ we can claim that the mean Bq are significantly different with a minimum of 95% confidence.
Interfaces with n < 1 have viscoelastic behavior and are described by a complex surface modulus. The storage and loss modulus (G′ and G′′) are calculated from MSD (or EMSD) vs. τ data using the equation,
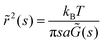 | (7) |
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 2(s) is the Laplace transform of the MSD, s is the Laplace frequency, and
2(s) is the Laplace transform of the MSD, s is the Laplace frequency, and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (s) is the modulus in Laplace space.25 Local power law fits, determined by the logarithmic time derivative of the MSD, are used to estimate the complex shear modulus. We use a second-order polynomial to locally smooth the MSD data and to numerically calculate the first- and second-order logarithmic derivatives of the MSD. By including the second-order logarithmic time derivatives of the MSD, we achieve a better estimate of the moduli.26
(s) is the modulus in Laplace space.25 Local power law fits, determined by the logarithmic time derivative of the MSD, are used to estimate the complex shear modulus. We use a second-order polynomial to locally smooth the MSD data and to numerically calculate the first- and second-order logarithmic derivatives of the MSD. By including the second-order logarithmic time derivatives of the MSD, we achieve a better estimate of the moduli.26
Absent PEPS, single point microrheology of the air–aqueous interfaces of buffer solutions and of buffer solutions containing 260 μM Tb3+ are viscous, with Bq ∼ 2 and Bq ∼ 5, respectively, indicating the presence of surface-active impurities in the buffer and Tb3+ components (Fig. S4, ESI†).
| χ(x,τ) = 〈χij(xsp(t,τ))〉 = 〈Δyi(t,τ)Δxpj(t,τ)δ2D(x − xsp(t))〉t,i,j | (8) |
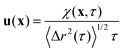 | (9) |
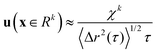 . For purely elastic interfaces, the same approach yields the shear strain field generated by the probe's Brownian displacement in the film
. For purely elastic interfaces, the same approach yields the shear strain field generated by the probe's Brownian displacement in the film 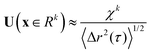 .
.For fluid interfaces, the spatial form of the flow field reveals an interfacial Stokeslet generated by “Brownian forcing” by a point force f directed along the y axis in an incompressible fluid interface. Surface viscosities slow the rate of spatial decay of the flow and generate signatures that can be used to quantify the surface viscosity. In particular, the y-directed velocities along the x and y axes depend strongly on the surface viscosity and can be fitted with the theoretical flow field using two parameters: the point force, f, and the Boussinesq length LB. The theoretical y component of the velocity uy for a point force acting in the interface is given by:
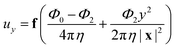 | (10) |
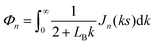 | (11) |
2.3 Interfacial tensiometry
The surface tension of PEPS:REE solutions is measured using pendant drop tensiometry in which a silhouette of a pendant droplet of solution is fitted with the Young–Laplace equation.31 Pendant droplets are formed at the end of an 18-gauge straight needle by a syringe and kept in a humidified chamber which limits evaporative losses. Silhouettes are captured using a camera (Basler acA720-520um) every 5 seconds for a total of one hour. The surface tension of clean air–water interfaces (γ = 72.8 mN m−1) is measured each time before a PEPS and REE mixture is measured to ensure cleanliness of the syringe and needle and to confirm proper calibration of the instrument. For peptide and REE solutions that do not come to equilibrium, but have continued weak relaxation of tension, we truncate this measurement at 45 minutes and report the surface tension values at that surface age as quasi-equilibrium surface tensions. For elastic interfaces, we report the apparent surface tension obtained from the pendant drop silhouette as an apparent surface tension, noting that its interpretation must be treated with care as the interface is covered in a thin solid film.2.4 Molecular dynamics
Molecular dynamics (MD) simulations were performed for the two peptides LBT5− and LBT3−. The conformation of LBT5− is taken from the protein data bank (ID 1TJB).12 To simulate the interfacial behavior, we employ a simulation box with an aqueous phase slab32 at the middle of the simulation box. The aqueous slab is surrounded by empty spaces which accommodate the vapor phase and create two surfaces (Fig. S8a, ESI†). The simulation box dimensions are 10 nm × 10 nm × 40 nm in the x-, y-, and z-directions, respectively. We applied periodic boundary conditions in the three directions. At t = 0, a layer of PEPS complexes is placed at each of the interfaces in the configuration shown in Fig. S8a (ESI†). The systems are simulated for at least 1 μs and up to 2 μs. We investigate the conformational evolution of the peptide complexes, the velocity profiles, and mean square displacement. We considered variable complex concentrations. The composition of the systems is given in Table S1 (ESI†). We conducted classical all-atom molecular dynamics (MD) simulations using the package GROMACS.33–35 The electrostatic and van-der-Waals interactions are considered using the parameters from the CHARMM force field.36 The electrostatic interactions are computed using the PME algorithm. We performed microsecond-MD simulations in the NVT ensemble at T = 298 K using a time-step of 2.5 fs. The temperature is controlled using the Nose–Hoover thermostat.37,38 The systems are equilibrated for 20 ns before a production run of at least 1 μs and up to 2 μs. Two and three replicated simulations are conducted for the systems. To calculate the mean square displacement, the system configurations are recorded every 20 ps. No significant differences are found by recording every 100 ps.2.5 Metadynamics simulation
Well-tempered metadynamics simulations were performed to construct the free energy landscape of the LBT5−:Tb3+ and LBT3−:Tb3+ complex at the air–water interface using the GROMACS package 2020.235 and Plumed 2.6.2 version.39 The initial configuration of the LBT5−:Tb3+ complex was obtained from X-ray measurements (PDB code: 1TJB).12 The initial configuration of the LBT3−:Tb3+ complex was obtained by residue mutation D11N using the Scwrl4 program.40 Metadynamics simulations of the two systems were performed under constant volume (rectangular box with 5 nm × 5 nm × 10 nm in XYZ direction, respectively) and the room temperature maintained by the stochastic velocity rescaling thermostat.41 The initial configurations for the two metadynamics simulations are obtained from the last configuration of 100 ns NVT simulations of LBT5−:Tb3+ complex and LBT3−:Tb3+ complex at the air–water interface. Here, we used two collective variables (CVs). First, the coordination number (CN) of Tb3+, which refers to the number of oxygen atoms (j) from the LBT peptide that have a separation distance with Tb3+ (i) less than rc = 0.27 nm, (d = 0.03) and do not include the oxygens of water, using the following equation:
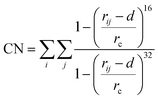 | (12) |
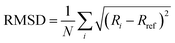 | (13) |
3 Results and discussion
3.1 Interfacial rheology of LBT5− and Tb3+ solutions
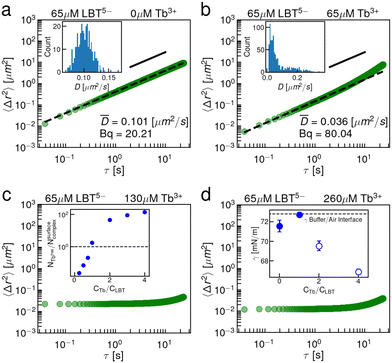
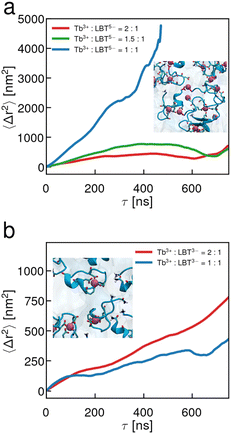
Interfaces of LBT5− solutions with excess Tb3+ cations above an equimolar concentration ratio undergo a viscous to elastic transition, as is evident in the single point microrheology data shown in Fig. 2. Absent Tb3+, the LBT5− laden interface is highly viscous, with Bq ∼ 20 (Fig. 2a); the significant dissipation in the interface may be attributed to the intrinsically disordered unbound peptide and resulting peptide–peptide interactions. For equimolar Tb3+ to LBT5− concentrations, the interface is even more sluggish, with Bq ∼ 80 (Fig. 2b). For excess Tb3+ (Fig. 2c) the EMSD shows the signature of elastic network formation. The nearly constant reduced EMSD at early lag times indicates that surface probes are caged within the network. The increase in EMSD at long lag times indicates that the probes can escape from these caging domains. As even more Tb3+ is added (Fig. 2d), the elastic network stiffens as indicated by the slight reduction in the MSD plateau. We find the storage modulus G′(ω = 1 s−1) = 82.9 mN m−1 and loss modulus G′′(ω = 1 s−1) = 15.4 mN m−1; G′ > G′′, indicating a transition to a thin solid film.This crossover can be related to the presence of excess unbound cations in solution that are not in binding loops. Molecular dynamics simulation of LBT5−:Tb3+ complexes in the interface yields a minimum area per molecule amin = 150 Å2 per molecule. Using this number and the known interfacial area of our chamber Asurface, we estimate the maximum number of moles of complexed peptide that can adsorb at the interface of our chamber, Nsurfacecomplex = Asurface/amin. Using the binding affinity of the LBT5−:Tb3+ complex in solution (KD = 150 nM), we also estimate the total unbound fraction of Tb3+ in solution NTbfree. For fixed peptide concentration, the ratio NTbfree/Nsurfacecomplex, shown in the inset to Fig. 2c, increases above unity (dashed line) for bulk concentrations of Tb3+ in excess of equimolar ratios to peptide. We hypothesize that these excess cations interact with the adsorbed LBT5−:Tb3+ complexes to form condensed domains of multimers of LBT5−:Tb3+ complexes that are chelated by Tb3+ through free anionic ligands present on the PEPS:REE complexes.
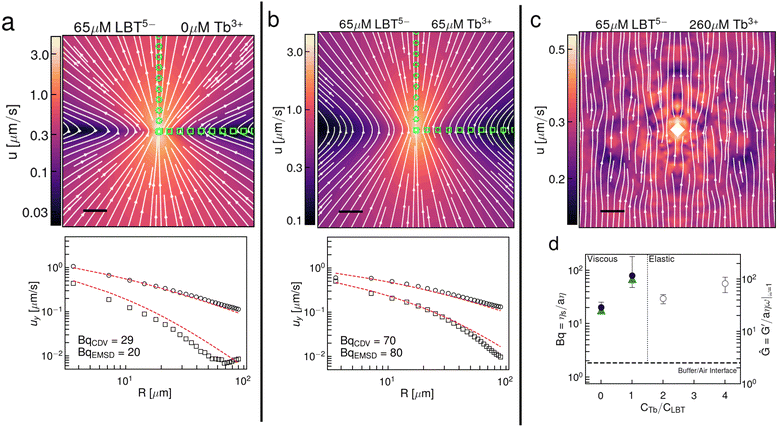
Using the same videos of Brownian particles in the interface, we also perform CDV and construct the interfacial flow generated around a Brownian colloid in the interface (Fig. 3a–c). The flow field has the form of a Stokeslet in a viscous, incompressible interface.27,28 In the presence of excess Tb3+ cations, the displacement field in the thin elastic film is nearly uniform (Fig. 3c), corresponding to that of a source particle generating unidirectional displacement of surface probes. These data corroborate the main single-point rheology result, i.e. that the interface transitions from a viscous fluid to a thin elastic solid film in the presence of excess Tb3+. Moreover, the measured values of Bq from CDV closely resemble the values measured by single point microrheology (Fig. 3d). This result is notable because CDV does not probe the interface in the direct vicinity of the particle, rather it reports on the region between two particles. This means the method is insensitive to any local interfacial structuring that could be brought on by the probe particle.42 The spatial form of the flow fields generated by Brownian colloids constructed by CDV for viscous interfaces (Fig. 3a and b) clearly shows that there is an incompressible layer, as expected for interfaces that are laden with surface-active species that do not ad/desorb rapidly between the interface and the fluid sublayer. The waist of the hourglass shape of the flow field expands with increasing surface viscosity and the velocity decays more slowly. We fit the y-directed velocities along the x and y axes to extract a Bq from the viscous flow fields. Theoretical flow fields and y-directed velocity profiles along the x and y axis are shown in Fig. S7 (ESI†).
In the above discussion, we have hypothesized that the elastic interface indicates non-specific binding in the interface by chelation of Tb3+ ions that link complexed LBT5−:Tb3+ in the interface. In this scenario, the coordination sphere of binding ligands forms and envelops a single Tb3+ cation, but the additional anionic ligands present outside of the coordination sphere interact with excess Tb3+ to form viscous aggregates and elastic networks. Alternatively, the binding loop could denature in the interface, thereby presenting many anionic ligands for network formation. Such denaturation could arise from two sources: the anisotropic environment of the air–aqueous interface itself, or electrostatic interaction between net negative complexes and excess Tb3+ ions.
3.2 Interfacial rheology of LBT3− and Tb3+ solutions
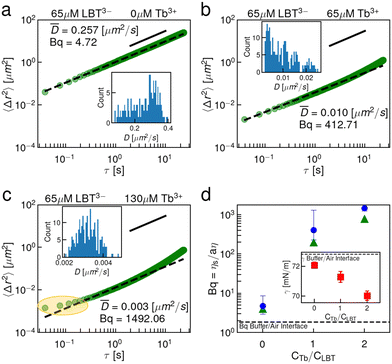
To assess the binding loop integrity, a less charged peptide surfactant, LBT3−, was selected. This peptide has identical coordinating ligands to LBT5− but forms neutral complexes with Tb3+ and contains no anionic ligands outside of its coordination sphere. Fig. 4 summarizes the interfacial rheology characterization of LBT3−. The EMSD data, shown in Fig. 4, show that the LBT3− and Tb3+ laden interfaces are viscous at all concentrations of Tb3+, over concentration ratios of Tb3+ to LBT3− from 0 to 2.0. Furthermore, the distributions of tracer diffusivities measured from individual particles’ MSDs are relatively unimodal, indicating that interfacial heterogeneity is not pronounced. The viscosity of these interfaces becomes extremely large with excess Tb3+. This highly dissipative behavior is likely driven by van der Waals interactions among the neutral LBT3−:Tb3+ complexes which have limited electrostatic repulsion. A careful scrutiny of the EMSD at Tb3+ to LBT3− concentration ratio of 2 shows an apparent plateau in EMSD at short lag times (Fig. 4c, highlighted). However, this plateau does not indicate the formation of an elastic film. Rather, the viscosity in this interface is so high in these layers that the particle displacement cannot be measured due to the resolution of the instrument (Fig. S2, ESI†). At lagtimes of 0.2 s and longer, probe motion can be resolved and the EMSD is diffusive. The surface tension of these solutions also differs from that of LBT5− solutions (Fig. 2d inset); the surface tension decreases monotonically over all Tb3+ to LBT3− concentration ratios (Fig. 4d inset). While for LBT5−, electrostatic repulsion was significantly reduced by chelation of excess cations, such effects are absent for LBT3− which lacks excess charge when complexed to drive Tb3+ chelation. A summary of Bq versus Tb3+ concentration (Fig. 4d) shows that the surface viscosity increases monotonically with Tb3+ and appears to plateau for Tb3+ in excess of equimolar ratios. Again, CDV was performed on these interfaces (Fig. S9, ESI†) and the Bq from CDV follows the same trend with similar magnitudes to the single point measurements (Fig. 4d).These LBT3−:Tb3+ results suggest that the coordination sphere of binding ligands around the Tb3+ cation is stable in the highly anisotropic environment at the air–water interface. Further, the elastic transition with excess Tb3+ for the negatively charged LBT5−:Tb3+ complex and the absence of such a transition for neutral LBT3−:Tb3+ complexes indicates that electrostatics play a key role in elastic structure formation. This concept is consistent with the hypothesis that neighboring LBT5−:Tb3+ complexes at the interface recruit Tb3+. It is not clear, however, whether the elastic film formation relies on the presence of complexes with net negative charge, which are linked by Tb3+ cations, or whether it depends more subtly on the location of the charged moieties in the bound complex.
3.3 Interfacial rheology of LBT3−:Ca2+ and RR-LBT3−:Tb3+ complexes
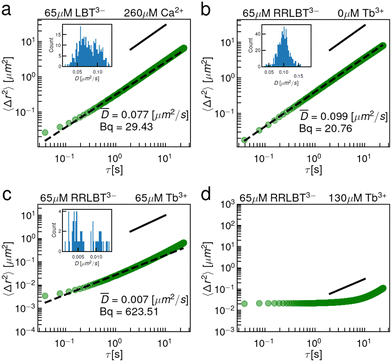
To address this question, we have performed two sets of single point microrheology experiments. First, we exploit the ability of LBT3− to bind Ca2+ to form a complex with a net negative charge. Ca2+ is an acceptable surrogate for Tb3+ because they are of similar size and the binding loop was derived from a Ca2+ binding protein.11 The results (Fig. 5a) show that the interface remains purely viscous in the presence of excess Ca2+, i.e. at a Ca2+ to LBT3− concentration ratio of 4.0. This result shows clearly that excess charge on the complex is not sufficient to promote network formation and suggests that a more subtle effect is at play. We hypothesize that elastic films do not form because LBT3−:Ca2+ complexes have no anionic ligands that are presented outside of the coordination sphere. Fig. S10 (ESI†) shows a simulation snapshot at 1 μs for LBT3−:Ca2+ at the air–water interface. In this snapshot, all anionic ligands are coordinating the Ca2+. Thus, while the LBT3−:Ca2+ complex has a net negative charge, it is not possible for the complex's anionic ligands to crosslink in the interface with additional Ca2+ outside the binding loop. To further probe the importance of ligands outside of the coordination sphere, another mutant, RR-LBT3−, was prepared, in which two positively charged arginine residues have been appended to the N-terminus of LBT5− and the C-terminus is amidated. Based on the KD of RR-LBT3−, shown in Fig. 1, we infer that this peptide binds Tb3+ similarly. This mutant is designed to form net neutral complexes with Tb3+. However, like LBT5−, RR-LBT3− presents a carboxylate outside of the coordination sphere at the D11 position. Fig. 5b–d shows that despite the RR-LBT3−:Tb3+ complex having a neutral charge, adsorbed RR-LBT3−:Tb3+ complexes form thin elastic films in the presence of excess Tb3+. Like LBT5−, RR-LBT3− undergoes a viscous to elastic transition where the interface is viscous for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 RR-LBT3−
1 RR-LBT3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tb3+ and 1
Tb3+ and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 RR-LBT3−
0 RR-LBT3−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tb3+.
Tb3+.
These data indicate that, even in the absence of net negative charge on the complex, the negatively charged D11 residue is locally attractive and sterically accessible to the trivalent cation. Furthermore, these results indicate that the two positively charged arginines outside of the binding pocket do not repel the additional cation, suggesting “patchy colloid”-like interactions among the exposed charged sites on the peptide at the interface. The bulk Debye length for these solutions is around 1 nm. In the air–water interface, where the dielectric constant is about half that of the bulk,43 the Debye length is closer to 0.5 nm which is sufficiently small such that patchy charges on these complexes could be distinguishable. This indicates that net neutral complexes are not sufficient to deter non-specific binding and a more stringent design criterion, having no anionic ligands outside the coordination sphere, is required.
To interrogate the coordination sphere in the presence of strong cationic perturbants, the rheology of PEPS laden interfaces was also probed in the presence of Al3+. We select the small Al3+ cation for two reasons. Its small size implies that its charge is highly concentrated, with a radius about half that of Ln3+.44 This relates to a charge density almost 10× larger. Furthermore, it is too small to form a coordination sphere with LBT3− due to steric hindrance of the backbone. The addition of Al3+ to LBT solutions is highly disruptive. Large extended aggregates form in the interface and in the bulk (Fig. S11, ESI†); such aggregated clumps are never present for Tb3+ or Ca2+. Interestingly, the addition of Al3+ to solutions of LBT3−:Tb3+ does not lead to such aggregate formation, providing additional evidence that the coordination sphere of LBT3−:Tb3+ is intact in the bulk and at the interface. Addition of Al3+ to solutions of LBT5−:Tb3+ results in aggregation, whereas addition of Al3+ to solutions of RR-LBT3−:Tb3+ shows no aggregation (Video S1–S3, ESI†). These results indicate that PEPS should be designed to be charge neutral to prevent electrostatic denaturation from cations with large charge densities in bulk solution. Future studies will assess interactions between PEPS and common transition metals like Fe. We do not expect that metal cations like Fe2+, which have lower charge and ionic radii only slightly smaller than Ln3+, would denature the binding loop in the same way as Al3+.
Scrambled peptides are often studied as controls to assess the importance of loop sequence in generating selective binding.45 However, here we study bi-functional LBTS with amphiphilicity to bring them to the interface and binding loops known to selectively bind REE. We seek to understand conditions for which selective binding is preserved and non-selective chelation is avoided upon LBTs adsorption. Peptides are unlikely preserve their bifunctionality, i.e. to have both intact binding loops and surfactancy. For this reason, a scrambled control is not studied in this work.
3.4 Molecular dynamics and metadynamics simulations
Our study of surface rheology suggests that the coordination spheres formed by the LBT-derived peptides do not denature at the interface, even in the presence of excess large ions like Tb3+ or Ca2+. Furthermore, the experimental results show that the presence of non-binding loop ligands is responsible for interfacial elasticity and network formation. To get insight into molecular conformations at the interface at various Tb3+ to peptide ratios, all-atom MD simulations were performed on air–aqueous interfaces of solutions of PEPS and Tb3+. The results from the MD simulations corroborate the findings of the particle tracking microrheology, in that the displacements are highly attenuated in the presence of excess cations (Fig. 6).Fig. 6 shows that LBT5− undergoes network formation as Tb3+ concentration increases past the stoichiometric ratio. The EMSD data is subtle, but for larger than stoichiometric ratios of Tb3+ (Fig. 6a) a plateau can be seen at later lag times around 200 ns. We attribute this late onset plateau to a characteristic length of the elastic network that forms. As such, PEPS move diffusively until they have moved far enough to strain the elastic network and then the PEPS EMSD shows a “caged” behavior. It appears that this characteristic length decreases with increasing Tb3+ concentration i.e. the plateaus occur at slightly lower MSD when greater excess Tb3+ is present indicating that more ions may crosslink the network more densely. In the simulations for LBT3−, the EMSDs are increasing during the entire duration of the simulation. This implies that the interface is viscous even when excess Tb3+ is present (Fig. 6b). Careful inspection of the inset MD snapshots reveals how excess ions are present in the interfacial layer for LBT5− and crosslink multiple LBT5− peptides together. While similar results are found for RRLBT3− (see Fig. S12, ESI†), this behavior is not seen for interfacial layers of LBT3−. Additional snapshots showing the sideview of the interface are shown in Fig. S8b–d (ESI†) which show how excess Tb3+ localizes at the interface for LBT5− but not for LBT3−. Lastly, the PEPS in the interfacial layer appear to have intact binding loops throughout the duration of the simulation which suggests the binding loop is robust, again corroborating the findings of microrheology. Animations of the simulations can be found in the ESI† (Video S4–S6).
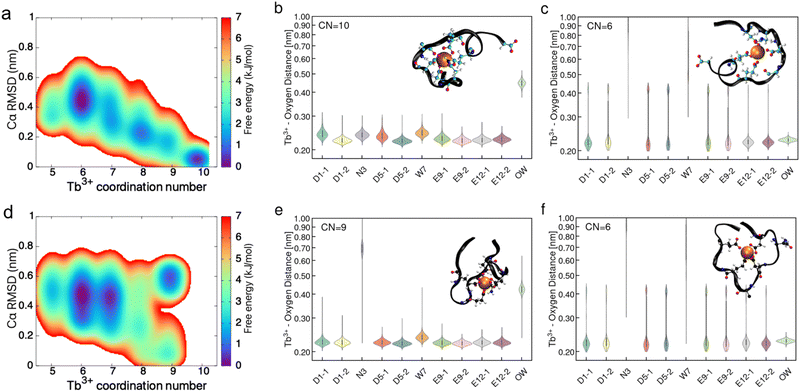
In addition to traditional MD, metadynamics simulations were performed to access PEPS conformations that may not be available to normal MD simulation. Fig. 7 shows the results of the metadynamics simulation. Here, we have performed well-tempered metadynamics simulations to further probe the molecular conformation of PEPS:Tb3+ binding complex at the air–water interface. The 2 dimensional free energy landscape is constructed from the metadynamics simulation trajectory using the histogram re-weighting method.46 Metadynamics simulations of the interface identified 5 to 6 PEPS:Tb3+ binding conformations with small free energy differences (ΔΔG ≤ 1 kcal mol−1), revealing the hidden complexity of the PEPS:Tb3+ binding complex conformations (Fig. 7a and d). For instance, LBT5− tends to sample three conformations with relatively higher probability (thus lower free energy) where Tb3+ is coordinated with 10, 8, and 6 oxygen atoms from LBT5− respectively (see Fig. S13, ESI† for the ranking of basin free energy value of each binding conformation). By comparison, LBT3− tends to have 9, 7, and 6 oxygen atoms coordinate with Tb3+ in the binding loop, suggesting that LBT3− may bind more weakly than LBT5− with Tb3+ at the interface. We report the residue oxygen–Tb3+ distance distances in violin plots (Fig. 7b, c, e and f), for the most highly coordinated and probable state and the least coordinated and probable state: 10 and 6 coordinate for LBT5− and 9 and 6 coordinate for LBT3−. The intermediate coordination states (8 coordinate for LBT5− and 7 coordinate for LBT3−) can be found in Fig. S14 (ESI†). Analysis of the residue oxygen–Tb3+ distance shows that in the case of both LBT5− and LBT3− all carboxylate ligands are bound to the Tb3+ cation in the interface even with lower coordinate structures. This implies that the elasticity seen with LBT5− comes from the non-binding loop ligands. For LBT3− no elasticity is observed and metadynamics reports that all anionic ligands are interacting with a Tb3+ in the binding loop. Since these anionic ligands are already in close contact with a cation inside the binding loop, they cannot be presented in such a way to crosslink with extra cations outside the binding loop.
4 Conclusion
This study demonstrates that microrheology by particle tracking can be used to infer molecular conformations of metal binding peptides that adsorb to air–water interfaces. The inferred molecular structures were further examined and confirmed by MD and metadynamics simulations. Recalling Fig. 1, we are able to categorize our PEPS into each of the scenarios. Scenario I represents PEPS that maintain their binding loop in the air–aqueous interface even in conditions with excess Tb3+. We demonstrate that LBT3− fits this scenario due to its purely viscous rheology, failure to denature upon addition of Al3+ to PEPS that have already bound Tb3+, and prior study that shows 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding. In addition, metadynamics simulation shows the lowest free energy conformations of LBT3− have all anionic binding loop ligands facing inward and interacting with the bound Tb3+ in the interface. In the presence of excess Ca2+, where the Ca2+:LBT3− complex carried negative charge, electrostatic interaction with excess Ca2+ was not strong enough to denature the coordination sphere and lead to elastic network formation. We suggest that the subtle detail of this PEPS which mitigates non-specific binding is the lack of anionic ligands outside of the binding loop and consider that a design criterion for future PEPS development. The other PEPS studied fall in scenario II. Both LBT5− and RR-LBT3− formed elastic networks at the air–aqueous interface of solutions containing excess Tb3+. Both of these PEPS contain anionic non-binding loop ligands, notably D11 in both and also the C-terminal carboxylate in LBT5−. While these PEPS form an elastic network, it should be emphasized that their binding loop is robust in the interface and likely stays coordinated. This is not only confirmed with careful mutation and ion selection (LBT3− with Ca2+), but also through interfacial MD and metadynamics studies which show the binding loop ligands are always interacting with the bound Tb3+ in the lowest energy configurations. Studies of PEPS with Al3+, a small and densely charged cation prone to denaturing PEPS, show that denatured PEPS form large extended aggregates which are never seen with LBT5− and RR-LBT3− in the presence of Tb3+. This evidence suggests that scenario III does not happen in interaction with Ln3+ cations and that the binding loops are robust in the interface. Interfacial elastic network formation likely occurs through interactions of Tb3+ with non-binding loop ligands that face outwards from the coordination sphere and is aided by the highly concentrated nature of molecules at fluid interfaces. Future work will be done to study the effect of the anionic ligands outside the binding loop on bulk aggregation. The Al3+ denaturation studies show another critical design criterion: PEPS must be net neutral to avoid non-Ln3+ induced denaturation and aggregation.
1 binding. In addition, metadynamics simulation shows the lowest free energy conformations of LBT3− have all anionic binding loop ligands facing inward and interacting with the bound Tb3+ in the interface. In the presence of excess Ca2+, where the Ca2+:LBT3− complex carried negative charge, electrostatic interaction with excess Ca2+ was not strong enough to denature the coordination sphere and lead to elastic network formation. We suggest that the subtle detail of this PEPS which mitigates non-specific binding is the lack of anionic ligands outside of the binding loop and consider that a design criterion for future PEPS development. The other PEPS studied fall in scenario II. Both LBT5− and RR-LBT3− formed elastic networks at the air–aqueous interface of solutions containing excess Tb3+. Both of these PEPS contain anionic non-binding loop ligands, notably D11 in both and also the C-terminal carboxylate in LBT5−. While these PEPS form an elastic network, it should be emphasized that their binding loop is robust in the interface and likely stays coordinated. This is not only confirmed with careful mutation and ion selection (LBT3− with Ca2+), but also through interfacial MD and metadynamics studies which show the binding loop ligands are always interacting with the bound Tb3+ in the lowest energy configurations. Studies of PEPS with Al3+, a small and densely charged cation prone to denaturing PEPS, show that denatured PEPS form large extended aggregates which are never seen with LBT5− and RR-LBT3− in the presence of Tb3+. This evidence suggests that scenario III does not happen in interaction with Ln3+ cations and that the binding loops are robust in the interface. Interfacial elastic network formation likely occurs through interactions of Tb3+ with non-binding loop ligands that face outwards from the coordination sphere and is aided by the highly concentrated nature of molecules at fluid interfaces. Future work will be done to study the effect of the anionic ligands outside the binding loop on bulk aggregation. The Al3+ denaturation studies show another critical design criterion: PEPS must be net neutral to avoid non-Ln3+ induced denaturation and aggregation.
Our work demonstrates that PEPS can be designed to carry Ln3+ to the air–aqueous interface and maintain the selective 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding loop structure in the interface even under perturbation from the anisotropic environment and excess ions. There are two criteria that should be met: net neutrality of the complex and no anionic ligands outside of the binding loop. In this way, PEPS can bind and retain REE cations in their binding loop at the interface without non-selective coulombic interactions to provide a means of green selective separation of REEs.
1 binding loop structure in the interface even under perturbation from the anisotropic environment and excess ions. There are two criteria that should be met: net neutrality of the complex and no anionic ligands outside of the binding loop. In this way, PEPS can bind and retain REE cations in their binding loop at the interface without non-selective coulombic interactions to provide a means of green selective separation of REEs.
Author contributions
KJS, IJD, CM, RST, CFN, RR, EJP designed the study, supervised research, and aided in interpretation of results. SAC performed all rheology experiments, analysis and interpretation with guidance from JD and MM. FJA performed and analyzed the molecular dynamics simulations, MOdlC participated in their interpretation. YW performed metadynamics simulations; RR aided in their design and interpretation. LEOM and JGM provided guidance in sample preparation. LEOM interpreted results. JGM carried out binding assays. The manuscript was drafted by SAC and reviewed and edited by all authors.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U. S. Department of Energy, Office of Science, Basic Energy Sciences under Award DE-SC0022240. J. G. M. acknowledges a graduate fellowship through the Vagelos Institute for Energy Science and Technology. We acknowledge Dr Nicholas. G. Chisholm's assistance with constructing theoretical interfacial Stokeslets.Notes and references
- B. S. Van Gosen, P. L. Verplanck, R. R. Seal Ii, K. R. Long and J. Gambogi, Rare-earth elements, U.S. Geological Survey Professional Paper Report 1802, 2017.
- K. Long, The future of rare earth elements—will these high-tech industry elements continue in short supply?, U.S. Geological Survey Open-File Report 1189, 2011.
- T. G. Goonan, Rare Earth Elements—End Use and Recyclability, U.S. Geological Survey Scientific Investigations Report 5094, 2011.
- E. O. Opare, E. Struhs and A. Mirkouei, Renewable Sustainable Energy Rev., 2021, 143, 110917 CrossRef CAS.
- T. C. Liu and J. Chen, Sep. Purif. Technol., 2021, 276, 119263 CrossRef CAS.
- T. Cheisson and E. J. Schelter, Science, 2019, 363, 489–493 CrossRef CAS.
- M. Y. Xu, Z. H. Su and J. N. Renner, Pept. Sci., 2019, 111, e24133 CrossRef CAS.
- Z. H. Su, J. D. Hostert and J. N. Renner, ACS ES&T Water, 2021, 1, 58–67 Search PubMed.
- J. D. Hostert, M. R. Sepesy, C. E. Duval and J. N. Renner, Soft Matter, 2023, 19, 2823–2831 RSC.
- L. L. Martin, B. R. Sculimbrene, M. Nitz and B. Imperiali, QSAR Comb. Sci., 2005, 24, 1149–1157 CrossRef CAS.
- K. J. Franz, M. Nitz and B. Imperiali, ChemBioChem, 2003, 4, 265–271 CrossRef CAS.
- M. Nitz, M. Sherawat, K. J. Franz, E. Peisach, K. N. Allen and B. Imperiali, Angew. Chem., Int. Ed., 2004, 43, 3682–3685 CrossRef CAS.
- L. Ortuno Macias, F. Jimenez-Angeles, J. G. Marmorstein, Y. Wang, S. A. Crane, S. KT, P. Sun, B. Sapkota, E. Hummingbird, W. Jung, B. Qiao, D. Lee, I. J. Dmochowski, R. Messinger, M. L. Schlossman, R. Radhakrishnan, E. J. Petersson, M. Olvera de la Cruz, W. Bu, M. Bera, B. Lin, R. Tu, K. Stebe and C. Maldarelli, ChemRxiv, 2024, preprint DOI:10.26434/chemrxiv-2024-8dzr2-v2.
- C. N. Pace, F. Vajdos, L. Fee, G. Grimsley and T. Gray, Protein Sci., 1995, 4, 2411–2423 CrossRef CAS PubMed.
- M. H. Lee, D. H. Reich, K. J. Stebe and R. L. Leheny, Langmuir, 2010, 26, 2650–2658 CrossRef CAS.
- J. Y. Deng, M. Molaei, N. G. Chisholm and K. J. Stebe, Langmuir, 2020, 36, 6888–6902 CrossRef CAS.
- M. A. Gharbi, M. Nobili, M. In, G. Prévot, P. Galatola, J. B. Fournier and C. Blanc, Soft Matter, 2011, 7, 1467–1471 RSC.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- D. B. Allan, T. Caswell, N. C. Keim, C. M. van der Wel and R. W. Verweij, soft-matter/trackpy: v0.6.2, 2024 DOI:10.5281/zenodo.10696534.
- P. G. Saffman and M. Delbruck, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3111–3113 CrossRef CAS PubMed.
- P. G. Saffman, J. Fluid Mech., 1976, 73, 593–602 CrossRef.
- B. D. Hughes, B. A. Pailthorpe and L. R. White, J. Fluid Mech., 1981, 110, 349–372 CrossRef CAS.
- T. M. Fischer, P. Dhar and P. Heinig, J. Fluid Mech., 2006, 558, 451–475 CrossRef.
- D. G. Altman and J. M. Bland, BMJ, 2005, 331, 903 CrossRef.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 74, 1250–1253 CrossRef CAS PubMed.
- B. R. Dasgupta, S. Y. Tee, J. C. Crocker, B. J. Frisken and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 051505 CrossRef.
- M. Molaei, N. G. Chisholm, J. Y. Deng, J. C. Crocker and K. J. Stebe, Phys. Rev. Lett., 2021, 126, 228003 CrossRef CAS PubMed.
- N. G. Chisholm and K. J. Stebe, J. Fluid Mech., 2021, 914, A29 CrossRef CAS.
- H. A. Stone and A. Ajdari, J. Fluid Mech., 1998, 369, 151–173 CrossRef CAS.
- V. Prasad, S. A. Koehler and E. R. Weeks, Phys. Rev. Lett., 2006, 97, 176001 CrossRef CAS.
- Y. Rotenberg, L. Boruvka and A. W. Neumann, J. Colloid Interface Sci., 1983, 93, 169–183 CrossRef CAS.
- F. Jiménez-Angeles, H. K. Kwon, K. Sadman, T. Wu, K. R. Shull and M. O. de la Cruz, ACS Cent. Sci., 2019, 5, 688–699 CrossRef PubMed.
- S. Páll, A. Zhmurov, P. Bauer, M. Abraham, M. Lundborg, A. Gray, B. Hess and E. Lindahl, J. Chem. Phys., 2020, 153, 134110 CrossRef.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS.
- S. Nose, J. Chem. Phys., 1984, 81, 511–519 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef CAS.
- G. G. Krivov, M. V. Shapovalov and R. L. Dunbrack, Proteins: Struct., Funct., Bioinf., 2009, 77, 778–795 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef.
- J. C. Crocker, M. T. Valentine, E. R. Weeks, T. Gisler, P. D. Kaplan, A. G. Yodh and D. A. Weitz, Phys. Rev. Lett., 2000, 85, 888–891 CrossRef CAS PubMed.
- M. Miller, Y. H. Liang, H. H. Li, M. Q. Chu, S. J. Yoo, W. Bu, M. O. de la Cruz and P. Dutta, Phys. Rev. Lett., 2019, 122, 058001 CrossRef CAS.
- R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- G. Verma, J. Hostert, A. A. Summerville, A. S. Robang, R. Garcia Carcamo, A. K. Paravastu, R. B. Getman, C. E. Duval and J. Renner, ACS Appl. Mater. Interfaces, 2024, 16, 16912–16926 CrossRef CAS.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00493k |
| This journal is © The Royal Society of Chemistry 2024 |