Charge transport in electrospinning of polyelectrolyte solutions

Abstract

This study elucidates the electrical charge transport during electrospinning of weak polyelectrolyte (poly(acrylic acid) (PAA)) solutions by employing current emission measurements. With pH variation, the PAA ionization degree could be controlled from uncharged at low pH to weakly charged at intermediate solution pH. Electrospinning neutral poly(vinylpyrrolidone) (PVP) as a reference polymer solution confirmed established current–flow rate scaling relationships as shown by De La Mora and Loscertales (1994), I ∼ (γKQ)^ν, independent of the applied electric field polarity, where ν = 0.5, K is the conductivity, γ is the surface tension, Q is the flow rate, and I is the current. Similarly, the uncharged PAA did not display any polarity dependence, yet ν ≈ 0.8. Negatively charged PAA, however, showed a marked deviation in the current–flow rate behavior, which was affected by the applied electric field polarity. In the case of negative polarity, ν = 0.99, whereas for a positive polarity ν = 0.68. Similarly, the voltage required for stable cone-jet electrospinning of charged PAA was significantly higher in the negative polarity configuration for all tested flow rates (300–1600 μL h⁻¹). As opposed to merely surface charges typically considered when electrospinning leaky dielectric fluids, as suggested by Melcher and Taylor (1969), our results suggest that the measured current is also affected by volumetric charges from charged PAA in the bulk of the jet. The proposed additional charge transport might affect the orientational order within PE-based nanofibers and their diameter.

---

1. Introduction

The production of fine sprays of charged, nanoscale droplets in the electrospraying process^1–6 and the formation of nanofibers by electrospinning^7–11 have an underlying jetting phenomenon in common. In both cases, a conducting liquid is supplied through a capillary to an orifice where a pendant drop forms. Under the action of a sufficiently strong capacitor-like electric field, the acting electrical Maxwell stress overcomes the droplet surface tension, yielding a breakup of the droplet and a stationary jet formation. Within a few millimeters of the orifice, the jet contains a straight section; however, initial small asymmetric jet radius distortions grow with increasing distance due to convective or bending instabilities.^7,8,10 In the case of electrospraying, the liquid can either break up into small droplets at the orifice^12,13 or within the jet,^14,15 where capillary instabilities arise. If the precursor solution, e.g., a polymer solution, provides sufficient viscoelastic properties, the capillary instability within the jet can be suppressed. After a marked stretching within the jet and significant solvent evaporation, nanofibers eventually form in the electrospinning process.¹⁶

The study of charge transport in electrospraying and electrospinning is important from a scientific and technological perspective. It provides insight into the electrohydrodynamic stability of processes and the expected diameter of nanofibers or drops formed during electrospinning or electrospraying, respectively. Studies have focused on elucidating the nature of the electric current, I, in the jet at a given flow rate, Q as well as applied electric field, E by using electrohydrodynamic (EHD) models.^17–20

Exemplary, by balancing stresses related to the surface tension and charge repulsion in a narrow jet, Fridrikh et al. suggested d ∼ (Q/I)^2/3 for the relationship between the final fiber diameter, d, the flow rate Q, and the electric current I.²¹ When electrospraying solutions with large but finite conductivity at large flow rates, Loscertales and Fernández de la Mora and Gañán-Calvo independently showed I ∼ (γKQ)^1/2, for the dependence of the surface tension γ, the conductivity K, and Q on the electric current.^17,18,22,23 Since the electric field E, which determines the jet dynamics, is on the order of (γ/r)^1/2 at large distances r from the Taylor cone apex,²⁴ it is indeed expected that the current will depend on γ. Alternatively, Bhattacharjee et al. predicted the emitted current based on the applied electric field strength when electrospinning neutral poly(methyl methacrylate) and suggested I ∼ EQ^1/2K^2/5.²⁵ For low conducting solutions where the surface tension stresses are small compared to the viscous and electric stresses, Higuera²⁶ found by numerical simulations an additional contribution of the viscosity, η, to the emitted current: I ∼ ε_m^1/3η^1/6K^1/2(EQ)^2/3, where ε_m is the liquid dielectric constant. Complementary to viscosity-dominated jets, Reznik and Zussman proposed, I ∼ ε_m^2/7γ^2/7K^3/7E^3/7Q^4/7 for capillary-dominated jets.²⁷ In this case, the capillary numbers, Ca = Qη/a₀²γ (a₀ is the orifice diameter), are sufficiently small, indicating that surface tension stresses dominate over the viscous stresses.

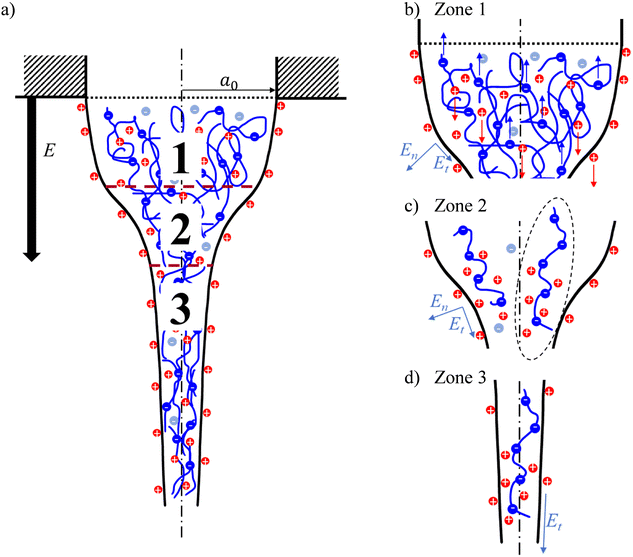
It is important to note that EHD models focus on the net charge owing to an excess of charged species rather than the concentration and distribution of certain species in detail.²⁸ For instance, the common EHD model, the Taylor and Melcher leaky dielectric model (LDM), considers only surface charges and assumes the bulk of the fluid to be depleted of free charges; that is, volumetric charges are absent in the jet.^29–31 Hence, the electrical Maxwell stresses regarded in this model act solely on the jet surface. The LDM is valid in cases when the charge relaxation time, τ_C ∼ ε_m/K, is shorter than any characteristic process time, τ_H ∼ a³/Q, where a is the characteristic jet radius. In electrospinning, the jet evolution below the orifice can be divided into three zones, as shown in Fig. 1a. The first zone comprises the Taylor cone and is characterized by τ_C ≪ τ_H and immediate ohmic migration of free charges from the bulk to the fluid surface in response to the applied external electric field. The second zone encompasses a transition zone where the jet diameter narrows significantly, accompanied by a marked solution acceleration along the jet. The third zone is characterized by a weakly tapered jet. The jet velocity is typically in the order of 1 m s⁻¹, so that τ_C ≈ τ_H and convection of surface charges dominates the current in zones two and three.³² Despite its limited suitability in fast hydrodynamic phenomena, such as within the second and the third jet zones, scaling relationships for the electric current derived from the LDM, as well as EHD-based models in general, agree with experimental observations when working with neutral polymers.²⁸

Fig. 1 Electrospinning of an anionic PE solution. (a) Schematic charge distribution and relevant jet zones; (b) zone 1: Taylor cone; (c) zone 2: cone-jet transition; (d) zone 3: jet zone. E_n and E_t are the normal and tangential components of the applied electric field E, acting on the solution surface.

Unlike neutral polymers, polyelectrolytes (PEs) are macromolecules with a significant portion of ionic or ionizable functional groups that render charged PEs water-soluble.^33,34 Emerging applications in biomedical and food engineering, personal care, and water purification, as well as the striving for “green processing” – that is, abstaining from the use of toxic organic solvents – raise interest in PEs.^35–37 Examples of naturally-occurring PEs include proteins, DNA or RNA, or certain polysaccharides such as xanthan, alginate, chitosan, hyaluronic acid, etc.³⁸ It is well-known that the behaviour of PEs in solution is significantly affected by the charges on the PE backbone and interactions with the corresponding oppositely charged counterions and cannot be modeled by superimposing the behaviours of uncharged polymers and electrolytes.³⁹ The description by a bulk solution ohmic conductivity, as in EHD models, can only insufficiently describe the asymmetry in ionic mobilities between PE chains and counterions inherent in PE solutions.

By utilizing an electrokinetic modeling approach, a recent work by López-Herrera et al. has indeed shown deviations in the Taylor cone profile depending on the applied electric field polarity when the solutions exhibited asymmetric ionic mobilities.²⁸ Thus, it is reasonable to believe that assumptions made within the LDM framework, e.g., depletion of free charges in the bulk, homogeneous permittivity in the liquid, neglecting the internal electric field within the jet, may not be valid when dealing with solutions containing charged PEs. Instead, the charge connectivity on the PE chains endows the solution with bulk volumetric charges that undergo electrophoretic motion (see Fig. 1).⁴⁰ Hence, a deviation from the proposed current-flow rate relationships might be observed in the case of charged PEs, indicating a different electrohydrodynamic behaviour of charged PEs compared to neutral polymers in the electrospinning jet. This could have far-reaching implications on the axial velocity profile in the jet cross-section and the macromolecule conformation, orientation and distribution in nanofibers comprised of PEs, ultimately affecting their diameter and mechanical properties. In the most extreme case, a variation in the applied electric field polarity might affect the spinnability of PE solutions by either enabling or preventing the formation of a continuous jet. To elucidate the charge transport in electrospinning PEs, the emitted current was measured as a function of flow rate and applied voltage for neutral poly(vinylpyrrolidone) (PVP) as a reference, as well as uncharged and partially ionized, model PE, poly(acrylic acid) (PAA), controlled by solution pH. In addition, the polarity of the applied electric field was varied. The results were compared to established scaling relationships for the emitted current.

2. Experimental

2.1. Materials

PVP (M_w = 300 kDa) was purchased from Sigma Aldrich (Israel). PAA (M_w = 450 kDa) was purchased from Polysciences Inc. (USA). NaOH pellets were obtained from Frutarom Ltd. (Haifa, Israel).

2.2. Solution preparation

PVP powder was dissolved in a Milli-Q water/ethanol (6/4 v/v) cosolvent mixture to obtain a 15 wt% solution. PAA solutions with 4 wt% concentration in (6/4 v/v) Milli-Q water/ethanol were prepared by dissolving the PAA powder overnight in Milli-Q water to create a 10 wt% PAA stock solution. The desired solution pH values of 2.8 and 4.5 for uncharged and charged solutions, respectively, were obtained by adding required amounts of 1 M NaOH. The final solution concentrations were adjusted by adding appropriate amounts of ethanol and Milli-Q water, followed by stirring overnight.

2.3. PAA ionization degree

The pH-dependent ionization degree of PAA was evaluated by ATR-FTIR on Nicolet 380 spectrometer (Thermo Fisher Scientific, USA) with 0.5 cm⁻¹ increments. For this purpose, 1 wt% PAA solutions were prepared in water/ethanol (6/4 v/v) at different solution pH, with 0.15 M NaCl added to diminish the effect of PE concentration. The obtained spectra were analyzed using OriginPro 2020 software (Originlab, USA). Deconvolution of the COOH band (at 1695 cm⁻¹) and COO− (1557 cm⁻¹) was conducted, and the ionization degree of PAA was calculated as:

α(pH) = (peak area of COO⁻)/((peak area of COOH) + (peak area of COO⁻)) (1)

Fitting was done according to the Henderson–Hasselbalch equation.

2.4. Conductometric titration

150 ml of 0.1 wt% PAA solution in Milli-Q water/ethanol (6/4 v/v) was prepared, followed by adding a small amount of 1 M HCl to deionize the PAA in solution entirely. Subsequently, the solution was titrated with 1 M NaOH under constant stirring and continuous conductivity and pH measurements. The solution conductivity was measured on a portable laboratory conductivity meter, XS Cond 7 Vio (XS instruments, Italy). The pH measurements were performed on SevenCompact pH meter S220 (Mettler Toledo, Switzerland).

2.5. Zeta potential

The electrophoretic mobility of PAA was measured at different solution pH values. For this purpose, 0.1 wt% PAA solution in Milli-Q water/ethanol (6/4 v/v) was prepared, and the pH was adjusted by adding appropriate amounts of 1 M NaOH or 1 M HCl. The measurements were conducted on Malvern Zetasizer Nano-ZS (Malvern Panalytical, UK) and repeated three times per specimen. The Zeta potential, ζ, was calculated using Henry's equation with Smoluchowski approximation:

ζ = μ_eη/ε₀ε_r (2)

where μ_e denotes the electrophoretic mobility, η the solution viscosity, and ε₀ and ε_r are the relative permittivity and the permittivity in vacuum, respectively.

2.6 Surface tension

The respective surface tensions of the solutions were evaluated using Tate's drop weight method.⁴¹ Briefly, Tate's law postulates a balance between the drop weight and a counteracting surface tension force, holding the pendant drop to the capillary tip:

mg = 2πRnγ (3)

where m denotes the droplet mass, g is the gravitational constant, R is the capillary radius, n denotes the number of drops, and γ is the surface tension. For each solution, n = 15 drops were supplied through a G27 (R = 0.21 mm) needle at 1 mL h⁻¹ flow rate and weighed to determine the surface tension. Experiments were conducted in triplicates and the results are reported as mean ± standard deviation.

2.7. Rheological characterization

The polymer solution shear viscosity was assessed on a DHR-2 rotational rheometer (TA Instruments) at different shear rates in the range of 0.2 up to 1000 s⁻¹. All measurements were performed at room temperature using a parallel plate geometry with a diameter of 40 mm and a 300 μm gap between the plates.

2.8. Electric current measurement

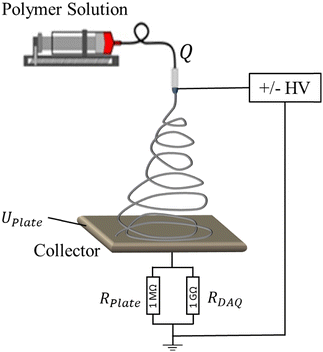
The measurements of emitted current during the electrospinning process were performed with a setup, schematically shown in Fig. 2. Briefly, the polymer solution was supplied by a syringe pump (Harvard Apparatus, PHD 2000) with a controllable flow rate, Q, to a metallic, blunt, 23G (0.337 mm inner diameter) needle, which was connected to a high voltage power supply. Experiments were conducted for positive and negative applied voltages. For a positive polarity, XRM30P (Gamma High Voltage Research) was used, whereas a negative electric potential was applied by XRM50N (Gamma High Voltage Research). The electrospray or electrospun fibers were collected on a thin steel plate with 20 cm radius and 5 cm distance to the needle tip. The collector was connected to the ground through an Ohmic resistance of R_Plate = 1 MΩ. In parallel to the Ohmic resistance, a digital acquisition device (DAQ) (USB-6211, National Instruments, USA) with an internal resistance of 1 GΩ was attached to measure the potential difference, U, over R_Plate.

Fig. 2 An experimental setup for measuring the emitted current during electrospinning.

Due to the expected low electric currents emitted during electrospinning (typically nano- to microampere), a large Ohmic resistance of R_Plate = 1 MΩ was required to generate a measurable potential difference over the resistance. At the same time, the DAQ internal resistance was large enough not to measurably affect the current. Finally, the data was transferred to the computer, and the emitted current, I, was calculated by Ohm's law:

I = U_Plate/R_Plate (4)

Electrospinning was conducted in a stable cone-jet mode, where the competing supply of the solution by the syringe pump and withdrawal by the electric field were in balance. Hence, the electric field strength, E, controlled by the applied voltage, V, and the solution flow rate could not be varied independently without affecting the electrospinning stability. Consequently, each applied flow rate (300, 350, 400, 500, 600, 800, 1000, 1200, and 1600 μL h⁻¹) permitted only a narrow range of applied voltages. Note that the electric field is highly nonuniform and much higher than the corresponding parallel capacitor field value. The emitted current of each flow rate-voltage combination was measured for 30 s at a refresh rate of 100 s⁻¹ and ultimately averaged. All results are presented as mean ± standard deviation in dimensionless form (I* = I/I₀, Q* = Q/Q₀, and E* = E/E₀, for the nondimensional current, flow rate, and electric field, respectively) following the scheme introduced by Gañán-Calvo.⁴² The intrinsic scales for electric current, I₀ = ε₀γρ^−1/2, flow rate Q₀ = ε₀γρ⁻¹K⁻¹, electric field E₀ = (2ε₀⁻¹γd₀⁻¹)^1/2, and diameter d₀ = (π⁻²ε₀²γρ⁻¹K⁻²)^1/3 have been shown to be on the smallest order possible in an electrohydrodynamic jet.^18,25,43

3. Results

3.1. PAA solution characterization

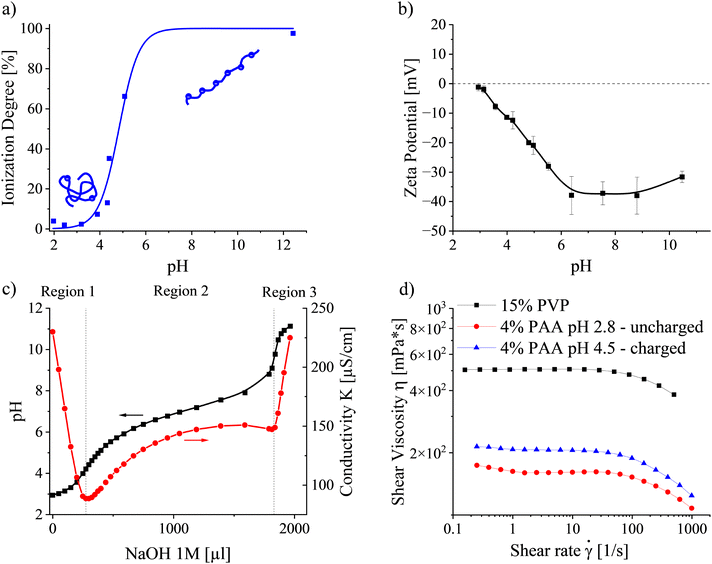
The behaviour of PAA in solution strongly depends on its ionization degree, controlled by the solution pH. FTIR spectroscopy was carried out to determine the pH-dependent ionization behaviour of PAA in water/ethanol (6/4 v/v) (Fig. 3a). Under acidic conditions, when the concentration of free hydrogen ions is high, the carboxylic acid of PAA appears mostly in its associated, protonated form. Thus, PAA can be considered uncharged and adopts a Gaussian coil conformation below solution pH 3. With increasing pH, the PAA ionization degree rises due to the deprotonation of the PAA carboxylic acid functional groups into negatively charged carboxylate ions. Simultaneously, the arising repulsion between neighboring charges along the chain causes it to take on a stretched conformation.⁴⁴ The apparent pK_a, describing the condition when the ionization degree reaches 50%, was determined at pH 4.84. Complete ionization of the PAA functional groups could be considered above pH 6.5.

Fig. 3 Electrical, physicochemical, and rheological properties of PAA solutions: (a) ionization degree as a function of solution pH in water/ethanol (6/4 v/v); (b) zeta potential depending on the solution pH; (c) conductometric titration; (d) steady state shear viscosity of PVP and uncharged/charged PAA at solution pH 2.8 and 4.5, respectively.

The dependence of the PAA zeta potential on the solution pH in Fig. 3b corroborates the results above. Below pH 3, PAA did not demonstrate any significant charges. Increases in the ionization degree with rising pH rendered the chains with a larger electrophoretic mobility, expressed by an increase in the absolute zeta potential up to pH ≈ 6.5. At higher pH values, charges were screened. Ultimately, the absolute zeta potential decreased, ascribed to a high ionic strength and consequent reduction of the double layer around the PAA chains at pH 10.5.

Conductometric titrations were performed to elucidate the contribution of each ionic species in the solution. Fig. 3c presents the solution pH and conductivity depending on the amount of added NaOH. The graph can be divided into three regions based on conductivity, corresponding to three distinct physicochemical processes. Region 1 is characterized by a steep decrease in conductivity, which is ascribed to neutralization of excess H⁺ (350 S cm² mol⁻¹) from the previously added HCl by Na⁺ ions with approximately 7 times lower ionic mobility (50.9 S cm² mol⁻¹):^45,46

NaOH + H⁺ + Cl⁻ ⇋ H₂O + Na⁺ + Cl⁻ (5)

Simultaneously, the decrease in the hydrogen ion concentration led to a slight pH increase. After reaching the first equivalence point, the addition of NaOH causes PAA carboxylic acid groups (−COOH) to dissociate, thus become ionized (−COO−) in Region 2:

−COOH + Na⁺ + OH⁻ ⇋ −COO⁻ + Na⁺ + H₂O (6)

The conductivity increase in this region is attributed to increasingly negatively charged PAA chains and Na⁺ counterions. Here, it is imperative to highlight that the ionization degree does not reflect the effective charge a PE chain possesses. In fact, the effective charge is determined by an interplay between electrostatic-driven counterion adsorption on the PE macromolecule and entropy-driven counterion disassociation into the solution.⁴⁷ Thus, above a specific PAA charge density, Na⁺ counterions begin to “condensate” on the negatively charged PAA chain, causing the observed conductivity plateau in Region 2.⁴⁸

Considering the popular Manning–Oosawa counterion condensation theory, the minimal distance between effective charges along a linear PE chain equals the Bjerrum length in solution, which depends on the solvent permittivity.⁴⁹ The water/ethanol cosolvent (6/4 v/v) used in this study has a permittivity, ε_r, of 59.2 at 25 °C which yields a Bjerrum length, l_B = e²/(ε_rk_BT) of l_B ≈ 0.95 nm.⁵⁰ Assuming a spacing of 0.27 nm between the carboxylic acid groups on the chain,⁵¹ the fraction of maximal effective charges is limited to ≈0.28, corresponding approximately to pH 4.5 (see Fig. 3a). Above this pH, additional PAA ionization causes counterions to condense on the macromolecule, effectively screening the charges. Note that Fig. 3c suggests an onset of PAA ionization only above pH 4.2 and counterion condensation to occur approximately above pH 6. The origin of this shift to higher pH values lies in the difference in PAA concentrations used for the essays in Fig. 3a and c.^52,53

The second equivalence point appears upon approaching complete PAA ionization in the titration experiment. Further NaOH addition causes a significant increase in conductivity owing to excess Na⁺ and highly mobile (192 S cm² mol⁻¹) OH⁻ ions in Region 3.⁵⁴ Concluding, for the following experiments, PAA with solution pH 2.8 (f ≈ 0.01) and pH 4.5 (f ≈ 0.28) were chosen to represent uncharged and charged PE solutions, respectively.

To eliminate any effects caused by different solvent properties such as permittivity, surface tension, etc., the current study used the same solvent composition for all polymer solutions. For this purpose, the chosen water/ethanol (6/4 v/v) cosolvent system was deemed appropriate to dissolve neutral PVP and PAA well in both the uncharged and charged states. In the charged state, charge repulsion stretches the PAA chain, yielding good water solubility. However, as the ionization degree decreases, the contribution of the hydrophobic backbone rises, ultimately rendering water a poor solvent for uncharged PAA. Pure ethanol has the opposite effect on PAA solubility. The charged chain collapses in this case, whereas it swells when PAA is protonated. For partially ionized PAA, simulations suggest water molecules interact mainly with the negatively charged carboxylate ions, while ethanol interacts with the protonated carboxylic acid and the polymer backbone.^55,56 Moreover, an unexpected nonlinearity has been recently reported after studying the solution viscosity of uncharged PAA at varying water/ethanol mixture compositions. Vats et al. obtained a positive deviation from the logarithmic mixing rule, with a maximal viscosity at a water-to-ethanol mole fraction of ≈0.65.⁵⁷

As the solution viscosity is an essential parameter in predicting the emitted current when electrospinning viscosity-dominated solutions, steady-state shear flow curves were collected for neutral PVP and uncharged and charged PAA, respectively. Fig. 3d presents the viscosities of 15 wt% PVP and 4 wt% PAA at pH 2.8 and 4.5 as a function of the applied shear rate. All samples exhibit pseudoplastic behaviour, typical for semidilute entangled polymer solutions. By extrapolating the flow curves to zero-shear conditions, the zero-shear viscosity, η₀, was obtained. For PVP, η₀ was determined as 505 mPs, whereas it reached 160 and 207 mPs for uncharged PAA at pH 2.8 and charged PAA at pH 4.5, respectively. The higher zero-shear viscosity of the charged PAA is ascribed to inter- and intramolecular charge repulsion, yielding a swollen polymer network compared to the uncharged state at pH 2.8. Table 1 summarizes the measured polymer solution properties.

Table 1 Polymer solution properties

Material	Ionization degree, f	Conductivity, K [μS cm^−1]	Surface tension, γ [mN m^−1]	Zero-shear viscosity, η0 [mPas]	Capillary number, Ca
PVP	0	44.5	36.8 ± 0.43	505	0.13
PAA – pH 2.8	≈0.01	167.7	29.2 ± 0.41	160	0.054
PAA – pH 4.5	≈0.28	745	30.3 ± 0.09	207	0.067

---

3.2. Measured current in electrospinning

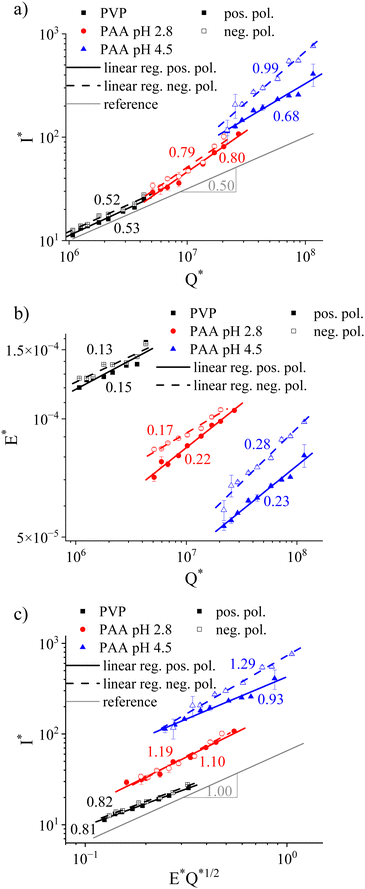
After establishing the relevant solution parameters, especially the pH values associated with uncharged and effectively fully charged PAA, the solutions were electrospun. The setup included a combination of a relatively short distance of 5 cm between the needle and the collector plate and a large collector radius of 20 cm, both of which were chosen to ensure collecting the entire current emitted in the process. Fig. 4 presents the relationship between the dimensionless parameters, that is, electric current I*, flow rate Q*, and applied electric field E*, obtained in a stable cone-jet electrospinning process of neutral PVP and uncharged (pH 2.8) and charged (pH 4.5) PAA. The polarity of the electric field was varied to reveal the effect of asymmetric mobilities inherent in charged PE solutions.

Fig. 4 Dependence of dimensionless electrospinning parameters for neutral PVP and uncharged (pH 2.8) and charged (pH 4.5) PAA in a stable cone-jet process, respectively. (a) Electrical current I* depending on flow rate Q*; (b) applied electric field E* vs. flow rate Q*; (c) electrical current I* as a function of E*Q*^1/2. Error bars are based on standard deviation.

For neutral PVP, the emitted current ranged between 40.3 ± 2 nA at 300 μL h⁻¹ to 90.7 ± 0.7 nA at 1200 μL h⁻¹ for a positively charged needle. The electric current was slightly larger when the needle was connected to the negative high-voltage power supply (44.9 ± 0.9 nA at 300 μL h⁻¹ to 98.7 ± 0.6 nA at 1200 μL h⁻¹, see Fig. S1, ESI†). Independent of the electric field direction, the current/flow rate relationship resembled the I* ∼ Q*^1/2 prediction by De la Mora & Loscertales (see Fig. 4a). Precisely, PVP demonstrated slopes in the log–log plot of 0.52 and 0.53 for positive and negative polarity, respectively. Note that maintaining a stable cone-jet process did not allow the applied electric field and the flow rate to be varied independently. Fig. 4b presents the normalized applied electric field E* depending on the flow rate Q*. For PVP, raising the flow rate required only small increases in the applied electric field, reflected by the weak E* ∼ Q*^0.15 or E* ∼ Q*^0.13 dependence for a positive and negative polarity, respectively. While a larger negative than positive electric field was required for stable electrospinning of the neutral PVP, this difference was minuscule at approximately 4% (0.73 vs. 0.69 kV cm⁻¹, see Fig. S2, ESI†). When considering the combined contribution of dimensionless electric field strength and flow rate on the current, a slope of 0.81 and 0.82 in the log–log plot was obtained for the positive and negative applied polarity, respectively (see Fig. 4c). Thus, the dependence was slightly lower than the empirical I* ∼ E*Q*^1/2 suggestion.

Considering the I* ∼ Q* dependence of the uncharged PAA solution at pH 2.8, the slope of ≈0.8 deviated significantly from the square root relationship obtained for PVP (see Fig. 4a). Analog to neutral PVP, the charge transport did not vary with the applied voltage polarity. For a positively charged needle, the results showed I = 82.7 ± 6 nA at Q = 300 μL h⁻¹ and I = 228.8 ± 7 nA at Q = 1200 μL h⁻¹, whereas for a negative applied voltage, we obtained I = 95.8 ± 7 nA at Q = 300 μL h⁻¹ and I = 286.0 ± 17.8 nA at Q = 1200 μL h⁻¹ (see Fig. S3, ESI†). The overall higher current in the case of PAA at pH 2.8 compared to PVP is ascribed to the higher solution conductivity of the former. As for PVP, in the case of PAA at pH 2.8, a lower positive than negative applied electric field was required for maintaining a stable cone jet, albeit with a larger difference of ≈15% at 300 μL h⁻¹ (0.59 vs. 0.69 kV cm⁻¹, see Fig. 4b and Fig. S4, ESI†). Interestingly, this difference decreased with higher flow rates as indicated by the slopes for the E* ∼ Q* relationship of 0.22 and 0.17 for positive and negative polarity, respectively. Consequently, fitting the current to the E*Q*^1/2 relationship suggested by Bhattacharjee et al. yielded a slope of 1.10 and 1.19 for the positive and negative applied polarity, respectively.

At pH 4.5, PAA is approximately 28% ionized (Fig. 3a), exhibiting maximum net negative charges. In contrast to neutral PVP and uncharged PAA, the relationship between emitted current, flow rate, and electric field strength depended significantly on the applied electric field polarity (see Fig. 4). For a positively charged needle, the measured current was I = 332.9 ± 29.6 nA at Q = 300 μL h⁻¹ and reached I = 1199.7 ± 292.6 nA at Q = 1600 μL h⁻¹, whereas I = 343.4 ± 85.3 nA at Q = 300 μL h⁻¹ and I = 2226.6 ± 41.2 nA at Q = 1600 μL h⁻¹ for a negative applied polarity (Fig. S5, ESI†). That is, the electric current increase with a rising flow rate was much less pronounced when the needle was connected to the positive rather than the negative high-voltage power supply with I* ∼ Q*^0.68 and I* ∼ Q*^0.99, respectively (see Fig. 4a). The overall higher current, measured when electrospinning charged compared to uncharged PAA, is due to its higher conductivity (see Table 1). From Fig. 4b, it is evident that maintaining a stable cone-jet process required an overall larger electric field when a negative instead of positive polarity was applied. The mean difference was 16.8% for charged PAA at pH 4.5 compared to 8.2% for uncharged PAA within the studied flow rate range of 300–1600 μL h⁻¹ (Fig. S4 and S6, ESI†). As opposed to uncharged PAA at pH 2.8, the applied electric field strengths diverged with increasing flow rates, reflected by E* ∼ Q*^0.23 and E* ∼ Q*^0.28 for positive and negative polarities, respectively. Combined, Fig. 4c confirms the marked dependence with exponents of 0.93 and 1.29 for the positive and negative polarity, respectively, when fitting I* ∼ E*Q*^1/2.

Fig. 5 summarizes the obtained exponents for scaling the electric current with the flow rate and electric field strength at either polarity, including previously proposed formulations for viscosity-dominated²⁶ and capillary-dominated jets,²⁷ respectively. Considering the parameters used in electrospinning the solutions, such as Q ∼ 1000 μL h⁻¹, 23G needle with a₀ = 0.169 mm, η₀ ≈ 160–505 mPas, and γ ≈ 30 mN m⁻¹, the capillary number was Ca ≈ 0.054–0.13, as listed in Table 1. Capillary or viscosity-dominated regimes are unequivocally defined for Ca ≪ 1 or Ca ≫ 1, respectively.¹⁶ The obtained Ca < 1 indicates a dominance of the surface tension over the viscous stress. Hence, capillary-dominated electrospinning could be assumed for all solutions. However, while for PVP the I* ∼ Q*^1/2 relationship yielded the best fit, uncharged PAA at pH 2.8 obeyed the scaling relationship for viscosity-dominated solutions of I ∼ ε_m^1/3η^1/6K^1/2(EQ)^2/3 remarkably well. Interestingly, averaging the obtained exponent values for the positive and negative polarity of charged PAA at pH 4.5 led to comparable results obtained for uncharged PAA, independent of the scaling model.

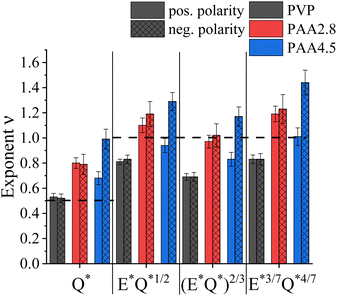Fig. 5 Summary of exponents ν obtained by fitting the measured current to different EHD-models. Error bars are based on standard deviation.

4. Discussion

When a pending droplet of a conducting solution is subjected to a capacitor-like electric field, free charges migrate to the surface and repel each other, ultimately generating a jet. The external electric field exerts a Coulomb force on the charges, accelerating them and adjacent liquid layers through viscous drag towards the respective oppositely charged electrode. The charge transport within the jet has been the subject of numerous studies. While the LDM in particular and EHD models in general predict the emitted current of conducting fluids containing monovalent salts or uncharged polymer solutions subjected to an electric field very well, the situation becomes more complicated when the solution comprises charged PEs. Charged PEs endow the solution with significant asymmetric ionic mobilities and complex viscoelastic properties and cannot be modeled by superposing the behaviour of uncharged polymers with an added simple electrolyte.^58–60

Measurements of the electric current during electrospinning give insight into the charge transport within the jet, which reflects on the acting forces. A qualitative comprehension of the forces is detrimental as they affect the macromolecule conformation, orientation and distribution, and consequently, the fiber diameter and mechanical properties.^61–64 While previous experimental works generally showed a power law relationship between the electric current, I, and various parameters in electrospinning (such as Q, E, K, γ, η, etc.), it should be noted that the exact values for the exponents can vary significantly for different materials.^9,65 Yet, for neutral PVP and uncharged PAA, our results indicate a symmetry in the charge transport behaviour, i.e., the relationship between the electric current and parameters mentioned above is independent of the polarity of E. Conversely, a significant polarity dependence was obtained for charged PAA at pH 4.5, indicating the presence of electrokinetic transport phenomena that require further elaboration. For this, the present electrostatic forces will be discussed, followed by reviewing the jet zones where they possibly occur.

The action of an electric field exerts an electrostatic Coulomb force, F_C = qE, upon each charge, q, in the solution, where the direction of F_C is determined by the polarity of E and the charge sign of q. In the case of uncharged polymer solutions, the Coulomb force acts only on free ions, typically introduced by impurities of the solvent and the polymer, eventually leading to the jetting phenomenon described in the introduction, driven by an electroosmotic flow.⁶⁶ In contrast, when the system encompasses charged PEs, F_C is additionally exerted upon the charge bearing macromolecules, generating an electrophoretic flow. Simultaneously, the Coulomb forces are acting in the opposite direction on the counterions surrounding the PE chains. Consequently, the diffuse counterion cloud becomes distorted, effectively polarizing the PE-counterion cloud entity.

The significant polarizability of PEs renders them susceptible to a dielectrophoretic force, F_DEP that arises in strongly nonuniform electric fields ∇|E|². While the dielectrophoretic force strength increases with the applied electric field, its gradient, and the difference in polarizability between solvent and PE, the direction of F_DEP along E is independent of the applied electric field polarity and is solely determined by the permittivity difference between solvent and PE. Aqueous PE solutions typically demonstrate a higher electrical permittivity than the pure solvent;^67–70 hence, we can assume positive dielectrophoresis for our water-ethanol 6–4 (v/v) cosolvent system, with the net force acting in the direction of increasing electric field.

Considering the three jet zones in electrospinning (Fig. 1a), we can contemplate the respective contributions of F_C and F_DEP in each zone. Within zone 1, the characteristic process time dominates the charge relaxation time by several orders of magnitude: τ_H ≫ τ_C. Thus, the solution can be considered as a conductor, where under the action of an external electric field, PEs and free counterions migrate in opposite directions, causing an internal electric field that opposes the external field. For the specific case of polyanionic PAA used in this work and in the case of a positive polarity of the applied electric field, the PAA chains migrate towards the positively charged needle, while free cationic H⁺ and Na⁺ counterions accelerate towards the liquid surface and eventually the grounded collector (see Fig. 1b), and vice versa for a negative applied electric field polarity. As a result of the so-called Onsager relaxation effect, the effective electric field inside the bulk, that affects the PE and counterion electrophoretic motion, is E − ΔE, with the correction term ΔE being proportional to the applied field strength.⁷¹ Thus, the electrophoretic motion abates once the system is in equilibrium.

From the perspective of a single PE chain, the surrounding counterion cloud becomes distorted by bound counterions, giving rise to a large dipole (exemplary sketched in Fig. 1c for zone 2). This, along with the large electric field gradient from the solution bulk to the surface, generates a significant radial dielectrophoretic contribution that drives the PE chains to the liquid surface.

Moving further along the jet axis into the cone-jet transition zone 2 (Fig. 1c), the solution is being significantly accelerated, which reduces the process time in this segment; thus, τ_H ≥ τ_C and the solution can be considered a leaky dielectric. That is, the charge distribution in the solution does not reach equilibrium, and an effective internal electric field remains, responsible for electrophoretic and electroosmotic motion of PEs and free counterions, respectively. Alongside the significant diameter decrease in this zone, a marked electric field gradient appears along the jet axis.²⁷ Consequently, in addition to a radially acting dielectrophoretic force, F_DEP also acts along the jet axis, further accelerating the polarized PE chains along the jet in the cone-jet zone.

Lastly, the jet in zone 3 is characterized by a small diameter of tens to hundreds of μm and a large flow velocity. The external applied electric field, where on the jet surface E_n ≪ E_t, efficiently penetrates the narrow jet (see Fig. 1d).⁷² Presumably, this jet zone is dominated by an electrophoretic contribution of PEs and free counterions. Note that solvent evaporation along the jet increases the solution viscosity, resulting in an increase in hydrodynamic friction, which opposes electrophoretic motion.

Specifically, when applying a positive voltage, the dielectrophoretic contribution yields PAA chain propagation to the liquid surface. There, the high concentration of positive H⁺ and Na⁺ counterions, migrated in response to the external field, leads to a reduction of the local pH and an increase in the ionic strength. Consequently, the PAA ionization degree decreases, accompanied by partial screening of remaining PAA charges. The resulting lower solution viscosity (see Fig. 3d) and lower conductivity eventually yield a lower electric current when electrospinning the anionic PAA with positive as opposed to negative polarity. Conversely, when electrospinning the negatively charged PE with applied negative electric field polarity, the needle attracts free cationic counterions. In contrast, the polarized PAA macromolecules migrate towards the liquid surface until the eventual viscosity increase and interchain electrostatic repulsion oppose the dielectrophoretic motion. Further along the jet, the tangential component of the electric field accelerates the anionic PAA chains within the jet towards the grounded collector, contributing to elevated charge transport.

In conclusion, for negatively charged PAA, the observed polarity dependence expressed by the exponent ν in the I ∼ (γKQ)^ν relationship of ν = 0.68 and ν = 0.99 for the positive and negative applied electric field polarity, respectively, indicates a contribution of the charged macromolecules in the electrospinning process, questioning the validity of the leaky dielectric model by Taylor and Melcher for charged PEs. Moreover, the polarity-dependent distribution and variable ionization degree of PAA chains along the jet radius invalidate the assumption of constant and isotropic solution properties, such as viscosity, surface tension, and conductivity, assumed in EHD-based models.⁷³ Here, we suggest, in addition to charge conduction in zone 1 and convection of surface charges in zones 2 and 3 of the jet, convection of PE charges in the bulk of the jet, so that:

I = KπEa²+ 2σQ/a ± σ_V(c,f)Q (7)

where σ_V(c,f) denotes the volumetric charge density, which is a function of the PE concentration c and the ionization degree f. The first term on the right-hand side describes charge conduction, followed by a term accounting for surface charge convection and the final term denoting the convection of PE charges in the bulk of the jet. For the setup used in this work, we can conclude a positive contribution to the electrical current if the applied electric field and net PE charge polarities match, whereas it is negative in the case of inequal polarities.

5. Conclusions

Exploiting the leaky dielectric model introduced by Taylor and Melcher, several power law relationships for the emitted current depending on the applied flow rate and electric field strength in electrospraying and -spinning have been suggested. The underlying assumption is charge depletion in the bulk of the jet, owing to charge migration to the surface, so that the internal electric field can be neglected. While this seems valid for solutions containing small ions when electrospinning neutral polymers, the situation is unclear regarding PE solutions characterized by charge connectivity and asymmetric ionic mobilities.

In this work, the emitted current, I, in electrospinning was measured as a function of flow rate, Q, applied electric field, E, and voltage polarity for a neutral polymer (PVP) and compared to a weak, anionic PE (PAA) in uncharged and charged state. For all examined materials, a good power law dependence I ∼ (γKQ)^ν was found, where K is the conductivity and γ is the surface tension. Albeit a difference in the obtained exponent, ν, neutral PVP and uncharged PAA at pH 2.8 demonstrated qualitatively the same behaviour, namely the scaling properties were independent on the applied voltage polarity. However, at pH 4.5 when PAA was ∼28% charged, a significant dependence of I on the applied electric field direction was observed. Here, ν = 0.68 was obtained for a positively charged needle, whereas ν = 0.99 when a negative high voltage was applied. Apart ohmic conduction of charges in the Taylor cone zone and convection of surface charges in the jet zone, established for neutral polymer solutions, our results indicate an additional convective transport of bulk charges in PE solutions: I_bulk = σ_V(c,f)Q, where the volumetric charge density, σ_V, depends on the PE concentration, c, and ionization degree, f, determined by pH for weak PEs. The direction of I_bulk depends on the polarity of E and the PE net charges. In the case of same polarities, I_bulk raises the total emitted current. Oppositely, unequal polarities generate a smaller I ∼ γKQ dependence. The additional polarity-dependent charge transport through convection of bulk charges might affect the orientational order within PE-based nanofibers with implications on their diameter and mechanical properties. Hence, variation of the applied electric field polarity should be considered a significant parameter for tuning the PE solution spinnability and eventually the fiber properties.

Author contributions

P. M.: conceptualization, investigation, data curation, formal analysis, validation, visualization, writing – original draft. E. Z.: conceptualization, resources, supervision, writing – review & editing.

Data availability

The data supporting this article have been included as part of the Supplementary Information.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the ISF – Israel Science Foundation 177/23. E. Z. acknowledges the financial support of the Winograd Chair of Fluid Mechanics and Heat Transfer at Technion.

Notes and references

1. J. Zeleny, Proc. Camb. Phil. Soc., 1915, 18, 71–83.
2. M. Cloupeau and B. Prunet-Foch, J. Electrost., 1989, 22, 135–159.
3. J. F. De La Mora, J. Fluid Mech., 1992, 243, 561.
4. R. T. Collins, K. Sambath, M. T. Harris and O. A. Basaran, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4905–4910.
5. A. M. Gañán-Calvo, J. M. López-Herrera, M. A. Herrada, A. Ramos and J. M. Montanero, J. Aerosol Sci., 2018, 125, 32–56.
6. J. Rosell-Llompart, J. Grifoll and I. G. Loscertales, J. Aerosol Sci., 2018, 125, 2–31.
7. D. H. Reneker, A. L. Yarin, H. Fong and S. Koombhongse, J. Appl. Phys., 2000, 87, 4531–4547.
8. M. M. Hohman, M. Shin, G. Rutledge and M. P. Brenner, Phys. Fluids, 2001, 13, 2201–2220.
9. S. A. Theron, E. Zussman and A. L. Yarin, Polymer, 2004, 45, 2017–2030.
10. A. L. Yarin, S. Koombhongse and D. H. Reneker, J. Appl. Phys., 2001, 90, 4836–4846.
11. D. H. Reneker, A. L. Yarin, E. Zussman and H. Xu, Advances in Applied Mechanics, Elsevier, 2007, vol. 41, pp. 43–346.
12. R. J. Pfeifer and C. D. Hendricks, AIAA J., 1968, 6, 496–502.
13. I. Marginean, P. Nemes and A. Vertes, Phys. Rev. Lett., 2006, 97, 064502.
14. R. T. Collins, M. T. Harris and O. A. Basaran, J. Fluid Mech., 2007, 588, 75–129.
15. A. R. Jones and K. C. Thong, J. Phys. D: Appl. Phys., 1971, 4, 316.
16. A. Arinstein and E. Zussman, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 691–707.
17. A. M. Gañán-Calvo, A. Barrero and C. Pantano-Rubiño, J. Aerosol Sci., 1993, 24, S19–S20.
18. J. F. De La Mora and I. G. Loscertales, J. Fluid Mech., 1994, 260, 155–184.
19. L. T. Cherney, J. Fluid Mech., 1999, 378, 167–196.
20. F. J. Higuera, J. Fluid Mech., 2003, 484, 303–327.
21. S. V. Fridrikh, J. H. Yu, M. P. Brenner and G. C. Rutledge, Phys. Rev. Lett., 2003, 90, 4.
22. A. M. Gañán-Calvo, J. Fluid Mech., 1997, 335, 165–188.
23. A. M. Gañán-Calvo, J. Aerosol Sci., 1999, 30, 863–872.
24. G. I. Taylor, Proc. R. Soc. London, Ser. A, 1964, 280, 383–397.
25. P. K. Bhattacharjee, T. M. Schneider, M. P. Brenner, G. H. McKinley and G. C. Rutledge, J. Appl. Phys., 2010, 107, 044306.
26. F. J. Higuera, J. Fluid Mech., 2006, 558, 143.
27. S. N. Reznik and E. Zussman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 026313.
28. J. M. López-Herrera, M. A. Herrada and A. M. Gañán-Calvo, J. Fluid Mech., 2023, 964, 1–24.
29. J. R. Melcher and G. I. Taylor, Annu. Rev. Fluid Mech., 1969, 1, 111–146.
30. D. A. Saville, Annu. Rev. Fluid Mech., 1997, 29, 27–64.
31. J. Fernández de la Mora, Annu. Rev. Fluid Mech., 2007, 39, 217–243.
32. A. V. Subbotin, Polym. Sci., Ser. A, 2021, 63, 172–179.
33. M. Hara, Polyelectrolytes: science and technology, Marcel Dekker, 1993.
34. M. Hess, R. G. Jones, J. Kahovec, T. Kitayama, P. Kratochvíl, P. Kubisa, W. Mormann, R. F. T. Stepto, D. Tabak, J. Vohlídal and E. S. Wilks, Pure Appl. Chem., 2006, 78, 2067–2074.
35. M. Boas, A. Gradys, G. Vasilyev, M. Burman and E. Zussman, Soft Matter, 2015, 11, 1739–1747.
36. M. Boas, P. Martin, G. Vasilyev, J. Lee, R. Vilensky, C. Xu, A. Greiner and E. Zussman, Carbohydr. Polym., 2021, 266, 118131.
37. X. Meng, S. L. Perry and J. D. Schiffman, ACS Macro Lett., 2017, 6, 505–511.
38. C. Warwar Damouny, P. Martin, G. Vasilyev, R. Vilensky, R. Fadul, I. Redenski, S. Srouji and E. Zussman, Biomacromolecules, 2022, 23, 3222–3234.
39. C. E. Sing, Adv. Colloid Interface Sci., 2017, 239, 2–16.
40. D. A. Hoagland, E. Arvanitidou and C. Welch, Macromolecules, 1999, 32, 6180–6190.
41. T. Tate, London, Edinburgh Dublin Philos. Mag. J. Sci., 1864, 27, 176–180.
42. A. M. Gañan-Calvo, J. Aerosol Sci., 1998, 29, S975–S976.
43. A. M. Gañán-Calvo, J. Dávila and A. Barrero, J. Aerosol Sci., 1997, 28, 249–275.
44. A. K. Gupta and U. Natarajan, Mol. Simul., 2017, 43, 625–637.
45. F. Rouessac and A. Rouessac, Chemical Analysis: Modern Instrumentation Methods and Techniques, Wiley, 2nd edn, 2007, p. 101.
46. S. Ötleş, Handbook of food analysis instruments, CRC Press, 2008, p. 173.
47. C. Cametti, Polymers, 2014, 6, 1207–1231.
48. H. P. Van Leeuwen, R. F. M. J. Cleven and P. Valenta, Pure Appl. Chem., 1991, 63, 1251–1268.
49. G. S. Manning, J. Chem. Phys., 1969, 51, 924–933.
50. J. Wyman, J. Am. Chem. Soc., 1931, 53, 3292–3301.
51. L. Lamch, S. Ronka, I. Moszynśka, P. Warszynśki and K. A. Wilk, Polymers, 2020, 12, 1185.
52. R. Arnold, J. Colloid Sci., 1957, 12, 549–556.
53. L. Nová, F. Uhlík and P. Košovan, Phys. Chem. Chem. Phys., 2017, 19, 14376–14387.
54. S. Farris, L. Mora, G. Capretti and L. Piergiovanni, J. Chem. Educ., 2012, 89, 121–124.
55. S. Srikant, S. S. Muralidharan and U. Natarajan, Mol. Simul., 2013, 39, 145–153.
56. P. Sappidi and U. Natarajan, J. Mol. Graphics Modell., 2016, 64, 60–74.
57. S. Vats, L. W. Honaker, M. W. Frey, F. Basoli and J. P. F. Lagerwall, Macromol. Mater. Eng., 2022, 307, 1–8.
58. M. Rubinstein, R. H. Colby and A. V. Dobrynin, Phys. Rev. Lett., 1994, 73, 2776–2779.
59. R. H. Colby, D. C. Boris, W. E. Krause and J. S. Tan, J. Polym. Sci., Part B: Polym. Phys., 1997, 35, 2951–2960.
60. F. Bordi, R. H. Colby, C. Cametti, L. de Lorenzo and T. Gili, J. Phys. Chem. B, 2002, 106, 6887–6893.
61. D. Terada, H. Kobayashi, K. Zhang, A. Tiwari, C. Yoshikawa and N. Hanagata, Sci. Technol. Adv. Mater., 2012, 13, 015003.
62. C. Tang, A. E. Ozcam, B. Stout and S. A. Khan, Biomacromolecules, 2012, 13, 1269–1278.
63. X. Mu, Y. Liu, D. Fang, Z. Wang, J. Nie and G. Ma, Carbohydr. Polym., 2012, 90, 1582–1586.
64. D. P. Ura, J. Rosell-Llompart, A. Zaszczyńska, G. Vasilyev, A. Gradys, P. K. Szewczyk, J. Knapczyk-Korczak, R. Avrahami, A. O. Šišková, A. Arinstein, P. Sajkiewicz, E. Zussman and U. Stachewicz, Materials, 2020, 13, 4169.
65. G. Collins, J. Federici, Y. Imura and L. H. Catalani, J. Appl. Phys., 2012, 111, 044701.
66. O. Schnitzer and E. Yariv, J. Fluid Mech., 2015, 773, 1–33.
67. M. Mandel and A. Jenard, Trans. Faraday Soc., 1963, 59, 2158–2169.
68. M. Mandel, F. V. An and D. Touw, Polyelectrolytes, 1974, 285–300.
69. F. Bordi, C. Cametti and R. H. Colby, J. Phys.: Condens. Matter, 2004, 16, R1423–R1463.
70. F. Bordi, C. Cametti, T. Gili, S. Sennato, S. Zuzzi, S. Dou and R. H. Colby, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 031806.
71. R. M. Fuoss and L. Onsager, J. Phys. Chem., 1957, 61, 668–682.
72. C. F. Chamberlayne and R. N. Zare, J. Chem. Phys., 2020, 152, 1–10.
73. J. M. Montanero and A. M. Gañán-Calvo, Rep. Prog. Phys., 2020, 83, 097001.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00605d

---