Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quasi-two-dimensional dispersions of Brownian particles with competitive interactions: phase behavior and structural properties
Zihan
Tan
 *abc,
Vania
Calandrini
*abc,
Vania
Calandrini
 b,
Jan K. G.
Dhont
b,
Jan K. G.
Dhont
 ad and
Gerhard
Nägele
ad and
Gerhard
Nägele
 ad
ad
aBiomacromolecular Systems and Processes, Institute of Biological Information Processing, Forschungszentrum Jülich, 52428 Jülich, Germany
bComputational Biomedicine, Institute for Advanced Simulation, Forschungszentrum Jülich, 52428 Jülich, Germany
cInstitut für Theoretische Physik, Technische Universität Berlin, Hardenbergstrβe 36, 10623 Berlin, Germany. E-mail: zihan.tan@tu-berlin.de
dDepartment of Physics, Heinrich-Heine Universität Düsseldorf, D-40225 Düsseldorf, Germany
First published on 10th October 2024
Abstract
Competing short-range attractive (SA) and long range repulsive (LR) particle interactions can be used to describe three-dimensional charge-stabilized colloid or protein dispersions at low added salt concentrations, as well as membrane proteins with interaction contributions mediated by lipid molecules. Using Langevin dynamics (LD) simulations, we determine the generalized phase diagram, cluster shapes and size distributions of a generic quasi-two-dimensional (Q2D) dispersion of spherical SALR particles confined to in-plane motion inside a bulk fluid. The SA and LR interaction parts are modelled by a generalized Lennard-Jones potential and a screened Coulomb potential, respectively. The microstructures of the detected equilibrium and non-equilibrium Q2D phases are distinctly different from those observed in three-dimensional (3D) SALR systems, by exhibiting different levels of hexagonal ordering. We discuss a thermodynamic perturbation theory prediction for the metastable binodal line of a reference system of particles with SA interactions only, which in the explored Q2D-SALR phase diagram region separates cluster from non-clustered phases. The transition from the high-temperature (small SA) dispersed fluid (DF) phase to the lower-temperature equilibrium cluster (EC) fluid phase is characterised by a low-wavenumber peak height of the static structure factor (corresponding to a thermal correlation length of about twice the particle diameter) featuring a distinctly smaller value (≈1.4) than in 3D SALR systems. With decreasing temperature (increasing SA), the cluster morphology changes from disk-like shapes in the equilibrium cluster phase, to double-stranded anisotropic hexagonal cluster segments formed in a cluster-percolated (CP) gel-like phase. This transition can be quantified by a hexagonal order parameter distribution function. The mean cluster size and coordination number of particles in the CP phase are insensitive to changes in the attraction strength.
1 Introduction
During the past two decades, strong attention has been paid to Brownian particle dispersions with competitive short-range attractive (SA) and long-range repulsive (LR) inter-particle forces.1–3 The competition between attraction and repulsion makes these excellent model systems for exploring the physics of copious soft matter and biological systems, including charged-stabilized colloids with added depletants,1,4–8 lysozyme protein solutions under low-salinity conditions,1,9–14 Y-shaped monoclonal antibodies,15–17 and the reentrant liquid condensation of ribonucleoprotein-RNA complexes,18 to name just a few. Adjusting the respective influence of SA and LR forces allows to control the microstructure of the dispersions, which is relevant to applications such as in the formulation of pharmaceutical drugs and protein crystallization.2 Owing to their importance both for fundamental theory and in industrial applications, the structure and phase behavior of three-dimensional (bulk) dispersions of SALR particles have been extensively investigated theoretically, numerically and experimentally. For example, integral equation theory,19,20 discrete perturbation theory (DPT),21–23 density functional theory,24–27 and computer simulations23,28 have been used to study the phase behavior of 3D-SALR systems. In ref. 29 and the mini-review,30 Monte Carlo simulations in three dimensions (3D) have been reported for a SALR potential consisting of hard-core and short-range attractive square-well parts, augmented by a long-range linear repulsive ramp potential. In ref. 31 a phase diagram in two dimensions (2D) is obtained for a triangular lattice model where neighbouring particles are attractive and next-neighbour particles are repulsive. Here, a cluster phase is found, as well as stripe-like phases. Recent 3D-MD simulations of SALR particles in between two parallel walls with one wall being attractive32 have shown flattened clusters or stripes, respectively, formed by the adsorbed particles. Generic SALR pair interaction potentials have been also employed to mimick the behavior of aqueous lysozyme solutions for low added salt concentrations.13,14In contrast to pre-dominantly attractive particles fluids where macroscopic gas–liquid type phase separation is observed, the repulsive interaction part in SALR suspensions primarily stints the size of growing clusters, thus frustrating macroscopic phase separation.33–35 Due to the strongly differing length scales of attraction and repulsion, there is a rich phase behavior of 3D-SALR systems including equilibrium and gel-like cluster phases.23,36–38 Using Monte-Carlo simulations for two generic SALR potentials, Godfrin et al.23 have mapped out a generalized 3D phase diagram including four different phases distinguishable by their respective cluster size distribution (CFD) functions, namely equilibrium dispersed fluid (DF) and equilibrium cluster (EC) states, and random percolated (RP) and cluster percolated (CP) states. In the temperature versus particle concentration state diagram, the latter two states are separated from the former ones by a percolation line, while the EC and CP cluster states (non-clustered DF and RP states) are located below (above) the binodal line of a short-range attractive (SA) reference potential system. As argued by Ruiz-Franco and Zaccarrelli,3 the phase states observed by Godfrin et al. are located well above a so-called λ-line in the temperature-concentration state diagram representing systems for which the static structure factor diverges at a small but non-zero wavenumber qλ > 0. The λ-line marks the onset of a low-temperature region where the system becomes unstable to periodic density fluctuations of long wavelength 2π/qλ, giving rise to ordered modulated phases such as stripe or lamellar phases, self-organized from rather monodisperse clusters. We note that microphase separation into ordered modulated phases is not limited to colloidal systems, but also occurs in micellar systems where the micelles exhibit SALR-type interactions, as shown in ref. 39.
In contrast, the higher-temperature disordered EC and CP cluster phases identified by Godfrin et al. consist of finite-sized clusters with a broad size distribution. A rough estimate of the characteristic wavenumbers qc and qλ (λ-line) can be obtained using a simple random phase approximation calculation of the SALR static structure factor, with a hard-sphere or hard-disk reference potential in the 3D and 2D cases, respectively.27
Regarding the (metastable) binodal of the SA reference potential system separating the EC and CP phases from the higher-temperature DF and RP phases, the Noro–Frenkel extended law of corresponding states (ELCS) asserts that the thermodynamics (and equilibrium structure) of all three-dimensional SA systems is practically the same, independent of the details of the underlying SA potential, provided its attraction range is less than 25% of the particle diameter, for systems of equal temperature (attraction strength), second virial coefficient and volume fraction, expressed in units of the according critical point values at the liquid–liquid phase separation.40 For protein solutions where the electrostatic repulsion is strongly screened, it has been shown experimentally that near to the liquid–liquid phase separation, the ELCS behavior further extends to collective diffusion.41 While the ELCS does not hold as such for 3D-SALR systems,3 an universal state diagram is obtained, provided temperature and particle concentration are scaled by the critical point temperature and concentration of the SA reference system, respectively.23
As discussed in ref. 2 and 10, the (onset of) finite-sized particle clusters formation is globally indicated by a prepeak of the static structure factor, S(q), at a wavenumber, q = qc, distinctly smaller than the wavenumber, qm, of the principal peak associated with the nearest neighbor shell of particles. In contrast to qm, the prepeak position wavenumber qc is in general rather insensitive to changes in the particles concentration. The prepeak of S(q) is also commonly referred to as intermediate range order peak, to emphasize that its existence does not necessarily indicate a genuine clustered fluid phase.2,10 While the present work is not concerned with the dynamics of SALR systems, we note that a prepeak is theoretically predicted also for the hydrodynamic function, H(q), of 3D-SALR systems characterizing collective diffusion,28,42 and this feature has been experimentally detected for lyzosyme solutions under low-salt conditions in the DF phase region.14
For 3D-SALR systems, a notable effort was made to identify simple criteria characterizing the transition from the DF to the EC equilibrium phase. From their MC simulations, Godfrin et al.23 conclude that this transition is hallmarked by a prepeak height value S(qc) ≈ 2.7. This value is accidentally close to the Hansen–Verlet freezing transition value S(qm) ≈ 2.85 for the height of the static structure factor principal peak of a three-dimensional hard-sphere system, located at the wavenumber qm43,44 associated with the nearest neighbor shell of particles. The Hansen–Verlet freezing transition criterion can be mapped, incidentally, to a dynamic criterion in terms of the long-time self-diffusion coefficient, both for 3D and 2D systems.45 The freezing transition value is enlarged slightly to S(qm) = 3.1 for low-salt dispersions of highly charged colloids, in which case it signals a fluid to bcc crystal phase transition.46
Observation of the prepeak height value S(qc) = 2.7 is not sufficient to unambiguosly indicate a DF to EC phase transition in three dimensions. According to Bollinger and Truskett33 (see also ref. 3 and 47), this condition should be amended by the condition 2.0 ≲ ξT/σ ≲ 3.0 for the thermal correlation length ξT in units of the particle diameter σ, where ξT is identified as the inverse half-width of a quadratic fit of the inverse structure factor prepeak around qc. As we will discuss also in the context of Q2D dispersions, fluid-like systems with a distinct cluster peak S(qc) exhibit a damped, long-distance oscillatory part of the radial distribution function g(r) of characteristic wavelength 2π/qc. Additionally to the prepeak-associated indicators S(qc) and ξT, an empirical relation between particle coordination number and mean cluster size has been identified as being likewise indicative of the DF to EC transition.23 Since in the present study only the depth of the short-ranged attractive part of the potential is varied, phases additional to the ones reported here may appear, e.g., for stronger attraction strengths and a varying attraction to repulsion range ratio, akin to the stripe-like patterns in 3D discussed in ref. 27, 48 and 49. Moreover, there might be a hexatic phase specific to two-dimensional systems only. An intermediate hexatic phase has been observed, e.g., in the freezing/melting of a two-dimensional dispersions of hard disks, and of disks interacting by an attractive square-well potential50 which can be described by the celebrated Kosterlitz–Thouless–Halperin–Nelson–Young (KTHNY) theory of thermally driven dislocation or disclination pairs unbinding transitions.51–53
Exploring the structure and phase behavior of Q2D-SALR systems is particularly relevant for colloidal (or protein) particles confined at, or close to, a planar interface. In biology, the diffusion and self-organization of phospholipids and membrane-proteins into finite-sized domains, such as “lipid rafts”54–56 or protein clusters,57–59 are significant features in signal transduction, membrane sorting, protein processing, and virus trafficking.60–62 It has been evidenced that the interplay of SA (due, e.g., to lipid-mediated depletion, wetting, and hydrophobic mismatch, or direct chemical interactions between amino-acid side chains) and LR (induced, e.g., by mechanical deformation or fluctuations of the membrane) is crucial for the formation of membrane-protein clusters.63–68 In this context, systematic investigations of the phase behavior, and the structural and cluster properties, of Q2D-SALR particles are thus indispensable. Surprisingly, despite its fundamental importance, only little effort was invested so far in exploring systematically the structure and dynamics of (Q)2D-SALR systems. There exists, however, some theoretical and simulation works on (Q)2D-SALR systems showing that particles can self-assemble into various exotic microphases either in bulk fluid,69–72 or when trapped (pinned) by external forces73–75 or by confinement.25
In this work, using Langevin dynamics (LD) simulations, we explore the phase behavior, and the structural and clustering properties of a planar monolayer of SALR Brownian particles restricted to in-plane motion. The particles are described as Brownian spheres interacting via short-range generalized Lennard-Jones and long-range repulsive screened Coulomb forces of comparable interaction strengths. Our study covers a broad range of attraction strength and particle concentration values, and we identify and analyze the (Q)2D phases in this parameter space region. In addition to analyzing the observed cluster morphologies, we identify and quantify various (Q)2D indicators for the transition from a higher-temperature, non-clustered DF phase to a lower-temperature EC phase. The LD simulation results enable us not only to study static properties of Q2D-SALR systems as presented in this work, but also to gain (to some extent) insight into the dynamic properties of the different phases. The dynamics of Q2D-SALR systems will be discussed extensively in a subsequent paper which further addresses effects of interparticle hydrodynamic interactions not accounted for in LD simulations.76
The paper is organized as follows. Section 2 describes the employed pair potential and the LD simulation scheme for the Q2D-SALR model system of Brownian particles. Furthermore, we recap the theoretical tools used to identify and analyze the morphology of the encountered phases. Section 3 includes the main results of the paper. Notably, a generalized phase diagram is mapped out by analyzing the shapes of the cluster size distribution function. Akin to three-dimensional SALR systems, the Q2D-SALR diagram in reduced units is subsequently amended by a metastable binodal curve for a representative short-range attractive two-dimensional square-well (SW) fluid, obtained from a second-order thermodynamic perturbation theory calculation in local compressibility approximation. Furthermore, the intermediate range order prepeak in S(q) is investigated. Various indicators for the DF to EC phase transition in Q2D systems are discussed and compared with their 3D analogues. The level of hexagonal ordering in clusters belonging to different cluster phases is carefully examined. Section 4, finally, comprises our summary with conclusions.
2 Theoretical background
We discuss here the employed Q2D-SALR model of Brownian particles and the Langevin dynamics simulation scheme, in conjunction with the theoretical tools used in analyzing the simulation data.2.1 SALR pair potential
Our simplifying Q2D-SALR model system consists of a planar monolayer of monodisperse spherical particles embedded in a bulk fluid, with the motion of the particle centers confined to in-plane motion. The pair potential, u(r), for two particles i and j at center-to-center distance r = rij is thus taken to be equal to that of SALR particles in a three-dimensional dispersion, but with the constraint that r is an in-plane pair distance. We use here a standard soft SALR pair potential, namely28,69,77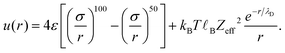 | (1) |
Concerning the results shown in this paper, the non-dimensionalized Debye screening length (repulsion range) is fixed to λD/σ = 1.794, and the non-dimensionalized electrostatic repulsion parameter to ℓBZeff2/σ = 3.588. The non-dimensionalized short-range attraction strength, ε* = ε/kBT, is varied in between 2–20, which amounts to a variation of the dimensionless effective temperature defined by
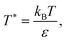 | (2) |
The employed SALR potential attains its minimal value, u(rmin) = uY(rmin) − ε ≈ 2kBT − ε, at the pair distance rmin ≈ 1.01σ which is practically independent of the attraction strength. The attraction range parameter λatt(ε) = r0(ε) − σ is defined here in terms of the distance r = r0(ε) located to the right of the potential minimum where u(r0) = 0. This distance is given approximately by r0(ε) ≈ (2ε*)1/50σ for ε* ≥ 4, so that λatt < 0.08σ in the considered range of attraction strength values. Considering that the electrostatic repulsion range, λD = 1.749σ, is distinctly larger than λatt, u(r) qualifies indeed as a SALR potential. The motivation for the employed λD is that it is comparable to the repulsion range in previous simulation works on 3D-SALR systems.2,23,78 Considering a colloidal suspension as an example, the employed reduced Debye screening length, λD/σ, is that of a dilute aqueous 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte solution of concentration ≈3 µM, and colloidal particle diameter σ ≈ 100 nm.
1 electrolyte solution of concentration ≈3 µM, and colloidal particle diameter σ ≈ 100 nm.
2.2 (Q)2D Langevin dynamics simulations
Consider Np disk-like and monodisperse particles interacting pairwise via the SALR pair potential given in eqn (1). The (underdamped) two-dimensional Brownian motion of the particles of mass M and diameter σ is described by the set of Np coupled two-dimensional Langevin dynamics (LD) equations,79,80M![[r with combining umlaut]](https://www.rsc.org/images/entities/b_i_char_0072_0308.gif) i(t) + γ0ṙi(t) = −∇iV(t) + Γ(t), i(t) + γ0ṙi(t) = −∇iV(t) + Γ(t), | (3) |
![[r with combining umlaut]](https://www.rsc.org/images/entities/b_i_char_0072_0308.gif) i(t) are the two-dimensional position vector, velocity, and acceleration of the ith particle at time t, and γ0 is the single-particle translational friction coefficient, associated with the single-particle translational diffusion coefficient by D0 = kBT/γ0. Bearing in mind that a planar monolayer of Brownian spheres embedded in bulk fluid is considered in actuality, the three-dimensional Stokes–Einstein relation D0 = kBT/(3πησ) can be used for stick hydrodynamic boundary conditions, where η is the shear viscosity of the suspending fluid.
i(t) are the two-dimensional position vector, velocity, and acceleration of the ith particle at time t, and γ0 is the single-particle translational friction coefficient, associated with the single-particle translational diffusion coefficient by D0 = kBT/γ0. Bearing in mind that a planar monolayer of Brownian spheres embedded in bulk fluid is considered in actuality, the three-dimensional Stokes–Einstein relation D0 = kBT/(3πησ) can be used for stick hydrodynamic boundary conditions, where η is the shear viscosity of the suspending fluid.
Furthermore, Γ(t) is an orthogonal, Gaussian white-noise random force vector, fully characterized by its zero mean,
| 〈Γ(t)〉 = 0, | (4) |
| 〈Γ(t)Γ(t′)〉 = 2γ0kBTÎδ(t − t′). | (5) |
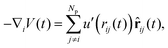 | (6) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij is the unit vector pointing from the centre of particle i to that of particle j, and u′(r) is the analytically obtained derivative of the soft SALR potential given in eqn (1).
ij is the unit vector pointing from the centre of particle i to that of particle j, and u′(r) is the analytically obtained derivative of the soft SALR potential given in eqn (1).
In our LD simulations, the pair potential is truncated at r = 5σ, and shifted slightly downwards to maintain its continuity everywhere.77 Using a two-dimensional square as the primary simulation box, periodic boundary conditions and the minimum image convention are invoked. The LD equations include no hydrodynamic coupling of particle positions and orientations, i.e. solvent-mediated inter-particle hydrodynamic interactions are disregarded. Hydrodynamic coupling would turn the considered monolayer system into a genuine quasi-2D system where the lateral (out-of-plane) extension of the fluid and particles matters. We are dealing here with static properties only where the influence of hydrodynamic interactions is negligible, provided the system is in thermodynamic equilibrium.
Energy in the employed LD simulation algorithm is expressed in units of the thermal energy kBT, length in units of σ, force in units of kBT/σ, and time in units of 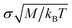 which is the single-particle momentum relaxation time. The according unit for the single-particle translational friction coefficient γ0 is
which is the single-particle momentum relaxation time. The according unit for the single-particle translational friction coefficient γ0 is 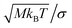 .
.
The LD simulations integrate the Langevin equation using a small time step of approximately 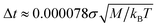 . The simulations run for at least 108 time steps, or 2 × 108 steps for attraction strengths larger than 10kBT. This is nearly 2 × 104 times the particle momentum relaxation time. Systems are prepared at different area fractions, with initial particle positions assigned according to a uniform distribution. Velocities are initialized according to a Maxwellian distribution at a temperature one order of magnitude larger than the target value. Each system is then quenched to the target temperature, and equilibration is monitored subsequently by calculating the average potential energy per particle and kBT, as function of the LD simulation time t. We note here that methods such as simulated annealing and parallel tempering have been implemented to improve the simulation convergence towards the stationary state.31,48,49,81 As shown by Imperio and Reatto in ref. 48 parallel tempering simulations actually achieve lower energy states, and allow a more precise computation of thermodynamic properties than plain simulations, although the overall picture on the structural features of the explored patterns does not change qualitatively.
. The simulations run for at least 108 time steps, or 2 × 108 steps for attraction strengths larger than 10kBT. This is nearly 2 × 104 times the particle momentum relaxation time. Systems are prepared at different area fractions, with initial particle positions assigned according to a uniform distribution. Velocities are initialized according to a Maxwellian distribution at a temperature one order of magnitude larger than the target value. Each system is then quenched to the target temperature, and equilibration is monitored subsequently by calculating the average potential energy per particle and kBT, as function of the LD simulation time t. We note here that methods such as simulated annealing and parallel tempering have been implemented to improve the simulation convergence towards the stationary state.31,48,49,81 As shown by Imperio and Reatto in ref. 48 parallel tempering simulations actually achieve lower energy states, and allow a more precise computation of thermodynamic properties than plain simulations, although the overall picture on the structural features of the explored patterns does not change qualitatively.
While LD simulations allow also for the calculation of dynamic properties including time correlation functions (but with hydrodynamic interactions disregarded), in the present work only static structural properties are considered which are not influenced by inertia effects (on a coarse-grained time scale much larger than 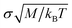 ) depending on the particle mass M. The dynamics of our Q2D-SALR model viewed on different time scales, and with hydrodynamic interaction effects included using additional multi-particle collision dynamics simulations, will be the topic of a subsequent paper.76
) depending on the particle mass M. The dynamics of our Q2D-SALR model viewed on different time scales, and with hydrodynamic interaction effects included using additional multi-particle collision dynamics simulations, will be the topic of a subsequent paper.76
2.3 Binodal of the SA reference system
Motivated by the works of Godfrin et al.23 on the phase behavior of 3D-SALR systems, for the considered Q2D-SALR model we discuss next our calculation of the binodal of the SA reference system. We define the pair potential, uref(r), of the short-range attractive reference system in terms of the SALR potential u(r) in eqn (1) as| uref(r) = u(r)Θ(r0(ε) − r), | (7) |
To determine the gas–liquid-type binodal of the reference potential system, we employ 2nd-order (discrete) thermodynamic perturbation theory,22,23,82–84 but now applied to a two-dimensional fluid. To avoid cumbersome numerical calculations, triggered by the complex form of uref(r), we map the reference system summarily onto a two-dimensional square well (SW) fluid of comparable attraction range. The pair potential of the 2D-SW fluid is
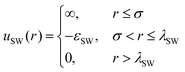 | (8) |
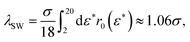 | (9) |
The binodal line of the so-specified 2D-SW fluid can be easily calculated using the 2nd-order thermodynamic perturbation theory parameterization in local compressibility approximation, as worked out by Trejos et al.85 in the framework of the statistical associating fluid theory for potentials of variable range (SAFT-VR).86–88 In a nutshell, thermodynamic perturbation theory computes the free energy approximately by treating the pair potential of the interacting particles system as perturbation of the hard-disk potential. For the radial distribution function (RDF) input of hard disks, Trejos et al. use an analytic superposition of the exact RDF of hard rods (Tonk gas) and the approximate RDF of a three-dimensional hard-sphere system in Percus–Yevick approximation.
The explicit form of the 2D-SW reference system binodal, as determined in this work using the semi-analytic scheme by Trejos et al., is shown in the upcoming Section 3, and it is amended by a discussion of the applicability of 2nd order perturbation theory to 2D fluids for which thermal fluctuations are stronger than in 3D.
2.4 Identification of phases
To gain insight into the phase behavior of the Q2D-SALR dispersion, using the LD simulation data we analyze the cluster size distribution (CSD) function defined as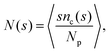 | (10) |
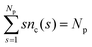 , which in turn implies the normalization condition
, which in turn implies the normalization condition 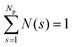 . The mean cluster size is given by
. The mean cluster size is given by 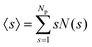 . Whether two interacting particles i and j belong to the same cluster is determined by their mutual center-to-center distance rij, which for a common cluster is required to be smaller than the threshold distance, rmax(ε), with rmax(ε) > r0(ε), where the potential in eqn (1) attains its local maximum. For particles pair distances rmin < rij < rmax(ε), the two particles attract each other. The cluster threshold distance varies in between 1.11 < rmax(ε)/σ < 1.17 for the considered range of attraction strength values. The Q2D-SALR phases discussed in Section 3 are identified essentially on basis of the generated CSD functions.
. Whether two interacting particles i and j belong to the same cluster is determined by their mutual center-to-center distance rij, which for a common cluster is required to be smaller than the threshold distance, rmax(ε), with rmax(ε) > r0(ε), where the potential in eqn (1) attains its local maximum. For particles pair distances rmin < rij < rmax(ε), the two particles attract each other. The cluster threshold distance varies in between 1.11 < rmax(ε)/σ < 1.17 for the considered range of attraction strength values. The Q2D-SALR phases discussed in Section 3 are identified essentially on basis of the generated CSD functions.
2.5 Hexagonal order parameter
It will be shown in Section 3 that particles with SALR interactions tend in two-dimensional settings to form clusters with hexagonal ordering.71 The degree of hexagonal ordering can be analyzed, e.g., using the particle-specific local hexagonal orientational order parameter |q(i)6|2 ∈ [0,1] for a given particles configuration which quantifies the sixfold planar orientational order in the neighborhood of a particle i.51,52,89–92 Its complex-valued amplitude factor is given by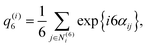 | (11) |
Using our LD simulations data for the orientational order parameter subdivided into thin bins including values in between zero and one, we have furthermore calculated the orientational distribution function, P(|q6|2), where P(|q6|2) d|q6|2 is the probability of finding particles in the two-dimensional system with hexagonal order parameter values in an infinitesimal interval d|q6|2 centered around |q6|2. This continuous distribution function is normalized according to
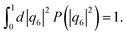 | (12) |
3 Results
We explore the microstructure and phase behavior of the employed Q2D-SALR system by considering at least 8 different values for the reduced effective temperature T* = kBT/ε in the range [0.05–0.5], and 4 different values for the area fraction of particles, ϕ2D = n2Dπσ2/4, in the interval [0.1–0.5], where n2D = Np/L2 is the area concentration of particles. The number, Np, of particles in the LD simulations is fixed, while the areal simulation box length L is varied for setting up the considered values of ϕ2D.For each parameter pair (ϕ2D,T*) refered to as state point, quantities of interest such as N(s) and P(|q6|2) are calculated as time averages in a LD production simulation run, following an equilibration run executed over a sufficiently long time span until steady-state is reached. It was checked that the steady state value of the average energy is independent of the initial (uniform) particle configuration and the initial Maxwellian velocity distribution. However, as in ref. 48,81 a very slow logarithmic drift of the average potential energy is monitored over the entire duration of the thermalization simulation run, for cluster and percolated states at ε ≥ 10kBT. If not specified otherwise, the presented results are for Np = 1024 particles in the two-dimensional primary simulation box of area L × L. The particle number Np = 1024 commonly used in our simulations is in line with previous 2D and 3D studies.23,29,48,49,81 A larger particle number, Np = 4096, was used in our simulations for specific state points (ϕ2D,T*) = (0.5, ≤0.1), for improved statistics and as a check of internal consistency.
3.1 Generalized phase diagram
As it is thoroughly discussed in the context of 3D-SALR systems,3,23 the shape of the discrete cluster size distribution (CSD) function N(s) introduced in eqn (10) is indicative of the phase state of a considered system. For a total of 34 different Q2D-SALR systems of particles interacting by the pair potential described in Section 2.1, which are specified by respective (ϕ2D,T*) state points, we have calculated the according N(s) functions. Recall from Section 2.4 that N(s) is the mean number of clusters consisting of s particles. Inspection of the N(s) curves has led us to the identification of four different disordered (modulated) phases described in the following.Fig. 1(a) depicts the shapes of N(s) characteristic of the four identified (Q)2D-SALR phases. Akin to the phase diagram of 3D-SALR systems discussed in ref. 3 and 23, the identified phases encompass a dispersed fluid (DF) phase (blue squares) consisting mainly of particle monomers, an equilibrium cluster (EC) phase (red squares) with clusters having a preferential size, a random percolated (RP) gel-like phase (green diamonds) exhibiting area-spanning clusters formed basically by monomers, and a cluster percolation (CP) gel-like phase (magenta triangles) where the system-spanning clusters consist of finite cluster subunits. As noticed from the figure, the N(s) describing a DF phase system (depicted in blue) at state point (ϕ2D,T*) = (0.2,0.5) decays monotonically with increasing s, and has its maximum at s = 1. In contrast, the CSD function of an EC fluid phase system (in red) at state point (0.2,0.125) reveals a local peak, indicative of the preferential cluster size. A RP system (depicted in green) at (0.5,0.25) is characterized by a slow, monotonic decay of N(s) terminating in a pronounced peak at s ≈ Np, indicative of clusters spanning the two-dimensional primary simulation box with Np = 1024 particles. Furthermore, the N(s) of a CP state system (in magenta, at (0.38,0.1)) showcases likewise a system-spanning cluster peak at s ≈ Np, plus additional peaks reflecting smaller cluster subunits.
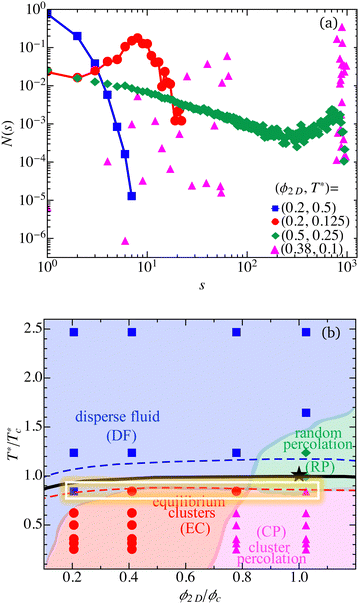 | ||
Fig. 1 (a) Cluster size distribution function, N(s), of Q2D-SALR systems for area fraction and effective temperature state points (ϕ2D,T*) corresponding to the dispersed fluid (DF: blue squares), equilibrium cluster (EC: red circles), random percolation (RP: green diamonds), and cluster percolation (CP: magenta triangles) phases. (b) Corresponding reduced Q2D-SALR phase diagram. The considered 34 state points are marked according to the identified four phases. The lines are the binodals of the two-dimensional square-well (SW) reference fluid, for attraction range parameter values λSW = 1.075 (dashed blue), 1.06 (solid black) and 1.05 (dashed red), respectively, calculated using the 2nd order thermodynamic perturbation theory method proposed by Trejos et al.85 All state points are normalized by the critical point values 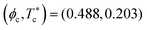 (black star) of the 2D-SW reference fluid with λSW/σ = 1.06. The horizontal white rectangle includes the four state points whose static structure factors are shown in Fig. 3(a). (black star) of the 2D-SW reference fluid with λSW/σ = 1.06. The horizontal white rectangle includes the four state points whose static structure factors are shown in Fig. 3(a). | ||
Based on the CSD functions determined for the 34 considered state points, we obtain the Guggenheim-type (reduced) phase diagram displayed in Fig. 1(b). The (Q)2D-SALR phase diagram resembles globally that for 3D-SALR systems.23 At comparatively high effective temperatures T* but small area fractions ϕ2D, the systems are in the monomer-dominated DF phase space region, while the gel-like RP phase region is entered for ϕ2D ≳ 0.37. Notice in comparison that the maximal area fraction of a planar monodisperse hard-disk layer is 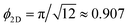 , attained at hexagonal closed packing. The EC and CP cluster phases are observed for lower T* ≲ 0.2 only, and for non-small ϕ2D. The transition from the EC fluid phase to the CP gel-like phase occurs roughly for area concentrations exceeding ϕ2D ≈ 0.35.
, attained at hexagonal closed packing. The EC and CP cluster phases are observed for lower T* ≲ 0.2 only, and for non-small ϕ2D. The transition from the EC fluid phase to the CP gel-like phase occurs roughly for area concentrations exceeding ϕ2D ≈ 0.35.
Akin to 3D-SALR systems, the lower-temperature two-dimensional EC and CP cluster phases in the phase diagram of Fig. 1(b) are qualitatively demarcated from the higher-temperature, non-clustered DF and RP phases by the (metastable) gas–liquid coexistence line (binodal) of a SA reference fluid of particles including short-range attractions only, with the SA pair potential defined in eqn (7) of Section 2.3. For simplicity, and as detailed in Section 2.3, we have calculated the binodal approximatively only, by mapping the SA system onto a two-dimensional square-well (SW) fluid whose attraction range parameter is fixed, according to eqn (9), to λSW/σ = 1.06. As another simplification, the SW potential depth εSW is identified with the attraction strength ε of the SALR potential. We use the 2D-SW fluid here as a simple model for the SA reference fluid, since different from the 3D case93 no analytic expression is available in 2D for the free energy of the limiting case of an adhesive hard-disk system.
We have calculated the binodal characterizing the metastable gas–liquid phase coexistence of the 2D-SW fluid using second-order thermodynamic perturbation theory in local compressibility approximation, as conveniently worked out in a semi-analytic form by Trejos et al.85 The resulting binodal for λSW/σ = 1.06 is shown in Fig. 1(b) as the solid black curve. Its critical point is located at 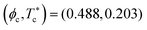 . These critical point values are used to scale the area fraction ϕ2D and effective temperature, T* = kBT/ε, respectively, in the depicted phase diagram. On a qualitative level, the 2D-SW reference fluid binodal separates the non-clustered from the clustered phases, supporting thus the physical interpretation of the EC and CP cluster phases as modulated phases originating from gas–liquid-type demixing, macroscopically frustrated by the long-range interaction part of the SALR potential. In accord with physical expectation, and as shown in the figure, the binodal is shifted upwards (and its critical point temperature and concentration shifted to larger and smaller values, respectively) when the attraction range λSW is increased (see dashed lines).
. These critical point values are used to scale the area fraction ϕ2D and effective temperature, T* = kBT/ε, respectively, in the depicted phase diagram. On a qualitative level, the 2D-SW reference fluid binodal separates the non-clustered from the clustered phases, supporting thus the physical interpretation of the EC and CP cluster phases as modulated phases originating from gas–liquid-type demixing, macroscopically frustrated by the long-range interaction part of the SALR potential. In accord with physical expectation, and as shown in the figure, the binodal is shifted upwards (and its critical point temperature and concentration shifted to larger and smaller values, respectively) when the attraction range λSW is increased (see dashed lines).
We refrain from a more quantitative discussion of SA reference fluid binodals, since first these are not central to the present discussion of Q2D-SALR systems, and second since the binodals in Fig. 1(b) are mean-field results based on thermodynamic 2nd-order perturbation theory. The mean-field binodals overestimate 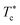 and underestimate ϕc, owing to the underestimated thermal fluctuations. These fluctuations are more pronounced for smaller-range attractions as the ones considered here, and are stronger in 2D than in 3D. In this context, notice in Fig. 1(b) the strong sensitivity of the 2D mean-field binodal on the attraction range, which is likely due to the underestimation of thermal fluctuations in the employed 2nd-order perturbation scheme. Moreover, the mean-field coexistence curves underestimate the pronounced flatness of binodals generated by computer simulations,85 and the mean-field critical point exponent β = 1/2 in the near-critical
and underestimate ϕc, owing to the underestimated thermal fluctuations. These fluctuations are more pronounced for smaller-range attractions as the ones considered here, and are stronger in 2D than in 3D. In this context, notice in Fig. 1(b) the strong sensitivity of the 2D mean-field binodal on the attraction range, which is likely due to the underestimation of thermal fluctuations in the employed 2nd-order perturbation scheme. Moreover, the mean-field coexistence curves underestimate the pronounced flatness of binodals generated by computer simulations,85 and the mean-field critical point exponent β = 1/2 in the near-critical 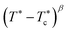 dependence of the liquid–gas concentration difference, determined along the mean-field binodal close to the critical point, differs distinctly from the exponent β = 1/8 of the 2D Ising model universallity class. The latter critical exponent is expected to apply to two-dimensional SA fluids. As noted already in Section 1, Godfrin et al.23 discuss binodals of the 3D-SA reference fluid based on the Noro–Frenkel extended law of corresponding states (ELCS), known to hold to good accuracy for 3D fluid systems with short-range attractions where the gas–liquid type coexistence is metastable against crystallization. To our knowledge, no general validation of the ELCS has been made to date for 2D-SA fluids using computer simulations. Such a validation is more demanding in 2D than in 3D owing to stronger thermal fluctuations in 2D, and an accordingly more pronounced flatness of binodals in the (ϕ2D,T*) diagram complicating the determination of critical points. In 2D, there is also an enhanced tendency for crystallization.
dependence of the liquid–gas concentration difference, determined along the mean-field binodal close to the critical point, differs distinctly from the exponent β = 1/8 of the 2D Ising model universallity class. The latter critical exponent is expected to apply to two-dimensional SA fluids. As noted already in Section 1, Godfrin et al.23 discuss binodals of the 3D-SA reference fluid based on the Noro–Frenkel extended law of corresponding states (ELCS), known to hold to good accuracy for 3D fluid systems with short-range attractions where the gas–liquid type coexistence is metastable against crystallization. To our knowledge, no general validation of the ELCS has been made to date for 2D-SA fluids using computer simulations. Such a validation is more demanding in 2D than in 3D owing to stronger thermal fluctuations in 2D, and an accordingly more pronounced flatness of binodals in the (ϕ2D,T*) diagram complicating the determination of critical points. In 2D, there is also an enhanced tendency for crystallization.
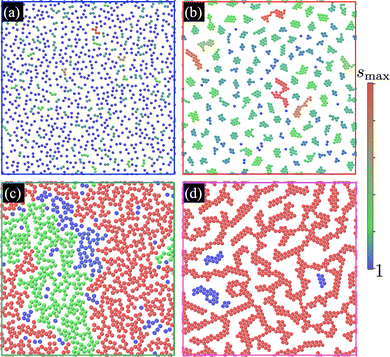
It is instructive to analyze simulation snapshots of the four detected phases. Fig. 2 includes configurational snapshots of Q2D-SALR particles for the same four state points (ϕ2D,T*) as in Fig. 1(a). Particles belonging to clusters of different size s are distinguished by colors, selected according to the vertical color bar spanning the range from s = 1 up to s = smax, where smax denotes the maximal cluster size at specific (ϕ2D,T*). In the DF system snapshot depicted in Fig. 2(a), mostly monomers are observed, but also loosely packed small clusters of varying size s are occasionally recognized. In Fig. 2(b) visualizing the EC phase of equilibrium clusters, the clusters have a preferred size (here, around s = 10), due to the increased attraction (decreased T*) in comparison with the DF phase. The RP phase snapshot in Fig. 2(c) features system-spanning clusters. It can be viewed as a crowded DF phase. Accordingly, the RP phase lacks orientational order of clusters. In contrast, the cluster percolated (CP) phase system in Fig. 2(d) has a system-spanning cluster, formed by compact and locally elongated structures with pronounced internal hexagonal order.
A comment is in order about why globally the same phases are observed in the present (Q)2D study as in the works by Godfrin et al. on 3D-SALR systems. This can be attributed to our selection of the SALR potential parameters {ε/kBT,lBZeff2/σ,λD/σ} similar to those by Godfrin et al., and our focus on the phase space region around the SA fluid reference binodal. Well outside the explored phase space region, there is the possibility of finding ordered modulated phases (at low T*), as well as a hexatic phase encountered in 2D systems only. Finally, in the explored phase space region, we have no evidence of a Wigner (cluster) glass which different from the CP phase has no percolated clusters.
3.2 Prepeak characteristics at DF to EC phase transition
As mentioned in Section 1, the transition from the equilibrium DF to the modulated equilibrium EC phase of 3D-SALR systems is signalled by a characteristic height, S(qc), of the static structure factor prepeak (intermediate range order peak) centered around the wavenumber qc, in conjuction with a characteristic half-width, 2/ξT, of the prepeak where S(qc ± 1/ξT) ≈ S(qc)/2. According to Monte-Carlo simulation data by Godfrin et al.,23 this transition occurs in 3D when the prepeak height exceeds the characteristic value S(qc) ≈ 2.7. Moreover, as argued by Bollinger and Truskett,33,47 for a clear-cut identification of the DF to EC transition, the prepeak height criterion should be amended by the condition that the length ξT slightly exceeds the Debye screening length, λD, of the repulsive long-range Yukawa part of the SALR potential in eqn (1). Explicitly, ξT ≳ λD is required, or more generally for an arbitrary SALR potential that 2.0 ≲ ξT ≲ 3.0. The length ξT is also refered to as thermal correlation length. Both in 3D and 2D, ξT is obtained from a fit of the prepeak region of S(q) around q ≈ qc, using the inverse (Bollinger–Truskett) quadratic form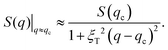 | (13) |
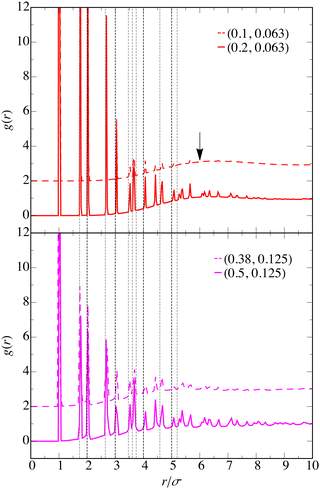
Fig. 3(b) shows LD simulation results for the static structure factor,
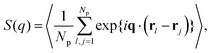 | (14) |
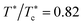 ), and for four different area fractions ϕ2D = 0.1–0.5, representative of three out of the four detected phases. The brackets indicate an average over a stationary ensemble of particle configurations, and q is the scattering wavevector of magnitude q ≥ 2π/L (with L the linear dimension of the simulation square), selected according to the invoked periodic boundary conditions. The prepeaks visible at wavenumber position qcσ ∼ 1.5 increase in height and become more narrow with increasing area fraction. A distinctive prepeak (in blue) is visible already for the DF phase system at ϕ2D = 0.1. While qc remains nearly constant for the DF and EC systems, it is shifted to a somewhat smaller value for the CP system (magenta curve) at ϕ2D = 0.5, for which the nearest-neighbor shell peak of S(q) at qm ≈ 2π/σ > qc is distinctly higher than the prepeak. That qc is rather insensitive to changes in particle concentrations is observed also for 3D-SALR systems. Akin to the 3D case, the concentration insensitivity of qc can be qualitatively explained using a simple random phase approximation where the static structure factor of the (Q)2D-SALR system is related approximately to the static structure factor, Shd(q), of a hard-disk reference system. On noting that Shd(q ≲ qc) ≈ Shd(q = 0), it is predicted in random phase approximation that qc is independent of ϕ2D, and determined only by the competing attraction/repulsion interaction parameters of the SALR potential. In actuality, qc can be mildly ϕ2D-dependent for fixed pair potential.
), and for four different area fractions ϕ2D = 0.1–0.5, representative of three out of the four detected phases. The brackets indicate an average over a stationary ensemble of particle configurations, and q is the scattering wavevector of magnitude q ≥ 2π/L (with L the linear dimension of the simulation square), selected according to the invoked periodic boundary conditions. The prepeaks visible at wavenumber position qcσ ∼ 1.5 increase in height and become more narrow with increasing area fraction. A distinctive prepeak (in blue) is visible already for the DF phase system at ϕ2D = 0.1. While qc remains nearly constant for the DF and EC systems, it is shifted to a somewhat smaller value for the CP system (magenta curve) at ϕ2D = 0.5, for which the nearest-neighbor shell peak of S(q) at qm ≈ 2π/σ > qc is distinctly higher than the prepeak. That qc is rather insensitive to changes in particle concentrations is observed also for 3D-SALR systems. Akin to the 3D case, the concentration insensitivity of qc can be qualitatively explained using a simple random phase approximation where the static structure factor of the (Q)2D-SALR system is related approximately to the static structure factor, Shd(q), of a hard-disk reference system. On noting that Shd(q ≲ qc) ≈ Shd(q = 0), it is predicted in random phase approximation that qc is independent of ϕ2D, and determined only by the competing attraction/repulsion interaction parameters of the SALR potential. In actuality, qc can be mildly ϕ2D-dependent for fixed pair potential.
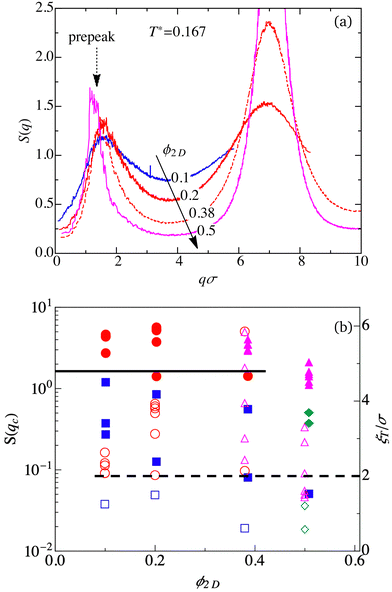 | ||
| Fig. 3 (a) Static structure factor, S(q), as function of the non-dimensionalized wavenumber qσ, for reduced temperature T* = 0.167 (ε = 6kBT) and four different area fractions as indicated. The according four state points are included in the horizontal white rectangle in Fig. 1(b). The dashed vertical arrow points to the locations, qcσ, of the intermediate range order prepeaks. (b) Static structure factor prepeak height S(qc) (logarithmic left ordinate, filled symbols) and reduced thermal correlation length ξT/σ (right ordinate, open symbols) as functions of area fraction. The color code for the different phases is as in Fig. 1. The solid (dashed) horizontal line marks the identified transition value S(qc) ≈ 1.4 (ξT/σ ≈ 2), separating approximately the DF from the EC phase for ϕ2D ≲ 0.4. | ||
Fig. 3(b) summarizes our results for the height, S(qc), of the prepeak of S(q) (filled symbols and left ordinate), and for the corresponding thermal correlation length ξT/σ (open symbols and right ordinate), the latter obtained from a best fit of the simulated (Q)2d-SALR prepeak using the analytic form in eqn (13). Different from the figure part (a), T* is not fixed in figure part (b) so that all explored state points are considered, the colors labeling different phases are selected as in Fig. 1.
Quite interestingly, the characteristic prepeak height S(qc) ≈ 1.4 signaling the transition from the DF to the EC phase for ϕ2D < 0.4 (solid horizontal line) is distinctly smaller than the according characteristic value S(qc) ≈ 2.7 in the 3D. This is in accord with our expectation that cluster formation is facilitated in 2D, since the local order in 2D is sixfold in all observed phases. As noted in Section 1 already, the DF to EC transition height S(qc) ≈ 2.7 in 3D-SALR systems23 is close to the Hansen–Verlet freezing transition criterion values, S(qm) ≈ 2.85–3.1, for the nearest-neighbor peak at qm. The latter peak heights signal a macroscopic fluid to crystal (freezing) transition in 3D systems with dominantly repulsive pair interactions. The freezing transition value S(qm) ≈ 2.85 is attained for hard spheres at volume fraction ϕ3D = 0.494, while the upper value 3.1 is characteristic for the freezing of complex fluids having long-range repulsive interactions such as charge-stabilized suspensions of low salt ion content. This should be contrasted with the according Hansen–Verlet freezing transition peak values for 2D systems, obtained from simulations, which span the range from S(qm) ≈ 4.4 for a hard-disk system at freezing for ϕ2D ≈ 0.70, up to S(qm) ≈ 5.7 for particles repelling each other by a soft 1/r12 pair potential where freezing occurs at ϕ2D ≈ 0.77.94–97 For super-paramagnetic particles at a planar gas–liquid interface interacting by a long-range repulsive 1/r3 pair potential, an even larger Hansen–Verlet value S(qm) ≈ 10 is found experimentally at the hexatic to crystalline phase transition point.98 Characteristic of 2D systems at freezing is a strong change of S(qm) across the freezing point.97,98
The freezing transition peak height, S(qm), of 2D systems with (dominantly) repulsive interactions is thus more than three times larger than the prepeak value S(qc) ≈ 1.4 signalling DF to EC transition in (Q)2D-SALR systems. However, one needs to distinguish the different mechanisms driving the respective transitions. Macroscopic freezing is driven by particles packing/caging effects. While the mesoscale DF to EC transition is driven by the competition of SA and LR pair forces. In this context, notice from Fig. 3(b) the pronounced increase in S(qc) with increasing area (packing) fraction, causing for fixed temperature 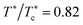 the subsequent transitions DF → EC → CP. The distinctly larger Hansen–Verlet peak heights S(qm) as compared to 3D systems, and the larger area concentration values at 2D freezing, can be attributed to stronger critical thermal fluctuations in 2D, which necessitates stronger interparticle correlations to stabilize two-dimensional crystals exhibiting quasi long-range order only.
the subsequent transitions DF → EC → CP. The distinctly larger Hansen–Verlet peak heights S(qm) as compared to 3D systems, and the larger area concentration values at 2D freezing, can be attributed to stronger critical thermal fluctuations in 2D, which necessitates stronger interparticle correlations to stabilize two-dimensional crystals exhibiting quasi long-range order only.
Having identified the prepeak height S(qc) ≈ 1.4 as an approximative indicator of the DF to EC transition in (Q)2D-SALR systems, we analyze next our simulation results for the thermal correlation length ξT depicted in Fig. 3(b) (open symbols and right ordinate). As indicated by the horizontal dashed line, the EC phase region for ϕ2D ≲ 0.4 is reached approximately, in progressing from the DF phase region, provided ξT ≳ 2σ. This threshold value implies that to form (Q)2D equilibrium clusters, ξT should exceed the Debye screening length λD in the LR Yukawa part of the SALR potential in eqn (1), whose range is fixed to λD = 1.794σ in our study. Our finding for the characteristic value of ξT is therefore similar to the one by Bollinger and Truskett for 3D-SALR systems,33 but we cautionally recall that no span of different λD values is covered in the present simulations.
It is instructive to analyze asymptotically the two-dimensional, real-space Fourier back transform,
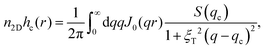 | (15) |
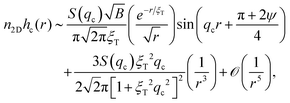 | (16) |
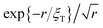 . This clarifies the physical meaning of ξT as the range of pair correlations. The second polynomial term decaying proportional to 1/r3 arises from the linear in q contribution of the denominator, 1 + ξT2(q − qc)2, of the integrand, and it dominates the asymptotics of hc(r) at large distances. The second polynomial term on the right-hand side of eqn (16) is non-zero, and the first term is oscillating away from a Fisher–Widom line where qc = 0.99 In comparison, the long-distance oscillatory part of hc(r) in 3D decays more strongly as exp{−r/ξT}/r, and the polynomial term dominating the long-distance decay of hc(r) in 3D is proportional to 1/r4. Our asymptotic 2D pair correlation expression in eqn (16) which is distinctly different from the 3D case, could prove useful for analyzing experimentally determined or simulated pair correlations in (Q)2D cluster phases such as studied, e.g., in ref. 32.
. This clarifies the physical meaning of ξT as the range of pair correlations. The second polynomial term decaying proportional to 1/r3 arises from the linear in q contribution of the denominator, 1 + ξT2(q − qc)2, of the integrand, and it dominates the asymptotics of hc(r) at large distances. The second polynomial term on the right-hand side of eqn (16) is non-zero, and the first term is oscillating away from a Fisher–Widom line where qc = 0.99 In comparison, the long-distance oscillatory part of hc(r) in 3D decays more strongly as exp{−r/ξT}/r, and the polynomial term dominating the long-distance decay of hc(r) in 3D is proportional to 1/r4. Our asymptotic 2D pair correlation expression in eqn (16) which is distinctly different from the 3D case, could prove useful for analyzing experimentally determined or simulated pair correlations in (Q)2D cluster phases such as studied, e.g., in ref. 32.
In concluding this subsection, akin to corresponding 3D criteria by Godfrin et al.,23 and Bollinger et al.,33,47 we propose the following characteristic prepeak values to localize approximately the DF to EC transition in Q2D-SALR systems: first, the prepeak height should surpass S(qc) ≈ 1.4, and second, the reduced thermal correlation length ξT/σ should be not smaller than 2.0. We caution that the characteristic values for S(qc) and ξT/σ indicating the DF to EC transition in 2D, may depend to some extent on the shape of the SALR potential. In 3D, the corresponding characteristic values appear to be insensitive to the SALR potential shape, which can be attributed to some extent to the validity of the Noro–Frenkel extended law of corresponding states for 3D particles systems with short-range attraction (SA). Whether this extended law remains valid in 2D – SA systems is the topic of an ongoing simulation study, into which the present authors are involved.
3.3 Local hexagonal ordering and cluster properties
In the following, we discuss first the local hexagonal ordering of (Q)2D-SALR particles, which in two dimensions is energetically favored, and progress next to the analysis of cluster properties in the different phases.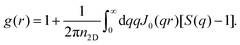 | (17) |
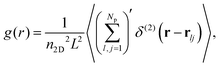 | (18) |
Fig. 4 displays LD simulation results for g(r) of clustered Q2D-SALR systems in the EC phase (upper panel, in red) and in the CP phase (lower panel, in magenta). Two state points (ϕ2D,T*) are considered for each phase, of values given in the figure. The (dashed) curves of g(r) for the lower-concentrated system in each phase are shifted upwards by two units, to render them better distinguishable from the g(r) of the more concentrated systems (solid curves). The vertical dotted lines at 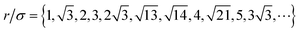 mark the next, overnext and so on interparticle distances, of ascending magnitude, of close-packed disks of diameter σ centered at the vertices of an ideal two-dimensional hexagonal (triangular) lattice. These interparticle distances are readily obtained as the vector lengths of linear superpositions of the hexagonal lattice basis vectors b1 =
mark the next, overnext and so on interparticle distances, of ascending magnitude, of close-packed disks of diameter σ centered at the vertices of an ideal two-dimensional hexagonal (triangular) lattice. These interparticle distances are readily obtained as the vector lengths of linear superpositions of the hexagonal lattice basis vectors b1 = ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) and
and 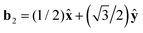 , with inner product b1·b2 = cos(60°), where
, with inner product b1·b2 = cos(60°), where ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) and ŷ are unit vectors along the orthogonal x and y directions, respectively.
and ŷ are unit vectors along the orthogonal x and y directions, respectively.
Consider first the two EC systems in the upper panel at equal effective temperature T* = 0.063. The EC g(r) for the smaller area fraction ϕ2D = 0.1 (dashed red curve, shifted upwards by two units) reveals already well-developed, longer-range inter-particle correlations, quantified by several sharp peaks in g(r) of sizeable heights, persisting to inter-particle distances r of about five times the particle diameter σ. The peaks in g(r) are centered at the above noted interparticle distances separating the vertices of a 2D hexagonal lattice, which indicates pronounced local hexagonal ordering inside the equilibrium clusters. These characteristic features of g(r) become sharpened and more pronounced for the EC system at the larger area fraction ϕ2D = 0.2 (solid red curve).
Notice, in particular, the existence of a broad and very shallow peak region of g(r) with maximum at about r ≈ 6σ (pointed at by the short black arrow in the upper panel of Fig. 4), which is close to the distance rc = 2π/qc associated with the mean distance of neighboring clusters. Incidentally, such an extended shallow peak region of g(r) at larger pair distances is also observed in multiparticle collision dynamics simulation results for 3D-SALR systems in the EC phase region.42
Consider next the two RDFs of the percolated CP systems in the lower panel of Fig. 4. These are at a temperature T* = 0.063 higher than the one of the EC systems in the upper panel, but the two area concentrations are now distinctly larger. As seen in the figure, the RDFs of the cluster percolated particles are similar to those of the EC systems, with peaks likewise positioned at the inter-vertices distances of an ideally hexagonal lattice. However, the peak heights for r/σ > 1 are in general smaller. Moreover, the shallow peak region at larger r is flattened out in comparison to the non-percolated EC systems, indicative of a more random distribution of particles at larger pair distances r ≳ 6σ (see black arrow).
Typical configurational simulation snapshots for 20 different state points (ϕ2D,T*) encompassing clustered EC and CP systems and non-clustered DF and RP systems, are displayed in Fig. 5. The local hexagonal order parameter of each individual particle is color-coded by the vertical bar on the right-hand side of the figure. This color coding of different hexagonal ordering should be distinguished from the four-colors code used throughout this work to label the four different phases. In the dispersed fluid (DF) snapshot for ϕ2D = 0.2 and T* = 0.167, enclosed in a thick blue frame, for most particles it is |q(i)6|2 ≈ 0, i.e., there is no local hexagonal order. This is the case also for the random percolated (RP) system at ϕ2D = 0.5 and T* = 0.25, whose snapshot is depicted in the top left corner of the figure enclosed by a green frame. It has no pronounced orientational order even though it has system-spanning clusters. In contrast, there is significant local hexagonal order in the 11 snapshots of the equilibrium cluster (EC) systems, shown in the figure for three area fractions and six different effective temperature values. The EC systems are the ones inside the red frames. In comparison with the DF system, there is a noticeable reduction in the fraction of particles with zero local order parameter. For the lowest-concentrated EC system at (0.1,0.125), only few hexagonally packed small clusters are formed, as reflected by a small number of particles with |q(i)6|2 ≈ 1. In fact, there is still a substantial fraction of non-clustered particles characterized by |q(i)6|2 ≈ 0. Intermediate values 0 < |q(i)6|2 < 1 characterize cluster particles with less than 6 nearest neighbors. Recall from Section 2.5 that for a cluster particle, it is more likely that its neighbors belong to its own cluster than to other ones.
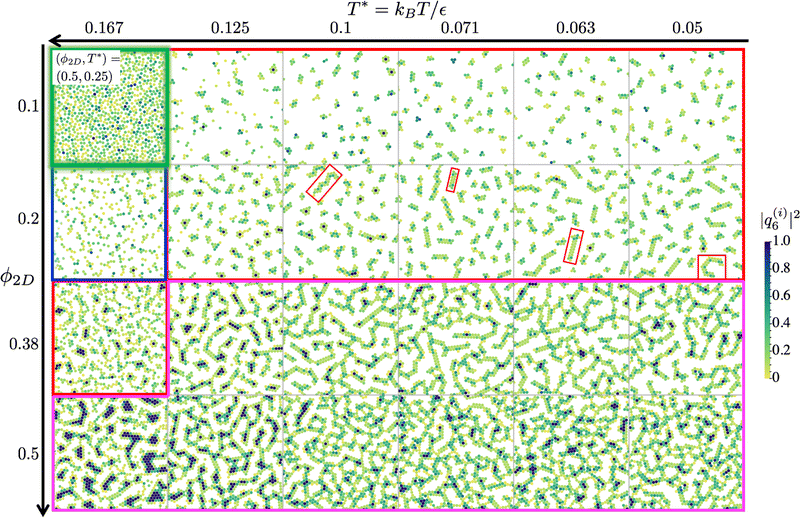 | ||
| Fig. 5 Typical configurational snapshots at four different area fractions, ϕ2D, and six different effective temperatures, T*, as indicated, except for the snapshot at the top left corner, demarcated by thick green lines, which corresponds to (ϕ2D,T*) = (0.5,0.25). The particle-specific hexagonal order parameter |q(i)6|2 ∈ [0,1] is color-coded by the vertical bar on the right hand side. Snapshots of systems representing the same phase are encompassed by a frame with color as used in Fig. 1, i.e., DF (blue), EC (red), RP (green), and CP (magenta), respectively. A selection of four double-strands hexagonal clusters are marked by small red rectangles. See main text for details. | ||
In addressing EC systems with stronger short-range attraction where T* ≲ 0.1, an interesting change in the cluster morphology is observed. Decreasing T* from 0.125 down to 0.1, the cluster shapes progressively change from mainly disk-like to elongated, whereas the cluster sizes s have not changed significantly yet. Only for T* > 0.1 and the larger area fractions ϕ2D = 0.1 and 0.2, a larger fraction of elongated clusters emerges. These clusters are mainly double-stranded, i.e., they consist of two strings of particles in a locally hexagonal arrangement. Four examples of these double-stranded hexagonal clusters are marked in Fig. 5 by red rectangles.
Double-stranded hexagonal particles arrangements are omnipresent in the cluster percolated (CP) phase. According snapshots of eleven CP systems are enclosed in Fig. 5 by a magenta-colored frame. As attraction is increased by lowering T*, the initially quite open percolated cluster network increasingly develops branch points, which are more numerous for the largest considered area fraction ϕ2D = 0.5. For the lowest temperature T* = 0.167, the system-spanning network consists to a larger degree of particles belonging to perfectly hexagonally ordered cluster segments where |q(i)6|2 ≈ 1. Particles in the double-stranded cluster segments of the percolated cluster network are typically bonded to 4 neighbors. The mean length of the segments decreases with decreasing temperature.
An analogous formation of elongated clusters has been observed previously for 3D systems under two specific conditions. First, Toledano et al.81 found elongated clusters at large particle concentrations close to and above the percolation threshold, for a long-range screening length of λD = 2σ. Second, for distinctly shorter screening lengths of a fraction of σ, quasi-one-dimensional clustering and the formation of peculiar Bernal spirals was observed both in simulations100 and experiments.5 The double-stranded hexagonal clusters seen in the Q2D-SALR systems of this work are in line with according findings in ref. 81. Their existence can be ascribed to inter-cluster interactions favoring anisotropic structures instead of isotropic ones to lower potential energy. We point out that enlarged short-range attraction induces anisotropic cluster formation even for small particle concentrations, far below the percolation threshold value. We argue that the outer cluster particles preferentially arrange themselves into elongated shapes, to counterbalance the net repulsion by the inner cluster particles, thus minimizing the system free energy. Especially at lower T*, it is energetically more favorable for additional particles to connect to a cluster along the elongated direction, since for a connection along the short cluster axis a larger kinetic barrier has to be surpassed.77,101
Additional information on the hexagonal ordering of clusters in different phases is contained in the normalized, continuous probability distribution function, P(|q6|2), of the hexagonal order parameter |q6|2 introduced in Section 2.5. Simulation results for P(|q6|2) are presented in Fig. 6, for area fractions ϕ2D = 0.1, 0.2, 0.38 and 0.5, respectively, and three effective temperatures as indicated. The hexagonal order distribution function of DF systems at high temperatures (cf., the blue curves in Fig. 6(a)–(c)) decays monotonically, expressesing lack of hexagonal ordering.
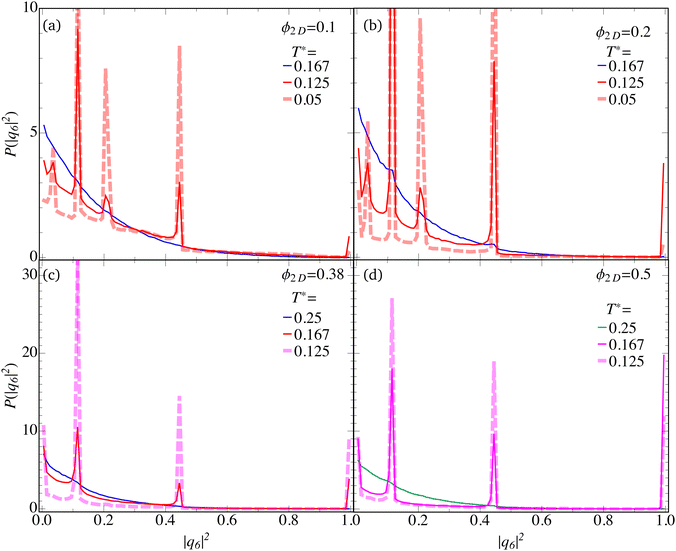 | ||
| Fig. 6 Probability density function of the hexagonal order parameter, P(|q6|2), for area fractions (a) ϕ2D = 0.1, (b) ϕ2D = 0.2, (c) ϕ2D = 0.38, and (d) ϕ2D = 0.5, respectively, and for three reduced temperature values T* as indicated. The color code indicating different phases is as in Fig. 1. For better visibility, some curves are dashed or semi-transparent. | ||
A monotonic decay of P(|q6|2) is likewise observed for the RP system (green curve) in Fig. 6(d), at state point (ϕ2D,T*) = (0.5,0.25), since different from EC and CP systems there are basically no double-stranded hexagonal cluster (segments) in RP phase systems (see Fig. 2(c)). Akin to DF systems, the particles in the higher-temperature RP phase region forming system-spanning networks are locally mobile which allows them to readjust their relative orientations.
In contrast, at lower temperatures, the presence of hexagonally ordered clusters in the EC phase systems at ϕ2D = 0.1 and 0.2 (red curves in Fig. 6(a) and (b)) is reflected by multiple sharp peaks in P(|q6|2). The smaller peak at |q6|2 = 1 is due to a modest amount of six-bonds neighboring particles inside disk-shaped clusters, as it is noticed from Fig. 5. In addition, more pronounced peaks of P(|q6|2) are located at |q6|2 = 1/9, 1/4, and 4/9. These peaks are mainly due to particles positioned at the fringe of the clusters which have less than six next neighbors. The peak at |q6|2 = 1/9, e.g., is mainly due to particles at the lateral corners of double-stranded clusters with two nearest neighbors only. Increasing the attraction strength or area fraction enhances the peak heights (dashed orange curves), since more double-stranded EC clusters of elongated shape are formed wherein the cluster particles have four or two nearest neighbors. There is an according suppression of the peak at |q6|2 = 1. Interestingly, for equilibrium cluster (EC) systems, there is a certain amount of s = 5 and s = 6 clusters with hexagonal order such that |q6|2 = 0.233 and |q6|2 = 0.198, respectively. Since these two values are close to each other, they both contribute to essentially a single peak in P(|q62|), visible in the figure at |q6|2 ≈ 0.2. In the percolated RP and CP phases, the clusters are very extended and hence this additional peak is not present any more.
Consider next P(|q6|2) of the cluster percolated (CP) systems (solid and dashed magenta curves) in Fig. 6(c) and (d), where the system-spanning, branched network is put together mainly by double-stranded hexagonal cluster segments. As seen, the peak at |q6|2 = 1/9 becomes strongly enhanced with increasing attraction, consistent with an overall enthalpic strengthening of local hexagonal order for decreasing effective temperature. An enhancement of this peak with increasing concentration at fixed temperature (such as for the EC systems), could be expected on first sight also for the CP systems in Fig. 6(c) and (d). Conversely, however, this peak decreases when ϕ2D is increased from 0.38 to 0.5. We attribute this to the increased branching of the system-spanning network, as it is visible in Fig. 2, with an accompanying loss of network particles having two nearest neighbors.
Fig. 7 shows the configuration-averaged, hexagonal order parameter, 〈|q6|2〉, i.e., the first moment of P(|q6|2), plotted as function of T*, for four different area fractions as indicated. The phase assignment of state points is marked by symbols and colors selected as in Fig. 1. State points of equal ϕ2D are connected by black line segments. Notice that particles belonging to different clusters are not clearly discriminated in computing 〈|q6|2〉, since it invokes an ensemble average over all particles. The depicted average orientational order parameter increases with decreasing temperature (T* < 0.18) towards a plateau value, whereas for ϕ2D = 0.38 and in particular for ϕ2D = 0.5 a sharp non-monotonic variation of 〈|q6|2〉 is observed in the interval T* = 0.1–0.2. In comparing the cluster percolated (CP) states at (ϕ2D = 0.5,T* ≤ 0.167) and (ϕ2D = 0.38,T* ≤ 0.125), the latter ones have more particles in double-stranded cluster segments connecting the branch points of the system-spanning clusters. This implies less overall hexagonal ordering for the lower-concentrated CP systems, as seen in Fig. 5.
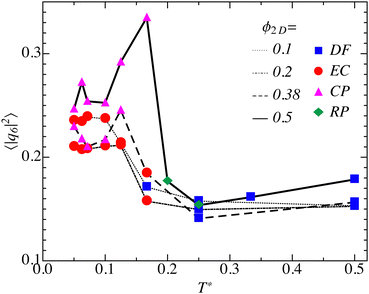 | ||
| Fig. 7 Configuration-averaged hexagonal order parameter, 〈|q6|2〉, as function of the effective temperature T*, for four different area fractions as indicated. The phase state membership of state points is indicated by symbols and colors as in Fig. 1. State points of equal ϕ2D are connected by black line segments. | ||
The temperature dependence of 〈s〉 is analyzed in Fig. 8(a) for the area fractions ϕ2D = 0.1, 0.2, 0.38 and 0.5. As expected, 〈s〉 decreases with increasing T* at constant ϕ2D, and it increases with increasing ϕ2D for constant T*, which is characteristic for the percolated cluster phase. In comparison, while still being large, the mean cluster size of the random percolated systems (green diamonds) at ϕ2D = 0.5 is smaller, which conforms with the overall flat shape of the RP phase CSD function in Fig. 1(a).
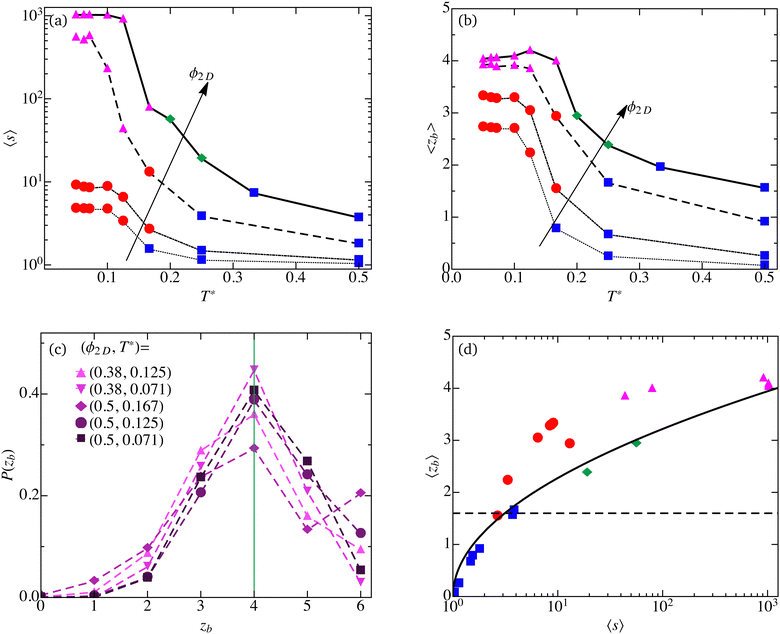 | ||
| Fig. 8 (a) Mean cluster size, 〈s〉, and (b) coordination number (average number of bonds per particle), 〈zb〉, as functions of effective temperature T* = kBT/ε. Simulation points of equal ϕ2D are linked by black line segments. The arrows point towards increasing area fraction values ϕ2D = 0.1, 0.2, 0.38, and 0.5. (c) Probability distribution of bond number per particle, P(zb), for cluster percolated (CP) phase systems at five different indicated state points (magenta symbols, linked by dashed lines). (d) Coordination number, 〈zb〉, as function of average cluster size 〈s〉, for various (ϕ2D,T*) state points. The dashed horizontal black line marks the threshold value 〈zb〉 ≈ 1.6 separating DF from EC phase systems. The thick solid black curve represents the empirical relation in eqn (19), as discussed in the main text. Symbols and colors indicating different phases are selected as in Fig. 1. | ||
Interestingly, DF systems (blue squares) at higher concentrations can have larger mean cluster sizes than EC phase systems (red circles) at lower concentration and temperature, owing to packing effects coming into play at higher particle concentration. An example in case is the DF system at (ϕ2D,T*) = (0.38,0.25) if compared with the EC system at (0.2,0.125). However, clusters of the EC phase are distinctly more persistent than the transiently formed small clusters in the DF phase. The depicted curves of 〈s〉 as functions of T* have sigmoidal shapes, reaching a plateau at low T* whose height is larger for larger ϕ2D. A close inspection of N(s) for T* < 0.1 (data not shown here) reveals that the CSD function becomes insensitive to T* in the low temperature range, while clusters of size close to the mean value 〈s〉 are more likely to occur. In this context, note that in their 3D-SALR systems analysis based on classical nucleation theory, Zhang et al.101 predict an initial increase of 〈s〉 when the attraction strength is increased, in accord with our simulation results for ε/kBT ≤ 10, while for stronger attraction (ε ≈ 16kBT) they detect a decrease in 〈s〉.
Simulation results for 〈zb〉 are shown in Fig. 8(b) as functions of T*, for area fractions as in Fig. 8(a). The coordination number curves follow the same trends as the mean cluster size curves in Fig. 8(a). In particular, they share similar sigmoidal shapes, with 〈zb〉 attaining a constant value for low temperatures. Most notably, the coordination number of the CP systems (magenta circles) at low T* is close to 4.
To elucidate this observation, we analyze next the full statistical information on the bond number zb encoded in the discrete distribution function, P(zb), of bond numbers, which is normalized such that  . Simulation results of P(zb) are depicted in Fig. 8(c) for five CP systems (magenta color) whose respective state points are given in the figure. For each CP system (state point), the values of P(zb) at the discrete bond numbers zb = 0–6 are linked by straight line segments, for better visibility. The bond number distribution functions of all five CP systems have the maximum located at zb = 4, and the value of the maximum increases with decreasing temperature for constant ϕ2D. The maximum of P(zb) at zb = 4 is due to the composition of the system-spanning network by double-stranded cluster segments, whose constituting particles are surrounded mainly by four next neighbors. While the probability for encounting monomers (i.e., for zb = 0) is close to zero, all considered CP systems have a small but non-zero probability for zb = 6. The CP system at state point (ϕ2D,T*) = (0.5,0.167) falls out of line in having a 20% probability for 〈zb〉 = 6. This enlarged probability is compensated by an accordingly smaller probability for zb = 4 such that the normalization of P(zb) is conserved.
. Simulation results of P(zb) are depicted in Fig. 8(c) for five CP systems (magenta color) whose respective state points are given in the figure. For each CP system (state point), the values of P(zb) at the discrete bond numbers zb = 0–6 are linked by straight line segments, for better visibility. The bond number distribution functions of all five CP systems have the maximum located at zb = 4, and the value of the maximum increases with decreasing temperature for constant ϕ2D. The maximum of P(zb) at zb = 4 is due to the composition of the system-spanning network by double-stranded cluster segments, whose constituting particles are surrounded mainly by four next neighbors. While the probability for encounting monomers (i.e., for zb = 0) is close to zero, all considered CP systems have a small but non-zero probability for zb = 6. The CP system at state point (ϕ2D,T*) = (0.5,0.167) falls out of line in having a 20% probability for 〈zb〉 = 6. This enlarged probability is compensated by an accordingly smaller probability for zb = 4 such that the normalization of P(zb) is conserved.
Analogous to earlier findings for 3D-SALR systems,23,100 and as suggested by the similarity of the sigmoidal curves for 〈s〉(T*) and 〈zb〉(T*) in Fig. 8(a) and (b), respectively, a monotonic relation between 〈zb〉 and 〈s〉 is expected also for Q2D-SALR systems. A qualitative reasoning for such a relation to exist has been given for the 3D case by Godfrin et al.:23 with increasing mean cluster size 〈s〉, more particles are integrated into clusters which enlarges the mean number of nearest neighbors. Moreover, and once again similar to the 3D case, for a given 〈s〉 the coordination number of clustered phases can be expected to be larger than that of non-clustered ones. That this reasoning applies also to Q2D-SALR systems is evident from Fig. 8(d), encompassing all state points considered in this work. Additionally shown in the figure as solid black line is the curve of the empirical relation23
| 〈zb〉 = 1.5(ln〈s〉)1/2, | (19) |
The discussed DF to EC transition indicator values in 2D and 3D are summarized and compared in Table 1. Incidentally, as shown for 3D-SALR systems,28 there exists also a dynamic indicator for the DF to EC transition in terms of the mean cluster lifetime, whose slope as function of the attraction strength ε changes abruptly at the transition value. Whether this dynamic indicator remains valid also for Q2D-SALR systems will be analyzed in subsequent work.76
| S(qc) | ξ T/σ | 〈zb〉c | 〈s〉c | |
|---|---|---|---|---|
| 2D | 1.4 | >2.0 | 1.6 | 3.1 |
| 3D | 2.7 | >2.0 ∧ <3.0 | 2.4 | 12.9 |
In a nutshell, we have established a comprehensive and coherent picture of cluster properties in Q2D-SALR fluids of pair potential form given in eqn (1), for a broad range of effective temperatures and concentrations. Using LD simulations, we have shown that Q2D-SALR clusters have pronounced local hexagonal order. For sufficiently strong short-range attraction, the system tends to form elongated double-stranded hexagonal clusters even at low area fractions. At higher concentrations, branched percolated networks are formed whose morphology is still dominated by the double-stranded hexagonal pattern of cluster segments. We caution that SALR potentials different from eqn (1) may lead to distinctly different (Q)2D mean cluster sizes and coordination numbers, for comparable attraction and repulsion strength parameters.
4 Conclusions
Using LD simulations, we have investigated the phase behavior and structural properties of Q2D-SALR systems of monolayers of Brownian spheres, confined to translational in-plane motion in an embedding fluid, and interacting by a generalized Lennard-Jones–Yukawa pair potential with competing short-range attractive (SA) and long-range repulsive (LR) interaction parts. A broad range of area concentrations and effective temperatures has been covered in our study. A generalized phase diagram was mapped out, by analysing the cluster size distribution function. We have identified four distinct phases: a dispersed fluid (DF), equilibrium cluster (EC), random percolation (RP), and cluster percolation (CP) phase. While these phases resemble those for 3D-SALR systems, they are distinctly different in their microstructure invoking different levels of hexagonal ordering.Using a second-order thermodynamic perturbation scheme applied to a two-dimensional reference SW fluid related to the SA part of the SALR potential, we determined a binodal curve delineating approximately the non-clustered from the cluster phases. The strong sensitivity of the binodal on the attraction range, noticed from Fig. 1(b), is likely an artifact of the perturbation scheme which in 2D is distinctly less accurate close to a critical point than in 3D. For this reason, we have refrained from studying the extended law of corresponding states (ELCS) behavior of the 2D reference fluid using perturbation theory. However, a detailed 2D Monte-Carlo simulation study of the ELCS behavior of short-range attractive SW and Mie potential fluids is in progress, in which part of the present authors are involved.
Furthermore, various indicators have been analyzed for the transition from the higher (effective) temperature DF to the lower (effective) temperature EC phase region, in comparison with their 3D analogues. The DF to EC transition is signalled by the threshold value S(qc) ≈ 1.4 of the low-wavenumber peak of the static structure factor, and the thermal correlation length ξT ≳ 2σ exceeding in particular the Debye screening length λD quantifying the repulsion range of the SALR potential. While the (Q)2D criterion for ξT agrees practically with that for 3D-SALR systems, the characteristic prepeak height S(qc) ≈ 1.4 is distinctly smaller than that in three dimensions (S(qc) ≈ 2.7). The smaller prepeak height complies with the favored local hexagonal ordering in the 2D phases, which facilitates cluster formation. Different from the 3D case, however, the Hansen–Verlet concentration peak height S(qm) ≈ 4.4–5.7 of the static structure factor signalling freezing into a 2D crystalline phase is more than three times larger than the prepeak height at SALR equilibrium cluster formation. This can be attributed to stronger thermal concentration fluctuations in 2D destabilizing crystal formation.
We have conducted a thorough analysis of local hexagonal ordering in the four detected phases. As the attraction strength ε is increased (typically up to more than 10kBT) at lower area concentrations, the finite-sized equilibrium clusters present in the EC phase change from nearly disk-like to elongated shapes. The observed elongated clusters are mainly double strands, i.e., they are composed of two parallel linear strings of particles arranged hexagonally. This type of 2D clusters resembles the Bernal spirals observed in 3D systems.100 Bernal spiral formation is either triggered by a short electrostatic screening length, or by intra- and inter-cluster interactions in the case of larger screening lengths. The double-strands pattern is dominant also in the CP phase region of large concentrations, in form of the cluster segments of the branched percolation network.
The mean cluster size, 〈s〉, increases with increasing concentration, ϕ2D, and increasing attraction strength (decreasing effective temperature T* = kBT/ε), as expected. It has a sigmoidal-shape as function of increasing attraction strength, i.e., 〈s〉 grows gradually for weak attractions, followed by a sharp increase for intermediate attractions, and finally reaching a saturation value for highly attractive particles. The coordination number, 〈zb〉, follows a similar trend as 〈s〉 for varying attraction strength. For the Q2D-SALR systems, we observe a threshold value 〈zb〉 ≈ 1.6 separating the DF from the EC phase region. The corresponding threshold value in 3D-SALR systems is 〈zb〉 = 2.4, which complies with the rigidity percolation threshold value at 3D covalent glass formation.23,102
For the EC and CP cluster phases, the probability distribution of bond numbers, P(zb), attains its maximum in the bond number range zb ≥ 2. Provided the cluster morphology is dominated by double-stranded clusters, at concentrations below or above the percolation threshold, the peak in P(zb) persistently occurs at zb = 4. Intriguingly, the empirical relation by Godfrin et al.23 between 〈zb〉 and 〈s〉 in eqn (19), which delineates cluster from non-clustered SALR phases, remains applicable also to Q2D systems. According to this relation, the DF to EC transition threshold value 〈zb〉 = 1.6 corresponds to a mean cluster size of 〈s〉 ≈ 3.1.
The presented simulation study of the phase behavior and structure of a generic Q2D-model of SALR particles allows to gain qualitative insight into the clustering properties of more complex Q2D systems such as particles confined to a fluid–fluid interface with viscosity contrast,103 and into biologically relevant membrane protein aggregation effects at the intracellular level. A natural extension of this study is the exploration of the (cluster) dynamics of the employed Q2D-SALR model, including the role of the hydrodynamic interactions for diffusion and surface-rheological properties. Work in this direction is in progress, and its results will be reported in a subsequent paper.76 Finally, as done for 3D – SALR systems using grand canonical MC simulations,104 an in-depth thermodynamic characterization of the transitions between the different 2D structural patterns could be another valuable follow-up of this work.
Author contributions
GN, JKGD and CV conceived the research project. ZT developed the simulation code, conducted the simulation, and analyzed the obtained data. GN and ZT conducted the 2nd-order perturbation theory calculations. All authors participated in discussing the results and writing the manuscript.Data availability
The simulation code and cluster analysis scripts used to generate the data in this paper are available in the referenced source.105Conflicts of interest
There are no conflicts to declare.Acknowledgements
ZT and GN thank Shibananda Das (GAU Göttingen), Kai Qi (2020 X-Lab Shanghai) and Roland G. Winkler (FZ Jülich) for insightful discussions, and for sharing their cluster analysis codes. The authors gratefully acknowledge computing time granted through JARA-HPC on the supercomputer JURECA at Forschungszentrum Jülich.106References
- A. Stradner, H. Sedgwick, F. Cardinaux, W. C. Poon, S. U. Egelhaaf and P. Schurtenberger, Nature, 2004, 432, 492 CrossRef CAS PubMed
.
- Y. Liu and Y. Xi, Curr. Opin. Colloid Interface Sci., 2019, 39, 123 CrossRef CAS PubMed
.
- J. Ruiz-Franco and E. Zaccarelli, Annu. Rev. Condens. Matter Phys., 2021, 12, 51 CrossRef CAS
.
- H. Sedgwick, S. U. Egelhaaf and W. C. K. Poon, J. Phys.: Condens. Matter, 2004, 16, S4913 CrossRef CAS
.
- A. I. Campbell, V. J. Anderson, J. S. van Duijneveldt and P. Bartlett, Phys. Rev. Lett., 2005, 94, 208301 CrossRef PubMed
.
- C. L. Klix, C. P. Royall and H. Tanaka, Phys. Rev. Lett., 2010, 104, 165702 CrossRef PubMed
.
- M. Kohl, R. Capellmann, M. Laurati, S. U. Egelhaaf and M. Schmiedeberg, Nat. Commun., 2016, 7, 1 Search PubMed
.
- N. Krishna Reddy, Z. Zhang, M. Paul Lettinga, J. K. G. Dhont and J. Vermant, J. Rheol., 2012, 56, 1153 CrossRef CAS
.
- F. Cardinaux, A. Stradner, P. Schurtenberger, F. Sciortino and E. Zaccarelli, EPL, 2007, 77, 48004 CrossRef
.
- Y. Liu, L. Porcar, J. Chen, W.-R. Chen, P. Falus, A. Faraone, E. Fratini, K. Hong and P. Baglioni, J. Phys. Chem. B, 2011, 115, 7238 CrossRef CAS PubMed
.
- F. Cardinaux, E. Zaccarelli, A. Stradner, S. Bucciarelli, B. Farago, S. U. Egelhaaf, F. Sciortino and P. Schurtenberger, J. Phys. Chem. B, 2011, 115, 7227 CrossRef CAS PubMed
.
- P. D. Godfrin, S. D. Hudson, K. Hong, L. Porcar, P. Falus, N. J. Wagner and Y. Liu, Phys. Rev. Lett., 2015, 115, 228302 CrossRef PubMed
.
- P. D. Godfrin, P. Falus, L. Porcar, K. Hong, S. D. Hudson, N. J. Wagner and Y. Liu, Soft Matter, 2018, 14, 8570 RSC
.
- J. Riest, G. Nägele, Y. Liu, N. J. Wagner and P. D. Godfrin, J. Chem. Phys., 2018, 148, 065101 CrossRef PubMed
.
- E. Yearley, P. Godfrin, T. Perevozchikova, H. Zhang, P. Falus, L. Porcar, M. Nagao, J. Curtis, P. Gawande, R. Taing, I. Zarraga, N. Wagner and Y. Liu, Biophys. J., 2014, 106, 1763 CrossRef CAS PubMed
.
- P. D. Godfrin, I. E. Zarraga, J. Zarzar, L. Porcar, P. Falus, N. J. Wagner and Y. Liu, J. Phys. Chem. B, 2016, 120, 278 CrossRef CAS PubMed
.
- A. Chowdhury, N. Manohar, G. Guruprasad, A. T. Chen, A. Lanzaro, M. Blanco, K. P. Johnston and T. M. Truskett, J. Phys. Chem. B, 2023, 127, 1120 CrossRef CAS PubMed
.
- I. Alshareedah, T. Kaur, J. Ngo, H. Seppala, L.-A. D. Kounatse, W. Wang, M. M. Moosa and P. R. Banerjee, J. Am. Chem. Soc., 2019, 141, 14593 CrossRef CAS PubMed
.
- D. Pini, A. Parola and L. Reatto, J. Phys.: Condens. Matter, 2006, 18, S2305 CrossRef CAS
.
- G. Foffi, G. D. McCullagh, A. Lawlor, E. Zaccarelli, K. A. Dawson, F. Sciortino, P. Tartaglia, D. Pini and G. Stell, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031407 CrossRef PubMed
.
- A. L. Benavides and A. Gil-Villegas, Mol. Phys., 1999, 97, 1225 CrossRef CAS
.
- G. Jiménez, S. Santillán, C. Avendaño, M. Castro and A. Gil-Villegas, Oil Gas Sci. Technol., 2008, 63, 329 CrossRef
.
- P. D. Godfrin, N. E. Valadez-Pérez, R. Castañeda-Priego, N. J. Wagner and Y. Liu, Soft Matter, 2014, 10, 5061 RSC
.
- A. J. Archer, D. Pini, R. Evans and L. Reatto, J. Chem. Phys., 2007, 126, 014104 CrossRef CAS PubMed
.
- B. Chacko, C. Chalmers and A. J. Archer, J. Chem. Phys., 2015, 143, 244904 CrossRef PubMed
.
- A. J. Archer and N. B. Wilding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 031501 CrossRef PubMed
.
- A. J. Archer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031402 CrossRef PubMed
.
- S. Das, J. Riest, R. G. Winkler, G. Gompper, J. K. Dhont and G. Nägele, Soft Matter, 2018, 14, 92 RSC
.
- Y. Zhuang and P. Charbonneau, J. Phys. Chem. B, 2016, 120, 6178 CrossRef CAS PubMed
.
- Y. Zhuang and P. Charbonneau, J. Phys. Chem. B, 2016, 120, 7775 CrossRef CAS PubMed
.
- N. G. Almarza, J. Pekalski and A. Ciach, J. Chem. Phys., 2014, 140, 164708 CrossRef CAS PubMed
.
- M. Litniewski and A. Ciach, J. Chem. Phys., 2019, 150, 234702 CrossRef CAS PubMed
.
- J. A. Bollinger and T. M. Truskett, J. Chem. Phys., 2016, 145, 064902 CrossRef
.
- M. Seul and D. Andelman, Science, 1995, 267, 476 CrossRef CAS PubMed
.
- D. Andelman and R. E. Rosensweig, J. Phys. Chem. B, 2009, 113, 3785 CrossRef CAS PubMed
.
- H. Serna, A. D. Pozuelo, E. G. Noya and W. T. Góźdź, Soft Matter, 2021, 17, 4957 RSC
.
- G. M. Grason, J. Chem. Phys., 2016, 145, 110901 CrossRef
.
- J. V. Selinger, Annu. Rev. Condens. Matter Phys., 2022, 13, 49 CrossRef CAS
.
- A. Ciach, J. Pekalski and W. T. Gozdz, Soft Matter, 2013, 9, 6301 RSC
.
- M. G. Noro and D. Frenkel, J. Chem. Phys., 2000, 113, 2941 CrossRef CAS
.
- J. Hansen, S. U. Egelhaaf and F. Platten, Phys. Chem. Chem. Phys., 2023, 25, 3031 RSC
.
- J. Riest and G. Nägele, Soft Matter, 2015, 11, 9273 RSC
.
- J.-P. Hansen and L. Verlet, Phys. Rev., 1969, 184, 151 CrossRef CAS
.
- J.-P. Hansen, Phys. Rev. A: At., Mol., Opt. Phys., 1970, 2, 221 CrossRef
.
- G. Nägele, A. J. Banchio, M. Kollmann and R. Pesché, Mol. Phys., 2002, 100, 2921 CrossRef
.
- J. Gapinski, G. Nägele and A. Patkowski, J. Chem. Phys., 2014, 141, 124505 CrossRef PubMed
.
- R. B. Jadrich, J. A. Bollinger, K. P. Johnston and T. M. Truskett, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 042312 CrossRef PubMed
.
- A. Imperio and L. Reatto, J. Phys.: Condens. Matter, 2004, 16, S3769 CrossRef CAS
.
- A. Imperio and L. Reatto, J. Chem. Phys., 2006, 124, 164712 CrossRef CAS PubMed
.
- J. C. Armas-Pérez, J. Quintana-H, G. A. Chapela, E. Velasco and G. Navascués, J. Chem. Phys., 2014, 140, 064503 CrossRef PubMed
.
- B. I. Halperin and D. R. Nelson, Phys. Rev. Lett., 1978, 41, 121 CrossRef CAS
.
- D. R. Nelson and B. I. Halperin, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 2457 CrossRef CAS
.
- K. J. Strandburg, Rev. Mod. Phys., 1988, 60, 161 CrossRef CAS
.
- K. Simons and E. Ikonen, Nature, 1997, 387, 569 CrossRef CAS PubMed
.
- I. Levental, K. R. Levental and F. A. Heberle, Trends Cell Biol., 2020, 30, 341 CrossRef CAS PubMed
.
- E. Sezgin, I. Levental, S. Mayor and C. Eggeling, Nat. Rev. Mol. Cell Biol., 2017, 18, 361 CrossRef CAS PubMed
.
- K. S. Ramamurthi, S. Lecuyer, H. A. Stone and R. Losick, Science, 2009, 323, 1354 CrossRef CAS PubMed
.
- E. Merklinger, J.-G. Schloetel, P. Weber, H. Batoulis, S. Holz, N. Karnowski, J. Finke and T. Lang, eLife, 2017, 6, e20705 CrossRef PubMed
.
- E. J. Dufourc, J. Chem. Biol., 2008, 1, 63 CrossRef PubMed
.
- O. M. Schütte, I. Mey, J. Enderlein, F. Savić, B. Geil, A. Janshoff and C. Steinem, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E6064 CrossRef PubMed
.
- R. E. Lamerton, A. Lightfoot, D. J. Nieves and D. M. Owen, Front. Immunol., 2021, 12, 564 Search PubMed
.
- R. A. Dwek, T. D. Butters, F. M. Platt, T. M. Cox and T. Harder, Phil. Trans. R. Soc. B, 2003, 358, 863 CrossRef
.
- N. Destainville, M. Manghi and J. Cornet, Biomolecules, 2018, 8, 104 CrossRef PubMed
.
- V. Wasnik, N. S. Wingreen and R. Mukhopadhyay, PLoS One, 2015, 10, 1 CrossRef CAS PubMed
.
- J. J. Sieber, K. I. Willig, C. Kutzner, C. Gerding-Reimers, B. Harke, G. Donnert, B. Rammner, C. Eggeling, S. W. Hell, H. Grubmüller and T. Lang, Science, 2007, 317, 1072 CrossRef CAS PubMed
.
- T. Gurry, O. Kahramanohgullari and R. G. Endres, PLoS One, 2009, 4, e6148 CrossRef PubMed
.
- N. Destainville, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 011905 CrossRef PubMed
.
- N. Destainville and L. Foret, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051403 CrossRef CAS PubMed
.
- P. Charbonneau and D. R. Reichman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 050401 CrossRef CAS PubMed
.
- D. F. Schwanzer and G. Kahl, J. Phys.: Condens. Matter, 2010, 22, 415103 CrossRef PubMed
.
- D. F. Schwanzer, D. Coslovich and G. Kahl, J. Phys.: Condens. Matter, 2016, 28, 414015 CrossRef PubMed
.
- C. Bores, N. G. Almarza, E. Lomba and G. Kahl, J. Phys.: Condens. Matter, 2015, 27, 194127 CrossRef PubMed
.
- Y. H. Liu, L. Y. Chew and M. Y. Yu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 066405 CrossRef CAS PubMed
.
- J.-X. Chen, J.-W. Mao, S. Thakur, J.-R. Xu and F.-Y. Liu, J. Chem. Phys., 2011, 135, 094504 CrossRef PubMed
.
- L. Q. Costa Campos, S. W. S. Apolinario and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 042313 CrossRef CAS PubMed
.
- Z. Tan, V. Calandrini, J. K. G. Dhont and G. Nägele, to be submitted Search PubMed.
- E. Mani, W. Lechner, W. K. Kegel and P. G. Bolhuis, Soft Matter, 2014, 10, 4479 RSC
.
- F. Sciortino, S. Mossa, E. Zaccarelli and P. Tartaglia, Phys. Rev. Lett., 2004, 93, 055701 CrossRef PubMed
.
-
J. Dhont, An Introduction to Dynamics of Colloids, Elsevier Science, 1996 Search PubMed
.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 1989 Search PubMed
.
- J. C. F. Toledano, F. Sciortino and E. Zaccarelli, Soft Matter, 2009, 5, 2390 RSC
.
- G. A. Chapela, F. del Río, A. L. Benavides and J. Alejandre, J. Chem. Phys., 2010, 133, 234107 CrossRef PubMed
.
- J. Torres-Arenas, L. A. Cervantes, A. L. Benavides, G. A. Chapela and F. del Río, J. Chem. Phys., 2010, 132, 034501 CrossRef CAS PubMed
.
- N. E. Valadez-Pérez, A. L. Benavides, E. Schöll-Paschinger and R. Castañeda-Priego, J. Chem. Phys., 2012, 137, 084905 CrossRef PubMed
.
- V. M. Trejos, A. Santos and F. Gámez, J. Chem. Phys., 2018, 148, 194505 CrossRef PubMed
.
- A. Martinez, M. Castro, C. McCabe and A. Gil-Villegas, J. Chem. Phys., 2007, 126, 074707 CrossRef PubMed
.
- V. M. Trejos, M. Becerra, S. Figueroa-Gerstenmaier and A. Gil-Villegas, Mol. Phys., 2014, 112, 2330 CrossRef CAS
.
- V. M. Trejos, A. Martínez and A. Gil-Villegas, Fluid Phase Equilib., 2018, 462, 153 CrossRef CAS
.
- J. Bialké, T. Speck and H. Löwen, Phys. Rev. Lett., 2012, 108, 168301 CrossRef PubMed
.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef PubMed
.
- M. Theers, E. Westphal, K. Qi, R. G. Winkler and G. Gompper, Soft Matter, 2018, 14, 8590 RSC
.
- P. S. Ruiz, Q.-L. Lei and R. Ni, Commun. Phys., 2019, 2, 1 CrossRef
.
- R. J. Baxter, J. Chem. Phys., 1968, 49, 2770 CrossRef CAS
.
- J. Q. Broughton, G. H. Gilmer and J. D. Weeks, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25, 4651 CrossRef CAS
.
- G. P. Hoffmann and H. Löwen, J. Phys.: Condens. Matter, 2001, 13, 9197 CrossRef CAS
.
- Z. Wang, A. M. Alsayed, A. G. Yodh and Y. Han, J. Chem. Phys., 2010, 132, 154501 CrossRef PubMed
.
- Z. Wang, W. Qi, Y. Peng, A. M. Alsayed, Y. Chen, P. Tong and Y. Han, J. Chem. Phys., 2011, 134, 034506 CrossRef PubMed
.
- P. Dillmann, G. Maret and P. Keim, J. Phys.: Condens. Matter, 2012, 24, 464118 CrossRef PubMed
.
-
J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Oxford University Press, 4th edn, 2013 Search PubMed
.
- F. Sciortino, P. Tartaglia and E. Zaccarelli, J. Phys. Chem. B, 2005, 109, 21942 CrossRef CAS PubMed
.
- T. H. Zhang, J. Klok, R. Hans Tromp, J. Groenewold and W. K. Kegel, Soft Matter, 2012, 8, 667 RSC
.
- H. He and M. F. Thorpe, Phys. Rev. Lett., 1985, 54, 2107 CrossRef CAS PubMed
.
- Z. Tan, V. Calandrini, J. K. G. Dhont, G. Nägele and R. G. Winkler, Soft Matter, 2021, 17, 7978 RSC
.
- A. P. Santos, J. Pekulski and A. Z. Panagiotopoulos, Soft Matter, 2017, 13, 8055 RSC
.
- Z. Tan, 2024 DOI:10.5281/zenodo.11694635.
- Jülich Supercomputing Centre, J. Large-Scale Res. Facil., 2018, 4, A132.
| This journal is © The Royal Society of Chemistry 2024 |