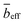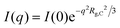Open Access Article
Open Access ArticleInfluence of counterion type on the scattering of a semiflexible polyelectrolyte†
Anish
Gulati
 a,
Jack F.
Douglas
a,
Jack F.
Douglas
 b,
Olga
Matsarskaia
b,
Olga
Matsarskaia
 c and
Carlos G.
Lopez
c and
Carlos G.
Lopez
 *ad
*ad
aInstitute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, 52056 Aachen, Germany
bMaterials Science and Engineering Division, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, USA
cInstitut Laue-Langevin DS/LSS, 71 avenue des Martyrs, CS 20156, 38042 Grenoble Cedex 9, France
dDepartment of Material Science and Engineering, The Pennsylvania State University, University Park, Pennsylvania 16802, USA. E-mail: cvg5719@psu.edu
First published on 21st October 2024
Abstract
Understanding the influence of counterion and backbone solvation on the conformational and thermodynamic properties of polyelectrolytes in solution is one of the main open challenges in polyelectrolyte science. To address this problem, we study the scattering from semidilute solutions of a semiflexible polyelectrolyte, carboxymethyl cellulose (CMC) with alkaline and tetra-alkyl-ammonium (TAA) counterions in aqueous media using small-angle neutron scattering (SANS), and small-angle X-ray scattering (SAXS), which allow us to probe concentration fluctuations of the polymer backbone and counterions. In SAXS, the calculated contrast arises primarily from the polymer backbone for both alkaline and TAA salts of CMC. In SANS, however, the contrast is dominated by the counterions for the TAA salts and the polymer backbone for the alkaline salts. Solutions are found to display a correlation peak in their scattering function, which at low concentrations is independent of counterion type. At moderate salt concentrations (c ≳ 0.1 M), the peak positions obtained from SANS and SAXS for the CMC salts with the TAA counterions differ. This divergence suggests a decoupling in the lengthscale over which the couterions and the polymer fluctuate. Upturns in the scattering intensity in the low-q region signal the presence of long-ranged compositional inhomogeneities in the solutions. The strength of these decreases with increasing counterion–solvent interaction strength, as measured by the viscosity B coefficient, and are strongest for the corresponding sodium salt of CMC.
I. Introduction
Polyelectrolytes are polymers with charged groups covalently bonded to their backbone. The presence of these charges lends them an array of properties leading to a significantly different behaviour compared to their neutral counterparts.1–3 These properties can be further modified by altering the interaction between the charges by, for instance, the addition of low molecular weight salts, or by varying the counterion type.3–14 The importance of biological polyelectrolytes such as DNA, RNA, hyaluronic acid or proteoglycans makes understanding the physics of charged polymers crucial for understanding fundamental biological phenomena and molecular interactions.15,16The role of counterion solvation, which was usually not considered in early polyelectrolyte solution theories,17–22 has received increasing attention in recent years5,23–27 and this phenomenon is thought to be responsible for some hitherto unexplained phenomena in polyelectrolyte solutions, such as the low-q upturn observed in the structure factor of solutions of low ionic strength. Several recent simulation studies discuss the effect of counterion solvation on the properties of polyelectrolyte solutions. For example, it is known that the relative quality of the solvent for the polymer backbone and counterions can influence the distribution of counterions around the chain.28 Using a coarse-grained model of polyelectrolyte solutions with explicit solvents, Chremos and Douglas concluded that with increasing affinity of the counterions to the solvent, the solution becomes increasingly heterogeneous due to supramolecular chain association.23,29 This phenomenon naturally gives rise to a stronger upturn in the scattering intensity at low-q, a phenomenon ubiquitously observed in synthetic polyelectrolytes, as well as proteins, and many other biomolecule solutions.23 This finding was further backed by another molecular dynamics simulation study that investigated the effect of altering the relative solvation of the counterions and the backbone. The latter study indicated a stronger upturn at low-q for a preferential solvation of the counterion.25 Another molecular dynamics (MD) simulation study found that the stronger solvation of the charged species (counterion and backbone alike) leads to the disappearance of the correlation peak and a strong low-q upturn,24 a behaviour observed in aggrecan30 and other highly charged bottlebrush polyelectrolyte molecules in which the sidegroups are highly hydrophilic. This result was interpreted as arising from the appearance of short and long-ranged attractive forces induced by the better-solvated counterions, which leads to the formation of heterogeneous multichain structures. The work of Wang et al.31 provides additional evidence for the importance of solvent-specific effects32 on the electrostatic interactions between charged objects in solution, that are not captured by continuum electrostatics. According to their model, polar solvents can order around charged objects in a way that strongly depends on the sign of the charge on the object, suggesting another level of subtlety in the interactions between charged particles and polymers in solution.
The existence and behaviour of the multichain domains in polyelectrolyte solutions have been studied in the literature, primarily using dynamic light scattering (DLS).3,5,33–40 These domains have been recognised as the source of the slow mode on the DLS correlation curves, and the low-q upturn in small-angle neutron scattering (SANS)/small-angle X-ray scattering (SAXS) curves38,41,42 and have been found to exist for a range of systems. Their response to different stimuli, such as ionic strength34 and mechanical filtration,36,39 and their stability over time37 have been reported. These domains have been found to be stable for long periods of time under no-added salt conditions for systems such as sodium polystyrene sulfonate, and ionised solutions of polyacrylic acid and polymethacrylic acid.37 Filtering has been shown to transiently alter their properties and non-equilibrium effects have sometimes been observed.36,39
In the present work, we study the scattering of carboxymethyl cellulose aqueous solutions as a function of counterion type. Carboxymethyl cellulose (CMC), usually employed as its sodium salt NaCMC, is a weak, semiflexible polyelectrolyte which is widely employed as a rheology and texture modifier in food, drinks, pharmaceutical products and in drilling muds.43–46 With a market size of over USD 1 billion,47 it is the most widely employed cellulose ether as well as the most important ionic derivative of cellulose.48
The monomer structure of CMC is shown in Fig. 1. R = H in all three positions corresponds to cellulose. The degree of substitution (DS) is the average number of R = CH2COO−X+ groups per monomer, out of a maximum of 3. The structural and rheological properties of NaCMC have been extensively studied in earlier publications.49–59 Grades with DS ≳ 1 are labelled as “highly substituted” and usually display “hydrophilic” behaviour in aqueous solution,52,54 meaning that inter-chain associations are relatively weak and no crystalline aggregates of unsubstituted cellulose are present.50,51,60–63 In aqueous solution, NaCMC displays a locally rigid conformation,50,51,64 independent of degree of substitution. Its rheological properties in excess salt show similar features to those of other semiflexible polysaccharides (neutral or charged).43,65,66 Despite extensive investigations into the properties of CMC, literature on the influence of counterion on the solution behaviour of CMC are limited to a few studies on their electrical conductivity.67,68
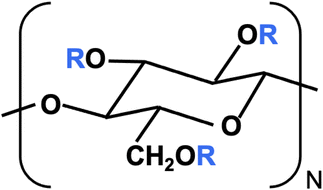 | ||
| Fig. 1 Carboxymethyl cellulose monomer where R = H or CH2COO−X+ and X+ is the counterion. The degree of substitution (DS) is the number of R = CH2COO−X+ per monomer, out of a maximum of three. | ||
II. Background theory
The relatively expanded nature of polyelectrolytes in salt-free solutions, compared to their uncharged counterparts, means that the overlap concentration2,52 is very low, and semidilute or concentrated solutions are usually of interest. The scaling theory of Dobrynin et al.17 models semidilute polyelectrolyte solutions based on the assumption of well-dispersed chains with a characteristic mesh size known as the correlation length ξ, which, in the absence of added salts, is predicted to scale with polymer concentration (c) as,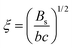 | (1) |
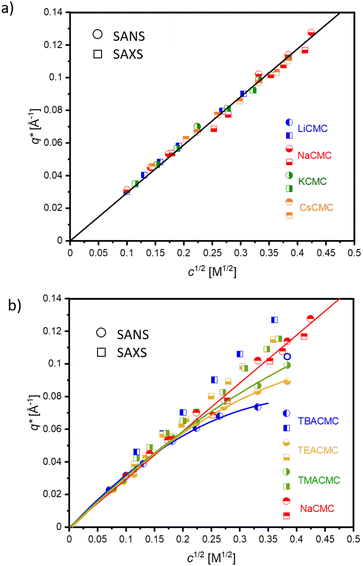
For example, the predicted variation of ξ ∝ c−1/2 from this model is consistent with reports on many experimental studies on flexible,2,69–72 semiflexible50,51,64,73 and rigid polyelectrolyte systems.74 In this scaling model, the correlation length (ξ) characterizes the lengthscale at which polyelectrolyte chains become flexible, in agreement with experimental observations for polystyrene sulfonate.75
Although a scaling exponent having a magnitude near 1/2 is common, this exponent is not universal. Values of this scaling exponent near 1/3 have been observed in mucin bottlebrush polyelectrolytes76 and proteoglycan molecules from cartilage77 where strongly hydrating side-groups exist, as in the case of aggrecan. This exponent also matches the observation of Kaji et al. for polyelectrolytes in dilute solutions.78,79 Chremos and Douglas29 found by simulation with an explicit solvent that the magnitude of this scaling exponent can be reduced from 1/2 when the counterions or polymer are strongly hydrating and a smaller magnitude exponent has been observed in polyionene solutions with certain counterions.80 Simulation and measurement also indicated an exponent having a value near 1/3 in star polymer polyelectrolytes81,82 and an exponent value near 1/3 has been observed in dendrimer polyelectrolytes,83,84 globular proteins85,86 and other relatively compact-shaped charged polymers and charged particles such as charged micelles.87,88 Changes in the value of the polyelectrolyte peak scaling exponent might then provide a clue about new physics in these solutions becoming important. We will see this situation arise below in our discussion of tetraalkylammonium counterions of carboxymethyl cellulose.
A. Partial structure factors and scattering contrast
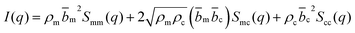 | (2) |
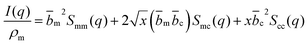 | (3) |
The contrast factors for SANS are given by,
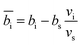 | (4) |
If the concentration fluctuations of counterions and the polymer backbone occur on the same lengthscale, which is expected, for example, if a large fraction of the counterions are condensed onto the backbone, we can simplify eqn (2) using the approximation Sm,m(q) ≃ Sm,c(q) ≃ Sc,c(q). The structure factor can then be calculated from the scattering intensity as:
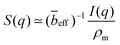 | (5) |
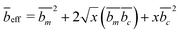 | (6) |
has units of length squared.
B. Scattering functions for semidilute polyelectrolyte solutions
The total structure factor S(q) can be written as the sum of an interparticle contribution, known as the form factor (P(q)) and an intermolecular term H(q):| Sm,m(q) = NP(q) + ρH(q) | (7) |
For sufficiently high wave-vectors,89,90H(q) ≃ 0, and we approximate Sm,m ≈ NP(q). Chains are expected to be in a rigid configuration inside the correlation blob, so that for q ≫ 2π/ξ, P(q) may be approximated by the form factor of a rod:89
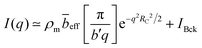 | (8) |
Polyelectrolytes, normally, display a peak in their scattering function at wave-vector q*, which defines a correlation length as:17,19
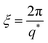 | (9) |
For wave-vectors Rg,C ≲ q ≪ 2π/q*, where Rg,C is the radius of gyration of the clusters, the scattering intensity can be described by a power-law:
| I(q) = Dq−m | (10) |
For sufficiently small wave-vectors q ≲ 1/Rg,C, the Guinier law describes the scattering intensity:
III. Materials and methods
Materials
NaCMC was purchased from Sigma-Aldrich, with a nominal mass average molar mass (Mw) of 250 kg mol−1 and degree of substitution (DS) = 1.2. Characterisation of the sample in an earlier study96 yielded Mw ≃ 2.1 × 105 g mol−1 and DS = 1.3. The Spectra/Por dialysis membranes98 with a Molecular Mass Cut-Off of 6 to 8 kDa were used and were purchased from VWR. A viscosity standard solution N2 purchased from VWR. The bases used for the preparation of CMC salts were acquired from Sigma Aldrich and their characteristics are reported in Table ST2 in the ESI.†Preparation of CMC salts
As a precursor to the CMC salt preparation, the NaCMC was converted to its acid form (HCMC) by displacement using 0.1 mol L−1 HCl at pH ≈ 2 and then dialysing the resulting solution against DI water to remove the excess ions. The end point of the dialysis was determined by examining the conductivity of the dialysis bath at the point when the conductivity stayed below 2 μS cm−1 beyond, at least, 4 h from the last exchange. The resulting solution was frozen using liquid nitrogen and dried under vacuum at a pressure of 0.4 mbar for 72 h to 96 h.For the preparation of the CMC salts with alkali metal and quaternary ammonium counterions, the resulting dry HCMC was neutralized with excess of the respective bases. The neutralized solutions were again subjected to the same dialysis and freeze-drying process to obtain the pure salts.
Sample preparation
The CMC salts were stored in the vacuum freeze dryer for ≈24 h before any samples were prepared. The samples were prepared in polypropylene microcentrifuge tubes, previously washed with deionized (DI) water and dried at 60 °C. All the sample components were added by weight using a weighing balance with a least count of 0.1 mg and, therefore, a typical error of ±0.05 mg.Densitometry
The density measurements were performed using the Anton Paar DMA 5000 densitometer with a least count of 10−6 g cm−3. The accuracy of the instrument was calibrated using DI water.Thermogravimetric analysis
The PerkinElmer STA 6000 was used for the thermogravimetric measurements to estimate the residual water content in all the CMCs. The sample temperature was increased to 120 °C at 10 °C min−1, and was allowed to reach equilibrium. The temperature was then increased to 550 °C to estimate the point of CMC degradation.Conductivity and pH
The conductivity measurements were made using the Mettler Toledo S47 SevenMulti conductivity meter. All the pH measurements were made using the Metrohm 744 pH meter at room temperature.Small-angle neutron scattering
The SANS measurements were carried out at NG30m at NIST Center for Neutron Research (NCNR), Maryland, USA, D11 at Institut Laue-Langevin (ILL), Grenoble, France and SANS-1 at Paul Scherrer Institute (PSI), Switzerland. The sample-to-detector distances (SDD) used at NCNR were 1.5 m and 7 m which covered a q-range of (0.003 to 0.42) Å−1 (λ = 6 Å). The measurements at D11 were performed at five different SDDs (1.7 m, 5.5 m, 8 m, 12 m and 28 m) covering a q-range of (0.002 to 0.55) Å−1 (λ = 6 Å). The measurements at SANS-1 were conducted at two different SDDs (3 m and 11 m) covering a q-range of (0.005 to 0.36) Å−1 (λ = 6 Å). The samples were measured in banjo cells with path lengths of 1 mm, 2 mm or 5 mm depending on polymer concentration.Small-angle X-ray scattering
The SAXS measurements were carried out at the SPring-8 synchrotron facility, Hyogo, Japan and at the Institute of Physical Chemistry, Rheinisch-Westfälische Technische Hochschule (RWTH) Aachen using an in-house instrument. The sample-to-detector distances of 2 m and 4 m were used at SPring-8, providing a q-range of (0.0023 to 0.2) Å−1 using a beam energy of 10 keV. A Peltier heating system was used to maintain the sample temperature at 25 °C. The in-house instrument consists of a 3-pinhole S-Max3000 system with a MicroMax002+ X-ray microfocus generator from Rigaku and a 2D multiwire detector with an active diameter of 200 mm. The sample-to-detector distance of 2.6 m was used, which covered a q-range of (0.005 to 0.4) Å−1 (λ = 1.54 Å, Cu radiation). The samples were measured in sealed 1.5 mm (in-house experiments) or 2 mm (synchrotron experiments) borosilicate capillaries from WJM Glas Müller GmbH.All the measurements were performed at 25 °C, except the conductivity and pH measurements, which were carried out at room temperature (≈22 °C). All the data for this study are provided in tabulated form in the ESI.†
IV. Results and discussion
A. Density measurements
The partial molar volume (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) of various CMC salts were determined from density measurements of solutions using:99
) of various CMC salts were determined from density measurements of solutions using:99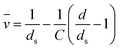 | (11) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) for the various counterions studied, see Table 1. Values for the PMV of counterions available in literature have also been provided in the table. These are found to be in reasonable agreement with our data except for K+ and Cs+.
for the various counterions studied, see Table 1. Values for the PMV of counterions available in literature have also been provided in the table. These are found to be in reasonable agreement with our data except for K+ and Cs+.
![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) i) with respect to D2O (SANS) and H2O (SAXS) and partial molar volume for the CMC monomer (DS = 1.3) and the various counterions studied. The values in brackets for the PMV are taken from literature
i) with respect to D2O (SANS) and H2O (SAXS) and partial molar volume for the CMC monomer (DS = 1.3) and the various counterions studied. The values in brackets for the PMV are taken from literature
| Scattering unit | b i SANS [fm] | b i SAXS [fm] |
![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) i
2 SANS [fm2]
i
2 SANS [fm2] |
![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) i
2 SAXS [fm2]
i
2 SAXS [fm2] |
PMV (lit.) [cm3 mol−1] |
|---|---|---|---|---|---|
| a Ref. 100. b Ref. 101. | |||||
| CMC− monomer | 54.39 | 360.39 | 7680 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
133.90 |
| Li+ | −1.90 | 5.64 | 7.7 | 18.8 | 0.83a |
| Na+ | 3.63 | 28.2 | 1.0 | 591 | 2.47 (2.68a) |
| K+ | 3.67 | 50.7 | 110 | 893 | 13.3 (6.63a) |
| Cs+ | 5.42 | 155 | 960 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
34.3 (12.39a) |
| TMA+ | −8.91 | 121 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
418 | 90.6 (84.85b) |
| TEA+ | −12.24 | 211 | 3620 | 2610 | 168 (143.53b) |
| TBA+ | −18.90 | 392 | 141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
337 (271.18b) |
Table 1 lists the contrast factors for the CMC monomer and the various counterions studied in D2O. Both SANS and SAXS contrast factors for alkali salts in D2O and H2O respectively are dominated by the polymer backbone so that I(q) ∝ Sm,m(q), with the exception of CsCMC, where the SAXS intensity contains a significant contribution from the counterions. On the other hand, for the TAA salts in D2O, the SANS contrast is dominated by the counterions, such that I(q) ∝ Sc,c(q). The SAXS contrast for the TAA salts in H2O, however, arises primarily from the polymer backbone (eqn (2)), with the exception of TBACMC, for which the backbone and counterion contribute similarly to S(q). The contrast conditions are summarised in Table 2.
B. Influence of counterion on scattering properties of CMC
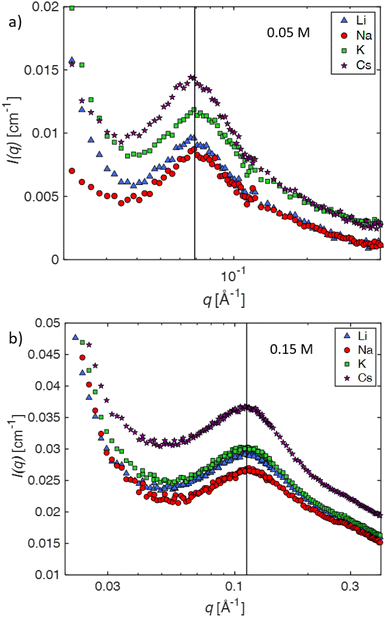
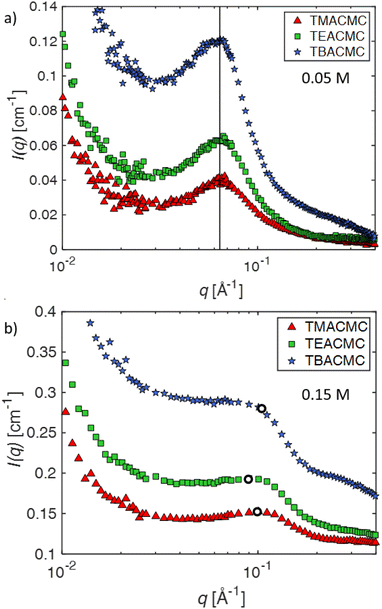
The SANS profiles of CMC with tetra-alkyl-ammonium counterions, where the alkyl chain = C1, C2 and C4 in D2O solutions are plotted in Fig. 3. At c = 0.05 mol L−1, there is no discernible influence of counterion type on the position of the peak position q* (Fig. 3(a)). At high concentrations, however, the correlation peak broadens and moves to a lower q for the larger counterions. For sufficiently high concentrations (c ≃ 0.15 mol L−1), the peak in TBACMC solutions develops into a scattering plateau (i.e. no discernible maxima) where a polynomial fit is no longer possible. Here, we fit two linear functions to either side of the scattering plateau, following the approach of Salamon et al.,73 and take their point of the intersection to be the ‘position’ of the scattering plateau (see Fig. S4 in the ESI†). If this method is applied for samples with a distinct peak, the difference in q* compared to the value extracted from fitting a polynomial is always smaller than ≈20%. For reference, the viscosity B-coefficients of tetraalkylammonium ions, characterizing their relative strength of the hydration102,103 are listed in Table 3. These complex ions are strongly “kosmotropic” (i.e. have large positive B-coefficient values) according to the conventional nomenclature, but this designation must be made with caution for large counter-ions since large positive concentration virial coefficients for the viscosity, i.e., the “intrinsic viscosity”, are characteristic of polymer solutions. The TAA counter-ion molecules have an alkane polymer component that probably does not hydrate very well so that a large contribution to the viscosity B-coefficient probably derives from a hydrodynamic effect rather than from the strength of the ion–water interaction as in the case of alkaline and other elemental ions.27
| Ion | Jones–Dole B coefficient [L mol−1] |
|---|---|
| Li+ | 0.146 |
| Na+ | 0.085 |
| K+ | −0.009 |
| Cs+ | −0.047 |
| TMA+ | 0.123 |
| TEA+ | 0.385 |
| TBA+ | 1.275 |
The concentration dependence of the correlation length for the alkaline salts of CMC agrees well with the scaling prediction (eqn (1)), as expected based on previous SANS and SAXS studies on aqueous solutions of NaCMC.50,51,64 Applying eqn (1) and (9), the stretch parameter is estimated to be in the range of Bs ≃ 1.3 ± 0.1 for all samples, see Table 4. These values are similar to the stretch parameter of Bs ≃ 1.1 ± 0.1 reported by Lopez et al.50 for solutions of NaCMC with DS ≃ 1.06 in D2O and Bs ≃ 1.25 and reported by Hou et al.105 for NaCMC with DS ≃ 0.98 in H2O.
| CMC salt | B s,SANS | c-range [M] | B s,SAXS | c-range [M] |
|---|---|---|---|---|
| LiCMC | 1.4 | 0.05–0.147 | 1.24 | 0.009–0.087 |
| NaCMC | 1.2 | 0.01–0.18 | 1.40 | 0.033–0.15 |
| KCMC | 1.36 | 0.05– 0.147 | 1.27 | 0.012–0.096 |
| CsCMC | 1.43 | 0.05–0.147 | 1.31 | 0.021–0.132 |
| TMACMC | 1.22 | 0006–0.033 | 1.08 | 0.013–0.126 |
| TEACMC | 1.32 | 0.006–0.05 | 1.07 | 0.012–0.119 |
| TBACMC | 1.18 | 0.003–0.017 | 0.92 | 0.025–0.121 |
The independence of the peak position on counterion type for the alkaline series contrasts with results for aqueous solutions of ionenes, where the scaling of the peak position with concentration of halide salts of the same polymer depends on the counterion.80,106,107 Note that Kaji et al. report a weak dependence of the peak position on counterion type for the alkaline salts of poly(vinyl hydrogen sulfate).108 These results are apparently in line with the simulations observations of Chremos and co-workers discussed previously indicating that stronger ion and polymer solvation, acting together, can alter the concentration scaling of q*.
The tetra-alkyl-ammonium salts of CMC display similar behaviour to the alkaline salts at low concentrations: the correlation length is independent of ion type, matching the values observed for alkaline CMCs (see Fig. 4(b)), the maxima in Smm(q) and Scc(q) coincide and the common scaling q* ∼ c1/2 is observed. These observations accord with literature reports for polystyrene sulfonate (PSS). Prabhu et al. report the correlation lengths for TMAPSS in D2O (3.7 < c < 46 g L−1), measured by SANS,109 which are nearly identical values to those reported for NaPSS in H2O obtained using SANS and SAXS.78,110–113
At high concentrations, however, the behaviour of TAA salts differs in several ways from those of alkaline salts. First, the peak position in the SANS signal, which measures Scc(q), shifts to lower q values and its shape becomes broader, eventually morphing into a scattering “plateau”. The magnitude of these changes depends on the length of the alkyl chain, with larger ions showing more pronounced effects, see for example Fig. 4b. The maxima in the SAXS signal, which corresponds approximately to Smm(q) is almost the same as for the alkaline counterions. These results indicate that (1) polymer correlation scale (inferred from q*) is not greatly altered by the nature of the counterions and (2) the concentration fluctuations of the polymer backbone and the counterions become decoupled at high concentrations if the counterions are strongly kosmotropic, i.e., relatively large positive values of B, see Table 3. For a discussion on the decoupling of polymer and charge concentration fluctuations, see also ref. 114 and 115.
The partial molar volume of the TBA+ ion can be used to calculate an ionic radius of ≃0.5 nm, in agreement with the radius expected from bond lengths. At the highest concentrations studied, this corresponds to the bare ions occupying a volume fraction of ≃0.05. If a hydration volume corresponding to 20–40 water molecules per ion is added,116 the volume fraction of the hydrated TAA ions increases to 0.1–0.15. This might be sufficient for the hydrated ions to percolate, which we anticipate influences the average intermolecular potential between the polyelectrolytes deriving from the competitive association of hydrated counter-ions and water molecules with the polyelectrolyte chains. In particular, we expect the extended counter-ion cloud found for low-concentration polyelectrolyte solutions to become delocalized when the counter-ion concentration becomes sufficiently large that their hydration layers percolate, suppressing the large-scale fluctuations in the concentration of the counter-ions about the polyelectrolyte chains responsible for the long-range attractive interactions between polymers having a like charge sign. However, this proposed mechanism of the polyelectrolyte peak suppression remains to be checked by molecular dynamics simulation and we simply offer this as a tentative hypothesis.
An important implication of this hypothesis for the progressive suppression of the polyelectrolyte peak at high salt concentrations seems to be supported by our measurements is that percolation concentration or “overlap concentration” of the counter-ion molecules should govern the concentration at which this transition in polyelectrolyte solution should occur. As in the case of neutral polymer solutions, the concentration corresponding to the TAA counterion overlap becomes smaller when their molecular mass becomes larger. We note that the suppression of the polyelectrolyte peak at high salt concentrations is a well-known trend in polyelectrolyte solutions,117 although it is by no means established that this trend is simply due to charge screening in the simple Debye–Huckel sense. Here, we are simply suggesting that the percolation of the hydrated counterions is influencing the strength of the many-body intermolecular interaction strength between the polyelectrolytes.
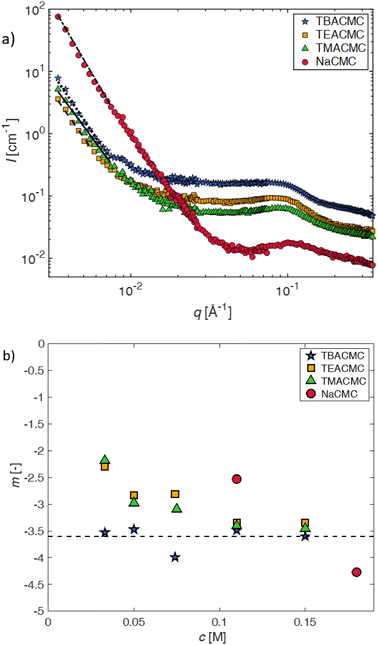 | ||
| Fig. 5 (a) SANS scattering intensity of CMC with different counterions for a fixed concentration of c = 0.11 mol L−1. Lines are power-law fits (eqn (10)) to the low-q upturn region. (b) Best-fit exponent -m as a function of polymer concentration for various salts of CMC. | ||
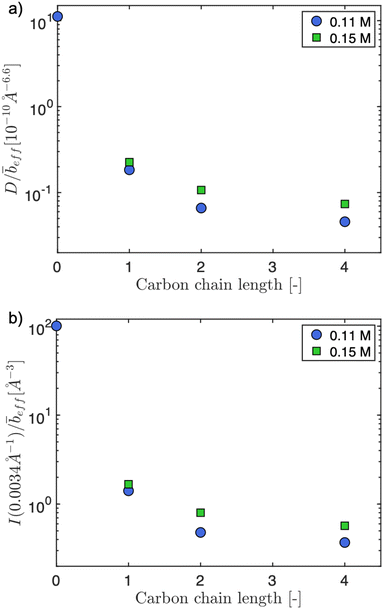
The pre-factor, D, to the low-q power-law in eqn (10) is plotted as a function of ion type in Fig. 6(a) for c = 0.11 mol L−1 and c = 0.15 mol L−1. For this plot, we use fits with the exponent m fixed to a value of 3.6, so that the units of the pre-factor are independent of concentration. We have divided D by ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) eff to reduce the influence of neutron contrast. Further, we compare the scattering intensity at the lowest measured wave vector (q = 0.0034 Å−1) at c = 0.11 mol L−1 for the various salts studied. Lacking a more rigorous framework to evaluate the low-q region, both D/
eff to reduce the influence of neutron contrast. Further, we compare the scattering intensity at the lowest measured wave vector (q = 0.0034 Å−1) at c = 0.11 mol L−1 for the various salts studied. Lacking a more rigorous framework to evaluate the low-q region, both D/![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) eff and I(0.0034 Å−1)/
eff and I(0.0034 Å−1)/![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) eff serve as measures for the ‘clustering strength’.118–121 The trends observed in Fig. 6 therefore support an earlier finding by molecular dynamics simulations29 that preferential counterion solvation can lead to enhanced clustering in polyelectrolyte solutions. The general increase of the clustering strength parallels the growth of the viscosity B-coefficient values122 of the tetra-alkylammonium counterions.
eff serve as measures for the ‘clustering strength’.118–121 The trends observed in Fig. 6 therefore support an earlier finding by molecular dynamics simulations29 that preferential counterion solvation can lead to enhanced clustering in polyelectrolyte solutions. The general increase of the clustering strength parallels the growth of the viscosity B-coefficient values122 of the tetra-alkylammonium counterions.
V. Conclusions
We have studied the scattering properties of semiflexible polyelectrolyte carboxymethyl cellulose with different counterions in aqueous solutions. The correlation peak of the various alkaline salts studied follows the same q* ∝ c1/2 scaling law and the peak positions measured by SANS and SAXS agree, indicating that concentration fluctuations of the polymer backbone and counterions occur on approximately the same lengthscales.Solutions with hydrophobic counterions display similar features to the alkaline salts at low concentrations. However, beyond a characteristic concentration, a different scaling behaviour emerges. First, in this regime, the c-dependence of q*, obtained from SANS, becomes increasingly weaker with an increasing degree of counterion hydrophobicity. However, the q* ∝ c1/2 scaling persists in the results obtained from SAXS, even for the most hydrophobic counterion studied. We interpret this as a “decoupling” of the concentration fluctuations of the polymer backbone and counterions, but we, currently, lack any convincing explanation for the physical mechanism underpinning this behaviour. A further examination of the nature of counterion-solvent interactions using other techniques, such as rheology, could provide better insights into this behaviour. In this regard, a recent study of polystyrene sulfonate with sodium and tetra-alkyl ammonium counterions showed that the viscosity of PSS salts is independent of counterion type at low (c ≲ 0.1 M) concentrations, but differs strongly at high concentrations.12 Another key observation at higher concentrations is the broadening of the SANS correlation peaks with increasing counterion hydrophobicity. This is accompanied by a shift in the correlation peak position as well.
As with other polyelectrolyte systems, the solutions studied here displayed an upturn at low q, which signals the presence of large-scale inhomogeneities in the solution. A comparison of solutions of sodium and tetra-alkyl-ammonium salts of CMC revealed that the clustering intensity, when adjusted for contrast, decreases as the ions become larger and more hydrophobic. The nature of hydration in these complex ions requires further investigation.
Author contributions
CRediT: Anish Gulati: formal analysis, investigation, data curation, methodology, writing – original draft, writing – review & editing. Jack F. Douglas: formal analysis, investigation, writing – original draft, writing – review & editing. Olga Matsarskaia: data curation, investigation, methodology, writing – review & editing Carlos G. Lopez: conceptualization, formal analysis, funding acquisition, investigation, data curation, methodology, supervision, writing – original draft, writing – review & editing.Data availability
All the scattering datasets from this study are included in xls format as ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the support of the National Institute of Standards and Technology, U.S. Department of Commerce, in providing the neutron research facilities used in this work. We thank Dr Susan Krueger for assistance during the SANS experiments at NIST and help with data reduction. We thank the ILL (doi: 10.5291/ILL-DATA.9-11-1994 and doi: 10.5291/ILL-DATA.9-13-985), the Paul-Scherrer Institute and the SPring-8 synchrotron radiation facility (proposal number: 2024A1203) for beamtime and Dr. Noboru Ohta and Dr. Albert Mufundirwa for their help with the SAXS experiments. We also thank Prof. Takaichi Watanabe (Okayama University), Prof. Atsushi Matsumoto (University of Fukui), Can Hou and Hannes Luhmann (RWTH Aachen University) for their help with the experiments at Spring-8. The authors acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG) (project: GO 3250/2-1). Certain commercial equipment, instruments, software, or materials are identified in this paper to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.References
- A. V. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118 CrossRef CAS.
- R. H. Colby, Rheol. Acta, 2010, 49, 425–442 CrossRef CAS.
- C. G. Lopez, A. Matsumoto and A. Q. Shen, Soft Matter, 2024, 20, 2635–2687 RSC.
- C. G. Lopez, F. Horkay, M. Mussel, R. L. Jones and W. Richtering, Soft Matter, 2020, 16, 7289–7298 RSC.
- Y. Zhang, J. F. Douglas, B. D. Ermi and E. J. Amis, J. Chem. Phys., 2001, 114, 3299–3313 CrossRef CAS.
- E. Dubois and F. Boué, Macromolecules, 2001, 34, 3684–3697 CrossRef CAS.
- J.-S. Jan and V. Breedveld, Macromolecules, 2008, 41, 6517–6522 CrossRef CAS.
- I. Kagawa and R. M. Fuoss, J. Polym. Sci., 1955, 18, 535–542 CrossRef CAS.
- M. Beer, M. Schmidt and M. Muthukumar, Macromolecules, 1997, 30, 8375–8385 CrossRef CAS.
- R. Schweins, J. Hollmann and K. Huber, Polymer, 2003, 44, 7131–7141 CrossRef CAS.
- A. Gulati, M. Jacobs, C. G. Lopez and A. V. Dobrynin, Macromolecules, 2023, 56, 2183–2193 CrossRef CAS.
- A. Gulati and C. G. Lopez, ACS Macro Lett., 2024, 13, 1079–1083 CrossRef CAS PubMed.
- A. Matsumoto and A. Q. Shen, Soft Matter, 2022, 18, 4197–4204 RSC.
- E. Seyrek and P. Dubin, Adv. Colloid Interface Sci., 2010, 158, 119–129 CrossRef CAS PubMed.
- A. Katchalsky, Biophys. J., 1964, 4, 9–41 CrossRef CAS.
- M. Rubinstein and G. A. Papoian, Soft Matter, 2012, 8, 9265–9267 RSC.
- A. V. Dobrynin, R. H. Colby and M. Rubinstein, Macromolecules, 1995, 28, 1859–1871 CrossRef CAS.
- P. Pfeuty, J. Phys. Colloq., 1978, 39, C2-149 CrossRef.
- P. D. Gennes, P. Pincus, R. Velasco and F. Brochard, J. Phys., 1976, 37, 1461–1473 CrossRef.
- M. Yamaguchi, M. Wakutsu, Y. Takahashi and I. Noda, Macromolecules, 1992, 25, 470–474 CrossRef CAS.
- A. V. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118 CrossRef CAS.
- A. V. Dobrynin and M. Jacobs, Macromolecules, 2021, 4, 1859–1869 CrossRef.
- A. Chremos and J. F. Douglas, J. Chem. Phys., 2017, 147, 241103 CrossRef.
- A. Chremos and F. Horkay, Phys. Rev. E, 2020, 102, 012611 CrossRef CAS PubMed.
- A. Chremos and J. F. Douglas, J. Chem. Phys., 2018, 149, 163305 CrossRef PubMed.
- C. Hotton, G. Ducouret, J. Sirieix-Plénet, T. Bizien, L. Porcar and N. Malikova, Macromolecules, 2023, 56, 923–933 CrossRef CAS.
- J. A. Clark and J. F. Douglas, J. Phys. Chem. B, 2024, 128, 6362–6375 Search PubMed.
- A. Chremos and J. F. Douglas, Gels, 2018, 4, 20 CrossRef PubMed.
- A. Chremos and J. F. Douglas, J. Chem. Phys., 2018, 149, 163305-1–163305-11 Search PubMed.
- F. Horkay, A. Chremos, J. F. Douglas, R. Jones, J. Lou and Y. Xia, J. Chem. Phys., 2021, 155, 074901-1–074901-13 CrossRef PubMed.
- S. Wang, R. Walker-Gibbons, B. Watkins, M. Flynn and M. Krishnan, Nat. Nanotechnol., 2024, 1–9 Search PubMed.
- A. Behjatian, R. Walker-Gibbons, A. A. Schekochihin and M. Krishnan, Langmuir, 2022, 38, 786–800 CrossRef CAS.
- M. Sedlák and E. J. Amis, J. Chem. Phys., 1992, 96, 826–834 CrossRef.
- M. Sedlak, J. Chem. Phys., 1996, 105, 10123–10133 CrossRef CAS.
- M. Sedlák, Langmuir, 1999, 15, 4045–4051 CrossRef.
- M. Sedlák, J. Chem. Phys., 2002, 116, 5236–5245 CrossRef.
- M. Sedlák, J. Chem. Phys., 2002, 116, 5246–5255 CrossRef.
- B. D. Ermi and E. J. Amis, Macromolecules, 1998, 31, 7378–7384 CrossRef CAS.
- S. Ghosh, R. M. Peitzsch and W. F. Reed, Biopolymers, 1992, 32, 1105–1122 CrossRef CAS.
- M. Sedlak, Macromolecules, 1993, 26, 1158–1162 CrossRef CAS.
- C. Kosgallana, M. Senanayake, S. S. Mohottalalage, S. Wijesinghe, L. He, G. S. Grest and D. Perahia, Macromolecules, 2024, 1688–1698 CrossRef CAS.
- C. G. Lopez, S. E. Rogers, R. H. Colby, P. Graham and J. T. Cabral, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 492–501 CrossRef CAS PubMed.
- C. Clasen and W.-M. Kulicke, Prog. Polym. Sci., 2001, 26, 1839–1919 CrossRef CAS.
- T. Garlick and P. Miner, US Pat., 3597416, 1993 Search PubMed.
- J. N. Bemiller and R. L. Whistler, Industrial gums: polysaccharides and their derivatives, Academic Press, 1992 Search PubMed.
- J. K. Fink, Water-based chemicals and technology for drilling, completion, and workover fluids, Gulf Professional Publishing (Elsevier), 2015 Search PubMed.
- F. B. Insights, Market Research Report, 2021.
- H. Chen, Lignocellulose biorefinery engineering, Elsevier, 2015 Search PubMed.
- J. S. Behra, J. Mattsson, O. J. Cayre, E. S. J. Robles, H. Tang and T. N. Hunter, ACS Appl. Polym. Mater., 2019, 1, 344–358 CrossRef CAS.
- C. G. Lopez, S. E. Rogers, R. H. Colby, P. Graham and J. T. Cabral, J. Polym. Sci., Part B: Polym. Phys., 2014, 53, 492–501 CrossRef PubMed.
- C. G. Lopez, R. H. Colby and J. T. Cabral, Macromolecules, 2018, 51, 3165–3175 CrossRef CAS.
- C. G. Lopez, J. Rheol., 2020, 64, 191–204 CrossRef CAS.
- C. Barba, D. Montané, M. Rinaudo and X. Farriol, Cellulose, 2002, 9, 319–326 CrossRef CAS.
- C. Barba, D. Montané, X. Farriol, J. Desbrières and M. Rinaudo, Cellulose, 2002, 9, 327–335 CrossRef CAS.
- P. Wagner, S. Różańska, E. Warmbier, A. Frankiewicz and J. Różański, Materials, 2023, 16, 418 CrossRef CAS PubMed.
- L. N. Jimenez, C. D. Martnez Narváez and V. Sharma, Phys. Fluids, 2020, 32, 012113 CrossRef CAS.
- L. N. Jimenez, C. D. Martinez Narvaez and V. Sharma, Macromolecules, 2022, 8117–8132 CrossRef CAS.
- D. Truzzolillo, F. Bordi, C. Cametti and S. Sennato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011804 CrossRef CAS.
- D. Ray, R. De and B. Das, J. Chem. Thermodyn., 2016, 101, 227–235 CrossRef CAS.
- E. deButts, J. A. Hudy and J. Elliott, Ind. Eng. Chem., 1957, 49, 94–98 CrossRef CAS.
- L. Xiqua, Q. Tingzhu and Q. Shaoqui, Acta Polym., 1990, 41, 220–222 CrossRef.
- G. Dürig and A. Banderet, Helv. Chim. Acta, 1950, 33, 1106–1118 CrossRef.
- J. Enebro, D. Momcilovic, M. Siika-Aho and S. Karlsson, Biomacromolecules, 2007, 8, 3253–3257 CrossRef CAS PubMed.
- W. N. Sharratt, R. O’Connell, S. E. Rogers, C. G. Lopez and J. T. Cabral, Macromolecules, 2020, 53, 1451–1463 CrossRef CAS.
- C. Castelain, J. Doublier and J. Lefebvre, Carbohydr. Polym., 1987, 7, 1–16 CrossRef CAS.
- C. G. Lopez, L. Voleske and W. Richtering, Carbohydr. Polym., 2020, 234, 115886 CrossRef CAS.
- H. Vink, Macromol. Chem. Phys., 1982, 183, 2273–2283 CrossRef CAS.
- H. Vink, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 699–709 RSC.
- S. Dou and R. H. Colby, Macromolecules, 2008, 17, 6505–6510 CrossRef.
- J. Combet, M. Rawiso, C. Rochas, S. Hoffmann and F. Boué, Macromolecules, 2011, 44, 3039–3052 CrossRef CAS.
- P. Lorchat, I. Konko, J. Combet, J. Jestin, A. Johner, A. Laschewski, S. Obukhov and M. Rawiso, Europhys. Lett., 2014, 106, 28003 CrossRef.
- C. G. Lopez, F. Horkay, R. Schweins and W. Richtering, Macromolecules, 2021, 54, 10583–10593 CrossRef CAS.
- K. Salamon, D. Aumiler, G. Pabst and T. Vuletic, Macromolecules, 2013, 46, 1107–1118 CrossRef CAS.
- L. Wang and V. A. Bloomfield, Macromolecules, 1991, 24, 5791–5795 CrossRef CAS.
- C. G. Lopez and W. Richtering, J. Chem. Phys., 2018, 148, 244902 CrossRef.
- T. Waigh, A. Papagiannopoulos, A. Voice, R. Bansil, A. Unwin, C. Dewhurst, B. Turner and N. Afdhal, Langmuir, 2002, 18, 7188–7195 CrossRef CAS.
- W. F. Reed, J. Chem. Phys., 1994, 100, 7825–7827 CrossRef CAS.
- K. Kaji, H. Urakawa, T. Kanaya and R. Kitamaru, J. Phys., 1988, 49, 993–1000 CrossRef CAS.
- K. Nishida, K. Kaji and T. Kanaya, J. Chem. Phys., 2001, 115, 8217–8220 CrossRef CAS.
- N. Malikova, A.-L. Rollet, S. Čebašek, M. Tomšič and V. Vlachy, Phys. Chem. Chem. Phys., 2015, 17, 5650–5658 RSC.
- A. Chremos and J. F. Douglas, J. Chem. Phys., 2017, 147, 044906 CrossRef PubMed.
- F. Boué, J. Combet, B. Demé, M. Heinrich, J.-G. Zilliox and M. Rawiso, Polymers, 2016, 8, 228 CrossRef.
- G. Nisato, R. Ivkov and E. J. Amis, Macromolecules, 1999, 32, 5895–5900 CrossRef CAS.
- A. Ramzi, R. Scherrenberg, J. Joosten, P. Lemstra and K. Mortensen, Macromolecules, 2002, 35, 827–833 CrossRef CAS.
- H. Inoue and T. Matsumoto, J. Rheol., 1994, 38, 973–984 CrossRef CAS.
- D. Renard, M. A. Axelos, F. Boué and J. Lefebvre, Biopolymers, 1996, 39, 149–159 CrossRef CAS.
- F. Muller, M. Delsanti, L. Auvray, J. Yang, Y. Chen, J. Mays, B. Demé, M. Tirrell and P. Guenoun, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 3, 45–53 CrossRef CAS.
- P. Guenoun, M. Delsanti, D. Gazeau, J. Mays, D. Cook, M. Tirrell, M. Tirrell and L. Auvray, Eur. Phys. J. B, 1998, 1, 77–86 CrossRef CAS.
- K. Kassapidou, W. Jesse, M. Kuil, A. Lapp, S. Egelhaaf and J. Van der Maarel, Macromolecules, 1997, 30, 2671–2684 CrossRef CAS.
- K. Nishida, K. Kaji, T. Kanaya and T. Shibano, Macromolecules, 2002, 35, 4084–4089 CrossRef CAS.
- We neglect here the scattering from the counterions, which is a valid approximating under certain conditions, as discussed later in the manuscript.
- L. Schulz, B. Seger and W. Burchard, Macromol. Chem. Phys., 2000, 201, 2008–2022 CrossRef CAS.
- P. W. Schmidt, The fractal approach to heterogeneous chemistry, 1989, pp. 67–79 Search PubMed.
- F. Cousin, J. Gummel, D. Ung and F. Boué, Langmuir, 2005, 21, 9675–9688 CrossRef CAS.
- P. Vallat, J.-M. Catala, M. Rawiso and F. Schosseler, Macromolecules, 2007, 40, 3779–3783 CrossRef CAS.
- C. G. Lopez and W. Richtering, Cellulose, 2019, 26, 1517–1534 CrossRef CAS.
- S. Pyett and W. Richtering, J. Chem. Phys., 2005, 122, 034709 CrossRef PubMed.
- Certain commercial equipment, instruments, or materials are identified in this paper to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.
- C. Wandrey, A. Bartkowiak and D. Hunkeler, Langmuir, 1999, 15, 4062–4068 CrossRef CAS.
- Y. Marcus, J. Phys. Chem. B, 2009, 113, 10285–10291 CrossRef CAS.
- L. H. Blanco and E. F. Vargas, J. Solution Chem., 2006, 35, 21–28 CrossRef CAS.
- M. Andreev, A. Chremos, J. de Pablo and J. F. Douglas, J. Phys. Chem. B, 2017, 121, 8195–8202 CrossRef CAS PubMed.
- M. Andreev, J. J. de Pablo, A. Chremos and J. F. Douglas, J. Phys. Chem. B, 2018, 122, 4029–4034 CrossRef CAS.
- H. D. B. Jenkins and Y. Marcus, Chem. Rev., 1995, 95, 2695–2724 CrossRef CAS.
- C. Hou, T. Watanabe, C. G. Lopez and W. Richtering, Carbohydr. Polym., 2025, 347, 122287 CrossRef CAS.
- N. Malikova, S. Čebašek, V. Glenisson, D. Bhowmik, G. Carrot and V. Vlachy, Phys. Chem. Chem. Phys., 2012, 14, 12898–12904 RSC.
- C. Hotton, Y. Sakhawoth, A.-L. Rollet, J. Sireix-Plénet, L. Tea, S. Combet, M. Sharp, I. Hoffmann, F. Nallet and N. Malikova, C. R. Chim., 2024 DOI:10.26434/chemrxiv-2024-drcrc.
- K. Kaji, H. Urakawa, T. Kanaya and R. Kitamaru, Macromolecules, 1984, 17, 1835–1839 CrossRef CAS.
- V. M. Prabhu, E. J. Amis, D. P. Bossev and N. Rosov, J. Chem. Phys., 2004, 121, 4424–4429 CrossRef CAS PubMed.
- V. Prabhu, M. Muthukumar, G. D. Wignall and Y. B. Melnichenko, J. Chem. Phys., 2003, 119, 4085–4098 CrossRef CAS.
- J. Combet, F. Isel, M. Rawiso and F. Boué, Macromolecules, 2005, 38, 7456–7469 CrossRef CAS.
- K. Nishida, K. Kaji and T. Kanaya, J. Chem. Phys., 2001, 114, 8671–8677 CrossRef CAS.
- M. Nierlich, F. Boue, A. Lapp and R. Oberthür, Colloid Polym. Sci., 1985, 263, 955–964 CrossRef CAS.
- M. Jacobs, C. G. Lopez and A. V. Dobrynin, Macromolecules, 2021, 54, 9577–9586 CrossRef CAS.
- A. V. Dobrynin and M. Jacobs, Macromolecules, 2021, 54, 1859–1869 CrossRef CAS.
- Y. Marcus, J. Solution Chem., 2008, 37, 1071–1098 CrossRef CAS.
- B. D. Ermi and E. J. Amis, Macromolecules, 1997, 30, 6937–6942 CrossRef CAS.
- B. Hammouda, F. Horkay and M. L. Becker, Macromolecules, 2005, 38, 2019–2021 CrossRef CAS.
- B. Hammouda, Polymer, 2009, 50, 5293–5297 CrossRef CAS.
- F. Horkay and B. Hammouda, Colloid Polym. Sci., 2008, 286, 611–620 CrossRef CAS.
- B. Hammouda, J. Chem. Phys., 2010, 133(8), 084901 CrossRef PubMed.
- R. L. Kay, T. Vituccio, C. Zawoyski and D. Evans, J. Phys. Chem. B, 1966, 70, 2336–2341 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00874j |
| This journal is © The Royal Society of Chemistry 2024 |