Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pickering emulsions for stimuli-responsive transdermal drug delivery: effect of rheology and microstructure on performance†
Simona
Migliozzi
 *a,
Yiting
He
*a,
Yiting
He
 ab,
Maryam
Parhizkar
ab,
Maryam
Parhizkar
 c,
Yang
Lan
c,
Yang
Lan
 ab and
Panagiota
Angeli
ab and
Panagiota
Angeli
 *a
*a
aDepartment of Chemical Engineering, University College London, London, UK. E-mail: s.migliozzi@ucl.ac.uk; p.angeli@ucl.ac.uk
bCentre for Nature Inspired Engineering, University College London, London, UK
cSchool of Pharmacy, University College London, London, UK
First published on 15th October 2024
Abstract
This work investigates the design of stimuli-responsive Pickering emulsions (PEs) for transdermal drug delivery applications, by exploring the impact of stabilising microgels size and interactions on their rheological and release properties. Temperature-responsive poly(N-isopropylacrylamide) microgels modified with 1-benzyl-3-vinylimidazolium bromide (pNIPAM-co-BVI) are synthesized in varying sizes and used to stabilise jojoba oil-in-water concentrated emulsions. The results reveals two distinct behaviours: for small microgels (∼300 nm), the PEs exhibit a smooth, uniform structure characterised by a mild yield stress, characteristic of soft glassy systems. Conversely, larger microgels (∼800 nm) induce droplet clustering, resulting in increased elasticity and a more complex yielding process. Interestingly, transdermal delivery tests demonstrate that microstructure, rather than bulk rheology, governs sustained drug release. The release process can be modelled as diffusion-controlled transport through a porous medium with random traps. At room temperature, the trap size corresponds to the droplet size, and the release time scales with the total dispersed phases volume fraction. However, at physiological temperature (37 °C), above the volume-phase transition temperature of the microgels, the release time increases significantly. The trap size approaches the microgel size, suggesting that microgel porosity becomes the dominant factor controlling drug release. Overall, the results highlight the critical role of microstructure design in optimising stimuli-responsive PEs for controlled transdermal drug delivery.
1 Introduction
In recent decades, the development of targeted drug delivery systems has received significant scientific and industrial interest. Traditional methods often require high dosages and frequent administrations, which can lead to poor patient compliance and severe side effects.1 Significant efforts have been devoted towards designing and fabricating delivery systems that achieve greater specificity, improved stability of the drugs, and controlled sustained release.1–6 Among various delivery technologies, topical drug delivery through the skin (transdermal drug delivery) holds significant appeal due to several key benefits: (i) it offers an extended and controlled duration of therapeutic action, thereby reducing dosing frequency; (ii) it bypasses the gastrointestinal tract, minimising the impact on metabolism; and (iii) it can be non-invasive.7–9In this context, optimal formulations should be semisolid, spreadable materials, ideally dosed with nanostructured microcarriers to allow localised drug transport to the diseased sites through the skin layers.7,8,10,11 Pickering emulsions (PEs) are a promising strategy that combines these desired characteristics. PEs are surfactant-free dispersions of two phases, stabilised by nanoparticles absorbed at the interface. This approach offers the potential to create formulations with both the appropriate texture for topical application and the ability to deliver drugs.8,12,13 By carefully engineering the stabilising nanoparticles, PEs offer design flexibility, where novel formulations with improved stability, specific rheological properties, increased shelf life and stimuli-responsive release functions can be tailored for a variety of different therapeutic applications, from transdermal delivery of drugs for the treatment of heart failure,14 to injectable formulations for the release of hydrophobic drugs or biologics (i.e., proteins, antibodies and enzymes).15 In all these applications, ensuring the mechanical resistance of the microdroplets to applied stresses, and at the same time, optimal bulk functionality, is fundamental to preserve the drug stability and its sustained release.
To this aim, soft-crosslinked nanoparticles of hydrophilic polymers, known as microgels (MGs), emerge as promising interface stabilisers. Thanks to the rapid development of polymer particle synthesis techniques, MGs with desired properties and complex stimuli-responsive attributes can be designed for very targeted applications16 as well as to address bio-compatibility and toxicity issues often related to the use of common molecular surfactants.17,18 Although several studies explored the use of novel microgel (MG)-stabilised Pickering emulsions in different bioapplications,8,19,20 they primarily focused on the final performance and stability of specific oil and MG chemistry combinations. A gap remains in understanding the key physical attributes that influence the final properties of these formulations.
Microgels exhibit more intricate behaviour at interfaces compared to standard solid particles due to their unique dual particle/polymer nature. Similar to solid particles, MGs can irreversibly bind at interfaces. However, their polymeric structure allows them to stretch significantly along the interface plane.21–23 The significant structural deformation, combined with the interpenetration of their polymer chains, controls MGs assembly at the interface, ultimately impacting the microstructure, stability and rheology of MG-stabilised PEs.22–25 The ability of microgels to stretch and deform is, in turn, influenced by specific attributes, such as size, crosslinking degree and charge.26–28 These properties can therefore be used as tuning parameters to design formulations with desired functionalities. For instance, larger MGs typically have a more uneven internal structure, which leads to a less uniform interfacial layer.27 This less dense layer promotes bridging between neighbouring droplets, resulting in Pickering emulsions that are more prone to flocculation.27 Conversely, smaller MGs stabilise more uniform and well-dispersed PEs due to their ability to create a denser and more uniform interfacial layer.23,27 The degree of droplet aggregation significantly affects the rheology of the final emulsions.29–32 This, in turn, is further influenced by other design parameters, such as the total volume fraction of oil droplets and the total amount of stabilising microgels added.32–37 These factors complicate the design of PEs, especially for transdermal applications where smooth texture and good spreadability are essential. The microstructure formed by the assembly of all dispersed phases in the formulation also impacts its responsive behaviour. For instance, faster drug release is frequently observed when an external stimulus is applied to promote PEs destabilisation. This is usually attributed to the breakdown of the uniform external layer formed by the stabilising particles.38,39 However, some studies have reported opposing trends for microgels-stabilised PEs,40 highlighting the intricate interplay between microgel properties, the resulting microstructure, and the release kinetics of the encapsulated drug.
Hence, this study aims to elucidate the connection between the specific characteristics of responsive microgel particles and the overall performance of the resulting emulsions. In particular, we investigate how microgel size influences the microstructure and rheology of the resulting Pickering emulsions and explore how both aspects ultimately affect the final responsive drug release properties. To this end, we fabricated model Pickering emulsions stabilised with pNIPAM-based microgels of two distinct sizes. PNIPAM (poly(N-isopropylacrylamide)) microgels were chosen due to their well-established thermal responsiveness.23,41 This responsiveness allows control over their swelling behaviour using temperature as external stimulus. Notably, pNIPAM undergoes a structural collapse at temperatures exceeding 32 °C.42,43 This characteristic makes it an ideal candidate to investigate the performance of PEs stabilised by such microgels at physiological temperature (i.e., 37 °C).
The general aspect and microstructural properties of the resulting PEs were analysed through bright-field and confocal microscopy, while strain amplitude oscillatory sweep measurements and time-resolved rheological analysis were performed to obtain a detailed characterisation of the PEs rheological properties and gain insights into the microstructure of the different formulations. Finally, the sustained release properties of the formulations were evaluated with the Franz-cell method44,45 at both room and physiological temperatures, using levosimendan as a model lipophilic drug.14 Through this multi-scale investigation, we wish to guide the design of PEs with tailored properties to achieve desired functionalities. By studying the material behaviour across a wide range of strain amplitudes, we aim to identify various microstructural rearrangements and gain insights into the underlying interactions. This approach provides valuable insights for designing these formulations from a physical perspective. This knowledge will be instrumental in optimising these systems for controlled drug delivery and other fields where controlled release is essential.
2 Materials and methods
2.1 Chemicals
N-Isopropylacrylamide (NIPAM), N,N′-methylenebis(acrylamide) (Bis), 2,2′-azobis(2-methyl-propionamidine)dihydrochloride (AIBA), benzyl bromide (BBr), 1-vinylimidazole (VImi), Rhodamine B isothiocyanate (RhodB), 2-aminoethyl methacrylate hydrochloride (AEMA-HC) and Nile Red were sourced from Sigma-Aldrich. Diethyl ether was from Acros Organics, cetyltrimethylammonium bromide (CTAB) was purchased from MP Biomedicals, LLC and Jojoba oil was supplied by Santa Cruz Biotechnology, Inc.2.2 Microgels synthesis and characterisation
Monodisperse p(NIPAM-co-BVI) microgels (pNIPAM-co-BVI MGs), composed of monomer NIPAM and BVI, were synthesised in two different sizes through batch emulsion polymerization,46 following the same procedure reported in a previous work.25 In brief, BVI was first synthesised as described by Liu et al.47 Next, microgels with a swollen size ∼800 nm (M800) were fabricated by dissolving NIPAM (54.65 mmol), Bis (1.40 mmol) and BVI (0.86 mmol) in 298 mL DI water. The mixture was then purged with nitrogen for 20 minutes and 2 mL of AIBA (0.12 M) solution were injected into the flask to start the radical polymerization. The reaction was carried out at 70 °C and stirring speed of 700 rpm for 8 hours. To obtain microgels with smaller sizes, ∼300 nm (M300), 0.42 mmol CTAB were added to the initial mixture before purging. After polymerization, the microgels were purified with DI water by dialysis for one week, with DI water changed daily, and then concentrated with a rotavapor to obtain stock solutions at MG mass fractions higher than 8 wt%. To obtain fluorescently-tagged microgels for confocal imaging, 40 μL of 0.002 mM RhodB and AEMA–HC mixture (molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were added to the reaction mixture before heating. The characteristic sizes (dp) and surface charge of the microgels synthesised as above were then determined using dynamic light scattering (DLS) and electrophoretic tests (Anton Paar Litesizer 100). For this purpose, 4 mL of 0.02 wt% solutions of M800 and M300 were prepared from the respective stock solutions and placed in a quartz cuvette. A temperature ramp (20 °C to 40 °C) was applied, and the temperature-dependent sizes and zeta-values (ζ) were measured at increments of 2.5 °C.
1) were added to the reaction mixture before heating. The characteristic sizes (dp) and surface charge of the microgels synthesised as above were then determined using dynamic light scattering (DLS) and electrophoretic tests (Anton Paar Litesizer 100). For this purpose, 4 mL of 0.02 wt% solutions of M800 and M300 were prepared from the respective stock solutions and placed in a quartz cuvette. A temperature ramp (20 °C to 40 °C) was applied, and the temperature-dependent sizes and zeta-values (ζ) were measured at increments of 2.5 °C.
2.3 Emulsion preparation and characterisation
Pickering emulsions (PEs) were prepared with a fixed oil-to-water volume ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 through high shear homogenisation. Jojoba oil and microgel aqueous dispersions were emulsified using a high-shear mixer (Silverson, L5 series) at 10
1 through high shear homogenisation. Jojoba oil and microgel aqueous dispersions were emulsified using a high-shear mixer (Silverson, L5 series) at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 90 seconds. To investigate both the effect of microgel size and loading, for each of the two microgel sizes, three different microgel concentrations were tested, 6 wt% (C1), 4 wt% (C2), and 2 wt% (C3), for a total of six configurations.
000 rpm for 90 seconds. To investigate both the effect of microgel size and loading, for each of the two microgel sizes, three different microgel concentrations were tested, 6 wt% (C1), 4 wt% (C2), and 2 wt% (C3), for a total of six configurations.
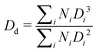 | (1) |
To further observe the distribution of the microgels at the droplet interface, the PEs were also observed through confocal fluorescence microscopy (LSM 710 equipped with Plan-Apochromat 63×–40×/1.4 Oil DIC M27, Zeiss). Details of the sample preparation can be found in a previous publication.25
To investigate the influence of microgel size and loading on the microstructure of the material, strain amplitude oscillatory sweep tests were conducted. These measurements analyse the viscoelastic response of a material under small to large sinusoidal deformations, providing valuable insights into the physical mechanisms governing material yielding and, consequently, its microstructure. The tests were performed at a constant angular frequency (ω) of 10 rad s−1 and a variable strain amplitude (γ0) ranging from 10−4 to 102. The choice of an angular frequency of 10 rad s−1 was primarily driven by technical considerations. Preliminary measurements revealed that lower frequencies (e.g., 1 rad s−1) introduced significant noise into the raw waveforms, especially for low-strain amplitudes and low viscoelasticity formulations (M300-C2/C3). To ensure data quality and enable reliable analysis, we opted for the higher frequency. While a different oscillating frequency could potentially explore distinct microstructural processes, we believe that the chosen frequency adequately samples the microstructure of our samples. The frequency-dependent viscoelastic moduli, obtained through small amplitude oscillatory sweeps for reference samples M300-C1/C3 and M80-C1/C3, are reported in the ESI† (S8). At each amplitude, the oscillations were maintained until a stable periodic signal was achieved. Subsequently, time-resolved data were collected over several oscillation periods. The acquired strain, shear rate, and stress waveforms were then analysed using the sequence of physical processes (SPP) approach. This technique, developed by Rogers,49 offers a unique method for interpreting raw strain amplitude oscillatory sweep data, revealing the underlying physical processes responsible for yielding behaviour.50–55 All data processing was performed using the MATLAB-based SPPplus v2 software53 (kindly provided by Prof. Rogers). The software first employs Fourier-domain filtering to reconstruct the data, utilising all detectable odd harmonics, then applies the SPP framework, which will be further discussed in the following section.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt). Here, γ(t) is the instantaneous strain, γ0 is the strain amplitude of the sinusoidal signal, and ω is the angular frequency. Within the linear viscoelastic regime (LVER), the stress response to an applied sinusoidal strain can be described by a single odd harmonic (I1 ≡ σ1) from which the conventional storage (G′) and loss (G′′) moduli can be retrieved.55,56 Above the LVER regime, the onset of nonlinearities causes a distortion of the simple sinusoidal response, and the stress can be decomposed as:
sin(ωt). Here, γ(t) is the instantaneous strain, γ0 is the strain amplitude of the sinusoidal signal, and ω is the angular frequency. Within the linear viscoelastic regime (LVER), the stress response to an applied sinusoidal strain can be described by a single odd harmonic (I1 ≡ σ1) from which the conventional storage (G′) and loss (G′′) moduli can be retrieved.55,56 Above the LVER regime, the onset of nonlinearities causes a distortion of the simple sinusoidal response, and the stress can be decomposed as: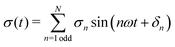 | (2) |
The SPP framework offers a unique method for interpreting stress signals for any type of material. For complex materials that exhibit neither purely elastic nor purely viscous behaviour, the stress response σ(t) to a periodic deformation depends on both the applied strain γ(t) and the induced shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t). This translates into a three-dimensional visualisation of the stress response within a single deformation period, where the axes of this space are given by the instantaneous deformation, the normalised instantaneous shear rate and the stress, [γ(t),
(t). This translates into a three-dimensional visualisation of the stress response within a single deformation period, where the axes of this space are given by the instantaneous deformation, the normalised instantaneous shear rate and the stress, [γ(t), ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t)/ω, σ(t)]. Projections of this 3D curve onto the [γ(t), σ(t)] and [
(t)/ω, σ(t)]. Projections of this 3D curve onto the [γ(t), σ(t)] and [![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t)/ω, σ(t)] planes provide the classic Lissajous–Bowditch curves.52,57 The specific physical processes governing the material's response during each sinusoidal deformation cycle influence the dynamic evolution of the 3D stress trajectory. Using infinitesimal steps, the instantaneous tridimensional stress can be decomposed into two components: one in phase with the strain (representing the instantaneous elastic contribution,
(t)/ω, σ(t)] planes provide the classic Lissajous–Bowditch curves.52,57 The specific physical processes governing the material's response during each sinusoidal deformation cycle influence the dynamic evolution of the 3D stress trajectory. Using infinitesimal steps, the instantaneous tridimensional stress can be decomposed into two components: one in phase with the strain (representing the instantaneous elastic contribution, 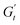 ) and one in phase with the shear rate (representing the instantaneous viscous contribution,
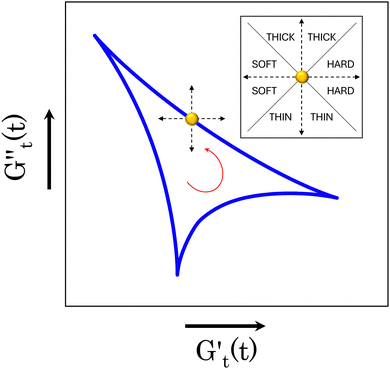
) and one in phase with the shear rate (representing the instantaneous viscous contribution, 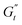 ). These instantaneous moduli are defined as partial derivatives of the stress with respect to the strain and the shear rate, allowing for a clear separation of elastic and viscous contributions. For the complete mathematical derivation please refer to Rogers’ original work.51 All rheological transitions within a deformation cycle can be described by the changes in these two instantaneous moduli. For easier visualisation, these changes are typically reported in a Cole–Cole plot (Fig. 1). This graphical representation allows for straightforward interpretation of the evolving rheological behaviour during each strain cycle. Horizontal movements on the plot indicate elastic changes, with an increase in
). These instantaneous moduli are defined as partial derivatives of the stress with respect to the strain and the shear rate, allowing for a clear separation of elastic and viscous contributions. For the complete mathematical derivation please refer to Rogers’ original work.51 All rheological transitions within a deformation cycle can be described by the changes in these two instantaneous moduli. For easier visualisation, these changes are typically reported in a Cole–Cole plot (Fig. 1). This graphical representation allows for straightforward interpretation of the evolving rheological behaviour during each strain cycle. Horizontal movements on the plot indicate elastic changes, with an increase in 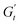 signifying stiffening and vice versa. Similarly, vertical movements represent viscous transitions, with an increase in
signifying stiffening and vice versa. Similarly, vertical movements represent viscous transitions, with an increase in 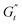 indicating thickening and vice versa.51–54 For infinitesimal strain amplitudes, the trajectories would converge to a single point representing the bulk storage G′ and loss G′′ moduli, signifying the absence of any microstructural rearrangements within the material, as expected in the LVER.
indicating thickening and vice versa.51–54 For infinitesimal strain amplitudes, the trajectories would converge to a single point representing the bulk storage G′ and loss G′′ moduli, signifying the absence of any microstructural rearrangements within the material, as expected in the LVER.
2.4 Drug release tests
The transdermal delivery performance of the Pes was evaluated using permeation studies of levosimendan in a Franz cell. The Franz cell, equipped with a hydrophobic polysulfone membrane (0.45 μm porosity, Omicron Research Ltd), mimics the permeation process through the skin (a schematic of the cell can be found in the ESI,† Fig. S.1A). A stock solution of levosimendan (0.1 mg mL−1) was prepared in jojoba oil and then emulsified with aqueous microgel solutions as described in Section 2.3. For each formulation, 1 mL of the emulsion was placed in the donor chamber, resulting in a consistent total drug mass of 0.05 mg (as half the volume of each formulation is oil). Standard PBS buffer solution (5 mL) served as the receiver phase. Samples (2 mL) were periodically withdrawn from the receiver compartment and replaced with fresh buffer solution to maintain a constant volume throughout the 190-hour experiment. The concentration of released levosimendan at each time point was measured using a double-beam Cary-60 UV-vis spectrometer (Agilent UK) at 400 nm. The instrument was initially calibrated using a series of 10 levosimendan solutions at known concentration in PBS buffer (Fig. S.1B in ESI†). The cumulative percentage of drug released (CR%) was then calculated as CR% = cR/c0 × 100, where cR is the concentration of levosimendan accumulated in the receptor chamber at a specific time, and c0 is the initial drug concentration. To assess the permeability of the drug to the polysulfone membrane, a reference experiment was conducted using a simple jojoba oil solution containing levosimendan (0.05 mg mL−1) (Fig. S.1C in ESI†). All experiments were performed at both room temperature (T = 21 °C) and physiological temperature (T = 37 °C) to investigate the thermoresponsive behaviour of the Pes on sustained release.3 Results and discussion
3.1 Microgels sizes and surface charge
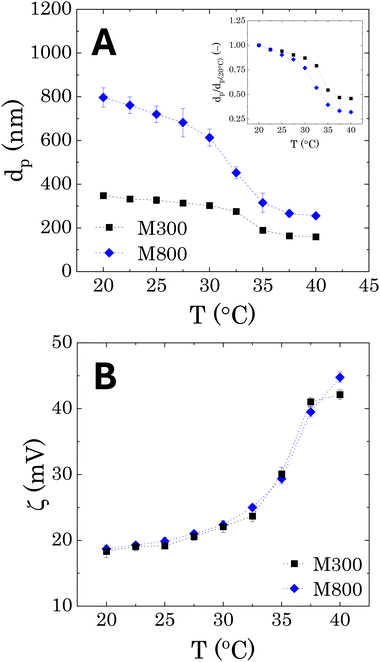
The DLS results, reporting the average sizes of the pNIPAM-co-BVI microgels used to stabilise the Pickering emulsions are reported in Fig. 2A as a function of temperature. An average swollen diameter of 348 ± 4 nm and 796 ± 44 nm is found for samples M300 and M800, respectively at 20 °C. The microgels show the same qualitative behaviour of conventional pNIPAM microgels. At low temperatures, the crosslinked cores swell to their maximum dimension thanks to the higher hydrophilicity of the NIPAM chains. As the temperature increases, the polymer becomes more hydrophobic, causing a collapse of the network and a reduction of the microgels diameters. The temperature transition is consistent for both microgels, showing a lower critical solution temperature (LCST) around 32.5 °C, which corresponds to the typical value reported for pNIPAM in the literature.25,46,58 However, a difference is observed in the shape of the volume transition, when the average diameters are normalised with the values obtained at T = 20 °C (dp(20°C)). In both cases, the microgels shrink linearly with temperature, until reaching the LCST, where the diameters suddenly collapse to half the original size (inset in Fig. 2A). Bigger microgels present a more pronounced gradient, showing a final collapse of more than half the original swollen size. In addition, a higher variability is observed for the measured sizes of microgels M800 in the swollen configuration, as highlighted by the larger error bars in Fig. 2A. Both aspects can be related to the core–shell morphology of pNIPAM-MGs, characterised by a denser crosslinked core and external dangling ends.58,59 These external chains are typically longer for bigger microgels and therefore can assume a wider range of relaxed conformations, which will affect the hydrodynamic diameter of the microgel particles and their temperature-dependent transition.58–60In terms of surface charge (Fig. 2B), the zeta-potential measurements show a positive charge of approximately +18 mV, which is related to the presence of BVI at the external periphery of the microgels.25 We note that, as already found in the literature for pNIPAM microgels, as the particle shrinks at increasing temperatures, the surface charge increases because of a higher charge density in the external boundary of the microgels.61 Overall, the two microgels do not show any differences in surface charge, indicating a similar binding efficiency of the external BVI molecules.
3.2 Calculation of microgels effective volume fraction
To estimate the degree of coverage of the MG-stabilised drops and obtain a proper comparison between different MG sizes, the effective particle volume fraction (ϕ) and in turn the number concentration (np) need to be calculated. The effective ϕ can be found using a rheological approach. For suspensions of repulsive particles, it is in fact predicted that the relative zero-shear viscosity is a function of the particle volume fraction, usually showing divergence as the critical jamming concentration is approached.62,63 If a linear relation is assumed between the mass concentration c and the resulting volume fraction ϕ, expressed as ϕ = kMc, the constant kM can be determined by fitting the measured relative zero-shear viscosity of the MG suspensions, ηr(c). In Fig. 3, we report the results for microgels M300 and M800. Both sets of data can be fitted together with the equation derived by Mooney64 for concentrated suspensions of spherical particles: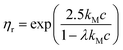 | (3) |
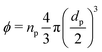 | (4) |
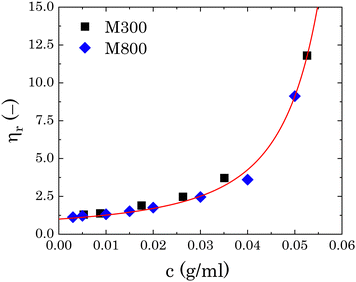 | ||
| Fig. 3 Relative viscosity as a function of microgel mass fraction for both sets of microgels. The red line is the fitting of eqn (3) to the experimental points. | ||
Note that in previous works, np was obtained assuming an effective density of the microgels, which takes into account their porosity.24,65,66 This method does not consider possible changes in the swollen conformation of the microgels and can overestimate the effective volume fraction of the microgels.
3.3 Pickering emulsions – appearance and droplet size distribution
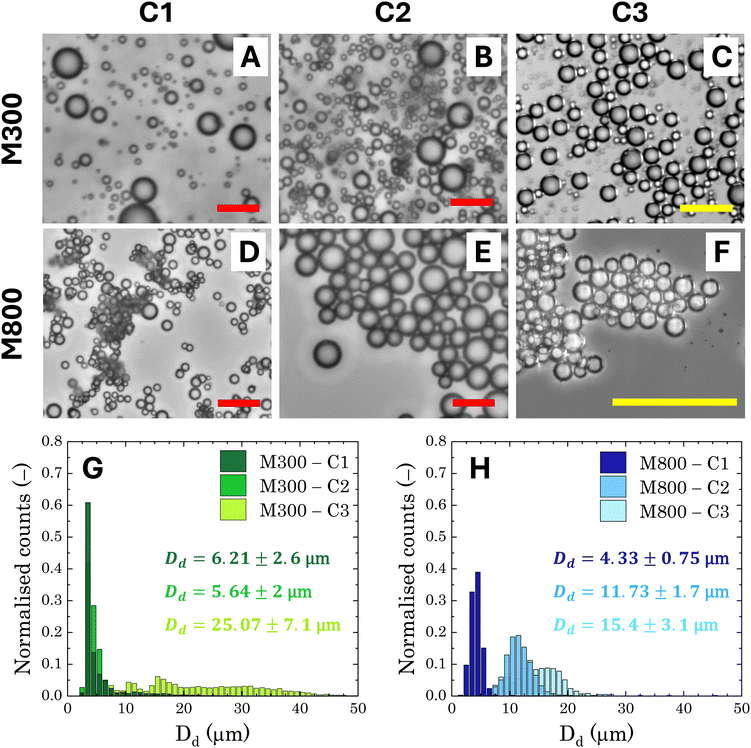
The general appearance and droplet size distribution (DSD) of Pickering emulsions stabilised with microgels M300 and M800 were investigated at various microgel loadings. The appearance of the PEs is significantly influenced by the size of the microgel particles. Regardless of the microgel concentration, samples stabilised with smaller particles appear smooth and fluid, whereas those stabilised with larger microgels have a paste-like consistency with a granular texture (Fig. S.2 in ESI†). As the microgel content decreases, samples stabilised with M300 microgels become more prone to creaming, evidenced by the residual layer of aqueous microgel dispersions at the bottom of the test vials. In contrast, PEs stabilised with larger M800 microgels do not show any creaming, with only a small amount of water visible at the bottom of the test vial at the lowest microgel concentration (sample M800-C3 in Fig. S.2). As opposed to M300-stabilised samples, in this case, the water layer appears transparent, indicating that most microgels remain in the emulsion phase. This suggests differences in the stabilising mechanism of the two microgel sizes. To further investigate these differences at the microscale, we analysed the characteristic DSD of all the samples using bright-field, fluorescent, and confocal microscopy. An example of the images obtained from bright-field microscopy, along with the corresponding droplet size distributions, is shown in Fig. 4.Both microgel size and concentration have a direct effect on the size distributions of the droplets obtained. For smaller microgels, i.e. sample M300, small droplets with average sizes around ∼5 μm and a fairly narrow size distribution are observed for both samples C1 and C2. However, at the lowest concentration, there is a significant shift towards larger droplet sizes, reaching an average size of approximately ∼25 μm, with a broad size distribution. A more progressive shift of the size distributions is instead observed for PEs stabilised with microgels M800. Similarly to sample M300, the highest microgel concentration, sample M800-C1, shows an average size of ∼5 μm, but the average droplet diameter increases with a decrease in microgels loading, yet maintaining fairly narrow size distributions. A plot summarising the average droplet sizes (eqn (1)) for all samples is reported in Fig. 5A. In the graph, the average sizes are reported against the number of microgels available in the aqueous phase, normalised by the theoretical number required to obtain a coverage of 0.78 (i.e., limit of maximum random packing of spherical objects in 2D67), for a fixed average droplet size equivalent to the process-controlled dimension (i.e., ∼5 μm). Typically, above the limited coalescence threshold, i.e. when particles are in excess, the average droplet size of Pickering emulsions is primarily determined by the details of the emulsification process.27,68 For a given set of fluids, the key factors influencing droplet size are the geometry of the homogeniser, the rotational speed, and the homogenisation time. Once these parameters are fixed, the initial drop size created by the homogeniser remains constant because there are enough particles to cover the interface of the drops. With a decrease in particle concentration, a diminishing proportion of the interface remains shielded by particles. This facilitates droplet coalescence until a stable size is achieved.27
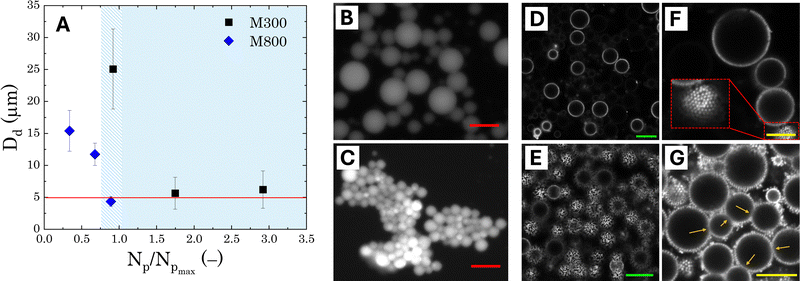
In the present system, the average attainable droplet size is around 5 μm, as demonstrated by the average sizes observed at the highest microgel loadings. However, while the onset of the limited coalescence regime occurs at a normalised particle number of 1 for small microgels, as expected, the threshold is shifted to lower values for larger microgels. This shift indicates that fewer large microgels are needed to stabilise the average size of the droplets at the process-controlled size, highlighting a fundamental difference in the microstructure of emulsions stabilised with different microgel sizes. Thanks to their more homogeneous crosslinking distribution, smaller microgels are expected to form a more uniform and densely packed shield around the droplets, resulting in emulsions with droplets that are less prone to aggregation.27 Conversely, large microgels result in Pickering emulsions with a more heterogeneous coverage, which are more prone to droplet adhesion. In particular, the increased adhesion has been attributed to a bridging effect, due to the presence of shared microgels simultaneously adsorbed at the interface of two droplets.27 This phenomenon is favoured in the presence of larger microgels because, once adsorbed at the interface, they present a lower mobility, resulting in a more disordered coverage.69 This leaves free interface for other microgels, allowing bridging between two droplets. Fluorescence micrographs confirm this scenario: stable 3D clusters of droplets are clearly identifiable in samples prepared with M800 microgels (Fig. 5C), while more dispersed and solitary droplets are observed in samples prepared with M300 microgels (Fig. 5B). Confocal microscopy reveals additional details regarding the assembly of microgels. Samples stabilised with M300 exhibit a uniform microgel coating, as evidenced by the consistent ring surrounding the droplets (Fig. 5D–F) and the packed assembly of the microgels at the droplet interface (inset in Fig. 5F). In contrast, M800-stabilised samples display a less dense microgel distribution. Here, we observe droplets with exposed areas (Fig. 5E) alongside bridged droplets where microgels appear shared at the interface (Fig. 5G). Given the charged nature of the microgels, beyond the direct effect of different microgel morphologies, electrostatic interactions can also contribute to the discrepancy observed. While the presence of charges contributes to a more ordered interfacial structure for small sizes, this has no effect on large microgels, where the interactions, and thus the interfacial organisation, are prevalently dominated by volume effects.28
Overall, the microscopic analysis confirms what already reported in the literature,27,69 showing significant differences in the microstructure of the Pickering emulsions obtained with the two different microgel sizes. These differences in microgels arrangement and interfacial coverage can have a profound impact on the rheological behaviour of the formulations. For instance, a more dispersed droplet distribution with minimal inter-droplet connections would likely exhibit more fluid-like behavior. This translates to lower viscosities, which in turn, would lead to faster release kinetics due to the increased diffusion coefficients. Conversely, the presence of droplet clusters, could introduce more pronounced elastic properties, which can influence the mobility of the emulsion, thus inducing slower release properties. Therefore, investigating the nonlinear rheological properties is fundamental to provide further insights into the connection between microstructure and performance.
3.4 Rheological characterisation
Fig. 6A illustrates the dependence of the storage (G′) and loss (G′′) moduli on the strain amplitude for all the investigated samples, measured at an oscillation frequency ω = 10 rad s−1. All the PEs exhibit a type III strain response,72 characterised by an elasticity-dominated linear viscoelastic regime (LVER) at low strains, and a G′′ overshoot. At low strain amplitudes, G′ maintains a constant plateau, exceeding G′′. As the strain increases, a crossover is observed where G′′ surpasses G′, while going through an overshoot. The crossover point indicates the final threshold of the strain-induced solid-to-liquid transition, and it is followed by a decrease of both moduli at higher strain amplitudes (strain-thinning). This type of response is commonly observed in soft glassy and jammed materials,53,63,73 and reflects the microstructural rearrangements that the material undergoes during the yielding process. At low strains, the viscoelastic response is dominated by the elastic restoring force of the jammed dispersed phase,74–76 in this case represented by the Pickering droplets. As the strain amplitude increases, the stress applied overcomes the elastic response, and the droplets escape their positions at rest, sliding against each other, thus enabling the material to flow (crossover point). The transition between the elasticity-dominated and the liquid-like responses, i.e. the yielding transition, is progressive and encompasses various microstructural rearrangements, which culminate in the peak of the viscous component, associated to the release of energy dissipated during the reorganisation of the material.53,63,76
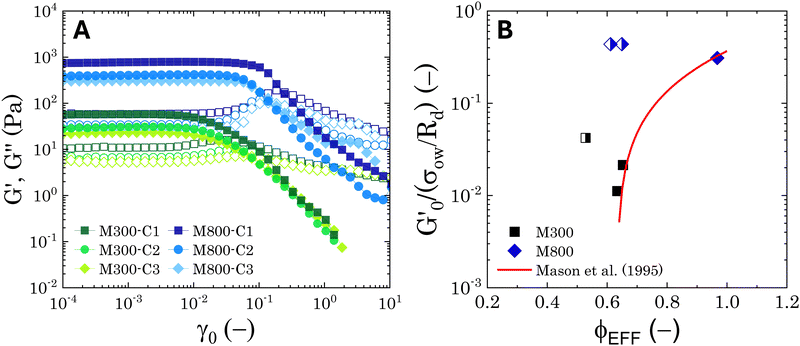 | ||
Fig. 6 Average viscoelastic moduli from strain amplitude oscillatory tests. (A) Strain amplitude dependence of the storage (closed symbols) and loss (hollow symbols) moduli obtained from strain amplitude oscillatory experiments at ω = 10 rad s−1 for the Pickering emulsions tested. (B) Zero-shear plateau storage modulus 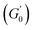 scaled by the Laplace pressure of the dispersed droplets (σow/Rd), plotted against the effective dispersed volume fraction (ϕEFF) defined as in Kaganyuk and Mohraz (2019).33 Red line is the prediction found by Mason et al. (1995),30 scaled by the Laplace pressure of the dispersed droplets (σow/Rd), plotted against the effective dispersed volume fraction (ϕEFF) defined as in Kaganyuk and Mohraz (2019).33 Red line is the prediction found by Mason et al. (1995),30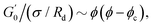 where ϕc ≈ 0.635. Half-filled symbols highlight the points that do not align with Mason's prediction. where ϕc ≈ 0.635. Half-filled symbols highlight the points that do not align with Mason's prediction. | ||
Despite the similarities in the general trends, PEs stabilised with different microgel sizes exhibit some key distinctions. PEs stabilised with small microgels display lower elasticity, as shown by the lower LVE plateaus of G′ in Fig. 6A, and a shorter extension of the LVER. The impact of microgel loading on the overall viscoelastic behaviour appears small for PEs stabilised with the same microgel size. While a slight reduction of the elastic plateau 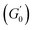 is observed for both types of PEs as microgel concentration decreases (Fig. S.3 in the ESI†), there is a significant jump between M300 and M800-stabilised PEs, even though the oil fraction remains constant across all formulations. To accurately account for these observed differences,
is observed for both types of PEs as microgel concentration decreases (Fig. S.3 in the ESI†), there is a significant jump between M300 and M800-stabilised PEs, even though the oil fraction remains constant across all formulations. To accurately account for these observed differences, 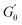 should be reported as a function of the effective dispersed phase volume fraction (ϕEFF). This metric considers the increased volume fraction due to the microgel monolayer at the droplet interface.33 Additionally, changes in microgel loading also affect droplet size in both PE sets, which is known to influence the elastic modulus plateau.30,33 Therefore, to account for both factors, we normalise
should be reported as a function of the effective dispersed phase volume fraction (ϕEFF). This metric considers the increased volume fraction due to the microgel monolayer at the droplet interface.33 Additionally, changes in microgel loading also affect droplet size in both PE sets, which is known to influence the elastic modulus plateau.30,33 Therefore, to account for both factors, we normalise 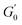 by the Laplace pressure of a single droplet, σow/Rd, and report it as a function of ϕEFF (for details on the calculation of ϕEFF, please refer to Section S5 of the ESI†). Here, σow is the interfacial tension between the oil phase and the aqueous microgel dispersion (see Table S.3 in the ESI†), and Rd = Dd/2 is the average droplet radius.
by the Laplace pressure of a single droplet, σow/Rd, and report it as a function of ϕEFF (for details on the calculation of ϕEFF, please refer to Section S5 of the ESI†). Here, σow is the interfacial tension between the oil phase and the aqueous microgel dispersion (see Table S.3 in the ESI†), and Rd = Dd/2 is the average droplet radius.
Fig. 6B presents these results alongside the predictions of Mason et al.30 The scaling suggests that the elastic moduli of the samples tested follow the prediction only at high effective volume fractions higher than ϕc ≈ 0.635. Although measures at multiple volume fractions are required to confirm the generality of the trend for the system at hand, this hints towards a shift in the dominant factors governing elasticity. At high ϕEFF, when the dispersed phase is effectively jammed, the elasticity of the material is primarily determined by the elasticity of the individual droplets. In contrast, at lower ϕEFF, the long-range structuring of the PEs becomes more important for elasticity. For M300-stabilised PEs, the higher elasticity observed at lower ϕEFF (i.e., sample M300-C3) can be attributed to the presence of excess microgels in the continuous phase (see Tables S.1 and S.2 in the ESI†), which can likely influence droplet interactions near the jamming threshold. In fact, for sample M300-C3, ϕEFF ≈ 0.53 and the total volume fraction of the dispersed phases (i.e., ϕTOT = ϕEFF + ϕm, where ϕm is the volume fraction of excess microgels) reaches a value of ϕTOT ≈ 0.59. Conversely, for M800-stabilised PEs, the sustained elasticity at lower ϕEFF is likely due to the presence of droplet clusters, which contribute to a more robust structure even at lower effective volume fractions. Notably, deviations from the LVE behaviour occur at strains γ0 ∼ 10−2 and γ0 ∼ 10−1 for PEs stabilised with microgels M300 and M800, respectively. The shorter LVER for M300-stabilised PEs indicates a lower tolerance for deformation, and therefore stress, before yielding.71,77 This translates in a significant difference in the yield stress (σy) observed for the PEs stabilised by the two different microgel sizes (see Fig. S.3B, ESI†), which differ of two orders of magnitude. These results suggest smaller microstructural units within the material, and they align with the microscopy data, which show no tendency for clustering in PEs stabilised by small microgels. In this case, the “cage” formed by surrounding droplets can be considered as the microstructural unit. Conversely, the presence of droplet clusters in PEs stabilised by M800 microgels implies a more intricate yielding process. Here, droplets rearrange within the cluster before complete yielding occurs. This is further supported by the higher normalised peaks of the loss moduli observed for M800-stabilised samples compared to M300 (see Fig. S4 and S7, ESI†), which highlight the higher dissipation associated to multiple rearrangements.78,79
Following the G′′ overshoot and the crossover point where G′′ surpasses G′, both types of PEs exhibit a similar strain-thinning behaviour, with both G′ and G′′ following a power-law decay of the type G′ ∼ γ−μ and G′′ ∼ γ−ν, with a ratio μ/ν ∼ [2.2–3.1]. This aligns with observations for soft glassy materials.63,79,80 Interestingly, for both PE systems, a second shoulder appears in the strain dependence of the loss modulus as the microgel loading is reduced. This is more evident in the normalised moduli presented in Fig. S.4A and B (ESI†), where a smaller peak can be observed around γ0 = 1–10. The presence of this secondary peak in G′′ is often associated with a more complex microstructure. In such cases, the flow transition involves a sequence of microstructural rearrangements at different scales: smaller-scale rearrangements within clusters (e.g., droplet rearrangement) and larger-scale rearrangements involving cluster breakage.71,78,79
These observations suggest the occurrence of complex yielding phenomena within the PEs. The presence of a multi-step flow transition and the dependence on microgel loading point towards a strong interplay between the microstructure and the mechanical response of the Pickering emulsions, motivating further investigation into the intracycle nonlinear stress response using quantitative methods.
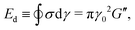 and the energy dissipated by a perfect plastic material at the same deformation value, obtained as Edp = 4γ0σmax, where σmax is the maximum stress reached by the material during a full cycle.55,81 Following this definition, the dissipation mechanism can be classified in three extreme behaviours: (i) DR ≡ Ed/Edp = 1 purely plastic deformation, (ii) DR = 0 purely elastic deformation, (iii) DR = 0.785 Newtonian fluid deformation.81
and the energy dissipated by a perfect plastic material at the same deformation value, obtained as Edp = 4γ0σmax, where σmax is the maximum stress reached by the material during a full cycle.55,81 Following this definition, the dissipation mechanism can be classified in three extreme behaviours: (i) DR ≡ Ed/Edp = 1 purely plastic deformation, (ii) DR = 0 purely elastic deformation, (iii) DR = 0.785 Newtonian fluid deformation.81
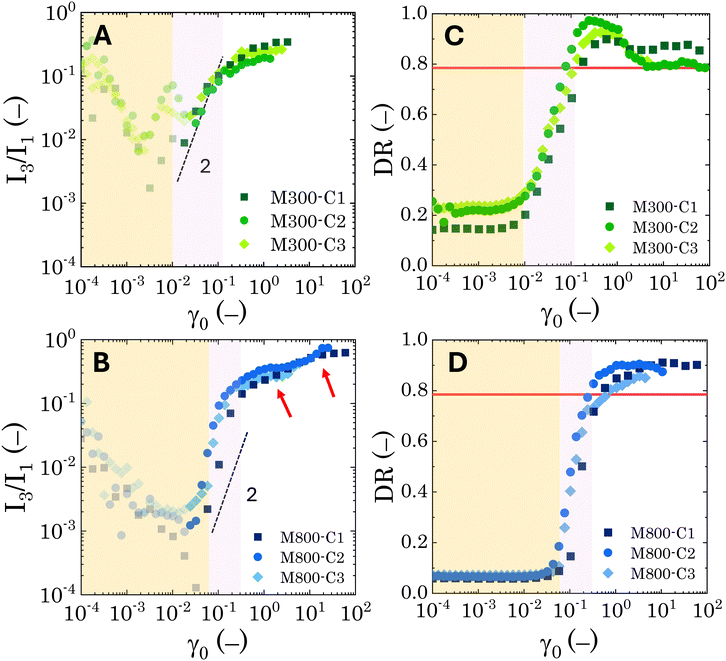
While no significant dependence on microgel loading is observed for either microgel sizes (M300 or M800), the results reveal clear differences in the nonlinear behaviour between the two PEs types. For M300-stabilised PEs, above the instrumentation limits (i.e. semi-transparent symbols in Fig. 7A and B), the coefficient I3/I1 follows a power-law trend with an exponent of approximately 2 within the MAOS region, where yielding occurs. This aligns with observations in the literature, which report a similar coefficient for soft glassy systems.55,82 Beyond the MAOS region, I3/I1 plateaus at a constant value of approximately 0.25. In contrast, M800-stabilised PEs exhibit a sharper rise in the I3/I1 ratio, starting just before the end of the LVER, and increasing with a power-law exponent slightly higher than 2 during yielding. This sharper rise, corresponding to a narrower yielding window, is then followed by a first plateau at 0.36, a second small rise around γ0 = 3, and finally another plateau at a higher value of 0.65. The higher plateau values, together with the occurrence of multiple flow steps, suggest stronger nonlinearities associated to multiple restructuring events within the emulsions. Here, smaller-scale rearrangements within clusters might occur first, followed by cluster breakage at higher deformations. Notably, the presence of these plateaus indicates that the emulsions maintain some structure even at high deformations and for effective volume fractions below 0.64 (as observed for sample M800-C3).
Similar conclusions can be drawn from the analysis of the dissipation ratio, Fig. 7C and D. In the initial LVER, for both PE types, the low DR values indicate a predominantly elastic response. Specifically, for M800-stabilised PEs, the initial DR plateaus at around 0.065 for all microgel loadings. Conversely, M300-stabilised PEs exhibit some variability, with progressively higher LVE plateaus ranging from 0.14 to 0.2, indicating overall a bigger deviation from the pure elastic regime compared to M800 samples. A sharp increase in DR is observed as the LVER is surpassed. Notably, for samples M800, DR increases with a power-law of 2 during yielding, independent of microgel loading. In contrast, M300-stabilised PEs display a smoother increase with a power-law of approximately 0.5 (see Fig. S.5 in the ESI,† for log-scale plots). After the yielding transition, the DR for M800 samples plateaus at high values ∼0.9, indicating a tendency towards plastic dissipation.55 Conversely, M300-stabilised PEs exhibit a peak in plasticity, just after yielding, followed by a return to a Newtonian-like behaviour. This further corroborates the structural differences between the two PE types, with M800-stabilised PEs exhibiting greater interconnectivity and more microstructural rearrangements. To gain further insights into the transient rheological behaviour that these two types of PEs undergo during larger strain amplitudes, we report the evolution of the Cole–Cole trajectories of the transient storage  and loss
and loss  moduli for two indicative samples, i.e. M300-C1 and M800-C1 (Fig. 8A and B).
moduli for two indicative samples, i.e. M300-C1 and M800-C1 (Fig. 8A and B).
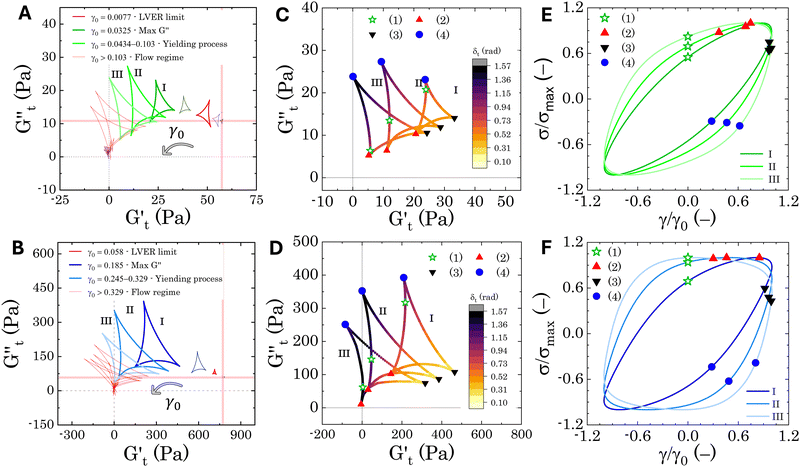
The Cole–Cole plots for both samples exhibit the characteristic deltoid shape, reflecting the dominance of the third harmonic.52,54,83 However, the orientation and enclosed area of the cycles progressively change with increasing strain amplitude. These two features offer valuable insights into the sequence of microstructural rearrangements the material undergoes during each oscillation cycle. The orientation of the trajectory reflects the nature of the material's deformation transition, while the enclosed areas relate to the extent of intra-cycle rheological transitions. A larger enclosed area indicates a broader spectrum of microstructural rearrangements within the material.55,83 Notably, in the LVER the size of the deltoids in both cases is significantly small, with the values of 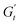 and
and 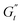 converging to the values of
converging to the values of 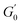 and
and 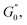 respectively. Increasing strain amplitude leads to a departure from linearity, as evidenced by the evolving orientation and size of the deltoid curves in the Cole–Cole plots (Fig. 8A and B). Interestingly, key distinctions in the evolution are observed between the two PEs types. For M300-stabilised PEs, the deltoid trajectories maintain a similar orientation after departing from the LVER (e.g., magenta curve in Fig. 8A) and the areas progressively grow until the final yielding point (see Fig. S.6 in the ESI,† reporting the evolution of the areas of the deltoids, AD, normalised by the area in the LVER, AD0). Beyond this point, the size of the deltoids decreases again, until reaching very small areas at γ0 > 1. These results imply that PEs stabilised with small microgels undergo their widest range of microstructural rearrangements around the yield point, where the solid-to-liquid transition is accompanied by some degree of structural recovery.54,55,83 However, at even higher strains, the structure breaks down more severely, hindering recovery and leading to a complete collapse of the microstructure. In contrast, the area changes for M800-stabilised PEs exhibit a less gradual increase, with a rapid rise observed around the G′′ overshoot. After the yield point, the areas decrease progressively but remain at relatively high values (see Fig. S.6 in the ESI†). This trend reinforces the presence of a more interconnected network within PEs stabilised by larger microgels. Here, the droplet clusters are capable of yielding and recovering within each deformation cycle, demonstrating resilience against complete breakdown at the tested amplitudes. The difference in microstructure between the two types of PEs is further evident in the details of the trajectories around the yielding point.
respectively. Increasing strain amplitude leads to a departure from linearity, as evidenced by the evolving orientation and size of the deltoid curves in the Cole–Cole plots (Fig. 8A and B). Interestingly, key distinctions in the evolution are observed between the two PEs types. For M300-stabilised PEs, the deltoid trajectories maintain a similar orientation after departing from the LVER (e.g., magenta curve in Fig. 8A) and the areas progressively grow until the final yielding point (see Fig. S.6 in the ESI,† reporting the evolution of the areas of the deltoids, AD, normalised by the area in the LVER, AD0). Beyond this point, the size of the deltoids decreases again, until reaching very small areas at γ0 > 1. These results imply that PEs stabilised with small microgels undergo their widest range of microstructural rearrangements around the yield point, where the solid-to-liquid transition is accompanied by some degree of structural recovery.54,55,83 However, at even higher strains, the structure breaks down more severely, hindering recovery and leading to a complete collapse of the microstructure. In contrast, the area changes for M800-stabilised PEs exhibit a less gradual increase, with a rapid rise observed around the G′′ overshoot. After the yield point, the areas decrease progressively but remain at relatively high values (see Fig. S.6 in the ESI†). This trend reinforces the presence of a more interconnected network within PEs stabilised by larger microgels. Here, the droplet clusters are capable of yielding and recovering within each deformation cycle, demonstrating resilience against complete breakdown at the tested amplitudes. The difference in microstructure between the two types of PEs is further evident in the details of the trajectories around the yielding point.
In Fig. 8C and D, we report the trajectories obtained for M300- and M800-stabilised PEs, respectively, including a colormap of the instantaneous phase angle, δt. This value directly indicates the type of transition the material undergoes at each point within the deformation cycle. Typically, δt < 0.785 suggest elastic behaviour, while values exceeding 0.785 indicate liquid-like behaviour.53,55 The colormap clearly reveals that sample M800-C1 experiences more extensive structural rearrangements. This is evident from the wider range of δt values spanned within a single cycle for this sample compared to M300-C1. In particular, M300-C1 exhibits a more progressive yielding process (Fig. 8C–E). Trajectory I, starting from an initial instantaneous strain equal to zero (point 1), shows a strong initial thinning with minimal softening, leading to a minimum in both 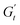 and
and 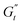 at point 2. During this transition, both the strain amplitude and the total instantaneous stress are increasing, as can be seen in the Lissajous-Bodwditch plots in Fig. 8E, indicating the breakdown of the initial structure as strain increases. As the strain reaches its maximum and reverses (point 2 to 3), the emulsion experiences a restructuring, indicated by rising
at point 2. During this transition, both the strain amplitude and the total instantaneous stress are increasing, as can be seen in the Lissajous-Bodwditch plots in Fig. 8E, indicating the breakdown of the initial structure as strain increases. As the strain reaches its maximum and reverses (point 2 to 3), the emulsion experiences a restructuring, indicated by rising 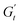 and
and 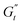 values (coupled thickening/stiffening). As the flow reverses in the opposite direction, approaching again an instantaneous strain of zero, the structure breaks down, dissipating stored elasticity and reaching a maximum
values (coupled thickening/stiffening). As the flow reverses in the opposite direction, approaching again an instantaneous strain of zero, the structure breaks down, dissipating stored elasticity and reaching a maximum 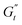 (point 3 to point 4). Beyond this point, the structure thins again, returning to its initial state and repeating the cycle. This qualitative behaviour persists at higher nominal strain amplitudes (trajectories II and III), with a gradual reorientation of the deltoids towards a more plastic response. The initial stress increase becomes weaker, and the structure exhibits more liquid-like behaviour later in the cycle, as shown by the δt colormap.
(point 3 to point 4). Beyond this point, the structure thins again, returning to its initial state and repeating the cycle. This qualitative behaviour persists at higher nominal strain amplitudes (trajectories II and III), with a gradual reorientation of the deltoids towards a more plastic response. The initial stress increase becomes weaker, and the structure exhibits more liquid-like behaviour later in the cycle, as shown by the δt colormap.
Sample M800-C1 displays a different response around the yielding point (Fig. 8D–F). Trajectory I, corresponding to the G′′ overshoot, shares some similarities with M300-C1, but the δt colormap indicates a wider range of restructuring within the material. As the strain amplitude increases (trajectory II), the behaviour transitions to a plastic-type response, as shown by the quasi-constant stress response with an increase of the instantaneous strain amplitude (point 1 to 2 in Fig. 8F), followed by strain-thinning at a higher nominal strain amplitude (trajectory III). This transition corresponds to the G′/G′′ crossover point. Here, 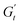 becomes negative and the total stress slightly reduces, indicating a softening of the microstructure and suggesting complete material flow (1 to 2). As the strain increases further and reverses, the structure first undergoes a nearly purely viscous thickening, followed by purely elastic stiffening until reaching the maximum
becomes negative and the total stress slightly reduces, indicating a softening of the microstructure and suggesting complete material flow (1 to 2). As the strain increases further and reverses, the structure first undergoes a nearly purely viscous thickening, followed by purely elastic stiffening until reaching the maximum 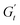 (2 to 3). During the subsequent strain reversal (3 to 4), the accumulated elastic energy dissipates viscously, indicating disruption of the internal microstructure. This process continues until a purely viscous regime is reached (negative
(2 to 3). During the subsequent strain reversal (3 to 4), the accumulated elastic energy dissipates viscously, indicating disruption of the internal microstructure. This process continues until a purely viscous regime is reached (negative 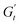 ). A negative
). A negative 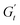 signifies that stress decreases with increasing strain, reflecting a shift from elastic storage to complete viscous dissipation.52,53,83 This indicates complete yielding and flow behaviour by point 4. Finally, as the strain returns to zero, viscous dissipation reduces, and the elastic modulus gradually recovers, closing the loop at point 1.
signifies that stress decreases with increasing strain, reflecting a shift from elastic storage to complete viscous dissipation.52,53,83 This indicates complete yielding and flow behaviour by point 4. Finally, as the strain returns to zero, viscous dissipation reduces, and the elastic modulus gradually recovers, closing the loop at point 1.
Overall, the intracycle analysis reveals that M300-stabilised PEs experience yielding through disruption and deformation of the close-packed droplet cages. In contrast, M800-stabilised PEs exhibit a more complex yielding process due to the presence of droplet clusters. These clusters introduce greater heterogeneity within the sample, leading to progressive deformation, stretching, and flow of the initial microstructure as the strain amplitude increases. These results reveal a clear difference in the microstructure of the two types of PEs, which is crucial for optimizing their application in transdermal drug delivery. For instance, M800-stabilised PEs, characterised by more complex droplet clusters, might exhibit a slower and potentially controlled release profile. The following section delves into the transdermal drug delivery properties of these PEs, exploring how the observed microstructural variations translate to drug release kinetics.
3.5 Transdermal release properties
The release profiles of all the investigated PEs are evaluated at room temperature and at physiological temperature (37 °C) using the procedure described in Section 2.4. Fig. 9A presents representative curves for the normalised cumulative release of samples M300-C1/C3 and M800-C1/C3 at room temperature. This comparison emphasises the impact of microgel loading on the release profiles. Fig. 9B focuses on the thermoresponsive behaviour by depicting the normalised cumulative release of samples M300-C1 and M800-C1 at both room and physiological temperatures. All samples exhibit a cumulative release trend characteristic of diffusion-controlled kinetics.2,84 This is typically characterised by an initial, steeper rise in concentration followed by a plateau as time approaches infinity. The release profiles clearly demonstrate the influence of both microgel loading and temperature. Interestingly, the bulk rheological properties do not appear to directly govern the release kinetics. This is evident from the slower release observed for sample M300-C1 compared to M800-C3 (Fig. 9A), despite M300-C1 having a lower storage modulus and yield stress (by 1 and 2 orders of magnitude, respectively). Conversely, a higher microgel loading appears to slow down the release kinetics, suggesting that the presence of microgels within the PEs structure contributes to the controlled release mechanism. Another intriguing observation is the significant decrease in release rate at higher temperatures for all samples. This might seem counter intuitive, as temperatures exceeding the microgel volume phase transition temperature (VPTT) are typically expected to induce phase separation in PEs due to the collapsed state of the microgels, thus causing release of the species from the single droplets acting as drug carriers.42,85 However, the appearance of the PEs in the donor chamber after the release experiment is strikingly different for samples stored at physiological temperature (Fig. 9C). While room temperature samples retain their original consistency with some creaming, those exposed to 37 °C appear as textured cylindrical structures. To further investigate their internal structure, we sectioned a portion of these samples for observation under fluorescence microscopy. The results for reference samples M300-C3 and M800-C3 are shown in Fig. 9C. Bright areas represent the microgels, which are fluorescently labelled. As observed, microgels in both cases collapse, inducing significant clustering that immobilises the emulsions within a porous medium characterised by varying void sizes. M300-stabilized samples exhibit sparse round voids, left by oil droplets (as indicated by the arrows in Fig. 9C), while the dense microgel structures within the droplet clusters of M800-stabilised samples make it more challenging to distinguish individual voids.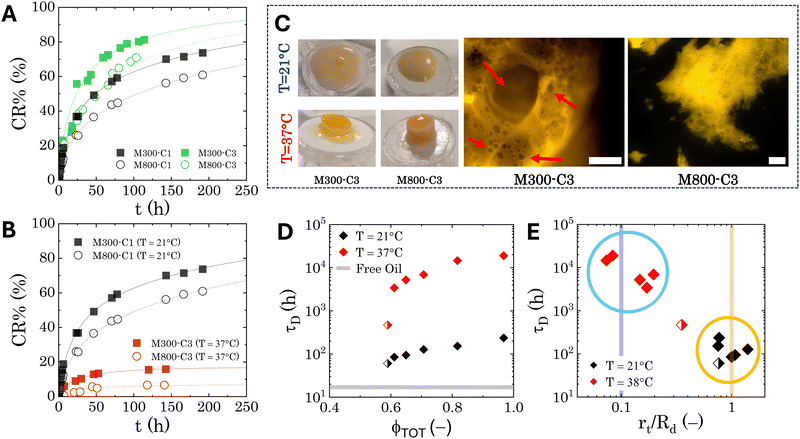 | ||
| Fig. 9 Transdermal drug release model: results. (A) Normalised cumulative drug release at room temperature for M300- and M800-stabilized PEs containing different loadings of microgels. (B) Normalised cumulative drug release for samples M300-C1 and M800-C1 at both room temperature and physiological temperature. In both panels, the lines represent the fitting of the data to eqn (7). (C) Left: General appearance of the PEs after the release tests (approximately 190 hours) at room temperature (top row) and physiological temperature (bottom row). Right: Details of the microstructure of the samples treated at physiological temperature, obtained through fluorescence microscopy. The scale bars indicate 250 μm. The red arrows indicates some of the round voids left by droplets. (D) Characteristic diffusion time as a function of the total dispersed phase volume fraction (ϕTOT). The grey line reports the reference value for simple jojoba oil. (E) Characteristic diffusion time as a function of the normalised characteristic dimension of the traps obtained from fitting of eqn (7). The two vertical lines indicate the order of magnitude of the droplet size (yellow line) and the microgel size (blue line). Half-filled symbols in panels (D) and (E) indicate the formulation with ϕTOT < 0.6. | ||
To gain a deeper understanding of the relationship between microstructure and release kinetics, and to obtain more quantitative results, we employ a semi-empirical model to analyse all the release profiles. Considering the microstructural features of both fresh and temperature-treated samples, along with the geometry of the Franz cell, we model the drug transport as a two-step diffusive process: (i) transport within the PEs and (ii) transport across the polysulfone membrane of the Franz cell. For the first diffusion mechanism, we utilize a model for species transport within a porous medium containing randomly distributed traps.86 This model predicts the following decay of concentration from the donor compartment:
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (t) ∼ exp[−(t/τD)d/(d+2)] (t) ∼ exp[−(t/τD)d/(d+2)] | (5) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (t) represents the remaining drug concentration at time t. τD is the characteristic diffusion time between traps, defined as
(t) represents the remaining drug concentration at time t. τD is the characteristic diffusion time between traps, defined as 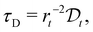 where rt represents the characteristic size of the traps, and
where rt represents the characteristic size of the traps, and 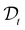 is the diffusion coefficient. Finally, d is the spatial dimension, which equals 3 for a 3D system, resulting in a total exponent of 0.6. The characteristics of the second diffusion mechanism are determined using a control experiment with pure jojoba oil. The release profile follows a first-order diffusion decay (see SI-3 in the ESI†) described by the following equation:
is the diffusion coefficient. Finally, d is the spatial dimension, which equals 3 for a 3D system, resulting in a total exponent of 0.6. The characteristics of the second diffusion mechanism are determined using a control experiment with pure jojoba oil. The release profile follows a first-order diffusion decay (see SI-3 in the ESI†) described by the following equation:![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (t) ∼ exp[−(t/τ0)] (t) ∼ exp[−(t/τ0)] | (6) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) (t) = k (t) = k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(t/τD)0.6] + (1 − k)exp(−t/τ0) exp[−(t/τD)0.6] + (1 − k)exp(−t/τ0) | (7) |
Table 1 summarises the fitting results for all investigated PEs. Because the presence of microgels in the continuous phase significantly alters the PEs microstructure at physiological temperature, we also report the total dispersed phase volume fraction, ϕTOT. This value is calculated as the sum of the effective volume fraction, ϕEFF, and the residual microgel volume fraction within the continuous phase, ϕm. Details regarding the calculations of these volume fractions can be found in the ESI,† S5. For all Pickering emulsions, the partition constant consistently exceeds 0.7, indicating that the first diffusion mechanism within the PEs remains the dominant factor controlling release kinetics under all tested conditions. Notably, M800-stabilised samples exhibit significantly higher partition constant values, with most exceeding 0.9. This could be attributed to a higher degree of interconnection between droplets within M800-stabilised PEs and a lower residual microgel content in the continuous phase. This combination results in a more interconnected porous structure, where the porosity is primarily dictated by the distribution of droplets. Interestingly, when plotting the characteristic diffusion times against the total volume fraction ϕTOT, we observe two distinct trends for each temperature, as shown in Fig. 9D. In both cases, the characteristic release time exhibits a strong positive correlation with the total volume fraction, showing an initial jump at a threshold value around 0.6, which is close to random packing conditions. At physiological temperature, when the microgels deswell, the entire curve shifts upwards by two orders of magnitude. This shift indicates a significant change in the characteristic size of the porosity of the material. To further investigate this, Fig. 9E plots the characteristic times against the characteristic size of the traps, normalised by the average radius of the droplets for each formulation. This visualisation reveals a transition in the dominant trap size. At room temperature, the characteristic size falls within the same order of magnitude as the droplet size. However, at physiological temperature, the characteristic size becomes comparable to the size of the microgels. The shift observed might be related to an increase in polymer density at the oil–water interface upon heating, caused by the hydrophobic collapse of the microgel network.87 Additionally, the change in hydrophobicity can alter the interactions of the drug with the polymeric chains of the microgels, thus slowing down the release. Further investigations to properly characterise the mechanism at hand are surely required, however the present results highlight the crucial role of the local microstructure of the PEs in regulating sustained drug release.
| Sample | ϕ TOT | τ D (h) | k | |
|---|---|---|---|---|
| T = 21 °C | M300-C1 | 0.817 | 152.9 | 0.808 |
| M300-C2 | 0.707 | 127.54 | 0.851 | |
| M300-C3 | 0.59 | 60.45 | 0.783 | |
| M800-C1 | 0.967 | 236.5 | 0.925 | |
| M800-C2 | 0.65 | 94.5 | 0.953 | |
| M800-C3 | 0.611 | 84.96 | 1 | |
| T = 37 °C | M300-C1 | 0.817 | 1.46 × 10+4 | 0.894 |
| M300-C2 | 0.707 | 6.88 × 10+2 | 0.8 | |
| M300-C3 | 0.59 | 4.70 × 10+2 | 0.707 | |
| M800-C1 | 0.967 | 1.9 × 10+4 | 0.981 | |
| M800-C2 | 0.65 | 5.21 × 10+3 | 0.917 | |
| M800-C3 | 0.611 | 3.41 × 10+3 | 0.854 | |
4 Conclusions
In this study, we investigate how microgel size and thermoresponsive behaviour specifically influence the microstructure and rheology of Pickering emulsions to aid the design of transdermal drug delivery systems. To this end, we use model PEs stabilised with pNIPAM-based microgels of two distinct sizes (M300 and M800). PNIPAM microgels were chosen due to their well-established thermal responsiveness, allowing us to control their swelling behaviour using temperature as an external stimulus. The size of the resulting droplets was analysed using bright-field microscopy, while confocal microscopy revealed the arrangement of microgels at the droplet interface. Rheological properties were characterised using strain amplitude oscillatory sweep measurements and time-resolved analysis. Finally, the sustained release of levosimendan, a model lipophilic drug, was evaluated via the Franz-cell method at both room and physiological temperatures.The microscopic analysis confirms that microgel size significantly affects microgel arrangement and interfacial coverage, ultimately impacting the PEs' rheological behaviour. Smaller M300 microgels form a more uniform and densely packed layer around the droplets, leading to less aggregation compared to PEs stabilised with larger M800 microgels. This difference in interfacial organisation translates to distinct rheological behaviours of the different formulations. More dispersed droplets with minimal inter-droplet connections exhibit a more fluid-like behaviour, while the presence of droplet clusters in the larger-microgel PEs introduces a more complex yielding process. The analysis of the intracycle nonlinear stress response suggests that M300-stabilised PEs yield through disruption and deformation of the close-packed droplet cages. In contrast, M800-stabilised PEs exhibit a more complex process due to rearrangements within the droplet clusters. These microstructural differences have a significant impact on the sustained drug release performance. For both PE types, the internal microstructure of the emulsions dominates the release kinetics. Notably, the characteristic release times directly correlate with the total volume fraction of the dispersed phases. The release mechanism can be modelled by considering the emulsion as a porous medium with randomly distributed traps. At room temperature, when the emulsions maintain their original structure, the characteristic size of these traps approximates the average droplet sizes. However, at physiological temperature, when the microgels significantly deswell, the characteristic release time increases significantly for both sets of PEs. Additionally, the dominant trap size shifts towards the microgel size. These findings highlight that microgel porosity also plays a crucial role in the sustained release of molecules from the PEs. It should be pointed out that, given the complex phase-change that the PEs undergo at physiological temperature, transient drug/MG interactions could also affect the release kinetics. Future studies should explore this aspect in more detail.
Overall, this study provides valuable insights into the relationship between microgel properties, microstructure, and the performance of PEs for drug delivery applications. In contrast to other drug delivery methods, such as hydrogel-based systems, where rheology and porosity are intrinsically linked, our study shows that PEs offer greater flexibility in decoupling rheological design from delivery properties. This decoupling allows for a wider range of formulation possibilities. Further investigations are required to explore the long-term stability and bio-compatibility of these PEs for in vivo applications, as well as the effect of shear flow on the release kinetics, relevant to the direct use of these formulation. Additionally, optimising the microgel design to achieve a balance between microstructure and desired release kinetics is an important area for future research.
Author contributions
Conceptualisation: SM, YL, PA, MP; data curation: SM, YL; formal analysis: SM; funding acquisition: YL, PA, SM; investigation: SM, YH; methodology: SM, YH; project administration: YL, PA, SM; resources: YL, PA, MP; supervision: YL, PA; visualization: SM; writing/original draft: SM; writing/review and editing: YL, PA, MP.Data availability
All the data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from UK Engineering and Physical Sciences Research Council (EPSRC) Programme Grant PREMIERE (PA, SM), HemoSmart Medical Technology Gift Fund (YL), CNIE Inspiration Grant (part of EPSRC “Frontier Engineering” (2015-2019)) (SM, YL), and China Scholarship Council (CSC) 202008430157 (YH).Notes and references
- J. Li and D. J. Mooney, Nat. Rev. Mater., 2016, 1, 1–17 Search PubMed.
- S. Hiranphinyophat, A. Otaka, Y. Asaumi, S. Fujii and Y. Iwasaki, Colloids Surf., B, 2021, 197, 111423 CrossRef CAS PubMed.
- K. Wood, M. R. Szewczuk, D. Rousseau and R. J. Neufeld, Oncotarget, 2018, 9, 12754–12768 CrossRef PubMed.
- C. Pacheco, A. Baião, T. Ding, W. Cui and B. Sarmento, Adv. Drug Delivery Rev., 2023, 194, 114724 CrossRef CAS PubMed.
- W. Y. Jeong, M. Kwon, H. E. Choi and K. S. Kim, Biomater. Res., 2021, 25, 24 CrossRef PubMed.
- M. I. Khan, M. I. Hossain, M. K. Hossain, M. H. K. Rubel, K. M. Hossain, A. M. U. B. Mahfuz and M. I. Anik, ACS Appl. Bio Mater., 2022, 5, 971–1012 CrossRef CAS PubMed.
- J. Marto, A. Ascenso, S. Simoes, A. J. Almeida and H. M. Ribeiro, Expert Opin. Drug Delivery, 2016, 13, 1093–1107 CrossRef CAS PubMed.
- S. Peito, D. Peixoto, I. Ferreira-Faria, A. Margarida Martins, H. Margarida Ribeiro, F. Veiga, J. Marto and A. Cláudia Paiva-Santos, Int. J. Pharm., 2022, 615, 121455 CrossRef CAS PubMed.
- F. Sabbagh and B. S. Kim, J. Controlled Release, 2022, 341, 132–146 CrossRef CAS PubMed.
- V. Phatale, K. K. Vaiphei, S. Jha, D. Patil, M. Agrawal and A. Alexander, J. Controlled Release, 2022, 351, 361–380 CrossRef CAS PubMed.
- S. Chaturvedi and A. Garg, J. Drug Delivery Sci. Technol., 2021, 62, 102355 CrossRef CAS.
- A. Sharkawy, F. M. Casimiro, M. F. Barreiro and A. E. Rodrigues, Int. J. Biol. Macromol., 2020, 147, 150–159 CrossRef CAS PubMed.
- F. B. de Carvalho-Guimarães, K. L. Correa, T. P. de Souza, J. R. Rodríguez Amado, R. M. Ribeiro-Costa and J. O. C. Silva-Júnior, Pharmaceuticals, 2022, 15, 1413 CrossRef PubMed.
- R. Valjakka-Koskela, J. Hirvonen, J. Mönkkönen, J. Kiesvaara, S. Antila, L. Lehtonen and A. Urtti, Eur. J. Pharm. Sci., 2000, 11, 343–350 CrossRef CAS PubMed.
- R. S. Riley, C. H. June, R. Langer and M. J. Mitchell, Nat. Rev. Drug Discovery, 2019, 18, 175–196 CrossRef CAS PubMed.
- G. Agrawal and R. Agrawal, Polymers, 2018, 10, 418 CrossRef PubMed.
- B. Wu, Y. Li, Y. Li, H. Li, S. Ji and Q. Xia, React. Funct. Polym., 2021, 169, 105074 CrossRef CAS.
- B. Pang, H. Liu and K. Zhang, Adv. Colloid Interface Sci., 2021, 296, 102522 CrossRef CAS PubMed.
- T. Zhang, F. Liu, J. Wu and T. Ngai, Particuology, 2022, 64, 110–120 CrossRef CAS.
- H. Jiang, Y. Sheng and T. Ngai, Curr. Opin. Colloid Interface Sci., 2020, 49, 1–15 CrossRef CAS PubMed.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed.
- M. Rey, M. A. Fernandez-Rodriguez, M. Karg, L. Isa and N. Vogel, Acc. Chem. Res., 2020, 53, 414–424 CrossRef CAS PubMed.
- M. A. Fernandez-Rodriguez, A. Martín-Molina and J. Maldonado-Valderrama, Adv. Colloid Interface Sci., 2021, 288, 102350 CrossRef CAS PubMed.
- F. Pinaud, K. Geisel, P. Massé, B. Catargi, L. Isa, W. Richtering, V. Ravaine and V. Schmitt, Soft Matter, 2014, 10, 6963–6974 RSC.
- S. Migliozzi, Y. He, P. Angeli and Y. Lan, Colloids Surf., A, 2024, 134538 CrossRef CAS.
- M. Destribats, V. Lapeyre, M. Wolfs, E. Sellier, F. Leal-Calderon, V. Ravaine and V. Schmitt, Soft Matter, 2011, 7, 7689–7698 RSC.
- M. Destribats, M. Eyharts, V. Lapeyre, E. Sellier, I. Varga, V. Ravaine and V. Schmitt, Langmuir, 2014, 30, 1768–1777 CrossRef CAS PubMed.
- M. M. Schmidt, S. Bochenek, A. A. Gavrilov, I. I. Potemkin and W. Richtering, Langmuir, 2020, 36, 11079–11093 CrossRef CAS PubMed.
- S. Aben, C. Holtze, T. Tadros and P. Schurtenberger, Langmuir, 2012, 28, 7967–7975 CrossRef CAS PubMed.
- T. G. Mason, J. Bibette and D. A. Weitz, Phys. Rev. Lett., 1995, 75, 2051–2054 CrossRef CAS PubMed.
- B. P. Binks, J. H. Clint and C. P. Whitby, Langmuir, 2005, 21, 5307–5316 CrossRef CAS PubMed.
- S. S. Datta, D. D. Gerrard, T. S. Rhodes, T. G. Mason and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041404 CrossRef PubMed.
- M. Kaganyuk and A. Mohraz, J. Colloid Interface Sci., 2019, 540, 197–206 CrossRef CAS PubMed.
- J. S. Hong, H. J. Kong, K. Hyun, J. Bergfreund, P. Fischer and K. H. Ahn, Rheol. Acta, 2019, 58, 453–466 CrossRef CAS.
- J. Hou, H.-N. Xu, L. Wang and L. Zhang, Langmuir, 2022, 38, 4599–4605 CrossRef CAS PubMed.
- P. L. Fuhrmann, S. Breunig, G. Sala, L. Sagis, M. Stieger and E. Scholten, J. Colloid Interface Sci., 2022, 607, 389–400 CrossRef CAS PubMed.
- W. Jin, J. Zhu, Y. Jiang, P. Shao, B. Li and Q. Huang, J. Agric. Food Chem., 2017, 65, 1401–1409 CrossRef CAS PubMed.
- Y. Chen, W. Wei, Y. Zhu, J. Luo, R. Liu and X. Liu, ACS Appl. Mater. Interfaces, 2020, 12, 4821–4832 CrossRef CAS PubMed.
- Y. Ming, Y. Xia and G. Ma, Aggregate, 2022, 3, e162 CrossRef CAS.
- L. Dai, Y. Li, F. Kong, K. Liu, C. Si and Y. Ni, ACS Sustainable Chem. Eng., 2019, 7, 13497–13504 CrossRef CAS.
- M.-h Kwok, J. Ambreen and T. Ngai, J. Colloid Interface Sci., 2019, 546, 293–302 CrossRef CAS PubMed.
- T. Ngai, S. H. Behrens and H. Auweter, Chem. Commun., 2005, 331–333 RSC.
- X. Wang, X. Qiu and C. Wu, Macromolecules, 1998, 31, 2972–2976 CrossRef CAS.
- R. Neupane, S. H. Boddu, J. Renukuntla, R. J. Babu and A. K. Tiwari, Pharmaceutics, 2020, 12(2), 152 CrossRef CAS PubMed.
- F. Iliopoulos, P. J. Caspers, G. J. Puppels and M. E. Lane, Pharmaceutics, 2020, 12(9), 887 CrossRef CAS PubMed.
- X. Wu, R. Pelton, A. Hamielec, D. Woods and W. McPhee, Colloid Polym. Sci., 1994, 272, 467–477 CrossRef CAS.
- J. Liu, C. S. Y. Tan, Z. Yu, N. Li, C. Abell and O. A. Scherman, Adv. Mater., 2017, 29, 1605325 CrossRef PubMed.
- S. Arditty, C. Whitby, B. Binks, V. Schmitt and F. Leal-Calderon, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 11, 273–281 CrossRef CAS PubMed.
- S. A. Rogers, J. Rheol., 2012, 56, 1129–1151 CrossRef CAS.
- S. A. Rogers and M. P. Lettinga, J. Rheol., 2012, 56, 1–25 CrossRef CAS.
- S. A. Rogers, Rheol. Acta, 2017, 56, 501–525 CrossRef CAS.
- J. Choi, F. Nettesheim and S. A. Rogers, Phys. Fluids, 2019, 31, 073107 CrossRef.
- G. J. Donley, J. R. de Bruyn, G. H. McKinley and S. A. Rogers, J. Non-Newtonian Fluid Mech., 2019, 264, 117–134 CrossRef CAS.
- S. Migliozzi, P. Angeli and L. Mazzei, Materials, 2021, 14, 1782 CrossRef CAS PubMed.
- J. Xu, P. Wang, Z. Zhou, B. Yuan and H. Zhang, J. Rheol., 2024, 68, 491–508 CrossRef CAS.
- M. Wilhelm, D. Maring and H. W. Spiess, Rheol. Acta, 1998, 37, 399–405 CrossRef CAS.
- R. H. Ewoldt, A. E. Hosoi and G. H. McKinley, J. Rheol., 2008, 52, 1427–1458 CrossRef CAS.
- G. Del Monte, D. Truzzolillo, F. Camerin, A. Ninarello, E. Chauveau, L. Tavagnacco, N. Gnan, L. Rovigatti, S. Sennato and E. Zaccarelli, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2109560118 CrossRef PubMed.
- E. Ponomareva, B. Tadgell, M. Hildebrandt, M. Krüsmann, S. Prévost, P. Mulvaney and M. Karg, Soft Matter, 2022, 18, 807–825 RSC.
- R. Acciaro, T. Gilanyi and I. Varga, Langmuir, 2011, 27, 7917–7925 CrossRef CAS PubMed.
- R. Pelton, H. Pelton, A. Morphesis and R. Rowell, Langmuir, 1989, 5, 816–818 CrossRef CAS.
- D. Vlassopoulos and M. Cloitre, Curr. Opin. Colloid Interface Sci., 2014, 19, 561–574 CrossRef CAS.
- S. Migliozzi, G. Meridiano, P. Angeli and L. Mazzei, Soft Matter, 2020, 16, 9799–9815 RSC.
- M. Mooney, J. Colloid Sci., 1951, 6, 162–170 CrossRef CAS.
- V. Schmitt and V. Ravaine, Curr. Opin. Colloid Interface Sci., 2013, 18, 532–541 CrossRef CAS.
- M.-C. Tatry, E. Laurichesse, J. Vermant, V. Ravaine and V. Schmitt, J. Colloid Interface Sci., 2023, 629, 288–299 CrossRef CAS PubMed.
- E. L. Hinrichsen, J. Feder and T. Jøssang, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 4199–4209 CrossRef CAS.
- H. Zhao, Y. Yang, Y. Chen, J. Li, L. Wang and C. Li, Chem. Eng. Sci., 2022, 248, 117085 CrossRef CAS.
- M. Destribats, V. Lapeyre, E. Sellier, F. Leal-Calderon, V. Ravaine and V. Schmitt, Langmuir, 2012, 28, 3744–3755 CrossRef CAS PubMed.
- N. Koumakis, A. Pamvouxoglou, A. S. Poulos and G. Petekidis, Soft Matter, 2012, 8, 4271–4284 RSC.
- B. C. Munro, S. B. Hall and C. P. Whitby, Colloids Surf., A, 2022, 637, 128237 CrossRef CAS.
- K. Hyun, S. H. Kim, K. H. Ahn and S. J. Lee, J. Non-Newtonian Fluid Mech., 2002, 107, 51–65 CrossRef CAS.
- D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005 CrossRef.
- A. Ghosh, G. Chaudhary, J. G. Kang, P. V. Braun, R. H. Ewoldt and K. S. Schweizer, Soft Matter, 2019, 15, 1038–1052 RSC.
- M. Cloitre, R. Borrega, F. Monti and L. Leibler, Phys. Rev. Lett., 2003, 90, 068303 CrossRef PubMed.
- J. Seth, L. Mohan, C. Locatelli-Champagne, M. Cloitre and R. T. Bonnecanze, Nat. Mater., 2011, 10, 838–843 CrossRef CAS PubMed.
- C. P. Whitby and M. Krebsz, Soft Matter, 2014, 10, 4848–4854 RSC.
- N. Koumakis and G. Petekidis, Soft Matter, 2011, 7, 2456–2470 RSC.
- K. N. Pham, G. Petekidis, D. Vlassopoulos, S. U. Egelhaaf, W. C. K. Poon and P. N. Pusey, J. Rheol., 2008, 52, 649–676 CrossRef CAS.
- C. Pellet and M. Cloitre, Soft Matter, 2016, 12, 3710–3720 RSC.
- R. H. Ewoldt, P. Winter, J. Maxey and G. H. McKinley, Rheol. Acta, 2010, 49, 191–212 CrossRef CAS.
- S. Wojno, A. Ahlinder, A. Altskär, M. Stading, T. Abitbol and R. Kádár, Carbohydr. Polym., 2023, 308, 120622 CrossRef CAS PubMed.
- J. D. Park and S. A. Rogers, Phys. Fluids, 2020, 32, 063102 CrossRef CAS.
- J. Siepmann, F. Lecomte and R. Bodmeier, J. Controlled Release, 1999, 60, 379–389 CrossRef CAS PubMed.
- Z. Li, W. Richtering and T. Ngai, Soft Matter, 2014, 10, 6182–6191 RSC.
- D. Tartakovsky and M. Dentz, Transp. Porous Med., 2019, 130, 105–127 CrossRef.
- D. Kleinschmidt, K. Nothdurft, M. V. Anakhov, A. A. Meyer, M. Mork, R. A. Gumerov, I. I. Potemkin, W. Richtering and A. Pich, Mater. Adv., 2020, 1, 2983–2993 RSC.
Footnote |
† Electronic supplementary information (ESI) available: (S1) Theoretical interfacial coverage of the Pickering droplets; (S2) drug release experiments; (S3) Pickering emulsions general aspect; (S4) zero-shear elastic plateau  and yield stress σy as a function of microgel loading; (S5) calculation of the effective droplet volume fraction and of the total dispersed phases volume fraction; (S6) interfacial tension of the oil/microgel dispersions interface; (S7) additional graphs from strain amplitude sweep tests; (S8) small-amplitude oscillatory frequency sweeps. See DOI: https://doi.org/10.1039/d4sm00993b and yield stress σy as a function of microgel loading; (S5) calculation of the effective droplet volume fraction and of the total dispersed phases volume fraction; (S6) interfacial tension of the oil/microgel dispersions interface; (S7) additional graphs from strain amplitude sweep tests; (S8) small-amplitude oscillatory frequency sweeps. See DOI: https://doi.org/10.1039/d4sm00993b |
| This journal is © The Royal Society of Chemistry 2024 |