Open Access Article
Open Access ArticleA computational method for rapid analysis polymer structure and inverse design strategy (RAPSIDY)†
Vinson
Liao
 a,
Tristan
Myers
a,
Tristan
Myers
 a and
Arthi
Jayaraman
a and
Arthi
Jayaraman
 *abc
*abc
aDepartment of Chemical and Biomolecular Engineering, University of Delaware, Colburn Lab, 150 Academy Street, Newark, DE 19716, USA. E-mail: arthij@udel.edu
bDepartment of Materials Science and Engineering, University of Delaware, 201 DuPont Hall, Newark, Delaware 19716, USA
cData Science Institute, University of Delaware, Ammon Pinizzotto Biopharmaceutical Innovation Center, Suite 147, 590 Avenue 1743, Newark, DE 19713, USA
First published on 30th September 2024
Abstract
Tailoring polymers for target applications often involves selecting candidates from a large design parameter space including polymer chemistry, molar mass, sequence, and architecture, and linking each candidate to their assembled structures and in turn their properties. To accelerate this process, there is a critical need for inverse design of polymers and fast exploration of the structures they can form. This need has been particularly challenging to fulfill due to the multiple length scales and time scales of structural arrangements found in polymers that together give rise to the materials’ properties. In this work, we tackle this challenge by introducing a computational framework called RAPSIDY – Rapid Analysis of Polymer Structure and Inverse Design strategY. RAPSIDY enables inverse design of polymers by accelerating the evaluation of stability of multiscale structure for any given polymer design (sequence, composition, length). We use molecular dynamics simulations as the base method and apply a guiding potential to initialize polymers chains of a selected design within target morphologies. After initialization, the guiding potential is turned off, and we allow the chains and structure to relax. By evaluating similarity between the target morphology and the relaxed morphology for that polymer design, we can screen many polymer designs in a highly parallelized manner to rank designs that are likely to remain in that target morphology. We demonstrate how this method works using an example of a symmetric, linear pentablock, AxByAzByAx, copolymer system for which we determine polymer sequences that exhibit stable double gyroid morphology. Rather than trying to identify the global free-energy minimum morphology for a specific polymer design, we aim to identify candidates of polymer design parameter space that are more stable in the desired morphology than others. Our approach reduces computational costs for design parameter exploration by up to two orders-of-magnitude compared to traditional MD methods, thus accelerating design and engineering of novel polymer materials for target applications.
1. Introduction
Block copolymers (BCPs) are a class of macromolecules consisting of two or more monomers covalently linked together. BCPs have been shown to phase-separate into a variety of multiscale structures (or morphologies) to balance energetic driving forces arising from chemical incompatibility between the constituent monomers and entropic driving forces favoring mixed states.1–3 The multiple length scales, ranging from a few angstroms to hundreds of nanometers, of structural arrangements in the assembled morphology give rise to the macroscopic material properties4 which, in turn, make BCPs desirable for a variety of applications such as membranes,5 drug delivery,6 photovoltaics,7 and microelectronics.8 With advances in high-throughput techniques and synthetic schemes enabling higher precision in synthesis of polymers than ever before,9–13 there is a critical need for computational methods that can efficiently screen the optimal designs of polymers that lead to the desired multiscale arrangement of monomers and polymer chains and, in turn, the desired macroscale property.Rather than beginning with a set of design parameters (such as degree-of-polymerization and block composition) and determining the resulting equilibrium morphology and material property (also known as “forward design”),14 the inverse problem involves starting with a target morphology or material property and searching for designs that meet the specified criteria (also known as “inverse design”).15 Inverse design is challenging because it requires intelligent and efficient navigation of a high-dimensional design space and is often ill-posed (or weakly conditioned) with a non-unique solution.16 It also requires robust methods of forward design, and in the case of BCPs, efficient methodologies of determining the correct multi-length scale morphology for a chosen set of design parameters.
There are additional aspects of macromolecular materials that make this inverse-design problem more challenging than other classes of materials. Unlike inorganic materials whose precise crystalline structure (in most cases) gives rise to their properties, polymers properties are governed by a combination of disordered and ordered amorphous (non-crystalline), and in some cases, semi-crystalline, multiscale arrangements of monomers (angstroms), chains (1–10 nm), and domains (10 nm to microns). Furthermore, the free energy landscape of the assembled structures has several local minima leading to degeneracy in their spatial arrangements. Lastly, the design parameter space for polymer chains is much larger than that of small inorganic or organic molecules. If we consider the inverse design strategy for the simple case of linear diblock copolymers, one could independently vary the monomer chemistries A and B, their segregation strength χAB (or temperature), block compositions fA, and the degree-of-polymerization, N. Thus, even in the case of the simplest BCP, the number of unique designs is uncountably large and cannot be efficiently explored with naïve sampling approaches. This problem is only compounded as one increases the complexity of the BCP by introducing new chain design parameters such as varying the topology17,18 (i.e., linear, branched, etc.) and number of blocks (i.e., triblock, tetrablock, etc.). As such, the seemingly infinite size of the BCP design space has been dubbed the “ménages en blocs” problem in literature.19 Thus, any inverse design strategy must effectively and efficiently test the stability of desired multiscale assembled structures as one varies the synthetically feasible values of the copolymer design parameter space.
The seemingly infinite design space of block copolymers has led to the development of theoretical and computational approaches for “forward design”. Field-theoretic methods, in which discrete coarse-grained polymer chains are approximated in a mean-field manner, has emerged as a powerful tool for forward modeling and has been applied to a wide range of interacting polymer systems. Energetic interactions are described using an effective Hamiltonian, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , and explicitly depend on system parameters like effective interaction strength and chain architecture. There are two major categories of field-based methods, the first of which is self-consistent field theory20,21 (SCFT), and the second of which are field-theoretic simulations22,23 (FTS). Both methods seek to find solutions and corresponding free energy minima within the theoretical Hamiltonian framework. SCFT seeks to find saddle points of
, and explicitly depend on system parameters like effective interaction strength and chain architecture. There are two major categories of field-based methods, the first of which is self-consistent field theory20,21 (SCFT), and the second of which are field-theoretic simulations22,23 (FTS). Both methods seek to find solutions and corresponding free energy minima within the theoretical Hamiltonian framework. SCFT seeks to find saddle points of ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , and neglects system fluctuations, and solves the governing equations deterministically. FTS incorporates system fluctuations through stochastic sampling, thus sampling a distribution of saddle points. Field-based methods have shown success in reproducing experimentally derived phase diagrams for block copolymers, determining order–disorder transition (ODT) temperatures, and has aided in the discovery of novel BCP morphologies.24–26
, and neglects system fluctuations, and solves the governing equations deterministically. FTS incorporates system fluctuations through stochastic sampling, thus sampling a distribution of saddle points. Field-based methods have shown success in reproducing experimentally derived phase diagrams for block copolymers, determining order–disorder transition (ODT) temperatures, and has aided in the discovery of novel BCP morphologies.24–26
The success of field-based methods as engines for forward design has led to their use for driving efficient inverse design. For example, Tsai and Fredrickson use a global optimization technique, known as particle swarm optimization (PSO), in tandem with SCFT, and developed a combined method termed PSO-SCFT, to determine novel, globally stable and low-lying meta-stable morphologies of block copolymers.27 The authors benchmarked PSO-SCFT by recovering existing globally stable morphologies of two systems, (1) AB diblock copolymer and (2) miktoarm star polymer AB4, which both have well-established phase diagrams, and discovered a novel, energetically competitive, “mystery” morphology for miktoarm AB4 polymer. Work by Khadilkar et al. also used PSO as a global optimizer driven by SCFT for the inverse design of multiblock polymers to target 3D network morphologies within the high-dimensional parameter space.28 They optimize parameters such as block fraction, blend fractions, and interaction strength to directly determine viable designs. While field-based methods have shown promise in accelerating block copolymer design, these methods (a) sacrifice molecular details, such as configurations and dynamics of individual polymer chains, (b) are only valid at the limit of infinite chain length, and (c) neglect excluded volume interactions. These molecular details are important in determining macroscopic properties such as mechanical strength, viscosity, and thermal conductivity.29–31 Particle-based simulations, such as molecular dynamics simulations, provide chain level details and enable computations of macroscopic material properties such as tensile strength and transport properties,32,33 but are often expensive, especially for dense polymer melts, due to slow system dynamics.34
In this work, we introduce a high-throughput computational framework for the inverse design of self-assembled block copolymers for targeted morphologies; an approach we named RAPSIDY – Rapid Analysis of Polymer Structure and Inverse Design strategY. Using molecular dynamics (MD) simulations and an external guiding potential, we preplace polymer chains with a chosen chain design within a specified target morphology, a process we call structural biasing. We study the relative stability and compatibility between the chosen sequence design and targeted morphology. Our goal is not to identify the global free-energy minimum morphology for a polymer design but rather to identify viable candidates within the polymer design parameter space that are more stable in the desired morphology than others. We measure relative morphological stability using a stability metric that compares the scattering profiles of the structures against the target structure. Finally, the design loop is closed by repeating this process, now with a different sequence design.
Our methodology accelerates design space exploration by two orders-of-magnitude over traditional molecular dynamics simulation methods used in forward modeling and is designed for parallelization and high-throughput screening. We showcase our methodology by identifying symmetric, linear pentablock copolymer AxByAzByAx designs that exhibit stable double gyroid morphology, a highly desirable microphase separated structure for applications that need favorable mechanical and transport properties. Our pipeline directly addresses the traditional difficult inverse design problem and aids in the intelligent engineering of novel, next-generation high-performance polymeric materials.
2. Polymer coarse-grained (CG) model
For this work, we focus our efforts on studying a symmetric, linear pentablock copolymer (pentaBCP) AxByAzByAx system, where both the degree of polymerization (DP) of the end A blocks are equivalent and the DP of the middle B blocks are equivalent. We chose this specific polymer because we have extensive results from our recent work using traditional forward modeling methods of molecular dynamics and self-consistent field theory which we use to benchmark computational times and compare results to.35 Our recent work shows that the melt phase behavior of this specific pentaBCP with equal statistical segment lengths (bA = bB), at a given segregation strength, χ, can be expressed in terms of two independent variables: (1) the total volume fraction of A, fA = (2x + z)/N, and (2) the volume fraction of A that is within the middle block versus the total volume fraction of A, τA = z/(2x + z), where x and z refer to the A block DPs of the AxByAzByAx pentaBCP and N is the total number of Kuhn segments. Even though we restrict our demonstration of RAPSIDY in this paper to this specific pentaBCP, the methodologies developed in this work can be extended to the any one of the intractable designs among the vast BCP design space and are not limited to symmetric, linear pentaBCPs, which we simply use as a benchmark system.We model each pentaBCP as a coarse-grained (CG) bead-spring chain with two types of beads (hereon, referred to as A and B) with each bead size chosen to be the statistical segment length b of that monomer; we consider the case where bA = bB = 1σ. The adjacent beads in each chain are connected via harmonic bonds with a potential of the form, Ubond(r) = kbond(r − r0)2. Here, r refers to the bead–bead separation measured from the center of each bead and r0 is the equilibrium bond length. The equilibrium bond length, r0, is set to the arithmetic mean of the statistical segment length of the two species involved, which, in our case, is 1σ. The force constant is set to kbond = 50kbT/σ2. Each polymer chain in our study consists of N beads. We model the pentaBCP polymers as flexible chains and, therefore, do not employ any angle or torsional/dihedral potentials.
All pairs of nonbonded beads interact via a cut-and-shifted LJ potential, Ucut:
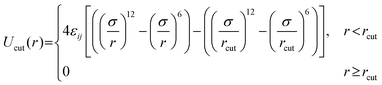 | (1) |
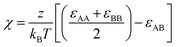 | (2) |
3. RAPSIDY approach
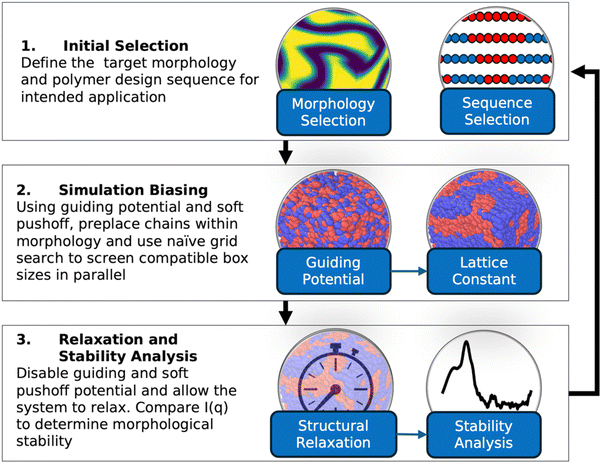
Fig. 1 shows a schematic of the RAPSIDY framework which is composed of three major steps: (1) initial selection, (2) structural biasing, and (3) structural relaxation and stability analysis. The workflow begins with an initial selection of a target morphology for inverse design and a test BCP design sequence. Next, using a method which we call “structural biasing”, we directly place the polymer chains in a simulation box within the targeted morphology using an external guiding potential and a soft pushoff potential. We screen multiple lattice constants in parallel using a grid-search approach to determine compatible periodic box sizes. Finally, in the structural relaxation and stability analysis step, we use MD simulations to let the system relax without any bias to its global free energy minimum (equilibrium structure) or one of its local free energy minima (metastable structure) by replacing the guiding and soft pushoff potentials with the system's natural non-bonded and bonded potentials. We analyze the relaxation trajectory to quantitatively determine the stability of the targeted morphology with the selected polymer design by comparing the computed scattering profiles of structures during relaxation and the scattering profile of the target morphology. Finally, the design loop is closed and repeated with the selection of another design sequence in an efficient and parallelizable nature that allows for high-throughput screening of the design space. Our pipeline is highly amenable to high-performance computing and machine learning methodologies, like active learning,38 to quickly and optimally query points within a high-dimensional BCP design space. In the subsequent sections, we elaborate on each step of RAPSIDY and demonstrate the efficiency of our methodology compared to traditional MD simulations for determining viable double gyroid polymer design sequences within the symmetric, linear pentablock copolymer design space. We showcase that RAPSIDY can independently screen many block copolymer designs using multiple CPUs and accelerates computational wall times required by two orders of magnitude over traditional MD, even when using a naïve grid-search approach. Incorporating optimal design space querying to RAPSIDY using machine learning based active learning is the scope of future work.3.1. Copolymer designs and target morphologies
We benchmark our inverse design methodology on a model symmetric, linear AxByAzByAx pentaBCP system with A and B having same statistical segment length. At any value of χ that defines the extent of incompatibility between A and B, we can define the design space of our system in terms of two variables: (1) the volume fraction of A, fA = (2x + z)/N, and (2) the volume fraction of A middle block versus the total volume fraction of A, τA = z/(2x + z), where where x and z are the number of beads in the A blocks of the AxByAzByAx pentaBCP and N is the total degree of polymerization. We work with symmetric, linear AxByAzByAx pentaBCP system with fA = 0.4, τA = 0.8, and N = 50.For canonical target morphologies, we consider double gyroid (DG), hexagonally packed cylinders (C6), lamellar (L), face-centered cubic (FCC) and body-centered cubic (BCC); many of these find use in various applications. For non-canonical target morphology, we choose a hypothesized checkerboard morphology.
3.2. Simulation system and box sizes
We simulate M number of chains of length N in a cubic, periodic simulation box, where M is chosen to match the target volume density of ρ = 0.45 in the simulation box to mimic dense melt conditions, as in previous studies of similar systems.36,37,39,40 The typical number of beads within a simulation box (N*M) studied in this work ranges from 3000 to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 beads. At the beginning of our workflow, M chains are placed randomly in a cubic simulation box of a predetermined size. It is a well-known challenge when simulating BCP self-assembly that incommensurability between simulation box sizes and the intrinsic periodic unit cell, which is often not known a priori, can affect the formation of specific phases.41,42 Certain 1D and 2D phases, like L and C6, respectively, are more resilient to incompatible box dimensions as they can morphologically rotate to minimize internal strain. However, 3D phases, like DG, cannot morphologically rotate and are prone to being impacted by box size incommensurability. Thus, stability analysis of ordered phases for any given polymer design requires both choosing a compatible (1) morphology and (2) box size commensurate with the domain spacing of that morphology; domain spacing is a function of the segregation strength, χN. To understand the effects of cubic simulation box size, for each target morphology, we run the workflow on different simulation box sizes. This makes RAPSIDY amenable to high-throughput computing and parallelization because each biased structure (with a different box size) can be relaxed independently in a separate CPU or GPU.
000 beads. At the beginning of our workflow, M chains are placed randomly in a cubic simulation box of a predetermined size. It is a well-known challenge when simulating BCP self-assembly that incommensurability between simulation box sizes and the intrinsic periodic unit cell, which is often not known a priori, can affect the formation of specific phases.41,42 Certain 1D and 2D phases, like L and C6, respectively, are more resilient to incompatible box dimensions as they can morphologically rotate to minimize internal strain. However, 3D phases, like DG, cannot morphologically rotate and are prone to being impacted by box size incommensurability. Thus, stability analysis of ordered phases for any given polymer design requires both choosing a compatible (1) morphology and (2) box size commensurate with the domain spacing of that morphology; domain spacing is a function of the segregation strength, χN. To understand the effects of cubic simulation box size, for each target morphology, we run the workflow on different simulation box sizes. This makes RAPSIDY amenable to high-throughput computing and parallelization because each biased structure (with a different box size) can be relaxed independently in a separate CPU or GPU.
For our model linear pentaBCP system with N = 50, fA = 0.4, τA = 0.8, χN = 120, and various target morphologies of DG, C6, L, FCC, and BCC, we work with an array of box sizes. For each morphology (except C6), we screen the stability of each cubic box size with equal side lengths from 15σ to 35σ, in increments of 5σ, at the limit of low, intermediate, and high segregation strengths (χN = 60, 90, 120). The unit cell of C6 does not have a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in the x–y dimensions like the other morphologies (i.e., DG, L, BCC, FCC), but rather exhibits a 2
1 ratio in the x–y dimensions like the other morphologies (i.e., DG, L, BCC, FCC), but rather exhibits a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31/2 ratio. To keep system sizes comparable between morphologies, we set the length of the x and z-directions, equivalently, from 15σ to 35σ, in increments of 5σ, and scale the y-direction accordingly.
31/2 ratio. To keep system sizes comparable between morphologies, we set the length of the x and z-directions, equivalently, from 15σ to 35σ, in increments of 5σ, and scale the y-direction accordingly.
3.3. Structure biasing
During “structure biasing”, we start with the random initial configuration of M chains with the specific design placed in a cubic simulation box of specific size and generate configurations that match the target canonical or non-canonical morphologies by applying an external biasing potential, Vext. This approach is similar to those employed by Nowak and Escobedo to study stability of gyroid systems,43 Müller and Daoulas44 to study free energies of self-assembled structures via thermodynamic integration, and Lequieu to study the equivalence of self-consistent field theory and particle-based simulations.45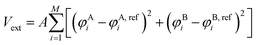 | (3) |
In eqn (3), φji and φj,refi refers to the number density of bead type j within the simulation and reference morphology, respectively, at mesh point i, M is the total number of mesh points, and A is a positive user-defined scaling constant. When the simulation density is far away from the target morphological density field, the system potential energy is heavily penalized, but tends to 0 as the system is closer to the target morphology. Here, the density refers to the number density of each species (in this case, A or B) at a particular location within the simulation box. Mathematical derivations of the density fields describing the morphologies studied in this work are described and plotted in the ESI† (Fig. S1–S6). The scaling constant, A, controls the magnitude of the forces exerted on the beads. We choose A such that the external forces are comparable in magnitude to the forces exerted by the existing bonded and non-bonded interactions for system stability. In our case, we found A = 100 to be a reasonable tradeoff between stability and equilibration speed. During structural biasing, we modify the non-bonded interactions in the system by using a force-capped LJ potential, defined as follows:
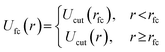 | (4) |
The methodology of using a force-capped potential, known as a soft pushoff procedure, slowly introduces excluded volume interactions and allows beads and chains to overlap. This push-off procedure has been shown to significantly accelerate equilibration of dense melts due to allowing chain movements that are traditionally unphysical in a traditional LJ potential.34 We set the cutoff radius to rfc = 0.8σ initially and increase it linearly over 5000 timesteps to rfc = 21/2σ over the course of the structural biasing procedure.
We perform molecular dynamics simulations using the large-scale atomic/molecular massively parallel dimulator (LAMMPS)46 and allow the system to evolve in the canonical ensemble using the Nosé–Hoover thermostat at a reduced temperature of T* = 1 with the push-off potential and the external guiding potential for 5000 timesteps. The timestep is chosen as Δt = 0.01τ, where τ is in reduced LJ units of time. The combination of the external guiding potential coupled with the force-capped LJ potential allows all chains to settle within their desired morphologies within 5000 timesteps. At the end of this structural biasing step, the structures we obtain are referred to as “biased structures”.
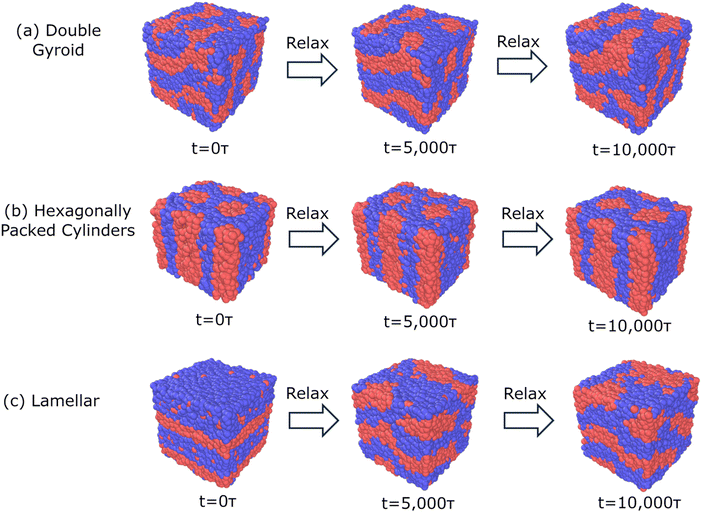
For our model linear pentaBCP system with N = 50, fA = 0.4, τA = 0.8, χN = 120, and various target morphologies, Fig. 2 shows the starting (a) random disordered melt and the different biased structures for the chosen canonical target morphology of (b) double gyroid (DG), (c) hexagonally packed cylinders (C6), (d) lamellar (L), (e) face-centered cubic (FCC), and (f) body-centered cubic (BCC), as well as a non-canonical, hypothesized checkerboard morphology after structural biasing from a (a) random disordered melt. All biased structures shown are periodic in the x, y, and z directions and represent 1 period of the primitive unit cell (except for L, which we have used 2 periods to achieve a comparable system size).
Visual inspection of the structures shows that structural biasing has “forced” the random disordered melt of ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chains of A2B15A16B15A2 design to adopt the six different target morphologies. Our previous work using SCFT calculation and traditional MD simulations showed that this polymer design would adopt the C6 morphology at χN = 120 at equilibrium.
000 chains of A2B15A16B15A2 design to adopt the six different target morphologies. Our previous work using SCFT calculation and traditional MD simulations showed that this polymer design would adopt the C6 morphology at χN = 120 at equilibrium.
Besides visual inspection, we also quantify the structures using the scattering profile, I(q), which we calculate using the Debye equation:47
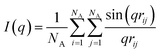 | (5) |
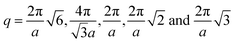 , respectively, where a is the corresponding lattice constant of the morphology. In all morphologies, except L and C6, the lattice constant is equivalent to the side length of the simulation box. For L, the lattice constant is half the length of the simulation box because we simulate two periods of the morphology rather than one for the other morphologies. For C6, the lattice constant refers to the center-to-center cylinder distance.
, respectively, where a is the corresponding lattice constant of the morphology. In all morphologies, except L and C6, the lattice constant is equivalent to the side length of the simulation box. For L, the lattice constant is half the length of the simulation box because we simulate two periods of the morphology rather than one for the other morphologies. For C6, the lattice constant refers to the center-to-center cylinder distance.
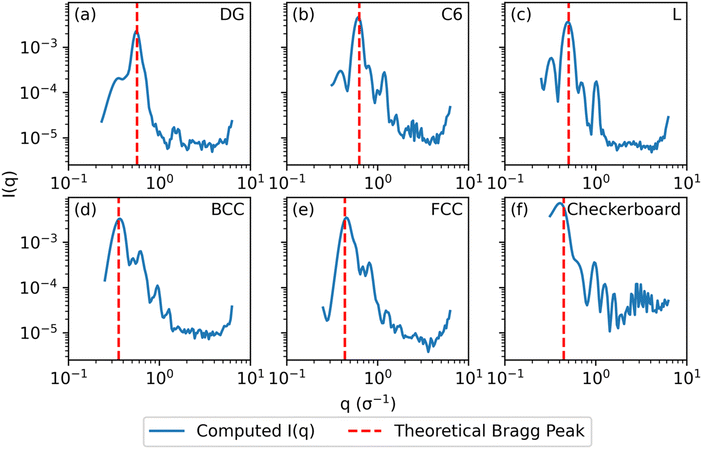 | ||
Fig. 3 Computed scattering profiles for biased structures of canonical morphologies shown in Fig. 2 (b) through (g) with theoretical primary Bragg peaks overlaid. Shown morphologies are (a) double gyroid, (b) hexagonally packed cylinders, (c) lamellar, (d) body-centered cubic, (e) face-centered cubic, and (f) checkerboard. The locations of the theoretical primary Bragg peaks are 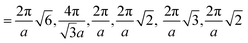 , respectively, where a is the lattice constant of the morphology. , respectively, where a is the lattice constant of the morphology. | ||
We also include an example of applying structural biasing using a non-canonical “checkerboard” morphology to demonstrate that our guiding field can also initialize non-traditional (or undiscovered) phases. The only requirement is that the volume fraction of the target density field is consistent with the sequence design by conservation of mass. Mathematically, this constraint is given by the following equation: 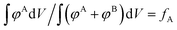 . The numerator,
. The numerator, 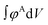 , integrates to the total number of A beads in the system and the denominator,
, integrates to the total number of A beads in the system and the denominator, 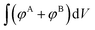 , integrates to the total number of beads in the system. The quotient of these two quantities, thus, must be equivalent to the volume fraction of A of the chosen sequence design. Our checkerboard morphology was defined such that the integrated fraction of species A,
, integrates to the total number of beads in the system. The quotient of these two quantities, thus, must be equivalent to the volume fraction of A of the chosen sequence design. Our checkerboard morphology was defined such that the integrated fraction of species A, 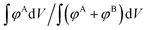 , is 0.4, which is equivalent to the chosen volume fraction, fA = 0.4, and thus is compatible with the chosen pentaBCP design in this example. We theoretically derive the primary Bragg peak to be
, is 0.4, which is equivalent to the chosen volume fraction, fA = 0.4, and thus is compatible with the chosen pentaBCP design in this example. We theoretically derive the primary Bragg peak to be 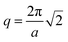 , which corresponds to diffraction resulting from scattering by the (110) crystal plane, the diagonal crystal plane perpendicular to the x–y plane that represents periodicity of A beads within the checkerboard grid. Here, the lattice constant, a, is the side length of the simulation box. The computed scattering profile and theoretical Bragg peak for our checkerboard morphology is shown in Fig. 3(f).
, which corresponds to diffraction resulting from scattering by the (110) crystal plane, the diagonal crystal plane perpendicular to the x–y plane that represents periodicity of A beads within the checkerboard grid. Here, the lattice constant, a, is the side length of the simulation box. The computed scattering profile and theoretical Bragg peak for our checkerboard morphology is shown in Fig. 3(f).
It is also important that we quantify the time required to perform the structural biasing stage versus allowing the system to naturally evolve from their random configuration to their equilibrated structure, as in traditional MD simulations. The structural biasing process using our guiding and soft push-off potentials requires 5000 timesteps for each of the morphologies studied, which takes ∼5 minutes of wall time on an M1 Macbook Pro. Traditional MD methodologies, like the ones used in our previous work,35 require ∼4 orders-of-magnitude additional timesteps to reach equilibrium morphologies from a disordered melt. Specifically, in our previous work, it took ∼2 days for similar system sizes on a 40-node supercomputer running an Intel Xeon Gold 6230 processor.
3.4. Structural relaxation
After completing our “structural biasing” stage and obtaining our biased structures that exhibit our target morphologies, we allow the chains in the structure to relax after disabling the external guiding and push-off potentials and switching to their natural non-bonded and bonded potentials. Using unbiased MD simulations in canonical ensemble, we watch the system evolve to a global or local free energy minimum. We find that allowing the system to relax for only 106 timesteps, or 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ, has been sufficient to determine if the chains of a specific design choose to remain in the biased structure or not. Each combination of morphology, box size, and segregation strength can be independently biased and relaxed, and thus, can be performed in parallel using high-performance computing resources.
000τ, has been sufficient to determine if the chains of a specific design choose to remain in the biased structure or not. Each combination of morphology, box size, and segregation strength can be independently biased and relaxed, and thus, can be performed in parallel using high-performance computing resources.
For our model system (N = 50, fA = 0.4, τA = 0.8, χN = 120, A2B15A16B15A2), Fig. 4 shows examples of snapshots of trajectories with biased structures consisting of DG, C6, and L target morphologies over the course of the relaxation at the limit of high segregation, χN = 120, with identical box sizes of 30σ. We find that both the DG and C6 bias structures remain within their target morphology after 5000τ and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ, suggesting that there is a compatibility between both the prescribed morphology and prescribed box size. However, the system initiated as L, for all box sizes studied, quickly transitions away from L (after 5000τ) towards a perforated layer morphology, after 10
000τ, suggesting that there is a compatibility between both the prescribed morphology and prescribed box size. However, the system initiated as L, for all box sizes studied, quickly transitions away from L (after 5000τ) towards a perforated layer morphology, after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ. This morphological behavior is consistent for all box sizes studied over three replicates and shows that L is quite unstable; it is not even a meta-stable kinetically trapped state within the free energy surface, even at the limit of high segregation strength of χN = 120. At high segregation strengths, BCPs are more prone to kinetic trapping and increase the prevalence of meta-stable states.
000τ. This morphological behavior is consistent for all box sizes studied over three replicates and shows that L is quite unstable; it is not even a meta-stable kinetically trapped state within the free energy surface, even at the limit of high segregation strength of χN = 120. At high segregation strengths, BCPs are more prone to kinetic trapping and increase the prevalence of meta-stable states.
We observe similar morphological stability behavior for an intermediate segregation strength of χN = 90 but observe microphase separation for DG, C6, and L at the limit of low segregation strength of χN = 60, within analogous box sizes ranging from 15σ to 35σ. We also find that BCC and FCC target morphologies are not stable in any of the box sizes or values of segregation strengths screened.
While we cannot comment on the relative stability (i.e., difference in free energy) of C6versus DG phases for this polymer design (N = 50, τA = 0.8, χN = 90, 120), previous studies on kinetic pathways towards the formation of DG structures show that the L to DG transition proceeds through two possible intermediate structures, a hexagonal perforated lamellar structure and a fluctuating perforated layer structure.48,49 The latter fluctuating perforated layer structure is observed in the system initialized as L at both t = 5000τ and t = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ and suggests that the system could be restructuring towards DG. A rigorous relative phase stability (i.e., free energy of C6versus DG) and global phase stability analysis (i.e., free energy of formation of DG from disordered state, as well as associated free energy barrier) would require expensive free energy calculations methods, such as thermodynamic integration44 or Widom insertions.50
000τ and suggests that the system could be restructuring towards DG. A rigorous relative phase stability (i.e., free energy of C6versus DG) and global phase stability analysis (i.e., free energy of formation of DG from disordered state, as well as associated free energy barrier) would require expensive free energy calculations methods, such as thermodynamic integration44 or Widom insertions.50
The ability to systematically identify and study multiple meta-stable morphologies for a chosen BCP sequence design cannot be trivially accomplished using traditional MD methods, such as simulated annealing, in which the final morphology is predetermined by the chosen sequence, initial random seed, and annealing rate, and showcases the strength of our RAPSIDY methodology in screening commensurable morphologies and their corresponding periodic box sizes.
3.5. Stability analysis
In this section, we discuss the final step of our methodology for automated and high-throughput structure stability analysis. In the previous sections, we manually determined the formation and stability of specific morphologies using a combination of visual inspection and analysis of the scattering profile, I(q), after the biased structures were relaxed. Such a manual approach is not amenable to automated high-throughput analysis and motivates the need for a quantitative metric to determine stability.To quantitatively determine the stability of the biased morphology, we compare the scattering profile of the biased structure (this serves as a known morphological reference) prior to relaxation, to the scattering profile of final relaxed structure after t = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ. The biased structure that is formed using our external guiding potential is guaranteed to exhibit the targeted morphology and is an excellent reference for comparison as it is more realistic with appropriate fluctuations due to the BCP chain packing. Several quantitative metrics have been reported in the literature to compare scattering intensities from two different material samples such as χ2 metric and the Pearson correlation coefficient.51 In this work, we choose to use a similarity metric developed by Hura et al. known as volatility-of-ratio (Vr), which operates on the ratio of two scattering curves (rather than the difference like χ2 and Pearson correlation coefficient), I(q), and is defined as follows:52
000τ. The biased structure that is formed using our external guiding potential is guaranteed to exhibit the targeted morphology and is an excellent reference for comparison as it is more realistic with appropriate fluctuations due to the BCP chain packing. Several quantitative metrics have been reported in the literature to compare scattering intensities from two different material samples such as χ2 metric and the Pearson correlation coefficient.51 In this work, we choose to use a similarity metric developed by Hura et al. known as volatility-of-ratio (Vr), which operates on the ratio of two scattering curves (rather than the difference like χ2 and Pearson correlation coefficient), I(q), and is defined as follows:52
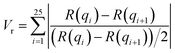 | (6) |
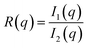 | (7) |
Scattering intensities are calculated over 25 bins equally spaced bins between the lowest wavevector of 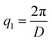 , where D is the smallest dimension of the simulation box, and the highest wavevector of
, where D is the smallest dimension of the simulation box, and the highest wavevector of 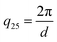 , where d is the diameter of the smallest bead in the simulation box. This volatility-of-ratio (Vr) provides a robust distance metric for comparing two scattering curves to determine structural similarity and has the advantages of not giving increased weight to low resolution regions of I(q) like χ2 and the Pearson correlation coefficient. Smaller values of Vr imply higher similarity between the two compared scattering profiles. We utilize the Vr metric and a prescribed cutoff value to compare I(q) of the biased structure and I(q) of the relaxed structure to determine if the prescribed morphology is maintained.
, where d is the diameter of the smallest bead in the simulation box. This volatility-of-ratio (Vr) provides a robust distance metric for comparing two scattering curves to determine structural similarity and has the advantages of not giving increased weight to low resolution regions of I(q) like χ2 and the Pearson correlation coefficient. Smaller values of Vr imply higher similarity between the two compared scattering profiles. We utilize the Vr metric and a prescribed cutoff value to compare I(q) of the biased structure and I(q) of the relaxed structure to determine if the prescribed morphology is maintained.
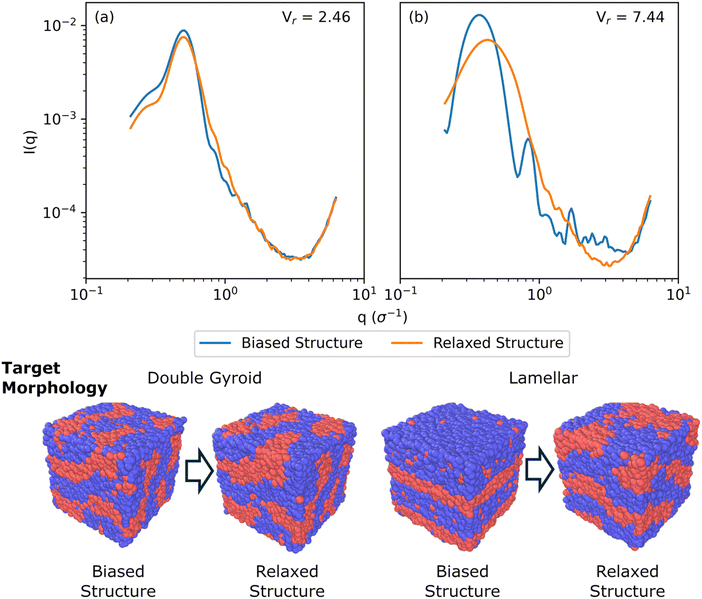
Fig. 5 shows a comparison of biased structures and relaxed structures and their corresponding Vr similarity metrics for a symmetric, linear pentablock copolymer A2B15A16B15A2 design with fA = 0.4 and τA = 0.8 at χN = 120, with a box size of 30σ, with target morphologies of DG and L, respectively; these are the same systems shown in Fig. 4(a) and (c).
For the DG biased structure (Fig. 5(a)), the peak location, intensity, and breadth of the scattering profiles of the biased structure and relaxed structure agree; they exhibit similar primary scattering peaks of 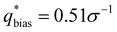 and
and 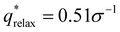 and a similarity metric of Vr = 2.46. The primary scattering peak of the biased structure is approximately equal to the theoretical DG Bragg peak of
and a similarity metric of Vr = 2.46. The primary scattering peak of the biased structure is approximately equal to the theoretical DG Bragg peak of 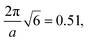 where the lattice constant, a, is the box size (30σ), and supports our choice of reference profile.
where the lattice constant, a, is the box size (30σ), and supports our choice of reference profile.
For the L biased structure (Fig. 5(b)), however, there is qualitative disagreement between the scattering profiles of the biased structure and relaxed structure; they exhibit different primary scattering peaks of 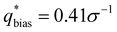 and
and 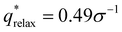 , respectively, and a similarity metric of Vr = 7.44. The primary scattering peak of the biased structure is approximately equal to the theoretical L Bragg peak of
, respectively, and a similarity metric of Vr = 7.44. The primary scattering peak of the biased structure is approximately equal to the theoretical L Bragg peak of 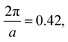 where the lattice constant, a, is half the box size (15σ) because we simulate two periods.
where the lattice constant, a, is half the box size (15σ) because we simulate two periods.
The similarity metric of the DG system (Vr = 2.46) is lower than the similarity metric of the L system (Vr = 7.44) and is consistent with visual inspection of morphological stability. Vr can sufficiently capture differences in scattering profiles and can quantitatively serve as a metric for determining stability. For the rest of our study, we found that a cutoff value of Vr < 3.5 for determining if two structures are morphologically congruent was consistent with our visual observations. This is contrary to the heuristic cutoff of Vr < 2.8 prescribed by the original authors for their system;35 we urge readers to adjust the cutoff accordingly depending on the system and that expert domain knowledge is needed to select an appropriate cutoff value. In cases where multiple box sizes meet the user prescribed stability cutoff (Vr < 3.5), the one with the lowest Vr value is deemed the most compatible box size with the chosen morphology and polymer design sequence.
4. Inverse BCP design for target morphology of double gyroid using RAPSIDY
Having described the RAPSIDY workflow in the previous section, we now demonstrate its use for high-throughput exploration of the BCP design space and sequence-engineering for targeted morphologies. In this section, we specifically focus on one case study targeting symmetric, linear pentaBCP design sequences for target double gyroid (DG) morphology. Network morphologies, like DG, have been shown to exhibit desirable materials properties such as enhanced electronic conductivity and mechanical stability due to the bicontinuous nature of the structure and have been used in applications such as active membranes in photovoltaic cells53,54 and electrochemical cells.55 However, the window of stability of the DG phase is often very narrow within the BCP design space. This smaller stable window for DG phase has been attributed to what is described in the literature as “packing frustration” - the entropic penalty associated with overstretching chains to fit within bulky DG nodes.56 This practical use of DG morphology and the goal to widen DG phase windows motivates our search for new polymer designs.We screen the stability of the DG phase using our approach outlined in the previous sections for pentaBCP designs with fA = 0.5 and τA ∈ (0,1) using a grid search approach; this specific pentaBCP design has been chosen due to our recent work using SCFT and traditional MD simulations that provides us results to compare to.35
We chose a total degree-of-polymerization of 48 and screen discrete values of τA = 1/12, 2/12,…,11/12 with box sizes from 10σ to 35σ, in increments of 5σ at low, intermediate, and high segregation limits (χN = 60, 90, 120). For each set of (τA, box size, χN) parameters, we perform structural biasing (into DG), followed by structural relaxation (for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ), and stability analysis with a cutoff value of Vr < 3.5 to determine DG stability. A design (τA, χN) is considered DG stable if any box size screened has a stability cutoff value of Vr < 3.5.
000τ), and stability analysis with a cutoff value of Vr < 3.5 to determine DG stability. A design (τA, χN) is considered DG stable if any box size screened has a stability cutoff value of Vr < 3.5.
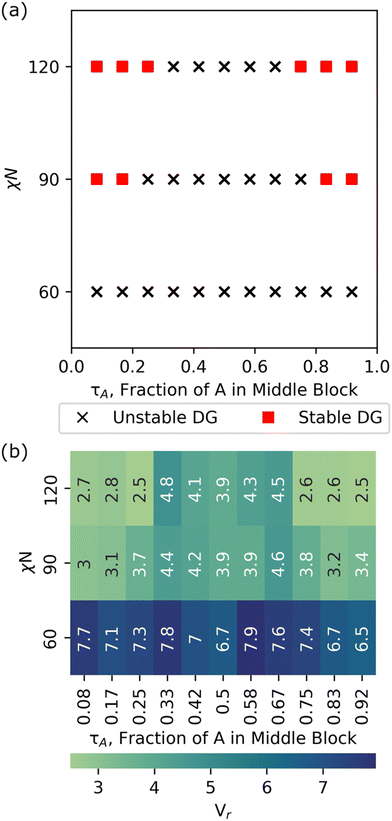
Fig. 6 shows a phase diagram with DG stability screened using our grid search approach at χN = 60, 90, and 120. At χN = 60, there is no region of stability or metastability for the DG phase and visual inspection of the trajectories show that the systems shift to disordered microphase separated (DM) state. This observation of DM is consistent with our previous study, which studied symmetric, linear pentaBCPs using simulated annealing, and found order–disorder transitions at segregation strengths of (χN)ODT > 80.35 We used the height of the contact peak of the A–B radial distribution function, gAB(r ≅ 1σ), as a measure of microphase separation in the melt. We found that gAB(r ≅ 1σ) = 1.76 ± 0.06 was the transition point from disordered microphase separated to disordered (DS) phase (i.e., the limit of χ → 0). Lower values of gAB(r ≅ 1σ) <1.76 visually exhibited ordered structures or more pronounced phase separated domains. Further detail on the distinction between the DS and DM phases is available in our previous work.35 The radial distribution function of A and B from our relaxed structures show the gAB(r ≅ 1σ) contact peak to be ∼0.86, which suggests that our systems exhibit DM rather than DS behavior.
At χN = 90, we see two DG windows forming, one spanning τA = 1/12 to 2/12 and another spanning τA = 10/12 to 11/12. Analysis of the scattering similarity metric, Vr, shows that the expanded points of τA = 3/12 and τA = 9/12 had similarity metrics of 3.7 and 3.8, respectively, at χN = 90, which just misses our prescribed cutoff of Vr < 3.5, and suggests that we are approaching the ODT for the chosen τA values. At χN = 120, DG windows expand to τA = 1/12 to 3/12 and τA = 9/12 to 11/12, respectively.
In this study, the DG stability of each pentaBCP design was screened in ∼2 hours of wall time on a 40-node supercomputer with Intel Xeon Gold 6230 processor, whereas benchmarks using our traditional MD approach required upwards of 4 days of wall time for the formation of a stable morphology (which often was not the targeted DG morphology) on the same architecture.
In this case study, due to the fast calculations, we employed a naïve grid-search approach with two design parameters, τA and χN, simply to showcase the proof-of-concept ability for high-throughput screening of morphological stability for many block copolymer design sequences. Our methodology can easily be combined with high-throughput optimization techniques, such as active learning and Bayesian optimization, to efficiently query a high-dimensional design space with many design parameters and is the scope of future work. Our methodology is highly parallelizable as the stability results of each polymer sequence design are independent of one another and offers significant runtime improvement over traditional MD methods.
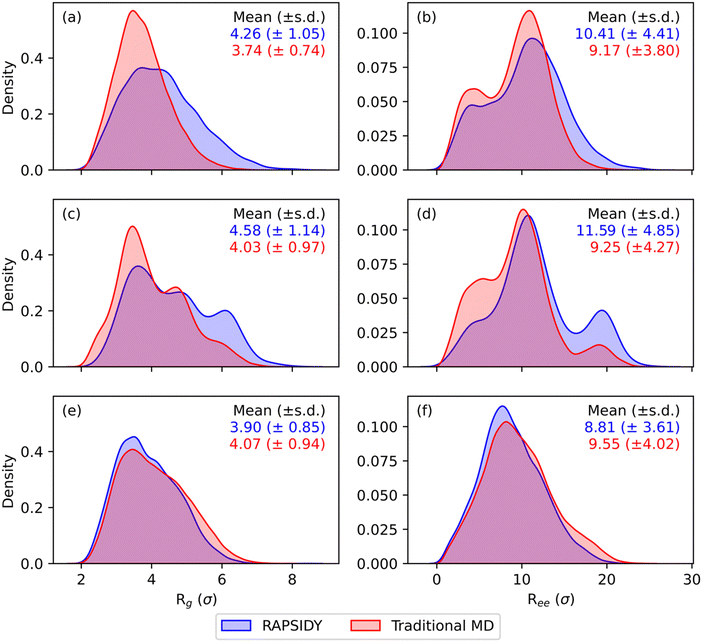
While our methodology has been shown to significantly accelerate the formation of and stability testing of targeted morphologies, we have not discussed how physically correct the individual chain level details and conformations that form within these morphologies are. Chain level metrics, such as the radius-of-gyration (Rg) and end-to-end distance (Ree), serve as key indicators into polymer chain conformations and dynamics within a melt, and directly influence macroscopic material properties such as mechanical strength, viscosity, and thermal conductivity.29–31 It is critical to show that our RAPSIDY approach does not trap the chains in unphysical configurations after our biasing and relaxation steps. The chain conformations analyzed for the various phases obtained for symmetric, linear AxByAzByAx pentaBCP system with fA = 0.4, N = 50, χN = 120 at varying values of τA obtained in our recent work serve as comparison for our RAPSIDY approach's chain conformations. Specifically, we wish to verify that distributions of Rg and Ree, are quantitatively consistent for structures from the two methods – fast RAPSIDY and slow, rigorous “traditional MD” that uses simulated annealing.
We perform structural biasing and structural relaxation for each pentaBCP design sequence (N = 50, fA = 0.4, and τA = 0.2, 0.4, 0.5, 0.6, 0.8), targeting the morphology that was predicted to be the free energy minimum from traditional MD (DG, L, L, L, C6, respectively) at χN = 120. During structural relaxation, we follow the same protocol discussed in the previous sections and screen the stability of each box size from 15σ to 35σ, in increments of 5σ. The compatible lattice constant for each pentaBCP design sequence is known a priori from our traditional MD results (e.g., the box size needed to simulate a single repeat unit of the morphology) by analyzing the location of the primary scattering peak, q*, which we use to compare to the corresponding q* for the most compatible box size found from our structural relaxation procedure.
Table 1 shows the comparison of the morphology stability (Vr) and computed q* after relaxation of the most stable box size (i.e., smallest value of Vr) found from RAPSIDY compared to traditional MD. The sequence design of τA = 0.8 has been tested in a previous section in Fig. 5(a), and the results are repeated in this table. We find quantitative agreement in morphology stability, as determined by Vr, and qualitative agreement in q* values. All morphologies exhibit stability metrics of our prescribed stability cutoff of Vr < 3.5. Slight differences in q* values computed via after structural biasing and structural relaxation can be attributed to the discrete box sizes we screen using our methodology. All sequence designs studied exhibited highest stability at box sizes of 25σ and 30σ, in which the corresponding theoretical q* values bracket the q* values found by traditional MD, suggesting the true intrinsic box size is appropriately bounded.
| τ A | Morphology | q*, traditional MD (σ−1) | q*, RAPSIDY (σ−1) | Morphology stability, Vr |
|---|---|---|---|---|
| 0.2 | DG | 0.57 | 0.60 | 3.38 |
| 0.4 | L | 0.66 | 0.63 | 2.34 |
| 0.5 | L | 0.64 | 0.63 | 2.79 |
| 0.6 | L | 0.68 | 0.62 | 2.86 |
| 0.8 | C6 | 0.58 | 0.51 | 2.46 |
Fig. 7 shows the distributions of Rg and Ree found from RAPSIDY versus traditional MD simulations for τA = 0.2, 0.5, and 0.8, which form DG, L, and C6 morphologies, respectively; irrespective of morphology, we find agreement in breadth and modality of the distributions from RAPSIDY versus traditional MD simulations. Distributions of Rg and Ree for τA = 0.4 and 0.6, which both form L, are shown in Fig. S7 (ESI†). Consistency in both the breadth and modality of the distributions suggest that the chain conformations adopted by systems found by both methods are similar. Slight deviations in the distributions is expected and can be attributed to differing system sizes because the number of chains needed to simulate an integer number of periods of that morphology within the simulation box is unknown.
In summary, we showcase the ability of RAPSIDY to rapidly screen viable double gyroid candidates within the symmetric, linear pentablock copolymer design space. We find that no designs with fA = 0.5 are DG viable at the limit of low segregation (χN = 60) but find windows of DG stability for designs with 0 < τA < 0.25 and 0.75 < τA < 1 at the limit of high segregation (χN = 120). Our methodology yields chain conformations and lattice constants that are consistent with those obtained from traditional MD, while reducing computational time by two orders of magnitude, even when employing a naïve grid-search approach.
5. Conclusions
In this work, we presented a high-throughput computational framework, RAPSIDY – Rapid Analysis of Polymer Structure and Inverse Design strategY – for the inverse design of self-assembled block copolymers targeting specific morphologies. We showcase our methodology by rapidly identifying symmetric, linear pentablock copolymer AxByAzByAx designs that exhibit a stable double gyroid morphology, a highly desirable microphase separated structure for applications that need favorable mechanical and transport properties, and accelerate the design procedure by two orders-of-magnitude over traditional MD simulations. Our work is amendable to parallelization through high-performance computing and can be used in tandem with machine learning methodologies like active learning for intelligent design space querying. While our methodology offers significant reduction in computational cost over traditional MD, RAPSIDY is limited to quickly identifying designs that exhibit higher or lower stability for a desired morphology rather than predict the true global free energy minimum structure for that design. We expect the knowledge we gain by using RAPSIDY to be highly valuable for guiding synthesis of materials and accelerating creation of the next generation of novel, high-performance polymeric materials.Data availability
All data needed to evaluate the conclusions in the paper are available either in the main text or ESI.† RAPSIDY is available as open-access code in our lab's GitHub repository, https://github.com/arthijayaraman-lab.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was financially supported by the Army Research Office through the Multi-disciplinary University Research Initiative (MURI) award number W911NF2310260. This research was supported in part through the use of Information Technologies (IT) resources at the University of Delaware, specifically the high-performance computing resources.References
- F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38 CrossRef CAS.
- M. W. Matsen and M. Schick, Macromolecules, 1994, 27, 6761–6767 CrossRef CAS.
- F. Bates and G. Fredrickson, Annu. Rev. Phys. Chem., 1990, 41, 525–557 CrossRef CAS PubMed.
- S. K. Siddique, H. Sadek, T.-L. Lee, G.-M. Manesi, A. Avgeropoulos, C.-W. Wang, C.-C. Lee, E. L. Thomas and R.-M. Ho, Giant, 2024, 17, 100205 CrossRef CAS.
- S. P. Nunes, Macromolecules, 2016, 49, 2905–2916 CrossRef CAS.
- C. Allen, D. Maysinger and A. Eisenberg, Colloids Surf., B, 1999, 16, 3–27 CrossRef CAS.
- C. Guo, Y.-H. Lin, M. D. Witman, K. A. Smith, C. Wang, A. Hexemer, J. Strzalka, E. D. Gomez and R. Verduzco, Nano Lett., 2013, 13, 2957–2963 CrossRef CAS PubMed.
- D. J. C. Herr, J. Mater. Res., 2011, 26, 122–139 CrossRef CAS.
- J.-F. Lutz, J.-M. Lehn, E. W. Meijer and K. Matyjaszewski, Nat. Rev. Mater., 2016, 1, 1–14 Search PubMed.
- D. Pasini and D. Takeuchi, Chem. Rev., 2018, 118, 8983–9057 CrossRef CAS.
- N. Badi and J.-F. Lutz, Chem. Soc. Rev., 2009, 38, 3383–3390 RSC.
- X. Li, J. Iocozzia, Y. Chen, S. Zhao, X. Cui, W. Wang, H. Yu, S. Lin and Z. Lin, Angew. Chem., Int. Ed., 2018, 57, 2046–2070 CrossRef CAS.
- H. Dau, G. R. Jones, E. Tsogtgerel, D. Nguyen, A. Keyes, Y.-S. Liu, H. Rauf, E. Ordonez, V. Puchelle, H. Basbug Alhan, C. Zhao and E. Harth, Chem. Rev., 2022, 122, 14471–14553 CrossRef CAS PubMed.
- K. R. Gadelrab, A. F. Hannon, C. A. Ross and A. Alexander-Katz, Mol. Syst. Des. Eng., 2017, 2, 539–548 RSC.
- A. Zunger, Nat. Rev. Chem., 2018, 2, 1–16 CrossRef.
- J. Wang, Y. Wang and Y. Chen, Materials, 2022, 15, 1811 CrossRef CAS PubMed.
- C.-Y. Chang, G.-M. Manesi, J. Xie, A.-C. Shi, T. Shastry, A. Avgeropoulos and R.-M. Ho, Macromolecules, 2024, 57(15), 7087–7097 CrossRef CAS.
- W. Jiang, Y. Qiang, W. Li, F. Qiu and A.-C. Shi, Macromolecules, 2018, 51, 1529–1538 CrossRef CAS.
- F. S. Bates, M. A. Hillmyer, T. P. Lodge, C. M. Bates, K. T. Delaney and G. H. Fredrickson, Science, 2012, 336, 434–440 CrossRef CAS.
- A. Arora, J. Qin, D. C. Morse, K. T. Delaney, G. H. Fredrickson, F. S. Bates and K. D. Dorfman, Macromolecules, 2016, 49, 4675–4690 CrossRef CAS.
- M. W. Matsen, J. Phys.: Condens. Matter, 2001, 14, R21 CrossRef.
- V. Ganesan and G. H. Fredrickson, in Handbook of Materials Modeling: Methods, ed S. Yip, Springer Netherlands, Dordrecht, 2005, pp. 2645–2656 Search PubMed.
- M. C. Villet and G. H. Fredrickson, J. Chem. Phys., 2014, 141, 224115 CrossRef PubMed.
- M. W. Matsen and F. S. Bates, Macromolecules, 1996, 29, 1091–1098 CrossRef CAS.
- B. Zhao, W. Jiang, L. Chen, W. Li, F. Qiu and A.-C. Shi, ACS Macro Lett., 2018, 7, 95–99 CrossRef CAS PubMed.
- B. Zhao, C. Wang, Y. Chen and M. Liu, Langmuir, 2021, 37, 5642–5650 CrossRef CAS PubMed.
- C. L. Tsai and G. H. Fredrickson, Macromolecules, 2022, 55, 5249–5262 CrossRef CAS.
- M. R. Khadilkar, S. Paradiso, K. T. Delaney and G. H. Fredrickson, Macromolecules, 2017, 50, 6702–6709 CrossRef CAS.
- S. Sen, S. K. Kumar and P. Keblinski, Macromolecules, 2005, 38, 650–653 CrossRef CAS.
- T. Zhou, Z. Wu, H. K. Chilukoti and F. Müller-Plathe, J. Chem. Theory Comput., 2021, 17, 3772–3782 CrossRef CAS PubMed.
- R. H. Colby, L. J. Fetters and W. W. Graessley, Macromolecules, 1987, 20, 2226–2237 CrossRef CAS.
- J. Koyanagi, N. Takase, K. Mori and T. Sakai, Compos., Part C: Open Access, 2020, 2, 100041 CAS.
- F. Müller-Plathe, J. Chem. Phys., 1997, 106, 6082–6085 CrossRef.
- R. Auhl, R. Everaers, G. S. Grest, K. Kremer and S. J. Plimpton, J. Chem. Phys., 2003, 119, 12718–12728 CrossRef CAS.
- S. Jung Park, T. Myers, V. Liao and A. Jayaraman, Mol. Syst. Des. Eng., 2024 10.1039/d4me00138a.
- G. S. Grest, M. Lacasse, K. Kremer and A. M. Gupta, J. Chem. Phys., 1996, 105, 10583–10594 CrossRef CAS.
- A. Kulshreshtha, R. C. Hayward and A. Jayaraman, Macromolecules, 2022, 55, 2675–2690 CrossRef CAS.
- B. Settles, Active Learning Literature Survey, University of Wisconsin-Madison Department of Computer Sciences, 2009 Search PubMed.
- M. Murat, G. S. Grest and K. Kremer, Macromolecules, 1999, 32, 595–609 CrossRef CAS.
- H. Guo and K. Kremer, J. Chem. Phys., 2003, 119, 9308–9320 CrossRef CAS.
- Y. Feng, J. Wu, B. Li and Q. Wang, Soft Matter, 2022, 18, 2750–2756 RSC.
- F. J. Martínez-Veracoechea and F. A. Escobedo, J. Chem. Phys., 2006, 125, 104907 CrossRef.
- C. Nowak and F. A. Escobedo, J. Chem. Theory Comput., 2018, 14, 5984–5991 CrossRef CAS.
- M. Müller and K. Ch Daoulas, J. Chem. Phys., 2008, 128, 024903 CrossRef PubMed.
- J. Lequieu, J. Chem. Phys., 2023, 158, 244902 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- P. Debye, J. Phys. Chem., 1947, 51, 18–32 CrossRef CAS.
- N. Ji, P. Tang, F. Qiu and A.-C. Shi, Macromolecules, 2015, 48, 8681–8693 CrossRef CAS.
- M. Imai, K. Sakai, M. Kikuchi, K. Nakaya, A. Saeki and T. Teramoto, J. Chem. Phys., 2005, 122, 214906 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Elsevier, 2023 Search PubMed.
- D. T. Murray, D. S. Shin, S. Classen, C. A. Brosey and G. L. Hura, Methods Enzymol., 2023, 678, 411–440 Search PubMed.
- G. L. Hura, H. Budworth, K. N. Dyer, R. P. Rambo, M. Hammel, C. T. McMurray and J. A. Tainer, Nat. Methods, 2013, 10, 453–454 CrossRef CAS.
- E. J. W. Crossland, M. Kamperman, M. Nedelcu, C. Ducati, U. Wiesner, D.-M. Smilgies, G. E. S. Toombes, M. A. Hillmyer, S. Ludwigs, U. Steiner and H. J. Snaith, Nano Lett., 2009, 9, 2807–2812 CrossRef CAS.
- S.-S. Sun, Sol. Energy Mater. Sol. Cells, 2003, 79, 257–264 CrossRef CAS.
- M. Adachi, A. Okumura, E. Sivaniah and T. Hashimoto, Macromolecules, 2006, 39, 7352–7357 CrossRef CAS.
- M. W. Matsen and M. Schick, Phys. Rev. Lett., 1994, 72, 2660–2663 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01037j |
| This journal is © The Royal Society of Chemistry 2024 |