Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamics of phase-separated microdroplets near the contact line of evaporating all-aqueous drops†
Rahul
Rai‡
,
Maheshwar
Gopu‡
 ,
Senthan Pugalneelam
Parameswaran
,
Tapan Chandra
Adhyapak
* and
Dileep
Mampallil
,
Senthan Pugalneelam
Parameswaran
,
Tapan Chandra
Adhyapak
* and
Dileep
Mampallil
 *
*
Indian Institute of Science Education and Research Tirupati, Yerpedu P.O. PIN 517619, Tirupati, AP, India. E-mail: adhyapak@iisertirupati.ac.in; dileep.mampallil@iisertirupati.ac.in
First published on 2nd October 2024
Abstract
Evaporation of multicomponent drops can induce liquid–liquid phase separation and spatial reconfiguration of phases. Here, we unveil several novel dynamics near the contact line of evaporating multicomponent drops containing polyethylene glycol and dextran. The interplay between background Marangoni flow and self-migration of nucleated microdroplets creates both unstable and stable equilibrium points. This leads to either continuous migration or stepwise advancement of microdroplets, influenced by random coalescence events. Tiny dextran microdroplets nucleating at the contact line can migrate toward the bulk only by growing in size with coalescence events. Our findings offer new insights into the fundamental understanding of evaporating multicomponent drops and factors influencing the spatial segregation of phases in evaporative liquid–liquid phase separation with implications in prebiotic biomolecular reactions to industrial applications.
Evaporation of drops, a process rich in physics, has profound implications in various applied processes.1–6 A less explored system is the evaporating multicomponent drops. They undergo out-of-equilibrium processes, leading to liquid–liquid phase separation (LLPS),7–11 particularly near the three-phase liquid–solid–air contact line, where significant evaporative fluxes occur.12–18 In general, LLPS of aqueous two-phase systems8,9 has applications in broad areas such as environmental remediation, water purification, synthetic biology, and biomedicine.7,8,10,11 For example, LLPS can form microdroplets resembling membraneless organelles occurring in cells. LLPS by spontaneous evaporation has been shown to concentrate RNA molecules in compartments, as seen in protocells,19–21 delineating the possible implications in the origin of life. Evaporative deposition of polymer components also has implications for the bottom-up construction of polymer-based systems with wide industrial applications.22–24
Evaporating multicomponent drops are complex systems containing intricate dynamics such as driving of nucleated microdroplets at the contact line through asymmetric interfacial stresses,25–28 large-scale convection driven by strong recirculating solutal Marangoni flow,12,14,20,29 and radial capillary flows.4,30 In evaporative multiphase drop systems, hydrodynamic effects influence the spatial organization of the phases. For example, capillary and Marangoni background flows in multiphase sessile-drop evaporation in oil-coated surfaces could generate stagnation points stabilizing the hierarchically compartmentalized microdroplets.21 In a different context, it was demonstrated that when partially immersed in oil (as an emulsion), evaporating multiphase polymer microdroplets separate into distinct phases.31,32 In the widely used model system of polyethylene glycol (PEG) and dextran (DEX), sessile drop evaporation drives inward migrations of nucleated DEX microdroplets, resulting in a DEX-rich center (Fig. 1(a and b)) as also reported in previous studies.12,20,28 Unfortunately, several complex dynamics of evaporating multicomponent drops are not well understood. For example, the interplay between the dynamics of the nucleated phases at the contact line and the background flow in the drop has been overlooked in previous studies.
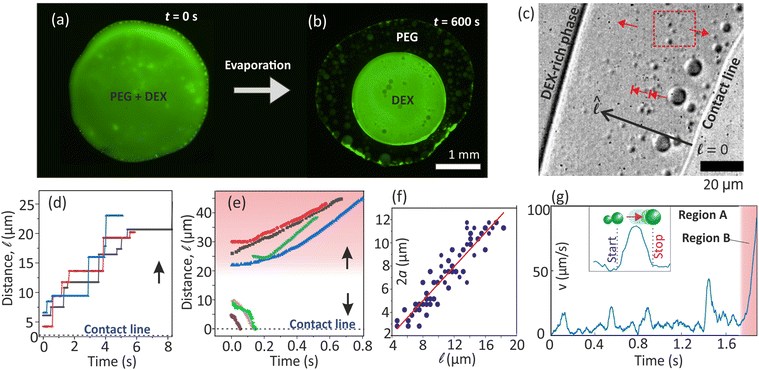 | ||
Fig. 1 (a) and (b) Bottom-view images of PEG-(FITC-DEX) drop. (c) DEX microdroplets at the contact line move stepwise (blunt-head arrows) toward the bulk upon coalescence. (d) Stepwise position change over time (Video S1, ESI†). (e) Tiny microdroplets (red dashed rectangle in (c)) nucleated away from the contact line move continuously towards the bulk or contact line, based on their nucleating point. (f) Size of stepwise migrating microdroplets as a function of distance from the contact line. (g) In the stepwise motion, velocity peaks upon a coalescence, and the resulting droplet halts at a new position. After multiple coalescence events, the resulting large droplet reaches a position where it migrates to the bulk without intermittent halting (marked as region B). The regions A & B are spatial regions near the contact line. Relative PEG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEX concentration was 2 DEX concentration was 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 wt%. 10 wt%. | ||
Here, we unveil several previously unexplored dynamics surrounding the contact line during the evaporating PEG-DEX drop. We study the previously overlooked dynamics of nucleated DEX and, importantly, its interaction with the background flow. We show that DEX nuclei can migrate from the contact line to the bulk only by growing via coalescence, manifesting a stepwise motion with intermittent halts (Fig. 1(c and d)). Conversely, DEX nucleating slightly away moves continuously, either towards or away from the contact line, depending on its initial nucleation position (Fig. 1(e)). Our analysis, supported by theory, reveals that these dynamics arise from the complex interplay between nucleated DEX and convective flow gradients near the contact line. Our findings offer broad insights into transport dynamics within evaporating multicomponent drops.
1 Experiments
In the experiments, we evaporated a polymer mixture drop of volume 1 μL deposited on an ethanol–oxygen plasma-cleaned dry glass slide at laboratory conditions (25 °C and humidity 50 ± 2%). The initial concentrations of individual polymers (DEX, Mw = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 and PEG, Mw = 6000 g mol−1) were prepared at 2–10 wt% in deionized water. We also used DEX tagged with FITC (fluorescein isothiocyanate; λem = 517 nm) for fluorescent imaging. The drop edge was imaged using an inverted fluorescence microscope (Nikon Eclipse Ti2) and cameras (Nikon DS-Qi2 and Vision Research Lab-110) at 24–200 frames per s with a maximum resolution of 0.33 μm per pix with 90× objective.
000 g mol−1 and PEG, Mw = 6000 g mol−1) were prepared at 2–10 wt% in deionized water. We also used DEX tagged with FITC (fluorescein isothiocyanate; λem = 517 nm) for fluorescent imaging. The drop edge was imaged using an inverted fluorescence microscope (Nikon Eclipse Ti2) and cameras (Nikon DS-Qi2 and Vision Research Lab-110) at 24–200 frames per s with a maximum resolution of 0.33 μm per pix with 90× objective.
2 Results
2.1 Microdroplet dynamics observed near the contact line
Henceforth, the PEG-DEX sessile drop will be referred to as the “drop,” while the micro-sized droplets that nucleate at the drop edge will be referred to as “microdroplet(s).” We imaged near the contact line, i.e., within about 30 μm from the edge. The contact line is pinned on the substrate and does not move.(i) The DEX microdroplets nucleating at the contact line can migrate away only by coalescence-induced growth and stepwise advancement (Fig. 1(d) and Video S1, ESI†). It is also reflected in their size distribution as shown Fig. 1(f). In Fig. 1(g), we display the velocity of a microdroplet in stepwise motion over time (Video S2, ESI†). Peaks indicate intermittent advancements of the microdroplet, rising from zero to a maximum post-coalescence before returning to near-zero velocity.
(ii) After coalescence cascades, resulting large microdroplets move continuously (region B in Fig. 1(g)) toward the bulk. The velocity of these continuously moving microdroplets increases over time.
(iii) Extremely small DEX microdroplets (diameter < 2 μm) nucleate slightly away from the contact line, possibly from a precursor film of denser DEX on the substrate. They move in the direction of the contact line or towards the bulk if they nucleate relatively closer to these corresponding regions, as depicted in Fig. 1(e) and (Video S1, ESI†).
Mainly, we observe that the nucleated DEX microdroplets move close to the substrate (liquid–solid interface). DEX stays near the substrate as its density (∼1049 kg m−3) is higher than that of the PEG-rich phase (∼1017 kg m−3).28 We do not expect any pinning of the DEX microdroplets on the substrate as they are surrounded by liquid.
2.2 Understanding the microdroplet dynamics
When DEX nucleates, the drop edge undergoes a compositional change where it becomes predominantly composed of PEG. The gradient in the polymer concentration generates a corresponding gradient in the interfacial tension along the interface between the microdroplets and the surrounding liquid.12,28 The resulting Marangoni stress pushes the liquid on the microdroplet surface, assisting them to ‘swim’ in the opposite direction, i.e., towards the drop center.28Assuming that the interfacial tension, σdl, between the DEX microdroplet and surrounding liquid varies linearly, the Marangoni force of the microdroplets is given as,28
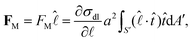 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
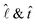 the unit vectors along the inverse radius of the drop (
the unit vectors along the inverse radius of the drop (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0 at the contact line, [see Fig. 1(c)]) and the local tangent to the droplet surface, respectively. The direction
= 0 at the contact line, [see Fig. 1(c)]) and the local tangent to the droplet surface, respectively. The direction ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) of FM is inferred directly from the symmetry of the setup.
of FM is inferred directly from the symmetry of the setup.
In the low Reynolds number limit, the hydrodynamic drag force on the droplet is, FD = −γvM, where the drag coefficient γ of the microdroplet,33 is linear in the radius a. Here, vM = v − uf is the velocity of the microdroplet relative to the background flow uf, while v is the velocity in the laboratory frame. Therefore, force-balance, FM + FD = 0, predicts a continuous motion of droplets with vM ∝ a as demonstrated by May et al.28 (also see Fig. S3, ESI†). However, we show that this continuous motion occurs only for relatively large microdroplets at region B, after reaching there in a step-wise manner by a cascade of coalescence events. Interestingly, we also see that the measured microdroplet velocity (v) increases continuously in region B. Below, we explain all these aspects considering the interplay between the convective flow uf and the opposing Marangoni force FM.
The low surface tension towards the drop edge at the drop–air interface induces a large-scale Marangoni convective recirculation flow inside the drop.20,28 Its velocity ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
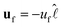 is radially outward near the drop–substrate interface. Writing γ = CHRa, where CHR is the constant in Hadamard–Rybczynski drag equation,33 the lab frame velocity of the microdroplets is read from eqn (1), as
is radially outward near the drop–substrate interface. Writing γ = CHRa, where CHR is the constant in Hadamard–Rybczynski drag equation,33 the lab frame velocity of the microdroplets is read from eqn (1), as
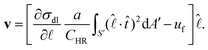 | (2) |
The droplet moves radially inward step by step if its radius a increases through coalescence, and the external flow velocity uf also increases inward radially. This scenario leads to multiple consecutive equilibrium positions with v = 0.
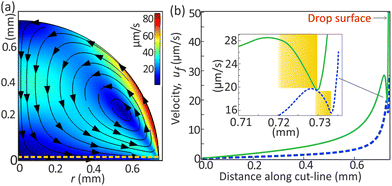
The strong Marangoni flow generated at the liquid–air interface of the drop expands in its bulk as a circulating flow. We expect gradients in the flow strength, especially near the corners, as they are far away from the circulation path. Although it is experimentally challenging to visualize this gradient in the small region near the drop edge, numerical simulations of Marangoni convective flow do reveal it.34–36 We also performed numerical simulations (see ESI†), excluding nucleation processes and complexities caused by microdroplets near the contact line. Such a flow can occur when surface tension is relatively higher towards the apex of the drop, which is a scenario usually occurring by solutal or thermal gradients. Although the flow in our drop is driven by solutal Marangoni stress, our simulations easily produced the correct flow direction, as shown in Fig. 2(a), through evaporatively generated thermal gradients ∇T, which induce interfacial stress (dσ/dT)∇T. The circulating flow pattern persists even under very large interfacial stresses, similar to solutal Marangoni flow (Fig. S4, ESI†), as demonstrated in other studies.34–36 The interaction between the DEX microdroplets and the background flow is independent of the specific origin of the flow.
Fig. 2(b) shows the numerically calculated flow magnitude just above the substrate. Moving radially inward (along ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
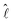 ) from the contact line, the fluid velocity strength increases (highlighted in the inset) creating a barrier for self-migrating microdroplets along
) from the contact line, the fluid velocity strength increases (highlighted in the inset) creating a barrier for self-migrating microdroplets along ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . This increased flow strength transitions to a decrease towards the drop center.
. This increased flow strength transitions to a decrease towards the drop center.
The flow strength varies along the horizontal cutline due to the drop's shape, with reduced fluid velocity near the drop's edge. This is illustrated by the dark blue band emanating from the drop edge in Fig. 3(a), consistent with numerical calculations by others for thermal and solutal Marangoni flows.34–36 The effect of the corner depends upon the flow-circulation position (Fig. S5, ESI†) and appears to be stronger with decreasing contact angle of the drop.35,37 Experimentally, the circulation appears to be closer to the drop edge where the surface tension gradients exist at the drop–air interface.
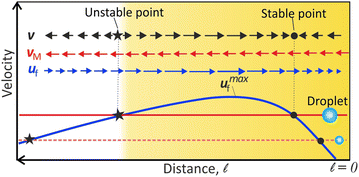
The peak-like variation of uf near the contact line has an important consequence: the condition v = vM + uf = 0 produce locations of stable and unstable equilibrium. It is schematically illustrated in Fig. 3. Now we can explain all the droplet dynamics observed near the contact line.
The existence of the unstable equilibrium position can explain why the very small DEX microdroplets formed from the precursor film, away from the contact line, move continuously. When microdroplets nucleate between the unstable and stable regions, they flow towards the contact line, as uf(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) > vM. Conversely, microdroplets, nucleating beyond the unstable equilibrium, flow directly towards the bulk along the substrate as vM > uf(
) > vM. Conversely, microdroplets, nucleating beyond the unstable equilibrium, flow directly towards the bulk along the substrate as vM > uf(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) (Video S1, ESI†).
) (Video S1, ESI†).
On the other hand, due to the flow barrier as highlighted region Fig. 2(b)-inset or Fig. 3, the small microdroplets nucleating at the contact line can migrate to the bulk only by coalescence-induced size increase. Each coalescence causes vM > uf(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), and results in the migration of the microdroplet to the next stable equilibrium position where vM + uf(
), and results in the migration of the microdroplet to the next stable equilibrium position where vM + uf(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) = 0.
) = 0.
After multiple coalescence events, the resulting large daughter droplet has vM > umaxf, where umaxf is the maximum flow velocity (see Fig. 3). At this stage, no stable equilibrium is possible, and therefore, the microdroplet flows continuously towards the bulk (as reported in ref. 28). However, the droplet velocity steadily increases (region B in Fig. 1(g)) since the convective flow velocity (uf) decreases towards the drop center, as inferred in Fig. 2(b).
Apart from the migration of the DEX microdroplets near and parallel to the substrate, rarely do we observe that the tiny microdroplets get trapped in the large background recirculating flow. They move upward near the liquid–air interface and flow back to the contact line, similar to the dynamics described in PEG-DEX drops28 and also in the Marangoni ring formation in evaporating water–glycerol drops.29
2.3 Velocity change during individual coalescence
In Fig. 1(g), each coalescence event shifts a resting microdroplet to a new position, showcasing a velocity pattern starting from zero, peaking, and then returning to zero. Concurrently, the shape of the coalescing microdroplets is found to undergo a systematic pattern change, as shown in Fig. 4(a): first, the two merging spheres are connected through a neck which grows until the shape becomes an ellipsoid;38,39 subsequently, relaxing to a final larger sphere.40 In the following, for simplicity, we assume that the neck growth and the relaxation back to the sphere happens sequentially and independent of each other.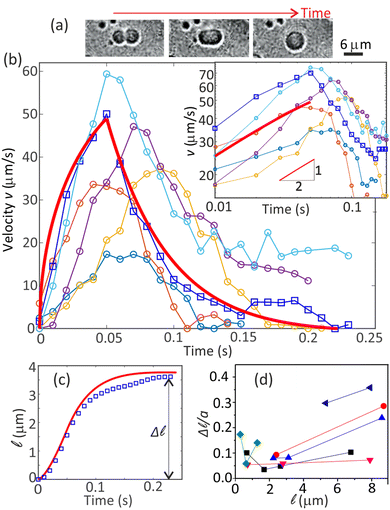 | ||
Fig. 4 (a) Shape change during the coalescence of two microdroplets. (b) Experimental velocity (v) peaks during coalescence events (also Fig. 1(g)). The solid red curve is from theory and represents one of the experimental curves (squares). The inset shows t1/2 growth of the velocity. (c) The distance traveled by the drop upon a coalescence. The plot corresponds to the data with connected open squares in (b). The solid red curve is theoretically calculated. (d) The scaled step length (Δ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /a) increases towards small and large /a) increases towards small and large ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , where corresponding small m values exist. The uncertainties in the values of v and , where corresponding small m values exist. The uncertainties in the values of v and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) correspond to at least one pixel. Given a resolution of 0.33 μm per pixel, this translates to uncertainties of at least 2 μm s−1 for v and 0.33 μm for correspond to at least one pixel. Given a resolution of 0.33 μm per pixel, this translates to uncertainties of at least 2 μm s−1 for v and 0.33 μm for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . . | ||
A correlation between the velocity peak and the shape change can be predicted from the time variation of the factor 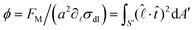 of eqn (1). Being a non-dimensonalized factor, ϕ depends only on the shape of the surface S′. For spheres coalescing along the radial direction, ϕ peaks when S′ is ellipsoidal (because ellipsoids aligning along
of eqn (1). Being a non-dimensonalized factor, ϕ depends only on the shape of the surface S′. For spheres coalescing along the radial direction, ϕ peaks when S′ is ellipsoidal (because ellipsoids aligning along 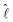 maximizes
maximizes 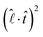 for most part of S′). Assuming a to be an average linear size of the combined microdroplets, we infer that the time dependence of FM is predominantly due to that of ϕ. Therefore, it follows from above that FM, too, peaks at the ellipsoidal shape, qualitatively explaining the peak in the relative velocity vM (the peaking of ϕ can easily be demonstrated in a numerical experiment of coalescence of two 2D droplets as shown in the ESI†).
for most part of S′). Assuming a to be an average linear size of the combined microdroplets, we infer that the time dependence of FM is predominantly due to that of ϕ. Therefore, it follows from above that FM, too, peaks at the ellipsoidal shape, qualitatively explaining the peak in the relative velocity vM (the peaking of ϕ can easily be demonstrated in a numerical experiment of coalescence of two 2D droplets as shown in the ESI†).
The effect of the background flow uf to the above analysis can be deduced from eqn (2) which implies that during a coalescence, 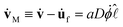 , where D = ∂
, where D = ∂![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) σdl/CHR. Identifying
σdl/CHR. Identifying 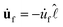
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) as −mv, with m = duf/d
as −mv, with m = duf/d![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) the slope of uf in the linear region [Fig. 2(b)], we find the lab-frame velocity v to evolve as:
the slope of uf in the linear region [Fig. 2(b)], we find the lab-frame velocity v to evolve as:
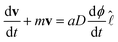 | (3) |
The factors D and m are experimentally estimable (see Appendix). The coalescence of two drops, or the factor ϕ, follows a dynamics characterized by the fast growth of the neck radius initially as t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t followed by t1/2.38,39,41 Our experiments cannot capture the early time t
t followed by t1/2.38,39,41 Our experiments cannot capture the early time t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t dynamics. After the initial growth, the ellipsoidal drop recovers to the final spherical shape in a nearly exponential manner.40 With the corresponding forms of ϕ, eqn (3) predicts the theoretical solution v(t) (see Appendix), which is plotted in Fig. 4(b) (solid red line), whereas the displacement during a coalescence,
t dynamics. After the initial growth, the ellipsoidal drop recovers to the final spherical shape in a nearly exponential manner.40 With the corresponding forms of ϕ, eqn (3) predicts the theoretical solution v(t) (see Appendix), which is plotted in Fig. 4(b) (solid red line), whereas the displacement during a coalescence, 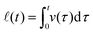 , is plotted in Fig. 4(c) (solid red line).
, is plotted in Fig. 4(c) (solid red line).
The experimental data was obtained by tracking the microdroplets near the contact line within a range of about 20 μm. It is achieved by a well-established tracking algorithm42 available publicly (included in the data in ESI†). The experimental velocities and displacement are also shown alongside in Fig. 4(b and c), respectively. While the experimental plots are in qualitative agreement with the exponential decay, the t1/2 growth dynamics is evident from both theory and experiments [inset, Fig. 4(b)]. Accordingly, displacements ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (t) have a good agreement between theory and experiments, showing deviations only slightly in the decay regions [Fig. 4(c)].
(t) have a good agreement between theory and experiments, showing deviations only slightly in the decay regions [Fig. 4(c)].
The strength of the background flow gradient (or slope m) decreases near and far from the contact line as inferred from Fig. 2(b) inset (also Fig. S6, ESI†). A decrease in the gradient allows the microdroplet to step a longer distance. Thus, we expect Δ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) to have larger values very close to and far away from the contact line, also as seen in Fig. 4(d). A similar effect can be seen for v during the coalescence-induced motion (Fig. S7, ESI†). Our analytical model also predicts this trend for Δ
to have larger values very close to and far away from the contact line, also as seen in Fig. 4(d). A similar effect can be seen for v during the coalescence-induced motion (Fig. S7, ESI†). Our analytical model also predicts this trend for Δ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and a peak of v during the coalescence (see Appendix and Fig. S8 and S9, ESI†).
and a peak of v during the coalescence (see Appendix and Fig. S8 and S9, ESI†).
Based on our model, we can anticipate certain microdroplet behavior during coalescence. When m is large, the condition vM + uf(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) = 0 may occur before complete shape relaxation to a sphere. In such instances, the decreasing vM with shape relaxation must make v negative, causing a slight droplet retraction (see Appendix and Fig. S10, ESI†).
) = 0 may occur before complete shape relaxation to a sphere. In such instances, the decreasing vM with shape relaxation must make v negative, causing a slight droplet retraction (see Appendix and Fig. S10, ESI†).
In our discussions, we have omitted factors such as the weak evaporation-driven capillary flow,4 viscosity gradient near the contact line, or effects of surrounding microdroplets.
3 Summary
In summary, we show that DEX nuclei, forming at the contact line of evaporating PEG-DEX drop, can migrate towards the bulk only by growing with random coalescence events. The interplay between the increasing size and gradient in the background flow strength leads to stepwise migration of these DEX nuclei. Understanding the interplay between the transport of nucleated phases and the background flows in the evaporating multiphase drops allows the development of strategies to control the self-organization of the phases. Thus, our findings provide valuable fundamental insights and opportunities for developing control of evaporation of multicomponent drops, LLPS-based membraneless compartment systems,19–21 and multiphase polymer systems of industrial applications such as inkjet printing,22,23 fabrication of biomaterials,24 and biomedical applications.43Author contributions
R. R., M. G., and S. P. P. performed the experiments, analyzed the data. DM designed the project, and TCA and DM performed the modeling and wrote the manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflicts of interest.Appendix
Analytical model of coalescence-induced motion
Neglecting the inertial effects we have the equation of motion, FD + FM = 0. Or,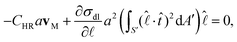 | (4) |
The velocity of the DEX nuclei in the lab frame is given as
| v = vM + uf | (5) |
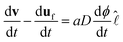 | (6) |
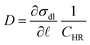 and
and 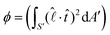 , which is a numerical factor depending upon the shape of the droplet during coalescence. We have the following directional relationships:
, which is a numerical factor depending upon the shape of the droplet during coalescence. We have the following directional relationships: 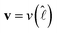 ,
, 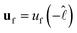 , and
, and 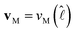 . Writing
. Writing 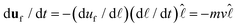 , where m is the gradient (slope) of the flow, results in eqn (3).
, where m is the gradient (slope) of the flow, results in eqn (3).
The coalescence process involves two parts: first is the merging of two droplets to form an ellipsoidal droplet. The second part is the relaxation of the ellipsoidal droplet to a final spherical one.
We can consider ϕ ∼ (t/τ0)1/2 and eqn (3) can be rewritten as,
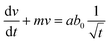 | (7) |
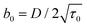 .
.
The solution of eqn (7) can be obtained as,
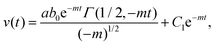 | (8) |
Eqn (3) can be written as,
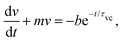 | (9) |
The solution of eqn (9) can be obtained as,
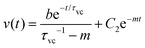 | (10) |
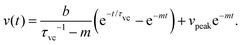 | (11) |
Taking a = 5 μm, μ = 10 mPa s, σdl = 1 μN m−1, and δρ = 32 kg m−3, we estimate the parameters and shown in the Table 1.
| Estimate | In Fig. 4(c) | |
|---|---|---|
| m | 2.5 s−1 | 5.0 s−1 |
| b 0 | 540* s−3/2 | 49 s−3/2 |
| b | 10 × 10−4 m s−2 | 8.4 × 10−4 m s−2 |
| τ vc | 0.05 s | 0.05 s |
We used the values shown in the Table to plot a representative theoretical curve for one of the experimental data plotted in Fig. 4(c) in the manuscript. The droplet radius was a = 4.7 μm. The time period for drop merging was 0.05 s (the time point where the velocity peak appears). Thus, eqn (8) was calculated for a duration 0–0.05 s. Eqn (11) was calculated until the velocity becomes zero.
![[small script l]](https://www.rsc.org/images/entities/b_char_e146.gif) upon each coalescence.
We can integrate eqn (8) and (11) for the duration of the droplet movement to obtain the distance traveled by the droplet. It also gives the step length Δ
upon each coalescence.
We can integrate eqn (8) and (11) for the duration of the droplet movement to obtain the distance traveled by the droplet. It also gives the step length Δ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) .
.
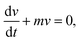 | (12) |
| v(t) = v0e−mt | (13) |
Acknowledgements
DM and TCA acknowledge grants CRG/2020/003117 and CRG/2021/004759, respectively, from the Science and Engineering Research Board (India).Notes and references
- S. K. Wilson and H.-M. D'Ambrosio, Annu. Rev. Fluid Mech., 2023, 55, 481–509 CrossRef.
- D. Mampallil and H. B. Eral, Adv. Colloid Interface Sci., 2018, 252, 38–54 CrossRef PubMed.
- H. Hu and R. G. Larson, J. Phys. Chem. B, 2006, 110, 7090–7094 CrossRef.
- A. G. Marín, H. Gelderblom, D. Lohse and J. H. Snoeijer, Phys. Rev. Lett., 2011, 107, 085502 CrossRef.
- S. Shiri, S. Sinha, D. A. Baumgartner and N. J. Cira, Phys. Rev. Lett., 2021, 127, 024502 CrossRef PubMed.
- W. D. Ristenpart, P. G. Kim, C. Domingues, J. Wan and H. A. Stone, Phys. Rev. Lett., 2007, 99, 234502 CrossRef PubMed.
- L.-P. Bergeron-Sandoval, N. Safaee and S. W. Michnick, Cell, 2016, 165, 1067–1079 CrossRef PubMed.
- M. Iqbal, Y. Tao and S. Xie, et al. , Biol. Proced. Online, 2016, 18 DOI:10.1186/s12575-016-0048-8.
- C. P. Brangwynne, P. Tompa and R. V. Pappu, Nat. Phys., 2015, 11, 899–904 Search PubMed.
- C. D. Keating and R. V. Pappu, J. Phys. Chem. B, 2021, 125, 12399–12400 CrossRef.
- A. A. M. André and E. Spruijt, Int. J. Mol. Sci., 2020, 21, 18 Search PubMed.
- B.-U. Moon, L. Malic, K. Morton, M. Jeyhani, A. Elmanzalawy, S. S. H. Tsai and T. Veres, Langmuir, 2020, 36, 14333–14341 CrossRef PubMed.
- C. H. Ooi, E. Bormashenko, A. V. Nguyen, G. M. Evans, D. V. Dao and N.-T. Nguyen, Langmuir, 2016, 32, 6097–6104 CrossRef PubMed.
- C. Diddens, H. Tan, P. Lv, M. Versluis, J. G. M. Kuerten, X. Zhang and D. Lohse, J. Fluid Mech., 2017, 823, 470–497 CrossRef.
- H. Tan, C. Diddens, P. Lv, J. G. M. Kuerten, X. Zhang and D. Lohse, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8642–8647 CrossRef PubMed.
- Y. Li, P. Lv, C. Diddens, H. Tan, H. Wijshoff, M. Versluis and D. Lohse, Phys. Rev. Lett., 2018, 120, 224501 CrossRef.
- H. Sadafi, R. Rabani, S. Dehaeck, H. Machrafi, B. Haut, P. Dauby and P. Colinet, Colloids Surf., A, 2020, 602, 125052 CrossRef CAS.
- Y. Li, P. Lv, C. Diddens and D. Lohse, J. Fluid Mech., 2022, 946, A37 CrossRef.
- H. M. Fares, A. E. Marras, J. M. Ting, M. V. Tirrell and C. D. Keating, Nat. Commun., 2020, 11, 5423 CrossRef PubMed.
- W. Guo, A. B. Kinghorn, Y. Zhang, Q. Li, A. D. Poonam, J. A. Tanner and H. C. Shum, Nat. Commun., 2021, 12, 1–13 CrossRef.
- C. Qi, X. Ma, Q. Zeng, Z. Huang, S. Zhang, X. Deng, T. Kong and Z. Liu, Nat. Commun., 2024, 15, 1107 CrossRef PubMed.
- U. S. B. J. de Gans and P. C. Duineveld, Adv. Mater., 2016, 16 DOI:10.1186/s12575-016-0048-8.
- J. F. Dijksman, P. C. Duineveld, M. J. J. Hack, A. Pierik, J. Rensen, J.-E. Rubingh, I. Schram and M. M. Vernhout, J. Mater. Chem., 2007, 17, 511–522 RSC.
- S. M. Park and D. K. Yoon, Mater. Horiz., 2024, 11, 1843–1866 RSC.
- S. Michelin, Annu. Rev. Fluid Mech., 2023, 55, 77–101 CrossRef.
- C. C. Maass, C. Krüger, S. Herminghaus and C. Bahr, Annu. Rev. Condens. Matter Phys., 2016, 7, 171–193 CrossRef CAS.
- Z. Izri, M. N. van der Linden, S. Michelin and O. Dauchot, Phys. Rev. Lett., 2014, 113, 248302 CrossRef PubMed.
- A. May, J. Hartmann and S. Hardt, Soft Matter, 2022, 18, 6313–6317 RSC.
- L. Thayyil Raju, C. Diddens, Y. Li, A. Marin, M. N. van der Linden, X. Zhang and D. Lohse, Langmuir, 2022, 38, 12082–12094 CrossRef PubMed.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 756–765 CrossRef PubMed.
- M. Kumar, M. Gopu, S. Pugalneelam Parameswaran, P. Joshi and D. Mampallil, JCIS Open, 2024, 13, 100101 CrossRef.
- M. Gopu and D. Mampallil, Phys. Fluids, 2022, 34, 102110 CrossRef.
- G. L. Leal, Advanced Transport Phenomena, Cambridge University Press, Cambridge, 2007 Search PubMed.
- R. van Gaalen, H. Wijshoff, J. Kuerten and C. Diddens, J. Colloid Interface Sci., 2022, 622, 892–903 CrossRef PubMed.
- M. R. Barmi and C. D. Meinhart, J. Phys. Chem. B, 2014, 118, 2414–2421 CrossRef.
- B. Bozorgmehr and B. T. Murray, ACS Omega, 2021, 6, 12577–12590 CrossRef.
- Z. Pan, S. Dash, J. A. Weibel and S. V. Garimella, Langmuir, 2013, 29, 15831–15841 CrossRef PubMed.
- J. Eggers, J. R. Lister and H. A. Stone, J. Fluid Mech., 1999, 401, 293–310 CrossRef.
- X. Xia, C. He and P. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 23467–23472 CrossRef PubMed.
- H.-X. Zhou, J. Chem. Phys., 2021, 155, 145102 CrossRef PubMed.
- L. Duchemin, J. Eggers and C. Josserand, J. Fluid Mech., 2003, 487, 167–178 CrossRef.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef.
- Y. Chao and H. C. Shum, Chem. Soc. Rev., 2020, 49, 114–142 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01056f |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2024 |