Open Access Article
Open Access ArticleTowards a greener electrosynthesis: pairing machine learning and 3D printing for rapid optimisation of anodic trifluoromethylation†
Nipun Kumar
Gupta‡
 af,
Yilin
Guo‡
af,
Yilin
Guo‡
 b,
Soon Yee
Chang‡
b,
Jing
Lin‡
b,
Soon Yee
Chang‡
b,
Jing
Lin‡
 c,
Zi Hui Jonathan
Khoo
c,
Zi Hui Jonathan
Khoo
 af,
Riko
I. Made
af,
Riko
I. Made
 a,
Zi En
Ooi
a,
Zi En
Ooi
 a,
Carina Yi Jing
Lim
a,
Carina Yi Jing
Lim
 a,
Chow Hern
Lee
a,
Chow Hern
Lee
 d,
M.
Sivapaalan
e,
Yee-Fun
Lim
d,
M.
Sivapaalan
e,
Yee-Fun
Lim
 af,
Edwin
Khoo
af,
Edwin
Khoo
 *c,
Lu Wen
Feng
*b,
Yanwei
Lum
*a and
Albertus D.
Handoko
*c,
Lu Wen
Feng
*b,
Yanwei
Lum
*a and
Albertus D.
Handoko
 *af
*af
aInstitute of Materials Research and Engineering (IMRE), Agency for Science, Technology and Research (A*STAR), 2 Fusionopolis Way, Innovis #08-03, Singapore 138634, Republic of Singapore. E-mail: lum_yanwei@imre.a-star.edu.sg; Handoko_Albertus@isce2.a-star.edu.sg
bNUS Centre for Additive Manufacturing (AM.NUS), E3-02-07, E3, Engineering Block 2, Engineering Drive 3, Singapore 117581. E-mail: mpelwf@nus.edu.sg
cInstitute for Infocomm Research (I2R), Agency for Science, Technology and Research (A*STAR), 1 Fusionopolis Way, Connexis #21-01, Singapore 138632, Republic of Singapore. E-mail: edwin_khoo@i2r.a-star.edu.sg
dSchool of Chemical and Biomedical Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798
eSchool of Materials Science and Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798
fInstitute of Sustainability for Chemicals, Energy and Environment (ISCE2), Agency for Science, Technology and Research (A*STAR), 1 Pesek Road, Jurong Island, Singapore 627833, Republic of Singapore
First published on 26th December 2023
Abstract
Applying electro-organic synthesis in flow configuration can potentially reduce the pharmaceutical industry's carbon footprint and simplify the reaction scale-up. However, the optimisation of such reactions has remained challenging due to the convoluted interplay between various input experimental parameters. Herein, we demonstrate the advantage of integrating a machine learning (ML) algorithm within an automated flow microreactor setup to assist in the optimisation of anodic trifluoromethylation without transition metal catalysts. The ML algorithm is able to optimise six reaction parameters concurrently and increase the reaction yield of anodic trifluoromethylation by >270% within two iterations. Furthermore, we discovered that suppression of electrode fouling and even higher reaction yields could be achieved by integrating 3D-printed metal electrodes into the microreactor. By coupling multiple analytical tools such as AC voltammetry, kinetic modelling, and gas chromatography, we gained holistic insights into the trifluoromethylation reaction mechanism, including potential sources of faradaic efficiency and reactant losses. More importantly, multiple electrochemical and non-electrochemical steps involved in this process are elucidated. Our findings highlight the potential of synergistically combining ML-assisted flow systems with advanced analytical tools to rapidly optimise complex electrosynthetic reactions sustainably.
Sustainability spotlightElectro-organic synthesis is a relatively new approach for making valuable molecules driven by electricity as an energy input. When coupled with flow configuration under optimum operating conditions, high energy transfer efficiency with minimum reagent wastage can be achieved, significantly reducing the environmental impact. However, the optimisation of flow electro-organic synthesis is highly challenging due to the convoluted interplay between various experimental parameters and the desired product(s) yields. Herein, we demonstrate how integrating a machine-learning algorithm and 3D printed electrodes in a flow electro-organic synthesis reactor can help rapidly optimise the reaction yield and address pertinent issues of electrode fouling in anodic trifluoromethylation reactions. Further analyses of the reaction data using advanced electrochemical techniques and kinetic modelling shed light on the reaction mechanisms. We believe that this work and the dataset contained within will benefit the concerted effort towards realising electro-organic synthesis as an efficient and versatile synthetic tool, minimising the footprint of reaction optimisation and helping to realise an environmentally friendly approach to chemical synthesis. This work advances efforts towards the following UN sustainable development goals: industry, innovation, and infrastructure (SDG 9), responsible consumption and production (SDG 12), and climate action (SDG 13). |
Introduction
Effective and targeted synthesis methods for pharmaceutical products with a reduced carbon footprint are highly sought after.1 Electrosynthesis can tap into renewable low-carbon electricity sources to drive specific synthetic reactions at targeted areas near the electrode, improving energy transfer efficiency while reducing the consumption of expensive and volatile reagents,2,3 potentially making the pharmaceutical industry more sustainable. However, the application of electrosynthesis in the pharmaceutical industry is still limited today, more than 170 years after Kolbe's first demonstration.4 One of the reasons could be the poorly understood mechanism of electrosynthesis, which involves complex relationships between the precursor, substrate, solvent, electrode, electrons, and other reaction parameters.5 The common use of hazardous solvents, redox mediators, and transition metal catalysts also limits the appeal of electrosynthesis.6,7In this regard, microreactors powered by machine learning (ML) algorithms can offer practical solutions to optimise a large number of parameters with non-trivial interdependency compared to a systematic Edisonian approach. Microreactors have a much smaller footprint and use tiny amounts of reagents, while offering precise control over the temperature, residence time, pressure of the reactor vessel, and a high surface-to-volume ratio.8,9 In addition, the short inter-electrode separation in flow reactors allows the flow reactor's operation without a reference electrolyte, which can simplify future scale-up.10 A multi-input problem such as electrosynthesis in flow microreactors is a prime test-bed for ML algorithms, as it can eliminate blind spots and biases that may prevent the discovery of global minima during manual optimisation.5,11,12 Furthermore, learnings obtained from the optimisation process may be transferrable to related reactions through transfer optimisation.13
In this work, an automated microflow electrosynthesis reactor is integrated with ML algorithms and a 3D-printed electrode under direct and alternating current (DC and AC) conditions to optimise the yield of trifluoromethylation of caffeine and investigate the challenging issue of reactor fouling. Trifluoromethylation was selected as the reaction has been demonstrated in both cathodic and anodic configurations,14,15 and it has significant applications in pharmacology.16 Caffeine was selected as the substrate as it is the most consumed psychoactive substance globally17 and is an inhibitor of AchE.18 Caffeine is also a challenging substrate for typical trifluoromethylation reactions, as the multiple N atoms in its structure can easily poison traditional transition metal catalysts.19 Here, we aim to move away from transition metal catalysts or redox mediators and optimise electrofluorination using a greener solvent (acetonitrile20) and widely available graphite anodes. A series of advanced analytical techniques are applied to get a holistic understanding of the electrochemical trifluoromethylation reaction. Finally, detailed kinetics based on a reaction network incorporating candidate mechanisms and side reactions with kinetic parameters were modelled and fitted to the experimental data. The fitting results help us discern probable reaction paths and side reactions and guide us to simplify the reaction network and distil the dominant mechanisms.
Materials and methods
Tetrabutylammonium perchlorate (TBAP, >98%, see ESI Section 9 for precaution†) and sodium trifluoromethanesulphinate (CF3SO2Na, >95%) were purchased from TCI chemicals. Caffeine was purchased from Sigma (>98.5%), and acetonitrile (chromatography grade) was purchased from VWR chemicals. All chemicals were utilised without any further purification.Microflow electrosynthesis cells with PEEK construction and 4 mm graphite electrodes were purchased from Electrocell North America. 3 mm expanded PTFE gaskets were purchased from James Walker. A Foxy R1 fraction collector (Teledyne ISCO) was used to collect reaction products for high-fidelity NMR quantitation. Cell temperature was controlled using a recirculating water cooler (CP-300F, Julabo GmbH). Flow pumps were purchased from Tacmina Corporation (Series Q). A preparative degasser (model 186002488) was purchased from Waters Corporation, and a potentiostat (IviumStat.h standard) was used to control the current or voltage. Square wave current pulses with variable upper and lower bound magnitudes and times were used to drive the reaction. The automation of the flow electrosynthesis setup was conducted through a unified LabView interface. Details of the setup can be viewed in ESI Section S1.†
Six parameters were investigated: (a) flow rate (constrained between 0.25 and 2.00 mL min−1), (b) first current pulse (ON current, constrained between 40 and 80 mA), (c) second current pulse (OFF current, constrained between 40 and −80 mA), (d) frequency of the AC pulse (F, constrained between 0.1 and 100 Hz), (e) temperature (T, constrained between 5 and 65 °C), and (f) duty cycle (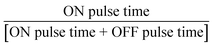 , constrained between 0.5 and 1.0). AC pulses were investigated as they have been reported to improve mass transport, improve stability, and enhance the electrode surface in other electrocatalytic reactions.21,22 Gaseous side products were collected and analysed with a GC-MS system to confirm the gas-phase side products from the trifluoromethylation reaction. We leverage our ML framework for optimising the six input parameters simultaneously within constraints. The initial sampling was performed with the experimental parameters generated via the Latin hypercube sampling (LHS) algorithm23 as implemented in scikit-optimize.24 LHS was chosen to maximise the range of exploration with the minimum number of initial datasets, while minimising the overlap between the experimental conditions. We then construct a surrogate artificial neural network (ANN) – as implemented in the Keras/TensorFlow framework,25 as an estimator for the target output, given the input parameters. The choice of the surrogate machine learning model is based on prior optimisation studies, where we observed comparatively faster convergence with the ANN model as compared to other machine learning algorithms (ESI Section S6†). We opted for the batched optimisation approach as it is more efficient, allowing us to take multiple suggestions to simultaneously operate in both exploration and exploitation modes and is less prone to noise and saddle point trapping.26–28
, constrained between 0.5 and 1.0). AC pulses were investigated as they have been reported to improve mass transport, improve stability, and enhance the electrode surface in other electrocatalytic reactions.21,22 Gaseous side products were collected and analysed with a GC-MS system to confirm the gas-phase side products from the trifluoromethylation reaction. We leverage our ML framework for optimising the six input parameters simultaneously within constraints. The initial sampling was performed with the experimental parameters generated via the Latin hypercube sampling (LHS) algorithm23 as implemented in scikit-optimize.24 LHS was chosen to maximise the range of exploration with the minimum number of initial datasets, while minimising the overlap between the experimental conditions. We then construct a surrogate artificial neural network (ANN) – as implemented in the Keras/TensorFlow framework,25 as an estimator for the target output, given the input parameters. The choice of the surrogate machine learning model is based on prior optimisation studies, where we observed comparatively faster convergence with the ANN model as compared to other machine learning algorithms (ESI Section S6†). We opted for the batched optimisation approach as it is more efficient, allowing us to take multiple suggestions to simultaneously operate in both exploration and exploitation modes and is less prone to noise and saddle point trapping.26–28
The 3D electrode design is conducted using computer-aided design (CAD) software, including SolidWorks and nTopology (v3.31.2). The evaluation of the geometry parameters, such as the surface area and porosity of the electrode structure, are calculated using the CAD software. The computational fluid dynamic (CFD) simulations are conducted using ANSYS Fluent (2022 R1) to understand and compare the hydrodynamic behaviour of the fluid between the conventional planar electrode and the proposed lattice-based body-centred cubic (BCC) structure, emphasising the flow distribution visualisation and residence time distribution (RTD) curve. Subsequently, the proposed electrode designs are 3D printed with industrial-level laser powder bed fusion (LPBF) additive manufacturing machine – EOS M290 with an SS 316L material and integrated into the flow system for performance evaluation.
AC voltammetry techniques were performed on a Gamry 600+ potentiostat coupled with a Digielch v8.0 as a measurement and analysis tool. The DC voltage was swept between 0.5 and 2.5 V vs. a leakless Ag/AgCl electrode (eDAQ) at a scanning speed of 0.04 V s−1. The AC amplitude and frequency were set at 0.15 V and ∼22 Hz (depending on the actual DC range and the number of AC cycles per step). The delay time was set at 2 s, and the potentiostat current range was fixed at 600 μA with a 200 kHz IE filter. iR compensation was added at 85% of the measured uncompensated solution resistance. The number of data points was collected at 2n, with n = 16. Fitting of the Fourier-transformed AC/DC voltammetry (FTAC) data was performed on Digielch v8.0, following the Marcus-Hush model. The initial concentration was assumed to be 0.05 mol L−1, and chemical potential (E0), symmetry of the electron transfer energy barrier (α), steady-state rate constant (ks) and diffusivity (D) of the electrochemical transfer reaction and species are fitted. For kinetic modelling, Python libraries such as SciPy29 and scikit-optimize24 were used to perform the estimation of kinetic parameters by fitting a reaction network to experimental concentration values.
Results and discussion
Trifluoromethylation reaction mechanism
The trifluoromethylation of caffeine is schematically represented in Fig. 1. The anodic electrosynthetic route towards trifluoromethylation of arenes has been suggested to follow the oxidation of the trifluoromethanesulphinate anion (CF3SO2−) to a trifluoromethanesulphinate radical (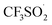 , Step 1) followed by its disintegration into a trifluoromethyl radical
, Step 1) followed by its disintegration into a trifluoromethyl radical 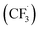 and SO2 (Step 2).30–32 The
and SO2 (Step 2).30–32 The 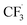 is proposed to react readily with caffeine to form a transition complex that is quickly converted to the caffeine–CF3 reaction complex through Step 3. Earlier studies have proposed that the caffeine–CF3 reaction complex converts trifluoromethylated caffeine (1,3,7-trimethyl-8-(trifluoromethyl)-3,7-dihydro-1H-purine-2,6-dione, referred to as I) exclusively through electrochemical Step 4a.30,31 Herein, our experimental observations of the by-products (red fonts in Fig. 1) and kinetic modelling point out the coexistence of a parallel chemically driven Step 4b. We shall discuss this in greater detail in the following sections.
is proposed to react readily with caffeine to form a transition complex that is quickly converted to the caffeine–CF3 reaction complex through Step 3. Earlier studies have proposed that the caffeine–CF3 reaction complex converts trifluoromethylated caffeine (1,3,7-trimethyl-8-(trifluoromethyl)-3,7-dihydro-1H-purine-2,6-dione, referred to as I) exclusively through electrochemical Step 4a.30,31 Herein, our experimental observations of the by-products (red fonts in Fig. 1) and kinetic modelling point out the coexistence of a parallel chemically driven Step 4b. We shall discuss this in greater detail in the following sections.
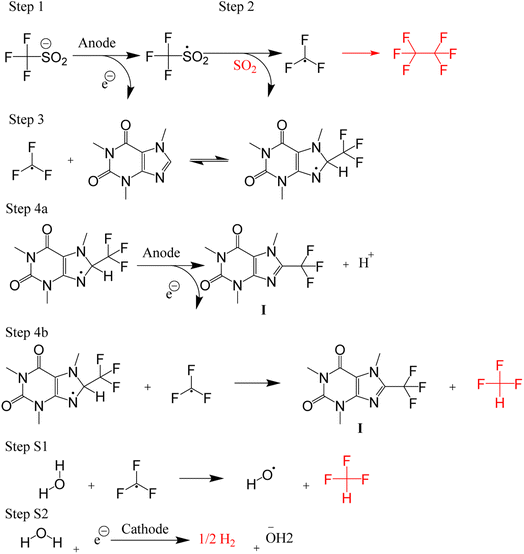 | ||
| Fig. 1 A schematic of the proposed mechanism for trifluoromethylation of caffeine. The gaseous side products are drawn in red colour. | ||
Electrochemistry characterisation
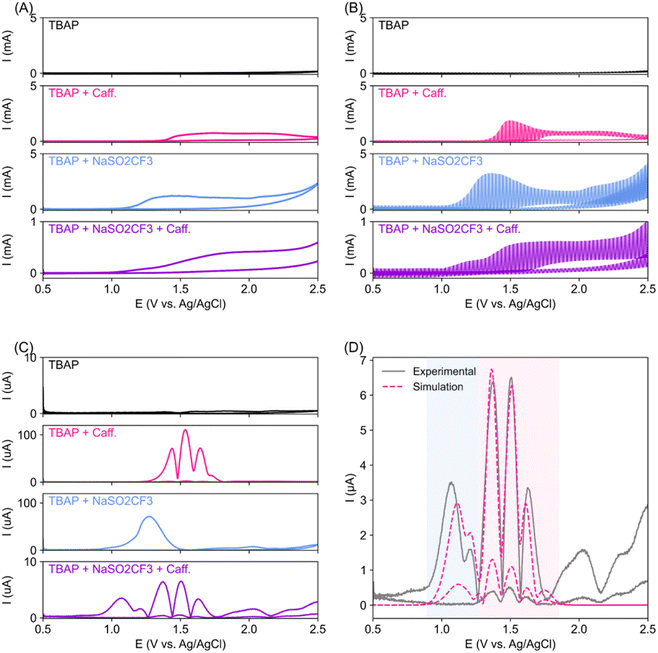
We first employed a superimposed AC/DC voltammetry technique33,34 to conduct a thorough analysis of the oxidation event surrounding the reactant near the electrodes. AC/DC voltammetry can extract minute electron transfer of surface-bound species that DC voltammetry often misses (Fig. 2A), as the contribution from the capacitance background current is removed by the fast-oscillating AC component.35 Flat AC/DC scan (black trace, Fig. 2B) indicates the stability of the TBAP electrolyte and solvent up to 2.5 V vs. Ag/AgCl. The oxidation of caffeine observed from 1.5 V vs. Ag/AgCl was indeed irreversible (pink trace), with no reduction event observed on the reverse (cathodic going) scan. The oxidation of NaSO2CF3 appears to occur a little bit earlier, at around 1.0 V vs. Ag/AgCl, as compared to caffeine. When all reactants are mixed (purple trace), the NaSO2CF3 oxidation features dominate, but caffeine oxidation peaks are still visible, although smaller and shifted to a more anodic potential. Inverse Fourier transformation (IFT) was then performed on fourth harmonic Fourier transformed AC/DC voltammetry (FTAC), resulting in multiple sets of peaks that correspond to electron transfer events (Fig. 2C). Notably, the reagent mixture (purple trace) contains features consistent with caffeine and NaSO2CF3 but shifted towards less anodic potential with some notable changes in the peak shape.Fitting of the caffeine's fourth harmonic IFT FTAC features suggests that the caffeine oxidation event follows two back-to-back two-electron transfer steps, first at 1.37 V followed by another at 1.63 V (ESI Fig. S2A and Table S1†). Our observations corroborate previously reported caffeine anodic oxidation that follows two consecutive 2-electron transfer reactions to 1,3,7 trimethyl uric acid, and subsequently to 4,5 diol uric acid.36 On the other hand, the anodic activation of NaSO2CF3 is often described as a single electron transfer process, followed by chemical transformation.30,37 Interestingly, our NaSO2CF3 FTAC signal fit best with two back-to-back single electron transfer events at around 1.18 and 1.53 V (ESI Fig. S2B and Table S2†), suggesting an unknown side reaction during NaSO2CF3 anodic oxidation. With higher oxidation potential, the caffeine substrate is expected to be more stable in the presence of NaSO2CF3. However, traces of caffeine oxidation are still present in the FTAC of the mixed reagent (Fig. 2C, purple trace), suggesting that caffeine oxidation may still be a potential side reaction that could lower the electron and caffeine utilisation efficiency. The mixed reagents' IFT FTAC fits well with combined caffeine and NaSO2CF3 oxidation events (Fig. 2D and Table S3†). However, we note that both oxidation events have earlier E0 when compared to the individual components, indicating possible interaction between the reagent mixtures during electrosynthesis.
Preliminary study on the microflow reactor
We then started the flow electrosynthesis experiments with a flat stainless steel (SS) plate as a cathode in chronoamperometry mode to simplify the reactor setup. The microflow reactor setup is described in ESI Section S1† while the quantitation methods utilised herein are described in ESI Section S3.† After a short period of the constant current operation of 20–40 min, we observed a significant deposit of deleterious reaction by-products on the electrode (Fig. S4†) that frequently leads to flow obstruction and cell leakage. These white solid deposits were identified as sulphates and fluorides of sodium based on powder XRD experiments (ESI Section S4, Fig. S5†). This observation is unexpected as it suggests that the trifluoromethyl radicals can undergo a reduction reaction at the cathode electrode to form fluoride anions, especially near the cathode where the local pH is expected to be alkaline in the presence of water.38In addition to the solid precipitates, we investigate the gaseous emission from the microflow reactor. Carbon dioxide (CO2), fluoroform (CF3H), and hexafluoroethane (C2F6) gases were detected (ESI Section S4, Fig. S6 and S7†). The CO2 likely evolved from the oxidation of the carbon at the graphite electrode. Whilst the evolution of C2F6 is expected, the evolution of the CHF3 formation is surprising and leads us to suggest that Step 4a of the trifluoromethylation reaction (Fig. 1) may not be the only pathway towards I. Based on the detection of CHF3 gas, we hypothesise that the 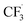 radicals generated in the second step can abstract an H˙ from the caffeine–CF3 complex due to their likely proximity near the anode electrode (Step 4b, Fig. 1).39 Alternatively, the
radicals generated in the second step can abstract an H˙ from the caffeine–CF3 complex due to their likely proximity near the anode electrode (Step 4b, Fig. 1).39 Alternatively, the 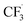 radical may also attack the water in the solvent (Step S1, Fig. 1) to form CHF3 gas and a hydroxide radical. Water is assumed to reduce to H2 and OH− on the cathode surface as a competing reaction (Step S2, Fig. 1).
radical may also attack the water in the solvent (Step S1, Fig. 1) to form CHF3 gas and a hydroxide radical. Water is assumed to reduce to H2 and OH− on the cathode surface as a competing reaction (Step S2, Fig. 1).
To address the reaction fouling, AC waveforms and 3D-printed SS electrodes were explored. AC conditions have been shown to improve reaction yield while lowering energy consumption.43 When optimised correctly, it can improve electrosynthesis reaction efficiency and selectivity.40,41 On the other hand, 3D-printed electrodes can improve reagent mixing42 and mass transfer to electrodes,43 while increasing the reaction turnover by virtue of increased surface area.
A simple BCC geometry with a unit cell of 6 mm (referred to as BCC-6 mm, Fig. 3C and ESI Table S4†) was then selected based on the evaluation of optimum surface area, porosity and residence times of electrode structures (see ESI Section S5†). The results showed that using a BCC-6 mm electrode structure increases the electrode surface by 3-fold and reduces the porosity by 25% as compared to the planar electrode. More importantly, the BCC-6 mm almost doubles the maximum velocity of fluid flow (at height 2 mm above the electrode) from ∼3.4 × 10−4 m s−1 to ∼5.5 × 10−4 m s−1 (ESI Table S5†), which we posit to be the key to reducing the fouling accumulation.
To understand how the electrode design and AC conditions contribute to the yield, we compared the 3D printed BCC-6 mm patterned SS electrode with a flat SS plate as cathodes under AC and DC conditions. We observe that flat SS electrodes have a markedly lower yield as compared to the 3D-printed BCC-6 mm SS electrodes (ESI Table S7†) as well as severe reaction fouling (ESI Fig. S4†). This could be linked to the larger surface area and longer and more spread-out retention time, as observed in the CFD RTD simulation (ESI Fig. S8†). Thus, we chose to use 3D-printed BCC-6 mm SS electrodes for the optimisation in this study due to the comparatively higher reaction yields compared to flat SS electrodes.
ML-guided reaction optimisation
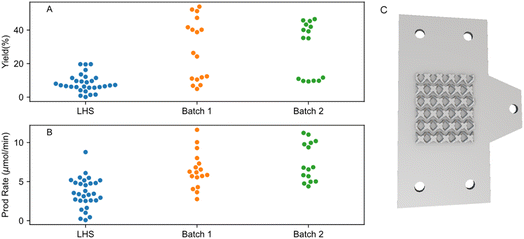
ML algorithm-assisted optimisation of the reaction was performed by first obtaining an initial sampling dataset suggested by the LHS algorithm. The initial dataset is then used as a prior to construct surrogate models capable of relating the objective (reaction yield and production rate) and the input parameters. After selecting the best models, the optimisation process is then done by the Bayesian Optimisation (BO) method.44 Further details of the optimisation modelling are presented in ESI Section S6†. For the reaction yield objective, a minimum and maximum yield of 0.10% and 19.64% were observed in the initial sampling dataset respectively (Fig. 3, labelled as LHS). Surprisingly, the first BO iteration already resulted in significantly enhanced maximum and minimum yield of 53.99% and 4.90% respectively (Fig. 3A, batch_1). A second iteration was then done by re-training the models with updated prior that contains new results from batch_1. A minimum and maximum yield of 9.35% and 46.63% was observed respectively. No further iteration was done as no improvement in the maximum yield was observed. Full results of the ML-aided optimisation results can be seen in Tables S7–S9 and Fig. S11.†Similar trends were also observed for the production rate objective, where the maximum production rate increased by almost 50% from 8.78 to 11.63 μmol min−1, for the experiments from the initial sampling run and the experiments with the parameters suggested by the ML model from the first BO, respectively (Fig. 2B). The second iteration of the BO did not improve the production rate, with the maximum and minimum rates being 11.23 μmol min−1 and 4.39 μmol min−1, respectively. From these results, it appears that we have the appropriate size of initial sampling parameters and that the ML model can find out the underlying parameters in relation to the yield and production rate relatively quickly, hence achieving the global maxima early.
We can now comment on the relationship between the input parameters and objectives. We see some interesting relationships between the input parameters chosen herein and the dependent parameters, i.e. yield and production rate, with the help of SHAP feature importance maps45 (Fig. 4). The input parameters are represented on the y-axis, and their respective Shapley values are presented on the x-axis. Input parameters that strongly influence the output have a wider spread of the Shapley values, and input parameters that have minimal influence on the output have clustered Shapley values. We observe that the flow rate has a strong inverse correlation with the yield (Fig. 4A). Conversely, there is a strong direct correlation with the production rate (Fig. 4B). Based on the spread of the Shapley values along the x-axis for the various input parameters, we observe that the flow rate, duty cycle, and T strongly influence the yield and the production rate compared to the current pulses and the frequency. However, the exact order varies for both metrics. We also observe that all other parameters are directly correlated to the yield (except for the flow rate) and the production rate. On the other hand, F appears to influence the production rate negligibly.
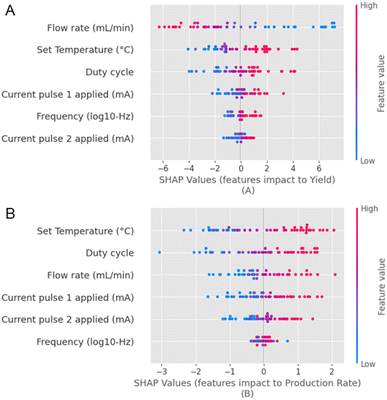 | ||
| Fig. 4 A representation of the feature importance for all the independent input and dependent output parameters, which are (A) the yield and the (B) production rate with a SHAP waterfall map. | ||
In this work, non-continuous parameters such as the reactor geometry, electrode material, and substrate scope were not optimised, leading to a relatively lower (absolute) reaction yield and production rate compared to the literature with similar reagents.19,46–49 However, we wish to highlight that the implementation of our workflow has successfully optimised the reaction within two iterations. This approach can be extended to many other electrosynthesis reactions without a strict need for reaction chemistry knowledge.
Reaction kinetics and analysis
The datasets obtained from the optimisation steps contain valuable information that can be used to model detailed reaction kinetics following a prescribed reaction network and its associated rate laws. Kinetics modelling incorporates physical constraints and considers the whole dynamic process to provide a mechanistic understanding of the reaction, allowing for better generalisation to different reactor setups and facilitating scaling up. To build a kinetic model, we first hypothesise several candidate reaction pathways based on the mechanism proposed by Deng et al.30 and the experiments performed in previous sections, which contain various intermediate species and speculated side reactions, as shown in eqn (1)–(8).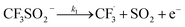 | (1) |
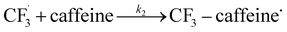 | (2) |
 | (3) |
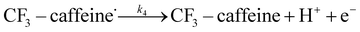 | (4) |
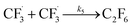 | (5) |
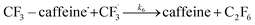 | (6) |
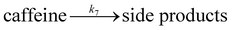 | (7) |
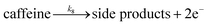 | (8) |
We want to distinguish the mechanism suggested by the experimental data. First, note that we include both the chemical and electrochemical steps for producing I, corresponding to eqn (3) and (4), respectively. Second, we incorporate three radical termination steps as eqn (3), (5) and (6) that produce various gas side products detected by GC-MS. Besides, comparing the molar concentrations of the reacted NaSO2CF3 and I (Fig. S13†) shows that the reacted NaSO2CF3 is typically 2 to 4 times as much as I. We expect the dimerisation of the 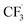 and the formation of CHF3 from
and the formation of CHF3 from 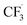 and CF3–caffeine˙ to be the major side reactions related to NaSO2CF3. Third, we add both the chemical and electrochemical side reactions of caffeine in eqn (7) and (8), respectively.
and CF3–caffeine˙ to be the major side reactions related to NaSO2CF3. Third, we add both the chemical and electrochemical side reactions of caffeine in eqn (7) and (8), respectively.
Looking at the total faradaic efficiency (FE) at the anode as a metric of electron utilisation, if anodic oxidation of NaSO2CF3 is taken as the only electron donating reaction, we found the average total FE to be very far from unity, approx. 53.8(±13.8)%. We posit that the missing FE could stem from the side electrochemical process, such as the caffeine oxidation detected in the AC voltammetry experiment (Fig. 2). As we have shown that caffeine is stable in the reagent without current (Fig. S2†), the average caffeine loss of about 3.7(±2.6) mM (Table S10†) should originate from anodic oxidation. These losses translate to 18.7(±9.9)% FE if the two back-to-back two-electron steps suggested by AC voltammetry are followed. When caffeine oxidation is considered, the total FE becomes closer to unity at 72.2(±17.3)%. We add both the chemical and electrochemical mechanisms to the network, attempting to discern the dominant one from the data. However, comparing the reacted caffeine and I (Fig. S15†) implies that side reactions involving caffeine are mild, so this reaction might not be discernible. The remainder of the missing FE could represent other side reactions that are not quantified, such as CO2 generation from the anode.
We assume that all the rate laws are elementary. To fit the rate constants in these rate laws to the concentration measurements, we also need a reactor model that governs the transport of the species. For the efficiency of parameter fitting, we make several simplifications. From the reaction data, we observed that the dominant conditions affecting the yield are the residence time t = lwhε/![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) , and the anode temperature, where l, w, h, and ε denote the length, width, thickness, and porosity of the flow reactor channel, respectively, while
, and the anode temperature, where l, w, h, and ε denote the length, width, thickness, and porosity of the flow reactor channel, respectively, while ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) is the volumetric flow rate. The mean anodic current Ī = ρmax{I1,0} + (1 − ρ)max{I2,0} also has an apparent influence on the yield, where ρ is the duty cycle ratio. In contrast, the role of pulsing (Fig. S12†) is relatively ambiguous. Therefore, we make the simplification of using a constant average current without accounting for pulsing only to capture the dominant effects on the yield.
is the volumetric flow rate. The mean anodic current Ī = ρmax{I1,0} + (1 − ρ)max{I2,0} also has an apparent influence on the yield, where ρ is the duty cycle ratio. In contrast, the role of pulsing (Fig. S12†) is relatively ambiguous. Therefore, we make the simplification of using a constant average current without accounting for pulsing only to capture the dominant effects on the yield.
We further assume that species concentration is uniform over each cross-section of the channel and only varies along the flow. This is because the inter-electrode thickness is much lower than the other two dimensions, also considering the spanwise homogeneity (Fig. S14†). We further ignore the residence time distribution for simplicity and thus apply the plug-flow reactor conditions50 to this case and identify the flow-wise coordinate with time. Therefore, the full reactor model reduces to a system of ODEs characterising how the species concentrations vary with time, which are solved using the Python library scipy.integrate.29
All candidate reaction pathways share the same initial step, where NaSO2CF3 is oxidised at the anode to generate 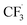 and kick off the whole reaction. Using an irreversible version of the Butler–Volmer equation formulated in terms of the electrode potential rather than overpotential, the first step is decoupled from the rest and governed by eqn (9).
and kick off the whole reaction. Using an irreversible version of the Butler–Volmer equation formulated in terms of the electrode potential rather than overpotential, the first step is decoupled from the rest and governed by eqn (9).
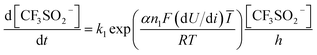 | (9) |
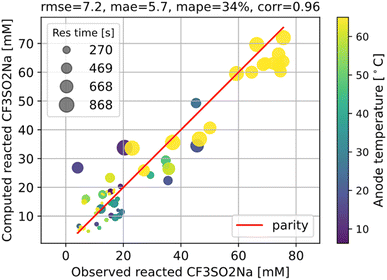
Hence, using the measurements of CF3SO2− at the exit, we can fit the kinetic parameters for this first step separately as shown in Fig. 5.
The rest of the kinetic parameters are fitted to caffeine and I molar using nonlinear least squares implemented by the Python library scipy.optimize.29 When fitting the full reaction network as formulated in eqn (1)–(8) (fitting results shown in Fig. S15†), we find that the full network can essentially be simplified to a subset of it, which is extracted and adapted as the simplified model as follows (eqn (10)–(14)).
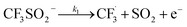 | (10) |
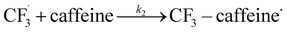 | (11) |
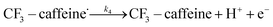 | (12) |
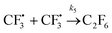 | (13) |
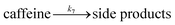 | (14) |
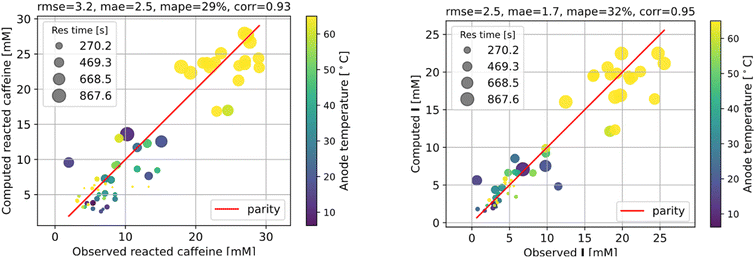
The fitting results shown in Fig. 6 are as good as those of the full model. As we can see, the agreement with measurements is reasonably good, with the error in the final I product prediction being around 2 mM, well within the uncertainty of an NMR molar measurement. The kinetic parameters from fitting are listed in Table 1, with the rate constant for each step represented by the Arrhenius equation k = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E/RT), where A is the pre-exponential factor and E is the activation energy.
exp(−E/RT), where A is the pre-exponential factor and E is the activation energy.
| Step | k 1 | k 2 | k 4 | k 5 | k 7 |
|---|---|---|---|---|---|
| A | 3.3 × 10−6 m s−1 | 7.2/(mM s) | 3.1 m s−1 | 6.8/(mM s) | 4.7 × 10−4 s−1 |
| E [in kJ mol−1] | 4.1 | 21 | 17 | 7.0 | 2.1 |
We must emphasise that the flow reactor experiments in this work have been designed to optimise the yield rather than discern the detailed reaction mechanisms. With the aggressive simplifying approximation made regarding the reactor to make kinetic parameter fitting feasible, the obtained kinetic model should be viewed as a preliminary attempt to elucidate the kinetic processes rather than a conclusive mechanistic study. The model can decently capture the dominant effects of temperature, residence time, and average current on the reaction progression, but much work is still needed to verify the detailed mechanisms and associated kinetic parameters.
Conclusions
Our work demonstrates how a synergistic combination of the ML algorithm with advanced analytical tools can be very efficient in optimising complex electrosynthetic reactions rapidly and sustainably without prior knowledge of the chemical reactions. Specifically, we found the ANN model to be the most suitable algorithm to reach the optimum conditions with just two iterations. While training datasets are required in this work, newer concepts of transfer optimisation envision that diverse optimisation datasets from related reactions can be exploited in the future. This will enable rapid deployment of electrosynthetic approaches to produce complex functionalised molecules relevant to the pharmaceutical and specialty chemical industries in a greener manner whilst eliminating the need for transition metal catalysts and hazardous redox intermediate compounds.Furthermore, advances in electrochemical techniques, such as superimposed AC/DC voltammetry, can be applied to discern possible electron transfer events during the reaction, enabling rapid evaluation of solvent, reagent, and substrate suitability and compatibility. We also hypothesise a reaction network with elementary rate laws and fit the kinetic parameters to the experimental data to study the detailed reaction mechanisms. We find that not only the initial oxidation of NaSO2CF3 is electrochemical, but the final product I is also likely to be generated through an electrochemical step. The fitting results also indicate that the dimerisation of 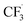 is the dominant side reaction of NaSO2CF3. Due to the mildness of the side reaction for caffeine, it is not clear from the fitting whether its major mechanism is electrochemical. Finally, we also simplify the full reaction network to a much more parsimonious one while preserving most of the accuracy, showing that it captures the major reaction mechanism.
is the dominant side reaction of NaSO2CF3. Due to the mildness of the side reaction for caffeine, it is not clear from the fitting whether its major mechanism is electrochemical. Finally, we also simplify the full reaction network to a much more parsimonious one while preserving most of the accuracy, showing that it captures the major reaction mechanism.
Electrode fouling is also a formidable challenge in electrosynthesis. Here, we discover that applying AC pulses and integrating 3D-printed cathodes suppress the fouling significantly and increase the experimental yield by >270%. CFD simulations suggest that the protrusions on the electrode increase the cell's turbulence and the components' mixing. Also, the increased surface area of the electrode further enhances the surface-to-volume ratio of the reaction, promoting the conversion of the reactant into the product. As such, the combination can be readily adopted for continuous electrosynthesis of many desired compounds. Although only unpressurised microflow reactors are used in this study, further optimisation of the reactor and process design, such as increasing working pressure, adding gaseous vents, and implementing process loops, can improve the electron and reagent utilisation efficiency significantly.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
Dr Yuan C. H. Steven and the NUS CMMAC are acknowledged for assisting with the experiments to identify the gaseous side products. Associate Professor Kedar Hippalgaonkar from the School of Materials Science and Engineering, Nanyang Technological University and the Institute of Materials Research and Engineering (IMRE), Agency for Science, Technology and Research (A*STAR) is acknowledged for assistance with the development of the machine learning frameworks. This work was funded by A*STAR under the Pharma Innovation Programme Singapore (PIPS) grant (A20B3a0131, A20B3a0133, and A20B3a0134), the Accelerated Materials Development for Manufacturing Programme (A1898b0043), the Accelerated Catalysis Development Platform (A19E9a0103) and HTCO seed fund (C231218004). We acknowledge the subject matter experts from Pfizer, Syngenta, MSD, and GSK overseeing the combined electrochemistry project C13 for their support, guidance, and feedback.References
- R. Cernansky, Nature, 2015, 519, 379–380 CrossRef PubMed.
- B. K. Peters, K. X. Rodriguez, S. H. Reisberg, S. B. Beil, D. P. Hickey, Y. Kawamata, M. Collins, J. Starr, L. Chen, S. Udyavara, K. Klunder, T. J. Gorey, S. L. Anderson, M. Neurock, S. D. Minteer and P. S. Baran, Science, 2019, 363, 838–845 CrossRef CAS PubMed.
- E. J. Horn, B. R. Rosen and P. S. Baran, ACS Cent. Sci., 2016, 2, 302–308 CrossRef CAS.
- H. Kolbe, J. Prakt. Chem., 1847, 41, 137–139 CrossRef.
- V. Sans and L. Cronin, Chem. Soc. Rev., 2016, 45, 2032–2043 RSC.
- S. Cembellín and B. Batanero, Chem. Rec., 2021, 21, 2453–2471 CrossRef PubMed.
- R. Francke, Curr. Opin. Electrochem., 2022, 36, 101111 CrossRef CAS.
- M. I. Awad and T. Ohsaka, J. Power Sources, 2013, 226, 306–312 CrossRef CAS.
- T. Noël, Y. Cao and G. Laudadio, Acc. Chem. Res., 2019, 52, 2858–2869 CrossRef PubMed.
- T. P. Nicholls, C. Schotten and C. E. Willans, Curr. Opin. Green Sustainable Chem., 2020, 26, 100355 CrossRef.
- A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Chem. Eng. J., 2018, 352, 277–282 CrossRef CAS.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89–96 CrossRef CAS PubMed.
- A. Gupta, Y.-S. Ong and L. Feng, IEEE Trans. Emerg. Top. Comput. Intell., 2018, 2, 51–64 Search PubMed.
- W. Jud, S. Maljuric, C. O. Kappe and D. Cantillo, Org. Lett., 2019, 21, 7970–7975 CrossRef CAS PubMed.
- R. P. Bhaskaran and B. P. Babu, Adv. Synth. Catal., 2020, 362, 5219–5237 CrossRef CAS.
- A. S. Nair, A. K. Singh, A. Kumar, S. Kumar, S. Sukumaran, V. P. Koyiparambath, L. K. Pappachen, T. M. Rangarajan, H. Kim and B. Mathew, Processes, 2022, 10, 2054 CrossRef CAS.
- A. Nehlig, Neurosci. Biobehav. Rev., 1999, 23, 563–576 CrossRef CAS PubMed.
- N. R. Jabir, F. R. Khan and S. Tabrez, CNS Neurosci. Ther., 2018, 24, 753–762 CrossRef CAS PubMed.
- X.-A. Liang, D. Liu, H. Sun, C. Jiang, H. Chen, L. Niu, K. Mahato, T. Abdelilah, H. Zhang and A. Lei, Adv. Synth. Catal., 2020, 362, 1138–1143 CrossRef CAS.
- D. Prat, O. Pardigon, H.-W. Flemming, S. Letestu, V. Ducandas, P. Isnard, E. Guntrum, T. Senac, S. Ruisseau, P. Cruciani and P. Hosek, Org. Process Res. Dev., 2013, 17, 1517–1525 CrossRef CAS.
- R. Casebolt, K. Levine, J. Suntivich and T. Hanrath, Joule, 2021, 5, 1987–2026 CrossRef CAS.
- A. Engelbrecht, C. Uhlig, O. Stark, M. Hämmerle, G. Schmid, E. Magori, K. Wiesner-Fleischer, M. Fleischer and R. Moos, J. Electrochem. Soc., 2018, 165, J3059–J3068 CrossRef CAS.
- M. D. McKay, R. J. Beckman and W. J. Conover, Technometrics, 1979, 21, 239–245 Search PubMed.
- T. Head, M. Coder, G. Louppe, I. Shcherbatyi Fcharras, Z. Vinícius Cmmalone, C. Schröder, N. Campos, T. Young, S. Cereda, T. Fan, R. Rex, K. K. Shi, J. Schwabedal, C. H. Labs, M. Pak, F. Callaway, L. Estève, L. Besson, M. Cherti, K. Pfannschmidt, F. Linzberger, C. Cauet, A. Gut, A. Mueller and A. Fabisch, scikit-optimize/scikit-optimize: v0.5.2, GitHub, 2018, https://github.com/scikit-optimize/scikit-optimize Search PubMed.
- F. Chollet, Keras, Github, 2015, https://github.com/fchollet/keras Search PubMed.
- S. L. Smith, P.-J. Kindermans and Q. V. Le, Sixth International Conference on Learning Representations, Vancouver, Canada, 2018 Search PubMed.
- R. Ge, F. Huang, C. Jin and Y. Yuan, The 28th Conference on Learning Theory, JMLR Workshop and Conference Proceedings, Paris, France, 2015, pp. 797–842 Search PubMed.
- D. R. Jones, M. Schonlau and W. J. Welch, J. Glob. Optim., 1998, 13, 455–492 CrossRef.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. Van Der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. Vanderplas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. Van Mulbregt, A. Vijaykumar, A. P. Bardelli, A. Rothberg, A. Hilboll, A. Kloeckner, A. Scopatz, A. Lee, A. Rokem, C. N. Woods, C. Fulton, C. Masson, C. Häggström, C. Fitzgerald, D. A. Nicholson, D. R. Hagen, D. V. Pasechnik, E. Olivetti, E. Martin, E. Wieser, F. Silva, F. Lenders, F. Wilhelm, G. Young, G. A. Price, G.-L. Ingold, G. E. Allen, G. R. Lee, H. Audren, I. Probst, J. P. Dietrich, J. Silterra, J. T. Webber, J. Slavič, J. Nothman, J. Buchner, J. Kulick, J. L. Schönberger, J. V. De Miranda Cardoso, J. Reimer, J. Harrington, J. L. C. Rodríguez, J. Nunez-Iglesias, J. Kuczynski, K. Tritz, M. Thoma, M. Newville, M. Kümmerer, M. Bolingbroke, M. Tartre, M. Pak, N. J. Smith, N. Nowaczyk, N. Shebanov, O. Pavlyk, P. A. Brodtkorb, P. Lee, R. T. Mcgibbon, R. Feldbauer, S. Lewis, S. Tygier, S. Sievert, S. Vigna, S. Peterson, S. More, T. Pudlik, T. Oshima, T. J. Pingel, T. P. Robitaille, T. Spura, T. R. Jones, T. Cera, T. Leslie, T. Zito, T. Krauss, U. Upadhyay, Y. O. Halchenko and Y. Vázquez-Baeza, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- Y. Deng, F. Lu, S. You, T. Xia, Y. Zheng, C. Lu, G. Yang, Z. Chen, M. Gao and A. Lei, Chin. J. Chem., 2019, 37, 817–820 CrossRef CAS.
- Z. Ruan, Z. Huang, Z. Xu, G. Mo, X. Tian, X.-Y. Yu and L. Ackermann, Org. Lett., 2019, 21, 1237–1240 CrossRef CAS PubMed.
- Z. Zhang, L. Zhang, Y. Cao, F. Li, G. Bai, G. Liu, Y. Yang and F. Mo, Org. Lett., 2019, 21, 762–766 CrossRef CAS PubMed.
- J. Zhang, S.-X. Guo, A. M. Bond and F. Marken, Anal. Chem., 2004, 76, 3619–3629 CrossRef CAS.
- C. Y. J. Lim, M. Yilmaz, J. M. Arce-Ramos, A. D. Handoko, W. J. Teh, Y. Zheng, Z. H. J. Khoo, M. Lin, M. Isaacs, T. L. D. Tam, Y. Bai, C. K. Ng, B. S. Yeo, G. Sankar, I. P. Parkin, K. Hippalgaonkar, M. B. Sullivan, J. Zhang and Y.-F. Lim, Nat. Commun., 2023, 14, 335 CrossRef CAS PubMed.
- M. J. A. Shiddiky, A. P. O'Mullane, J. Zhang, L. D. Burke and A. M. Bond, Langmuir, 2011, 27, 10302–10311 CrossRef CAS PubMed.
- Y. Tadesse, A. Tadese, R. C. Saini and R. Pal, Int. J. Electrochem., 2013, 2013, 1–7 CrossRef.
- D. Deng, K. S. Novoselov, Q. Fu, N. Zheng, Z. Tian and X. Bao, Nat. Nanotechnol., 2016, 11, 218–230 CrossRef CAS PubMed.
- M. Schatz, S. Jovanovic, R.-A. Eichel and J. Granwehr, Sci. Rep., 2022, 12, 8274 CrossRef CAS PubMed.
- G. O. Pritchard, H. O. Pritchard, H. I. Schiff and A. F. Trotman-Dickenson, Trans. Faraday Soc., 1956, 52, 849 RSC.
- Y. Kawamata, K. Hayashi, E. Carlson, S. Shaji, D. Waldmann, B. J. Simmons, J. T. Edwards, C. W. Zapf, M. Saito and P. S. Baran, J. Am. Chem. Soc., 2021, 143, 16580–16588 CrossRef CAS PubMed.
- L. E. Sattler, C. J. Otten and G. Hilt, Chem.–Eur. J., 2020, 26, 3129–3136 CrossRef CAS.
- A. Ambrosi, R. R. S. Shi and R. D. Webster, J. Mater. Chem. A, 2020, 8, 21902–21929 RSC.
- R. A. Márquez-Montes, V. H. Collins-Martínez, I. Pérez-Reyes, D. Chávez-Flores, O. A. Graeve and V. H. Ramos-Sánchez, ACS Sustain. Chem. Eng., 2020, 8, 3896–3905 CrossRef.
- Y.-F. Lim, C. K. Ng, U. S. Vaitesswar and K. Hippalgaonkar, Adv. Intell. Syst., 2021, 3, 2100101 CrossRef.
- S. M. Lundberg and S.-I. Lee, 31st Conference on Neural Information Processing Systems (NIPS), ed. U. v. Luxburg, I. Guyon, S. Bengio, H. Wallach and R. Fergus, Curran Associates Inc., Long Beach, CA, USA, 2017, pp. 4768–4777 Search PubMed.
- R. D. Baxter and D. G. Blackmond, Tetrahedron, 2013, 69, 5604–5608 CrossRef CAS.
- S. Rodrigo, C. Um, J. C. Mixdorf, D. Gunasekera, H. M. Nguyen and L. Luo, Org. Lett., 2020, 22, 6719–6723 CrossRef CAS PubMed.
- A. G. O'Brien, A. Maruyama, Y. Inokuma, M. Fujita, P. S. Baran and D. G. Blackmond, Angew. Chem., Int. Ed., 2014, 53, 11868–11871 CrossRef PubMed.
- J. Struwe and L. Ackermann, Faraday Discuss., 2023, 247, 79–86 RSC.
- H. S. Fogler, Elements of Chemical Reaction Engineering, Pearson Education, Inc., 2016 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3su00433c |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |