Open Access Article
Open Access ArticleGraph theory and graph neural network assisted high-throughput crystal structure prediction and screening for energy conversion and storage†
Joshua
Ojih
a,
Mohammed
Al-Fahdi
 a,
Yagang
Yao
b,
Jianjun
Hu
a,
Yagang
Yao
b,
Jianjun
Hu
 c and
Ming
Hu
c and
Ming
Hu
 *a
*a
aDepartment of Mechanical Engineering, University of South Carolina, SC 29208, USA. E-mail: hu@sc.edu
bNational Laboratory of Solid State Microstructures, College of Engineering and Applied Sciences, Jiangsu Key Laboratory of Artificial Functional Materials, and Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China
cDepartment of Computer Science and Engineering, University of South Carolina, Columbia, SC 29208, USA
First published on 6th March 2024
Abstract
Prediction of crystal structures with desirable material properties is a grand challenge in materials research, due to the enormous search space of possible combinations of elements and their countless arrangements in 3D space. Despite the recent progress of a few crystal structure prediction algorithms, most of those methods only target a few specific material families or are restricted to simple systems with limited element diversity. Moreover, these algorithms are usually coupled with first principles calculations and thus are computationally expensive and very time consuming. Therefore, establishing a workflow that can generate a large number of hypothetical structures with diverse elements and quickly optimize and screen out stable structures is urgently needed for the crystal structure prediction field. In this study, we take 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277 compositions involving 63 elements across the periodic table from the open quantum materials database (OQMD) and use a graph theory assisted universal structure searcher (MAGUS) to generate more than 3.4 million hypothetical structures. We employ a pre-trained universal interatomic potential named Crystal Hamiltonian Graph neural Network (CHGNet) to rapidly optimize this large number of hypothetical structures. Subsequently, we validate these optimized structures using density functional theory (DFT) and find 4145 structures are successfully optimized and 2368 structures have energy lower than those from the original OQMD. 647 structures are further identified to be dynamically stable using CHGNet. Moreover, the stability of 123 out of 200 randomly chosen structures are validated by DFT, corresponding to a high success rate of 61.5%. We further use 4706 DFT data points to train 3 graph neural network models to predict lattice thermal conductivity (LTC) and heat capacity. Numerous structures with ultralow LTC and high heat capacity, which are promising for advanced energy conversion and energy storage, have been identified. The success of our workflow demonstrates that combining graph theory with pre-trained universal interatomic potential is highly expected to accelerate the search for new both thermodynamically and dynamically stable structures with target material properties.
277 compositions involving 63 elements across the periodic table from the open quantum materials database (OQMD) and use a graph theory assisted universal structure searcher (MAGUS) to generate more than 3.4 million hypothetical structures. We employ a pre-trained universal interatomic potential named Crystal Hamiltonian Graph neural Network (CHGNet) to rapidly optimize this large number of hypothetical structures. Subsequently, we validate these optimized structures using density functional theory (DFT) and find 4145 structures are successfully optimized and 2368 structures have energy lower than those from the original OQMD. 647 structures are further identified to be dynamically stable using CHGNet. Moreover, the stability of 123 out of 200 randomly chosen structures are validated by DFT, corresponding to a high success rate of 61.5%. We further use 4706 DFT data points to train 3 graph neural network models to predict lattice thermal conductivity (LTC) and heat capacity. Numerous structures with ultralow LTC and high heat capacity, which are promising for advanced energy conversion and energy storage, have been identified. The success of our workflow demonstrates that combining graph theory with pre-trained universal interatomic potential is highly expected to accelerate the search for new both thermodynamically and dynamically stable structures with target material properties.
1 Introduction
Crystal structures with desired material properties are the starting point and cornerstone of modern materials research. Determining both chemically and dynamically stable crystal structures is the first step to achieve this but remains a pivotal challenge across various research disciplines, mainly because most stable crystal structures only have the lowest Gibbs free energy at certain chemical compositions as well as given external conditions, such as temperature and pressure.1 To evaluate whether a compound is thermodynamically stable, one needs to compare its Gibbs free energy with that of its competing phases.2 Finding a structure with the lowest Gibbs free energy is cumbersome because each crystal structure has 3N − 3 atomic coordinates, where N is the number of atoms in the unit cell. Considering 6 additional lattice parameters (a, b, c, α, β, and γ), the search space is thus 3N + 3-dimensional. However, the complexity of searching for stable crystals does not solely scale linearly with the number of atoms, because during the search one also needs to consider the possibility of different combinations of elements occupying the lattice sites, which usually leads to exponential scaling with the number of atoms in the unit cell. Also, it is hard to obtain the global minima among many local minima in the complex potential energy surface.3 Traditional experimental techniques, including X-ray powder diffraction (XRD) and neutron scattering, have historically been the primary means of crystal structure determination. However, experiments are too expensive and both time and facility resource consuming, making large-scale hypothetical materials screening and testing impossible. Recently, the emergence of computational methods has offered an alternative avenue, thanks to the advancement of computational software and the availability of supercomputing resources.4,5 This high-throughput computation of crystal structure prediction (CSP) at the quantum level, although accurate to the largest extent, is also time and computer resource consuming. Hence, to date, it is still computationally expensive to search for large-scale new and stable structures, despite some success on a few specific material families or small number of systems.6In the past decade, several algorithms have been developed to search for new hypothetical structures. For example, CALYPSO7 uses particle swarm optimization (PSO) to predict the high pressure phase of many different combinations of compositions. USPEX8 uses an evolutionary algorithm (EA) to find many stable structures as well. Some recent CSP methods or algorithms in this line include crystal diffusion variational autoencoder9 and machine learning (ML) enabled or accelerated general inverse design of inorganic crystals10 and porous materials.11 These newer methods aim to use ML algorithms to capture the physical inductive bias of material stability and hidden rules of periodic arrangements of atoms among all possible combinations of elements. Despite the huge success, there is at least one major issue associated with these approaches: the number of local minima in the vast material space grows exponentially with the number of atoms, and the cost of density functional theory (DFT) calculations used for local structure optimization grows rapidly with the number of atoms and huge amount of hypothetical structures. Hence, the first motivation of this work is to think about an alternative approach that can bypass the tedious optimization of hypothetical structures. In recent years, machine learning techniques have gained rapid adoption as a precise and efficient tool for atomistic simulations, enabling the resolution of a wide array of fundamental problems.12 This trend has given rise to a novel class of interatomic potentials known as machine learning potentials (MLPs). Notable examples include Gaussian approximation potential (GAP),13–15 higher order equivariant message passing neural networks (MACE),16,17 high-dimensional neural network potential (HDNNP),18 moment tensor potential (MTP),19 spectral neighbor analysis potential (SNAP),20 spatial density neural network force fields (SDNNFFs)21 and deep potential for molecular dynamics (DeepMD).22 MLPs have found applications across a diverse spectrum of materials systems, consistently delivering high accuracy compared to the conventional DFT approaches. Based on these studies, we expect that the state-of-the-art MLPs would be straightforwardly applied to solve the issue in CSP by speeding up energy and force evaluation necessary for structure optimization.
Another issue in high-throughput CSP with desired material properties is to quickly screen or accurately predict the physical properties of hypothetical structures after successfully optimizing structures. Some physical properties are easy to train with ML models while some are not. For instance, most mechanical properties such as Young's modulus, bulk modulus, etc. can be well trained and predicted with high accuracy by both traditional ML models23 and newly developed models such as graph neural networks.24 Unfortunately, the lattice thermal conductivity (LTC) we are interested in in this work belongs to the latter case. Screening and predicting the LTC of materials is crucial in the design of thermal management, energy conversion, and energy storage systems such as thermoelectrics, electronic cooling, solid-state phase change, etc. A recent study25 established a strong correlation between the thermal conductivity of amorphous GaOx and mass density, O to Ga composition ratio, and structural similarity factor (SSF) which inherits the sensitivity of the smooth overlap of atomic positions (SOAP) descriptor to density and composition. These results demonstrate that combining SOAP and SSF could be very promising for identifying more hidden relationships or correlations between thermal transport and structural features. Despite the ubiquitous application of thermal materials, it is hard to train a good ML model to quantitatively predict LTC across diverse material types and families or sometimes the developed ML model involves material descriptors that are hard to compute in a high-throughput manner due to the nonlinear relationship between atomic structure and thermal transport properties.26,27 Furthermore, another obstacle before the struggling LTC training and prediction is to judge whether a crystal is dynamically stable, i.e., there should be no imaginary phonon frequencies in the full Brillouin zone. Without ensuring the dynamical stability of a crystalline structure, predicting its thermal transport properties would be physically meaningless. To this end, the second motivation of this work is to use ML models to screen dynamically stable materials with high speed and high accuracy so that the prediction on the LTC of the final promising structures will have a high success rate.
In this paper, we established a workflow consisting of hypothetical structure generation, fast structure optimization, and quick screening of dynamical stability for searching for ultralow LTC for thermoelectric energy conversion and high heat capacity for thermal energy storage. We first use an ML algorithm called “machine learning and graph theory assisted universal structure searcher (MAGUS)4” for the generation of large-scale hypothetical structures, followed by fast structure optimization and quick screening of dynamical stability using a pre-trained MLP named “Crystal Hamiltonian Graph neural Network (CHGNet)”.28 The LTC and heat capacity of the filtered structures in the previous steps are predicted by our separately trained graph neural network (GNN) models. Selected promising candidates were validated by full DFT calculations. In all, after generating 200 hypothetical structures each for the 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277 unstable structures from the OQMD, we found 4145 of those structures to be successfully optimized by DFT. Furthermore, 647 structures were found to be dynamically stable by our CHGNet model, and 123 out of 200 randomly selected structures were verified to be indeed dynamically stable by full DFT calculations, showing a high success rate of screening dynamically stable structures by using pre-trained MLPs.
277 unstable structures from the OQMD, we found 4145 of those structures to be successfully optimized by DFT. Furthermore, 647 structures were found to be dynamically stable by our CHGNet model, and 123 out of 200 randomly selected structures were verified to be indeed dynamically stable by full DFT calculations, showing a high success rate of screening dynamically stable structures by using pre-trained MLPs.
2 Computational method and machine learning model training
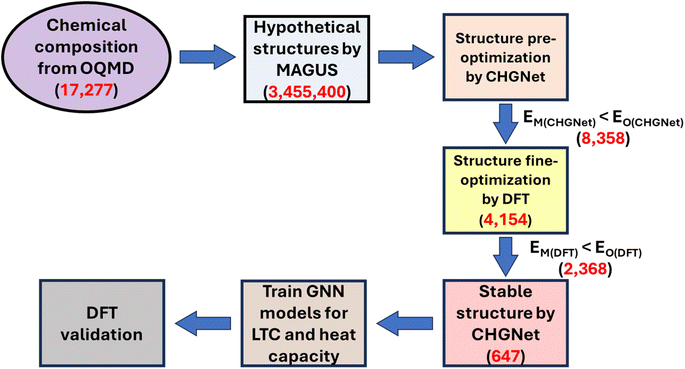
Our workflow comprises six major steps as shown in Fig. 1: (1) hypothetical structure generation by MAGUS; (2) structure pre-optimization by CHGNet; (3) fine structure optimization by DFT; (4) dynamical stability screening by CHGNet; (5) training a regression ML model to recommend structures with ultralow LTC and high heat capacity; (6) DFT calculations of selected promising material candidates for ML model validation.2.1 Hypothetical structure generation by a graph theory assisted universal structure searcher
In this work, we use MAGUS for the generation of hypothetical structures, which uses EA in the generation of hypothetical structures. EA is inspired by the mechanism of biological evolution in nature. When adapting the algorithm for CSP, we treat a single potential structure as an individual and a collection of these individuals as a population. These individuals produce new populations with the fittest individual having a greater chance of survival. The fundamental difference between MAGUS and the recent new ML-assisted CSP methods9–11 is that the MAGUS algorithm does not learn the pattern of arrangements of atoms in space. Instead, MAGUS generates new populations called offspring by crossover and mutation, and the individuals with good fitness are superior and survive. One of the important input parameters to the MAGUS package is the composition or chemical formula. Here, the compositions refer to the constituent elements and their ratios, such as K2YTlBr6, while the hypothetical structures refer to the corresponding atomic arrangements in space including lattice parameters, symmetry, and internal atomic positions. To generate completely new crystalline structures to the greatest extent that are different from the existing open quantum materials database (OQMD), we selected 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277 chemical compositions as individuals. In order to save some computational cost, we first narrow down our new search to compositions containing less than 10 atoms and also exclude lanthanide and actinide elements (very hard to calculate in the DFT optimization step). For noncubic structures we also exclude zero bandgap materials. There were much more unstable cubic structures from the beginning but in order to have a balanced distribution with cubic structures and also due to computational limitation, we finally only randomly chose 10
277 chemical compositions as individuals. In order to save some computational cost, we first narrow down our new search to compositions containing less than 10 atoms and also exclude lanthanide and actinide elements (very hard to calculate in the DFT optimization step). For noncubic structures we also exclude zero bandgap materials. There were much more unstable cubic structures from the beginning but in order to have a balanced distribution with cubic structures and also due to computational limitation, we finally only randomly chose 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cubic compositions. This finally leads to 10
000 cubic compositions. This finally leads to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compositions from cubic structures and 7277 compositions from noncubic structures. All 17
000 compositions from cubic structures and 7277 compositions from noncubic structures. All 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277 structures have been predicted to have negative frequencies in the Brillouin zone, i.e., dynamically unstable. The dynamical instability was either checked by direct DFT calculations or predicted by our recently developed high-fidelity Elemental Spatial Density Neural Network Force Field (Elemental-SDNNFF).29,30 Our hypothesis is that there could exist a different structure other than those in the OQMD but with the same chemical composition. For each chemical composition we use the MAGUS package to generate 200 hypothetical structures (population).
277 structures have been predicted to have negative frequencies in the Brillouin zone, i.e., dynamically unstable. The dynamical instability was either checked by direct DFT calculations or predicted by our recently developed high-fidelity Elemental Spatial Density Neural Network Force Field (Elemental-SDNNFF).29,30 Our hypothesis is that there could exist a different structure other than those in the OQMD but with the same chemical composition. For each chemical composition we use the MAGUS package to generate 200 hypothetical structures (population).
2.2 Pre-optimization of hypothetical structures by pre-trained universal neural network potential
CHGNet is an ML potential trained on energies, atomic forces, virial stresses, and magnetic moments from the Materials Project trajectory dataset. This pre-trained universal MLP helps to bridge the gap between quantum accuracy and classical efficiency. For each composition, we use the CHGNet MLP to optimize the 200 hypothetical structures generated by MAGUS, and then filter out the one with the lowest energy among the 200 total structures. We further check this lowest energy structure with the energy of the original OQMD structure obtained by the same CHGNet MLP. The pre-trained CHGNet MLP gives the same result of energy, atomic forces, etc., whenever it is used to predict on the same material, regardless of the number of times the CHGNet model is invoked. In other words, the prediction results by CHGNet only depend on the input structure, such as lattice cell size, shape, constituent atom species, internal atomic positions, etc. The reason why we use the same MLP to evaluate the total energy is to exclude the possible error induced by the MLP as compared with full DFT calculations. We then collect the structures into a separate pool when the energy of the structure newly generated by MAGUS is lower than the original OQMD structure, which means the MAGUS probably identifies a new structure with even lower energy than the original one.2.3 Dynamical stability screening by pre-trained universal neural network potential
After successfully finding hypothetical structures that are lower in energy than the original OQMD structures, we further screen the structures for dynamical stability by using the pre-trained CHGNet MLP. For each structure, we construct a supercell and generate 50 different configurations with random atomic displacements using the PHONOPY package.31 The supercell size in a specific crystallographic direction depends on the lattice parameter in the same direction, and we try to make the length of the supercell in all three directions the same to a large extent. The supercell is generated to ensure that the total number of atoms in the supercell should be at least 80 but generally not more than 300. The magnitude of random atomic displacements is set as 0.01 Å, which is a widely used number if only the second order interatomic force constants (IFCs) are concerned most. After evaluating the atomic forces in the supercell configurations by CHGNet, the second order IFCs are extracted and fitted by PHONOPY, followed by the imaginary phonon frequency check in the full Brillouin zone. A threshold value of negative frequency of −0.01 THz is applied, i.e., if any frequency less than −0.01 THz is found in the Brillouin zone, the corresponding structure is discarded.2.4 Fine optimization of potential low energy structures with DFT
After filtering out dynamically unstable structures by the CHGNet MLP, we continue to optimize the rest of the structures by full DFT calculations with the projector augmented wave (PAW) method as implemented in the Vienna Ab Initio Simulation Package (VASP) software.32–34 The exchange–correlation functional implemented in this work is the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA).35 A plane wave energy cutoff of 520 eV is used for all DFT calculations. For global structure optimization, a criterion of 10−8 eV and 10−6 eV Å−1 for energy and atomic force convergence respectively was applied. For electrons, the Brillouin zone was sampled using the Monkhorst–Pack k-mesh depending on the lattice constants, with the product of the number of k-points in the crystallographic direction of the primitive cell and the corresponding lattice constant at least 60 Å to guarantee high quality DFT structure optimization. The structures with successfully converged DFT optimization will go to the next step.2.5 Graph neural network model training for structure properties prediction
We trained 3 graph neural networks, namely atomistic line graph neural network (ALIGNN),36 orbital graph convolution neural network (OGCNN)37 and global attention graph neural network (deeperGATGNN),38 for LTC and heat capacity and then used the models to predict the LTC and heat capacity of the final structure pool we obtained. The data used for the training were obtained from our separate DFT calculations on 4706 crystal structures taken from the OQMD (specifically, 3827 cubic structures and 879 noncubic structures). Part of the data has been used in our recent work.29,30 80% of our data was used for training, while 20% was used for testing. In the case of noncubic structures where the LTC typically exhibits anisotropy, we opted to train our ML models using the mean LTC values along the crystallographic x, y, and z directions. It is important to note that our previous experience shows the ML models were trained with much higher accuracy when using the log-scale values for the LTC. We thus used the log-scale values of the LTC for training and prediction of all GNN models.2.6 DFT calculations of LTC and heat capacity for ML model validation
For DFT validation of randomly selected structures predicted by the ML LTC model, we use the same supercells as in the previous step of fast screening of dynamic stability but this time we displace the atoms by 0.03 Å in random directions to ensure better capture of the complex potential energy landscape and facilitate accurate fitting of higher order IFCs, the quality of which is crucial for the accuracy of LTC calculation. For each structure, 30 supercell configurations with random atomic displacements are generated by PHONOPY. Self-consistent DFT calculations are then conducted to evaluate the atomic forces in the displaced supercells. The same plane wave energy cutoff is used in the DFT calculations. An energy convergence criterion of 10−6 eV is used. For electrons the Monkhorst–Pack k-mesh depends on the lattice constants of the supercells, with the product of the number of k-points in a crystallographic direction and the corresponding lattice constant being at least 60 Å. The second and third order IFCs are then fitted by the compressive sensing lattice dynamics (CSLD).39 The LTC of the structures is obtained subsequently by iteratively solving the phonon Boltzmann transport equation (BTE) with the ShengBTE package.40 The n-grids for sampling q-points for phonons when solving the phonon BTE are dense enough to ensure that the total number of scattering channels is larger than 108. Our DFT calculations following OQMD settings have yielded very good accuracy in predicting phonon related properties, such as heat capacity and LTC in comparison with experiments, as reported in our recent papers.23,303 Results and discussion
3.1 Hypothetical structure generation, optimization, and dynamic stability screening
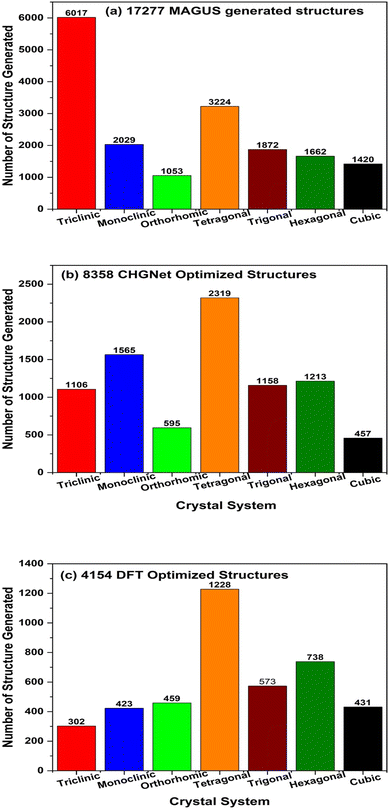
Fig. 2a shows the distribution of our 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277 MAGUS generated structures across the crystal systems. We can see that the triclinic crystal system has the highest occurrence while the remaining 6 crystal systems have more or less the same occurrence. After optimizing the total 3
277 MAGUS generated structures across the crystal systems. We can see that the triclinic crystal system has the highest occurrence while the remaining 6 crystal systems have more or less the same occurrence. After optimizing the total 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455
455![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 (200 × 17
400 (200 × 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277) hypothetical structures by the CHGNet MLP, we obtain the structure with the lowest energy by CHGNet and compare it with the original OQMD structure energy predicted by the same CHGNet MLP. We found that 8358 hypothetical structures have lower energy than the original OQMD structures, whose crystal system distribution is shown in Fig. 2b. The monoclinic, tetragonal, trigonal, and hexagonal systems have a high optimization success rate (>60%), partially proving that the MAGUS algorithm is very efficient at generating structures in those crystal systems for our given compositions. We continue to compare the volume and space group number of the structures before and after optimization by CHGNet. The majority of the structures have different volumes after optimization, as well as space group numbers. There is a clear trend that the volume of lattice cells after optimization is smaller than the originally generated ones (results not shown here for brevity), which means the MAGUS algorithm overestimates the bonding distance between atoms. The space group number of the majority of MAGUS generated structures changes after optimization, meaning that the original material symmetry cannot be maintained during the optimization process when the lowest possible global energy with other symmetries is pursued. This implies that the MAGUS algorithm can be further improved by incorporating the ML model to quickly evaluate energies during the initial hypothetical structure generation, such that lower energy states can be found with a higher success rate. Nevertheless, deploying CHGNet to do structure optimization was successful on the huge number of hypothetical structures generated by the MAGUS package (3
277) hypothetical structures by the CHGNet MLP, we obtain the structure with the lowest energy by CHGNet and compare it with the original OQMD structure energy predicted by the same CHGNet MLP. We found that 8358 hypothetical structures have lower energy than the original OQMD structures, whose crystal system distribution is shown in Fig. 2b. The monoclinic, tetragonal, trigonal, and hexagonal systems have a high optimization success rate (>60%), partially proving that the MAGUS algorithm is very efficient at generating structures in those crystal systems for our given compositions. We continue to compare the volume and space group number of the structures before and after optimization by CHGNet. The majority of the structures have different volumes after optimization, as well as space group numbers. There is a clear trend that the volume of lattice cells after optimization is smaller than the originally generated ones (results not shown here for brevity), which means the MAGUS algorithm overestimates the bonding distance between atoms. The space group number of the majority of MAGUS generated structures changes after optimization, meaning that the original material symmetry cannot be maintained during the optimization process when the lowest possible global energy with other symmetries is pursued. This implies that the MAGUS algorithm can be further improved by incorporating the ML model to quickly evaluate energies during the initial hypothetical structure generation, such that lower energy states can be found with a higher success rate. Nevertheless, deploying CHGNet to do structure optimization was successful on the huge number of hypothetical structures generated by the MAGUS package (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455
455![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 herein) in terms of acceptable timeframe. It is worth noting that the total CPU time is only roughly 2400 core hours (i.e., 10 parallel jobs, each running on a single core for 10 days) for optimizing the total 3.4 million hypothetical structures, which means the pre-trained CHGNet potential should be at least several orders of magnitude faster in screening and optimizing hypothetical structures as compared with full DFT calculations. This shows great potential for developing more sophisticated, more accurate universal MLPs to accelerate or even replace traditionally largely used but computationally expensive DFT calculations. We further optimized the 8358 structures with full DFT calculations and found 4154 to be successfully optimized. There are lots of structures with optimization iterations reaching the preset maximum step (NSW = 100 in VASP settings, i.e., we allow the box size, shape, and internal atomic positions to change 100 times). As a standard procedure, some of these materials might be able to be successfully optimized at the end if more rounds of optimization are conducted. However, due to the high computational cost of DFT calculations, we did not continue such procedure. Fig. 2c shows the distribution of the crystal systems of the 4154 DFT optimized structures that have lower energy than the original OQMD structures. The distribution of crystal systems by DFT optimization is more or less the same as that by CHGNet optimization, with the tetragonal system as the highest occurrence, which implicitly proves the accuracy of the pre-trained CHGNet MLP in evaluating the relative total energies among different atom species and structural symmetries. After fine optimization of these 4154 structures by DFT, we compare their energy with that of the original OQMD structure and finally found 2368 structures to have energy lower than that of the original OQMD structures. This is the pool for screening dynamically stable structures.
400 herein) in terms of acceptable timeframe. It is worth noting that the total CPU time is only roughly 2400 core hours (i.e., 10 parallel jobs, each running on a single core for 10 days) for optimizing the total 3.4 million hypothetical structures, which means the pre-trained CHGNet potential should be at least several orders of magnitude faster in screening and optimizing hypothetical structures as compared with full DFT calculations. This shows great potential for developing more sophisticated, more accurate universal MLPs to accelerate or even replace traditionally largely used but computationally expensive DFT calculations. We further optimized the 8358 structures with full DFT calculations and found 4154 to be successfully optimized. There are lots of structures with optimization iterations reaching the preset maximum step (NSW = 100 in VASP settings, i.e., we allow the box size, shape, and internal atomic positions to change 100 times). As a standard procedure, some of these materials might be able to be successfully optimized at the end if more rounds of optimization are conducted. However, due to the high computational cost of DFT calculations, we did not continue such procedure. Fig. 2c shows the distribution of the crystal systems of the 4154 DFT optimized structures that have lower energy than the original OQMD structures. The distribution of crystal systems by DFT optimization is more or less the same as that by CHGNet optimization, with the tetragonal system as the highest occurrence, which implicitly proves the accuracy of the pre-trained CHGNet MLP in evaluating the relative total energies among different atom species and structural symmetries. After fine optimization of these 4154 structures by DFT, we compare their energy with that of the original OQMD structure and finally found 2368 structures to have energy lower than that of the original OQMD structures. This is the pool for screening dynamically stable structures.
Here, we would like to discuss the accuracy of the CHGNet MLP which plays a significant role in obtaining more structures compared to DFT calculations. However, it is extremely hard to train a highly accurate universal MLP that can cover the vast space of different combinations of elements across the periodic table and various atomic arrangements in space to the largest extent. To the best of our knowledge, so far there are only two such types of pre-trained universal MLPs that are publicly accessible, namely CHGNet (the one used herein) and M3GNEt.41 These pre-trained universal MLPs are expected to accelerate discovery of novel materials through fast evaluation and screening of large previously unexplored materials space. Both MLPs were trained on the raw data from the Materials Project database gathered in the past 10 years or even longer. The biggest advantage of these pre-trained universal MLPs is that they can cover different combinations of elements across the periodic table and various atomic arrangements in space, such that one can immediately use them to quickly evaluate and screen a very large number of hypothetical systems (3.4 million in this work) in an acceptable timeframe. We would also like to point out that the development of these MLPs is still in their infancy and their accuracy needs more comprehensive testing on different structures in the vast materials space. Fine tuning or even re-training a universal MLP would require a large amount of new DFT calculations, which is not an easy task. The main barrier is to identify the unseen and to-be-poorly-predicted configurations by the pre-trained CHGNet model out of the large amount of hypothetical structures and subsequently perform DFT calculations to serve as new training data. Very recently, we also noticed that the Google DeepMind team42 claimed that their newly developed universal MLP outperforms CHGNet. This might be true considering two facts: (1) huge amounts of high quality DFT data might be generated in that work, and thus it is not surprising to train an ML model better than previous ones. (2) The statistics or distribution of materials for the 384![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 materials42 is fundamentally different from the Materials Project database. For example, our quick screening found that at least 78% of the materials reported by the DeepMind team have lanthanide or actinide elements, while this percentage in the Materials Project database is only 25.5% (data downloaded on Jan. 3rd, 2022). Therefore, it is not surprising that the CHGNet model that was trained on different materials datasets has poor performance on predicting the lanthanide/actinide dominated material pool. Comprehensive evaluation of the accuracy of CHGNet would require more careful work and a fair materials dataset for comparison.
938 materials42 is fundamentally different from the Materials Project database. For example, our quick screening found that at least 78% of the materials reported by the DeepMind team have lanthanide or actinide elements, while this percentage in the Materials Project database is only 25.5% (data downloaded on Jan. 3rd, 2022). Therefore, it is not surprising that the CHGNet model that was trained on different materials datasets has poor performance on predicting the lanthanide/actinide dominated material pool. Comprehensive evaluation of the accuracy of CHGNet would require more careful work and a fair materials dataset for comparison.
Regarding the difference in the number of structures between CHGNet screening and DFT confirmation, one of the main reasons is there could be tons of new local atomic environments that have not been seen in the training data of the CHGNet MLP and thus will be poorly predicted by the ML model. Such phenomenon is very common when dealing with huge numbers of hypothetical structures. A very standard procedure is to use the ML model to do screening first, due to its fast speed. In this step, accuracy is not a big concern since the finally obtained “good” structures will still be large. Nevertheless, despite some discrepancies as compared with full DFT calculations, CHGNet is a great success in predicting the energy of a given cell and atomic forces therein with fast speed. In fact, our success rate of 28.3% is way higher than in a recent study using transfer learning to predict stable materials.43 The relatively higher success rate is due to the different screening/filtering procedure and the different ML model used.
We then combine the CHGNet MLP and PHONOPY package to obtain the second order IFCs for all 2368 MAGUS structures. After checking phonon frequencies in the full Brillouin zone, we identify 647 structures to be dynamically stable (a positive dispersion percentage of 27.3%), i.e., no negative phonon frequencies are found. We would rate the percentage of positive frequency as normal, although the total number of dynamically stable structures is not impressively large. This judgement is based on our recent observation of generally positive dispersion percentages between 23% and 28% on some other material datasets and families. We would like to emphasize that it is much stricter for a crystal structure to be dynamically stable than simply being optimized. Negative formation energy and even energy above hull close to zero does not necessarily guarantee dynamical stability. In other words, the low percentage of predicted dynamically stable structures is more likely due to the small amount of truly stable structures found. Nevertheless, we are still able to use the workflow developed herein to discover some new stable structures. A higher success rate of finding dynamically stable structures would require a more sophisticated ML model to understand the intrinsic nature and physical/chemical feature of dynamic stability, and an equally important thing is to generate structures in the previously unexplored vast space of compositions and arrangements of atoms.
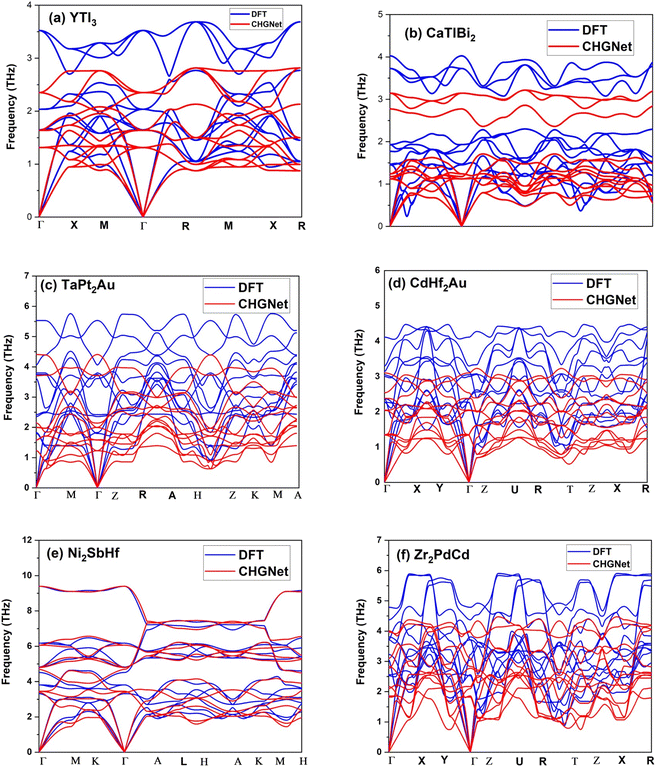
To validate the success rate of dynamic stability screening by CHGNet, we randomly selected 200 structures and performed full DFT calculations for their phonon dispersions. Due to the expensive computational cost by DFT calculations of full interatomic force constants required for evaluating phonon frequencies, in particular for complex structures with low material symmetry, we only randomly selected 200 structures for DFT validation. We found 123 out of 200 structures to be dynamically stable, corresponding to a success rate of 61.5%. Despite one-time sampling, the success rate is comparable to our separate validation on another material family with prototype ABC2D6 and noncubic symmetry (results have not been published yet). Therefore, we believe that the CHGNet MLP has decent accuracy in predicting dynamic stability. The 61.5% success rate of positive dispersions as validated by DFT calculations is good enough for high-throughput screening of a large number of previously unexplored structures if the initial screening pool is very large (say >104 predicted positive dispersions). The DFT validation result confirms the high success rate of using the pre-trained CHGNet MLP for quickly screening dynamic stability, which would have taken much longer simulation time and resources if running by full DFT calculations. Fig. 3a–f show the phonon dispersion comparison between CHGNet and DFT for 6 selected structures. All 6 structures show no imaginary frequency along the high symmetry paths. It should be noted that there are indeed some discrepancies between the phonon dispersions by CHGNet and DFT. For instance, it seems that there is a systematic underestimation of frequencies by CHGNet as compared with DFT. The discrepancy is understandable considering that the DFT data used for training CHGNet is quite different from the DFT calculations performed by us, in terms of both structure and element diversity. This leaves some room for further improvement of the CHGNet model. It is well-known that the size and quality of the training data determine the accuracy of an MLP. When more DFT data is added into training in the future, the CHGNet MLP will be more accurate. Nevertheless, generally speaking, the frequency near the Γ-point is well predicted by CHGNet, while the high frequency optical phonons are under-predicted as compared with DFT results, and the pre-trained CHGNet is efficient in predicting a wide range of structures with elements across the entire periodic table and material symmetry across all 230 space groups.
3.2 Screening materials with ultralow lattice thermal conductivity for thermoelectrics and thermal insulation
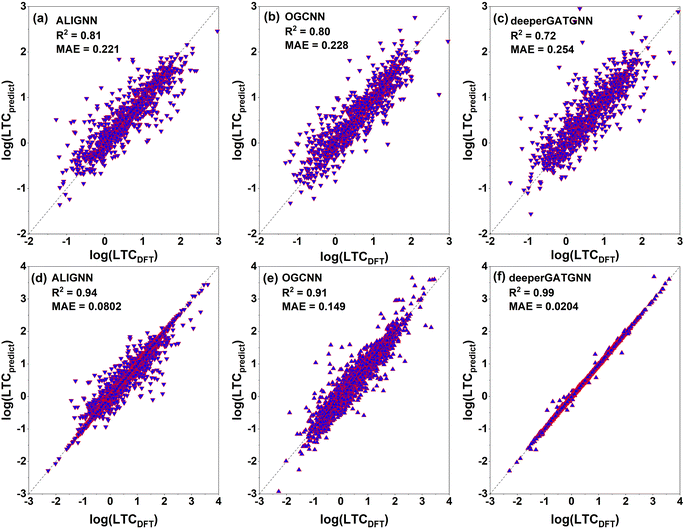
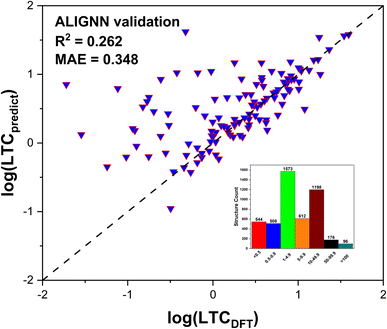
After training 3 GNN models for LTC, we test the model performance by comparing the model prediction results with full DFT calculations. The testing results of LTC for all 3 trained GNN models are shown in Fig. 4a–c. The ALIGNN model exhibits the best performance among the 3 models as evidenced by the smaller mean square error (MAE) of 0.221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(Wm−1 K−1) and high R2 value of 0.81, meaning that the predicted LTC is on average within 1.663 times the DFT value. The ALIGNN model incorporates bond angle information as a descriptor, which helps to increase the accuracy of the model since many material properties are sensitive to slight changes in bond angles. Bond angles can also be regarded as the representation of the relative orientation between atoms' neighbors, which plays a critical role in determining the anharmonicity of a material and thus is expected to facilitate training of LTC. It should be noted that the GNN models do not require explicit definitions of structural descriptors and rather directly predict LTC values based on input structures composing of lattice cell size, shape, constituent elements, and internal atomic positions. Such treatment is hardly doable to representative cells of amorphous materials as studied previously25 in terms of quantitative structure–property (LTC) prediction, primarily due to the usually large number of atoms (on the order of at least a few hundreds). In general, all our trained GNN models are at the same accuracy level as previous studies.29,44 We then further used the trained ALIGNN model to predict on the 647 reoptimized stable structures to find ultralow LTC structures which are suitable candidates for thermoelectrics and thermal insulation. We validate the model prediction by randomly selecting 200 structures predicted by the ALIGNN model. 123 out of the 200 structures turned out to be dynamically stable as verified by our DFT calculations. The comparison between ALIGNN predicted LTC and DFT calculations is shown in Fig. 5. It is found that the LTC above 1 W m−1 K−1 is well predicted by the ALIGNN model, while ultralow LTC materials (below 1 W m−1 K−1) are over-predicted by the model. This can be explained by three plausible aspects: (1) the majority of our LTC training data is above 1 W m−1 K−1, i.e., smaller percentage in the ultralow LTC region, making the medium LTC region well presented by training data and thus it is natural to see the trained model has better prediction performance in the same region as well. As shown in the inset of Fig. 5, only about 22% of our LTC training data are below 1 W m−1 K−1. Separate training tests by removing partial training data in the medium to high LTC region turns out not to improve the overall performance of the GNN models in predicting the ultralow LTC region. In general, the behavior in Fig. 5 is very common to see in many ML models as the model approaches the boundaries and training data are usually scarce. A significant improvement of the models in the lower bound or data scarce LTC region would thus require a substantially large amount of new training data. (2) The ALIGNN shows a trend of slightly higher LTC in the ultralow LTC range during the training process, as indicated in Fig. 4a (for LTC less than 1 W m−1 K−1, there are more data points above the perfect dashed line than the data points below). (3) The absolute values of ultralow LTCs are usually very “sensitive” to specific computational parameters even if full DFT calculations are performed, such as the accuracy level of the atomic forces, converged cutoff distance for 3rd order IFC truncation, and large enough q-grids when solving the phonon BTE. That is to say, there is also uncertainty coming from the DFT calculation itself. Although we do not expect there will be orders of magnitude uncertainty for the DFT-LTC values, there still could be sub-1 W m−1 K−1 differences (rough estimate). Despite such small absolute value, the uncertainty could be significant or even in the same order as the original DFT-LTC itself. However, such potential effect was not considered in ML training since the model simply treats all data as “true” values.
log(Wm−1 K−1) and high R2 value of 0.81, meaning that the predicted LTC is on average within 1.663 times the DFT value. The ALIGNN model incorporates bond angle information as a descriptor, which helps to increase the accuracy of the model since many material properties are sensitive to slight changes in bond angles. Bond angles can also be regarded as the representation of the relative orientation between atoms' neighbors, which plays a critical role in determining the anharmonicity of a material and thus is expected to facilitate training of LTC. It should be noted that the GNN models do not require explicit definitions of structural descriptors and rather directly predict LTC values based on input structures composing of lattice cell size, shape, constituent elements, and internal atomic positions. Such treatment is hardly doable to representative cells of amorphous materials as studied previously25 in terms of quantitative structure–property (LTC) prediction, primarily due to the usually large number of atoms (on the order of at least a few hundreds). In general, all our trained GNN models are at the same accuracy level as previous studies.29,44 We then further used the trained ALIGNN model to predict on the 647 reoptimized stable structures to find ultralow LTC structures which are suitable candidates for thermoelectrics and thermal insulation. We validate the model prediction by randomly selecting 200 structures predicted by the ALIGNN model. 123 out of the 200 structures turned out to be dynamically stable as verified by our DFT calculations. The comparison between ALIGNN predicted LTC and DFT calculations is shown in Fig. 5. It is found that the LTC above 1 W m−1 K−1 is well predicted by the ALIGNN model, while ultralow LTC materials (below 1 W m−1 K−1) are over-predicted by the model. This can be explained by three plausible aspects: (1) the majority of our LTC training data is above 1 W m−1 K−1, i.e., smaller percentage in the ultralow LTC region, making the medium LTC region well presented by training data and thus it is natural to see the trained model has better prediction performance in the same region as well. As shown in the inset of Fig. 5, only about 22% of our LTC training data are below 1 W m−1 K−1. Separate training tests by removing partial training data in the medium to high LTC region turns out not to improve the overall performance of the GNN models in predicting the ultralow LTC region. In general, the behavior in Fig. 5 is very common to see in many ML models as the model approaches the boundaries and training data are usually scarce. A significant improvement of the models in the lower bound or data scarce LTC region would thus require a substantially large amount of new training data. (2) The ALIGNN shows a trend of slightly higher LTC in the ultralow LTC range during the training process, as indicated in Fig. 4a (for LTC less than 1 W m−1 K−1, there are more data points above the perfect dashed line than the data points below). (3) The absolute values of ultralow LTCs are usually very “sensitive” to specific computational parameters even if full DFT calculations are performed, such as the accuracy level of the atomic forces, converged cutoff distance for 3rd order IFC truncation, and large enough q-grids when solving the phonon BTE. That is to say, there is also uncertainty coming from the DFT calculation itself. Although we do not expect there will be orders of magnitude uncertainty for the DFT-LTC values, there still could be sub-1 W m−1 K−1 differences (rough estimate). Despite such small absolute value, the uncertainty could be significant or even in the same order as the original DFT-LTC itself. However, such potential effect was not considered in ML training since the model simply treats all data as “true” values.
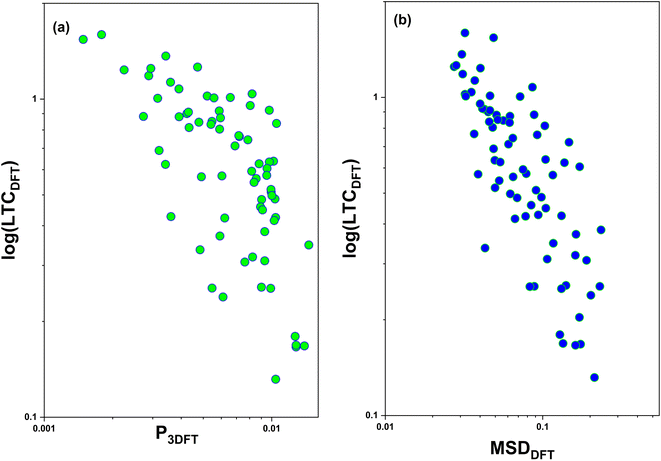
We further show the relationship between the material properties P3 parameter and mean square displacement (MSD) with LTC in Fig. 6a and b, respectively. The P3 parameter corresponds to the availability of three-phonon scattering opportunities throughout the entire Brillouin zone. A high P3 parameter value indicates the presence of numerous pathways for phonon–phonon interaction (scattering) within the crystal lattice, which in turn usually results in a low LTC.45,46 The MSD offers information about how atomic positions in crystals change with temperature, shedding light on how atoms deviate from their equilibrium positions in a harmonic phonon lattice. The large MSD value leads to the identification of rattling atoms within the crystal.47,48 Both the P3 parameter and MSD serve as valuable material descriptors, allowing for a rapid screening of crystalline materials with exceptionally ultralow LTC. These plots depict the relationship between LTC and the P3 parameter and MSD for the 123 DFT verified structures. It is evident that this observation is consistent with the established knowledge that the LTC generally decreases as the MSD or P3 parameter increases, showcasing an inverse proportionality.
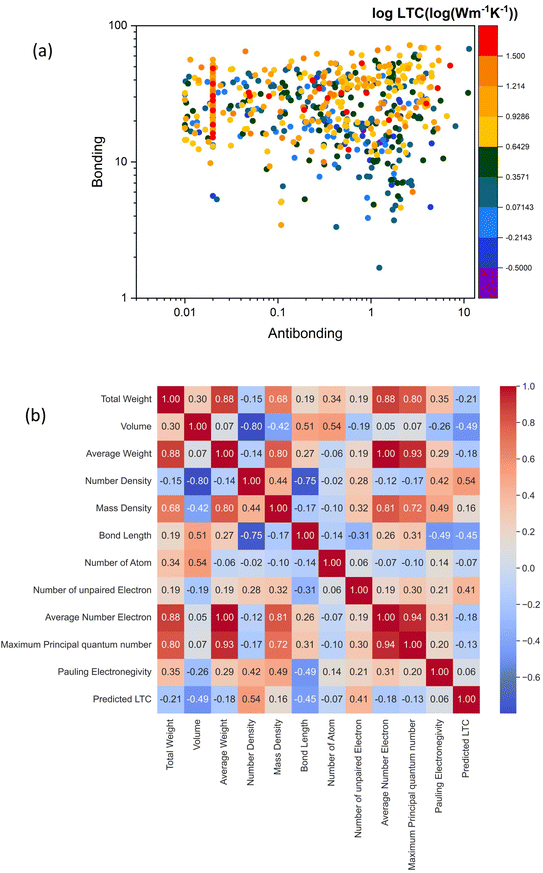
To gain deep insight into the electronic level understanding of ultralow LTC materials, we conducted a more in-depth analysis of our predicted LTC using Crystal Orbital Hamilton Population (COHP)49 to measure the contribution of bonding and antibonding states. The single values of bonding and antibonding for each structure are obtained by performing integration over COHP curves for each atomic pair as evaluated by the LOBSTER package and then taking the average for all pairs in the primitive cell. This analysis helps us to understand how chemical bonding influences thermal transport properties such as LTC. In Fig. 7a, we illustrate bonding and antibonding states, highlighting the log value of predicted LTC. From the kinetic theory of phonon transport, the lattice thermal conductivity of a crystal can be expressed as 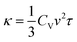 , where Cv, ν, and τ are the volumetric heat capacity, average phonon group velocity, and average phonon relaxation time, respectively. In principle, the group velocity and relaxation time are determined by the harmonic and anharmonic characteristics of the lattice, respectively, which can be roughly correlated with the bonding and antibonding COHP, respectively. Generally speaking, low bonding COHP and high antibonding COHP would more likely lead to low LTC, as reflected by the lower-right corner of Fig. 7a. When bonding values are less than 10 and antibonding greater than 0.01, the structures exhibit LTC less than 1 W m−1 K−1, i.e., the LTC is ultralow. In this region, the interatomic bonding strengths are weak while phonon anharmonicity is strong, resulting in exceptionally low LTC. This observation is consistent with our recent big data analysis of bonding–antibonding states on 13
, where Cv, ν, and τ are the volumetric heat capacity, average phonon group velocity, and average phonon relaxation time, respectively. In principle, the group velocity and relaxation time are determined by the harmonic and anharmonic characteristics of the lattice, respectively, which can be roughly correlated with the bonding and antibonding COHP, respectively. Generally speaking, low bonding COHP and high antibonding COHP would more likely lead to low LTC, as reflected by the lower-right corner of Fig. 7a. When bonding values are less than 10 and antibonding greater than 0.01, the structures exhibit LTC less than 1 W m−1 K−1, i.e., the LTC is ultralow. In this region, the interatomic bonding strengths are weak while phonon anharmonicity is strong, resulting in exceptionally low LTC. This observation is consistent with our recent big data analysis of bonding–antibonding states on 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 718 stable structures.29 In contrast, high antibonding COHP does not necessarily lead to low LTC. This is because the phonon group velocity (the harmonic term in the kinetic theory) competes with the phonon relaxation time (the anharmonic term). Therefore, medium to high LTC materials can happen in a broad range of antibonding. Also note that the absolute value of high LTC materials shown in Fig. 7a only ranges from 16 W m−1 K−1 to 32 W m−1 K−1, which is not very high at all compared with the really high values of many other LTC materials. Thus, in Fig. 7a it is easy to find some materials with harmonic terms overwhelming the anharmonic terms and then showing relatively high LTC. Such trend can be clearly seen from more data (13
718 stable structures.29 In contrast, high antibonding COHP does not necessarily lead to low LTC. This is because the phonon group velocity (the harmonic term in the kinetic theory) competes with the phonon relaxation time (the anharmonic term). Therefore, medium to high LTC materials can happen in a broad range of antibonding. Also note that the absolute value of high LTC materials shown in Fig. 7a only ranges from 16 W m−1 K−1 to 32 W m−1 K−1, which is not very high at all compared with the really high values of many other LTC materials. Thus, in Fig. 7a it is easy to find some materials with harmonic terms overwhelming the anharmonic terms and then showing relatively high LTC. Such trend can be clearly seen from more data (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 718 cubic structures in total) in our recent work.29
718 cubic structures in total) in our recent work.29
 | ||
| Fig. 7 (a) Insight into the relationship between bonding and antibonding with color coded by the log-value of predicted LTC. (b) Pearson correlation between material descriptors and LTC. | ||
Furthermore, we explore the correlation between our predicted LTC values and material descriptors which are simple characteristics that can help quickly screen structures with low LTC. This serves as a bridge between DFT accuracy and classical level efficiency. In Fig. 7b, we present the Pearson correlation between some representative material descriptors with LTC. The Pearson correlation coefficient is the most common way of measuring a linear correlation between two variables. The Pearson correlation number is between −1 and +1 that measures the strength and direction of the relationship between two variables, with −1 meaning strong negative correlation and +1 meaning strong positive correlation. Volume of the primitive cell, bond length, total weight and average number of electrons exhibit negative correlations with LTC, with Pearson correlation values of −0.49, −0.45, −0.21 and −0.18, respectively. This means higher values of these descriptors correspond to structures with low LTC. Physically speaking, this trend is understandable since a larger cell volume or longer bond length usually corresponds to loose bonding between atoms, and thus leads to low phonon group velocities. On the other hand, atom number density, the number of unpaired electrons, and mass density are positively correlated with LTC, with Pearson correlation values of 0.54, 0.41 and 0.16, respectively. Higher atom number density means denser packing of atoms in space and thus usually corresponds to strong interatomic bonding and thus high phonon group velocities, which facilitates phonon energy transport in the lattice. Meanwhile, descriptors like the total number of atoms, maximum principal quantum number, and Pauling electronegativity show almost no correlations or weak correlations with LTC. The positive and negative correlated descriptors identified herein are expected to accelerate the screening process of even larger-scale hypothetical structures in the future.
3.3 Screening materials with high heat capacity for thermal energy storage
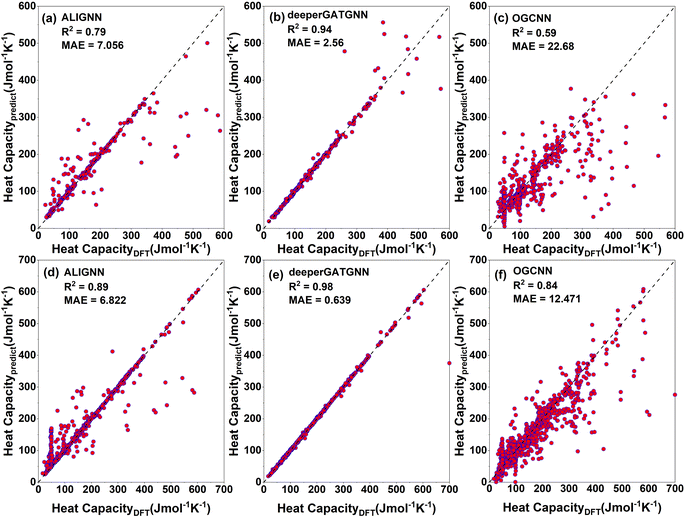
After training 3 GNN models for heat capacity with the same 4706 DFT data points, we test the performance of our heat capacity training by comparing with DFT calculations. The testing result is shown in Fig. 8a–c. This time the deeperGATGNN model shows the best performance compared to other models with a smaller MAE value and higher R2 score. The deeperGATGNN model trains a very deep neural network with the number of layers being greater than those of the OGCNN and ALIGNN models, and thus has better performance. We then used the trained deeperGATGNN model to predict on the 647 reoptimized stable structures to find high heat capacity materials, which hold great potential for thermal energy storage (TES) systems. Like LTC, we continue to validate our heat capacity model with the 123 structures calculated by DFT, and the validation result is shown in Fig. 9. We could not find any structures with heat capacity exceeding the Dulong–Petit limit at room temperature.23 However, we do find some structures with heat capacity very close to the Dulong–Petit limit. Here, the Dulong–Petit limit for constant volume heat capacity is calculated as 3NR, where R is the universal gas constant (8.314 J mol−1 K−1) and N is the number of atoms in the unit cell. Table 1 shows the top 20 structures with the highest ratio of heat capacity to the Dulong–Petit limit. The phonon dispersions of the top two structures (YTl3 with space group no. 221 and CaTlBi2 with space group no. 123) with the highest ratio of heat capacity to the Dulong–Petit limit are shown in Fig. 3a and b, respectively. Their high heat capacity can be understood in terms of the relatively low cutoff frequencies below 4 THz, which is attributed to the medium to heavy elements in materials such as Y, Tl, and Bi. The Bose–Einstein distribution function of phonons says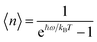 , where ℏ is Planck's constant, kB is the Boltzmann constant, ω is the phonon frequency, and T is the absolute temperature. Thus, we can estimate the characteristic frequency for the phonon energy comparable to kBT at room temperature as
, where ℏ is Planck's constant, kB is the Boltzmann constant, ω is the phonon frequency, and T is the absolute temperature. Thus, we can estimate the characteristic frequency for the phonon energy comparable to kBT at room temperature as 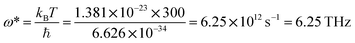 . This means the phonon modes with frequency less than 6.25 THz can be excited near room temperature. As shown in Fig. 3a and b, the phonon frequencies in the two structures YTl3 and CaTlBi2 are below 4 THz, and then all phonon modes can be populated near room temperature and thus contribute to the heat capacity. This is the fundamental reason for these two materials having high heat capacities.
. This means the phonon modes with frequency less than 6.25 THz can be excited near room temperature. As shown in Fig. 3a and b, the phonon frequencies in the two structures YTl3 and CaTlBi2 are below 4 THz, and then all phonon modes can be populated near room temperature and thus contribute to the heat capacity. This is the fundamental reason for these two materials having high heat capacities.
 | ||
| Fig. 9 DFT validation of deeperGATGNN prediction for the 123 structures randomly selected from the final dynamically stable structure pool (647) as screened by the workflow in this work. | ||
| MAGUS ID | Formula | Symmetry | Space group number | Formation energy (eV per atom) | LTC (W m−1 K−1) | Heat capacity (J mol−1 K−1) | Ratio of heat capacity to Dulong–Petit limit |
|---|---|---|---|---|---|---|---|
313![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161_167 161_167 |
YTl3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
221 | −0.23374 | 1.780 | 98.7352 | 0.9896 |
546![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287_12 287_12 |
CaTlBi2 | P4/mmm | 123 | −0.47185 | 1.078 | 98.7321 | 0.9896 |
310![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222_80 222_80 |
CaBi3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
221 | −0.50218 | 1.471 | 98.7256 | 0.9896 |
313![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873_43 873_43 |
CaPb3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
221 | −0.32828 | 4.031 | 98.5031 | 0.9873 |
371![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 322_34 322_34 |
YTl2In | P4/mmm | 123 | −0.28082 | 2.228 | 98.4791 | 0.9871 |
453![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 343_147 343_147 |
YIn2Bi | P4/mmm | 123 | −0.41288 | 1.512 | 98.4355 | 0.9866 |
499![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 515_125 515_125 |
LiBiPb2 | P4/mmm | 123 | −0.19219 | 0.742 | 98.3930 | 0.9862 |
468![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 937_47 937_47 |
BiPd2Pt | P4/mmm | 123 | −0.20358 | 1.003 | 98.1140 | 0.9834 |
454![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 575_137 575_137 |
ScIn2Pb | P4/mmm | 123 | −0.21603 | 1.474 | 98.0507 | 0.9828 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 548 548![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 987_90 987_90 |
K2YTlBr6 |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
147 | −1.67237 | 0.096 | 245.111 | 0.9827 |
314![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 264_194 264_194 |
Ag3Ge | Amm2 | 38 | 0.113334 | 0.029 | 97.9828 | 0.9821 |
416![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 611_76 611_76 |
Hf2CdAu |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
2 | −0.19819 | 0.177 | 97.9752 | 0.9820 |
308![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064_41 064_41 |
TaAu3 | P4/mmm | 123 | −0.05549 | 0.628 | 97.8864 | 0.9811 |
312![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610_45 610_45 |
CaIn3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
221 | −0.31326 | 1.804 | 97.7639 | 0.9799 |
314![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157_46 157_46 |
RhAu3 |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
164 | 0.138769 | 0.150 | 97.7346 | 0.9796 |
515![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810_43 810_43 |
CdPdAu2 | P4/mmm | 123 | −0.26516 | 2.601 | 97.7262 | 0.9795 |
308![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890_145 890_145 |
TaPt3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
221 | −0.54038 | 2.168 | 97.7192 | 0.9795 |
463![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270_167 270_167 |
Pd2PtPb | P4/mmm | 123 | −0.24499 | 3.143 | 97.5625 | 0.9779 |
311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765_44 765_44 |
ScIn3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
221 | −0.28857 | 3.058 | 97.4223 | 0.9765 |
308![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939_100 939_100 |
Pd3Pb |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
221 | −0.30703 | 3.652 | 97.3603 | 0.9759 |
4 Conclusion
In summary, recent crystal structure prediction algorithms are only targeting a few specific material families or are restricted to simple systems with limited element diversity. Moreover, these algorithms invoke frequent first principles calculations and thus are time and resource consuming. To alleviate these issues, in this work we establish a workflow that can generate a large number of hypothetical structures with diverse atom species and then quickly optimize and screen out stable structures. Specifically, using a machine learning and graph theory assisted universal structure searcher, we generated more than 3.4 million hypothetical structures covering 63 elements across the periodic table with unstable structure composition and formula screened from the OQMD, with hypothesis to find phases that are stable. We optimized these structures with pre-trained universal CHGNet machine learning potential and obtained 8358 successfully optimized structures. We compared the energy of these structures with the original OQMD structures optimized by CHGNet, to obtain structures with lower energy than the original OQMD structures. We further used CHGNet to generate a second order interatomic force constant to quickly screen dynamically stable structures. Finally, 647 structures were obtained, and we randomly verified 200 of these structures with DFT and got 123 new structures with dynamic stability confirmed by DFT, i.e., success rate of 61.5%. We also trained 3 GNN models, namely ALIGNN, deeperGATGNN, and OGCNN, and predicted on the new stable structures to find structures with ultralow LTC and high heat capacity. The ALIGNN model gave the best performance for the LTC while the deeperGATGNN model gave the best performance for heat capacity, which were used to predict LTC and heat capacity, respectively, for the 647 stable structures. Among all stable structures, we found 71 structures with LTC less than 1 W m−1 K−1 with 13 confirmed by full DFT calculations. We also found some structures whose heat capacities are very close to the Dulong–Petit limit at room temperature. This study of combining MAGUS with CHGNet has paved the way for accelerating the discovery of new stable structures for broad materials applications.Data availability
The data for the 647 screened dynamically stable structures with predicted LTC, along with relevant information and LTC for the 123 DFT verified structures, are available in the ESI† as an Excel file, “SI_pred_val_data_pub.xlsx”. The POSCAR files for the 647 dynamically stable structures are provided in “POSCAR_MAGUS_647str.json”.Conflicts of interest
The authors declare no competing financial or non-financial interests.Acknowledgements
This work was supported by the NSF (award numbers 2030128, 2110033, 2311202, 2320292), SC EPSCoR/IDeA Program under NSF OIA-1655740 (23-GC01) and an ASPIRE grant from the Office of the Vice President for Research at the University of South Carolina (project 80005046). M. A. acknowledges the financial support by the SPARC Graduate Research Grant (project 80004800).References
- C. C. Pantelides, C. S. Adjiman and K. Andrei V, Prediction and Calculation of Crystal Structures, ed. S. A.-E. A. Aspuru-Guzik, Springer Cham, 2014, pp. 25–58 Search PubMed.
- H. Callen, Thermodynamics and an Introduction to Thermostatistics, John Wiley & Sons, 1985 Search PubMed.
- B. C. Revard, W. W. Tipton and R. G. Hennig, Structure and Stability Prediction of Compound with Evolutionary Algorithm, 2014 Search PubMed.
- J. Wang, H. Gao, Y. Han, C. Ding, S. Pan, Y. Wang, Q. Jia, H.-T. Wang, D. Xing and J. Sun, Natl. Sci. Rev., 2023, 10(7), nwad128 CrossRef CAS PubMed.
- R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746 CrossRef CAS.
- J. Ojih, M. Al-fahdi, A. D. Rodriguez and K. Choudhary, npj Comput. Mater., 2022, 1–12 Search PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, Crystal Diffusion Variational Autoencoder for Periodic Material Generation, 2021, pp. 1–20 Search PubMed.
- Z. Ren, S. I. P. Tian, J. Noh, F. Oviedo, G. Xing, J. Li, Q. Liang, R. Zhu, A. G. Aberle, S. Sun, X. Wang, Y. Liu, Q. Li, S. Jayavelu, K. Hippalgaonkar, Y. Jung and T. Buonassisi, Matter, 2022, 5, 314–335 CrossRef CAS.
- B. Kim, S. Lee and J. Kim, Sci. Adv., 2020, 6, 1–8 Search PubMed.
- Q. Tong, P. Gao, H. Liu, Y. Xie, J. Lv, Y. Wang and J. Zhao, J. Phys. Chem. Lett., 2020, 11, 8710–8720 CrossRef CAS PubMed.
- A. P. Bartõk and G. Csányi, Int. J. Quantum Chem., 2015, 115, 1051–1057 CrossRef.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 1–4 CrossRef PubMed.
- A. P. Bartók, J. Kermode, N. Bernstein and G. Csányi, Phys. Rev. X, 2018, 8, 41048 Search PubMed.
- I. Batatia, D. P. Kovács, G. N. C. Simm, C. Ortner and G. Csányi, Adv. Neural Inf. Process. Syst., 2022, 35, 11423–11436 Search PubMed.
- D. P. Kovács, I. Batatia, E. S. Arany and G. Csányi, J. Chem. Phys., 2023, 159(4), 044118 CrossRef PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 1–4 CrossRef PubMed.
- A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef.
- M. A. Wood and A. P. Thompson, J. Chem. Phys., 2018, 148, 241721 CrossRef PubMed.
- A. Rodriguez, Y. Liu and M. Hu, Phys. Rev. B, 2020, 102, 35203 CrossRef CAS.
- H. Wang, L. Zhang, J. Han and W. E, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS.
- J. Ojih, U. Onyekpe, A. Rodriguez, J. Hu, C. Peng and M. Hu, ACS Appl. Mater. Interfaces, 2022, 14, 43277–43289 CrossRef CAS PubMed.
- J. Ojih, A. Rodriguez, J. Hu and M. Hu, Energy AI, 2023, 14, 100286 CrossRef.
- Y. Liu, H. Liang, L. Yang, G. Yang, H. Yang, S. Song, Z. Mei, G. Csányi and B. Cao, Adv. Mater., 2023, 35, 1–13 Search PubMed.
- G. Qin, Y. Wei, L. Yu, J. Xu, J. Ojih, A. D. Rodriguez, H. Wang, Z. Qin and M. Hu, J. Mater. Chem. A, 2023, 5801–5810 RSC.
- C. Loftis, K. Yuan, Y. Zhao, M. Hu and J. Hu, J. Phys. Chem. A, 2021, 125, 435–450 CrossRef CAS PubMed.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031–1041 CrossRef.
- A. Rodriguez, C. Lin, C. Shen, K. Yuan, M. Al-Fahdi, X. Zhang, H. Zhang and M. Hu, Commun. Mater., 2023, 4, 61 CrossRef CAS.
- A. Rodriguez, C. Lin, H. Yang, M. Al-Fahdi, C. Shen, K. Choudhary, Y. Zhao, J. Hu, B. Cao, H. Zhang and M. Hu, npj Comput. Mater., 2023, 9, 20 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef.
- R. A. Vargas-Hernández, J. Phys. Chem. A, 2020, 124, 4053–4061 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- M. Karamad, R. Magar, Y. Shi, S. Siahrostami, I. D. Gates and A. Barati Farimani, Phys. Rev. Mater., 2020, 4, 1–6 Search PubMed.
- S. S. Omee, S.-Y. Louis, N. Fu, L. Wei, S. Dey, R. Dong, Q. Li and J. Hu, Patterns, 2021, 3, 100491 CrossRef PubMed.
- F. Zhou, W. Nielson, Y. Xia and V. Ozoliņš, Phys. Rev. B, 2019, 100, 1–15 Search PubMed.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef PubMed.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85 CrossRef CAS PubMed.
- J. Schmidt, N. Hoffmann, H. C. Wang, P. Borlido, P. J. M. A. Carriço, T. F. T. Cerqueira, S. Botti and M. A. L. Marques, Adv. Mater., 2023, 35, 2210788 CrossRef CAS PubMed.
- T. Zhu, R. He, S. Gong, T. Xie, P. Gorai, K. Nielsch and J. C. Grossman, Energy Environ. Sci., 2021, 14, 3559–3566 RSC.
- L. Elalfy, D. Music and M. Hu, Phys. Rev. B, 2021, 103, 75203 CrossRef CAS.
- T. Ouyang and M. Hu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 1–13 CrossRef.
- S. Ju, R. Yoshida, C. Liu, S. Wu, K. Hongo, T. Tadano and J. Shiomi, Phys. Rev. Mater., 2021, 5, 1–2 Search PubMed.
- A. Jain, H. P. Veeravenkata, S. Godse and Y. Srivastava, arXiv, 2022, arXiv:2204.03628, DOI:10.48550/arXiv.2204.03628.
- R. Dronskowski and P. E. Blochl, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta06190f |
| This journal is © The Royal Society of Chemistry 2024 |