Open Access Article
Open Access ArticleNa vs. Li metal anodes for batteries: unraveling thermodynamic and electronic origins of voids and developing descriptors for artificial surface coatings†
Victor
Venturi
 *,
Rodrigo
Freitas
*,
Rodrigo
Freitas
 and
Iwnetim Iwnetu
Abate
and
Iwnetim Iwnetu
Abate
 *
*
Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA. E-mail: vventuri@mit.edu; iabate@mit.edu
First published on 24th September 2024
Abstract
Techno-economic, humanitarian, and safety concerns limit the possible uses of conventional lithium-ion and lithium-metal batteries. Sodium-based batteries constitute a promising alternative to address these issues; however, due to the similarities between the two alkali metals, they present similar failure modes as their lithium counterparts. In this work, we focus on one of such failure mechanisms: the thermodynamically-driven accumulation of vacancies on the surface of the metallic anode, which leads to the formation of voids and pits, detrimental to battery performance and cycle life. We investigate the differences in behavior between anode/coating interfaces of both lithium and sodium. Adhesion energy, a descriptor previously argued to be a reliable design principle for lithium metal anodes, is found to not exhibit the same predictive power for sodium metal architectures: in cases where vacancy congregation is not thermodynamically favorable for isolated sodium slabs, we find strong interfacial interactions to have adverse effects on void formation. By studying select coating materials, we also reveal that these material interactions at alkali/coating interfaces are highly nuanced, and that the field of surface science and engineering is ripe with opportunities for further discovery and tuning of surface properties via coating selection.
Introduction
Owing to their high energy density, large voltage window, and versatility,1–4 lithium (Li) ion batteries (LIBs) have, over the last two decades, taken over a significant share of the battery market. The substitution of standard graphite-based anodes by Li metal would enable such technology to achieve its theoretical maximum energy density.3–5 However, successful widespread use of Li metal anodes has not been feasible, partially due to phenomena happening at the surface of the anode, such as growth of dendritic structures, and formation of voids and pits.6–11Moreover, the low safety, high costs, and sustainability concerns related to LIBs have limited their use to emerging markets, namely, portable electronics, automotive transportation, and electric aviation,12–16 all of which require energy densities matched only by LIBs. Other applications, such as stationary storage of renewable energy, can only be achieved with cheaper, more reliable alternatives to LIBs.
Among such options, the use of sodium (Na) ions as the charge carrier is one of the most promising alternatives: sodium is orders of magnitude more abundant on the Earth's crust, and its mining is more cost-effective than lithium.17 Additionally, the cathodes of sodium ion batteries (NIBs) can be synthesized with manganese (Mn) or iron (Fe), while stable LIB cathodes require cobalt (Co) and nickel (Ni), elements which are rarer and have higher supply risks.17–19 While Na-metal simply cannot rival the energy density of corresponding Li-metal batteries, it still exceeds that of Li-ion by a factor of three (for sulfur-based systems).20 Furthermore, since both Li and Na are alkali metals, they have very similar electrochemical properties:20 production lines of LIBs can be easily adapted to NIBs, and many of the strides made in LIB technology have a high likelihood of being fruitful in NIBs. However, this also means that failure modes in Li metal batteries (LMB) are also consistently observed in Na metal batteries (NMB), such as the formation of dendrites20 and voids21 at the anode surface.
Since voids are precursors to dendrite formation in metallic anodes,22,23 in this article, the first step associated with void formation is investigated at interfaces between different coating materials and either Li or Na. By combining thermodynamic modeling and simulations of interfacial dynamics using density functional theory (DFT) and molecular dynamics (MD) methods, we evaluate the tendencies of vacancy accumulation at interfaces between metal and solid electrolyte interphase (SEI) components, and compare the similarities and disparities between the behavior exhibited by Li and Na. Numerous experimental studies have demonstrated that battery performance can be significantly improved by using coatings to tune surface properties of either the metallic anode23–33 or of the current collector.34–36 We also extend our formalism to two-dimensional (2D) material coatings, which are promising candidates as protective surface coatings in metallic anode batteries.26–32,34,36
While first-principles investigations of heterogeneous metal/coating and metal/electrolyte interfaces abound, they are generally centered around interface stability37–40 or dendrite suppresion,41–43 with few being dedicate to void and pit growth.44–46 These past studies have identified adhesion energy between Li metal and coating materials as a promising descriptor for the likelihood of void formation: the weaker the adhesion, the more void prone the interface.44–46 In this work, by probing interfaces of metallic anodes and coating materials, we reveal previously undetected nuances of the relationship between interfacial interactions and tendency for vacancy accumulation, including factors such as adhesion energy, surface deformations, geometric lattice matching, and charge redistribution. For instance, we observed that, for metallic surfaces which, when isolated, exhibit a thermodynamic driving force towards vacancy accumulation, adhesion with a coating material can partially alleviate this tendency; however, for cases where vacancy congregation is not naturally favorable, strong interfacial interactions can lead to detrimental behavior. The results in this work indicate that our grasp of the fundamentals of the void formation phenomenon has much to mature, as well as open new directions for further research.
Methods
Vacancy interactions
The formation of voids and pits in Li metal has been previously studied through a variety of computational techniques.23,44–47 In the current work, we use the method proposed by Venturi and Viswanathan44 in order to estimate whether the initial steps associated with the void formation process can occur at room temperature for several Li and Na interfaces. This approach is based on a regular solution formalism, which has shown great accuracy at modeling a wide variety of mixture system, including, but not limited to, binary48 and high-entropy alloys, surfaces with adsorbates,49,50 and grain boundary complexions.51 While this methodology does not account for kinetics, and its predictions are based on a mean-field nearest-neighbor approach, it has been shown to correctly capture experimentally observable void formation phenomena in similar Li-metal systems.23In this model, the regular solution formalism is employed to evaluate the mixing behavior between occupied and vacant sites in the material: at temperatures where a miscibility gap exists, vacancies congregate and start forming voids. A full derivation of the model can be found in Venturi and Viswanathan.44 The tendency for vacancy accumulation is captured through the Gibbs free energy of mixing:
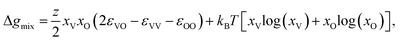 | (1) |
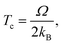 | (2) |
The interaction parameters εij are obtained from high-accuracy first principles DFT simulations for selected surface facets of Li and Na, as well as their interfaces with other materials, using the methods described by Venturi and Viswanathan.44 For a direct comparison between Li and Na system, the interfaces modeled in this work were chosen to match those from previous studies,44–46 which have already considered surface energetics in their selections. Simulation cells of surface slabs and interface systems were created using the Atomic Simulation Environment (ASE).52 Interfacial systems were built by setting the alkali slab as the substrate in the coherent interfaces module implemented within the pymatgen package,53 and by minimizing lattice mismatch between the two surfaces under consideration. An additional constraint of maximum strain of 4% was also applied. As the aim of this work is to study several different alkali/coating interfaces in search of commonalities and of differences between Li and Na, we focus solely on pristine interfaces. However, we would also like to highlight the importance of off-stoichiometric and other defective surfaces, which play a critical role in battery materials.11,54–56 While the location(s), concentration(s), and type(s) of defects (vacancies, interstitials, Schottky, Frenkel, etc.) can impact the energetics of the interfaces, an exhaustive analysis of all their effects falls outside the scope of this study.
DFT calculations were carried out with the real-space projector-augmented wave (PAW) method as implemented in GPAW.57,58 The Perdew–Burke–Ernzerhof (PBE)59 exchange correlation function was used in the Na/NaF calculations, and the Bayesian error estimation functional (BEEF-vdW)60 was used for the alkali/2D interfaces due to its similarity to PBE,5,60 but also because of its capability to include non-local van der Waals correlations in a self-consistent manner. All systems are charge-neutral, and dipole correction is employed in all surface and interfacial calculations.61 Simulations of bulk systems were all converged to a maximum force of 0.01 eV Å−1. All surface and interfacial systems were converged to a maximum force of 0.05 eV Å−1, had their Brillouin-zone sampled at a 6 Å−1k-point density, and employed at least 15 Å of vacuum.
Surface fluctuations
To capture surface morphologies at larger length scales than what is possible with DFT, we turned to capillary-fluctuation theory (CFT),62–64 which, to our knowledge, has not been previously used to investigate metallic battery anodes. CFT has been primarily used to probe the stiffness of solid–liquid metallic interfaces near and below the melting point, for the purpose of understanding crystallization behavior. However, it has also been successfully employed to describe experimental observations in surface step fluctuations (a process driven significantly by vacancies),65 grain boundary stiffness66 and premelting,67 as well as other solid–solid heterophase interfaces.68 Furthermore, its core idea is similar to that of the DFT-informed solution model: to capture naturally occurring surface oscillations. The CFT model expresses the surface free energy of a quasi-two-dimensional periodic surface slab (b ≪ W) as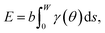 | (3) |
The Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) software69 was used to perform MD simulations. The interatomic potentials used for Li and Na systems were, respectively, a quadratic spectral neighbor analysis potential (q-SNAP) developed by Zuo et al.70 and an embedded atom model (EAM) based potential of Finnis–Sinclair type developed by Nichol and Ackland.71 These potentials were chosen due to their outstanding ability of simulating the desired alkali metals, as tabulated in the Open Knowledgebase of Interatomic Models (OpenKIM).72,73 A standard hysteresis-based analysis for estimating the melting point of both materials was conducted, which also allowed for evaluation of their thermal expansion behavior, shown in Fig. S5 and S6.†
Results
Susceptibility to vacancy accumulation
Using the thermodynamic model for void formation described in the Methods section,23,44 the critical temperature associated with vacancy accumulation was calculated for isolated slabs of Na of different facets. The comparison between the values obtained for Li and Na can be found on Table 1.| Facet | (100) | (110) | (111) | |||
|---|---|---|---|---|---|---|
| Alkali element | Li | Na | Li | Na | Li | Na |
| T c (11) K | 1980 | 1170 | 1600 | 500 | 100 | 0 |
| T c (12) K | 1340 | 700 | 70 | 200 | 0 | 0 |
The regular solution formalism dictates that, at temperatures above Tc, vacancies are fully soluble in the mixture and will be uniformly distributed on the surface. At temperatures below Tc, two phases coexist: one dominated by vacancies, and one, by occupied sites. The high vacancy phase corresponds to the onset of void formation. Based on this, lower values of Tc are desirable, as they indicate that, at operating temperature conditions (near 300 K), vacancies will tend to move away from one another, rather than accumulate and give rise to increased surface roughness.
From Table 1, it is clear that, for all facets, and all possible interactions, values of Tc follow the same trend for both Li and Na: the largest values occur for the (100) facet, followed by the (110), and then by the (111) facet. Similarly, the critical temperature values describing interactions between vacancies and occupied sites on the same Miller plane (Tc(11)) are generally larger than those that capture interactions across Miller planes (Tc(12)). Curiously, for the (111) facet, both Li and Na exhibit critical temperature values far below 300 K, suggesting that these surfaces are unlikely to develop voids if isolated. This is the opposite of what happens with the (100) facet, for which the surface of both alkali metals is predicted to form voids. For the (110) facet, even though Tc(12) < 300 K, since Tc(11) > 300 K in Li and Na, voids are expected to evolve through a stepping mechanism described in previous works.44 Interestingly, the values of Tc are consistently smaller for Na than for Li, indicating that vacancies on the surface of Na slabs become soluble at lower temperatures, and that void formation is less prone to occur in Na than in Li.
To ensure that these results are valid at larger length scales, we compared them to the predictions from our CFT investigation, under the assumption that stiffer surfaces are more resistant to void evolution, and, therefore, have lower values of Tc. As discussed in the next section, there is general agreement between DFT and MD predictions: both methods suggest that Na is stiffer than Li, despite its lower melting point, and that the relative surface facet resistance to void formation follows the trend (111) > (110) > (100).
With DFT, it is possible to investigate solid–solid interfaces more reliably than with MD, given the latter's requirement for interatomic potentials capable of describing each component independently as well as in tandem. Therefore, we also employ DFT to evaluate how the presence of sodium fluoride (NaF) can impact the results shown in Table 1. NaF is a common SEI component of Na-ion batteries,74,75 – especially if the electrolyte contains NaPF6 salt – and has the same rock-salt symmetry as lithium fluoride (LiF). The similarities between Li/Na and LiF/NaF can thus also provide additional insight into the behavior of these alkali metals. Interfaces between the different surface facets of the alkali metals and their respective fluoride structures were created and simulated with DFT under the same lens of the regular solution model shown in eqn (1). Examples of the structures used can be found on Fig. S7 and S8.†
The results from our analysis for Li/LiF and Na/NaF are shown in Tables 2 and 3, respectively. Similar trends exist between the two metals: for the (100) and (110) facets, the presence of the fluoride species has either negligible or negative impacts in the metals' ability to prevent vacancy accumulation. This can be seen from the values of the critical temperatures reported, which either stay the same or increase as XF (X = Li or Na) is introduced in the vicinity of the metal slabs with different facets. Interestingly, while the resistance to void formation of Li(111) surface decreases upon introduction of LiF, NaF had different effects on Na(111). This can be understood by evaluating how these interfaces change configurations before and after structural relaxation. In the Na(111)/NaF(111) case, depicted in Fig. S7,† strong interactions between the atoms in the Na slab and the dangling F bonds in NaF cause large deformations to the surface of Na, pushing atoms from the top two Miller planes of Na closer to the NaF slab. This, in turn, modifies the energetic landscape of these Na atoms considerably, largely altering their regular solution behavior. For cases in which these Na–F interactions are not as strong, and more evenly distributed along the plane of the interface, such as in Na(111)/NaF(100), shown in Fig. S8,† the thermodynamic parameters for Na are more akin to those observed in the simulations of isolated slabs, indicating this particular interface may still be resistant to Na vacancy accumulation. These interactions are particularly pronounced in the interfaces involving NaF(111), but, in the cases of Na(100) and Na(110), they only affect the Na atoms of the top Miller plane of the Na slab. In the interfacial Li systems, these alkali–halide interactions, while present, were not as strong as in the Na systems, likely due to lithium's higher ionization potential of 520 kJ mol−1, compared to sodium's 496 kJ mol−1.76
| Li(100) | Li(110) | Li(111) | |
|---|---|---|---|
| LiF(100) | T c (11) ≈ 1200 K | T c (11) ≈ 2000 K | T c (11) ≈ 300 K |
| T c (12) ≈ 1200 K | T c (12) ≈ 1200 K | T c (12) ≈ 600 K | |
| LiF(110) | T c (11) ≈ 900 K | T c (11) ≈ 2000 K | T c (11) ≈ 1700 K |
| T c (12) ≈ 1000 K | T c (12) ≈ 800 K | T c (12) ≈ 1200 K |
| Na(100) | Na(110) | Na(111) | |
|---|---|---|---|
| NaF(100) | T c (11) ≈ 1100 K | T c (11) ≈ 1000 K | T c (11) ≈ 0 K |
| T c (12) ≈ 800 K | T c (12) ≈ 120 K | T c (12) ≈ 0 K | |
| NaF(110) | T c (11) ≈ 1100 K | T c (11) ≈ 670 K | NA |
| T c (12) ≈ 800 K | T c (12) ≈ 0 K | ||
| NaF(111) | T c (11) > 104 K | T c (11) ≈ 0 K | T c (11) > 104 K |
| T c (12) > 104 K | T c (12) ≈ 1600 K | T c (12) > 104 K |
From these results, it can be postulated that the role of alkali-philicity is dubious. It has been argued that, for Li, stronger lithiophilicity reduces the likelihood of void evolution.44–46 However, for Na, we observed cases (such as the Na(111)/NaF(111) interface) where strong interactions with NaF material can promote vacancy congregation on the surface of Na. Nevertheless, for Na(110)/NaF(110) and Na(110)/NaF(111), weaker levels of sodiophilicity were able to reduce the critical temperatures related with void dissolution. This can also be seen in Fig. S9,† where values of the both Ω(11) and Ω(12) are plotted against approximate interface adhesion. A more in-depth discussion of the relationship (or lack thereof) between approximate adhesion and thermodynamic parameters can be found in the ESI.† Our results from studying Na/SEI interfaces suggest that, for cases where the isolated Na slabs can already prevent vacancy accumulation, strong interactions seem to bring adverse consequences, while, for the slabs that present a thermodynamic driving force to bring vacancies together, medium-strength interactions can be advantageous. This phenomenon could also be partially observed in Li, but, as discussed above, its effects are not as evident due to weaker interactions: the Li(111) interfaces, which, by themselves, are naturally resistant to voids, when interacting with LiF, become prone to vacancy accumulation.
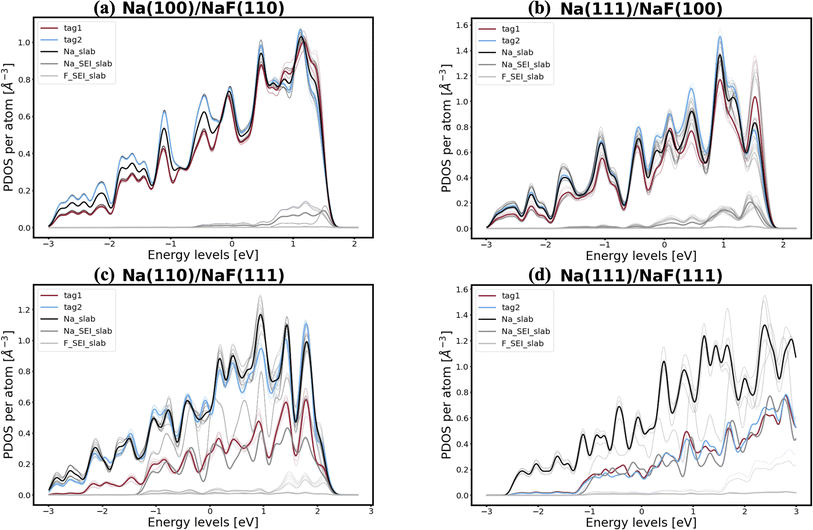
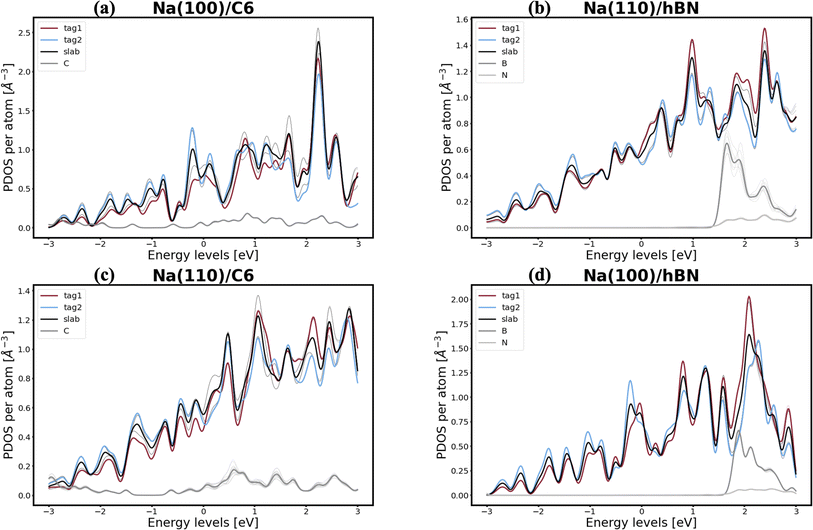
In pursuit of a more accurate and universal descriptor for void formation at metallic anode interfaces, we investigate the role of charge density and projected density of states (PDOS), a method which has been succesfully employed in previous studies to understand relevant interfaces in Li-metal batteries.37 In experimental examinations of Na/NASICON interfaces, Wang et al.21 identified a possible correlation between charge transfer and void formation at the surface of the metallic anode. To investigate this hypothesis further, we combine the PDOS and the charge densities of the explicit interfaces as a metric of the alkali-coating interactions. In Fig. 1, we can see four examples of PDOS of different interfaces. In the case of a Na(100)/NaF(110) interface (Fig. 1a) – for which the predicted behavior is of vacancy accumulation, the same as for isolated Na(100) – it is evident that all Na atoms in the metallic slab have equivalent PDOS, and do not strongly interact with NaF. Similarly, as shown in Fig. 1b, there is little interaction between Na and NaF in the Na(111)/NaF(100) interface, which does not exhibit tendency for vacancy accumulation, akin to the isolated Na(111) slab. Conversely, as shown in Fig. 1c, interactions between Na(110) and NaF(111), indicative of favorable adhesion, can help lower the critical temperatures associated with the initial steps of void formation when compared to the corresponding isolated Na slab. However, too strong interactions can lead to disadvantageous behavior, as exemplified by the Na(111)/NaF(111) interface, which has very high critical temperatures for vacancy accumulation compared to the isolated Na(111) slab. The PDOS of this interface is shown in Fig. 1d: Na atoms on the two top-most Miller planes (denoted by tag1 and tag2) of the metallic slab have a PDOS more similar to Na atoms in NaF. These results reveal that, while the PDOS analysis can serve as a great descriptor for understanding the strength of alkali-philicity of interfaces, a direct, quantitative connection between PDOS and tendency for vacancy accumulation remains elusive.
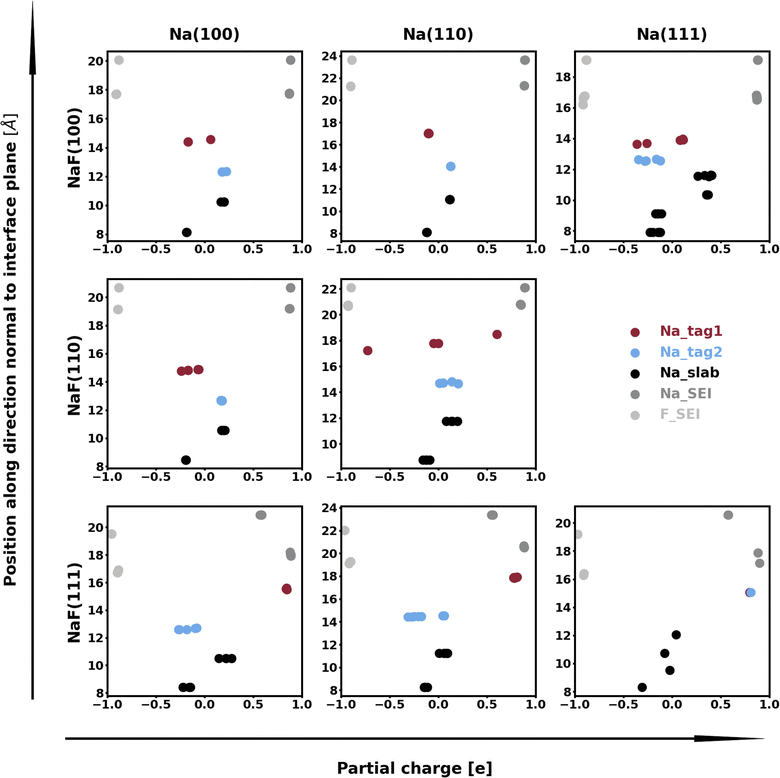
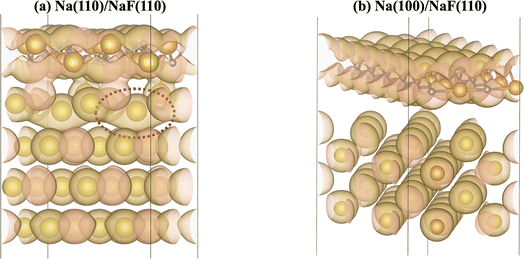
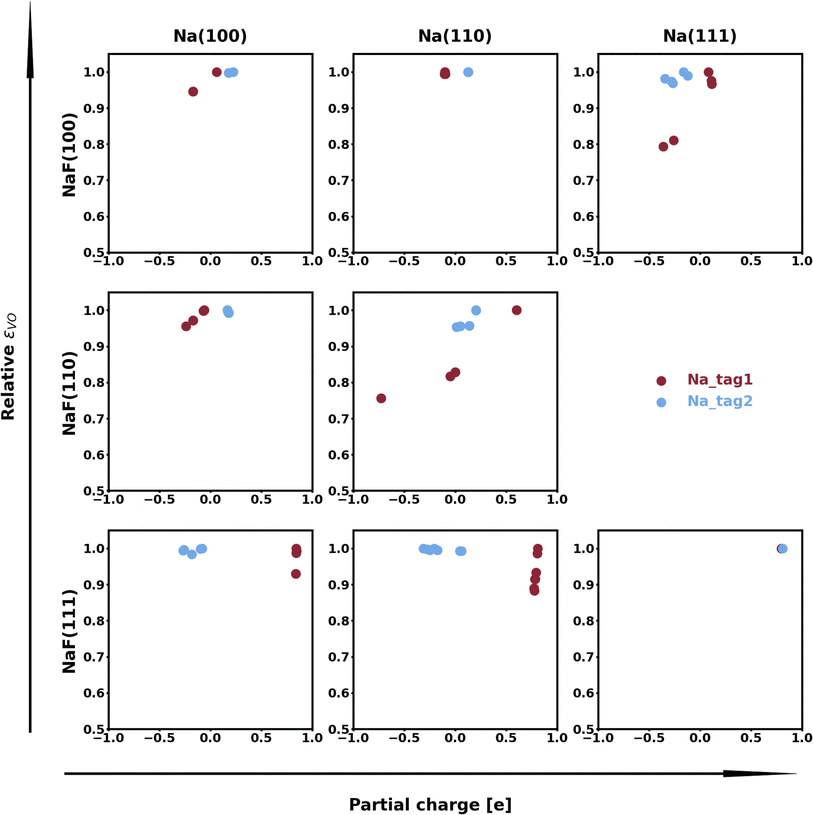
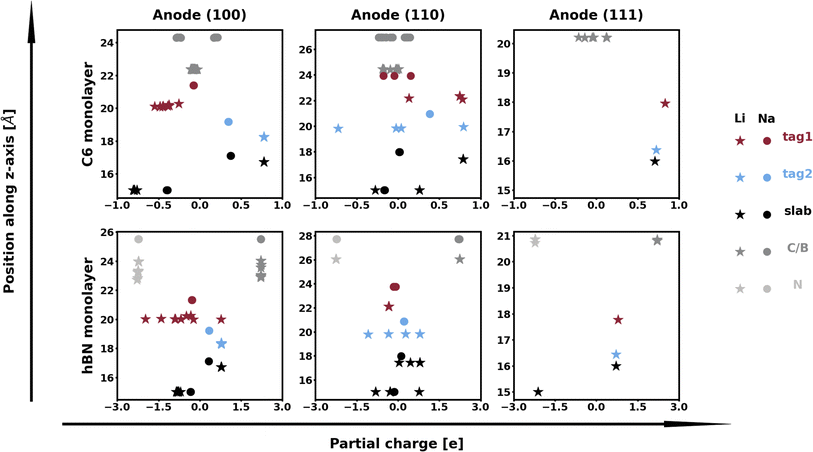
The calculation of Bader charges77 (done as implemented by Henkelman et al.78) can also be used to further examine these interfacial interactions. In Fig. 2, we plot the position of the atoms in the system along the direction normal to the interfacial plane (z-direction) and their respective Bader charges. As expected, in the NaF layer, the species are in their ionized forms: Na1+ and F1−. For the systems with weaker adhesion, while some degree of polarization can be observed within the Na slab, the partial charges remain within the range [−0.5, +0.5]. For interfaces with stronger interactions, the Na atoms on the top-most Miller plane of the Na-slab generally present an oxidation state of +1, having donated their valence electron to the metallic electron gas (whose charge density gets redistributed to the Na atoms in the slab by the Bader method). In the particular case of interfaces with NaF(111), these interactions are strong enough to have partially reduced the Na+ ions in the SEI material. In the Na(110)/NaF(110) interface, the Bader partitioning method assigns large negative charges to some Na atoms on the top-most Miller plane due to high spatial heterogeneity in the electron gas: since all atoms in the NaF slab are at their maximum allowed oxidation state, the extra electrons from first-plane Na+ ions are non-uniformly redistributed to the Na-slab metallic electron gas. This can be seen in Fig. 3: in panel (a), some of the Na atoms of type tag1 on the Na(110)/NaF(110) system have apparent larger charge volumes, which can be attributed to the heterogeneous electron gas around them, as indicated by the red dotted ellipse; in cases of weak to no interactions, such as the Na(100)/NaF(110) one in panel (b), we can see the charge distribution in the Na-slab remains homogeneous.
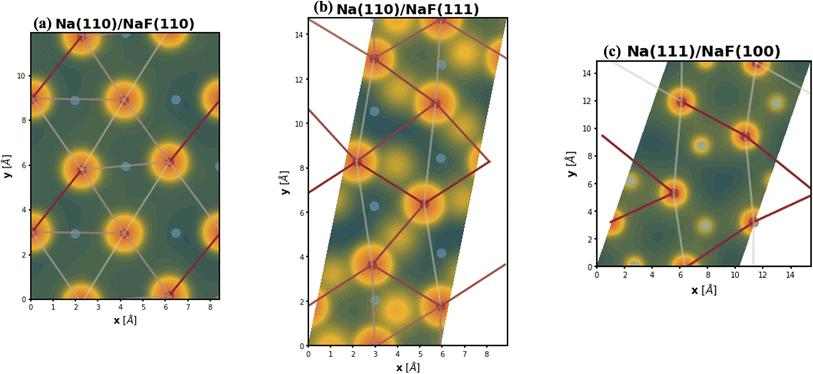
The spatial heterogeneity in the charge distribution appears to be correlated with the thermodynamic parameters in our model, as can be seen in Fig. 4, 5, S10, and S11.† First, we can try to capture the charge density on the plane of the interface by integrating its values along vertical lines (of constant x and y coordinates within the super-cell) between values of the z coordinate given by the average of the top position of a tag2 atom and the bottom position of a tag1 atom (zmin) and by the average of the top tag1 atom and lowest SEI atom (zmax). The base-10 logarithm of this planar integral is displayed as a contour plot in Fig. 4, with brighter contours indicating larger values. Red circles denote the positions of atoms of type tag1, and blue ones, of those of type tag2. The lines correspond to the calculated values of the εVV(11) parameter, with darker, more opaque lines corresponding to stronger interactions, and lighter, more transparent lines corresponding to weaker interactions. A similar plot for εVV(12) is shown in Fig. S10.† It can be observed that there exists some relationship between charge density heterogeneity and thermodynamic parameters, despite it not being substantial. For instance, in Fig. 4b, the strongest interactions happen between Na atoms which share a F atom, while those that have no bonds to a common F species display weaker interactions (even though all Na atoms are effectively fully oxidized). A more pronounced correlation is seen between this heterogeneity and the εVO parameter, as displayed in Fig. 5, in which partial charge is used as a proxy for heterogeneity in charge density. It can be seen that, for the most part, variations in the value of εVO are associated with a change in the partial charge of the corresponding Na atom.
While the correlation between thermodynamic parameters and spatial heterogeneity of the metallic electron gas is not overt, the results from our Bader charge analysis reinforce the hypothesis that, when the isolated Na slab is naturally prone to surface vacancy accumulation, adhesion can partially help diminish the thermodynamic driving force for this phenomenon; however, in cases where vacancy congregation is not thermodynamically favorable on the isolated Na-slab, too strong interactions can have adverse effects for the issue of void formation.
Numerous studies have identified 2D materials as promising coatings for metallic anodes.26–32,34 In experimental studies, few-layer graphene (C6)26,29,32 and hexagonal boron nitride (hBN)30,79 in particular have generally demonstrated enhanced performance. By applying our methodology to interfaces between metallic slabs (of either Li or Na) and 2D monolayers of coating materials (graphene C6 or hexagonal boron nitride hBN), we can examine how these materials impact the thermodynamic driving forces for the initial steps of void formation. The results of the thermodynamic analysis, reported in Table 4, indicate that none of the 2D coatings investigated in this study are capable of preventing vacancy accumulation on the surface of Na metal, and the same is true for hBN coatings on Li slabs. However, vacancy dissolution is favorable in the Li(110)/C6 and Li(111)/C6 interfaces. Therefore, for Na metal systems and architectures with hBN coatings, the enhanced performance observed experimentally is unlikely to stem from a reduction of void formation tendencies, but more probably originates from improvements related to other phenomena, such as dendrite suppression.
| Facet | (100) | (110) | (111) | |||
|---|---|---|---|---|---|---|
| Alkali element | Li | Na | Li | Na | Li | |
| C6 | T c (11) K | ≈104 | 0 | ≈6700 | 0 | |
| T c (12) K | ≈1250 | ≈104 | 0 | ≈4320 | 0 | |
| hBN | T c (11) K | ≈1340 | ≈104 | ≈6500 | >104 | ≈5450 |
| T c (12) K | ≈1200 | ≈104 | ≈3600 | ≈104 | ≈3590 | |
This behavior can in part be explained by evaluating the electronic interactions between the interfacing materials. The Bader charge analysis in Fig. 6 shows that Li and Na have generally similar behavior: the alkali atoms on the second (and, in most cases, third) Miller plane(s) tends to partially donate their electrons to the metallic electron cloud. However, this effect is much more pronounced in the systems with Li, and remains more muted for the Na systems, which do not interact with the 2D coating materials, as evidenced by the PDOS plots shown in Fig. 7 and charge isosurfaces in Fig. S13.† This explains in part why the Na/2D interfaces show similar predictions to their corresponding isolated Na slabs. Fig. S14 and S15† also show the absence of any relationship between charge density heterogeneity and thermodynamic parameter values, unlike what we observed for the Na/NaF systems, likely due to the weak interacting nature of the Na/2D interfaces.
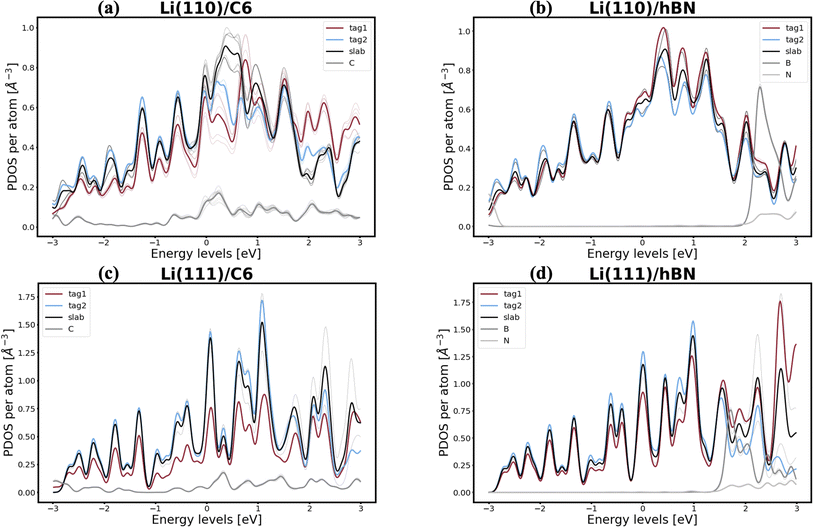
Interestingly, lithium's behavior is much more nuanced and varied, as well as more promising, since two out of the six interfaces investigated appear to be resistant to the first steps of void formation. The apparent polarization suggested by the Bader analysis is, similarly to the Na/NaF interfaces, a product of spatial heterogeneity in the electron gas distribution, as evidenced by the charge density isosurfaces in Fig. S12.† Additionally, the per-atom and type-averaged PDOS of the Li/2D systems displayed in Fig. 8 show there is no interaction between Li and hBN (panels b and d), and weak interactions between Li and C6 (panels a and c). Curiously, the Li(111) facet, which resists vacancy accumulation in the absence of coating (Table 1), maintains its behavior while exhibiting small interactions in its interface with C6, however, it loses its vacancy dissolution character when coupled in non-interacting fashion with hBN. Moreover, the similarly small C6 interactions are also capable of making the Li(110) facet resistant to vacancy congregation, while the non-interacting hBN does not affect its vacancy-accumulation inducing behavior.
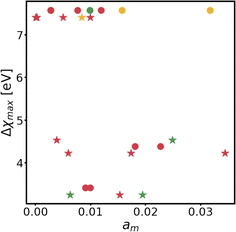
Changes in electronic structure observed in the coherent interfaces stem from interactions between the constituent materials as well as their geometric structure, including atom reorganization and strains caused by lattice mismatch (as seen in Fig. S7 and S8†). It is thus important to investigate possible relationships between these two features and the overall performance of the interface to help guide coating design. To measure electronic interactions between anode and coating slabs, we used the Mulliken electronegativity values of the elements, as explained in the ESI† and shown in Fig. S16.† The lattice mismatch between the interfacing surfaces was used as a surrogate for geometric considerations in this analysis. We employed two methods of quantifying this lattice mismatch. The first was by constructing all possible O-lattices80 between the 2D unit cells of the interfacing slabs (considering all possible relative rotations of the two lattices) and considering only the smallest value of the area of the reduced O-lattice. Generally, smaller O-lattices correspond to interfaces with fewer strained or frustrated regions. One example is the case of twisted bilayer graphene, where a small twist angle gives rise to very large O-lattices (akin to Moiré patterns), while larger angles reduce the magnitude of the supercell lattice vectors. The other way for measuring lattice mismatch is inspired by the method of building interfaces proposed by Zur and McGill81 (which was used to build the interfaces in this study): the ratio between the areas of the reduced lattices of the interfacing materials was calculated (ar = aalkali/a2D), and compared against the closest rational number 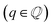 that can be written as a fraction of integers smaller than or equal to eight. The difference between these two numbers is what we denote by the area mismatch coefficient am = |ar − q|. The smaller this value, the less the individual (but repeated) unit cells had to be strained to form a coherent, computationally tractable interface. Based on the results shown in Fig. S16,† we found am to be a more descriptive parameter: not only is it capable of more clearly distinguishing the systems under investigation when compared to the O-lattice method, it also allows for the observation of explainable trends, as discussed below. The results of our analysis are shown in Fig. 9. It is important to note that, since cases of partial or full resistance to vacancy accumulation are a minority, any statistics derived from them is associated with high degrees of uncertainty. We observed that, for systems with higher lattice mismatch (am ≥ 0.02), the polarization ability of the coating material can help achieve at least partial resistance to vacancy accumulation. Additionally, lattice mismatch seems to be correlated with void resistant: for a given Δχmax value, most of the interfaces with some vacancy dissolution character have elevated am values. However, we observe a number of systems with low values of am which are still capable of preventing vacancy accumulation at the surface of the anode. This further corroborates the idea that adhesion and interfacial interactions are highly nuanced, and that a one-size-fits-all approach is not appropriate.
that can be written as a fraction of integers smaller than or equal to eight. The difference between these two numbers is what we denote by the area mismatch coefficient am = |ar − q|. The smaller this value, the less the individual (but repeated) unit cells had to be strained to form a coherent, computationally tractable interface. Based on the results shown in Fig. S16,† we found am to be a more descriptive parameter: not only is it capable of more clearly distinguishing the systems under investigation when compared to the O-lattice method, it also allows for the observation of explainable trends, as discussed below. The results of our analysis are shown in Fig. 9. It is important to note that, since cases of partial or full resistance to vacancy accumulation are a minority, any statistics derived from them is associated with high degrees of uncertainty. We observed that, for systems with higher lattice mismatch (am ≥ 0.02), the polarization ability of the coating material can help achieve at least partial resistance to vacancy accumulation. Additionally, lattice mismatch seems to be correlated with void resistant: for a given Δχmax value, most of the interfaces with some vacancy dissolution character have elevated am values. However, we observe a number of systems with low values of am which are still capable of preventing vacancy accumulation at the surface of the anode. This further corroborates the idea that adhesion and interfacial interactions are highly nuanced, and that a one-size-fits-all approach is not appropriate.
Surface stiffness
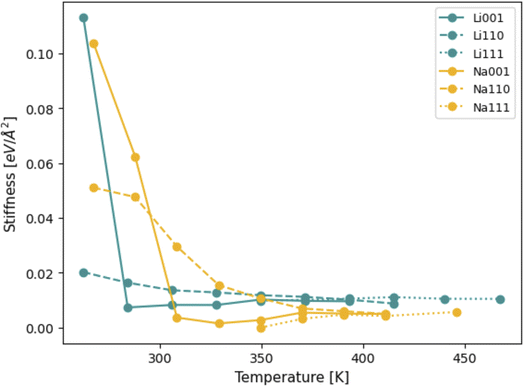
CFT allows for computations of interfacial stiffness by decomposing oscillations of surface height into their Fourier modes, as shown in eqn (S.4)–(S.6).† Each Fourier mode is fully defined by its wavenumber k and respective amplitude Ak. Eqn (S.6)† demonstrates that linear fits of 〈|Ak|〉−1 × k2 (as shown in Fig. S3†) can be used to compute the stiffness of the different Li and Na facets considered. The behavior of stiffness as a function of temperature is shown in Fig. 10. Unsurprisingly, as temperatures increase, the stiffness of all facets goes down, since they approach their liquid state.Interestingly, at first glance, the (111) surface facet appears to be the less stiff of all of them, for both Li and Na. At lower temperatures, the (111) facets for both Li and Na did not show any signs of capillary fluctuations in the timescale of the simulation due to their high stiffness. The profile of the surface provides a likely explanation for this behavior: all deviations from a perfectly flat (111) surface originate from individual, isolated adatoms, as well as small thermal oscillations in the atomic coordinates. This is evidence that the (111) facet surface-vacuum interfaces are too stiff to be appropriately understood with the timescale of MD simulations, unlike the (100) and (110) cases. The fact that the (111) facets only melt at higher temperatures, when compared to their (100) and (110) counterparts, also reinforces this hypothesis (the plot in Fig. 10 includes temperatures up to which the slabs could be considered solid, and constituent atoms were still mostly in a body-centered configuration). Therefore, other than believing the (111) facets to be stiffer than the others, we will only draw conclusions from the (100) and (110) facets of Li and Na.
Fig. 10 also shows that, at temperatures smaller than 310 K, Na surfaces are stiffer than Li, that is, more likely to resist void formation. While this might seem surprising, seeing as the mechanical moduli of Li is slightly larger than those of Na,20 it is important to note that the stiffness pertaining to CFT does not necessarily relate to the response of the whole system to mechanical stress, but instead only represents an energy penalty associated with perturbing surfaces.62–64 This result is in agreement with our predictions from DFT, shown in Table 1: stiffer systems are less likely to favor vacancy accumulation and subsequent evolution of large surface fluctuations. Therefore, higher stiffness values are, in general, expected to be correlated to smaller values of Tc for vacancy congregation, in line with our DFT results. For Na in particular, it would appear that estimations from both MD and DFT are qualitatively similar, as both predict the order of stiffness for isolated Na surface slabs to be (111) > (110) > (100). The same, however, cannot be said for Li: MD and DFT calculations are not in agreement regarding which facet among (100) and (110) is stiffer. Moreover, as seen in Table 1, while DFT calculations would indicate that the Li(110) should be more resistant to voids than the Li(100) facet, the temperatures associated with spontaneous vacancy accumulation are not too dissimilar between these two facets. On the other hand, MD results indicate the Li(100) facet to be significantly more resistant to surface perturbations than the (110). Notably, this only appears to be valid below 280 K, and, at temperatures higher than this value, the situation is reversed and the match between MD and DFT predictions is re-established. It is possible that, at such low homologous temperatures, and in the absence of a liquid system, the capillary method may not reliably capture the interface stiffness of certain facets, especially those that only melt at more elevated temperatures.
Conclusions
In this work, we explore the initial steps required for void formation in Li and Na metal batteries, namely, the accumulation of vacancies at the surface of the metal anodes. First, we investigated the thermodynamics of spontaneous surface roughening through the lens of capillary fluctuation theory, and showed that it can make similar predictions as a regular solution model with parameters obtained from first-principles. Coupling the regular solution model with DFT, we surveyed numerous alkali/coating interfaces. Our work shows that adhesion energy, a property previously identified as an appropriate descriptor for both thermodynamics and kinetics of void formation in Li metal batteries, does not appropriately capture the same thermodynamics in Na metal interfaces. We demonstrated that too strong alkali-philicity can lead to significant structural distortions on the metallic Na slab, negatively impacting driving forces for vacancy dissolution. However, our results also indicate that interactions of moderate intensity can be beneficial for preventing vacancy accumulation. Electronic and geometric considerations reveal that alkali/coating interfacial interactions are highly nuanced, and that, for Na metal batteries, an adequate descriptor for the vacancy congregation tendency is still lacking. In order to address this issue, our future work will continue to apply and further develop the formalism described here to diverse types of coating materials.Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†Author contributions
V. V. and I. I. A. conceived the project. R. F. supervised the MD calculations. I. I. A. supervised both the DFT and MD calculations. V. V. designed and performed computational simulations and data analysis. V. V. wrote the manuscript with inputs from all authors; I. I. A. directed the overall research.Conflicts of interest
There are no conflicts to declare.Acknowledgements
V. V. was supported in part by the MIT Climate & Sustainability Consortium. Acknowledgement is also made to Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) grants number MAT230005, MAT230014, and MAT230050, as well as to administrators of the Expanse and Engaging computer clusters in San Diego and at MIT, respectively. We thank Prof. Ju Li for insightful discussions.References
- Y. Sun, N. Liu and Y. Cui, Promises and Challenges of Nanomaterials for Lithium-Based Rechargeable Batteries, Nat. Energy, 2016, 1, 1–12 Search PubMed.
- D. Aurbach, E. Zinigrad, H. Teller and P. Dan, Factors Which Limit the Cycle Life of Rechargeable Lithium (Metal) Batteries, J. Electrochem. Soc., 2000, 147, 1274–1279 CrossRef CAS.
- D. Lin, Y. Liu and Y. Cui, Reviving the Lithium Metal Anode for High-Energy Batteries, Nat. Nanotechnol., 2017, 12, 194–206 CrossRef CAS PubMed.
- W. Xu, J. Wang, F. Ding, X. Chen, E. Nasybulin, Y. Zhang and J.-G. Zhang, Lithium Metal Anodes for Rechargeable Batteries, Energy Environ. Sci., 2014, 7, 513–537 RSC.
- C. Fu, V. Venturi, J. Kim, Z. Ahmad, A. W. Ells, V. Viswanathan and B. A. Helms, Universal Chemomechanical Design Rules for Solid-Ion Conductors to Prevent Dendrite Formation in Lithium Metal Batteries, Nat. Mater., 2020, 19, 758–766 CrossRef CAS PubMed.
- A. Bhowmik, I. E. Castelli, J. M. Garcia-Lastra, P. B. Jørgensen, O. Winther and T. Vegge, A Perspective on Inverse Design of Battery Interphases Using Multi-Scale Modelling, Experiments and Generative Deep Learning, Energy Storage Mater., 2019, 21, 446–456 CrossRef.
- A. Sharafi, E. Kazyak, A. L. Davis, S. Yu, T. Thompson, D. J. Siegel, N. P. Dasgupta and J. Sakamoto, Surface Chemistry Mechanism of Ultra-Low Interfacial Resistance in the Solid-State Electrolyte Li7La3Zr2O12, Chem. Mater., 2017, 29, 7961–7968 CrossRef CAS.
- K. S. Exner, Constrained Ab Initio Thermodynamics: Transferring the Concept of Surface Pourbaix Diagrams in Electrocatalysis to Electrode Materials in Lithium-Ion Batteries, ChemElectroChem, 2017, 4, 3231–3237 CrossRef CAS.
- K. S. Exner, A Short Perspective of Modeling Electrode Materials in Lithium-Ion Batteries by the Ab Initio Atomistic Thermodynamics Approach, J. Solid State Electrochem., 2018, 22, 3111–3117 CrossRef CAS.
- M. A. Gialampouki, J. Hashemi and A. A. Peterson, The Electrochemical Mechanisms of Solid–Electrolyte Interphase Formation in Lithium-Based Batteries, J. Phys. Chem. C, 2019, 123, 20084–20092 CrossRef CAS.
- Z. Ahmad, V. Venturi, S. Sripad and V. Viswanathan, Chemomechanics: Friend or Foe of the “AND Problem” of Solid-State Batteries?, Curr. Opin. Solid State Mater. Sci., 2022, 26, 101002 CrossRef CAS.
- S. Sripad and V. Viswanathan, Performance Metrics Required of Next-Generation Batteries to Make a Practical Electric Semi Truck, ACS Energy Lett., 2017, 2, 1669–1673 CrossRef CAS.
- W. L. Fredericks, S. Sripad, G. C. Bower and V. Viswanathan, Performance Metrics Required of Next-Generation Batteries to Electrify Vertical Takeoff and Landing (VTOL) Aircraft, ACS Energy Lett., 2018, 3, 2989–2994 CrossRef CAS.
- A. Bills, S. Sripad, W. L. Fredericks, M. Singh and V. Viswanathan, Performance Metrics Required of Next-Generation Batteries to Electrify Commercial Aircraft, ACS Energy Lett., 2020, 5, 663–668 CrossRef CAS.
- A. Bills, S. Sripad, W. L. Fredericks, M. Guttenberg, D. Charles, E. Frank and V. Viswanathan, Universal Battery Performance and Degradation Model for Electric Aircraft, arXiv, 2020, preprint, arXiv:2008.01527, DOI:10.48550/arXiv.2008.01527.
- A. H. Epstein and S. M. O'Flarity, Considerations for Reducing Aviation's CO2 with Aircraft Electric Propulsion, J. Propul. Power, 2019, 35, 572–582 CrossRef.
- C. Vaalma, D. Buchholz, M. Weil and S. Passerini, A Cost and Resource Analysis of Sodium-Ion Batteries, Nat. Rev. Mater., 2018, 3, 1–11 CrossRef.
- H. Kim, Sodium-Ion Battery: Can It Compete with Li-Ion?, ACS Mater. Au, 2023, 571–575 CrossRef CAS PubMed.
- H. S. Hirsh, Y. Li, D. H. S. Tan, M. Zhang, E. Zhao and Y. S. Meng, Sodium-Ion Batteries Paving the Way for Grid Energy Storage, Adv. Energy Mater., 2020, 10, 2001274 CrossRef CAS.
- B. Lee, E. Paek, D. Mitlin and S. W. Lee, Sodium Metal Anodes: Emerging Solutions to Dendrite Growth, Chem. Rev., 2019, 119, 5416–5460 CrossRef CAS PubMed.
- W. Wang, S. Hu, Z. Jian and W. Chen, Insight into the Evolution of Voids at the NASICON/Na Interface and Suppressing Void Accumulation by a Semiliquid Wetting Strategy, ACS Appl. Energy Mater., 2023, 6, 7837–7846 CrossRef CAS.
- Y. Zhao, R. Wang and E. Martínez-Pañeda, A Phase Field Electro-Chemo-Mechanical Formulation for Predicting Void Evolution at the Li–Electrolyte Interface in All-Solid-State Batteries, J. Mech. Phys. Solids, 2022, 167, 104999 CrossRef CAS.
- V. Raj, V. Venturi, V. R. Kankanallu, B. Kuiri, V. Viswanathan and N. P. B. Aetukuri, Direct Correlation between Void Formation and Lithium Dendrite Growth in Solid-State Electrolytes with Interlayers, Nat. Mater., 2022, 1–7 Search PubMed.
- Y.-J. Liu, R.-Y. Fang and D. Mitlin, NASICON Solid Electrolyte Coated by Indium Film for All-Solid-State Li-metal Batteries, Tungsten, 2022, 4, 316–322 CrossRef.
- Y. Deng, J. Zheng, Q. Zhao, J. Yin, P. Biswal, Y. Hibi, S. Jin and L. A. Archer, Highly Reversible Sodium Metal Battery Anodes via Alloying Heterointerfaces, Small, 2022, 18, 2203409 CrossRef CAS PubMed.
- H. Wang, C. Wang, E. Matios and W. Li, Critical Role of Ultrathin Graphene Films with Tunable Thickness in Enabling Highly Stable Sodium Metal Anodes, Nano Lett., 2017, 17, 6808–6815 CrossRef CAS PubMed.
- H. Tian, Z. W. Seh, K. Yan, Z. Fu, P. Tang, Y. Lu, R. Zhang, D. Legut, Y. Cui and Q. Zhang, Theoretical Investigation of 2D Layered Materials as Protective Films for Lithium and Sodium Metal Anodes, Adv. Energy Mater., 2017, 7, 1602528 CrossRef.
- E. Cha, M. D. Patel, J. Park, J. Hwang, V. Prasad, K. Cho and W. Choi, 2D MoS2 as an Efficient Protective Layer for Lithium Metal Anodes in High-Performance Li–S Batteries, Nat. Nanotechnol., 2018, 13, 337–344 CrossRef CAS PubMed.
- J.-S. Kim, D. W. Kim, H. T. Jung and J. W. Choi, Controlled Lithium Dendrite Growth by a Synergistic Effect of Multilayered Graphene Coating and an Electrolyte Additive, Chem. Mater., 2015, 27, 2780–2787 CrossRef CAS.
- J. Xie, L. Liao, Y. Gong, Y. Li, F. Shi, A. Pei, J. Sun, R. Zhang, B. Kong, R. Subbaraman, J. Christensen and Y. Cui, Stitching H-BN by Atomic Layer Deposition of LiF as a Stable Interface for Lithium Metal Anode, Sci. Adv., 2017, 3, eaao3170 CrossRef PubMed.
- D. Zhang, S. Wang, B. Li, Y. Gong and S. Yang, Horizontal Growth of Lithium on Parallelly Aligned MXene Layers towards Dendrite-Free Metallic Lithium Anodes, Adv. Mater., 2019, 31, 1901820 CrossRef PubMed.
- Z. Lu, Q. Liang, B. Wang, Y. Tao, Y. Zhao, W. Lv, D. Liu, C. Zhang, Z. Weng, J. Liang, H. Li and Q.-H. Yang, Graphitic Carbon Nitride Induced Micro-Electric Field for Dendrite-Free Lithium Metal Anodes, Adv. Energy Mater., 2019, 9, 1803186 CrossRef.
- C.-F. Xiao, J. H. Kim, S.-H. Cho, Y. C. Park, M. J. Kim, K.-B. Chung, S.-G. Yoon, J.-W. Jung, I.-D. Kim and H.-S. Kim, Ensemble Design of Electrode–Electrolyte Interfaces: Toward High-Performance Thin-Film All-Solid-State Li–Metal Batteries, ACS Nano, 2021, 15, 4561–4575 CrossRef CAS PubMed.
- J. Zheng, et al., Reversible Epitaxial Electrodeposition of Metals in Battery Anodes, Science, 2019, 366, 645–648 CrossRef CAS PubMed.
- Y. Wang, Y. Liu, M. Nguyen, J. Cho, N. Katyal, B. S. Vishnugopi, H. Hao, R. Fang, N. Wu, P. Liu, P. P. Mukherjee, J. Nanda, G. Henkelman, J. Watt and D. Mitlin, Stable Anode-Free All-Solid-State Lithium Battery through Tuned Metal Wetting on the Copper Current Collector, Adv. Mater., 2023, 35, 2206762 CrossRef CAS PubMed.
- J. H. Lee, Y.-G. Cho, D. Gu and S. J. Kim, 2D PdTe2 Thin-Film-Coated Current Collectors for Long-Cycling Anode-Free Rechargeable Batteries, ACS Appl. Mater. Interfaces, 2022, 14, 15080–15089 CrossRef CAS PubMed.
- N. D. Lepley and N. A. W. Holzwarth, Modeling Interfaces between Solids: Application to Li Battery Materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214201 CrossRef.
- M. Ebadi, C. Marchiori, J. Mindemark, D. Brandell and C. M. Araujo, Assessing Structure and Stability of Polymer/Lithium-Metal Interfaces from First-Principles Calculations, J. Mater. Chem. A, 2019, 7, 8394–8404 RSC.
- X.-Q. Zhang, X.-B. Cheng, X. Chen, C. Yan and Q. Zhang, Fluoroethylene Carbonate Additives to Render Uniform Li Deposits in Lithium Metal Batteries, Adv. Funct. Mater., 2017, 27, 1605989 CrossRef.
- L. E. Camacho-Forero, T. W. Smith, S. Bertolini and P. B. Balbuena, Reactivity at the Lithium–Metal Anode Surface of Lithium–Sulfur Batteries, J. Phys. Chem. C, 2015, 119, 26828–26839 CrossRef CAS.
- Z. Liu, Y. Qi, Y. X. Lin, L. Chen, P. Lu and L. Q. Chen, Interfacial Study on Solid Electrolyte Interphase at Li Metal Anode: Implication for Li Dendrite Growth, J. Electrochem. Soc., 2016, 163, A592 CrossRef CAS.
- Z. Ahmad, Z. Hong and V. Viswanathan, Design Rules for Liquid Crystalline Electrolytes for Enabling Dendrite-Free Lithium Metal Batteries, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 26672–26680 CrossRef CAS PubMed.
- L. Shi, A. Xu and T. Zhao, First-Principles Investigations of the Working Mechanism of 2D h-BN as an Interfacial Layer for the Anode of Lithium Metal Batteries, ACS Appl. Mater. Interfaces, 2017, 9, 1987–1994 CrossRef CAS PubMed.
- V. Venturi and V. Viswanathan, Thermodynamic Analysis of Initial Steps for Void Formation at Lithium/Solid Electrolyte Interphase Interfaces, ACS Energy Lett., 2022, 1953–1959 CrossRef CAS.
- C.-T. Yang and Y. Qi, Maintaining a Flat Li Surface during the Li Stripping Process via Interface Design, Chem. Mater., 2021, 33, 2814–2823 CrossRef CAS.
- M. Yang and Y. Mo, Interfacial Defect of Lithium Metal in Solid-State Batteries, Angew. Chem., Int. Ed., 2021, 60, 21494–21501 CrossRef CAS PubMed.
- H. Yan, K. Tantratian, K. Ellwood, E. T. Harrison, M. Nichols, X. Cui and L. Chen, How Does the Creep Stress Regulate Void Formation at the Lithium-Solid Electrolyte Interface during Stripping?, Adv. Energy Mater., 2022, 12, 2102283 CrossRef CAS.
- H. K. Hardy, A “Sub-Regular” Solution Model and Its Application to Some Binary Alloy Systems, Acta Metall., 1953, 1, 202–209 CrossRef CAS.
- T. Murakami, S. Ono, M. Tamura and M. Kurata, On the Theory of Surface Tension of Regular Solution, J. Phys. Soc. Jpn., 1951, 6, 309–312 CrossRef CAS.
- G. Barbero, L. R. Evangelista and I. Lelidis, Effective Adsorption Energy and Generalization of the Frumkin-Fowler-Guggenheim Isotherm, J. Mol. Liq., 2021, 327, 114795 CrossRef CAS.
- P. R. Cantwell, M. Tang, S. J. Dillon, J. Luo, G. S. Rohrer and M. P. Harmer, Grain Boundary Complexions, Acta Mater., 2014, 62, 1–48 CrossRef CAS.
- A. H. Larsen, et al., The Atomic Simulation Environment—a Python Library for Working with Atoms, J. Phys.: Condens.Matter, 2017, 29, 273002 CrossRef PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (Pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- M. W. Swift and Y. Qi, First-Principles Prediction of Potentials and Space-Charge Layers in All-Solid-State Batteries, Phys. Rev. Lett., 2019, 122, 167701 CrossRef PubMed.
- J. Pan, Q. Zhang, X. Xiao, Y.-T. Cheng and Y. Qi, Design of Nanostructured Heterogeneous Solid Ionic Coatings through a Multiscale Defect Model, ACS Appl. Mater. Interfaces, 2016, 8, 5687–5693 CrossRef CAS PubMed.
- Z. Ahmad, V. Venturi, H. Hafiz and V. Viswanathan, Interfaces in Solid Electrolyte Interphase: Implications for Lithium-Ion Batteries, J. Phys. Chem. C, 2021, 125, 11301–11309 CrossRef CAS.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Real-Space Grid Implementation of the Projector Augmented Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola and H. A. Hansen, et al., Electronic Structure Calculations with GPAW: A Real-Space Implementation of the Projector Augmented-Wave Method, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Density Functionals for Surface Science: Exchange-correlation Model Development with Bayesian Error Estimation, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- L. Bengtsson, Dipole Correction for Surface Supercell Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301–12304 CrossRef CAS.
- J. J. Hoyt, M. Asta and A. Karma, Method for Computing the Anisotropy of the Solid-Liquid Interfacial Free Energy, Phys. Rev. Lett., 2001, 86, 5530–5533 CrossRef CAS PubMed.
- N. T. Brown, E. Martinez and J. Qu, Solid-Liquid Metal Interface Definition Studies Using Capillary Fluctuation Method, Comput. Mater. Sci., 2019, 168, 65–73 CrossRef CAS.
- P. Saidi, R. Freitas, T. Frolov, M. Asta and J. J. Hoyt, Free Energy of Steps at Faceted (111) Solid–Liquid Interfaces in the Si–Al System Calculated Using Capillary Fluctuation Method, Comput. Mater. Sci., 2017, 134, 184–189 CrossRef CAS.
- R. Freitas, T. Frolov and M. Asta, Capillary Fluctuations of Surface Steps: An Atomistic Simulation Study for the Model Cu(111) System, Phys. Rev. E, 2017, 96, 043308 CrossRef PubMed.
- S. M. Foiles and J. J. Hoyt, Computation of Grain Boundary Stiffness and Mobility from Boundary Fluctuations, Acta Mater., 2006, 54, 3351–3357 CrossRef CAS.
- J. J. Hoyt, Z. T. Trautt and M. Upmanyu, Fluctuations in Molecular Dynamics Simulations, Math. Comput. Simulat., 2010, 80, 1382–1392 CrossRef.
- Y. Mishin, Calculation of the γ/Γ′ Interface Free Energy in the Ni–Al System by the Capillary Fluctuation Method, Modell. Simul. Mater. Sci. Eng., 2014, 22, 045001 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS - a Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, Performance and Cost Assessment of Machine Learning Interatomic Potentials, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS PubMed.
- A. Nichol and G. J. Ackland, Property Trends in Simple Metals: An Empirical Potential Approach, Phys. Rev. B, 2016, 93, 184101 CrossRef.
- E. van der Giessen, et al., Roadmap on Multiscale Materials Modeling, Modell. Simul. Mater. Sci. Eng., 2020, 28, 043001 CrossRef.
- E. B. Tadmor, R. S. Elliott, J. P. Sethna, R. E. Miller and C. A. Becker, The Potential of Atomistic Simulations and the Knowledgebase of Interatomic Models, JOM, 2011, 63, 17 CrossRef.
- L. Gao, J. Chen, Q. Chen and X. Kong, The Chemical Evolution of Solid Electrolyte Interface in Sodium Metal Batteries, Sci. Adv., 2022, 8, eabm4606 CrossRef CAS PubMed.
- J. Fondard, E. Irisarri, C. Courrèges, M. R. Palacin, A. Ponrouch and R. Dedryvère, SEI Composition on Hard Carbon in Na-Ion Batteries After Long Cycling: Influence of Salts (NaPF6, NaTFSI) and Additives (FEC, DMCF), J. Electrochem. Soc., 2020, 167, 070526 CrossRef CAS.
- A. Kramida, Y. Ralchenko, J. Reader and NIST ASD Team, NIST Database of Ionization Potentials. NIST Atomic Spectra Database (Ver. 5.10), National Institute of Standards and Technology, Gaithersburg, MD, 2022, https://physics.nist.gov/asd Search PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, The International Series of Monographs on Chemistry 22, Clarendon Press; Oxford University Press, Oxford [England]: New York, 1994 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- K. Yan, H.-W. Lee, T. Gao, G. Zheng, H. Yao, H. Wang, Z. Lu, Y. Zhou, Z. Liang, Z. Liu, S. Chu and Y. Cui, Ultrathin Two-Dimensional Atomic Crystals as Stable Interfacial Layer for Improvement of Lithium Metal Anode, Nano Lett., 2014, 14, 6016–6022 CrossRef CAS PubMed.
- W. Bollmann, Crystal Defects and Crystalline Interfaces, Softcover Reprint of the Original, Springer, 1st edn, 2012 Search PubMed.
- A. Zur and T. C. McGill, Lattice Match: An Application to Heteroepitaxy, J. Appl. Phys., 1984, 55, 378–386 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta00971a |
| This journal is © The Royal Society of Chemistry 2024 |