Enhancement of hole capture and water dissociation on rutile TiO₂(110) by intermolecular hydrogen bonding: time-domain ab initio study

Abstract

Photocatalytic water splitting has been a focal point of research to solve energy and environmental issues. However, the understanding of photocatalytic water splitting and coupled dynamics of photogenerated charge carriers at molecule/semiconductor interfaces is still limited. We have combined ab initio molecular dynamics, real-time time-dependent density functional theory, and nonadiabatic molecular dynamics to study the dissociation of water and capture of photogenerated holes on the pristine rutile TiO₂(110) surface. Our simulations indicate that intermolecular hydrogen bonding (IHB) between water molecules facilitates water dissociation. The dissociation energy of water molecules in a pristine, non-dissociated structure is reduced by 15%, from 0.26 eV to 0.21 eV, due to IHB. In the semi-dissociated structure, the dissociation energy of a water molecule is only 0.13 eV, owing to proton transfer induced by IHB. In the semi-dissociated structure, IHB between H₂O and terminal hydroxyl (O_tH) stabilizes the dissociated structure. Furthermore, IHB promotes spatial isolation of O_tH and bridging hydroxyl (O_brH) and inhibits their recombination. The stabilized dissociated structure activates high-frequency vibrational modes that increase the nonadiabatic coupling and promote hole capture on a femtosecond timescale, accelerating the capture rate by 36%. The findings provide important insights into photo-dissociation of water on rutile TiO₂(110), particularly shedding light on the impact of key intermediates on the photocatalytic process.

---

1. Introduction

Hydrogen energy, as an efficient and clean energy source, holds tremendous potential for addressing the energy crisis and reducing carbon emissions. Photolysis of water, a crucial technique, harnesses solar energy to split water into hydrogen and oxygen, thereby enabling efficient hydrogen production.^1–3 Since the pioneering discovery of photocatalytic water splitting on TiO₂ electrodes under ultraviolet light by Fujishima and colleagues in 1972,⁴ photocatalytic water splitting on TiO₂ has garnered significant attention and serves as a model system for studying water dissociation.^5–12 The dissociation of water on the TiO₂ surface is influenced by various factors, such as surface defects, adsorption structures, surface water coverage, and charge distribution.^13–24 Many current efforts focus on photocatalytic reactivity mediated by defects. For example, numerous experiments and theoretical studies suggest that the dissociation of water on rutile TiO₂(110) occurs at surface bridging oxygen (O_br) vacancies, but the dissociation of H₂O on perfect rutile (p-rutile) TiO₂(110) remains elusive.^13,25–30

Over the years, numerous experimental and theoretical studies have attempted to elucidate whether water molecules dissociate on the p-rutile TiO₂(110) surface, but the current conclusions remain controversial. On the one hand, some experimental and theoretical studies suggest that water molecule dissociation occurs only on oxygen vacancies of the TiO₂(110) surface. For example, using scanning tunneling microscopy (STM), Brookes et al. observed that only bridging hydroxyl (O_brH) is formed by the dissociation of water at oxygen vacancies on the rutile TiO₂(110) surface.^13,25 They did not observe terminal hydroxyl (O_tH) adsorbed on five-coordinated Ti sites (Ti_5c) formed by the dissociation of water at non-oxygen vacancies, and therefore they suggested that water molecules cannot dissociate on the p-rutile TiO₂(110) surface. Density functional theory (DFT) simulations conducted by Liu et al. indicated that water molecules do not dissociate on the p-rutile TiO₂(110) surface at coverages of 0.5 mol L⁻¹ and 1 mol L⁻¹.³¹ On the other hand, some studies suggest that water molecules can dissociate on the p-rutile TiO₂(110) surface. Walle et al. utilized synchrotron radiation photoelectron spectroscopy to find that water dissociation at oxygen vacancies competes with dissociation in defect-free regions.^26,29 Using STM, Yang et al. observed the appearance of O_tH on the Ti_5c site of p-rutile TiO₂(110) under ultraviolet light exposure.^30,32 Their work provides direct evidence for photoinduced water dissociation on the p-rutile TiO₂(110) surface. In addition to the experiments, quantum molecular dynamics (MD) simulations also revealed that the assistance of surface O_br contributes to the water dissociation on p-rutile TiO₂(110).³³

Although some studies suggest that water molecules can dissociate on the p-rutile TiO₂(110) surface, experimental results demonstrate that the efficiency of photocatalytic water decomposition on this surface is very low. Consequently, most studies conclude that surface-bridging oxygen vacancies are the key factor facilitating water dissociation. Du et al. observed through high-resolution STM that once O_brH and O_tH occupy adjacent positions, they immediately disappear due to the reformation of water.³⁴ This discovery provides a clue for explaining the low efficiency of photoinduced water molecule dissociation on p-rutile TiO₂(110). It is hard for the O_tH species generated by the dissociation of water to desorb from Ti_5c and migrate along the surface, preventing separation of O_brH and O_tH and leading to the formation of O_brH/O_tH pairs, referred to as “pseudo-dissociated” water.³⁵ Car–Parrinello MD simulations also indicated that O_brH/O_tH pairs undergo rapid recombination on p-rutile TiO₂(110).³⁶ Thus, the rapid recombination of O_brH/O_tH pairs in the pseudo-dissociated state may be the key factor limiting effective photoinduced dissociation of water. It is noteworthy that both experiments and theoretical simulations indicate that the adsorption of water molecules on rutile TiO₂(110) in the form of dimers or one-dimensional water chains is more favorable compared to monomer adsorption, with these molecules interconnected through hydrogen bonds.^15,37,38 Experiments show that water molecules adsorbed in the dimeric form exhibit a higher dissociation efficiency compared to monomer adsorption, which is attributed to cooperativity mediated by strong intermolecular hydrogen bonding (IHB).³² Up to now, the detailed mechanism of water molecule dissociation on p-rutile TiO₂(110) remains unclear, particularly regarding how to overcome the recombination of the O_brH/O_brH pairs in the pseudo-dissociated state and effectively capture photogenerated holes. Further research is needed to address these questions.

Numerous first-principles calculations and molecular dynamics simulations of the water-splitting process focused on the electronic and thermodynamic aspects. These simulations are based on the Born–Oppenheimer approximation, and thus, are conducted in the ground electronic state. More advanced methods are needed for studying the dynamics of photogenerated hole capture at the surface, which is important for a comprehensive understanding of the mechanism of water splitting on surfaces. Time-domain ab initio nonadiabatic molecular dynamics (NAMD) simulations can investigate excited-state charge transfer, relaxation, and recombination processes at photocatalytic interfaces at the atomic level, providing new insights into the mechanisms of photocatalytic surface reactions.³⁹ Using NAMD simulations, Kaxiras, Meng et al., studied the photo-driven oxidation and dissociation of H₂O and CH₃OH on the rutile TiO₂(110) surface.^40,41 Their work revealed the reaction intermediates, adsorption structures, and timescales of photogenerated carrier capture. Zhao et al. discovered through ab initio NAMD simulations that the activation of the bending and asymmetric stretching vibrational modes of CO₂ molecules is key to capturing photogenerated electrons, a process that can be completed within 100 fs.⁴² The capture of surface photogenerated charges has become an essential aspect of studying photocatalytic reaction mechanisms.

In this study, we employed DFT, time-dependent DFT (TD-DFT), and nonadiabatic (NA) MD methods to investigate the dynamics of water dissociation and capture of photogenerated holes on p-rutile TiO₂(110). Ab initio MD (AIMD) simulations reveal that the water monolayer undergoes spontaneous partial dissociation (semi-dissociation). Strong hydrogen bonds (HBs) between O_brH and O_tH in the semi-dissociated system stabilize the dissociated structure and inhibit recombination of O_brH/O_tH pairs. Moreover, the dissociation of water with a lowered reaction barrier, induced by HBs, leads to spatial isolation of the O_brH and O_tH species, further preventing their recombination. NAMD simulations show that capture of photogenerated holes in the semi-dissociated system is significantly accelerated compared to in the monolayer system and occurs on a femtosecond timescale. This is primarily attributed to the enhanced nonadiabatic coupling between adjacent states. The electron-vibrational interaction analysis reveals that hole capture is mainly promoted by high-frequency vibration modes that are activated after the initial semi-dissociation. The stronger electron–phonon coupling and enhanced high-frequency vibrational modes accelerate energy relaxation leading to the photogenerated hole capture. Our study emphasizes the importance of intermediates during the photocatalytic water dissociation process on metal oxide surfaces.

2. Computational methods

A 2 × 1 supercell comprised of five layers of rutile TiO₂ (O–Ti–O) is constructed as our model for water splitting. To eliminate dangling bonds, pseudo-hydrogens were added to saturate the bottom Ti and O atoms, with assigned charges of +1.33e and +0.66e, respectively, based on the previous work.^39,43 The calculated rutile TiO₂(110) surface model has lattice parameters of a = 5.93 Å, b = 6.57 Å, and c = 30.70 Å. The model consists of 64 atoms, including 40 oxygen atoms, 20 titanium atoms, and 4 pseudo-hydrogens. A 15 Å vacuum layer was added perpendicular to the surface to eliminate interactions introduced by the periodic arrangement.

The geometry optimization, electronic structure calculations, and adiabatic molecular dynamics simulations were performed using the Vienna Ab initio Simulation Package (VASP) software.⁴⁴ The Perdew–Burke–Ernzerhof (PBE)⁴⁵ functional was employed to handle the electronic correlation and exchange energy, and the interaction between valence electrons and atomic cores was described using the Projected Augmented Wave (PAW)^46–48 pseudopotentials. The energy cutoff for the plane wave basis was set to 500 eV. The DFT-D3 method⁴⁹ was employed to describe the weak van der Waals interactions. Geometry optimization and electronic structure calculations were performed using 3 × 3 × 1 and 6 × 6 × 1 Monkhorst–Pack k-point grids,⁵⁰ respectively. The search for the minimum energy paths and transition state optimizations for the dissociation of water molecules were performed using the Climbing Image Nudged Elastic Band (CI-NEB)⁵¹ method. In all calculations, the energy convergence criterion for the electronic self-consistent field was 10⁻⁵ eV, and the structures were fully optimized until the ionic forces were less than 0.02 eV Å⁻¹. After obtaining the optimized geometry at 0 K, the system was heated to 200 K using velocity rescaling. Subsequently, a 12 ps adiabatic molecular dynamics trajectory was obtained in the microcanonical ensemble with a time step of 1 fs. To simulate the quantum dynamics of the capture of photogenerated holes by H₂O, 1000 structures were selected from the 12 ps trajectory as initial structures for the NAMD simulation. The NAMD simulations were carried out using fewest switches surface hopping (FSSH) implemented within the time-dependent Kohn–Sham theory.^52–54 This method has been proven to be reliable in simulating the dynamics of photogenerated charge carriers in various condensed-phase materials and systems.^55–70

3. Results and discussion

3.1 Geometric structure

The dissociation of water molecules on the TiO₂ surface is an endothermic reaction. Water molecules are more likely to adsorb on the five coordinated Ti atoms (Ti_5c) on the surface as intact molecules, forming a Ti_5c–*OH₂ structure. The dissociated *OH and *H tend to recombine and regenerate water molecules, as observed in the experiments.³⁴ We studied adsorption of a water monolayer on the p-rutile TiO₂(110) surface. Our model includes adsorption of one water molecule on each surface Ti_5c site, with an adjacent water molecule interacting with the first one by IHB and forming HBs with the bridging oxygen atoms on the surface, as shown in Fig. 1a and b. Fig. 1c and d demonstrate that dissociation of the water molecule in the monolayer system leads to formation of a semi-dissociated structure with surface adsorbed H₂O–O_tH species. After water molecule dissociation, the length of the IHB in the semi-dissociated structure decreases from 2.11 Å to 1.71 Å, indicating that the IHB strength increases. The IHB facilitates the dissociation of H₂O, making the adsorption of water on TiO₂ stronger. Compared to the non-dissociated monolayer system, the length of the bonds between Ti and O_w (oxygen atoms in water) are significantly reduced in the semi-dissociated system. In particular, the Ti–O_w1 bond length is reduced by 0.33 Å. This indicates that the dissociation of a water molecule in the monolayer system enhances stability of the water adsorption on the TiO₂ surface. The IHBs between H₂O and O_tH in the semi-dissociated system play a crucial role in stabilizing the O_brH and O_tH pairs, and further facilitates the dissociation of H₂O.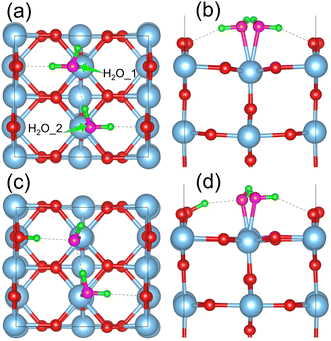

Fig. 1 Top and side views of water molecules adsorbed on the p-rutile TiO₂(110) surface in (a and b) monolayer and (c and d) semi-dissociated forms. The two water molecules are labeled as H₂O_1 and H₂O_2 in part (a). The side views in (b) and (d) only show the top two O–Ti–O layers. Fig. S1† presents 2 × 2 supercells to demonstrate the adsorption structures more clearly. The light blue and red balls represent the Ti and O atoms in TiO₂, respectively, while the pink and green balls represent the O and H atoms in water molecules, respectively. The visualization is achieved with the VESTA software.⁷¹

In practical TiO₂ photocatalytic water splitting systems, the TiO₂ surface typically has multiple layers of adsorbed water molecules, forming a more complex HB network. In such cases, the monolayer adsorption structure on the TiO₂ surface is augmented by additional IHBs. We chose monolayer water adsorption on the TiO₂ surface as our study model for the following reasons. First, stable monolayer water adsorption structures have been observed experimentally on both rutile and anatase TiO₂ surfaces.^72,73 This provides a direct connection between our work and the experiment. Second, the monolayer water adsorption model provides a simple and efficient model to study the effect of IHBs on the dissociation of water molecules and hole capture on TiO₂.

3.2 Dissociation of H₂O on rutile TiO₂(110)

The dissociation barrier is a critical factor for assessing the dissociation efficiency of water. To evaluate the effect of hydrogen bonding on water dissociation, we calculated the dissociation barriers for water molecules in both the non-hydrogen bonded (monomer adsorption) system and the monolayer system, as shown in Fig. 2a. The dissociation barrier of a water molecule in a monomer adsorption system is 0.26 eV, in agreement with the previous reports of ∼0.3 eV.^19,74 It is noteworthy that the reverse dissociation barrier is only 0.09 eV, and the low barrier implies that the O_brH/O_tH pairs tend to recombine to regenerate water molecules. This phenomenon, known as “pseudo-dissociation” in previous literature, is a crucial factor limiting the efficiency of water dissociation on the p-rutile TiO₂(110) surface.^34,35 Compared to the dissociation of a water molecule in a monomer adsorption system, the dissociation barrier of a water molecule in the monolayer system is reduced to 0.21 eV, indicating that the IHBs make the dissociation more favorable. The reverse barrier for the O_brH/O_tH pairs to recombine is 0.11 eV, slightly increased compared to that of the monomer adsorption system. This suggests that the HB between H₂O and O_tH can inhibit the recombination of O_brH/O_tH pairs to some extent.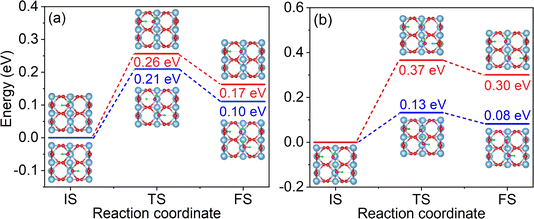

Fig. 2 (a) Minimum energy pathways for water dissociation on p-rutile TiO₂(110) for a non-hydrogen bonded system (monomer adsorption system) (red line) and monolayer water molecule adsorption (blue line). (b) Two pathways for H₂O_2 molecule dissociation in the semi-dissociated system. One pathway is the dissociation of H₂O_2 to form O_tH and O_brH, and the other pathway is induced by IHB between O_tH and H₂O_2. Fig. S2† shows enlarged views of the initial state (IS), transition state (TS), and final state (FS) structures.

As shown in Fig. 2b, there are two possible water dissociation pathways in the semi-dissociated system. One pathway leads to the formation of O_brH on O_br, with a dissociation barrier as high as 0.37 eV (red line). The other pathway involves dissociation of the H₂O_2 molecule induced by the HB between O_tH and H₂O_2. The dissociation barrier for the second pathway is much lower, 0.13 eV (blue line), making the dissociation of water molecules much more likely. Importantly, the dissociation of H₂O_2 induced by the IHB leads to spatial isolation of O_brH and O_tH, effectively preventing their recombination.

3.3 Dynamic structure induced by water dissociation on rutile TiO₂(110)

Fluctuations in bond lengths in AIMD simulations characterize the motion of H atoms, revealing the stability of the dissociated structure after water molecule dissociation. Fig. 3 presents distributions of lengths of the O_brH bond and the IHB in the monolayer and semi-dissociated systems over the 12 ps MD trajectory. Fig. 3a shows that the O_brH bond lengths in the monomer adsorption system range from 1.4 Å to 2.1 Å, with the peak at around 1.7 Å. The typical bond length of a hydroxyl group is in the 0.96 Å to 1.02 Å range. The calculated values are significantly larger, indicating that the O_brH bond is highly unstable and that the hydrogen atom in O_brH returns to the oxygen atom in O_tH. The AIMD trajectory reveals that the O_brH/O_tH pair undergoes fast recombination within 0.2 ps, as shown in Fig. S3.† This is consistent with the experiments showing that O_brH/O_tH pairs rapidly disappear in the pseudo-dissociated state.³⁴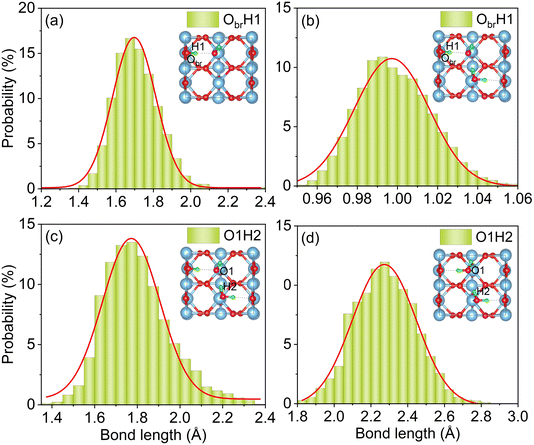

Fig. 3 Probability distributions of O_brH bond lengths in (a) a single water molecule and (b) monolayer systems, and IHB lengths (c) after and (d) before water dissociation in the monolayer system.

In contrast, the distribution of the O_brH bond lengths in the semi-dissociated structure, as shown in Fig. 3b, formed after dissociation of a water molecule in the monolayer system, ranges from 0.96 Å to 1.04 Å, which is typical for the hydroxyl bond length. Thus, the H atom produced after water dissociation can be stably adsorbed on O_br. The evolutions of the O_brH and O_tH bond lengths during the AIMD trajectory are shown in Fig. S4,† indicating that the dissociated water molecule in the monolayer system did not undergo recombination. The lengths of the IHBs reflect the bond strength: as the IHB length decreases, the IHB strength increases. Compared to the monolayer system, as shown in Fig. 3d, the IHB in the semi-dissociated system is significantly shorter, primarily distributed at around 1.75 Å, as shown in Fig. 3c. This indicates a significant enhancement in the IHB strength between O_tH and H₂O_2. Although the strengthening of the IHB between O_tH and H₂O_2 in the semi-dissociated system did not induce a permanent intermolecular proton transfer, the increased HB strength stabilized the O_brH/O_tH pairs and suppressed the O_brH/O_tH pair recombination in the pseudo-dissociated state.

As shown in Fig. 3c and d, the dissociation of H₂O enhances the strength of IHB, which in turn promotes the dissociation of H₂O_2. The dissociation energy barrier induced by IHB is only 0.13 eV. Fig. S5† shows the evolution of the H–O bond length in H₂O_2 in both the monolayer and semi-dissociated systems during the MD process. It can be observed that the H–O bond length increases in the semi-dissociated system due to the enhanced IHB. An increase in the bond length indicates a weakening of the bond, making the H–O bond more prone to dissociation, rationalizing the significantly reduced energy barrier for dissociation of H₂O_2 induced by IHB. Additionally, Fig. 3 demonstrates that the O–H bond length fluctuates more in the semi-dissociated system compared to the monolayer system. The enhanced movement of H atoms is accompanied by a stronger electron-vibrational coupling in the system, accelerating relaxation and capture of holes by H₂O_2. Chu et al. discovered through both theoretical and experimental studies that methanol molecules adsorbed on the TiO₂ surface significantly enhance the ability to capture excited state holes due to the quantized motion of protons, thereby improving the efficiency of the photochemical reaction.⁷⁵ Overall, the increased IHB strength in the semi-dissociated system leads to higher efficiency of water dissociation, according to our thermodynamic analysis, and accelerated capture of photogenerated holes, according to our kinetic analysis.

3.4 Electronic structure

Fig. 4a and b display the projected density of states (PDOS) for the monolayer and semi-dissociated systems, respectively. Although computationally efficient, the PBE DFT functional mistreats electron–electron interactions among d electrons in strongly correlated systems, and as a result, underestimates the TiO₂ band gap. To correct the band gap, we refer to prior experimental and theoretical studies and introduce a “scissor operator” expanding the gap to match the experimental value.^77–79 We determined the locations of the highest occupied molecular orbital (HOMO) of water in the monolayer and semi-dissociated systems by studying charge density distributions of the electronic states. The positions of the HOMO energy levels are presented by red arrows in Fig. 4a and b, and the corresponding charge densities are presented on the right side of the figure, in particular, depicting the O_p orbital features of the water HOMOs. Water molecule dissociation has an impact on the position of the HOMO energy level. Compared to the monolayer system, as shown in Fig. 4a, the water HOMO energy level shifts by 0.3 eV towards the valence band maximum in the semi-dissociated system, as shown in Fig. 4b, and the H₂O contribution to the DOS increases in this energy range. More advanced electronic structure methods, e.g., hybrid functionals, should exhibit qualitatively similar results. The charge density plots also show higher charge (hole) density on the adsorbed water molecules in the semi-dissociated system, which facilitates trapping of photogenerated holes and subsequent dissociation of water molecules.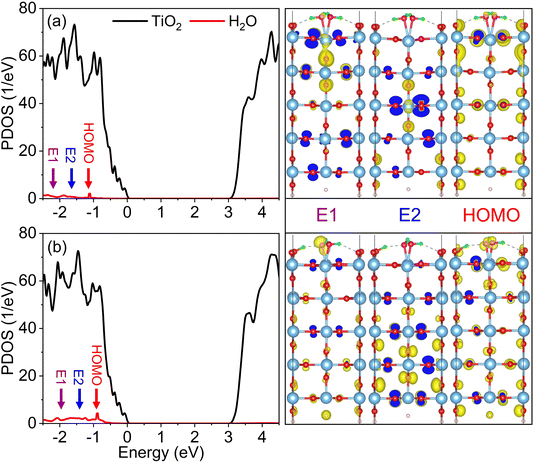

Fig. 4 PDOSs for (a) monolayer and (b) semi-dissociated systems. The PDOS of water is doubled for clarity. The purple, blue, and red arrows indicate the high (E1) and low energy (E2) photogenerated hole states, and the HOMO energy level. The charge densities are visualized with the VASPKIT and VESTA software.^71,76

3.5 Hole capture and energy relaxation dynamics

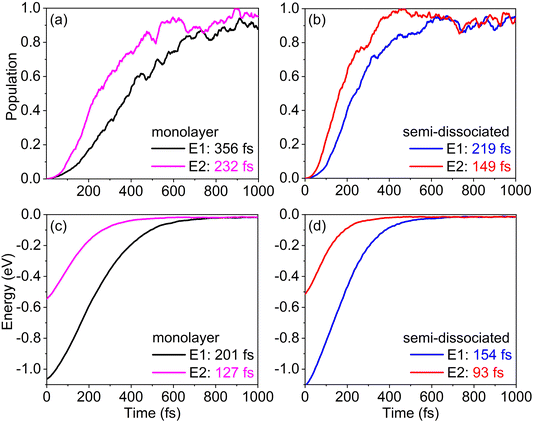
The capture of photogenerated holes is a key factor in driving the dissociation of surface water molecules.^30,80–83 The rate of hole capture determines the efficiency of water molecule dissociation on the rutile TiO₂(110) surface. With the HOMO energy level of water serving as the hole acceptor, we study hole capture dynamics starting with the hole at higher and lower energies in TiO₂, 1.0 eV and 0.5 eV above the water HOMO level, E1 and E2, respectively. Fig. 5a and b present the dynamics of hole capture by the HOMO of water in the monolayer and semi-dissociated systems, respectively. We employed a Gaussian function, P(t) = 1 − exp[−0.5 × (−t/τ)²], to fit the curves and obtain time scales of the photogenerated hole capture. The data shown in Fig. 5a and b demonstrate that if the hole starts at a lower energy, its capture is faster, and importantly, that hole capture is notably faster in the semi-dissociated system than the monolayer system, 219 fs vs. 356 fs for the higher initial energy condition, and 149 fs vs. 232 fs for the lower initial energy. This implies that the semi-dissociated system not only effectively suppresses the recombination of O_brH and O_tH pairs, but also accelerates hole capture, thereby promoting the subsequent rapid dissociation of H₂O. During the relaxation of the hole from a TiO₂ donor state to the water HOMO level, the photogenerated hole loses energy through coupling with phonons. As shown in Fig. 5c and d, the relaxation of energy in the monolayer and semi-dissociated systems occurs within 100–200 fs, faster than the corresponding hole capture. Thus, holes lose significant amounts of energy before transferring to H₂O, forming holes that are not “sufficiently hot”. The insufficiently hot holes may not have enough energy for oxidation of water molecules, which can be another factor restricting the oxidation of water on rutile TiO₂(110).

Fig. 5 (a and b) Dynamics of hole capture by the water HOMO in the monolayer and semi-dissociated systems, respectively. E1 and E2 represent high- and low-energy photogenerated hole donor states. (c and d) Energy relaxation processes in the monolayer and semi-dissociated systems, with E1 and E2 as the initial states.

The hole capture process involves transitions between adiabatic electronic states, induced by nonadiabatic coupling (NAC). NAC induces energy exchange between the electronic and vibrational subsystems, and the rate of electron-vibrational energy exchange leading to hole capture is determined by using the NAC magnitude. NAC is defined as d_ij = −iℏ〈φ_i|∇_R|φ_j〉·Ṙ, and it is a scalar product of the electronic matrix element of the atomic gradient vector operator, 〈φ_i|∇_R|φ_j〉, and the atomic velocity, Ṙ. Therefore, the magnitude of NAC depends on the overlap of wave functions between orbitals and the extent of atomic motion. Fig. S5† demonstrates that H atoms fluctuate much more in the semi-dissociated system than the monolayer system, rationalizing the larger NAC and faster hole capture.

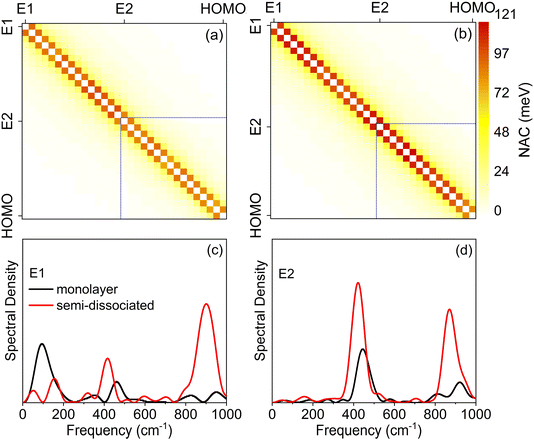
Fig. 6a and b present two-dimensional heat maps of the average absolute NAC between electronic states involved in the hole capture process for the monolayer and semi-dissociated systems, respectively. The deeper the color, the stronger the NAC. The NAC is the strongest between adjacent states, followed by the next nearest states. The stronger NAC between adjacent states implies that hole relaxation and capture is a sequential process, i.e., the hole hops down in energy through the manifold of TiO₂ states before being captured by the water HOMO. The NAC is stronger in the semi-dissociated system than the monolayer system. This is because the vigorous movement of H atoms in the semi-dissociated system generates larger NAC (as shown in Fig. S5†). Table 1 summarizes the energy ranges and the averaged absolute NACs for the hole capture processes starting from the higher, E1 and lower, E2 energies in TiO₂ to the water HOMO. The larger NAC in the semi-dissociated system explains the faster hole transfer (E1 to HOMEO: 14.19 meV vs. 16.75 meV and E2 to HOMO: 23.06 meV vs. 30.13 meV), quantitatively rationalizing why water molecules in the semi-dissociated system can capture photogenerated holes more quickly, Fig. 5.

Fig. 6 (a and b) Average absolute NACs between pairs of electronic states involved in hole relaxation in the monolayer and semi-dissociated systems, respectively. (c and d) Spectral densities obtained from FTs of unnormalized autocorrelation functions for the fluctuation of energy gaps between the donor states (E1 and E2) and the acceptor state (water HOMO).

Table 1 Energy range and average absolute NACs for hole transfer from E1 and E2 in TiO₂ to the water HOMO in the monolayer and semi-dissociated systems

System	E1-HOMO		E2-HOMO
	Energy range (eV)	NAC (meV)	Energy range (eV)	NAC (meV)
Monolayer	1.06	14.19	0.54	23.06
Semi-dissociated	1.11	16.75	0.51	30.13

---

Spectral density plots, shown in Fig. 6c and d, identify vibrational modes that couple to the electronic subsystem, accommodate the excess energy released during hole relaxation and facilitate hole transfer. The spectral densities corresponding to the hole transfer process are obtained by Fourier transforms (FTs) of the unnormalized autocorrelation functions of the energy gap fluctuations between the hole donor and acceptor states. The locations of the peaks in the spectral densities identify frequencies of the active vibrations, while the intensities of the peaks represent the strength of the electron–phonon coupling to the vibration at the corresponding frequency. At a given temperature, higher frequency vibrational modes generate faster atomic velocities, creating larger NAC, and larger NAC accelerates electron-vibrational energy exchange and hole capture. The spectral densities demonstrate that the hole transfer is primarily coupled with high-frequency vibrations, and that low-frequency vibrations have relatively small contributions to hole transfer. The peak at around 150 cm⁻¹ corresponds to the B_1g vibration of TiO₂ and the vibration of H_br,⁸⁴ while the peak at around 400 cm⁻¹ represents the E_g mode arising from the stretching vibration of O–Ti–O.^85,86 The peak near 900 cm⁻¹ corresponds to the bending motion of water molecules.⁸⁷ As shown in Fig. 6c for the higher initial energy TiO₂ state E1, the semi-dissociated system exhibits a stronger high-frequency electron–phonon coupling, especially near 900 cm⁻¹, enhancing the NAC between E1 and the acceptor state. For the lower initial energy state E2, as shown in Fig. 6d, hole transfer is driven only by the high-frequency vibrations near 400 cm⁻¹ and 900 cm⁻¹. Low-frequency contributions are insignificant in this case. The signals at both 400 cm⁻¹ and 900 cm⁻¹ are stronger for the semi-dissociated system than the monolayer system. The stronger signals seen in the spectral densities correspond to the larger NAC, and rationalize faster hole relaxation and capture in the semi-dissociated system. Overall, for the relaxation of high energy (E1) and low energy (E2) initial excited state holes, the stronger high-frequency vibrational modes coupled to the hole relaxation process in the semi-dissociated system generate larger NAC. This accelerates the capture of photogenerated holes by water molecules, thereby improving the oxidation efficiency of water.

4. Conclusion

In summary, the quantum dynamics of water dissociation and capture of photogenerated holes by a water monolayer and an isolated water molecule adsorbed on the rutile TiO₂(110) surface were studied using the DFT, real-time TD-DFT, and NAMD methods. DFT calculations indicate that IHBs between water molecules lower the barrier of water molecule dissociation, facilitating the process. AIMD results demonstrate that strengthening of IHBs in the semi-dissociated system stabilizes the dissociated structure, and inhibits recombination of O_brH/O_tH pairs. Furthermore, IHBs facilitate spatial isolation of O_brH/O_tH pairs, breaking the “pseudo-dissociated” state.

NAMD simulations reveal that the capture of photogenerated holes is significantly accelerated in the semi-dissociated system compared to the pristine system. The hole capture time is reduced by 36%, primarily due to the enhanced NAC between neighboring electronic states. The fast hole capture implies a higher dissociation efficiency for subsequent water splitting, which is a key factor for improving the yield of photocatalyzed splitting of water on TiO₂. Stronger coupling of holes to high-frequency vibrations and additional active high-frequency vibrational modes in the semi-dissociated structure contribute to the accelerated capture of photogenerated holes as well. None of these effects are observed for isolated water molecules on TiO₂.

The findings reported in this work are expected to apply to other metal oxide surfaces, such as RuO₂ and SrTiO₃, especially for recognizing the importance of IHB in the hole capture and water dissociation processes. Water adsorption structures in other classes of materials, such as metal nitrides and carbon nitrides, are likely to differ from those in metal oxides. Still, IHB should play a key role there as well. Related phenomena can take place in other cases, such as the photocatalytic oxidation of CH₃OH on TiO₂ surfaces. Capture of photogenerated holes depends on the properties of the CH₃O⁻ intermediate formed after CH₃OH dissociation, and the HB should also be a significant factor influencing the capture of photogenerated holes in CH₃OH. Future theoretical studies can focus on modeling ultrafast chemical reactions induced by photogenerated holes. For this purpose, one can employ the impulsive two-state method.^39,42 Additional modeling studies on other classes of material systems and with other molecules are required in order to establish the generality of the conclusions reported in this work, and to formulate common theoretical principles underlying atomistic dynamics of photocatalytic reactions. Experimental studies combining spatial and temporal resolutions, e.g., using scanning tunneling microscopy and time-resolved spectroscopy, can provide important data to test and verify theoretical work and create new insights for constructing a detailed and comprehensive picture of water photolysis and related photocatalytic reactions.

Our work offers a detailed investigation of surface reaction kinetics and photogenerated hole capture dynamics during the dissociation of water adsorbed on p-rutile TiO₂(110) surfaces. By exploring the role of special intermediates in photocatalyzed water splitting, our work deepens understanding of the complex reactions occurring on metal oxide surfaces.

Data availability

The data that support the findings of this study are available from the corresponding author, RL, upon reasonable request.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by the National Natural Science Foundation of China, grant no. 92372121. R. L. acknowledges the Fundamental Research Funds for the Central Universities. C. C. acknowledges financial support by the Guangdong Basic and Applied Basic Research Foundation (no. 2023A1515110101). O. V. P. acknowledges support of the US National Science Foundation (grant CHE-2154367).

References

1. J. O. Abe, A. Popoola, E. Ajenifuja and O. M. Popoola, Int. J. Hydrogen Energy, 2019, 44, 15072–15086.
2. S. Nandy, T. Hisatomi, T. Takata, T. Setoyama and K. Domen, J. Mater. Chem. A, 2023, 11, 20470–20479.
3. F. Xu and B. Weng, J. Mater. Chem. A, 2023, 11, 4473–4486.
4. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
5. J. S. Schubert, J. Popovic, G. M. Haselmann, S. P. Nandan, J. Wang, A. Giesriegl, A. S. Cherevan and D. Eder, J. Mater. Chem. A, 2019, 7, 18568–18579.
6. X. Ma, Y. Shi, J. Liu, X. Li, X. Cui, S. Tan, J. Zhao and B. Wang, J. Am. Chem. Soc., 2022, 144, 13565–13573.
7. X. Zhang, C. Bo, S. Cao, Z. Cheng, Z. Xiao, X. Liu, T. Tan and L. Piao, J. Mater. Chem. A, 2022, 10, 24381–24387.
8. J. Tang, J. R. Durrant and D. R. Klug, J. Am. Chem. Soc., 2008, 130, 13885–13891.
9. J.-Q. Li, Y. Sun and J. Cheng, J. Mater. Chem. A, 2023, 11, 943–952.
10. J. Lian, K. Shibata, Y. Xiao, S. Du, T. Tanaka, Y. Qi, O. Ishitani, K. Maeda, Z. Feng and F. Zhang, J. Mater. Chem. A, 2023, 11, 141–148.
11. Q. Guo, Z. Ma, C. Zhou, Z. Ren and X. Yang, Chem. Rev., 2019, 119, 11020–11041.
12. J. Yan, Y. Zhang, S. Liu, G. Wu, L. Li and N. Guan, J. Mater. Chem. A, 2015, 3, 21434–21438.
13. R. Schaub, P. Thostrup, N. Lopez, E. Lægsgaard, I. Stensgaard, J. K. Nørskov and F. Besenbacher, Phys. Rev. Lett., 2001, 87, 266104.
14. O. Bikondoa, C. L. Pang, R. Ithnin, C. A. Muryn, H. Onishi and G. Thornton, Nat. Mater., 2006, 5, 189–192.
15. J. Lee, D. C. Sorescu, X. Deng and K. D. Jordan, J. Phys. Chem. Lett., 2013, 4, 53–57.
16. H. Hussain, G. Tocci, T. Woolcot, X. Torrelles, C. Pang, D. Humphrey, C. Yim, D. Grinter, G. Cabailh and O. Bikondoa, Nat. Mater., 2017, 16, 461–466.
17. P. J. Lindan, N. Harrison and M. Gillan, Phys. Rev. Lett., 1998, 80, 762–765.
18. C. Zhang and P. J. Lindan, J. Chem. Phys., 2003, 118, 4620–4630.
19. P. J. Lindan and C. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075439.
20. R. Schaub, E. Wahlstrom, A. Rønnau, E. Lægsgaard, I. Stensgaard and F. Besenbacher, Science, 2003, 299, 377–379.
21. L. A. Harris and A. A. Quong, Phys. Rev. Lett., 2004, 93, 086105.
22. Y. Ji, B. Wang and Y. Luo, J. Phys. Chem. C, 2012, 116, 7863–7866.
23. J. Chen, C. Penschke, A. Alavi and A. Michaelides, Phys. Rev. B, 2020, 101, 115402.
24. S. Selcuk and A. Selloni, Nat. Mater., 2016, 15, 1107–1112.
25. I. Brookes, C. Muryn and G. Thornton, Phys. Rev. Lett., 2001, 87, 266103.
26. L. Walle, D. Ragazzon, A. Borg, P. Uvdal and A. Sandell, Surf. Sci., 2014, 621, 77–81.
27. M. A. Henderson, Surf. Sci., 1996, 355, 151–166.
28. L. Walle, A. Borg, P. Uvdal and A. Sandell, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235436.
29. R. L. Kurtz, R. Stock-Bauer, T. E. Msdey, E. Román and J. De Segovia, Surf. Sci., 1989, 218, 178–200.
30. S. Tan, H. Feng, Y. Ji, Y. Wang, J. Zhao, A. Zhao, B. Wang, Y. Luo, J. Yang and J. Hou, J. Am. Chem. Soc., 2012, 134, 9978–9985.
31. L.-M. Liu, C. Zhang, G. Thornton and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 161415.
32. W. Yang, D. Wei, X. Jin, C. Xu, Z. Geng, Q. Guo, Z. Ma, D. Dai, H. Fan and X. Yang, J. Phys. Chem. Lett., 2016, 7, 603–608.
33. W. Zhang, J. Yang, Y. Luo, S. Monti and V. Carravetta, J. Chem. Phys., 2008, 129, 064703.
34. Y. Du, N. A. Deskins, Z. Zhang, Z. Dohnálek, M. Dupuis and I. Lyubinetsky, J. Phys. Chem. C, 2009, 113, 666–671.
35. S. Wendt, J. Matthiesen, R. Schaub, E. K. Vestergaard, E. Lægsgaard, F. Besenbacher and B. Hammer, Phys. Rev. Lett., 2006, 96, 066107.
36. W. Langel, Surf. Sci., 2002, 496, 141–150.
37. J. Matthiesen, J. Hansen, S. Wendt, E. Lira, R. Schaub, E. Lægsgaard, F. Besenbacher and B. Hammer, Phys. Rev. Lett., 2009, 102, 226101.
38. B. Hammer, S. Wendt and F. Besenbacher, Top. Catal., 2010, 53, 423–430.
39. C. Cheng, O. V. Prezhdo, R. Long and W.-H. Fang, J. Am. Chem. Soc., 2022, 145, 476–486.
40. G. Kolesov, D. Vinichenko, G. A. Tritsaris, C. M. Friend and E. Kaxiras, J. Phys. Chem. Lett., 2015, 6, 1624–1627.
41. P. You, D. Chen, X. Liu, C. Zhang, A. Selloni and S. Meng, Nat. Mater., 2024, 23, 1100–1106.
42. W. Chu, Q. Zheng, O. V. Prezhdo and J. Zhao, J. Am. Chem. Soc., 2020, 142, 3214–3221.
43. W. Chu, W. A. Saidi, Q. Zheng, Y. Xie, Z. Lan, O. V. Prezhdo, H. Petek and J. Zhao, J. Am. Chem. Soc., 2016, 138, 13740–13749.
44. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
47. W. Chu, Q. Zheng, A. V. Akimov, J. Zhao, W. A. Saidi and O. V. Prezhdo, J. Phys. Chem. Lett., 2020, 11, 10073–10080.
48. W. Chu and O. V. Prezhdo, J. Phys. Chem. Lett., 2021, 12, 3082–3089.
49. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
50. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
51. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
52. J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071.
53. S. A. Fischer, B. F. Habenicht, A. B. Madrid, W. R. Duncan and O. V. Prezhdo, J. Chem. Phys., 2011, 134, 024102.
54. C. F. Craig, W. R. Duncan and O. V. Prezhdo, Phys. Rev. Lett., 2005, 95, 163001.
55. Y. Wei, W.-H. Fang, Q. Fang and R. Long, J. Phys. Chem. C, 2018, 122, 7041–7050.
56. X. Wang and R. Long, J. Phys. Chem. Lett., 2021, 12, 7553–7559.
57. X. Wang and R. Long, J. Phys. Chem. Lett., 2021, 12, 2763–2769.
58. Y. Wei, L. Li, W. Fang, R. Long and O. V. Prezhdo, Nano Lett., 2017, 17, 4038–4046.
59. D. Liu, Y. Wu, A. S. Vasenko and O. V. Prezhdo, Nanoscale, 2023, 15, 285–293.
60. X. Zhao, A. S. Vasenko, O. V. Prezhdo and R. Long, J. Phys. Chem. Lett., 2022, 13, 11375–11382.
61. D. Liu, Y. Wu, M. R. Samatov, A. S. Vasenko, E. V. Chulkov and O. V. Prezhdo, Chem. Mater., 2024, 36, 2898–2906.
62. K. Hyeon-Deuk and O. V. Prezhdo, ACS Nano, 2012, 6, 1239–1250.
63. V. V. Chaban, V. V. Prezhdo and O. V. Prezhdo, J. Phys. Chem. Lett., 2013, 4, 1–6.
64. L. Zhang, A. S. Vasenko, J. Zhao and O. V. Prezhdo, J. Phys. Chem. Lett., 2019, 10, 1083–1091.
65. L. Qiao, W. H. Fang, R. Long and O. V. Prezhdo, Angew. Chem., 2020, 132, 4714–4720.
66. R. Long, O. V. Prezhdo and W. Fang, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, 1–29.
67. Z. Zhang, L. Liu, W.-H. Fang, R. Long, M. V. Tokina and O. V. Prezhdo, Chem, 2018, 4, 1112–1127.
68. C. Cheng, W.-H. Fang, R. Long and O. V. Prezhdo, JACS Au, 2021, 1, 550–559.
69. S. Agrawal, B. Wang, Y. Wu, D. Casanova and O. V. Prezhdo, Nanoscale, 2024, 16, 8986–8995.
70. X. Ma, W.-H. Fang, R. Long and O. V. Prezhdo, J. Am. Chem. Soc., 2024, 146, 16314–16323.
71. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
72. G. A. Kimmel, M. Baer, N. G. Petrik, J. VandeVondele, R. Rousseau and C. J. Mundy, J. Phys. Chem. Lett., 2012, 3, 778–784.
73. C. Dette, M. A. Pérez-Osorio, S. Mangel, F. Giustino, S. J. Jung and K. Kern, J. Phys. Chem. C, 2018, 122, 11954–11960.
74. Q. Guo, C. Xu, Z. Ren, W. Yang, Z. Ma, D. Dai, H. Fan, T. K. Minton and X. Yang, J. Am. Chem. Soc., 2012, 134, 13366–13373.
75. W. Chu, S. Tan, Q. Zheng, W. Fang, Y. Feng, O. V. Prezhdo, B. Wang, X.-Z. Li and J. Zhao, Sci. Adv., 2022, 8, eabo2675.
76. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
77. D. C. Cronemeyer, Phys. Rev., 1952, 87, 876–886.
78. L. Lin, S. Mo and D. Lin, J. Phys. Chem. Solids, 1993, 54, 907–912.
79. C. Cheng, Y. Zhu, W.-H. Fang, R. Long and O. V. Prezhdo, JACS Au, 2021, 2, 234–245.
80. H. Zhou, X. Zhang, J. Zhang, H. Ma, F. Jin and Y. Ma, J. Mater. Chem. A, 2021, 9, 7650–7655.
81. G. A. Tritsaris, D. Vinichenko, G. Kolesov, C. M. Friend and E. Kaxiras, J. Phys. Chem. C, 2014, 118, 27393–27401.
82. H. Sun, D. J. Mowbray, A. Migani, J. Zhao, H. Petek and A. Rubio, ACS Catal., 2015, 5, 4242–4254.
83. J. Chen, Y.-F. Li, P. Sit and A. Selloni, J. Am. Chem. Soc., 2013, 135, 18774–18777.
84. G. C. Vásquez, D. Maestre, A. Cremades and J. Piqueras, J. Raman Spectrosc., 2017, 48, 847–854.
85. O. Frank, M. Zukalova, B. Laskova, J. Kürti, J. Koltai and L. Kavan, Phys. Chem. Chem. Phys., 2012, 14, 14567–14572.
86. E. Shojaee and M. Mohammadizadeh, J. Phys.: Condens. Matter, 2009, 22, 015401.
87. S. A. Fischer, W. R. Duncan and O. V. Prezhdo, J. Am. Chem. Soc., 2009, 131, 15483–15491.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta04750h

---