The effect of the halogen on the structural, optoelectronic, and luminescent properties of hybrid (1,5-pentanediamine)PbX4 (X = Cl, Br, I) perovskites†
D. S.
Shtarev
 *ab,
M. I.
Balanov
ab,
A. Ju.
Major
bc,
A. V.
Gerasimenko
d,
R.
Kevorkyants
*ab,
M. I.
Balanov
ab,
A. Ju.
Major
bc,
A. V.
Gerasimenko
d,
R.
Kevorkyants
 e,
D. A.
Zharovov
e,
D. A.
Zharovov
 e,
K. M.
Bulanin
f,
D. V.
Pankin
fg,
A. V.
Rudakova
e,
K. M.
Bulanin
f,
D. V.
Pankin
fg,
A. V.
Rudakova
 f,
D. A.
Chaplygina
b,
N. I.
Selivanov
f,
D. A.
Chaplygina
b,
N. I.
Selivanov
 e and
A. V.
Emeline
e
e and
A. V.
Emeline
e
aDepartment of Materials Science, Shenzhen MSU-BIT University, Shenzhen, People's Republic of China. E-mail: shtarev@mail.ru; balanov.mi@dvfu.ru
bInstitute of High Technologies and Advanced Materials of the Far Eastern Federal University, Russky Island, Ajax, 10, Vladivostok, 690022, Russian Federation. E-mail: mayor@iacp.dvo.ru; chaplygina.dal@dvfu.ru
cInstitute of Automation and Control Processes, Far Eastern Branch, Russian Academy of Sciences, Vladivostok, Russian Federation
dInstitute of Chemistry, Far Eastern Branch, Russian Academy of Sciences, Vladivostok, Russian Federation. E-mail: gerasimenko@ich.dvo.ru
eSaint-Petersburg State University, Laboratory Photoactive Nanocomposite Materials, Saint-Petersburg, Russian Federation. E-mail: ruslan.kevorkyants@gmail.com; dmzharovov@gmail.com; selivanov_chem@mail.ru; alexei.emeline@spbu.ru
fSaint-Petersburg State University, Laboratory Photonics of Crystals, Saint-Petersburg, Russian Federation. E-mail: k.bulanin@spbu.ru; dmitrii.pankin@spbu.ru; aida.rudakova@spbu.ru
gSaint-Petersburg State University, Center for Optical and Laser Materials Research, Saint-Petersburg, Russian Federation
First published on 27th November 2023
Abstract
The present work reports on the experimental structures, and optoelectronic and luminescence properties of a series of low-dimensional hybrid organic–inorganic (1,5-pentanediamine) PbX4 (X = Cl, Br, I) perovskites. Single-crystal XRD data revealed that the chloride and bromide compounds form quasi 2D perovskite-like structures, whereas the iodide is a quasi 1D compound. In accordance with the experiment, DFT modeling predicts that the chloride and bromide are direct bandgap semiconductors. In contrast, the iodide is an indirect bandgap semiconductor. The experimentally and theoretically established bandgap widths of the perovskites follow the same trend. Finally, the luminescent properties of the perovskites were investigated. The study shows that the halogen anions determine the degree of disorder of the perovskite crystal lattices and the degree of distortion of the PbX6 octahedra therein. Both structural phenomena affect the dimensionality, optoelectronic, and luminescent properties of the studied perovskites.
1. Introduction
Hybrid organic–inorganic perovskites or perovskite-like structures (Ruddlesden–Popper, Dion–Jacobson phases) are among the most promising light-transforming materials. They are mainly intended for use in solar panels for a direct transformation of solar radiation into electric current1 or in light-emitting diodes (LEDs) for white light sources, narrow-band light of a specific color, and even for laser generation.2–6 Whereas hybrid 3D perovskites are best suited for photovoltaics, low-dimensional quasi 1D and 2D perovskites can be used in various light-emitting applications.In hybrid quasi 2D halide perovskites the layers of inorganic octahedra MX6 are separated from each other by the layers of organic cations. The latter often represent diamines. Two amino groups of such cations form hydrogen bonds with neighboring layers of inorganic MX6 octahedra. This choice of organic cation is intended to increase the stability of the perovskite crystal.7 The number of organic cations used to form quasi 2D perovskite structures is ever-increasing. At present, several hundreds of them are already known.8
A particular sub-family of low-dimensional hybrid halide perovskites contain alkanediamine cations with terminal amino-groups, i.e. NH3–(CH2)n–NH3. In contrast to hybrid halide perovskites with aromatic organic cations demonstrating a strong interaction of an inorganic electronic subsystem with an organic one, members of this sub-family feature only hydrogen bonding interactions between inorganic and organic subsystems. Their alkyl chain lengths are directly related to the distance between the layers of inorganic MX6 octahedra. However, their electronic and optical properties are not directly affected by the length of the alkyl chain, being governed solely by the inorganic subsystem composition as we have shown recently using 1,6-hexamethylenediaminium perovskite as an example.9
As a rule, quasi 2D hybrid perovskites show complex luminescence properties10 combining narrow-band and broadband luminescence. The narrow-band luminescence is usually attributed to the luminescence of free excitons.11 While still debated, the nature of broadband luminescence is attributed to both the luminescence of autolocalized excitons11 and to the luminescence at crystal lattice defects.12
Generally, the luminescence properties of hybrid low-dimensional perovskites are considered through the prism of the structure of their organic cation (linear,13 branched or cyclic, presence or absence of double bonds, etc.11). Much less attention is paid to the structural role of the halogen.
Here, we focus on haloplumbates with 1,5-pentamethylenediaminium (PDA) cations. It is known that the use of PDA as a cation in the synthesis of hybrid lead iodide perovskite leads to the formation of low-dimensional (quasi 1D) crystals in which chains of the inorganic Pbl6 octahedra are oriented along the [111] crystallographic direction.14 This was the only piece of information one could find in the literature until very recently. More detailed information about the crystal structure, electronic, and optical properties of PDAPbCl4 was reported not that long ago.15 Here, a comparative study of the effect of the halogen on the dimensionality, structure, and optoelectronic, vibrational, and luminescence properties of PDAPbX4 (X = Cl, Br, I) perovskites is conducted.
2. Experimental and modeling techniques
2.1. Synthesis
The samples of PDAPbX4 (X = Cl, Br, I) were prepared using a ‘wet-chemistry’ approach.2.2. Characterization
The powder diffraction data of PDAPbX4 (X = Cl, Br, I) were collected at room temperature using a Colibri powder diffractometer (Bourevestnik, Cu-Kα radiation) and a linear VANTEC detector. The step size of 2θ was 0.02° and the counting time was 35.4 s per step.The full profile X-ray analysis of PDAPbBr4 and PDAPbCl4 single-crystals was performed using a Bruker Kappa Apex II diffractometer with graphite-monochromatized MoKα radiation16 at 100 K. The data reduction and multi-scan absorption correction was carried out using original software.
Diffuse reflectance spectra were recorded in the spectral range 200–800 nm under ambient conditions using a Lambda 950 UV/vis/NIR spectrophotometer. An optical-grade BaSO4 powder was used as a reference standard.
The Raman spectra of the samples (PDAPbBr4 and PDAPbI4 single crystals and PDAPbCl4 powder) were obtained using a Senterra (Bruker) Raman spectrometer equipped with Olympus BX51 microscope in backscattering geometry. The Raman scattering was excited using a 785 nm solid state laser. The laser power under the 20× lens with a 14 μm spot diameter was ∼1 mW. The diffraction grating was 400 L mm−1, and the aperture was 25 × 1000 μm. The accumulation time was 150 s with 6 repetitions.
FTIR spectra of the powdered samples were obtained using a Nicolet 8700 (Thermo Scientific) FTIR spectrometer with ATR diamond accessory. A KBr beam splitter and a liquid nitrogen cooled mercury–cadmium–telluride type (MCT-A) detector were used. The spectra were obtained with 4 cm−1 resolution and the Blackman–Harris apodization function. 150 scans were accumulated of each spectrum. The phase correction was performed according to the Mertz method.
Low-temperature luminescence spectra and luminescence excitation spectra of the perovskite samples in the spectral range 250–850 nm were registered using the spectrofluorometer Jobin-Yvon FluoroMax Plus. All the recordings were performed using the modified sample holder enabling a precise setup at every spectrum registration stage. The radiation within particular spectral ranges was filtered with glass color filters. Prior to the spectra recordings, the vacuumized samples were placed in the optical nitrogen cooled cryostat LN-121-SPECTR (Cryotrade engineering, Russia) compatible with the spectrofluorometer Jobin-Yvon FluoroMax Plus. The cryostat windows are made from high quality quartz KY-1 transparent in all the studied spectral regions. The temperature control was accomplished via the integrated thermocouple and thermoregulation unit TPM-210. The luminescence lifetimes were determined using a setup described in detail in the ESI.†
2.3. Computational approach
The electronic structures of PDAPbX4 perovskites were modeled theoretically using a periodic DFT approach. This was accomplished by employing the plane augmented wave (PAW) approach17 in conjunction with the generalized gradient approximation (GGA) Perdew–Burke–Ernzerhof (PBE)18,19 density functional as implemented in the VASP 5.4.4 program.20–23 The P21/c spatial symmetry of the perovskite crystal lattices determined by XRD was employed. The perovskite unit cells correspond to the chemical formula Pb4X16C20N8H64 (X = Br, I). The chloride unit cell is twice as large. The reason for this is given later in the text. The SCF energy convergence criterion was set to 1.0 × 10−7 eV. The atomic kinetic energy cutoffs were set to their default values. Brillouin Zones (BZ) were sampled over the Monkhorst–Pack grid24 of 7 × 9 × 9 k-points (9 × 9 × 3 k-points for the monocrystalline chloride perovskite). Electronic band structures were computed at 181 k-points along the high symmetry path Γ–A–C–D–D1–E–X–Y–Y1–Z of monoclinic BZ. Electronic band structures and density of states were plotted using the Gnuplot 5.2 software package.25 Throughout the text, chemical structures are visualized using the program VESTA.26For the PDAPbI4 perovskite, the calculations of phonon properties at the Γ-point were carried out in the framework of GGA PBE density functional and norm-conserving pseudopotentials as implemented in the CASTEP software (Materials Studio).27,28 The plane wave basis cutoff energy was set to 1000 eV. The SCF energy convergence criterion was set to 5 × 10−7 eV. The dimensions of k-space were chosen in order to provide a step of 0.05 1 Å−1 in k-space. The Monkhorst–Pack grid was chosen. At the initial stage, the geometry optimization was carried out with the aid of the Limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) method29 to achieve residual forces and stresses below 0.01 eV Å−1 and 0.02 GPa, respectively. For the optimized structure, the phonon frequencies were calculated using the linear response method (density functional perturbation theory).30
3. Results
3.1. Crystal structure of the PDAPbX4 perovskites
Powder XRD patterns of the three hybrid perovskites are shown in Fig. S1 (ESI†). The reference XRD data are available only for PDAPbI4.14 The XRD pattern of PDAPbI4 matches well with the reference XRD pattern indicating the formation of the perovskite. XRD patterns of the chloride and bromide compounds significantly differ from that of the iodide sample. The single main reflection at ∼8° in both XRD patterns correspond to the interplane distances of 11.25 Å and 10.12 Å for the chloride and bromide perovskite, respectively. This observation suggests a quasi 2D structure for the chloride and bromide species.The structures of PDAPbCl4 and PDAPbBr4 perovskites were investigated using a single crystal XRD technique as well. The resolved non-hydrogen atomic positions were refined by the least-squares method in anisotropic approximation. All the hydrogen atoms were placed in geometrically idealized positions which were then refined using the riding-model approximation with r(C–H) = 0.99 Å, r(N–H) = 0.91 Å, and Uiso(H) = 1.2 or 1.5 times Ueq(C, N). The determination and refinement of the structures were carried out using the SHELXTL program.31 Some details of the data collection, processing, and refinement are given in Table S1 (ESI†). Further details can be obtained from the Cambridge Crystallographic Data Center by quoting the depository number CCDC – 2269541 (for NH3(CH2)5NH3PbCl4) and CCDC – 2269539 (for NH3(CH2)5NH3PbBr4).†
Resolved structures of the chloride and bromide perovskites as well as the known structure of the iodide are illustrated in Fig. 1. Both the chloride and bromide species demonstrate a quasi 2D perovskite-like structure in which corner-sharing inorganic octahedra form 2D sheets separated from each other by organic cations. Based on the single crystal XRD patterns of the chloride and bromide perovskite their powder XRD patterns were simulated. Both of them are demonstrated in Fig. S1 (ESI†) as well. It shows a good match between the experimental and calculated data.
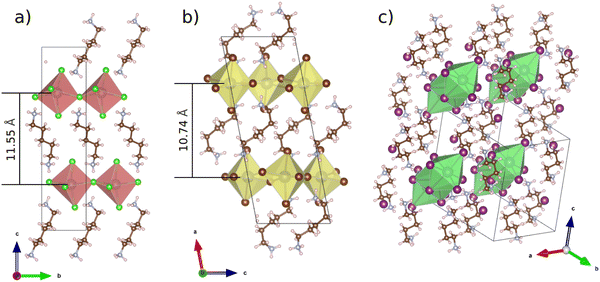 | ||
| Fig. 1 Single crystal XRD structures of (a) PDAPbCl4, (b) PDAPbBr4 and literature data for (c) PDAPbI4. | ||
The obtained structural data enables analysis of the sizes of inorganic octahedra PbX6 and the degrees of their disorder and distortion as a function of halogen type (see Table 1). Average Pb–X distances (dav), the degree of PbX6 octahedra distortion (Δd) as well as the octahedral angle variance σoct2 were calculated according to the following formulae:32
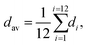 | (1) |
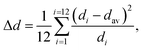 | (2) |
 | (3) |
| Compound | Pb–X, Å | Δd, Å | X–Pb–X σoct2 | Pb–X–Pb Θav |
|---|---|---|---|---|
| PDAPbCl4 | 2.8624 | 5.45 × 10−5 | 231.62 | 145.83 |
| PDAPbBr4 | 2.9916 | 3.48 × 10−4 | 20.37 | 150.53 |
| PDAPbI4 | 3.2260 | 1.12 × 10−3 | 28.89 | 75.19 |
The value dav serves as a measure of an average size of the PbX6 octahedra. Table 1 shows that in the sequence Cl–Br–I the octahedra sizes increase. This dependence takes place due to two effects. First, the halogen anion sizes increase in the same sequence. Second, the electronegativity of the halogen anions decreases in that sequence.
The perovskite octahedra appear to be distorted which is manifested by a dispersion in the Pb–X bond lengths (eqn (2)) and/or by a displacement of lead cations away from the octahedra centers (eqn (3)). As shown in Table 1, the dispersion in the Pb–Cl bond lengths is about an order of magnitude smaller than that in the Pb–Br bond lengths. In this respect, the PbI6 octahedra are the most distorted. At the same time, the PbCl6 octahedra feature the largest displacement of lead cations from the centers of the octahedra. In the case of PbBr6 and PbI6 octahedra this displacement is an order of magnitude smaller.
Yet another type of perovskite inorganic subsystem structural phenomenon is a tilt of the octahedra PbX6 with respect to each other. Usually, it is characterized by an angle Pb–X–Pb (denoted as Θav in Table 1).33 The more it deviates from 180° (the Pb–X–Pb angle in ideal 3D perovskites), the stronger the perovskite crystal lattice disorder. Table 1 shows that PbX6 octahedra tilting in the chloride perovskite (Θav = 145.83°) is just slightly stronger than in the bromide one (Θav = 150.53°). Both tilting angles, however, deviate insignificantly from the ideal angle of 180° enabling the formation of a quasi 2D perovskite structure. In contrast, in the iodide perovskite, the PbI6 octahedra tilting is very large (Θav = 75.19°). This results in the edge- and face-sharing PbI6 octahedra leading to a quasi 1D perovskite structure.
Furthermore, for all the perovskites, the distances from the nitrogen atom to the nearest halogen atoms were determined. For the iodide species, the –NH3+ groups are arranged between the zigzag-like chains of the PbI6 octahedra. The distances from the –NH3+ groups to the nearest three iodine atoms appear to be 3.53 Å, 3.67 Å, and 3.98 Å. In the chloride perovskite, the –NH3+ groups are located in cavities formed by four PbCl6 octahedra which share corners so that there are three nearest chlorine atoms, and the N⋯Cl distance varies within 0.2 Å: 3.21 Å, 3.28 Å, and 3.38 Å. As mentioned above, in the bromide perovskite, two sets of –NH3+ groups insignificantly differing in distance from the nitrogen atom to three nearest bromine atoms were found. The distances r(N⋯Br) for the first set were 2.94 Å, 3.35 Å, and 3.41 Å, and for the second set were 3.09 Å, 3.34 Å, and 3.46 Å. The PbBr6 octahedra in PDAPbBr4 perovskite are arranged in a way similar to that of the PbCl4 octahedra in the corresponding species. Thus, distances from the –NH3+ groups to the bromine atoms allow the formation of weak hydrogen bonds N–H⋯X.
Fig. 1 also shows the distances between the planes formed by lead atoms in the quasi 2D perovskites PDAPbCl4 (11.55 Å) and PDAPbBr4 (10.74 Å). These values derived from the single crystal XRD data are very close to their counterparts obtained from the analysis of the powder X-ray diffraction patterns: 11.25 Å (PDAPbCl4) and 10.12 Å (PDAPbBr4). Presumably, these differences in interplane distances between the chloride and bromide compounds cannot be related to the sizes of inorganic octahedra alone. Here, the organic cation orientation could play an important role as well. Indeed, Fig. 1 shows that in the chloride perovskite the organic cation is oriented almost perpendicular to the planes formed by the lead atoms, whereas in the bromide perovskite the organic cation is inclined to them at the angle of ∼45.0°.
3.2. Vibrational spectroscopic studies
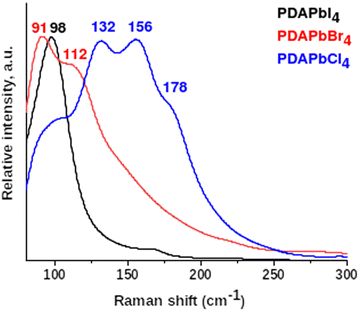
FTIR and Raman spectra of PDAPbX4 samples were recorded at room temperature in the spectral regions 700–4000 cm−1 and 70–4000 cm−1, respectively (see Fig. S2 and S3, ESI†). The majority of observed bands are interpreted in Table S2 (ESI†). The computed vibrational modes of PDAPbI4 active in the IR absorption spectrum are given there as well. The calculated and experimental data show very good agreement and help to identify vibrational modes for PDAPbCl4 and PDAPbBr4 (Fig. S2, ESI†). The Raman spectra low-frequency region in Fig. 2 is due to lattice vibrations involving heavy Pb and X atoms. The PDA cations are inactive in this spectral region and behave as rigid species.Fig. 2 shows that the breathing modes of PDAPbI4 are represented by a single intense peak at 98 cm−1. Phonon spectra of the bromide and chloride compounds show two (91 cm−1 and 112 cm−1) and four (98 cm−1, 132 cm−1, 156 cm−1, and 178 cm−1) peaks, respectively. This difference in the lattice phonon vibrational region can be explained based on the structure of the considered compounds. The inorganic framework of PDAPbI4 consists of identical, side-by-side arranged chains of almost regular face-sharing PbI6 octahedra, while the layered structures of PDAPbBr4 and PDAPbCl4 are formed by corner-sharing PbBr6 and PbCl6 octahedra of several types. The higher number of peaks in the spectrum of PDAPbCl4 as compared to that in the spectrum of PDAPbBr4 is attributed to the following. The PbCl6 octahedra feature a larger displacement of Pb cations from the octahedron centers as compared to the PbBr6 octahedra. Besides, the PbCl6 octahedra are more tilted than the PbBr6 octahedra.
The higher frequency vibrations (>200 cm−1) are due to the PDA cations. At these frequencies the heavy lead and halogen ions remain almost stationary.
The broad-band components are noted in the high-frequency range 2800–3300 cm−1 (see Fig. 3a). The peaks at ∼2863 cm−1 and ∼2929 cm−1 correspond to the symmetric and antisymmetric stretching vibrations in the PDA methylene groups.34,35
 | ||
| Fig. 3 FTIR spectra of PDAPbX4 in the ν(NH) (a) and δ(NH) (b) frequency regions: 1 – PDAPbI4, 2 – PDAPbBr4, 3 – PDAPbCl4. The spectra of solid PDA (4) and PDA dihydrochloride (5) diluted in KBr pellets are presented for comparison.40 | ||
The absorption band maxima near 3093 cm−1, 3025 cm−1, and 3030 cm−1 for the iodide, bromide, and chloride compounds, respectively, can be assigned to the N–H stretching vibrations (see spectra 1–3). Due to the hydrogen bonding, these bands for salts of primary aliphatic amines are downshifted by ∼250–300 cm−1 as compared to those for primary aliphatic amines in condensed phase or diluted in non-polar solvents.35,41,42 The H-bonding effect on the band shape and band position can be clearly seen for the PDA salt (spectrum 5) and PDA (spectrum 4), both diluted in potassium bromide.40 In general, the greater the band downshift, the stronger the H-bonding. This results in wider absorption bands featuring more types of H-bonds in a system. It is known that for molecular complexes of ammonia or amines with hydrogen halides in a gas phase or in cryogenic matrices, the energy required for dissociation of HX increases in the series I–Br–Cl–F.36–39 Thus, the gradual weakening of the H–X bond promotes the formation of such complexes.
In cryogenic matrices and in the gas phase, the halogen-involving vibrations of N⋯H⋯X and H–X types were detected for NH3⋯HX complexes.36,43 This kind of vibration was not detected even for PDAPbCl4 which is apparently due to the large number of halogen atoms weakening the intermolecular interactions.
Downshifts of ν(NH) are about the same for the bromide and chloride perovskites and greatly exceed those for the iodide compound. This may indicate a stronger interaction of nitrogen with protons of –NH3+ groups surrounded by halogens of the PbX6 octahedra in PDAPbBr4 and PDAPbCl4 as compared to PDAPbI4. It should be noted that the absorption range of N–H fragments involved in the formation of N–H⋯X-type bonds in PDAPbBr4 is wider than that in PDAPbCl4 and PDAPbI4.
A thorough examination of the structures obtained from crystallographic data (Fig. 1) allowed us to determine the nearest halogen environment for the nitrogen atoms in each sample. As a result, it was determined that in the structures of PDAPbI4 and PDAPbCl4 nitrogen atoms in the –NH3+ groups are arranged uniformly throughout the structure, while for PDAPbBr4 there are two slightly different configurations of the arrangement of –NH3+ groups in cavities formed by PbBr6 octahedra.
Following classification of the hydrogen bond by strength depending on the N–H distance and the relative Δν(NH) shift,44 the binding of the PDA ammonium groups with halogen atoms of the inorganic framework should be considered weak for all the perovskites. The analysis of structural data confirmed the conclusions about the strength and diversity of interactions of the N–H⋯X type in the studied perovskite materials made from spectroscopic data (Fig. 3a).
The spectral manifestation of the H-bond can also be traced in the N–H deformation vibration range.35,45 H-bonding shifts the N–H deformation band frequency to higher values.
In the FTIR spectra, the most prominent features below 1600 cm−1 are complex absorption bands (see Fig. 3b). The band at ∼1622 cm−1 attributed to the alkyl-diamine NH2 scissoring mode (spectrum 4) is absent in the spectra of PDA salt (spectrum 5) and PDA halide perovskites (spectra 1–3) that confirms the high affinity of nitrogen in –NH3+ to the proton. In the range 1420–1500 cm−1, the C–H bending vibrations contribute to the complex band shape at ∼1440–1450 cm−1, as demonstrated by the Raman and FTIR spectra in Fig. S2 and S3 (ESI†). The peaks with maxima at 1450–1500 cm−1 and 1550–1625 cm−1 are related to the symmetric and antisymmetric bending vibrations in the –NH3+ group, respectively.35,41,46 The δs(NH) and δasym(NH) frequencies are as follows (see Fig. 3b and Table S2, ESI†). For PDAPbI4: 1464 cm−1 (the shoulder at 1450 cm−1) and 1574 cm−1 (the shoulder at 1565 cm−1). For PDAPbBr4: doublet with maxima at 1483 cm−1 and 1467 cm−1 and doublet with maxima at 1587 cm−1 and 1575 cm−1. For PDAPbCl4: 1487 cm−1 (shoulder at 1469 cm−1) and 1602 cm−1 (shoulder at 1585 cm−1). Obviously, with decreasing halogen size, a shift of both bands towards higher frequencies is observed. This result also confirms the strengthening of the hydrogen bond N–H⋯X in the same halogen sequence.45
Predominantly one narrow band in the iodide perovskite spectrum indicates a weak and uniform halogen environment of the –NH3+ groups in the inorganic matrix, and for bromide perovskite the presence of doublets for δs(NH) and δasym(NH) bands indicates the coexistence of two types of –NH3+ groups in the perovskite structure (Fig. 3b). It should also be noted that the spectra of all the perovskites reveal a band below 2000 cm−1 (see Fig. S4, ESI†) attributed to a combination of the C–C–N torsional vibration and the antisymmetric deformation vibration of –NH3+ groups (1550–1625 cm−1).35,42 The presence of this spectral feature may indicate the lack of threefold symmetry of the pentadiamine cations.42
The effect of the H-bond on the primary amine spectra is the most clearly manifested in the range 700–1000 cm−1 where the broad absorption of weak-to-medium intensity alters in shape and position depending on the number of H-bonds present (compare spectra 1–4 with spectrum 5 in Fig. S5, ESI†). This range is mainly due to the combination of bands involving the H–N–H twisting (τ) and rocking (ρ) vibrations (see Table S2, ESI†). Unfortunately, vibrations associated with the C–C–N angles and C–N bonds which are active in this spectral range as well complicate understanding of the H-bonding picture.
Thus, as far as the perovskite crystal structures are concerned the data obtained using IR spectroscopy confirm and complement the data obtained through XRD analysis. While the XRD method is well-suited for studies of the inorganic subsystem of the perovskite crystal lattices, IR spectroscopy allows us to describe interactions between their inorganic and organic subsystems. It was demonstrated that all the hydrogen atoms of the –NH3+ groups participate in the formation of N–H⋯X bonds. This is evidenced by the fact that in the IR spectra all the N–H vibrations are perturbed by H-bonding. No bands belonging to free N–H vibrations were observed.
3.3. Refinement of the PDAPbBr4 perovskite crystal structure
In contrast to PDAPbCl4 and PDAPbI4, the structure of PDAPbBr4 was poorly resolved and demonstrated duplicated atoms. In order to refine it a combinatorics approach was employed. First, out of the eight PDA chains present in the original unit cell of PDAPbBr4 four distinct conformations, meaningful from a chemical viewpoint and each containing four such chains, were identified. This manipulation let us get rid of duplicated C, N, and H atoms. Further analysis of the symmetry of the four PDA chain conformations revealed that only two of them are unique. Then, using a combinatorics approach again, 16 out of the 32 bromine anions present in the original perovskite unit cell were chosen. This resulted in 16 (organic chains conformation # 1) and 736 (organic chains conformation # 2) perovskite structures of non-trivial spatial symmetry i.e. belonging to a space group other than P1. The generated structures feature either triclinic (space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) or monoclinic (space groups P21, Pc, and P21/c) syngony. In total, fourteen highest symmetry structures (space group P21/c) were found. Space groups of other perovskites structures are subgroups of the space group P21/c. We therefore concluded that an actual bromide perovskite has the space group symmetry P21/c, while other perovskites symmetries are simply artifacts of the employed combinatorics approach. The final step of the PDAPbBr4 structure refinement was to choose a single P21/c structure out of the fourteen available. This was done based on total energy computations. The lowest energy structure was assumed to be a true one.
) or monoclinic (space groups P21, Pc, and P21/c) syngony. In total, fourteen highest symmetry structures (space group P21/c) were found. Space groups of other perovskites structures are subgroups of the space group P21/c. We therefore concluded that an actual bromide perovskite has the space group symmetry P21/c, while other perovskites symmetries are simply artifacts of the employed combinatorics approach. The final step of the PDAPbBr4 structure refinement was to choose a single P21/c structure out of the fourteen available. This was done based on total energy computations. The lowest energy structure was assumed to be a true one.
3.4. Electronic structures of the PDAPbX4 perovskites
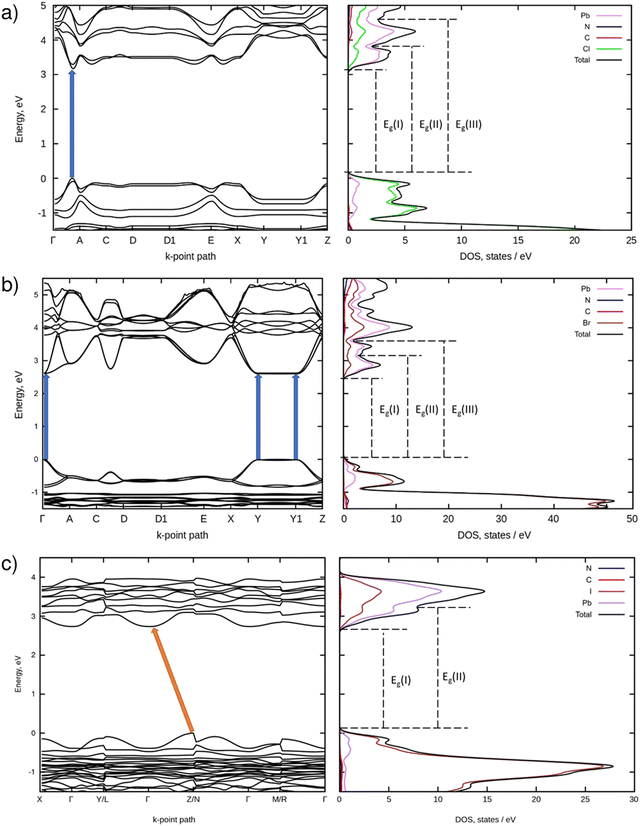
Fig. 4 demonstrates electronic BS and DOS of the perovskites modeled using DFT. As can be seen from Fig. 4a, the quasi 2D chloride perovskite (monoclinic; C2) is a semiconductor with the direct VB → CB electronic transition occurring in-between the Γ and A k-points. The computed electronic bandgap equals 3.20 eV. This value matches well the bandgap of 3.036 eV recently reported for the same perovskite by W. Yang et al.15 However, the BS plot of PDAPbCl4 presented in Fig. 5b therein differs considerably from the one illustrated in Fig. 4a of this work. Despite the similar structure (monoclinic; P21/c) the BS of PDAPbCl4 features a direct electronic transition at the Γ-point.15 At present, we cannot offer any explanation for this discrepancy. What we found even more confusing is the reported high symmetry k-point path.15 To the best of our knowledge, monoclinic syngony features no high symmetry k-points A1, R, and S.47Fig. 4b shows that the quasi 2D bromide perovskite (monoclinic; P21/c) is a direct bandgap semiconductor as well. In contrast to the chloride, it features several energetically close VB → CB electronic transitions. They occur at the Γ, Y, and Y1 k-points. The computed electronic bandgap amounts to ∼2.60 eV.
According to Fig. 4c, the quasi 1D iodide perovskite (triclinic; P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) is an indirect bandgap semiconductor. In this compound, electrons can be excited from the k-point of the VB located in-between the Z and N k-points onto the Γ k-point of the CB. For this perovskite, the calculations predict an electronic bandgap of 2.73 eV.
) is an indirect bandgap semiconductor. In this compound, electrons can be excited from the k-point of the VB located in-between the Z and N k-points onto the Γ k-point of the CB. For this perovskite, the calculations predict an electronic bandgap of 2.73 eV.
3.5. Optical properties of the PDAPbX4 perovskites
Fig. 5a shows diffuse reflectance spectra of the studied perovskites.One can see that the chloride and bromide feature sharper edges of fundamental absorption as compared to the iodide, which could be related to the larger number of defects in the latter. Optical bandgaps of the perovskites were determined as cross-points of the diffuse reflectance spectra derivatives with the X-axis (Fig. 5b). They decrease in the sequence Cl–Br–I as follows: Eg = 3.69 eV (Cl), Eg = 2.96 eV (Br), and Eg = 2.88 eV (I), which is typical of metal halide perovskites. Fig. 5b also shows that the second maxima of the derivatives are shifted towards higher energies. We have observed and explained this behavior in 1,6-hexamethylenediamine perovskites previously.9
As one can see from Table 2, there is a discrepancy between the theoretical (electronic) and experimental (optical) bandgaps of the perovskites. There are several reasons for this.48 We shall remind the reader that the results of the DFT calculations presented here formally correspond to 0 K as opposed to a finite temperature at which the diffuse reflectance spectra were recorded. It is known that many materials including semiconductors undergo thermal expansion often resulting in optical bandgaps which are larger than the predicted electronic ones. This could be one of the reasons why the optical bandgaps listed in Table 2 are somewhat larger than their theoretical counterparts. Taking this into account we may conclude that the agreement between the experimental and theoretical bandgaps is rather satisfactory.
| Compound | Experiment, eV | Theory, eV |
|---|---|---|
| PDAPbCl4 | 3.69 | 3.20 |
| PDAPbBr4 | 2.96 | 2.60 |
| PDAPbI4 | 2.88 | 2.73 |
As speculated previously, the second maxima in Fig. 5b could be associated with VB → CB + 1 electronic transitions.9 In the case of chloride perovskite, the second maximum is observed experimentally at 3.89 eV, while the theoretical value predicted by DFT amounts to 3.62 eV. In the case of bromide perovskite, the second maximum is observed experimentally at 3.17 eV, whereas DFT predicts a value of 3.09 eV. Finally, in the case of iodide perovskite, the second maximum is observed experimentally at 3.32 eV, while DFT predicts 3.24. Thus, all the studied perovskites show very good agreement between the calculated and experimental energies of VB → CB + 1 electronic transitions.
3.6. Luminescent properties of PDAPbX4
Low-temperature luminescence spectra of the PDAPbCl4 perovskite are demonstrated in Fig. 6a.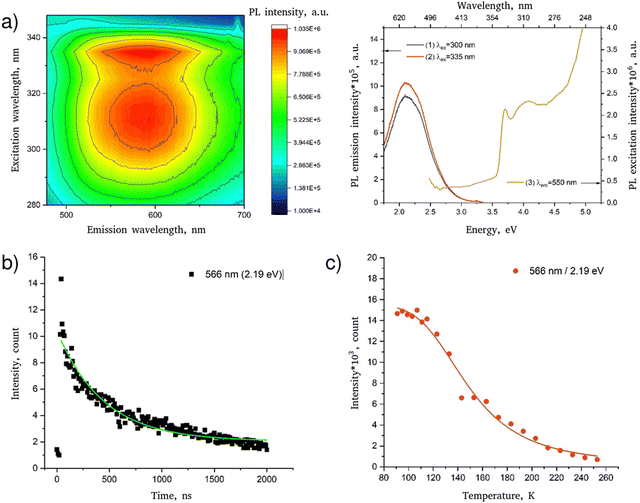 | ||
| Fig. 6 Luminescent properties of PDAPbCl4: (a) luminescence spectrum represented as a 3D map (left) and spectral lines (right); (b) low-temperature (78 K) decay kinetics of luminescence (the line corresponds to the fitting of the experimental data according to eqn (4)); (c) temperature dependence of the intensity of the luminescence band (the line corresponds to the fitting of the experimental data according to eqn (5)). | ||
In agreement with the data reported previously,15 this hybrid perovskite is characterized by a single broad luminescence band in the region 450–700 nm (curves 1–2) with a maximum at ∼550 nm which is most effectively excited by radiation with wavelengths of 335 and 315 nm (curve 3). The sharp edge of the broadband luminescence at 340 nm agrees well with the determined optical bandgap of 3.69 eV (336 nm) meaning that the broadband luminescence of PDAPbCl4 is due to interband excitation.
Fig. 6b shows the decay kinetics of the characteristic luminescence band intensities of PDAPbCl4. The kinetics of this process follows the exponential dependence:
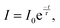 | (4) |
Fitting the data for PDAPbCl4 into eqn (4) results in the broadband luminescence life-time of 458 ± 77 ns.
As temperature increases, the luminescence band intensity of the studied perovskites decreases due to the increase in efficiency of nonradiative recombination channels. Generally, the temperature dependence of the luminescence intensity is well described by the Mott–Seitz equation49,50:
 | (5) |
Fig. 6c shows that the temperature quenching of broadband luminescence of PDAPbCl4 with a maximum at 566 nm (2.19 eV) is well described by eqn (5) with Ea = ∼67.8 ± 6.5 meV.
Fig. 7a illustrates the luminescence spectra and the spectra of luminescence excitation of PDAPbBr4. Therein, one can see two components: the narrow band, short wavelength with the maximum at 414 nm and the wide band, long wavelength with the maximum at 530 nm. The peaks of both luminescence spectra coincide.
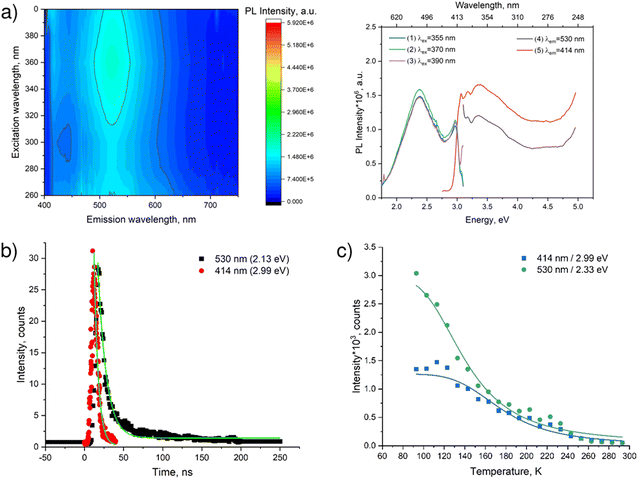 | ||
| Fig. 7 Luminescent properties of PDAPbBr4: (a) luminescence spectrum represented as a 3D map (left) and spectral lines (right); (b) low-temperature (78 K) decay kinetics of luminescence (the lines correspond to the fitting of the experimental data according to eqn (4)); (c) temperature dependence of the intensity of the luminescence bands (the lines correspond to the fitting of the experimental data according to eqn (5)). | ||
The edge of the long wavelength luminescence excitation reaches 427 nm (2.90 eV) matching the perovskite optical bandgap (2.96 eV). Interestingly, the excitation spectra of both luminescence bands look alike. This might indicate that both channels of the radiative relaxation originate from the same excitation pathways due to the intrinsic light absorption.
The decay kinetics of the characteristic luminescence band intensities of PDAPbBr4 is demonstrated in Fig. 7b. In this perovskite, the luminescence decay occurs much faster as compared to that in PDAPbCl4. An application of eqn (4) to the experimental decay kinetics data results in characteristic life-times of 11 ± 0.3 ns and 5 ± 0.2 ns for the luminescence bands with the maxima at 530 nm and 414 nm, respectively. The latter value is very close to the duration of excitation laser pulse in Fig. S6 (ESI†). This is the reason why an actual life-time of the narrow-band luminescence of PDAPbBr4 could not be determined. Seemingly, it does not exceed 10 ns. Anyway, the difference in decay time for two luminescence bands infers that there exist two different channels of radiative relaxation corresponding to the two observed luminescence bands.
The quenching of both narrow- and broad-band luminescence of PDAPbBr4 (Fig. 7c) is also well described by eqn (5). For the narrow-band luminescence with a maximum at 414 nm (2.99 eV) Ea = 100.4 ± 9.4 meV, whereas for the broadband luminescence with a maximum at 530 nm (2.33 eV) Ea = 68.4 ± 6.9 meV.
The luminescence spectra and the spectra of luminescence excitation of PDAPbI4 are shown in Fig. 8a. Therein, one can see two overlapping luminescence bands: the short wavelength in the range 575–725 nm and the long wavelength in the range 650–850 nm. The long wavelength luminescence excitation spectrum reaches 430 nm (2.88 eV) which corresponds to the interband excitation of this perovskite. The luminescence excitation spectrum is complex and consists of several bands. Most efficiently the luminescence is excited by radiation with the wavelengths of 240 nm, 330 nm, and 410 nm.
 | ||
| Fig. 8 Luminescent properties of PDAPbI4: (a) luminescence spectrum represented as a 3D map (left) and spectral lines (right); (b) low-temperature (78 K) decay kinetics of luminescence (the lines correspond to the fitting of the experimental data according to eqn 4); (c) temperature dependence of the intensity of luminescence bands (the lines correspond to the fitting of the experimental data according to eqn (5)). | ||
Fig. 8b shows the kinetics of decay of the short and long wavelength luminescence of PDAPbI4. Having approximated the data according to eqn (4), we obtain characteristic life-times of 11.4 ± 0.52 ns and 12.11 ± 0.8 ns for the luminescence bands with the maxima at 650 nm and 800 nm, respectively. Such similar lifetimes of the luminescence might indicate a similarity in the relaxation mechanisms for both luminescence bands.
The quenching of both closely spaced luminescence bands (with maxima at 650 nm and 800 nm) in PDAPbI4 (Fig. 8c) occurs with activation energies in the order of 49 meV (49.4 ± 1.9 meV and 49.1 ± 1.8 meV, respectively).
Table 3 shows how the luminescent properties of PDAPbX4 (X = Cl, Br, I) depend on the type of halogen atom. According to this, the bromide perovskite features two luminescence channels: free excitons (FE) and self-trapped excitons (STE). Noteworthy, the narrow-band FE-luminescence is more stable than the broad-band STE-luminescence. The other compounds demonstrate just one radiative recombination channel which is STE. The two luminescence bands in the iodide perovskite case correspond to two types of STE localization states.
| Compound | L. max at 83 K | Lifetime | L. quenching Ea |
|---|---|---|---|
| PDAPbCl4 | 566/2.19 | 458 ± 77 | 67.8 ± 6.5 |
| PDAPbBr4 | 414/2.99 | ≤5 | 100.4 ± 9.4 |
| PDAPbBr4 | 530/2.33 | 11.0 ± 0.30 | 68.4 ± 6.9 |
| PDAPbI4 | 650/1.91 | 11.4 ± 0.52 | 49.4 ± 1.9 |
| PDAPbI4 | 800/1.55 | 12.11 ± 0.8 | 49.1 ± 1.8 |
4. Discussion
The considered PDAPbX4 (X = Cl, Br, I) perovskites differ from each other only in the type of constituting halogen atom. This lets us uncover how halogen atoms affect the perovskite crystal structures and, as a result, their optoelectronic properties.There are two ways halogen atoms influence the formation of crystal structures of low-dimensional perovskites. The first one is a dimensionality factor. Indeed, the halogen atoms differ in size which increases in the sequence Cl–Br–I. The second is the strength with which the halogen atom interacts with the organic cation and lead atom. This strength depends on halogen atom electronegativity which decreases in the same sequence. The cumulative effect of both leads to the formation of a wide variety of hybrid perovskites with different anionic compositions.
The inorganic PbCl6 octahedra network within the chloride perovskite structure undergoes both disorder and distortion. The former manifests itself in significant PbCl6 octahedra tilts with respect to each other, while the latter results in slight asymmetry of the octahedra themselves. Thus, in the case of the chloride perovskite, the optimal positions of the PbCl6 octahedra with respect to the PDA amino groups are achieved via tilting of the former. In contrast, in the case of bromide perovskite the same goal is achieved through PbBr6 octahedra distortion. Yet another scenario is realized in the iodide perovskite case. As a matter of fact, optimal interactions between the organic and inorganic subsystems in this perovskite are fulfilled when the PbI6 octahedra are connected with each other through common faces and edges forming a quasi 1D structure.
Electrostatic interactions between cations and anions of a perovskite play an important role in its formation. In the context of this study, they arise between lead, halogen, and PDA ions. An optimal arrangement of the PDA protonated amino groups within the perovskite crystals is such that their three hydrogens point toward the nearest halogens thereby forming H-bonds. This is confirmed by the IR spectra lacking bands due to non-interacting N–H bonds. Thus, an optimal PDA orientation with respect to the PbX6 octahedra implies the formation of three H-bonds between the protonated amino groups and halogens.
We would like to emphasize that, here, H-bonds play a rather minor role as they are much weaker than the electrostatic interactions occurring between the perovskite ions. Nevertheless, all three considered perovskites feature H-bond formation that leads to total energy lowering.
In fact, the recorded XRD data revealed that PDA+ in the PDAPbBr4 perovskite have two distinct conformations as shown in Fig. 9. The major difference between them is the orientation of one of the amino groups with respect to the neighboring PbBr6 octahedra (compare positions of the atoms N2 and N2A in Fig. 9). This can also be regarded as a manifestation of the intention of a perovskite to form as many H-bonds N–H⋯X as possible thereby stabilizing its structure.
As indicated by the excitation spectra and decay times of the luminescence, the excitation mechanism in all three perovskites involves band to band transitions. However, the observed structure of the luminescence excitation spectra manifests the different character of these transitions between different electronic band states. In the case of the luminescence spectra of PDAPbCl4 perovskite, the wavelength of 335 nm (3.70 eV) corresponds to the electron transition from the top of the VB to the bottom of the CB (denoted as Eg(I) in Fig. 4). This transition matches well with the experimentally determined optical bandgap of 3.69 eV. In contrast, the wavelength of 315 nm (3.93 eV) seems to correspond to the VB → CB + 1 electron transition (denoted as Eg(II) in Fig. 4). This transition is observed by diffuse reflectance spectroscopy and corresponds to the second maximum of the absorption derivative reported in section 3.4 (3.89 eV). These features of the electronic structure and optical behavior of the synthesized materials can be attributed to the quantum size confinement effect that, in turn, creates strong optical and electronic anisotropy in crystals reflecting the strong crystal structure anisotropy typical of low dimensional perovskites and their derivatives.
The obtained luminescence spectra can be represented as dots on the CIE 1931 color space shown in Fig. 10. As shown, PDAPbBr4 is a material with great white light emission potential.
5. Conclusions
In the present work, the synthesis, structure, and optoelectronic and luminescence properties of PDAPbX4 (X = Cl, Br, I) hybrid perovskites are reported. In contrast to their quasi 1D iodide analog, the chloride and bromide haloplumbates possess quasi 2D perovskite-like structures.The role of the size of halogen anion and the strength of its interaction with the PDA and lead cations is elucidated. It is shown that the halogen anions determine the degree of the PbX6 octahedra distortion and overall disorder of the perovskite crystal lattices. The PbX6 octahedra distortion may result in asymmetry of the Pb–X bond lengths and/or in the displacement of lead cation from its ideal position within the octahedron. Overall perovskite crystal lattice disorder is achieved through the PbX6 octahedra tilting. In an extreme case (PDAPbI4), the PbX6 octahedra tilting may lead to their specific connection pattern in which the neighboring PbX6 octahedra share their edges and faces as opposed to the corner-sharing pattern observed in PDAPbCl4 and PDAPbBr4. The orientation of the terminal protonated amino groups also changes subject to a type of halogen atom. An optimal perovskite structure explores all of the above-mentioned possibilities. One of the manifestations of this structure is the formation of as many H-bonds N–H⋯X as possible.
Author contributions
Conceptualization: D. S. Shtarev, A. V. Emeline. Data curation: M. I. Balanov, D. A. Zharovov, K. M. Bulanin. Formal analysis: D. S. Shtarev, A. V. Gerasimenko, R. Kevorkyants, D. A. Chaplygina, K. M. Bulanin, D. V. Pankin, A. V. Rudakova. Funding acquisition: D. S. Shtarev. Investigation: R. Kevorkyants, M. I. Balanov, A. Ju. Major, A. V. Gerasimenko, D. A. Zharovov, K. M. Bulanin. Methodology: D. S. Shtarev, R. Kevorkyants. Project administration: N. I. Selivanov. Resources: D. S. Shtarev, A. Ju. Major, A. V. Gerasimenko, A. V. Emeline. Software: R. Kevorkyants, D. V. Pankin. Supervision: D. S. Shtarev. Validation: A. V. Emeline, N. I. Selivanov. Visualization: R. Kevorkyants, D. S. Shtarev. Writing – original draft: D. S. Shtarev, R. Kevorkyants. Writing – review & editing: D. S. Shtarev, R. Kevorkyants, K. M. Bulanin, A. V. Rudakova, A. V. Emeline.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The study was supported by the FEFU Foundation, project No. 22-03-03 004 and I Ministry of Science and Higher Education of the Russian Federation (Mega Grant no. 075-15-2022-1112). Luminescence spectral studies were performed in the laboratory “Photoactive nanocomposite materials” supported by Saint-Petersburg University (project ID: 94030186). The authors are very grateful to the staff of the Joint Center for Collective Use of FEFU, as well as to the NanoPhotonics Resource Center, Centre for Optical and Laser Materials Research, Computing Center of the Research Park at the Saint Petersburg State University for their valuable assistance.References
- M. A. Green, E. D. Dunlop, J. Hohl-Ebinger, M. Yoshita, N. Kopidakis and A. W. Y. Ho-Baillie, Solar cell efficiency tables (Version 55), Prog. Photovolt. Res. Appl., 2020, 28, 3–15 CrossRef
.
- H. Cho, S. Jeong, M. Park, Y. Kim, C. Wolf, C. Lee, J. H. Heo, A. Sadhanala, N. Myoung, S. Yoo, S. Im, R. Friend and T. Lee, Overcoming the electroluminescence efficiency limitations of perovskite light-emitting diodes, Science, 2015, 350, 1222–1225, DOI:10.1126/science.aad1818
.
- N. Wang, L. Cheng, R. Ge, S. Zhang, Y. Miao, W. Zou, C. Yi, Y. Sun, Y. Cao, R. Yang, Y. Wei, Q. Guo, Y. Ke, M. Yu, Y. Jin, Y. Liu, Q. Ding, D. Di, L. Yang, G. Xing, H. Tian, C. Jin, F. Gao, R. H. Friend, J. Wang and W. Huang, Perovskite light-emitting diodes based on solution-processed self-organized multiple quantum wells, Nat. Photonics, 2016, 10, 699–704, DOI:10.1038/nphoton.2016.185
.
- Z. Xiao, R. A. Kerner, L. Zhao, N. L. Tran, K. M. Lee, T.-W. Koh, G. D. Scholes and B. P. Rand, Efficient perovskite light-emitting diodes featurianometertre-sized crystallites, Nat. Photonics, 2017, 11, 108–115, DOI:10.1038/nphoton.2016.269
.
- X. Li, Y. Wu, S. Zhang, B. Cai, Y. Gu, J. Song and H. Zeng, CsPbX3 quantum dots for lighting and displays: Room-temperature synthesis, photoluminescence superiorities, underlying origins and white light-emitting diodes, Adv. Funct. Mater., 2016, 26, 2435–2445, DOI:10.1002/adfm.201600109
.
- H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X. Y. Zhu, Lead halide perovskite nanowire lasers with low lasing thresholds and high quality factors, Nat. Mater., 2015, 14, 636–642, DOI:10.1038/nmat4271
.
- S. K. Abdel-Aal, G. Kocher-Oberlehner, A. Ionov and R. N. Mozhchil, Effect of organic chain length on structure, electronic composition, lattice potential energy, and optical properties of 2D hybrid perovskites [(NH3)(CH2)n(NH3)]CuCl4, n = 2–9, Appl. Phys. A: Mater. Sci. Process., 2017, 123, 531, DOI:10.1007/s00339-017-1150-8
.
- J. A. McNulty and P. Lightfoot, Structural chemistry of layered lead halide perovskites containing single octahedral layers, Chem. crystallogr. Cryst. Eng., 2021, 8, 485–513, DOI:10.1107/S2052252521005418
.
- M. I. Balanov, O. A. Brylev, V. V. Korochencev, R. Kevorkyants, A. V. Emeline, N. I. Selivanov, Y. V. Chizhov, A. V. Syuy and D. S. Shtarev, Crystal structure and electronic properties of low-dimensional hexamethylenediaminium lead halide perovskites, Dalton Trans., 2023, 52, 6388–6397, 10.1039/D3DT00438D
.
- L. Mao, P. Guo, M. Kepenekian, I. Spanopoulos, Y. He, C. Katan, J. Even, R. Schaller, R. Seshadri, C. C. Stoumpos and M. G. Kanatzidis, Organic cation alloying on intralayer A and interlayer A′ sites in 2D hybrid Dion-Jacobson lead bromide perovskites (A′)(A)Pb2Br7, J. Am. Chem. Soc., 2020, 142, 8342–8351, DOI:10.1021/jacs.0c01625
.
- E. J. Crace, A. C. Su and H. I. Karunadasa, Reliably obtaining white light from layered halide perovskites at room temperature, Chem. Sci., 2022, 13, 9973–9979, 10.1039/d2sc02381d
.
- S. Kahmann, D. Meggiolaro, L. Gregori, E. K. Tekelenburg, M. Pitaro, S. D. Stranks, F. De Angelis and M. A. Loi, The origin of broad emission in 100 two-dimensional perovskites: Extrinsic vs. intrinsic processes, ACS Energy Lett., 2022, 7, 4232–4241 CrossRef CAS
.
- C. Deng, G. Zhou, D. Chen, J. Zhao, Y. Wang and Q. Liu, Broadband photoluminescence in 2D organic−inorganic hybrid perovskites: (C7H18N2)PbBr4 and (C9H22N2)PbBr4, J. Phys. Chem. Lett., 2020, 11, 2934–2940, DOI:10.1021/acs.jpclett.0c00578
.
- D. G. Billing and A. Lemmerer, Bis(pentane-1,5-diammonium) decaiodotriplumbate(II), Acta Cryst., 2004, C60, m224–m226, DOI:10.1107/S0108270104007553
.
- W. Yang, X. Xiao, H. He, G. Tong, J. Hu, X. Xiao, J. Chen, M. Li and Y. He, Intermolecular hydrogen-bonding correlated structure distortion and broadband white-light emission in 5-ammonium valeric acid templated lead chloride perovskites, Cryst. Growth Des., 2021, 21, 5731–5739, DOI:10.1021/acs.cgd.1c00566
.
- A. P. E. X. Bruker, 2. BrukerAXS Inc., Madison, Wisconsin, USA, 2008.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775, DOI:10.1103/PhysRevB.59.1758
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Erratum: Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS
; J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef
.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561, DOI:10.1103/PhysRevB.47.558
.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mat. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186, DOI:10.1103/PhysRevB.54.11169
.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192, DOI:10.1103/PhysRevB.13.5188
.
- T. Williams, C. Kelley, E. A. Merritt, C. Bersch, H.-B. Bröker, J. Campbell, R. Cunningham, D. Denholm, G. Elber, R. Fearick, C. Grammes, L. Hart, L. Hecking, P. Juhász, T. Koenig, D. Kotz, E. Kubaitis, R. Lang, T. Lecomte, A. Lehmann, J. Lodewyck, A. Mai, B. Märkisch, P. Mikulík, D. Sebald, C. Steger, S. Takeno, T. Tkacik, J. van der Woude, J. R. van Zandt, A. Woo and J. Zellner, Gnuplot 5.2: An interactive plotting program, 2018.
- K. Momma and F. J. Izumi, VESTA: A three-dimensional visualization system for electronic and structural analysis, J. Appl. Crystallogr., 2008, 41, 653–658, DOI:10.1107/S0021889808012016
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P.
J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr. Cryst. Mater., 2005, 220, 567–570, DOI:10.1524/zkri.220.5.567.65075
.
- K. Refson, P. R. Tulip and S. J. Clark, Variational density functional perturbation theory for dielectrics and lattice dynamics, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114, DOI:10.1103/PhysRevB.73.155114
.
- J. Aarons, A new CASTEP and ONETEP geometry optimiser, https://www.hector.ac.uk/cse/distributedcse/reports/castep-geom/castep-geom/HTML/dCSE_project.html.
- X. Gonze and C. Lee, Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355, DOI:10.1103/PhysRevB.55.10355
.
- G. M. Sheldrick, SHELXT – Integrated space-group and crystal-structure determination, Acta Cryst., 2015, A71, 3–8, DOI:10.1107/S2053273314026370
.
- D. Cortecchia, J. Yin, A. Petrozza and C. Soci, White light emission in low-dimensional perovskites, J. Mater. Chem. C, 2019, 7, 4956–4969, 10.1039/c9tc01036j
.
- C. C. Stoumpos and M. G. Kanatzidis, The renaissance of halide perovskites and their evolution as emerging semiconductors, Acc. Chem. Res., 2015, 48, 2791–2802, DOI:10.1021/acs.accounts.5b00229
.
-
D. W. Mayo, F. A. Miller and R. W. Hannah, Course notes on the interpretation of infrared and Raman spectra, John Wiley & Sons Inc., 2004 Search PubMed
.
-
G. Socrates, Infrared and Raman characteristic group frequencies: Tables and charts, John Wiley & Sons Inc., 2004 Search PubMed
.
- A. C. Legon, The nature of ammonium and methylammonium halides in the vapour phase: hydrogen bonding versus proton transfer, Chem. Soc. Rev., 1993, 22, 153–163, 10.1039/CS9932200153
.
- A. J. Barnes and M. P. Wright, Strongly hydrogen-bonded molecular complexes studied by matrix isolation vibrational spectroscopy. Part 3. Ammonia–hydrogen bromide and amine–hydrogen bromide complexes, J. Chem. Soc., Faraday Trans. 2, 1986, 82, 153–164, 10.1039/F29868200153
.
- S. M. Pratik, S. Chakraborty, S. Mandal and A. Datta, Cooperativity in a new role: Stabilization of the ammonium salts in the solid state over their H-bonded complexes in the gas phase, J. Phys. Chem. C, 2015, 119, 926–933, DOI:10.1021/jp510479n
.
- J. A. Snyder, R. A. Cazar, A. J. Jamka and F.-M. Tao, Ab initio study of gas-phase proton transfer in ammonia−hydrogen halides and the influence of water molecules, J. Phys. Chem. A, 1999, 103, 7719–7724, DOI:10.1021/jp991918j
.
- https://webbook.nist.gov/cgi/cbook.cgi?ID=C462942; https://webbook.nist.gov/cgi/cbook.cgi?ID=B6009315.
- M. E. Baldwin, The infrared spectra of some diamines and diamine salts, Spectrochim. Acta, 1962, 18, 1455–1461, DOI:10.1016/0371-1951(62)80006-X
.
- A. Cabana and C. Sandordy, The infrared spectra of solid methylammonium halides, Spectrochim. Acta, 1962, 18, 843–861, DOI:10.1016/0371-1951(62)80089-7
.
- L. Andrews, X. Wang and Z. Mielke, Infrared spectrum of the H3N–HCl complex in solid Ne, Ne/Ar, Ar, and Kr. Matrix effects on a strong hydrogen-bonded complex, J. Phys. Chem. A, 2001, 105, 6054–6064, DOI:10.1021/jp010323x
.
- T. Steiner, The hydrogen bond in the solid state, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS
.
-
K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination compounds, Wiley and Sons Inc., 4th edn, 1986 Search PubMed
.
- J. Bellanato, Infra-red spectra of ethylenediamine dihydrochloride and other amine hydrochlorides in alkali halide disks, Spectrochim. Acta, 1960, 16, 1344–1357 CrossRef CAS
.
- W. Setyawan and S. Curtarolo, High-throughput electronic band structure calculations: Challenges and tools, Comput. Mater. Sci., 2010, 49, 299–312 CrossRef
.
- J. Wiktor, U. Rothlisberger and A. Pasquarello, Predictive determination of band gaps of inorganic halide perovskites, J. Phys. Chem. Lett., 2017, 8, 5507–5512 CrossRef CAS PubMed
.
-
N. F. Mott and R. W. Gurney, Electronic Processes in Ionic Crystals, Oxford University
Press, London, 2nd edn, 1948 Search PubMed
.
- F. Seitz, Speculations on the properties of the silver halide crystals, Rev. Modern Phys., 1951, 23, 328–352 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2269539 and 2269541. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3tc02767h |
| This journal is © The Royal Society of Chemistry 2024 |