Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding trends in conductivity in four isostructural multifunctional crystals of Se substituted bis-dithiazolyl radicals†‡
C.
Roncero-Barrero
 a,
M. A.
Carvajal
a,
J.
Ribas-Ariño
a,
M. A.
Carvajal
a,
J.
Ribas-Ariño
 *a,
I.
de P. R. Moreira
*a,
I.
de P. R. Moreira
 a and
M.
Deumal
a and
M.
Deumal
 *b
*b
aDepartament de Ciència de Materials i Química Física and IQTCUB, Universitat de Barcelona, Martí i Franquès 1-11, E-08028 Barcelona, Spain. E-mail: j.ribas@ub.edu
bSerra-Húnter Fellow, Departament de Ciència de Materials i Química Física and IQTCUB, Universitat de Barcelona, Martí i Franquès 1-11, E-08028 Barcelona, Spain. E-mail: merce.deumal@ub.edu
First published on 28th November 2023
Abstract
Materials based on stable organic radicals are very promising for the development of single-component organic conductors. However, the lack of studies addressing the quantitative calculation of the parameters defining their conductivity hampers progress. To contribute to this field, we computationally study four isostructural compounds with different Se-contents belonging to the key pyridine-bridged bisdithiazolyl family (namely, (S,S)-bisdithiazolyl, (S,Se) and (Se,S) mixed-thiaselenazolyl, and (Se,Se)-bisdiselenazolyl) with remarkable variation in the electrical conductivity (σSS < σSeS < σSSe < σSeSe) that cannot be explained on simple grounds. This trend here is explained by analyses of the local microscopic parameters playing the leading role in charge transport mediated by the molecular hopping mechanism: reorganization energy (λ), electronic couplings (HDA), electron-transfer rate constants (kDA), and charge-carrier density (ρc). Our results reveal the preference for hole conduction. The lowest conductivity of (S,S) arises from its largest λ, and smallest HDA's and ρc, resulting in a 1D conductor along the π-stack. Instead, the largest conductivity of (Se,Se) originates in its smallest λ, largest ρc and a set of HDA electronic couplings that not only are the largest but also define a 3D topology of conduction pathways along both lateral contacts and π-stacking. Comparison of (Se,S) and (S,Se) shows that although (Se,S) features the largest kDA and the smallest λ values, (S,Se) exhibits the largest electrical conductivity since it shows a 3D conduction topology because of lateral contacts and has a larger ρc value. Our take-home message is that one needs to master a holistic view of the parameters governing the charge transport process (namely, λ, HDA, topology of conduction paths, and ρc) to understand the trends in conductivity in radical-based molecular materials.
Introduction
Organic radical conductors constitute an important research line of multifunctional materials with interesting technological applications.1–5 These materials are targeted to exhibit a large variety of magnetic, electric and optical properties by means of chemical modulation of the organic building blocks, endowing them with great potential for applications such as battery components,6–8 organic light-emitting diodes (OLEDs),9–11 and as components in organic electronics12–14 and organic spintronics.15–19 Organic semiconductors with magnetic properties are a cheaper, light-weight and less environmentally harmful alternative to conventional inorganic materials based on scarce rare earth and transition metals.20–23 The use of organic materials in spin electronics overcomes the problem of the exceedingly fast spin relaxation times that inorganic materials have, making them a promising substitute for spintronic devices.24–27 However, despite these advantages, the relatively low conductivity of these materials, in comparison with traditional metals or inorganic semiconductors, has been a limitation for their technological applications. The use (or incorporation) of paramagnetic centers as building blocks of these molecular materials potentially enhances their electronic and magnetic properties28 and sometimes, additionally, gives rise to entanglement between both properties.16,29 In general, there is a large body of information regarding spin exchange pathways in organic radical based multifunctional materials.30 In stark contrast, with the exception of certain family of polymers,31–34 there is no detailed information on which parameters control their conductivity, namely density of charge carriers, electronic couplings, electron–phonon coupling and a detailed description of all possible conduction paths in the material. The lack of this knowledge prevents the efficient use of the wide possibilities of chemical modulation for a rational design of their properties. Therefore, it is exceedingly important to carry out studies aimed at determining all these parameters to establish realistic models for understanding their magnetic and conducting properties. Computational modelling is an invaluable tool to obtain these parameters as well as structure–property relationships that can provide essential information to design new materials with potential technological applications. However, the open-shell nature of the molecular building blocks makes these systems a challenge for quantum chemistry methods. Indeed, the competition between charge localization to enhance magnetism, and charge transport to enhance conductivity is a difficult scenario for present day electronic structure methods that require special care and analysis. In addition, the local nature of electron hopping in molecular materials limits the validity of using the band structure of the ground state of the material to interpret its conductivity and requires the exploration of cluster models to evaluate these parameters.In this work, we will focus on a subset of molecular compounds belonging to the family of bisdithiazolyl (bisDTA)-derived materials,35–51 which is one of the most important families of single-component organic conductors based on molecular radicals. Within the bisDTA family of compounds, the delocalization of unpaired electrons over the molecular skeleton and a wise choice of the substituents of the central ring make them stable over dimerization, which is a typical problem encountered in radical-based molecular materials. In fact, π- or σ-dimerization of bisDTA radicals has been thus far reported only for a few systems,39,40,42,52–55 which means that they are robust π-radical-based materials. These organic π-radicals are thus regarded as promising building blocks for the synthesis of multifunctional materials since (1) they have a planar molecular structure leading to a possible π-stacking in the crystal providing a feasible path for electron conduction,28,56–68 and (2) the unpaired electron of the radical centers opens the possibility for interesting magnetic and spintronic properties because this unpaired electron resides in a frontier orbital of the constituent molecular entities that will also participate in the electron conductivity process of the material. The resulting crystallographic arrangement of these building blocks will thus define the properties of the materials, which can be tailored by changing the bulky substituents bonded to the central ring.35,38,44,69–72 Moreover, the substitution of sulphur atoms by a heavier alternative, such as selenium, has been proven to increase conductivity and modify the magnetic response of the material leading to a wide range of multifunctional responses ranging from weak to moderate ferromagnetic (FM) or antiferromagnetic (AFM) semiconductors to metallic conductors.38,41,53,69,71–76
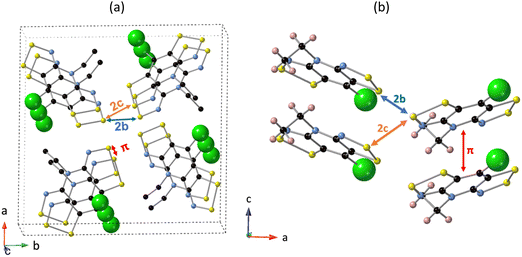
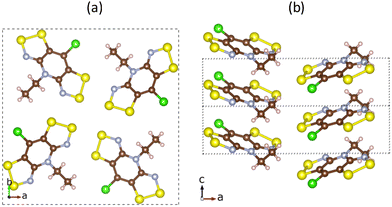
To understand the structure–property relationships in the bisDTA-family of materials, we believe that a comparison of the electronic structures and a detailed analysis of the electron hopping process of a series of closely related materials with similar molecular and crystal structural features will provide a well-defined set of systems to rationalize their distinct properties. A particularly interesting family of isostructural materials based on bisDTA analogues includes the bisdithiazolyl, thiaselenazolyl, and bisdiselenazolyl molecular crystals, which have been studied in detail by Robertson et al.41 (see Fig. 1a for bisDTA common building block, where the E1 and E2 positions are occupied either by S or Se atoms and the resulting molecular materials have been named according to their S/Se substitutions at (E1,E2) positions as bisdithiazolyl (S,S), bisdiselenazolyl (Se,Se), and mixed thiaselenazolyl (Se,S) and (S,Se) molecular materials). The experimental results showed that Se-substitutions significantly affect both the charge transport and the magnetic response of the materials. Electric conductivity (σE1,E2) increases depending on the S/Se ratio as σSS < σSeS < σSSe < σSeSe (see Fig. 1b for values of σ at 300 K in S cm−1). Although a conductivity increase was expected with the incorporation of Se, mixed thiaselenazolyl (S,Se) and (Se,S) materials demonstrate that the particular position occupied by the heteroatoms within the ring also affects the magnitude of the conductivity, with the σSSe at 300 K being one order of magnitude larger than σSeS. Activation energies (Ea) obtained using the experimental conductivity data range from 0.43 eV to 0.19 eV (see Ea values listed in Fig. 1b), indicating that a hopping mechanism is expected to prevail over electronic band conduction in this family of bisDTA compounds.
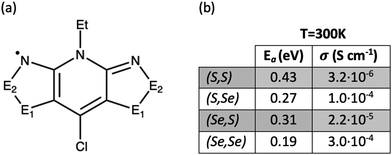 | ||
| Fig. 1 (a) General molecular representation of bisDTA radicals studied in this work, classified according to whether E1 and E2 positions are occupied by S or Se atoms. In the following, the constituent radical building blocks (and the corresponding materials) will be referred to as (E1,E2), namely, bisdithiazolyl (S,S) radical, mixed thiaselenazolyl (S,Se) and (Se,S) radicals, and bisdiselenazolyl (Se,Se) radical. (b) Activation energy (Ea) and conductivity (σ) at 300 K extracted from ref. 41. | ||
A detailed knowledge of the influence of the S-by-Se substitution on the microscopic parameters that govern conductivity of bisDTA compounds displayed in Fig. 1a would be the key to rationalize their different charge transport properties and, more broadly, to obtain structure–property correlations in bisDTA materials. In this work, we will present the results of a computational study carried out to obtain the density of charge carriers (ρc), the electronic couplings (HDA), and the electron–phonon couplings (in terms of the reorganization energy (λ)) of the here-selected multifunctional materials. A detailed description of all possible conduction paths of these materials in terms of the relevant electron-transfer rate constants (kDA) between nearby molecular pairs, together with a description of their overall conduction dimensionality, will also be provided. Note that all these parameters are very important to characterize charge transport in molecular materials, regardless of the transport mechanism (band, hopping or intermediate regime) operative in the material under study. As previously mentioned, the few examples in the literature that deal with this problem are mainly related to nonconjugated radical polymers.31–34 Therefore, to the best of our knowledge, this is the first work in which all the parameters that control the conductivity of a molecular crystal of a single-component radical conductor are obtained. Furthermore, our contribution here is not only to explain the tendencies in conductivity (which increases two orders of magnitude from (S,S) to (Se,Se) compounds41) but also to identify the key microscopic parameters behind their different transport properties.
Methods
Theoretical background
Charge transport has been typically studied through model Hamiltonians according to the prevailing charge transport mechanism in the material under study. These models are usually classified into three regimes based on the degree of charge delocalization of valence electrons upon the material. There are two limiting models, namely, itinerant band transport77 and localized hopping78–80 mechanisms, and a possible third regime intermediate to both. Recently, more intricate models based on electron dynamics to describe charge mobility have also been proposed.81–89 However, their use compared to model Hamiltonians is too complex to be applied in a regular basis to molecular systems. Therefore, although very recently some research has turned to the intermediate regime,90 when it comes to molecular materials, one has to basically resort to either rigid band transport or molecular hopping approaches.Band transport assumes the delocalization of charge carriers in electronic bands of the crystal (either valence or conduction).77 On the other hand, the hopping regime regards charge transport as realized by discrete localized “jumps” of charge between neighbor donor and acceptor sites. Broadly speaking, systems constituted by strong cohesive forces (metals, simple inorganic conductors and semiconductors, conjugated polymers, etc.) have been successfully modelled in the delocalized band regime. Yet, disordered materials and organic crystals with neutral building blocks (whose cohesive forces between molecular entities are dispersion and weak electrostatic interactions) have been mainly studied from a hopping perspective or a mixture of both limits.91–94 The computational evaluation of the model Hamiltonian parameters that describe the charge transport process in both regimes has been widely tested in different closed-shell organic molecular materials.95–99 However, as far as we know, the evaluation of all the parameters required to fully characterize charge transport in open-shell molecular materials is currently still not well established. Note that the few examples in the literature that deal with this problem are mainly related to organic polymers.31–34
At the crossroad whether to address the study of the title isostructural bisDTA-compounds from either a band or a hopping perspective, recent periodic calculations100 have shown that the band structure of the ground state of each of the four compounds exhibits narrow bands of 0.2–0.3 eV dispersion and indirect insulating band gaps of 1.15–1.40 eV. These calculated data are significantly larger than the measured activation energies for the conduction process and, hence, the result is insufficient to explain their conductivity in terms of the rigid band model (i.e., by using the energetic features of the valence and conduction bands of the electronic ground state of the system). In addition, a small energy difference (ca. 0.25 eV per unit formula) between the magnetic semiconductor ground state and a metallic diamagnetic (i.e., closed-shell) electronic solution was observed. This result suggested that the electronic conduction has contributions from a hopping mechanism that involves local excitations with activation energy well below the insulating band gap found for the electronic ground state, thus precluding a simple rationalization using a rigid band model. Notice that the former energy difference is of the same order of magnitude as the activation energies for the conduction process (Ea values range from 0.43 eV to 0.19 eV, see Fig. 1b). This piece of information further supports the evaluation of additional parameters that govern conductivity using a hopping approach to interpret the observed experimental trends. It must be also stressed that no experimental evidence indicates whether the resulting electric conductivity is due to holes or electrons and, thus, both mechanisms will have to be investigated. Let us here remind that within the hopping transport regime framework, the mobile charge (electron or hole) is trapped in the organic radicals and the conductivity remains activated above a given temperature. The charge transport mechanism can hence be described as charge hopping from the donor (D) to the acceptor (A) molecular moieties. It is then possible to calculate the macroscopic conductivity of the material by computing the rate of that process at the microscopic level using several cluster models of the system to describe the electron or hole hopping process between different nearby pairs of molecules.
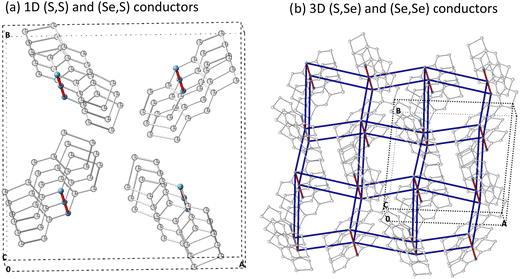
Finally, despite slight differences in distance and tilting angles between planes containing the molecular skeleton, let us mention that analogous crystal packing is displayed by all four materials, whose unit cell shares tetragonal P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m symmetry. The packing of these materials consists of π-stacks of four symmetry equivalent molecules around a C4 axis, parallel to the c-crystalline direction (see Fig. 2 for a representation of the crystal packing). It should be mentioned that Se-substitution does not just enhance conductivity, but also modifies the macroscopic magnetic response of the materials, which ranges from no-magnetic-order at low temperatures to bulk ferromagnetism. Computationally,101 these reported experimental magnetic data have been very recently rationalized for all four isostructural materials in terms of a 3D magnetic topology of FM and AFM JAB magnetic interactions which compete to result in the overall observed magnetism. The sign of the lateral and π-stacking JAB magnetic interactions has been found to be highly dependent on the Se-substitution and on small structural variations driven by the substitution itself or by external stimuli, like temperature. In view of these results and assuming a hopping limiting regime, the study of the charge transfer processes between radicals will consider both lateral and π-stacking radical–radical contacts. Within this framework, rate constants for electron and hole transfer processes will then be evaluated using the well-known Marcus rate equation between pairs of molecules (see eqn (1))102,103
21m symmetry. The packing of these materials consists of π-stacks of four symmetry equivalent molecules around a C4 axis, parallel to the c-crystalline direction (see Fig. 2 for a representation of the crystal packing). It should be mentioned that Se-substitution does not just enhance conductivity, but also modifies the macroscopic magnetic response of the materials, which ranges from no-magnetic-order at low temperatures to bulk ferromagnetism. Computationally,101 these reported experimental magnetic data have been very recently rationalized for all four isostructural materials in terms of a 3D magnetic topology of FM and AFM JAB magnetic interactions which compete to result in the overall observed magnetism. The sign of the lateral and π-stacking JAB magnetic interactions has been found to be highly dependent on the Se-substitution and on small structural variations driven by the substitution itself or by external stimuli, like temperature. In view of these results and assuming a hopping limiting regime, the study of the charge transfer processes between radicals will consider both lateral and π-stacking radical–radical contacts. Within this framework, rate constants for electron and hole transfer processes will then be evaluated using the well-known Marcus rate equation between pairs of molecules (see eqn (1))102,103
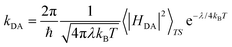 | (1) |
 | ||
| Fig. 2 Crystal structure of pure bisdithiazolyl (S,S) material. View of (a) ab-plane of the unit cell with a 4-fold pinwheel-like center, and (b) π-stacked radicals along the c-axis. | ||
The reorganization energy λ (in eqn (1)) evaluates how the geometry of the charge carriers (λin) and their surrounding (λex) is affected during the charge migration (i.e., the effects of electron–phonon coupling to assist the charge reorganization due to the moving charge during the hopping process of a hole or an electron between two molecules). Therefore, both contributions give rise to λ, which is usually expressed as λ = λin + λex. The λin term accounts for the effect of geometry adjustment that D donor and A acceptor moieties undergo after the charge transfer has taken place. It is usually computed following a 4-point scheme, which splits the term into two contributions, namely, λO for donor (where O stands for oxidation process, i.e., D → D+ + 1e−) and λR for acceptor (where R stands for reduction process, i.e., A+ + 1e− → A). The λin term can be thus calculated according to eqn (2) (note that EC) denotes the energy of the charged system (anion (D−) or cation (A+) for electron and hole transport, respectively), EN is the energy of the neutral system, and RN (RC) are the equilibrium geometries of the neutral (charged) radicals. Geometries of each species (RN and RC) are obtained by performing geometry optimizations of the isolated either neutral (N) or charged (C) species.
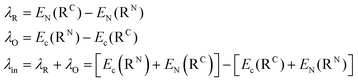 | (2) |
The HDA electronic coupling (in eqn (1)) is the Hamiltonian matrix element between diabatic DA+ and D+A charge localized states for the process of a single hole transfer at the transition state (TS) geometry 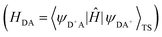 . Note that, for electron transfer, the diabatic states involved would be D−A and DA−. Here, HDA for hole and electron transfers has been obtained using the following equations:96,108,109
. Note that, for electron transfer, the diabatic states involved would be D−A and DA−. Here, HDA for hole and electron transfers has been obtained using the following equations:96,108,109
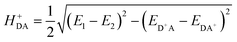 | (3a) |
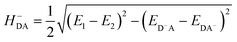 | (3b) |
Once all relevant rate constants between D donor and A acceptor pairs have been evaluated via the Marcus equation (eqn (1)), we can have access to the macroscopic charge transport properties of our title bisDTA compounds, such as mobility and conductivity. Given the lack of experimental data using single crystals to validate our calculations, we have decided to estimate mobilities from the Einstein–Smoluchowski relation, which provides the bulk isotropic mobility of the material as:
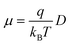 | (4) |
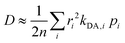 | (5) |
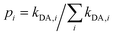 ). Notice that eqn (5) averages over all crystal directions to provide an estimate of the macroscopic diffusion coefficient. Let us also remind here that the experimental σ conductivity measurements on the four bisDTA-derivatives of interest were performed using powder samples.41 Therefore, the measured conductivity of a polycrystalline system does not bring any information regarding the anisotropy of the conductivity, and will be closer to an averaged estimation between all possible directions.
). Notice that eqn (5) averages over all crystal directions to provide an estimate of the macroscopic diffusion coefficient. Let us also remind here that the experimental σ conductivity measurements on the four bisDTA-derivatives of interest were performed using powder samples.41 Therefore, the measured conductivity of a polycrystalline system does not bring any information regarding the anisotropy of the conductivity, and will be closer to an averaged estimation between all possible directions.
Finally, the electric conductivity (σ) of each bisDTA material can be defined by the bulk isotropic mobility (μ), the density of the charge carriers (ρc), and the charge (q) of each one of those (see eqn (6)).
| σ = ρcqμ | (6) |
Computational details
We will next describe the computational details to calculate the parameters that control the kDA rate constants (namely, reorganization energy λin and electronic coupling HDA) and, hence, the electric conductivity, σ. To that aim, we have used two different cluster models: an isolated radical to calculate the λin reorganization energy and a cluster model to evaluate the HDA electronic coupling between neighboring pairs of radicals within the solid. Both models have been extracted from reported X-ray crystallographic data at 100 K.41 Since there is no experimental evidence to unequivocally discriminate between hole transport and electron transport as the predominant conductivity mechanism in bisDTA-derivative materials, both options have been considered. Hence, from now on, all reference to a charged cluster will encompass both negatively (anion, electron transport) and positively (cation, hole transport) charged molecular moieties, unless otherwise specified.The reorganization energy term, λin, has been computed for all four bisDTA-derivative compounds using an isolated radical. Geometry relaxations have been conducted for neutral (RN) and charged (RC) isolated molecules at UB3LYP level,110 with a 6-311+G(d,p) basis set111–113 in vacuum. Secondly, EN(RN), EN(RC) and Ec(RN), Ec(RC) have been evaluated by means of single-point energy calculations with the previously neutral and charged optimized geometries. Finally, λin is obtained by means of eqn (2). All UDFT calculations have been performed using the Gaussian09 software.114 In addition, all four energies (namely, EN(RN), EN(RC) and Ec(RN), Ec(RC)) have been re-evaluated at CASSCF and CASPT2 levels using (6,7) and (8,7) active spaces for cation and anion, respectively, with OpenMolcas code115 and ANO RCC-type Gaussian basis functions116 (see ESI,‡ Section S1 for a discussion on the selection of the active spaces). The contractions of the atomic basis sets were the following: [9s8p3d] for Se, [7s6p1d] for S and Cl, [5s4p1d] for C and N, and [3s1p] for H. The standard zeroth order Hamiltonian for CASPT2 calculations uses an IPEA shift of 0 a.u. and a shift equal to 0.2 a.u.
The evaluation of the HDA electronic couplings requires the selection of pairs of charge carriers. Accordingly, a complete analysis of each crystal has been performed to select the pairs of bisDTA radicals that are to be candidates to present a non-negligible HDA. Robertson et al.41 have stressed the importance of the E2⋯E2 contacts (see Fig. 1) to rationalize the different conducting and magnetic responses encountered in their experiments, since it has been found that contraction of E2⋯E2 distances correlates with an enhancement of conductivity and magnetism. Therefore, the E2⋯E2 distance has been taken as selection criteria for D⋯A pairs of bisDTA-radicals, with a 7.0 Å threshold (note that van der Waals E2⋯E2 distance is ca. 3.9 Å117). These analyses resulted in 13 pairs of radicals as potential candidates (see ESI,‡ Section S2 for a detailed analysis of the selection of D⋯A pairs of bisDTA radicals). Tests were then conducted using an adapted Koopmans' theorem for open-shell systems based on ROB3LYP/6-311+G(d,p) calculations to screen those pairs of molecules with the largest HDA electronic coupling (see ESI,‡ Section S3). The electronic coupling for those successfully screened candidates was obtained by optimizing the diabatic charge localized states (either D+A/DA+ or D−A/DA−) via state-specific CASSCF calculations, and then evaluating the adiabatic energies (E1, E2) in eqn (3) using the RASSI module of OpenMolcas (see paragraph above for basis set details). The active spaces used in the state-specific calculations were (13,14) and (15,14) for cation (D+A/DA+) and anion (D−A/DA−) pairs, respectively (see ESI,‡ Section S4 for selection of the active spaces). For bisDTA title compounds, it must be stressed that (ED+A − EDA+) and (ED−A − EDA−) cannot be neglected specially for the screened pairs of molecules showing lateral contacts.
Referring to the calculation of the D diffusion coefficient, one should address the choice of distances between bisDTA moieties (namely, ri in eqn (5)), which we take as the shortest distance between N⋯E1 atoms. In parallel, the density of charge carriers that is required to evaluate conductivity (ρc in eqn (6)) is obtained by calculating the density of states (DOS) diagram of the electronic ground state of each bisDTA crystal. In an intrinsic pure semiconductor, the concentration of electrons (or holes) comes from the excitation of electrons from the valence to the conduction bands and, using the quadratic approach of these bands, DOS can be evaluated by means of the band gap (Eg) and, hence, ρc can be expressed as:
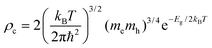 | (7) |
Results and discussion
Calculation of λ at UB3LYP, CASSCF and CASPT2 levels of theory provides insight on the energy cost for the radical to adapt to the charge transfer in order to adjust the extra charge. Our results reveal that calculated λ values show a consistent preference for the cationic form (λ+ < λ−), irrespective of the method (see Table 1). This is relevant because it hints at the conductivity being mainly driven by hole transport. Here let us remark that a large λSS indicates a higher energy cost for the (S,S) radical to adjust the extra charge compared to (Se,Se), which can be understood in terms of Se being a more polarizable element. Note also that mixed materials have the same content of S and Se but λSSe is larger than λSeS. The difference in reorganization energy between mixed (S,Se) and (Se,S) isomers can be qualitatively understood by analyzing the variation of the Mulliken charge distribution on the N−E1−E2 moiety upon structure relaxation in response to the redox process,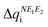 where i = oxidation/reduction (see ESI,‡ Section S5). We focus on the N−E1−E2 moiety because this is the region in which the excess charge is mostly delocalized. Considering that smaller values of
where i = oxidation/reduction (see ESI,‡ Section S5). We focus on the N−E1−E2 moiety because this is the region in which the excess charge is mostly delocalized. Considering that smaller values of 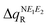 and
and 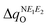 are expected to lead to smaller energy penalties, and thus to smaller values of λR and λO (see eqn (2)), we can rationalize the difference between the two isomers in terms of
are expected to lead to smaller energy penalties, and thus to smaller values of λR and λO (see eqn (2)), we can rationalize the difference between the two isomers in terms of 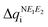 in (Se,S) being smaller than in (S,Se) (see Fig. 3). Although the relative ordering of reorganization energies has a plausible explanation, the trends observed (λSS > λSSe > λSeS > λSeSe) partially follow the opposite trend than experimentally measured conductivity (σSS < σSeS < σSSe < σSeSe). Remarkably, the ordering of the reorganization energy for (S,Se) and (Se,S) is in conflict with the ordering of their conductivities (see ESI,‡ Section S6 for the qualitative explanation of this trend). As expected, the reorganization energy on its own cannot rationalize the tendencies in conductivity of the four isostructural pyridine-bridged bisDTA compounds. Therefore, the electronic couplings between pairs of nearby molecules corresponding to different potential hopping paths will be next assessed.
in (Se,S) being smaller than in (S,Se) (see Fig. 3). Although the relative ordering of reorganization energies has a plausible explanation, the trends observed (λSS > λSSe > λSeS > λSeSe) partially follow the opposite trend than experimentally measured conductivity (σSS < σSeS < σSSe < σSeSe). Remarkably, the ordering of the reorganization energy for (S,Se) and (Se,S) is in conflict with the ordering of their conductivities (see ESI,‡ Section S6 for the qualitative explanation of this trend). As expected, the reorganization energy on its own cannot rationalize the tendencies in conductivity of the four isostructural pyridine-bridged bisDTA compounds. Therefore, the electronic couplings between pairs of nearby molecules corresponding to different potential hopping paths will be next assessed.
| (S,S) | (S,Se) | (Se,S) | (Se,Se) | ||
|---|---|---|---|---|---|
| λ + | UB3LYP | 202.43 | 183.93 | 167.77 | 152.45 |
| CASSCF | 258.47 | 238.69 | 209.80 | 192.43 | |
| CASPT2 | 219.25 | 200.70 | 196.92 | 183.16 | |
| λ − | UB3LYP | 384.15 | 333.63 | 302.79 | 257.34 |
| CASSCF | 373.66 | 320.71 | 279.39 | 241.35 | |
| CASPT2 | 454.50 | 381.06 | 355.60 | 295.56 | |
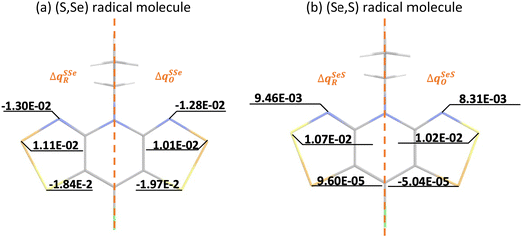 | ||
| Fig. 3 Atomic Mulliken charge analysis of the neutral (RN) and charged (RC) geometries of (a) (S,Se) and (b) (Se,S) materials. In each image, the charge difference Δq for acceptor (A, reduction ΔqXYR) and donor (D, oxidation ΔqXYO) are shown in the half left and half right parts of the XY radical molecules, respectively, since the main changes between (S,Se) and (Se,S) systems are localized in N − E2 − E1 atoms. Note that Δq on the missing half of the molecules is equivalent to the one represented. See ESI,‡ Section S5 for the remaining systems. | ||
The analysis based on the adapted Koopmans' theorem for open-shell species indicates that, for the four title compounds, there are only three types of bisDTA radical pairs that may lead to significantly large values of the HDA electronic coupling, namely, π-stack, 2b- and 2c-pairs (see ESI,‡ Section S3 for data on the screening, and Fig. 4 for a representation of bisDTA pairs with relevant HDA). The computed HDA values of the selected pairs at CASSCF level show a predominance of Hπ in all the systems under study, and among Hπ the hole transport is favored since H+π > H−π, reinforcing the take-home message extracted from the reorganization energy data (see Table 2). A comparison of HDA values using the adapted Koopman's theorem and at CASSCF level shows that their order of magnitude agrees. However, the trends of the CASSCF results are at odds with the Koopman's estimated values according to which H2b and H2c were predominant (see ESI,‡ Section S3). Hence the need to perform higher level state-specific charge localized CASSCF calculations to evaluate electronic couplings.
| (S,S) | (S,Se) | (Se,S) | (Se,Se) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r i | H +DA | H −DA | r i | H +DA | H −DA | r i | H +DA | H −DA | r i | H +DA | H −DA | |
| π | 3.53 | 34.60 | 17.18 | 3.55 | 55.88 | 28.75 | 3.58 | 50.51 | 28.09 | 3.65 | 65.45 | 49.53 |
| 2b | 3.35 | 9.87 | 15.89 | 3.41 | 32.34 | 37.49 | 3.28 | 4.99 | 21.46 | 3.34 | 30.10 | 40.04 |
| 2c | 3.53 | 2.47 | 4.14 | 3.56 | 2.82 | 2.73 | 3.65 | 10.69 | 20.51 | 3.70 | 9.90 | 15.34 |
Our data reveal that all three types of HDA electronic couplings increase from (S,S) to (Se,Se) with the Se content, meaning charge-transport is favored in (Se,Se). This result is in agreement with the conclusion drawn from λSS > λSeSe, which indicates that (Se,Se) can better accommodate the extra charge. Interestingly, for mixed thiaselenazolyl materials, Hπ and H2b increase when Se is in the E2 position. This result is in conflict with the observed trend for λSSe > λSeS. Mixed (S,Se) and (Se,S) compounds are a clear example of the complex interplay of the electronic coupling and reorganization energy in shaping the overall conductivity: the former favors (S,Se), while the latter favors (Se,S). Remarkably, our computed HDA electronic couplings and λ reorganization energy show that all four compounds can be described using the polaronic hopping model since all HDA's < λ/2.96,119 Within this framework, we have calculated kDA rate constants using Marcus equation (eqn (1)) to quantify the interplay between both electronic couplings and reorganization energies and, in turn, the potential conducting pathways. As a final comment, the Marcus rate equation relies on the fact that vibrational levels assist the electronic transition between D and A moieties and, hence, is dependent on temperature being high.119 This fact restricts the analysis of the reported experimental data on the conductivity of the systems and, thus, we focus on the T = 300 K values only (see Table 3 for calculated hole and electron transport kDA values).
| (S,S) | (S,Se) | (Se,S) | (Se,Se) | |||||
|---|---|---|---|---|---|---|---|---|
| k +DA | k −DA | k +DA | k −DA | k +DA | k −DA | k +DA | k −DA | |
| π | 3.24 | 0.22 | 10.65 | 1.10 | 12.23 | 1.68 | 25.44 | 8.11 |
| 2b | 0.26 | 0.19 | 3.57 | 1.87 | 0.12 | 0.98 | 5.38 | 5.30 |
| 2c | 0.02 | 0.01 | 0.02 | 0.01 | 0.55 | 0.89 | 0.58 | 0.78 |
The calculated kDA data enables us to conclude (see values in Table 3): (1) a preference for hole conduction is observed by comparing the dominant rate constants for both hole (k+DA) and electron (k−DA) charge conductions at 300 K, and (2) the π-stacking prevails as the most probable direction for the charge hopping mechanism in all four materials. Nevertheless, it must be stressed that (Se,Se) shows the largest contribution of electron transport among all four bisDTA compounds, not only along the π-stack but also along the 2b-pair direction. Having said that, if one now considers hole transport, (S,S) and (Se,S) are essentially 1D conductors along the π-stacking direction (see Fig. 5a). Instead, (Se,Se) and (S,Se) feature a dominant conduction path along the π-stack but with important lateral contacts between bisDTA radicals (see 2b pairs in Fig. 4 and 5b for conduction paths) that ultimately define them as 3D conductors. For (S,S) and (Se,Se), comparison of the largest k+π rate constants shows that k+π,SS < k+π,SeSe which means that (Se,Se) is a better conductor, in line with both our calculations on electronic couplings and reorganization energy, and experiment. In turn, the rate constants for mixed (S,Se) and (Se,S) lie in between the two limiting (S,S) and (Se,Se) cases, which agrees with experimental data. However, rationalization of the tendencies for mixed compounds is more subtle since, although k+π,SeS < k+π,SSe, (S,Se) has an extra conduction path along the 2b-pair direction rendering it as a 3D conductor, as above mentioned. Let us remark here that these lateral conduction paths would not have emerged from an exclusive analysis of the crystal packing. To move forward, we will now calculate mobilities using the computed rate constants (see eqn (4) and (5)).
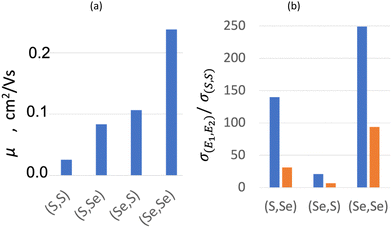
The resultant mobilities for both holes and electrons (μ+ and μ−, respectively) increase with the Se content from (S,S) to (Se,Se) (see Table 4), in agreement with experimental conductivity. The calculated values, which range from 0.026 to 0.238 cm2 V−1 s−1, are similar to those found for other organic semiconductors (10−3–101 cm2 V−1 s−1),91,107,120 and much smaller than those found for intrinsic inorganic semiconductors (101–105 cm2 V−1 s−1).121 Despite that μ+ shows a clear dominance in all bisDTA, as expected for a hopping semiconductor, relative contribution of μ− increases from ∼8% (μ−/μtotal, assuming μtotal = μ+ + μ−) in (S,S) to ∼23% in (Se,Se) material. Interestingly, the smaller total mobility of (S,Se) compared to (Se,S) (see Fig. 6a, and 0.084 vs. 0.106 cm2 V−1 s−1, respectively, in Table 4) is at odds with the experimental conductivity trend (see orange bars in Fig. 6b, and 1.00 × 10−4vs. 2.20 × 10−5 S cm−1, respectively, in Table 4). Therefore, the relative ordering of mobility is only partially consistent with the relative ordering of conductivity. Indeed, for mixed thiaselenazolyl (Se,S) and (S,Se), mobility by itself cannot justify their conductivity. The lack of consistency between computed mobilities and experimental conductivity values calls for the evaluation of the density of the charge carriers (see ρc in eqn (6)).
| μ + (cm2 V−1 s−1) | μ − (cm2 V−1 s−1) | μ (cm2 V−1 s−1) |
σ
Exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (S cm−1)
(S cm−1) |
E g (eV) |
ρ
estc
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1/m3)
(1/m3) |
|
|---|---|---|---|---|---|---|
| a Data from ref. 41. b Data from ref. 100. c ρ estc is calculated using eqn (6) with the computed total mobility (μ) and experimental conductivity (σExp). | ||||||
| (S,S) | 0.024 | 0.002 | 0.026 | 3.20 × 10−6 | 1.34 | 7.80 × 1020 |
| (S,Se) | 0.071 | 0.012 | 0.084 | 1.00 × 10−4 | 1.15 | 7.48 × 1021 |
| (Se,S) | 0.096 | 0.010 | 0.106 | 2.20 × 10−5 | 1.26 | 1.29 × 1021 |
| (Se,Se) | 0.184 | 0.054 | 0.238 | 3.00 × 10−4 | 1.17 | 7.87 × 1021 |
The estimated ρc (eqn (6)) depends on Eg, which is related to the activation energy associated with the charge transfer process, Ea (see Fig. 1b). However, our calculation of this activation energy is restricted to vertical gaps using the ground state data, i.e., between its valence band maximum and conduction band minimum (namely, the electronic band gap). Therefore, this rigid band model approach misses relaxation processes undergone by the conduction band upon charge transfer. As such, the calculated rigid Eg fails to fully capture the physics of the conductivity process in these molecular systems. However gross the approximation is, we will still use with caution the estimated rigid Eg values to interpret the observed conductivity in the title compounds. Analysis of the electronic band structure of the ground states of the present bisDTA-derivatives, reported in a previous study,100 showed that all four title materials presented similar bands with optic band gaps around 1.15–1.34 eV (see Table 4). Given that (1) these values are between 3 and 6 times larger than the experimentally determined Ea values (ranging from 0.43 to 0.19 eV) and (2) ρc depends exponentially on Eg, the resulting calculated ρc values are expected to be massively underestimated (see ESI,‡ Section S7). This will, in turn, imply that the calculated conductivities are to be smaller than the experimentally measured data. Since we are only interested in understanding the trends in conductivity in the four title isostructural compounds, hereafter we will report relative data. Results for (S,S) will be taken as reference owing to its smallest value of conductivity to compare both calculated and experimental conductivity data. As shown in Fig. 6b, a comparison between our calculated conductivity and the experimental data exhibits the same relative ordering, namely, σSS < σSeS < σSSe < σSeSe.
In view of the offset between relative conductivity values, we have estimated the density of charge carriers as a reality check. To do so, we have resorted to eqn (6) using the computed total mobilities and experimental conductivities (see Table 4 for values). Interestingly, our estimated values of the charge carrier density fit into the low charge density regime typically found in organic photovoltaic devices and organic light emitting diodes under operation (1021–1023![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m−3).122 The calculated as well as estimated values of ρc (see ESI,‡ Section S7 and Table 4) highlight the larger number of charge carriers in (S,Se), thus providing a rationale for (S,Se) exhibiting larger conductivity than (Se,S) despite having smaller mobility. The tendency observed for ρc in (S,Se) and (Se,S) can be further supported by the computed disproportionation energy (ΔEdisp) associated with the charge separation process (R˙ + R˙ → R+ + R−). Indeed, ΔEdisp for (S,Se) is slightly smaller than for (Se,S), which favors the generation of charge carriers in (S,Se). Notably, the tendency observed for (S,Se) mirrors data from cyclic voltammetry reported in ref. 41 (see ESI,‡ Section S8 for further details). Therefore, although absolute values for conductivity cannot be reproduced, we are certain that our results are able to capture the microscopic picture of the charge transfer process. In addition, our effective gaps for the charge transfer process and, in turn, the estimated charge carrier density, are compatible with small resistivity values. Accordingly, despite being semiconductors, the title compounds are corroborated to be quite good organic radical-based conductors, as realized experimentally.41
m−3).122 The calculated as well as estimated values of ρc (see ESI,‡ Section S7 and Table 4) highlight the larger number of charge carriers in (S,Se), thus providing a rationale for (S,Se) exhibiting larger conductivity than (Se,S) despite having smaller mobility. The tendency observed for ρc in (S,Se) and (Se,S) can be further supported by the computed disproportionation energy (ΔEdisp) associated with the charge separation process (R˙ + R˙ → R+ + R−). Indeed, ΔEdisp for (S,Se) is slightly smaller than for (Se,S), which favors the generation of charge carriers in (S,Se). Notably, the tendency observed for (S,Se) mirrors data from cyclic voltammetry reported in ref. 41 (see ESI,‡ Section S8 for further details). Therefore, although absolute values for conductivity cannot be reproduced, we are certain that our results are able to capture the microscopic picture of the charge transfer process. In addition, our effective gaps for the charge transfer process and, in turn, the estimated charge carrier density, are compatible with small resistivity values. Accordingly, despite being semiconductors, the title compounds are corroborated to be quite good organic radical-based conductors, as realized experimentally.41
To sum up, the take-home message is that Se-substitution affects both, charge mobility and density of carriers, depending on the position, and that only when both effects are considered the experimental tendency on σ is met. Final results show that improvement in conductivity by Se-substitution in bisDTA materials is, broadly speaking, due to two complementary effects: (i) for materials with the same conduction motif (namely, 1D for (S,S) and (Se,S), and 3D for (S,Se) and (Se,Se)), the Se-substitution has proved to favor charge migration, and (ii) when Se is placed in the E2 position (S,Se), the band gap shrinks and conductivity is enlarged thanks to an increase of the available charge carriers.
Finally, let us make a remark on the effect that anisotropy would have on the transport properties. Along this work, we have reported bulk isotropic mobilities and, thus, conductivities, since the experimental measurements were performed using powder samples. However, the differences in the magnitude of the charge transfer rate constants depending on the conduction path (see Table 2) hint at a potential role of anisotropy. Given that the π-stacking direction is most favored, one could envisage an experiment exploiting such anisotropy using single crystals with the electric field aligned along the π-stack. Specifically, hole and electron mobilities would only have contribution coming from that direction (k+π and k−π) (see ESI,‡ Section S9), and our results show that in the worst-case scenario, namely for (S,S) and (Se,S) 1D conductors, the mobility is enhanced by ca. 8%. Instead, the enhancement achieved by (S,Se) and (Se,Se) 3D conductors is about 14% and 20%, respectively. Consequently, within this family, the distinction between the least effective and most effective conductors would become more pronounced. Concerning anisotropy, one can come up with another possible experiment using single crystals, namely, switching the direction of the electric field, be it either along π or 2b charge channels (see ESI,‡ Section S8). Our estimates show that (Se,S) would feature the largest difference in terms of conductivities between the ‘on’ and ‘off’ states. However, this difference (ca. one order of magnitude) is likely too small to envisage possible applications.123
Conclusions
The variation in the electric conductivity of four isostructural pyridine-bridged bisDTA compounds with different Se-contents belonging to the same family of single-component organic conductors is remarkable (σSS < σSeS < σSSe < σSeSe) but cannot be explained based solely on the inspection of the crystal packing and rigid band models. We here elucidate this trend by analyzing the key parameters influencing charge transport, namely, reorganization energy (λ), electronic couplings (HDA), electron-transfer rate constants (kDA), dimensionality of the conduction path network, and density of charge carriers (ρc). These local parameters are suitably estimated by analyzing the hole or electron hopping process in cluster models including pairs of nearby molecules.Our results corroborate that all four title compounds can be described using the polaronic hopping model and reveal a preference for hole conduction. Furthermore, our analyses enable us to discriminate between their dimensionality in terms of their microscopic conduction paths within the crystal. An anisotropic conduction motif has emerged with larger charge transport rates along the π-stacking direction leading to a 1D conductor for the (S,S) and (Se,S) cases. Analogously, we can attribute a 3D conductive behavior to (S,Se) and (Se,Se) due to additional charge transfer paths with significant electronic couplings (namely, 2b lateral contacts) that interconnect the dominant π-stacking paths. It is important to remark that this dimensionality cannot be inferred from the direct observation of the crystal packing.
For (S,S) and (Se,Se), all key individual parameters per se (i.e., λ, HDA's and ρc) lead to the same conclusion: (S,S) and (Se,Se) are the worst and best conductors, respectively, within this pyridine-bridge family of bisDTA radicals. However, this does not hold for (S,Se) and (Se,S). In this case, it is the intricate interplay between this set of key parameters that allows us to justify their relative ordering in conductivity. The experimental conductivity trend can be indeed recovered when not only the set of charge transfer rates (kDA) is considered, but also the density of charge carriers is accounted for.
Referring to the density of charge carriers, it is proven that the rigid band model fails to quantitatively evaluate the activation energy for the conduction process in these molecular systems, as opposed to rigid inorganic systems. This arises from the fact that we use the ground state and vertical transitions, which is a drastic approximation when referring to the conductivity of the title compounds since it is mediated by means of the hopping mechanism. This highlights the limitations of both periodic approaches relying on the band structure of the electronic ground state and cluster models using HOMO–LUMO energy differences attempting to assess conductivity properties. The combination of experimental and computational data enables the estimation of the corresponding density of charge carriers. These results are consistent with typical values found in organic photovoltaic systems and organic light emitting diodes, thus, stressing the relevance of hybrid experimental and theoretical approaches to rationalize trends in conductivity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support from the Spanish Ministerio de Economía y Competitividad (Projects No. PID2019-109518GB-I00 and PID2020-117803GB-I00/AEI/10.13039/501100011033), Spanish Structures of Excellence María de Maeztu program (Grant No. CEX2021-001202-M), and Agència de Gestió d’Ajuts Universitaris i de Recerca of Generalitat de Catalunya (Project No. 2021 SGR 00354).References
- D. Yuan, W. Liu and X. Zhu, Chem., 2021, 7, 333–357, DOI:10.1016/j.chempr.2020.10.001.
- S. Dong and Z. Li, J. Mater. Chem. C, 2022, 10, 2431–2449, 10.1039/d1tc04598a.
- I. Ratera and J. Veciana, Chem. Soc. Rev., 2012, 41, 303–349, 10.1039/c1cs15165g.
- Z. X. Chen, Y. Li and F. Huang, Chem, 2021, 7, 288–332, DOI:10.1016/j.chempr.2020.09.024.
- T. Kubo, Bull. Chem. Soc. Jpn., 2021, 94, 2235–2244, DOI:10.1246/bcsj.20210224.
- K. Nakahara, K. Oyaizu and H. Nishide, Chem. Lett., 2011, 40, 222–227, DOI:10.1246/cl.2011.222.
- K. Nakahara, S. Iwasa, M. Satoh, Y. Morioka, J. Iriyama, M. Suguro and E. Hasegawa, Chem. Phys. Lett., 2002, 359, 351–354, DOI:10.1016/S0009-2614(02)00705-4.
- D. A. Wilcox, V. Agarkar, S. Mukherjee and B. W. Boudouris, in Annual Review of Chemical and Biomolecular Engineering, ed. M. F. Doherty, R. A. Segalman and R. S. Kane, ANNUAL REVIEWS, 4139 EL CAMINO WAY, PO BOX 10139, PALO ALTO, CA 94303-0139, 2018, Vol. 9, pp. 83–103 DOI:10.1146/annurev-chembioeng-060817-083945.
- P. Mayorga Burrezo, V. G. Jiménez, D. Blasi, I. Ratera, A. G. Campaña and J. Veciana, Angew. Chem., Int. Ed., 2019, 58, 16282–16288, DOI:10.1002/anie.201909398.
- Q. Peng, A. Obolda, M. Zhang and F. Li, Angew. Chem., Int. Ed., 2015, 54, 7091–7095, DOI:10.1002/anie.201500242.
- A. Obolda, X. Ai, M. Zhang and F. Li, ACS Appl. Mater. Inter., 2016, 8, 35472–35478, DOI:10.1021/acsami.6b12338.
- S. Mukherjee and B. W. Boudouris, Organic Radical Polymers: New Avenues in Organic Electronics, Springer Briefs in Materials, Springer International Publishing, Cham, Switzerland, 2017. ISBN: 978-3319585734 Search PubMed.
- X. Hu, W. Wang, D. Wang and Y. Zheng, J. Mater. Chem. C, 2018, 6, 11232–11242, 10.1039/c8tc04484h.
- T. Sukegawa, H. Omata, I. Masuko, K. Oyaizu and H. Nishide, ACS Macro Lett., 2014, 3, 240–243, DOI:10.1021/mz400644y.
- T. Y. Gopalakrishna, W. Zeng, X. Lu and J. Wu, Chem. Commun., 2018, 54, 2186–2199, 10.1039/c7cc09949e.
- T. Sugawara, H. Komatsu and K. Suzuki, Chem. Soc. Rev., 2011, 40, 3105–3118, 10.1039/c0cs00157k.
- R. Hayakawa, M. A. Karimi, J. Wolf, T. Huhn, M. S. Zöllner, C. Herrmann and E. Scheer, Nano Lett., 2016, 16, 4960–4967, DOI:10.1021/acs.nanolett.6b01595.
- C. Herrmann, G. C. Solomon and M. A. Ratner, J. Am. Chem. Soc., 2010, 132, 3682–3684, DOI:10.1021/ja910483b.
- S. Shil, D. Bhattacharya, A. Misra and D. J. Klein, Phys. Chem. Chem. Phys., 2015, 17, 23378–23383, 10.1039/c5cp03193a.
- DOE, Critical Supply Strategy, 2011, https://www.energy.gov/sites/prod/files/DOE_CMS2011_FINAL_Full.pdf.
- DOE, Critical Supply Strategy, 2021, https://www.energy.gov/sites/prod/files/2021/01/f82/DOE%20Critical%20Minerals%20and%20Materials%20Strategy_0.pdf.
- European Raw Materials Alliance, Rare Earth Magnets and Motors: A European Call for Action, 2021, https://eit.europa.eu/library/rare-earth-magnets-and-motors-european-call-action.
- V. Balaram, Geosci. Front., 2019, 10, 1285–1303, DOI:10.1016/j.gsf.2018.12.005.
- W. J. M. Naber, S. Faez and W. G. van der Wiel, J. Phys. D: Appl. Phys., 2007, 40, R205–R228, DOI:10.1088/0022-3727/40/12/R01.
- J. Devkota, R. Geng, R. C. Subedi and T. D. Nguyen, Adv. Funct. Mater., 2016, 26, 3881–3898, DOI:10.1002/adfm.201504209.
- S. Sanvito, Molecule-based magnets themed issue, in Chem. Soc. Rev., ed. J. S. Miller and D. Gatteschi, 2011, 40, pp. 3336–3355 10.1039/c1cs15047b.
- H. Gu, X. Zhang, H. Wei, Y. Huang, S. Wei and Z. Guo, Chem. Soc. Rev., 2013, 42, 5907–5943, 10.1039/c3cs60074b.
- J. M. Rawson, A. Alberola and A. Whalley, J. Mater. Chem., 2006, 16, 2560–2575, 10.1039/b603199d.
- H. Komatsu, M. M. Matsushita, S. Yamamura, Y. Sugawara, K. Suzuki and T. Sugawara, J. Am. Chem. Soc., 2010, 132, 4528–4529, DOI:10.1021/ja9109538.
- M. Deumal, S. Vela, M. Fumanal, J. Ribas-Arino and J. J. Novoa, J. Mater. Chem. C, 2021, 9, 10624–10646, 10.1039/d1tc01376a.
- Y. Tan, N. C. Casetti, B. W. Boudouris and B. M. Savoie, J. Am. Chem. Soc., 2021, 143, 11994–12002, DOI:10.1021/jacs.1c02571.
- T. W. Kemper, R. E. Larsen and T. Gennett, J. Phys. Chem. C, 2014, 118, 17213–17220, DOI:10.1021/jp501628z.
- T. W. Kemper, R. E. Larsen and T. Gennett, J. Phys. Chem. C, 2015, 119, 21369–21375, DOI:10.1021/acs.jpcc.5b06368.
- K. Sato, R. Ichinoi, R. Mizukami, T. Serikawa, Y. Sasaki, J. Lutkenhaus, H. Nishide and K. Oyaizu, J. Am. Chem. Soc., 2018, 140, 1049–1056, DOI:10.1021/jacs.7b11272.
- L. Beer, J. L. Brusso, A. W. Cordes, R. C. Haddon, M. E. Itkis, K. Kirschbaum, D. S. MacGregor, R. T. Oakley, A. A. Pinkerton and R. W. Reed, J. Am. Chem. Soc., 2002, 124, 9498–9509, DOI:10.1021/ja026118s.
- L. Beer, J. L. Brusso, A. W. Cordes, E. Godde, R. C. Haddon, M. E. Itkis, R. T. Oakley and R. W. Reed, Chem. Commun., 2002, 2562–2563, 10.1039/b207735n.
- L. Beer, J. F. Britten, O. P. Clements, R. C. Haddon, M. E. Itkis, K. M. Matkovich, R. T. Oakley and R. W. Reed, Chem. Mater., 2004, 16, 1564–1572, DOI:10.1021/cm035191u.
- J. L. Brusso, S. Derakhshan, M. E. Itkis, H. Kleinke, R. C. Haddon, R. T. Oakley, R. W. Reed, J. F. Richardson, C. M. Robertson and L. K. Thompson, Inorg. Chem., 2006, 45, 10958–10966, DOI:10.1021/ic061687c.
- K. Lekin, S. M. Winter, L. E. Downie, X. Bao, J. S. Tse, S. Desgreniers, R. A. Secco, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2010, 132, 16212–16224, DOI:10.1021/ja106768z.
- K. Lekin, H. Phan, S. M. Winter, J. W. L. Wong, A. A. Leitch, D. Laniel, W. Yong, R. A. Secco, J. S. Tse, S. Desgreniers, P. A. Dube, M. Shatruk and R. T. Oakley, J. Am. Chem. Soc., 2014, 136, 8050–8062, DOI:10.1021/ja502753t.
- C. M. Robertson, A. A. Leitch, K. Cvrkalj, R. W. Reed, D. J. T. Myles, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2008, 130, 8414–8425, DOI:10.1021/ja801070d.
- A. A. Leitch, C. E. McKenzie, R. T. Oakley, R. W. Reed, J. F. Richardson and L. D. Sawyer, Chem. Commun., 2006, 1088–1090, 10.1039/b517098b.
- A. A. Leitch, R. W. Reed, C. M. Robertson, J. F. Britten, X. Yu, R. A. Secco and R. T. Oakley, J. Am. Chem. Soc., 2007, 129, 7903–7914, DOI:10.1021/ja071218p.
- X. Yu, A. Mailman, P. A. Dube, A. Assoud and R. T. Oakley, Chem. Commun., 2011, 47, 4655–4657, 10.1039/c1cc10598a.
- A. Mailman, S. M. Winter, X. Yu, C. M. Robertson, W. Yong, J. S. Tse, R. A. Secco, Z. Liu, P. A. Dube, J. A. K. Howard and R. T. Oakley, J. Am. Chem. Soc., 2012, 134, 9886–9889, DOI:10.1021/ja303169y.
- X. Yu, A. Mailman, K. Lekin, A. Assoud, C. M. Robertson, B. C. Noll, C. F. Campana, J. A. K. Howard, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2012, 134, 2264–2275, DOI:10.1021/ja209841z.
- J. W. L. Wong, A. Mailman, K. Lekin, S. M. Winter, W. Yong, J. Zhao, S. V. Garimella, J. S. Tse, R. A. Secco, S. Desgreniers, Y. Ohishi, F. Borondics and R. T. Oakley, J. Am. Chem. Soc., 2014, 136, 1070–1081, DOI:10.1021/ja411057x.
- A. Mailman, J. W. L. Wong, S. M. Winter, R. C. M. Claridge, C. M. Robertson, A. Assoud, W. Yong, E. Steven, P. A. Dube, J. S. Tse, S. Desgreniers, R. A. Secco and R. T. Oakley, J. Am. Chem. Soc., 2017, 139, 1625–1635, DOI:10.1021/jacs.6b11779.
- A. Mailman, C. M. Robertson, S. M. Winter, P. A. Dube and R. T. Oakley, Inorg. Chem., 2019, 58, 6495–6506, DOI:10.1021/acs.inorgchem.9b00691.
- X. Yu, A. Mailman, K. Lekin, A. Assoud, P. A. Dube and R. T. Oakley, Cryst. Growth Des., 2012, 12, 2485–2494, DOI:10.1021/cg300107t.
- A. Mailman, S. M. Winter, J. W. L. Wong, C. M. Robertson, A. Assoud, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2015, 137, 1044–1047, DOI:10.1021/ja512235h.
- L. Beer, J. L. Brusso, R. C. Haddon, M. E. Itkis, A. A. Leitch, R. T. Oakley, R. W. Reed and J. F. Richardson, Chem. Commun., 2005, 1543–1545, 10.1039/b416352d.
- L. Beer, J. L. Brusso, R. C. Haddon, M. E. Itkis, H. Kleinke, A. A. Leitch, R. T. Oakley, R. W. Reed, J. F. Richardson, R. A. Secco and X. Yu, J. Am. Chem. Soc., 2005, 127, 18159–18170, DOI:10.1021/ja055122b.
- A. A. Leitch, X. Yu, C. M. Robertson, R. A. Secco, J. S. Tse and R. T. Oakley, Inorg. Chem., 2009, 48, 9874–9882, DOI:10.1021/ic901563n.
- H. Phan, K. Lekin, S. M. Winter, R. T. Oakley and M. Shatruk, J. Am. Chem. Soc., 2013, 135, 15674–15677, DOI:10.1021/ja4055806.
- R. C. Haddon, Nature, 1975, 256, 394–396, DOI:10.1038/256394a0.
- E. Coronado and P. Day, Chem. Rev., 2004, 104, 5419–5448, DOI:10.1021/cr030641n.
- S. K. Pal, M. E. Itkis, R. W. Reed, R. T. Oakley, A. W. Cordes, F. S. Tham, T. Siegrist and R. C. Haddon, J. Am. Chem. Soc., 2004, 126, 1478–1484, DOI:10.1021/ja037864f.
- S. K. Pal, M. E. Itkis, F. S. Tham, R. W. Reed, R. T. Oakley and R. C. Haddon, Science, 2005, 309, 281–284, DOI:10.1126/science.1112446.
- M. Vérot, J.-B. Rota, M. Kepenekian, B. Le Guennic and V. Robert, Phys. Chem. Chem. Phys., 2011, 13, 6657–6661, 10.1039/c0cp02124e.
- Y. Kobayashi, T. Terauchi, S. Sumi and Y. Matsushita, Nat. Mater., 2017, 16, 109–114, DOI:10.1038/NMAT4981.
- Y. Beldjoudi, M. A. Nascimento, Y. J. Cho, H. Yu, H. Aziz, D. Tonouchi, K. Eguchi, M. M. Matsushita, K. Awaga, I. Osorio-Roman, C. P. Constantinides and J. M. Rawson, J. Am. Chem. Soc., 2018, 140, 6260–6270, DOI:10.1021/jacs.7b12592.
- T. Murata, C. Yamada, K. Furukawa and Y. Morita, Commun. Chem., 2018, 1, #47, DOI:10.1038/s42004-018-0048-5.
- K. Molčanov, D. Stalke, A. Šantič, S. Demeshko, V. Stilinovič, Z. Mou, M. Kertesz and B. Kojić-Prodić, CrystEngComm, 2018, 20, 1862–1873, 10.1039/c7ce02146a.
- Y. Le Gal, T. Roisnel, P. Auban-Senzier, N. Bellec, J. Íñiguez, E. Canadell and D. Lorcy, J. Am. Chem. Soc., 2018, 140, 6998–7004, DOI:10.1021/jacs.8b03714.
- A. Mizuno, H. Benjamin, Y. Shimizu, Y. Shuku, M. M. Matsushita, N. Robertson and K. Awaga, Adv. Funct. Mater., 2019, 29, 1904181, DOI:10.1002/adfm.201904181.
- T. Kwon, J. Y. Koo and H. C. Choi, Angew. Chem., Int. Ed., 2020, 59, 16436–16439, DOI:10.1002/anie.202006263.
- J. Y. Koo, T. Kwon, Y. Ahn and H. C. Choi, J. Phys. Chem. C, 2021, 125, 10991–10997, DOI:10.1021/acs.jpcc.0c10644.
- J. W. L. Wong, A. Mailman, S. M. Winter, C. M. Robertson, R. J. Holmberg, M. Murugesu, P. A. Dube and R. T. Oakley, Chem. Commun., 2014, 50, 785–787, 10.1039/c3cc46686h.
- C. M. Robertson, A. A. Leitch, K. Cvrkalj, D. J. T. Myles, R. W. Reed, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2008, 130, 14791–14801, DOI:10.1021/ja8054436.
- J. S. Tse, A. A. Leitch, X. Yu, X. Bao, S. Zhang, Q. Liu, C. Jin, R. A. Secco, S. Desgreniers, Y. Ohishi and R. T. Oakley, J. Am. Chem. Soc., 2010, 132, 4876–4886, DOI:10.1021/ja100216c.
- A. A. Leitch, K. Lekin, S. M. Winter, L. E. Downie, H. Tsuruda, J. S. Tse, M. Mito, S. Desgreniers, P. A. Dube, S. Zhang, Q. Liu, C. Jin, Y. Ohishi and R. T. Oakley, J. Am. Chem. Soc., 2011, 133, 6050–6060, DOI:10.1021/ja200391j.
- J. L. Brusso, K. Cvrkalj, A. A. Leitch, R. T. Oakley, R. W. Reed and C. M. Robertson, J. Am. Chem. Soc., 2006, 128, 15080–15081, DOI:10.1021/ja0666856.
- A. A. Leitch, J. L. Brusso, K. Cvrkalj, R. W. Reed, C. M. Robertson, P. A. Dube and R. T. Oakley, Chem. Commun., 2007, 3368–3370, 10.1039/b708756j.
- C. M. Robertson, D. J. T. Myles, A. A. Leitch, R. W. Reed, B. M. Dooley, N. L. Frank, P. A. Dube, L. K. Thompson and R. T. Oakley, J. Am. Chem. Soc., 2007, 129, 12688–12689, DOI:10.1021/ja076841o.
- A. A. Leitch, X. Yu, S. M. Winter, R. A. Secco, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2009, 131, 7112–7125, DOI:10.1021/ja900853t.
- C. Kittel, Introduction to solid state physics, John Wiley & Sons, New York, 8th edn, 2004 Search PubMed.
- A. J. Heeger, Angew. Chem., Int. Ed., 2001, 40, 2591–2611 CrossRef CAS.
- J. L. Brédas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804–5809, DOI:10.1073/pnas.092143399.
- Z. Shuai, W. Li, J. Ren, Y. Jiang and H. Geng, J. Chem. Phys., 2020, 153, #080902, DOI:10.1063/5.0018312.
- T. Holstein, Ann. Phys., 1959, 8, 325–342, DOI:10.1016/0003-4916(59)90002-8; T. Holstein, Ann. Phys., 1959, 8, 343–389, DOI:10.1016/0003-4916(59)90003-X.
- K. Hannewald, V. M. Stojanovic, J. M. T. Schellekens, P. A. Bobbert, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, #075211, DOI:10.1103/PhysRevB.69.075211.
- A. Troisi and G. Orlandi, Phys. Rev. Lett., 2006, 96, #086601, DOI:10.1103/PhysRevLett.96.086601.
- S. Giannini, A. Carof, M. Ellis, H. Yang, O. G. Ziogos, S. Ghosh and J. Blumberger, Nat. Commun., 2019, 10, #3843, DOI:10.1038/s41467-019-11775-9.
- L. Song and Q. Shi, J. Chem. Phys., 2015, 142, #174103, DOI:10.1063/1.4919061.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315, DOI:10.1002/adfm.201502386.
- H. Ishii, H. Tamura, M. Tsukada, N. Kobayashi and K. Hirose, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, #155458, DOI:10.1103/PhysRevB.90.155458.
- A. Heck, J. J. Kranz, T. Kubar and M. Elstner, J. Chem. Theory Comput., 2015, 11, 5068–5082, DOI:10.1021/acs.jctc.5b00719.
- L. J. Wang, Q. Peng, Q. K. Li and Z. Shuai, J. Chem. Phys., 2007, 127, #044506, DOI:10.1063/1.2751191.
- T. Nematiaram, D. Padula, A. Landi and A. Troisi, Adv. Funct. Mater., 2020, 30, #2001906, DOI:10.1002/adfm.202001906.
- V. Stehr, J. Pfister, R. F. Fink, B. Engels and C. Deibel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, #155208, DOI:10.1103/PhysRevB.83.155208.
- S.-H. Wen, A. Li, J. Song, W.-Q. Deng, K.-L. Han and W. A. Goddard, J. Phys. Chem. B, 2009, 113(26), 8813–8819, DOI:10.1021/jp900512s.
- Y. Yang, B. Rice, X. Shi, J. R. Brandt, R. Correa Da Costa, G. J. Hedley, D. M. Smilgies, J. M. Frost, I. D. W. Samuel, A. Otero-De-La-Roza, E. R. Johnson, K. E. Jelfs, J. Nelson, A. J. Campbell and M. J. Fuchter, ACS Nano, 2017, 11, 8329–8338, DOI:10.1021/acsnano.7b03540.
- C. Wang, F. Wang, X. Yang, Q. Li and Z. Shuai, Org. Electron., 2008, 9, 635–640, DOI:10.1016/j.orgel.2008.04.003.
- J. L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104(11), 4971–5003, DOI:10.1021/cr040084k.
- H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357, DOI:10.1021/acs.chemrev.7b00086.
- J. Vura-Weis, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2010, 132, 1738–1739, DOI:10.1021/ja907761e.
- R. J. Cave and M. D. Newton, J. Chem. Phys., 1997, 106, 9213–9226, DOI:10.1063/1.474023.
- A. Kubas, F. Gajdos, A. Heck, H. Oberhofer, M. Elstner and J. Blumberger, Phys. Chem. Chem. Phys., 2015, 17, 14342–14354, 10.1039/c4cp04749d.
- C. Roncero-Barrero, J. Ribas-Ariño, M. Deumal and I. de P. R. Moreira, Phys. Chem. Chem. Phys., 2022, 24, 12196–12207, 10.1039/d2cp00415a.
- C. Roncero-Barrero, J. Ribas-Ariño, I. de P.R. Moreira and M. Deumal, Dalton Trans., 2022, 51, 13032–13045, 10.1039/d2dt01340a.
- R. A. Marcus, J. Chem. Phys., 1956, 24(5), 966–978, DOI:10.1063/1.1742723.
- R. A. Marcus, Angew. Chem., Int. Ed. Engl., 1993, 32(8), 1111–1121, DOI:10.1002/anie.199311113.
- V. Lemaur, M. Steel, D. Beljonne, J.-L. Brédas and J. Cornil, J. Am. Chem. Soc., 2005, 127, 6077–6086, DOI:10.1021/ja042390l.
- D. P. McMahon and A. Troisi, J. Phys. Chem. Lett., 2010, 1, 941–946, DOI:10.1021/jz1001049.
- J. E. Norton and J.-L. Brédas, J. Am. Chem. Soc., 2008, 130, 12377–12384, DOI:10.1021/ja8017797.
- I. Yavuz, B. N. Martin, J. Park and K. N. Houk, J. Am. Chem. Soc., 2015, 137, 2856–2866, DOI:10.1021/ja5076376.
- E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J. L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882–9886, DOI:10.1021/ja061827h.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J. L. Brédas, Chem. Rev., 2007, 107, 926–952, DOI:10.1021/cr050140x.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652, DOI:10.1063/1.464913.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648, DOI:10.1063/1.438980.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654, DOI:10.1063/1.438955.
- R. C. Binning and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206–1216, DOI:10.1002/jcc.540111013.
- M. J. Frisch, et al., Gaussian09, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, A. C. Borin, L. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. Fernández-Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P.-Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Mart, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, #214117, DOI:10.1063/5.0004835.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858, DOI:10.1021/jp031064+.
- A. Bondi, J. Phys. Chem., 1964, 68(3), 441–451, DOI:10.1021/j100785a001.
- The effective mass of electrons and holes (me, mh) has been assumed to be the free electron mass as a reference to estimate ρc values. We are aware that this introduces an error, but it is several orders of magnitude smaller than the error introduced by Eg, which is part of the argument of the exponential term of the ρc expression.
- A. Troisi, Chem. Soc. Rev., 2011, 40, 2347–2358, 10.1039/c0cs00198h.
- H. Dong, X. Fu, J. Liu, Z. Wang and W. Hu, Adv. Mater., 2013, 25, 6158–6183, DOI:10.1002/adma.201302514.
- in CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 2009 Search PubMed.
- C. G. Shuttle, R. Hamilton, J. Nelson, B. C. O'Regan and J. R. Durrant, Adv. Funct. Mater., 2010, 20, 698–702, DOI:10.1002/adfm.200901734.
- For instance, at 20 °C, the electric conductivity for graphite either parallel or perpendicular to the basal plane is ca. 3 × 103 and 3.0 S cm−1, respectively, which encompass three orders of magnitude. See H.O. Pierson, Handbook of carbon, graphite, diamond, and fullerenes: properties, processing, and applications, p. 61, William Andrew, 1993 ISBN 0-8155-1339-9.
Footnotes |
| † Dedicated to Prof. Juan J. Novoa, in memoriam. |
| ‡ Electronic supplementary information (ESI) available: Choice of active space for CASSCF calculations of reorganization energy and electronic coupling; crystal packing analysis and cluster model selection for evaluation of HDA electronic couplings; Koopman's theorem variation for open-shell materials constituted by monoradical centers; donor–acceptor charge distribution; qualitative insights into reorganization energy and electronic coupling of (S,Se) and (Se,S); calculation of density of charge carriers; analysis of disproportionation energies; effect of anisotropy on the transport properties. See DOI: https://doi.org/10.1039/d3tc03710j |
| This journal is © The Royal Society of Chemistry 2024 |