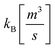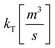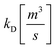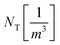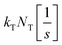Unravelling material properties of halide perovskites by combined microwave photoconductivity and time-resolved photoluminescence spectroscopy†
Christian
Kupfer
 *ab,
Vincent M.
Le Corre
a,
Chaohui
Li
a,
Larry
Lüer
ab,
Karen
Forberich
ab,
Masashi
Kato
c,
Andres
Osvet
a and
Christoph J.
Brabec
ab
*ab,
Vincent M.
Le Corre
a,
Chaohui
Li
a,
Larry
Lüer
ab,
Karen
Forberich
ab,
Masashi
Kato
c,
Andres
Osvet
a and
Christoph J.
Brabec
ab
aFriedrich-Alexander-Universität Erlangen-Nürnberg, Faculty of Engineering, Department of Material Science, Materials for Electronics and Energy Technology (i-MEET), Martensstraße 7, Erlangen 91058, Germany. E-mail: christian.kupfer@fau.de
bForschungszentrum Jülich GmbH, Helmholtz-Institut Erlangen-Nürnberg for Renewable Energy (HI ERN), Immerwahrstraße 2, Erlangen 91058, Germany
cDepartment of Electric and Mechanical Engineering, Nagoya Institute of Technology, Nagoya 466-8555, Japan
First published on 4th December 2023
Abstract
To take advantage of the huge compositional space of metal halide perovskites, a reliable and fast characterization method is required. By combining time-resolved photoluminescence (trPL) with microwave photoconductivity measurements, we are able to rapidly extract fundamental material properties of promising perovskite materials from bare films. This is achieved by incorporating a rate-equation model into a fitting algorithm based on Bayesian optimization to globally fit the experimental results. Including microwave photoconductivity measurements into our analysis significantly enhances the accuracy of estimating recombination rate constants. Additionally, it grants us the ability to determine the ratio of electron and hole mobilities, a crucial charge transport property that cannot be obtained solely through time-resolved photoluminescence measurements. Furthermore, the high sensitivity of microwave photoconductivity measurements to long-lived trap states yields information about the trap-assisted recombination, which is a major source of efficiency loss for solar devices and is difficult to assess from pure trPL measurements. In this work, we introduce the fundamental principles of microwave photoconductivity, along with the employed rate-equation model and fitting techniques. We then outline the procedure for conducting measurements and extracting the recombination rate constants, trap density, and mobility ratio. Subsequently, we highlight the benefits of combining both methods through a comparison of results from fits using only trPL with those from fits incorporating combined signals on a simulated dataset. We also discuss the merits of conducting intensity-dependent measurements. Finally, we present the annealing-dependent results obtained from a highly relevant triple-cation, mixed-halide perovskite, FA0.82MA0.13Cs0.05Pb(I0.87Br0.13)3, as an application example, where we uncover the presence of long-lived traps beyond 10 μs.
1. Introduction
The remarkable progress of perovskite solar cells beyond the 25% efficiency milestone in the last decade1 highlights the potential of this technology to assist in addressing the globally growing energy demand and the urgent climate crisis. Organic–inorganic metal halide perovskites based on lead are currently the most efficient members of this material group. Nonetheless, more work towards enhancing the stability of these compounds is required before their commercialization, and the presence of highly toxic lead poses a potential obstacle.To tackle these challenges, researchers are exploring the vast compositional space of perovskites and their related materials.2–5 The fabrication of complete solar cells, however, is a tedious and time-consuming process, necessitating a tool to rapidly gauge the capabilities of novel materials in advance. One of the most important parameters for solar cell performance is the charge carrier lifetime since it strongly influences the efficiency.
In previous efforts, Krückemeier et al. suggested the use of the differential lifetimes for describing recombination processes6 and reconciled time-resolved photoluminescence (trPL) and transient photovoltage (TPV) measurements to better understand charge carrier dynamics.7 Furthermore, rise and decay times of TPV signals were studied to extract recombination time constants.8 In another work, Musiienko et al. resolved transport properties of semiconductor materials by constant light induced magneto transport (CLIMAT) and used these values to predict the photoluminescence quantum yield (PLQY) of the material.9 Additionally, the combination of time-of-flight spectroscopy measurements with Monte Carlo simulations was used to investigate the dynamics of free charge carriers on the example of MAPbBr3 films.10 Finally, Lobo et al. performed comparative trPL and microwave photoconductivity measurements to investigate the presence of minority carrier traps in poly- and single-crystalline lead halide perovskites.11
Nonetheless, simple trPL measurements are still the most prevalently employed method to extract carrier lifetimes by a large majority of the research community, due to their contactless, reliable, fast, and non-destructive nature. Nevertheless, the extraction of material parameters from trPL measurements is not straightforward since the transients, especially for perovskites, are usually multi-exponential.6 Thus, signal analysis is oftentimes either limited to qualitative statements or relies on fitting multi-exponential or stretched exponential functions to the data. However, this causes a loss of information7 or, if not done carefully, can be potentially misleading since it does not accurately describe the underlying processes, which are governed by rate equations.12
Here we augment time-resolved photoluminescence measurements with the less-commonly used microwave photoconductivity technique to assess fundamental properties of raw materials in an accurate and comprehensive manner, while retaining the aforementioned advantages of reliability, speed, non-destructiveness, and non-requirement for electrical contacts. To achieve this, we perform simultaneous trPL and microwave photoconductivity measurements and analyse the data with a machine-learning-powered fitting algorithm based on Bayesian optimization to produce a global fit with a rate equation model. By fitting two signals from different measurements with a single underlying charge carrier density, we are able to deduce the rate constants and trap density of the investigated sample. Additionally, we gain access to the ratio of electron and hole mobilities, a property that cannot be determined by trPL measurements alone. This contributes to the understanding of charge transport properties of the material. Furthermore, in contrast to trPL, microwave photoconductivity measurements are highly sensitive to long-lived trap states and thus yield information about the duration that charge carriers stay trapped.13 This is expected to influence both recombination and transport properties.10
The fast and accurate extraction of fundamental material parameters in combination with the relative ease-of-use makes the demonstrated technique an ideal candidate for inclusion into state-of-the-art, high-throughput material development acceleration platforms. It allows researchers to quantify the result of their efforts directly after the synthesis of a given compound, without the need to produce a full device. Furthermore, it could potentially be used in the future to drive autonomous research.
In the following sections, the fundamentals of microwave photoconductivity and the rate-equation model are introduced and a brief mathematical description is presented. The main differences and similarities to trPL measurements are highlighted and the fitting procedure is introduced. Then the advantages from a combined fit are evaluated on synthetic data sets and the further improvement achievable through an intensity-dependent measurement is illustrated. Finally, results from measurements of FA0.82MA0.13Cs0.05Pb(I0.87Br0.13)3 films on glass, prepared under different annealing conditions, are presented and discussed. We find that the annealing-dependent changes in the trap-assisted recombination rate are difficult to obtain from trPL measurements alone but are directly visible from microwave conductivity data. Furthermore, we uncover the ratio of mobilities of the different charge carrier types.
2. Methodology
2.1 Working principle of microwave photoconductivity measurements
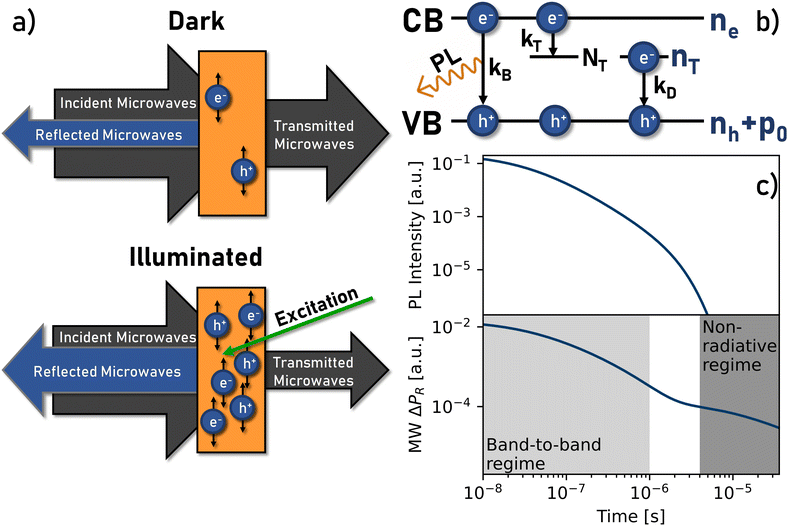
The interaction between matter and microwaves, which are electromagnetic waves within the frequency range between 3 GHz and 100 GHz,14 depends on the properties of the material, particularly its conductivity. Insulating materials are typically transparent to microwave radiation or experience heating effects due to polar molecules. In contrast, metals readily reflect microwaves due to the interaction with free charge carriers present in the metal. These charge carriers oscillate under the influence of the electromagnetic field and re-emit secondary waves, leading to a reflection of the incident signal.15 While semiconducting materials also exhibit some degree of microwave reflection, the extent of it depends heavily on the conductivity of the sample, which is determined by the density and mobility of available free charge carriers. This principle forms the basis for the presented technique. A semiconducting sample, such as a metal halide perovskite, is subjected to continuous microwave radiation and excess charge carriers are created by a pulsed laser (see Fig. 1a). By measuring the transient change in reflected microwave power, valuable information about changes in conductivity and, consequently, changes in charge carrier density can be obtained. This allows us to gain insight into the charge carrier dynamics and draw conclusions about fundamental material properties. Notably, for a successful measurement, a significant change in conductivity has to occur under excitation, which excludes samples with very high dark conductivity or electric contacts.2.2 Mathematical description
While a complete mathematical treatment of microwave photoconductivity can be found elsewhere,16–18 a short introduction will be given here. Consider a sample with conductivity σ that is irradiated with continuous microwaves. Upon excitation by a laser pulse, this conductivity changes σ → σ + Δσ and therefore, the power reflected by the sample PR(σ) changes accordingly: PR(σ) → PR(σ + Δσ). It can be shown that for small changes in reflected microwave power,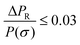 , the relative change in reflected microwave power
, the relative change in reflected microwave power 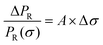 , where A is the so-called sensitivity factor and ΔPR = PR(σ + Δσ) − PR(σ).16 Therefore, the change in reflected microwave power is directly proportional to the change in conductivity as long as the low-injection condition is maintained:19
, where A is the so-called sensitivity factor and ΔPR = PR(σ + Δσ) − PR(σ).16 Therefore, the change in reflected microwave power is directly proportional to the change in conductivity as long as the low-injection condition is maintained:19| ΔPR ∝ Δσ | (1) |
Note that this is only true under the so-called low-injection condition as otherwise the proportionality is not guaranteed and nonlinearities are introduced. Furthermore, the change in conductivity can be expressed in terms of the charge carrier densities and mobilities for electrons and holes:
| Δσ = e × (neμe + nhμh) | (2) |
| ΔPR ∝ neμe + nhμh | (3) |
We furthermore assssume mobilities constant in time μe,h(t) = μe,h(t = 0) = μe,h, such that the only time dependency remains with the charge carrier densities. Note that this assumption is only true for sufficiently low excess charge carrier concentrations which do not significantly increase the scattering probability between charge carriers.20,21 Furthermore, by dividing by either of the mobilities (here μh), the equation can be rewritten as:
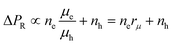 | (4) |
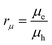 .
.
2.3 Bimolecular-trapping–detrapping model
To analyse the experimental data, it is necessary to employ a suitable physical model that describes the behaviour of the underlying charge carrier densities. In this study, we adopt the bimolecular-trapping–detrapping model described by Péan et al.12 In short, the recombination process of excited charge carriers is governed by three rate constants: the bimolecular (or band-to-band) recombination rate constant kB, the trapping rate constant kT, and the trap-assisted recombination rate constant kD (called detrapping rate constant in the original publication). These constants determine the rates with which charge carriers recombine in a radiative bimolecular process, get trapped, and recombine non-radiatively via traps respectively. The time-evolution of electron and hole densities is parametrized by these quantities, along with the density of electron traps NT and the p-type doping density p0.The model is described by the following set of differential equations:
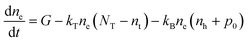 | (5) |
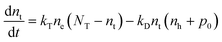 | (6) |
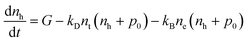 | (7) |
Here, G represents the charge carrier generation rate and nt is the density of trapped electrons. The model is schematically depicted in Fig. 1b. Notably, the model does not consider Auger recombination since this process typically only becomes significant at very high charge carrier densities.22
While the model in the original publication and the presented equations assume electron traps and p-type doping, our measurement method cannot distinguish between the types of charge carriers. Exchanging electron and hole densities simply changes the ratio of mobilities rμ to its inverse for the description of the microwave photoconductivity signal (see eqn (4)) and has no impact on the photoluminescence signal. Since the resulting signals would not change for hole traps and n-type doping, the trapping density NT and doping density p0 are not assigned to a specific type of charge carrier in our analysis. Furthermore, while there is some evidence of perovskite self-doping,23 for the purpose of this study, we assume the material to be mostly intrinsic and set the doping density to p0 = 0 since no intentional doping was performed.
In addition, the boundary conditions of the differential equations are determined by the experimental conditions. We assume that initially no charge carriers are trapped, nt(0) = 0, and that each absorbed photon creates exactly one electron–hole pair, ne(0) = nh(0) = N0, where N0 is the number of absorbed photons.
To relate the charge carrier densities to the experimental microwave photoconductivity signal, we use eqn (1) and (2) to obtain:
| SMW = ΔPR = IMW(nerμ + nh) | (8) |
Here, SMW represents the measured signal and IMW denotes a scaling factor.
2.4 Similarities and differences to time-resolved photoluminescence
One of the most frequently employed techniques for characterizing perovskite materials is time-resolved photoluminescence. Similar to microwave photoconductivity, excess charge carriers are generated using a pulsed laser, however, the signal is a consequence of a different physical phenomenon. Various processes can facilitate the return of excited charge carriers to their ground state, with recombination of a free electron and hole, accompanied by emission of a photon, being one of the most prominent. By measuring the number of photons emitted this way as a function of time after the excitation pulse, information about the charge carrier densities and recombination processes can be extracted. Since photon emission relies on the presence of both electrons and holes, the signal ultimately depends on the product of both charge carrier densities:| SPL = IPL × kBnenh | (9) |
Here, SPL is the photoluminescence signal and IPL is a scaling factor. In contrast, microwave conductivity depends on the sum of the charge carrier densities weighted by their mobilities (see eqn (2)). Consequently, it can be understood that for unequal excess charge carrier densities the trPL signal is most sensitive to the minority charge carrier type, while the microwave photoconductivity signal will follow the sum of charge carriers.11,16,24 This situation typically occurs in the presence of charge selective traps. In this case, the trPL signal diminishes quickly because minority charge carriers are either trapped or rapidly recombine due to the high density of majority carriers. The microwave photoconductivity signal, on the other hand, can persist for much longer times, as the majority carriers are unable to return to the ground state, due to a lack of minority carriers to recombine with, yet they still contribute to the signal. A simulation of both trPL and microwave photoconductivity signals is depicted in Fig. 1c. The shaded areas highlight the dominance of different recombination processes over the lifetime of the microwave photoconductivity signal.
Since both methods fundamentally probe the same physical processes, they can be regarded as two sides of the same coin, thus shining light onto the dynamics of charge carriers from different angles. Because of this, it is only natural to combine both methods in an attempt to obtain a clearer picture.
It is worth noting, that the contribution of excitons to the respective signals is significantly different; while trPL is sensitive to excitons because their recombination leads to luminescence, microwave photoconductivity measurements are unable to detect excitons due to their electric neutrality. However, the low binding energy of excitons that is typically observed in perovskites leads to a quick thermal dissociation at room temperature.25–28 Therefore, the excess charge carriers produced through laser excitation can be considered free charge carriers for the materials used in this study.
2.5 Fitting via Bayesian optimization for automatic research (BOAR)
The previously introduced model can be employed to simulate measurement signals for a given set of material parameters. However, the inverse problem of determining material parameters from measured data requires more effort. In this study, we employ a method called Bayesian optimization for automatic research (BOAR) to globally fit data from both experiments.29,30 The workflow of the algorithm is schematically illustrated in the ESI,† Fig. S3.Bayesian optimization is the method of choice to perform optimization on computationally expensive functions. The principle is relatively simple, first, we define a cost function that needs to be optimized. In our case, the cost function is the mean square error (MSE) between the experimental and simulated data which we aim to minimize. Then, we perform a random pre-sampling of the parameter space to get a first idea of the cost function. We subsequently use these points to train a so-called surrogate model of the cost function. The surrogate model tries to approximate the link between the material parameters and the MSE. In this work, we use Gaussian process regression (GPR) to build the surrogate. Once this model is trained, we can use it to predict the MSE for a new set of parameters. We then use an acquisition function to select the next set of parameters to evaluate. The acquisition function is a trade-off between exploration and exploitation. It tries to find the best compromise between exploring the parameter space to find the global minimum and exploiting the current best solution to find the local minimum. The process is repeated iteratively until the user is satisfied with the result.
The main advantage of using such a method is that contrary to usual fitting procedures based on gradient descent, it is not sensitive to local minima and does not rely on the initial guess. Moreover, Bayesian optimization typically performs well in high dimensional parameter space. Both advantages make it a better candidate for the optimization of the material parameters of the model. In fact, for new materials, it is difficult to predict a good initial guess and the parameter space is not only high dimensional with 7 parameters to be optimized, but each of those parameters can realistically vary over several orders of magnitude, making gradient based method very difficult and risky to use.
The optimized parameters kB, kT, kD, rμ, NT, IPL, IMW are determined and saved for further analysis. On a standard workstation PC, this procedure takes around 30 minutes per data set.
By using a rate equation model as the basis for our fitting, we are able to gain insight into the physical processes inside the semiconductor that govern the return of the photoexcited carriers to the ground state after illumination. This contrasts the empirical fitting of trPL signals with multiple exponential decay functions or stretched exponentials, which is still frequently employed in current publications. While the signal from a species of excited charge carriers returning to the ground state via a single monomolecular process, i.e. via a single rate constant, is correctly described by an exponential decay with a given lifetime τ (i.e.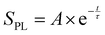 ), adding a second recombination pathway necessitates a deeper look at the underlying processes and physical principles. Notably, multi-path recombination is not accurately described by a sum of exponential decays or a stretched exponential.12
), adding a second recombination pathway necessitates a deeper look at the underlying processes and physical principles. Notably, multi-path recombination is not accurately described by a sum of exponential decays or a stretched exponential.12
3. Results and discussion
The simultaneous trPL and microwave photoconductivity measurements and subsequent analysis were performed as previously described on a set of FA0.82MA0.13Cs0.05Pb(I0.87Br0.13)3 films. The materials were deposited on glass via spin-coating and subsequently annealed under four different conditions for 20 min (25 °C, 60 °C, 100 °C and vacuum annealing). This material was chosen due to the high PCEs of over 20% which has previously been reported for very similar material compositions, which makes it highly relevant for future applications and research.31–33Details concerning the experimental setup, measurement conduct, sample specifications, data treatment, and fitting procedure can be found in the ESI.†
Fig. 2 shows the experimental trPL and microwave photoconductivity data of FA0.82MA0.13Cs0.05Pb(I0.87Br0.13)3 films on glass along with the corresponding global fits produced with BOAR for two different annealing temperatures (25 °C and 100 °C). The specific material parameters obtained from the analysis can be found in Table 1 and the fits of the 60 °C and vacuum annealing can be found in the ESI,† Fig. S6. It is evident that the experimentally obtained signals are very accurately reproduced by the employed fitting method and model. This is especially remarkable considering the significantly different shape of the microwave photoconductivity signal, which exhibits a long-lived tail way beyond 1 μs for the sample annealed at 25 °C but not for the one annealed at 100 °C. All microwave photoconductivity signals exhibit a very similar initial decay. Two main processes can in principle be responsible for the depopulation of the excited state: bimolecular recombination and trapping of charge carriers. Comparing the corresponding rate constants extracted by our fits, we find that the rate of bimolecular recombination exceeds the trapping rate by around an order of magnitude. Therefore, the early decay, where the number of electrons and holes is roughly equal due to their symmetric initial generation, is mostly governed by bimolecular recombination, as one would expect.
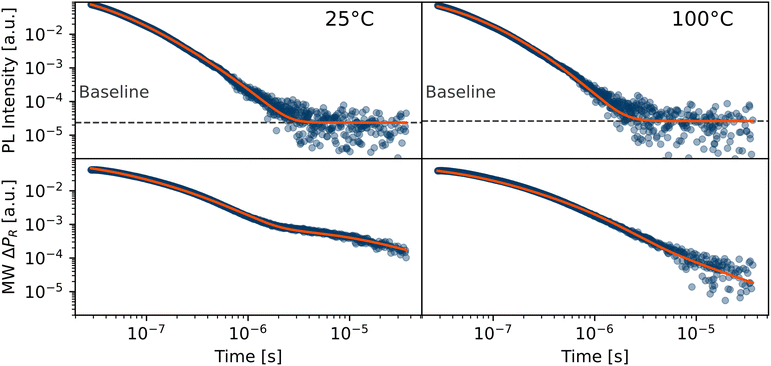 | ||
| Fig. 2 Experimental (blue dots) microwave photoconductivity (bottom) and time-resolved photoluminescence (top) data of FA0.82MA0.13Cs0.05Pb(I0.87Br0.13)3 films annealed for 20 min at 25 °C and 100 °C respectively. The orange lines are global fits of both trPL and microwave photoconductivity data, produced with BOAR. The dashed grey lines indicate the baselines of the photoluminescence signal (see ESI,† for further explanation). | ||
| Annealing condition | r μ | I PL[a.u.] | I MW[a.u.] | |||||
|---|---|---|---|---|---|---|---|---|
| Vacuum | 1.77 × 10−17 | 4.42 × 10−19 | 1.20 × 10−18 | 5.328 | 6.89 × 1023 | 1.01 × 10−32 | 1.05 × 10−26 | 3.0 × 105 |
| 25 °C | 2.54 × 10−17 | 5.43 × 10−18 | 1.75 × 10−18 | 4.699 | 1.31 × 1023 | 8.71 × 10−33 | 1.40 × 10−26 | 6.1 × 105 |
| 60 °C | 2.21 × 10−17 | 1.14 × 10−18 | 1.34 × 10−18 | 4.629 | 5.55 × 1023 | 8.96 × 10−33 | 1.32 × 10−26 | 6.3 × 105 |
| 100 °C | 1.85 × 10−17 | 8.94 × 10−18 | 6.95 × 10−17 | 0.3392 | 1.26 × 1023 | 8.42 × 10−33 | 4.41 × 10−26 | 1.1 × 106 |
Nevertheless, trapping still plays an important role since it skews the charge carrier equilibrium. This becomes evident when the minority carrier concentration diminishes and the bimolecular recombination subsides. At this point, the photoluminescence signals mostly cease (at around 1 μs), but the microwave photoconductivity signals, which do not require the presence of both charge carrier types simultaneously, show a long tail even beyond 10 μs. This tail is strongly pronounced in all but the 100 °C sample and originates from majority carriers that are unable to recombine due to the unavailability of the minority carriers which are still trapped.
The release of the minority carriers from their trapped state and subsequent recombination is mediated by the trap-assisted recombination rate constant kD. When the trap-assisted recombination rate has a comparable or lower magnitude as the trapping rate, a considerable fraction of traps becomes occupied initially and stays filled until most of the bimolecular recombination has occurred. However, when the trap-assisted recombination is much faster than the trapping, most traps can be considered empty. Interestingly, this leads to the conclusion that a fast trap-assisted recombination can have negative consequences for the device performance since it leads to more non-radiative recombination pathways by emptying previously occupied trap states.
The sample annealed at 100 °C exhibits exactly this behaviour, showing a trap-assisted recombination rate much larger than the trapping rate. This directly results in the disappearance of the long-lived tail in the microwave photoconductivity signal of this particular sample. Comparing the trap-assisted recombination rate of the 100 °C sample to the results from the other annealing conditions, we find that the trap-assisted recombination rate has increased by almost two orders of magnitude. As previously discussed, the trap-assisted recombination rate specifically is a parameter that is hardly obtained by trPL measurements alone. This is also evident by the signal shape, which barely differs for the trPL data but shows an obvious change in the microwave photoconductivity.
The mobility ratio we find is between 4.5 and 5.5 for the samples annealed at 25 °C, 60 °C, and in vacuum. As previously discussed, we cannot discern whether the electron or hole mobility is larger, however, we can conclude that for a mobility ratio larger than 1, the species which gets trapped has a larger mobility. This directly results from the definition of rμ as a fraction of both mobilities in combination with the rate constants, where the species of charge carriers that become trapped is in the enumerator and the un-trapped species is in the denominator of rμ (see eqn (4)–(7)). The sample annealed at 100 °C, on the other hand, produces a drastically different value of 0.3. However, as was shown in the synthetic data, this parameter carries a large uncertainty when the long-lived tail is strongly suppressed, as the mobility ratio is strongly related to the tail shape. However, the accuracy is likely to improve somewhat for intensity-dependent measurements.
Another interesting feature is the significantly lower product of the trapping rate and trap density of the vacuum-annealed sample, which can be seen as a proxy for the inverse lifetime of the trapping process. In combination with a mostly unchanged bimolecular recombination rate, this leads to a prolonged period before trapping becomes the dominant recombination process compared to the other samples. This is also evident in the position of the kink observed in the microwave photoconductivity signal along the time axis. Since trapping is generally considered detrimental to device performance, a slower trapping process suggests an extended time for charge extraction and thus an improved mobility-lifetime product μτ. This is in accord with observations from device fabrication, where vacuum-annealed samples exhibited better performance than thermally annealed devices (see ESI,† Fig. S7).
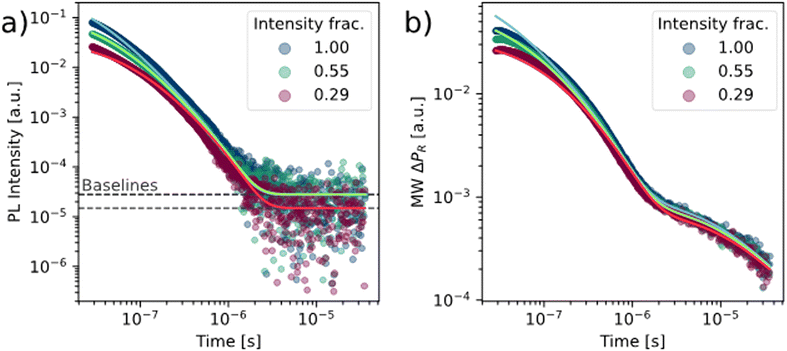
To increase the accuracy and reliability of the extracted parameters, the measurements were repeated with three different excitation intensities. The resulting signal and corresponding fit are exemplary presented in Fig. 3 for the sample annealed at 60 °C. As expected, the signal intensity of both measurements varies with the intensity of the illuminating laser. While there is some deviation between experiment and simulation especially in the microwave photoconductivity signal at early times, it is evident that the global fit is still able to sufficiently explain the measured data. This result highlights the robustness of the procedure. Simultaneously, we expect the intensity-dependent fit to also show enhanced precision of the extracted parameters and partially disentangle previously correlated parameters. This is evident for the mobility ratio rμ of the sample annealed at 100 °C, which for this analysis produces a value of 2.8, which is much closer to the values of the other samples. The other parameters deviate only slightly from the results obtained by fitting a single intensity, with the exception of the trap density and trapping rate, which can be attributed to the strong correlation of these parameters, as discussed previously. All extracted parameters from both the single-intensity and intensity-dependent measurements for the different annealing conditions can be found in the ESI,† Table S3.
Conclusions
While trPL measurements are commonly used in the research community to extract lifetimes for halide perovskite materials, the correct interpretation of the resulting signals and extraction of material properties is often difficult.In this work, we augmented trPL measurements with microwave photoconductivity data to rapidly extract the fundamental material parameters of halide perovskites in a contactless, reliable, and non-destructive manner. To achieve a physically correct and accurate fit to the experimental data, a rate-equation model was combined with machine-learning-assisted simulations to provide a global fit of both signals. Through the incorporation of microwave photoconductivity, we obtained access to the ratio of electron and hole mobilities, a parameter that is significant for understanding transport properties and cannot be extracted from trPL measurements alone.
By evaluating the fitting procedure on a synthetic dataset, we were able to prove that the combined method provides accurate results for the bimolecular and trap-assisted recombination rate constants, the product of trapping rate constant and trap density, and the mobility ratio of electrons and holes. Compared to trPL-only fits, the main improvement beyond the access to the mobility ratio was the drastically improved precision of the extracted trap-assisted recombination rate constant for the global fit. This parameter determines the trapping duration and is thus an important puzzle piece in understanding the processes governing charge carrier transport and recombination. For example, a slower trap-assisted recombination can have beneficial effects on the carrier lifetime by suppressing trapping of charge carriers after the traps are filled initially.
The excellent agreement of the global fit and the experimentally obtained data from FA0.82MA0.13Cs0.05Pb(I0.87Br0.13)3 films subjected to different annealing conditions proves the robustness and validity of our approach. We observe a substantial change of material properties with annealing condition, which shows the significance of carefully chosen sample treatment and also highlights the ability of the presented technique to inform such decisions. In the future, varying the excitation intensity over a larger range is anticipated to potentially decouple the trapping rate constant and the trap density, yielding independent values for those parameters. Furthermore, investigating the sample-to-sample variation under identical processing conditions can grant interesting insights into the robustness of the production process.
Author contributions
CK: conceptualization, investigation, methodology, visualization, writing – original draft VLC: methodology, software, writing – review & editing CL: investigation LL: software, conceptualization KF: conceptualization, writing – review & editing MK: supervision, writing – review & editing AO: supervision, conceptualization, writing – review & editing CJB: funding acquisition, project administration, supervision, conceptualization, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Christian Kupfer, Andres Osvet, Masashi Kato, and Christoph J. Brabec gratefully acknowledge financial support for this work by the Deutsche Forschungsgemeinschaft under GRK 2495/E. Chaohui Li gratefully acknowledges the funding from China Scholarship Council (CSC). Masashi Kato gratefully acknowledges the funding from the JSPS Japanese-German Graduate Externship (Grant No. 2019/R1).Notes and references
- NREL, Best Research-Cell Efficiency Chart, https://www.nrel.gov/pv/cell-efficiency.html, (accessed June 16, 2023).
- T. Nakajima and K. Sawada, J. Phys. Chem. Lett., 2017, 8, 4826–4831 CrossRef CAS.
- A. Jain, O. Voznyy and E. H. Sargent, J. Phys. Chem. C, 2017, 121, 7183–7187 CrossRef CAS.
- T. Wu and J. Wang, Nano Energy, 2019, 66, 104070 CrossRef CAS.
- M. A. Surmiak, T. Zhang, J. Lu, K. J. Rietwyk, S. R. Raga, D. P. McMeekin and U. Bach, Sol. RRL, 2020, 4, 2000097 CrossRef CAS.
- L. Krückemeier, B. Krogmeier, Z. Liu, U. Rau and T. Kirchartz, Adv. Energy Mater., 2021, 11, 2003489 CrossRef.
- L. Krückemeier, Z. Liu, B. Krogmeier, U. Rau and T. Kirchartz, Adv. Energy Mater., 2021, 11, 2102290 CrossRef.
- L. Krückemeier, Z. Liu, T. Kirchartz and U. Rau, Adv. Mater., 2023, 35, 2300872 CrossRef PubMed.
- A. Musiienko, F. Yang, T. W. Gries, C. Frasca, A. Al-Ashouri, E. Sağlamkaya, F. Lang, D. Kojda, Y.-T. Huang, R. Hoye, M. Ahmadi, A. Kanak and A. Abate, Resolving Electron and Hole Transport Properties in Semiconductor Materials by Constant Light Induced Magneto Transport, In Review, 2023 Search PubMed.
- A. Musiienko, J. Pipek, P. Praus, M. Brynza, E. Belas, B. Dryzhakov, M.-H. Du, M. Ahmadi and R. Grill, Sci. Adv., 2020, 6, eabb6393 CrossRef CAS.
- N. Lobo, T. Kawane, G. J. Matt, A. Osvet, S. Shrestha, L. Ievgen, C. J. Brabec, A. Kanak, P. Fochuk and M. Kato, Jpn. J. Appl. Phys., 2022, 61, 125503 CrossRef.
- E. V. Péan, S. Dimitrov, C. S. D. Castro and M. L. Davies, Phys. Chem. Chem. Phys., 2020, 22, 28345–28358 RSC.
- M. Kato, T. Asada, T. Maeda, K. Ito, K. Tomita, T. Narita and T. Kachi, J. Appl. Phys., 2021, 129, 115701 CrossRef CAS.
- D. M. Pozar, Microwave Engineering, Wiley, 4th edn, 2011 Search PubMed.
- J. Sun, W. Wang and Q. Yue, Materials, 2016, 9, 231 CrossRef.
- M. Kunst and G. Beck, J. Appl. Phys., 1986, 60, 3558–3566 CrossRef CAS.
- G. Beck and M. Kunst, Rev. Sci. Instrum., 1986, 57, 197–201 CrossRef CAS.
- M. Kunst and G. Beck, J. Appl. Phys., 1988, 63, 1093–1098 CrossRef CAS.
- M. Kato, Y. Mori and M. Ichimura, Jpn. J. Appl. Phys., 2015, 54, 04DP14 CrossRef.
- J. Lim, M. Kober-Czerny, Y.-H. Lin, J. M. Ball, N. Sakai, E. A. Duijnstee, M. J. Hong, J. G. Labram, B. Wenger and H. J. Snaith, Nat. Commun., 2022, 13, 4201 CrossRef CAS.
- C. Motta, F. El-Mellouhi and S. Sanvito, Sci. Rep., 2015, 5, 12746 CrossRef CAS PubMed.
- A. Alnuaimi, I. Almansouri and A. Nayfeh, AIP Adv., 2016, 6, 115012 CrossRef.
- G. Paul, S. Chatterjee, H. Bhunia and A. J. Pal, J. Phys. Chem. C, 2018, 122, 20194–20199 CrossRef CAS.
- T. Asada, Y. Ichikawa and M. Kato, JoVE J. Vis. Exp., 2019, e59007 CAS.
- M. Baranowski and P. Plochocka, Adv. Energy Mater., 2020, 10, 1903659 CrossRef CAS.
- A. Miyata, A. Mitioglu, P. Plochocka, O. Portugall, J. T.-W. Wang, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Nat. Phys., 2015, 11, 582–587 Search PubMed.
- K. Galkowski, A. Mitioglu, A. Miyata, P. Plochocka, O. Portugall, G. E. Eperon, J. T.-W. Wang, T. Stergiopoulos, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Energy Environ. Sci., 2016, 9, 962–970 RSC.
- D. M. Niedzwiedzki, H. Zhou and P. Biswas, J. Phys. Chem. C, 2022, 126, 1046–1054 CrossRef CAS.
- M. Wagner, A. Distler, V. M. L. Corre, S. Zapf, B. Baydar, H.-D. Schmidt, M. Heyder, K. Forberich, L. Lüer, C. J. Brabec and H.-J. Egelhaaf, 2023.
- V. M. Le Corre and L. Lüer, BOAR: Bayesian Optimization for Automatic Research, https://github.com/i-MEET/boar, (accessed March 15, 2023).
- M. Degani, Q. An, M. Albaladejo-Siguan, Y. J. Hofstetter, C. Cho, F. Paulus, G. Grancini and Y. Vaynzof, Sci. Adv., 2021, 7, eabj7930 CrossRef CAS.
- S. Yang, S. Chen, E. Mosconi, Y. Fang, X. Xiao, C. Wang, Y. Zhou, Z. Yu, J. Zhao, Y. Gao, F. De Angelis and J. Huang, Science, 2019, 365, 473–478 CrossRef CAS PubMed.
- S. Wu, Z. Li, M.-Q. Li, Y. Diao, F. Lin, T. Liu, J. Zhang, P. Tieu, W. Gao, F. Qi, X. Pan, Z. Xu, Z. Zhu and A. K.-Y. Jen, Nat. Nanotechnol., 2020, 15, 934–940 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc03867j |
| This journal is © The Royal Society of Chemistry 2024 |