Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the role of nitrogen-doping and surface topology in the binding of Fe(III)/Fe(II) to biobased carbon electrodes†
Anna
Bachs-Herrera
 a,
Isaac
Vidal-Daza
a,
Isaac
Vidal-Daza
 ab,
Emre B.
Boz
ab,
Emre B.
Boz
 c,
Antoni
Forner-Cuenca
c,
Antoni
Forner-Cuenca
 c and
Francisco J.
Martin-Martinez
c and
Francisco J.
Martin-Martinez
 *a
*a
aDepartment of Chemistry, Swansea University, Swansea, SA2 8PP, UK. E-mail: f.j.martin-martinez@swansea.ac.uk
bGrupo de Modelización y Diseño Molecular, Universidad de Granada, Granada, 18071, Spain
cElectrochemical Materials and Systems, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, PO Box 513, Eindhoven, MB 5600, The Netherlands
First published on 6th May 2024
Abstract
Low-cost and high performance electrodes are critical to advance electrochemical energy storage devices that decouple energy supply from demand. At their core, carbon is ubiquitously employed given its availability, chemical and electrochemical stability, electrical conductivity, and affordable cost. However, due to their relative inertness, carbonaceous electrodes suffer from limited wettability and kinetic activity with aqueous electrolytes. A common approach is to introduce heteroatoms, either through post-processing (thermal/acid activation) or by employing different precursors. Specifically, biobased carbons like hydrochar and biochar are rich in heteroatoms that are naturally incorporated through the production process into the electrode structure. However, achieving a fundamental understanding of the interactions between metal ions and carbon surfaces has proven elusive, leading researchers to rely on empirical approaches for heteroatom doping of carbons. To achieve a better understanding of the fundamental mechanisms, we performed density functional theory calculations of a commonly employed iron redox couple, Fe(III) and Fe(II). We investigated binding mechanisms in graphitic carbon model systems with different surface features, and explored the effect of nitrogen doping and surface topology on the binding energy, as well as the effect of ions' spin multiplicity in the carbon-metal coordination mechanisms. Our results suggest that the interactions of Fe(III) and Fe(II) ions with the nitrogen-doped carbon electrodes not only depend on the surface curvature or the nitrogen content and functionality, but also on the spin multiplicity of the metal ion. Iron ions always evolve into an open-shell electronic structure with a high number of unpaired electrons to increase their coordination sphere with the graphitic surface. We hope that our findings can assist the development of fit-for-purpose heteroatom-doped carbon electrodes with a tailored nanostructure for electrochemical devices utilizing the Fe(III)/Fe(II) redox couple.
Introduction
Electrochemical technologies for energy conversion and storage are poised to play a central role in the future energy economy. At the core of these devices, porous carbonaceous materials are critical to enable sustainable energy storage and energy conversion that alleviates intermittency from renewable sources, enhances grid resiliency, and decouples energy supply from demand.1,2 Prominent examples of using porous carbonaceous materials include catalyst supports for low temperature fuel cells,3 electrodes in redox flow batteries,4 and other technologies such as supercapacitors and metal–air batteries.5–7Carbon electrodes with low heteroatom content and high degrees of graphitisation are not ideally suited for several redox pairs. Furthermore, the low energy carbon surface provides limited wettability with aqueous solutions.8–10 Thus, carbon electrode materials are commonly functionalised to improve their key properties. For example, nitrogen doping results in increased wettability, which facilitates the access of the aqueous electrolyte to the electrode surface and enhances electrolyte-electrode interactions.11 The increase in wettability, in turn, decreases the kinetic overpotential in the battery, which improves the electrochemical performance.12,13 Although the mechanism is not fully understood, it is believed that the electron-donor properties of nitrogen induce faradaic reactions through its lone electron pair, which increase the pseudocapacitance,14 therefore adding to the capacitance produced from the electrochemically accessible surface area (ECSA).13,15 Heteroatoms also improve the charge transfer kinetics of common aqueous redox couples on carbon surfaces. Recent studies, both at an experimental and computational level, suggest that adding heteroatoms on the carbon surface increases the number of active adsorption sites due to charge delocalisation, enhancing then the electron transfer kinetics of the V(III)/V(II) pair,16 which increases the exchange current density of both V(III)/V(II) and V(IV)/V(V) couples in all-vanadium redox flow batteries (VRFB).15
Biobased carbon materials, i.e., derived from biomass that is already rich in heteroatoms, make great candidates for new-generation electrodes.14,15,17 The use of oxygen- and nitrogen-doped biobased carbons, such as hydrochars and biochars, coupled to aqueous electrolytes are a promising avenue to develop low-cost and high-performance devices. Hydrochar and biochar are carbon-rich solid materials predominantly produced from hydrothermal carbonisation (HTC) or pyrolysis of biomass, respectively. HTC uses wet biomass,18 while pyrolysis requires an initial drying step.19 During the thermal process, biomass heteroatoms are easily incorporated into the graphitic structure of the biobased carbon material, which leads to electrodes with increased wettability, and enhanced electrode–electrolyte interactions. Wan et al.13 showed that nitrogen-rich electrodes from hydrochars exhibited an enhanced capacitance and electrochemically accessible surface area (ECSA) in VRFBs, compared to those with no nitrogen in their structure, or carbon black. It has been demonstrated that nitrogen-doped biobased carbon electrodes not only increase the redox activity, but also have a better oxidation stability, especially in acidic electrolytes.17
Hydrochar and biochar possess high energy and mass density, and a porous structure that can be tailored. The physicochemical properties of these biobased carbon materials vary depending on the type of biomass, the specific processing conditions, the use of catalysts, and the application of any activation procedures,20 which lead to different chemical and physical characteristics, such as porosity and surface acidity. For example, oxygen-containing groups are usually associated with acidity on the carbon surface,21 while nitrogen doping provides basicity, enhancing the interactions with acidic molecules.22 Possible nitrogen-containing functional groups on carbon surfaces are amides, pyridinic, pyrrolic, and quaternary nitrogen.23,24 For example, the presence of pyridinic N enhances the pseudocapacitance of carbon, whereas pyrrolic N has the opposite effect on the normalised capacitance.25,26 Understanding the variety and role of these functional groups is critical to define the structure–property relationships of the material, since it modifies properties such as the electronic and crystalline structure, thermal stability, surface polarity, electronic conductivity, and electron-donor chemical features.27
The C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio in biomass, which in turn determines the C
N ratio in biomass, which in turn determines the C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio in hydrochar and biochar, is also critical since it affects porosity. While micro- and mesopores are observed28–31 in hydrochars from various biomass precursors, the abundancy of micropores slightly decreases with a decreasing C
N ratio in hydrochar and biochar, is also critical since it affects porosity. While micro- and mesopores are observed28–31 in hydrochars from various biomass precursors, the abundancy of micropores slightly decreases with a decreasing C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio25 It implies that pores seem to widen as more nitrogen in the form of pyridinic groups is introduced, and ion mobility is increased in the resulting mesopores compared to micropores,32–34 although the reasons behind these phenomena are still unclear. This increase of mesopores increases accessibility to existing micropores, increases ion mobility, reducing then the resistance to penetrating pores at high rates17 and also enhances the electrochemical performance because of the higher electric double-layer capacitance (EDLC) associated to them. Furthermore, biobased carbon electrodes, with pore sizes ranging between 0.7–0.8 nm, have demonstrated increased wettability,35 suggesting that this factor may be related to both the nitrogen content and the pore size.
N ratio25 It implies that pores seem to widen as more nitrogen in the form of pyridinic groups is introduced, and ion mobility is increased in the resulting mesopores compared to micropores,32–34 although the reasons behind these phenomena are still unclear. This increase of mesopores increases accessibility to existing micropores, increases ion mobility, reducing then the resistance to penetrating pores at high rates17 and also enhances the electrochemical performance because of the higher electric double-layer capacitance (EDLC) associated to them. Furthermore, biobased carbon electrodes, with pore sizes ranging between 0.7–0.8 nm, have demonstrated increased wettability,35 suggesting that this factor may be related to both the nitrogen content and the pore size.
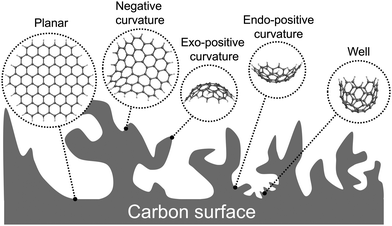
Modelling the surface of biobased electrodes with atomic resolution is challenging due to complexity of the carbon surface with several surface topologies, and the variety of functional groups and heteroatoms existing in the structure because of biomass processing. As a highly porous carbon material that can also present microspheres on the surface,36–38 the curvature of the carbon surfaces – in combination with the chemical functional groups – must be included in the models to investigate the electrode–electrolyte interaction mechanisms. Furthermore, the intrinsic size limitations of atomistic models call for an imaginative but representative selection of molecular model systems. This chemical complexity has hampered a detailed characterisation of the molecular structure of biobased carbon electrodes, with few articles reporting functional groups,37,39–42 or models of either hydrochar or biochar.43–47 This lack of characterisation has also limited the development of atomistic models, with only few density functional theory (DFT) studies44,45,47,48 involving hydrochar to date, and some fused benzene-rings models to simulate activated carbon.49
Porosity generates different types of curvatures on the electrode surface. Negatively curved surfaces may be found in biobased carbon materials in a similar way to those found in schwarzites. DFT calculations for the use of schwarzites as nodes in Li-ion batteries suggest that Li0 has a higher affinity for negatively curved surfaces than those with zero curvature (i.e. graphitic surfaces). Furthermore, there is an energetic decrease in the barrier for diffusion for Li+ in this type of surfaces than in graphene.50
To account for the role of nitrogen in graphitic surfaces of hydrochar, nitrogen-doped graphene has been used as a model system. Duan et al.51 studied the effect of nitrogen on different positions of the graphitic surface, including nitrogen replacing a carbon position in the middle of the flake (graphitic N) and a nitrogen atom on the edge of the flake (pyridinic N), as well as the pH and edge (zigzag and armchair) effects. Zigzag models have been proved to be more reactive than those with armchair edges,52 which could be related to the different distribution of aromaticity53,54 across the polycyclic aromatic structure, and potential radical electrons. In this case, it was observed that the binding energies of the chemical species involved in oxygen reduction reactions on the graphene surface were stronger at higher pH. As for the effect of the nitrogen atom, it was found that N doping at the zigzag edge (pyridinic N) deactivates the neighbouring carbon sites but activates the armchair edge. Graphitic N also showed a negative effect for both types of edge. On the contrary, when both types of doping, graphitic N and pyridinic N, are present on the graphitic surface, the adsorbate–surface interactions increased and even more so at higher pH. The conclusion was that an electron transfer is produced between the graphitic N and the pyridinic N.
On the electrolyte side, a low-cost, non-strategic,55,56 and abundantly available redox couple is Fe(III)/Fe(II),57 which is used as an electrolyte in redox flow batteries,57–59 and plays a role in several other relevant processes such us H2 generation by using a Zn–Fe battery with a Fe(III) reduction reaction.60 The Fe(III)/Fe(II) redox chemistry is a reversible one electron reaction with relatively fast kinetics, high solubility in aqueous solvents, and it does not require expensive catalysts.61,62 Moreover, this redox reaction is sensitive to the functional groups on the carbon surface, and certain groups, such as carbonyls, have been found to lead to faster Fe(III)/Fe(II) kinetics.61,63 Thus, iron cations are the ideal redox probes for computational and experimental studies, and in this work, we examined the interaction of nitrogen and curvature on graphitic carbon surfaces with iron in its two oxidation states, i.e., Fe(II) and Fe(III), in the context of the catalysis of the Fe(III)/Fe(II) redox reaction on a carbon electrode. To this end, we built finite atomistic models to represent graphitic carbon surfaces of the electrode (see Fig. 1) for a schematic representation of microscopic view of a carbon electrode. The aim of this study is to elucidate the effects of nitrogen-containing chemical functionalities and pore curvature of biobased carbon materials on the redox couple Fe(III)/Fe(II). Our findings suggest that the presence of nitrogen enhances, in general, the interactions of any of the adsorbates investigated with the surfaces in most curvatures. This work on biobased carbon electrodes utilising the Fe(III)/Fe(II) reaction opens further avenues to develop tailored biobased carbon materials for selected redox chemistries. The binding of water on this biobased graphitic carbon surfaces was also investigated, since it is a common solvent used in electrochemistry and that is known to form a coordination sphere around iron.64,65 Because iron is a transition metal, different spin states (S) were considered in the binding study of Fe(II) and Fe(III) on the different carbon surfaces, from spin multiplicity 1 for S = 0 to spin multiplicity 6 for S = 5/2 depending on the complex.
 | ||
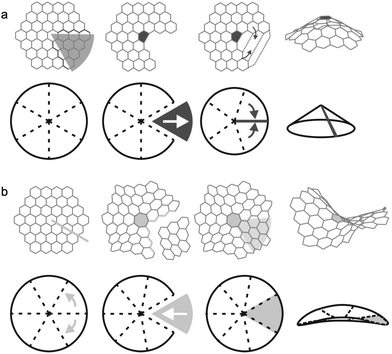
| Fig. 1 Schematic representation of the surface topology of a carbon electrocatalyst and the molecular models developed to describe the different features and pore sizes along this surface. | ||
The aim of this study is to elucidate the effects of nitrogen-containing chemical functionalities and pore curvature of biobased carbon materials on the redox couple Fe(III)/Fe(II). Our findings suggest that the presence of nitrogen enhances, in general, the interactions of any of the adsorbates investigated with the surfaces in most curvatures. This work on biobased carbon electrodes utilising the Fe(III)/Fe(II) reaction opens further avenues to develop tailored biobased carbon materials for selected redox chemistries.
Experimental
The finite models for the graphitic carbon surfaces models were generated with ChemDraw 21.0.0. Planar surfaces were built to represent meso- and macropores, where the pore curvature is almost neglectable compared to the size of the ions (see Fig. 1). We selected graphene flakes with zigzag edges because those edges are known to induce a more homogeneous electron distribution, minimising edge effects. To evaluate the effect of curvature in the smaller pores of a carbon electrode we built graphitic surfaces with positive and negative curvature. Fig. 2 shows a scheme of how the topology of a hexagonal honeycomb lattice changes upon the inclusion of defects (changing the central hexagonal ring for a pentagonal or a heptagonal ring). This topological characteristic has been used to create nanoscopic features of curved surfaces in a carbon electrode. As shown in Fig. 2a, positive curvatures are generated by introducing a pentagon at the centre of a hexagonal honeycomb lattice, which removes a section of the structure (in dark grey) creating a conical-like surface. Negative curvatures (Fig. 2b) are generated by the inclusion of a heptagon, which adds a section to the structure (in light grey), forming a saddle shape. In the actual models considered here, more than one pentagon is included in positive surfaces to generate more rounded pores rather than a conical structure.The initial geometries of the complexes formed by the of the graphitic carbon surfaces and the ions were generated with an in-house Python code that was created to automate the process.
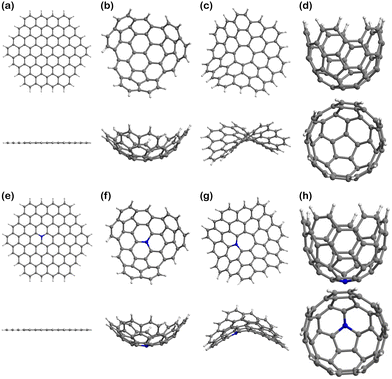
The geometry optimisations of the isolated graphitic carbon models (Fig. 3) and the ion–surface complexes (Fig. S1–S3 in, ESI†), as well as the single point calculations of the monoatomic ion species were performed with ORCA version 4.2.1.66
All DFT calculations were made with PBEh-3c67 functional, which implements the Perdew–Burke–Ernzerhoff (PBE) functional within the generalised gradient approximation (GGA).68,69 It includes a three-fold corrected Hartree–Fock method (HF-3c),70 which applies a three atom pair-wise correction terms for London dispersion interactions (D3 correction71 with Becke–Johnson damping72), and a geometrical counterpoise correction (gCP)73 that corrects both the basis set superposition error (BSSE) and the basis set incompleteness error (BSIE). The reason of selecting PBEh-3c relies in the fact that it has proven to provide an accurate description of non-covalent interactions in systems of up to hundreds of atoms,67 which makes it suitable for our purposes, in a less computationally demanding approach. Furthermore, the molecular calculations to develop this method were performed with ORCA, making it optimised for our study.67
As basis set we used a polarised valence-double-zeta basis set def2-mSVP for the elements from H to Ne, and the def2-SVP,74 for the rest of the elements, as they are included in ORCA and specially optimised for PBEh-3c. Both bases contain a d-polarisation function for p elements and a diffuse p set for d elements. In def2-mSVP, the missing p-polarisation functions on hydrogen atom are compensated by scaling the s-function components to account for increased effective nuclear charge.67
Solvent effects were included using an implicit solvent method as implemented by the conductor-like polarisable continuum model (CPCM),75 with water being the solvent present in the systems. In CPCM, the solute (i.e., the graphitic carbon models and their complexes with different ions) is embedded in a cavity formed by spheres centred on the atoms76 and the surface is then smoothed to simulate the solvent-excluded surface, which represents the boundary of the molecular volume with respect to a specific solvent.77 Inside the cavity, the dielectric constant is the same as in vacuo, whereas outside, its value is that of the solvent, which is water in this case.
Since most systems of study contain at least one unpaired electron, Unrestricted Kohn–Sham (UKS) DFT calculations were performed to account for the open-shell systems. Those with no unpaired electrons were also calculated as UKS so that all results were comparable.
Furthermore, unrestricted calculations of open-shell systems may incur in spin contamination, because α and β electrons are calculated separately so that the wavefunction is not an eigenfunction of the total spin, leading to some errors. As a rule of thumb, if the deviation between the total spin operator 〈S2〉 and S(S + 1) is more than 10%, it is considered that there is such spin contamination. This has been accounted for (Tables S1–S12 in ESI†) in this paper with the deviation value provided by the output files.
The SCF spin densities were calculated to study the distribution of unpaired electrons in open-shell systems and properties such as charge transfer adsorbate–surface interactions. Spin densities were obtained by calculating the difference between the α and β electron densities. The plots with positive isovalues show then the probability of finding an electron in the α state. The spin density plots were generated with a cube grid of 100 points of resolution by side to obtain smooth surfaces in the visualisation process. The final geometries as well as the spin densities were visualised with VMD.78
To calculate binding energies, the energies of the ions Fe(II) and Fe(III) (Fig. S4 in ESI†) were calculated at their respective possible spin multiplicities (M) depending on their total electronic spin (S)
| M = 2S + 1 | (1) |
| EB = Ecomplex − (Esurface + Eadsorbate) | (2) |
The global effect of N-doping on the binding energy was evaluated by subtracting the binding energy of the pristine complex EpristineB to the binding energy of the N-doped complex (EN-dopedB) as in eqn (3). This operation is repeated for each curvature studied. In the case of Fe(II) and Fe(III), the binding energies for each complex were those the spin multiplicity of which presented the lowest energy.
| ΔE = EN-dopedB − EpristineB | (3) |
Results & discussion
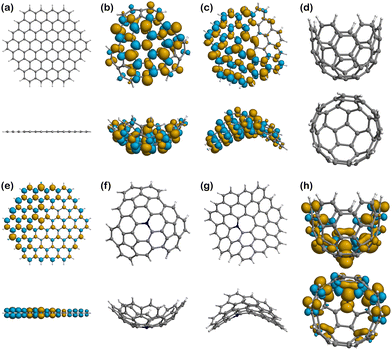
The models of finite graphitic surfaces used in this study are presented in Fig. 3. Pristine (Fig. 3a–d) and N-doped (Fig. 3e–h) models were created to represent pure carbon and nitrogen-rich biobased electrode surfaces, respectively. By using a sufficiently large hexagonal graphene-like flake with and without nitrogen in its structure, we evaluate the effect of nitrogen doping coming from biomass in the binding of iron electrochemical species at the surface of the carbon electrode. Furthermore, to evaluate the effect of curvature in combination with nitrogen doping, we used the surface curvatures already described: planar (Fig. 3a and e), abbreviated “Planar” and “N-Planar”, for pristine carbon and N-doped respectively; positive curvature (Fig. 3b and f), abbreviated “Endo” or “Exo” and “N-Endo” or “N-Exo” (depending on what side of the surface the binding takes place); negative curvature (Fig. 3c and g), abbreviated as “Negative” and “N-Negative”, and positive surface with a smaller curvature radius (Fig. 3d and f), abbreviated “Well” and “N-Well”, respectively. While planar surfaces are representative of the interior of meso- and macropores, in which the curvature is neglectable in comparison to the size of the electrolytes, curved surfaces represent the features of micropores, where the curvature is closer to the order of magnitude of the adsorbed species. Since hydrochar can also present microspheres on its surface, Endo and Exo binding were explored for surfaces with positive curvature. During the following discussion, the complexes are noted as adsorbate@surface, e.g., Fe(II)@pristine for the binding of Fe(II) on a pristine surface.Effect of curvature on the binding energy
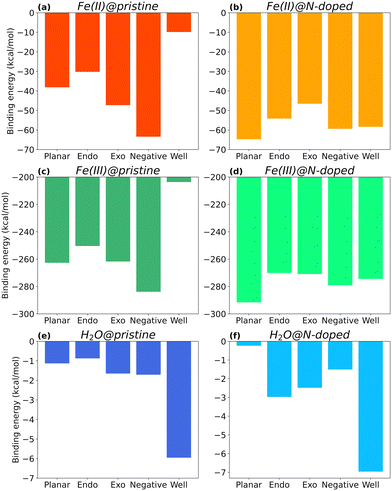
Fig. 4 shows the binding energies of Fe(II), Fe(III), and H2O to each type of surface, i.e., neutral (Planar), positive (with Endo and Exo binding), negative, and positive with higher curvature radius (Well), in their pristine and N-doped forms. Only the complexes in the most stable spin multiplicity configuration are discussed. Their final structures are available in ESI,† (Fig. S1–S3) together with energy results for other spin multiplicities (Fig. S5–S7, ESI†).As seen in Fig. 4, the type of curvature and nitrogen doping impact the interaction between the molecules and the surface, with Fe(III) complexes showing binding energies one order of magnitude larger than those of Fe(II), and two orders of magnitude larger than those with H2O.
Focusing on the three main curvature topologies without nitrogen doping, i.e., planar, negative, and positive (Endo), EB varies following this order: ENegative > EPlanar > EEndo, for all cases. For Fe(II)@pristine (Fig. 4a), the binding energy of Fe(II)@Negative is 47% and 57% more favourable than the binding energies of Fe(II)@Planar and Fe(II)@Endo surfaces, respectively. A similar trend applies to Fe(III)@pristine (Fig. 4b), but one order of magnitude stronger. These results indicate that carbon electrodes with higher proportion of negatively curved surfaces may be beneficial for the reduction of Fe(III) to Fe(II), since more Fe(III) ions become available for reduction at the carbon surface. H2O@pristine presented a much lower affinity (Fig. 4c), approximately 30 and 160 times weaker than those for Fe(II) and Fe(III), respectively, which rules out its competition for the binding sites.
In the specific case of surfaces with positive curvature, the binding at Exo position is more favourable than that at the Endo one for all cases, although in the case of Fe(III) the EB value for Exo is close to EB for Planar. In fact, Endo is the least favourable surface for binding overall, which suggests that this type of surface could be disadvantageous for achieving improved wettability in an electrode.
Within positive curvature surfaces, higher curvature radius in very small micropores is not beneficial. Both Fe(II) and Fe(III), show weaker binding to the Well surface than to the Endo one. EB of Fe(II)@pristine for Well surfaces is barely −10 kcal mol−1 (Fig. 4a), which is 3 times less favourable than the Endo complex. In the case of Fe(III)@pristine, EB is still below the −200 kcal mol−1 (Fig. 4b) with a ΔE = 46.7 kcal mol−1 between the Well and Endo complexes, most likely due to electronic hindrance. H2O@pristine shows a different trend (Fig. 4c), with the binding to the Well surface almost 7 times stronger than to the Endo one. Thus, a small micropore with higher curvature radius could be beneficial to increase its wettability. Even though the iron in both oxidation states show lowest affinity for the Well, the interaction is still favourable, especially in the case of Fe(III) and its reduction to Fe(II).
Overall, the affinities of Fe(II) and Fe(III) for the different pristine surfaces follow the trends ENegative > EExo > EPlanar > EEndo > EWell and ENegative > EExo ≈ EPlanar > EEndo > EWell respectively. Despite following a very similar pattern in terms of interaction, Fe(III) presents a much stronger affinity for the different surface topologies. In fact, binding energies between Fe(III) and the pristine surfaces are 4.5 to 20.7 times more favourable, being the largest difference for the Well surface. The higher affinity may be due to the fact that Fe(III) is more electron deficient than Fe(II) and therefore it seeks to compensate this deficiency by interacting with the electron-rich electrode's surface.
Surface curvature influence the interaction with electrolytes. Our findings suggest that negatively curved surfaces enhance the binding of Fe(III)/Fe(II) pair with respect to planar ones. Similar findings have been reported in DFT calculations for lithium.50
Effect of nitrogen content on the binding energy
Looking at Fig. 4d, Fe(II)@N-Planar shows the strongest interaction, which is comparable to the pristine Fe(II)@Negative. In general, in Fe(II)@N-doped, EB varies following this order: EN-Planar > EN-Negative ≈ EN-Well > EN-Endo > EN-Exo, which is different from the order in Fe(II)@pristine complexes. Fe(III) follows a similar trend (Fig. 4e), also with Fe(III)@N-Planar presenting the strongest binding energy.The curvature radius seems to have a similar effect on the binding of Fe(II) and Fe(III) on N-doped surfaces. In fact, the energy difference between N-Well and N-Endo for both Fe(II) and Fe(III) is −4 kcal mol−1, being the N-Well complex the slightly more stable one.
For H2O, the N-Well surface shows the highest binding energy, as it happens with H2O@Well, although the largest increment occurs for H2O@N-Endo, with an interaction 240% stronger than in H2O@Endo.
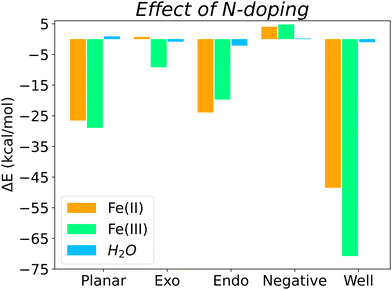
Overall, Fig. 5 shows the energy differences (calculated using eqn (3)) between N-doped and pristine surfaces with different curvatures complexed to Fe(II), Fe(III) and H2O. In general, nitrogen has a positive effect on the binding energy, with the exception of the Negative surfaces for Fe(II)@N-doped and Fe(III)@N-doped complexes. Although the effect over H2O is not so notorious as with the ions, with a ΔE < 1.0 kcal mol−1 in certain cases, it can be observed that H2O benefitted the most in the interaction with positive surfaces, especially Endo and Well, a finding that is supported by the experimental increase of wettability in pores ranging between 0.7 and 0.8 nm.35
The systems that benefited from the presence of nitrogen the most are Fe(II)@N-Well and Fe(III)@N-Well, followed by the N-Planar and N-Endo complexes. However, in the optimised geometries for N-Well and N-Endo both ions converged to the edge of the surface rather than to the centre (Fig. S1g, j and Fig. S2g, j, respectively, ESI†), which indicates that even though there are lower energy geometries, the interaction to the nitrogen atom is not favoured and the ions tend to leave the pore. This implies that it is N-Planar structure the most beneficial for the binding of Fe(II) and Fe(III) ion. Fe(III)@N-Exo was favourable as well, but the ΔE is one order of magnitude lower.
Regardless of the effect of nitrogen on Fe(III) and Fe(II), which varies depending on surface topology, Fe(III) always presents a more favourable surface interaction than Fe(II), i.e., the binding with to the biobased carbon electrode is stronger with Fe(III).
The presence of nitrogen increases binding strength for both species, with the exception of the surface with negative curvature. Binding energies of Fe(III) with any N-doped surface are 4.5 to 5.8 times stronger than those for Fe(II). This is specially relevant to use of nitrogen-rich biobased carbons as a cathode material, since a stronger interaction with the reagent, Fe(III), obeys the Sabatier principle.
On average, quaternary nitrogen doping in the graphitic surface of a carbon electrode favours the binding of both iron electrolytes and water, with the exception of surfaces with negative curvature, although those surfaces were already the best surface topology for binding in the pristine form. The electron-donor properties of nitrogen, derived from its lone pair of electrons, facilitate the interaction with the two species, which are electron deficient. Furthermore, nitrogen also favours the interaction with water, especially in micropores, and therefore improves the wettability of the biobased carbon electrode, in agreement with experimental results.14–17,35
The beneficial effects of nitrogen doping has also been described for other metal ions15,16,79 and electrolytes,14,17 which suggests that our findings are transferable to other redox pairs.
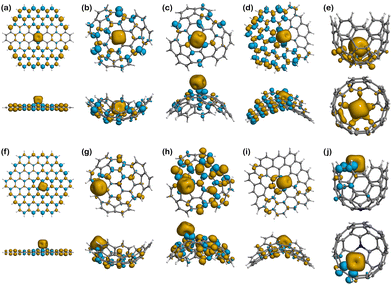
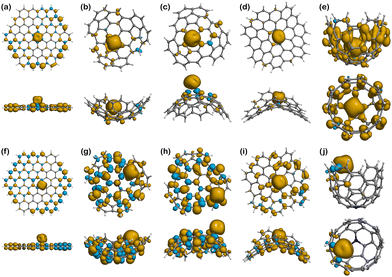
Spin density
Fig. 6–8 show the spin density plots for all the surfaces and their complexes with Fe(II) and Fe(III), calculated from the difference between α and β electron densities. Based on quantum mechanics, a high multiplicity state has increased stability because of the unpaired electrons of parallel spin (α and β by convention), which must reside in different spatial orbitals according to the Pauli exclusion principle. However, spin polarisation can be induced in some cases, especially in the presence of paramagnetic centres, and therefore structures may show some excess of β-electron density80–82 in addition to the expected α density one. In other words, the spin density plots that would expectingly represent the electron density associated to unpaired electrons with parallel α spin, may also present isosurfaces associated to unpaired β electrons. Thus, the plots of spin densities presented in Fig. 6–8 show the excess of both α and β electron densities. In addition, there are 4 surfaces with no spin density in Fig. 6, as they are closed-shell systems (with no unpaired electrons), i.e., Planar (Fig. 6a), Well (Fig. 6d), N-Positive (Fig. 6f), and N-Negative (Fig. 6g).The pristine positive surface (Fig. 6b) and the negative one (Fig. 6c) show a large delocalisation of unpaired electrons across the structure. The distribution is not symmetric, since the geometry induced by the presence of pentagonal and heptagonal rings in the structure broke the C6 symmetry of the graphitic network. Some of the lobes on the external (exo) side of the positive surface, especially in those atoms closer to the centre of the molecule, are larger in size, for a fixed value of isosurface, than their endo counterparts, which indicates a higher probability of locating the unpaired electron in that region. Accordingly, there could be a greater tendency to engage in radical reactions in the external and central part of the surface.
N-Planar and N-Well show some excess of α-electron density on the nitrogen atom and the adjacent carbons and is then delocalised along the structure of the surface. Like in the pristine positive, the lobes on the external (exo) side of the Well structure are larger than those in the endo side.
Looking at the binding of Fe(II), Fig. 7a shows that the 4 unpaired electrons from the metal ion are mostly concentrated on the metal centre, but also delocalised at the edges following a mirrored symmetry. The population analysis results show that the total spin in Fe(II)@Planar is 3.14, which is less than the 4 unpaired electrons of the isolated ion. This is indicative of a subtle covalent interaction between the metal ion and the surface. When nitrogen is added to the structure, Fig. 7f shows that the nitrogen atom, which initially contained an unpaired electron, does not show any spin density now, but the four closest atoms to the metal centre show an excess of β-electron density that is delocalised on alternating atoms, including nitrogen. However, the population analysis indicates that the total spin value for Fe(II) is 3.01, coinciding with the total spin value of the system, meaning no electrons from the ion are delocalised.
In Fe(II)@Endo (Fig. 7b), there is a change in the spin density distribution of the surface with respect to the surface prior to binding (Fig. 6b). The unpaired electrons are more localised in the ion. In fact, out of the 3 unpaired electrons of the system, 2.87 are localised in Fe(II). This could indicate a weaker interaction than in other binding systems, where the electrons are more delocalised between the ion and the surface. A different case is that of Fe(II)@N-Endo (Fig. 7g), where the geometry optimisation converged to a Fe(II)-edge interaction (Fig. S1g, ESI†) rather than to a binding mechanism to the nitrogen atom. Nevertheless, in both the pristine and N-doped systems, Fe(II) induced a β-spin density on the atoms it is mostly interacting with. The results are similar for Fe(II)@Exo (Fig. 7c), where there is less spin delocalisation than in other cases. In the case of Fe(II)@N-Exo (Fig. 7h), on the other hand, the spin delocalisation is larger, with 0.79 electrons delocalised along the surface, indicative of a subtle covalent interaction like in Fe(II)@Planar.
The complexes with the negative surfaces show quite different behaviour to the Positive ones. Fe(II)@Negative (Fig. 7d) presents electron delocalisation on most of the surface with a high degree of spin polarisation (β-electron density), whereas in Fe(II)@N-Negative (Fig. 7i) the unpaired electrons seem to be more localised and less polarised, which is supported by the Hirshfeld charge population analysis, where the total spin value of the system is 4 and 0.44 electrons are delocalised on the surface.
The only structure that does not present any polarisation of spin is Fe(II)@Well (Fig. 7e), although it is induced in the Fe(II)@N-Well (Fig. 7j), where the interaction happens at the edge, in interestingly the ion does not enter the pore.
Moving to Fe(III) binding structures, Fe(III)@Planar (Fig. 8a), shows an increase in the covalent character of the interaction compared to Fe(II)@Planar (Fig. 7a), which is measured by comparing the total spin of the system with the spin associated with Fe(III) in the Hirshfeld charge population analysis. The total spin population of the system is 5, although Fe(III) presents a total spin value of 3.09, indicating that two electrons are completely delocalised along the structure of the surface. Fe(III)@N-Planar (Fig. 8f) presents more spin density at the edges than in the centre of the surface, similar to its pristine counterpart and which differs from Fe(II)@N-Planar. In this case, out of the 4 unpaired electrons of the system, 0.81 is delocalised on the surface.
As it happened with Fe(II) systems, Fe(III)@Positive (Fig. 8b and c) present less spin density than other Fe(III) complexes, while Fe(III)@N-Positive (Fig. 8g and h) show both more spin delocalisation and polarisation and converged to the edges. Looking at the interactions in Fe(III)@N-Endo, out of the 5 unpaired electrons of the electronic configuration of Fe(III), 1.27 are delocalised throughout the carbon surface, which indicates a stronger covalent character than Fe(II)@N-Endo, with only 0.3 delocalised electrons along the positive surface, and also a bit stronger than Fe(III)@N-Exo with 1.19.
Different from other cases, there is no spin delocalisation or polarisation in Fe(III)@Negative (Fig. 8d), but it appears as a consequence of N-doping in Fe(III)@N-Negative (Fig. 8i).
Fe(III)@Well (Fig. 8e) shows the largest spin density and delocalisation out of all the complexes with Fe(III) having a spin value of 3.54 after binding compared to the 5 in the isolated ion. The excess of α-electron density is distributed throughout the surface of Well in a mostly even manner with no presence of spin polarisation. This situation changes for Fe(III)@N-Well (Fig. 8j), where the spin density is mostly concentrated in the ion with no delocalisation on the nitrogen atom.
Conclusions
This work provides a molecular-scale understanding of the interactions between a biobased electrode surface (N-doped carbon) and a model redox couple, Fe(III)/Fe(II), in its aqueous solutions. DFT calculations on model systems for micro- and meso- and macropores interacting with Fe(III)/Fe(II) electrolytes helped elucidating some fundamental binding mechanisms between the electrode and the electrolytes, especially in the reduction of Fe(III) to Fe(II). We evaluated the effect of surface topology and N-doping on the binding of Fe(II), Fe(III) and water molecules to the biobased carbon surface, from an atomic perspective.Our results indicate that:
• The presence of quaternary N-doping increases the binding of Fe(II) to low-curvature carbon surfaces by up to 80%, and by up to 10% in the case of Fe(III), which increases species availability at the surface for the reduction process and accelerates charging kinetics.12,13
• Binding energies of Fe(III) are 4.5–5.8 times higher than those of Fe(II), which is especially relevant for cathode electrodes, according to Sabatier principle.
• Structures rich in N-doped micropores improve the wettability at the molecular scale, with up to 240% higher binding energies to water molecules.
• An ideal biobased carbon electrode should combine N-doped large pores (planar surfaces), pristine areas with a negative curvature and micropores for increased wettability.
• Fe(III)/Fe(II) ions adopt an electronic configuration that maximises the number of unpaired electrons, increasing their ability to create a coordination sphere either with water molecules or upon binding to the carbon surface.
• Fe(III)/Fe(II) ions induce spin polarisation in the carbon surface upon binding, as described for some systems paramagnetic centres.80–82 The stronger the interaction electrolyte-surface, the more spin polarisation is induced.
Our findings provide fundamental knowledge with implications in the development of fit-for-purpose biobased carbon that increase wettability, accelerates kinetics due to increased binding, and improves electrochemical performance at a lower cost.
Author contributions
Anna Bachs-Herrera: conceptualization (supporting), investigation (lead), formal analysis (equal), visualization (equal), writing – original draft (equal). Isaac Vidal-Daza: investigation (supporting), writing – review and editing (supporting). Emre B. Boz: writing – review and editing (supporting). Antoni Forner-Cuenca: writing – review and editing (supporting). Francisco J. Martin-Martinez: conceptualization (lead), supervision (lead), investigation (supporting), formal analysis (lead), visualization (equal), funding acquisition (lead), project administration (lead).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Royal Society of Chemistry Enablement Grant (E21-7051491439), the Engineering and Physical Sciences Research Council's PhD scholarship ref. 2492554. The authors also acknowledge the support from the Google Cloud Research Credits program with the award GCP19980904, and the support of the Supercomputing Wales project. F. J. M.-M. acknowledges the Google Cloud Research Innovators program.References
- Z. Yang, J. Zhang, M. C. W. Kintner-Meyer, X. Lu, D. Choi and J. P. Lemmon, et al., Electrochemical Energy Storage for Green Grid, Chem. Rev., 2011, 111(5), 3577–3613 CrossRef CAS PubMed . Available from: https://pubs.acs.org/doi/10.1021/cr100290v.
- K. Gong, F. Xu, J. B. Grunewald, X. Ma, Y. Zhao and S. Gu, et al., All-Soluble All-Iron Aqueous Redox-Flow Battery, ACS Energy Lett., 2016, 1(1), 89–93 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/acsenergylett.6b00049.
- E. Hornberger, T. Merzdorf, H. Schmies, J. Hübner, M. Klingenhof and U. Gernert, et al., Impact of Carbon N-Doping and Pyridinic-N Content on the Fuel Cell Performance and Durability of Carbon-Supported Pt Nanoparticle Catalysts, ACS Appl. Mater. Interfaces, 2022, 14(16), 18420–18430 CrossRef CAS PubMed . Available from: https://pubs.acs.org/doi/10.1021/acsami.2c00762.
- A. Forner-Cuenca and F. R. Brushett, Engineering porous electrodes for next-generation redox flow batteries: recent progress and opportunities, Curr. Opin. Electrochem., 2019, 18, 113–122 CrossRef CAS . Available from: https://linkinghub.elsevier.com/retrieve/pii/S2451910319301668.
- H. Yang, X. Han, A. I. Douka, L. Huang, L. Gong and C. Xia, et al., Advanced Oxygen Electrocatalysis in Energy Conversion and Storage, Adv. Funct. Mater., 2021, 31(12), 1–29 CrossRef . Available from: https://onlinelibrary.wiley.com/doi/10.1002/adfm.202007602.
- L. Yaqoob, T. Noor and N. Iqbal, An overview of metal-air batteries, current progress, and future perspectives, J. Energy Storage, 2022, 56, 106075, DOI:10.1016/j.est.2022.106075.
- F. Shahbazi Farahani, M. S. Rahmanifar, A. Noori, M. F. El-Kady, N. Hassani and M. Neek-Amal, et al., Correction to “Trilayer Metal–Organic Frameworks as Multifunctional Electrocatalysts for Energy Conversion and Storage Applications”, J. Am. Chem. Soc., 2022, 144(34), 15903–15906 CrossRef CAS PubMed . Available from: https://pubs.acs.org/doi/10.1021/jacs.2c06864.
- Y. J. Shin, Y. Wang, H. Huang, G. Kalon, A. T. S. Wee and Z. Shen, et al., Surface-Energy Engineering of Graphene, Langmuir, 2010, 26(6), 3798–3802 CrossRef CAS PubMed . Available from: https://pubs.acs.org/doi/10.1021/la100231u.
- F. Taherian, V. Marcon, N. F. A. van der Vegt and F. Leroy, What Is the Contact Angle of Water on Graphene?, Langmuir, 2013, 29(5), 1457–1465 CrossRef CAS PubMed . Available from: https://pubs.acs.org/doi/10.1021/la304645w.
- R. Raj, S. C. Maroo and E. N. Wang, Wettability of Graphene, Nano Lett., 2013, 13(4), 1509–1515 CrossRef CAS PubMed . Available from: https://pubs.acs.org/doi/10.1021/nl304647t.
- R. L. McCreery, Advanced Carbon Electrode Materials for Molecular Electrochemistry, Chem. Rev., 2008, 108(7), 2646–2687 CrossRef CAS PubMed . Available from: https://pubs.acs.org/doi/10.1021/cr068076m.
- L. Wu, Y. Shen, L. Yu, J. Xi and X. Qiu, Boosting vanadium flow battery performance by Nitrogen-doped carbon nanospheres electrocatalyst, Nano Energy, 2016, 28, 19–28, DOI:10.1016/j.nanoen.2016.08.025.
- C. T. C. Wan, D. López Barreiro, A. Forner-Cuenca, J. W. Barotta, M. J. Hawker and G. Han, et al., Exploration of Biomass-Derived Activated Carbons for Use in Vanadium Redox Flow Batteries, ACS Sustainable Chem. Eng., 2020, 8(25), 9472–9482 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/acssuschemeng.0c02427.
- S. L. Candelaria, B. B. Garcia, D. Liu and G. Cao, Nitrogen modification of highly porous carbon for improved supercapacitor performance, J. Mater. Chem., 2012, 22(19), 9884 RSC . Available from: https://xlink.rsc.org/?DOI=c2jm30923h.
- M. A. Costa de Oliveira, C. Schröder, M. Brunet Cabré, H. Nolan, A. Forner-Cuenca and T. S. Perova, et al., Effects of N-functional groups on the electron transfer kinetics of VO2 +/VO2+ at carbon: Decoupling morphology from chemical effects using model systems, Electrochim. Acta, 2024, 475, 143640 CrossRef CAS . Available from: https://linkinghub.elsevier.com/retrieve/pii/S0013468623018042.
- M. Meskinfam Langroudi, C. S. Pomelli, R. Giglioli, C. Chiappe, M. Aysla Costa de Oliveira and B. Mecheri, et al., Interaction of vanadium species with a functionalized graphite electrode: A combined theoretical and experimental study for flow battery applications, J. Power Sources, 2019, 420, 134–142, DOI:10.1016/j.jpowsour.2019.02.083.
- A. B. Fuertes and M. Sevilla, Superior Capacitive Performance of Hydrochar-Based Porous Carbons in Aqueous Electrolytes, ChemSusChem, 2015, 8(6), 1049–1057 CrossRef CAS PubMed . Available from: https://chemistry-europe.onlinelibrary.wiley.com/doi/10.1002/cssc.201403267.
- A. Bachs-Herrera, D. York, T. Stephens-Jones, I. Mabbett, J. Yeo and F. J. Martin-Martinez, Biomass carbon mining to develop nature-inspired materials for a circular economy, iScience, 2023, 26(4), 106549, DOI:10.1016/j.isci.2023.106549.
- T. Kan, V. Strezov and T. J. Evans, Lignocellulosic biomass pyrolysis: A review of product properties and effects of pyrolysis parameters, Renewable Sustainable Energy Rev., 2016, 57, 1126–1140, DOI:10.1016/j.rser.2015.12.185.
- S. A. Nicolae, H. Au, P. Modugno, H. Luo, A. E. Szego and M. Qiao, et al., Recent advances in hydrothermal carbonisation: from tailored carbon materials and biochemicals to applications and bioenergy, Green Chem., 2020, 22(15), 4747–4800, 10.1039/d0gc00998a.
- M. Seredych, D. Hulicova-Jurcakova, G. Q. Lu and T. J. Bandosz, Surface functional groups of carbons and the effects of their chemical character, density and accessibility to ions on electrochemical performance, Carbon, 2008, 46(11), 1475–1488 CrossRef CAS . Available from: https://linkinghub.elsevier.com/retrieve/pii/S0008622308002911.
- W. Shen and W. Fan, Nitrogen-containing porous carbons: synthesis and application, J. Mater. Chem. A, 2013, 1(4), 999–1013 RSC . Available from: https://xlink.rsc.org/?DOI=C2TA00028H.
- A. A. Peterson, R. P. Lachance and J. W. Tester, Kinetic Evidence of the Maillard Reaction in Hydrothermal Biomass Processing: Glucose−Glycine Interactions in High-Temperature, High-Pressure Water, Ind. Eng. Chem. Res., 2010, 49(5), 2107–2117 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/ie9014809.
- X. Du, J. Li and M. E. Lindström, Modification of industrial softwood kraft lignin using Mannich reaction with and without phenolation pretreatment, Ind. Crops Prod., 2014, 52, 729–735, DOI:10.1016/j.indcrop.2013.11.035.
- P. Treeweranuwat, P. Boonyoung, M. Chareonpanich and K. Nueangnoraj, Role of Nitrogen on the Porosity, Surface, and Electrochemical Characteristics of Activated Carbon, ACS Omega, 2020, 5(4), 1911–1918 CrossRef CAS PubMed . Available from: https://pubs.acs.org/doi/10.1021/acsomega.9b03586.
- A. Borenstein, O. Hanna, R. Attias, S. Luski, T. Brousse and D. Aurbach, Carbon-based composite materials for supercapacitor electrodes: a review, J. Mater. Chem. A, 2017, 5(25), 12653–12672 RSC . Available from: https://xlink.rsc.org/?DOI=C7TA00863E.
- H. Chen, F. Sun, J. Wang, W. Li, W. Qiao and L. Ling, et al., Nitrogen Doping Effects on the Physical and Chemical Properties of Mesoporous Carbons, J. Phys. Chem. C, 2013, 117(16), 8318–8328 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/jp4017773.
- T. P. de Araújo, H. B. Quesada, R. Bergamasco, D. T. Vareschini and M. A. S. D. de Barros, Activated hydrochar produced from Brewer's spent grain and its application in the removal of acetaminophen, Bioresour. Technol., 2020, 310, 123399, DOI:10.1016/j.biortech.2020.123399.
- J. Fang, B. Gao, J. Chen and A. R. Zimmerman, Hydrochars derived from plant biomass under various conditions: Characterization and potential applications and impacts, Chem. Eng. J., 2015, 267, 253–259, DOI:10.1016/j.cej.2015.01.026.
- M. T. Reza, E. Rottler, L. Herklotz and B. Wirth, Hydrothermal carbonization (HTC) of wheat straw: Influence of feedwater pH prepared by acetic acid and potassium hydroxide, Bioresour. Technol., 2015, 182, 336–344, DOI:10.1016/j.biortech.2015.02.024.
- N. Guo, M. Li, X. Sun, F. Wang and R. Yang, Enzymatic hydrolysis lignin derived hierarchical porous carbon for supercapacitors in ionic liquids with high power and energy densities, Green Chem., 2017, 19(11), 2595–2602 RSC . Available from: https://xlink.rsc.org/?DOI=C7GC00506G.
- S. Shiraishi, in Electric Double Layer Capacitors, ed. Y. E. Ichi, M. Inagaki, K. Kaneko, M. Endo, A. Oya and Y. Tanabe, Elsevier, Carbon Alloys, Oxford, 2003, pp. 447–457. Available from: https://www.sciencedirect.com/science/article/pii/B9780080441634500279 Search PubMed.
- X. Wang, C. G. G. Liu, D. Neff, P. F. Fulvio, R. T. Mayes and A. Zhamu, et al., Nitrogen-enriched ordered mesoporous carbons through direct pyrolysis in ammonia with enhanced capacitive performance, J. Mater. Chem. A, 2013, 1(27), 7920 RSC . Available from: https://xlink.rsc.org/?DOI=c3ta11342f.
- T. N. Phan, M. K. Gong, R. Thangavel, Y. S. Lee and C. H. Ko, Enhanced electrochemical performance for EDLC using ordered mesoporous carbons (CMK-3 and CMK-8): Role of mesopores and mesopore structures, J. Alloys Compd., 2019, 780, 90–97 CrossRef CAS . Available from: https://linkinghub.elsevier.com/retrieve/pii/S0925838818344803.
- A. B. Fuertes, G. A. Ferrero and M. Sevilla, One-pot synthesis of microporous carbons highly enriched in nitrogen and their electrochemical performance, J. Mater. Chem. A, 2014, 2(35), 14439–14448 RSC . Available from: https://xlink.rsc.org/?DOI=C4TA02959C.
- Q. Wang, H. Li, L. Chen and X. Huang, Monodispersed hard carbon spherules with uniform nanopores, Carbon, 2001, 39(14), 2211–2214 CrossRef CAS . Available from: https://linkinghub.elsevier.com/retrieve/pii/S0008622301000409.
- M. M. Titirici, M. Antonietti and N. Baccile, Hydrothermal carbon from biomass: a comparison of the local structure from poly- to monosaccharides and pentoses/hexoses, Green Chem., 2008, 10(11), 1204 RSC . Available from: https://xlink.rsc.org/?DOI=b807009a.
- J. Pfersich, P. J. Arauzo, M. Lucian, P. Modugno, M. M. Titirici and L. Fiori, et al., Hydrothermal Conversion of Spent Sugar Beets into High-Value Platform Molecules, Molecules, 2020, 25(17), 3914 CrossRef CAS PubMed . Available from: https://www.mdpi.com/1420-3049/25/17/3914.
- S. Kang, X. Li, J. Fan and J. Chang, Characterization of Hydrochars Produced by Hydrothermal Carbonization of Lignin, Cellulose, D-Xylose, and Wood Meal, Ind. Eng. Chem. Res., 2012, 51(26), 9023–9031 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/ie300565d.
- M. Sevilla and A. B. Fuertes, Chemical and Structural Properties of Carbonaceous Products Obtained by Hydrothermal Carbonization of Saccharides, Chem. – Eur. J., 2009, 15(16), 4195–4203 CrossRef CAS PubMed . Available from: https://onlinelibrary.wiley.com/doi/10.1002/chem.200802097.
- M. Sevilla and A. B. Fuertes, The production of carbon materials by hydrothermal carbonization of cellulose, Carbon, 2009, 47(9), 2281–2289, DOI:10.1016/j.carbon.2009.04.026.
- L. Leng, S. Xu, R. Liu, T. Yu, X. Zhuo and S. Leng, et al., Nitrogen containing functional groups of biochar: An overview, Bioresour. Technol., 2020, 298, 122286, DOI:10.1016/j.biortech.2019.122286.
- A. B. Brown, B. J. McKeogh, G. A. Tompsett, R. Lewis, N. A. Deskins and M. T. Timko, Structural analysis of hydrothermal char and its models by density functional theory simulation of vibrational spectroscopy, Carbon, 2017, 125, 614–629, DOI:10.1016/j.carbon.2017.09.051.
- L. Cheng, Y. Ji and X. Liu, Insights into interfacial interaction mechanism of dyes sorption on a novel hydrochar: Experimental and DFT study, Chem. Eng. Sci., 2021, 233, 116432, DOI:10.1016/j.ces.2020.116432.
- X. Yang, D. Jiang, X. Cheng, C. Yuan, S. Wang and Z. He, et al., Adsorption properties of seaweed-based biochar with the greenhouse gases (CO2, CH4, N2O) through density functional theory (DFT), Biomass Bioenergy, 2022, 163, 106519 CrossRef CAS . Available from: https://linkinghub.elsevier.com/retrieve/pii/S0961953422001817.
- W. Mrozik, B. Minofar, T. Thongsamer, N. Wiriyaphong, S. Khawkomol and J. Plaimart, et al., Valorisation of agricultural waste derived biochars in aquaculture to remove organic micropollutants from water – experimental study and molecular dynamics simulations, J. Environ. Manage., 2021, 300, 113717 CrossRef CAS PubMed . Available from: https://linkinghub.elsevier.com/retrieve/pii/S0301479721017795.
- L. Delahaye, J. T. Hobson, M. P. Rando, B. Sweeney, A. B. Brown and G. A. Tompsett, et al., Experimental and Computational Evaluation of Heavy Metal Cation Adsorption for Molecular Design of Hydrothermal Char, Energies, 2020, 13(16), 4203 CrossRef CAS . Available from: https://www.mdpi.com/1996-1073/13/16/4203.
- Q. Chen, J. Zheng, J. Xu, Z. Dang and L. Zhang, Insights into sulfamethazine adsorption interfacial interaction mechanism on mesoporous cellulose biochar: Coupling DFT/FOT simulations with experiments, Chem. Eng. J., 2019, 356, 341–349, DOI:10.1016/j.cej.2018.09.055.
- W. Qu, F. Shen, H. Zu, S. Liu, J. Yang and Y. Hu, et al., Density Functional Theory Studies of the Adsorption and Interactions between Selenium Species and Mercury on Activated Carbon, Energy Fuels, 2020, 34(8), 9779–9786 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/acs.energyfuels.0c00759.
- D. Odkhuu, D. H. Jung, H. Lee, S. S. Han, S. H. Choi and R. S. Ruoff, et al., Negatively curved carbon as the anode for lithium ion batteries, Carbon, 2014, 66, 39–47, DOI:10.1016/j.carbon.2013.08.033.
- Z. Duan and G. Henkelman, Identification of Active Sites of Pure and Nitrogen-Doped Carbon Materials for Oxygen Reduction Reaction Using Constant-Potential Calculations, J. Phys. Chem. C, 2020, 124(22), 12016–12023 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/acs.jpcc.0c03951.
- P. Koskinen, S. Malola and H. Häkkinen, Self-Passivating Edge Reconstructions of Graphene, Phys. Rev. Lett., 2008, 101(11), 115502 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.101.115502.
- F. J. Martín-Martínez, S. Fias, G. Van Lier, F. De Proft, P. Geerlings and F. J. Martín-Martínez, et al., Electronic Structure and Aromaticity of Graphene Nanoribbons, Chem. – Eur. J., 2012, 18(20), 6183–6194 CrossRef PubMed . Available from: https://onlinelibrary.wiley.com/doi/10.1002/chem.201103977.
- A. D. Zdetsis and E. N. Economou, A Pedestrian Approach to the Aromaticity of Graphene and Nanographene: Significance of Huckel's (4n + 2)π Electron Rule, J. Phys. Chem. C, 2015, 119(29), 16991–17003 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/acs.jpcc.5b04311.
- G. Kear, A. A. Shah and F. C. Walsh, Development of the all-vanadium redox flow battery for energy storage: a review of technological, financial and policy aspects, Int. J. Energy Res., 2012, 36(11), 1105–1120 CrossRef CAS . Available from: https://onlinelibrary.wiley.com/doi/10.1002/er.1863.
- Á. Cunha, J. Martins, N. Rodrigues and F. P. Brito, Vanadium redox flow batteries: a technology review, Int. J. Energy Res., 2015, 39(7), 889–918 CrossRef . Available from: https://onlinelibrary.wiley.com/doi/10.1002/er.3260.
- D. M. Kabtamu, G. Y. Lin, Y. C. Chang, H. Y. Chen, H. C. Huang and N. Y. Hsu, et al., The effect of adding Bi 3+ on the performance of a newly developed iron–copper redox flow battery, RSC Adv., 2018, 8(16), 8537–8543 RSC . Available from: https://xlink.rsc.org/?DOI=C7RA12926B.
- L. W. Hruska and R. F. Savinell, Investigation of Factors Affecting Performance of the Iron-Redox Battery, J. Electrochem. Soc., 1981, 128(1), 18–25 CrossRef CAS . Available from: https://iopscience.iop.org/article/10.1149/1.2127366.
- J. Noack, M. Berkers, J. Ortner and K. Pinkwart, The Influence of Some Electrolyte Additives on the Electrochemical Performance of Fe/Fe 2+ Redox Reactions for Iron/Iron Redox Flow Batteries, J. Electrochem. Soc., 2021, 168(4), 040529 CrossRef CAS . Available from: https://iopscience.iop.org/article/10.1149/1945-7111/abf5a3.
- C. Chen, Z. Fu, F. Qi, Y. Chen, G. Meng and Z. Chang, et al., Fe2+/Fe3+ Cycling for Coupling Self-Powered Hydrogen Evolution and Preparation of Electrode Catalysts, Angew. Chem., Int. Ed., 2022, 61(32), e202207226 CrossRef CAS PubMed . Available from: https://onlinelibrary.wiley.com/doi/10.1002/anie.202207226.
- T. V. Sawant and J. R. McKone, Flow Battery Electroanalysis. 2. Influence of Surface Pretreatment on Fe(III/II) Redox Chemistry at Carbon Electrodes, J. Phys. Chem. C, 2019, 123(1), 144–152 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/acs.jpcc.8b09607.
- T. V. Sawant, C. S. Yim, T. J. Henry, D. M. Miller and J. R. McKone, Harnessing Interfacial Electron Transfer in Redox Flow Batteries, Joule, 2021, 5(2), 360–378, DOI:10.1016/j.joule.2020.11.022.
- P. Chen and R. L. McCreery, Control of Electron Transfer Kinetics at Glassy Carbon Electrodes by Specific Surface Modification, Anal. Chem., 1996, 68(22), 3958–3965 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/ac960492r.
- M. Radoń and G. Drabik, Spin States and Other Ligand–Field States of Aqua Complexes Revisited with Multireference ab Initio Calculations Including Solvation Effects, J. Chem. Theory Comput., 2018, 14(8), 4010–4027 CrossRef PubMed . Available from: https://pubs.acs.org/doi/10.1021/acs.jctc.8b00200.
- M. A. Esmaeilbeig, M. Khorram, S. Ayatollahi and A. R. Zolghadr, On the hydrolysis of iron ions: DFT-based molecular dynamics perspective, J. Mol. Liq., 2022, 367, 120323, DOI:10.1016/j.molliq.2022.120323.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152(22), 224108 CrossRef CAS PubMed . Available from: https://pubs.aip.org/aip/jcp/article/1061982.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, Consistent structures and interactions by density functional theory with small atomic orbital basis sets, J. Chem. Phys., 2015, 143(5), 054107 CrossRef PubMed . Available from: https://pubs.aip.org/aip/jcp/article/194086.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78(7), 1396 CrossRef CAS . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.78.1396.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110(13), 6158–6170 CrossRef CAS . Available from: https://pubs.aip.org/aip/jcp/article/110/13/6158-6170/476177.
- R. Sure and S. Grimme, Corrected small basis set Hartree-Fock method for large systems, J. Comput. Chem., 2013, 34(19), 1672–1685 CrossRef CAS PubMed . Available from: https://onlinelibrary.wiley.com/doi/10.1002/jcc.23317.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed . Available from: https://pubs.aip.org/aip/jcp/article/926936.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS PubMed . Available from: https://onlinelibrary.wiley.com/doi/10.1002/jcc.21759.
- H. Kruse and S. Grimme, A geometrical correction for the inter- and intra-molecular basis set superposition error in Hartree-Fock and density functional theory calculations for large systems, J. Chem. Phys., 2012, 136(15), 154101 CrossRef PubMed . Available from: https://pubs.aip.org/aip/jcp/article/941628.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297 RSC . Available from: https://xlink.rsc.org/?DOI=b508541a.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model, J. Comput. Chem., 2003, 24(6), 669–681 CrossRef CAS PubMed . Available from: https://onlinelibrary.wiley.com/doi/10.1002/jcc.10189.
- V. Barone and M. Cossi, Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model, J. Phys. Chem. A, 1998, 102(11), 1995–2001 CrossRef CAS . Available from: https://pubs.acs.org/doi/10.1021/jp9716997.
- P. Hermosilla, M. Krone, V. Guallar, P. P. Vázquez, À. Vinacua and T. Ropinski, Interactive GPU-based generation of solvent-excluded surfaces, Vis. Comput., 2017, 33(6–8), 869–881 CrossRef . Available from: https://link.springer.com/10.1007/s00371-017-1397-2.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38 CrossRef CAS PubMed . Available from: https://linkinghub.elsevier.com/retrieve/pii/0263785596000185.
- M. Ren, Z. Jia, Z. Tian, D. Lopez, J. Cai and M. Titirici, et al., High Performance N-Doped Carbon Electrodes Obtained via Hydrothermal Carbonization of Macroalgae for Supercapacitor Applications, ChemElectroChem, 2018, 5(18), 2686–2693 CrossRef CAS . Available from: https://chemistry-europe.onlinelibrary.wiley.com/doi/10.1002/celc.201800603.
- K. Boguslawski, C. R. Jacob and M. Reiher, Can DFT Accurately Predict Spin Densities? Analysis of Discrepancies in Iron Nitrosyl Complexes, J. Chem. Theory Comput., 2011, 7(9), 2740–2752 CrossRef CAS PubMed . Available from: https://pubs.acs.org/doi/10.1021/ct1006218.
- K. Boguslawski, K. H. Marti, Ö. Legeza and M. Reiher, Accurate ab Initio Spin Densities, J. Chem. Theory Comput., 2012, 8(6), 1970–1982 CrossRef CAS PubMed . Available from: https://pubs.acs.org/doi/10.1021/ct300211j.
- E. Ruiz, J. Cirera and S. Alvarez, Spin density distribution in transition metal complexes, Coord. Chem. Rev., 2005, 249(23), 2649–2660 CrossRef CAS . Available from: https://linkinghub.elsevier.com/retrieve/pii/S0010854505001207.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ya00622k |
| This journal is © The Royal Society of Chemistry 2024 |