Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A high frequency alternating current heater using the advantages of a damped oscillation circuit for low voltage Li-ion batteries
Joachim
Oehl
 *a,
Andreas
Gleiter
a,
Daniel
Manka
a,
Alexander
Fill
b and
Kai Peter
Birke
b
*a,
Andreas
Gleiter
a,
Daniel
Manka
a,
Alexander
Fill
b and
Kai Peter
Birke
b
aRobert Bosch GmbH, Robert-Bosch-Allee 1, Abstatt, 74232, Germany. E-mail: Joachim.Oehl@de.bosch.com
bInstitute for Photovoltaics, Electrical Energy Storage Systems, University of Stuttgart, Pfaffenwaldring 47, Stuttgart, 70569, Germany
First published on 25th September 2024
Abstract
In many cases, batteries used in light e-mobility vehicles such as e-bikes and e-scooters do not have an active thermal management system. This poses a challenge when these batteries are stored in sub-zero temperatures and need to be charged. In such cases, it becomes necessary to move the batteries to a warmer location and allow them to acclimatize before charging. However, this is not always feasible, especially for batteries installed permanently in vehicles. In this work, we present an internal high-frequency AC heater for a 48 V battery, which is used for light electric vehicles of EU vehicle classes L1e and L3e-A1 for a power supply of up to 11 kW. We have taken advantage of the features of a damped oscillating circuit to improve the performance of the heater. Additionally, only a small inductor was added to the main current path through a cable with three windings. Furthermore, as the power electronics of the heater is part of the battery main switch, fewer additional parts inside the battery are required and therefore a cost and space reduction compared to other heaters is possible. For the chosen setup we reached a heating rate of up to 2.13 K min−1 and it was possible to raise the battery temperature from −10 °C to 10 °C using only 3.1% of its own usable capacity.
1 Introduction
Large Li-ion batteries like those in battery electric vehicles (BEVs) have a battery thermal management system (BTMS) to heat and cool the cells to extend life time and improve efficiency.1–3 Batteries in smaller applications such as electric scooters, e-bikes or e-motorcycles usually do not have an active BTMS for cost and space reasons. If the cells get too hot, the battery will reduce or stop supplying power. Charging in sub-zero temperatures favors greater capacity reduction and lithium plating, which in the worst case can lead to a short circuit due to grown Li-dendrites4–10 and is therefore not recommended in most cases. The battery must then be moved to a warmer location and acclimatized to be able to be charged.In this scenario, internal battery heating methods utilizing their own energy could bridge this gap. A comprehensive overview of various heating techniques can be found in the research conducted by Wu et al.11 Most internal battery heaters generate alternating current to induce losses within the battery, and hence they are referred to as current excitation methods. Some of these methods utilize an external power supply, while others use the energy provided by the battery itself. The advantage here is that no additional power supply is required, and the circuitry can be integrated within the battery. Another benefit is that the heat is generated directly within the cell where it is needed.
A different approach was taken by Wang et al.12,13 and Zhang et al.,14 who introduced a self-heating lithium-ion battery (SHLB) incorporating a nickel-foil within the cells. However, this design limitation restricts the use of commercial cells and limits the battery's design flexibility. Nonetheless, the heating rate of 96 K min−1 is remarkably fast. Only 2.9% of the cell's own capacity was used to heat the 10 A h cell from −20 °C to 0 °C.
In this study, our focus is on current excitation methods, which utilize the current flowing through the cells to generate heat. These heaters discharge and charge the battery in order to heat it up through the ohmic losses that occur within the battery. Due to the desired losses within the battery and the undesired losses within the power electronics, which is needed to generate the alternating current, the alternating current is superimposed by a continuous discharge current.
Several power electronics were developed to produce an alternating current flow through the battery using its own energy, with the majority designed for a single cell.
Shang et al.15 developed a “compact resonant switched-capacitor heater” using two MOSFETs, an inductance and a capacitor. To achieve higher heating rates, the topology was doubled, resulting in a sinusoidal current waveform and a heating rate of 7.41 K min−1 at a switching frequency of 40 kHz for a 2.5 A h cell.
The work by Shang et al.16 generates a triangular current waveform based on a half-bridge and a full-bridge-structured topology. The half-bridge topology operates with two MOSFETs and one inductance, but it requires an electrical connection between two cells in a row and does not work for a single cell. To address this, the paper suggests a full-bridge topology, increasing the number of MOSFETs to four. The best results, with a heating rate of 3.75 K min−1, were achieved at 10 kHz, while the maximum tested frequency was 45 kHz. Tests were conducted with 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 cells with a capacity of 2.5 A h. To raise the temperature of the cells from −20 °C to 0 °C, 5.7% of their own energy was required.
650 cells with a capacity of 2.5 A h. To raise the temperature of the cells from −20 °C to 0 °C, 5.7% of their own energy was required.
Zhang et al.17 introduced a high frequency AC heater based on switched capacitors. Depending on the frequency used, the current waveform ranges between sinusoidal and triangular. This heater requires 5.4% of the energy to heat the cells from −20 °C to 0 °C, with the cells having a capacity of 2.5 A h. The optimal frequency for this heater is 10 kHz, achieving a heating rate of 9.43 K min−1. The heater consists of four MOSFETs and two capacitors. The required two inductances were not used as components, only utilizing the parasitic effects of the wires. A disadvantage here, as in the previously presented work, is that there must be a connection to the middle of the cells connected in series, and therefore, it will not work with a single cell.
In our previous work,18 a heating topology based on the boost converter achieved a heating rate of up to 38 K min−1 at a switching frequency of 50 kHz, using a triangular current waveform. This heater requires 3.5% of the capacity to heat the 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 cell from −10 °C to 10 °C, with a capacity of 3.5 A h. The heater needs two MOSFETs and a capacitor, and the inductance as a component was omitted, only using the parasitic inductances, similar to Zhang et al.17
650 cell from −10 °C to 10 °C, with a capacity of 3.5 A h. The heater needs two MOSFETs and a capacitor, and the inductance as a component was omitted, only using the parasitic inductances, similar to Zhang et al.17
Zhong et al.19 proposed a heater with a similar topology to that in our previous work, also consisting of two MOSFETs, a capacitor, and an inductance. However, the values of these components are much larger. This is primarily due to the modulation of a rectangular charge and discharge current at low frequencies of around 1 Hz, necessitating a much higher capacity as an energy reservoir. The heater achieves a heating rate of up to 6.7 K min−1, requiring 5.96% of the 2.8 A h cell capacity to raise the temperature from −20 °C to 0 °C.
Cai et al.20 employed several components, including two MOSFETs, four inductances, four additional switches, and a DCDC. The current waveform is triangular at a frequency of 1 Hz. They achieved a heating rate of 5.32 K min−1 for a 2.8 A h 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 cell.
650 cell.
A heater for an entire battery with a capacity of 35 A h was designed and tested by Jiang et al.21 The current waveform of this heater is sinusoidal, utilizing a full-bridge topology with four MOSFETs, an inductance, and a capacitor. The optimal switching frequency was found to be 754 Hz, achieving a heating rate of up to 2.29 K min−1. Less than 7% of the battery capacity was utilized to raise the temperature from −20 °C to 0 °C.
A summary of the shown heaters can be found in Table 1. As a reference the SHLB approach is included.
| Heater | Battery capacity | Heating components | Energy or capacity consumption for 20 K temperature rise | Max. heating rate | |
|---|---|---|---|---|---|
| Q Batt (A h) | Q Ex/QBatt (%) | E Ex/EBatt (%) | Ṫ Batt (K min−1) | ||
| Compact resonant switched-capacitor heater15 | 2.5 | 4 MOSFETs, 2 capacitors (138 nF to 4.4 μF), 2 inductances (1.2 μH to 18.43 μH) | — | — | 7.41 |
| High-frequency alternating-current heater16 | 2.5 | 4 MOSFETs, 1 inductance (2.1 μH to 98.5 μH) | — | 5.7 | 3.57 |
| High frequency AC heater based on switched capacitors17 | 2.5 | 4 MOSFETs, 2 capacitors (220 μF), 2 parasitic inductances (1.03 μH) | — | 5.4 | 9.43 |
| High frequency alternating current heating based on boost converter topology18 | 3.5 | 2 MOSFETs, 1 capacitor (3 mF), 1 parasitic inductance | 3.5 | — | 38 |
| Mutual pulse heating method based on multiplexing converters19 | 2.8 | 2 MOSFETs, a capacitor (1 μF), 1 inductance (100 μH) | 5.96 | — | 6.7 |
| Rapid self-heating strategy based on bidirectional pulse current20 | 2.8 | 2 MOSFETs, 4 switches, a DCDC, 4 inductances (12 μH to 40 μH) | — | — | 5.32 |
| Soft-switching resonance circuit heater21 | 35 | 4 MOSFETs, a capacity (1.5 mF), 1 inductance (29.76 μH) | <7 | — | 2.29 |
| SHLB14 | 10 | Nickel foil, switch | 2.9 | — | 96 |
The objective of this study is to develop a heater for an entire battery rather than a single cell, while minimizing the use of additional components to reduce cost and space. Particularly, inductances for high currents are both expensive and heavy. Additionally, we aim to achieve a competitive heating rate of at least 2 K min−1. Ultimately, this is a scalable factor, where the tradeoff between investing more in cost and space for the power electronic and the specific application needs to be defined. The capacity used to heat the battery by 20 K should also be comparable to values found in existing literature (Table 1).
In this study, the “high frequency heater based on a boost converter topology”18 (HF-heater) will be adapted for use with a 48 V battery for light electric vehicles, having been previously designed for a single 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 cell. One advantage is that this topology requires fewer components compared to others, and the required inductance is particularly small. Furthermore, due to the low inductance, the heater's topology can be integrated into the main current path for normal operation and included in the battery's main switch, further reducing cost and space. Additionally, the current flow during the heating process will be enhanced by leveraging the benefits of a damped oscillating circuit, ultimately increasing the efficiency of the heater.
650 cell. One advantage is that this topology requires fewer components compared to others, and the required inductance is particularly small. Furthermore, due to the low inductance, the heater's topology can be integrated into the main current path for normal operation and included in the battery's main switch, further reducing cost and space. Additionally, the current flow during the heating process will be enhanced by leveraging the benefits of a damped oscillating circuit, ultimately increasing the efficiency of the heater.
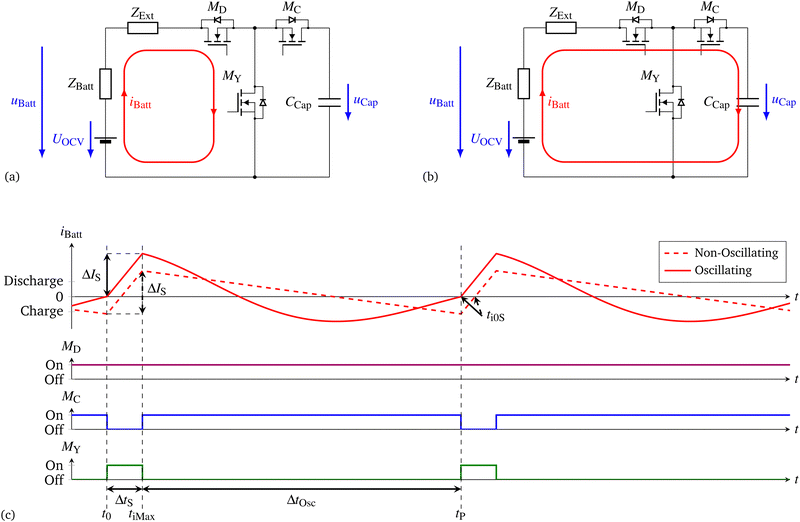
2 Basic function and circuitry of the HF-heater
The basic principle of the heater is to use the stored energy of the battery itself. The current iBatt that flows through the cells will heat up the cells caused by the power loss within the internal resistances of the cells. To improve the heating efficiency the root mean square (RMS) current IRMS has to be as high as possible compared to the discharge current (DC) IDC. That can be achieved by an alternating current (AC) IAC flowing out and into the battery.The basic function of the heater is based on the boost converter topology with an additional MOSFET to enable the topology to act in addition as battery main switch. We named the topology ‘YSSR’ for “Y-Solid State Relay”. The ‘Y’ describes the orientation of the MOSFETs. The equivalent circuit diagram (ECD) of the HF-heater, the idealized current waveforms and the switching states of the MOSFETs are presented in Fig. 1. The discharge MOSFET MD and the charge MOSFET MC can be used as the battery main switch. Those two MOSFETs in a common source configuration can prevent charge and discharge currents. During the heating process itself the MOSFET MD is not necessary and hence is always switched on.
The heating process can be separated into two main sequences.
In the first sequence, shown in Fig. 1a the Y-MOSFET MY will be switched on and shortens the whole battery. This sequence is termed as a short sequence with a time of ΔtS and starts at the point t0. The current iBatt increases and energy is stored within the inductive part of the battery and external components. If the second sequence concludes with a charge current flowing, the energy stored in the inductor must first be depleted again in order to be built up again in the discharge direction. The inductive part is summarized to LS displayed as part of the impedances ZBatt and ZExt respectively. The primary components that contribute to the impedance ZExt are the inductances located outside of the battery. The resulting resistance during this sequence is defined as RS. Both variables include all the resistances and inductances within the current path of iBatt in Fig. 1a. The sequence ends with the switching off of MY and leads to the second sequence displayed in Fig. 1b. This is also the point where the highest discharge current is flowing and is denoted tiMax.
During this sequence the current can be described as
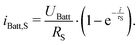 | (1) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = t − ti0S, t0 ≤ t < tiMax where ti0S represents the point at which the current crosses zero during the oscillation sequence, while tiMax denotes the time at which the maximum discharge current IMax occurs, marking the conclusion of the short sequence. The time constant is
= t − ti0S, t0 ≤ t < tiMax where ti0S represents the point at which the current crosses zero during the oscillation sequence, while tiMax denotes the time at which the maximum discharge current IMax occurs, marking the conclusion of the short sequence. The time constant is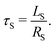 | (2) |
Alternatively, the slope through the origin can be used:
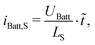 | (3) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = t − ti0S and t0 ≤ t ≤ tiMax. This simplification can be used when (tiMax − t0) = ΔtS ≪ τS.
= t − ti0S and t0 ≤ t ≤ tiMax. This simplification can be used when (tiMax − t0) = ΔtS ≪ τS.
Using the previous equation, the change in current iBatt,S during the short sequence can be expressed as
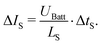 | (4) |
In the scenario of zero-current switching ΔIS is equivalent to IMax, as depicted in Fig. 1c.
The voltage UBatt describes the average battery voltage and depends on the open circuit voltage UOCV and the voltage drop across the batteries’ internal resistance RDC caused by a flowing current discharge (or charge) current IDC. It is measurable at the battery terminal. It can be described as
| UBatt = UOCV − IDC·RDC. | (5) |
The second sequence was further improved regarding our previous work18 and we took advantage of the properties of a damped oscillating circuit. This sequence is therefore termed an oscillation sequence with a time of ΔtOsc; the previous approach is further termed non-oscillating. The differences in the current waveform for the two approaches can be seen in Fig. 1c.
During the second sequence the MOSFET MY is turned off, the current iBatt is now forced to flow through MOSFET MC and the capacitor CCap. To minimize the losses MC will be switched on after a short deadtime to prevent an on-state of MC and MY at the same time. The voltage of the capacitor will increase while the current is decreasing until the stored energy in the inductances is reloaded into the capacitor. As soon the current iBatt = 0 A, the current direction changes and the battery will be charged. Latest by this time MC has to be switched on, to allow the current flowing back into the battery. The resistances and inductances for this sequence are summarized to ROsc and LOsc and includes the resistances and inductances within the current path of iBatt in Fig. 1b. The end of this sequence and the whole period is denoted as tP.
The oscillation approach offers a significant advantage over the non-oscillation approach. During the oscillation sequence, the absolute current of iBatt decreases at the end of the oscillation sequence due to the characteristics of a damped oscillation circuit, if the angular frequency is selected appropriately. Ideally, the goal is to achieve a current of iBatt = 0 A at the end of the oscillation sequence (tP). This results in the same switching losses but a higher RMS current IRMS of iBatt.
This can be attributed to the switching losses that occur in the MOSFETs. The switching losses for an inductive load can be roughly estimated for a single MOSFET, which represents one switching operation with
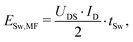 | (6) |
In the heater circuit, the losses during the switching on of the MOSFETs MY and MC can be disregarded because the current is already in the reverse direction and flows through the body diode. This is the case as long as the current flows in the charge direction at the start of the short phase t0. However, when switching off both MOSFETs, the full current must be disconnected. MOSFET MY carries the current IMax and MOSFET MC carries the current iBatt(t0) or in the case of zero current switching, 0 A while switching off. This leads to
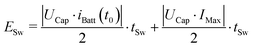 | (7) |
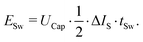 | (8) |
In other words, if the short phase begins at 0 A, the current IMax at the end of the short sequence will reach its highest possible maximum while keeping consistent switching losses.
A damped oscillator can be described with the fundamental differential form, using our defined variables (ROsc, LOsc and COsc) and the electrical charge Q(t) and its derivatives as
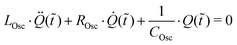 | (9) |
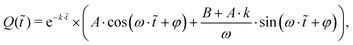 | (10) |
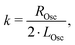 | (11) |
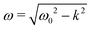 | (12) |
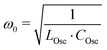 | (13) |
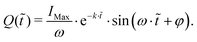 | (14) |
For heating up the cells the current is the important value so the previous equation has to be derived, leading to
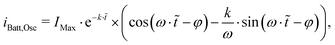 | (15) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = t − tiMax and tiMax ≤ t < tP.
= t − tiMax and tiMax ≤ t < tP.
In order to achieve zero current switching when transitioning from the oscillation sequence to the short sequence at tP = t0, the angular frequency ω must be selected based on the duration of the oscillation sequence ΔtOsc. To ensure that the following equations remain of reasonable size and are solvable, some simplifications are made.
Because electrical charge in a capacitor cannot change instantaneously, the charge at the beginning of the oscillation phase and at the end must be the same, assuming there is no leakage current during the short sequence discharging the capacitor. This implies that 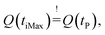 or in relation to the oscillating phase,
or in relation to the oscillating phase, 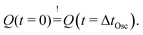 Utilizing this relation with eqn (14), it follows that
Utilizing this relation with eqn (14), it follows that
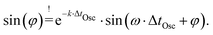 | (16) |
To solve this equation for φ, some assumptions are made. At the beginning of the oscillation phase, with the maximum current flowing, the electrical charge Q(t = 0) has to be close to the point of inflection so the slope at this point is sin(φ) = φ. Assuming a standard sine function, which represents an undamped circuit, to determine the maximum current at the beginning of the oscillation and at the end, where the current is 0 A, this would correspond to three-quarters of the sine function's period. This leads to the second assumption that at ΔtOsc, the function is close to its minimum, resulting in sin(ω·ΔtOsc − φ) = −1. These two assumptions lead to
| φ ≈ −e−k·ΔtOsc. | (17) |
The times for zero crossings of the current can be derived from eqn (15) by setting iBatt,Osc = 0. Furthermore, the exponential term IMax·e−k·![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) was omitted. This simplification can be made because, close to the zero crossing, the trigonometric functions have a much higher gradient compared to the exponential function. This results in
was omitted. This simplification can be made because, close to the zero crossing, the trigonometric functions have a much higher gradient compared to the exponential function. This results in
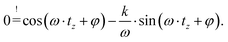 | (18) |
Solving for tz, which describes the zero-crossing points of iBatt,Osc yields
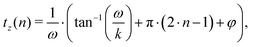 | (19) |
To solve for ω, the Laurent series
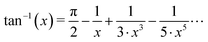 | (20) |
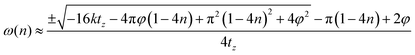 | (21) |
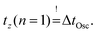 | (22) |
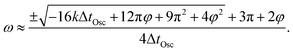 | (23) |
This leads to the angular frequency for achieving zero current switching at the first zero crossing with a positive gradient.
Out of the presented equations for the currents iBatt,S (eqn (1) and (3)) and iBatt,Osc (eqn (15)) and in Fig. 2a the average currents IRMS, IDC and IAC can be derived using the three following equations:
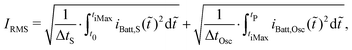 | (24) |
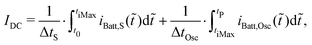 | (25) |
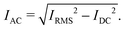 | (26) |
One switching period is
| ΔtP = ΔtS + ΔtOsc. | (27) |
The duty cycle of the heater is described as
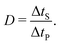 | (28) |
3 Test setup
3.1 Used hardware and its configuration
For the experiments a 48 V battery consisting of 195 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 cells in a 15p13s configuration was used. The used cell type in the battery is the NCR18650GA from Sanyo/Panasonic. The battery cells are linked together using spot welding. More specific data can be found in Table 2. Normally the battery is used for light electric vehicles in the EU vehicle class L1e and L3e-A1 for a power supply of up to 11 kW. For L3e-A1 vehicles up to three batteries in parallel can be used.
650 cells in a 15p13s configuration was used. The used cell type in the battery is the NCR18650GA from Sanyo/Panasonic. The battery cells are linked together using spot welding. More specific data can be found in Table 2. Normally the battery is used for light electric vehicles in the EU vehicle class L1e and L3e-A1 for a power supply of up to 11 kW. For L3e-A1 vehicles up to three batteries in parallel can be used.
| Parameter | Value |
|---|---|
| Battery | |
| Cells | NCR18650GA (Sanyo/Panasonic) |
| Configuration | 15p13s |
| Nominal voltage | 48 V |
| Min. discharge and max. charge voltage | 32.5 V, 54 V |
| Max. discharge and charge current | 120 A, 20 A |
| Discharge and charge temperature range | −20 °C to 60 °C, 0 °C to 50 °C |
| Capacity QBatt | 52.5 A h |
| Energy EBatt | 2.4 kW h |
| Resistance RBatt at 25 °C and 1 kHz | 48 mΩ (33 mΩ the cells) |
| MOSFETs | |
| Manufacturer number | IAUT300N10S5N015 (Infineon) |
| Nominal on-resistance RDS(ON) | 1.5 mΩ |
| Maximum drain to source voltage VDS | 100 V |
| Capacitors non-oscillating approach | |
| Type | Electrolytic |
| Capacity CCap | ≈10 mF |
| Voltage rating | 100 V |
| Capacitors oscillating approach | |
| Manufacturer number | C5750X7S2A106K230KB (TDK) |
| Type | Multi-layer ceramic |
| Capacity CCap | 20 × 10 μF = 200 μF |
| Voltage rating | 100 V |
To obtain the parameters for the heater, certain calculations and assumptions are made while considering system boundaries. One simplification is that LS = LOsc and RS = ROsc because the parasitic values and the difference in the current traces have minimal impact compared to the values of the battery. In the zero current switching approach, the ideal average voltage at the capacitor can be calculated using the equation of the boost converter
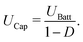 | (29) |
Because the battery is used in a low voltage system, an average voltage of 60 V should not be exceeded. This allows for a maximum duty cycle of D = 1/10, which leads to a fully charged battery with UBatt = 54 V to an average voltage at the capacitor of exactly UCap = 60 V. This is a worst-case assumption using the maximum open circuit voltage of the battery. During the heating process, the voltage will drop according to eqn (5). Furthermore, to keep the inductance low to reduce cost and space, the switching frequency should be high. Conversely, a too high frequency leads to higher switching losses in the MOSFETs. This was solved by an additional inductance, represented by ZExt on the PCB. This was realized with a wire with a 6 mm2 cross section and three windings. The outer diameter was 55 mm. Overall, the additional inductance doubles the overall inductance of the setup to around LS = LOsc≈ 850 nH. This means that LBatt ≈ LExt ≈ 425 nH. This solution needs not much space and is cost-effective.
In this case, the peak current IMax is determined by ensuring that a limit of 275 A is not exceeded to avoid triggering the short circuit detection. The current can be calculated using eqn (4) since iBatt(t0) = 0 A and therefore IMax = ΔIS.
The short time was set to ΔtS = 4 μs, resulting in a peak current of IMax = 254 A when the battery is fully charged with UBatt = 54 V. However, during the heating process, the voltage will decrease due to the discharge current and the resulting voltage drop as described by eqn (5).
Using eqn (27), this results in a period time of ΔtP = 40 μs, which in turn gives a switching frequency of fSW = 25 kHz.
By utilizing the measured battery resistance RBatt = 48 mΩ at 1 kHz from Table 2 and the inductance LS = LOsc ≈ 850 nH, the damping coefficient can be calculated as approximately k = 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 235 s−1 using eqn (11). Given a defined time for the oscillation sequence of ΔtOsc = 36 μs (eqn (27)), the phase shift can be calculated to φ = −20.7° using eqn (17), and then the angular frequency can be determined to ω 135
235 s−1 using eqn (11). Given a defined time for the oscillation sequence of ΔtOsc = 36 μs (eqn (27)), the phase shift can be calculated to φ = −20.7° using eqn (17), and then the angular frequency can be determined to ω 135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148 s−1 using eqn (23). With eqn (12) and 12 finally the natural angular frequency ω0 138
148 s−1 using eqn (23). With eqn (12) and 12 finally the natural angular frequency ω0 138![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 066 s−1 and the capacity COsc = 61.7 μF can be derived.
066 s−1 and the capacity COsc = 61.7 μF can be derived.
A straightforward method to calculate the maximum possible voltage across the capacitor, in order to determine the required voltage ratings for the components, is to consider the energy stored in the inductance at the end of the short sequence. At this stage, the maximum current I − Max occurs. The energy stored in the inductance must be equal to the energy change in the capacitor during the oscillation, resulting in
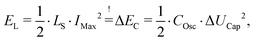 | (30) |
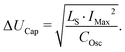 | (31) |
To obtain the maximum possible voltage, the previously calculated average value UCap = 60 V for the maximum capacitor voltage is added to half of the peak-to-peak value of ΔUCap, resulting in
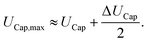 | (32) |
This results in a maximum capacitor voltage of UCap,max = 74.9 V and ΔUCap = 29.8 V and leads to the voltage rating of the capacitors and MOSFETs, which are rated for 100 V. The battery voltage uBatt will be close to zero during the short sequence and below UCap,max during the oscillation sequence with no external inductance LExt. The additional inductance, as in this case, will reduce the voltage swing at the battery, functioning as a voltage divider. This will result in approximately half of the battery voltage UBatt during the short sequence, as in this setup LBatt ≈ LExt.
The power electronic was being implemented on a 4-layer printed circuit board (PCB) with a copper thickness of 70 μm. The main current path was laid out over all 4 layers to minimize ohmic losses. Additionally, the traces were designed to be wide in order to reduce the inductance within the PCB. For the power electronic of the heater three MOSFETs were used; details can be found in Table 2. The MOSFETs were cooled directly via an axial fan.
The only difference between the non-oscillating and oscillating approach is the capacitors. For the non-oscillating approach capacitors with an overall capacity of around CCap ≈ 10 mF were used.
For the oscillating approach 20 multi-layer ceramic capacitors (MLCC) were considered in parallel with an overall rated capacity of CCap = 200 μF, which correlates with a usable capacity COsc = 65.1 μF. This is a slightly higher value than previously calculated for zero current switching with COsc = 61.7 μF. This results in switching during a small charge current, or in other words, premature switching. The usable capacity with the MLCC capacitors is lower because of the DC-Bias and was simulated by a model of the supplier in LT Spice, previously calculated to UCap = 60 V.
At this point, it must be noted that these values represent the worst-case scenario. A lower battery voltage UBatt due to a discharge current and the resulting voltage drop, or a lower State of Charge (SOC), will result in lower values. Additionally, a lower battery voltage will lead to a lower average voltage at the capacitor UCap, which, in turn, will lead to higher capacities COsc due to the DC-bias at MLCC capacitors. This will result in a lower angular frequency and, consequently, premature switching before the current reaches zero.
3.2 Test procedure
Prior to the experiment, the battery was charged to UBatt = 54 V with a charging current of 10 A, without a constant voltage phase. Following this, the whole setup was placed in a climate chamber at TAmb = −10 °C for 12 hours to fully acclimatize the entire system. Following that, the heating process was initiated. For the evaluation only the temperature in the middle of the battery was used as a reference. The temperature measurement was directly linked to the microcontroller of the heater, causing an oscilloscope to measure the current iBatt and voltage uBatt at every 5 K increment in temperature. The heating process was stopped upon reaching TBatt = 30 °C.Three different batteries were tested with the same PCB. In this work, we only present one result because the other two showed similar results. The small deviations in cell resistance within the tested three batteries have no measurable influence on the heater.
3.3 Data acquisition
The data acquisition can be primarily divided into two different areas.The battery temperature TBatt, current IDC, and voltage UBatt were measured every 0.5 s and were filtered with a moving average over 10 values. The current and voltage were filtered using a low-pass filter to measure the average value.
The temperatures of the MOSFETs (TM) are directly measured with NTCs placed close to the MOSFETs on the PCB. The measured values are filtered with a low-pass filter on the hardware side and communicated by the microcontroller of the heater in 1 °C steps. In the event of an overtemperature (TM > 100 °C) at the MOSFETs, the heating would stop.
The detailed waveforms of the current iBatt and voltage uBatt were measured using an oscilloscope with a 400 MHz bandwidth with a measurement point every 5 ns. The values were filtered with a moving average over 50 values, and for the plots, only every 10th value was used. The oscilloscope was triggered at every 5 K increment of TBatt.
An overview of the sample times, range, and error of the data acquisition can be found in Table 3.
| Value | Range | Error | Sample time |
|---|---|---|---|
| I DC | −150 A to 150 A | ± 0.1 A | 0.5 s |
| U Batt | 0 V to 100 V | ± 0.2 V | 0.5 s |
| T Batt | −20 °C to 65 °C | ± 0.5 °C | 0.5 s |
| T MOSFET | −30 °C to 200 °C | ± 2 °C | 0.5 s |
| i Batt | −500 A to 500 A | ± 1% | 5 ns |
| u Batt | 0 V to 400 V | ± 1% | 5 ns |
4 Results and discussion
This chapter will start with a short comparison of an oscillating and non-oscillating heater followed by a curve fitting of the current iBatt, both at TBatt = 0 °C. After that a complete heating process from TBatt = −10 °C up to 30 °C will be analyzed.All measurements started at an ambient temperature of TAmb = −10 °C with a completely acclimatized battery.
4.1 Oscillating vs. non-oscillating heater
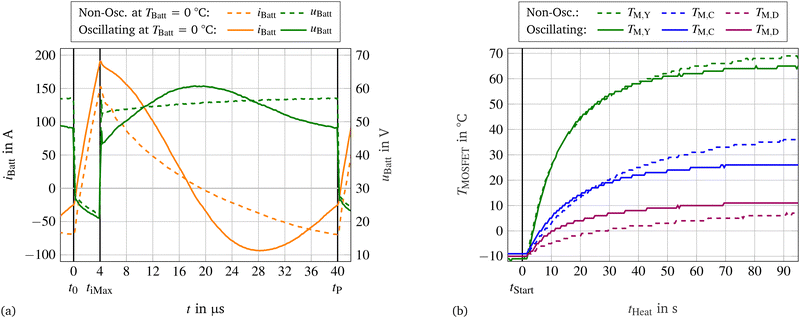
In the beginning a comparison of the non-oscillating and oscillating approach was made. For the non-oscillating approach electrolytic capacitors with an overall capacity of around CCap ≈ 10 mF were used and for the oscillating part MLCCs with a rated overall capacity of CCap = 200 μF. Due to the DC-Bias the usable capacity COsc is lower. Both setups used the same duty cycle D and short time ΔtS. The goal of both circuits was to have a comparable power loss in the power electronic.Fig. 2a displays the current and voltage profiles of both approaches at TBatt = 0 °C.
The period starts with the short sequence at t0, and the second sequence starts at tiMax while the maximum discharge current IMax is flowing. The end of the period is marked with tP. During the first sequence both approaches are similar, and the only difference is the current offset resulting out of the different starting point at t0. The maximum current IMax is about 40 A higher in the oscillating version.
In the second sequence the difference between the non-oscillating and oscillating approach is clearly visible. A higher maximum discharge current IMax and in amount a higher charge current is in comparison to the non-oscillating approach clearly visible. In addition, the switching point at t0 or tP is with the oscillating approach closer to zero and not the highest charge current compared to the non-oscillation circuit. The current iBatt follows the waveform described by eqn (15).
Out of the curves of iBatt presented in Fig. 2a the currents IRMS, IDC and the alternating current (AC) IAC can be derived with eqn (24)–(26).
As expected, the oscillating setup archived a higher RMS current and also the other currents increased as shown in Table 4.
| Heater | Currents | ||
|---|---|---|---|
| I RMS (A) | I DC (A) | I AC (A) | |
| Non-oscillating | 60.3 | 5.7 | 60.0 |
| Oscillating | 95.4 | 10.2 | 94.9 |
The voltages uBatt of the oscillating and non-oscillating approaches exhibit the same behavior during the short sequence. Due to the setup having an external inductance LExt, the voltage does not drop to zero but stays at around UBatt/2 due to the voltage divider with the inductance of the battery LBatt and the external one. Because they have about the same size, the voltage uBatt is about half of the average battery voltage UBatt at the beginning of the short sequence. The decreasing voltage during the sequence can be mostly attributed to the non-ideal inductive behavior of Li-ion cells and the transition from an inductive voltage divider to an ohmic voltage divider, which dominates at lower frequencies. The voltage uBatt of the non-oscillating circuit is slightly higher due to the lower discharge current IDC, resulting in a lower voltage drop (eqn (5)).
During the oscillation sequence of the non-oscillating heater, the transition from the inductive to the ohmic voltage divider can also be observed, as it gradually becomes more similar to the capacitor voltage UCap over time.
During the oscillation sequence of the oscillating heater, the voltage uBatt rises until reaching its maximum at the first zero crossing, after which it reduces its voltage again. This behavior is described by eqn (14) for the capacitor voltage uCap. The previously described behavior of the voltage divider also applies to the battery voltage uBatt in this case.
Fig. 2b displays the temperatures of the three MOSFETs for the first 90 s. It can be seen that the temperatures of the switching MOSFETs MC and MY are comparable, and even the oscillating circuit has marginal lower temperatures and hence lower power losses. The always switched on MOSFET MD has a higher temperature for the oscillating approach. That can be directly linked to the higher IRMS. Overall, this confirms eqn (8), demonstrating that the same ΔIS results in the same switching losses.
With the same power electronic hardware and reduced needed space due to the smaller capacitors a higher IRMS thru the battery is possible. Overall, it can be summarized that it is worth diving deeper into the oscillating approach.
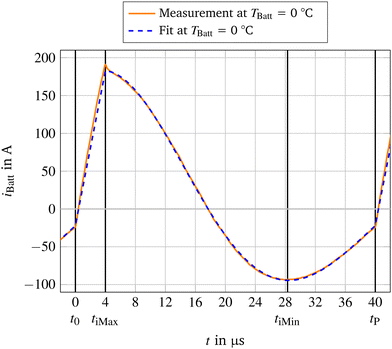
4.2 Curve fitting of the current
To derive the parameters of the measurements the current curves are fitted. For the oscillation sequence eqn (15) is used for t0 ≤ t ≤ tiMax and![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0 at the beginning of the sequence.
= 0 at the beginning of the sequence.
To fit the waveform for the short time, eqn (3) can also be rewritten as
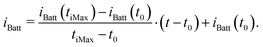 | (33) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = ΔtOsc.
= ΔtOsc.
In Fig. 3 the measured and the resulting fitted curve with the values of the fit can be seen. During the short sequence the fitted current has a lower gradient. This results from the fact that the fit neglects the current peak during switching. On top the behavior and losses during the switching times are neglected. For the oscillating phase the fit pairs quite well with the measurements.
The fitted parameters for every 5 K increment can be found in Table 6 in the following chapter and will be used to derive further values.
4.3 Evaluation of the heating process
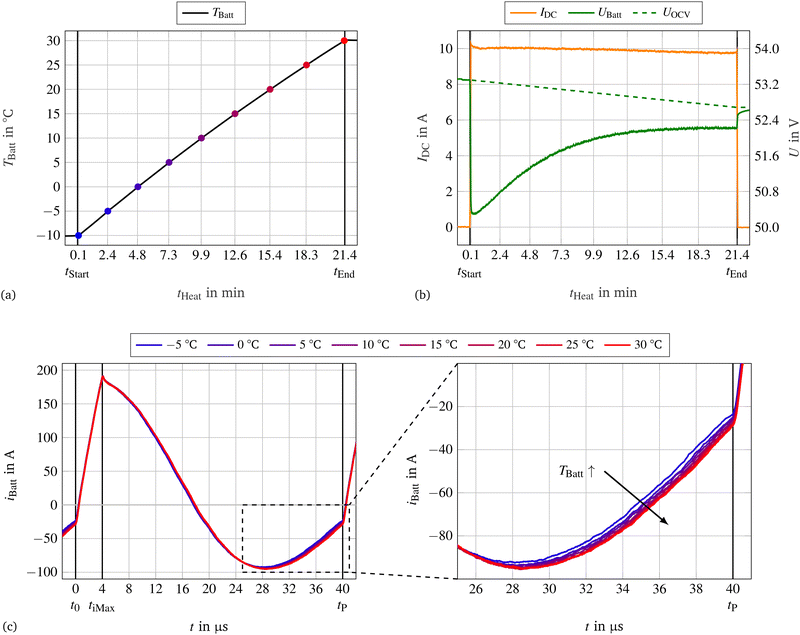
The battery was placed as previous mentioned in a climate chamber at an ambient temperature of around Tamb ≈ −10 °C, long enough to acclimatize. The temperature development during the heating process in the middle of the battery during the heating, starting with TBatt = −10 °C at tStart and end with TBatt = 30 °C at tEnd can be seen in Fig. 4a. The temperature is rising nearly linearly with a slightly decreasing gradient.The temperature gradient of each 5 K increment can be found in Table 5, starting from −10 °C to −5 °C with 2.13 K min−1.
| Temperature | Time | Currents | Voltages | Resistance | |||||
|---|---|---|---|---|---|---|---|---|---|
| T Batt (°C) | Ṫ Batt (K min−1) | t Heat (min) | I RMS (A) | I DC (A) | I AC (A) | U OCV (V) | U Batt (V) | U Cap (V) | R DC (mΩ) |
| −10 | — | 0.1 | — | 10.3 | — | 53.3 | 50.3 | 54.5 | 288.5 |
| −5 | 2.13 | 2.4 | 94.5 | 10.2 | 93.9 | 53.2 | 50.8 | 55.3 | 244.9 |
| 0 | 2.08 | 4.8 | 95.4 | 10.2 | 94.9 | 53.2 | 51.3 | 55.9 | 183.0 |
| 5 | 2.01 | 7.3 | 96.0 | 10.3 | 95.4 | 53.1 | 51.7 | 56.4 | 134.1 |
| 10 | 1.93 | 9.9 | 96.2 | 10.2 | 95.7 | 53.0 | 51.9 | 56.6 | 108.3 |
| 15 | 1.86 | 12.6 | 96.4 | 10.0 | 95.9 | 52.9 | 52.1 | 56.7 | 81.5 |
| 20 | 1.78 | 15.4 | 96.4 | 9.9 | 95.9 | 52.9 | 52.2 | 56.8 | 70.3 |
| 25 | 1.71 | 18.3 | 96.3 | 9.8 | 95.8 | 52.8 | 52.2 | 56.8 | 56.9 |
| 30 | 1.65 | 21.4 | 96.0 | 9.7 | 95.5 | 52.7 | 52.2 | 56.8 | 50.1 |
Fig. 4b shows the battery voltage UBatt and the discharge current IDC during the heating process. The open circuit voltage UOCV was calculated using
 | (34) |
The current IDC and the open circuit voltage UOCV is over time slightly decreasing, whereas UBatt increasing rapidly at the beginning of the heating. The voltage increase gets over time slower and ends in a plateau. The voltages and the current can also be found in Table 5 for each 5 K increment. In addition the voltage at the capacitor UCap is shown. The DC resistance for the whole battery was calculated using
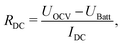 | (35) |
The detailed current curves for one switching period can be found in Fig. 4c, measured at each 5 K increment, starting with TBatt = −5 °C including the curve at TBatt = 0 °C already well known from the previous figures. From t0 to tiMax the battery is shortened (short sequence) and the current is nearly linear increasing to around iBatt = 190 A of discharge current at each temperature. The characteristics during the oscillation phase (oscillation sequence) is comparable for each TBatt. Still the absolute value of the current at the second switching point tP is increasing while the temperature is rising; this is more visible in the cutout. This goes along with a small reduction of the angular frequency.
Out of those presented curves of iBatt, the currents IRMS, IDC and IAC can be calculated (eqn (24)–(26)) and are summarized in Table 5. The DC current IDC was already directly measured all along not only at each 5 K increment. The currents IRMS and IAC increase slightly with a slightly decreasing value at the end of the heating process. In good approximation those values can be seen as constant.
As presented in Section 4.2 the current curves of iBatt were fitted for each battery temperature TBatt 5 K increment. The capacity was simulated based on the measured voltage UCap (Table 5) as previously mentioned because of the DC-Bias in MLCC-capacitors. With the known capacity COsc the other values can be derived with the equations presented in Section 2. The values are summarized in Table 6.
| Temperature | Capacity | Fitted parameters | Calculated values | Deviations | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T Batt (°C) | C Osc (μF) | φ (°) | I Max (A) | ω (s−1) | k (s−1) | ω 0 (s−1) | L Osc (nH) | R Osc (mΩ) | I RMS,c (A) | I DC,c (A) | ΔIRMS (%) | ΔIDC (%) |
| −5 | 71.4 | −21.00 | 180.1 | 127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 115 115 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 139 139 |
129![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 980 |
829 | 45.0 | 89.1 | 9.2 | −5.6 | −9.6 |
| 0 | 70.4 | −21.34 | 181.3 | 126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 671 671 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685 685 |
129![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 451 451 |
847 | 45.2 | 90.3 | 9.3 | −5.3 | −8.7 |
| 5 | 69.6 | −21.30 | 181.5 | 126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465 465 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431 431 |
129![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 198 |
860 | 45.5 | 90.7 | 9.2 | −5.5 | −10.4 |
| 10 | 69.2 | −21.47 | 181.7 | 126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 144 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 227 227 |
128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 842 842 |
870 | 45.6 | 91.1 | 9.3 | −5.3 | −9.5 |
| 15 | 69.1 | −21.39 | 181.5 | 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 958 958 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 907 |
128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 595 595 |
875 | 45.3 | 91.3 | 9.1 | −5.3 | −9.7 |
| 20 | 69.0 | −21.21 | 181.2 | 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 683 683 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 704 704 |
128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 284 284 |
881 | 45.3 | 91.3 | 8.9 | −5.3 | −10.2 |
| 25 | 69.0 | −20.98 | 180.4 | 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 486 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517 517 |
128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 054 |
884 | 45.1 | 91.1 | 8.6 | −5.4 | −11.8 |
| 30 | 69.0 | −20.98 | 180.0 | 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452 452 |
127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 794 794 |
888 | 45.2 | 90.9 | 8.6 | −5.3 | −11.0 |
It can be observed that while the temperature TBatt is rising the values ω, k and ω0 are decreasing while the inductance LOsc is increasing. The resistance ROsc, the phase shift φ and IMax remain nearly constant. The calculated current values IRMS,c and IDC,c showing the same behavior as the measured ones, this is also represented with the shown deviations ΔIRMS and ΔIDC. Both show nearly the same deviation over the complete heating process, for ΔIRMS always less than −6% and for ΔIDC less than −12%. That means, that the calculation always results in smaller values than the measurement.
In the following discussion the values at −10 °C will be excluded because there is no detailed current curve measured and the circuit, especially the power electronic has not reached a constant operating point, meaning a constant temperature of the components of the power electronic. Furthermore, it is assumed that the resistances and inductances during the two sequences are the same (RS ≈ ROsc, and LS ≈ LOsc) because the majority of both values are in the common current path and the MOSFETs (MY and MC) are identical.
As the resistance RDC drops as the temperature TBatt increases, the voltage UBatt increases despite a slight decrease in the voltage UOCV. The strong temperature dependence of RDC is well-known and has been documented by Zhang et al.23,24 and other researchers. Due to the properties of a boost converter, there is a linear relationship between the voltages UBatt and UCap. Due to the DC-bias of MLCC capacitors, the voltage UCap directly affects the capacitance COsc. However, the change is small in the area under consideration.
While the resistance within the oscillating circuit ROsc stays nearly the same over the whole temperature range, the inductance LOsc is increasing with increasing temperature. That was also reported by Dai et al.25 The almost constant resistance ROsc was expected to decrease slightly. In this case the resistance of the cell connectors with a positive temperature coefficient seems to balance the resistance of the cells with a slightly negative temperature coefficient. In addition the electrochemical impedance spectroscopies in the work of Dong et al.26 show a very low temperature dependency of the ohmic resistance of the NCR18650GA cell, confirming the stable value of ROsc over the measured temperature range. It follows from the eqn (11) and (12) that the small changes in k and ω arise mainly from the changed inductance LOsc.
The maximum current at the end of the short sequence IMax results in particular from the current at the beginning of the short sequence iBatt(t0) and the correlation in eqn (1) or simplified eqn (3). Since RS remains constant, the changes are due to the open circuit voltage UOCV and the inductance LS, since the duty cycle D and the switching period ΔtP and therefore the short time ΔtS remain constant. However, this also shifts the starting point slightly due to the small changes in ω and k caused by the increase of LOsc.
Since the values in the area under consideration ultimately only change slightly, the resulting current IAC remains nearly constant.
4.4 Temperature distribution within the battery
After the complete heating process up to a temperature of TBatt = 30 °C in the middle of the battery, the temperature at the coldest measured spot was at 25.9 °C the hottest at 33.7 °C, resulting in a temperature difference of 7.8 K.The coldest measured spot was observed at the outer edge of the battery, which was the furthest point from the power electronics. Conversely, the hottest spot was found near the power electronics. However, it is important to note that the battery and power electronic were not housed together and were not thermally connected, meaning that the temperature difference observed was not due to the power losses from the power electronic.
One obvious point is that the thermal resistance for the cells closer to the battery housing are smaller compared to the cells in the middle of the battery.
A further point is that different resistances within the parallel connections caused by cell tolerance but also by the cell connections and different temperatures lead to current variations.27–29
Another point is that the inductances within the current paths for the different cells are not the same. That is caused by different inductances within the cells due to mainly different temperatures25 and the geometry of the battery which influences the self-inductance of the current loops, based on the Faraday's law of induction.30 For example, if the current path covers a large area the inductance will be higher as for a smaller area. In this setup, the effect described above is most pronounced for the hottest measured temperature near the power electronics, where the area covered by the current path is relatively small.
A more symmetric current within all cells can be archived using different approaches. Some solutions are listed below:
• Before the current splits to the parallel connected cells an additional inductance can be included, which will lower the overall influence of the different inductances in the parallel current paths.
• Adding additional inductances within the parallel paths with lower inductances, but this is not particularly attractive.
• The power electronic can be thermally connected to the cells, preferably to the cells within a current path with a higher inductance. Unfortunately, they are spatially further away from the power electronic. Using the heat from the MOSFETs was also proposed by Xu et al.31 and additionally increase the overall efficiency.
• A segmentation of the power electronic, which means to use more power electronics on single cell levels or smaller subdivisions within the battery as proposed by Zhong et al.19
As mentioned, there are several solutions to make the internal heating uniform and should be considered while designing a new battery using the heating approach mentioned in this work or other high frequency heaters.
4.5 Efficiency of the heater
As a first step the expended energy EEx during the heating can be calculated with integral of the product of the average discharge current IDC and the open circuit voltage UOCV over time using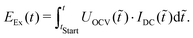 | (36) |
In the same way the expended capacity QEx can be calculated using
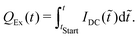 | (37) |
The energy and capacity needed for heating relatively to the overall energy and capacity of the battery is shown for each 5 K increment in Table 7. Comparing this energy with the nominal available energy of the battery EBatt leads to the ratio EEx/EBatt. To heat the battery by 20 K, the heater consumes 3.6% of its energy or 3.1% of its capacity.
| Temperature | Time | Energy | Capacity | Power | ||||
|---|---|---|---|---|---|---|---|---|
| T Batt (°C) | Ṫ Batt (K min−1) | t Heat (min) | E ex/EBatt (%) | Q ex/QBatt (%) | P Ex (W) | P DC (W) | P AC (W) | η Heat (%) |
| −10 | — | 0.1 | — | — | — | — | — | — |
| −5 | 2.13 | 2.4 | 0.9 | 0.8 | 535 | 25 | 351 | 70.2 |
| 0 | 2.08 | 4.8 | 1.8 | 1.5 | 533 | 18 | 360 | 71.0 |
| 5 | 2.01 | 7.3 | 2.7 | 2.3 | 530 | 13 | 367 | 71.7 |
| 10 | 1.93 | 9.9 | 3.6 | 3.1 | 527 | 11 | 370 | 72.2 |
| 15 | 1.86 | 12.6 | 4.6 | 4.0 | 523 | 8 | 369 | 72.1 |
| 20 | 1.78 | 15.4 | 5.6 | 4.9 | 520 | 7 | 368 | 72.2 |
| 25 | 1.71 | 18.3 | 6.7 | 5.8 | 516 | 5 | 366 | 71.9 |
| 30 | 1.65 | 21.4 | 7.8 | 6.7 | 515 | 5 | 365 | 71.8 |
In our previous work18 we archived the same with 3.5% of the capacity for a single cell and it is already very close to the SHLB14 with 2.9%. At this point it has to be mentioned, that the hardware is the same for the single cell and the battery presented here. Differences lie in the additional inductance, the MOSFETs (same package but different voltage levels), the shunt for the current measurement and the capacity and of course the usage of the damped oscillation. This means that the efficiency in terms of space increases.
To look now a little bit deeper into how much energy was really used to heat the battery up, a comparison of different power losses was made.
The expended power PEx for each 5 K step was determined using
| PEx = UOCV·IDC. | (38) |
The heating power in the battery can be divided into a DC and AC part, named PDC and PAC. The power PDC can be easily derived out of the equation:
| PDC = RDC·IDC2, | (39) |
For the AC part we know the resistance of the whole circuitry during the oscillating sequence. Because the RMS current IRMS is almost constant and due to this the temperatures of the MOSFETS as well, we assume that the AC resistance of the power electronic during the heating process after reaching the steady state is constant. The steady state is reached after around 90 s (Fig. 2b) and only not valid for the measurement at −10 °C. The AC resistance of the power electronic of the oscillating current path (Fig. 1b) is RAC,PE,Osc = 5.2 mΩ. Furthermore, we presuppose that the AC resistance of the battery RAC is the same during both sequences. This leads to RAC = ROsc − RAC,PE,Osc. Now we can reuse eqn (39) with the AC values instead of the DC values. The efficiency of the heater can be calculated as
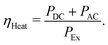 | (40) |
The calculated values are summarized in Table 7.
The slight decrease of Pex can be attributed to a decrease of the current IDC and the open circuit voltage UOCV.
The rapid reduction of PDC can be directly linked to the decreasing RDC which is as previously mentioned highly temperature dependent.
The AC power PAC remains nearly constant during the heating process in good agreement with the constant resistance RAC and the current IAC.
When comparing the generated AC and DC power, PDC is smaller than PAC by at least a factor of 14. This subordinate role of PDC is also reflected in the efficiency of the heater showing a nearly constant value with ηHeat > 70% throughout the heating process.
This means that around 30% of the power is mainly caused by losses in the power electronic and the supply lines. The majority of this arises from the switching losses within the MOSFETs.
To further improve efficiency the power loss of the power electronic could be used to heat the cells as proposed by Xu et al.31 A thermal connection to the battery housing could be a good approach.
On the other hand, the efficiency of the power electronic could be improved. Using a control system, the time of the oscillation phase tOsc could be adjusted to realize during different conditions like different states of charges (SOCs) and different temperatures a zero current switching. Further improvements can be made by adjusting the dead time and improve the switching behavior of the MOSFETs like for example that proposed by Oomori and Omura.32
4.6 Aging effects
The aging of battery cells can be a concern due to over-discharging and over-charging during the short and oscillation sequence. However, the average values are still within specifications.Uno et al.33 suggests that lower frequencies activate electrochemical processes, leading to accelerated degradation, while higher frequencies result in no additional degradation. Due to the high switching frequency of the heater, it is expected that there will be at least no additional degradation due to electrochemical processes caused by the alternating current.
In our previous study,18 1802 heating cycles from −10 °C to 10 °C were conducted with an NCR18650GA cell, resulting in an overall heating time of 52.7 hours and a capacity fading of 15%. This translates to a capacity fading of 85 ppm per heating. The cell was charged and discharged (through the heating process) 100 times from 3.15 V to 4.15 V, and the capacity fading was determined based on coulombic counting during the recharging of the cell. The experiment did not use additional inductance, as was done in this work, and had a duty cycle of D = 1/2, resulting in a cell voltage close to 0 V during the short sequence and doubled cell voltage for the other half of the period.
Applied to this work, this would imply that the voltage uBatt would periodically change approximately between 0 V and 100 V. However, as shown in Fig. 2, the voltage is only swinging from 22 V to around 62 V. This indicates that this profile is more challenging for the cell than in the current work, leading to the conclusion that the aging effects using this approach are lower than the measured 15%.
5 Conclusions
It turned out that with the same power electronic, but an oscillating approach, a higher RMS current and thus a higher heating output could be achieved compared to a non-oscillating approach, while keeping the switching losses comparable. Another advantage of the oscillation approach is that the capacitor can be smaller and more cost-effective. The heating power is almost independent of the cell temperature because the ohmic resistance component RAC of the battery in this setup was independent of the temperature and the heat generated by the alternating current was more than 14 times higher than the heat generated by direct current.The presented internal heater already achieves an efficiency of ηheat > 70%. However, there is still room for improvement, such as introducing a control system, adjusting the oscillation sequence time to achieve zero current switching or taking advantage of the generated heat from the power electronic to heat up the cells. In the future, a control system will also help to adapt the switching times to different conditions, for example to a different SOC.
A rise in temperature of 20 K was achieved using just 3.1% of the battery capacity, a percentage comparable to the SHLB approach, which involves using a nickel-foil within the battery to generate heat with 2.9% of the available capacity. The reached heating rate was 2.13 K min−1, limited due to short detection and the heat generation at the power electronics.
The heater can be integrated into the battery main switch and therefore does not require much more cost and space. In addition, the approach is scalable by connecting multiple MOSFETs in parallel and adapting them to the required heating power. However, this would require more space and increased costs, but it would also enable higher heating rates.
Additional inductances offer the benefit of reducing switching losses by lowering the switching frequency. However, they come with a cost and require space in the battery. In this study, an inductance made of a wire with three windings was added to double the overall inductance, representing a balanced tradeoff between cost and space requirements.
Author contributions
Joachim Oehl: conceptualization, investigation, methodology, validation, visualization, writing – original draft. Andreas Gleiter: validation, writing – review & editing. Daniel Manka: writing – review & editing. Alexander Fill: writing – review & editing. Kai Peter Birke: supervision, writing – review & editing.Data availability
The authors confirm that the data supporting the findings of this study are available within the article.Conflicts of interest
Some of the authors have filed a patent (DE102019212475A1) for the presented heating topology, which consists of three MOSFETs.Notes and references
- X. Hu, Y. Zheng, D. A. Howey, H. Perez, A. Foley and M. Pecht, Prog. Energy Combust. Sci., 2020, 77, 100806 CrossRef.
- A. G. Olabi, H. M. Maghrabie, O. H. K. Adhari, E. T. Sayed, B. A. Yousef, T. Salameh, M. Kamil and M. A. Abdelkareem, Int. J. Thermofluids, 2022, 15, 100171 CrossRef CAS.
- W. Li, Y. Zhou, H. Zhang and X. Tang, Energies, 2023, 16, 4845 CrossRef CAS.
- Q. Liu, C. Du, B. Shen, P. Zuo, X. Cheng, Y. Ma, G. Yin and Y. Gao, RSC Adv., 2016, 6, 88683–88700 RSC.
- T. Waldmann, B. I. Hogg and M. Wohlfahrt-Mehrens, J. Power Sources, 2018, 384, 107–124 CrossRef CAS.
- G. Zhang, X. Wei, G. Han, H. Dai, J. Zhu, X. Wang, X. Tang and J. Ye, J. Power Sources, 2021, 484, 229312 CrossRef CAS.
- Y. Qiu, X. Zhang, C. Usubelli, D. Mayer, C. Linder and J. Christensen, J. Power Sources, 2022, 541, 231632 CrossRef CAS.
- A. Laforgue, X. Z. Yuan, A. Platt, S. Brueckner, F. Perrin-Sarazin, M. Toupin, J. Y. Huot and A. Mokrini, J. Power Sources, 2022, 524, 231071 CrossRef CAS.
- E. Teliz, C. López-Vázquez and V. Díaz, Electrochim. Acta, 2024, 475, 143540 CrossRef CAS.
- M. Feinauer, M. Wohlfahrt-Mehrens, M. Hölzle and T. Waldmann, J. Power Sources, 2024, 594, 233948 CrossRef CAS.
- S. Wu, R. Xiong, H. Li, V. Nian and S. Ma, J. Energy Storage, 2020, 27, 101059 CrossRef.
- C.-Y. Wang, G. Zhang, S. Ge, T. Xu, Y. Ji, X. G. Yang and Y. Leng, Nature, 2016, 529, 515–523 CrossRef CAS PubMed.
- C.-Y. Wang, T. Xu, S. Ge, G. Zhang, X.-G. Yang and Y. Ji, J. Electrochem. Soc., 2016, 163, A1944–A1950 CrossRef CAS.
- G. Zhang, S. Ge, T. Xu, X. G. Yang, H. Tian and C. Y. Wang, Electrochim. Acta, 2016, 218, 149–155 CrossRef CAS.
- Y. Shang, K. Liu, N. Cui, N. Wang, K. Li and C. Zhang, IEEE Trans. Power Electron., 2020, 35, 7134–7144 Search PubMed.
- Y. Shang, C. Zhu, G. Lu, Q. Zhang, N. Cui and C. Zhang, J. Power Sources, 2020, 450, 227435 CrossRef CAS.
- Y. Zhang, Y. Yang, Y. Shang and N. Cui, J. Energy Storage, 2021, 42, 102977 Search PubMed.
- J. Oehl, A. Gleiter, D. Manka, A. Fill and K. P. Birke, J. Energy Storage, 2022, 53, 105169 CrossRef.
- H. Zhong, F. Lei, W. Zhu and J. Chen, J. Energy Storage, 2023, 67, 107441 CrossRef.
- F. Cai, H. Chang, Z. Yang, C. Duan and Z. Tu, J. Power Sources, 2022, 549, 232138 CrossRef CAS.
- J. Jiang, H. Ruan, B. Sun, L. Wang, W. Gao and W. Zhang, Appl. Energy, 2018, 230, 257–266 CrossRef.
- M. Thingvad, L. Calearo, A. Thingvad, R. Viskinde and M. Marinelli, UPEC 2020 – 2020 55th International Universities Power Engineering Conference, Proceedings, 2020.
- S. S. Zhang, K. Xu and T. R. Jow, J. Power Sources, 2003, 115, 137–140 CrossRef CAS.
- S. S. Zhang, K. Xu and T. R. Jow, Electrochim. Acta, 2004, 49, 1057–1061 CrossRef CAS.
- H. Dai, B. Jiang and X. Wei, Energies, 2018, 11, 220 CrossRef.
- M. Dong, X. Li, Z. Yang, Y. Chang, W. Liu, Y. Luo, W. Lei, M. Ren and C. Zhang, J. Power Sources, 2024, 603, 234386 CrossRef CAS.
- M. J. Brand, M. H. Hofmann, M. Steinhardt, S. F. Schuster and A. Jossen, J. Power Sources, 2016, 334, 202–212 CrossRef CAS.
- A. Fill, S. Koch, A. Pott and K. P. Birke, J. Power Sources, 2018, 407, 147–152 CrossRef CAS.
- A. Fill, T. Mader, T. Schmidt, A. Avdyli, M. Kopp and K. P. Birke, J. Energy Storage, 2022, 51, 104325 CrossRef.
- C. R. Paul, Inductance: Loop and Partial, John Wiley and Sons, 2010, pp. 1–379 Search PubMed.
- J. Xu, X. Mei, H. Wang and J. Wang, IEEE Trans. Ind. Inform., 2021, 17, 4714–4723 Search PubMed.
- H. Oomori and I. Omura, Power Electron. Dev. Components, 2022, 3, 100018 CrossRef.
- M. Uno and K. Tanaka, IEEE Trans. Veh. Technol., 2011, 60, 1505–1515 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |