Pressure-driven magnetic phase change in the CrI₃/Br₃Cr₂I₃ heterostructure

Abstract

Vertically stacked van der Waals (vdW) heterostructures not only provide a promising platform in terms of band alignment, but also constitute fertile ground for fundamental science and attract tremendous practical interest towards their use in various device applications. Beyond most two-dimensional (2D) materials, which are intrinsically non-magnetic, CrI₃ is a novel material with magnetism dependent on its vdW-bonded layers, promising potential spintronics applications. However, for particular device applications, a heterostructure is commonly fabricated and it is necessary to examine the effect of the interface or contact atoms on the magnetic properties of the heterostructure. Most importantly, the effect of assembly stress on the electronic and magnetic properties remains unclear. In this study, we design a vdW heterostructure from two-chromium tri-halides, namely the CrI₃/Br₃Cr₂I₃ heterostructure, where the Janus equivalent of the CrI₃ monolayer, Br₃Cr₂I₃, is also an intrinsically magnetic 2D material. Using state-of-the-art first-principles calculations, we uncover the effects of the contact atoms, as well as external pressure, on the electronic and magnetic properties of the CrI₃/Br₃Cr₂I₃ heterostructure. It is found that the heterostructure transitions from an antiferromagnetic (AFM) to ferromagnetic (FM) ground state with pressure larger than certain threshold. We also investigate the magneto-crystalline anisotropy energy (MAE) of the CrI₃/Br₃Cr₂I₃ heterostructure. Remarkably, it is found that the MAE is significantly influenced by both the stacking and the contact atoms, varying abruptly and inconsistently with the contact atoms and external pressure. Further, we also reveal a correlation between the MAE and the polar angle. The pressure-regulated magnetic properties of the CrI₃/Br₃Cr₂I₃ heterostructure as revealed in this study highlight its potential applications in spintronic devices.

---

I. Introduction

Two-dimensional (2D) van der Waals (vdW) materials offer an exciting platform for technological breakthroughs in several current practical applications. Therefore, due to their unusual structural, electronic, magnetic and optical properties, such 2D materials triggered a research explosion soon after the successful exfoliation of graphene.¹ Besides graphene, a wide variety of 2D materials have been attracting increasing attention in the last couple of years due their peculiar properties.^2–8 Transition metal dichalcogenides (TMDs), hexagonal boron nitride (hBN), silicene and black phosphorous are grouped together among 2D materials due to their exciting and novel properties.^9–13 Similarly, CuI has been reported, featuring a very low thermal conductivity.¹⁴ Layered TMDs constitute a wide family with a variety of distinct optical, electronic and mechanical properties.^12,13,15,16 For certain significant properties and device applications, some of the available 2D materials are combined to produce novel hetrostructures.¹⁵ However, most of the available 2D materials or nanoribbons are intrinsically nonmagnetic in their pristine form, which causes a major obstacle for their applications in spintronics.^17–19 Magnetism can be induced via some external means like doping, defect and edge engineering, and coupling with a ferromagnetic material. Therefore, there is a desire to explore novel 2D materials using a robust material with prominent intrinsic ferromagnetism.

Soon after the discovery of intrinsic magnetic order in low-dimensional materials, several noteworthy examples of these 2D magnetic materials have been focused on, both experimentally and theoretically, for instance CrI₃, Cr₂Ge₂Te₆ (CGT), FePS₃, VSe₂ and MnSe₂.^20–24 Moreover, due to the spin effect, CrI₃ has been reported to have high thermal conductivity.²⁵ It has been reported that CrI₃ and CGT monolayers are intrinsically ferromagnetic with measured Curie temperatures of 45 K and 28 K, respectively.^20,21 Meanwhile, for CrI₃ bilayers, an antiferromagnetic (AFM) ground state has been reported.²⁰ The chromium tri-halides CrX₃ (X = Br, I) have been extensively investigated, both theoretically and experimentally. These compounds are reported to have strong interlayer ferromagnetic interactions.^26–28 Further, it has been reported that the interlayer coupling is ferromagnetic (FM) in both CrBr₃ and CrI₃, with critical temperatures T_c = 32.5 and 68 K, respectively.²⁹

Interestingly, vdW-bonded magnetic materials are of great interest as building blocks for heterostructures in spin-based technologies. Heterostructures are based on layering of two-dimensional materials with a particular contact geometry. Therefore, in making a CrI₃/Br₃Cr₂I₃ heterostructure from CrI₃ and Janus Br₃Cr₂I₃, our primary goal is to explore the interface and contact-atom behavior in terms of the structural, electronic, and magnetic properties of the materials under study. The resemblance of the geometric structures of CrI₃ and Janus Br₃Cr₂I₃ (as Br₃Cr₂I₃ is a Janus equivalent of CrI₃) motivated us to systematically investigate the CrI₃/Br₃Cr₂I₃ heterostructure. Vertically stacked heterostructures have quite promising device applications.³⁰ Therefore, in the current study, we combine one monolayer of CrI₃ and a Janus monolayer of Br₃Cr₂I₃ to form the CrI₃/Br₃Cr₂I₃ heterostructure.

Prior theoretical and experimental findings demonstrate that both CrI₃ and Janus Br₃Cr₂I₃ monolayers are intrinsically ferromagnetic. However, bilayer CrI₃ possesses an antiferromagnetic ground state.³¹ Therefore, in the current study, we also expect an AFM ground state for the CrI₃/Br₃Cr₂I₃ heterostructure.^31,32 Further, in this work we systematically study the effect of interface atoms for tuning the structural, electronic, and magnetic properties of the CrI₃/Br₃Cr₂I₃ heterostructure under external vertical pressure. Our results reveal that a flip in the spin alignment of Cr atoms occurs from AFM to FM under high external pressure, but the magnetic moment of the Cr atoms remains constant. We expect that our results will provide new information to understand the magnetic ground state of the CrI₃/Br₃Cr₂I₃ heterostructure and will provide a new paradigm for useful spintronic devices.

II. Numerical method

In this study, the calculations have been carried out using the Vienna ab initio simulation package (VASP),³³ with the Perdew–Burke–Ernzerhof generalized gradient approximation (GGA)³⁴ within the framework of the projector augmented wave (PAW) method. Grimme's DFT-D3 scheme was adopted to describe the interlayer long-range vdW interactions.³⁵ In the CrI₃ bilayer, due to the 3d localized nature of the electrons in the Cr atom, we applied on-site Hubbard-type interactions for the Coulomb repulsion of the Cr 3d orbital. We used the rotationally invariant GGA+U method introduced by Liechtenstein et al.,³⁶ where we applied U = 2 and J = 1.76 eV, similar to our previous report.³² A plane-wave cut-off energy of 500 eV was used. The Brillouin zone has been sampled using the Monkhorst–Pack method³⁷ within an atomically generated k-mesh of 9 × 9 × 1. The stable lattice constant was determined by calculating the total energy as a function of the lattice constant. The convergence criterion for energy was set to 0.02 meV, while the atomic positions were optimized until the Hellmann–Feynman force on each atom became smaller than 10⁻⁴ eV Å⁻¹. To find the equilibrium lattice constant for the two different layers, first we consider the lattice constant of the CrI₃ monolayer and relax the CrI₃/Br₃Cr₂I₃ heterostructure. Then we decrease the lattice constant until it is consistent with the lattice constant of CrX₃ (X = I, Br) and relax the CrI₃/Br₃Cr₂I₃ heterostructure. To avoid artificial interactions between the images, a vacuum layer of more than 20 Å was applied along the z-axis. Besides spin polarization, we also apply spin–orbit coupling (SOC) to discuss the electrical properties. For the magnetic crystalline anisotropy (MAE) calculations, we use non-collinear spin–orbit interactions with a dense k-mesh of 21 × 21 × 1.³⁸

III. Results and discussion

A. Atomic structures

As we know, bulk chromium tri-halides CrX₃ (X = Br and I) crystallize in the rhombohedral BiI₃ structure (space group R3), which can be transformed to the monoclinic AlCl₃ structure (space group C2/m) at high temperature. Here, in the current study, we will focus on two different stackings of the CrI₃/Br₃Cr₂I₃ heterostructure. These two types of stackings are either AB (natural type) or AA, where AB stacking results when moving one layer over the other by ∼4 Å, while placing the second layer exactly on the first layer gives us AA stacking. There is about 64 meV energy difference between AB and AA stacking.³² Further, we demonstrate how the contact atoms affect the different properties of the Cr₂I₃Br₃/CrI₃ heterostructure. Interestingly, the two possibilities for the contact atoms in the CrI₃/Br₃Cr₂I₃ heterostructure are: firstly, there could be the same I atoms interfacing with each other, called the same interface and represented by AB-I and AA-I for AB and AA stacking, respectively; secondly, the Br atoms of the Janus monolayer will be in contact with the I atoms of the CrI₃ monolayer, called the different interface and represented by AB-II and AA-II for AB and AA stacking, respectively. Due to the different lattice constants of the two monolayers Cr₂I₃Br₃ (6.805 Å)³⁹ and Cr₂I₃ (7.07 Å),^40,41 we also need to calculate the lattice mismatch using the relation below:where a^H and a^M are the lattice constants of the Cr₂I₃Br₃/CrI₃ heterostructure and CrI₃ (Cr₂I₃Br₃) monolayers, respectively. Interestingly, using the above relation, we found a small lattice mismatch of only 0.22% by considering the lattice constants of Cr₂I₃Br₃ and the Cr₂I₃Br₃/CrI₃ heterostructure, resulting in a slight tensile strain. Similarly, considering the lattice constant of the CrI₃ monolayer and Cr₂I₃Br₃/CrI₃ heterostructure results in a slight compressive strain of 3.54 Å. The above lattice mismatch is for AB-II, AA-I and AA-II, while we found a negligible lattice mismatch for AB-I.

Schematic illustrations of the above four types of structure are shown in Fig. 1. The upper panels in Fig. 1 show the top views of the pristine relaxed structures, while the lower panels show the side views, for AB and AA stacking configurations.

Fig. 1 Structural illustrations of the CrI₃/Br₃Cr₂I₃ heterostructure for (a) and (e) AB-I (same interface) and (b) and (f) AB-II (different interface) types of AB stacking, and (c) and (g) AA-I (same interface) and (d) and (h) AA-II (different interface) types of AA stacking. The upper and lower panels respectively show the top and side views.

Now, to study the effect of the interface atoms on different physical properties, first we need a stable lattice constant for the CrI₃/Br₃Cr₂I₃ heterostructure. Therefore, we calculate the ground-state energy at different lattice constants. Fig. S1(a) of the ESI† shows the lattice constant vs. energy curve for the AB-I contact, with favorable ground-state energy at a lattice constant of 6.83 Å, while ESI† Fig. S1(b)–(d) show that the other three contacts have the same value of lattice constant, i.e. 6.805 Å, for favorable ground-state energy.

Next, we need to check the effect of external vertical pressure on different physical properties of the CrI₃/Br₃Cr₂I₃ heterostructure. For this purpose, first we compress the heterostructure by applying perpendicular pressures corresponding to 5, 10, 15 and 20% of the interlayer distance of the CrI₃/Br₃Cr₂I₃ heterostructure; these are equivalent to specific numerical values in units of GPa as respectively indicated in Tables 1 and 2 for AB and AA stacking. Similarly, the structural parameters of all four contacts are given in these two tables. The bond angles (θ₁, θ₂), bond lengths (b₁, b₂) and interlayer distances (δ) at zero and applied pressures are also shown. Table 1 shows that the interlayer distance accordingly decreases with an increase in pressure. It is clear from Tables 1 and 2 that both the interlayer distance and bond angles are greatly affected by the external pressure, irrespective of the interface atoms, while the bond-length behavior with the pressure is slightly contact dependent. Further, Table 1 shows that b₁ for the same interface first greatly decreases with pressure and then, with further increases in pressure, it linearly decreases. Similarly, b₂ decreases with increasing pressure irrespective of the interface. Table 1 shows the results for AB stacking with the same (AB-I) and different (AB-II) contact interface atoms, while Table 2 shows the results for AA stacking with the same (AA-I) and different (AA-II) contact atoms. From these tables, not only does the external pressure affect the structural properties, but the contact atoms, due to the different atomic sizes of I and Br atoms, result in notable changes in the physical properties of the CrI₃/Br₃Cr₂I₃ heterostructure.

Table 1 Structural information: interlayer distances δ, bond angles (θ₁, θ₂), bond lengths (b₁, b₂), ground-state energies ΔE (E_AFM − E_FM), and band gaps E_g of AB stackings with the same (AB-I) and different (AB-II) contacts under external pressure (P)

	AB-I					AB-II
P (GPa)	0	0.055	1.59	2.84	4.43	0	0.61	1.52	2.59	3.96
δ (Å)	6.51	6.24	6.0	5.74	5.49	6.24	5.96	5.67	5.44	5.2
θ 1°	90.33	90.77	92.17	93.12	94.46	92.53	92.92	93.44	94	94.66
θ 2°	86.86	86.78	93.91	85.47	84.85	87.16	86.8	85.92	86.34	85.35
b 1	2.71	2.54	2.53	2.52	2.51	2.71	2.7	2.68	2.69	2.66
b 2	2.71	2.71	2.69	2.68	2.67	2.71	2.67	2.67	2.68	2.65
ΔE (meV)	−1.99	−1.36	1.28	5.57	12.89	−2.62	−1.27	1.77	6.88	14.2
E g (eV)	1.70	1.72	1.63	1.28	1.31	1.30	1.33	1.33	1.38	1.29

---

Table 2 Structural information: interlayer distances δ, bond angles (θ₁, θ₂), bond lengths (b₁, b₂), ground-state energies ΔE (E_AFM − E_FM), and band gaps E_g of AA stacking with the same (AA-I) and different (AA-II) contacts under external pressure (P)

	(AA-I)					(AA-II)
P (GPa)	0	0.81	2.61	2.37	4.39	0	0.185	0.74	1.68	2.7
δ (Å)	6.62	6.32	6.03	5.57	5.51	6.45	6.16	5.87	5.59	5.33
θ 1°	101.06	101.57	102.09	102.65	103.37	92.54	92.91	93.26	93.79	94.42
θ 2°	87.06	86.70	86.27	85.79	85.13	87.09	86.86	86.54	86.09	85.57
b 1	2.54	2.53	2.52	2.51	2.5	2.71	2.71	2.7	2.69	2.67
b 2	2.71	2.7	2.69	2.68	2.67	2.71	2.7	2.7	2.69	2.68
ΔE (meV)	−3.67	−3.25	−1.34	3.7	10.98	−3.43	−2.71	−1.41	2.45	8.57
E g (eV)	1.62	1.62	1.61	1.37	1.23	1.3	1.3	1.31	1.28	1.2

---

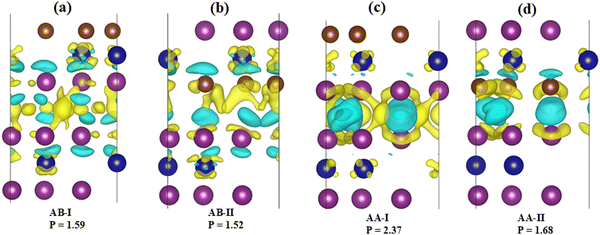
Further, we also determined the charge transfer by calculating the charge density difference at the pressure where the magnetic ground state transformed from AFM to FM. The charge density difference is calculated by using the relation below

Δ_ρ = ρ_Het − ρ_CrI3 − ρ_Br3Cr2I3 (2)

where ρ_Het, ρ_CrI3, and ρ_Br3Cr2I3 are, respectively, the charge densities of the CrI₃/Br₃Cr₂I₃ heterostructure, and CrI₃ and Br₃Cr₂I₃ monolayers, while Δ_ρ is the charge density difference, as shown in Fig. 2. The yellow and cyan colors respectively represent the charge accumulation and depletion. To further confirm the transfer of charges from one layer to the other, we also performed Bader charge analysis.^42,43 From the Bader charge analysis, in the case of AB-I, if we only consider the encircled atoms in Fig. 1, we find that the Cr atoms lose ∼0.14e. The other Cr atoms gain a charge of 0.18e and the Br atoms on the surface also gain about 0.198e. Similarly, the I atoms in the upper and lower layer respectively lose 0.11 and 0.067e, as can be seen in Fig. 1(a). In the case of AB-II, the contact Br atoms gain a charge of 0.258e, while the I atom loses a charge of 0.063e. Similarly, the encircled Cr atom loses a charge of 0.133e. Moreover, we also found a similar behavior for the AA configurations, as given in the ESI,† Table S1. Similarly, the results for the AB configuration are also included in Table S1 in the ESI.† Therefore, the charge density difference is further confirmed by the Bader charge analysis.

Fig. 2 Charge density difference of the CrI₃/Br₃Cr₂I₃ heterostructure for (a) AB-I (same interface) and (b) AB-II (different interface) types of AB stacking, and (c) AA-I (same interface) and (d) AA-II (different interface) types of AA stacking. The external pressure at which the spin flip from AFM to FM occurs is also given. The iso-surface value for (a) and (b) is 0.00003 and for (c) and (d) is 0.0009 e Å⁻¹.

B. Electronic properties

Here, we focus on the detailed electronic structure of the systems under study. Primarily, we focus on checking the effect of the same or different interface halide atoms on the electronic properties of the CrI₃/Br₃Cr₂I₃ heterostructure. Fig. 3 shows the electronic band structures of the AB-stacked CrI₃/Br₃Cr₂I₃ heterostructure with the same and different interfaces. The black lines depict the majority spin bands while the red lines show the minority spin bands. The Fermi level is fixed at zero. Fig. 3 shows a prominent effect of the interface atoms that can be clearly seen. All these band structures are indirect. The previously reported band gaps of CrI₃ and Janus Br₃Cr₂I₃ monolayers are 1.1 and 1.26 eV, respectively.³⁹ Similarly, in our previous report regarding the pristine bilayer CrI₃, the band gap is indirect with values of 1.71 and 1.68 eV for AB and AA stacking, respectively.³² In our present work, the measured band gaps for the pristine AB-stacked CrI₃/Br₃Cr₂I₃ heterostructure are 1.69 and 1.3 eV for (AB-I) and (AB-II) contact, while for AA stackings, they become 1.62 and 1.3, respectively, for AA-I and AA-II. Thus, in the case of different contact atoms, the band gap has the same value, irrespective of the stacking. The band gap remains indirect irrespective of the stackings and contacts. In addition to the transition and modulation of the magnetic state, the electronic properties of the CrI₃/Br₃Cr₂I₃ heterostructure show an interesting response to the external pressure. Therefore, we check the effect of pressure on the electronic properties and further check the possibility of transition from AFM to FM. Interestingly we found that not only is there a linear decrease in the band gap, but also a transition from AFM to FM occurs at different high pressures, as indicated in Tables 1 and 2 for both contacts in AB and AA-stacking, respectively, but the indirect nature of the band structures remains preserved. Fig. 3 shows the electronic band structures of the AB-stacked CrI₃/Br₃Cr₂I₃ heterostructure for the same contacts (upper panels) at zero to 4.43 GPa and different contacts (lower panels) at zero to 3.96 GPa, while for the AA-stacked CrI₃/Br₃Cr₂I₃ heterostructure, the electronic band structures at zero to 4.39 GPa for the same contacts (upper panel) and at zero to 2.7 GPa for different contacts (lower panel) are shown in Fig. 4. The band gap values of the CrI₃/Br₃Cr₂I₃ heterostructure for both contacts in AB and AA-stacking at different applied pressures are reported in Tables 1 and 2. Fig. 3 shows that as the pressure increases on the CrI₃/Br₃Cr₂I₃ heterostructure, the band gap gets narrower irrespective of the stacking and contacts atoms. Interestingly, it appears that the valence band maximum (VBM) remains almost constant while the conduction band minimum (CBM) moves down toward the Fermi level at high pressure. Besides this, the VBM also slightly shifted from Γ towards M, as shown in Fig. 3.

Fig. 3 Electronic band structures for the AB-stacked CrI₃/Br₃Cr₂I₃ heterostructure with (a)–(e) the same (AB-I) interface atoms from 0 to 4.43 GPa and (f)–(j) different (AB-II) interface atoms from 0 to 3.96 GPa.

Fig. 4 Electronic band structures for the AA-stacked CrI₃/Br₃Cr₂I₃ heterostructure with (a)–(e) the same (AA-I) interface atoms from 0 to 4.39 and (f)–(j) different (AA-II) interface atoms from 0 to 2.7 GPa.

C. Magnetic properties

Next, we need to explore the magnetic properties of the CrI₃/Br₃Cr₂I₃ heterostructure; therefore, to calculate the magnetic ground-state energy of the CrI₃/Br₃Cr₂I₃ heterostructure, we consider two different spin configurations, ferromagnetic (FM) and anti-ferromagnetic (AFM), as shown in Fig. 5(a). In the case of the FM configuration, the Cr atoms in both layers spin in the same direction, while for the AFM configuration, they have opposite spin directions, as shown in Fig. 5(a). The magnetic ground state can be calculated from the following equation:

ΔE = E_AFM − E_FM (3)

Here, ΔE is the energy difference between the AFM and FM magnetic ground state. As previously reported, the AFM ground state is stable in bilayer CrI₃, both theoretically and experimentally. Therefore, the CrI₃/Br₃Cr₂I₃ heterostructure of two chromium tri-halides is also expected to be in the AFM ground state irrespective of the stacking. In the AFM configuration, we consider that both layers in the CrI₃/Br₃Cr₂I₃ heterostructure are oppositely spin polarized to each other, as shown in Fig. 5(a). Interestingly, we found that the magnetic ground state of the heterostructure in the pristine form is AFM, with energy differences of −1.99, −2.63, −3.68 and −3.44 meV for the AB-I, AB-II, AA-I and AA-II interfaces, respectively. Not only does the stacking affect the magnetic ground state, but the interface atoms also prominently change the ground-state energy as well. Further, we investigated the effect of vertical pressure on the CrI₃/Br₃Cr₂I₃ heterostructure and found that at high pressure, a spin flip occurs in the systems under study. With increasing pressure, the AFM energy difference decreases and finally the AFM spin configurations flip to FM configurations. The ΔE values from zero to maximum external pressure for AB and AA stacking are respectively given in Tables 1 and 2.

Fig. 5 (a) Magnetic spin configurations and in-plane magnetic exchange coupling interactions are given as J₁, J₂ and J₃. (b) Total MAE for AB-I, AB-II, AA-I and AA-II stacking of the CrI₃/Cr₂I₃Br₃ heterostructure. The pressure is represented in steps of % for each stacking.

As the magneto-crystalline anisotropy energy (MAE) is an important quantity, we also explore the effect of the interface atoms of the CrI₃/Br₃Cr₂I₃ heterostructure on this quantity using different stackings at different applied external pressures. For this purpose, we performed non-collinear total energy calculations with spin–orbit coupling along the [100] and [001] directions, applying a denser k-mesh of 21 × 21 × 1. The [100] and [001] magnetic axes are called in-plane or parallel (‖) and out-of-plane or perpendicular (⊥), respectively. We carefully check the convergence of the total energy and finally the difference in energy along the parallel and perpendicular directions gives us the MAE.³⁸ Interestingly, the MAE of the CrI₃/Br₃Cr₂I₃ heterostructure is in accordance with that of the pure CrI₃ bilayer. The results for the MAE are shown in Fig. 5(b) for AB and AA stacking, both with the same and different interface atoms. Fig. 5(b) further shows that at high pressure, the AA-I stacking is more prominently enhanced than the other systems, followed by the AB-I stacking, while at high values of external perpendicular pressure, both AB-II and AA-II reach the same maximum values.

Fig. 5(b) shows that there is a strong perpendicular magnetic anisotropy irrespective of the stacking and contact interface atoms. Further, we saw a transition from AFM to FM in both stackings, either with the same or different interface atoms, which results in a robust enhancement in the perpendicular MAE of the CrI₃/Br₃Cr₂I₃ heterostructure. Interestingly, we found that for the same interface contact atoms (I–I), we have a large MAE, while for different contact atoms on the interface (I–Br), the MAE decreases irrespective of the stacking, which confirms that as the structure size increases, the MAE also increases. The MAE stems from the spin–orbit coupling (SOC) and further this SOC is dependent on the orbital character of both the occupied and unoccupied states of the CrI₃/Br₃Cr₂I₃ heterostructure. For same spins, the SOC for Δm = 0 states produces a perpendicular spin alignment, while for Δm = ±1 it results in an in-plane spin alignment. As demonstrated in Fig. 5(a), the heavy I atoms produce a high MAE, whereas the Br atoms provide a smaller value of the MAE, as previously reported for Janus materials.³⁹

Next, we also investigate the orbital contribution to the MAE from each atom of the CrI₃/Br₃Cr₂I₃ heterostructure as depicted in Fig. 5 for different interface atoms. Fig. 6(a)–(e) represent the orbital contributions of the Cr atom, ranging from 0 to 3.96 GPa pressure. Since the CrI₃/Br₃Cr₂I₃ heterostructure contains four Cr atoms, the orbital contribution for the Cr atom, which is indicated by the red dotted circle in Fig. 1(e)–(h), has a higher MAE value. Positive and negative values, respectively, reflect the out-of-plane and in-plane MAE. First, we will discuss the system at zero pressure, as shown in Fig. 6(a). Interestingly, the MAEs of the d_yz, d_z²−x² and d_xz orbitals have been determined to be 0.91, 0.21 and 0.065 meV, respectively. Additionally, due to the negative values of the other two orbitals (d_xy and d_x²−y²), these contribute to the in-plane MAE. Similarly, Fig. 6(g)–(k) illustrate the I atom contributions to the MAE from zero to 3.96 GPa, where the I atom is given in the blue dotted circle shown in Fig. 1(e)–(h). Fig. 6(f)–(j) show that p_z and p_y contribute to the out-of-plane MAE, while p_x and p_y contribute to the in-plane MAE. Further, we found an enhancement in the orbital contribution in the out-of-plane MAE but a decrease in the in-plane MAE of the I atom with increasing pressure. Now, we discuss the orbital contribution of the second halide element beside the I atom of the interface, Br, as shown by the green encircled Br atom in Fig. 1(e)–(h). In contrast to the I atom, we found that the Br atom contribution decreases with increasing pressure. Further, the orbital contribution is like that of the I atom with a sufficiently small MAE, which indicates that as we go down the group, the MAE increases in the Cr-trihalide 2D materials. It confirms that there is a size dependency of the MAE on the halogen elements with Cr. That is why we see a clear difference in the orbital contribution from the I (heavy atom) and Br atom (comparatively lighter than I), as shown in Fig. 6(f)–(j) for I and Fig. 6(k)–(o) for Br, respectively. Therefore, due to the strong spin–orbit coupling and heavy atoms, the MAE has giant value in the CrI₃/Br₃Cr₂I₃ heterostructure. Finally, we have a total MAE of ∼0.20 meV in the out-of-plane direction.

Fig. 6 SOC-resolved MAE for the different-interface AB stacking (AB-II) of the CrI₃/Cr₂I₃Br₃ heterostructure, (a)–(e) for Cr atoms, (f)–(j) for I atoms and (k)–(o) for Br atoms, from zero to 3.96 GPa pressure, respectively.

Similarly, we also explore the orbital contribution of the MAE for the same interface atoms (AB-I, AA-I). Interestingly, we found a comparatively larger value for the total MAE than for the different contact atoms, as expected, while the orbital contribution is equal from either layer of the CrI₃/Br₃Cr₂I₃ heterostructure, as shown in Fig. 6(f)–(o). This confirms the orbital character of the halogen atoms when changing the contact atoms in the Cr-trihalides.

Further, we also explore the atomic orbital contribution of each atom to the MAE for the AA stacking with different and same interface contacts, as shown in the ESI,† Fig. S2 and S3 respectively. Interestingly, we found a similar behavior for the same or different interface atoms in the AA stacking. Thus, this study showed the reason behind the different values of the MAE for the same or different interface atomic configuration in both stackings. Therefore, it is clear from Fig. 6 that, unlike the Cr atoms, the I and Br atoms have site- and pressure-dependent values for the MAE. Interestingly, it is also clear from Fig. 6 that for the different contact atoms, their contribution to the total MAE is smaller than that of the same contact atoms. The reason for the smaller contribution of the Br atoms than that of the I atoms is their atomic radii; thus, we concluded that as the atomic radius decreases, the MAE also decreases.

Subsequently, we investigated the atomic orbital contributions of the CrI₃/Br₃Cr₂I₃ heterostructure for AB stacking with the same interface atoms, as depicted in Fig. 7. Interestingly, in the case of AB-II, obviously both the contact atoms have the same contribution to the MAE, as depicted in Fig. 7(f)–(o), from zero to a maximum pressure of 4.43 GPa, respectively.

Fig. 7 SOC-resolved MAE for same-interface AB stacking (AB-I) of the CrI₃/Cr₂I₃Br₃ heterostructure, (a)–(e) for Cr atoms, (f)–(j) for I atoms and (k)–(o) for Br atoms, from zero to 4.43 GPa pressure, respectively.

To discuss the relationship between the angular dependency and spin orientation of the spins for both stackings, we explore the relation of the MAE with the polar (ϕ) and azimuthal angles (θ). We rotate the polar angle through the plane of the a and b axis of the CrI₃/Br₃Cr₂I₃ heterostructure, while keeping the spin orientation along the c axis (perpendicular to the plane), as shown in Fig. 8. Here, Fig. 8(a) shows the angular dependency of the AB stacking in both configurations of the contact atoms, same (AB-I) and different (AB-II), while Fig. 8(b) shows these configurations for the AA stacking. Interestingly, we noticed that when rotating the CrI₃/Br₃Cr₂I₃ heterostructure along the c-axis, the MAE is maximum at ϕ = 90°, while an increase or decrease in ϕ from 0 or 180° causes a decrease in the MAE, as shown by the brown and orange lines, respectively, for AB-I and AB-II. Furthermore, we found a similar behavior for the AA stacking. Meanwhile, in the case of the spin rotation in the ab plane, the MAE remains at zero for the same rotation of the polar angle from 0 to 180°, irrespective of the stacking of the CrI₃/Br₃Cr₂I₃ heterostructure. Therefore, we found that the MAE has a strong dependency on the polar angle and is independent of the azimuthal angle, as shown in Fig. 8(a) and (b) for AB and AA stacking, respectively.

Fig. 8 Angular dependence of the MAE of the CrI₃/Br₃Cr₂I₃ heterostructure for (a) AB and (b) AA stacking. The brown and orange lines in both panels represent the MAE along the [001] direction at ϕ = 0, while the grey and yellow lines represent the MAE along the ϕ = 0 [100] or ϕ = 3π/2 [010] or in-plane directions.

D. Curie temperature

We also calculate the Curie temperature (T_c) of the CrI₃/Br₃Cr₂I₃ heterostructure using VAMPIRE. We constructed a temperature-dependent magnetization curve using the Metropolis Monte Carlo (MC) simulation coded in the VAMPIRE software package⁴⁴ and then we extracted the Curie temperature (T_c). Here, we used the classical spin Heisenberg model, which can be written as:where J is the exchange coupling energy parameter of the nearest-neighbor atoms, and m_i and m_j show the magnetic moments of neighboring atoms related to each exchange interaction. Interestingly, we have three kinds of nearest-neighbor exchange interaction, called first, second and third nearest-neighbor exchange interactions, represented by J₁, J₂ and J₃, as shown in Fig. 5(a). J₁ and J₂ represent the intralayer exchange interaction, which leads to J > 0, while the third magnetic exchange interaction shows the interlayer exchange interaction, which is negative for certain values of external pressure; later, due to the transition from AFM to FM, this interaction also changes to a positive value. Therefore, in the current study, we only explore the Curie temperature for the magnetic flip point. Moreover, we consider that the intralayer exchange coupling interaction (J₁, J₂) remains constant for the two layers, irrespective of the external pressure. Here, J₁ and J₂ respectively have values of 4.46 × 10⁻²² and 5.03 × 10⁻²² J for the Br₃Cr₂I₃ and CrI₃ monolayers. Meanwhile, the third nearest-neighbor exchange interaction is given in the ESI,† in Tables S2 and S3 for AB and AA stacking, respectively. Further, the magnetic exchange interaction can be calculated using the relation , where N and m are, respectively, the total number of magnetic atoms per unit cell and the average magnetic moment per magnetic atom in the CrI₃/Br₃Cr₂I₃ heterostructure. For the MC simulation, we considered a large enough supercell of 50 × 50 × 1. Notably, we only calculate the Curie temperature at the transition point pressure, where the CrI₃/Br₃Cr₂I₃ heterostructure transformed from AFM to FM. Interestingly, we found that the T_c of the CrI₃/Br₃Cr₂I₃ heterostructure is ∼95 K irrespective of the CrI₃/Br₃Cr₂I₃ heterostructure configuration. This behavior confirms that there is a negligible effect on the Curie temperature by the configuration of the CrI₃/Br₃Cr₂I₃ heterostructure due to weak interlayer magnetic exchange interactions. Further, we also calculated the Curie temperature of the CrI₃ monolayer; this is estimated to be 46 K, which agrees well with the experimentally reported value of 45 K.⁴⁵ This comparison confirms the validity of our estimated results of the Curie temperature.

IV. Conclusion

In summary, we thoroughly investigate the effect of interface atoms in the CrI₃/Br₃Cr₂I₃ heterostructure using first-principles calculations. We not only note a prominent change in the structural properties for both the AA and AB stacking with the same (I–I) or different (I–Br) interface atoms; we also found a peculiar change in the charge transfer and electronic properties of the CrI₃/Br₃Cr₂I₃ heterostructure. Interestingly, for AB-II and AA-II, we found that the Br atoms gain more charge, which not only slightly enhances the band gaps but prominently results in a higher MAE than for the other configurations. Similarly, an increase in the external pressure does not affect the indirect-band-gap nature of the CrI₃/Br₃Cr₂I₃ heterostructure. However, a transition in the magnetic ground state from AFM to FM occurs with increasing external perpendicular pressure. Interestingly, an enhancement in the perpendicular magnetic anisotropy for the AB and AA stacking order was observed. However, this enhancement in the magnitude of the anisotropy energy was greatly affected by the interface atoms, with the same and different contact atoms in both stacking orders. For instance, compared with the pristine system, the magnitude of the MAE was almost doubled for AB stacking at a maximum pressure of 3.96 GPa, while the MAE was increased more than ∼20% for AA stacking at a maximum applied pressure of 2.27 GPa. This difference is due to the interface atoms, because in the I atoms, the p orbitals contribution is greater than the Br atoms. Through the SOC analysis, we found that both Cr and iodine atoms almost equally contributed to the MAE at zero pressure. With increasing pressure, the contribution for the perpendicular magnetization from the Cr was also increased, but the contribution from iodine atoms was more rapidly enhanced. Interestingly, we found that the MAE is independent of the azimuthal angle but has a strong dependency on the polar angle. Consequently, the role of iodine atoms in the anisotropy became more prominent. In particular, we found that the enhanced perpendicular magnetic anisotropy originated from the interface iodine atoms. Further, due to the smaller value of the third nearest-neighbor exchange interaction, we found an almost constant Curie temperature for all the configurations in our study.

Author contributions

G. Q. supervised the project. F. S. conceived the idea. F. S. carried out the DFT calculations and plotted the results. All the authors carefully checked the results and helped with writing and editing the manuscript.

Data availability

All data supporting the findings in this manuscript are available from the corresponding authors (Y. Z., Z. Q., and G. Q.) upon request.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (grant no. 52006057), the National Key R&D Program of China (2023YFB2408100), the Fundamental Research Funds for the Central Universities (grant no. 531119200237), the State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body at Hunan University (grant no. 52175013), the Natural Science Foundation of Chongqing, China (no. CSTB2022NSCQ-MSX0332), and the Outstanding Youth Project (23B0024) of the Hunan Provincial Department of Education. Z. Q. is supported by the National Natural Science Foundation of China (grant no. 12274374). The numerical calculations in this paper have been carried out on the supercomputing system of the E. T. Cluster, the National Supercomputing Center in Changsha, and the Hefei Advanced Computing Center.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric field effect in atomically thin carbon films, Science, 2004, 306, 666–669.
2. C.-D. Zhou, B. Liang, W.-J. Huang, J.-G. Noudem, X.-J. Tan and J. Jiang, Phonon engineering significantly reducing thermal conductivity of thermoelectric materials: a review, Rare Met., 2023, 42, 2825–2839.
3. L.-F. Yu, J.-Y. Xu, C. Shen, E. Zhou, J. Wu, H.-B. Zhang, X. Zheng, H.-M. Wang and G.-Z. Qin, Realizing ultra-low thermal conductivity by strong synergy of asymmetric geometry and electronic structure in boron nitride and arsenide, Rare Met., 2023, 42, 210–221.
4. S.-N. Wang, H.-C. Lu, D.-J. Li, Y. Jin, X.-Y. Li, Y. Yan, K. Gu, Y.-T. Qiu and L.-D. Zhao, Realizing p-type performance in low-thermal-conductivity BiSbSe3 via lead doping, Rare Met., 2023, 42, 3601–3606.
5. P.-D. Tao, S.-G. Wang, L. Chen, J.-F. Ying, L. Lv, L.-W. Sun, W.-B. Chu, K. Nishimura, L. Fu and Y.-Z. Wang, et al., Enhancement of in-plane thermal conductivity of flexible boron nitride heat spreaders by micro/nanovoid filling using deformable liquid metal nanoparticles, Rare Met., 2023, 42, 3662–3672.
6. Y.-X. Xu, H.-Z. Fan and Y.-G. Zhou, Quantifying spectral thermal transport properties in framework of molecular dynamics simulations: a comprehensive review, Rare Met., 2023, 42, 3914–3944.
7. P. Li, X. Wang, H. Wang, Q. Tian, J. Xu, L. Yu, G. Qin and Z. Qin, Biaxial strain modulated electronic structures of layered two-dimensional MoSiGeN4 Rashba systems, Phys. Chem. Chem. Phys., 2024, 26, 1891–1903.
8. Q. Tian, P. Li, J. Wei, Z. Xing, G. Qin and Z. Qin, Inverse Janus design of two-dimensional Rashba semiconductors, Phys. Rev. B, 2023, 108, 115130.
9. C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Boron nitride substrates for high-quality graphene electronics, Nat. Nanotechnol., 2010, 5, 722–726.
10. S. Cahangirov, M. Topsakal, E. Aktürk, H. Şahin and S. Ciraci, Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium, Phys. Rev. Lett., 2009, 102, 236804.
11. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Atomically Thin MoS₂: A New Direct-Gap Semiconductor, Phys. Rev. Lett., 2010, 105, 136805.
12. Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Electronics and optoelectronics of two-dimensional transition metal dichalcogenides, Nat. Nanotechnol., 2012, 7, 699–712.
13. L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Black phosphorus field-effect transistors, Nat. Nanotechnol., 2014, 9, 372–377.
14. J. Xu, A. Chen, L. Yu, D. Wei, Q. Tian, H. Wang, Z. Qin and G. Qin, The record low thermal conductivity of monolayer cuprous iodide (CuI) with a direct wide bandgap, Nanoscale, 2022, 14, 17401–17408.
15. A. K. Geim and I. V. Grigorieva, van der Waals heterostructures, Nature, 2013, 499, 419–425.
16. W. Han, R. K. Kawakami, M. Gmitra and J. Fabian, Graphene spintronics, Nat. Nanotechnol., 2014, 9, 794–807.
17. F. Subhan, M. U. Farooq and J. Hong, Bias-dependent transport properties of passivated tilted black phosphorene nanoribbons, Phys. Chem. Chem. Phys., 2018, 20, 11021–11027.
18. L. Zhang, J. Zhao, N. Cheng and Z. Chen, Intrinsic electronic and transport properties of graphene nanoribbons with different widths, Phys. Chem. Chem. Phys., 2020, 22, 3584–3591.
19. F. Subhan and J. Hong, Bias dependent transport property of defective hydrogen passivated tilted black phosphorene nanoribbon, Phys. E, 2019, 105, 151–155.
20. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature, 2017, 546, 270–273.
21. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals, Nature, 2017, 546, 265–269.
22. M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan and M. Batzill, Strong room-temperature ferromagnetism in VSe₂ monolayers on van der Waals substrates, Nat. Nanotechnol., 2018, 13, 289–293.
23. D. J. O’Hara, T. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta, D. W. McComb and R. K. Kawakami, Room Temperature Intrinsic Ferromagnetism in Epitaxial Manganese Selenide Films in the Monolayer Limit, Nano Lett., 2018, 18, 3125–3131.
24. J.-U. Lee, S. Lee, J. H. Ryoo, S. Kang, T. Y. Kim, P. Kim, C.-H. Park, J.-G. Park and H. Cheong, Ising-Type Magnetic Ordering in Atomically Thin FePS₃, Nano Lett., 2016, 16, 7433–7438.
25. G. Qin, H. Wang, L. Zhang, Z. Qin and M. Hu, Giant effect of spin–lattice coupling on the thermal transport in two-dimensional ferromagnetic CrI₃, J. Mater. Chem. C, 2020, 8, 3520–3526.
26. J. B. Goodenough, Theory of the Role of Covalence in the Perovskite-Type Manganites [La, M(II)]MnO₃, Phys. Rev., 1955, 100, 564–573.
27. J. Kanamori, Superexchange interaction and symmetry properties of electron orbitals, J. Phys. Chem. Solids, 1959, 10, 87–98.
28. P. W. Anderson, New Approach to the Theory of Super exchange Interactions, Phys. Rev., 1959, 115, 2–13.
29. R. W. Bené, Electron-Paramagnetic-Resonance Study of Cr Ions and Exchange-Coupled Cr Ion Pairs in the BiI₃ Structure, Phys. Rev., 1969, 178, 497–513.
30. X. Wu, X. Wang, H. Li, Z. Zeng, B. Zheng, D. Zhang, F. Li, X. Zhu, Y. Jiang and A. Pan, Vapor growth of WSe₂/WS₂ heterostructures with stacking dependent optical properties, Nano Res., 2019, 12, 3123–3128.
31. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature, 2017, 546, 270–273.
32. F. Subhan, I. Khan and J. Hong, Pressure-induced ferromagnetism and enhanced perpendicular magnetic anisotropy of bilayer CrI₃, J. Phys.: Condens. Matter, 2019, 31, 355001.
33. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
36. A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Density-functional theory and strong interactions: orbital ordering in Mott–Hubbard insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470.
37. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
38. D. Hobbs, G. Kresse and J. Hafner, Fully unconstrained noncollinear magnetism within the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 11556–11570.
39. M. Moaied, J. Lee and J. Hong, A 2D ferromagnetic semiconductor in monolayer Cr-trihalide and its Janus structures, Phys. Chem. Chem. Phys., 2018, 20, 21755–21763.
40. M. A. McGuire, H. Dixit, V. R. Cooper and B. C. Sales, Coupling of Crystal Structure and Magnetism in the Layered, Ferromagnetic Insulator CrI₃, Chem. Mater., 2015, 27, 612–620.
41. F. Subhan and J. Hong, Large Valley Splitting and Enhancement of Curie Temperature in a Two-Dimensional VI₃/CrI₃ Heterostructure, J. Phys. Chem. C, 2020, 124, 7156–7162.
42. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360.
43. W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204.
44. R. F. L. Evans, W. J. Fan, P. Chureemart, T. A. Ostler, M. O. A. Ellis and R. W. Chantrell, Atomistic spin model simulations of magnetic nanomaterials, J. Phys.: Condens. Matter, 2014, 26, 103202.
45. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature, 2017, 546, 270–273.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02066a

---