Thickness-dependent surface reconstructions in non-van der Waals two-dimensional materials

Abstract

Bismuth oxychalcogenides (Bi₂O₂X, X = S, Se, Te), a family of non-van der Waals (non-vdW) two-dimensional (2D) semiconductors, are attracting significant attention due to their outstanding semiconducting properties and huge potential in various applications of electronic and optoelectronic devices. Surface imperfections (e.g., surface vacancies) and surface reconstructions are more likely to appear and may cause intriguing physical properties and novel phenomena in the non-vdW 2D materials than the vdW cases. Here, we explore the impacts of surface vacancies and surface reconstructions on the properties of the surfaces and 2D structures of Bi₂O₂X by using the first-principles method. We find that the dimerization of surface X-vacancies occurs in Bi₂O₂S and Bi₂O₂Te (001) surfaces, like that happening in Bi₂O₂Se. Unexpectedly, the electronic structures of Bi₂O₂X (001) surfaces show strong tolerance to the order of surface X-vacancies. Furthermore, we find a phenomenon of thickness-dependent surface reconstructions for non-vdW Bi₂O₂X ultrathin films. For a monolayer, the zipper-surface is more stable, while the dimer-surface is generally more stable for thicker films. Calculated exfoliation energies of the Bi₂O₂X monolayer and multi-layers are close to those of common vdW 2D materials, indicating that 2D Bi₂O₂X belong to easily fabricated 2D materials, even though the inter-layer binding interaction is of the non-vdW type. Our results suggest that non-vdW 2D materials can possess intriguing properties because of surface imperfections and reconstructions in comparison with vdW 2D materials.

---

1. Introduction

Bi₂O₂Se is an emerging non-van der Waals (non-vdW) two-dimensional (2D) semiconductor with remarkable properties such as an ultrahigh carrier mobility and a moderate band gap.^1,2 More recently, superconductivity was demonstrated in Bi₂O₂Se via imposing external pressure and attributed to the flat-band near the Fermi level.³ These properties make it extremely promising for use in various electronic and optoelectronic devices such as field-effect transistors,^2,4 photodetectors,^5–7 memristors,⁸ and sensors.⁹ Surface imperfections such as vacancies have a significant impact on the physical properties of Bi₂O₂Se and the performance of the devices. For instance, the surface structures of Bi₂O₂Se including Se-vacancies (V_Se) and surface reconstructions play a decisive role in determining the performance of Bi₂O₂Se gas sensors.^9–12 Surface V_Se acting as an adsorption site for oxygen molecules help in realizing a feasible approach for detecting trace oxygen.⁹ Besides, surface defects were found to be responsible for a photo-gating effect and the strategy of passivating the defects upon vacuum annealing can be used to tune the photoconductivity of Bi₂O₂Se nanosheets.¹³

Intriguing patterns of V_Se have been discovered on the Bi₂O₂Se (001) surface. Chen et al. found an intertwined weave pattern of Se atoms and V_Se on the Bi₂O₂Se (001) surface, which is obtained by cleaving the single crystal in the ultrahigh vacuum (UHV) chambers.¹⁴ In this pattern, there are 50% of V_Se on the surface, and both remaining Se atoms and V_Se in the surface Se-layer tend to dimerize, resulting in a period of –V_Se–V_Se–Se–Se– along the x direction in the surface plane, namely 4 × 1 reconstruction (denoted as a dimer-surface, as shown in Fig. 1d), as characterized from atomic-resolution scanning tunneling microscopy (STM). Another remarkable feature is the non-existence of in-gap states, although plenty of V_Se occur in the surfaces.¹⁴ For the 4 × 1 dimer-surface, DFT calculations showed that the surface states at the Γ point give rise to a direct band gap.^15,16 Interestingly, another pattern of 2 × 1 reconstruction in which every other surface Se along the x direction is missing (i.e., a period of –V_Se–Se–V_Se–Se–, which is termed as zipper-surface) was also proposed on the (001) surface of 2D Bi₂O₂Se (see Fig. 1c).¹⁷ The discrepancy in the arrangements of Se and V_Se on the Bi₂O₂Se (001) surface poses two fundamental issues as to which pattern represents the most stable state for the surface and whether the most stable state depends on the thickness of the films. More fundamentally, the role that the surface vacancies and structure reconstructions play in determining the physical properties of non-vdW 2D Bi₂O₂Se, such as thermodynamic stability and electronic structures, remains largely unclear. It is essential to obtain a fundamental understanding of how surface imperfections and reconstructions affect the physical properties in non-vdW 2D materials.

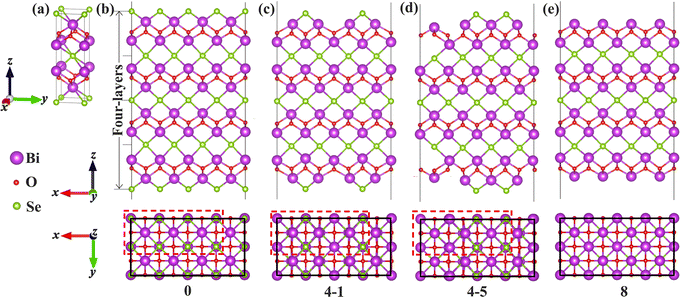Fig. 1 Structural model of Bi₂O₂Se bulk and (001) surfaces: (a) the bulk; (b) the surface terminated with the Se-layer without any V_Se (0); (c) the zipper-surface (4-1); (d) the dimer-surface (4-5); (e) the surface with 100% V_Se (8). Top views with the 2D periodicity indicated by black rectangles are shown below the side views. The red dashed-line rectangle in (b) shows the 4 × 2 arrangement of eight Se atoms on the surface layer. The 2 × 1 zipper- and 4 × 1 dimer-configurations are doubled along the y axis in (c) and (d), respectively. All possible configurations for each of V_Se compositions are shown in Fig. S1 (ESI†). Similar structural models are utilized for Bi₂O₂S and Bi₂O₂Te.

Apart from Bi₂O₂Se, two homologues Bi₂O₂S and Bi₂O₂Te are also attracting significant attention. Remarkable photoelectric properties were demonstrated for Bi₂O₂S within the visible light range.^18,19 An et al. reported the photo-induced structural reconstruction and the recovery under dark conditions in the Bi₂O₂S nanoplates.²⁰ Recently, near-infrared photoelectric response and 2D ferroelectricity were discovered in the ultrathin Bi₂O₂S nanosheets.^21,22 Bi₂O₂Te was first investigated as a thermoelectric material.^23,24 More recently, ultrahigh Hall mobility has been demonstrated in Bi₂O₂Te ultrathin films at low-temperature,^25–27 similar to Bi₂O₂Se.² Besides, significant anisotropic magnetoresistance and out-of-plane ferroelectricity have been found in Bi₂O₂Te.^27,28 An atomically sharp interface between Bi₂O₂Te and its native oxide Bi₂TeO₆ has been fabricated via layer-by-layer O intercalative oxidation.²⁹ However, up to now, the physical properties of Bi₂O₂S and Bi₂O₂Te surfaces are rarely involved. Particularly, there is a lack of systematic understanding of how surface imperfections and reconstructions affect the physical properties of 2D Bi₂O₂S and Bi₂O₂Te.

By taking Bi₂O₂X (X = S, Se, Te) as model systems, we investigate the impacts of surface X vacancies (V_X) and surface reconstructions on the properties of the surfaces and 2D structures of Bi₂O₂X by using the first-principles method. For the (001) surfaces of Bi₂O₂X bulks, we find that the dimerization of V_X in the surface X layer is a general phenomenon, giving rise to a dimer-surface as the ground state, which is consistent with the surface structures determined by STM for Bi₂O₂Se. We also find that surface reconstructions depend on the thickness of Bi₂O₂X ultrathin films. For a monolayer, the zipper-surface is more stable, while the dimer-surface is generally more stable for thicker films. We analyze the structural and electronic properties of the surfaces to elucidate the origin of the stability.

2. Results and discussion

2.1. Ground-states of Bi₂O₂X (001) surfaces

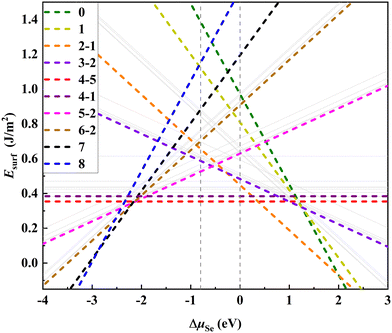
We first focus on the thermodynamic stability of the surfaces of Bi₂O₂X bulks. Taking Bi₂O₂Se as an archetype, we investigate the thermodynamic stability of the surfaces systematically for a series of surface V_Se including the 50%-V_Se structures found in experiments (i.e., the dimer- and zipper-surfaces). We use a 4 × 2 supercell model that expands four times along the x-axis and two times along the y-axis with respect to the unit cell. There are eight Se atoms in the surface Se-layer, allowing nine Se (or V_Se) compositions to be considered (Fig. 1b). We denote each of V_Se composition by a number n (0–8), which indicates the number of V_Se in the surface Se-layer, with the configurations 0 and 8 marking the Se- and Bi-terminated surfaces, respectively, as shown Fig. 1b and e. This model not only accounts for the dimer- and zipper-surfaces with 50% V_Se, but also allows us to consider the surfaces with other V_Se compositions. For each of V_Se composition, all possible arrangements of V_Se on the surface are considered, giving rise to several possible configurations for some compositions. These configurations are marked by two numbers n–m, with m differentiating the configurations for the n V_Se case, as shown in Fig. 1 and Fig. S1 (ESI†). To simulate the surface, a vacuum layer is imposed along z-axis. We calculate the surface energies to evaluate the thermodynamic stability of the surfaces (calculation methods in the ESI†). Test calculations indicate that slab thickness of four-layers can assure a reasonable convergence of the surface energies (Table S1 and discussion in the ESI†). Thus, four-layer slabs are used in simulating the surfaces.

Fig. 2 shows the surface energies of Bi₂O₂Se (001) surfaces as a function of Δμ_Se for a series of V_Se compositions The surface energies depend on Δμ_Se for non-stoichiometric surfaces, while being constants for stoichiometric surfaces, i.e., the configurations with 50% V_Se (4-m). We find that the dimer-surface (4-5) with 50% V_Se is the most stable with Δμ_Se varying from about −2 eV to 0 eV. For less-V_Se surfaces (0–3), their surface energies are reduced with increasing Δμ_Se, but are much higher than that of the dimer-surface even under the Se-rich conditions (i.e., Δμ_Se is close to 0 eV), suggesting that these surfaces are unstable. For more-V_Se surfaces (5–8), their surface energies exhibit inverse trends, implying that these surfaces may be more stable than the dimer-surface under Se-poor conditions (e.g., very low Δμ_Se like −3 eV). Notably, in a chemical potential range within which the bulk is stable (−0.799 eV < Δμ_Se < 0 eV, details in the ESI†), the ground state is the dimer-surface, which is consistent with the experimental characterization.¹⁴ Besides, the zipper-surface (4-1) is also more stable than other non-stoichiometric surfaces, although its surface energy is slightly higher than that of the dimer-surface. Therefore, stoichiometric surfaces display much higher stability than non-stoichiometric surfaces.

Fig. 2 Surface energies (E_surf) of the Bi₂O₂Se (001) surfaces for a series of V_Se compositions as a function of the chemical potential of Se (Δμ_Se, in eV units). Color dashed lines indicate the most stable configuration for each of V_Se composition. A set of gray lines parallel to a color dashed line stand for other meta-stable configurations. Two vertical dashed lines mark the chemical potential range within which the bulk is thermodynamically stable (−0.799 eV < Δμ_Se < 0 eV).

We also investigate the stability of Bi₂O₂S (001) and Bi₂O₂Te (001) surfaces and summarise the trend of the surface stability for Bi₂O₂X series. We utilize the dimer- and zipper-models to simulate the surface properties of these two homologues since these two types of surfaces, which have been identified experimentally,^14,17 exhibit better stability than other non-stoichiometric surfaces. The thicknesses of the slabs are four-layers, as used in Bi₂O₂Se. We make a comparison of the stability between two types of surfaces by evaluating the difference in total energies (ΔE, divided by the surface area) between the dimer and zipper surfaces. We find that the (001) surfaces of Bi₂O₂S and Bi₂O₂Te exhibit similar trends of stability to that of Bi₂O₂Se. The dimer-surface becomes the ground state after relaxation, while the unrelaxed zipper-surface is in a lower energy state. For unrelaxed surfaces, the ΔE values are 0.286 J m⁻², 0.259 J m⁻² and 0.192 J m⁻² for Bi₂O₂S, Bi₂O₂Se and Bi₂O₂Te, respectively. After relaxation, the ΔE values decrease to −0.021 J m⁻², −0.030 J m⁻² and −0.043 J m⁻² for Bi₂O₂S, Bi₂O₂Se and Bi₂O₂Te, respectively. This result clearly reveals that the dimer-surfaces are ground states for Bi₂O₂X (001) surfaces and structural relaxations have a significant impact on the surface stability. This not only explains the experimental observations for Bi₂O₂Se, but also demonstrates a universal rule for Bi₂O₂X.

2.2. Electronic structures of Bi₂O₂X (001) surfaces

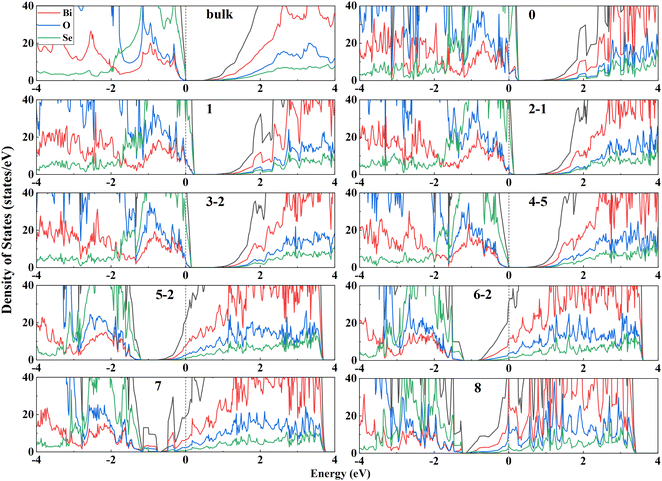
Surface electronic structures can provide deep insights into the surface stability. Fig. 3 shows the DOS of the most stable configuration for each of V_Se composition for Bi₂O₂Se (001) surfaces. It is seen that the less-V_Se surfaces (0–3) are doped with holes, as indicated by that the Fermi level crosses the top of the valence bands (VB). On the other hand, for more-V_Se surfaces (5–8), the bottom of conduction bands (CB) is filled with electrons. It is reasonable since these surfaces are unbalanced with charges. Particularly, two surfaces with full V_Se (8) and without any V_Se (0) are terminated with Bi-layer and Se-layer, respectively. The electronic structures of these two configurations are consistent with the calculated band structures of the Se- and Bi-terminated surfaces in a previous study.¹⁵ Note that these two surfaces are unstable, as indicated by the very large surface energies (Fig. 2). For the stoichiometric dimer-surface, the charges on the surface are balanced, making the surface semiconducting with a band gap. The band gap of the dimer-surface in the four-layer slab is 0.45 eV, which is slightly higher than the bulk value of 0.40 eV (the DOS of the bulk is shown in Fig. 3). This is consistent with an experimental observation that the band gap of Bi₂O₂Se bilayer is close to that of the bulk.³⁰ Thus, calculated electronic structures demonstrate that the stable surfaces should be stoichiometric and balanced in charges without hole-doped VB or electron-filled CB.

Fig. 3 Total (black lines) and projected (color lines) density of states (DOS) of the most stable surface for each composition. The DOS of the bulk is displayed as 16 times larger for a comparison with the surfaces. Zero energy indicates the Fermi level for non-stoichiometric surface or the maximum of VB for a stoichiometric surface.

We calculate the DOS of all configurations of stoichiometric Bi₂O₂Se (001) surfaces based on four-layer slabs, as shown in Fig. S2 (ESI†). The values of the band gaps for these surfaces are very close and in the range of 0.36–0.52 eV. Notably, there are no noticeable in-gap states for these surfaces even with many V_Se on the surfaces. This finding for the dimer-surface is consistent with experimental observations. For the dimer-surface, scanning tunneling spectroscopy (STS) spectra indicate a robust band gap without in-gap states, regardless of the surface positions (on Se atoms or V_Se).¹⁴ Thus, except for the dimer-surface, other surfaces with 50% V_Se also show robust, clean band gaps similar to the bulk (0.40 eV), indicating a universal character of the robustness of the band gaps against the surface V_Se. This seems to be very unexpected considering the dangling bonds and complex ordering of V_Se at the surfaces. For the dimer surface, this behavior was attributed to the ionicity of Bi₂O₂Se so that the formation of V_Se induces high doping-levels rather than the in-gap states.^14,31 It is worth noting that the (001) surfaces of Bi₂O₂S and Bi₂O₂Te exhibit similar features to Bi₂O₂Se (001) surfaces, i.e., no in-gap states occur to the stoichiometric surfaces with 50% V_X (Fig. S3 and S4, ESI†). These results indicate that in-gap states are absent for the Bi₂O₂X (001) surfaces with 50% vacancies of X anions, regardless of the arrangements of these vacancies. This implies that the electronic structures of Bi₂O₂X (001) surfaces show strong resistance to the order of the vacancies on the surfaces.

It is well-known that the band gaps of semiconductors are usually underestimated by the PBE functional. We make a comparison of the electronic structures obtained from PBE with those from HSE06 + SOC based on a typical small system, i.e., the Bi₂O₂Te zipper-bilayer (Fig. S5 and details in the ESI†). We find that the main features of the DOS are overall consistent with each other, indicating that PBE can provide a reasonable description about the electronic structures of Bi₂O₂X bulk and surfaces.

2.3. Origin of the stability of the dimer-surface

Now we might wonder the reason why the dimer-surfaces are the ground states in Bi₂O₂X. We analyze the energetics of cleaving surfaces and structural relaxation for Bi₂O₂X. The energy cost in cleaving the bulk into two surface parts is defined as cleavage energy (E_cl) and the energy released during surface relaxation is called relaxation energy (E_rel). In the first step, two surfaces are separated rigidly with the atomic positions fixed as in the bulk. Then, the surfaces are relaxed to the equilibrium states. Surface energy is contributed by the energies in these two processes, i.e. the sum of cleavage energy and relaxation energy (calculation methods in the ESI†). This decomposition allows us to separate the energy cost in producing rigid surfaces and the energy released from the surface relaxation.

Table 1 lists the cleavage energies and relaxation energies based on the dimer- and zipper-models for Bi₂O₂X (001) surfaces. For a comparison, beyond the dimer- and zipper-models, we also consider a uniform-surface model (the 4-9 model in Fig. S1, ESI†) in which V_X distribute evenly. For all compounds, the cleavage energies of the (001) surfaces decrease in order from the dimer- to zipper- to uniform-surfaces. Surface relaxation effects follow a similar decreasing trend, as indicated by the reduced absolute values of relaxation energies. The most stable configuration depends on the interplay of cleavage energy and relaxation energy. For Bi₂O₂X (001) surfaces, the dimer-surface exhibits a very strong relaxation effect, which offsets a large part of the cleavage energy cost and makes this type of surface ground state. In contrast, the relaxation effect of the uniform-surface is much weaker in comparison with the dimer-surface. For example, in Bi₂O₂Se, the relaxation energies of the dimer-, zipper- and uniform-surfaces are −0.663 J m⁻², −0.373 J m⁻² and −0.102 J m⁻², respectively. The difference in the relaxation energies between the dimer- and uniform-surfaces is −0.561 J m⁻², whose absolute value is larger than the difference (0.300 J m⁻²) in the cleavage energies. This leads to a lower surface energy of 0.354 J m⁻² for the dimer-surface and a higher surface energy of 0.614 J m⁻² for the uniform-surface. For the zipper-surface, both the cleavage energy and the relaxation energy are moderate. The difference in the relaxation energies between the dimer- and zipper-surfaces is −0.290 J m⁻² for Bi₂O₂Se, the absolute value of which is slightly larger than the difference (0.259 J m⁻²) in the cleavage energies. This results in a slightly lower surface energy for the dimer-surface. Therefore, the ground state character of the dimer-configurations of Bi₂O₂X (001) surfaces can be attributed to significant relaxation effects of the surfaces. Notably, the cleavage energies and relaxation energies show synchronous decreasing trends with X varying from S to Se to Te, resulting in close surface energies for three compounds.

Table 1 Cleavage energies (E_cl), relaxation energies (E_rel), and surface energies (E_surf) of Bi₂O₂X (001) surfaces in the dimer-, zipper- and uniform-models. All energetic quantities are in units of J m⁻²

Case	Dimer			Zipper			Uniform
	E cl	E rel	E surf	E cl	E rel	E surf	E cl	E rel	E surf
Bi2O2S	1.197	−0.863	0.334	0.911	−0.556	0.355	0.809	−0.269	0.541
Bi2O2Se	1.017	−0.663	0.354	0.758	−0.373	0.385	0.717	−0.102	0.614
Bi2O2Te	0.782	−0.462	0.320	0.590	−0.227	0.363	0.545	−0.047	0.498

---

Strong relaxation effects of the surfaces can be indicated by the changes of bond lengths and charge states. After structural relaxations, as shown in Fig. S6 and S7 (ESI†), the bond lengths of Bi–Se are reduced and the charge transfer is enhanced at the dimer- and zipper-surfaces of Bi₂O₂Se, suggesting stronger interaction strengths of surface ions and thus enhanced stability for the surfaces (a more detailed discussion in the ESI†). For Bi₂O₂S and Bi₂O₂Te, the dimer- and zipper-surfaces exhibit similar relaxation effects to those of Bi₂O₂Se, which are evidenced by the changes of bond lengths and charge states at the surfaces during the relaxation (Fig. S8–S11, ESI†). For instance, the lengths of surface Bi–S bonds are significantly reduced for both dimer- and zipper-surfaces in Bi₂O₂S (see Fig. S8 and S9, ESI†).

Based on the dimer-configurations, we obtain the surface energies of Bi₂O₂X (001) surfaces. The surface energy is moderate with a value of 0.354 J m⁻² for Bi₂O₂Se, which is much lower than those of perovskite oxide (001) surfaces (∼1 J m⁻²).³² The surface energies of Bi₂O₂S and Bi₂O₂Te (001) surfaces are close to that of Bi₂O₂Se (001) surface. Besides, the Bi₂O₂S (001) surface has a slightly lower surface energy than Bi₂O₂Se, which can be attributed to a stronger relaxation effect of the former.

2.4. Exfoliability of 2D Bi₂O₂X

Now we make a connection between the exfoliability of 2D Bi₂O₂X and the surface stability. We calculate the exfoliation energies (E_ex) of one-to-four layers by considering three types of surfaces (i.e., the dimer-, zipper- and uniform-surfaces) based on a rigorous method proposed Jung et al.³³ as shown in Fig. 4 (calculation details in the ESI† and structural models of 2D Bi₂O₂X in Fig. S12, ESI†). Generally, the lower exfoliation energy for a 2D structure, the higher stability for it, implying a larger possibility for it to be fabricated in experiments. Interestingly, the surface type with the lowest exfoliation energy depends on the thickness of 2D Bi₂O₂X. The exfoliation energies of Bi₂O₂Se and Bi₂O₂Te muti-layers in the dimer-model are the lowest in comparison with the zipper- and uniform-cases, indicating the best stability for the dimer pattern. This is also true for 2D Bi₂O₂S thicker than the bilayer. This result can be reasonably understood in that the surfaces of the bilayer, trilayer and quadruple-layer are like the surfaces of the bulks, giving rise to similar stability rules to the surfaces. This can also be evidenced from the fact that all of exfoliation energies converge to the double of the surface energies. This finding suggests that the energetic quantities of the surfaces such as surface energies are short-range quantities which are closely related to the very few atomic layers located at the surfaces and insensitive to the inner layers.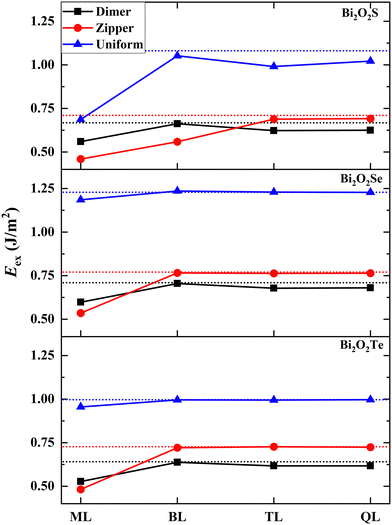

Fig. 4 Calculated exfoliation energies (E_ex, in the unit of J m⁻²) of monolayer (ML), bilayer (BL), trilayer (TL) and quadruple-layer (QL) for Bi₂O₂X. Three types of surfaces (i.e., the dimer-, zipper- and uniform-surfaces) are considered. The horizontal dot line indicates the double of the surface energy for each case. The E_ex values are also tabulated in Table S2 (ESI†).

However, the exfoliation energy of monolayer in the zipper-model is lower than those based on the dimer- and uniform-models, implying the higher stability of the zipper-monolayer. This is significantly different from that happens to thicker 2D structures and the surfaces. For bilayer Bi₂O₂S, the zipper-model is also favorable in energy. The relatively low exfoliation energies of Bi₂O₂X monolayer and Bi₂O₂S bilayer can be attributed to the special stability of these structures. We observe strong structural distortions in these structures, stabilizing these in lower energy states. Fig. S12d (ESI†) shows the structure of the Bi₂O₂Se zipper-monolayer in which 2 × 1 reconstruction emerges with alternating long and short Bi–Se bonds (3.390 and 2.806 Å) at the surface. This kind of structural distortions in the Bi₂O₂Se zipper-monolayer was also predicted in a previous study.³⁴ Our results provide an explanation for the zipper-type 2D structures found in experiments.¹⁷ In this experimental study, Wei et al. reported the sign of the existence of the Bi₂O₂Se zipper-monolayer at the position of line defects.

We make a comparison of the exfoliation energies of 2D Bi₂O₂X with those of common vdW 2D materials. The exfoliation energies of the most stable Bi₂O₂Se monolayer, bilayer and trilayer are calculated to 0.535 J m⁻² (or 33.4 meV Å⁻²), 0.705 J m⁻² (or 44.0 meV Å⁻²) and 0.678 J m⁻² (or 42.3 meV Å⁻²), respectively. Besides, the exfoliation energies of 2D Bi₂O₂S and Bi₂O₂Te are close to those of 2D Bi₂O₂Se. The exfoliation energies of monolayer and multi-layers for MoS₂, graphene, phosphorene and h-BN were calculated to be 17–32 meV Å⁻².³³ Thus, the exfoliation energies of the Bi₂O₂X monolayer and multi-layers are close to those predicted for common vdW 2D materials. Notably, the exfoliation energies of Bi₂O₂X monolayers are close to the upper bound of the exfoliation energy defining an easily exfoliable category of vdW 2D materials and lower than the exfoliation energy of potentially exfoliable category of vdW 2D materials.³⁵ These facts indicate that 2D Bi₂O₂X belong to easily fabricated 2D materials, even though the inter-layer binding interaction is of the non-vdW type. This finding is supported by a series of experiments where 2D Bi₂O₂S,²¹ Bi₂O₂Se,^1,2,36–39 and Bi₂O₂Te^25,26 were synthesized successfully.

3. Conclusions

In conclusion, we investigate the structural, energetic and electronic properties of Bi₂O₂X (001) surfaces systematically to understand the role that surface vacancies and surface reconstructions play in determining the thermodynamic stability and the electronic structures of the surfaces and 2D structures. We find that the dimerization of surface X-vacancies occurs in Bi₂O₂S and Bi₂O₂Te (001) surfaces, like that happening in Bi₂O₂Se. The origin of the stability of the dimer-surfaces can be attributed to strong relaxation effects of the surfaces. Interestingly, Bi₂O₂X (001) surfaces exhibit robust, clean band gaps against the order of surface X-vacancies. We also find that surface reconstructions depend on the thickness of Bi₂O₂X ultrathin films. For monolayer, the zipper-surface is more stable, while the dimer-surface is generally more stable for thicker films. This is different from that happening to vdW-type 2D materials, where monolayer and multi-layers are expected to be free of surface vacancies and thus share the same surface structure due to relatively weak inter-layer vdW interactions. Furthermore, the exfoliation energies of 2D Bi₂O₂X are found to be close to those of common vdW 2D materials, indicating that 2D Bi₂O₂X belong to easily fabricated 2D materials, even though the inter-layer binding interaction is of the non-vdW type. Our results provide important insights into understanding the properties of Bi₂O₂X, which lays a basis for further exploring the physical properties and device applications in Bi₂O₂X. Our work indicates that non-vdW 2D materials can exhibit more intriguing properties because of surface imperfections and reconstructions compared with vdW 2D materials.

4. Computational methods

We carried out all density functional theory (DFT) calculations by using the Vienna ab initio simulation package (VASP).^40,41 We utilized the projector-augmented-wave (PAW) method to describe the interaction between valence electrons and core.⁴² The generalized gradient approximation functional (PBE) was used as the exchange–correlation functional in the calculations. A cutoff energy of 600 eV was used for plane-wave expansion. A Monkhorst–Pack mesh of 8 × 8 × 3 was used for Bi₂O₂Se bulk.⁴³ A k-point grid of 8 × 8 × 1 was used for the 1 × 1 surface and scaled grids were used for expanded slabs. The convergence threshold of atomic forces was 0.001 eV Å⁻¹ for structure optimization. To simulate the surface, a vacuum layer of thicker than 20 Å is imposed along the z-axis. Two [Bi₂O₂] layers sandwiching one Se layer in the middle of the four-layers slabs are fixed to mimic the bulk. The optimized bulk structures utilized in building surface models are tetragonal phases for Bi₂O₂Se and Bi₂O₂Te, while it is the orthorhombic phase for Bi₂O₂S. More detailed information about the structural and electronic properties of Bi₂O₂X bulk was presented in our previous work.⁴⁴ All structure models are displayed in VESTA.⁴⁵ The calculation methods of energetic quantities including surface energy, cleavage energy, relaxation energy and exfoliation energy are presented in the ESI.†

Data availability

The main data supporting this article have been included as part of the ESI.† Other data are available from the authors upon reasonable request

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (11847150) and the Jiangxi Provincial Natural Science Foundation (20232BAB201029), and the University of Science and Technology of Jiangxi PhD Start-up Foundation (205200100527). This work was done using computing resources from Shanxi Supercomputing Center of China.

References

1. J. Wu, C. Tan, Z. Tan, Y. Liu, J. Yin, W. Dang, M. Wang and H. Peng, Nano Lett., 2017, 17, 3021–3026.
2. J. Wu, H. Yuan, M. Meng, C. Chen, Y. Sun, Z. Chen, W. Dang, C. Tan, Y. Liu, J. Yin, Y. Zhou, S. Huang, H. Q. Xu, Y. Cui, H. Y. Hwang, Z. Liu, Y. Chen, B. Yan and H. Peng, Nat. Nanotechnol., 2017, 12, 530.
3. H. Tian, T. Tu, X. Jin, C. Li, T. Lin, Q. Dong, X. Jing, B. Liu, R. Liu, D. Li, Z. Liu, Q. Li, H. Peng and B. Liu, J. Am. Chem. Soc., 2024, 146, 7324–7331.
4. T. Li, T. Tu, Y. Sun, H. Fu, J. Yu, L. Xing, Z. Wang, H. Wang, R. Jia, J. Wu, C. Tan, Y. Liang, Y. Zhang, C. Zhang, Y. Dai, C. Qiu, M. Li, R. Huang, L. Jiao, K. Lai, B. Yan, P. Gao and H. Peng, Nat. Electron., 2020, 3, 473–478.
5. J. Yin, Z. Tan, H. Hong, J. Wu, H. Yuan, Y. Liu, C. Chen, C. Tan, F. Yao, T. Li, Y. Chen, Z. Liu, K. Liu and H. Peng, Nat. Commun., 2018, 9, 3311.
6. Q. Fu, C. Zhu, X. Zhao, X. Wang, A. Chaturvedi, C. Zhu, X. Wang, Q. Zeng, J. Zhou, F. Liu, B. K. Tay, H. Zhang, S. J. Pennycook and Z. Liu, Adv. Mater., 2019, 31, 1804945.
7. U. Khan, Y. Luo, L. Tang, C. Teng, J. Liu, B. Liu and H.-M. Cheng, Adv. Funct. Mater., 2019, 29, 1807979.
8. B. Liu, Y. Zhao, D. Verma, L. A. Wang, H. Liang, H. Zhu, L.-J. Li, T.-H. Hou and C.-S. Lai, ACS Appl. Mater. Interfaces, 2021, 13, 15391–15398.
9. S. Xu, H. Fu, Y. Tian, T. Deng, J. Cai, J. Wu, T. Tu, T. Li, C. Tan, Y. Liang, C. Zhang, Z. Liu, Z. Liu, Y. Chen, Y. Jiang, B. Yan and H. Peng, Angew. Chem., Int. Ed., 2020, 59, 17938–17943.
10. J. K. Bae, H. H. Cho, H. Shin, Y. Kim, H. Ko, S. J. Lee, D. D. Megersa, G. T. Gudena, S. Chae, I. S. Cho and H. K. Yu, Sens. Actuators, B, 2023, 394, 134398.
11. S. Xu, C. Yang, Y. Tian, J. Lu, Y. Jiang, H. Guo, J. Zhao and H. Peng, ACS Sens., 2022, 7, 3764–3772.
12. A. Sirohi and J. Singh, IEEE. Nanotechnol., 2022, 21, 794–800.
13. M. T. Hossain, T. Jena, S. Debnath and P. K. Giri, J. Mater. Chem. C, 2023, 11, 6670–6684.
14. C. Chen, M. Wang, J. Wu, H. Fu, H. Yang, Z. Tian, T. Tu, H. Peng, Y. Sun, X. Xu, J. Jiang, N. B. M. Schröter, Y. Li, D. Pei, S. Liu, S. A. Ekahana, H. Yuan, J. Xue, G. Li, J. Jia, Z. Liu, B. Yan, H. Peng and Y. Chen, Sci. Adv., 2018, 4, eaat8355.
15. S. V. Eremeev, Y. M. Koroteev and E. V. Chulkov, Phys. Rev. B, 2019, 100, 115417.
16. S. W. Han, W. S. Yun, S. Seong, Z. Tahir, Y. S. Kim, M. Ko, S. Ryu, J.-S. Bae, C. W. Ahn and J. Kang, J. Phys. Chem. Lett., 2024, 15, 1590–1595.
17. Q. Wei, R. Li, C. Lin, A. Han, A. Nie, Y. Li, L.-J. Li, Y. Cheng and W. Huang, ACS Nano, 2019, 13, 13439–13444.
18. İ. A. KarİPer, Spectrochim. Acta, Part A, 2016, 163, 102–107.
19. X. Zhang, Y. Liu, G. Zhang, Y. Wang, H. Zhang and F. Huang, ACS Appl. Mater. Interfaces, 2015, 7, 4442–4448.
20. Y. An, Z. Xing, K. Zhu, H. Lin, H. Su and S. Yang, J. Phys. Chem. Lett., 2020, 11, 7832–7838.
21. R. Pathak, P. Dutta, K. Dolui, A. Vasdev, A. Ghosh, R. S. Roy, U. K. Gautam, T. K. Maji, G. Sheet and K. Biswas, Chem. Sci., 2024, 15, 7170–7177.
22. B. Chitara, T. B. Limbu, J. D. Orlando, Y. Tang and F. Yan, Nanoscale, 2020, 12, 16285–16291.
23. X. Tan, Y. Liu, K. Hu, G. Ren, Y. Li, R. Liu, Y.-H. Lin, J.-L. Lan and C.-W. Nan, J. Am. Ceram. Soc., 2018, 101, 326–333.
24. T. V. Quang and M. Kim, J. Appl. Phys., 2017, 122, 245104.
25. W. Ai, J. Chen, X. Dong, Z. Gao, Y. He, Z. Liu, H. Fu, F. Luo and J. Wu, Nano Lett., 2022, 22, 7659–7666.
26. H. Liu, R. Sun and X. Lu, Inorg. Chem., 2023, 62, 16752–16758.
27. X. Zou, R. Wang, M. Xie, F. Tian, Y. Sun and C. Wang, Nano Lett., 2023, 23, 11742–11748.
28. X. Zou, F. Tian, H. Liang, Y. Li, Y. Sun and C. Wang, ACS Nano, 2022, 16, 19543–19550.
29. X. Zou, H. Liang, Y. Li, Y. Zou, F. Tian, Y. Sun and C. Wang, Adv. Funct. Mater., 2023, 33, 2213807.
30. Y. Liang, Y. Chen, Y. Sun, S. Xu, J. Wu, C. Tan, X. Xu, H. Yuan, L. Yang, Y. Chen, P. Gao, J. Guo and H. Peng, Adv. Mater., 2019, 31, 1901964.
31. H. Fu, J. Wu, H. Peng and B. Yan, Phys. Rev. B, 2018, 97, 241203.
32. R. I. Eglitis, Integr. Ferroelectr., 2009, 108, 11–20.
33. J. H. Jung, C.-H. Park and J. Ihm, Nano Lett., 2018, 18, 2759–2765.
34. Z. Ge, W. Zhao, S. Yuan, Z. Gao, C. Hao, H. Ma, H. Ren and W. Guo, Appl. Surf. Sci., 2023, 611, 155528.
35. N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti and G. Pizzi, Nat. Nanotechnol., 2018, 13, 246–252.
36. X. Ding, M. Li, P. Chen, Y. Zhao, M. Zhao, H. Leng, Y. Wang, S. Ali, F. Raziq, X. Wu, H. Xiao, X. Zu, Q. Wang, A. Vinu, J. Yi and L. Qiao, Matter, 2022, 5, 4274–4314.
37. T. Li and H. Peng, Acc. Mater. Res., 2021, 2, 842–853.
38. Y. Liang, X. Zhou, W. Li and H. Peng, APL Mater., 2021, 9, 060905.
39. Y. Sun, J. Zhang, S. Ye, J. Song and J. Qu, Adv. Funct. Mater., 2020, 30, 2004480.
40. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
41. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
42. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
43. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192.
44. K. Gao, C. Hou and Y. Yang, J. Phys. Chem. C, 2024, 128, 2645–2655.
45. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03683b

---