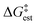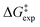Reactivity in Friedel–Crafts aromatic benzylation: the role of the electrophilic reactant

Abstract

Density functional theory is employed in understanding the reactivity in the TiCl₄ catalyzed Friedel–Crafts benzylation of benzene with substituted benzyl chlorides in nitromethane solvent. A series of ten substituted (in the aromatic ring) benzyl chlorides are characterized by theoretical reactivity indices. The theoretical parameters are juxtaposed to experimental relative rates of benzylation. It is established that the carbon–chlorine ionic bond dissociation energy and the Hirshfeld charge at the chlorine atom for the benzyl chlorides reactants – describe quite satisfactorily the reactivity trends. These results provide further insights into the factors governing reactivity in EAS reactions, which so far have been mostly focused on rate variations induced by changes in the structure of the aromatic substrate. The EAS benzylation investigated is quite unusual since, in contrast to most EAS reactions, the latest experimental kinetic results suggest that the aromatic substrate does not participate in the kinetic equation of the process. To shed more light on this unexpected result, we also conducted a theoretical study on the mechanistic pathway by applying M06-2X density functional computations combined with several basis sets: 6-311+G(d,p), 6-311+G(2df,2p), and def2-TZVPP. Because of the well-known difficulties in evaluating realistic free energy barriers for organic reactions, we tested two solvent models in determining the barrier for the TiCl₄-catalyzed Friedel–Crafts benzylation of benzene by benzyl chloride. Since all methods employed did not provide satisfactory results for the free energy barriers, we used a combination of theoretically estimated enthalpy barriers and the available (from kinetic experiments) entropy contribution. This approach enabled us to verify that indeed the rate of this EAS reaction does not depend on the nature of the aromatic substrate. The computations revealed the structure and relative energies of the critical structures along the mechanistic pathway. Four intermediates were established along the reaction route.

---

Introduction

The Friedel–Crafts electrophilic substitution of aromatic compounds provides effective routes for the synthesis of various alkylated or acylated systems, intermediates for further transformations, as well as numerous industrial products.^1–6 The kinetic and mechanistic studies of the Friedel–Crafts alkylation reactions have a long history.^5–12 In the present research we characterize the reactivity associated with a particular reaction from this class electrophilic aromatic substitution (EAS) reactions: the TiCl₄-catalyzed benzylation of benzene by benzyl chlorides in nitromethane solvent (eqn (1)). The kinetic results of Olah et al.⁷ provide a rare opportunity to investigate the role of the changing structure of the electrophilic reactant on the rate of an electrophilic aromatic substitution (EAS) reaction.So far, most studies on reactivity trends in EAS reactions have been centered on characterizing the rate variations induced by changes in the nucleophilic arene structures.^5,6,13–22 Extensive kinetic studies^7,11,12 on the reaction investigated form an excellent basis for consistent interpretation of the reactivity trends found. We apply density functional theory (DFT), aiming at quantifying the effects of structural variations in the electrophilic benzyl chloride reactants on the rates of the benzylation reaction. In addition, in the present research we report results from the computational modeling of the mechanistic pathway for the basic molecule from the benzyl chlorides series with the aim at providing deeper insights into the chemistry of this reaction. DeHaan et al.^11,12 reported an unusual result for an EAS reaction regarding the kinetics of the TiCl₄-catalyzed benzylation of benzene, toluene, and anisole by benzyl chloride in nitromethane solvent. The experiments of these authors suggested that the rate of these reactions does not depend on the arene substrate.

Early kinetic results^7–10 on the Friedel–Crafts alkylation revealed that depending on the type of reactants, catalyst, and solvent, alternative mechanistic pathways may be followed. The benzylation of arenes with substituted benzyl chlorides catalyzed by AlCl₃ in nitrobenzene suggested a displacement mechanism involving nucleophilic attack of the arene on the benzyl chloride-AlCl₃ initially formed complex.⁹ A third order kinetic equation was suggested:

Rate = k₃[RCl][AlCl₃][arene] (2)

For the gallium bromide-catalyzed alkylation of arenes, however, the kinetic results of Choi and Brown¹⁰ were more consistent with a rate-controlling step involving the formation of a Sigma complex (arenium ion) intermediate. First-order kinetics with respect to arene, alkyl bromide, and GaBr₃ was found:

Rate = k₃[RBr][GaBr₃][arene] (3)

The detailed investigation of Olah et al.⁷ on the electrophilic aromatic alkylation underlined the presence of different mechanistic routes for the reaction depending on the type of reactants, catalyst and the medium. The electrophilic alkylation of aromatics is usually described as passing via the classic S_EAr mechanism involving the formation of an arenium ion intermediate.⁶

The rate equation for the TiCl₄-catalyzed benzylation of benzene with benzyl chloride in nitromethane, reported by DeHaan et al.,^11,12 has the form:

Rate = k₃[PhCH₂Cl][TiCl₄]² (4)

For the benzylation with the weaker electrophile p-nitrobenzyl chloride, a fourth-order rate equation is found^11,12

Rate = k₄[ArCH₂Cl][TiCl₄]²[arene] (5)

Theoretical modeling of the mechanisms of EAS acylation and alkylation reactions have been also conducted.^23–27 Kim et al.²³ investigated the role of the Lewis acid interaction with the aromatic ring in the Friedel–Crafts reactions using the MP2/6-311++G(d,p) method. Yamabe et al.²⁵ applied B3LYP/6-31+(d,p) density functional theory computations in modeling the benzene acylation with acetyl chloride and the alkylation with 2-chloropropane. Catalysis by the Al₂Cl₆ dimer in simulated dichloromethane solvent was considered. For both reactions the formation of an arenium ion intermediate was shown to be an essential step. Gandon et al.²⁶ conducted M06-2X/6-311+G(2d,2p) computations in studying the GaCl₃-catalyzed methylation of benzene. These authors showed that a Ga₂Cl₆ adduct is a more active catalyst compared to the monomeric GaCl₃. Three alternative possible mechanistic pathways were considered. The results indicated that the reaction follows a concerted mechanism, which does not involve the formation of an arenium ion intermediate. Nogeira and Pliego²⁷ investigated the AlCl₃-catalyzed alkylation of benzene by isopropyl chloride in simulated benzene solution. The reaction pathways considering both AlCl₃ and Al₂Cl₆ catalysts were theoretically modeled using X3LYP/def2-SVP (ma-def2-SVP) computations. These authors showed that the energetically favored route involves catalysis by the Al₂Cl₆ adduct. The reaction pathway includes the formation of a CH₃CHCH₃⁺⋯Al₂Cl₇⁻ ion pair, which then reacts with benzene to form a Wheland (arenium ion) intermediate in the rate-controlling step of the process.

The chemical reactivity associated with electrophilic aromatic substitution (EAS) processes has been of prime interest over the long history of application of these reactions.^14–21 The progress on the topic has been presented in recent studies and reviews.^{17–21,28–36} Notably, theoretical parameters describing aromatic reactivity are frequently verified by comparisons with Hammett type substituent constants.^{13,17,18,21,28} Machine learning methods employing theoretically evaluated proton affinities that aimed at providing the experimental chemists with effective tools for the prediction of both relative reactivity and positional selectivity were also proposed.^34–36

As mentioned, we apply in the present research theoretically derived quantities characterizing the role of the electrophilic reactant on the rates of benzylation of benzene with substituted in the ring benzyl chlorides. The detailed experimental study of Olah et al.⁷ on the rates of the Lewis acid catalyzed benzylation of benzene and toluene with substituted benzyl chlorides provides an excellent platform to test the performance of theoretically derived quantities in describing reactivity. In Table 16 of ref. 7 these authors present results on the relative rates for the competitive benzylation of benzene by benzyl chloride and substituted in the aromatic ring derivatives under catalysis of TiCl₄ in nitromethane solvent. These kinetic results are employed in the present study as a basis for assessment of the applicability of theoretically derived parameters in describing the reactivity trends for these reactions. The interpretation of reactivity patterns is strongly associated with the mechanism of the reaction of Friedel–Crafts benzylation considered. We, therefore, report first the mechanistic features of this reaction.

Computational methods

The computational results discussed in most detail in the present research were conducted using the M06-2X density functional³⁷ combined with the 6-311+G(d,p) basis set.^38,39 This level of theory has been shown to provide reliable information on the energetics and mechanistic features of organic reactions.^40–44 To assess the influence of size and type of the basis set, we applied also the 6-311+G(2df,2p)^38,39 and def2-TZPVPP⁴⁵ basis sets with the M06-2X functional in evaluating the critical structures along the reaction paths. To assess the potential additional influences of dispersion effects on the computed reaction barriers we also performed M06-2X(D3)/6-311+G(d,p) computations using the zero-damping D3 correction.⁴⁶ Harmonic vibrational frequencies were calculated to verify that the optimized structures are true minima or saddle points on the potential energy surfaces. The effects of the nitromethane solvent were modeled using the CPCM method.⁴⁷ In view of the difficulties in evaluating reliable estimates of the entropy contributions to free energies,⁴⁸ we also tested the SMD solvent model of Marenich, Cramer, and Truhlar.⁴⁹ The computations employed ultrafine (99 590) integration grids and tight SCF convergence. The intrinsic reaction coordinate (IRC) method⁵⁰ was applied in connecting the critical structures along the reaction path for the TiCl₄ catalyzed Friedel–Crafts benzylation of benzene in nitromethane. The IRC computations employed the M06-2X/6-311+G(d,p) theoretical method. All computations were conducted with the Gaussian16 suite of programs.⁵¹

Results and discussion

Mechanism of benzylation

As discussed above, the kinetic equations for the TiCl₄ catalyzed benzylation of arenes in nitromethane derived by DeHaan et al.^11,12 differ substantially from earlier kinetic results referring to Friedel–Crafts benzylation employing other Lewis acids, such as AlCl₃, GaCl₃, and FeCl₃.^2,7–10 We conducted transition state theory computations on the potential energy landscapes of two possible reaction paths: (a) catalysis by two TiCl₄ molecules; (b) catalysis by a single TiCl₄ molecule. As mentioned, the basic approach in modeling the potential energy surfaces employed M06-2X/6-311+G(d,p) computations. To obtain more accurate energetics we also conducted M06-2X/6-311+G(2df,2p) and M06-2X/def2-TZVPP computations on the potential energy surface. Considering the paramount difficulties in the theoretical evaluation of the entropy contributions to free energies,^48,52,53 we present in Tables 1 and 2 the obtained theoretical estimates of the enthalpy shifts along the potential energy surfaces. The theoretical predictions of the free energy changes along the reaction pathway for all methods employed turned out highly overestimated (see Table S1 in the ESI†) compared to the experimental value reported by DeHaan et al.¹² To avoid uncertainties associated with the theoretical evaluation of the entropy contribution to free energy barriers,⁴⁸ we adopted a somewhat unusual approach. We discuss in the text the variations of the calculated ΔH^‡ values accompanied by discussion of the potential contributions to the free energies of the experimentally determined entropy shift ΔS^‡ for the reaction considered, ΔS^‡ = 78 J (deg mol)⁻¹, as reported by DeHaan et al.¹² The contribution from the TΔS^‡ term to the free energies for standard conditions is then −5.6 kcal mol⁻¹. This approach allows us to obtain more realistic comparisons of the barriers associated with the two alternative reaction paths (involving one or two TiCl₄ catalyst) considered. Similarly, the discussion of the relative heights of the sequential transition states along the same reaction route is based also on more solid grounds.

Table 1 Changes in enthalpies (in kcal mol⁻¹) associated with transition states and products for the TiCl₄-catalyzed benzylation of benzene in nitromethane along the route involving two catalyst molecules

Theoretical approach	ΔH
	TS1	TS2	P
a Using zero-damping D3 dispersion correction (ref. 46). b From ref. 12.
CPCM M06-2X/6-311+G(d,p)	7.5	−0.8	−7.9
CPCM M06-2X(D3)/6-311+G(d,p)^a	6.5	−2.7	−8.2
SMD M06-2X/6-311+G(d,p)	−2.1	−11.7	−7.7
CPCM M06-2X/6-311+G(2df,2p)	7.9	0.5	−7.5
CPCM M06-2X/def2-TZVPP	9.9	3.8	−7.8
Exp. value^b	12.7	—	—

---

Table 2 Reactants enthalpy and free energy shifts along the reaction pathway for the Friedel–Crafts benzylation of benzene with benzyl chloride. The results reflect catalysis by two molecules TiCl₄. The theoretical values are from M06-2X/6-311+G(d,p) computations

Structure	ΔH	^a	^b
a In this research, ΔG(est.) for TS1 and TS2 are obtained by summing the theoretical enthalpy shifts and the experimental TΔS contribution to the free energy shifts. The experimental value for ΔS of 78 J (deg mol)^−1 determined by DeHaan et al. (ref. 12) is employed. b From ref. 12.
R	0.0	0.0
Pre-reaction complex	−4.1	—
TS1	7.5	13.1	18.3
I2	−1.6	—
TS2	−0.8	4.8
I3 σ-complex	−3.8	—
P	−7.9	—

---

DeHaan et al.¹² discussed two distinct steps of the TiCl₄-catalyzed benzylation of benzene with benzyl chloride in nitromethane. Dissociation of the benzyl chloride and formation of a carbenium ion take place at the first step. These authors consider that this is the rate-controlling step of the reaction. It involves the electrophile and two molecules of the catalyst. At the second step, the formed ion interacts with the benzene substrate. DeHaan et al. assumed that this step results in the formation of a σ-complex intermediate. Removal of a proton leads to the final products. Still, there are several questions regarding the mechanism of the reaction: (a) How is the process initiated? (b) Does the rate-controlling step involves one or two TiCl₄ molecules? (c) What is the structure of potential intermediates? (d) Does the reaction route involves a Sigma complex intermediate?

It is of considerable interest to compare how the different levels of theory employed perform in predicting the barrier heights of the reaction investigated. Table 1 presents the enthalpy shifts associated with the two found transition states, theoretically estimated from the different methods applied. According to DeHaan et al.¹² the enthalpy shift associated with the dissociation of the C–Cl bond is 12.7 kcal mol⁻¹.¹²Table 1 shows that all three methods employing the CPCM simulation of the nitromethane solvent produce results for the highest energy transition state that are in reasonable agreement with the experimental enthalpy barrier. The M06-2X employing the largest basis set (def2-TZVPP) produces an enthalpy barrier (9.9 kcal mol⁻¹) that is in close correlation with the experimental ΔH^‡ value. In contrast, the application of the SMD solvation model⁴⁷ resulted in an enthalpy shift in poorer agreement with the experiment (Table 1). The application of the Grimme⁴⁶ zero-damping D3 dispersion correction reduces the TS1 enthalpy barrier by 1 kcal mol⁻¹ (Table 1). For the TS2 transition state, the dispersion corrections lead to a ΔH^‡ value, which is nearly 2 kcal mol⁻¹ lower. The enthalpy shifts associated with TS2 do not compare well with the experimental value. In brief, the theoretical computations conducted support the conclusions of DeHaan et al.¹² regarding the rate-controlling step of the reaction. Since all IRC computations were performed using the M06-2X/6-311+G(d,p) computations, in the subsequent section we discuss the found critical structures – intermediates and transition states – as obtained at this level of theory.

Benzylation of benzene catalyzed by two molecules TiCl₄. It is important to consider how the reaction begins. Ritter⁵⁴ showed that dimers of neutral TiCl₄ do not exist at ambient temperature. This author found by IR spectroscopy neutral dimers only at cryogenic temperatures. It is, therefore, expected that the initial interaction would be between the electrophilic reactant (benzyl chloride) and a single molecule of the catalyst to form a pre-reaction complex. This complex is then able to interact with a second catalyst molecule, thus starting the process leading to the first transition state (TS1). The optimized structures of the pre-reaction complex and TS1 are illustrated in Fig. 1. Forward IRC computations from TS1 reveal the formation of an intermediate (I1) containing an ion pair of a carbenium ion and a Ti₂Cl₉⁻ anion. (Fig. 1 and Table 2). The process then continues with the interaction of the I1 complex with the aromatic substrate (benzene). At the initial stage of this interaction, a second intermediate (I2) is formed. Backward IRC computations from the second transition state reveal the structure of I2. The reduced energy of I2 reflects the initial interaction of the I1 intermediate with the benzene molecule (Fig. 1). The reaction then proceeds toward the second transition state (TS2). TS2 reflects the formation of a carbon–carbon bond between the carbenium ion and the benzene substrate under catalysis by the dimeric Ti₂Cl₉⁻ ion. The normal coordinate corresponding to TS2 reveals shortening of the distance between the positively charged CH₂ group and the benzene substrate and the formation of the C–C bond between the two principal reactants. Importantly, forward IRC computations from TS2 reveal the formation of a Sigma complex intermediate (I3) (Fig. 1).

Fig. 1 Critical structures and enthalpy variations (in kcal mol⁻¹) along the reaction pathway for benzylation catalyzed by two TiCl₄ molecules in simulated nitromethane solvent. All from M06 2X/6-311+G(d,p) computations. Energies are relative to reactants (benzene and benzyl chloride) and two TiCl₄ molecules.

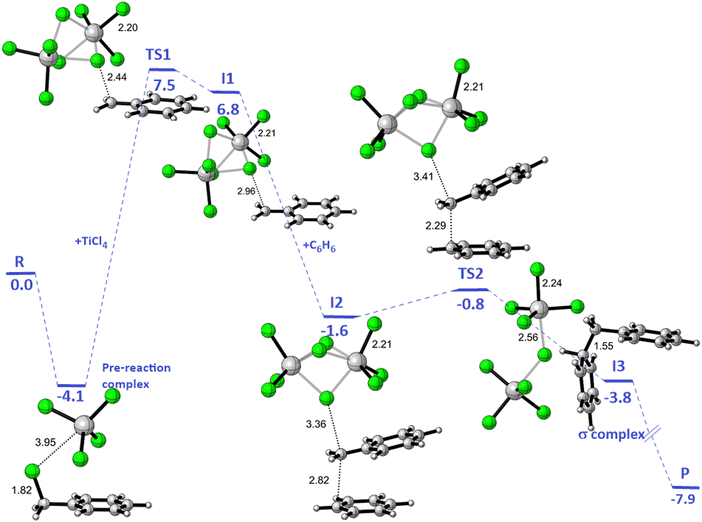
The enthalpy shifts accompanying the different steps of the reaction are provided in Table 2 and illustrated in Fig. 1. The transition state for the last step of the reaction – the removal of a proton – could not be located. Similar problems have been encountered in attempts to locate analogous transition states for other EAS reactions.²⁰ Liljenberg et al.²⁰ emphasized that the proton transfer is usually a low energy step. The results obtained in the present research clearly show that the rate-controlling step of the reaction is the dissociation of the carbon–chlorine bond in the benzyl chloride and formation of a carbenium ion. The interpretation considering the estimated free energy barrier 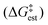confirms this finding. The theoretical enthalpy changes combined with the experimental TΔS contribution results in a ΔG^‡ barrier value of 13.1 kcal mol⁻¹ (Table 2). A more accurate value for this barrier comes from the M06-2X/def2-TZVPP computations (Table 1). The ΔG^‡ value for the reaction becomes 15.6 kcal mol⁻¹, in good accord with the experimentally determined barrier of 18.3 kcal mol⁻¹.¹² The fully theoretical computed ΔG^‡ value for TS1 from M06-2X/6-311+G(d,p) computations is 29.7 kcal mol⁻¹ (see Table S1 in ESI†). The contribution from the TΔS^‡ term is significantly overestimated when compared to the experimentally determined value. Overall, the results obtained clearly indicate that the TS1 barrier, associated with the dissociation of the C–Cl bond in the electrophilic reactant, governs the rate of the reaction. The reaction pathway includes four intermediates. In contrast to previous considerations, the initial attack does not involve a TiCl₄ dimer but a single catalyst TiCl₄ molecule.

Benzylation of benzene catalyzed by a single molecule of TiCl₄. Although less likely, we tested also the possibility of a mechanistic pathway for benzylation involving a single catalyst molecule. A third order kinetics of the type presented in eqn (2) has been discussed for alkylation reactions using more active catalysts.^7–10 For the benzylation catalyzed by TiCl₄ in nitromethane medium, however, the theoretical modeling disproved the possibility for a third order kinetics corresponding to eqn (2). Instead, the theory predicts a second order kinetics involving the benzyl chloride and the TiCl₄ molecule. Two distinct transition states on the potential energy surface, TS1 and TS2, are found. The first step involves interaction of the electrophile (benzyl chloride) with the catalyst resulting in the formation of a carbenium ion. The distinctly lower energy TS2 transition state corresponds to the formation of a C–C bond between the carbenium ion and the benzene molecule. The energies associated with this mechanistic route are given in Table S2 of the ESI.† Notably, the barrier associated with the formation of a carbenium ion along this pathway is 4.8 kcal mol⁻¹ higher compared to the mechanism involving catalysis by two TiCl₄ molecules (Table 2). Thus, the possibilities for a second order kinetics for the TiCl₄ catalyzed benzylation in nitromethane are rejected. As in the case of catalysis by two TiCl₄ molecules, participation of the aromatic substrate in the rate-controlling step of the reaction is not confirmed.

Reactivity trends

Theoretical reactivity indexes.
C–Cl dissociation energy (E_diss). The kinetic data of DeHaan et al.^11,12 for the TiCl₄ catalyzed benzylation of benzene in nitromethane show that the rate-controlling step of the reactions involves dissociation of the C–Cl bond in the electrophilic reactant. Our theoretical modeling confirmed this result. It appears, therefore, that the ionic C–Cl bond dissociation energy (E_diss) in the series of benzyl chlorides may well describe the experimentally determined kinetic trends. We estimated theoretically the dissociation energies for the series of the ten substituted in the aromatic ring benzyl chlorides considered (Table 3). These quantities were then juxtaposed to the experimental relative rates.

Table 3 Experimental relative rates^a and theoretical reactivity parameters^b for the TiCl₄ catalyzed benzylation of benzene by substituted benzyl chlorides in nitromethane

RC6H4CH2Cl	k R/kH^a	log kR/kH	E diss (kcal mol^−1)	q(Cl)^d (e)
a From ref. 7. b Theoretical parameters from M06-2X/6-311+G(2df,2p) computations. c Ionic dissociation energies for substituted benzyl chlorides. d Hirshfeld charge at the chlorine atom in ArCH2Cl. e Absolute values of correlation coefficients.
o-F	0.15	−0.8239	44.83	−0.1338
m-F	0.08	−1.0969	47.38	−0.1330
p-F	1.29	0.1106	41.28	−0.1407
o-Cl	0.07	−1.1549	46.49	−0.1343
m-Cl	0.06	−1.2219	47.56	−0.1321
p-Cl	0.22	−0.6576	43.14	−0.1360
H	1	0	42.94	−0.1412
o-CH3	3.23	0.5092	40.80	−0.1319
m-CH3	1.29	0.1106	42.10	−0.1435
p-CH3	12.4	1.09342	38.12	−0.1463
Correlation coef.^e with log kR/kH			0.968	0.971

---

Hirshfeld charges. Hirshfeld charges⁵⁵ at the reactive carbon centers in aromatic substrates were shown to correspond very well to theoretically estimated reaction barriers for the BF₃ catalyzed electrophilic chlorination of an extended series of substituted benzenes.⁵⁶ It was also demonstrated that Hirshfeld charges at the carbon atoms correlate strongly with the Hammett constants for substituted benzenes.⁵⁷ This type of population analysis has been successfully applied in rationalizing properties of various molecular systems (see, e.g. ref. 58 and 59). In the present research, the aromatic substrate is just the benzene molecule. Nonetheless, it was of interest to test whether this type of atomic charges would provide insights into the reactivity trends for systems, where the changes of structures are in the electrophile.

Table 3 presents the experimental relative rates for the benzylation of benzene with benzyl chloride and nine ring substituted derivatives as determined by Olah et al.⁷ The reactivity indexes are evaluated using DFT computations at the M06-2X/6-311+G(2df,2p) level, including CPCM modeling of the nitromethane solvent. As may be expected, in accordance with the rate equation (eqn (3)), the changes in the structure of the electrophile will lead to substantial differences in the relative rates of benzylation compared to the rate for the parent electrophile (benzyl chloride). The theoretically evaluated reactivity parameters are shown in Table 3. In most cases, the electron withdrawing chlorine and fluorine aromatic substituents cause strengthening of the C–Cl bond in the CH₂Cl moiety. The stronger C–Cl bonds in these compounds lead to higher bond dissociation energies (E_diss), resulting in slower reaction rates. Somewhat surprizingly, the p-F substituent increases the reactivity (Table 3). This influence is well reflected in the computed C–Cl dissociation energy (E_diss = 41.3 kcal mol⁻¹), which is lower than in the unsubstituted benzyl chloride (E_diss = 42.9 kcal mol⁻¹). The strong hyperconjugation effect of p-F group evidently overwhelms the reverse inductive (and through-space) influences of the same substituent. As expected, the hyperconjugation effects of the methyl group in the methyl substituted derivatives, in particular the para-methylbenzyl chloride, cause lowering of the C–Cl bond dissociation energies and, respectively, higher reaction rates. Altogether, the shifts in dissociation energies are in quite good accord with the experimental trends of relative rates (Table 3).⁷ The dependence between log k_R/k_H and E_diss is illustrated in Fig. 2.

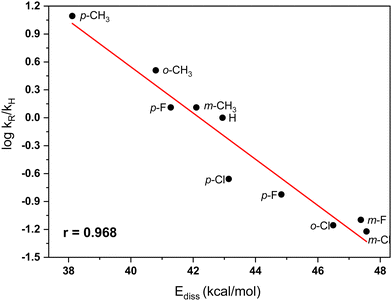Fig. 2 Plot of the dependence between C–Cl ionic bond dissociation energies in substituted benzyl chlorides and relative rates (ref. 7) of the TiCl₄-catalyzed Friedel–Crafts benzylation of benzene in nitromethane solvent.

The partial charge at the chlorine in the ArCH₂Cl molecules is expected to influence the interaction between the TiCl₄ catalyst and the electrophilic reactants. A good correlation between relative rates and Hirshfeld charges at the chlorine atom of the CH₂Cl group was found (r = 0.971). The relationship established shows again that Hirshfeld charges provide a useful theoretical approach in rationalizing molecular properties (see, e.g. ref. 56–59). Fig. 3 shows the plot between charges at the chlorine center and the rates of benzylation. An outlier for this correlation is the charge at the chlorine atom in the o-CH₃ derivative. A possible hydrogen bonding interaction between the chlorine and a methyl C–H bond may explain the deviation.

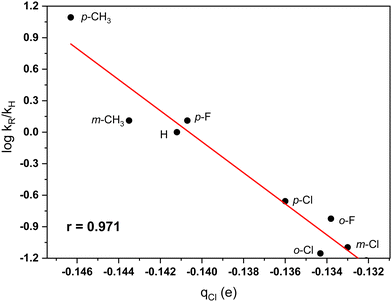Fig. 3 Plot of the dependence between Hirshfeld charges at the chlorine of the CH₂Cl group in substituted benzyl chlorides and relative rates (ref. 7) of the TiCl₄-catalyzed Friedel–Crafts benzylation of benzene in nitromethane solvent.

An interesting case for this type of Friedel–Crafts benzylation is the reaction involving p-nitrobenzyl chloride. The computed (at the same level of theory) C–Cl ionic dissociation energy for this derivative is 54.6 kcal mol⁻¹, higher than all values shown in Table 3. The strong electron-withdrawing effects of the nitro group invokes strengthening of the C–Cl bond. Based on this result, one might expect that the rate of the p-nitrobenzylation may also be determined by the C–Cl dissociation energy. However, the form of the kinetic equation (eqn (5)) suggests a very different mechanistic pathway for this reaction, with participation of the arene in the rate-controlling step. The Hirshfeld charge on the CH₂Cl chlorine in the p-nitrobenzyl chloride is −0.12 e. This value for the partial charge is less favorable for the initial interaction between the p-nitrobenzyl chloride and the catalyst.

The application of bond dissociation energy as a reactivity index for the Friedel–Crafts benzylation reactions investigated proved quite appropriate considering the mechanistic features of the reaction. The good correlations between relative rates and the theoretical reactivity parameters indicate that the ten TiCl₄-catalyzed benzylation reactions considered follow the same mechanistic route.

Conclusions

The experimental relative rates⁷ of the TiCl₄-catalyzed Friedel–Crafts benzylation of benzene by benzyl chloride and a series of ring substituted derivatives are investigated based on results from theoretical modeling of the mechanism of the reaction. Density functional theory computations employing the M06-2X functional combined with several types of basis sets and two alternative solvent models reveal the potential energy landscape for the basic reaction from the series. The usual difficulties in evaluation free energy barriers in solution are avoided by applying theoretically evaluated enthalpy shifts combined with experimental¹² entropy contributions to arrive at physically plausible potential energy surface. Our comprehensive mechanistic DFT computations reveal full details of the reaction pathway, including the structures of transition states as well as of four intermediates. Contrary to previous assumptions, the present results show that while the rate-controlling transition state involves two catalyst molecules, the initial interaction is between the electrophile and a single TiCl₄ molecule.

On the basis of the revealed mechanistic features, the reactivity trends for the series of reactions investigated are rationalized with the aid of reactivity descriptors. Most significantly, the computed C–Cl ionic dissociation energies for the benzyl chlorides correlate strongly with the relative rates of benzylation, thus confirming that the kinetics is governed by this process. Quite satisfactory correlations also exist between the experimental relative rates of benzylation⁷ and theoretically evaluated Hirshfeld charges at the reacting chlorine atom.

Data availability

The data supporting this article have been included in the ESI.†

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The research in Sofia is financed by the European Union-NextGenerationEU, through the National Recovery and Resilience Plan of the Republic of Bulgaria, project SUMMIT BG-RRP-2.004-0008-C01; the research in Georgia was supported by Department of Energy, Computational and Theoretical Chemistry Program, Contract DE-SC0018412.

References

1. (a) C. Friedel and J. M. Crafts, Sur Une Nouvelle Méthode Générale de Synthèse d’Hydrocarbures, d’Acétones, etc., Compt. Rend., 1877, 84, 1392–1395; (b) C. Friedel and J. M. Crafts, Sur Une Nouvelle Méthode Générale de Synthèse d’Hydrocarbures, d’Acétones, etc., Compt. Rend., 1877, 84, 1450–1454.
2. G. A. Olah, Friedel–Crafts and Related Reactions, Wiley, New York, 1963.
3. R. M. Roberts and A. A. Khalaf, Friedel–Crafts Alkylation Chemistry, Marcel Dekker, New York, 1984.
4. M. Rueping and B. J. Nachtsheim, A Review of New Developments in the Friedel–Crafts Alkylation – From Green Chemistry to Asymmetric Catalysis, Beilstein J. Org. Chem., 2010, 6, 6.
5. M. B. Smith and J. March, March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, Wiley, New York, 2007.
6. F. A. Carrey and R. J. Sandberg, Advanced Organic Chemistry. Part A: Structure and Mechanisms, Springer, New York, 5th edn, 2006.
7. G. A. Olah, S. Kobayashi and M. Tashiro, Aromatic Substitution. XXX. Friedel–Crafts Benzylation of Benzene and Toluene with Benzyl and Substituted Benzyl Halides, J. Am. Chem. Soc., 1972, 94, 7448–7461.
8. H. Jungk, C. R. Smoot and H. C. Brown, Kinetics of Methylation and Ethylation of Benzene and Toluene in 1,2,4-Trichlorobenzene under the Influence of Aluminum Bromide: Mechanism of the Alkylation Reaction, J. Am. Chem. Soc., 1956, 78, 2185–2190.
9. H. C. Brown and M. Grayson, Kinetics of the Reaction of Representative Benzyl Halides with Aromatic Compounds: Evidence for a Displacement Mechanism in the Friedel–Crafts Reaction of Primary Halides, J. Am. Chem. Soc., 1953, 75, 6285–6292.
10. S. U. Choi and H. C. Brown, Kinetic and Relative Rates of the Gallium Bromide-Catalyzed Reaction of Alkyl Bromides with Aromatic Compounds in 1,2,4-Trichlorobenzene Solution, J. Am. Chem. Soc., 1963, 85, 2596–2600.
11. F. P. DeHaan, G. L. Delker, W. D. Covey, J. Ahn, M. S. Anisman, E. C. Brehm, J. Chang, R. M. Chicz, R. L. Cowan, D. M. Ferrara, C. H. Fong, J. D. Harper, C. D. Irani, J. Y. Kim, R. W. Meinhold, K. D. Miller, M. P. Roberts, E. M. Stoler, Y. J. Suh, M. Tang and E. L. Williams, Electrophilic Aromatic Substitution. 8. A Kinetic Study of the Friedel–Crafts Benzylation Reaction in Nitromethane, Nitrobenzene, and Sulfolane. Substituent Effects in Friedel–Crafts Benzylation, J. Am. Chem. Soc., 1984, 106, 7038–7046.
12. F. P. DeHaan, W. H. Chan, J. Chang, T. B. Cheng, D. A. Chiriboga, M. M. Irving, C. R. Kaufman, G. Y. Kim, A. Kumar, J. Na, T. T. Nguyen, D. T. Nguyen, B. R. Patel, N. P. Sarin and J. H. Tidwell, Kinetic Studies of the TicCl₄ Catalyzed Reactions of Benzyl Chloride, p-Xylyl Chloride, and p-Nitrobenzyl Chloride with Benzene and Anisole in Nitromethane and Dichloromethane, J. Am. Chem. Soc., 1990, 112, 356–363.
13. L. P. Hammett, Some Relations Between Reaction Rates and Equilibrium Constants, Chem. Rev., 1935, 17, 125–136.
14. H. H. Jaffé, A Reexamination of the Hammett Equation, Chem. Rev., 1953, 53, 191–261.
15. C. Hansch, A. Leo and R. W. Taft, A Survey of Hammett Substituent Constants and Resonance and Field Parameters, Chem. Rev., 1991, 91, 165–195.
16. K. Fukui, T. Yonezawa and H. Shingu, A Molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons, J. Chem. Phys., 1952, 20, 722–725.
17. J. J. Brown and S. L. Cockroft, Aromatic Reactivity Revealed: Beyond Resonance Theory and Frontier Orbitals, Chem. Sci., 2013, 4, 1772–1780.
18. B. Galabov, S. Ilieva, G. Koleva, W. D. Allen, H. F. Schaefer and P. V. R. Schleyer, Structure-Reactivity Relationships for Aromatic Molecules: Application of the Electrostatic Potential at Nuclei and Electrophile Affinity Electronic Indices, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 37–55.
19. T. Brinck and M. Liljenberg, in Arene Chemistry: Reaction Mechanisms and Methods for Aromatic Compounds, ed. J. Mortier, Wiley, Hoboken, NJ, 2016, ch. 4.
20. M. Liljenberg, H. J. Stenlid and T. Brinck, Theoretical Investigation into Rate-Determining Factors in Electrophilic Aromatic Halogenation, J. Phys. Chem. A, 2018, 122, 3270–3279.
21. B. Galabov, S. Ilieva, D. Cheshmedzhieva, V. Nikolova, V. A. Popov, B. Hadjieva and H. F. Schaefer III, Mini-review on Structure-Reactivity Relationship for Aromatic Molecules: Recent Advances, ACS Omega, 2022, 7, 8199–8208.
22. (a) P. R. Rablen and A. Yett, The Relative Favorability of Placing Substituents Ortho or Para in the Cationic Intermediate for Electrophilic Aromatic Substitution, J. Phys. Org. Chem., 2022, e4457; (b) A. Yett and P. R. Rablen, A G4 Approach to Computing the Hammett Substituent Constants σ_p, σ_m, σ⁻, σ⁺, and σ⁺_m, J. Phys. Org. Chem., 2022, e4436.
23. P. Tarakeshwar, J. Y. Lee and K. S. Kim, Role of Lewis Acid (AlCl₃) – Aromatic Ring Interactions in Friedel–Crafts Reactions; An Ab Initio Study, J. Phys. Chem. A, 1998, 102, 2253–2258.
24. S. Csihony, H. Mehdi, Z. Homonnay, A. Vertes, O. Farkas and I. T. Horvath, In Situ Spectroscopic Studies Related to the Mechanism of the Friedel–Crafts Acetylation of Benzene in Ionic Liquids Using AlCl₃ and FeCl₃, J. Chem. Soc., Dalton Trans., 2002, 5, 680–685.
25. S. Yamabe and S. Yamazaki, A Remarkable Difference in the Deprotonation Steps of the Friedel–Crafts Acylation and Alkylation Reactions, J. Phys. Org. Chem., 2009, 22, 1094–1103.
26. S. Yang, C. Bour and V. Gandon, Superelectrophilic Gallium(III) Homodimers in Gallium Chloride Mediated Methylation of Benzene: a Theoretical Study, ACS Catal., 2020, 10, 3027–3033.
27. I. C. Nogueira and J. R. Pliego Jr., Friedel–Crafts Reaction: Theoretical Study of the Mechanism of Benzene Alkylation with Isopropyl Chloride Catalyzed by AlCl₃ and Al₂Cl₆, J. Braz. Chem. Soc., 2023, 34, 194–200.
28. (a) T. M. Krygowski and B. T. Stepien, Sigma- and pi-electron delocalization: focus on substituent effects, Chem. Rev., 2005, 105, 3482–3512; (b) H. Szatylowicz, T. Siodla, O. A. Stasyuk and T. M. Krygowski, Towards Physical Interpretation of Substituent Effects: The Case of meta- and para- substituted Anilines, Phys. Chem. Chem. Phys., 2016, 18, 1711–1721.
29. B. Galabov, G. Koleva, P. V. R. Schleyer and H. F. Schaefer III, Electrophile Affinity: Quantifying Reactivity for the Bromination of Arenes, J. Org. Chem., 2010, 75, 2813–2819.
30. M. Liljenberg, J. H. Stenlid and T. Brinck, Mechanism and Regioselectivity of Electrophilic Aromatic Nitration in Solution: The Validity of the Transition State Approach, J. Mol. Model., 2017, 24, 15.
31. (a) S. R. Gadre and C. H. Suresh, Electronic Perturbations of the Aromatic Nucleus: Hammett Constants and Electrostatic Potential Topography, J. Org. Chem., 1997, 62, 2625–2627; (b) S. R. Gadre, C. H. Suresh and N. Mohan, Electrostatic Potential Topology for Probing Molecular Structure, Bonding and Reactivity, Molecules, 2021, 26, 3289.
32. A. V. Salnikov, A. M. Genaev, G. E. Salnikov, H. S. Rzepa and V. G. Shubin, J. Comput. Chem., 2016, 37, 210–225.
33. X. He, M. Li, C. Rong, D. Zhao, W. Liu, P. W. Ayers and S. Liu, Some Recent Advances in Density-Based Reactivity Theory, J. Phys. Chem. A, 2024, 128, 1183–1196.
34. J. M. Kromann, J. H. Jensen, M. Kruszyk, M. Jessing and M. Jorgensen, Fast and Accurate Prediction of the Regioselectivity of Electrophilic Aromatic Substitution Reactions, Chem. Sci., 2018, 9, 660–665.
35. A. Tomberg, M. J. Johansson and P.-O. Norrby, A Predictive Tool for Electrophilic Aromatic Substitutions Using Machine Learning, J. Org. Chem., 2019, 84, 4695–4703.
36. K. Jorner, T. Brinck, P.-O. Norrby and D. Buttar, Machine Learning Meets Mechanistic Modelling for Accurate Prediction of Experimental Activation Energies, Chem. Sci., 2021, 12, 1163–1175.
37. Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 other Functionals, Theor. Chem. Acc., 2008, 120, 215–241.
38. W. J. Hehre, L. Radom, P. V. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986.
39. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, Efficient Diffuse Function-Augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-Row Elements, Li–F, J. Comput. Chem., 1983, 4, 294–301.
40. F. M. Bickelhaupt and K. N. Houk, Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model, Angew. Chem., Int. Ed., 2017, 56, 10070–10086.
41. Y. H. Lam, M. N. Grayson, M. C. Holland, A. Simon and K. N. Houk, Theory and Modeling of Asymmetric Catalytic Reactions, Acc. Chem. Res., 2016, 49(4), 750–762.
42. T. A. Hamlin, B. J. Levandowski, A. K. Narsaria, K. N. Houk and F. M. Bickelhaupt, Structural Distortion of Cycloalkynes Influences Cycloaddition Rates Both by Strain and Interaction Energies, Chem. – Eur. J., 2019, 25, 6342–6348.
43. M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, Performance of M06, M06-2X, and M06-HF Density Functionals for Conformationally Flexible Anionic Clusters: M06 Functionals Perform Better than B3LYP for a Model System with Dispersion and Ionic Hydrogen-Bonding Interactions, J. Phys. Chem. A, 2013, 117, 12590–12600.
44. K. Yang, J. L. Zheng, Y. Zhao and D. G. Truhlar, Tests of the RPBE, revPBE, τ-HCTHhyb, ω-B97X-D, and MOHLYP Density Functional Approximations and 29 Others Against Representative Database for Diverse Bond Energies and Barrier Heights in Catalysis, J. Chem. Phys., 2010, 132, 164117.
45. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
46. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465.
47. (a) V. Barone and M. Cossi, Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model, J. Phys. Chem. A, 1998, 102, 1995–2001; (b) M. Cossi, N. Rega, G. Scalmani and V. Barone, Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model, J. Comput. Chem., 2003, 24, 669–681.
48. E. Plata and D. A. Singleton, A Case Study of the Mechanism of Alcohol-Mediated Morita Baylis–Hillman Reactions. The Importance of Experimental Observations, J. Am. Chem. Soc., 2015, 137, 3811–3826.
49. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Co6stant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396.
50. K. Fukui, The Path of Chemical Reactions – the IRC Approach, Acc. Chem. Res., 1981, 141, 363–368.
51. M. J. Frisch, et al., Gaussian 16, Revision 16. B.01, Gaussian, Inc., Wallingford, CT, 2016.
52. J. N. Sanders, H. J. Jun, R. A. Yu, J. L. Gleason and K. N. Houk, Mechanism of an Organocatalytic Cope Rearrangement Involving Iminium Intermediates: Elucidating the Role of Catalyst Ring Size, J. Am. Chem. Soc., 2020, 142, 16877–16886.
53. D. Cheshnedzhieva, S. Ilieva, B. Hadjieva and B. Galabov, The Mechanism of Alkaline Hydrolysis of Amides: A Comparative Computational and Experimental Study of the Hydrolysis of N-Methylacetamide, N-Methylbenzamide, and Acetanilide, J. Phys. Org. Chem., 2009, 22, 619–631.
54. E. Ritter and S. Kvisle, Spectral Evidence for Dimerization of Titanium Tetrachloride at Cryogenic Temperatures, Inorg. Chem., 1985, 24, 640–642.
55. (a) F. L. Hirshfeld, Bonded-Atom Fragments for Describing Molecular Charge Densities, Theor. Chim. Acta, 1977, 44, 129–138; (b) J. P. Ritchie, Electron Density Distribution Analysis for Nitromethane, Nitromethide, and Nitramide, J. Am. Chem. Soc., 1985, 107, 1829–1837; (c) J. P. Ritchie and S. M. Bachrach, Some Methods and Applications of Electron Density Distribution Analysis, J. Comput. Chem., 1987, 8, 499–509.
56. S. Liu, Quantifying Reactivity for Electrophilic Aromatic Substitution Reactions with Hirshfeld Charge, J. Phys. Chem. A, 2015, 119, 3107–3111.
57. V. Nikolova, D. Cheshmedzhieva, S. Ilieva and B. Galabov, Atomic Charges in Describing Properties of Aromatic Molecules, J. Org. Chem., 2019, 84, 1908–1915.
58. K. B. Wiberg and P. R. Rablen, Atomic Charges, J. Org. Chem., 2018, 83, 15463–15469.
59. P. G. Seybold, Quantum Chemical-QSPR Estimation of the Acidities and Basicities of Organic Compounds, Adv. Quant. Chem., 2012, 64, 83–104.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03181d

---