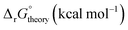Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the stability constants of metal–nitrate complexes in aqueous solutions†
Mohammadhasan
Dinpajooh
 *a,
Greta L.
Hightower
bc,
Richard E.
Overstreet
b,
Lori A.
Metz
b,
Neil J.
Henson
b,
Niranjan
Govind
*a,
Greta L.
Hightower
bc,
Richard E.
Overstreet
b,
Lori A.
Metz
b,
Neil J.
Henson
b,
Niranjan
Govind
 a,
Andrew M.
Ritzmann
b and
Nicolas E.
Uhnak
*b
a,
Andrew M.
Ritzmann
b and
Nicolas E.
Uhnak
*b
aPhysical & Computational Sciences Directorate, Pacific Northwest National Laboratory, Richland 99352, WA, USA. E-mail: hadi.dinpajooh@pnnl.gov; nicolas.uhnak@pnnl.gov
bNational Security Directorate, Pacific Northwest National Laboratory, Richland 99352, WA, USA
cUniversity of Hartford, West Hartford 06117, CT, USA
First published on 10th February 2025
Abstract
Stability constants of simple reactions involving addition of the NO3− ion to hydrated metal complexes, [M(H2O)x]n+ are calculated with a computational workflow developed using cloud computing resources. The computational workflow performs conformational searches for metal complexes at both low and high levels of theories in conjunction with a continuum solvation model (CSM). The low-level theory is mainly used for the initial conformational searches, which are complemented with high-level density functional theory conformational searches in the CSM framework to determine the coordination chemistry relevant for stability constant calculations. In this regard, the lowest energy conformations are found to obtain the reaction free energies for the addition of one NO3− to [M(H2O)x]n+ complexes, where M represents Fe(II), Fe(III), Sr(II), Ce(III), Ce(IV), and U(VI), respectively. Structural analysis of hundreds of optimized geometries at high-level theory reveals that NO3− coordinates with Fe(II) and Fe(III) in either a monodentate or bidentate manner. Interestingly, the lowest-energy conformations of Fe(II) metal–nitrate complexes exhibit monodentate or bidentate coordination with a coordination number of 6 while the bidentate seven-coordinated Fe(II) metal–nitrate complexes are approximately 2 kcal mol−1 higher in energy. Notably, for Fe(III) metal–nitrate complexes, the bidentate seven-coordinated configuration is more stable than the six-coordinated Fe(II) complexes (monodentate or bidentate) by a few thermal energy units. In contrast, Sr(II), Ce(III), Ce(IV), and U(VI) metal ions predominantly coordinate with NO3− in a bidentate manner, exhibiting typical coordination numbers of 7, 9, 9, and 5, respectively. Stability constants are accordingly calculated using linear free energy approaches to account for the systematic errors and good agreements are obtained between the calculated stability constants and the available experimental data.
1 Introduction
Chemical equilibria in aqueous solutions play an important role in determining the key factors that control the various processes governing chemical behavior. For instance, carbonic acid-carbonate equilibrium determines the pH in seawater,1 which is crucial for the marine life.2 In chemical engineering, chemical equilibria are very crucial to design the reactors.3 In chemical separation techniques, understanding ligand-exchange equilibria provides the necessary information needed to design new techniques.4 Chemical equilibria are also important for nuclear forensic analysis.5,6 For example, a fission event like that from a nuclear detonation, creates a large swath of the periodic table, both from the fission process as well as neutron activation of the local environment requiring prompt analysis. Nuclear forensics analyses involve isolating and quantifying a multitude of elements and isotopes; therefore, it provides information that allows for fundamental questions regarding the detonation to be answered. In this regard, chemical separations of aqueous metal ions are necessary for adequate analysis of debris collected from the environment.7 The complicated nature of these samples is magnified by the difficulty of analyzing the most important fission or activation products. By separating these more troublesome components from the bulk material, one can quantify those high impact fission or activation products and aid in answering the fundamental questions regarding the detonation. Therefore, understanding ligand-exchange equilibrium is essential to improve the separation procedures. This involves determining the thermodynamic speciation of numerous elements using the stability constants.In this work, we focus on chemical equilibria of simple ligand-exchange reactions that have applications in nuclear forensics and study the stability constants of metal–nitrate complexes in aqueous solutions. Such information is crucial for multiscale modeling of column chromatographic separation systems,8 where different metal species exist in the solution, usually at relatively low concentrations, and the distribution of these species influences how each species interacts with the hydrophobic stationary phase, or resin phase to simplify, as well as their overall mobility. For instance, the formation of stable metal–nitrate complexes can alter the retention time of the metal species in the chromatographic column, and complexes with higher stability constants might have different interactions with the resin phase. To this end, our group is working to establish a multiscale and multiphysics approach for modeling how metal ions are preferentially extracted by the commercially available UTEVA® (diamyl amyl phosphonate) resin and other resins.9 Here we focus on ab initio modeling of stability constants of metal ions in nitric acid solutions using continuum solvation models (CSMs)10–15 at the density functional theory (DFT) level.16–20 The justification for our DFT calculations is based on previous work including ours on similar systems, where DFT was shown to be sufficiently accurate to describe the spin and oxidation states and spectroscopies.21–29 Our long-term protocol is based on the DFT, which is a pragmatic approach to obtain thermodynamic properties for large molecular systems in complex environments. To mitigate situations where DFT breaks down, in future studies we will adapt our workflow to include higher order wavefunction-based approaches. However, these methods become prohibitively expensive for computations of large systems lacking high symmetry. Where appropriate, we will use small model complex surrogates of the full complexes to guide our understanding of the electronic structure with the more expensive approaches in order to validate DFT predictions.30–32
Considering the advances in cloud computing, which dynamically adjusts resources based on consumer demand,33 we use the computational resources provided by Microsoft,34 through their virtual machines optimized for high performance computing (Azure Quantum Elements), to develop a computational workflow. We use this workflow to explore a wide range of conformations relevant for free energy calculations, which are based on finding the minimum structures and can be challenging.35,36 The conformations are initially generated from previous literature or molecular dynamics (MD) simulations at low levels of theory and later optimized at high-level DFT. This is accompanied by conformational searches at a high level of theory to report enthalpies, entropies, and free energies of reactions. We have applied these approaches to study several aqueous metal nitrate complexes consisting of Sr(II), Fe(II), Fe(III), Ce(III), Ce(IV), and U(VI) ions, which are important metal ions in a nuclear forensics investigation for various reasons. Uranium is the primary fission fuel, strontium is a high-yield fission product, and cerium is a fission product that is representative of lanthanide series from a chemistry standpoint. Iron is one of the most abundant elements and is found in both structural as well as geological materials.37,38
In particular, we calculate the reaction free energies involving ligand exchange in metal complexes including their first solvation shells in the CSM framework. Our approach can complement other coordination-based computational approaches such as the molSimplify toolkit being developed by Kulik et al.,39,40 which are equipped with artificial neural networks to predict quantum-mechanically-derived properties including spin-state ordering and spin-state specific bond lengths in octahedral transition metal complexes. As one may notice, the second and higher solvation shells in the coordination-based approaches are completely absent, which are critical in monitoring the kinetics and mechanisms of ligand-exchange reactions and are subjects of future studies. In fact, explicit modeling of the second hydration shell in the CSM framework for the calculation of the reaction free energy calculation is limited because as the number of solvent molecules increases, adequate sampling of solute–solvent clusters and locating the minimum conformations become computationally challenging.41 However, previous studies have shown that the calculated properties based on the first solvation representation of a solvent can predict free energy of ion solvation42 and the relative stability of a series of metal complexes.41,43,44 Motivated by these studies, we consider the relative stability constants and apply linear free energy relations45,46 to calculate the stability constants relevant to the multiscale generative artificial intelligence approach we will develop in future studies. In addition, experimental studies can benefit from the data provided with the computational workflow presented in this work.
This paper is organized as follows: in the next section, the details of the developed computational workflow will be provided and it is discussed how the workflow generates the lowest energy conformations for hydrated metal complexes. This is followed by presenting the coordination chemistry properties and the ligand-exchange reactions for the studied metal–nitrate complexes. We then present the DFT-based stability constants and compare them with the available experimental results. Finally, the paper concludes with a summary of the findings, along with a discussion of the outlook and future directions.
2 Computational details & workflow
In the CSM framework, the solution-phase reaction free energy is obtained as the sum of the corresponding gas-phase free energy and the free energy of solvation. At a given temperature, the free energy of a ligand-exchange reaction may be given by13,47| ΔGrxn = ΔE + ΔGTRRHO + ΔδGTsolv | (1) |
The second term, GTRRHO, in eqn (1) for a given species is often referred as the thermal corrections for free energy calculations within the CSM and is the sum of both entropic and enthalpic contributions. The superscript T in GTRRHO indicates that this term is determined at a given temperature in the CSM framework while the superscript T in δGTsolv indicates that any non-canceling differences in the gas and solution phase thermal corrections are implicitly incorporated into the solvation model through parametrizations.14,15 The rigid rotor harmonic approximation (RRHO) is used to apply the thermal corrections at T = 298 K, which ignores anharmonicity in vibrations, coupling between vibrational and rotational motions (vibronic coupling), and centrifugal distortion in rotations and it only includes translational, rotational, and zero-point-vibrational energies for each species in the gas phase.48 Nevertheless, theoretically, when one performs MD simulations for the species in the reaction, they are sampled in an anharmonic potential, and at each MD step, the conformations are not at equilibrium, resulting in the appearance of imaginary frequencies if the Hessian is calculated at each MD step. In particular, the MD simulations represent ensembles of structures that correspond to a given thermodynamic state point and the occurrence of imaginary frequencies is expected. In these lines, when the optimized structures are calculated in the CSM framework, a few imaginary frequencies may also appear that are associated with low frequencies. In this work, the quasi-harmonic approximation is applied, which replaces very low frequencies (<50 cm−1) with a low enough frequency (50 cm−1) to avoid the vibrational entropy approaches unphysically infinite values and reduce the errors associated with the use of the harmonic oscillator partition function.47,49 Similarly, some imaginary frequencies (usually with magnitudes less than about 50 cm−1) in some conformations are replaced with their absolute values for entropy and thermal correction calculations. The accuracy of these approximations is demonstrated in the ESI.†
2.1 Conformational search
In eqn (1), the ΔE term is expected to be the dominant contribution suggesting that the reliability of results depends mostly on the accuracy of this term, but its accurate determination is not a trivial task because its value depends significantly on determining the lowest energy conformation. Such determinations for metal complexes can be quite challenging because the number of candidate local energy minima grows exponentially with the number of atoms.50,51 In this regard, a number of recent studies have developed workflows/toolkits to generate relevant conformations.39,40,52–54 Considering these, here we develop a computational workflow in conjunction with CSMs with the goal of determining the lowest energy structures. In particular, we combine low and high levels of theories with enhanced sampling techniques in MD simulations, which allows one to explore the reaction phase space reasonably in the CSMs. Fig. 1 shows a schematic of this workflow for the reactions of interest. Making use of MD simulations and enhanced sampling techniques (see below), a range of different starting configurations are examined to find the most stable structures at a DFT level of theory. | ||
| Fig. 1 The computational workflow for finding the lowest energy conformations. An initial search is done using the available resources such as machine learning models (e.g., molSimplify39,40) or previous literature to guess the conformations. If there are no available rigorous conformations available, a conformational search is performed at a low theoretical level of calculation (e.g. the CREST software program54 with the xTB method combined with enhanced sampling techniques) to add additional conformations. These are followed by high level DFT calculations with NWChem,55 which includes optimizations of selected conformations from CREST to find the lowest energy conformations. To explore the phase space around these candidate minimum conformations at room temperature and to locate other minima, ab initio molecular dynamics (AIMD) simulations are performed. These AIMD simulations are done to confirm that the candidate minimum conformation is stable, i.e. this conformation with a given coordination number remains stable at timescales smaller than the residence time, τres, for a given ligand-exchange reaction (see Section 3.1 for the definition of τres). If the conformation is not stable within this timescale, a conformation with a new coordination number is proposed for the reactant or the product. Otherwise, the lowest energy conformations are found using all conformers found. | ||
To calculate eqn (1) for the reactions of interest, one needs to know the coordination number of metal complexes. The initial metal coordination numbers for hydrated metal ions are obtained from the literature.56 In general, for metal–nitrate complexes less information is available from the literature about the coordination number; therefore, the workflow uses the available information for hydrated metal ions56 to replace the water molecules with NO3− ligands in various metal–nitrate complexes, but considering monodentate and bidentate arrangements of NO3−, the stable conformation may keep or lose water molecules in these metal–nitrate complexes. Therefore, significant uncertainties can be introduced in the calculations of the free energy calculations. Later, we discuss how the workflow handles the coordination of metal complexes in the framework of CSM, but we first present the general scheme of the workflow.
As shown in step 1 of the workflow in Fig. 1, the initial configurations for all metal complexes are either obtained from previous studies (e.g., ab initio MD simulations25,26,57) or from the optimizations using the standard molecular mechanics force fields.58,59 In general, the workflow can be integrated to automated first-principles toolkits such as molSimplify39,40 to generate the initial metal complexes coordinated by ligands in a mono- or multi-dentate fashion once the ligands are available in such toolkits. Step 2 of the workflow uses these configurations as inputs to perform conformational searches at a low level of theory. Here, we use the conformer-rotamer ensemble sampling tool (CREST) software program54 for the efficient and automated exploration of molecular chemical space at the extended tight-binding (xTB) level. In short, the automated exploration in CREST involves performing a block of metadynamics simulations using the Cartesian root-mean-square deviation as the collective variables (see ref. 54 for details). The GFN2-xTB method in the CREST program is used for geometry optimizations and energy calculations and only conformers within a given energy (15 kcal mol−1) of the lowest-energy conformer are considered for conformational search. In step 3 of the workflow, tens or hundreds of output geometries from the CREST software program or step 1 are selected based on the energy criterion. This involves choosing the 10 lowest conformations and the rest conformations in the intervals n/10, with n as the total number of conformations. These geometries from CREST or step 1 are then optimized at the DFT level to obtain an accurate reasonable ensemble of conformations. From these DFT candidate conformations, the workflow in step 4 finds the lowest energy conformation. It is worth stressing that one may skip steps 2 if the previous conformations in step 1 are already obtained from rigorous conformational searches.
Considering the existence of many local minima for metal complexes, one may wonder whether the optimized candidate DFT conformation from step 4 of the workflow can be significantly higher in energy from the nearby local minima. Generally, such nearby local minima can be accessed by performing AIMD simulations using enhanced techniques, which is the subject of future studies. However, if the optimized candidate DFT conformation is located at an extreme point with relatively low barrier heights, even relatively short AIMD simulations can demonstrate that the conformation is unstable. Therefore, in step 5 of the workflow, the AIMD simulations are performed on the selected conformations optimized at DFT to assess whether the candidate for the lowest energy conformation is stable or not. If the candidate for the lowest energy conformation is not stable with a given timescale (see Section 2.2), then the conformation is adjusted and the conformational search will be repeated (see Fig. 1). If the candidate for the lowest energy conformation is stable, the workflow adds new conformations from AIMD to the set for the optimization calculations and performs a final search to find the minimum structures. The significance of this step is further discussed below in Section 3.1 especially for UO22+ and Sr2+ metal complexes, where at various levels of theories metal complexes turn out to be most stable with different number of water molecules due to monodentate or bidentate structures of NO3− with these metal ions.
To find the lowest energy conformations with no imaginary frequencies, the workflow optimizes the lowest energy conformation. If the optimized conformation has zero imaginary frequencies, then the conformation is labeled as the lowest energy conformation for a given metal complex; otherwise, at least 20 more optimizations are performed along the displacement vectors of the first 20 frequency modes to locate the minimum conformations with no or least number of imaginary frequencies. Therefore, all or most of the imaginary frequencies are removed. The workflow verifies that the magnitudes of any remaining imaginary frequencies are less than about 100 cm−1. The significance of imaginary frequencies in the calculation of thermodynamical properties (second term in eqn (1)) is addressed in the ESI† for this study. Finally, before reporting the lowest-energy conformers, it is worth considering alternative reasonable conformations that may not have been initially accounted for but appear plausible as part of the iterative learning process.
Given that many conformations have been optimized at DFT level using the initial configurations provided by CREST, we also report Boltzmann average thermodynamical properties whose weights are determined by comparing the available conformation energies with the lowest one. Setting the minimum electronic energy as the reference energy, Emin, for a given thermodynamical property B, the average B (〈B〉) may be reported as
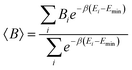 | (2) |
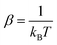 and kB as the Boltzmann constant. Considering the Boltzmann averaging of the conformations, the quasi-harmonic approximation, and the existence of imaginary frequencies, in the ESI,† we show that for a frequency cutoff of 50 cm−1, the Boltzmann Gibbs free energies are in excellent agreement with the Gibbs free energy obtained only from the lowest energy conformations with zero imaginary frequencies noting that the enthalpies and temperature times entropies are only different by about 1–2 kcal mol−1. Larger differences are observed for a frequency cutoff of 100 cm−1, when the reaction thermodynamical properties are compared with the ones with the lowest energy conformations with zero imaginary frequencies but the differences remain by about 0.5–1 kcal mol−1. Therefore, for these reactions, the results indicate that possible errors associated with including the imaginary frequencies within the quasi-harmonic approximation remain to be about 0.5–1 kcal mol−1. In what follows, we report the reaction thermodynamical properties based on both the lowest energy conformations and the Boltzmann averaging.
and kB as the Boltzmann constant. Considering the Boltzmann averaging of the conformations, the quasi-harmonic approximation, and the existence of imaginary frequencies, in the ESI,† we show that for a frequency cutoff of 50 cm−1, the Boltzmann Gibbs free energies are in excellent agreement with the Gibbs free energy obtained only from the lowest energy conformations with zero imaginary frequencies noting that the enthalpies and temperature times entropies are only different by about 1–2 kcal mol−1. Larger differences are observed for a frequency cutoff of 100 cm−1, when the reaction thermodynamical properties are compared with the ones with the lowest energy conformations with zero imaginary frequencies but the differences remain by about 0.5–1 kcal mol−1. Therefore, for these reactions, the results indicate that possible errors associated with including the imaginary frequencies within the quasi-harmonic approximation remain to be about 0.5–1 kcal mol−1. In what follows, we report the reaction thermodynamical properties based on both the lowest energy conformations and the Boltzmann averaging.
Fig. 2 shows the lowest energy conformations that are obtained from the workflow for the studied hydrated metal ions, [M(H2O)x]n+. It is worth mentioning that the predicted hydration structures surrounding these ions are consistent with the previous studies using high-resolution X-ray absorption fine structure experiments25,26,57,60–62 (also see ESI†). In the next sections, we discuss the consequences of the addition of NO3− to these metal complexes and formations of bidentate and monodentate structures and address how workflow helps the calculations of reaction free energies using eqn (1), but we first present more computational details.
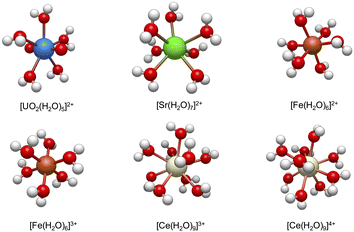 | ||
| Fig. 2 The lowest energy configurations of the studied hydrated metal ions, [M(H2O)x]n+ at B3LYP level of theory (see Section 2.2 for the numerical details). | ||
2.2 CSM and AIMD computational details
Here we study the thermodynamic aspects of ligand-exchange reactions when the first hydration shell of metal complexes is treated explicitly and the other solvation effects are characterized in the CSM framework in which the other solvent effects are captured by the dielectric constant of solvent representing the nuclear rearrangements.10,11,13,15,63 Unless mentioned otherwise, the low theoretical level of calculations are performed at the extended tight-binding (xTB) level,64 while the high-level calculations are performed with the NWChem software program at the DFT16,17 level with the global hybrid B3LYP exchange–correlation functional.18,65–68 The exchange part of the B3LYP combines 20% Hartree–Fock exact exchange with 80% Slater exchange and a 72% non-local correction from Becke's 1988 functional. The correlation part of the B3LYP combines 19% Vosko–Wilk–Nusair (VWN) correlation with 81% Lee–Yang–Parr (LYP) correlation. The metal ions are represented with the Stuttgart relativistic small core (RSC) effective core potential (ECP) and basis set69,70 and the oxygen and nitrogen atoms are represented by the 6-311++G(2d,2p) basis set and the hydrogen atoms with the 6-311G* basis set.71 These choices are made based on the sufficient accuracy of DFT and the basis sets that we have observed in previous studies.21–29,71 The DFT-D3BJ method55,72 is used to account for the dispersion corrections in interactions and the COSMO solvent continuum model10,11 with a dielectric constant of 78.4 is used to account for solvent effects beyond the first solvation shell. The most stable electronic states for the studied metal ions are determined from the literature and verified by standard DFT calculations in their local environment (first solvation shell). For Fe(II) and Fe(III), the high spin states of quintet and sextet, respectively turn out to be more stable than the low spin and intermediate spin states for all studied metal complexes (see Table S3 in the ESI†) and be consistent with previous studies.73 For all other metals the singlet states are stable except the Ce4+, which has a stable doublet state.38,62As mentioned above, the workflow in step 5 checks the stabilities of the selected DFT optimized structures by running AIMD simulations. The AIMD simulation are performed using the “qmd” module in the NWChem software program.74 The nuclei are integrated using the velocity-Verlet algorithm. The AIMD simulations are performed at 298 K using the Nosé–Hoover thermostat to control the temperature with a frequency of 300 cm−1 as the interaction with the heat bath making use of three Nosé–Hoover chains. The electronic potentials are provided by the same Gaussian basis set-based methods used for the minimization, which use the spherical basis sets.
The AIMD simulations are performed over a shorter timescale relative to the longer ligand residence time, τres,75–77 to assess whether the metal complex is relatively stable. Running these AIMD simulations allow one to determine the optimized metal complexes that are not in a relatively stable state and their ligands tend to leave the metal complex at relatively short timescales (smaller than long residence time) due to small barrier heights. By long residence time we mean the residence time for the ligand departure when the metal complex is in a relatively stable conformation. For instance, if the optimized conformation in the workflow involves a bidentate conformation of the NO3− in a metal complex when only one water molecule has been replaced with one NO3− ligand, this state can be in a relatively unstable state when the NO3− ligand occupies two sites of the metal complex and the departure of another water molecule can lead to a more stable conformation. Due to computational limitations, we choose to run the AIMD simulations for about 4.8 ps. It is an interesting future project to improve the AIMD simulation protocols using enhanced sampling techniques. It is worth noting that the AIMD simulations in the CSM framework can qualitatively provide the long residence times for ligand departures consistent with experimental results.75–78
3 Results: ligand-exchange with NO3−
3.1 Coordination chemistry properties
Understanding the coordination chemistry of metal complexes in the CSM framework is essential to understand their thermodynamics and stability constants. As we show in the next section, this allows one to write simple ligand-exchange reactions. We discuss the coordination chemistry when the NO3− ion replaces water in the studied metal complexes in an aqueous solution, where monodentate or bidentate configurations can compete with each other.A rigorous way to understand the competition between the monodentate and bidentate configurations require condensed-phase AIMD simulations.28,79–85 For instance, for the CO32− ion, such simulations have indeed shown that both bidentate and monodentate configurations are possible when they approach the Ca2+ ion in an aqueous solution with barrier heights on the order of the thermal energy.80 However, the workflow can perform significant conformational searches and can overcome the barrier heights to generate both monodentate or bidentate conformations of the [M(NO3)(H2O)x](n−1)+. Considering the relatively small number of degrees of freedom in the CSM framework, this allows one to get the stability constants of metal ions with a given coordination number, which is currently a reasonable method of choice when compared to the condensed-phase AIMD simulations noting that the thermodynamical properties in the CSM framework can be very sensitive to the determination of the lowest energy conformation to introduce uncertainties. In what follows, the estimates of such uncertainties are provided by comparing the results obtained from the lowest energy conformations with the ones from the Boltzmann average of all relevant conformations. In particular, in the next sections, we discuss how the workflow can determine the coordination chemistry of these metal–nitrate complexes by generating tens to hundreds of conformations and discuss how the lowest energy conformations are obtained from the workflow.
We first present the lowest energy conformations obtained from the workflow in Fig. 3. As can be seen, the bidentate conformations are, in general, most stable for all metal complexes except the Fe(II) metal–nitrate complexes. Unlike other metal complexes, the lowest energy conformations for the iron metal complexes consist of both monodentate and bidentate conformations with energy differences that can be less than 2 kcal mol−1 and this will be rigorously demonstrated in details in the next section.
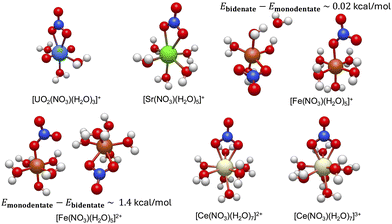 | ||
| Fig. 3 The resulting lowest minimum structures of the studied hydrated metal ions, [M(NO3)(H2O)x](n−1)+ at B3LYP level of theory (see Section 2 for the numerical and workflow details). The lowest energy conformations for both monodentate and bidentate conformations for [Fe(NO3)(H2O)5]1+/2+ metal complexes are shown. The energy difference between them are also reported, which is on the order of thermal motions. The structural properties of these lowest energy conformations are discussed in Section 3.1 and summarized in Table 1 below. | ||
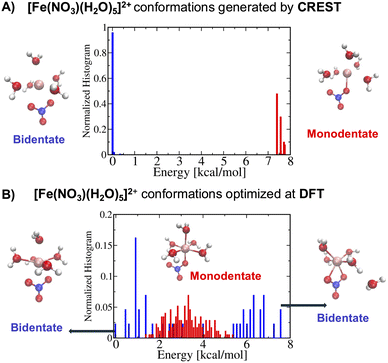
Following step 2 of the workflow in Section 2.1, one may extend the accessibility of the phase space with enhanced sampling techniques at a low-level of theory using the CREST. Panel A of Fig. 4 shows that the CREST can generate several hundreds of conformations with energy ranges less than 1.5 kcal mol−1 for [Fe(NO3)(H2O)5]+ metal complexes and all of the conformations are bidentate. Adding these configurations to the previously reasonable generated conformations, we select a few hundreds of them for optimizations at a DFT level. Panel B of Fig. 4 shows the optimized structures at DFT revealing that the monodentate and bidentate conformations with coordination numbers of 6 are both stable and their energy differences are on the order of thermal energy units. Interestingly, the seven-coordinated bidentate conformations of [Fe(NO3)(H2O)5]+ are observed but their energies are about 2 kcal mol−1 higher than the lowest energy conformations found (Fig. 4B).
On the other hand, for the [Fe(NO3)(H2O)5]2+ metal complexes, Fig. 5A shows that CREST can generate both monodentate and bidentate conformations with monodentate conformations to be about 7–8 kcal mol−1 higher in energy. Once selected conformations are optimized at the DFT level of theory, the energies of monodentate conformations turn out to be much closer to the bidentate conformations (see Fig. 5B). In particular, the lowest monodentate conformation is only 1.4 kcal mol−1 higher in energy than the lowest energy bidentate conformation. Compared to the Fe2+ metal–nitrate complexes, the Fe3+ metal–nitrate complexes have greater stability in their seven-coordinated bidentate conformations than in the six-coordinated ones, by approximately 4–7 kcal mol−1. These seven-coordinated structures represent the lowest-energy conformations, as revealed by extensive conformational searches and optimizations, and are confirmed by having zero imaginary frequencies. This observation can be attributed to the higher charge density of Fe3+ compared to Fe2+ in metal–nitrate complexes.
 | ||
| Fig. 5 (A) The normalized energy histogram obtained from 277 monodentate and 376 bidentate conformations for [Fe(NO3)(H2O)5]2+ generated from CREST. (B) The normalized energy histogram obtained from 172 monodentate and 43 bidentate selected conformations for [Fe(NO3)(H2O)5]2+ each of which is optimized at DFT. Other details are similar to the ones in Fig. 4. | ||
A useful metric is the metal–oxygen distance(s) between one or two closest oxygen atoms of the NO3− ligand to the metal center, depending on whether the conformation is monodentate or bidentate, respectively. In general, the metal–oxygen, dFe–O, distances of the monodentate conformations are smaller than the ones from the bidentate conformations by about 0.1–0.2 Å. In particular, the average dFe–O distance of the monodentate [Fe(NO3)(H2O)5]+ conformers is about 2.15 Å while the average dFe–O distance of the bidentate [Fe(NO3)(H2O)5]+ conformers is 2.23 Å. Similarly, the average dFe–O distance of the monodentate [Fe(NO3)(H2O)5]2+ conformers is about 1.94 Å while the average dFe–O distance of the bidentate [Fe(NO3)(H2O)5]2+ conformers is 2.12 Å. More structural analyses of the monodentate and bidentate conformations optimized at DFT are presented in the Fig. S1 in the ESI.† The histograms of dFe–O distances for the monodentate conformations show Gaussian distributions while the histograms of the dFe–O distances for the bidentate conformations resemble bimodal distributions indicating the existence of six- and seven-coordinated metal complexes noting that the dM–O in bidentate conformations are mostly not identical. The important exception is the lowest energy conformation of seven-coordinated bidentate [Fe(NO3)(H2O)5]2+ conformation with dFe–O bond lengths of about 2.15 Å.
Therefore, making use of hundreds of conformations, the workflow confirms the formations of both monodentate and bidentate conformations for [Fe(NO3)(H2O)5]1+/2+ at DFT level and this is rigorously demonstrated through several complementary AIMD simulations of these metal complexes at 298 K (step 5 of the workflow), revealing that monodentate conformations are either stable or can transition to stable bidentate conformations, and vice versa. It is worth noting that the formations of monodentate conformations in solutions are consistent with the crystallographic observation that NO3− ion attaches to the Fe3+ metal ion in a monodentate fashion.86 In addition, the formations of seven-coordinated [Fe(NO3)(H2O)5]1+/2+ metal complexes are consistent with previous studies of transition metals coordinated with other ligands.87–90
Alternatively, one may consider the formations of significantly different conformations in the thermodynamics limit by removing two water molecules from the hydrated metal complexes and replacing them with one NO3− ligand to form [Fe(NO3)(H2O)4]+ and [Fe(NO3)(H2O)4]2+ metal complexes. Interestingly, using the same workflow steps stated above, stable conformations are also formed, where the NO3− ligand is attached to the metal in a bidentate fashion. However, the seven-coordinated bidentate conformations of the [Fe(NO3)(H2O)4]1+/2+ complexes are not observed noting that an octahedral substitution of water with NO3− require that the two oxygen atoms of NO3− to occupy the octahedral sites. Therefore, care is required to design the first solvation shells in the CSM framework in the coordination-based approaches such as our approach and molSimplify considering the artifacts that exist due to absence of second hydration shells.
Fig. 6 shows the normalized energy histograms for the DFT optimized structures of [Sr(NO3)(H2O)5]+ conformers including 99 monodentate (red bars) and 512 bidentate (blue bars) conformers. As can be seen, the bidentate conformations are in general more stable than the monodentate conformations such that the lowest energy bidentate conformer is about 2 kcal mol−1 more stable than the lowest energy monodentate conformer. In addition, the dSr–O distances of the monodentate conformations are, in general, smaller than the ones from the bidentate conformations. In particular, the average dSr–O distance of the monodentate [Sr(NO3)(H2O)5]+ conformers is about 2.53 Å while the average dSr–O distance of the bidentate [Sr(NO3)(H2O)5]+ conformers is 2.63 Å.
We first discuss the possibility of the formation of [UO2(NO3)(H2O)4]+ metal complexes. If one starts from the initial guess conformation of the [UO2(NO3)(H2O)4]+ metal complex with a coordination number of 6 and minimize this structure, one can get a minimized bidentate structure consisting of one NO3− ligand and 4 water molecules attached to U with a UO distance of ∼2.6 Å. However, when one proceeds to step 5 of the workflow to perform 4.8 ps AIMD simulations at 298 K, after about 3.6 ps one water molecule leaves the metal complex suggesting that the coordination number of UO2 tends to remain 5. Interestingly, the water molecule that departs the first solvation shell, remains close to within an average UO distance of 4.1 Å as compared with UO average distances of 2.4 Å for water molecules attached directly to U in the first solvation shell. This may attributed to many factors such as the interplay between the continuum solvent field, relatively strong hydrogen bonding between water molecules, and the charge density of metal complex. For consistency, another minimum structure of the [UO2(NO3)(H2O)4]+ was chosen to run the MD simulations for another 4.8 ps and it was observed that the separated water molecule tend not to leave and attach to U over the course of MD simulations. Importantly, among all optimized conformations for [UO2(NO3)(H2O)4]+ metal complexes (40 configurations), the minimum structure appears to be the one with a coordination number of 5, where the remaining water molecule tend to be at location with a UO distance of 4.1 Å as compared with UO distances of 2.4 Å for water molecules attached directly to U. A few percentage of monodentate conformations are also observed in the AIMD simulations whose optimized energies appear to be at least ∼2.5 kcal mol−1 higher than the lowest energy bidentate conformation. Overall, one can consider the formation of the bidentate [UO2(NO3)(H2O)4]+ conformations reasonable in the solution in the CSM framework.
On the other hand, one can conceive the formation of the [UO2(NO3)(H2O)3]+ metal complexes, in which three water molecules attach to U and one NO3− ligand attaches to U in a bidentate fashion to satisfy a coordination number of 5. The AIMD simulations of this type of metal complex demonstrates that all ligands stay attached to U over the course of 4.8 ps molecular simulations. Fig. 7 shows the energy and bond histograms extracted from the conformations of [UO2(NO3)(H2O)3]+ optimized at DFT level. Panel A shows that the conformations of [UO2(NO3)(H2O)3]+ only consist of bidentate conformations. Interestingly, in the lowest energy bidentate conformation for the [UO2(NO3)(H2O)3]+ metal complex, 4 water molecules coordinate with U atom with a UO bond length of ∼2.5 Å and a NO3− ligand attaches to U atom in a bidentate fashion with an average UO bond length of ∼2.5, which confirms the coordination number of 5 for this metal complex.
Although the workflow can generate a considerable number of monodentate conformations for [Ce(H2O)7(NO3)]2+ and [Ce(H2O)7(NO3)]3+, the energies of their optimized structures at DFT turn out to be significantly higher than the corresponding bidentate conformations (ranging from 8 to 90 kcal mol−1 higher in energy). An examination of these high-energy DFT optimized monodentate structures reveals the presence of nitric acid and OH− species (results not shown). These structures result from DFT optimization of the initial configurations generated by CREST. Therefore, the monodentate conformations do not contribute significantly to the thermodynamical properties according to eqn (2) because their Boltzmann weights are almost negligible. In fact, this is a good demonstration that the workflow can disregard irrelevant conformations for the stability constant calculations that we present in the next sections.
A simple metric to characterize the structural properties of the metal–nitrate complexes is the distance between metal center and the nitrogen atom of nitrate (dM–N). Table 1 shows that the dM–N value for the monodentate conformer is about 0.5 Å larger than the bidentate conformer of [Fe(NO3)(H2O)5]+. Comparing the bidentate conformations of the metal–nitrate complexes, the dM–N values are highest for [Sr(NO3)(H2O)5]+ and the smallest for [Fe(NO3)(H2O)5]+, which has one water molecule in the outer-shell.
| Product | LEC | d M–N [Å] | d M–O1 [Å] (BO) | d M–O2 [Å] |
|---|---|---|---|---|
| [Fe(NO3)(H2O)5]+ | Monodentate | 3.13 | 2.16 (0.254) | NA |
| [Fe(NO3)(H2O)5]+ | Bidentate | 2.62 | 2.18 (0.285) | 2.26 |
| [Fe(NO3)(H2O)5]2+ | Bidentate | 3.00 | 2.14 (0.644) | 2.15 |
| [Sr(NO3)(H2O)5]+ | Bidentate | 3.07 | 2.65 (0.173) | 2.65 |
| [UO2(NO3)(H2O)3]+ | Bidentate | 2.93 | 2.48 (0.359) | 2.49 |
| [Ce(NO3)(H2O)7]2+ | Bidentate | 3.01 | 2.57 (0.476) | 2.58 |
| [Ce(NO3)(H2O)7]3+ | Bidentate | 2.90 | 2.44 (0.843) | 2.45 |
A more important metric is the closest two oxygen–metal distances of NO3−1 (dM–O1 and dM–O2). Table 1 shows these bond length distances for all bidentate conformations are almost identical except for the [Fe(NO3)(H2O)5]+ metal complex with a percentage difference of ∼4%. A detailed analysis of the lowest-energy conformation of the bidentate [Fe(NO3)(H2O)5]+ metal complex reveals a coordination number of 6. This structure exhibits two distinct metal–oxygen distances for the four remaining water molecules: 2.10 Å for those in the same plane as the NO3− group and 2.15 Å for those nearly perpendicular to this plane. Additionally, an outer-shell water molecule is positioned at 3.77 Å from the Fe metal center. Interestingly, the competing monodentate conformation of the [Fe(NO3)(H2O)5]+ metal complex has also a coordination number of 6 but with metal–oxygen bond lengths of ∼2.15 Å for all water molecules and the closest distance oxygen of NO3−1. A detailed discussion of the competition between the monodentate and bidentate conformations for [Fe(NO3)(H2O)5]1+/2+ is presented in Section 3.1.1 above.
A closer look on the closest oxygen–metal distances of NO3−1 (dMO) for all bidentate conformations presented in Table 1 suggest a general trend. The dMO values are smallest for Fe2+/3+ (with ionic radii of 0.65/0.78 Å) and largest for Sr2+ (with an ionic radius of 1.18 Å).38 This can be attributed to higher charge densities of [Fe(NO3)(H2O)5]1+/2+ metal complexes as compared with the [Sr(NO3)(H2O)5]+ metal complexes (see Table S1 in the ESI†). For the lanthanide and actinide metals studied here, the closest oxygen–metal distances of NO3−1 range from 2.45 to 2.57 Å. Although no clear trend is observed for dMO values based solely on charge densities, a consistent pattern seems to hold based on the ionic radii for Ce3+/4+ (ionic radii: 1.01/0.87 Å) whose dMO values are larger than those of Fe2+/3+ (ionic radii: 0.65/0.78 Å) but smaller than those of Sr2+ (ionic radius: 1.18 Å).
Mayer bond order92 analyses are reported for M–O1 and M–O2 bonds in the ESI.† The analyses indicate that the bond orders for both M–O1 and M–O2 bonds are relatively close to each other for all bidentate lowest energy conformations except the [Fe(NO3)(H2O)5]2+, which has significantly different dM–O1 and dM–O2 as shown in Table 1. The highest bond order for these bonds is observed in [Ce(NO3)(H2O)7]3+, while the lowest is found in [Sr(NO3)(H2O)5]+. Among the M3+ metal ions, the bond order of [Fe(NO3)(H2O)5]2+ appear to be, in general, larger than the one for [Ce(NO3)(H2O)7]2+. The bond orders of [UO2(NO3)(H2O)3]1+ for these bonds are less than that of [Ce(NO3)(H2O)7]2+ but greater than those of [Fe(NO3)(H2O)5]+ and [Sr(NO3)(H2O)5]+.
Hydrogen bond analyses for all available DFT optimized conformations of all studied metal–nitrate complexes based on a Wernet criterion93 show that the hydrogen bond between the NO3− ligand and nearby water molecules only exists in their monodentate conformations and all studied bidentate conformations show no presence of such hydrogen bond interactions. For the lowest-energy monodentate conformation of Fe[(H2O)5(NO3)]1+/2+, we find the distance between O of NO3− and H of water to be 1.78/1.89 Å and the distance between O of NO3− and O of water to be 2.71/2.74 Å while the hydrogen bonding (O–H⋯O) angle is 157/143 degrees. Interestingly, in the lowest-energy monomer conformation of Sr[(H2O)5(NO3)]+, which is about 2 kcal mol−1 higher in energy than the lowest-energy bidentate conformation, the distance between O of NO3− and H of water is 1.81 Å and the distance between O of NO3− and O of water is 2.78 Å while the hydrogen bonding (O–H⋯O) angle is 166 degrees. No monodentate conformation is found among all explored conformations of [UO2(NO3)(H2O)3]+. The monodentate conformations for Ce metal–nitrate complexes turn out to include HNO3 and OH− species and significantly higher in energy (∼>8 kcal mol−1) than the bidentate conformations (see Section 3.1.4).
These hydrogen bond analyses are further verified by quantum topological atom-in-molecule (QTAIM) analyses94,95 in which the properties of the metal-complexes are represented in terms of electron density critical points at which the gradients of electron densities vanish. A bond critical point (BCP) is located between two atomic centers and denotes the presence of a bond. A good example to illustrate this is to compare the hydrogen bonding in the lowest-energy conformations of the [Fe(NO3)(H2O)5]+ metal complexes using QTAIM analyses. The left side of Fig. 8 shows the BCP of the hydrogen bond between NO3− and the nearby water molecule for the monodentate conformation of [Fe(NO3)(H2O)5]+. The QTAIM analyses predict a binding energy of about 14 kcal mol−1 for this hydrogen bond corresponding to a medium hydrogen bond.95,96 A similar QTAIM analysis for the lowest-energy monodentate conformation of [Sr(NO3)(H2O)5]+ confirms that the hydrogen bond between NO3− and the nearby water molecule is a medium hydrogen bond (a binding energy of 13 kcal mol−1). On the other hand, the right side of Fig. 8 shows the BCP of the hydrogen bond between the outer-shell water molecule and the two nearby water molecules for the lowest energy bidentate conformation of [Fe(NO3)(H2O)5]+. The QTAIM analyses for each of these two hydrogen bonds predict their binding energies around 6–7 kcal mol−1 corresponding to weak-to-medium hydrogen bonds. Therefore, the binding energy of a hydrogen bond between NO3− and a water molecule in the first solvation shell is almost twice as much as the one between two water molecules in metal–nitrate complexes when they can form close to the first solvation shell.
Similar Wernet and QTAIM analyses of the studied [M(H2O)x]n+ reactants show no signatures of hydrogen bonding within the first solvation shell. Therefore, at this CSM level of theory, one can conclude that the hydrogen bonding mainly stabilizes the metal–nitrate products. In the monodentate conformations of the products, the primary hydrogen bond is present between NO3− and water molecules while in the bidentate conformations, this type of hydrogen bonding plays no significant role. Interestingly, as discussed above (Fig. 8) for the seven-coordinated Fe metal–nitrate bidentate complexes, hydrogen bonds between water molecules can also contribute to the stabilization of the metal–nitrate complexes while for the other studied metal–nitrate bidentate conformations, no signatures of hydrogen bonds are found. Considering the limitations of CSM used in this work, this might suggest that the hydrogen bonds between NO3− and water molecules can be attributed as one of the driving forces to form the monodentate conformations while they are not very significant for the formation of the bidentate conformations. However, complete analyses of hydrogen bonding effects on the reaction free energies require incorporating more hydration shells for both reactants and products. Therefore, in the next sections we hesitate to report hydrogen bonds effects on the reaction free energies in the CSM framework using the first solvation shells. This is an interesting future project to study the roles of hydrogen bonding on the reaction free energies using the condensed-phase AIMD simulations.79
3.2 Ligand-exchange reactions
Formations of bidentate and monodentate conformations can have significant effects on the ligand-exchange reactions. Per the calculations and arguments above, in this section, we suggest the following ligand-exchange reactions of the NO3− ligand in the hydrated metal complexes to form [M(NO3)(H2O)x](n−1)+ within the CSM framework at the DFT/B3LYP level of theory: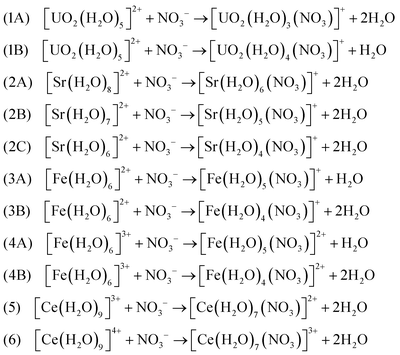 | (3) |
Several comments about these reactions should be noted. Reaction 1A implies that a coordination number of 5 is conceived for [UO2(H2O)3(NO3)]+ and NO3− attaches to U in a bidentate conformation. The reason that reaction 1B is also considered for the UO22+ metal complex with the bidentate conformation, is due to the fact that four water molecules tend to remain close to the first solvation shell, which is confirmed by several independent AIMD simulations (see Section 3.1.3) as well as inorganic textbooks.38
There exists an uncertainty in the coordination numbers of Sr2+. Consistent with previous studies,56 here we consider the coordination numbers of 7 and 8 to be reasonable (reactions 2A and 2B) noting that the NO3− ligand attaches to Sr2+ in bidentate conformations. The coordination number of 6 for Sr2+ (reaction 2C) is mainly investigated in this work to study the sensitivity of the thermodynamic quantities to the coordination numbers. However, the AIMD simulations at CSM level suggest that the coordination numbers of 8 and 7 are more probable than 6.
The competitions between the monodentate and bidentate conformations for iron–nitrate metal complexes are considered in reactions 3A and 4A, where their products can be both monodentate and bidentate with slightly different energies. Therefore, the reaction properties estimated by eqn (2) can provide some insights about these competitions and the roles of entropy and energetics on their reaction free energies. On the other hand, simple stoichiometry analyses of reactions show that entropy can play a significant role in reactions 3B and 4B. Similar statement can be made for reactions 5 and 6 for [Ce(H2O)7(NO3)]3+ metal–nitrate complexes, where the bidentate conformations dominate. These statements will be demonstrated quantitatively in the next section.
3.3 Stability constants
Table 2 reports the calculated thermodynamical quantities for the reactions presented in eqn (3) for the metal complexes of interest. Interestingly, all reactions are favorable with negative ΔG values. When the bidentate conformations dominate the products of the studied metal nitrate complexes with their normal coordination numbers, the reaction entropies are positive with TΔS values ranging from 5 to 8 kcal mol−1, which is due to the departures of two water molecules in reactions shown in eqn (3). Therefore, the main driving force for these reactions is mostly entropic with one main exception. For the [Ce(H2O)7(NO3)]3+ metal complexes for which the enthalpic reaction energy is about −11 kcal mol−1. On the other hand, when monodentate conformations dominate the products, the reaction entropies are negative with TΔS values ranging from −4 to −1 kcal mol−1 showing that for these reactions the driving force is mostly enthalpic with the negative enthalpic contributions with magnitudes ranging from −15 to −6 kcal mol−1.| Metal ion | Reaction | S | ΔEtot (kcal mol−1) | ΔrH (kcal mol−1) | TΔrS (kcal mol−1) | ΔrG (kcal mol−1) |
|---|---|---|---|---|---|---|
| Lowest energy conformers | ||||||
| UO22+ | 1A | 1 | −1.5 | −3.8 | 8.3 | −12.1 |
| UO22+ | 1B | 1 | −8.6 | −9.7 | −0.8 | −8.9 |
| Sr2+ | 2A | 1 | 2.5 | 1.2 | 6.6 | −5.4 |
| Sr2+ | 2B | 1 | 1.8 | 0.4 | 4.9 | −4.5 |
| Sr2+ | 2C | 1 | 3.0 | 1.8 | 5.7 | −3.9 |
| Fe2+ | 3A | 5 | −5.8 | −6.3 | −2.9 | −3.4 |
| Fe2+ | 3B | 5 | 3.0 | 1.0 | 6.5 | −5.5 |
| Fe3+ | 4A | 6 | −16.3 | −16.3 | −2.9 | −13.4 |
| Fe3+ | 4B | 6 | −1.3 | −3.7 | 7.2 | −10.9 |
| Ce3+ | 5 | 2 | 0.8 | −0.3 | 6.6 | −6.8 |
| Ce4+ | 6 | 1 | −7.6 | −10.8 | 8.0 | −18.8 |
| Boltzmann averaging: all structures | ||||||
| UO22+ | 1A | 1 | −1.5 | −3.9 | 7.4 | −11.3 |
| UO22+ | 1B | 1 | −8.7 | −9.0 | −2.7 | −6.3 |
| Sr2+ | 2A | 1 | 2.4 | 1.2 | 5.6 | −4.4 |
| Sr2+ | 2B | 1 | 1.3 | −0.1 | 5.0 | −5.1 |
| Sr2+ | 2C | 1 | 2.9 | 1.6 | 5.3 | −3.7 |
| Fe2+ | 3A | 5 | −5.9 | −6.6 | −3.0 | −3.6 |
| Fe2+ | 3B | 5 | 3.2 | 0.6 | 6.8 | −6.2 |
| Fe3+ | 4A | 6 | −15.3 | −16.1 | −2.4 | −13.7 |
| Fe3+ | 4B | 6 | −0.9 | −3.8 | 7.4 | −11.2 |
| Ce3+ | 5 | 2 | 0.8 | −1.0 | 6.8 | −7.8 |
| Ce4+ | 6 | 1 | −7.6 | −11.4 | 8.9 | −20.3 |
The top and bottom panels of Table 2 report the reaction free energies for all metal complexes based on the lowest energy conformations (LECs) and their Boltzmann-average reaction free energies based on eqn (2). Generally the differences between the LEC and Boltzmann-average reaction free energies are less than 2 kcal mol−1. This confirms that when the LECs are found reasonably well, the Boltzmann-average values can provide good insights about the uncertainties associated with reaction free energies. This is particularly demonstrated for reaction 3A, where the difference between the LEC and Boltzmann-averaged reaction free energies is approximately 0.2 kcal mol−1. This discrepancy is relatively small considering that in the Boltzmann average approach, the product [Fe(H2O)5(NO3)]+ includes both monodentate and bidentate conformations. Similar observation is made for reaction 4A. On the other hand, the differences between the reaction free energies of reactions 3A/4A and 3B/4B turn out to be more than 2 kcal mol−1 noting that in reactions 3B/4B, in the CSM framework, the maximum number of sites that the Fe metal can attach to ligands is six and does not consider the possibility of other scenarios that may be important in the closest solvation shell. A similar but larger discrepancy exists for reactions 1A and 1B, noting that for [UO2(H2O)x(NO3)]+ metal complexes, the bidentate conformations dominate. These discrepancies, to the extent that they can be explained, hinge on more rigorous determinations of reaction free energies (e.g., via condensed-phase ab initio AIMD simulations) and remain an open question.
We conclude this section by presenting the following interesting trends from Table 2. It is worth mentioning that these trends can be rationalized through quantitative structure–property relationships, enabling the development of machine learning models, such as artificial neural networks,39,97 that utilize relevant descriptors.95,97–99 The exploration of such models is reserved for future studies. In this work, we focus on presenting and interpreting the observed trends based on the interplay between the metal ion's charge, ionic radius, and the bond order for the bond the metal atom and the closest oxygen atoms of NO3− in metal–nitrate complexes. As we show below the trends in the bond order metric aligns with trends observed in the reaction free energy trends.
• Among all the M2+ metal ions examined, UO22+ has the most negative (and therefore the most favorable) reaction free energy. Sr2+ follows as the next most favorable, while Fe2+ has the least negative reaction free energy among the M2+ ions. This is interesting noting that among metal–nitrate complexes, [UO2(H2O)3(NO3)]+ exhibits the highest bond order.
• About 1.5 kcal mol−1 difference in the reaction free energies of Sr2+ is observed when the coordination number changes from six to eight.
• The reaction free energy of Fe3+ metal ion is about 11 kcal mol−1 more favorable (negative) than the one for the Fe2+ metal ion, which is in general consistent with the Mayer bond order analysis in which [Fe(H2O)5(NO3)]2+ has a higher bond order than [Fe(H2O)5(NO3)]+. In addition, the ionic radius Fe3+ is greater than Fe2+.
• The reaction free energy of Fe3+ metal ion is about 5 kcal mol−1 more favorable (negative) than the one for the Ce3+ metal ion. This is also in general consistent with the Mayer bond order analysis in which [Fe(H2O)5(NO3)]2+ has a higher bond order than [Ce(H2O)7(NO3)]2+. In addition, the ionic radius Fe3+ is greater than Ce3+.
• The reaction free energy of Ce4+ metal ion is about 12 kcal mol−1 more favorable (negative) than the one for the Ce3+ metal ion, which is consistent with the trends in the Mayer bond orders and ionic radius trends.
• The reaction free energies are more favorable (negative) for metal ions with larger positive charge. In particular, Ce4+ shows the most favorable reaction free energy followed by Fe3+, and then UO22+. This trend is supported by the trends in the Mayer bond orders as discussed above. The ionic radius of Ce4+ is 0.87 Å and the ionic radius of Fe3+ is 0.65 Å; therefore, the ionic radius trend breaks down for this case of comparison.
In the next section, we provide a method to compare these reaction free energies with the experimental ones by accounting for the factors that cannot be directly or easily implemented in the CSM framework.
3.4 Comparison with available experimental data
A direct comparison of the computational DFT results with the experimental stability constants is not straightforward considering there are various sources of errors in both experiments and calculations.100 Experimental measurements of stability constants can be subject to systematic, methodological, and random errors.101–106 Importantly, methodological errors may occur in experiments due to incorrect assumptions about the nature of the metal complexes and various species formed in solution during the experiments. In addition, systematic errors can happen due to calibration errors in equipment (e.g., pH meters, spectrophotometers), impurities in reagents or solvents, and ionic strength controls, and random errors can originate from inherent instrumental noise.Similar to experiments, various errors can occur in DFT calculations in the framework of CSM. In general, when one fails to locate the lowest energy conformations of metal complexes, random errors can occur. The larger the metal complexes, the more challenging it is to locate the lowest energy conformation, and more errors can be introduced when predicting the stability constants of reactions in the CSM framework. Such random errors may be mitigated by making use of advanced conformational search algorithms52–54 as used in this workflow. The influence of methodological choices (e.g., basis sets and exchange–correlation functionals) is addressed in Section 3.5. In addition, systematic errors can occur when the reactants or products are represented as reduced models in which a few solvent water molecules may surround them. Therefore, insufficient representations of solvation structures in the framework of CSM can, in general, be one source of systematic errors.107 In this work, it is assumed that metal complexes are represented by the first solvation shells and one water and one NO3− ion are representatives of side-products and reactants (NO3− and H2O in eqn (3)), respectively. Alternatively, one can solvate NO3− and H2O with several water molecules to address the effect of solvation structure on the overall reaction. However, finding the lowest energy conformations becomes very challenging as the number of water molecules increases to represent the solvation structures for NO3− and H2O and in the framework of CSM, it is plausible to use the first solvation shell. Therefore, systematic errors exist for all reported thermodynamic quantities by using a reduced solvation structure. In what follows, we present a simple procedure based on linear free energy relations45 to correct the systematic errors in calculations.
Linear free energy relations have been successfully used to estimate the stability constants of various metal complexes.45,46 Following these lines, one can estimate the systematic errors in calculations by comparing the calculated free energies with the ones from the experimental data (see Appendix A for details). Table 3 compares the corrected theoretical reaction free energies with the available experimental data from the NIST database108 for the first addition of NO3− to hydrated metal complexes. Several observations are noteworthy for the studied reaction free energies:
• Both experimental and theoretical results indicate that reaction free energy for Ce4+ is about 0.2–0.3 kcal mol−1 more favorable than the one for Ce3+ consistent with the fact the charge density of Ce4+ is higher than Ce3+.
• Both experimental and theoretical results indicate that reaction free energy for Fe3+ with an empirical radius of 0.65 Å is more favorable than the one for Ce3+ with an empirical radius of 1.0 Å.38 This is more pronounced in experiments noting that the ionic strength changes in the experiments.
• Experimentally, the reaction free energy for Fe3+ is most negative (−1.36 kcal mol−1) while theoretically the reaction free energy for Ce4+ is most negative (−1.09 kcal mol−1). The origin of the discrepancy may be attributed to ionic strength of 3.5 used in experiments for Ce4+ and other assumptions used in the analyses of experiments and optimized structures as discussed above. Simple estimations of charge densities for [Ce(H2O)9]4+ and [Fe(H2O)6]3+ (see ESI†) show that their charge densities are almost the same while the charge density of [Ce(H2O)7(NO3)]3+ is higher than the charge density of [Fe(H2O)5(NO3)]2+ by about 25%.
• Experimentally, the reaction free energy for UO22+ is less negative than the one for Sr2+ while theoretically the reaction free energy for UO22+ is more negative. Such discrepancies may indicate the significance of errors in the experimental measurements. In fact, ref. 102 states that the experimental thermodynamical data for nitrate complexes are of doubtful significance. When one considers the empirical ionic radius of UO22+ (0.89 Å) is smaller than Sr2+ (1.18 Å),38 one can notice that the charge density of the UO22+ ion is significantly higher than that of the Sr2+ ion, which is supported by simple charge density calculations for [UO2(H2O)5]2+ and [Sr(H2O)7]2+ (see ESI†). However, the charge density of [UO2(H2O)3(NO3)]+ is only 5% higher than the charge density of [Sr(H2O)5(NO3)]+.
• Theoretical results indicate that reaction free energy for Fe3+ is about 0.3 kcal mol−1 more favorable than the one for Fe2+ noting that no experimental data is available for Fe2+.
3.5 Sensitivity of calculations
In this section, we study the reaction free energies using different functionals and basis sets. In particular, we compare the results for BLYP,19 PBE,20 and B3LYP18,65–68 functionals, which have different levels of exchange–correlation treatment. These functionals span a range of Jacob's ladder,109 with BLYP and PBE as a pure generalized gradient approximation (GGA) functionals, offering computational efficiency without Hartree–Fock exchange. B3LYP is a hybrid functional, which mixes some exact (Hartree–Fock) exchange with GGA (BLYP) exchange for improved accuracy in systems with localized electrons, albeit at higher computational cost. This selection provides a relatively comprehensive analysis of functional performance across varying exchange–correlation treatments. These DFT functionals are used with the ECP-type basis sets that involve Stuttgart RSC 1997 ECP,69,70 Stuttgart RLC 1997 EPC,69,70 and Lanl2dz ECP.110Detailed analyses of the calculated thermodynamical properties are presented in Appendix B, which indicate that the difference in reaction free energies from different functionals and basis sets can be as high as 6 kcal mol−1 without applying linear free energy corrections. Here we report the reaction free energies with linear free energy corrections46 (see Appendix A) and focus on their significance when compared with experimental stability constants. Table 4 shows the sensitivities of the reaction free energies (with the linear free energy corrections) of reactions 1A and 1B involving [UO2(H2O)5]2+ metal complexes in eqn (3) to the choices of the functionals and basis sets. The top part of Table 4 presents the free energies from the lowest energy conformation while the bottom panel shows the free energies from the Boltzmann averaging from the workflow discussed earlier. In general, the free energies estimated from all functionals and ECP-type basis sets are about 2–3 times larger than the reported experimental values noting that the complex chemistry of uranyl ion has introduced special challenges in the experimental determination of thermodynamical properties.101,102 However, the difference between theoretical and experimental values is only about 0.5–0.7 kcal mol−1 after the free energies in the CSM model have been corrected with the linear free energy approach. Therefore, establishing linear free energy corrections for a given reaction free energy calculated in the CSM framework is significant. The results in Table 4 show that the difference between the reaction free energies obtained from various functionals and basis sets is about 0.4 kcal mol−1, which is relatively small.
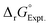 is reported as −0.41 kcal mol−1
is reported as −0.41 kcal mol−1
| Functional | Reaction | Basis set | |
|---|---|---|---|
| Lowest energy conformers | |||
| B3LYP | 1A | LANL2DZ | −0.87 |
| B3LYP | 1A | Stuttgart RSC | −0.91 |
| BLYP | 1A | Stuttgart RSC | −1.0 |
| PBE | 1A | Stuttgart RSC | −1.1 |
| B3LYP | 1B | LANL2DZ | −0.83 |
| B3LYP | 1B | Stuttgart RLC | −0.73 |
| B3LYP | 1B | Stuttgart RSC | −0.83 |
| BLYP | 1B | Stuttgart RSC | −0.97 |
| PBE | 1B | Stuttgart RSC | −0.88 |
| Boltzmann averaging: all structures | |||
| B3LYP | 1A | LANL2DZ | −0.91 |
| B3LYP | 1A | Stuttgart RSC | −0.89 |
| BLYP | 1A | Stuttgart RSC | −1.0 |
| PBE | 1A | Stuttgart RSC | −1.1 |
| B3LYP | 1B | LANL2DZ | −0.84 |
| B3LYP | 1B | Stuttgart RLC | −0.72 |
| B3LYP | 1B | Stuttgart RSC | −0.76 |
| BLYP | 1B | Stuttgart RSC | −0.97 |
| PBE | 1B | Stuttgart RSC | −0.89 |
4 Summary and conclusions
We have successfully used cloud computing resources (Azure Quantum Elements of Microsoft33,34) to develop a computational workflow to determine the coordination chemistry of metal–nitrate complexes and calculate the stability constants of ligand-exchange reactions. In particular, we have demonstrated that the computational workflow can determine the reaction free energies of additions of NO3− to hydrated metal ions in the CSM framework at DFT level of theory by exploring a large number of conformations and various coordination numbers of metal ions. Therefore, this study demonstrates that cloud environments can be adapted and optimized to meet the high demands of high-performance computing (HPC) workloads.The computational workflow starts from the best-guess conformations obtained either from previous literature, AIMD simulations, or standard procedures using molecular mechanics or molSimplify (see Fig. 1). Added to these conformations, the workflow performs a conformational search using enhanced sampling MD techniques with low-level electronic structure calculations. Based on energy criteria, 20–40 conformations are selected and optimized at a high-level theory whose stabilities are checked by independent DFT MD simulations at the same level of theory. If they are stable, then the lowest energy conformations are determined from all selected conformations including the ones from the latter DFT MD simulations. Otherwise, the workflow adjusts the conformations and iterates.
The lowest energy conformations for the hydrated metal ions, [M(H2O)x]n+, of UO22+, Sr2+, Fe2+, Fe3+, Ce3+, and Ce4+ are shown in Fig. 2 suggesting that the coordination numbers are 5, 7, 6, 6, 9, and 9, respectively. The workflow predicts that when one NO3− ion reacts with [M(H2O)x]n+, one or two water molecules may leave them, resulting in monodentate and bidentate conformations. For the iron metal–nitrate complexes of Fe2+ and Fe3+, the workflow shows that monodentate and bidentate conformations can compete with each other and their energy differences can be on the order of thermal motions. This is also confirmed by AIMD simulations in the CSM framework which the monodentate conformations can transition to the bidentate conformations. These results are consistent with the previous periodic condensed-phase ab initio MD simulations for CO32− ion.80 On the other hand, the other metal ions mainly prefer the bidentate conformations keeping their coordination numbers the same as [M(H2O)x]n+ metal complexes. Overall, the workflow predicts the reactions presented in eqn (3) from which it calculates the reaction free energies. Interestingly, the workflow allows one to get the Boltzmann average reaction free energies by taking a weighted average of the free energies of possible reaction states. Comparing Boltzmann average reaction free energies and the reaction free energies from the lowest energy conformation shows that their differences are usually less than 10%.
The conformational searches and reaction free energy calculations in the workflow only involve the first solvation shells, which allows one to reasonably find the lowest conformations through advanced conformational searches.53,54 An advantage of this workflow is its ability to explore higher coordination numbers for a given metal complex, as demonstrated with [Fe(NO3)(H2O)5]1+/2+ and [Fe(NO3)(H2O)4]1+/2+ in Section 3.1.1. The findings underscore the importance of carefully designing the first solvation shell within the CSM framework. Specifically, metal–nitrate complexes with a coordination number of 7 are prevalent in bidentate conformations of [Fe(NO3)(H2O)5]1+/2+, whereas steric constraints limit the coordination number to 6 for [Fe(NO3)(H2O)4]1+/2+ in the resulting bidentate conformations.
It becomes vastly more difficult if the computational workflow includes the second and higher solvation shells. In this regard, the workflow uses linear free energy relations to correct the systematic errors that occur in the computations due to the absence of the higher solvation shells in the CSM framework. The linear free energy approach only requires a few experimental data, which are often available and can be applied to the newly calculated free energy of reactions whose experimental values are unavailable. Table 3 presents the resulting reaction free energies from the workflow and compares them with the experimental values. In general, the workflow reaction free energies are in good agreement with the experimental results with deviations that may be attributed to experimental uncertainties. The general trend in the workflow predictions shows that the stability constants are largest for Ce4+ and Fe3+ having the highest charge densities for [M(H2O)x]n+. The trend in the calculated reaction free energies align well with the trend in the Mayer bond order92 for the bond between the metal and the closest oxygen of NO3− ligand. Interestingly, the experimental data shows that the stability constant for Fe3+ is largest while the stability constant for Ce4+ (at an ionic strength of 3.5) is among the lowest ones. Unlike the reported experimental data, the reaction free energy of UO22+ from the workflow is close to the one for Fe3+ and it is about 0.5 kcal mol−1 more negative resulting in relatively high theoretical stability constants among the studied metal ions. Such discrepancies might be attributed to errors in the experiments as stated in ref. 102 but its remains to future studies to explain them.
In this study, the stability constants are calculated based on relatively simple coordination and bonding chemistry by excluding the complexities that may arise due to the inclusion of higher hydration shells.28,81,111 The sensitivity of reaction free energies to various functionals and basis sets are reported for the UO22+ reaction using the linear free energy corrections. The differences between the reaction free energies for all functionals and basis sets turn out to be less than 0.5 kcal mol−1 showing the significance of linear free energy relations for the workflow calculations. The effects of concentrations, ionic strength, speciations, and pH in the CSM framework on the reaction free energies may be incorporated using standard thermodynamic equations.112,113 An extension would be to study these reactions with explicit modeling of higher solvation shells in the condensed phase ab initio molecular simulation techniques at various ionic strengths.79–85 This is the subject of future studies, where we are exploring machine learning potentials,85,114,115 which can significantly increase the time and length scales accessible in MD simulations.85
In summary, we demonstrate that one can use cloud computing resources to carry out a relatively complex computational workflow equipped with conformational searches to predict the coordination chemistry and the resulting stability constants of various alkaline earth, transition, actinide, and lanthanide metal–nitrate complexes in the CSM framework relevant to the separation processes. This is accompanied by applying linear free energy relations to report the stability constants that show good agreement the experimental values. In a future work, our cloud computing workflow will be further developed to study the stability constants for bis, tris, tetrakis metal nitrate complexes in aqueous solutions and the metal complexes involving water, nitrate and organic molecules in various resins. These data will be used to develop a generative artificial intelligence approach to predict more complex chemical reactions relevant to separation and nuclear forensics projects.
Data availability
The ESI† includes the optimized structures of the studied metal complexes and the related structural analyses.Conflicts of interest
There are no conflicts to declare.Appendices
A Determination of reaction free energies: systematic errors & linear free energy relations
As discussed in the main text, the main source of systematic errors in the CSMs can arise from an insufficient number of solvent molecules (inaccurate solvent structure) around the reactants and products. Interestingly, when one increases the number of solvent molecules around the reactants or products, finding the minimum structures becomes extremely challenging, introducing more errors. Therefore, one may argue that it is plausible to keep the system size small in the CSM framework and find alternative ways to correct the systematic errors in the theoretical/computational data when compared to the experimental data. In this regard, one can use a linear correction model. One can assume that the systematic errors are consistent across all data points. Let's denote the available experimental data points (reaction free energies) as e = (e1, e2, …, en) and the corresponding calculated data as c = (c1, c2, …, cn). To correct the systematic errors, one can consider a linear regression model of the form:| ei = a·ci + b | (4) |
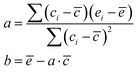 | (5) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) and ē the means of the calculated and experimental data, respectively, and can be determined using least-square fitting. Another feature of this linear free energy correction is that it can capture the standard-state corrections for comparisons with the experimental solution-phase free energies. Since the solvent (water) concentration remains nearly constant in the studied ligand-exchange reactions, linear free energy corrections can be applied to capture the standard-state corrections13,47,112,113 for the formation of metal–nitrate complexes, whether in monodentate or bidentate conformations (see Tables 3 and 4). A more rigorous connection between the coefficients of linear free energy approach and the standard-state corrections is the subject of future research.
and ē the means of the calculated and experimental data, respectively, and can be determined using least-square fitting. Another feature of this linear free energy correction is that it can capture the standard-state corrections for comparisons with the experimental solution-phase free energies. Since the solvent (water) concentration remains nearly constant in the studied ligand-exchange reactions, linear free energy corrections can be applied to capture the standard-state corrections13,47,112,113 for the formation of metal–nitrate complexes, whether in monodentate or bidentate conformations (see Tables 3 and 4). A more rigorous connection between the coefficients of linear free energy approach and the standard-state corrections is the subject of future research.
Once a and b are known for a given set of reactions, one can apply the correction to any related calculated data points, ccorrected, as
| ccorrected = a·c + b | (6) |
In this study, we used three experimental data, namely, the data available for the first addition of NO3− for UO22+, Sr2+, and Fe3+ metal complexes as presented in Table 3 to empirically determine a and b as 0.026 and −0.59 kcal mol−1, respectively.
B Choice of functionals and basis sets
In this section, we study the reaction free energies using different functionals and basis sets. The DFT functionals are based on the local electron density and its gradient, and include B3LYP (hybrid),18 BLYP (non-hybrid),19 and PBE (non-hybrid)20 functionals. In general, B3LYP is often used for molecular systems while PBE might be preferred for solid-state applications and BLYP can be a good choice for systems where dispersion interactions play a significant role. The ECP-type basis sets involve Stuttgart RSC 1997 ECP,69,70 Stuttgart RLC 1997 EPC,69,70 and Lanl2dz ECP,110 which are widely used ECP-type basis sets and it is commonly observed that for various properties the RLC ECPs tend to produce less accurate results than those using RSC ECPs and Lanl2dz ECP.116Table 5 compares the reaction free energies obtained using the workflow at different levels of theory with the functionals of B3LYP, BLYP, and PBE for UO22+ metal complexes. We also show the sensitivity of the thermodynamic properties to various basis sets.
| Functional | Reaction | Basis set | ΔEtot (kcal mol−1) | ΔrH (kcal mol−1) | TΔrS (kcal mol−1) | ΔrG (kcal mol−1) |
|---|---|---|---|---|---|---|
| Lowest energy conformers | ||||||
| B3LYP | 1A | LANL2DZ | −2.1 | −3.8 | 6.6 | −10.4 |
| B3LYP | 1A | Stuttgart RSC | −1.5 | −3.8 | 8.3 | −12.1 |
| BLYP | 1A | Stuttgart RSC | −3.5 | −6.1 | 9.6 | −15.7 |
| PBE | 1A | Stuttgart RSC | −4.8 | −8.0 | 9.7 | −17.7 |
| B3LYP | 1B | LANL2DZ | −11.5 | −11.7 | −2.8 | −8.9 |
| B3LYP | 1B | Stuttgart RLC | −7.8 | −8.0 | −2.8 | −5.2 |
| B3LYP | 1B | Stuttgart RSC | −8.6 | −9.7 | −0.8 | −8.9 |
| BLYP | 1B | Stuttgart RSC | −13.3 | −14.5 | −0.1 | −14.4 |
| PBE | 1B | Stuttgart RSC | −11.7 | −12.4 | −1.4 | −11.0 |
| Boltzmann averaging: all structures | ||||||
| B3LYP | 1A | LANL2DZ | −2.2 | −4.4 | 7.7 | −12.1 |
| B3LYP | 1A | Stuttgart RSC | −1.5 | −3.9 | 7.4 | −11.3 |
| BLYP | 1A | Stuttgart RSC | −3.4 | −6.2 | 9.8 | −16.0 |
| PBE | 1A | Stuttgart RSC | −4.9 | −8.0 | 10.2 | −18.2 |
| B3LYP | 1B | LANL2DZ | −11.5 | −11.9 | −2.4 | −9.5 |
| B3LYP | 1B | Stuttgart RLC | −7.7 | −7.9 | −3.0 | −4.9 |
| B3LYP | 1B | Stuttgart RSC | −8.7 | −9.0 | −2.7 | −6.3 |
| BLYP | 1B | Stuttgart RSC | −13.3 | −14.6 | −0.4 | −14.2 |
| PBE | 1B | Stuttgart RSC | −12.3 | −12.8 | −1.6 | −11.2 |
Acknowledgements
We thank Edoardo Aprà, Eric J. Bylaska, Shawn M. Kathmann, John L. Fulton, Christopher J. Mundy, Paul Rigor, Daniel Mejia-Rodriguez, and Gregory K. Schenter for their helpful discussions. The research described herein was funded by the Generative AI for Science, Energy, and Security Science & Technology Investment under the Laboratory Directed Research and Development Program at Pacific Northwest National Laboratory (PNNL), a multiprogram national laboratory operated by Battelle for the U.S. Department of Energy. This work was also supported by the Center for AI and Center for Cloud Computing at PNNL.Notes and references
- K. Adamczyk, M. Prémont-Schwarz, D. Pines, E. Pines and E. T. J. Nibbering, Science, 2009, 326, 1690–1694 CrossRef CAS PubMed
.
- D. Qi, Z. Ouyang, L. Chen, Y. Wu, R. Lei, B. Chen, R. A. Feely, L. G. Anderson, W. Zhong, H. Lin, A. Polukhin, Y. Zhang, Y. Zhang, H. Bi, X. Lin, Y. Luo, Y. Zhuang, J. He, J. Chen and W.-J. Cai, Science, 2022, 377, 1544–1550 CrossRef CAS PubMed
.
- M. P. Dudukovic, Science, 2009, 325, 698–701 CrossRef CAS PubMed
.
- T. Cheisson and E. J. Schelter, Science, 2019, 363, 489–493 CrossRef CAS PubMed
.
- D. E. Hanson, J. R. Garrison and H. L. Hall, J. Radioanal. Nucl. Chem., 2011, 289, 213–223 CrossRef CAS
.
- M. D. Straub, J. Arnold, J. Fessenden and J. L. Kiplinger, Anal. Chem., 2021, 93, 3–22 CrossRef CAS PubMed
.
- M. S. Wren, A. B. Weberg, A. A. Salazar, M. R. Klosterman, S. J. Eaton, T. L. Goehring, S. M. Herman, B. D. Pierson, E. J. Warzecha, G. E. Dale, N. Fotiades, I. May and S. K. Hanson, Talanta, 2024, 275, 126140 CrossRef CAS PubMed
.
- F. M. Burrell, P. E. Warwick, I. W. Croudace and W. S. Walters, Analyst, 2021, 146, 4049–4065 RSC
.
- D. R. McAlister, H. Kurosaki, S. Happel and E. P. Horwitz, Bunseki, 2020, 2, 44–50 Search PubMed
.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC
.
- D. M. York and M. Karplus, J. Phys. Chem. A, 1999, 103, 11060–11079 CrossRef CAS
.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed
.
-
C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, Johns Wiley & Sons Ltd, 2004 Search PubMed
.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS PubMed
.
- J. Ho and M. Z. Ertem, J. Phys. Chem. B, 2016, 120, 1319–1329 CrossRef CAS PubMed
.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef
.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- Y. Zhang, S. Mukamel, M. Khalil and N. Govind, J. Chem. Theory Comput., 2015, 11, 5804–5809 CrossRef CAS PubMed
.
- M. Ross, A. Andersen, Z. W. Fox, Y. Zhang, K. Hong, J.-H. Lee, A. Cordones, A. M. March, G. Doumy and S. H. Southworth,
et al.
, J. Phys. Chem. B, 2018, 122, 5075–5086 CrossRef CAS PubMed
.
- D. R. Nascimento, E. Biasin, B. I. Poulter, M. Khalil, D. Sokaras and N. Govind, J. Chem. Theory Comput., 2021, 17, 3031–3038 CrossRef CAS PubMed
.
- D. Boglaienko, A. Andersen, S. M. Heald, T. Varga, D. R. Mortensen, S. Tetef, G. T. Seidler, N. Govind and T. G. Levitskaia, J. Alloys Compd., 2022, 897, 162629 CrossRef CAS
.
- S. Ghosh, H. Agarwal, M. Galib, B. Tran, M. Balasubramanian, N. Singh, J. L. Fulton and N. Govind, J. Phys. Chem. Lett., 2022, 13, 6323–6330 CrossRef CAS PubMed
.
- D. Mejia-Rodriguez, A. A. Kunitsa, J. L. Fulton, E. Aprà and N. Govind, J. Phys. Chem. A, 2023, 127, 9684–9694 CrossRef CAS PubMed
.
- C. B. Larsen, K. Ledbetter, D. R. Nascimento, E. Biasin, M. Qureshi, S. H. Nowak, D. Sokaras, N. Govind and A. A. Cordones, J. Am. Chem. Soc., 2024, 146, 28561–28571 CAS
.
- N. N. Intan, B. A. Sorenson, Y. K. Choi, J. J. Choi, J. L. Fulton, N. Govind, S. D. Kelly, G. K. Schenter, P. Clancy and C. J. Mundy, Chem. Mater., 2024, 36, 8424–8436 CrossRef CAS
.
- G. Prampolini, A. Andersen, B. I. Poulter, M. Khalil, N. Govind, E. Biasin and M. Pastore, J. Chem. Theory Comput., 2024, 20, 1306–1323 CrossRef CAS PubMed
.
- J. P. Janet and H. J. Kulik, Chem. Sci., 2017, 8, 5137–5152 RSC
.
- S. Roy Chowdhury and S. Mishra, J. Chem. Phys., 2018, 149, 234302 CrossRef PubMed
.
- S. Roy Chowdhury, N. Nguyen and B. Vlaisavljevich, J. Phys. Chem. A, 2023, 127, 3072–3081 CrossRef CAS PubMed
.
- E. J. Bylaska, A. Panyala, N. P. Bauman, B. Peng, H. Pathak, D. Mejia-Rodriguez, N. Govind, D. B. Williams-Young, E. Aprà, A. Bagusetty, E. Mutlu, K. A. Jackson, T. Baruah, Y. Yamamoto, M. R. Pederson, K. P. K. Withanage, J. N. Pedroza-Montero, J. A. Bilbrey, S. Choudhury, J. Firoz, K. M. Herman, S. S. Xantheas, P. Rigor, F. D. Vila, J. J. Rehr, M. Fung, A. Grofe, C. Johnston, N. Baker, K. Kaneko, H. Liu and K. Kowalski, J. Chem. Phys., 2024, 161, 150902 CrossRef CAS PubMed
.
- Microsoft, Azure, https://azure.microsoft.com, 2024, Cloud computing service.
- A. M. Maldonado, S. Hagiwara, T. H. Choi, F. Eckert, K. Schwarz, R. Sundararaman, M. Otani and J. A. Keith, J. Phys. Chem. A, 2021, 125, 154–164 CrossRef CAS PubMed
.
- G. Norjmaa, G. Ujaque and A. Lledós, Top. Catal., 2022, 65, 118–140 CrossRef CAS
.
- P. Söderlind, O. Eriksson, B. Johansson, J. M. Wills and A. M. Boring, Nature, 1995, 374, 524–525 CrossRef
.
-
F. A. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, Advanced Inorganic Chemistry, Wiley-Interscience, 6th edn, 1999 Search PubMed
.
- E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, J. Comput. Chem., 2016, 37, 2106–2117 CrossRef CAS PubMed
.
- A. Nandy, C. Duan, J. P. Janet, S. Gugler and H. J. Kulik, Ind. Eng. Chem. Res., 2018, 57, 13973–13986 CrossRef CAS
.
- S. Vukovic, B. P. Hay and V. S. Bryantsev, Inorg. Chem., 2015, 54, 3995–4001 CrossRef CAS PubMed
.
- D. T. Gomez, L. R. Pratt, D. N. Asthagiri and S. B. Rempe, Acc. Chem. Res., 2022, 55, 2201–2212 CrossRef CAS PubMed
.
- J. R. Rustad, D. A. Dixon, K. M. Rosso and A. R. Felmy, J. Am. Chem. Soc., 1999, 121, 3234–3235 CrossRef CAS
.
- D. Devarajan, P. Lian, S. C. Brooks, J. M. Parks and J. C. Smith, ACS Earth Space Chem., 2018, 2, 1168–1178 CrossRef CAS
.
- P. W. Dimmock, P. Warwick and R. A. Robbins, Analyst, 1995, 120, 2159–2170 RSC
.
- N. E. Uhnak, Sep. Sci. Technol., 2018, 53, 725–733 CrossRef CAS
.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed
.
-
D. A. McQuarrie, Statistical Mechanics, University Science Books, New York, 2000 Search PubMed
.
- J. R. Rustad and E. J. Bylaska, J. Am. Chem. Soc., 2007, 129, 2222–2223 CrossRef CAS PubMed
.
- L. T. Wille and J. Vennik, J. Phys. A:Math. Gen., 1985, 18, L419 CrossRef CAS
.
- D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288–291 CrossRef CAS PubMed
.
- M. Steiner, T. Holzknecht, M. Schauperl and M. Podewitz, Molecules, 2021, 26, 1793 CrossRef CAS PubMed
.
- R. A. Talmazan and M. Podewitz, J. Chem. Inf. Model., 2023, 63, 5400–5407 CrossRef CAS PubMed
.
- P. Pracht, S. Grimme, C. Bannwarth, F. Bohle, S. Ehlert, G. Feldmann, J. Gorges, M. Müller, T. Neudecker, C. Plett, S. Spicher, P. Steinbach, P. A. Wesołowski and F. Zeller, J. Chem. Phys., 2024, 160, 114110 CrossRef CAS PubMed
.
- E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Brunauer, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning Jr, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102 CrossRef PubMed
.
- I. Persson, Liquids, 2022, 2, 210–242 CrossRef CAS
.
- P. Nichols, E. J. Bylaska, G. K. Schenter and W. de Jong, J. Chem. Phys., 2008, 128, 124507 CrossRef PubMed
.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS
.
- Avogadro Chemistry, Avogadro, https://avogadro.cc/.
- L. X. Dang, G. K. Schenter and J. L. Fulton, J. Phys. Chem. B, 2003, 107, 14119–14123 CrossRef CAS
.
- J. L. Fulton, E. J. Bylaska, S. Bogatko, M. Balasubramanian, E. Cauët, G. K. Schenter and J. H. Weare, J. Phys. Chem. Lett., 2012, 3, 2588–2593 CrossRef CAS PubMed
.
- C. A. Buchanan, D. Herrera, M. Balasubramanian, B. R. Goldsmith and N. Singh, JACS Au, 2022, 2, 2742–2757 CrossRef CAS PubMed
.
- D. M. York and M. Karplus, J. Phys. Chem. A, 1999, 103, 11060–11079 CrossRef CAS
.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2021, 11, e1493 CAS
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed
.
- M. N. S. H. Vosko and L. Wilk, Can. J. Phys., 1980, 58, 1200–1211 CrossRef
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS
.
- P. J. Stephens, F. J. Devlin, C. S. Ashvar, C. F. Chabalowski and M. J. Frisch, Faraday Discuss., 1994, 99, 103–119 RSC
.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS
.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS
.
- V. S. Bryantsev, M. S. Diallo, A. C. T. van Duin and W. A. I. Goddard, J. Chem. Theory Comput., 2009, 5, 1016–1026 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- Y. Yang, M. A. Ratner and G. C. Schatz, J. Phys. Chem. C, 2013, 117, 21706–21717 CrossRef CAS
.
- S. A. Fischer, T. W. Ueltschi, P. Z. El-Khoury, A. L. Mifflin, W. P. Hess, H.-F. Wang, C. J. Cramer and N. Govind, J. Phys. Chem. B, 2016, 120, 1429–1436 Search PubMed
.
- L. Helm and A. E. Merbach, Chem. Rev., 2005, 105, 1923–1960 CrossRef CAS PubMed
.
- B. Rode, C. Schwenk, T. Hofer and B. Randolf, Coord. Chem. Rev., 2005, 249, 2993–3006 CrossRef CAS
.
- S. Karimi, L. Tei, M. Botta and L. Helm, Inorg. Chem., 2016, 55, 6300–6307 Search PubMed
.
- L. Helm and A. E. Merbach, Chimia, 2019, 73, 179 CrossRef CAS PubMed
.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed
.
- K. Henzler, E. O. Fetisov, M. Galib, M. D. Baer, B. A. Legg, C. Borca, J. M. Xto, S. Pin, J. L. Fulton, G. K. Schenter, N. Govind, J. I. Siepmann, C. J. Mundy, T. Huthwelker and J. J. D. Yoreo, Sci. Adv., 2018, 4, eaao6283 CrossRef PubMed
.
- M. Pouvreau, E. Martinez-Baez, M. Dembowski, C. I. Pearce, G. K. Schenter, K. M. Rosso and A. E. Clark, Inorg. Chem., 2020, 59, 18181–18189 CrossRef CAS PubMed
.
- M. Dinpajooh, E. Biasin, E. T. Nienhuis, S. T. Mergelsberg, C. J. Benmore, G. K. Schenter, J. L. Fulton, S. M. Kathmann and C. J. Mundy, J. Chem. Phys., 2024, 161, 151102 CrossRef CAS PubMed
.
- M. Dinpajooh, N. N. Intan, T. T. Duignan, E. Biasin, J. L. Fulton, S. M. Kathmann, G. K. Schenter and C. J. Mundy, J. Chem. Phys., 2024, 161, 230901 CrossRef CAS PubMed
.
- A. Gomez, M. de la Puente, R. David and D. Laage, C. R. Chim., 2024, 1–17 CrossRef CAS
.
- R. David, M. de la Puente, A. Gomez, O. Anton, G. Stirnemann and D. Laage, Digital Discovery, 2025, 4, 54–72 Search PubMed
.
- H. Schmidt, A. Asztalos, F. Bok and W. Voigt, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 2012, 68, i29–i33 CrossRef CAS PubMed
.
- H. S. Soo, M. T. Sougrati, F. Grandjean, G. J. Long and C. J. Chang, Inorg. Chim. Acta, 2011, 369, 82–91 CrossRef CAS
.
- M. Grau, J. England, R. Torres Martin de Rosales, H. S. Rzepa, A. J. P. White and G. J. P. Britovsek, Inorg. Chem., 2013, 52, 11867–11874 CrossRef CAS
.
- F. Villafañe, Coord. Chem. Rev., 2014, 281, 86–99 CrossRef
.
- B. Ramezanpour, M. Mirzaei, V. Jodaian, M. Niknam Shahrak, A. Frontera and E. Molins, Inorg. Chim. Acta, 2019, 484, 264–275 CrossRef CAS
.
- I. Persson, Pure Appl. Chem., 2010, 82, 1901–1917 CAS
.
- I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274 CrossRef CAS
.
- P. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, M. Odelius, H. Ogasawara, L. Näslund, T. K. Hirsch, L. Ojamäe, P. Glatzel, L. G. M. Pettersson and A. Nilsson, Science, 2004, 304, 995–999 CrossRef CAS PubMed
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed
.
- T. Lu, J. Chem. Phys., 2024, 161, 082503 CrossRef CAS PubMed
.
- S. Emamian, T. Lu, H. Kruse and H. Emamian, J. Comput. Chem., 2019, 40, 2868–2881 CrossRef CAS PubMed
.
- L. Himanen, M. O. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS
.
- L. B. Kier, Quant. Struct.-Act. Relat., 1985, 4, 109–116 CrossRef CAS
.
- T. Zhou, E. Martinez-Baez, G. Schenter and A. E. Clark, J. Chem. Phys., 2019, 150, 134102 Search PubMed
.
-
A. E. Martell and R. J. Motekaitis, Determination and Use of Stability Constants, VCH Publishers, Dallas, 1992 Search PubMed
.
- S. Ahrland, Acta Chem. Scand., 1951, 5, 1271 CrossRef CAS
.
- R. A. J. Day and R. M. Powers, J. Am. Chem. Soc., 1954, 76, 3895–3897 CrossRef CAS
.
- D. Peppard, G. Mason and I. Hucher, J. Inorg. Nucl. Chem., 1962, 24, 881–888 CrossRef
.
- V. I. Levin, G. V. Korpusov, N. M. Man'ko, E. N. Patrusheva, N. P. Prokhorova and G. F. Platnov, Sov. At. Energy, 1964, 15, 828–835 CrossRef
.
- W. Masterton and L. Berka, J. Phys. Chem., 1966, 70, 1924–1929 CrossRef CAS
.
- P. Danesi, R. Chiarizia, G. Scibona and G. D'Alessandro, J. Inorg. Nucl. Chem., 1971, 33, 3503–3510 CrossRef CAS
.
- J. R. Pliego Jr and J. M. Riveros, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2020, 10, e1440 Search PubMed
.
-
D. R. Burgess, NIST SRD 46. Critically Selected Stability Constants of Metal Complexes: Version 8.0 for Windows, 2004 Search PubMed
.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS
.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS
.
- M. Dinpajooh and D. V. Matyushov, Phys. Rev. Lett., 2015, 114, 207801 CrossRef PubMed
.
- R. Ibragimova, M. J. Puska and H.-P. Komsa, ACS Nano, 2019, 13, 9171–9181 CrossRef CAS PubMed
.
- R. Bhattacharjee and P. Miró, Inorg. Chem., 2022, 61, 14718–14725 CrossRef CAS PubMed
.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed
.
- L. Zhang, D.-Y. Lin, H. Wang, R. Car and E. Weinan, Phys. Rev. Mater., 2019, 3, 023804 CrossRef CAS
.
- S. O. Odoh and G. Schreckenbach, J. Phys. Chem. A, 2010, 114, 1957–1963 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Optimized structures of the studied metal complexes and the related structural analyses. See DOI: https://doi.org/10.1039/d4cp04295f |
| This journal is © the Owner Societies 2025 |

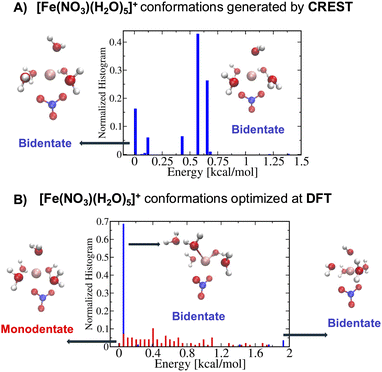
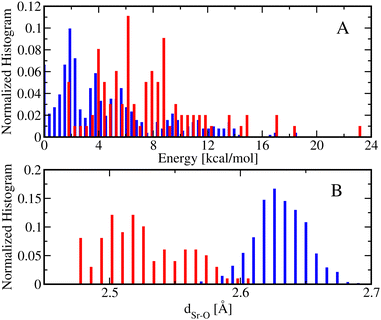
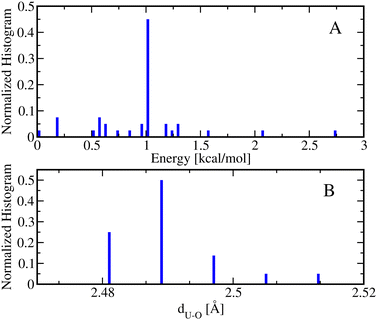
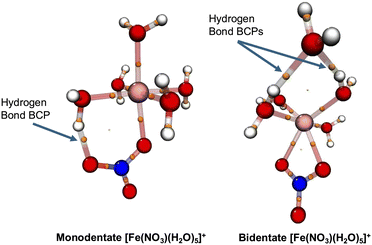
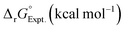
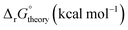
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)