Role of explicit solvation and level of theory in predicting the aqueous reduction potential of carbonate radical anion by DFT

Abstract

Chemical oxidation reactions, a key class of electron transfer processes, have broad applications, including the treatment of persistent and mobile pollutants. Marcus theory, paired with density functional theory (DFT) simulations, enables quantification of thermodynamic properties in these reactions. However, accurately modeling species with complex solvent interactions, especially radicals, requires careful selection of computational methods. Reduction potentials provide critical benchmarks for evaluating solvent models and functional choices by comparing simulated values to literature data. In this study, we used the carbonate radical, known for its strong intermolecular interactions, as a model to assess solvation models and computational functionals. Implicit solvation methods significantly underperformed, predicting only one-third of the measured reduction potential. Accurate results were obtained using explicit solvation with 18 water molecules for ωB97xD/6-311++G(2d,2p) and 9 water molecules for M06-2X/6-311++G(2d,2p). B3LYP/6-311++G(2d,2p) showed improvement with additional explicit solvation but failed to match literature benchmarks. Functional performance differences, analyzed through natural bond orbital (NBO) and charge transfer calculations, emphasized the critical role of dispersion corrections. Testing various dispersion correction methods revealed consistent improvements in reduction potential accuracy. These findings highlight the necessity of explicit solvation for modeling electron transfer reactions with extensive solvent interactions and underscore the importance of selecting appropriate functionals and dispersion corrections for reliable predictions.

---

Introduction

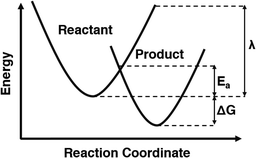
Chemical oxidation reactions are electron transfer (ET) reactions that can be investigated using Marcus theory. Marcus theory is a mathematical approach that can be used to estimate rates of ET reactions, among other applications.¹ Marcus theory is uniquely able to calculate an activation energy for processes that do not have an identifiable transition state such as ET.² This is accomplished by modelling the energetic surfaces of the reactants and products as distinct but overlapping parabolas, and using the reorganization energy (λ) and geometric principles to calculate the energy at which they meet, providing the height of the activation barrier as illustrated in Fig. 1. For many applications, calculating activation energies using Marcus theory is a useful screening step to quantitatively assess the thermodynamic feasibility of the proposed reaction. Using pollutant treatment as an example, radical species which have low barriers and fast rates for electron transfer with target pollutants will be promising to study for degradation applications. Calculating these barriers and rates using Marcus theory as a screening step is possible using the myriads of computational chemistry techniques, but caution must still be taken to ensure correct treatment.

Fig. 1 Simplified depiction of Marcus theory.

Accurate potential energy surfaces are essential for reliable results in Marcus theory. Using experimental values as benchmarks helps validate computational methods, such as calculating a measured property. The most obvious choice is to use a measured rate constant, but these are not always available. Instead, reduction potentials (E°) are a more common measured property that can be used for validating the computational methods. Reduction potentials quantify a chemical's ability to gain an electron, with standard reduction potential referring to electron transfer from hydrogen specifically.³ Comparing the standard reduction potentials (E°s) of the electron donor and the electron acceptor quantifies the thermodynamic favorability of an ET reaction between them.⁴ Marcus theory for electron transfer from an ion such as carbonate requires both an ion (reactant) and radical (product) complexes to be modelled individually. The calculated energies of these two species can be used to determine the reduction potential which can then be compared to a literature value. Accurate reduction potentials indicate that both the product and reactant of the ET reaction have been modelled correctly.

Obtaining E° values through computational methods can be difficult, primarily due to differences in charges and solvation atmosphere of the oxidant radical and the resulting product.⁵ Researchers are left with several choices to make, such as the choice of level of theory and solvation model to best represent the target species. On one hand, implicit solvation models can be used to treat these species. Implicit solvation applies an electric continuum across the simulation to gently push and pull electron density as if a solvent were present. Implicit solvent models estimate the energy of the solvent environment as a perturbation to the gas-phase Hamiltonian of the solute. This perturbation includes both electrostatic processes, such as permanent dipole attraction, and non-electrostatic processes, such as dispersion and solvent cavity formation based on how the solute interacts with the electric continuum. Each model approaches these energy components differently, with their mathematical distinctions detailed in a recent review.⁶ For this investigation, the universal solvation model (SMD) was chosen due to its general accuracy matching experimental data.⁷ On the other hand, explicit solvation includes individual solvent molecules in the simulation to overtly simulate intermolecular interactions such as hydrogen-bonding. The key advantage lies in capturing complex phenomena beyond the capabilities of implicit solvation models, such as strong hydrogen bonding that pulls the solvent closer and reduces cavity size, as well as charge transfer to the solvent, which influences electrostatic dipole interactions. However, we cannot simply add many explicit solvent molecules into simulations without drastically increasing the computational cost. Therefore, it is essential to investigate the relationship between the solvation and the reduction potential to identify the most accurate and efficient treatment for use in future Marcus theory calculations.

Carbonate radical (CO₃˙⁻) was selected as the model species due to its relevance in oxidation applications and its extensive intermolecular interactions. Carbonate radical is present in biological systems,⁸ can react with many organic species,^9,10 and is easily generated with bicarbonate or carbonate and a photosensitizer in UV light.¹¹ Importantly, reduction potential of carbonate radical has also been measured, and it has a reported reduction potential of 1.57 V.¹² Carbonate has three oxygen atoms sharing negative charge, meaning it can be involved extensively in hydrogen bonding with its solvent. Due to the multiple strong solvent interactions of carbonate ions, it is referred to as a kosmotropic ion, or a “structure maker”.¹³ However, the best choice of computational parameters for simulating carbonate radical is still uncertain.

Previous research on the sulfate radical showed that explicit solvation was necessary for accurate reduction potential predictions.⁵ Since sulfate distributes its charge across four oxygen atoms, carbonate, with a slightly higher charge density, likely has even stronger intermolecular interactions. This earlier study highlighted the need for explicit solvation but left questions about its application to other molecules and the impact of other computational choices. Our investigation extends this work to carbonate, examining solvation models and theoretical levels more deeply to identify an accurate approach for future research. As computational methods evolve, understanding their successes and limitations is crucial for selecting optimal methods moving forward.

Previous research on carbonate ion reduction potential highlights the need for further exploration. DFT studies have shown that the choice of theory level significantly affects results and that explicit solvation leads to notable charge transfer.¹⁴ Building on this, we examine these variables as a function of explicit solvation to identify key trends. Prior studies suggest that increasing explicit solvation improves accuracy, but the optimal amount remains undetermined.¹⁵ Additionally, research indicates that carbonate's hydrogen bonding motifs influence atmospheric chemistry, yet high levels of explicit solvation have not been thoroughly studied.^16,17 Given carbonate's ability to form highly coordinated clusters, six explicit water molecules may be insufficient to capture its structured solvation shell, as seen with the sulfate radical.

This study evaluated the impact of solvation model and level of theory on the reduction potential of carbonate radical. Explicit solvation proved essential for accurately modeling the extensive hydrogen-bonding of carbonate radical in DFT calculations. Three common functionals were tested, and it seems only functionals with built in dispersion corrections can accurately model the extensive electron dispersion happening in the solvated carbonate system. Therefore, future simulations of electron transfer reactions should use explicit solvation with an in-built dispersion correction.

Methods

Carbonate's radical and ionic forms were modelled individually using density functional theory (DFT). The DFT calculations were performed using the Gaussian 16 software suite.¹⁸ The functionals tested were the popular Becke's 3-parameter exchange functional with Lee–Yang–Parr correlation functional (B3LYP), a variant of ωB97 functional that accounts for dispersion (ωB97xD), and variants of the Minnesota ’06 functionals (M06, M06-L, and M06-2X).^19–22 The 6-311++G(2d,2p) basis set was used, and this choice was based on its use in previous research.^5,23,24 The implicit solvation was also incorporated using the SMD solvation model of water.⁷ Explicit solvent molecules were placed manually. For the simulations with explicit water molecules, the implicit solvation model was still active. All stationary points were characterized as a minimum energy structure by the absence of any imaginary vibration modes. The energy difference between the oxidant (carbonate radical anion) and the reduced species (carbonate dianion) was converted into the reduction potential (E°) with respect to the standard hydrogen electron potential using eqn (1):

ΔG_rxn = −nFE⁰ − E_SHE (1)

where F is the Faraday constant, E⁰ is the potential, n is the number of electrons being transferred in the reaction which is 1 in this case, and E_SHE is the standard hydrogen electrons potential, 4.47 V.²⁵ The energy term, ΔG_rxn, is the difference in the Gibbs free energy of the radical species and the ionic form.

For the explicitly solvated systems, three different geometries were prepared to generate replicate reduction potential values to make sure the value was repeatable. Each replicate had carbonate in the center and the same number of waters, but the angles and positions of the explicit water molecules were varied to sample the conformational space. Geometries were verified to ensure the carbonate species maintained strong intermolecular interactions, particularly hydrogen bonding, with the solvent cage. Without these interactions, the solvent would primarily interact with itself, leading to inaccurate simulations. While achieving this balance was challenging at low solvation levels due to limited conformational variety, at higher solvation levels, the abundance of explicit water consistently ensured numerous hydrogen bonds with the carbonate. Once a satisfactory geometry was optimized, the energies of these geometries were taken and used for the potential calculation, and the potentials were averaged together. This solution generates error bars for the data points with the standard deviation of the three potentials calculated for each solvation level. All of the partial atomic charges were computed using the natural bond orbital (NBO) analysis as implemented in Gaussian16 software suite.¹⁸

Results

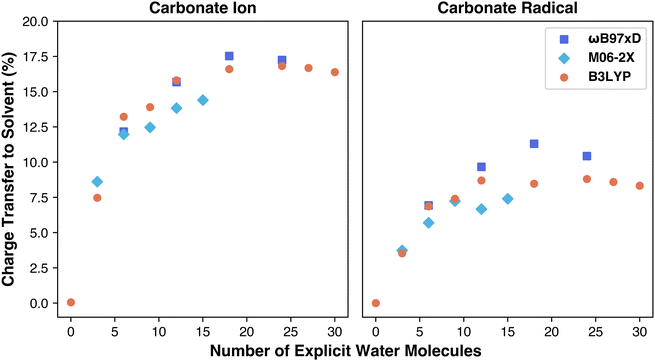
The results indicate that implicit solvation models alone cannot accurately predict the reduction potential of carbonate radical. Implicit models, like SMD, simplify solvent effects by allowing the electron density of solute to interact with the dielectric field of the solvent, making them a logical starting point. However, these models overlook key non-covalent interactions, such as hydrogen bonding and dispersion forces, which are critical for accurate predictions. The initial reduction potential calculated using B3LYP/6-311++G(2d,2p) and the SMD implicit solvation model was 0.42 V, which has an error greater than 1 V compare to the experimental value of 1.57 V.¹² The significant discrepancy suggests that the implicit solvation model fails to accurately simulate the molecule, likely due to the kosmotropic nature of carbonate and its extensive hydrogen bond network, which implicit models do not capture. This indicates that explicit solvation is necessary for accurate treatment of the carbonate radical. Thus, calculations were repeated using varying numbers of explicit water molecules.

Including explicit water molecules in the simulation demonstrates the kosmotropic, or “structure-making,” nature of carbonate. As shown in Fig. 2, each oxygen atom on carbonate can form two hydrogen bonds (indicated by blue dashed lines). This raised the question of how many water molecules are needed for accurate modeling. Although six water molecules seem to form a complete inner shell, additional solvent molecules may still be necessary. To account for potential impact of secondary solvation shell, we extended simulations to include up to 30 explicit water molecules, ensuring any impact on the inner shell structure and overall results was considered.

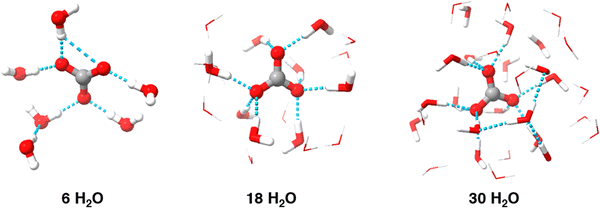Fig. 2 Example minimized geometries for various solvation levels. Outer sphere explicit H₂O have been illustrated as wireframes to increase visibility of carbonate radical and the inner shell.

As more explicit water molecules were included in the simulation, the calculated reduction potential became increasingly accurate. To start, three explicit water molecules were added. The result of this was a calculated potential of 0.67 V, a number that does come closer to the reference value (1.57 V) than the calculated potential with no explicit solvation (0.42 V), nonetheless, it is still inaccurate. With six explicit water molecules, the reduction potential increases to 0.94 V, and with nine water molecules it increased to 1.05 V. The trend shows that the reduction potential became more accurate as more explicit water molecules were added to the solution, which agrees with data for sulfate radical.⁵

The calculated reduction potential values as a function of the number of explicit water molecules are displayed in Fig. 3. The data shows a clear upward trend, indicating that increasing the number of water molecules brings the results closer to the reference value, as expected. However, the number of water molecules needed to match the reference value varies depending on the functional used. The data demonstrates how DFT significantly underestimates the reduction potential of the carbonate radical in systems with fewer explicit solvent molecules. The data for the reduction potentials calculated using B3LYP/6-311++G(2d,2p) level of theory reach an asymptote suggesting the solvation is sufficient, but this asymptote is still below the reference value suggesting the lack of some key non-covalent interactions such as dispersion which are not taken into account with B3LYP functional.

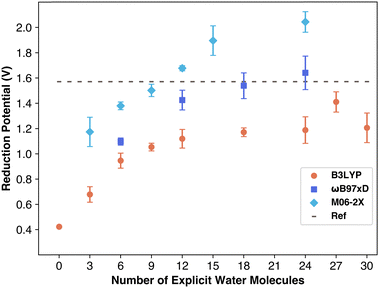Fig. 3 Average reduction potential of carbonate from simulations. Error bars are standard deviation between replicates.

Reduction potentials obtained using the ωB97xD/6-311++G(2d,2p) level of theory reach the reference value with high amounts of explicit solvation. The results are included in Table S1 (ESI†). As can be seen in Fig. 3 with six explicit water molecules forming an incomplete shell around the carbonate, a value of only 1.1 V is obtained. The calculated reduction potential data is near reference with 12 explicit molecules while it reaches the reference value with 18 water molecules. The ωB97xD functional was specifically designed with in-built dispersion corrections to capture long range interactions accurately. The excellent performance of ωB97xD is further supported by a previous report that evaluated the reduction potential of per- and polyfluoroalkyl substances with B3LYP and ωB97xD functionals and found that ωB97xD outperforms B3LYP functional in terms of accuracy.²⁶

The Minnesota functional variant M06-2X, tested with the 6-311++G(2d,2p) basis set, showed similar trends to other functionals: results fell below the reference until sufficient explicit solvent was included. This combination required the fewest explicit water molecules, closely approaching the reference value with only nine water molecules. The increase in potential with additional water molecules remained consistent, though M06-2X began to overestimate the carbonate radical anion's reduction potential at 12 or more water molecules, aligning with prior findings that M06-2X overestimates reduction potentials for PFAS molecules.²⁶

These findings align well with recent research showing that carbonate radical potential increases with the number of water molecules.²⁷ Barrios and Minakata found that, using M06-2X/aug-cc-pVDZ, the reduction potential increased from 1.08 to 1.42 V with additional explicit solvation up to three water molecules, affirming that explicit water improves Marcus theory accuracy. They attributed this to increasing charge transfer between carbonate and solvent, observing a rise from ∼8% to ∼21% charge transfer with 1 to 3 water molecules. They reasoned that ion stabilization relies on strong solvent interactions, which are better modeled with explicit solvation. However, they did not perform these computations with more water molecules, and as can be seen in Fig. 3 the M06-2X functional begins to overestimate the reduction potential of carbonate radical.

To explore the charge transfer from carbonate to solvent shell, we conducted NBO calculations to measure percentage charge transfer, aiming to determine if charge transfer differences account for the variation in functional performance. NBO calculations are performed on optimized geometries to determine the charges and spin of each atom in the simulation. By summing the total charges on the carbonate species separately from the charges on the solvent, we quantify the portion of the carbonate ion's original −1 or −2 charge transferred to the water molecules. This transfer is expressed as a percentage of the overall charge shifted from solute to solvent. The results are included in Table S2 (ESI†). As shown in Fig. 4, charge transfer increases with explicit solvation, asymptoting at 12–18 water molecules, similar to the reduction potential behavior. The carbonate ion transfers more charge than the radical, consistent with previous findings performed using only the M06-2X functional.²⁷ Prior work, however, resulted in a higher total charge transfer (∼21%) compared to our maximum (∼17%) in case of M06-2X functional, suggesting that aug-cc-pVDZ basis set accounts for a higher charge transfer.²⁷ We also aimed to examine if charge transfer differences contributed to functional performance variations, as each functional models charge sharing with water molecules differently. For example, M06-2X includes stronger dispersion and a doubled nonlocal exchange term (hence “2X”), possibly influencing charge distribution with water. Surprisingly, M06-2X predicted the lowest charge transfer while overestimating the reduction potential, meaning the effect of doubling nonlocal exchange on charge transfer is not straightforward. As for the NBO spin calculations, every radical geometry for each functional performed the same with minimal (0.01) spin transfer from the carbonate radical to the surrounding water. Overall, our analysis indicates that while all functionals similarly modeled total charge transfer, another factor likely underlies the observed performance differences.

Fig. 4 Plot of carbonate charge transfer % vs. number of explicit water molecules.

We compared three Minnesota functional variants to isolate the impact of exchange–correlation terms. As shown in Fig. 5, the quantity of nonlocal exchange in the functional leads to different performance outcomes: M06-L, using only local exchange, severely underestimates the reduction potential, underscoring the importance of nonlocal exchange for overall energy. M06 results were similar to M06-2X but slightly below it. The linear data increase—unaffected by solvation—suggests that overestimation could stem from exchange–correlation contributions, which add a fixed energy value independent of solvation. Based on these findings, M06-L would likely plateau below the reduction potential, similar to B3LYP. Barrios and Minakata observed a similar overestimation with M06-2X using the aug-cc-pVTZ basis set for one molecule, attributing this to an overestimation of the standard-state Gibbs free energy of solvation, regardless of the explicit solvent quantity. Nonetheless, explicit solvation appears not to severely affect the exchange–correlation term's contribution unless the secondary solvation shell of carbonate species is complete as indicated by data points with 24 water molecules.

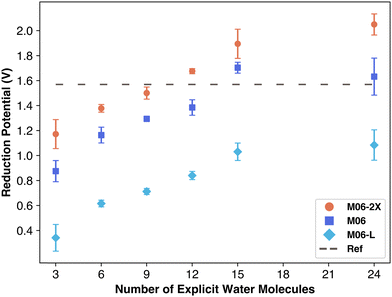Fig. 5 Reduction potential vs. number of explicit water molecules for three M06 functional variants.

To evaluate the role of the dispersion corrections, we attempted to use Grimme's empirical dispersion corrections to see how it affected the data. We first applied Grimme's GD3 empirical correction to the M06, M06-L, and M06-2X optimized geometries. The results are summarized in the ESI† (Table S3). Surprisingly, this led to only a minor average change of 0.2% in predicted reduction potential. M06 functionals, parameterized using a large dispersion-corrected dataset, appear to inherently account for dispersion interactions. The disadvantage is that these parameters are fixed and not directly tied to a physical representation of dispersion interactions. Instead, they adjust the data to align with a dispersion dataset, which may contribute to the overestimations observed with M06 functionals. This lack of accessibility also prevents exploration of potential modifications. However, we can isolate the effects of dispersion corrections by using them with the B3LYP functional.

To further evaluate the impact of dispersion interactions in computing the reduction potentials, we performed single point dispersion corrections as well as complete geometry optimizations with dispersion interactions being taken in account at each change of the geometry using the B3LYP functional. Unlike ωB97xD, which includes built-in dispersion corrections, and M06, which is trained on dispersion data, B3LYP lacks these features, making it a better candidate for evaluating the isolated impact of dispersion corrections. We applied DFT-D2, DFT-D3 and DFT-D3BJ corrections with and without geometry re-optimization. The results of these corrections are summarized in Fig. 6 and Table S4 (ESI†). It is important to note the DFT-D3 and DFT-D3BJ corrections were computationally less expensive to apply than the outdated DFT-D2 correction, despite their increased complexity. With the help of the corrections, each data point became closer to the reference, even reaching it with 24 explicit water molecules. If these empirical dispersion corrections were applied after the geometry has been optimized, calculated reduction potentials were slightly closer to the reference compared to empirical dispersion corrections being invoked during the geometry optimization. Nonetheless, comparison of the uncorrected and corrected data in Fig. 6 demonstrates the importance of taking into account the empirical dispersion corrections when calculating properties of a kosmotropic species. As a result, it is important to use a functional such as ωB97xD that has in-built dispersion corrections or to utilize empirical corrections with a functional that does not consider dispersion such as B3LYP functional.

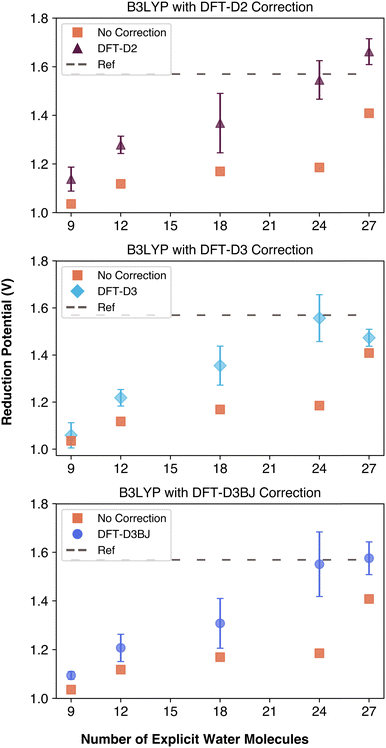Fig. 6 Comparison of dispersion corrections applied to B3LYP geometries throughout the geometry optimization process.

A cautionary note on entropy in this experiment: we used the free energies of two carbonate forms calculated in the solution phase, which introduces concerns due to the challenges in accurately modeling the entropic contribution. In Gaussian, the translational component of entropy is calculated in the gas phase, where molecules can move freely.²⁸ However, in the solution phase, molecular motion is highly restricted, leading to discrepancies.²⁹ A recent review discusses methods for modeling solution-phase translational entropy.^6,30 However, the SMD implicit solvation model used in this experiment applies a fixed correction to free energy and cannot be used with these methods, possibly contributing to its poor performance.

Explicit solvation models also present challenges, as adding more explicit solvent molecules introduces many low-frequency vibrational modes, which can be problematic in Gaussian.³¹ This effect becomes more pronounced at high solvation levels (>12 molecules) and could explain the increasing errors observed in our results.

For future studies, researchers should carefully account for entropy, either by using methods that explicitly calculate it (unlike the SMD model) or by inspecting the vibrational modes of solvated geometries for consistency across reactants and products. If the modes are consistent, the excess entropy may cancel out when comparing reactant and product energies. Alternatively, post-processing tools like GoodVibes could be used to exclude contributions from low-frequency vibrational modes, potentially improving accuracy.³²

Conclusions

Explicit water molecules are needed in calculations to accurately determine the reduction potential of the carbonate radical anion. This finding aligns with previous work on the sulfate radical anion, highlighting the importance of capturing solvent–solute interactions, which significantly influence the chemical properties that facilitate electron transfer.⁵ Future simulations of the carbonate radical must consider this explicit solvation effect to achieve accurate results. One such specific example is in the context of Marcus theory, which is the most studied method to probe redox reactions computationally. Accurate modeling requires capturing and comparing the electron density before and after the electron transfer reaction in the Marcus theory. The ability to transfer electrons is influenced by the surrounding environment, especially for kosmotropic species, which significantly shift their electron density away from themselves when coordinated with solvent molecules. It is crucial that our models reflect this effect. This study demonstrates that the reduction potential of the carbonate radical anion is significantly affected by surrounding water molecules. Future studies will seek to confirm this conclusion by examining the role of explicit solvation on the reduction potential of chemicals that do not have these strong solvent interactions, such as chaotropes.

Abbreviations

PFAS	Per- and polyfluoroalkyl substances
AOP	Advanced oxidative process
ET	Electron transfer
DFT	Density functional theory
IRC	Intrinsic reaction coordinate

Data availability

The data used in this article is included in the ESI.† This includes the reduction potentials, the energies of the structures, NBO results, and the optimized geometries.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Science Foundation (CHE-2109210). Financial support from US Army Corp of Engineers through cooperative agreement W912HZ-23-2-0009 is also gratefully acknowledged. Authors also acknowledge the computational resources allocated by the high-performance computing facility at the Colorado School of Mines.

References

1. R. A. Marcus, Chemical and Electrochemical Electron-Transfer Theory, Annu. Rev. Phys. Chem., 1964, 15(1), 155–196,  DOI:10.1146/annurev.pc.15.100164.001103.
2. R. A. Marcus, Electron Transfer Reactions in Chemistry. Theory and Experiment, Rev. Mod. Phys., 1993, 65(3), 599–610,  DOI:10.1103/RevModPhys.65.599.
3. J. Ho, M. L. Coote, C. J. Cramer and D. G. Truhlar, Theoretical Calculation of Reduction Potentials, Org. Electrochem., 2016, 5, 229–259.
4. E. J. Piechota and G. J. Meyer, Introduction to Electron Transfer: Theoretical Foundations and Pedagogical Examples, J. Chem. Educ., 2019, 96(11), 2450–2466,  DOI:10.1021/acs.jchemed.9b00489.
5. A. E. Carre-Burritt, D. J. Van Hoomissen and S. Vyas, Role of Explicit Hydration in Predicting the Aqueous Standard Reduction Potential of Sulfate Radical Anion by DFT and Insight into the Influence of pH on the Reduction Potential, J. Phys. Chem. A, 2022, 126(8), 1422–1428,  DOI:10.1021/acs.jpca.1c09459.
6. S.-C. Liu, X.-R. Zhu, D.-Y. Liu and D.-C. Fang, DFT Calculations in Solution Systems: Solvation Energy, Dispersion Energy and Entropy, Phys. Chem. Chem. Phys., 2023, 25(2), 913–931,  10.1039/D2CP04720A.
7. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396,  DOI:10.1021/jp810292n.
8. O. Augusto, M. G. Bonini, A. M. Amanso, E. Linares, C. C. X. Santos and S. L. De Menezes, Nitrogen Dioxide and Carbonate Radical Anion: Two Emerging Radicals in Biology, Free Radical Biol. Med., 2002, 32(9), 841–859,  DOI:10.1016/S0891-5849(02)00786-4.
9. L. Wojnárovits, T. Tóth and E. Takács, Rate Constants of Carbonate Radical Anion Reactions with Molecules of Environmental Interest in Aqueous Solution: A Review, Sci. Total Environ., 2020, 717, 137219,  DOI:10.1016/j.scitotenv.2020.137219.
10. Y. Zhou, C. Chen, K. Guo, Z. Wu, L. Wang, Z. Hua and J. Fang, Kinetics and Pathways of the Degradation of PPCPs by Carbonate Radicals in Advanced Oxidation Processes, Water Res., 2020, 185, 116231,  DOI:10.1016/j.watres.2020.116231.
11. S. Yan, Y. Liu, L. Lian, R. Li, J. Ma, H. Zhou and W. Song, Photochemical Formation of Carbonate Radical and Its Reaction with Dissolved Organic Matters, Water Res., 2019, 161, 288–296,  DOI:10.1016/j.watres.2019.06.002.
12. D. A. Armstrong, R. E. Huie, W. H. Koppenol, S. V. Lymar, M. Gabor, P. Neta, B. Ruscic, D. M. Stanbury, S. Steenken and P. Wardman, Standard Electrode Potentials Involving Radicals in Aqueous Solution: Inorganic Radicals (IUPAC Technical Report), Pure Appl. Chem., 2015, 87(11–12), 1139–1150,  DOI:10.1515/pac-2014-0502.
13. Y. Marcus, Effect of Ions on the Structure of Water: Structure Making and Breaking, Chem. Rev., 2009, 109(3), 1346–1370,  DOI:10.1021/cr8003828.
14. S. Zilberg, A. Mizrahi, D. Meyerstein and H. Kornweitz, Carbonate and Carbonate Anion Radicals in Aqueous Solutions Exist as CO₃(H₂O)₆²⁻ and CO₃(H₂O)₆—Respectively: The Crucial Role of the Inner Hydration Sphere of Anions in Explaining Their Properties, Phys. Chem. Chem. Phys., 2018, 20(14), 9429–9435,  10.1039/C7CP08240A.
15. S. P. Hebert and H. B. Schlegel, Computational Study of the pH-Dependent Competition between Carbonate and Thymine Addition to the Guanine Radical, Chem. Res. Toxicol., 2019, 32(1), 195–210,  DOI:10.1021/acs.chemrestox.8b00302.
16. M. G. Münst, M. Ončák, M. K. Beyer and C. van der Linde, Infrared Spectroscopy of CO₃˙⁻(H₂O)1,2 and CO₄˙⁻(H₂O)1,2, J. Chem. Phys., 2021, 154(8), 084301,  DOI:10.1063/5.0038280.
17. P. Rublev, N. V. Tkachenko, P. A. Dub and A. I. Boldyrev, On the Existence of CO₃²⁻ Microsolvated Clusters: A Theoretical Study, Phys. Chem. Chem. Phys., 2023, 25(20), 14046–14055,  10.1039/D3CP00955F.
18. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Forseman and D. J. Fox, Gaussian 16, 2016.
19. A. D. Becke, Density-functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98(7), 5648–5652,  DOI:10.1063/1.464913.
20. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789,  DOI:10.1103/PhysRevB.37.785.
21. D. Jacquemin, E. A. Perpète, I. Ciofini and C. Adamo, Assessment of the ωB97 Family for Excited-State Calculations, Theor. Chem. Acc., 2011, 128(1), 127–136,  DOI:10.1007/s00214-010-0783-x.
22. Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals, Theor. Chem. Acc., 2008, 120(1), 215–241,  DOI:10.1007/s00214-007-0310-x.
23. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions, J. Chem. Phys., 1980, 72(1), 650–654,  DOI:10.1063/1.438955.
24. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, Efficient Diffuse Function-Augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-Row Elements, Li–F, J. Comput. Chem., 1983, 4(3), 294–301,  DOI:10.1002/jcc.540040303.
25. A. V. Marenich, J. Ho, M. L. Coote, C. J. Cramer and D. G. Truhlar, Computational Electrochemistry: Prediction of Liquid-Phase Reduction Potentials, Phys. Chem. Chem. Phys., 2014, 16(29), 15068–15106,  10.1039/C4CP01572J.
26. D. J. Van Hoomissen and S. Vyas, Early Events in the Reductive Dehalogenation of Linear Perfluoroalkyl Substances, Environ. Sci. Technol. Lett., 2019, 6(6), 365–371,  DOI:10.1021/acs.estlett.9b00116.
27. B. Barrios and D. Minakata, Aqueous-Phase Single-Electron Transfer Calculations for Carbonate Radicals Using the Validated Marcus Theory, Environ. Sci. Technol. Lett., 2023, 10(2), 204–209,  DOI:10.1021/acs.estlett.2c00913.
28. J. W. Ochterski, Thermochemistry in Gaussian, Gaussian Inc., 2000.
29. B. O. Leung, D. L. Reid, D. A. Armstrong and A. Rauk, Entropies in Solution from Entropies in the Gas Phase, J. Phys. Chem. A, 2004, 108(14), 2720–2725,  DOI:10.1021/jp030265a.
30. M. Mammen, E. I. Shakhnovich, J. Deutch and G. M. Whitesides, Estimating the Entropic Cost of Self-Assembly of Multiparticle Hydrogen-Bonded Aggregates Based on the Cyanuric Acid melamine Lattice, J. Org. Chem., 1998, 63, 3821–3830.
31. J. W. Ochterski, Vibrational Analysis in Gaussian, Gaussian Inc., 1999.
32. G. Luchini, J. V. Alegre-Requena, I. Funes-Ardoiz and R. S. Paton, GoodVibes: Automated Thermochemistry for Heterogeneous Computational Chemistry Data, F1000Research, 2020, 9, 291,  DOI:10.12688/f1000research.22758.1.

---

Footnote

† Electronic supplementary information (ESI) available: All optimized geometries, energies, natural bond order charges, and calculated reduction potentials. See DOI: https://doi.org/10.1039/d4cp04487h

---