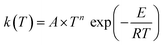Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular conformational effects on the overall rate constant and the branching ratios of the n-heptane + OH reaction: an ab initio and variational transition state theory study†
M.
Belmekki
 ,
M.
Monge-Palacios
,
M.
Monge-Palacios
 *,
T.
Wang
and
S. M.
Sarathy
*,
T.
Wang
and
S. M.
Sarathy

King Abdullah University of Science and Technology (KAUST), Physical Sciences and Engineering Division, Clean Energy Research Platform (CERP), Thuwal (Makkah), 23955-6900, Saudi Arabia. E-mail: manuel.mongepalacios@kaust.edu.sa
First published on 20th February 2025
Abstract
The oxidation of fuels by hydroxyl radical (OH) is a crucial initiation step in both combustion and atmospheric processes. In the present work, we explore the site-specific hydrogen atom abstraction reactions by OH from n-heptane through high level ab initio and sophisticated kinetic calculations. Rate constants for each of the four distinct abstraction sites were computed, for the first time, over a wide temperature range (200–3000 K) and using multistructural torsional variational transition state theory (MS-T-VTST) with small curvature tunneling (SCT) corrections. Optimized geometries, vibrational frequencies and minimum energy paths (MEPs) were determined using the M06-2X/aug-cc-pVTZ level of theory, with single-point energy refinements performed at the CCSD(T)/aug-cc-pVTZ level of theory to refine the energy of the optimized stationary points whose energy is up to 1 kcal mol−1 of their respective global minimum conformer. Our findings reveal that the overall rate constants obtained from our site-specific calculations align closely with experimental data, with a maximum deviation factor (kexp/ktheory) of 1.5 at 1000 K. More importantly, we provide branching ratios that are based on first-principles calculations, identifying the secondary site neighboring the primary site as the dominant abstraction channel—data not previously reported in the literature, thereby adding value to our kinetic study. Moreover, we demonstrate that, as long as multi-structural torsional anhamonicity effects are implemented, appropriate density functional methods with large enough basis sets can yield rate constants that are comparable to those from much more computationally demanding levels of theory that are based on wave function methods. The demonstrated protocol, in which we have also tested the effect of different energy cuttoffs for the computationally intensive single-point energy refinements, effectively handles large and conformationally complex chemical systems, offering a reliable framework for future investigations in this field involving similar chemical systems whose kinetics is barely known or simply based on estimations.
1. Introduction
In the quest for reliable predictions in combustion processes, the accuracy of chemical kinetic models is paramount. These models are typically simplified through computational reduction of complex reaction mechanisms to achieve practical computational efficiency. However, this simplification can compromise the precision of such predictive models, potentially leading to significant errors in numerical combustion simulations. Therefore, preserving the integrity of the original detailed reaction mechanism is crucial.Within combustion models, uncertainties in kinetic parameters can propagate, significantly affecting key combustion properties. Accurate determination of rate constants for critical reaction pathways is essential for ensuring the reliability of reduced mechanisms. High-level quantum chemistry and kinetic calculations offer a robust pathway to reach this precision, especially for dominant elementary reactions whose experimental measurements are challenging or infeasible. However, difficulties arise when it comes to applying these methods for the calculation of the rate constants of reactions involving large and flexible molecules.
Among the reactions of interest, hydrogen abstraction reactions by OH radicals are of particular relevance due to the pivotal role of these chain carriers in hydrocarbon oxidation. It is also well established that OH is a key reactive species in both combustion and atmospheric chemistry. Consequently, the hydrogen abstraction reactions by OH radicals from alkanes, including large alkanes (≥C4), have been extensively studied in the literature. For instance, Huynh et al.1 used the reaction class transition state framework to estimate rate constants for such reactions. This method combines transition state theory with structural similarities among reaction class members, allowing insights from one system to be extrapolated to others. These well-studied reactive systems can serve as reliable benchmarks for validating state-of-the-art theoretical calculations. The latter represent an alternative to experiments for the calculation of rate constants and branching ratios within wide temperature ranges that are inaccessible experimentally.
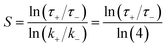 | (1) |
As a benchmark, this study focuses on the hydrogen atom abstraction reaction by OH radical from n-heptane, a widely used surrogate representing large alkanes in combustion studies. In order to prove that the associated elementary reactions of interest have a significant impact on macroscopic combustion properties such as ignition delay times, we performed a brute force sensitivity analysis using the mechanism developed by Zhang et al.2 and the Cantera3 simulation tool. For our analyses, we perturbed each rate constant by first doubling and then halving them in the original mechanism, leading to k+ and k− values and their corresponding simulated ignition delay times, τ+ and τ−, to calculate the sensitivity coefficient, defined as follows:
Fig. 1 shows the 20 most sensitive reactions for the combustion of n-heptane (NC7H16) in air at φ = 1, p = 20 bar, and T = 700 K, 1000 K, 1200 K, and 1500 K, from our sensitivity analysis. At low and intermediate temperatures (700–1200 K), the H-atom abstractions by OH from large species such as n-heptane (highlighted in bold font) are crucial pathways, while at high temperature (1500 K), the chemistry of smaller radicals takes over. Practical combustors, such as internal combustion engines, work under temperature conditions where these rate constants are highly sensitive; hence, it is important to determine them accurately.
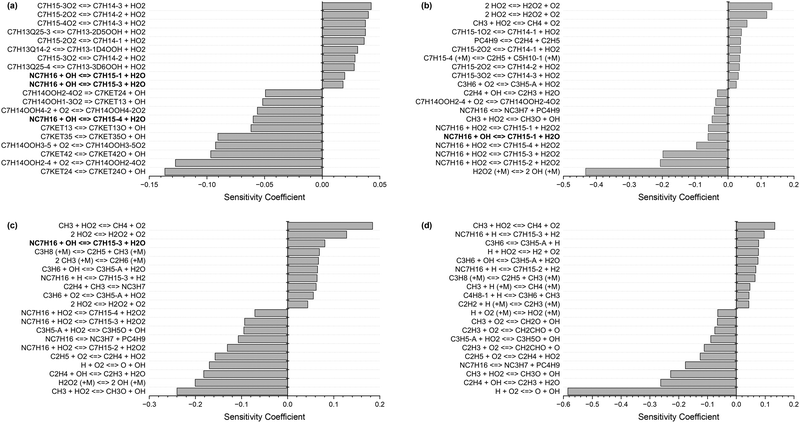 | ||
| Fig. 1 Ignition delay time sensitivity analysis for n-heptane at φ = 1, p = 20 bar, and (a) T = 700 K, (b) T = 1000 K, (c) T = 1200 K, and (d) T = 1500 K. | ||
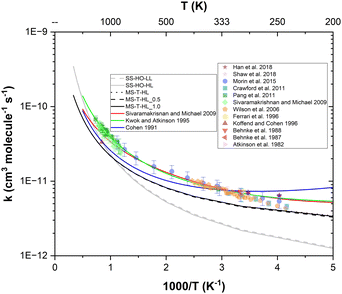
The overall rate constants for this reaction have been the subject of numerous experimental campaigns. The literature inventories as many as twelve experimental campaigns gathered in Table 1 covering a wide temperature range.4–15 At high temperatures, the sets of rate constants measured in shock tube reactors by both Sivaramakrishnan and Michael14 and Pang et al.15 are in very good agreement with one another, while the data reported by Koffend and Cohen13 seems to be underestimated despite using a similar device and method. At low temperatures, minor discrepancies are noticeable between the sets of available data possibly due to variations in experimental techniques and advancements in measurement accuracy over time.
| Authors | Year | Device | Method | T (K) | P (bar) |
|---|---|---|---|---|---|
| Atkinson et al.4 | 1982 | FEP Teflon reaction bag | Gas chromatography | 300 | 0.98 |
| Behnke et al.5 | 1987 | Smog chamber | Gas chromatography | 300 | 1 |
| Behnke et al.6 | 1988 | Smog chamber | Gas chromatography | 300 | 1 |
| Koffend and Cohen13 | 1996 | Shock tube reactor | Absorption spectroscopy | 1186 | 1.09–1.23 |
| Ferrari et al.7 | 1996 | Smog chamber | Gas chromatography | 295 | 1 |
| Wilson et al.8 | 2006 | Flow tube reactor | Gas chromatography | 241–406 | 1.01 |
| Sivaramakrishnan and Michael14 | 2009 | Shock tube reactor | Absorption spectroscopy | 838–1287 | 0.01–0.04 |
| Pang et al.15 | 2011 | Shock tube reactor | Absorption spectroscopy | 869–1364 | 0.85–2.09 |
| Crawford et al.9 | 2011 | Flow tube reactor | Mass spectrometry | 240–340 | 0.001 |
| Morin et al.12 | 2015 | Flow tube reactor | Mass spectrometry | 248–896 | 1.01 |
| Shaw et al.11 | 2018 | Flow tube reactor | Gas chromatography | 323 | 1 |
| Han et al.10 | 2018 | Smog chamber | Gas chromatography | 248, 288 | 1 |
Given the extensive availability of experimental data and the sound understanding of its kinetics, the hydrogen abstraction reaction from n-heptane by OH is an excellent test case for developing a protocol based on the available methods and theories that is practical to describe such large and flexible systems, yet accurate. The possible deviations between our calculations and the wide range of experimental data will help us identify potential sources of errors. Once validated, this protocol can be extended to other similar large and flexible chemical systems, where computational challenges arise due to the presence of several abstraction pathways, each associated with numerous conformers for the reactants and saddle points. The multiplicity of both pathways and conformers makes the application of robust quantum chemistry and kinetic calculations significantly difficult.
Due to the symmetry of n-heptane that results in equivalent abstractable H atoms, four distinct abstraction pathways can occur from the terminal site to the central site:
| CH3(CH2)5CH3 + OH˙ → CH2˙(CH2)5CH3 + H2O | (R1) |
| CH3CH2(CH2)4CH3 + OH˙ → CH3CH˙(CH2)4CH3 + H2O | (R2) |
| CH3CH2CH2(CH2)3CH3 + OH˙ → CH3CH2CH˙(CH2)3CH3 + H2O | (R3) |
| CH3CH2CH2CH2(CH2)2CH3 + OH˙ → CH3CH2CH2CH˙(CH2)2CH3 + H2O | (R4) |
Using high-level ab initio and sophisticated kinetic calculations, we computed the rate constants of each of the four different abstraction sites over a wide temperature range, i.e., 200–3000 K. We employed the multistructural torsional variational transition state theory (MS-T-VTST) with small curvature tunneling (SCT) corrections.16 This approach accounts for multistructural anharmonicity, arising from the presence of multiple conformational structures of the reactants and saddle points that can be converted into each other by internal rotations, and torsional anharmonicity, reflecting deviations of those internal rotations or torsions from the simple harmonic oscillator approach. Both anharmonicity effects are expected to be particularly pronounced in large and flexible species such as n-heptane and its corresponding H-abstraction saddle points, highlighting the importance of an accurate and practical protocol.
Moreover, site-specific rate constants are indispensable to model and understand the fate of intermediate products that influence combustion outcomes. Experiments cannot provide such information, and available empirical schemes are based on approximate structure–activity relationships.14,17,18 Cohen17 first developed reaction rate approximations for reactions between alkanes and OH based on group-additivity relationships linked to his transition-state theory results. Building on Cohen's work, Kwok and Atkinson18 updated and extended these rate estimations to other organic molecules by using an extensive experimental database. More recently, Sivaramakrishnan and Michael14 established a more formal classification for the type of surrounding neighboring group for each specific carbon site from where hydrogen atom can be abstracted. Their so-called next-nearest-neighbor method lists the rate parameters for different type of C–H bonds, depending on both their type (primary, secondary, or tertiary) and the ones of the adjacent carbon atoms. Our work is the first first-principle kinetic study to provide the branching ratios for each investigated abstraction pathways, which are expected to be more robust and accurate than those from previous estimations.
2. Computational details and methodology
2.1 Electronic structure calculations and conformational search
We employed the M06-2X/aug-cc-pVTZ level of theory19,20 as implemented in the Gaussian16 software21 to perform ab initio calculations. The M06-2X functional was reported to be an accurate functional in predicting the barrier heights of hydrogen-transfer reactions with a moderate computational expense19 while the aug-cc-pVTZ basis set is a large basis set that is expected to accurately describe the electronic structure of the chemical system being investigated. All the stationary points of the potential energy surface (PES), i.e., reactants, intermediate complexes, saddle points and products, were initially guessed and then optimized and characterized by means of vibrational frequency analysis, i.e., the saddle points are associated with one and only one imaginary frequency while the other stationary points have none and were thus confirmed as a minimum. The QST3 method22 was used to find an initial structure for the saddle point as it facilitates the search of the other conformers.To account for multi-structural torsional anharmonicity, we first performed conformational searches for n-heptane and the saddle point species of all channels using the MSTor 2013 software.23 We did not perform any conformational search for the product species as they do not affect the calculation of the forward rate constants within the VTST formulation. For a more comprehensive exploration of the conformational space, each dihedral (except terminal methyl groups) was iteratively and alternatively rotated by 120° from a previously optimized inputted structure of each of the considered stationary points. Methyl groups were not included in the conformational searches as their rotation yields undistinguishable conformers. The resulting guessed conformers were then optimized at the M06-2X/aug-cc-pVTZ level of theory using the Gaussian16 software. Single point energy calculations were performed with the CCSD(T) coupled cluster method24 and the same basis set aug-cc-pVTZ for a better energetic description of the unique optimized conformers that lie within up to 1.0 kcal mol−1 with respect to their respective global minimum. Although the CCSD(T)/aug-cc-pVTZ level provides more accurate energy values than M06-2X/aug-cc-pVTZ, we did not extend the use of the former to all the conformers as it is too computationally intensive and not affordable for large systems such as the one studied here. Instead, we only refined the energy of the conformers within the 1.0 kcal mol−1 threshold because they are expected to contribute to the rate constant to a larger extent than those beyond the threshold. We have previously tested the combination of the CCSD(T) and M06-2X methods in conjunction with different Dunning correlation consistent basis sets for the calculation of the rate constants of not only hydrogen-transfer reactions by OH,25,26 but also of other kinds of chemical reactions.27–29 Good agreement between calculations and experiments was observed, thus supporting the use of the selected level of theory.
For the calculation of the minimum energy path (MEP), we used the geometry of the global minimum conformer of each species. The GaussRate17 software30 was employed with the Page-McIver method31 to calculate the MEP with the reaction coordinate ranging from −1.6 to 1.6 Å, using a step size of 0.05 Å and a mass scaling factor of 1.0 amu. The region near the saddle point was refined by using a smaller step size of 0.02 Å between −0.5 and 0.5 Å since the location of the variational transition states and the evaluation of the tunnelling coefficients are more sensitive to an accurate description of this region of the MEP. Hessians were evaluated at every three points along the MEP.
2.2 Rate constant calculations
The way to calculate rate constants has been exhaustively described previously.25 The rate constants kCVT/SCTMS–T for the hydrogen abstraction reactions n-heptane + OH → n-heptyl + H2O are obtained using the canonical variational transition state theory (CVT) with a coupled torsional potential (T), multi-structural torsional (MS), and small curvature tunneling (SCT) corrections. First, we computed the canonical variational rate constants kCVT/SCTSS–HO using only single structures (SS), i.e., the global minimum conformers of the reactants and saddle point, the harmonic oscillator approximation (HO), and the SCT method with the Polyrate 2016-2A code.32 We included the 2Π1/2 low-lying electronically excited state of the OH radical (140 cm−1) to take the spin–orbit coupling into account while calculating its electronic partition function. Then, we also included multi-structural and torsional anharmonicity by calculating the multi-structural torsional anharmonicity partition functions with a coupled torsional potential using the MSTor 2017 software.23,33 The extent of multi-structural torsional anharmonicity in a given reaction is in practice represented by a general multi-structural torsional anharmonicity factor for the reaction, FMS–T, defined as the ratio of two multi-structural torsional anharmonicity factors, i.e., that of the saddle point FMS–T, to that of the reactants, FMS–T,R. Both are themselves calculated as the ratio of two rovibrational partition functions: the multi-structural (MS) one taking into account all conformers with a torsional (T) potential QrovibMS–T,χto the single-structural (SS) one only taking into account the global minimum (GM) conformer with a harmonic oscillator (HO) potential QMrovibSS–HO,χ,G, where χ stands for the n-heptane reactant (R) or saddle point (‡) species. The formula below provides the final rate constant that includes all the features and corrections described above:| kCVT/SCTMS–T = kCVT/SCTSS–HO × FMS–T | (2) |
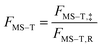 and
and 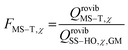 .
.
The final rate constant considers both quantum tunneling effects and multi-structural torsional anharmonicity as described in the following equation:
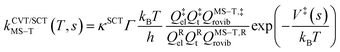 | (3) |
The transmission coefficient, κSCT, which takes into account quantum effects along the reaction coordinates s, is calculated here with the small curvature tunneling (SCT) approach.34 Variational effects are implemented through the recrossing factor Γ, which is defined as the ratio of variational transition state rate constant to the non-variational one. The Boltzmann's and Plank's constants are respectively designated by kB and h, while the potential energy barrier and the temperature are abbreviated by V‡(s) and T, respectively. The electronic, translational, and rovibrational partition functions of stationary point χ are respectively designated by Qχel, Qχt, and QMS–T,χrovib, χ representing either the alkane reactant (R) or saddle point (‡). Unlike the electronic partition functions and translational partition functions, the rovibrational partition functions depend on conformer c as the vibrational frequencies and moment of inertia depend on the spatial arrangement of the atoms within the chemical structure. They are calculated as follows:
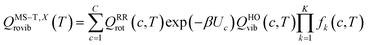 | (4) |
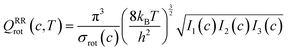 | (5) |
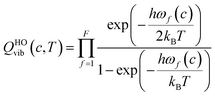 | (6) |
The corrective factor fk(c, T) accounts for the torsional anharmonicity of a set of coupled torsional motions k in conformer c and K is the number of coupled torsions. Coupled torsions are torsions whose motion is merged with that of other torsions (i.e., they can be described by a common normal mode and vibrational frequency). The product is computed as follows:
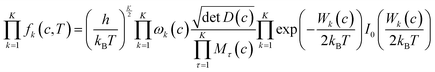 | (7) |
3. Results and discussion
3.1 Conformational analysis
The results of our conformational search are summarized in Fig. 2 as it shows the number of optimized and characterized distinguishable conformers for n-heptane and the saddle points along with their potential energy defined with respect to that of the corresponding global minimum. The optimized structures and vibrational frequencies for all conformers of the reactant n-heptane and the saddle points of reactions (R1)–(R4) are provided in Table S1 of the ESI,† while the corresponding global minimum conformers are depicted in Fig. 3. The calculated potential energies of these conformers, together with their T1 diagnostic values, are gathered in Table S2 of the ESI.† The T1 values are below 0.02 and 0.04 for the closed- and open-shell species, respectively, confirming the validity of our selected single reference methods.36 In total, we found 22, 42, 30, 31, and 22 unique conformers for n-heptane, SP1, SP2, SP3, and SP4, respectively. The number of conformers for the reactant is the same as the one reported by Nasiri and Luo37 who studied the H-abstraction reactions from n-heptane by the H radical.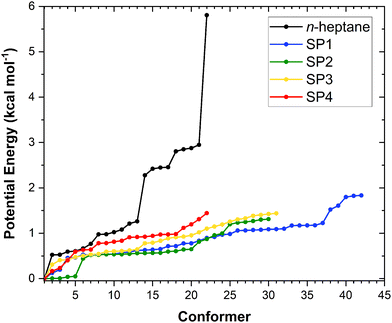 | ||
| Fig. 2 Potential energy distribution of the conformers of the n-heptane and saddle point (SP) species of reactions (R1)–(R4) at the M06-2X/aug-cc-pVTZ level. Energy values are defined with respect to that of the lowest-energy conformer of the corresponding stationary point. | ||
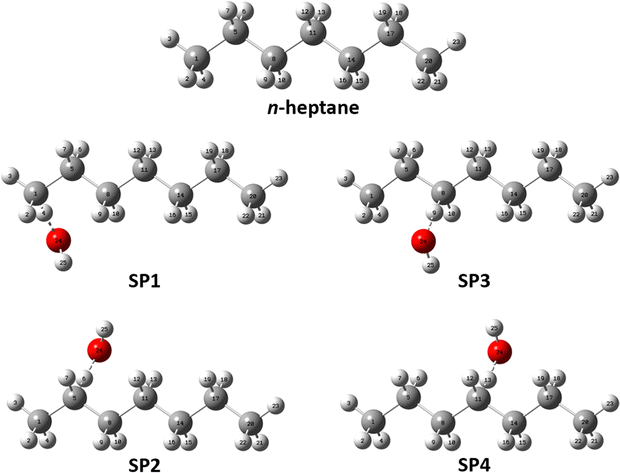 | ||
| Fig. 3 Optimized geometries of the global minimum conformers of the reactant and saddle point species at the M06-2X/aug-cc-pVTZ level of theory. | ||
The fact that SP1 has the highest number of conformers can be explained by the terminal site of n-heptane having the least steric hindrance from neighboring atoms, allowing greater flexibility for the attacking position and angle of the OH radical. In contrast, SP4 has the lowest number of conformers because the central location of the reactive center is the most sterically hindered, limiting the possibilities for OH to abstract a hydrogen atom at this site. In between, SP2 and SP3 have intermediate numbers of conformers since their reactive centers are in the middle of these extreme positions.
From Fig. 2 it can be inferred that, from a purely multi-structural anharmonicity perspective, i.e., neglecting the effect of torsional anharmonicity, one can expect reaction (R1) to be enhanced to a larger extent than reactions (R2)–(R4) due to the much larger number of conformers of its saddle point (SP1) compared to that of the reactant. On the contrary, the saddle point of reaction (R4) (SP4), which corresponds to the abstraction from the central C site, is the one with the fewest conformers. Moreover, the fact that the abstraction pathways (R1)–(R3) have two equivalent C sites for abstraction while (R4) has only one, would hinder the latter compared to the others from a symmetry perspective.
Another interesting feature of the potential energy distributions shown in Fig. 2 is the larger stability of the conformers of SP2 compared to those of the other stationary points, especially the first 4 conformers of SP2 whose energy with respect to that of the corresponding global minimum is below 0.04 kcal mol−1. This would contribute to enhance reaction (R2) among the others since the lower the energy of the conformers of a given saddle point the more positive effect of multi-structural anharmonicity on the corresponding reaction.
3.2 Potential energy surfaces
The minimum energy path (MEP) computed at the M06-2X/aug-cc-pVTZ level for each of the four different H-abstraction sites for the reaction of heptane + OH is shown in Fig. 4. For the sake of clarity, the values of the relative adiabatic potential energy and imaginary frequencies for the stationary points are compiled in Table 2. As expected, abstraction from the terminal site (R1) is the least kinetically favored since it leads to the formation of a least stable primary radical. The most favored H-abstraction site is the central one (R4) as it generates the most stable secondary radical due to the cumulative positive inductive effect from the surrounding methyl groups. Note that both secondary sites (R3) and (R4) almost coincide.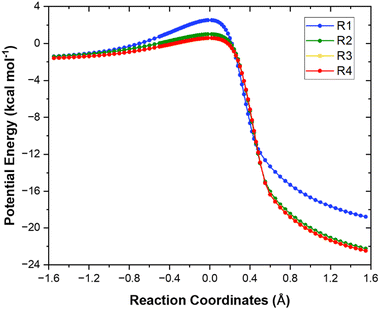 | ||
| Fig. 4 Minimum energy paths of reactions (R1)–(R4) calculated at the M06-2X/aug-cc-pVTZ level. | ||
| Species name | Energya (kcal mol−1) | Imaginary frequency (cm−1) |
|---|---|---|
| a ZPE-corrected energy of the saddle points and corresponding products relative to the reactants and calculated at the CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ level of theory. For the saddle point species, the global minimum conformers were considered. b The values shown in parentheses are calculated at the M06-2X/aug-cc-pVTZ level. | ||
| SP1 | 1.72 (1.30)b | −692.66 |
| SP2 | 0.07 (0.02)b | −489.13 |
| SP3 | −0.46 (−0.44)b | −477.11 |
| SP4 | −0.52 (−0.47)b | −477.80 |
| n-Hept-1-yl + H2O | −15.89 (−16.99)b | None |
| n-Hept-2-yl + H2O | −18.59 (−20.37)b | None |
| n-Hept-3-yl + H2O | −18.21 (−20.11)b | None |
| n-Hept-4-yl + H2O | −18.59 (−20.67)b | None |
3.3 Multi-structural torsional anharmonicity
The effects of the presence of multiple conformers and torsional anharmonicity were accounted for by calculating the relevant partition functions with the MSTor 2017 software, as explained in the Computational details and methodology section. Within the “Nearly Separable![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Strongly Coupled” (NS
Strongly Coupled” (NS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SC) scheme implemented in the MSTor software (0
SC) scheme implemented in the MSTor software (0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, 5
6, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 1
3, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, 1
7, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, and 1
7, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 for n-heptane, SP1, SP2, SP3, and SP4, respectively), multi-structural torsional anharmonicity factors (FMS–T) were calculated with different approaches that are referred to as M06-2X and CCSD(T)_N, corresponding to the use of potential energy values at the M06-2X/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ levels of theory, respectively. In the latter, N represents an energy threshold (in kcal mol−1) such that the reactant and saddle point conformers whose potential energy, defined with respect to that of the corresponding global minimum, is below that threshold are implemented in MSTor at the CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ level while the others were only considered at the M06-2X/aug-cc-pVTZ level, i.e., without a single point energy refinement. We applied this threshold to make our calculations feasible since the CCSD(T)/aug-cc-pVTZ level of theory would be computationally prohibitive if applied to all the numerous conformers that we found. Therefore, the level of theory CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ was only used in two scenarios, i.e., CCSD(T)_0.5 and CCSD(T)_1.0. The three calculated sets of FMS–T factors are plotted as a function of temperature in Fig. 5a and b for each species and reaction pathway, respectively, with the goal of assessing the impact of the extent of the computationally expensive CCSD(T)/aug-cc-pVTZ single point energy calculations in the multi-structural torsional treatment of large and flexible chemical reactive systems. The ultimate goal of this assessment is to facilitate the implementation of multi-structural torsional anharmonicity in the kinetics of large chemical reactions in which numerous conformers of reactants and saddle points are involved.
7 for n-heptane, SP1, SP2, SP3, and SP4, respectively), multi-structural torsional anharmonicity factors (FMS–T) were calculated with different approaches that are referred to as M06-2X and CCSD(T)_N, corresponding to the use of potential energy values at the M06-2X/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ levels of theory, respectively. In the latter, N represents an energy threshold (in kcal mol−1) such that the reactant and saddle point conformers whose potential energy, defined with respect to that of the corresponding global minimum, is below that threshold are implemented in MSTor at the CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ level while the others were only considered at the M06-2X/aug-cc-pVTZ level, i.e., without a single point energy refinement. We applied this threshold to make our calculations feasible since the CCSD(T)/aug-cc-pVTZ level of theory would be computationally prohibitive if applied to all the numerous conformers that we found. Therefore, the level of theory CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ was only used in two scenarios, i.e., CCSD(T)_0.5 and CCSD(T)_1.0. The three calculated sets of FMS–T factors are plotted as a function of temperature in Fig. 5a and b for each species and reaction pathway, respectively, with the goal of assessing the impact of the extent of the computationally expensive CCSD(T)/aug-cc-pVTZ single point energy calculations in the multi-structural torsional treatment of large and flexible chemical reactive systems. The ultimate goal of this assessment is to facilitate the implementation of multi-structural torsional anharmonicity in the kinetics of large chemical reactions in which numerous conformers of reactants and saddle points are involved.
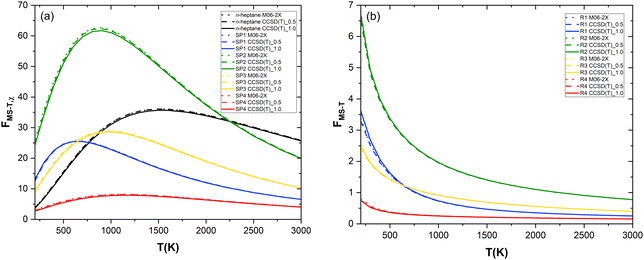 | ||
| Fig. 5 Temperature dependence of multi-structural torsional anharmonicity factors: (a) for the n-heptane reactant and the saddle points and (b) for each reaction pathway. | ||
As can be seen in Fig. 5a, the level of theory chosen hardly impacts the values of the anharmonicity factors for each species. Hence, we recognize that describing the most important conformers (i.e., those that are lowest in energy) with more accuracy has a negligible impact on the result. In the entire temperature range studied, the anharmonicity factor for SP4 is lower than that of n-heptane while the trend is opposite for the other saddle points except at lower temperatures for SP1 and SP3 (T < 800 K and T < 900 K, respectively) and at higher temperature for SP2 (T > 2200 K), the latter displaying the largest gap with respect to the reactant.
As a result, Fig. 5b shows that, compared to the single structure treatment, multi-structural torsional anharmonicity hinders the reactivity of (R4) within the entire temperature range considered (FMS–T < 1) while it enhances the reactivity of (R2) the most, especially at low temperatures. Fig. 5b evidences the important role played by multi-structural torsional anharmonicity in the investigated chemical reactions and thus the need for its implementation in chemical kinetic studies to derive accurate rate constants and branching ratios.
The effect of the pre-reaction complexes was estimated with the canonical unified statistical theory (CUS)38 as we did in our previous works.26,39 Pre-reaction complexes are expected to have an effect only at low or very low temperatures when the outer barrier, or barrier to the formation of the complex, can control reactivity. The CUS model defines the rate constant of a stepwise mechanism via a pre-reaction complex as:
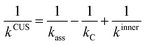 | (8) |
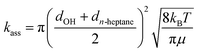 | (9) |
3.4 Overall rate constants
The site-specific rate constants for all four reaction pathways (R1), (R2), (R3) and (R4) in the temperature range 200–3000 K were computed using different levels of theory. First, we calculated the single-structural (SS-HO-LL) rate constants at the lower level M06-2X/aug-cc-pVTZ, and then we calculated them at the higher level CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ (SS-HO-HL) by updating the barrier heights. We further improved the rate constant calculations by implementing the effects of multi-structural torsional anharmonicity as described in the previous section, leading to three other sets of rate constants: MS-T-HL, MS-T-HL_0.5, and MS-T-HL_1.0 with F factors from M06-2X, CCSD(T)_0.5, and CCSD(T)_1.0, respectively (note that in the MS-T-HL case, only the global minimum conformers are refined at the CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ level, i.e. threshold = 0.0 kcal mol−1). The overall calculated rate constants, which are obtained by summing those corresponding to each reaction pathway, are compared to other estimations and experimental data from the literature in Fig. 6.The aim of these comparisons is to assess the effect of the corresponding features on the rate constant values and help to identify the most important sources of errors. Overall, all data display a positive temperature dependence and non-Arrhenius behavior. Both SS-HO-LL and SS-HO-HL approaches yield similar values for the overall rate constants, which is due to the similar barrier heights predicted by the two levels of theory used in our calculations (see Table 2). Thus, we conclude that, within the SS scheme, there is negligible effect in refining the barrier heights obtained for the global minimum conformers at the lower level M06-2X/aug-cc-pVTZ by using the higher level CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ, indicating a similar performance of the former at a much lower computational cost. When comparing for the same high level of theory, the single structural harmonic oscillator approach (SS-HO-HL) with the addition of the multi-structural treatment (MS-T-HL), it is evident that the latter provides a considerably better agreement with experimental data, especially at low and intermediate temperatures. Hence, the inclusion of the multistructural torsional anharmonicity feature cannot be overlooked, meaning that the integration of both multiple conformers and deviation from the harmonic oscillator model is critical and highly recommended for such large and flexible systems. All MS-T multi-structural rate constants agree reasonably well with the trends of both experimental data and estimations from both Kwok and Atkinson18 and Sivaramakrishnan and Michael.14 Our most refined one, i.e. MS-T-HL_1.0, shows negligible difference with the least refined ones, i.e. MS-T-HL_0.5 and MS-T-HL. Hence the inclusion of computationally expensive single-point energy calculations at the CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ level is not necessary and the M06-2X//aug-cc-pVTZ level of theory is actually sufficient to accurately describe the kinetics of the investigated reactive system as long as the multistructural torsional anharmonicity contribution is implemented.
Consequently, the final and recommended approach is MS-T-HL_1.0 for which we observe a maximum deviation from estimations of a factor of 1.5 at 1000 K. However, the MS-T-HL approach arises as the most computationally efficient one in terms of accuracy and cost, and may be the most convenient approach for other large, flexible and linear hydrocarbons for which the application of expensive coupled cluster methods is not feasible.
Two main sources of errors may explain the observed discrepancies. One is the potential overestimation of the barrier height which could be resolved by using higher levels of theory. However, this would require, for instance, using larger basis sets, which is impractical and defeats the purpose of our protocol that aims at determining a practical yet accurate way to calculate the rate constants of reactions involving large and complex chemical systems. Another one is the extent of the energy distribution refinements, that is, its extension to all conformers regardless of their energy. However, the high number of conformers that lay above the 1 kcal mol−1 threshold would result in an approach that would again defeat the purpose of practicality.
3.5 Branching ratios
Site-specific rate constants are key to understanding the fate of intermediate product radicals and necessary to incorporate in combustion mechanisms for greater accuracy. However, such data is inaccessible to retrieve through experiments, as these typically track the decay of reactants who are blind to the fate of products. As a consequence, experimental datasets provide no direct insight into the preferential reaction pathways. To address this gap, our theoretical study also includes branching ratios, offering valuable information on the relative prominence of each pathway.From our most refined site-specific rate constants MS-T-HL_1.0, we extracted the branching ratios shown in Fig. 7a. Notably, (R1) and (R4) exhibit similar reactivity, as do (R2) and (R3), with more pronounced differences at low temperatures. (R2) emerges as the most favored pathway, while (R1) is the least favored, except at high temperature where (R4) becomes less reactive than (R1). These branching ratios are controlled by both the barrier heights and the FMS–T factors.
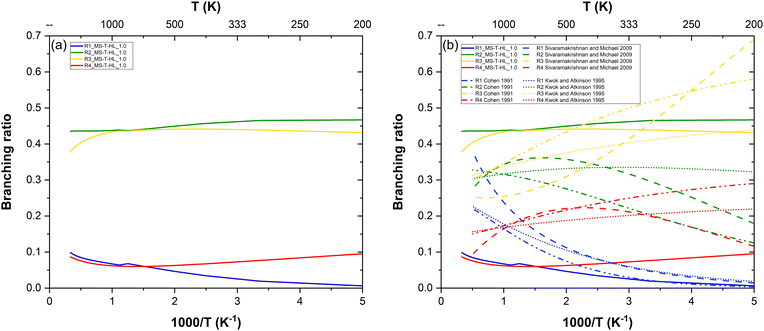 | ||
| Fig. 7 Branching ratios of the n-heptane + OH reaction: (a) our MS-T-HL_1.0 results in solid lines only and (b) compared to estimations in interrupted lines.14,17,18 | ||
(R1) having the highest barrier height, is the least kinetically favored pathway. Additionally, while (R1) and (R3) share similar FMS–T factors, the latter has a lower barrier height, making it more prominent. Conversely, despite (R4) having the lowest barrier height, its reactivity is hindered by multistructural torsional anharmonicity, characterized by the fewest conformers and the lowest FMS–T factors. Interestingly, (R2), though not associated with the lowest barrier height, benefits significantly from multistructural torsional anharmonicity. Its highest FMS–T factors render it the most dominant pathway, substantially surpassing (R4) in prominence.
In Fig. 7b, we also compared our branching ratio results to the ones obtained from the site-specific rate constants estimations available in the literature.14,17,18 In the low temperature range, all works predict that the reactivity follows the order: (R3) > (R2) > (R4) > (R1). At intermediate temperatures, both Cohen17 and Sivaramakrishnan and Michael14 display a swapped reactivity preference between (R2) and (R3), making the former the dominant pathway. At low temperatures, all works also predict (R4) to become the least reactive pathway with a swapped reactivity between (R1) and (R4), although according to Sivaramakrishnan and Michael,14(R1) is surprisingly the most reactive pathway. Our results generally follow a similar trend to the estimations of Kwok and Atkinson18 with less temperature variability than those from other works. However, our branching ratios display more extreme values, highlighting potential limitations of estimation methods which are expected to be less accurate than first-principle calculations. This suggests that such methods may not always achieve the accuracy required for detailed combustion modeling.
For example, Cohen's semi-empirical approach,17 while valuable, is inconclusive. The author acknowledges that his method does not surpass simpler empirical approaches, such as that of Kwok and Atkinson,18 due to the limited database of relevant rate constants available at the time. Moreover, Cohen's methodology relies on several assumptions and is fine-tuned to reproduce high-temperature shock-tube experiments by extrapolating transition state theory (TST) calculations conducted at room temperature. Kwok and Atkinson,18 on the other hand, report that their structure–reactivity approach provides rate constants for abstraction reactions from alkanes by OH radicals with an accuracy within a factor of two. Sivaramakrishnan and Michael14 proposed their own three-parameter Arrhenius fits for these site-specific rate constants by solving systems of equations derived from overall rate constants. Their methodology assumes additivity rules based on similarities between abstraction sites across different alkanes, following Cohen's nomenclature. To ensure validity over a broad temperature range, they combined their high-temperature measurements (with an uncertainty of 15%) with earlier low-temperature experimental data published by other authors, thereby incorporating more experimental uncertainties into their empirical model. In comparison, our study is entirely theoretical and based on first-principle and robust calculations, generating precise data independent from any experimental findings. This independence ensures that our results provide a reliable and robust foundation for advancing the understanding of site-specific preferences in hydrogen abstraction reactions from large and linear hydrocarbons.
3.6 Impact on ignition delay time predictions
Our site-specific rate constants were fitted to a three-parameter Arrhenius expression in the form of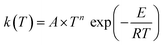 . The derived Arrhenius parameters for each reaction channel are compiled in Table 3.
. The derived Arrhenius parameters for each reaction channel are compiled in Table 3.
In Fig. 8, we compared the results of n-heptane ignition delay times upon updating with our values the rate parameters of reactions (R1)–(R4) in the original kinetic mechanism published by Zhang et al.2 who adopted these rate constants from the work of Sivaramakrishnan and Michael.14 Simulations were conducted using the ANSYS Chemkin 2024 R2 software.40 First, we can observe a significant discrepancy between both models at intermediate temperatures, coined as low temperature in the combustion field. This coincides with the earlier observation made regarding the high sensitivity of reactions (R1), (R3) and (R4) in these temperature ranges and highlights the importance of precisely determining these rate constants. Overall, our updated rate constants lead to an overestimation of ignition delay times at intermediate temperatures compared to the original rate constants which are in better alignment with experimental data.2,41 However, for this assessment, it should be kept in mind that ignition delay times are calculated based on all the reactions present in the mechanism, especially the highly sensitive ones. As displayed in Fig. 1, there are other highly sensitive reactions in the lower temperature region that happen to usually be poorly determined or tuned to fit macroscopic combustion properties. Revisiting the rate constants of reactions (R1)–(R4) is important but does not solve the problem of accurately predicting ignition delay times as other reactions need to be reviewed as well.
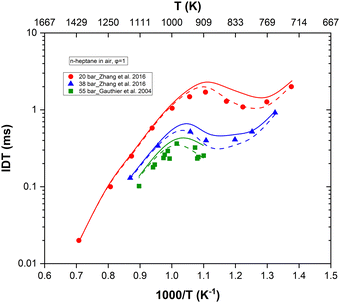 | ||
| Fig. 8 Comparison of n-heptane ignition delay time predictions at φ = 1, p = 20 bar, p = 38 bar, and p = 55 bar. Symbols are experiments2,41 while solid and dashed lines respectively correspond to simulations with and without the implementation of the updated rate constants for reactions (R1)–(R4) in the original mechanism.2 | ||
4. Conclusions
This study provides a comprehensive investigation into the hydrogen atom abstraction reactions of n-heptane by OH radicals, focusing on the impact of conformational effects on rate constants and branching ratios. Using multistructural torsional variational transition state theory (MS—VTST) with small curvature tunneling (SCT) corrections, we computed site-specific rate constants across a broad temperature range (200–3000 K). Our results demonstrate good agreement with numerous experimental data as deviations remain within a maximum factor of 1.5 at 1000 K.In addition to providing accurate rate constants, our work presents the branching ratios for the n-heptane + OH reaction, which is crucial data that is not accessible from experiments. These results revealed that the secondary abstraction site adjacent to the primary site is the dominant reaction pathway, offering new insights into the preferential reactivity of n-heptane.
This study highlights the significance of multistructural torsional anharmonicity effects in large and flexible molecular systems, emphasizing the necessity of considering conformational diversity to achieve accurate kinetic predictions.
Another important conclusion derived from our work is the fact that high levels of theory, such as those involving the common and computationally expensive coupled cluster method with large basis sets, may not be necessary for the refinement of the energy of the numerous conformers formed by the reactants and saddle points. Instead, a more computationally efficient and appropriate DFT method such as M06-2X, combined with a large enough basis set, may show comparable accuracy for similar linear and large hydrocarbons.
Therefore, our results demonstrate the applicability of the described protocols when it comes to calculating the rate constants and branching ratios of other unexplored hydrogen abstraction reaction systems involving other abstracting species as well as other substrates with multiple abstraction sites and conformers. We believe that the identification and implementation of these practical yet robust protocols can help with the development of accurate kinetic models that are essential for combustion and atmospheric applications.
Author contributions
M. Belmekki, M. Monge-Palacios, and T. Wang conceptualized the idea of this research work and conducted the analysis and data curation. M. Belmekki and M. Monge-Palacios wrote the original draft. S. M. Sarathy was responsible for funding acquisition and project administration, and also reviewed the original draft.Data availability
The data supporting this article have been included as part of the ESI.† The software and version used for the calculations and simulations have been stated in the main article and can be obtained upon request to the developers, with the exception of Gaussian16 and Chemkin 2024 R2 software, which is are commercial.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge funding from King Abdullah University of Science and Technology (KAUST) in Thuwal, Saudi Arabia. For computer time, this research used the resources of the KAUST Supercomputing Laboratory (KSL). The authors also acknowledge the support provided by the team in charge of the IBEX and SHAHEEN clusters at the KSL.References
- L. K. Huynh, A. Ratkiewicz and T. N. Truong, J. Phys. Chem. A, 2006, 110, 473–484 CrossRef CAS PubMed.
- K. Zhang, C. Banyon, J. Bugler, H. J. Curran, A. Rodriguez, O. Herbinet, F. Battin-Leclerc, C. B'Chir and K. A. Heufer, Combust. Flame, 2016, 172, 116–135 CrossRef CAS.
- D. G. Goodwin, H. K. Moffat, I. Schoegl, R. L. Speth and B. W. Weber, Zenodo, 2023 Search PubMed.
- R. Atkinson, S. M. Aschmann, W. P. L. Carter, A. M. Winer and J. N. Pitts Jr, Int. J. Chem. Kinet., 1982, 14, 781–788 CrossRef CAS.
- W. Behnke, F. Nolting and C. Zetzsch, J. Aerosol Sci., 1987, 18, 65–71 CrossRef CAS.
- W. Behnke, W. Holländer, W. Koch, F. Nolting and C. Zetzsch, Atmos. Environ., 1988, 22, 1113–1120 CrossRef CAS.
- C. Ferrari, A. Roche, V. Jacob, P. Foster and P. Baussand, Int. J. Chem. Kinet., 1996, 28, 609–614 CrossRef CAS.
- E. W. Wilson, W. A. Hamilton, H. R. Kennington, B. Evans, N. W. Scott and W. B. DeMore, J. Phys. Chem. A, 2006, 110, 3593–3604 CrossRef CAS PubMed.
- M. A. Crawford, B. Dang, J. Hoang and Z. Li, Int. J. Chem. Kinet., 2011, 43, 489–497 CrossRef CAS.
- L. Han, F. Siekmann and C. Zetzsch, Atmosphere, 2018, 9, 320 CrossRef.
- J. T. Shaw, R. T. Lidster, D. R. Cryer, N. Ramirez, F. C. Whiting, G. A. Boustead, L. K. Whalley, T. Ingham, A. R. Rickard, R. E. Dunmore, D. E. Heard, A. C. Lewis, L. J. Carpenter, J. F. Hamilton and T. J. Dillon, Atmos. Chem. Phys., 2018, 18, 4039–4054 CrossRef CAS.
- J. Morin, M. N. Romanias and Y. Bedjanian, Int. J. Chem. Kinet., 2015, 47, 629–637 CrossRef CAS.
- J. B. Koffend and N. Cohen, Int. J. Chem. Kinet., 1996, 28, 79–87 CrossRef CAS.
- R. Sivaramakrishnan and J. V. Michael, J. Phys. Chem. A, 2009, 113, 5047–5060 CrossRef CAS PubMed.
- G. A. Pang, R. K. Hanson, D. M. Golden and C. T. Bowman, Z. Phys. Chem., 2011, 225, 1157–1178 CrossRef CAS.
- R. T. Skodje, D. G. Truhlar and B. C. Garrett, J. Chem. Phys., 1982, 77, 5955–5976 CrossRef CAS.
- N. Cohen, Int. J. Chem. Kinet., 1991, 23, 397–417 Search PubMed.
- E. S. Kwok and R. Atkinson, Atmos. Environ., 1995, 29, 1685–1695 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. L. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, 2016 Search PubMed.
- C. Peng and H. B. Schlegel, Isr. J. Chem., 1993, 33, 449–454 CrossRef CAS.
- J. Zheng, R. Meana-Pañeda and D. G. Truhlar, Comput. Phys. Commun., 2013, 184, 2032–2033 CrossRef CAS.
- R. J. Bartlett, J. Phys. Chem., 1989, 93, 1697–1708 CrossRef CAS.
- J. E. Chavarrio Cañas, M. Monge-Palacios, E. Grajales-González and S. M. Sarathy, J. Phys. Chem. A, 2021, 125, 3177–3188 CrossRef PubMed.
- S. Y. Mohamed, M. Monge-Palacios, B. R. Giri, F. Khaled, D. Liu, A. Farooq and S. M. Sarathy, Phys. Chem. Chem. Phys., 2022, 24, 12601–12620 RSC.
- Y. Duan, M. Monge-Palacios, E. Grajales-Gonzalez, D. Han and S. M. Sarathy, Fuel, 2022, 326, 125046 CrossRef CAS.
- Y. Duan, M. Monge-Palacios, E. Grajales-Gonzalez, D. Han, K. H. Møller, H. G. Kjaergaard and S. M. Sarathy, Combust. Flame, 2020, 219, 20–32 CrossRef CAS.
- E. Grajales-González, G. Kukkadapu, S. S. Nagaraja, C. Shao, M. Monge-Palacios, J. E. Chavarrio, S. W. Wagnon, H. J. Curran, W. J. Pitz and S. Mani Sarathy, Combust. Flame, 2022, 242, 112206 CrossRef.
- J. Zheng, J. L. Bao, S. Zhang, J. C. Corchado, R. Meana-Paneda, Y.-Y. Chuang, E. L. Coitino, B. A. Ellingson and D. G. Truhlar, Gaussrate 17, 2017, University of Minnesota, Minneapolis (USA), 2017 Search PubMed.
- M. Page and J. W. McIver, J. Chem. Phys., 1988, 88, 922–935 CrossRef CAS.
- J. Zheng, J. L. Bao, R. Meana-Paneda, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. Fernandez-Ramos, B. A. Ellingson, V. S. Melissas, J. Villa, I. Rossi, E. L. Coitino, J. Pu and T. V. Albu, POLYRATE, version 2016-2A, University of Minnesota, Minneapolis, 2016 Search PubMed.
- J. Zheng, S. L. Mielke, J. L. Bao, R. Meana-Pañeda, K. L. Clarkson and D. G. Truhlar, MSTor computer program, version 2017, University of Minnesota, Minneapolis, 2017 Search PubMed.
- D. H. Lu, T. N. Truong, V. S. Melissas, G. C. Lynch, Y. P. Liu, B. C. Garrett, R. Steckler, A. D. Isaacson, S. N. Rai, G. C. Hancock and J. G. Lauderdale, Comput. Phys. Commun., 1992, 71, 235–262 CrossRef CAS.
- J. E. Kilpatrick and K. S. Pitzer, J. Chem. Phys., 1949, 17, 1064–1075 CrossRef CAS.
- T. J. Lee, Chem. Phys. Lett., 2003, 372, 362–367 CrossRef CAS.
- R. Nasiri and K. H. Luo, Combust. Flame, 2018, 193, 170–176 CrossRef CAS.
- B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1982, 76, 1853–1858 CrossRef CAS.
- M. Monge-Palacios, E. Grajales-Gonzalez and S. M. Sarathy, J. Phys. Chem. A, 2018, 122, 9792–9805 CrossRef CAS PubMed.
- Reaction Design, Inc., Chemkin-Pro, San Diego, CA, 422, 2011, p. 396.
- B. M. Gauthier, D. F. Davidson and R. K. Hanson, Combust. Flame, 2004, 139, 300–311 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tabulation of the: (1) geometries and vibrational frequencies for all conformers of n-heptane and the saddle points optimized at the M06-2X/aug-cc-pVTZ level of theory, (2) computed energies of all the conformers for the stationary points at the M06-2X/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ levels of theory along with their associated T1 diagnostic values, (3) rate constants for each pathway computed with different approaches. See DOI: https://doi.org/10.1039/d5cp00301f |
| This journal is © the Owner Societies 2025 |