Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An embedding scheme for constraint-based orbital-optimized excitations in molecular and bulk environments†
Yannick
Lemke‡
 a,
Jörg
Kussmann‡
a,
Jörg
Kussmann‡
 *a and
Christian
Ochsenfeld
*a and
Christian
Ochsenfeld
 *ab
*ab
aChair of Theoretical Chemistry, Department of Chemistry, Ludwig-Maximilians-Universität München, Butenandtstr. 5–13, Munich D-81377, Germany. E-mail: joerg.kussmann@uni-muenchen.de; christian.ochsenfeld@uni-muenchen.de
bMax-Planck-Institute for Solid State Research, Heisenbergstr. 1, Stuttgart, D-70659, Germany
First published on 29th May 2025
Abstract
We recently presented a novel approach to variationally determine electronically excited states based on constrained density functional theory calculations. The constraint-based orbital-optimized excited state method (COOX) [Kussmann et al., J. Chem. Theory Comput., 2024, 20, 8461–8473] allows the evaluation of arbitrary electronic excitations and has several advantages compared to other methods like ΔSCF. In this work, we present an embedding scheme for COOX where the constraint potential is drawn from a sub-system calculation. This approach enables the accurate evaluation of specific excited states within complex environments that are difficult to obtain with conventional methods. The validity and range of applicability of the presented method are investigated for first exemplary calculations.
Nowadays, electronic structure methods to determine electronic excitations are a crucial tool to investigate photoinduced chemical processes and for the design of energy materials. While many different theoretical models to evaluate electronic excitations as well as excited state properties are available,1–8 linear-response time-dependent density functional theory (LR-TDDFT) evolved to be the main workhorse for excited state simulations due to its overall good accuracy in combination with relatively low computational cost.
However, there are some well-known limitations to LR-TDDFT like its restriction to single electron excitations only or the poor description of charge transfer- or core-excitations due to the linear-response ansatz. In these cases, variational excited state methods like ΔSCF9–11 and improvements thereupon like MOM12,13 or STEP14 can strongly improve the overall accuracy, although only clearly defined orbital excitation patterns (e.g., HOMO → LUMO) can be simulated. Furthermore, these orbital-optimized TDDFT methods (OO-TDDFT) often suffer from instabilities, i.e., a collapse of the wave function to the ground state, which can be prevented by the squared gradient minimization method (SGM).15 Our recently proposed constraint-based orbital-optimized excited state method (COOX)16,17 rectifies several of the shortcomings of ΔSCF-type methods, i.e., by showing a stable convergence behavior for arbitrary excited states while also providing accurate excited state properties.
In this work, we present an embedding scheme for our COOX method that draws the constraint potential from an isolated sub-system to determine specific excited states within a complex environment. Note that in some cases these states can be very difficult or almost impossible to calculate with conventional linear-response methods as a large number of excitations have to be evaluated within the Davidson scheme.18
In the following, we will briefly recap the COOX method and outline the new embedded COOX scheme (e-COOX). Finally, we will analyze the validity and accuracy of our method for first illustrative calculations.
1 Theory
The COOX method variationally determines the electronically excited state employing the constrained DFT method (cDFT)19–21 by optimizing the energy functional:| E[ρ,λc;Nc] = E0[ρ] + λc(Tr[WcP] − Nc), | (1) |
For the COOX method, the constraint potential Wc is derived from the static part of the excited state difference density matrix obtained with LR-TDDFT:16
| Wc = S(ΔPvirt − ΔPocc)S, | (2) |
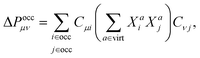 | (3) |
 | (4) |
1.1 Embedded COOX for complex environments
Our COOX embedding scheme (e-COOX) aims at evaluating the excited states of photoactive substrates in complex environments. Therefore, the constraint in eqn (2) is evaluated from the transition coefficient X of the isolated photoactive site. If this sub-system is well separated from the environment, i.e., if the interactions with the environment are negligible, the unmodified constraint of the sub-system could be used. However, realistically, the electron distributions of the active site and the environment interact, so that the constraint needs to be modified. Here, it is important to stress that Wc is not only a purely spatial constraint, but also a constraint on the occupied and virtual molecular orbital (MO) subspaces, thus ensuring the excitation of a single electron from the occupied into the virtual MO space,| Tr[SP0occSΔPocc] = 1, Tr[SP0virtSΔPocc] = 0, | (5) |
| Tr[SP0virtSΔPvirt] = 1, Tr[SP0occSΔPvirt] = 0, | (6) |
| ϕsuba ⊥ ϕtoti, ϕsubi ⊥ ϕtota, ϕsubi ⊥ ϕsuba, | (7) |
The embedding scheme is summarized as follows: 1. Evaluate the ground state for the complete system. 2. Perform a LR-TDDFT calculation for the isolated photoactive sub-system. 3. Reorthogonalize the sub-system MOs ϕsub with respect to the occupied/virtual MO subspaces of the complete system (eqn (7)). 4. Form the COOX constraint potential (eqn (2)) using the reorthogonalized sub-system MOs and transition coefficients. 5. Run the COOX calculation for the complete system.
At this point, it should be stressed that we use the term “embedding” in a more literal sense than existing embedding methods such as multi-scale quantum mechanics/molecular mechanics (QM/MM) approaches, wherein a sub-system which is treated at a high quantum-mechanical level of theory is “embedded” into an environment which is treated at a lower level of theory: in e-COOX, the sub-system constraint is properly embedded into the basis of the complete system, which is then altogether treated at the high quantum-mechanical level of theory.
To illustrate the effect of the embedding on the constraint potential as well as the difficulty to access some excitations with conventional linear-response methods, we investigate the HOMO → LUMO excitation of a carbon monoxide molecule embedded in a single C60 fullerene. Apparently, the fullerene itself features many excited states with a lower energy than the excitation of interest. Using the Davidson algorithm, we would have to evaluate hundreds of roots for the complete system, so that we opted to use the simplified TDA-TDDFT (sTDA) algorithm22 instead. Using PBE/def2-SVP,23,24 the 455th root can be identified as the carbon monoxide HOMO → LUMO excitation. Due to the small volume of the fullerene cavity, there is a significant overlap between the carbon monoxide orbitals and the fullerene, i.e., the impact of reorthogonalization is clearly visible from the constraint potential shown in Fig. 1. It should be stressed that the pure HOMO → LUMO excitation of carbon monoxide is not necessarily obtained with any density functional, i.e., often mixed excitation patterns including the HOMO−1 and LUMO+1 orbitals arise. The e-COOX scheme yields a slightly lower excitation energy of 7.50 eV compared to the isolated system (7.55 eV) which is in line with a reduced difference in the orbital energies. Using the unmodified sub-system constraint, however, produces a wrong trend by increasing the excitation energy (7.71 eV). This results from the missing orthogonality of the occupied and virtual constraint potentials with respect to the MOs of the complete system. The projection of the virtual part onto the occupied subspace and the occupied constraint onto the virtual subspace should vanish but instead considerably overlap with the supposedly orthogonal subspaces (Tr[SP0occSΔPvirt] = 0.002 and Tr[SP0virtSΔPocc] = 0.847). Drawing the constraint potential from the complete system, i.e., the 455th excitation from the sTDA calculation, one should expect a better result than using the plain sub-system constraint. However, due to the packed nature of our artificial test system, the strong overlap of the carbon monoxide orbitals with those from the fullerene cage results in a higher electron delocalization and thus leakage into the environment. An unscaled COOX calculation will result in a double excitation, so that a rather large scaling factor for the virtual part of the constraint potential16 is obtained which in turn slightly overcompensates and therefore results in only 0.89 electrons transitioning. As a result, the excitation energy is far too low at 4.5 eV.
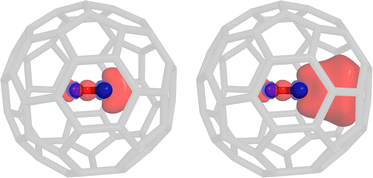 | ||
| Fig. 1 COOX constraint potential for the HOMO → LUMO excitation of carbon monoxide. The pure sub-system potential (left) as well as the embedded potential (right) are shown (sTDA-PBE/def2-SVP). | ||
Although this test system is highly artificial, it clearly illustrates how the e-COOX approach solves several issues. First, the computational overhead to execute a LR-TDDFT calculation for a large system to construct the COOX constraint is strongly reduced, and secondly, the identification of the desired target state is easier and clear. Finally, the embedded sub-system constraint does not suffer from any contamination like an unphysical charge-transfer character due to the use of approximate functionals, which in turn ensures accurate results and a stable convergence of the COOX calculation.
2 Illustrative calculations
All presented methods have been implemented using our FermiONs++ program package.25–27 The def2-SVP and def2-TZVP basis sets24 have been employed, except for PBEh-3c.28 Tight integral thresholds (ϑint = 10−10) and an SCF convergence threshold of ϑscf = 10−7 for the norm of the commutator [F,P]− have been used throughout. Two-electron integrals were evaluated with an improved RI-Coulomb integral engine29 using the universal auxiliary basis “def2-universal-jfit”30 and the sn-LinK method31–33 with a gm4 grid.34 For all COOX calculations, an electronic temperature of 1000 K has been chosen. For all DFT calculations, the gm5 grid34 has been employed and the libxc,35,36 DFT-D3,37–39 and gCP28,40 libraries have been used where required. The PyMol program41 was used to generate depictions of molecular structures and difference density plots.2.1 Uracil: solvation effects
In order to investigate the validity of our proposed embedded COOX scheme, we first analyze the first two singlet excitations, i.e., the n → π* (S1) and π → π* (S2) excitations, of the uracil molecule in solvation. This system has been investigated by Lange and Herbert42 to analyze the impact of spurious charge-transfer (CT) contamination in LR-TDDFT calculations. Here, a growing hydration shell introduces an increasing number of CT excitations at a similar or lower energy level compared to the valence excitations of the isolated uracil molecule. Therefore, this system presents an ideal test case for our new embedding scheme.As a proof of concept, we first analyze the impact of a single water molecule at different distances from the uracil molecule on the S1 and S2 states using PBE043/def2-TZVP. The results obtained with LR-TDA-TDDFT and ADC(3) (computed with Q-Chem 5.144) are compared to the complete COOX calculation and the embedded COOX scheme (e-COOX) using the unmodified (non-orthogonal) and reorthogonalized constraints obtained from the isolated uracil molecule as shown in Fig. 2, where only the difference to the corresponding excitation energy of the uracil molecule is shown. Note that the minimum energy for the ground state is obtained for a distance of 3 Å, so that the largest deviations can be seen for the more strained configurations with a smaller distance, where the TDA-TDDFT amplitudes for the complete system are likely less reliable. This is illustrated for the S2 state when using the scaled constraint potential (eqn (14) in ref. 16), for which the full COOX calculation shows a wrong trend, i.e., an increased excitation energy at small distances (see Fig. S2 in the ESI†). The figures containing the absolute excitation energies are found in the ESI† (Fig. S3 and S4).
We also investigate the influence of a full hydration shell similar to that described in ref. 42, although we generated the geometries using the Quantum Cluster Growth algorithm45 of the CREST program46 instead of using molecular dynamics snapshots. The resulting structure is shown in Fig. 3. Since the observed double excitation character is small for both considered states (<20%), we use the unscaled constraint potentials throughout this section. In Table 1, we compare the results for uracil within a water shell containing 100 solvent molecules obtained with our proposed e-COOX method compared to sTDA-TDDFT and COOX calculations of the complete system. The precise state ordering of n → π* and π → π* is highly method-dependent, with LR-TDDFT42 and CC247 predicting the π → π* state to fall below the n → π* state whereas EOM-CC methods predict the n → π* state as S148 (at least for the respective geometries used in these studies). Nevertheless, the methods agree on a substantially larger solvatochromic shift for the n → π* state, which is shown in Table 2. Most COOX calculations follow the trend of LR-TDDFT and CC2, i.e., the π → π* state appears below the n → π* state, though energetic differences are generally small. While the calculations using constraints from the complete system generally show good agreement with higher-level methods regarding the solvatochromic shift, it should be stressed that, especially in the case of PBE, the assignment of the sTDA roots in question (31st and 56th, respectively) becomes increasingly difficult – in contrast, the sub-system roots considered for e-COOX are always S1 and S2 (S1 and S3 for PBE) regardless of the size of the hydration shell. Furthermore, although the complete system calculations yield satisfactory excitation energies, the constraint potentials are considerably contaminated by charge-transfer contributions from the solvent. For scaled constraint potentials, the S1 state using B3LYP/TZVP failed to converge, while the S2 calculation converged only after 44 iterations. This again indicates the general problem of linear-response TDDFT, as the solvated system produces an S1 state with a significant long-range charge-transfer character for the B3LYP/TZVP calculation in contrast to the PBEh-3c results, which features a significantly larger amount of exact exchange. This is illustrated by the corresponding constraint potentials in Fig. S5 and S6 in the ESI† for S1 and S2, respectively. Since PBEh-3c employs a smaller basis set, we also analyzed the constraint potential for BHandHLYP49/TZVP with 50% of exact exchange, which yields a similar constraint potential to PBEh-3c. Considering e-COOX, which besides the previously mentioned case of B3LYP with scaled constraint potentials showed fast convergence, the solvatochromic shifts are on the same order as sTDA results and appear to be much less dependent on the choice of the functional than for the regular COOX calculations in the complete system as well as the underlying linear-response TDDFT calculations.
| Functional | S1 (n → π*) | S2 (π → π*) | ||||||
|---|---|---|---|---|---|---|---|---|
| sTDA | COOX | e-COOX [n.o.] | e-COOX | sTDA | COOX | e-COOX [n.o.] | e-COOX | |
| a Ref. 47, aug-cc-pVDZ basis set, QM/MM embedding. b Ref. 48, 6-31G(d) basis set, QM/MM embedding. | ||||||||
| PBE | 4.40 (31) | 5.15 | 5.33 | 5.71 | 4.68 (56) | 5.29 | 5.31 | 5.69 |
| B3LYP | 5.31 (7) | 5.78 | 5.94 | 6.34 | 5.32 (8) | 5.80 | 5.97 | 6.32 |
| PBE0 | 5.37 (5) | 6.17 | 6.07 | 6.45 | 5.36 (4) | 5.86 | 6.04 | 6.48 |
| PBEh-3c | 5.86 (2) | 6.88 | 6.55 | 6.97 | 5.83 (1) | 6.63 | 6.14 | 6.79 |
| CC2a | 5.37 | 5.20 | ||||||
| EOM-CCSDt(II)b | 5.75 | 5.96 | ||||||
| Functional | S1 (n → π*) | S2 (π → π*) |
|---|---|---|
| a Ref. 47, aug-cc-pVDZ basis set, QM/MM embedding. b Ref. 48, 6-31G(d) basis set, QM/MM embedding. | ||
| PBE/TZVP | ||
| sTDA | 0.57 | −0.09 |
| COOX | 0.28 | 0.12 |
| e-COOX | 0.83 | 0.52 |
| B3LYP/TZVP | ||
| sTDA | 0.70 | 0.06 |
| COOX | 0.28 | −0.14 |
| e-COOX | 0.84 | 0.38 |
| PBE0/TZVP | ||
| sTDA | 0.70 | 0.07 |
| COOX | 0.55 | −0.32 |
| e-COOX | 0.83 | 0.29 |
| PBEh-3c | ||
| sTDA | 0.87 | 0.13 |
| COOX | 0.83 | 0.13 |
| e-COOX | 0.92 | 0.29 |
| Reference | ||
| CC2a | 0.43 | −0.20 |
| EOM-CCSDt(II)b | 0.44 | 0.07 |
Compared to the more dense fullerene/CO test system, the impact of reorthogonalization instead of using the unmodified, i.e., non-orthogonal, sub-system constraint is smaller. The deviation from orthogonality with the occupied/virtual subspaces of the complete system is larger for the S2 state, which in turn is reflected in a larger deviation in the excitation energies.
We also present the results for three hydration shells containing 25, 50, and 100 water molecules in Table 3. In concert with the findings of ref. 42, the number of low-lying excited states below S1 and S2 of the isolated uracil molecule increases with the size of the hydration shell. As expected, the most artificial CT excitations below the target excited state energies occur for the pure PBE functional, while the addition of exact exchange clearly suppresses the delocalization effect of approximate functionals. Additional results obtained with LR-TDA-TDDFT and COOX using a constraint from a complete system and the unmodified sub-system constraint are shown in the ESI† (Tables S1–S3).
| Functional | S1 (n → π*) | S2 (π → π*) | ||||||
|---|---|---|---|---|---|---|---|---|
| Gas phase | 25 H2O | 50 H2O | 100 H2O | Gas phase | 25 H2O | 50 H2O | 100 H2O | |
| PBE | 4.87 (1) | 5.81 (8) | 6.20 (23) | 5.71 (31) | 4.45 (3) | 5.37 (17) | 5.47 (29) | 5.69 (56) |
| B3LYP | 5.46 (1) | 6.43 (4) | 6.92 (7) | 6.34 (7) | 4.89 (2) | 6.06 (3) | 6.14 (2) | 6.32 (8) |
| PBE0 | 5.58 (1) | 6.62 (4) | 7.04 (4) | 6.45 (5) | 5.12 (2) | 6.18 (1) | 6.21 (1) | 6.48 (4) |
| PBEh-3c | 6.00 (1) | 7.14 (2) | 7.60 (2) | 6.97 (2) | 5.43 (2) | 6.53 (1) | 6.72 (1) | 6.79 (1) |
2.2 Chlorophyll
As a fundamental part of photosystems I and II, chlorophyll is the focus of many research works, both theoretically and experimentally. Here, as a proof of concept regarding its applicability to large systems, we test our e-COOX method to analyze the impact of explicit solvent molecules on the Q-band gap (Qx–Qy) of the chlorophyll a chromophore. Due to the multi-reference character of these states, the scaled COOX variant has been employed. To generate the solvated complex structures, we used CREST45,46 to grow different solvation shells containing 25, 50, and 100 acetone molecules. The system with 100 solvent molecules are shown in Fig. 4.The most accurate theoretical results to date were obtained with DFT/MRCI, where gas phase calculations determine an energy gap for the Q-band of 0.23 eV.50 It should be stressed, however, that the results strongly depend on the solvent and experimental values range between 0.09 and 0.28 eV.51,52 The results for different solvation shells and methods are shown in Table 4.
| Functional | Gas phase | 25 Solv. | 50 Solv. | 100 Solv. | |||
|---|---|---|---|---|---|---|---|
| COOX | e-COOX | e-COOX | e-COOX | e-COOX [n.o.] | COOX | sTDA | |
| PBE | 0.26 | 0.05 | 0.00 | 0.10 | 0.13 | −0.06 | −0.13 |
| B3LYP | 0.22 | 0.09 | 0.09 | 0.12 | 0.22 | 0.14 | −0.06 |
| PBE0 | 0.20 | 0.05 | 0.04 | 0.07 | 0.25 | 0.12 | −0.04 |
| PBEh-3c | 0.16 | 0.12 | 0.14 | 0.17 | 0.16 | 0.11 | 0.07 |
Here, e-COOX again yields results closer to the experimental values than the competing methods, particularly sTDA. The COOX calculations using the constraint formed from the complete system again show the flaws resulting from charge-transfer contamination of the TDA-TDDFT calculation.
The excitation energies for the individual states for both Q- and B-bands are shown in Tables S4 and S5 in the ESI.† Note that in the case of the difficult Bx and By states, COOX does not appear to offer a significant improvement over other conventional single-reference methods.53
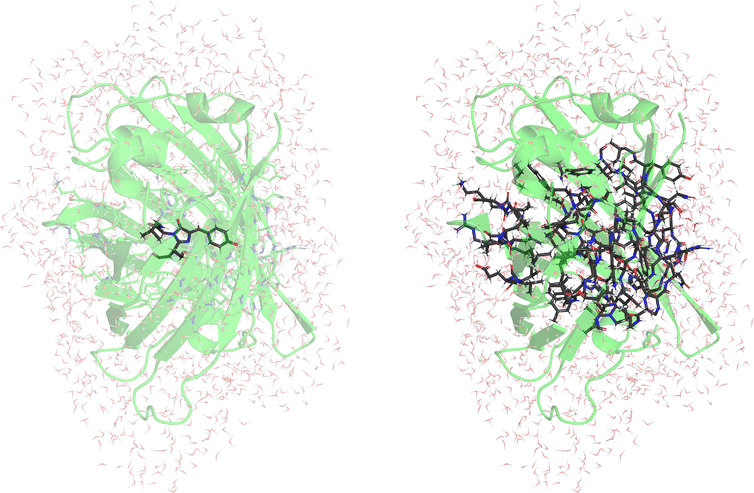
2.3 Green-fluorescent protein
As a further example for the scalability of e-COOX, we evaluate the energy difference between the neutral A- and anionic B-form of wild-type green fluorescent protein (GFP) by explicitly considering the environment,54 using a QM/MM embedding scheme with the Amber03 force field55,56 and the TIP3P water model.57 To better accommodate the anionic form in particular, we again use the scaled COOX constraint potentials in both cases.In contrast to previous works, we evaluate the excitations within a larger QM-region (chromophores and all residues and water molecules within 8 Å) containing 1182 and 1213 atoms for the neutral and anionic systems, respectively. The sub-system constraint is determined from the isolated chromophore within a QM/MM embedding setup. Note that the QM/MM approach in this case requires cutting through covalent bonds, i.e., using hydrogen as link atoms. In the large QM region, link atoms are placed between Cα–COOH for residues within the chain and Cβ–Cα for residues not within the chain; for the chromophore, we placed link atoms along the COOH–Cα bond of Phe64 and the Cα–COOH bond of Val68.
If link atoms are used within the QM/MM scheme, the sub-system constraint embedding has to first discard basis functions of link atoms and be renormalized. Thereafter, the reorthogonalization within the basis of the complete system is applied. In these cases, it is obviously important to ensure that the link atoms are spatially well separated from the region of the electronic excitation.
The results using COOX as well as TDA-TDDFT and CASPT254 using a QM/MM scheme with a small QM-region containing the chromophore only (52/51 QM-atoms) are shown in Table 5 (Fig. 5, left). The structures provided in ref. 54 have been used.
| GFP | Exp.a | PBE/TZVP | PBE0/TZVP | B3LYP/TZVP | PBEh-3c | CASPT2(16,14)a | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| TDA | COOX | TDA | COOX | TDA | COOX | TDA | COOX | ANO-S-PVDZ | ||
| a Ref. 54, ANO-S-PVDZ basis set, Amber99 force field, 40/39 atom QM-region containing the chromophore with link hydrogens placed between Cα–COOH of Phe64 and N–Cα of Val68. | ||||||||||
| Neutral | 3.05 | 3.49 | 2.40 | 3.63 | 3.15 | 3.56 | 2.99 | 3.88 | 3.83 | 3.53 |
| Anionic | 2.63 | 3.38 | 2.19 | 3.49 | 2.82 | 3.45 | 2.64 | 3.66 | 3.04 | 2.82 |
| Δ | 0.42 | 0.10 | 0.21 | 0.14 | 0.33 | 0.11 | 0.35 | 0.22 | 0.79 | 0.71 |
Here, in general, the COOX result improves on those obtained with TDA-TDDFT, where B3LYP/TZVP in particular reproduces the bathochromic shift of the experimental results accurately. It should also be noted again that the linear-response results are blue-shifted and too close to the gas-phase results, including those obtained with CASPT2.
As mentioned, to improve the description of the environment, we also evaluated the excitation energies within a QM/MM scheme with large QM-region as shown in Table 6 (Fig. 5, right).
The constraint is obtained from QM/MM calculations of the chromophore only containing 52 and 51 QM-atoms for the neutral and anionic systems, respectively. Again, the e-COOX results using B3LYP/TZVP nicely reproduce the experimentally obtained results, but in general the deviation from the results obtained with the small QM-region are small.
One important aspect, however, is that the electrostatic environment is also crucial for the determination of the sub-system constraint. Employing a constraint with the small QM-region only within the gas-phase, we observe the constraint spilling into the link region of the Phe64 residue (see Fig. S7 in the ESI†) and the results are severely blue-shifted and in most cases deliver a wrong or vanishing energy difference between the neutral and anionic forms. The results are shown in the ESI† (Table S6).
2.4 X-Ray absorption spectrum of liquid water
As a final example, we show an illustrative calculation of the X-ray absorption spectrum (XAS) of liquid water. High-level coupled-cluster studies of this system indicate a substantial charge-transfer contribution from the first and even second solvation shell upon core excitation, particularly in the main- and post-edge region of the spectrum,58 making this system especially well suited for demonstrating the importance of selecting a sensible sub-system for the e-COOX approach.We again used the Quantum Cluster Growth algorithm of CREST45,46 to place a solvent shell of 100 water molecules around a central water from which the O 1s core-electron will be excited. For illustrative purposes, we limit our calculations to this single geometry; note that an in-depth investigation of this system would require the generation of multiple snapshots from a (path integral) molecular dynamics simulation as was done, e.g., in ref. 58. For the XAS computation, we adopted our methodology from ref. 17, i.e., we computed broken-symmetry solutions followed by a spin-purification procedure. The scaled scalar-relativistic zero-order regular approximation (ZORA) Hamiltonian59–61 with the effective potential developed by van Wüllen62 was applied for the description of relativistic effects, and Coulomb integrals and energies were computed without the application of density fitting. For a good balance between accuracy and computational feasibility, we used the aug-pcX-2 basis set63 on the central water molecule, the aug-pcseg-2 basis set64 on all solvent molecules within a 5 Å radius, and the smaller pcseg-2 basis set64 for all remaining molecules. We then computed e-COOX X-ray absorption spectra from core–valence separated (CVS-)TDA amplitudes using the PBE0 functional, with the sub-system consisting of (i) only the central water molecule (35 CVS-TDA roots) and (ii) the central water and four closest solvent molecules (120 CVS-TDA roots). The obtained line spectra were artificially broadened using Voigt profiles with a half width at half maximum (HWHM) of 0.2 eV for both the Gaussian and Lorentzian components.
The spectra are shown in Fig. 6 alongside the XAS of the isolated monomer and the experimental spectrum from ref. 65, where we have applied a manual offset to align the computed spectra on the pre-edge peak at ∼535 eV. We would like to stress again that the computed spectra are obtained from a single CREST-optimized structure and that quantitative agreement with the experimental data is therefore not to be expected. Indeed, we found that we need to apply relatively large offsets of up to −3.3 eV to align the spectra, which does not match our observations from ref. 17, where COOX@PBE0 was shown to yield very accurate core excitations with average errors well below 1 eV, and reproduced the carbon and oxygen XAS of formaldehyde accurately without the need for a manual offset. As stated above, a more in-depth analysis using a multitude of molecular dynamics snapshots is certainly desirable, but well beyond the scope of this work.
 | ||
| Fig. 6 (a) Experimental and (b)–(d) computed X-ray absorption spectra of liquid water. The experimental spectrum is adapted from ref. 65 and computed spectra are obtained using e-COOX@PBE0/aug-pcX-2/aug-pcseg-2/pcseg-2 (see the text for further details). Line spectra broadened with Voigt profiles with a HWHM of 0.2 eV for both Gaussian and Lorentzian components. | ||
Considering Fig. 6, there is a clear effect of embedding even when including only the central water molecule in the sub-system; most notably, the post-edge peaks appear red-shifted by nearly 2 eV compared to the monomer in a vacuum. In addition, we computed the “charge-transfer number” as defined in ref. 58, i.e., the Löwdin charges of the relaxed e-COOX difference density
| ΔPe-COOX = Pe-COOX − P0 | (8) |
on the central water molecule:
 | (9) |
These are shown for both e-COOX calculations by the color of the line spectra in Fig. 6. Evidently, not including the first solvation shell within the sub-system only recovers a moderate amount of charge-transfer from the environment, whereas for the larger sub-system which includes the first solvation shell, stronger charge-transfer character in the main- and post-edge region is observed in accordance with the coupled-cluster results from ref. 58.
3 Conclusions
We presented a new COOX embedding scheme to evaluate specific excited states within complex environments that make these states difficult to determine within conventional approaches. The e-COOX method constructs the constraint potential from the transition coefficients of the isolated photoactive sub-system and its MOs, which are reorthogonalized with respect to the occupied and virtual orbital spaces of the complete system.It has been shown for first illustrative examples that the embedded sub-system constraint yields a correct description of the electronic excitation within the full complex. In contrast, a conventional linear-response approach may require the evaluation of a large number of roots to obtain the state of interest. Depending on the chosen functional, LR-TDDFT often produces contaminated excitations, e.g., a mixture of multiple orbital rotations due to near-degeneracy, so that a clear identification or correlation with the excitation in the isolated system is difficult. Using examples such as uracil in water and chlorophyll a in acetone, it became apparent that it is often advantageous to draw the constraint from the isolated chromophore, as potential charge-transfer contamination in the full system negatively impacts the COOX constraint potential. Within the e-COOX embedding scheme, however, these effects are avoided while the variational optimization of the excited state electronic structure is performed within the full system, i.e., a relaxation with the electrons of the environment is ensured. In cases where charge-transfer interactions with parts of the environment, e.g., the first solvation shell, are indeed desired, it is advisable to consider the respective solvent molecules as part of the sub-system to prevent a bias towards too little charge-transfer character, as we have demonstrated for the X-ray absorption spectrum of liquid water.
To illustrate the advantages of e-COOX, we also applied our method to larger systems like the aforementioned chlorophyll a and the green-fluorescent protein. These systems have been investigated by many research groups and represent a significant challenge to theoretical methods due to their size and complex environment. As has been shown, our embedding scheme allows specific electronic excitations to be accurately targeted at a low computational cost. For example, using a hybrid functional with the def2-TZVP basis, excitation energies for the largest GFP system in this work containing 1213 atoms can be obtained within a day on a single compute node.
Apart from the kind of application presented in this work, it should be straightforward to apply our e-COOX scheme to any condensed system, e.g., also for crystalline structures. Furthermore, e-COOX can also provide a pathway for more complex excitation patterns such as two-photon–two-electron excitations. The application of e-COOX to these more challenging excitations will be investigated in future works.
Author contributions
Yannick Lemke: investigation (equal), methodology (equal), data curation, formal analysis (equal), validation (equal), visualization (equal), software (equal), and writing – review and editing (equal). Jörg Kussmann: conceptualization, supervision, investigation (equal), methodology (equal), formal analysis (equal), validation (equal), visualization (equal), software (equal), writing – original draft, and project administration (equal). Christian Ochsenfeld: writing – review and editing (equal), supervision, project administration (equal), and funding acquisition.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Y. L. thanks Alexandra Stan-Bernhardt and Judit Katalin Szántó for assistance with the QM/MM setup. The authors acknowledge financial support by the “Deutsche Forschungsgemeinschaft”' (DFG) via the Collaborative Research Centre 325-444632635 (“Assembly Controlled Chemical Photocatalysis”) and the Cluster of Excellence (EXC 2089/1 – 390776260) “e-conversion”. C.O. further acknowledges financial support from the Max-Planck-Fellow at the MPI-FKF Stuttgart. Open Access funding provided by the Max Planck Society.References
- L. González, D. Escudero and L. Serrano-Andrés, ChemPhysChem, 2012, 13, 28–51 CrossRef PubMed.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- A. Dreuw and M. Wormit, WIREs Comput. Mol. Sci., 2015, 5, 82–95 CrossRef CAS.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- P. Pulay, Int. J. Quantum Chem., 2011, 111, 3273–3279 CrossRef CAS.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- K. Sneskov and O. Christiansen, WIREs Comput. Mol. Sci., 2012, 2, 566–584 CrossRef CAS.
- R. J. Bartlett, WIREs Comput. Mol. Sci., 2012, 2, 126–138 CrossRef CAS.
- P. S. Bagus, Phys. Rev., 1965, 139, A619 CrossRef.
- T. Kowalczyk, S. R. Yost and T. Van Voorhis, J. Chem. Phys., 2011, 134, 054128 CrossRef PubMed.
- D. Hait and M. Head-Gordon, J. Phys. Chem. Lett., 2021, 12, 4517–4529 CrossRef CAS PubMed.
- A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed.
- G. M. J. Barca, A. T. B. Gilbert and P. M. W. Gill, J. Chem. Theory Comput., 2018, 14, 1501–1509 CrossRef CAS PubMed.
- K. Carter-Fenk and J. M. Herbert, J. Chem. Theory Comput., 2020, 16, 5067–5082 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2020, 16, 1699–1710 CrossRef CAS PubMed.
- J. Kussmann, Y. Lemke, A. Weinbrenner and C. Ochsenfeld, J. Chem. Theory Comput., 2024, 20, 8461–8473 CrossRef CAS PubMed.
- Y. Lemke, J. Kussmann and C. Ochsenfeld, J. Phys. Chem. A, 2024, 128, 9804–9818 CrossRef CAS PubMed.
- E. R. Davidson, J. Comput. Phys., 1975, 17, 87–94 CrossRef.
- P. H. Dederichs, S. Blügel, R. Zeller and H. Akai, Phys. Rev. Lett., 1984, 53, 2512 CrossRef CAS.
- Q. Wu and T. Van Voorhis, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 024502 CrossRef.
- B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2012, 112, 321–370 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Phys., 2013, 138, 244104 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. Kussmann and C. Ochsenfeld, J. Chem. Phys., 2013, 138, 134114 CrossRef PubMed.
- J. Kussmann and C. Ochsenfeld, J. Chem. Theory Comput., 2015, 11, 918–922 CrossRef CAS PubMed.
- J. Kussmann and C. Ochsenfeld, J. Chem. Theory Comput., 2017, 13, 3153–3159 CrossRef CAS PubMed.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- J. Kussmann, H. Laqua and C. Ochsenfeld, J. Chem. Theory Comput., 2021, 17, 1512–1521 CrossRef CAS PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- H. Laqua, T. H. Thompson, J. Kussmann and C. Ochsenfeld, J. Chem. Theory Comput., 2020, 16, 1456–1468 CrossRef CAS PubMed.
- H. Laqua, J. Kussmann and C. Ochsenfeld, J. Chem. Phys., 2021, 154, 214116 CrossRef CAS PubMed.
- H. Laqua, J. C. B. Dietschreit, J. Kussmann and C. Ochsenfeld, J. Chem. Theory Comput., 2022, 18, 6010–6020 CrossRef CAS PubMed.
- H. Laqua, J. Kussmann and C. Ochsenfeld, J. Chem. Phys., 2018, 149, 204111 CrossRef PubMed.
- S. Lehtola, C. Steigemann, M. J. T. Oliveira and M. A. L. Marques, SoftwareX, 2018, 7, 1–5 CrossRef.
- libxc, https://gitlab.com/libxc/libxc, downloaded in Feb. 2023.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- Simple-DFTD3, https://github.com/dftd3/simple-dftd3, downloaded in Jan. 2023.
- gCP, https://github.com/grimme-lab/gcp, downloaded in Jan. 2023.
- PyMol Version 3.1, Schrödinger LLC, https://pymol.org.
- A. Lange and J. M. Herbert, J. Chem. Theory Comput., 2007, 3, 1680–1690 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, A. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, A. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, I. DePrince, A. Eugene, J. DiStasio, A. Robert, A. Dreuw, B. D. Dunietz, T. R. Furlani, I. Goddard, A. William, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, I. Woodcock, H. Lee, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- S. Spicher, C. Plett, P. Pracht, A. Hansen and S. Grimme, J. Chem. Theory Comput., 2022, 18, 3174–3189 CrossRef CAS PubMed.
- P. Pracht, S. Grimme, C. Bannwarth, F. Bohle, S. Ehlert, G. Feldmann, J. Gorges, M. Müller, T. Neudecker, C. Plett, S. Spicher, P. Steinbach, P. A. Wesołowski and F. Zeller, J. Chem. Phys., 2024, 160, 114110 CrossRef CAS PubMed.
- J. M. Olsen, K. Aidas, K. V. Mikkelsen and J. Kongsted, J. Chem. Theory Comput., 2010, 6, 249–256 CrossRef CAS PubMed.
- E. Epifanovsky, K. Kowalski, P.-D. Fan, M. Valiev, S. Matsika and A. I. Krylov, J. Phys. Chem. A, 2008, 112, 9983–9992 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- S. Reiter, L. Bäuml, J. Hauer and R. de Vivie-Riedle, Phys. Chem. Chem. Phys., 2022, 24, 27212–27223 RSC.
- M. Umetsu, Z.-Y. Wang, M. Kobayashi and T. Nozawa, Biochim. Biophys. Acta, Bioenerg., 1999, 1410, 19–31 CrossRef CAS PubMed.
- L. L. Shipman, T. M. Cotton, J. R. Norris and J. J. Katz, J. Am. Chem. Soc., 1976, 98, 8222–8230 CrossRef CAS PubMed.
- J. P. Goetze, F. Anders, S. Petry, J. F. Witte and H. Lokstein, Chem. Phys., 2022, 559, 111517 CrossRef CAS.
- C. Filippi, F. Buda, L. Guidoni and A. Sinicropi, J. Chem. Theory Comput., 2012, 8, 112–124 CrossRef CAS PubMed.
- Y. Duan, C. Wu, S. Chowdhury, M. C. Lee, G. Xiong, W. Zhang, R. Yang, P. Cieplak, R. Luo, T. Lee, J. Caldwell, J. Wang and P. Kollman, J. Comput. Chem., 2003, 24, 1999–2012 CrossRef CAS PubMed.
- M. C. Lee and Y. Duan, Proteins, 2004, 55, 620–634 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- S. D. Folkestad, A. C. Paul, R. Paul, S. Coriani, M. Odelius, M. Iannuzzi and H. Koch, Nat. Commun., 2024, 15, 3551 CrossRef CAS PubMed.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281–293 CrossRef CAS.
- J. van Lenthe, S. Faas and J. Snijders, Chem. Phys. Lett., 2000, 328, 107–112 CrossRef CAS.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- M. A. Ambroise and F. Jensen, J. Chem. Theory Comput., 2019, 15, 325–337 CrossRef CAS PubMed.
- F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085 CrossRef CAS PubMed.
- J. A. Sellberg, S. Kaya, V. H. Segtnan, C. Chen, T. Tyliszczak, H. Ogasawara, D. Nordlund, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2014, 141, 034507 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00839e |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2025 |