Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Applications of the density functional method combined with the electron–positron correlation-polarization potential to positron binding to hydrocarbons and water clusters†
Daisuke
Yoshida
 *a,
Toshiyuki
Takayanagi
*a,
Toshiyuki
Takayanagi
 b,
Yukiumi
Kita
c,
Tomomi
Shimazaki
b,
Yukiumi
Kita
c,
Tomomi
Shimazaki
 c and
Masanori
Tachikawa
c and
Masanori
Tachikawa
 c
c
aDepartment of Physics, Tohoku University, Aramaki Aza-Aoba 6-3, Aoba-ku, Sendai, Miyagi 980-8578, Japan. E-mail: daisuke.yoshida.b1@tohoku.ac.jp
bDepartment of Chemistry, Saitama University, Shimo-Okubo 255, Sakura-ku, Saitama, Saitama 338-8570, Japan
cQuantum Chemistry Division, Yokohama City University, Seto 22-2, Kanazawa-ku, Yokohama 236-0027, Japan. E-mail: tachi@yokohama-cu.ac.jp
First published on 6th May 2025
Abstract
We present benchmark calculations using the electron–positron correlation-polarization potential (CPP) method with the atomic polarizability model to evaluate the positron affinities of key categories of polyatomic hydrocarbons and water microclusters. The universal model parameter of the generalized gradient approximation for CPP is optimized based on the experimentally measured positron affinities of the representative hydrocarbon molecules. Using this method, the positron affinities and positron binding features of water clusters up to hexamers are investigated. The present CPP calculations revealed reasonable size-dependence on positron binding energies and conformer-dependent properties for each cluster size for these water clusters. The bound positrons are also trapped internally within cavities of the three-dimensional water clusters, similar to the behavior of bound excess electrons in water cluster anions. However, since the positronic binding energies are smaller than the electronic binding energies in water cluster anions, the bound positrons exhibit delocalized features extending into the electronegative oxygen atoms of the water molecules acting as the multiple hydrogen donor. Such behavior differs from the water cluster anions, resulting in isomeric conformational dependence.
1 Introduction
The positron (e+), the antimatter counterpart of the electron, has been utilized in practical applications across a wide range of scientific and technological fields, for example, in studies of antimatter physics,1 materials science,2,3 and biomedical applications.4,5 In bulk materials, positrons are trapped by open-volume defects and annihilated with electrons, emitting gamma rays. Positron annihilation (lifetime) spectroscopy enables non-invasive characterization of various types of bulk defects.2,3 Recent advances in slow positron beam techniques have enabled the characterization of individual molecules,6–8 where the temporary positron–(neutral) molecule bound states, formed by Feshbach resonant positron capture, have been observed by experimental measurements. Positrons also have the potential to be used as probes for identifying conformational structures of molecules.9 Various conformational effects on positron binding properties were identified through further theoretical investigations of molecules10,11 and molecular clusters.12,13The nature of positron (the excess positive charge) binding to the molecule is often compared and contrasted with that of electron binding. The excess electron attachment to neutral molecules is a key issue that has been studied extensively due to its relevance to radiation biophysics, atmospheric chemistry, and interstellar chemistry. In particular, water cluster anions have been well-studied due to their chemical significance associated with the role of the hydrated electron.14,15 Water cluster anions (H2O)n− of various sizes are observed experimentally,16 and the vertical electron detachment energies (VEDEs), which correspond to the one-electron removal energy from the cluster anion, exhibit systematic size-dependent trends: there are two distinct linear correlations of VEDEs with respect to n−1/3 (indicating the mean cluster radius), associated with different types of binding properties of the excess electrons.16–21 The electron binding features localized on the cluster surfaces exhibit considerably lower VEDEs than those localized internally within the clusters. The interior electronic state appears like the bulk hydrated electron, which has been rationalized by extrapolating to the bulk water situation.
Turning to positron binding in solvents, similar characterization may be possible for positron trapping by water micro-clusters or hydrated electrons. Recent theoretical studies using multi-scale simulations, combining quantum and molecular mechanical calculations extended for positronic complexes, have addressed positron–water interactions in the hydration states of a positronium (a hydrogen-like bound state between an electron and a positron, Ps)22 and in aqueous amino acid complexes.23 These have provided important theoretical insights into schemes of positrons trapped in solute cavities or cluster surfaces, as well as their solvent effects. For fundamental excess positron–water clusters, however, there have been no such systematic investigations, except for the water dimer.12 Thus, the size-dependent properties of the hydrated positron are still not as well understood as the hydrated electron.
To unveil mechanisms of positron trapping by molecules, it is necessary to perform accurate calculations including the electron–positron correlation effect that plays a crucial role in quantifying the stability of positronic complexes. Effective methods have been extended to different scales of the finite size systems. For few-body or comparatively fewer multi-atomic systems, very accurate calculations can be achieved by using the explicitly correlated method24–26 and the quantum Monte Carlo method.27–31 Molecular orbital (MO)-based calculations extended to exotic systems containing particles distinguishable from bound electrons (e.g., positrons and protons), represented by the multi-component molecular orbital (MC_MO)32–34 and any-particle molecular orbital (APMO)35,36 calculations, have been effectively employed to predict the existence of positronic bound states for various molecules. The MO calculations in combination with the effective model potentials9,37 and the many-body quasi-particle calculations38 have provided quantitative agreement with the experimental measurements. However, highly accurate correlated calculations become computationally expensive with the increasing size of molecules. Meanwhile, the density functional theory (DFT) extended to the positron–electron system has been widely employed for studies of positron annihilations in bulk systems.39–45 In recent years, DFT-based approaches, such as the correlation-polarization potential (CPP)10,46–50 and the extended wavefunction theory (WFT)-in-DFT embedding methods,51 have been proposed and effectively applied to positron-containing systems. The DFT approach is thus a practical alternative, reducing the computational cost and enabling calculations of positronic complexes with molecular aggregates.
In the DFT-CPP method, the positron–molecule interaction of the effective Hamiltonian is described approximately as a combination of the molecular electrostatic and correlation-polarization potentials.50 The short-range correlation of the CPP model is expressed in terms of the density functional theory: the two-component local density approximation (LDA),40 along with the generalized gradient approximation (GGA) correction with a gradient correction parameter,41 was proposed for the electron–positron correlation functional. The asymptotic long-range behavior can be represented by the attractive polarization potential with the dipole polarizability of the host system.52 By fitting the GGA model parameter, this approach also provides reasonable positron binding energies universally for small hydrocarbons and some organic heteroatom categories.10 However, the parameter often exhibits remarkable size dependence as the molecular size increases,50 and, hence, it needs to be adjusted for each molecular size referencing the experimental values.
For more practical use, the model potential, including the model parameter determined size-independently, is useful and applicable to theoretical predictions. Considering the proportional behaviors of dipole polarizabilities of simple covalent bonded atoms and molecular clusters, where the simple additivity rule53 is invoked, an effective approach is to construct polarization potentials with polarizabilities decomposed into locations of constituent atoms, as proposed in the previous studies.9 In this paper, we demonstrate the DFT-CPP calculation combined with the atomic hybrid polarizabilities53 and present benchmark studies for positron binding to hydrocarbons and water clusters. The calculations for positronic complexes with a homolog series of hydrocarbons were performed to test the present DFT-CPP calculation, where the size-independent GGA parameter is determined through comparison with the experimental data.54–56 Using this fitted model, positronic complexes of small water clusters up to hexamers are calculated to figure out the positron binding properties of small water microsolvents.
2 Theoretical method
The effective Hamiltonian for the positron–molecule complex, in atomic units, is given by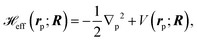 | (1) |
 | (2) |
The electron–positron correlation Vcorr(rp) for the short-range part can be represented in terms of the generalized gradient approximation (GGA)41 (here and henceforth fixed atomic nuclear coordinates, R, are omitted),
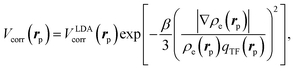 | (3) |
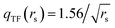 is the local Thomas–Fermi screening length57 with a Wigner–Seitz radius
is the local Thomas–Fermi screening length57 with a Wigner–Seitz radius  in the atomic units. The density ρe(rp) represents the probabilities for electrons that coalesce with a positron at rp. The factor β is an adjustable parameter to be fitted for targets.42,44 The original form of Vepcorr[ρe] was presented by Arponen and Pajanne,39 which was formulated based on the random-phase approximation (RPA) with the assumption of interacting bosons, regarding a positron as a charged impurity in a homogeneous electron gas. The interpolated general LDA formulae Vepcorr[ρe, ρp] for the positron density ρp in the full range of the parameter rs were proposed by Boroński and Nieminen.40 This formalism for ρp ≪ ρe reproduces the above RPA result in the limit of ρp → 0. In this work, we employed Vepcorr[ρe] by Boroński and Nieminen (BN), given by the following equations in the full range.
in the atomic units. The density ρe(rp) represents the probabilities for electrons that coalesce with a positron at rp. The factor β is an adjustable parameter to be fitted for targets.42,44 The original form of Vepcorr[ρe] was presented by Arponen and Pajanne,39 which was formulated based on the random-phase approximation (RPA) with the assumption of interacting bosons, regarding a positron as a charged impurity in a homogeneous electron gas. The interpolated general LDA formulae Vepcorr[ρe, ρp] for the positron density ρp in the full range of the parameter rs were proposed by Boroński and Nieminen.40 This formalism for ρp ≪ ρe reproduces the above RPA result in the limit of ρp → 0. In this work, we employed Vepcorr[ρe] by Boroński and Nieminen (BN), given by the following equations in the full range.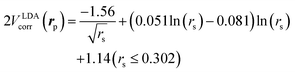 | (4a) |
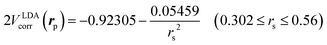 | (4b) |
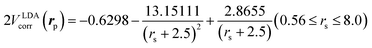 | (4c) |
2VLDAcorr(rp) = −0.524 − 179![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 856.2768ρe2 + 186.4207ρe (rs ≥ 8.0). 856.2768ρe2 + 186.4207ρe (rs ≥ 8.0). | (4d) |
A more sophisticated LDA parametrization of the electron–positron correlation energy, derived from quantum Monte Carlo calculations, was presented by Drummond et al.58 We have examined this accurate correlation functional (hereafter referred to as DLNP functional) in comparison with the BN functional in eqn (4). This DLNP functional yields PA values approximately 30–40% smaller than those obtained by the BN functional, due to slight differences that arise in the low-density region (i.e., at larger rs). To compensate for this, optimal values of the gradient correction parameter β can be identified from our demonstrative calculations, which suggest slightly smaller values of β = 0.34–0.35 (see Section S1 of the ESI†). Although the DLNP LDA functional is thus available at the current stage, in this study, we have applied the BN functional with the aim of comparing the impact of the present modification for CPP with those in the previous studies10 that employed the same functional.
The long-range interactions between an external charged particle (e.g., an electron or a positron) and a host molecule (or an atom) can be described by the polarization potential, which is given in terms of the second-order perturbation for the multipole expansion of their Coulomb interaction. This leads to the asymptotic form as the attractive interaction (independently of the charge sign of the external particle),
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are the static multipole polarizabilities and here rp represents the distance from the center of mass of the molecule. The lowest order
are the static multipole polarizabilities and here rp represents the distance from the center of mass of the molecule. The lowest order ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 term gives rise to the contribution of the induced dipole with the static dipole polarizability, associated with the electron density perturbed by the presence of the positron. This polarization potential combined with the local correlation functional has been applied for electron scattering52,59,60 as well as positron scattering.46–48,61 In recent studies using DFT-CPP, the second-order scheme of the polarization potential with the anisotropic polarizability has been utilized for investigating the influence of the conformational structures on spatial extents of bound positrons,10 where the above adjustable GGA parameter is fixed by reference to experimental PAs. Similar approaches combined with ab initio calculations have been constructed based on the many-body perturbation expansion,62,63 and also similar practical model potential methods have been utilized by Swann and Gribakin9,64 and Mitroy and his coworkers.65–69 These are also semi-empirical approaches with adjustable factors for the polarization potential to improve numerical results.
= 1 term gives rise to the contribution of the induced dipole with the static dipole polarizability, associated with the electron density perturbed by the presence of the positron. This polarization potential combined with the local correlation functional has been applied for electron scattering52,59,60 as well as positron scattering.46–48,61 In recent studies using DFT-CPP, the second-order scheme of the polarization potential with the anisotropic polarizability has been utilized for investigating the influence of the conformational structures on spatial extents of bound positrons,10 where the above adjustable GGA parameter is fixed by reference to experimental PAs. Similar approaches combined with ab initio calculations have been constructed based on the many-body perturbation expansion,62,63 and also similar practical model potential methods have been utilized by Swann and Gribakin9,64 and Mitroy and his coworkers.65–69 These are also semi-empirical approaches with adjustable factors for the polarization potential to improve numerical results.
In this study, we adopt the polarization potential within the lowest-order term, approximated by a sum over the atom-located dipole polarizabilities,
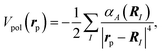 | (5) |
Switching of Vcp(rp) from the long-range asymptotic form to the short-range correlation is performed regarding some numerical criteria: in the original CPP scheme, these are connected at their crossing distance rc,52 while the recent DFT-CPP calculations used the simple formula as Vcp = max[Vcorr, Vpol]. We also employ the latter formalism for the present CPP calculations. To avoid numerical discontinuity at switching regions by the maximum function, we introduce an ad hoc representation by the following two-dimensional matrix for Vcp(rp),
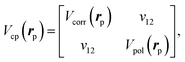 | (6) |
The eigenvalue of the effective Hamiltonian in eqn (1) gives the one-positron energy εp, and its negative value corresponds to the vertical positron affinity PA (positron binding energy) for the equilibrium structure of the host system, namely,
| PA = −εp. | (7) |
For accurate numerical calculations of the positron affinities, it is often essential to take into account the effect of the virtual Ps formation channel within the framework of the many-body quasiparticle calculation,38 which enhances the electron–positron overlap locally within the molecular system and increases the positron binding energy beyond the mean-field approximation. Similar effects can be observed in the wavefunction expansion approach,12,72 where a part of the effect associated with the virtual Ps is incorporated through the higher-order electronic/positronic excited configurations. In the present DFT-CPP framework, the calculation for eqn (7) does not account for the relaxation of the electron density induced by the presence of a bound positron. However, for more rigorous treatments, a self-consistent field (SCF) procedure would be necessary to obtain accurate numerical results for electron–positron superpositions. Nevertheless, since the electronic structure is not considered to be significantly disrupted for systems near the threshold of breaking up into e+ + X (where X is a host molecule), the electron density obtained from well-established electronic structure calculations is a better approximation for evaluating the correlation energy using the well-designed electron–positron correlation functional in combination with the perturbative long-range potential.
3 Computational details
The Schrödinger equation for the Hamiltonian in eqn (1) is solved by means of the discrete-variable representation (DVR) method73 with the particle-in-a-box basis functions.74 In this study, we calculate the lowest energy positronic states for a positron by the direct relaxation method. The space for the effective potential well is taken to be cubic with a side length L and with the origin fixed at the center of mass of a host molecular system, i.e., the ranges of −L/2 ≤ (x, y, z) ≤ L/2. We chose L = 100a0–140a0 (a0 is the Bohr radius) depending on the molecular size, and used 512 equally spaced grid points for each dimension. A cut off energy of 20 hartree for the potentials is applied to avoid numerical divergence especially due to Coulomb repulsions between a positron and positively charged nuclei. The relaxation calculations were performed with an energy convergence criterion of 10−9 hartree. These computational conditions are sufficient for the required level of accuracy. The supporting data are available in Section S2 of the ESI.†We selected means of the electronic structure calculations to obtain the electron density ρe as reproducing molecular polarizabilities. The comparatively low-level electronic structure calculations, for example, the Hartree–Fock (HF) approximation, LDA, and simple GGA functionals, are known to systematically yield significant errors for the electrostatic properties, while the well-tuned hybrid functionals, as well as correlation methods such as the second-order Møller–Plesset (MP2)75 and coupled cluster (CC),76–79 can provide results in good agreement.50,80 Additionally, inclusions of diffuse functions into the basis sets are also essential for improving accuracy.80 In this study, the electronic structure calculations are performed by using the dispersion-corrected range-separated hybrid functional,81 ωB97X-D, with Dunning's augmented correlation-consistent split-valence basis sets,82 aug-cc-pVDZ, for both alkanes and aromatics. Only for the water clusters, the single-component artificial force induced reaction (SC-AFIR) method, implemented in GRRM-17 software,83,84 combined with the ωB97X-D/aug-cc-pVDZ calculation was used for obtaining candidate equilibrium structures of conformers. Using these structures as starting points, the optimized structures were obtained by the ωB97X-D calculations with the aug-cc-pVTZ basis sets.82
Atomic hybrid polarizabilities (AHPs) αA assigned to elements A of constituent atoms used in this paper are as follows (in units of a03): αH = 2.611 for all the molecules, αC = 7.159 for alkanes, αC = 9.123 for benzene, αC = 12.794 only for bridgehead C atoms of naphthalene, and αO = 4.298 for water clusters, which are extracted from the literature.53 For water clusters (H2O)n, the calculated polarizabilities vary with the conformational structures, while by the definition of AHP, the additivity method gives the isotropic polarizabilities as 9.52n. The AHP values for n = 2–6 reasonably approximate the calculated polarizabilities of the overall conformational structures as will be shown later, but slightly underestimate them by 3%.
All structure optimization procedures are carried out using the Gaussian 16 program.85 Information on accessing the optimized geometries of all studied structures is provided in Section S3 of the ESI.† All calculations for the positronic complexes were performed using the DFT-CPP method at the GGA level, as described in the preceding section.
4 Results and discussion
4.1 Positronic bound states in n-alkanes and aromatics
We performed test calculations of PAs for n-alkanes (CNH2N+2 with N = 2–16), benzene (C6H6), and naphthalene (C10H8) to determine the universal GGA-β parameter employed in this work. These numerical details are shown in Table 1, where the experimental polarizabilities are retrieved from ref. 53 and 86. The ωB97X-D/aug-cc-pVDZ calculations reproduce isotropic polarizabilities within a deviation of 3% from the experimental data54–56 for all the presented hydrocarbons, and the additivity method for the atomic hybrid polarizabilities (AHPs) yields consistent results with these calculations. For the positronic ground states of n-alkanes, β = 0.38 provides fairly consistent results with the experimental PAs up to N = 12 but gradually underestimates them for N = 14 and 16, while for both benzene and naphthalene, a slightly smaller value of β = 0.36 improves agreements with the experimental PAs.| Molecule | α iso (a03) | PA (meV) | |||
|---|---|---|---|---|---|
| Expt. | Calc. | AHP | Expt. | Calc. | |
| n-Alkanes (first bound states) | |||||
| C2H6 | 29.6 | 28.9 | 30.2 | 3 | 2.9 |
| C3H8 | 42.5 | 41.2 | 42.6 | 16 | 16.8 |
| C4H10 | 54.6 | 53.5 | 55.1 | 37 | 37.8 |
| C5H12 | 67.4 | 65.9 | 67.5 | 67 | 69.3 |
| C6H14 | 79.6 | 78.3 | 79.9 | 93 | 101.5 |
| C7H16 | 92.4 | 91.0 | 92.4 | 118 | 127.3 |
| C8H18 | 104.5 | 103.6 | 104.8 | 147 | 154.0 |
| C9H20 | 117.4 | 116.3 | 117.3 | 178 | 172.3 |
| C10H22 | 129.5 | 129.0 | 129.7 | 193 | 191.6 |
| C11H24 | — | 141.8 | 142.2 | — | 204.0 |
| C12H26 | 154.5 | 154.5 | 154.6 | 225 | 218.1 |
| C13H28 | — | 167.4 | 167.1 | — | 226.6 |
| C14H30 | 179.5 | 180.3 | 179.5 | 265 | 237.3 |
| C15H32 | — | 193.1 | 192.0 | — | 243.6 |
| C16H34 | 204.4 | 205.8 | 204.4 | 295 | 251.4 |
| n-Alkanes (second bound states) | |||||
| C12H26 | 154.5 | 154.5 | 154.6 | 5 | 9.3 |
| C13H28 | — | 167.4 | 167.1 | — | 32.3 |
| C14H30 | 179.5 | 180.3 | 179.5 | 45 | 56.2 |
| C15H32 | — | 193.1 | 192.0 | — | 75.4 |
| C16H34 | 204.4 | 205.8 | 204.4 | 75 | 95.8 |
| Aromatic hydrocarbons | |||||
| C6H6 | 70.1 | 69.2 | 70.4 | 132 | 136.0 |
| C10H8 | 117.4 | 119.2 | 119.4 | 300 | 290.8 |
In previous DFT-CPP calculations employing centrally fixed anisotropic polarizabilities for the polarization potential, the β parameter often needs to be optimized separately for different molecular size ranges, as seen in the case of hydrocarbons presented here.10,50,87 This drawback of size-specific features can be overcome by the present approach, allowing the universal parameter to be successfully determined for both saturated homologous and unsaturated hydrocarbons.
The size dependence of PAs for n-alkanes is shown in Fig. 1 where the calculated and experimental PAs are plotted as a function of the number of backbone carbon atoms in n-alkanes. The increasing trend of PAs is weakened for the positronic ground states in the sizes of N ≥ 12, and in this region, the calculations underestimate the experimental values. This can be explained by the conformer effects that appear particularly in large alkanes: according to the previous report by Swann and Gribakin,9 the lowest energy conformations with all-trans(t) shape and/or t-rich geometries tend to exhibit the smallest PAs for each size, while energetically low-lying curved or bent alkane chains exhibit larger PAs, contributing to higher thermal averages that approach the experimental PA values. Therefore, lower PAs of all-t shape alkane chains compared to the experimental values provide rather reasonable results.
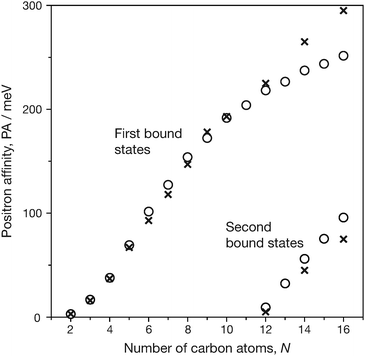 | ||
| Fig. 1 Positron affinities of n-alkanes CNH2N+2. Crosses and open circles are experimental and calculated values, respectively. | ||
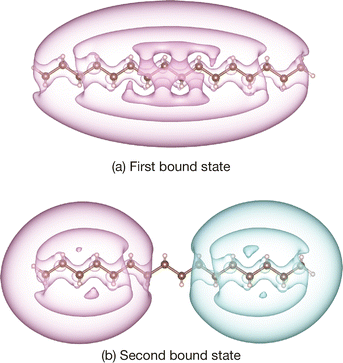
Using the same calculation conditions, we calculated the second positronic bound states of large n-alkanes, CNH2N+2 with N = 12–16, where the experimental data are available for N = 12, 14, and 16. These calculation results are also included in Table 1 and Fig. 1. With the universal β parameter, we also successfully obtained reasonable qualitative results for the second bound states, although these PAs are slightly overestimated compared to the experimental values for larger sizes. The calculation results presented by Gribakin and Swann,9 which employed a similar model potential with the exponentially cut-off factors adjusted empirically, show better agreement with experimental PAs. The calculated positronic wavefunctions of the system [C16H34; e+] are illustrated in Fig. 2. The first positronic bound state has an elliptical extent of the nodeless wavefunction, while the second bound state exhibits antisymmetric character with respect to the molecular center. These closely resemble those presented in the previous paper.64
We thus obtained a range of the GGA parameters that universally fit the PAs of hydrocarbons for different sizes. By using the size-independent model, we will address the positron binding to small water clusters in the following section.
4.2 Water clusters
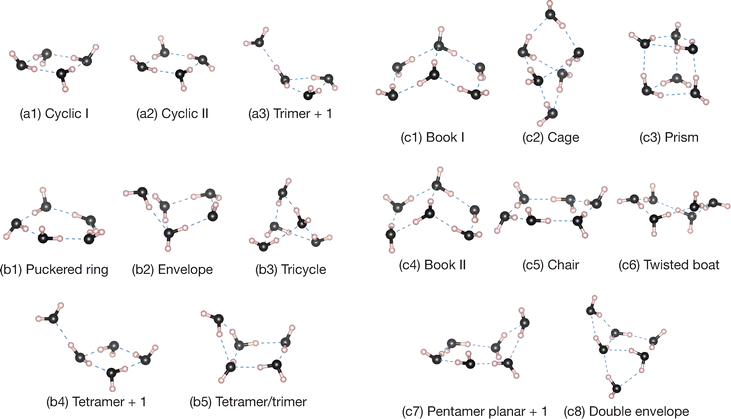
Finally, we present benchmark calculations of PAs for small water clusters, (H2O)n clusters with n = 2–6. According to previous reports, an isolated water molecule, as well as typical hydrogen inorganic species such as hydrogen halides and ammonia, exhibit near-zero PAs despite the polar systems, whereas the binary molecular clusters formed by the hydrogen bond (HB) are predicted to have positron binding abilities.12 Although these previous calculations evaluated the vertical PAs for the neutral binary clusters without the nuclear configuration relaxations, features of the bound positrons may differ from the excess electrons of water anions. In the anion case, the bound excess electron tends to be located near less-screened H atoms (protons) associated with the polar covalent O–H bond(s), whereas in the [H2O; e+] complex, such H atoms are unfavored in positron binding and it results in the positron unbound. For the dimer anion (H2O)2−, there are two stable structures that the excess electron is located around the positively charged H atoms: near the dangling H atoms (free from HB) of the acceptor in the linear geometry, and in the intermediate region in the H-bridged cyclic geometry.88 In contrast to the dimer anion, the bound positron for the linear (H2O)2 structure is located near the negatively charged O atom of the donor, showing the opposite dipole-supported binding character. This stabilization is allowed by the enhanced polarity in cooperation with partial screening of HB-free H atoms of the donor due to electron density rearrangements induced by the hydrogen bond.Here, we applied the present DFT-CPP method for vertical PAs of (H2O)n with up to n = 6. The optimized structures for n = 4–6 are shown in Fig. 3; we have three, five, and eight conformers, respectively, where the notations for n = 5 and 6 are defined in accordance with the ref. 89 and 90. The relative energies and electrostatic properties are given in Table 2. For the pentamer and hexamer, low-lying equilibrium structures within ≲0.1 eV in relative energy are examined, while exceptionally for the tetramer a higher energy conformer denoted as “trimer + 1” is included to consider the effect of different types of conformational structures.
| Structure | ΔE (eV) | μ (D) | α iso (a03) | PA (meV) |
|---|---|---|---|---|
| Dimer (H2O)2 | ||||
| 0.000 | 2.53 | 19.57 | 35.1 | |
| Trimer (H2O)3 | ||||
| Cyclic | 0.000 | 1.12 | 29.28 | 10.4 |
| Tetramer (H2O)4 | ||||
| Cyclic (I) | 0.000 | 0.00 | 39.18 | 34.1 |
| Cyclic (II) | 0.029 | 0.00 | 39.21 | 67.6 |
| Trimer + 1 | 0.262 | 3.43 | 39.26 | 173.2 |
| Pentamer (H2O)5 | ||||
| Puckered ring | 0.000 | 1.00 | 49.20 | 123.8 |
| Envelope | 0.057 | 2.17 | 48.66 | 132.9 |
| Tricycle | 0.076 | 4.25 | 48.48 | 215.2 |
| Tetramer/trimer | 0.125 | 2.55 | 48.71 | 157.6 |
| Tetramer + 1 (II) | 0.140 | 2.49 | 49.14 | 212.2 |
| Hexamer (H2O)6 | ||||
| Book (I) | 0.000 | 2.42 | 58.73 | 218.7 |
| Cage | 0.001 | 2.19 | 58.00 | 186.1 |
| Prism | 0.002 | 2.66 | 57.60 | 168.1 |
| Book (II) | 0.006 | 2.50 | 58.62 | 205.0 |
| Chair | 0.023 | 0.00 | 59.26 | 180.9 |
| Twisted boat | 0.058 | 0.82 | 59.09 | 203.8 |
| Pentamer planar + 1 | 0.070 | 2.73 | 58.78 | 175.9 |
| Double envelope | 0.127 | 1.82 | 58.34 | 140.7 |
As is well-known, the trimer, tetramer, and pentamer have the global minimum (GM) structures with the cyclic geometries, where all water fragments behave like one-hydrogen donor and acceptor. For cyclic tetramers, here we showed only two structures, denoted as I and II, which are identified by directions of dangling H atoms with respect to a tetramer plane; the GM structure has alternatively arranged “up” and “down” dangling H atoms, and the next lowest conformer II has adjacent two up and down dangling H atoms. In a similar manner, various conformations differentiated by arrangements of the HB-free H atoms exist.91 For pentamers, our calculation results of relative energies ΔE are fairly consistent with CCSD(T) calculations in the theoretical report,90 except for the “tetramer/trimer” structure. This lies about 0.12 eV above the GM, while the previous report predicted 0.03–0.06 eV.90 In the case of the hexamer, it was reported that 24 conformers exist by theoretical calculations,89 and a three-dimensional “prism” structure was obtained as the GM.89,92,93 Subsequently, the “cage” and “book” structures are competitive as the next-lowest conformers, but the order of relative energies varies with their computational methods. In the present calculations, these three conformations exhibit almost isoenergetic, and it is difficult to differentiate these stabilities in energy. Nevertheless, the results reproduce the important trend that three-dimensional structures are preferential in water microclusters for n ≥ 6 and that the prism, cage, and book structures become the lowest energies, which are also identified experimentally94 and agree with the later theoretical calculations.89
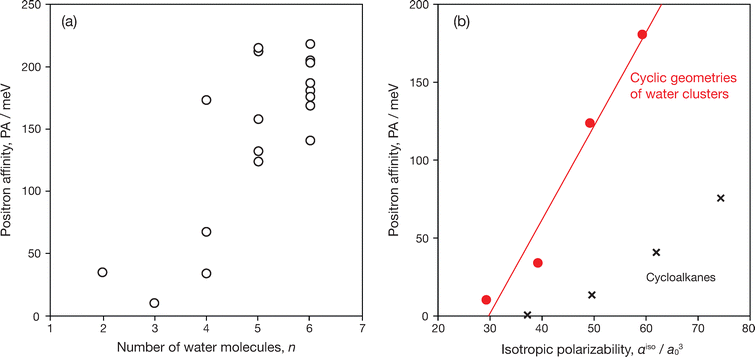
The calculation results of PAs for all structures presented above are included in Table 2. For the dimer, DFT-CPP provided PA = 35 meV and the electron–positron contact density of δep = 1.95 × 10−3a0−3, which is in agreement with the MC_CI result, PA = 38 meV and δep = 1.58 × 10−3a0−3.12 Also, for all (H2O)n with n = 3–6, PAs of all presented conformations are predicted to be positive. It was previously conjectured that PAs may become smaller in cyclic structures compared to the dimer,12 because the polarization effect associated with the dipole–dipole interaction scheme may be cancelled out, resulting in a schematically less polar overall structure due to the donor–acceptor characteristics of all H2O fragments. In comparison with the dimer, indeed, the PA of the cyclic trimer decreases to 10 meV, and that of the cyclic GM tetramer is increased to 34 meV which is close to the PA of the dimer. In larger sizes, however, against the early expectation, the PAs of cyclic structures increase almost linearly, at least up to the hexamer. Since these cyclic geometries are less polar species, this size-dependent property is analogous to the cases of hydrocarbons represented by alkane chains as well as the aromatic hydrocarbons as seen in the previous section, which can be interpreted as the dipole polarizability dependence.
Fig. 4(a) shows the correlation between PAs and cluster sizes n. Overall, PAs tend to increase as the cluster size n increases across the entire data. As mentioned above, the PAs of cyclic geometries for n = 3–6 exhibit a pronounced linear relationship with respect to n, suggesting that the trend for these cyclic forms can be characterized simply by the dependency on dipole polarizability, as shown in Fig. 4(b). These planar structures of a cyclic HB network show the lowest PAs for cases of n = 3, 4 and 5, whereas only for n = 6 the three-dimensional structures of the lowest energy conformations, such as prism and cage, have smaller PAs competitive with the PA of the cyclic (chair) structure.
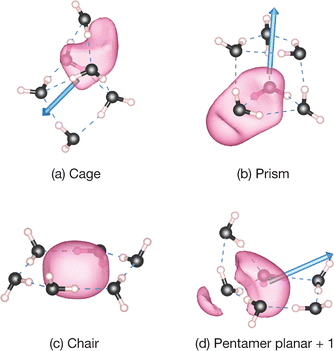
The bound positron densities of four conformations of n = 6; the cage, prism, chair, and pentamer planar + 1, are illustrated in Fig. 5. In the chair (cyclic) structure, the bound positron density has a single density lobe surrounded by water molecules. Analogous density distributions also appear in cyclic structures of other smaller cluster sizes. Similar positron binding features are observed in the cases of cycloalkanes as well as benzene. In comparison with the polarizability dependence of PAs for cycloalkanes,9 as shown in Fig. 4(b), the cyclic forms of water clusters exhibit a steeper linear relationship with respect to the polarizability αiso. This trend suggests that local polarities by polar-covalent O–H bonds contribute to enhancing positron binding abilities.
The spatial extents of the positron densities for the representative three-dimensional structures are seen in Fig. 5(a), (b), and (d), and all are polar structures with the gross dipole moments of μ = 2.1–2.7 D: these have noticeable delocalized features that are extending both inside and outside of the HB network. In both the cage and prism structures, the majority of positron densities are located internally in their cavities with some portions leaking into outer regions near an O atom. Also, in the pentamer planar + 1 structure, which consists of a pentamer and a trimer cycle sharing a hydrogen bonded two H2O molecules, the positronic distribution appears to extend across these two HB cycles and slightly leaks toward the O atom of the bridgehead double H donor H2O molecule. In the case of water hexamer anions with prism structures, the bound excess electron is either almost accommodated within a cavity or is distributed outside of the prism structures, following locations of the (dangling) H atoms (the positive end of the dipole moment).95 Importantly, while the excess electrons in water cluster anions tend to be attracted to the HB-free H atoms of a double H acceptor H2O moiety,96,97 the delocalized bound positron densities in water hexamers are located in the vicinity of the O atoms of a double H donor H2O moiety. As shown in Fig. 5(a), (b), and (d), these delocalized positrons appear to align with the gross dipole moment vectors. However, since these features are not fully dipole-supported binding, therefore it results in a weak correlation with the magnitude of the dipole moment, as indicated in Table 2. For larger clusters, it may be observed that the bound positron is fully accommodated within such three-dimensional structures or exhibit dipole-supported binding due to the increased polarity.
The present calculations provided the reasonable size-dependent properties of PAs for water clusters by using the universal model parameter as well as hydrocarbons. It was also suggested that the increasing trend of PAs may be suppressed and eventually saturated as the size of microsolvent clusters increases, similar to the VEDE-n−1/3 trend observed in the water cluster anions. However, such asymptotic behavior may be expected to appear in larger clusters, e.g., n ≳ 11 for anions16,18,19 and, therefore, cannot be addressed within the small clusters presented in this work. It is worth investigating positron trapping by larger microsolvent clusters and the effects of the donor/acceptor properties of solvent molecules associated with the HB network structures. In the present cases, which focused on non- or weakly-polar systems, long-range correlation effects described by the polarization potentials play a significant role in positron attachment, while for strongly-polar systems by possessions of strong polar covalent bonds, it may be necessary to redefine the gradient correction parameter of CPP associated with rapid density gradients to improve numerical results.
5 Conclusions
We have developed a density functional theory calculation combined with the electron–positron correlation-polarization potential (CPP) utilizing the atom-located polarizabilities towards applications to positronic complexes with arbitrary multi-atomic systems. The parameter of generalized gradient approximation is determined through test calculations for simple hydrocarbons, where both the first and second bound states of positrons for large n-alkanes can be reproduced reasonably by using the universal model parameter. We applied to the case study for positron binding with small water clusters. Positron binding of water clusters also exhibits the conformer dependence, which shows strongly delocalization behaviors reflecting hydrogen bonding network structures. The positron binding properties in water clusters as well as the excess electron state of the water cluster anions are also intriguing. We could confirm the capabilities of the present modifications of CPP for positronic complexes with large molecular systems, while it is able to be more applicable for various material properties by combining with more sophisticated decomposition algorithms for atomic polarizability models based on the ab initio calculations and density relaxation calculations of both bound electrons and an attached positron. These further improvements will be addressed in our future work.Data availability
The data supporting the findings of this study, including benchmark results, are available in the ESI,† specifically in Sections S1 and S2. The geometry data for all optimized molecular structures studied are provided in Section S3 of the ESI,† including a compressed archive containing the XYZ files.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by JSPS KAKENHI Grant Numbers 23H03993, 23H05462, and 23K17905 (to M. T.) and by the JSPS MEXT Grant Number 21K04983 (to Y. K.) The computations were partly performed using Research Center for Computational Science, Okazaki, Japan (Project No. 23-IMS-C008 and 24-IMS-C007 to M. T.).Notes and references
- P. Peŕez, D. Banerjee, F. Biraben, D. Brook-Roberge, M. Charlton, P. Cladé, P. Comini, P. Crivelli, O. Dalkarov, P. Debu, A. Douillet, G. Dufour, P. Dupré, S. Eriksson, P. Froelich, P. Grandemange, S. Guellati, R. Guérout, J. M. Heinrich, P.-A. Hervieux, L. Hilico, A. Husson, P. Indelicato, S. Jonsell, J.-P. Karr, K. Khabarova, N. Kolachevsky, N. Kuroda, A. Lambrecht, A. M. M. Leite, L. Liszkay, D. Lunney, N. Madsen, G. Manfredi, B. Mansoulié, Y. Matsuda, A. Mohri, T. Mortensen, Y. Nagashima, V. Nesvizhevsky, F. Nez, C. Regenfus, J.-M. Rey, J.-M. Reymond, S. Reynaud, A. Rubbia, Y. Sacquin, F. Schmidt-Kaler, N. Sillitoe, M. Staszczak, C. I. Szabo-Foster, H. Torii, B. Vallage, M. Valdes, D. P. van der Werf, A. Voronin, J. Walz, S. Wolf, S. Wronka and Y. Yamazaki, Hyp. Int., 2015, 233, 21–27 CrossRef
.
- F. Tuomisto and I. Makkonen, Rev. Mod. Phys., 2013, 85, 1583–1631 CrossRef CAS
.
- Y. Nagai, T. Chiba, Z. Tang, T. Akahane, T. Kanai, M. Hasegawa, M. Takenaka and E. Kuramoto, Phys. Rev. Lett., 2001, 87, 176402 CrossRef CAS PubMed
.
- M. Reivich, D. Kuhl, A. Wolf, J. Greenberg, M. Phelps, T. Ido, V. Casella, J. Fowler, E. Hoffman, A. Alavi, P. Som and L. Sokoloff, Circ. Res., 1979, 44, 127–137 CrossRef CAS PubMed
.
- R. L. Wahl, B. A. Siegel, R. Edward Coleman and C. G. Gatsonis, J. Clin. Oncol., 2004, 22, 277–285 CrossRef PubMed
.
- L. D. Barnes, S. J. Gilbert and C. M. Surko, Phys. Rev. A, 2003, 67, 032706 CrossRef
.
- L. D. Barnes, J. A. Young and C. M. Surko, Phys. Rev. A, 2006, 74, 012706 CrossRef
.
- J. R. Danielson, J. A. Young and C. M. Surko, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 235203 CrossRef
.
- A. R. Swann and G. F. Gribakin, J. Chem. Phys., 2020, 153, 184311 CrossRef CAS PubMed
.
- Y. Sugiura, H. Suzuki, T. Otomo, T. Miyazaki, T. Takayanagi and M. Tachikawa, J. Comput. Chem., 2020, 41, 1576–1585 CrossRef CAS PubMed
.
- Y. Sugiura, T. Takayanagi and M. Tachikawa, Int. J. Quantum Chem., 2020, 120, e26376 CrossRef CAS
.
- D. Yoshida, Y. Kita, T. Shimazaki and M. Tachikawa, Phys. Chem. Chem. Phys., 2022, 24, 26898–26907 RSC
.
- M. Furushima, M. Takagi, D. Yoshida, Y. Kita, T. Shimazaki and M. Tachikawa, Phys. Chem. Chem. Phys., 2023, 25, 625–632 RSC
.
- B. C. Garrett, D. A. Dixon, D. M. Camaioni, D. M. Chipman, M. A. Johnson, C. D. Jonah, G. A. Kimmel, J. H. Miller, T. N. Rescigno, P. J. Rossky, S. S. Xantheas, S. D. Colson, A. H. Laufer, D. Ray, P. F. Barbara, D. M. Bartels, K. H. Becker, K. H. Bowen, Jr, S. E. Bradforth, I. Carmichael, J. V. Coe, L. R. Corrales, J. P. Cowin, M. Dupuis, K. B. Eisenthal, J. A. Franz, M. S. Gutowski, K. D. Jordan, B. D. Kay, J. A. LaVerne, S. V. Lymar, T. E. Madey, C. W. McCurdy, D. Meisel, S. Mukamel, A. R. Nilsson, T. M. Orlando, N. G. Petrik, S. M. Pimblott, J. R. Rustad, G. K. Schenter, S. J. Singer, A. Tokmakoff, L. Wang, C. Wittig and T. S. Zwier, Chem. Rev., 2005, 105, 355–389 CrossRef CAS PubMed
.
- L. Turi and P. J. Rossky, Chem. Rev., 2012, 112, 5641–5674 CrossRef CAS PubMed
.
- J. R. R. Verlet, A. E. Bragg, A. Kammrath, O. Cheshnovsky and D. M. Neumark, Science, 2005, 307, 93–96 CrossRef CAS PubMed
.
- R. N. Barnett, U. Landman, C. L. Cleveland and J. Jortner, J. Chem. Phys., 1988, 88, 4429–4447 CrossRef CAS
.
- J. V. Coe, G. H. Lee, J. G. Eaton, S. T. Arnold, H. W. Sarkas, K. H. Bowen, C. Ludewigt, H. Haberland and D. R. Worsnop, J. Chem. Phys., 1990, 92, 3980 CrossRef CAS
.
- J. Kim, I. Becker, O. Cheshnovsky and M. A. Johnson, Chem. Phys. Lett., 1998, 297, 90–96 CrossRef CAS
.
- B. Abel, U. Buck, A. L. Sobolewskic and W. Domcke, Phys. Chem. Chem. Phys., 2012, 14, 22–34 RSC
.
- A. Herburger, E. Barwa, M. Ončák, J. Heller, C. van der Linde, D. M. Neumark and M. K. Beyer, J. Am. Chem. Soc., 2019, 141, 18000–18003 CrossRef CAS PubMed
.
- M. Bergami, A. L. D. Santana, J. M. Charry, A. Reyes, K. Coutinho and M. T. do N Varella, Phys. Chem. Chem. Phys., 2022, 126, 2699–2714 CrossRef CAS PubMed
.
- M. Bergami, J. Charry, A. Reyes, K. Coutinho and M. T. do N Varella, J. Phys. Chem. B, 2024, 128, 10178–10188 Search PubMed
.
- J. Mitroy, S. Bubin, W. Horiuchi, Y. Suzuki, L. Adamowicz, W. Cencek, K. Szalewicz, J. Komasa, D. Blume and K. Varga, Rev. Mod. Phys., 2013, 85, 693–749 CrossRef
.
- T. Yamashita, M. Umair and Y. Kino, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 205002 CrossRef
.
- T. Yamashita and Y. Kino, Phys. Rev. A, 2019, 100, 062511 CrossRef CAS
.
- Y. Yamada, Y. Kita and M. Tachikawa, Phys. Rev. A, 2014, 89, 062711 Search PubMed
.
- S. Ito, D. Yoshida, Y. Kita and M. Tachikawa, J. Chem. Phys., 2020, 153, 224305 CrossRef CAS
.
- D. Bressanini, J. Chem. Phys., 2021, 154, 224306 Search PubMed
.
- D. Bressanini, J. Chem. Phys., 2021, 155, 054306 CrossRef CAS PubMed
.
- S. Ito, D. Yoshida, Y. Kita and M. Tachikawa, J. Chem. Phys., 2023, 158, 204303 Search PubMed
.
- M. Tachikawa, K. Taneda and K. Mori, Int. J. Quantum Chem., 1999, 75, 497–510 CrossRef CAS
.
- M. Tachikawa and Y. Osamura, J. Chem. Phys., 2000, 113, 4942 Search PubMed
.
- M. Tachikawa, Chem. Phys. Lett., 2001, 350, 269–276 CrossRef CAS
.
- S. A. González, N. F. Aguirre and A. Reyes, Int. J. Quantum Chem., 2008, 108, 1742–1749 CrossRef
.
- J. Romero, E. Posada, R. Flores-Moreno and A. Reyes, J. Chem. Phys., 2012, 137, 074105 CrossRef PubMed
.
- A. R. Swann, G. F. Gribakin, J. R. Danielson, S. Ghosh, M. R. Natisin and C. M. Surko, Phys. Rev. A, 2021, 104, 012813 CrossRef CAS
.
- J. Hofierka, B. Cunningham, C. M. Rawlins, C. H. Patterson and D. G. Green, Nature, 2022, 606, 688–693 CrossRef CAS PubMed
.
- J. Arponen and E. Pajanne, Ann. Phys., 1979, 121, 343–389 CAS
.
- E. Boroński and R. M. Nieminen, Phys. Rev. B, 1986, 34, 3820 CrossRef PubMed
.
- B. Barbiellini, M. J. Puska, T. Torsti and R. M. Nieminen, Phys. Rev. B, 1995, 51, 7341 CrossRef PubMed
.
- B. Barbiellini, M. J. Puska, T. Torsti and R. M. Nieminen, Phys. Rev. B, 1996, 53, 16201 CrossRef CAS PubMed
.
- B. Barbiellini, M. Hakala, M. J. Puska, R. M. Nieminen and A. A. Manuel, Phys. Rev. B, 1997, 56, 7136 CrossRef CAS
.
- J. Kuriplach and B. Barbiellini, Phys. Rev. B, 2014, 89, 155111 CrossRef
.
- B. Barbiellini and J. Kuriplach, Phys. Rev. Lett., 2015, 114, 147401 Search PubMed
.
- F. A. Gianturco, T. Mukherjee and P. Paioletti, Phys. Rev. A, 1997, 56, 3638 CrossRef CAS
.
- F. A. Gianturco, P. Nichols, T. L. Gibson and R. R. Lucchese, Phys. Rev. A, 2005, 72, 032724 CrossRef
.
- R. Carey, R. R. Lucchese and F. A. Gianturco, Phys. Rev. A, 2008, 78, 012706 CrossRef
.
- J. Franz and F. A. Gianturco, Eur. Phys. J. D, 2014, 68, 279 CrossRef
.
- Y. Sugiura, T. Takayanagi, Y. Kita and M. Tachikawa, Eur. Phys. J. D, 2019, 73, 162 CrossRef
.
- F. Moncada and A. Reyes, J. Chem. Phys., 2023, 158, 134101 CrossRef CAS PubMed
.
- J. K. O’Connell and N. F. Lane, Phys. Rev. A, 1983, 27, 1893 CrossRef
.
- K. J. Miller, J. Am. Chem. Soc., 1990, 112, 8533–8542 CrossRef CAS
.
- G. F. Gribakin, J. A. Young and C. M. Surko, Rev. Mod. Phys., 2010, 82, 2557–2607 CrossRef CAS
.
- S. Ghosh, J. R. Danielson and C. M. Surko, Phys. Rev. Lett., 2022, 129, 123401 CrossRef CAS PubMed
.
- J. R. Danielson, S. Ghosh, E. Arthur-Baidoo, D. R. Witteman and C. M. Surko, Phys. Rev. A, 2023, 108, 032801 CrossRef CAS
.
- B. Barbiellini-Amidei, Phys. Lett. A, 1989, 134, 328–330 CrossRef CAS
.
- N. D. Drummond, P. López Ríos, R. J. Needs and C. J. Pickard, Phys. Rev. Lett., 2011, 107, 207402 CrossRef CAS PubMed
.
- N. T. Padial and D. W. Norcross, Phys. Rev. A, 1984, 29, 1742 Search PubMed
.
- X. Zhang, J. Sun and Y. Liu, J. Phys. B: At., Mol. Opt. Phys., 1992, 25, 1893–1897 CrossRef CAS
.
- K. Fedus, J. Franz and G. P. Karwasz, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 062701 CrossRef
.
- V. A. Dzuba, V. V. Flambaum, G. F. Gribakin and C. Harabati, Phys. Rev. A, 1999, 60, 3641 CrossRef CAS
.
- V. A. Dzuba, V. V. Flambaum and C. Harabati, Phys. Rev. A, 2000, 62, 042504 CrossRef
.
- A. R. Swann and G. F. Gribakin, Phys. Rev. Lett., 2019, 123, 113402 Search PubMed
.
- J. Mitroy and G. Ryzhikh, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, 1375–1383 CrossRef CAS
.
- J. Mitroy and G. G. Ryzhikh, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 2001–2007 Search PubMed
.
- J. Mitroy and I. A. Ivanov, Phys. Rev. A, 2002, 65, 042705 Search PubMed
.
- M. W. J. Bromley and J. Mitroy, Phys. Rev. A, 2002, 65, 062505 CrossRef
.
- J. Mitroy, M. W. J. Bromley and G. G. Ryzhikh, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, R81–R116 CrossRef CAS
.
- L. H. R. Dos Santos, A. Krawczuk and P. Macchi, J. Phys. Chem. A, 2015, 119, 3285–3298 CrossRef CAS PubMed
.
- F. Yang, X. Wang, M. Yang, A. Krishtal, C. van Alsenoy, P. Delaruec and P. Senet, Phys. Chem. Chem. Phys., 2010, 12, 9239–9248 Search PubMed
.
- D. Yoshida and M. Tachikawa, Eur. Phys. J. D, 2024, 78, 1 CrossRef
.
- J. C. Light, I. P. Hamilton and J. V. Lill, J. Chem. Phys., 1985, 82, 1400 CrossRef CAS
.
- R. Kosloff and H. Tal-Ezer, Chem. Phys. Lett., 1986, 127, 223–230 CrossRef CAS
.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 Search PubMed
.
- J. Čížek, J. Chem. Phys., 1966, 45, 4256 CrossRef
.
- J. Čížek and J. Paldus, Int. J. Quantum Chem., 1971, 5, 359–379 Search PubMed
.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910 Search PubMed
.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 Search PubMed
.
- A. L. Hickey and C. N. Rowley, J. Phys. Chem. A, 2014, 118, 3678–3687 CrossRef CAS PubMed
.
- J. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC
.
- D. E. Woon and T. H. Dunning, Jr, J. Chem. Phys., 1994, 100, 2975 CrossRef CAS
.
- S. Maeda, K. Ohno and K. Morokuma, Phys. Chem. Chem. Phys., 2013, 15, 3683–3701 RSC
.
- S. Maeda, Y. Harabuchi, M. Takagi, K. Saita, K. Suzuki and T. Ichino, J. Comput. Chem., 2017, 39, 233–250 CrossRef PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed
.
- S. Heitz, D. Weidauer, B. Rosenow and A. Hese, J. Chem. Phys., 1992, 96, 976–981 CrossRef CAS
.
- R. Iida, H. Suzuki, T. Takayanagi and M. Tachikawa, Phys. Rev. A, 2021, 104, 062807 CrossRef CAS
.
- T. Tsurusawa and S. Iwata, Chem. Phys. Lett., 1998, 287, 553–562 Search PubMed
.
- G. Hincapié, N. Acelas, M. Castaño, J. David and A. Restrepo, J. Phys. Chem. A, 2010, 114, 7809–7814 CrossRef PubMed
.
- F. Ramírez, C. Z. Hadad, D. Guerra, J. David and A. Restrepo, Chem. Phys. Lett., 2011, 507, 229–233 Search PubMed
.
- D. J. Wales and T. R. Walsh, J. Chem. Phys., 1997, 106, 7193 Search PubMed
.
- B. J. Mhin, J. Kim, S. Lee, J. Y. Lee and K. S. Kim, J. Chem. Phys., 1994, 100, 4484 Search PubMed
.
- E. S. Kryachko, Chem. Phys. Lett., 1999, 314, 353–363 Search PubMed
.
- C. Pérez, M. T. Muckle, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Science, 2012, 336, 897–901 CrossRef PubMed
.
- S. Lee, S. J. Lee, J. Y. Lee, J. Kim, K. S. Kim, I. Park, K. Cho and J. D. Joannopoulos, Chem. Phys. Lett., 1996, 254, 128–134 Search PubMed
.
- N. I. Hammer, J. Shin, J. M. Headrick, E. G. Diken, J. R. Roscioli, G. H. Weddle and M. A. Johnson, Science, 2004, 306, 675–679 CrossRef CAS PubMed
.
- T. Takayanagi, T. Yoshikawa, H. Motegi and M. Shiga, Chem. Phys. Lett., 2009, 482, 195–200 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00893j |
| This journal is © the Owner Societies 2025 |