Open Access Article
Open Access ArticlePredicting impact sensitivities for an extended set of energetic materials via the vibrational up-pumping model: molecular-based structure–property relationships identified†
Jack M.
Hemingway
a,
Heather M.
Quayle
 a,
Cian
Byrne
a,
Colin R.
Pulham
a,
Cian
Byrne
a,
Colin R.
Pulham
 a,
Subrata
Mondal
a,
Subrata
Mondal
 bc,
Adam A. L.
Michalchuk
bc,
Adam A. L.
Michalchuk
 *d and
Carole A.
Morrison
*d and
Carole A.
Morrison
 *a
*a
aEaStCHEM School of Chemistry and Centre for Science at Extreme Conditions, The University of Edinburgh, King's Buildings, David Brewster Road, Edinburgh EH9 3FJ, UK. E-mail: c.morrison@ed.ac.uk
bFederal institute for Materials Research and Testing (BAM), Richard-Wilstaetter-Str 11, Berlin, 12489, Germany
cInnovation & Translational Research Hub (iTRH), Department of Physics, Presidency University, Bangalore-560064, India
dSchool of Chemistry, University of Birmingham, Edgebaston, Birmingham, B15 2TT, UK. E-mail: a.a.l.michalchuk@bham.ac.uk
First published on 15th May 2025
Abstract
We have applied the vibrational up-pumping model to predict the mechanically-induced impact sensitivities of 33 molecular energetic crystals. Overall, the current model successfully identifies and ranks the compounds that are most sensitive to mechanical initiation, but offers poorer differentiation between compounds with lower sensitivity. Further developments to include the effects of trigger bond activation led to significant improvements in predictive capability. We show that this structure–property model highlights the importance of molecular flexibility in predicting impact sensitivity, and furthermore, we show that the Kier molecular flexibility index, which can be obtained from a SMILES string, offers a simple molecular-based descriptor that goes some way towards predicting the sensitivity of energetic materials.
1. Introduction
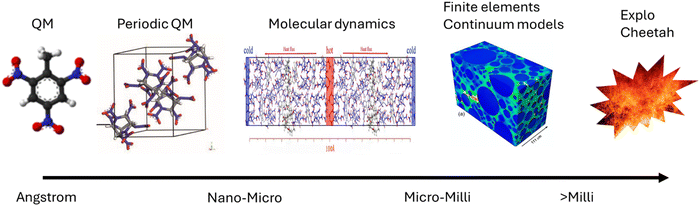
Energetic materials (EMs, explosives, propellants, pyrotechnics, and gas generators) release large amounts of energy when exposed to an external stimulus such as heat, electrostatic discharge, friction, or impact.1 As these materials are used in both military and civilian applications, their behaviour must be reliable and reproducible. This is especially true given that EMs are routinely stored for long durations and can be (often inadvertently) exposed to elevated temperatures, shocks, or impacts. Minimising the sensitivity of EMs to the latter (their impact sensitivity, IS) reduces the potential for accidental initiation and creates materials that are inherently safer to store and handle. The ability to design an EM with a particular IS response therefore creates a drive to understand how this property is directed by its structure.Computational modelling is at the forefront of modern efforts to understand the process of EM initiation, with a broad range of techniques employed to explore the various contributions to the initiation phenomenon (see Fig. 1). At one end are the thermochemical, continuum and large-scale molecular dynamics approaches, which facilitate the milli- and micro-scale modelling of EMs.2 Such models allow for the bulk performance parameters of EM compositions to be approximated, which usually include combinations of an energetic component (a crystalline solid) mixed with polymer binders to modify the mechanical properties. These models are very useful to probe the formation and behaviour of hot spots, and the effects of bulk structural defects such as voids, grain boundaries and other inhomogeneities. However, models at this scale tend to be less useful for probing the chemical origins of EM behaviour, and thus are not typically used to guide the design of new energetic components. This is a particular challenge given the growing need to replace existing energetic molecules whose combustion products are toxic or otherwise unsafe for the environment.3
To tackle questions on the chemical origins of initiation, the modelling focus must shift to the sub-micro-scale, with use of (typically) quantum mechanical methods to probe the behaviour of the pure energetic component itself. Here correlations have been reported with the amount of free space per molecule in its corresponding crystal lattice,4–6 electronic band gaps,7 bond dissociation energies,8,9 and electrostatic surface potentials.10,11 However, these approaches tend to report structure/property relationships for closely related classes of molecular structures only, and cannot account for differences that arise due to polymorphism12 or by crystallising an energetic molecule with a second molecule (i.e. to make a salt or cocrystal).13,14 To include the effects of the crystal packing environment, more computationally expensive methods are required. These include models which are rooted in mechanochemistry via the vibrational up-pumping model,15–17 such as those by Ye, Bernstein, Bondarchuk, Bidault, and Michalchuk.18–23 In these models the crystalline energetic component of the EM is considered, where it is usually described as an idealised, defect-free crystalline lattice with molecules vibrating on the picosecond timescale. Anharmonic phonon scattering events facilitate the transfer of energy from the low-frequency lattice vibrations that are excited by mechanical impact, into higher frequency, localised molecular vibrations. In this way, the mechanical impact energy causes the excitation of bond stretching, angle and torsional bending modes, leading to bond rupture and the onset of EM initiation.24 Moreover, as phonon scattering occurs on the timescale of molecular vibrations (typically picoseconds), it therefore manifests much earlier than the milli-scale hotspot creation (typically attributed to 10−5–10−3 seconds),25,26 and can therefore be considered to be an intrinsic first response measure of IS.
As nano-scale models relate directly to the crystal and molecular structures of an EM, it allows us to build a connection that links the chemical structure to its property. This raises the tantalising prospect that, once this connection is known, it can be explored in either direction, i.e. for a given structure we can predict its corresponding property, while for a desired property we can deduce the structural features that are most likely to give rise to it. For EM research, having access to such a design model would be highly valued, as current practice requires that novel EMs are synthesised and experimentally tested to obtain IS behaviour, work that is time-consuming, costly, and extremely hazardous. Moreover, experimental IS measurements, typically obtained with a BAM fall hammer apparatus (or related variants), are well documented to yield highly-variable data, with variations depending on temperature, humidity, sample purity, crystallinity, particle size, and even on operator experience.27 Reducing these issues with measurement reliability further bolsters the need to develop theoretical tools to rationalise the underlying trends that link structure to IS.
We have previously reported the performance of the vibrational up-pumping model for a proof-of-concept set of common EMs (grey box, Fig. 2). Using this set we have shown how our model can correctly rank the compounds on a scale of relative IS, as compared to their experimentally measured ordering. While this has allowed the IS of these materials to be rationalised in terms of the up-pumping model itself, and has suggested some correlations with molecular features like molecular flexibility,23 the existing data set is too small to extract broader trends that relate IS to chemical structure. Herein we look to address this by significantly expanding the list of compounds studied to include previously reported examples of pyrazoles, tetrazoles, nitrated toluenes, and nitrate esters (red, blue, yellow and green boxes, Fig. 2). We look to assess how well the vibrational up-pumping model performs over this extended data set, and to explore in more detail the important role that covalent bond strengths play in the up-pumping process. We also assess what molecular design features can be extracted from the vibrational up-pumping model that influence this important structure–property relationship.
2. Background theory
Full details on our vibrational up-pumping model, which build on the earlier models,15–17 are available elsewhere.23,28 They are summarised briefly here and in Fig. 3. The mechanical impact energy is first deposited into the lattice acoustic vibrations, where it equilibrates rapidly across the delocalised low frequency phonon bath (external lattice) modes, ω. We define an upper limit for the phonon bath as Ωmax, which is typically found at 200 ± 50 cm−1. In response to this mechanical impact, these low energy modes reach quasi-temperatures on the order of thousands of degrees (denoted by Tshock),29 and their excited vibrational populations scatter through anharmonic phonon–phonon interactions, described by the two-phonon density of states, ρ(2) (eqn (1)).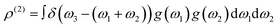 | (1) |
In practise, our impact sensitivity model takes as input the phonon density of states g(ω), calculated for the optimised crystal structure using plane-wave density functional theory (DFT). Using g(ω) the two-phonon density of states ρ(2) is generated according to the scattering pathways outlined above. This new curve is then projected onto g(ω) to reflect the amount of energy that can be ‘captured’ by the crystal. This projected curve is integrated from 1–3Ωmax and normalised to the number of molecules in the unit cell over which the captured energy is distributed. It is this number that provides a semi-quantitative metric that relates to the relative impact sensitivity of each EM.
3. Computational details
Crystal structures for all compounds were obtained from the CSD31 (see ESI†) and processed using Seekpath32 to generate input files for CASTEP v16.33 Where multiple polymorphs have been reported for a given compound the most stable structure defined at ambient pressure and temperature conditions was selected, i.e. α-RDX, α-FOX-7, α-NTO, β-HMX, ε-CL20 and m-TNT. All crystal structures were optimised using the generalised gradient approximation (GGA) functional of Perdew–Burke–Ernzerhof (PBE)34 with the TS dispersion correction scheme.35 The nuclear Coulomb potential was attenuated using norm-conserving pseudopotentials generated on-the-fly in CASTEP, alongside a plane wave basis set expressed to an expansion of at least 800 eV. The following convergence criteria were adhered to: residual atomic forces ≤ 0.005 eV Å−1, atomic displacements ≤ 5 × 10−4 Å, wavefunction self-consistency ≤ 5 × 10−6 eV and lattice vector stresses ≤0.01 GPa. The fine Fourier grids used for charge density projection was set using a grid of at least 2.0. Each optimised structure returned a calculated unit cell typically within ca. 5% of the experimentally determined structure (see ESI,† S1). Phonon frequencies were calculated at the Brillouin zone centre Γ (k = 0) for the optimised structure within the linear response formalism as implemented in CASTEP,36 and the density of states g(ω) were generated using a Gaussian smearing of 5 cm−1.The top of the phonon bath, Ωmax, was located by tracking the molecular centre of mass change across each of the normal mode eigenvectors, with the transition from external to internal mode behaviour taken to have occurred once the centre of mass change dropped to 10% of its maximum value (see ESI,† S2). The temperature of the phonon bath that results from mechanical impact Tshock, which is used to initiate our up-pumping calculation, was obtained from the ratio of the bulk heat capacity to the phonon bath heat capacity, Ctot/Cph, calculated analytically from the Gaussian broadened g(ω) (see ESI,† S3). This completes the input data required for the vibrational up-pumping model, which are collated in the ESI,† S4.
To determine the relative bond strengths for each EM, the mass-independent local force constants were extracted from the gas phase normal vibrational mode force constant matrix using LModeA-nano.37 In each case the normal force constant matrix was calculated using Gaussian v.16 at the B3LYP/6-31G* level.38
For each unique energetic molecule, the Kier molecular flexibility (KMF, Φ) indices were calculated via their corresponding SMILES strings, generated by Chemdraw and processed using RDKit.39 The KMF is obtained from the one-bond (1κ) and two-bond (1κ) Kappa shape indices (eqn (2) and (3)).40
| 1κ = (NSA + α)(NSA + α − 1)2/(1P + α)2 | (2) |
| 2κ = (NSA + α − 1)(NSA + α − 2)/(2P + α)2 | (3) |
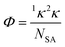 | (4) |
4. Results and discussion
The phonon density of states g(ω) and the two-phonon density of states ρ(2) that result from the phonon scattering processes are shown in Fig. 4 for a subset of EMs (grey box, Fig. 2; remainder are reported in the ESI,† S5). As we have discussed in previous reports, there is limited information regarding EM IS that can be extracted from visual analysis of these plots, with no obvious correlation between IS and features like Ωmax or the absolute magnitude of ρ(2). However, once ρ(2) is projected onto g(ω) and integrated across 1–3Ωmax for each EM we begin to observe clear trends (Fig. 5). | ||
| Fig. 4 Calculated vibrational density of states (g(ω) (grey)), alongside the two-phonon density of states, ρ(2) (× 103, a.u., red) and eigenvector displacement contributions from the weakest bonds (blue). Colour scheme: C–NO2 (filled squares), C–N ring or side chain bonds (open circles), and N–NO2 (solid triangles). Data for the remaining compounds are given in the ESI,† Section S5. | ||
 | ||
| Fig. 5 Vibrational up-pumping densities vs. experimental impact sensitivity values (a) projected onto all molecular vibrations that fall between 1–3Ωmax, and (b) only those molecular vibrations that contain weak bond stretch character, and (c) further scaled according to weak bond strengths. Colour scheme relates to compound classes shown in Fig. 2. Experimental impact sensitivities are taken from ref. 27 and 41–57. | ||
In its current form, the up-pumping model provides reasonable differentiation between sensitive EMs (high up-pumped energy, low experimental impact energies) and insensitive EMs (low up-pumped energy, high experimental impact energies), Fig. 5(a). To date this is the largest data set presented for the up-pumping model. Two noticeable outliers exist, however, with 1,4-DADNP and TET-6 sitting far above the general trend line. This suggests an intrinsic deficiency in the current up-pumping model and a need for further adjustment to the procedure.
Within the current model (Fig. 5(a)), we consider the up-pumped energy projecting onto all the vibrational modes that fall within the up-pumping window (1–3Ωmax), thereby assuming all modes in this region are equally important in the initiation process. This approximation is based on the existence of dense intramolecular states that facilitate rapid intramolecular vibrational energy redistribution,58 and that the likelihood of rupturing covalent bonds with a given quantity of energy is equivalent for all molecules. This has generally worked well for compounds comprising similar bonding patterns. Perhaps unsurprisingly, with the larger and more diverse dataset presented in this work, this simplification begins to breakdown, requiring a more detailed consideration of the breadth of chemistry across the EM dataset.
As a first attempt to improve the up-pumping model, we turn to the concept of trigger modes: i.e. that there exists a single (or subset) of defined normal modes whose excitation leads to transient metallisation of the EM (population of antibonding states induced by the structural distortions of a molecular vibration) that subsequently leads to the rupture of covalent bonds.24 While this model is straightforward to investigate for simple molecules like linear azides, it is less clear how individual normal modes can be isolated for complex molecules like ring systems. In fact, for more complex molecules the covalent bonds likely to be associated with initiation are expected to contribute to many normal modes within the 1–3 Ωmax window. This renders the task of identifying the individual vibrations likely to be involved in the chemical initiation pathway considerably harder. However, the fact that we observe contributions of the same covalent bond to many normal mode frequencies in the up-pumping window does offer an alternative strategy to recast our up-pumping model.
Starting from the widely held assumption that initiation begins with weak bond (also known as trigger bond) activation,30 we can interrogate the molecular eigenvectors to identify which vibrational modes significantly active these bonds, and which ones do not. In this way we can ‘mask out’ the vibrational modes that fall in the up-pumping window that are not associated with weak bond activation, with the aim to reduce the current limitation in our up-pumping model where we count the excitation of all modes in the 1–3Ωmax window.
To do this, we calculated the local mode force constants for all the energetic molecules in our test set, to quantify the strengths of all bond types (see ESI† S6). Consistent with earlier work our analysis showed that R–NO2 bonds (where R = C, N or O) are generally the weakest types of bonds, although there are exceptions (see ESI† S6). Across the whole dataset we find local force constants for R–NO2 bonds of 4.0 ± 0.8, 3.3 ± 0.6, and 2.1 ± 0.1 mDyn Å−1 for R = C, N, or O, respectively. Notably, the aliphatic C–N and C–O bonds were found to be of comparable strength (4.1 ± 0.4 and 3.4 ± 0.1 mDyn Å−1, respectively), as were C–Nar (Nar denoting N atoms within aromatic rings), N–NH2 and C–P bonds (4.6 ± 0.2, 4.7, and 2.3 ± 0.03 mDyn Å−1, respectively). Thus, it seems likely that the conventional definition of EM trigger bonds should be broadened beyond the conventional R–NO2 type. We note that weak bonds beyond the type R–NO2 have been reported to break during molecular dynamics simulations of nitrate esters.59 The other covalent bonds in our test molecules have significantly higher local force constants (for example, C–C bonds within aromatic rings 6.2 ± 0.8 mDyn Å−1, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds 9.9 ± 0.9 mDyn Å−1, and N–H bonds 7.1 ± 0.5 mDyn Å−1).
O bonds 9.9 ± 0.9 mDyn Å−1, and N–H bonds 7.1 ± 0.5 mDyn Å−1).
Next, for each EM we quantified the degree of weak bond activation (i.e. deviation from the optimised bond length) for a defined pair of atoms across all the solid-state eigenvectors, normalised against the molecular mode vibration that displayed the most pronounced distortion. This process was repeated for all weak bonds, with the output corresponding to the blue data points in Fig. 4 (plots for the other compounds are in ESI,† S5). This analysis allowed us to modify the structure of the up-pumping window for each EM by selecting only those normal modes which contain trigger bond normalised distortion behaviour of greater than 10%. Using this modified up-pumping window for the projection of ρ(2) provides a significant improvement to the prediction (Fig. 4(b)). As expected, by only summing the integrations for ρ(2) projecting onto modes associated with weak bond distortions, the predicted up-pumping values fall for nearly all our EMs. The exception is ε-CL-20, for which all vibrational modes in its up-pumping window contain trigger bond motion. Modifying the up-pumping window projection in this way leads to significant improvements in the predictions for 1,4-DADNP and TET-6 although they remain slightly overestimated. However, overall this data set shows some clear trends. For the compounds represented in the grey panel in Fig. 2, ε-CL-20 and HNB are correctly predicted to be the most sensitive, and the ordering β-HMX > α-RDX is correct. The three least sensitive compounds, α-FOX-7, α-NTO and TATB are ranked as insensitive on near equal parity, despite large differences in their experimental IS values. This shows that the up-pumping model effectively flatlines for mechanically insensitive EMs. BP-1 and NP-1 are correctly predicted to be more sensitive to mechanical impact than any of the other pyrazoles (red stars, Fig. 5), for which the model struggles to offer any other meaningful differentiation. The tetrazoles (blue triangles, Fig. 5) fare better: TET-1 is correctly predicted to be the most sensitive, while the other data points for this class sit reasonably well on the decay line, except for the aforementioned TET-6. For the compounds closely related to TNT (yellow diamonds), while m-TNT is slightly over-predicted, the other three compound are correctly ordered. Finally, for the nitrate esters (green squares) while PETN and PO-PETN are correctly predicted to be more sensitive than CH-PETN and NG, the latter two are incorrectly ordered.
While this approach to modifying the up-pumping integration provides a notable improvement, it still treats all trigger bonds as essentially equivalent in terms of their bond strength. However, we know this information through the local force constant analysis, and so this can be straightforwardly accounted for through the introduction of a scaling term. In this way we create a more direct link between the up-pumping model and previous gas-phase models that are based on bond dissociation energies.56,60 Noting that a local mode force constant (kloc) is inversely proportional to the bond dissociation probability we can define,
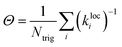 | (5) |
It follows from the above discussion that, while the present description of the vibrational up-pumping model offers good differentiation between sensitive (<10 Nm) and insensitive (>10 Nm) EMs, its ability to offer more detailed differentiation is somewhat limited. There are many reasons for this low resolution, with the two most significant being: (1) an under sampling of the phonon dispersion (here we are up-pumping g(ω) obtained from the Brillouin zone centre vibrational modes only), and (2) an assumption that all the phonon scattering pathways highlighted in Fig. 3 are permissible and occur at identical scattering rates in all EMs. Whilst many of these issues can – in principle – be addressed, they all come at significant computational cost that would render the model unfeasible for processing large datasets or for compound screening for novel EMs with a desired IS behaviour. It also should not be forgotten that the experimental data, presented on the x-axis on the plots shown in Fig. 5 will be subject to experimental error, given these measurements are derived from drop-weight experiments with known variability issues.27 Several of the data points (specifically, 1,4-DADNP, 3-NP and TET-6) are presented at their minimum initiation energies, while that presented for TATB is a widely accepted estimated value. The predicted data, presented on the y-axis, will also be subject to errors, which reside, in part, with the limitations in the accuracy of the DFT-based phonon calculations and the limitations in the up-pumping model, as documented above.
The vibrational up-pumping model is essentially a resonance model: those crystal lattices containing distributions of vibrational modes in favourable positions to accentuate the phonon scattering pathways, and the localisation of this scattering energy into its molecular vibrations, give a higher predicted mechanical initiation response. The reasonable success of this physical model, across a broad scope of molecular EM structures, suggests that simplified molecular descriptors associated with vibrational resonance may provide useful features for a machine learning approach, which could then be utilised for a much higher throughput study into the targeted design of new EMs with tailored properties.
To this end, we looked to identify any molecular-based features that appear to be influencing the vibrational up-pumping model. Previous reports have shown a correlation between the number of doorway modes (Qd) and impact sensitivity,17,22 a trend that is also seen in this work. Counting the number of modes that fall in the region 1–2Ωmax, and dividing by the number of molecules in the corresponding unit cell and the size of the doorway window gives the doorway density, which is plotted vs. experimental impact sensitivity in Fig. 6 (see also ESI,† S5). While the specific ordering between compounds in the different chemical classes is much poorer than for the vibrational up-pumping data shown in Fig. 5, the differentiation between sensitive and insensitive EMs is clearly apparent.
 | ||
| Fig. 6 Doorway density versus experimental impact sensitivity. Colour scheme relates to compound classes shown in Fig. 2. | ||
Classically, we know that vibrational frequencies are proportional to the strength of interatomic force constants, with stronger interactions leading to higher frequencies. It follows that to engineer molecules with a greater number of low frequency vibrational modes (i.e. falling in the doorway region), we need to consider structures with a greater degree of flexibility. Following our previous success linking molecular flexibility to impact sensitivity for a small data set,23 we have calculated the Kier molecular flexibility (KMF) index viaeqn (4) for all of our EMs (see Fig. 7). The result is a positive correlation between increasing KMF (flexibility) and IS. Our analysis also shows that KMF correlates positively with the number of trigger bonds, Ntrig, although this link was expected as KMF essentially counts the number of freely rotating bonds which naturally aligns with the count of weak trigger bonds.
We stress that KMF is a fairly primitive metric that does not account for structural rigidity arising from non-covalent interactions e.g. via hydrogen bonding within or between molecules, or rigidity imposed by a crystal lattice. This is why TATB, a flat rigid molecule, presents with a higher than anticipated KMF value. On the other hand, CL-20, a highly strained cage structure, presents with quite a low KMF, indicating that a direct correlation with IS is far from perfect. However, the appeal in having a molecular-based feature calculated from just a SMILES string that can guide the design of EMs, prior to their synthesis and testing, cannot be understated. This is a positive start for a machine learning study, using molecular-based descriptors that are easily obtainable and inspired by the vibrational up-pumping model. This work is currently underway.
5. Conclusions
Herein we have applied the vibrational up-pumping model to an extended set of molecular energetic compounds and found a favourable correlation with experimental impact sensitivity. The model, which is based on the phonon scattering of Brillouin zone-centred DFT generated density of states, offers good differentiation between highly sensitive and insensitive EMs. By counting the phonon scattering onto vibrational modes in the up-pumping window that activate trigger bonds only, we show that the relative ranking of EM sensitivity improves significantly. Further extension to account for differences in average trigger bond strengths for each EM led to only minor improvements for the most mechanically sensitive compounds. Overall, while the up-pumping model performs well for sensitive EMs, it essentially flatlines for insensitive EMs, offering little in the way of meaningful differentiation.The importance in being able to correctly predict the impact sensitivity behaviour for structurally diverse EMs from first principles should not be underestimated. It is clear that the up-pumping model has an important contribution to make in understanding the nano-scale response of EMs to mechanical impact. In this respect it offers a complementary approach to the longer length scale continuum models, by accounting for the different resonant properties of the crystalline components of EM compositions, and offers a route to encode for more of the material properties in a finite element approach.
The application of the vibrational up-pumping model in any large-scale screening capacity designed to identify new energetic materials with desired properties is unlikely. However, having a physical model that successfully links structure with property provides opportunities to learn simpler, more readily obtainable metrics that could be utilised in this way. It is clear that the up-pumping model works by vibrational resonance, and in particular the availability of low-lying vibrations that occupy the doorway region of the up-pumping window. This is typically around 200–400 cm−1, and therefore points to the likelihood that EMs that are highly sensitive to mechanical impact will have many low-lying vibrational modes. While this information has been known for some time, our work here shows this phenomenon holds across a broader range of molecular EMs than have been studied before. Moreover, we show that a simply determined molecular-based metric, the Kier molecular flexibility index, can successfully separate the sensitive EMs from the insensitive, and is therefore a powerful molecular-based descriptor that could be utilised in a supervised machine learning study. This work is currently underway.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
J. M. H. thanks the Air Force Office of Scientific Research (FA8655-20-1-7000) for the award of a PhD studentship. H. M. Q. thanks the UK MoD for funding of a PhD studentship through contract number WSTC1079. S. M. acknowledges funding for an Adolf-Martens Fellowship. We are grateful for the computational support from the UK Materials and Molecular Modelling Hub, which is partly funded by the EPSRC (EP/PO20194 and EP/TO22213), for which access was obtained via the UKCP consortium (EP/PO22561/1). Some computations in this paper were performed using the University of Birmingham's BlueBEAR HPC service.References
- J. Akhavan, The Chemistry of Explosives, The Royal Society of Chemistry, 4th edn, 2022 Search PubMed.
- C. A. Handley, B. D. Lambourn, N. J. Whitworth, H. R. James and W. J. Belfield, Appl. Phys. Rev., 2018, 5, 011303 Search PubMed.
- Chemical Rocket Propulsion: A comprehensive survey of Energetic Materials, ed. L. T. De. Luca, T. Shimada, V. P. Sinditskii and M. Calabro, Springer, Cham, 2016 Search PubMed.
- S. Zeman, N. Liu, M. Jungová, A. K. Hussein and Q.-L. Yan, Def. Technol., 2018, 14, 93–98 Search PubMed.
- M. Pospíšil, P. Vávra, M. C. Concha, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 895–901 Search PubMed.
- P. Politzer and J. S. Murray, J. Mol. Model., 2014, 20, 2223 Search PubMed.
- W. Zhu and H. Xiao, Struct. Chem., 2010, 21, 657–665 Search PubMed.
- X. Song, X. Cheng, X. Yang, D. Li and R. Linghu, J. Hazard. Mater., 2008, 150, 317–321 Search PubMed.
- D. Mathieu, J. Phys. Chem. A, 2013, 117, 2253–2259 Search PubMed.
- J. S. Murray, P. Lane and P. Politzer, Mol. Phys., 1995, 85, 1–8 Search PubMed.
- B. M. Rice and J. J. Hare, J. Phys. Chem. A, 2002, 106, 1770–1783 Search PubMed.
- B. W. Asay, B. F. Henson, L. B. Smilowitz and P. M. Dickson, J. Enery Mater., 2003, 21, 223–235 Search PubMed.
- O. Bolton, L. Simke, P. F. Pagoria and A. J. Matzger, Cryst. Growth Des., 2012, 12, 4311–4314 Search PubMed.
- S. R. Kennedy and C. R. Pulham, Co-crystals: Preparation, Characterisation and Applications, ed C. B. Aakeröy and A. S. Sinha, The Royal Society of Chemistry, 2018, ch. 6, pp. 231–266 Search PubMed.
- C. S. Coffey and E. T. Toton, J. Chem. Phys., 1982, 76, 949–954 Search PubMed.
- F. J. Zerilli and E. T. Toton, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 5891–5902 Search PubMed.
- D. D. Dlott and M. D. Fayer, J. Chem. Phys., 1990, 92, 3798–3812 Search PubMed.
- S. Ye, K. Tonokura and M. Koshi, Combust. Flame, 2003, 132, 240–246 Search PubMed.
- J. Bernstein, J. Chem. Phys., 2018, 148, 084502 Search PubMed.
- V. Bondarchuk, Theory of impact sensitivity revisited: mechanical-to-vibrational energy transfer phenomenon, FirePhysChem, 2022, 2, 334–339 Search PubMed.
- X. Bidault and S. Chaudhuri, Can a shock-induced phonon up-pumping model relate to impact sensitivity of molecular crystals, polymorphs and cocrystals?, RSC Adv., 2022, 12, 31282–31292 Search PubMed.
- A. A. L. Michalchuk, M. Trestman, S. Rudić, P. Portius, P. T. Fincham, C. R. Pulham and C. A. Morrison, J. Mater. Chem. A, 2019, 7, 19539–19553 Search PubMed.
- A. A. L. Michalchuk, J. Hemingway and C. A. Morrison, J. Chem. Phys., 2021, 154, 064105 Search PubMed.
- A. A. L. Michalchuk, S. Rudić, C. R. Pulham and C. A. Morrison, Phys. Chem. Chem. Phys., 2018, 20, 29061–29069 Search PubMed.
- F. P. Bowden and A. D. Yoffe, Initiation and Growth of Explosion in Liquids and Solid, Cambridge University Press, 1952 Search PubMed.
- K. E. Field, Acc. Chem. Res., 1992, 25, 489–496 Search PubMed.
- R. M. Doherty and D. S. Watt, Propellants, Explos. Pyrotech., 2008, 33, 4–13 Search PubMed.
- I. L. Christopher, C. R. Pulham, A. A. L. Michalchuk and C. A. Morrison, J. Chem. Phys., 2023, 158, 124115 Search PubMed.
- B. P. Johnson, X. Zhou, H. Ihara and D. D. Dlott, J. Phys. Chem. A, 2020, 124, 4646–4653 Search PubMed.
- M. J. Kamlet and H. G. Adolph, Propellants, Explos. Pyrotech., 1979, 4, 30–34 Search PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., 2016, B72, 171–179 Search PubMed.
- Y. Hinuma, G. Pizzi, Y. Kumagai, F. Oba and I. Tanaka, Comput. Mater. Sci., 2017, 128, 140–184 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 Search PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 Search PubMed.
- K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114 Search PubMed.
- E. Kraka, W. Zou and Y. Tao, Decoding chemical information from vibrational spectroscopy data: Local vibrational mode theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10(5), e1480 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.01, 2016 Search PubMed.
- An overview of the RDKit—The RDKit 2024.09.5 documentation https://www.rdkit.org/docs/Overview.html Search PubMed.
- L. B. Kier and L. H. HallThe Kappa Indices for Modeling Molecular Shape and Flexibility in Topological Indices and Related Descriptors in QSAR and QSPR, ed. J. Devillers and A. T. Balaban, Gordon and Breach Science Publishers, 1999 Search PubMed.
- W. S. Wilson, D. E. Bliss, S. L. Christian and D. J. Knight, Explosive Properties of Polynitroaromatics (Defense Technical Information Center Fort Belvoir, VA 1990) Search PubMed.
- R. L. Simpson, P. A. Urtiew, D. L. Ornellas, G. L. Moody, K. J. Scribner and D. M. Hoffman, Propellants, Explos. Pyrotech., 1997, 22, 249–255 Search PubMed.
- R. L. Simpson, P. A. Urtiew, D. L. Ornellas, G. L. Moody, K. J. Scribner and D. M. Hoffman, Propellants, Explos., Pyrotech., 1997, 22, 249–255 Search PubMed.
- N. V. Latypov, J. Bergman, A. Langlet, U. Wellmar and U. Bemm, Tetrahedron, 1998, 54, 11525–11536 Search PubMed.
- C. B. Storm, J. R. Stine and J. F. Kramer, Sensitivity Relationships in Energetic Materials, in Chemistry and Physics of Energetic Materials, ed. S. N. Bulusu, Springer, Dordrecht, 1990, vol. 309 DOI:10.1007/978-94-009-2035-4_27.
- G. Hervé, C. Roussel and H. Graindorge, Angew. Chem., Int. Ed., 2010, 49, 3177–3181 Search PubMed.
- M. F. Bölter, A. Harter, T. M. Klapötke and J. Stierstorfer, ChemPlusChem, 2018, 83, 804–811 Search PubMed.
- N. V. Muravyev, D. M. Meerov, K. A. Monogarov, I. N. Melnikov, E. K. Josareva, L. L. Fershtat, A. B. Sheremetev, I. L. Dalinger, I. V. Fomenkov and A. N. Pivkina, Chem. Eng. J., 2021, 421, 129804 Search PubMed.
- I. L. Dalinger, I. A. Vatsadze, T. K. Shkineva, A. V. Kormanov, M. I. Struchkova, K. Y. Suponitsky, A. A. Bragin, K. A. Monogatoc, V. P. Sinditskii and A. B. Sheremetev, Chem. Asian J., 2015, 10, 1987–1996 Search PubMed.
- N. V. Muravyev, A. A. Bragin, K. A. Monogarov, A. S. Nikiforova, A. A. Korlyukov, I. V. Formenkov, N. I. Shishov and A. N. Pivkina, Propellants, Explos. Pyrotech., 2016, 41, 999–1005 Search PubMed.
- M.-X. Zhang, P. F. Pagoria, G. H. Imler and D. Parrish, J. Heterocycl. Chem., 2019, 56, 781–787 Search PubMed.
- C. He, J. Zhang, D. A. Parrish and J. M. Shreeve, J. Mater. Chem. A, 2013, 1, 2863–2868 Search PubMed.
- K. V. Domasevitch, I. Gospodinov, H. Krautscheid, T. M. Klapötke and J. Stierstorfer, New J. Chem., 2019, 43, 1305–1312 Search PubMed.
- N. Fischer, K. Karaghiosoff, T. M. Klapötke and J. Stierstorfer, Z. Kristall., 2010, 636, 735–749 Search PubMed.
- B. M. Rice and J. J. Hare, J. Phys. Chem. A, 2002, 106, 1770–1783 Search PubMed.
- V. W. Manner, M. J. Cawkwell, E. M. Kober, T. W. Myers, G. W. Brown, H. Tian, C. J. Snyder, R. Perriot and D. N. Preston, Chem. Sci., 2018, 9, 3649–3663 Search PubMed.
- M. L. Jones and E. Lee, J. Energ. Mater., 1997, 15, 193–204 Search PubMed.
- A. Tokmakoff, M. D. Fayer and D. D. Dlott, J. Phys. Chem., 1993, 97, 1901–1913 Search PubMed.
- V. W. Manner, M. C. Cawkwell, E. M. Kober, T. W. Myers, G. W. Brown, H. Tian, C. J. Snyder, R. Perriot and D. N. Preston, Chem. Sci., 2018, 9, 3649–3663 Search PubMed.
- M. J. Cawkwell, J. David, N. Lease, F. W. Marrs, A. Burch, S. Ferreira and V. W. Manner, ACS Phys. Chem. Au, 2022, 2, 448–458 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00852b |
| This journal is © the Owner Societies 2025 |