 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural stability of chromophore-grafted Ubiquitin mutants in vacuum†
Emiliano
De Santis
 *ab,
Thomas
Mandl
*ab,
Thomas
Mandl
 cd,
Jocky C. K.
Kung
cd,
Jocky C. K.
Kung
 efg,
Khon
Huynh
hi,
Steven
Daly
j,
Lorenza A.
D'Alessandro
efg,
Khon
Huynh
hi,
Steven
Daly
j,
Lorenza A.
D'Alessandro
 fg,
Luke
MacAleese
fg,
Luke
MacAleese
 e,
Charlotte
Uetrecht
e,
Charlotte
Uetrecht
 fg,
Erik G.
Marklund
fg,
Erik G.
Marklund
 b and
Carl
Caleman
b and
Carl
Caleman
 *ck
*ck
aDepartment of Physics, University of Rome Tor Vergata and INFN, I-00133 Rome, Italy. E-mail: edesantis@roma2.infn.it
bDepartment of Chemistry - BMC, Uppsala University, Box 576, SE-751 23 Uppsala, Sweden
cDepartment of Physics and Astronomy, Uppsala University, Box 516, SE-751 20 Uppsala, Sweden. E-mail: carl.caleman@physics.uu.se
dUniversity of Applied Sciences Technikum Wien, Höchstädtplatz 6, A-1200 Wien, Austria
eInstitut Lumière Matière (iLM), Université Claude Bernard Lyon 1 & CNRS, UMR5306, F-69100, Villeurbanne, France
fCSSB Centre for Structural Systems Biology, Deutsches Elektronen Synchroton DESY, Leibniz Institute of Virology, University of Lübeck, Notkestraße 85, 22607 Hamburg, Germany
gInstitute of Chemistry and Metabolomics, University of Lübeck, Ratzeburger Allee 160, 23562 Lübeck, Germany
hLeibniz Institute of Virology (LIV), Martinistraße 52, 20251 Hamburg, Germany
iSchool of Biomedical Engineering, International University, Vietnam National University, Ho Chi Minh City, Vietnam
jMS Vision, Televisieweg 40, 1322 AM Almere, The Netherlands
kCenter for Free-Electron Laser Science CFEL, Deutsches Elektronen-Synchrotron DESY, Notkestraße 85, 22607 Hamburg, Germany
First published on 30th May 2025
Abstract
Structural biology is witnessing a transformative era with gas-phase techniques such as native mass spectrometry (MS), ion mobility, and single-particle imaging (SPI) emerging as critical tools for studying biomolecular assemblies like protein capsids in their native states. SPI with X-ray free-electron lasers has the potential to allow for capturing atomic-resolution structures of proteins without crystallization. However, determining particle orientation during exposure remains a major challenge, compounded by the heterogeneity of the protein complexes. Gas-phase Förster resonance energy transfer (FRET) offers a promising solution to assess alignment-induced structural perturbations, providing insights into the stability of the tertiary structure under various activation methods. This study employs molecular dynamics (MD) simulations to explore chromophore integration's effect on ubiquitin's structure and alignment properties in vacuum. Ubiquitin serves as an ideal model due to its small size, well-characterized properties, and computational simplicity. By investigating chromophore placement, we identified optimal sites for monitoring gas-phase denaturation and unfolding processes, advancing SPI applications and a broader understanding of protein stability in the gas phase.
1 Introduction
Structural biology has entered an exciting era where gas-phase techniques, such as native mass spectrometry (MS), ion mobility, and single-particle imaging (SPI), are emerging as invaluable tools to study the structural dynamics of protein supramolecular assemblies, such as capsids, in their native and dynamic states. Recent advancements in SPI using X-ray free-electron lasers (XFELs) have underscored the importance of protein homogeneity in providing high-resolution structural insights. The principle of SPI lies in introducing individual protein molecules or complexes into an X-ray beam, where each is exposed to an ultrashort XFEL pulse. This pulse induces intense ionization and ultimately destroys the sample. However, the use of ultrafast pulses allows data collection from intact structures before disintegration, enabling the acquisition of single-particle X-ray scattering images.1 To build a consistent 3D dataset, hundreds of thousands of measurements have to be collected to reduce signal-to-noise ratios and achieve reliable reconstructions.2 The achievement of high-resolution SPI outcomes critically depends on the structural homogeneity of proteins introduced into the X-ray beam. The variability between individual protein molecules could pose a more significant challenge to SPI than radiation damage.3 Despite this, many feasibility studies have focused mainly on addressing radiation damage,1,4,5 with limited attention to the challenges posed by sample heterogeneity. To address this issue, the European consortium MS SPIDOC6 has proposed innovative methods to improve protein sample homogeneity for SPI experiments. These include native MS for mass selection, ion-mobility separation for conformational filtering, and the development of prototypes designed to couple with the EuXFEL.7,8 Furthermore, orienting proteins using external electric fields has been suggested to enhance SPI conditions.Both static fields8,9 and laser fields10–12 have been explored for small molecules and have recently also been applied to proteins.13 Strong alignment fields inevitably affect protein structures,14 although simulations identify experimental conditions under which alignment occurs before denaturation.15
Beyond simulations, experimental tools are needed to evaluate alignment efficiency and measure structural perturbations induced by alignment fields. This is especially important in the gas-phase, where such tools are lacking. Förster resonance energy transfer (FRET) represents a promising technique to address these challenges.16,17 On the basis of dipole–dipole interactions between donor and acceptor chromophores, FRET is highly sensitive to changes in donor–acceptor distances, making it suitable for probing the effects of alignment fields on protein structure. Gas-phase FRET18–30 and variants of FRET, including action self-quenching,31 offer potential for sensitive and efficient measurements. Notably, these techniques, when applied to strategically engineered protein mutants, could elucidate stepwise unfolding processes under various activation methods, such as collisions, electric fields, or thermal activation. The grafting of chromophores at two intentional sites within the protein can provide insight into the differential stability of tertiary substructures in the gas-phase. Therefore, a deeper understanding of how chromophores influence protein stability and structural properties in the gas-phase is essential. Although similar questions have been extensively studied in solution-phase FRET, their relevance to gas-phase systems remains underexplored. Addressing this knowledge gap could provide valuable insights into the interplay between chromophore placement, protein stability, and alignment efficiency.
In this study, we employ classical molecular dynamics (MD) simulations to investigate the impact of chromophore integration on protein structure and alignment properties in vacuum. We focus on ubiquitin, a small globular protein, for several reasons: (i) its small size allows us to explore structural effects more prominently than in larger proteins; (ii) ubiquitin is well-characterized experimentally and has been studied using FRET related techniques;23,32 and (iii) its computational simplicity and extensive literature on vacuum stability make it an ideal model.3,9,33,34 We also focus on a model with the same chromophore on both mutation sites, to mimic action self-quenching experiments31 rather than tradition FRET experiments. This reduces complexity in both simulation and in the future real-world experiments that we plan to perform. The primary questions we aim to answer are: (1) how does the integration of chromophores affect ubiquitin's structure in the gas phase? (2) what is the impact of the placement of the chromophore on the properties of the field alignment of ubiquitin? (3) which chromophore sites are optimal for monitoring gas phase denaturation and unfolding processes? By addressing these questions, we hope to establish a robust framework for studying protein stability and alignment in the gas phase, advancing the application of SPI and related techniques to structural biology.
2 Methods
We conducted a series of classical MD simulations using the amber99sb force field,35 incorporating ATTO520-cysteine adduct as the chromophore. This specific chromophore was chosen because it is known to work well in self-quenching experiments.31 The non-standard ATTO520-cysteine adduct was first geometry-optimized at the HF/6-31G* level36 in Gaussian37 with its total charge constrained to +1e. The resulting electrostatic potential was then used to fit RESP charges and used by Antechamber38 to generate GAFF atom types and bonded parameters. All atom types and bonded terms were chosen to match amber99 conventions, ensuring seamless integration with the protein force field and avoiding spurious electrostatic polarization of neighboring residues. The force field parameters for the chromophore, including its functionalization onto cysteine residues, are provided in the “ATTO520 parametrization” section in the ESI† and all associated files are available in the public repository.39The initial wild-type (WT) ubiquitin structure was obtained from the Protein Data Bank (PDB ID: 1UBQ).40 The mutants were generated by substituting, in the WT sequence, the amino acid at the position of interest with a cysteine residue, which was subsequently functionalized with the ATTO520 chromophore (Fig. 1). In each mutant, two residues were replaced by an ATTO520-tagged cysteine: residue 73 was replaced in all cases, and additionally one of the residues at position 6, 20, 35, or 48 was substituted. Accordingly, we labeled the mutants based on the non-73 replacement as ubi6, ubi20, ubi35, and ubi48.
To make the simulations similar to a potential experiment, an additional amino acid sequence of ELALVPR was added to the C-terminus of each variant. This is due to the anticipation of the necessary inclusion of a cleavable HIS-tag to the protein for production and purification purposes. This ELALVPR amino acid sequence would be left behind after purification and enzymatic cleavage reaction.
The simulation strategy we used, identical for all the simulations, is the following. First, the ubiquitin structures are relaxed by performing a steepest descent minimization followed by a 60 ns long simulation in water at physiological pH and in the isothermal–isobaric ensemble. The temperature was kept constant at 300 K by using the v-rescale thermostat41 with a 0.1 ps coupling time. Pressure was kept constant at 1 bar by using the Berendsen barostat42 with a 1 ps coupling time and an isothermal compressibility of 4.5 × 10−5 bar−1. The tip4p water model was used for water molecules.43 Periodic boundary conditions were imposed to the system and the Particle Mesh Ewald algorithm44 was employed in dealing with the long-range Coulomb interactions. The MD integration time step was 2 fs. From each of these bulk simulations, five different structures, replicas, were extracted and used as starting points for the gas-phase simulations. For each replica, we then assigned the amino acids protonation states to match the net charge expected in mass spectrometry experimental data. We thus modeled any system to have a net charge of +6e, +7e, +8e. The choice of which amino acids are most likely to be protonated in vacuo was driven by their different gas-phase basicity.45 A comprehensive list of all the amino acid charges for all the simulated systems is shown in Table 1. Relaxation in vacuum was performed using the steepest descent algorithm. We then performed 250 ps simulation with Berendsen thermostat,42 using 300 K, 400 K, 500 K, 700 K and 1000 K temperatures. Note that these “temperatures” are used purely as surrogates for increasing levels of experimental internal energy deposition and should not be taken as literal gas-phase temperatures. The MD integration time step in vacuum was 0.5 fs. Long-range electrostatic forces were captured using no cutoffs for nonbonded interactions and no periodic boundary conditions were applied. A total of 375 independent simulations were performed (five molecules, three net charges, five replicas, and five temperatures). Bulk simulations were performed using Gromacs 2019.146 simulation package. Gas-phase simulations were performed using Gromacs 4.647 compiled in double precision.
![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) , their color reflect the cartoon representation shown in Fig. 1. The location of the amino acid partial charges along the linear sequence are indicated for the three different net charges of the simulated systems. The charges are given in units of elementary charge, e
, their color reflect the cartoon representation shown in Fig. 1. The location of the amino acid partial charges along the linear sequence are indicated for the three different net charges of the simulated systems. The charges are given in units of elementary charge, e
3 Results
3.1 Validating the position of the chromophore (ATTO520) for ubiquitin
Experiments in solution have shown that adding chromophores to amino acids 6, 20, 35, 48, and 73 does not significantly affect the folding of ubiquitin, preserving a structure similar to that of the native form.23,48,49 To assess the dynamical behavior of these positions in gas-phase ubiquitin, we conducted simulations at various temperatures and compared the resulting structures. We used the same simulation protocol that was used in Mandl et al.34 We then calculated the distances between all α-carbons and compared those distances between simulations at different temperatures. This way we could predict what parts of the structures of the protein are the most dynamic, i.e. which connections in the protein would be the first ones to break. Fig. 2 shows the difference in distances between the protein simulated at 325 K and 275 K. The results clearly indicate that some parts of the protein become more dynamic with temperature than others. The regions that we found to be most dynamic are the distances between alpha carbons 5–15, 28–36, and 62–71. These findings seem to be in general agreement with earlier observations, including experimental results23 and simulations of unfolding induced by an external electric field.14,15The experimentally feasible chromophore positions (at amino acid 6, 20, 35, 48 and 73) overlap reasonably well with the protein regions our simulations identify as the most dynamics parts of the proteins, see Fig. 2. Therefore, for the rest of the study, we focused on four ubiquitin mutants (ubi6, ubi20, ubi35 and ubi48), along with WT ubiquitin. Henceforth, we will refer to both WT ubiquitin and the mutants as variants. Fig. 1 and Table 1 illustrate the variants and the positions in the sequence where the chromophores were introduced.
 | ||
| Fig. 1 Cartoon representation of ubiquitin variants structure prior to the vacuum exposure. Secondary structure elements are given, in orange, green and cyan for helix, extended and coil regions, respectively. The chromophores are shown in licorice representation. Their colors resemble the position in the linear sequence presented in Table 1. | ||
 | ||
| Fig. 2 Average distance difference between all alpha carbons in WT ubiquitin, comparing simulations at 325 K and 275 K. White markers indicate the positions where the chromophores are placed. | ||
3.2 Structural stability of the variants in vacuum
After determining the optimal locations for the chromophores, we conducted simulations involving five replicas of each variant across three distinct charge states, each simulation lasting 250 ps. To replicate the energy absorption similar to a FRET experiment and potentially provide guidance for future experiments, we conducted simulations at varying temperatures. We subsequently analyzed the final trajectories using five distinct methods, aiming to understand the stability and similarities in behavior among the different variants when in a vacuum environment. | ||
| Fig. 3 (a) In the left column, intra-variant RMSD values (extracted from the diagonal of the pairwise RMSD matrix) are plotted for each ubiquitin variant, reflecting the mean structural variability across replica simulations. In the right column, WT-referenced RMSD values, calculated relative to the wild-type structure, illustrate the divergence of each variant from the reference. In both columns, each row corresponds to a system at a distinct net charge (q = +6e, +7e, +8e), and RMSD values are plotted as a function of simulation temperature. RMSD values are expressed in Å, with lower values (<5 Å) indicating high structural similarity and higher values (>5 Å) reflecting significant divergence. The complete pairwise RMSD matrix is presented in Fig. S1 of the ESI,† while additional detailed comparisons among the replicas can be found in (Fig. S2–S16b, ESI†) global hierarchical clustering of the five ubiquitin variants using the UPGMA algorithm on the distance matrix D defined in eqn (1). Branch heights (in Å) correspond to the average Cα RMSD between variant pairs: shorter branches denote greater structural similarity. | ||
From the figures, we can clearly see that for all charge states, the simulations at temperatures up to 500 K, the average RMSD between the structures is mostly below 10 Å. Within the same mutants, the RMSD is mostly below 5 Å, showing low sample heterogeneity. This holds for all three charges.
Another general trend is that the RMSD seems to increase slightly with the charge. This is in line with experimental evidence of many gaseous proteins, including ubiquitin.51–54 This statement is not true for all proteins at all temperatures and charges, but it is true if we consider the average RMSD for all proteins at a given charge state and temperature.
To assess the overall structural relationships among our five ubiquitin variants, we first constructed a “global” distance matrix D. Each entry
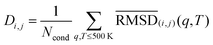 | (1) |
 denotes the average of the submatrix comparing the five frames of variant i to those of variant j under condition (q,T), and Ncond is the total number of (q,T) pairs. We chose the 500 K cutoff because our initial RMSD analyses showed that, below this temperature, all variants retained the native fold across charge states—thus focusing the clustering on biologically relevant conformational variability rather than high-temperature denaturation. This global distance matrix D was then subjected to agglomerative hierarchical clustering using the Unweighted Pair Group Method with Arithmetic Mean (UPGMA55) as implemented in the SciPy library.56 The resulting dendrogram (Fig. 3(b)) visualizes the mutual structural similarity of the five variants, with branch heights corresponding to mean–RMSD distances in Å. Across all charges and temperatures, the dendrogram shows:
denotes the average of the submatrix comparing the five frames of variant i to those of variant j under condition (q,T), and Ncond is the total number of (q,T) pairs. We chose the 500 K cutoff because our initial RMSD analyses showed that, below this temperature, all variants retained the native fold across charge states—thus focusing the clustering on biologically relevant conformational variability rather than high-temperature denaturation. This global distance matrix D was then subjected to agglomerative hierarchical clustering using the Unweighted Pair Group Method with Arithmetic Mean (UPGMA55) as implemented in the SciPy library.56 The resulting dendrogram (Fig. 3(b)) visualizes the mutual structural similarity of the five variants, with branch heights corresponding to mean–RMSD distances in Å. Across all charges and temperatures, the dendrogram shows:
• ubi35 and ubi48 form the tightest pair (smallest branch height ≈1.9 Å), indicating these two site-specific variants are most structurally similar.
• WT joins that cluster next (merge height ≈2.5 Å), showing that the native protein more closely resembles the ubi35/48 mutants than the ubi6 or ubi20 variants.
• ubi6 merges at a higher RMSD (≈4.1 Å), and ubi20 is the most divergent, joining only at the top of the tree (≈4.7 Å).
Thus, on average across all simulated conditions, ubi35 and ubi48 preserve the native fold most faithfully, while ubi6—and especially ubi20—induces the largest conformational shifts. Table 1 lists the modification sites; no obvious positional trend explains the observed deviations from WT, implying a complex interplay of local and long-range effects.
The results indicate that at temperatures up to 700 K, the distance between the chromophores is rather well defined and stable. The effect of increasing the charge state on the inter-chromophore distance is barely noticeable at 500 K (and only for mutant ubi48) and becomes more significant starting from 700 K. In other words, it is only at higher temperatures that charge-state-induced unfolding becomes significant. Overall, this suggests that the experimental selection of an arbitrary charge state (usually guided by pragmatic signal-to-noise considerations) may not be of paramount importance for experiments targeting the structural characterization of a given protein sample. This is promising for experiments measuring the chromophore distances, such as FRET performed at room temperature. At 1000 K, on the other hand, the spread in distances is wide, and it will be hard to draw any reasonable conclusion about the state of the molecule based solely on the chromophore distances. At this temperature the proteins are denaturated, and from the figure it is clear that higher charges result in a more unfolded protein.
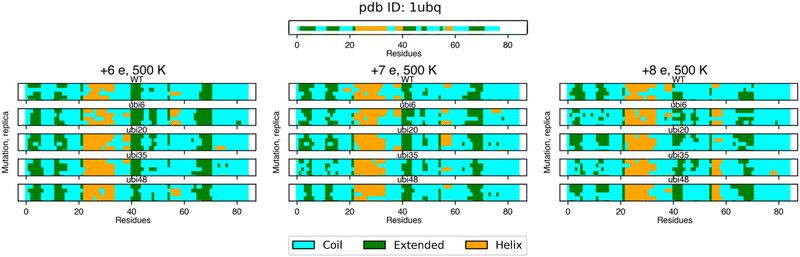 | ||
| Fig. 6 Secondary structure analysis of ubiquitin is shown for the crystal structure, PDB ID: 1UBQ (top) and simulations performed at 500 K (bottom). Each line represents a replica for a specific mutant and net charge of the systems, where coil, extended, and helix structures are depicted in cyan, green, and orange, respectively. | ||
In Fig. 8, we present the intrinsic dipole of ubiquitin as a function of time, temperature, and net charge in the simulated systems. The dipole moment ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) was computed as
was computed as  , where qi is the partial charge of atom i and
, where qi is the partial charge of atom i and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i is its position,
i is its position, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) COM is the center of mass of the protein, and N is the total number of atoms. This definition ensures translational invariance and is commonly used in simulations of charged systems.
COM is the center of mass of the protein, and N is the total number of atoms. This definition ensures translational invariance and is commonly used in simulations of charged systems.
We observe that for the cases of net charges +7e and +8e at temperatures of 300 K and 400 K, the protein's intrinsic dipole in the variants consistently surpasses that of the WT, thus confirming our speculation. In the case of a net charge of +8e, we also observed that the dipole of the mutants is larger compared to the WT at a temperature of 500 K. However, this trend is not observed for the net charge of +7e. Among the mutants, ubi48 exhibits the least influence on its dipole due to the presence of the chromophore. Thus, the dipole enhancement effect is more pronounced at high charge state and low temperature, which is interesting for experiments performed at room temperature on sample with similar dimensions as ubiquitin. This effect might nevertheless be less pronounced for larger proteins and protein complexes classically investigated by native mass spectrometry and which present typical mass and charge states both increased by 10- to 100-fold factor with regards to ubiquitin.
4 Discussion and conclusion
We have used molecular dynamics to perform gas-phase simulations of ubiquitin with the ATTO520 chromophore attached at four pairs of positions to investigate how the chromophore affects the dynamics and structure of the protein, comparing these results to the dynamics and structure of wild-type ubiquitin. We selected ubiquitin because it is a well-characterized protein and relatively small, which enabled us to simulate the aforementioned systems, each represented with three different net charges and at several temperatures. While the simulated time scales are shorter than those typically explored experimentally, they were sufficient to capture key dynamic and structural features, offering insights that are highly relevant to experimental studies.In classical molecular dynamics the charges are fixed during the simulations, and any effects caused by charge migration (due to a proton or an electron changing its position) are neglected. This includes processes such as proton hopping or charge scrambling, which are known to occur in the gas phase and can influence the detailed structure and dynamics of highly charged or partially unfolded proteins. While recent methods have begun to address such effects,63 there is currently no widely accepted or computationally efficient approach to accurately model charge mobility within standard MD frameworks. Nonetheless, fixed-charge MD simulations have been shown to offer qualitatively reliable insights into gas-phase protein behavior, particularly in capturing relative stability trends.64–67
Our simulations are also limited in the sense that they only simulate one charge distribution per total charge state, whereas in experiments over ensembles of molecules (such as mass spectrometry experiments where all ions with a given mass-to-charge ratio are simultaneously selected), multiple populations of charge distributions might be present at the same time, therefore also potentially affecting the secondary and tertiary structures of the protein, producing conformation ensembles within the same charge state. Our simulations only consider one charge distribution per molecule and charge state i.e., our model does not allow for any charge transfer, which is a limitation. However, by including an initial equilibration in solution at physiological pH, we selected charge distributions that we believe provide a realistic and representative model of experimental conditions.
Furthermore, it is worth pointing out that the applied simulation “temperatures” serve as tunable proxies for varying levels of internal vibrational energy deposition (e.g., in action-FRET experiments), rather than literal gas-phase temperatures. Because each protein's energy uptake and redistribution depend on chromophore placement, net charge, and the specifics of the excitation mechanism, there is no one-to-one mapping between an MD temperature and a precise experimental energy input, reinforcing their role as qualitative surrogates for relative activation.
Our simulations show that introducing the chromophore affects the dynamics of the protein. For all chromophore positions and charges, a general conclusion is that the structures are well kept and similar to the WT up to 500 K (moderate energy deposition).
Moreover we notice that the mutant where the distance between the two chromophores is the most affected by temperature is ubi6. At low temperatures (up to 500 K) the distance is below 20 Å, but at 1000 K (high energy deposition) the distance is around 30 Å, Fig. 5. This indicates that ubi6 might be the best mutant to use for measuring the structural stability in an FRET experiment. This conclusion holds for all charge states, but is more obvious at +7e and +8e compared to +6e. In ubi20 the chromophores are also separated by more than 30 Å at 1000 K, but since they start further apart than the chromophores in ubi6 the difference is less. Interestingly, ubi6 and ubi20 are also the mutants that show the greatest structural deviation from WT in our clustering analysis, suggesting a correlation between chromophore displacement and overall structural divergence. Judging from our simulations it is not straightforward to use chromophores at different positions in ubiquitin to monitor the temperature-induced unfolding using FRET. Our simulations do not reveal a pattern where the two chromophores in the protein are separated in a way that corresponds to their position in the amino acid sequence, at least at the temperatures when the protein structure is close the original, folded, state. At 1000 K, however the distance between the chromophores mirrors their position in amino acid chain. Adding the chromophores in general increases the dipole of the system, which could be beneficial for dipole orientation, however our simulations only show an increase for the two higher charge states (see Fig. 8). Since the structure of the proteins is not drastically affected by the presence of the chromophores, it might be a good idea to consider adding chromophores to proteins for dipole orientation.
In summary our main findings are: (i) all mutants are structurally stable at temperatures up to 500 K; (ii) below this temperature threshold, dendrogram analysis reveals that ubi35 and ubi48 retain conformations most similar to WT, while ubi20 diverges significantly; (iii) functionalization with chromophores increases the overall dipole moment without substantially altering the protein structure, making them promising tools for monitoring and potentially assisting dipole alignment in gas-phase proteins.
Author contributions
Conceptualization: CC, EDS, JCKK, LMA, EGM; methodology: CC, EDS, TM, EGM; formal analysis and investigation: CC, EDS, TM; visualization: EDS; writing – original draft: CC, EDS; writing – review & editing: All the authors contributed to the editing of the manuscript. All authors read and approved the final manuscript.Data availability
The data supporting this article have been included as part of the ESI,† or can be requested from the authors. The main software, GROMACS is available from https://www.gromacs.org.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Project grants from the Swedish Research Council (2018-00740, 2019-03935), MS SPIDOC Horizon 2020 research and innovation program (GA801406), SPIDoc's HORIZON-MSCA-2022-DN (GA101120312) and Röntgen Ångström Cluster grant provided by the Swedish Research Council and the Bundesministerium für Bildung und Forschung (2021-05988 and 05K22PSA), as well as the Helmholtz Association through the Center for Free-Electron Laser Science at DESY. The computations were enabled by resources in project UPPMAX SNIC 2018/3-476 and 2022/23-36.Notes and references
- R. Neutze, R. Wouts, D. Van der Spoel, E. Weckert and J. Hajdu, Nature, 2000, 406, 752–757 CrossRef CAS.
- E. Sobolev, S. Zolotarev, K. Giewekemeyer, J. Bielecki, K. Okamoto, H. K. Reddy, J. Andreasson, K. Ayyer, I. Barak, S. Bari, A. Barty, R. Bean, S. Bobkov, H. N. Chapman, G. Chojnowski, B. J. Daurer, K. Dörner, T. Ekeberg, L. Flückiger, O. Galzitskaya, L. Gelisio, S. Hauf, B. G. Hogue, D. A. Horke, A. Hosseinizadeh, V. Ilyin, C. Jung, C. Kim, Y. Kim, R. A. Kirian, H. Kirkwood, O. Kulyk, J. Küpper, R. Letrun, N. D. Loh, K. Lorenzen, M. Messerschmidt, K. Mühlig, A. Ourmazd, N. Raab, A. V. Rode, M. Rose, A. Round, T. Sato, R. Schubert, P. Schwander, J. A. Sellberg, M. Sikorski, A. Silenzi, C. Song, J. C. Spence, S. Stern, J. Sztuk-Dambietz, A. Teslyuk, N. Timneanu, M. Trebbin, C. Uetrecht, B. Weinhausen, G. J. Williams, P. L. Xavier, C. Xu, I. A. Vartanyants, V. S. Lamzin, A. Mancuso and F. R. Maia, Commun. Phys., 2020, 3, 97 CrossRef.
- C. Östlin, N. Timneanu, C. Caleman and A. Martin, Struct. Dyn., 2019, 6, 044103 CrossRef.
- M. Bergh, N. Tmneanu and D. van der Spoel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051904 CrossRef.
- S. P. Hau-Riege, R. A. London, G. Huldt and H. N. Chapman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061919 CrossRef.
- MS SPIDOC, https://www.ms-spidoc.eu/.
- A. Kadek, K. Lorenzen and C. Uetrecht, Drug Discovery Today: Technol., 2021, 39, 89–99 CrossRef CAS.
- T. Kierspel, A. Kadek, P. Barran, B. Bellina, A. Bijedic, M. N. Brodmerkel, J. Commandeur, C. Caleman, T. Damjanović and I. Dawod, et al. , Anal. Bioanal. Chem., 2023, 415, 4209–4220 CrossRef CAS PubMed.
- E. G. Marklund, T. Ekeberg, M. Moog, J. L. Benesch and C. Caleman, J. Phys. Chem. Lett., 2017, 8, 4540–4544 CrossRef CAS.
- S. Pabst, Eur. Phys. J.: Spec. Top., 2013, 221, 1–71 Search PubMed.
- P. Salén, M. Basini, S. Bonetti, J. Hebling, M. Krasilnikov, A. Y. Nikitin, G. Shamuilov, Z. Tibai, V. Zhaunerchyk and V. Goryashko, Phys. Rep., 2019, 836, 1–74 CrossRef.
- C. P. Koch, M. Lemeshko and D. Sugny, Rev. Mod. Phys., 2019, 91, 035005 CrossRef CAS.
- M. Amin, J.-M. Hartmann, A. K. Samanta and J. Kupper, J. Am. Chem. Soc., 2025, 147, 7445–7451 CrossRef CAS PubMed.
- A. Sinelnikova, T. Mandl, C. Östlin, O. Grånäs, M. N. Brodmerkel, E. G. Marklund and C. Caleman, Chem. Sci., 2021, 12, 2030–2038 RSC.
- A. Sinelnikova, T. Mandl, H. Agelii, O. GrÅnäs, E. G. Marklund, C. Caleman and E. De Santis, Biophys. J., 2021, 120, 3709–3717 CrossRef CAS PubMed.
- C. A. Royer, Chem. Rev., 2006, 106, 1769–1784 CrossRef CAS.
- B. Schuler and W. A. Eaton, Folding and Binding/Protein-nucleic acid interactions, 2008, vol. 18, pp. 16–26 Search PubMed.
- S. Daly, F. Poussigue, A.-L. Simon, L. MacAleese, F. Bertorelle, F. Chirot, R. Antoine and P. Dugourd, Anal. Chem., 2014, 86, 8798–8804 CrossRef CAS.
- A. Kulesza, S. Daly, L. MacAleese, R. Antoine and P. Dugourd, J. Chem. Phys., 2015, 143, 025101 CrossRef.
- S. Daly, A. Kulesza, F. Poussigue, A.-L. Simon, C. M. Choi, G. Knight, F. Chirot, L. MacAleese, R. Antoine and P. Dugourd, Chem. Sci., 2015, 6, 5040–5047 RSC.
- A. Kulesza, S. Daly, C. M. Choi, A.-L. Simon, F. Chirot, L. MacAleese, R. Antoine and P. Dugourd, Phys. Chem. Chem. Phys., 2016, 18, 9061–9069 RSC.
- S. Daly, L. MacAleese, P. Dugourd and F. Chirot, J. Am. Soc. Mass Spectrom., 2017, 29, 133–139 CrossRef.
- S. Daly, G. Knight, M. A. Halim, A. Kulesza, C. M. Choi, F. Chirot, L. MacAleese, R. Antoine and P. Dugourd, J. Am. Soc. Mass Spectrom., 2016, 28, 38–49 CrossRef.
- F. O. Talbot, A. Rullo, H. Yao and R. A. Jockusch, J. Am. Chem. Soc., 2010, 132, 16156–16164 CrossRef CAS PubMed.
- M. F. Czar, F. Zosel, I. Konig, D. Nettels, B. Wunderlich, B. Schuler, A. Zarrine-Afsar and R. A. Jockusch, Anal. Chem., 2015, 87, 7559–7565 CrossRef CAS PubMed.
- M. F. Czar and R. A. Jockusch, Curr. Opin. Struct. Biol., 2015, 34, 123–134 CrossRef CAS.
- C. Kjær, Y. Zhao, M. H. Stockett, L. Chen, K. Hansen and S. B. Nielsen, Phys. Chem. Chem. Phys., 2020, 22, 11095–11100 RSC.
- J. Langeland, T. T. Lindkvist, C. Kjær and S. B. Nielsen, Mass Spectrom. Rev., 2024, 43, 477–499 CrossRef CAS.
- R. Wu, J. B. Metternich, P. Tiwari, L. R. Benzenberg, J. A. Harrison, Q. Liu and R. Zenobi, J. Am. Chem. Soc., 2022, 144, 14441–14445 CrossRef CAS.
- R. Wu, J. B. Metternich, A. S. Kamenik, P. Tiwari, J. A. Harrison, D. Kessen, H. Akay, L. R. Benzenberg, T.-W. D. Chan, S. Riniker and R. Zenobi, Nat. Commun., 2023, 14, 2913 CrossRef CAS.
- S. Daly, C. M. Choi, F. Chirot, L. MacAleese, R. Antoine and P. Dugourd, Anal. Chem., 2017, 89, 4604–4610 CrossRef CAS PubMed.
- J. W. Lee, S. W. Heo, S. J. C. Lee, J. Y. Ko, H. Kim and H. I. Kim, J. Am. Soc. Mass Spectrom., 2012, 24, 21–29 CrossRef PubMed.
- A. Patriksson, E. Marklund and D. van der Spoel, Biochemistry, 2007, 46, 933–945 CrossRef CAS.
- T. Mandl, C. Östlin, I. E. Dawod, M. N. Brodmerkel, E. G. Marklund, A. V. Martin, N. Timneanu and C. Caleman, J. Phys. Chem. Lett., 2020, 11, 6077–6083 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins: Struct., Funct., Bioinf., 2010, 78, 1950–1958 CrossRef CAS.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Am. Chem. Soc., 2001, 222, U403 Search PubMed.
- E. De Santis, T. Mandl, J. C. K. Kung, K. Huynh, S. Daly, L. D'Alessandro, L. MacAleese, C. Uetrecht, E. G. Marklund and C. Caleman, Structural stability of chromophore-grafted Ubiquitin mutants in vacuum, 2025 DOI:10.5281/zenodo.15270985.
- S. Vijay-Kumar, C. E. Bugg and W. J. Cook, J. Mol. Biol., 1987, 194, 531–544 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. Berendsen, J. v Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- R. Marchese, R. Grandori, P. Carloni and S. Raugei, PLoS Comput. Biol., 2010, 6, e1000775 CrossRef PubMed.
- Lindahl, Abraham, Hess and van der Spoel, GROMACS 2019.1 Manual, 2019.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS.
- J.-r Huang and S. Grzesiek, J. Am. Chem. Soc., 2010, 132, 694–705 CrossRef CAS.
- M. Aznauryan, L. Delgado, A. Soranno, D. Nettels, J.-R. Huang, A. M. Labhardt, S. Grzesiek and B. Schuler, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E5389–E5398 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, et al. , J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- S. Daly, G. Knight, M. A. Halim, A. Kulesza, C. M. Choi, F. Chirot, L. MacAleese, R. Antoine and P. Dugourd, J. Am. Soc. Mass Spectrom., 2017, 28, 38–49 CrossRef CAS PubMed.
- S. J. Valentine, A. E. Counterman and D. E. Clemmer, J. Am. Soc. Mass Spectrom., 1997, 8, 954–961 CrossRef CAS.
- K. Breuker, H. Oh, D. M. Horn, B. A. Cerda and F. W. McLafferty, J. Am. Chem. Soc., 2002, 124, 6407–6420 CrossRef CAS PubMed.
- T. Wyttenbach and M. T. Bowers, J. Phys. Chem. B, 2011, 115, 12266–12275 CrossRef CAS.
- D. Müllner, arXiv, 2011, preprint, arXiv:1109.2378 DOI:10.48550/arXiv.1109.2378.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS.
- W. Kabsch and C. Sander, Biopolymers, 1983, 22, 2577–2637 CrossRef CAS.
- M. Heinig and D. Frishman, Nucleic Acids Res., 2004, 32, W500–W502 CrossRef CAS.
- B. Brutscher, R. Brüschweiler and R. R. Ernst, Biochemistry, 1997, 36, 13043–13053 CrossRef CAS.
- M. N. Brodmerkel, E. De Santis, C. Caleman and E. G. Marklund, Protein J., 2023, 42, 205–218 CrossRef CAS PubMed.
- H. Agelii, E. L. Jakobsson, E. De Santis, G. Elfrink, T. Mandl, E. Marklund and C. Caleman, Phys. Chem. Chem. Phys., 2025 10.1039/D5CP00073D.
- A. Wollter, E. De Santis, T. Ekeberg, E. G. Marklund and C. Caleman, J. Chem. Phys., 2024, 160, 114108 CrossRef CAS.
- L. Konermann, J. Phys. Chem. B, 2017, 121, 8102–8112 CrossRef CAS PubMed.
- M. Landreh, E. G. Marklund, P. Uzdavinys, M. T. Degiacomi, M. Coincon, J. Gault, K. Gupta, I. Liko, J. L. Benesch and D. Drew, et al. , Nat. Commun., 2017, 8, 13993 CrossRef CAS PubMed.
- M. N. Brodmerkel, L. Thiede, E. De Santis, C. Uetrecht, C. Caleman and E. G. Marklund, Phys. Chem. Chem. Phys., 2024, 26, 13094–13105 RSC.
- H. M. Britt, T. Cragnolini and K. Thalassinos, Chem. Rev., 2021, 122, 7952–7986 CrossRef.
- M. L. Abramsson, C. Sahin, J. T. Hopper, R. M. Branca, J. Danielsson, M. Xu, S. A. Chandler, N. Osterlund, L. L. Ilag and A. Leppert, et al. , JACS Au, 2021, 1, 2385–2393 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01297j |
| This journal is © the Owner Societies 2025 |





