Quantum-mechanical treatment of thermal effects on the structure and ¹³C NMR shielding of buckminsterfullerene C₆₀

Abstract

We investigate thermal effects on the structure and ¹³C nuclear magnetic resonance (NMR) shielding of buckminsterfullerene, C₆₀, using a quantum-mechanical treatment of thermal rovibrational motion at the density functional theory (DFT) level. Volumes calculated from the temperature-dependent effective geometries confirm that C₆₀ fullerene indeed experiences negative thermal expansion (NTE). However, the NTE is much smaller and occurs at temperatures higher than previously predicted by classical MD simulations, above T = 100 K. The normal mode analysis of the contributions to the effective geometry reveals that the NTE is caused by a single low-frequency, fully symmetric, A_g(1) breathing mode instead of previously alleged quadrupolar modes. Although the effect of centrifugal distortion on the A_g(1) mode monotonically increases the volume of C₆₀ at finite temperatures, the NTE is caused by the negative anharmonic vibrational correction that activates above T = 100 K and reaches a minimum around T = 320 K. The validity of the current rovibrational approach is further confirmed by good agreement with the experimental results of temperature dependence of ¹³C NMR shielding as well as its secondary isotope shifts. For them, the harmonic vibrational correction is the main contribution and also plays a dominant role in thermal effects,whereas the effective geometry contributionis smaller. The temperature dependence of the harmonic vibrational correction is due to several low-frequency normal modes different from A_g(1), and therefore, the NTE is not observed in ¹³C NMR shielding and isotope shifts.

---

1. Introduction

Buckminsterfullerene, C₆₀, is a naturally occurring fullerene, which can be produced by common phenomena, such as flames,^1,2 but is also created by lightning strikes³ or meteor impacts.^4,5 Due to its icosahedral I_h symmetry point group,⁶ it is also easier than other fullerenes to study computationally. Consequently, it is regularly studied as a simple model system of fullerenes and other carbon nanostructures that have many interesting properties, such as their electric^7–9 and thermal^10–12 conductivities.

An intriguing property of C₆₀ is the negative thermal expansion (NTE), suggested by Kwon et al.,^13,14 i.e. shrinking when heated as opposed to most materials that expand as temperature increases. Kwon et al. carried out classical molecular dynamics (MD) simulations and predicted the NTE in C₆₀ well below room temperature, and the minimum volume was found around T = 150 K. However, these results were claimed to be accidental due to the absence of quantum mechanical effects.¹⁵ Furthermore, in classical MD simulations of C₆₀ by Chen et al.,¹⁶ the NTE was observed only with a single sampling frequency of the average sampling method used by Kwon et al., while other sampling frequencies and methods lead to a monotonic positive thermal expansion in all temperature ranges.

Several experimental studies of C₆₀ using IR, Raman, and X-ray methods have claimed to see signs of NTE.^17–19 Other methods, such as nuclear magnetic resonance (NMR) spectroscopy, might offer an additional insight into the NTE. NMR is very sensitive to the local structural and chemical environment of the observed magnetic nucleus without interfering with molecular processes. However, while phase transitions of solid C₆₀ have been studied by ¹³C NMR,²⁰ there has been no study on the NTE in fullerenes. Although there are also no computational studies on the thermal effects of ¹³C NMR, there are some studies on ¹³C NMR shielding, σ(¹³C), of fullerenes in static geometries.^21–24

Here, we carry out, to our knowledge, for the first time, a quantum-mechanical (QM) rovibrational thermal averaging of the C₆₀ structure and ¹³C NMR shielding at both absolute zero and finite temperatures. The chosen approach provides a definitive answer to the existence and size of NTE in C₆₀ as well as a detailed normal-mode analysis of its vibrational origin.

Furthermore, the approach used enables studying another interesting property of C₆₀, the two small peaks observed next to the main peak in its solution state ¹³C NMR spectrum.²⁵ These side peaks are caused by the so-called secondary isotope shift in two isotopomers, in which another ¹³C atom shares a bond, as seen in Fig. 1, either between two hexagon rings ([HH–¹³C₂]–C₆₀) or a hexagon ring and a pentagon ring ([HP–¹³C₂]–C₆₀). Isotope shifts have been experimentally observed for a long time.^26–28 They are purely QM parameters, i.e., they cannot be treated classically and therefore require the rovibrational QM treatment of NMR shielding,^29,30 which provides quantitative primary and secondary isotope shifts in small molecules.^31–35 However, the secondary isotope shifts of C₆₀ have not been studied computationally before. Here, we confirm the magnitude and temperature dependence of the experimental isotope shifts and, more importantly, reveal the degrees of freedom behind these effects by normal mode analysis. Furthermore, we study if the NTE has an effect on ¹³C NMR shielding and isotope shifts.

Fig. 1 Structure of C₆₀ with the atoms changed to ¹³C in different isotopomers pictured in gold colour and ¹²C in light blue colour. Hexagon (H) and pentagon (P) rings are named to illustrate the positions of HH and HP bonds at their edges.

2. Methodology

2.1. Rovibrational averaging

Although thermal effects on molecular geometry, NMR shielding, and isotope shifts could be treated with Taylor expansion around the equilibrium geometry;^29–35 another way is to first generate the temperature-dependent effective geometry Q^eff_K at zero and finite temperatures^36,37 as follows:where Q^eq_K is the normal coordinate K with a harmonic frequency ω_K, F^eq_KLL is the third derivative of the electronic energy with respect to normal coordinates K, L computed at equilibrium geometry (eq), and k_B is the Boltzmann constant. The hyperbolic cotangent function takes care of the finite temperature Boltzmann averaging over vibrational states. The last term is the centrifugal distortion effect,^37,38 where I_αα is the moment-of-inertia tensor at the equilibrium geometry and a^(αα)_K is the expansion coefficient of I_αα in the normal coordinate Q_K. Effective geometries Q^eff_K therefore cover the NTE on the volume of C₆₀.

A molecular property, such as NMR shielding σ_eff, computed at a fixed effective geometry contains the leading-order anharmonic rovibrational effects. However, temperature-dependent harmonic vibrational corrections computed at the same effective geometry are needed to obtain the full leading-order thermally averaged shielding^37–40

The effective geometry Q^eff_K represents the average structure of the molecule at a given temperature, accounting for both vibrational anharmonicity and centrifugal distortion effects. Physically, it captures how thermal and zero-point motions shift nuclear positions away from their equilibrium values, thereby influencing geometry-sensitive properties like NMR shielding. Eqn (1) includes contributions from third-order force constants, which introduce anharmonicity, and from rotational averaging via the centrifugal term. Calculating NMR shielding at this effective geometry yields σ_eff, which reflects the geometry-driven component of thermal shifts. To obtain the full leading-order temperature-dependent shielding, an additional vibrational correction is added, as in eqn (2), where the second derivatives of shielding with respect to normal modes capture the explicit vibrational averaging over thermally populated states.

2.2. Isotope shifts

Changing isotopic masses of the atoms affects their thermal motions, which is accounted for in the normal mode frequencies and moment-of-inertia tensors of vibrational and centrifugal distortion corrections of the rovibrational treatment, respectively. Therefore, thermal averages of ¹³C NMR shielding, σ^13C, for different isotopomers^33–35 enable computing secondary isotope shifts of experimentally observed ¹³C NMR chemical shifts, δ^13C, in the C₆₀ fullerene²⁵i.e. the shielding (chemical shift) differences between the main [¹³C₁]–C₆₀ isotopomer with a single ¹³C atom and two different isotopomers with two ¹³C atoms that share either a HH bond ([HH–¹³C₂]–C₆₀) or a HP bond ([HP–¹³C₂]–C₆₀) (see Fig. 1).

2.3. Electronic structure calculations

Electronic structure calculations of the three ¹³C isotopomers of C₆₀, [¹³C₁]–C₆₀, [HH–¹³C₂]–C₆₀ and [HP–¹³C₂]–C₆₀, were performed at the level of non-relativistic density functional theory (DFT) using the Dalton code,^41,42 which was chosen because it uniquely supports rovibrational averaging at finite temperatures of both the molecular structure and properties, such as nuclear magnetic shielding, within a single framework and consistent theoretical treatment. For the three isotopomers, the optimization of the structure, the calculation of the effective geometry and the NMR shielding calculations were performed without symmetry using the PBE0 functional^43,44 with the pcSseg-1 basis set.⁴⁵ The effective geometries in eqn (1) were calculated at several temperatures ranging from 0 K to 500 K. The effects of different DFT functionals and basis sets were also studied, and the results are presented in the ESI.† From these tests, we learned that, with a pure DFT functional, PBE, the temperature dependence of contributions from the vibrational normal modes is not consistent between the isotopomers, prompting us to use a hybrid PBE0 functional. The basis set used was the largest in its basis set family that did not encounter SCF convergence issues due to linear dependencies in the test calculations.

2.4. Structure and NMR shielding analysis

The Turbomole code^46,47 was used to verify that the optimized equilibrium structure of C₆₀ was in the correct icosahedral I_h symmetry before being used as starting equilibrium geometries for the calculations of the three ¹³C isotopomers of C₆₀ with the Dalton code. Furthermore, the normal modes of the Dalton calculations were assigned by comparing their frequencies with those obtained using the Turbomole code at the same level of theory for the I_h symmetric ¹²C isotopomer of C₆₀.

The volume of C₆₀ as a function of temperature was extracted from the corresponding effective geometries at each temperature. The details of the volume calculation are explained in the ESI.† The volume data also allowed the derivation of the volumetric thermal expansion coefficient 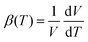that is listed and discussed in the ESI.† The origins of the C₆₀ volume changes due to vibrational and centrifugal effects are analyzed in terms of contributions from different normal modes according to eqn (1).

The harmonic vibrational corrections on the ¹³C shielding constant in eqn (2) were carried out at effective geometries and added to the value of σ_eff for each isotopomer in temperatures between 0 K and 400 K. Thermal effects on ¹³C shielding and secondary isotope shifts due to effective geometry and harmonic vibrational corrections are also analyzed in terms of normal mode contributions. The effect of temperature on the ¹³C NMR chemical shift is discussed in the ESI.†

3. Results

3.1. Volume changes

The absolute volume changes of the three different C₆₀ isotopomers and their relative volume changes with respect to the values of T = 0 K are presented in Fig. 2(a) and (b), respectively. As seen in Fig. 2(a), the heavier [HH–¹³C₂]–C₆₀ and [HP–¹³C₂]–C₆₀ isotopomers with two ¹³C atoms have volumes quite similar at all temperatures and are clearly smaller than those of the main isotopomer [¹³C₁]–C₆₀ with only one ¹³C atom. This is expected since heavy isotope substitution shortens the bonds⁴⁸ and consequently shrinks the C₆₀ cage. However, as seen in Fig. 2(b), the relative volume change with respect to T = 0 K is very similar in all isotopomers throughout the temperature range, indicating that the temperature dependence of the NMR isotope shift (vide infra) does not reflect volume changes.

Fig. 2 (a) Temperature dependence of the absolute volume in the three studied C₆₀ isotopomers. Inset: The contribution of the A_g(1) normal mode. (b) Temperature dependence of relative volumes (ΔV/V₀ = (V − V₀)/V₀) of each isotopomer with respect to the volumes at T = 0 K. Inset: The relative change in different contributions, vibrational (vibr.) and centrifugal (centr.) to the main A_g(1) normal mode contribution of ¹³C₁ isotopomer.

The most important observation is that the C₆₀ molecule clearly exhibits negative thermal expansion (NTE). At very low temperatures, the volume of C₆₀ increases, but the NTE begins around T = 100 K. It continues until T = 320 K, where the minimum volume of the C₆₀ molecule is reached and the normal positive thermal expansion recovers.

A closer inspection of the contributions to the effective geometry by vibrational normal modes can be found in the ESI.† It reveals that contributions of only a few normal modes have a considerable effect on effective geometry and hence volume changes. As shown in Fig. S2 in the ESI,† by far the largest effective geometry correction is due to the mode number 148, which is a nondegenerate, Raman active, fully symmetric, radial A_g(1) mode.⁴⁹ As seen in Fig. S3 in the ESI,† it is clearly the only mode that has the same temperature trend as the relative volume change shown in Fig. 2(a). The effective geometry correction due to this low-frequency mode (calculated, 505.9 cm⁻¹ vs. experimental, 500.9 cm⁻¹ (ref. 50)) is the only one significantly affected by the centrifugal distortion effect (CDE) as shown in the inset of Fig. 2(b). The CDE begins to increase linearly immediately above T = 0 K, which is the sole reason for the increase in the volume of C₆₀ at low temperatures because all the anharmonic vibrational contributions are frozen. The first vibrational effect activated is the A_g(1) contribution to the effective geometry at T ≈ 100 K. As shown in Fig. 2(b), it first gives a negative change to the effective geometry, and being a radial mode, it causes shrinkage of the carbon cage. This continues up to T = 320 K, where the minimum volume is also reached. The trend of the A_g(1) term is then reversed and contributes to the normal, positive, thermal expansion of C₆₀ at higher temperatures, above T = 320 K. At high temperatures, the monotonically increasing CDE on the A_g(1) mode gives a considerable contribution.

Although the effective geometry corrections of the other normal modes are activated around T = 100 K, they start to show some significance only above T = 200 K. They behave systematically; i.e., the either negative or positive contribution increases monotonically with temperature. The second most T-dependent normal mode contribution is the other A_g(2) mode (18, calculated, 1511.4 cm⁻¹ vs. experimental, 1472.4 cm⁻¹ (ref. 50)). However, the volume of C₆₀ seems not to be affected much by the other than A_g(1) mode. This indicates that the other modes do not change the average radius of the C₆₀ cage due to their tangential nature or the mutual cancellation of their small radial contributions.

The results clearly show that the thermal effects on the C₆₀ geometry are due to quantum mechanical modes that are frozen at low temperatures. Therefore, the NTE of C₆₀ cannot be described by classical MD simulations, such as those of Kwon et al.,¹³ in which the NTE starts immediately above T = 0 K and a minimum volume is already reached at ca. T = 150 K, well below the currently observed T = 320 K. In addition, the magnitude of the relative volume change is much greater, ca. −1 × 10⁻³, than the current observation of about −4.5 × 10⁻⁵. Furthermore, Kwon et al.¹³ found that the softest quadrupolar normal modes in the ω ≈ 200 m⁻¹ region are responsible for the NTE. This is not supported by the current QM treatment, in which the effective geometry corrections of the softest 5-fold degenerate H_g quadrupolar normal modes⁵¹ (modes 170–174, calculated, 268 cm⁻¹ vs. experimental, 277.2 cm⁻¹ (ref. 50)) behave monotonically and are negligible above T = 200 K.

The anomalous softening trend (decreasing frequency) with decreasing temperature of the T_1u(1) mode (calculated, 533 cm⁻¹ vs. experimental 526.2 cm⁻¹ (ref. 50)) observed with high-resolution far infrared spectroscopy (IR) was connected to NTE by Brown et al.¹⁸ The current QM analysis shows that the effective geometry correction corresponding to the T_1u(1) mode has practically no temperature dependence. Therefore, the observed softening of the T_1u(1) mode has no direct connection with the NTE and may only have an indirect dependence on it.

The other phenomenon observed experimentally, which is related to the possible NTE of the C₆₀ cage, is the decrease of the distance between the carbon and the endohedral noble gas atom observed by extended X-ray absorption fine structure (EXAFS) of Ar¹⁹ or Kr^17,18 at the K edge. The shortening of Ar–C and Kr–C distances with increasing temperature is quite significant. As it is interpreted to be due to the shrinkage of the carbon cage, the estimated negative thermal expansion coefficient is also quite large, β ≈ −10⁻⁵ K⁻¹. This is an order of magnitude larger than the current one, β = −0.411 × 10⁻⁶ K⁻¹ (see the ESI†). Therefore, instead of resulting from the shrinkage of the cage, the decrease of the Ar/Kr–C distance can be alternatively explained to be due to the increasing thermal motion of the noble gas atom, which brings it on average closer to the carbon atoms and therefore leads to an overestimation of the negative coefficient β.

In conclusion, the current QM rovibrational treatment at the first principles DFT level shows unequivocally that the decrease of the C₆₀ volume, i.e., NTE, in the temperature range of T = 100–320 K as well as a large part of normal thermal expansion at higher temperatures, is due to the effective geometry correction in the A_g(1) normal mode and is dominated by the anharmonic vibrational contribution.

3.2. Temperature dependence of the ¹³C NMR shielding constant

The temperature dependence of the ¹³C NMR shielding constant in the [¹³C₁]–C₆₀ isotopomer is shown in Fig. 3. The zero-point vibrational (ZPV) correction on shielding is −3.46 ppm (σ^r_e = 37.27 ppm and σ^T=0K = 33.81 ppm), of which −1.08 ppm is due to anharmonic vibrational contributions to the effective geometry since the centrifugal distortion effect (CDE) is absent at absolute zero temperature. The larger portion of the ZPV correction, −2.39 ppm, comes from the harmonic vibrational correction to shielding at the effective geometry.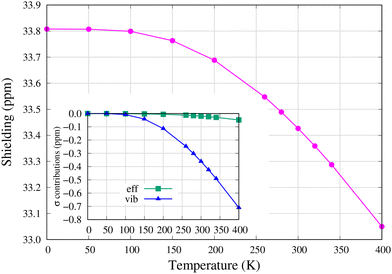

Fig. 3 ¹³C NMR shielding constant in the [¹³C₁]–C₆₀ isotopomer. The effective geometry (eff) and vibrational (vib) contributions with respect to their T = 0 K values are displayed in the inset. The absolute values are found in Table S3 in the ESI.†

Temperature has hardly any effect on shielding below T ≈ 100 K, but negative harmonic vibrational corrections (vib) dominate the monotonic decrease in ¹³C shielding at higher temperatures. As seen in the inset of Fig. 3, the contribution of effective geometry (eff) only slightly adds to the decrease at temperatures higher than T = 200 K. In the temperature interval T = 260–300 K, the temperature derivative of ¹³C shielding, dσ_C/dT = −3.02 × 10⁻³ ppm K⁻¹, has a somewhat greater magnitude than the experimental value for the ¹³C NMR chemical shift in C₆₀, dδ_C/dT = 1.88 × 10⁻³ ppm K⁻¹ (opposite sign due to the definition of the chemical shift, δ = σ_ref − σ).²⁰ The difference is at least partly due to intermolecular interactions in solid-state NMR experiments as well as thermal effects on the shielding of the reference compound (see the ESI†).

Obviously, as shown in Fig. 3, ¹³C NMR shielding is not affected by NTE. The dominant harmonic vibrational correction (vib) to ¹³C NMR shielding, the second term in eqn (2), has several normal mode contributions with considerable magnitude and temperature dependence (see Fig. S5 and Table S6 in the ESI†). However, the contribution due to A_g(1) is not one of them and therefore ¹³C NMR shielding is not affected by it. This also explains why NTE features are not present in the very small effective geometry (eff) contribution in Fig. 3.

Generally, the substitution of the ¹³C isotope removes the I_h symmetry and, hence, the degeneracy of several normal modes. In particular, a large frequency change is observed in the mode with a large effect on ¹³C shielding. Most of the harmonic vibrational normal mode contributions, especially the high-frequency ones, do not depend much on temperature. However, there is considerable dependence in many modes below 800 cm⁻¹, which cover over 85% of the temperature effect. Of them, the 10 most important modes are shown in Fig. S5(a and c) in the ESI.† These are quite low-frequency modes below 600 cm⁻¹ with radial character that changes the local geometry around the ¹³C atom. Only one of them, the soft H_g mode 173, also belongs to the 10 largest contributions as shown in Fig. S5(b and d) in the ESI.†

Generally, the magnitudes of the individual normal mode contributions are quite small, at most a few percent of the total harmonic vibrational correction. The high-frequency mode 30, one of the five Raman-active H_g modes, gives the largest ca. +5% contribution. It has a lower frequency than the other H_g modes (1465 → 1458 cm⁻¹) due to ¹³C isotopic substitution. However, it is not affected much by temperature as seen in Fig. S5(d) in the ESI.† One of the three T_1g modes (mode 83) also experiences a considerable frequency change (845 → 751 cm⁻¹) and gives the greatest negative contribution, ca. −5%. Another large frequency change (803 → 780 cm⁻¹) is seen in mode 86, one of the three T_2g symmetry modes with large negative contributions. Both these T_1g and T_2g modes have a strong tangential character and cause large changes in local bond lengths and angles around the ¹³C atom, leading to a large harmonic vibrational contribution to shielding.

3.3. Secondary isotope shifts

The temperature dependence of the calculated ¹Δ_HH (eqn (3)) and ¹Δ_HP (eqn (4)) isotope shifts is compared with the experimental results of Bacanu et al.²⁵ in Fig. 4. Furthermore, their effective geometry and harmonic vibrational contributions are displayed. Although the current rovibrational treatment slightly underestimates isotope shifts, they have the correct sign and magnitude. In particular, the temperature behavior is very close to the experimental observations in the temperature interval of T = 260–340 K, as, for example, the temperature derivative of the HH isotope shift, d¹Δ_HH/dT = −17.29 × 10⁻³ ppb K⁻¹ (vib: −12.11 × 10⁻³ ppb K⁻¹, eff: −5.18 × 10⁻³ ppb K⁻¹), is in excellent agreement with the experimental result, −17.38 × 10⁻³ ppb K⁻¹.²⁵ While also the temperature derivative of the HP isotope shift, d¹Δ_HP/dT = −16.93 × 10⁻³ ppb K⁻¹ (vib: −14.26 × 10⁻³ ppb K⁻¹, eff: −2.68 × 10⁻³ ppb K⁻¹) is only slightly overestimated (exp: −12.47 × 10⁻³ ppb K⁻¹ (ref. 25)), and there is good overall compatibility with the experimental data. Isotope shifts are computationally very demanding, purely quantum mechanical properties that are sensitive to both the chosen DFT functional and the basis set (see the ESI†). These results further confirm that the rovibrational method used is capable of adequately treating thermal effects on C₆₀.

Fig. 4 Contributions from effective geometry (eff, green) and harmonic vibrational corrections (vib, blue) to the total calculated isotope shift (total, magenta) compared with experimental (exp, black) values for the (a) ¹Δ_HH isotope shift in eqn (3) and (b) ¹Δ_HP isotope shift in eqn (4). The experimental data are from the study by Bacanu et al.²⁵

Although the overall agreement between the theory and the experiment is very good, especially in terms of the temperature derivatives and qualitative trends, small quantitative discrepancies remain. In particular, the absolute values of the computed isotope shifts are slightly underestimated across the temperature range. These differences may arise from limitations in the level of theory employed. Isotope shifts are highly sensitive to subtle changes in the potential energy surface, which is affected by the incompleteness of the basis set as well as deficiencies in the description of the electron correlation by the chosen DFT functional.^33–35 It is also shown that the neglect of higher-order anharmonicity does not have a significant effect on property averages.^36,52 Furthermore, the experimental data reflect the liquid-phase environment of C₆₀, while the current calculations are for isolated molecules. Although the temperature dependence of the NMR chemical shift is affected by solvent effects, they cancel out in isotope shifts that are dominated by intramolecular phenomena.^33–35 Despite these sources of uncertainty, the excellent match in temperature dependence suggests that the main physical mechanisms are correctly captured by the rovibrational averaging approach.

As seen in Fig. 4, the temperature dependence of both isotope shifts and their contributions is significant only above T = 100 K, which is very similar to the behavior of ¹³C shielding. Therefore, below T = 100 K, the values are close to the values at absolute zero, 12.4 ppb (¹Δ_HH) and 8.9 ppb (¹Δ_HP). By adding the difference with respect to the experimental values at room temperature as a correction, we can estimate the isotope shifts at absolute zero (T = 0 K) to be about 22 ppb and 14 ppb, respectively.

A clear NTE effect, a small “bump” in the T = 150–350 K interval, is seen in the small negative and positive, respectively, effective geometry contributions for ¹Δ_HH and ¹Δ_HP. However, it is not visible in the total isotope shifts as a result of larger and more temperature-dependent harmonic vibrational correction. The latter decreases linearly above T = 100 K, and the NTE contribution only slightly increases the non-linearity of the total temperature dependence of both isotope shifts.

Changes in contributions from different normal modes are displayed in Fig. S8 in the ESI.† In contrast to shielding with predominantly negative contributions of different normal modes, isotope shifts obtain large contributions, both positive and negative, which largely cancel each other out. Therefore, no individual mode can be assigned to cause the isotope shift or its temperature dependence. Although several high-frequency modes give large contributions, thermal effects are mainly due to low-frequency modes. All modes that have a high impact on isotope shifts also contribute significantly to shielding. However, the effects of some modes with significant roles in shielding, such as previously mentioned normal modes 83 and 86, largely cancel each other out in both isotope shifts. Cancellation also occurs within contributions from similar modes, i.e., the degenerate modes with the same symmetry in I_h.

Unlike the case for shielding or NTE, isotope shifts arise from more distributed vibrational contributions, with many modes contributing in opposite directions. This results in partial cancellations and makes direct mode-by-mode interpretation less meaningful for these parameters.

4. Conclusions

We have carried out first-principles rovibrational modeling of thermal effects on buckminsterfullerene C₆₀. The fully quantum-mechanical treatment provides effective geometries at finite temperatures affected by anharmonicity of the potential-energy hypersurface as well as centrifugal distortion due to the rotation of the fullerene cage. The approach enabled us to estimate volume changes at finite temperatures with respect to the absolute zero-point reference value. Harmonic vibrational corrections to the ¹³C NMR shielding were calculated in effective geometries of the three C₆₀ isotopomers studied to obtain the temperature dependence of both the ¹³C NMR shielding and its isotope shifts.

We observe the negative thermal expansion (NTE) of fullerenes caused solely by anharmonic vibrational effects due to the totally symmetric A_g(1) “breathing” normal mode. It is frozen below T = 100 K, and causes the NTE until T = 320 K. Centrifugal distortion affects through the same A_g(1) mode and causes a monotonic increase of volume with temperature. The other normal modes only add to the positive thermal expansion at high temperatures, above T = 200 K. In conclusion, the current quantum-mechanical treatment generates a considerably smaller NTE at much higher temperatures and is not dependent on the soft quadrupolar phonon modes, as previously predicted with classical MD simulations.¹³

The temperature dependence of ¹³C NMR shielding for an isolated C₆₀ molecule is qualitatively in agreement with the experimental results for the ¹³C chemical shift affected by environmental effects.²⁰ Furthermore, the observed trends in the temperature dependence of the two ¹³C secondary isotope shifts match well with the experimental observations.²⁵ Zero point vibrational (ZPV) corrections as well as thermal effects on the ¹³C shielding and its isotope shifts are dominated by harmonic vibrational corrections. The smaller effective geometry contributions are quite insensitive to temperature, and the NTE has no effect on the ¹³C shielding. Although the effective geometry contributions to both ¹³C isotope shifts are affected by NTE, it is hidden behind the larger temperature effects due to harmonic vibrational corrections. Several high-frequency normal modes are among the main contributors to the magnitudes of ¹³C shielding and its isotope shifts, whereas the temperature dependence is affected mainly by low-frequency modes.

In summary, the current study underscores the quantum-mechanical nature of thermal effects on the structure and NMR parameters of molecules. Therefore, these phenomena cannot be treated classically, and either the current rovibrational approach or the quantum path-integral simulations are necessary.

Author contributions

Tiia Jacklin: data curation, formal analysis, investigation, visualization, writing – original draft, and writing – review and editing. Petr Štěpánek: supervision and writing – review and editing. Perttu Lantto: conceptualization, funding acquisition, project administration, resources, supervision, and writing – review and editing.

Data availability

The curated data supporting this article have been included as part of the ESI.† The raw data for this article, including input and output files of the calculations are available at https://doi.org/10.23729/fd-729f01ad-f7e2-3b76-a5bb-2bb17520c465.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support from the Research Council of Finland (grant no. 354575) and the Kvantum Institute, University of Oulu. The authors thank Juha Vaara for insightful discussions. The authors also thank George Bacanu for providing the experimental reference values for the secondary isotope shifts. The computational resources were provided by CSC – IT Center for Science (Espoo, Finland) and the Finnish Grid and Cloud Infrastructure project (persistent identifier url: urn:nbn:fi:research-infras-2016072533).

References

1. J. B. Howard, J. T. McKinnon, Y. Makarovsky, A. L. Lafleur and M. E. Johnson, Nature, 1991, 352, 139–141.
2. J. B. Howard, A. L. Lafleur, Y. Makarovsky, S. Mitra, C. J. Pope and T. K. Yadav, Carbon, 1992, 30, 1183–1201.
3. T. K. Daly, P. R. Buseck, P. Williams and C. F. Lewis, Science, 1993, 259, 1599–1601.
4. F. Radicati di Brozolo, T. E. Bunch, R. H. Fleming and J. Macklin, Nature, 1994, 369, 37–40.
5. L. Becker, J. L. Bada, R. E. Winans, J. E. Hunt, T. E. Bunch and B. M. French, Science, 1994, 265, 642–645.
6. R. D. Johnson, G. Meijer and D. S. Bethune, J. Am. Chem. Soc., 1990, 112, 8983–8984.
7. T. Arai, Y. Murakami, H. Suematsu, K. Kikuchi, Y. Achiba and I. Ikemoto, Solid State Commun., 1992, 84, 827–829.
8. A. Hamed, Y. Sun, Y. Tao, R. Meng and P. Hor, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 10873.
9. S. Kazaoui, R. Ross and N. Minami, Solid State Commun., 1994, 90, 623–628.
10. J. Olson, K. Topp and R. Pohl, Science, 1993, 259, 1145–1148.
11. X. Wang, C. D. Liman, N. D. Treat, M. L. Chabinyc and D. G. Cahill, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 075310.
12. A. Giri and P. E. Hopkins, J. Phys. Chem. Lett., 2017, 8, 2153–2157.
13. Y.-K. Kwon, S. Berber and D. Tománek, Phys. Rev. Lett., 2004, 92, 015901.
14. Y.-K. Kwon, S. Berber and D. Tománek, Phys. Rev. Lett., 2005, 94, 209702.
15. P. Keblinski and P. K. Schelling, Phys. Rev. Lett., 2005, 94, 209701.
16. W.-H. Chen, C.-H. Wu and H.-C. Cheng, Comput. Mater. Contin., 2011, 25, 195–214.
17. S. Ito, A. Takeda, T. Miyazaki, Y. Yokoyama, M. Saunders, R. J. Cross, H. Takagi, P. Berthet and N. Dragoe, J. Phys. Chem. B, 2004, 108, 3191–3195.
18. S. Brown, J. Cao, J. L. Musfeldt, N. Dragoe, F. Cimpoesu, S. Ito, H. Takagi and R. J. Cross, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 125446.
19. N. Dragoe, A. Flank, P. Lagarde, S. Ito, H. Shimotani and H. Takagi, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155448.
20. H. He, J. T. Dias, J. Foulkes and J. Klinowski, Phys. Chem. Chem. Phys., 2000, 2, 2651–2654.
21. T. Heine, G. Seifert, P. Fowler and F. Zerbetto, J. Phys. Chem. A, 1999, 103, 8738–8746.
22. G. Sun and M. Kertesz, J. Phys. Chem. A, 2000, 104, 7398–7403.
23. A. R. Tulyabaev, I. I. Kiryanov, I. S. Samigullin and L. M. Khalilov, Int. J. Quantum Chem., 2017, 117, 7–14.
24. P. A. Christy, A. J. Peter and C. W. Lee, Solid State Commun., 2018, 283, 22–26.
25. G. R. Bacanu, G. Hoffman, M. Amponsah, M. Concistrè, R. J. Whitby and M. H. Levitt, Phys. Chem. Chem. Phys., 2020, 22, 11850–11860.
26. H. Batiz-Hernandez and R. A. Bernheim, Prog. Nucl. Magn. Reson. Spectrosc., 1967, 3, 63–85.
27. C. J. Jameson, J. Chem. Phys., 1977, 66, 4983–4988.
28. P. E. Hansen, Prog. Nucl. Magn. Reson. Spectrosc., 1988, 20, 207–255.
29. A. Kantola, S. Ahola, J. Vaara, J. Saunavaara and J. Jokisaari, Phys. Chem. Chem. Phys., 2007, 9, 481–490.
30. A. M. Kantola, P. Lantto, J. Vaara and J. Jokisaari, Phys. Chem. Chem. Phys., 2010, 12, 2679–2692.
31. J. Lounila, J. Vaara, Y. Hiltunen, A. Pulkkinen, J. Jokisaari, M. Ala-Korpela and K. Ruud, J. Chem. Phys., 1997, 107, 1350–1361.
32. J. Vaara, J. Lounila, K. Ruud and T. Helgaker, J. Chem. Phys., 1998, 109, 8388–8397.
33. P. Lantto, J. Vaara, A. M. Kantola, V.-V. Telkki, B. Schimmelpfennig, K. Ruud and J. Jokisaari, J. Am. Chem. Soc., 2002, 124, 2762–2771.
34. P. Lantto, S. Kangasvieri and J. Vaara, J. Chem. Phys., 2012, 137, 214309.
35. P. Lantto, S. Kangasvieri and J. Vaara, Phys. Chem. Chem. Phys., 2013, 15, 17468–17478.
36. P.-O. Åstrand, K. Ruud and P. R. Taylor, J. Chem. Phys., 2000, 112, 2655–2667.
37. T. A. Ruden and K. Ruud, Ro-vibrational corrections to NMR parameters, in Calculation of NMR and EPR Parameters: Theory and Applications, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley-VCH, Weinheim, 2004, pp. 153–173.
38. M. Toyama, T. Oka and Y. Morino, J. Mol. Spectrosc., 1964, 13, 193–213.
39. K. Ruud, P.-O. Åstrand and P. R. Taylor, J. Chem. Phys., 2000, 112, 2668–2683.
40. R. Faber, J. Kaminsky and S. P. Sauer, Rovibrational and temperature effects in theoretical studies of NMR parameters, in Gas phase NMR, ed. K. Jackowski and M. Jaszuński, Royal Society of Chemistry, London, UK, 2016, vol. 6, pp. 218–266.
41. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani and P. Dahle, et al., Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284.
42. Dalton, a molecular electronic structure program, Release v2020.1, 2022, see https://daltonprogram.org.
43. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
44. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
45. F. Jensen, J. Chem. Theory Comput., 2015, 11, 132–138.
46. TURBOMOLE V7.7 2022, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, available from https://www.turbomole.com.
47. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding and C. Hättig, et al., J. Chem. Phys., 2020, 152, 184107.
48. L. Bartell, K. Kuchitsu and R. DeNeui, J. Chem. Phys., 1961, 35, 1211–1218.
49. H.-J. Eisler, S. Gilb, F. H. Hennrich and M. M. Kappes, J. Phys. Chem. A, 2000, 104, 1762–1768.
50. F. Cimpoesu, S. Ito, H. Shimotani, H. Takagi and N. Dragoe, Phys. Chem. Chem. Phys., 2011, 13, 9609–9615.
51. H.-J. Eisler, F. H. Hennrich, S. Gilb and M. M. Kappes, J. Phys. Chem. A, 2000, 104, 1769–1773.
52. P.-O. Åstrand, K. Ruud and D. Sundholm, Theor. Chem. Acc., 2000, 103, 365–373.

---

Footnote

† Electronic supplementary information (ESI) available: Figures and numerical data for volumetric thermal expansion coefficient, bond lengths, ¹³C chemical shift, secondary isotope shifts, vibrational mode analysis, and functional and basis set tests. See DOI: https://doi.org/10.1039/d5cp01484k

---