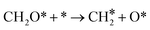A computational study of K promotion of CO dissociation on Hägg carbide

Abstract

The dissociation of CO is a critical step in producing long-chain hydrocarbons in the Fischer–Tropsch (FT) synthesis reaction. Although potassium (K) is known to enhance CO conversion and the selectivity to olefins of Fe-carbide FT catalysts, its precise mechanistic role remains unclear. In this work, we used density functional theory to show that K₂O facilitates C–O bond dissociation in CO, HCO, and COH by increasing the electron density of the Fe surface atoms of Hägg carbide (χ-Fe₅C₂) that bind these surface intermediates. This leads to a higher electron density in anti-bonding orbitals and enhanced electron–electron repulsion between the bonding orbitals of the CO, COH, and HCO intermediates and the Fe atoms. Effective promotion of C–O bond dissociation requires K to be adjacent to the active site on the χ-Fe₅C₂ surface.

---

1. Introduction

Fischer–Tropsch synthesis is a chemical process for the production of clean fuels and valuable chemical building blocks from synthesis gas, a mixture of CO and H₂, which can be derived from non-petroleum feedstocks, such as coal, shale gas, natural gas and biomass.^1–4 The Fischer–Tropsch (FT) reaction is a polymerization reaction with in situ generation of monomers from the CO reactant.⁵ One of the most critical steps in the FT reaction is the activation of the CO bond, which leads to the CH_x intermediates acting as the monomers. Without a low barrier for C–O bond scission, the rate of monomer formation is too low for effective chain growth, leading to unwanted light hydrocarbon products such as methane. Co, Fe and Ru are the transition metals that display high activity in the FT reaction.^6–9 Despite its high activity, the scarcity of Ru precludes its use in practical FT catalysts. Co is typically employed in low-temperature FT synthesis using synthesis gas mixtures obtained from natural gas. The benefits of Fe are its very low price, high selectivity to lower olefins and activity in the water–gas shift (WGS) reaction. This latter aspect is relevant when utilizing synthesis gas with low H₂/CO ratios, such as those derived from coal and biomass.^10–15 Under typical FT synthesis conditions, the Fe-based catalysts will typically convert into Fe-carbides, such as ε-Fe₂C, ε′-Fe_2.2C, χ-Fe₅C₂, θ-Fe₃C, and Fe₇C₃.^15–17 X-ray diffraction (XRD) and Mössbauer spectroscopy have been instrumental in linking the FT activity to these Fe-carbide phases.^3,18–21 Among them, Hägg carbide (χ-Fe₅C₂) is usually reported as the dominant and most active phase for CO activation and chain growth.^13,21,22

The performance of Fe-based catalysts can be tuned by incorporating promoters.²³ Promoters can increase the CO conversion or change the product distribution, increase the selectivity to long-chain hydrocarbons and suppress the methane selectivity.²⁴ Promoters such as Zn, Cu, S and alkali metals are known to increase the CO conversion and the selectivity to lower olefins.^25–30 Li, Na and K were found to increase the catalytic activity and the selectivity to lower olefins.³¹ K is usually the most effective promoter for increasing the FT reaction among these. K also promotes the WGS reaction and inhibits the methane selectivity, presumably by increasing the chain-growth probability.^32–35

The precise role of the K promoter in the mechanism of the FT reaction on Fe-carbide has not been established yet. Amoyal et al. found that K promoter makes Fe-carbide more resistant against oxidation, enhancing CO conversion.³⁴ Huo et al. suggested based on transmission electron microscopy (TEM) and XRD in conjunction with density functional theory (DFT) calculations that the main function of K is to stabilize the active Fe-carbide phases.³⁶ Ribeiro et al. show that K increases the Fe carburization rate by facilitating CO dissociation at the catalyst surface while suppressing methane formation.³⁷ An increased rate of Fe carburization by K was also concluded in the work of Cheng et al.³⁸ They identified a linear relationship between the surface basicity and the Hägg carbide concentration. Using DFT calculations, Petersen et al. reported that K increased CO and O adsorption energies on Hägg carbide.³⁹ Despite these insights, the nature of K species under FT conditions and their mechanistic role in promoting the FT reaction remains unclear.

As it has been challenging to resolve the role of K by experiments, we here adopt a theoretical approach to study the impact of K on the dissociation of the C–O bond, which leads to the surface monomers required for the FT reaction. DFT calculations are carried out for four representative active site configurations on χ-Fe₅C₂. It is found that the K enhances the CO dissociation by injecting additional electrons into the surface, leading to increased occupation of anti-bonding orbitals and increased electron–electron repulsion in bonding orbitals of C–O, weakening the C–O bond in CO, HCO and COH intermediates. Moreover, the effective promotion of C–O bond dissociation requires K to be adjacent to the active site on the χ-Fe₅C₂ surface. If K is placed directly at the active site or a greater distance under higher loading conditions, it has little effect or can even inhibit the reaction. This finding differs from the experimental explanation, where a high loading of the K promoter increases the particle size and C deposition, decreasing the CO conversion.³⁸

2. Computational methods

2.1 Density functional theory calculations

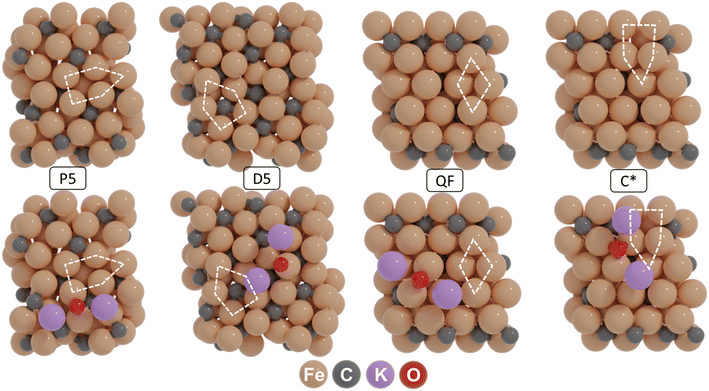
All quantum-chemical simulations were performed using spin-polarized density functional theory (DFT), wherein effective ion cores are described by projector-augmented wave (PAW) potentials, as implemented in the Vienna ab initio simulation package (VASP 5.4.4).^40–42 The exchange and correlation energies were computed using the Perdew–Burke–Ernzerhof (PBE) functional.⁴³ The PBE + D3 method was used to include dispersion corrections in our calculations.⁴⁴ The plane-wave basis set cut-off energy was 400 eV. Geometry optimization was conducted using the conjugate gradient method with a force-based stopping criterion of 0.05 eV/Å for each Cartesian direction and for each atom. The climbing-image nudged elastic band method (CI-NEB) was used to explore the transition states for all reaction pathways.^45,46 A frequency analysis was performed for all states, where stable states were verified to have no imaginary frequencies, while all transition states were verified by the presence of a single imaginary frequency in the direction of the reaction coordinate. The Hessian matrix for frequency analysis was determined using the finite difference approach in which individual atoms were displaced in each Cartesian direction. The corresponding normal mode vibrations were used to calculate the zero-point energy (ZPE). The Brillouin zone was sampled using a 1 × 1 × 1 Monkhorst–Pack grid (Γ-point only).

We used four representative active site configurations to describe the reactivity of χ-Fe₅C₂, namely (i) the planar five-fold site (P5) on Fe₅C₂(510), (ii) a distorted five-fold site (D5) on Fe₅C₂(111), (iii) a quasi-fourfold rectangle (FR) and (iv) a C-defect five-fold site (C*5), the latter two on Fe₅C₂(010). The first two layers of the solid, including the adsorbed molecules, were allowed to relax while keeping the atoms in the bottom layers frozen during geometry optimization. A vacuum layer of 15 Å was added perpendicular to the surface to mitigate spurious interactions between neighbouring slabs.

To analyze the electronic structure, crystal orbital Hamilton population (COHP) and density of states (DOS) analyses are conducted using the Lobster software (version 4.1.0).^47,48 The DDEC6 charge analysis method was applied to calculate net charges on atoms using the Chargemol software (version 3.5).^49,50 Electronic density differences between slab, adsorbate and adsorbate-on-slab configurations were constructed by the VTST electronic tools (version 5.4).⁵⁰ Electronic structure analysis using electron density differences was performed by projecting the three-dimensional scalar fields onto two-dimensional planes. Analysis and visualization of the electron density were conducted using the EDP program (version 2.0.3).⁵¹

3. Results and discussion

3.1 Surface models

Before constructing the surface terminations hosting the four active site configurations, the monoclinic unit cell (space group C2/c) corresponding to bulk χ-Fe₅C₂ was optimized using DFT. The computed lattice parameters of 11.53 Å × 4.50 Å × 4.95 Å and angles β = 97.75° (α = γ = 90°) are in good agreement with the experimental values for Hägg carbide (a = 11.588 Å, b = 4.579 Å, c = 5.059 Å, and β = 97.75°).⁵² The optimized unit cell is shown in the ESI† (Fig. S1). Based on the optimized bulk unit cell, four slab models were created, corresponding to the (510), (111), (010) and (010*) surface terminations. Fig. 1 shows these surface terminations exhibiting four distinct active site configurations, corresponding to P5, D5, QF and C* sites. It should be mentioned that the latter surface is created by removing a lattice C atom, residing in a fourfold site in the pristine surface. These active configurations were selected as they are sufficiently distinct and stable and are expected to exhibit different reactivity patterns under CO hydrogenation conditions.^53–56 Among these models, the P5 site has recently been identified as a highly reactive site, where direct CO dissociation is the dominant pathway.⁵⁷ The D5 site is one of the most active sites on the (111) surface, although the CO dissociation has a significantly higher barrier than sites on other χ-Fe₅C₂ surfaces.⁵⁵ The QF site represents the most active site on the (010) surface, where hydrogen-assisted CO dissociation is the most feasible pathway.⁵⁶ CO dissociation on a C vacancy site is studied on the C* site. By employing these representative models, we can reasonably capture the promotional effect of potassium (K) on Hägg carbide (χ-Fe₅C₂).

Fig. 1 (Top row) Active site configurations of the P5, D5, QF and C* sites as exposed on the (510), (111), (010) and (010*) surface terminations of χ-Fe₅C₂. (Bottom row) Most stable adsorption sites for the K₂O species.

To understand K promotion of χ-Fe₅C₂ in the FT reaction, we first established the most likely state of K on the surface by exploring the stability of K, KO, K₂O, KOH and K₂CO₃ as candidates on all the surfaces during CO hydrogenation. The potential energy diagrams of these reactions are shown in Fig. S2.† Among the considered species, K₂O is kinetically favored over other forms of K, with relatively low barriers for the interconversion between K, KO, and K₂O. In contrast, the formation of KOH from KO and K₂CO₃ from K₂O involves significantly higher barriers. For instance, metallic K is very easily oxidized to KO on all four surfaces. Furthermore, KO is readily oxidized to K₂O, with barriers of 24 kJ mol⁻¹ on (510), 56 kJ mol⁻¹ on (111), 23 kJ mol⁻¹ on (010) and 34 kJ mol⁻¹ on (010*). In contrast, its hydrogenation to KOH is less favorable, with significantly higher barriers that exceed 80 kJ mol⁻¹ on all surfaces. K₂CO₃ formation is kinetically hindered due to the considerably higher barriers of CO₂ formation (>140 kJ mol⁻¹ on the surfaces considered). To further evaluate the stability of these species, a phase diagram was constructed, showing the stability of the different forms of K on the considered surfaces as a function of the CO and H₂ pressure and temperature (Fig. S3†). This analysis confirms that K₂O is the most stable state of K on χ-Fe₅C₂ under FT synthesis conditions, which is in good agreement with other studies.^31,33,58

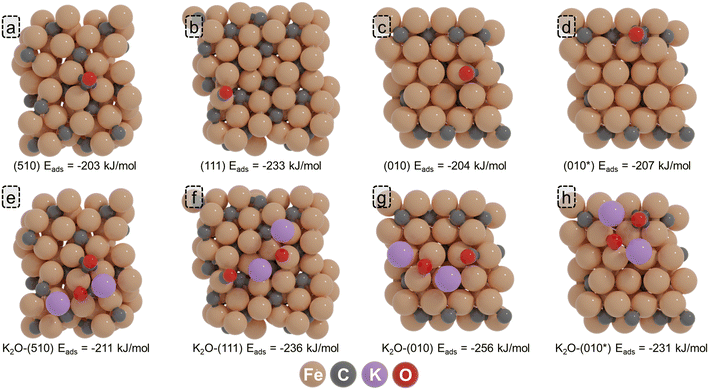
Next, we considered K₂O adsorption modes on the (510), (111), (010), and (010*) surfaces. Fig. S4–S7† shows the adsorption configurations and corresponding adsorption energies. It was found that K₂O is most stable on a bridge site of the (510) surface (−588 kJ mol⁻¹), a top site of the (111) surface (−546 kJ mol⁻¹), a semi-fourfold site of the (010) surface (−613 kJ mol⁻¹), and a 3-fold site of the (010*) surface (−586 kJ mol⁻¹). The geometries of the corresponding K₂O-containing surfaces are given in Fig. 1.

3.2 CO activation

3.2.1 Adsorption of CO and H. The adsorption energy of the reactants and the stability of the reaction intermediates critically determine the surface composition under reaction conditions and the reaction rate. Therefore, we investigated the influence of K₂O on the adsorption of CO and H on the four surface models. Top, bridge, three-fold, four-fold and five-fold adsorption modes were considered for CO and H. The most stable adsorption geometries and their corresponding adsorption energies of CO and H on the four adsorption sites, with and without the K₂O promoter, are provided in Fig. 2 and 3, respectively.

Fig. 2 The most stable adsorption structures and energy values of CO on (a–d) the pristine and (e–h) K₂O-promoted (510), (111), (010) and (010*) surfaces of χ-Fe₅C₂.

Fig. 3 The most stable adsorption structures and energy values of H* on (a–d) the pristine and K₂O-(e–h) promoted (510), (111), (010) and (010*) surfaces of χ-Fe₅C₂.

On the (510) surface, the most stable CO adsorption position corresponds to a four-fold site within the P5 site. A relatively low adsorption energy of −203 kJ mol⁻¹ was found, in agreement with the results found by Pham et al.⁵⁹ In the presence of K₂O, CO binds stronger at −211 kJ mol⁻¹. On the (111) surface, the highest adsorption energy of CO, corresponding to −233 kJ mol⁻¹, is obtained for a top configuration on one of the Fe atoms of the D5 site. In the presence of K₂O, the adsorption is almost the same. On the (010) surface, CO preferentially adsorbs on a quasi-fourfold site, where its C atom binds to four Fe atoms. An adsorption energy of −204 kJ mol⁻¹ was found for this configuration. In the presence of K₂O, the CO adsorption energy becomes more exothermic by 52 kJ mol⁻¹. Finally, on the C-vacancy site C* of the (010*) surface, CO adsorbs with an adsorption energy of −207 kJ mol⁻¹, which is further enhanced to −231 kJ mol⁻¹ in the presence of K₂O. It can be observed that the promoter can be near the adsorbate, with a shorter distance (2.58 Å) compared to the intrinsic bond distance of the K–O bond (2.68 Å). Irrespective of the surface, we observe an enhanced CO adsorption strength in the presence of K₂O, in line with the earlier findings of Petersen et al.³⁹

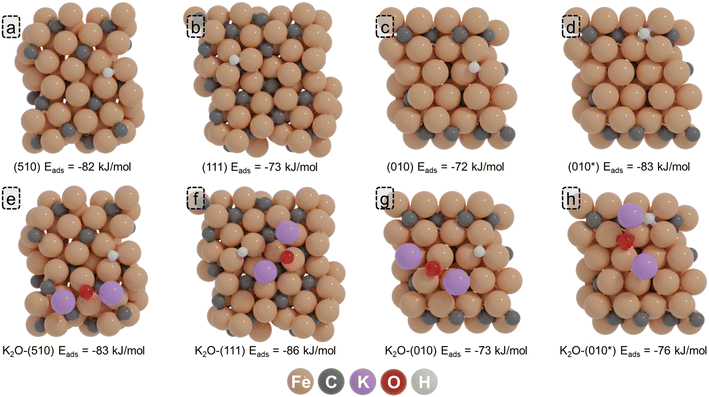
Due to the strong Fe–H bond, molecular H₂ readily dissociates upon adsorption over both the pristine and K₂O-promoted surfaces. On the (510) surface, H* preferentially adsorbs on a threefold site within the P5 site with an adsorption energy of −82 kJ mol⁻¹ referenced against gaseous H₂. In the presence of K₂O, this adsorption becomes slightly more exothermic with an adsorption energy of −83 kJ mol⁻¹. On the (111) surface, the most stable adsorption geometry is obtained at a three-fold site adjacent to the D5 site, with an adsorption energy of −73 kJ mol⁻¹. In the presence of K₂O, H adsorption becomes more exothermic by 13 kJ mol⁻¹. For the (010) surface, the H adsorption energy is −72 kJ mol⁻¹ which only becomes marginally more exothermic (1 kJ mol⁻¹) in the presence of K₂O. In contrast to the other surfaces, it was found for the (010*) surface that the presence of K₂O lowers the H* adsorption strength. Whereas for the unpromoted surface, the adsorption energy is −83 kJ mol⁻¹, it is marginally lower for the K₂O-promoted surface (−76 kJ mol⁻¹).

3.2.2 CO activation. The activation of adsorbed CO is known to be a crucial step in FT synthesis, producing the monomers for hydrogenation and chain growth.^59,60 CO dissociation can proceed either in a direct fashion by which the C–O bond is broken directly after CO adsorption or in a hydrogen-assisted fashion wherein first the C or O atom is hydrogenated before C–O bond scission.⁶¹ We investigate how K₂O promotion influences the adsorption energy and dissociation of the CO reactant on the pristine and promoted surfaces. The barriers of CO dissociation via the direct and H-assisted pathways are listed in Table 1. The corresponding geometries of the initial state (IS), transition state (TS) and final state (FS) involved in these pathways on the four considered surfaces are provided in Fig. S8–S15.†

Table 1 Forward reaction barriers (E_f), backward reaction barriers (E_b) and reaction energies (E_rxn) of CO dissociation via direct and H-assisted pathways on the four considered surfaces of χ-Fe₅C₂

Surface	Active site	Elementary steps	Pristine surface			Promoted surface
			E f (kJ mol^−1)	E b (kJ mol^−1)	E rxn (kJ mol^−1)	E f (kJ mol^−1)	E b (kJ mol^−1)	E rxn (kJ mol^−1)
(510)	P5	CO* + * → C* + O*	116	231	−115	106	195	−89
(510)	P5	CO* + H* → HCO* + *	143	10	133	126	2	124
(510)	P5	CO* + H* → COH* + *	180	104	76	150	50	100
(510)	P5	HCO* + * → CH* + O*	69	261	−195	51	201	−150
(510)	P5	COH* + * → C* + OH*	195	298	−97	95	171	−76
(111)	D5	CO* + * → C* + O*	178	94	84	153	51	101
(111)	D5	CO* + H* → HCO* + *	156	12	144	147	2	145
(111)	D5	CO* + H* → COH* + *	210	39	171	238	36	202
(111)	D5	HCO* + * → CH* + O*	139	215	−76	88	47	41
(111)	D5	COH* + * → C* + OH*	136	176	−40	101	252	−151
(010)	QF	CO* + * → C* + O*	163	200	−27	137	113	24
(010)	QF	CO* + H* → HCO* + *	119	61	58	108	22	86
(010)	QF	CO* + H* → COH* + *	160	67	93	170	44	126
(010)	QF	HCO* + * → CH* + O*	66	173	−107	45	110	−65
(010)	QF	COH* + * → C* + OH*	100	148	−48	77	124	−47
(010)	QF	HCO* + H* → CH2O* + *	127	49	78	99	15	84
(010)	QF		73	188	−115	56	127	−71
(010*)	C*	CO* + * → C* + O*	127	241	−114	106	184	−78
(010*)	C*	CO* + H* → HCO* + *	158	26	132	139	17	122
(010*)	C*	CO* + H* → COH* + *	200	108	92	181	82	99
(010*)	C*	HCO* + * → CH* + O*	131	326	27	88	251	−163
(010*)	C*	COH* + * → C* + OH*	93	213	−120	40	162	−122

---

From Table 1, it can be seen that K₂O induces a decrease in the barrier for direct CO dissociation for all four surfaces under consideration. The barriers decrease by 10 kJ mol⁻¹ on the (510), 25 kJ mol⁻¹ on the (111) surfaces, 26 kJ mol⁻¹ on the (010) surface and 21 kJ mol⁻¹ on the (010*) surface. Comparing the FS geometries of CO dissociation on the pristine and promoted surfaces, it is found that the O moiety formed upon C–O bond scission moves closer to the K₂O promoter, the latter effectively stabilizing O*.

Barriers for CO hydrogenation to form HCO show little effect due to the presence of K₂O. For C–O bond scission in HCO, the presence of K₂O results in a decrease in the dissociation barriers (ΔE^{promoted-pristine}_act,forward = −18, −51, −21, and −43 kJ mol⁻¹ for the (510), (111), (010) and (010*) surfaces, respectively), similar to the result observed for direct CO dissociation. For the (510) surface, we observe a decrease in the barrier for CO hydrogenation to HCO from 143 to 126 kJ mol⁻¹. For the (111), (010) and (010*) surfaces, the barriers decrease by −9, −11 and −19 kJ mol⁻¹ values, respectively.

The same trend for K₂O promotion is observed for C–O bond scission via COH. Whereas a systematic decrease in the C–O bond scission in COH is found in the presence of K₂O, no trend can be established for initial CO hydrogenation to COH. Moreover, we did not find a trend in whether K₂O acts as a promoting or inhibiting agent for CO hydrogenation, either to HCO or to COH, for the same surface. K₂O acts as a promoter for HCO formation on (111), (010) and (010*). In contrast, for COH formation, K₂O acts as a promoter for the (510) and (010*) surfaces by decreasing the hydrogenation barrier by −30 and −19 kJ mol⁻¹, respectively. For the (111) and (010) surfaces, the barrier increases by 28 and 10 kJ mol⁻¹, respectively. In contrast, C–O bond scission barriers in COH are substantially decreased due to K₂O by −100, −35, −23, and −53 kJ mol⁻¹ for the (510), (111), (010) and (010*) surfaces, respectively.

Based on the above results, it is evident that the K₂O promoter reduces the C–O bond strength in CO, HCO, and COH. To fully understand how K₂O facilitates the dissociation of these species, electronic analysis, which will be discussed in the next section.

To evaluate the most facile CO activation pathway and assess how K₂O affects this, we calculated the overall C–O bond scission barrier with respect to co-adsorbed CO* and H*. The results are listed in Table 2. The corresponding energy diagram that compares these pathways is provided in Fig. S16–S19.†Table 2 shows that CO preferentially dissociates via the direct dissociation pathway on the (510), (111) and (010*) surfaces with overall barriers of 116 kJ mol⁻¹, 178 kJ mol⁻¹ and 127 kJ mol⁻¹, respectively. In the presence of K₂O, these barriers decrease by 10 kJ mol⁻¹ (510), 25 kJ mol⁻¹ (111), and 21 kJ mol⁻¹ (010*). The direct CO dissociation pathway remains the dominant pathway on the (510), (111) and (010*) surfaces in the presence of K₂O. In contrast, for the (010) surface, where K₂O promotion changes the preferred pathway from direct CO dissociation to the HCO pathway. The latter offers a more facile pathway in the presence of K₂O, with an overall barrier of 131 kJ mol⁻¹ compared to 137 kJ mol⁻¹ for the direct CO dissociation pathway.

Table 2 Overall barriers of CO dissociation in CO direct dissociation and H-assisted pathways on considered four surfaces of χ-Fe₅C₂

Overall barrier (kJ mol^−1)	CO direct dissociation	HCO pathway	COH pathway
(510)	116	202	271
K2O-(510)	106	176	195
(111)	178	283	307
K2O-(111)	153	233	303
(010)	163	124	193
K2O-(010)	137	131	203
(010*)	127	263	185
K2O-(010*)	106	210	139

---

It should be emphasized that the overall barriers for the direct and HCO pathways over (010) are very similar. This also holds for the overall barriers for the direct and COH pathways over (010*). As such, these pathways are envisioned to be competitive, and it is likely that under CO hydrogenation conditions, both pathways participate in the overall reaction.

We next investigated the influence of CO coverage on the promotional effect of K. For this purpose, we determined the CO dissociation barrier at a higher CO coverage. To ensure that the contribution of lateral interactions is not included in the change of K promotion, CO dissociation was also studied at the higher CO coverage on the unpromoted surfaces. Table 3 presents two sets of calculations: (i) CO dissociation on the unpromoted and promoted surfaces and (ii) CO dissociation on these surfaces in the presence of an additional CO adsorbate. The corresponding geometries of the IS, TS and FS involved in the CO dissociation at the higher CO coverage of 0.2 ML are provided in Fig. S20–S23.†Table 3 shows that the promotional effect of K₂O is maintained at the higher CO coverage considered for all surfaces, except for the (010*) surface. Overall, these findings indicate that an increasing CO coverage does not significantly affect the promotional effect of K₂O on CO dissociation. It should be noted that it is usually assumed that Fe-carbide FT catalysts operate in the chain growth-limited regime, where CO dissociation is fast. This implies a relatively low CO coverage under steady-state conditions.

Table 3 Overall barriers of CO direct dissociation at 0.1 and 0.2 ML CO coverage on the considered χ-Fe₅C₂ surfaces

Surface	CO (0.1 ML)	CO (0.2 ML)
(510)	116	116
K2O-(510)	106	107
(111)	178	179
K2O-(111)	153	158
(010)	163	156
K2O-(010)	137	132
(010*)	127	136
K2O-(010*)	106	131

---

3.2.3 Electronic structure analysis. Table 1 shows that C–O bond scission barriers in CO, COH and HCO decrease in the presence of K. To understand the way K₂O impacts C–O bond activation, density of states (DOS) and crystal orbital Hamilton population (COHP) analyses^47,48 were conducted on the C–O bonds of CO, COH and HCO.

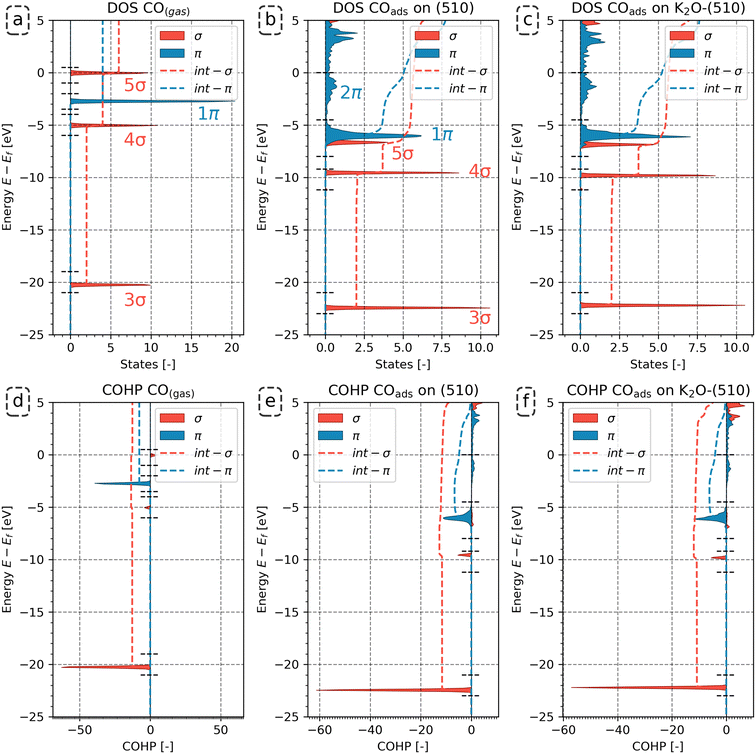
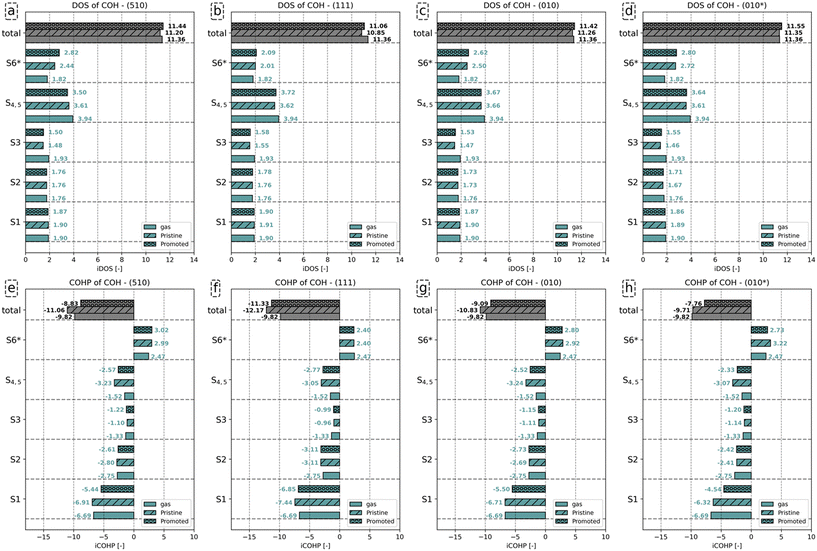
The analysis for the CO molecule in Fig. 4 compares the electronic structure of CO in the gas phase with CO adsorbed on the (510) surface, both in the presence and absence of K₂O. Based on the canonical molecular orbital solutions of CO in the gas phase⁶² (see also Fig. S24 in the ESI†), the Kohn–Sham states are categorized into distinct energy ranges, as indicated by the dashed horizontal lines in the DOS and COHP analyses in Fig. 4. From the lowest to highest energy, these energy ranges are labeled as 3σ, 4σ, 1π and 5σ for gaseous CO (Fig. 4a and d). The energy ranges corresponding to 1π and 5σ will overlap upon adsorption (Fig. 4b and c). By projecting the Kohn–Sham states onto localized atomic orbitals, we could deconvolute these interactions and distinguish between σ and π contributions, based on the procedure of CO dissociation on Co by Krösschell et al.⁶³ By orienting the atomic basis functions for the projection such that the p_z orbitals are aligned with the C–O bonding axis, the s–s, s–p_z and p_z–p_z interactions corresponding to σ contributions were identified, whereas p_x–p_x, p_x–p_y, p_y–p_x and p_y–p_y interactions correspond to π contributions. In this way, we could distinguish between 1π and 5σ contributions. Fig. 4 shows that, upon CO adsorption, the 3σ and 4σ molecular orbitals shift with respect to the Fermi level. Yet, their DOS features remain sharp, indicative that these orbitals do not readily mix with the d-states on the metal. This result is to be expected as these orbitals are compact in size (Fig. S24 in the ESI†). In contrast, the 1π and 5σ MOs broaden. As these molecular orbitals are more diffuse, they will mix with the d-states of the metal. Above the energy range assigned to the 1π and 5σ MOs, a new set of occupied states can be observed following CO adsorption. These states are labeled as 2π as they predominantly correspond to the unoccupied 2π* orbitals mixing with the d-states, resulting in their shift from above to below the Fermi level, thus becoming occupied upon adsorption of CO to the surface.

Fig. 4 DOS of C–O bond of CO (a) in gas phase; (b) on (510) surface; (c) on K₂O promoted (510) surface; COHP of C–O bond of CO (d) in gas phase; (e) on (510) surface; (f) on K₂O promoted (510) surface.

Fig. 4d–f shows how this redistribution of the Kohn–Sham state results affects the bond stability by observing the COHP features per energy range. Among these energy ranges, the 3σ and 1π orbitals are strongly bonding, while the 4σ and 5σ orbitals show minor (anti-)bonding contributions. Upon adsorption of CO, antibonding features emerge due to partial filling of the 2π orbital. The change in bonding characteristics was quantified by integrating the COHP features in the corresponding energy ranges to quantify the change. The dashed curves show the integrated COHP as a function of the state energy. The integrated COHP (iCOHP) and the integrated DOS (iDOS) per energy range for gaseous and adsorbed CO for the (510) surface are depicted in Fig. 5a. Similarly, the iDOS and iCOHP values for the other surfaces are shown in Fig. 5b–d. The original DOS and COHP diagrams used to construct Fig. 5 can be found in the ESI† in Fig. S25–S27.

Fig. 5 (a)–(d) iDOS and (e)–(h) iCOHP of C–O bond of CO in gas phase, CO absorbate on pristine surfaces and K₂O promoted surfaces. The red bars correspond to σ-interactions whereas the blue bars refer to π-interactions. The results for the pristine and K₂O-promoted surfaces are indicated by hashed and dotted bars, respectively.

From Fig. 5a–d, it can be seen that CO adsorption leads to additional electron density on the CO molecule. Whereas gaseous CO has 10 valence electrons (core electrons are part of the pseudopotential and are not shown in the DOS/COHP analyses), the total number of occupied states of CO increases by 0.69 on (510), 0.40 on (111), 0.85 on (010), and 0.87 on (010*). In the presence of K₂O, a further 0.15, 0.11, 0.23 and 0.21 states for the (510), (111), (010) and (010*) are occupied upon adsorption. Considering the states, we observe that the number of states corresponding to the 3σ molecular orbital (MO) on CO remains constant upon adsorption. In contrast, fewer states are assigned to the 4σ, 5σ and 1π molecular orbitals. The 2π orbital, unoccupied in gaseous CO, gains electron density upon adsorption. The number of states (electrons) gained by the 2π MO is larger than the number of states lost by the other orbitals. This electron accumulation in the 2π MO is further enhanced in the presence of K₂O. For example, it is observed for the (510) surface that with respect to the combined number of states lost in the 4σ, 5σ and 1π molecular orbitals, the 2π orbital gains 0.85 and 0.89 more electrons for the pristine and promoted surfaces, respectively.

To understand how the redistribution of the Kohn–Sham states affects the bond stability and how the presence of K₂O affects this, we consider Fig. 5e–h. In this analysis, we primarily focus on the 3σ, 1π and 2π as these orbitals were most important in describing CO bond activation.⁶³ For gaseous CO, the 3σ and 1π orbitals are strongly bonding with iCOHP values of −12.75 and −7.73, respectively, whereas the 4σ and 5σ show minor (anti-)bonding contributions of −0.78 and 0.91, respectively. Upon adsorption of CO, the bonding contributions become less bonding, while the anti-bonding features become more anti-bonding. For instance, for the pristine surfaces, it is observed that the iCOHP value of 3σ orbital increases by 1.19, 0.64, 1.45 and 1.77 for (510), (111), (010) and (010*) surfaces, respectively. In the presence of K₂O, a further increase of 0.73, 0.41, 0.91 and 1.16 for (510), (111), (010) and (010*) surfaces are found, respectively. As the 3σ peak in the DOS does not show any significant broadening upon CO adsorption, mixing of the 3σ orbital with the surface states is considered negligible. In lieu of any mixing effects, the decrease in bonding character can only be assigned to the increased electron–electron repulsion due to the increased proximity of this orbital with the surface electron density. Similarly, the 1π orbitals also become less bonding upon adsorption, yet in contrast to the 3σ orbital, here the loss of bonding character is assigned to the mixing of this orbital with surface states, as can be readily assessed from the peak broadening observed in Fig. 4 and S25–S27.† Akin to the 3σ orbital, the loss in bonding character is also observed to be more pronounced in the presence of K₂O. Besides losing overall bonding character, the additional occupation of the anti-bonding 2π states further destabilizes the C–O bond. For the 2π states, iCOHP values of 2.22, 1.75, 2.36 and 2.36 are found for the pristine (510), (111), (010) and (010*) surfaces, respectively. For the promoted surfaces, the iCOHP values increase to 2.53, 1.98, 2.90 and 2.56, respectively.

Based on these results, we infer that the role of K₂O is to inject additional electron density into the surface, as shown in Fig. S28.† The Blyholder concept of σ-donation and π-backdonation also leads to charge accumulation on the CO adsorbate, as shown in Fig. S29.† Compared to the situation where K₂O is absent, this charge injection into the surface, and indirectly into CO, has a twofold effect. For CO, it results in the occupation of additional 2π anti-bonding states. For the surface, the increased electron density enhances electron–electron repulsion in the 3σ and 1π orbitals. Since K₂O injects additional electron density into the surface, which is redirected to the CO adsorbate, both these effects contribute to the enhanced activation of the C–O bond in the presence of K₂O.

Besides CO, we also conducted the same analysis for the HCO and COH adsorbates as shown in Fig. 6 and 7, respectively. This analysis is performed in a similar manner as for CO, with the notable difference that for these molecules, a further distinction between σ and π contributions is not possible due to these complexes being non-linear upon adsorption. To categorize the Kohn–Sham states in terms of energy for adsorbed CO, we compared the adsorbed state with its fictitious gaseous counterpart (COH⁻ and HCO⁻). This yields the set of energy ranges shown in Fig. S30–S37 in the ESI.†

Fig. 6 (a)–(d) iDOS and (e)–(h) iCOHP of C–O bond of HCO⁻ in gas phase, HCO absorbate on pristine surfaces; and K₂O promoted surfaces. The result for the pristine and K₂O-promoted surfaces are indicated by hashed and dotted bars, respectively.

Fig. 7 (a)–(d) iDOS and (e)–(h) iCOHP of C–O bond of COH⁻ in gas phase, COH absorbate on pristine surfaces; and K₂O promoted surfaces. The results for the pristine and K₂O-promoted surfaces are indicated by hashed and dotted bars, respectively.

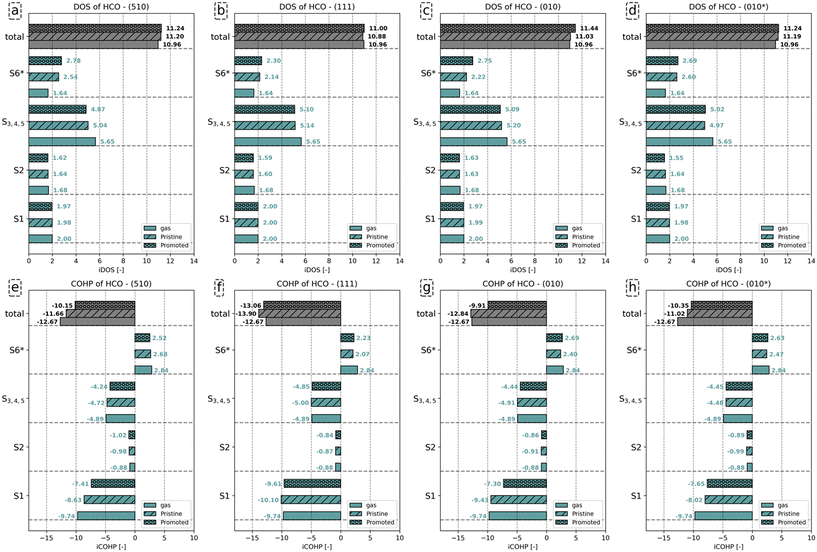
Fig. 6a–d show that the total number of electrons assigned to the C–O bond in HCO corresponds to 10.96. Including the number of electrons assigned to H in HCO⁻, a total of 12 electrons is found. Upon adsorption, we observe that the number of states assigned to the S1 and S2 orbitals remains largely the same, irrespective of the presence of K₂O. The number of electrons assigned to orbitals S3–S5, for convenience purposes taken together in this analysis, decreases upon adsorption and even more so in the presence of K₂O. The converse is valid for the anti-bonding S6 states, which gain electrons upon adsorption and more so upon K₂O promotion. From the total iCOHP value, it is found that HCO⁻ has a weaker C–O bond in the gas phase (−12.67) than in the adsorbed state on the pristine (111) surface (−13.90) and the pristine (010) surface (−12.84). This is mainly caused by the fact that HCO⁻ in lieu of an octet configuration is coordinately unsaturated and thus unstable in the gas phase. In a sense, the coordinative unsaturation is repaired upon adsorption to these surfaces, leading to enhanced stability. The effect of electron density rearrangement in the C–O bond can be found in Fig. 6e–h. In the presence of K₂O, the C–O bond is readily activated, as seen from the increase in the iCOHP values by 1.51 (510), 0.84 (111), 2.93 (010), and 0.67 (010*). Comparing the iCOHP values for the various orbitals between pristine and promoted surfaces, we observe a large decrease in bonding character for the S1 orbital in the presence of K₂O. Also, the S3–S5 orbitals become slightly less bonding, and the S6 orbitals become slightly more anti-bonding. For HCO, the role of K₂O in activating the C–O bond is mainly due to a destabilization of the S1 states by enhanced electron–electron repulsion between this state and the enhanced electron density on the Fe atoms as well as an additional occupation of anti-bonding S6* orbitals. These results are similar to how K₂O affects C–O bond activation in CO.

Fig. 7a–d shows that the total charge on the C–O bond is comparable between gaseous and adsorbed COH⁻, with little effect on whether K₂O promotes the surface. Analysis of the individual orbitals reveals that the number of electrons assigned to the S1 and S2 orbitals differs little between the three configurations. Compared to the number of states for the S3 orbitals of gaseous COH⁻ (1.93), a decrease by 0.45 (510), 0.38 (111), 0.46 (010) and 0.47 (010*), is found upon adsorption. Only minimal differences in the number of occupied states for the S3 orbital between the pristine and promoted surface are found. For the S4 and S5 orbitals, a similar decrease in the number of states is observed upon COH adsorption. Whereas gaseous COH⁻ hosts (3.94) states for the S4 and S5 orbitals, 3.61, 3.62, 3.66 and 3.61 are observed for these orbitals for the pristine (510), (111), (010) and (010*) surfaces, respectively. Upon K₂O promotion, these values decrease to 3.50, 3.72, 3.67, and 3.64, respectively. Finally, for the S6 orbital the number of states corresponds to 2.44 on (510), 2.01 on (111), 2.50 on (010), and 2.72 (010*) for the pristine surface. K₂O promotion results in a further increase in states by 0.38 on (510), 0.08 on (111), 0.12 on (010), and 0.08 (010*).

Similar to HCO, the C–O bond in the gas phase is less stable as compared to the C–O bond for adsorbed COH⁻ due to the COH⁻ not having an octet configuration in the gas phase. Also similar to HCO, surface promotion by K₂O results in a further activation of this C–O bond. Indeed, the iCOHP value for the C–O bond in COH adsorbed on the K₂O-promoted surface is lower than its counterpart found for the pristine surface. This difference in total iCOHP value between the pristine and promoted surfaces originates predominantly from a decreased bonding character for the S1, S4 and S5 orbitals. The other orbitals show little difference in their iCOHP values between the pristine and promoted surfaces. Conclusively, the mechanism of C–O bond activation by K₂O is, akin to its role for HCO, due to enhanced electron–electron repulsion between the increased surface charge and the S1, S4 and S5 orbitals and the enhanced occupation of S6 states.

3.3 Effect of K₂O location

In a previous experimental study conducted by Cheng et al., the effect of K promotion in Fe-based FT synthesis was studied.³⁸ These authors observed that K promotion results in an increase of the size of the Hägg carbide nanoparticles, which the authors assigned as the origin of the lower CO conversion. Furthermore, an increased thickness of the carbon layer as a function of increasing K content was observed, hinting at the ability of K to enhance C deposition, which can result in the poisoning of active sites, facilitating CO dissociation as observed in other experimental studies.^35,64 As an alternative to decreasing the active site by enhanced carbide size and C deposition, we consider the possibility of K₂O inhibiting C–O bond scission by directly poisoning the active site responsible for CO dissociation.

Compared to the most stable adsorption energy of K₂O (−588 kJ mol⁻¹), where K₂O adsorbs in the vicinity of the P5 active site (K₂O-(510)_a; Fig. 8b), we explored two alternative K₂O adsorption sites (K₂O-(510)_b and K₂O-(510)_c; Fig. 8c and d) that portray similar K₂O adsorption energies (−581 and −578 kJ mol⁻¹). We calculated the CO direct dissociation barriers for these surface sites and compared the result with the pristine surface. The CO direct dissociation barrier is found to be decreased by 10 kJ mol⁻¹ when K₂O is in the vicinity of the P5 site. However, when K₂O resides at the P5 site, with one K atom occupying the center of the P5 site, direct CO dissociation is significantly inhibited, resulting in an increase of the CO direct dissociation barrier by 74 kJ mol⁻¹ and by 124 kJ mol⁻¹ for the two configurations shown in Fig. 8c and d, respectively. These results suggest that K₂O can also exhibit an inhibiting role towards CO dissociation, which becomes more prevalent upon high loadings of K.

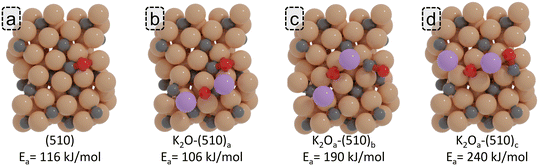Fig. 8 ZPE corrected reaction barriers and transition states geometries of CO direct dissociation on (a) pristine (510) surface and (b)–(d) K₂O promoted surfaces.

We also explored the impact of the position of K₂O on the (010*) surface. We considered one alternative configuration of K₂O near the active site for CO dissociation, as shown in Fig. 9c. Compared to the most stable adsorption configuration of K₂O (K₂O-(010*)_a; Fig. 9b) for the (010*) surface (−586 kJ mol⁻¹), this alternative configuration yields a similar adsorption energy of −583 kJ mol⁻¹. Whereas the K₂O-(010*)_a gives a CO dissociation barrier of 106 kJ mol⁻¹, the K₂O-(010*)_b configuration shows a CO dissociation barrier of 131 kJ mol⁻¹, only 4 kJ mol⁻¹ higher than the barrier found for the unpromoted surface. We assign this minor difference to K₂O being more distanced with respect to the active site.

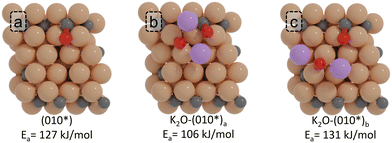Fig. 9 ZPE corrected reaction barriers and transition states geometries of CO direct dissociation on the (a) pristine (010*) and (b) and (c) K₂O-promoted surfaces.

These results show that the location of K₂O with respect to the active site is important. When K₂O resides at the active site, it will inhibit the reaction due to steric effects. When K₂O is not at the active site yet near it, C–O bond scission is promoted via charge injection into the catalyst surface and the CO moiety. Finally, when K₂O is at a greater distance from the reacting surface intermediate, its beneficial effects become negligible due to the charge injection being very localized in nature, only affecting the first coordination shell of K₂O.

Conclusions

To investigate the mechanistic role of K₂O on C–O bond scission, we calculated dissociation barriers for direct and hydrogen-assisted CO dissociation for several active site configurations in the presence and absence of K₂O. The results show that the K₂O promoter can strengthen the adsorption of CO while decreasing the C–O bond strength when the K₂O promoter adsorbs in the vicinity of the active site. Enhanced CO bond activation due to the presence of K₂O, leading to lower dissociation barriers, is assigned to its ability to inject additional electrons into the catalytic surface, which also results in an enhanced charge on the CO, HCO, or COH adsorbates. The effect of this charge injection is twofold; it destabilizes low-lying bonding orbitals due to increased electron–electron repulsion and increased occupation of high-lying anti-bonding orbitals. For CO, this predominantly entails decreased bonding of the 3σ and 1π orbitals and enhanced antibonding of the 2π orbitals. For HCO and COH, the same pattern is observed for the analogous orbitals. The propensity of K₂O to effectively promote C–O bond scission depends on its proximity to the active site for (hydrogen-assisted) CO dissociation. When K₂O resides at the active site, it will act as an inhibitor due to vastly increased steric repulsion. If K₂O is adjacent to the active site such that K and C share one or more Fe atoms, it can act as a promoting agent via a charge injection mechanism. The nature of this effect is, however, very localized. As soon as K₂O is at a greater distance with respect to the active site such that none of the Fe atoms can be shared between K and the adsorbate, its promoting effect becomes negligible and similar barriers as found for the unpromoted situation are observed.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

We acknowledge the financial support from the China Scholarship Council. The authors acknowledge NWO and SurfSARA for providing computational resources to carry out the DFT simulations. This work was supported by the National Key Research and Development Program of China (No. 2022YFB4101400) and CHN Energy Science and Technology innovation project (No. GJPT-23-18).

References

1. F. Fischer and H. Tropsch, Brennst.-Chem., 1923, 4, 276–285.
2. H. M. Torres Galvis and K. P. de Jong, ACS Catal., 2013, 3, 2130–2149.
3. P. Wang, W. Chen, F.-K. Chiang, A. I. Dugulan, Y. Song, R. Pestman, K. Zhang, J. Yao, B. Feng, P. Miao, W. Xu and E. J. M. Hensen, Sci. Adv., 2018, 4, eaau2947.
4. F. Jiao, J. Li, X. Pan, J. Xiao, H. Li, H. Ma, M. Wei, Y. Pan, Z. Zhou, M. Li, S. Miao, J. Li, Y. Zhu, D. Xiao, T. He, J. Yang, F. Qi, Q. Fu and X. Bao, Science, 2016, 351, 1065–1068.
5. G. P. Van Der Laan and A. A. C. M. Beenackers, Catal. Rev.: Sci. Eng., 1999, 41, 255–318.
6. Y. Xu, X. Li, J. Gao, J. Wang, G. Ma, X. Wen, Y. Yang, Y. Li and M. Ding, Science, 2021, 371, 610–613.
7. P. Senecal, S. D. M. Jacques, M. Di Michiel, S. A. J. Kimber, A. Vamvakeros, Y. Odarchenko, I. Lezcano-Gonzalez, J. Paterson, E. Ferguson and A. M. Beale, ACS Catal., 2017, 7, 2284–2293.
8. Y. Zhang, X. Su, L. Li, H. Qi, C. Yang, W. Liu, X. Pan, X. Liu, X. Yang, Y. Huang and T. Zhang, ACS Catal., 2020, 10, 12967–12975.
9. W. Chen, I. A. W. Filot, R. Pestman and E. J. M. Hensen, ACS Catal., 2017, 7, 8061–8071.
10. M. E. Dry, Catal. Lett., 1990, 7, 241–251.
11. A. P. Steynberg, M. E. Dry, B. H. Davis and B. B. Breman, Stud. Surf. Sci. Catal., 2004, 152, 64–195.
12. H. M. Torres Galvis, A. C. J. Koeken, J. H. Bitter, T. Davidian, M. Ruitenbeek, A. I. Dugulan and K. P. de Jong, J. Catal., 2013, 303, 22–30.
13. E. de Smit, F. Cinquini, A. M. Beale, O. V. Safonova, W. van Beek, P. Sautet and B. M. Weckhuysen, J. Am. Chem. Soc., 2010, 132, 14928–14941.
14. T. H. Pham, Y. Qi, J. Yang, X. Duan, G. Qian, X. Zhou, D. Chen and W. Yuan, ACS Catal., 2015, 5, 2203–2208.
15. E. de Smit and B. M. Weckhuysen, Chem. Soc. Rev., 2008, 37, 2758–2781.
16. Y. Li, Z. Li, A. Ahsen, L. Lammich, G. J. A. Mannie, J. W. H. Niemantsverdriet and J. V. Lauritsen, ACS Catal., 2018, 9, 1264–1273.
17. S. Lyu, L. Wang, Z. Li, S. Yin, J. Chen, Y. Zhang, J. Li and Y. Wang, Nat. Commun., 2020, 11, 6219.
18. Q. Chang, C. Zhang, C. Liu, Y. Wei, A. V. Cheruvathur, A. I. Dugulan, J. W. Niemantsverdriet, X. Liu, Y. He, M. Qing, L. Zheng, Y. Yun, Y. Yang and Y. Li, ACS Catal., 2018, 8, 3304–3316.
19. T. Qiu, L. Wang, S. Lv, B. Sun, Y. Zhang, Z. Liu, W. Yang and J. Li, Fuel, 2017, 203, 811–816.
20. K. Xu, B. Sun, J. Lin, W. Wen, Y. Pei, S. Yan, M. Qiao, X. Zhang and B. Zong, Nat. Commun., 2014, 5, 5783.
21. C. Yang, H. Zhao, Y. Hou and D. Ma, J. Am. Chem. Soc., 2012, 134, 15814–15821.
22. T. Herranz, S. Rojas, F. Perezalonso, M. Ojeda, P. Terreros and J. Fierro, J. Catal., 2006, 243, 199–211.
23. J. Yang, W. Ma, D. Chen, A. Holmen and B. H. Davis, Appl. Catal., A, 2014, 470, 250–260.
24. W. D. Mross, Catal. Rev.: Sci. Eng., 1983, 25, 591–637.
25. C. Zhang, C. Cao, Y. Zhang, X. Liu, J. Xu, M. Zhu, W. Tu and Y.-F. Han, ACS Catal., 2021, 11, 2121–2133.
26. Y.-N. Wang, W.-P. Ma, Y.-J. Lu, J. Yang, Y.-Y. Xu, H.-W. Xiang, Y.-W. Li, Y.-L. Zhao and B.-J. Zhang, Fuel, 2003, 82, 195–213.
27. J. Benziger and R. J. Madix, Surf. Sci., 1980, 94, 119–153.
28. T. C. Bromfield and N. J. Coville, Appl. Catal., A, 1999, 186, 297–307.
29. B. Graf and M. Muhler, Phys. Chem. Chem. Phys., 2011, 13, 3701–3710.
30. B. Shi, Z. Zhang, B. Zha and D. Liu, Mol. Catal., 2018, 456, 31–37.
31. M. E. Dry and G. J. Oosthuizen, J. Catal., 1968, 11, 18–24.
32. J. C. Park, S. C. Yeo, D. H. Chun, J. T. Lim, J.-I. Yang, H.-T. Lee, S. Hong, H. M. Lee, C. S. Kim and H. Jung, J. Mater. Chem. A, 2014, 2, 14371–14379.
33. S. Zhao, X.-W. Liu, C.-F. Huo, Y.-W. Li, J. Wang and H. Jiao, Appl. Catal., A, 2015, 493, 68–76.
34. M. Amoyal, R. Vidruk-Nehemya, M. V. Landau and M. Herskowitz, J. Catal., 2017, 348, 29–39.
35. Y. Yang, H.-W. Xiang, Y.-Y. Xu, L. Bai and Y.-W. Li, Appl. Catal., A, 2004, 266, 181–194.
36. C. F. Huo, B. S. Wu, P. Gao, Y. Yang, Y. W. Li and H. Jiao, Angew. Chem., Int. Ed., 2011, 50, 7403–7406.
37. M. C. Ribeiro, G. Jacobs, B. H. Davis, D. C. Cronauer, A. J. Kropf and C. L. Marshall, J. Phys. Chem. C, 2010, 114, 7895–7903.
38. Y. Cheng, J. Lin, K. Xu, H. Wang, X. Yao, Y. Pei, S. Yan, M. Qiao and B. Zong, ACS Catal., 2015, 6, 389–399.
39. M. A. Petersen, M. J. Cariem, M. Claeys and E. van Steen, Appl. Catal., A, 2015, 496, 64–72.
40. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
41. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
42. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
44. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
45. D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 134106.
46. D. Sheppard, P. Xiao, W. Chemelewski, D. D. Johnson and G. Henkelman, J. Chem. Phys., 2012, 136, 074103.
47. V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
48. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
49. N. G. Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747.
50. T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801.
51. I. A. W. Filot, J. Open Source Softw., 2023, 8(87), 5417.
52. J. J. Retief, Powder Diffr., 1999, 14, 130–132.
53. Q. Y. Liu, C. Shang and Z. P. Liu, J. Am. Chem. Soc., 2021, 143, 11109–11120.
54. Q.-Y. Liu, D. Chen, C. Shang and Z.-P. Liu, Chem. Sci., 2023, 14, 9461–9475.
55. S. Zhao, X.-W. Liu, C.-F. Huo, Y.-W. Li, J. Wang and H. Jiao, Appl. Catal., A, 2017, 534, 22–29.
56. R. J. P. Broos, B. Zijlstra, I. A. W. Filot and E. J. M. Hensen, J. Phys. Chem. C Nanomater. Interfaces, 2018, 122, 9929–9938.
57. Q. Y. Liu, D. Chen, C. Shang and Z. P. Liu, Chem. Sci., 2023, 14, 9461–9475.
58. G. Pirug, G. Brodén and H. P. Bonzel, Surf. Sci., 1980, 94, 323–338.
59. T. H. Pham, X. Duan, G. Qian, X. Zhou and D. Chen, J. Phys. Chem. C, 2014, 118, 10170–10176.
60. M. O. Ozbek and J. W. Niemantsverdriet, J. Catal., 2014, 317, 158–166.
61. B. Chen, D. Wang, X. Duan, W. Liu, Y. Li, G. Qian, W. Yuan, A. Holmen, X. Zhou and D. Chen, ACS Catal., 2018, 8, 2709–2714.
62. W. Jorgensen, The organic chemist's book of orbitals, Elsevier, 2012.
63. R. D. E. Krösschell, E. J. M. Hensen and I. A. W. Filot, J. Phys. Chem. C Nanomater. Interfaces, 2024, 128, 8947–8960.
64. W. Ma, E. L. Kugler and D. B. Dadyburjor, Energy Fuels, 2007, 21, 1832–1842.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cy01463d

---