Open Access Article
Open Access ArticleDisappearance of electric double layer effects on electrochemical reactions: the case of a chemisorbed small species on a metal surface at the electrode/electrolyte–solution interface†
Kenji
Iida
 *,
So
Kato
and
Jun-ya
Hasegawa
*,
So
Kato
and
Jun-ya
Hasegawa

Institute for Catalysis, Hokkaido University, N21 W10 Kita-ku, Sapporo, 001-0021 Hokkaido, Japan. E-mail: k-iida@cat.hokudai.ac.jp; hasegawa@cat.hokudai.ac.jp
First published on 24th April 2025
Abstract
The electric double layer (EDL) consisting of a charged electrode and an electrolyte solution hosts numerous electrochemical reactions. In this study, the oxygen reduction reaction (ORR) at the interface between a Pt electrode and a HClO4 aqueous solution was investigated using a hybrid method combining density functional theory and a statistical mechanical theory for molecular liquids, the three-dimensional reference interaction site model (3D-RISM) theory. This method can reveal the EDL structure at the atomic scale by explicitly considering the EDL charging owing to the electrode potential variation. Our calculation clarified that the solvation effect changes the ORR energy profile because of the local interaction between the adsorbate and the electrolyte solution. The charge distribution and solvation structure remarkably change depending on the electrode potential owing to the EDL formation; nevertheless, the energy profile of the dissociative mechanism is unaffected by the EDL formation. To elucidate the disappearance of the EDL effect on the energy profile, we analyzed the electrostatic potential change by the EDL formation and found that the O and OH adsorbates merge with the charged electrode surface. Therefore, the EDL does not affect the stability of the adsorbates. Detailed analysis further indicates that the EDL effect on electrochemical reactions will depend on the adsorption structure and size of adsorbates on the electrode surface. This study affords atomic-scale insights into the relationship between the EDL structure and electrochemical reactions.
1 Introduction
The electric double layer (EDL) consisting of a charged electrode and an electrolyte solution hosts various electrochemical reactions.1,2 The interaction between an electrode and an electrolyte solution has been a central topic in numerous electrochemical studies for a long time.3–10 The competitive adsorption of anions in the electrolyte solution on an electrode has been regarded as a main factor controlling electrode catalysis, where the initial step, more specifically, the adsorption of a reactant on the electrode is inhibited by the adsorbed anion.4 However, recent experimental studies indicated other roles of electrolyte solutions.11–15 For example, experimental studies reported that the ORR activity increases as the cation size increases. The findings from the studies also indicate that the electrolyte solution affects not only the initial O2 adsorption step but also the stability of intermediates.11,12 Despite these extensive investigations, the role of the electrolyte solution remains unclear because of the complexity of electrochemical interfaces.13The EDL consists of not only an electrolyte solution but also a charged electrode. Indeed, another subject for electrochemical reactions is the charging of an electrode and reactants owing to the electrode potential variation. The role of the charging in the electrode catalysis has only recently attracted considerable attention. For example, the charging of a molecule adsorbed on a single-atom catalyst affects the reaction energy profile,16,17 and that of a semiconductor electrode crucially changes its catalysis of the oxygen evolution reaction.18,19 However, these studies did not merely discuss the role of the electrolyte solution in the electrochemical reaction. In this context, it is necessary to gain a deeper insight into the interactions induced by the charged electrode, electrolyte solution, and reactant molecules.
Theoretical and computational methods are widely used to investigate chemical reactions.20–25 However, applying these methods to electrochemical systems remains difficult because calculations at a constant chemical potential of electrons (μ) are required.26–32 The finite-temperature density functional theory (FT-DFT), a generalized formula of DFT for the grand canonical ensemble of electrons, is a representative theoretical formula for the constant-μ calculation.33 FT-DFT has been applied to electrochemical systems.34–43 An additional difficulty in using FT-DFT is in the modeling of a charged material under the periodic boundary conditions due to the divergence of the electrostatic potential. Therefore, theoretical methods have been proposed to calculate a charged slab.35,39,44
In addition to the above mentioned difficulties, it is further required to appropriately evaluate the solvation effect by the electrolyte solution on the electrochemical reaction. To accurately represent the dilute electrolyte solutions commonly used in real experimental systems, the interface between the electrode and electrolyte solution should contain a large number of solvent molecules, in addition to electrolyte ions. The solvation effect has been widely investigated using the dielectric continuum model.45,46 However, this model approximates the electrolyte solution as a continuum medium using the dielectric permittivity which is predetermined by input parameters. The reference interaction site model (RISM) theory is a statistical mechanical formula for molecular liquids,47–49 and is useful for the calculation of dilute solutions at a reasonable computational cost.50,51 Three-dimensional-RISM-self-consistent field (3D-RISM-SCF) is a hybrid approach combining quantum mechanics and 3D-RISM theory for investigating 3D solvation structures.49,51–53 3D-RISM-SCF has been extended to address the problem of divergence in the calculation of charged materials.51,54–56 Further, the grand canonical ensembles of electrons and molecular liquids can be treated using FT-DFT and the RISM theory, respectively. 3D-RISM-SCF that consists of the two theories can give the ensemble average of the EDL structure by explicitly considering the EDL charging at a certain electrode potential. Therefore, 3D-RISM-SCF is suitable for investigating electrochemical reaction mechanisms governed by the EDL structure.
We proposed a theoretical and computational method based on 3D-RISM-SCF for modeling large electrochemical interfaces.56 In our method, an analytical formula is used to evaluate the contribution of the diverging electrostatic potential to the solvation structure. Because of using this analytical formula, the 3D-RISM theory is readily combined with FT-DFT to construct the 3D-RISM-SCF framework. Furthermore, calculations are performed using the SALMON software, which is suitable for investigating large materials owing to its high parallel efficiency.57 Therefore, complex interfaces consisting of a large charged-materials and an electrolyte solution can be calculated in almost the same manner as the 3D-RISM-SCF calculation for charge-neutral materials. Using our method, the EDL structure can be obtained without predetermined input parameters with respect to, for example, the Debye length. Furthermore, the molecular-level interactions such as the hydrogen bonding between an electrolyte solution and a molecule adsorbed on an electrode are explicitly considered. This enables the detailed, atomic-scale understanding of the EDL structure.
In this study, the ORR at the interface between a Pt electrode and a HClO4 aqueous solution was investigated using our method. We particularly focused on the stability of the intermediates and analyzed the charge distribution, solvation structure, and electrostatic potential profile of the EDL; thereby, we elucidated why the energy profile is unaffected by the EDL formation.
2 Computational models and details
The main part of our method has been presented in a previous study,56 and further details are provided in section S1 of the ESI.† In this study, we further extended our method to calculate the free energy of a charged material using the theoretical formula proposed by Lozovoi et al.35Fig. 1 shows the computational model, which consists of a Pt slab, 1.0 M HClO4 aqueous solution, and reactant molecule. The length of the supercell along the z-axis was set to 144 Å, and the surface area to 11.18 Å × 9.69 Å along the x and y directions, respectively. The Pt electrode was modeled using a tri-layer (light gray balls), to which a classical force-field layer consisting of 12 Pt atomic layers (dark gray small balls) was added. Owing to the presence of this classical region, the EDL was generated only on the right-hand side of the Pt slab, on which reactants (i.e., O or OH) were adsorbed. The total charge of the electrolyte solution at the left-hand side of the Pt slab is negligibly small (−0.02e) compared with the total EDL charge (−0.69e). Because the energy monotonically depends on the EDL charge, the small residual charge does not affect the discussion in this study.
The distribution function of the homogeneous 1.0 M HClO4 aqueous solution was calculated using the dielectrically consistent reference interaction site model (DRISM) implemented in the AMBER program.50,58 DRISM yields better results, particularly for electrolyte solutions, than the standard RISM theory. The Lennard-Jones parameters for the 3D-RISM calculations were obtained from the literature and are summarized in Table 1. An extended simple point charge (SPC/E)-like water model was employed,59 and the parameters for ClO4−, Pt, H2O, and H3O+ were taken from the literature.59–61 The same force field as that in our study for water and Pt was used in a previous 3D-RISM study wherein the hydration structure at the Pt(111)/water interface was well reproduced.62 It should be noted that the specific adsorption or chemisorption of ClO4− on the Pt electrode is considered to be absent,63–65 demonstrating the validity of the present hybrid model based on the 3D-RISM-SCF theory.
| Charge/e | σ/Å | ε/kcal mol−1 | |
|---|---|---|---|
| Pt (ref. 60) | — | 2.5340 | 7.8000 |
| O (on Pt)59 | — | 3.1660 | 0.1554 |
| H (on Pt)59 | — | 1.0000 | 0.0460 |
| Ow (ref. 59) | −0.8476 | 3.1660 | 0.1554 |
| Hw (ref. 59) | +0.4238 | 1.0000 | 0.0460 |
| Oc (ref. 66) | −0.5000 | 3.1640 | 0.1550 |
| Hc (ref. 66) | +0.5000 | 0.4000 | 0.0460 |
| Cla (ref. 61) | +1.1760 | 3.5000 | 0.1180 |
| Oa (ref. 61) | −0.5440 | 2.9000 | 0.2100 |
Although the 3D-RISM-SCF results depend on the force fields,67,68 it is difficult to improve the force fields because they (e.g., the SPE/E model) have been already carefully determined by referring to experimental and computational data. Reliance on the results of theoretical calculations such as AIMD is often useful for the design of force fields. However, DFT calculations include errors due to the functional approximation. For example, the water distribution differs between the PBE (GGA level) and SCAN (meta-GGA level) results.69 Further detailed consideration of the force field is beyond the scope of this study. The numerical error of the RISM calculation also depends on the closure;70,71 thus, the development of the closure has been performed.71
Geometry optimization of the vacuum system (i.e., without the electrolyte solution) was performed using the standard DFT method with the dispersion-corrected PBE functional (PBE-D3)72–75 implemented in the Quantum Espresso package.76 The supercell length along the direction perpendicular to the interface was set to 30 Å, which is shorter than that used in the 3D-RISM-SCF calculations (144 Å). The cutoff energy for geometry optimization was set to 80 Ry, and the number of k-points was 2 × 2 × 1. The bottom Pt layer was fixed to the bulk Pt metal structure. The closed-shell DFT method was adopted except for an oxygen molecule in the gas phase because the energy difference of the others using spin-polarized calculation is only ∼1 × 10−4 eV compared with the closed-shell calculation.
Using the optimized geometry, the 3D-RISM-SCF calculation based on FT-DFT were performed with the PBE functional. To do so, we used the SALMON program to which the 3D-RISM-SCF method was implemented. The grid widths were set to 0.112 Å for the x- and z-axes and 0.101 Å for the y-axis in accordance with the cell size, and the number of k-points was 2 × 2 × 1. The temperature (T) for the FT-DFT and 3D-RISM calculations was set to 298.15 K. Thermodynamic corrections were not performed in this study. Evaluating the translational and rotational entropy in the solution phase is still a difficult problem, and theoretical methods for this evaluation are still under development.77 The effective core potentials were obtained using the Troullier–Martins scheme implemented in the fhi98PP program.78,79 Visualization was performed using the VESTA program package.80 Bader charge analysis was conducted to determine the atomic charges.81–84
Our method explicitly considers the electrode potential and EDL formation based on the grand canonical ensemble framework. The electrode potential was given as the difference between the Fermi level and the computational value of the standard hydrogen electrode potential (SHE), whereas some theoretical studies used the experimental SHE value.15,85 Computational details of determining the electrode potential are provided in sections S2 and S3.†
3 Results and discussion
3.1 Free energy profiles
Fig. 2 shows the free energy profiles of the ORR relative to the final state via the dissociative mechanism, which has been widely investigated as one of the main ORR mechanisms in previous theoretical studies31 The reaction steps are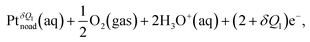 | (1) |
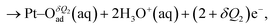 | (2) |
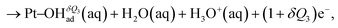 | (3) |
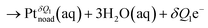 | (4) |
 | ||
| Fig. 2 Free energy profiles of the ORR in a vacuum using the CHE model at 0 V (black dash) and 0.53 V (aqua dash), at the potential of zero charge (pzc) of Ptnoad (blue), and at 0.90 V vs. SHE (red). | ||
The black dashed line in Fig. 2 represents the free energy profile in the gas phase (i.e., without the electrolyte solution) obtained using the computational standard hydrogen electrode (CHE) model at 0 V relative to the SHE.31 In the following, the electrode potential is given as the relative value to the SHE. In the CHE model, the energies of H2 and H2O in the gas phase are used instead of those of H3O+ and H2O in the HClO4 solution to evaluate the reaction energy at a certain electrode potential. The surface charge is not considered in the CHE model (i.e., δQi is set to 0); thus, the surface charge at 0 V of the CHE model is different from that at 0 V of the real system. However, avoiding explicit treatment of solvation and electrode charging, the conventional DFT approach can be readily used to investigate electrochemical reactions. Using the CHE model, the energies of the Pt–Oad state (2) and Pt–OHad state (3) relative to the final state (4) are 1.21 and 0.76 eV, respectively, whereas the results of a previous study are 1.53 and 0.78 eV.31 The numerical difference between the present and previous studies would be attributed to differences in the computational details and model such as the number of the Pt atom layers and the surface area.31,86,87 It is also noted that the molecular adsorption energies are slightly overestimated in this study because of neglecting the zero-point and free-energy corrections, which are ∼0.39 and ∼0.23 eV for the O and OH adsorptions, respectively.31
The free energy profile in the HClO4 solution at the potential of zero charge (pzc) of Ptnoad is represented by the blue line in Fig. 2. In this study, the calculated pzc of Ptnoad was 0.53 V. Accordingly, the result of the CHE model at 0.53 V is also shown in Fig. 2. The calculated pzc is in qualitative agreement with previous experimental and theoretical values ranging from 0.23 to 0.56 V.88–94 Details of the calculation of the electrode potential relative to the SHE are provided in sections S2 and S3.† In the classical electrochemistry and the CHE model, the dependence of the redox reaction on the electrode potential is simply estimated as ΔQtot·Upot, where ΔQtot is the variation in the total charge owing to the redox reaction (see the number of electrons in eqn (1)–(4)), and Upot is the electrode potential. The free energy of the Ptnoad state is almost equal to the CHE model result at 0.53 V (aqua dash). The subtle difference by 0.05 eV is due to the reactant molecules computed (H2 in the CHE model and H3O+ in our method). The energies of the Pt–Oad and Pt–OHad states are higher than the CHE model results by 0.24 eV and 0.26 eV, respectively. This indicates that the Pt–OHad state was faintly destabilized owing to the solvation effect compared with the Pt–Oad state by ∼0.02 eV. A previous study using 3D-RISM-SCF also showed that the Pt–OHad state is more destabilized compared with the Pt–Oad state.68
The increase in energy by the solvation effect on the Pt–Oad and Pt–OHad states was larger by ∼0.1 eV as compared to a previous study;68 this is attributed to the use of the gas-phase geometry in this study. This small difference is presumably because the adsorption structure is mainly governed by the strong chemical bond and less affected by the solvation.
The free energy profile at 0.90 V (the red line) is shown in Fig. 2. The ORR at 0.90 V has been widely investigated to determine its standard activity.95–97 The free energies decrease as the electrode potential increases from 0.53 V (the pzc of Ptnoad) to 0.90 V. The Ptnoad, Pt–Oad, and Pt–OHad states are stabilized by 0.73 eV, 0.71 eV, and 0.39 eV, respectively. These energy changes (represented by the blue-red arrows in Fig. 2) are in good agreement with the simple estimation of the electrode potential dependence (i.e., 2·(0.90–0.53) and 1·(0.90–0.53) eV). Thus, the energy difference between our method and the CHE model at 0.90 V is almost the same as the difference at the pzc, although the EDL is generated at 0.90 V. In our calculation, the electrode charging and the solvation structure are explicitly considered and both of them remarkably change via the EDL formation by increasing the electrode potential as discussed below. Nevertheless, the resultant energy dependence on the electrode potential is in agreement with the simple estimation wherein the EDL is neglected. Indeed, the electrode potential dependence of the energy profile using a 0.2 M HClO4 solution is also in good agreement with the simple estimation (section S4†). Therefore, we further analyzed the electrode potential dependence to elucidate the negligible effect of the EDL on the energetics of the present electrochemical system.
3.2 Charge analysis
Table 2 lists the result of the Bader charge analysis. The total charge per unit cell is decomposed into the contribution from the Pt slab and adsorbates O and OH. The adsorbate and Pt surface are negatively and positively charged, respectively, indicating the charge transfer from Pt to O or OH. When the electrode potential increases from 0.53 V (the pzc of Ptnoad) to 0.90 V, the charge on the three models (Ptnoad, Pt–Oad, and Pt–OHad) increases by +0.69e. The double-layer capacitances using 1.0 M and 0.2 M HClO4 solutions were calculated to be 28 μF cm−2 and 26 μF cm−2 on average from the pzc potential to 0.90 V, respectively. A previous theoretical study also showed that the capacitance becomes large as the concentration increases.68 Further, our results are qualitatively in agreement with the experimental result of 20 μF cm−2 using a 0.1 M HClO4 solution.89 We used the DRISM theory which affords better results for electrolyte solutions compared with the standard RISM theory. The electrode potential variation causes the charging of the Pt atoms of Pt–Oad and Pt–OHad by +0.67e, whereas the adsorbates remain negatively charged at 0.90 V (−0.77e and −0.32e for Pt–Oad and Pt–OHad, respectively). The charge variations in the O and OH moieties are approximately +0.02e which are small but not negligible compared with the average variation per surface Pt atom (+0.04e).| Ptnoad | Pt–Oad | Pt–OHad | ||||||
|---|---|---|---|---|---|---|---|---|
| Gas & pzc | 0.90 V | Gas | pzc | 0.90 V | Gas | pzc | 0.90 V | |
| Total | 0.00 | +0.69 | 0.00 | −0.10 | +0.59 | 0.00 | +0.05 | +0.74 |
| Sum of Pt | 0.00 | +0.69 | +0.76 | +0.69 | +1.36 | +0.36 | +0.39 | +1.06 |
| O or OH | — | — | −0.76 | −0.79 | −0.77 | −0.36 | −0.35 | −0.32 |
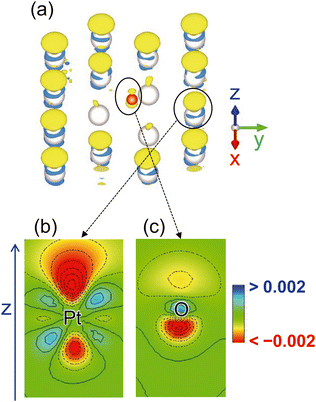
To elucidate the charging mechanism, we determined the change in the electron density distribution on the Pt–Oad surface owing to the electrode potential change from 0.53 V (the pzc of Ptnoad) to 0.90 V. The results are shown in Fig. 3. Only the surface Pt and O atoms are shown for the visibility of the distribution in Fig. 3(a). Enlarged cross sections of the electron density around the Pt and O atoms are shown in Fig. 3(b) and (c), respectively. The electron density mainly decreases in the upper side of the Pt atom (Fig. 3(b)) whereas the decreases are observed in the lower side of the adsorbed O atom near the Pt surface (Fig. 3(c)). These distributions indicate that the charging mechanism around the O atoms is different from that around the surface Pt atoms because of the solvation effect as further discussed below.
3.3 Solvation structure
Fig. 4 shows the average density distribution of the 1.0 M HClO4 solution along the z-axis perpendicular to the Pt surface, , where z is the average distance from the surface Pt atoms, S is the surface area, and g denotes the density distribution. The definition of g is given in section S1.† The distributions of the Cl site of ClO4− (Cla) and O site of H3O+ (Oc) are shown in the figure, those of the other sites are shown in section S5,† and the results of 0.2 M HClO4 solution are shown in section S6.†Fig. 4(a) shows the distributions at 0.53 V (the pzc of Ptnoad). In this study, the water coverage with respect to the surface Pt atoms of Ptnoad was 0.76, which is in good agreement with the AIMD result of 0.68.98 A similar value has previously been reported in an experimental study; two-thirds water coverage has been observed for a water monolayer formed in an ultrahigh vacuum.99 In AIMD calculation, the double peaks were observed at 2.1 Å and 3.0 Å, and their heights were 2.9 and 3.6, respectively.98 When the peak heights and positions are averaged, the resultant averaged values are close to our results (peak position and height of 2.8 Å and 4.5, respectively). The double peak structure itself cannot be reproduced by our method, as our method does not account for the chemisorption of water molecules on the electrode surface. The Cla and Oc distributions have the first peak at ∼4 Å, which is caused by the ions directly attached to the Pt surface. When the adsorbate (O or OH) is present, the distribution of Cla decreases because of repulsion between the negatively charged adsorbate (Table 2) and ClO4−.
, where z is the average distance from the surface Pt atoms, S is the surface area, and g denotes the density distribution. The definition of g is given in section S1.† The distributions of the Cl site of ClO4− (Cla) and O site of H3O+ (Oc) are shown in the figure, those of the other sites are shown in section S5,† and the results of 0.2 M HClO4 solution are shown in section S6.†Fig. 4(a) shows the distributions at 0.53 V (the pzc of Ptnoad). In this study, the water coverage with respect to the surface Pt atoms of Ptnoad was 0.76, which is in good agreement with the AIMD result of 0.68.98 A similar value has previously been reported in an experimental study; two-thirds water coverage has been observed for a water monolayer formed in an ultrahigh vacuum.99 In AIMD calculation, the double peaks were observed at 2.1 Å and 3.0 Å, and their heights were 2.9 and 3.6, respectively.98 When the peak heights and positions are averaged, the resultant averaged values are close to our results (peak position and height of 2.8 Å and 4.5, respectively). The double peak structure itself cannot be reproduced by our method, as our method does not account for the chemisorption of water molecules on the electrode surface. The Cla and Oc distributions have the first peak at ∼4 Å, which is caused by the ions directly attached to the Pt surface. When the adsorbate (O or OH) is present, the distribution of Cla decreases because of repulsion between the negatively charged adsorbate (Table 2) and ClO4−.
Fig. 4(b) shows the distributions at 0.90 V. The first peak of Cla increases whereas that of Oc decreases compared with the result at 0.53 V. The variations in the peak heights indicate that ClO4− accumulates near the Pt surface whereas H3O+ moves away from the surface as the electrode potential increases. Therefore, these distributions at 0.90 V are attributed to the generation of the EDL that mainly consists of a positively charged Pt surface and ClO4− in the electrolyte solution.
Fig. 5 shows the 3D density distributions g(r) of the electrolyte ions around the adsorbate O or OH at 0.53 V (the pzc of Ptnoad). The results of water are given in section S5.† The left and right panels of Fig. 5 show the results for Pt–Oad and Pt–OHad, respectively. The Cla site is mainly distributed above the Pt surface, compared with the area around the O and OH owing to the electrostatic repulsion between ClO4− and the negatively charged adsorbates. In Fig. 5(c) and (d), the Oc site in H3O+ is distributed around the adsorbates, in particular around O. It is due to the attractive interaction between H3O+ and the negatively charged O moiety. Therefore, the peak height of the Oc distribution in Fig. 4 is almost unchanged for Pt–Oad compared with that for Ptnoad despite the steric hindrance due to the O adsorbate.
 | ||
| Fig. 5 3D density distributions g(r) at 0.53 V of Cla at g(r) > 7 for (a) Pt–Oad and (b) Pt–OHad and Oc at g(r) > 4 for (c) Pt–Oad and (d) Pt–OHad. | ||
These 3D solvation structures explain the solvation mechanism of the O and OH adsorbates. Their adsorption on the Pt surface causes destabilization because of the removal of solution from the Pt surface, followed by the stabilization that is mainly caused by the electrostatic interaction. The O adsorbate has a larger negative charge than the OH adsorbate and is stabilized by interaction with positively charged sites (H of H2O and H3O+). In the case of the OH adsorbate, its O moiety locally interacts with positively charged sites (H of H2O and H3O+), and the H moiety interacts with negatively charged sites (O of H2O and ClO4−). The resultant energy change by the solvation effect on the Pt–OHad state then becomes similar to that on the Pt–Oad state, as shown by Fig. 2.
Fig. 6 shows the 3D density distributions g(r) at 0.90 V. The results using different threshold values are shown in section S5.† The Cla distribution is qualitatively unchanged compared with the result at 0.53 V, which is consistent with the moderate increase of the peak height associated with the electrode potential increase (Fig. 4). However, the Oc distribution decreases and is found only around the adsorbate, which is also consistent with the peak height decrease. An experimental study has demonstrated that the ORR activity increases as the cation size becomes large.11 According to our result, it is expected that the interaction strength between the adsorbate and the cation becomes weak as the cation size increases. Consequently, the destabilization of Pt–Oad would promote the formation of the product H2O.
 | ||
| Fig. 6 3D density distributions g(r) at 0.90 V of Cla at g(r) > 7 for (a) Pt–Oad and (b) Pt–OHad and Oc at g(r) > 4 for (c) Pt–Oad and (d) Pt–OHad. | ||
The charge distribution shown in Fig. 3 can be well rationalized from the solvation structure shown in Fig. 6. The anion distributions above the adsorbates are small and do not induce the positive charging of the adsorbates. It is in contrast to the surface Pt atoms on which a large anion distribution is observed. Therefore, the positive charge is distributed on the lower side around the adsorbed O but on the upper side of the surface Pt atoms owing to the Pt–ClO4− electrostatic interaction.
Fig. 5 and 6 show that ClO4− accumulates near the Pt surface whereas the H3O+ moves away from the surface as the electrode potential increases. Therefore, the electrostatic interaction between the negatively charged adsorbate and the electrolyte solution becomes repulsive in total as the electrode potential increases. As a result, the free energies of the Pt–Oad and Pt–OHad states are expected to destabilize relative to that of the Ptnoad state due to the repulsive interaction if their stabilities are solely determined by the electrostatic interaction between the adsorbate and electrolyte solution. However, this expectation about the stability contradicts our result. The free energy profile (Fig. 2) is independent of the EDL formation even though the electron density and solvation structure crucially change. Therefore, the dependence of the energy profile on the electrode potential cannot be rationalized only from the solvation effect.
3.4 Electrostatic potential profiles
The charge density and solvation structure remarkably changed by the EDL formation depending on the electrode potential as aforementioned. Nevertheless, these changes have a negligible effect on the energy profile. To elucidate the negligible effect of the EDL on energetics, in Fig. 7, we show the cross-section of the change in the electrostatic potential, Vps(r) + Vh(r) + Vsol(r) (see section S1† for the definition), due to the increase from 0.53 V (the pzc of Ptnoad) to 0.90 V. The electrode potential increases by 0.37 V; thus, we visualized the electrostatic potential change, ΔVpot, from −0.37 V to 0.37 V. The EDL is almost absent at the pzc but is present at 0.90 V. Therefore, Fig. 7 can be regarded as the electrostatic potential profile of the EDL at 0.90 V. The cross section is obtained by cutting through the position of the adsorbate (O or OH). In Fig. 7(a) for Ptnoad, the negative (blue) distribution above the Pt surface is generated by the electrolyte solution, and the positive (red) distribution in the Pt electrode is due to its positive charging by the electrode potential increase. In Fig. 7(b) and (c), the position of the adsorbed O atom is marked with “+”. The negative distribution becomes smaller above the adsorbate because the anion distribution is smaller than that on the Pt surface. The positive ΔVpot is distributed uniformly and covers the adsorbates and Pt electrode.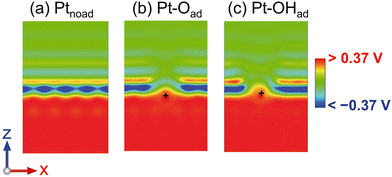 | ||
| Fig. 7 (a)–(c) Cross sections of the change in the electrostatic potential due to the 0.37 V increase relative to the potential of zero charge (pzc) for Ptnoad, Pt–Oad, and Pt–OHad, respectively. The color gradation maps from −0.15 V to 0.15 V are shown in section S7.† | ||
The above results elucidate the dependence of the ORR energy profile on the electrode potential. The electrostatic interaction energy is given as the product of the electrostatic potential Vpot and the charge Q, Vpot·Q. The change in Q, ΔQ, caused by the electrode potential variation is small for the adsorbates compared with the original value of Q, as shown in Table 2. Further, ΔQs of Ptnoad, Pt–Oad, and Pt–OHad are almost the same. Thus, ΔVpot·Q determines the variation in Vpot·Q depending on the electrode potential. The negatively charged adsorbate is stabilized by the positive ΔVpot that covers the adsorbates (the red distributions in Fig. 7(b) and (c)), while the surface Pt atoms are positively charged and thus destabilized by the positive ΔVpot. The total potential Vpot is different in space; however, the potential difference, ΔVpot, is uniform in space as seen from Fig. 7. Thus, the stabilization of the adsorbate induced by the EDL formation is offset by the corresponding destabilization of the surface Pt atoms. Therefore, the electrostatic potential change by the EDL formation does not affect the reaction energy profile.
Fig. 8(a) illustrates the EDL structure revealed by the present study. The electrolyte solution generates the negative ΔVpot in area I, which is above the positively charged Pt surface (area II). The adsorbate is negatively charged independent of the electrode potential. However, as the electrode potential increases to 0.9 V, the magnitude of this negative charge decreases, indicating a relative increase in positive character of the adsorbate (area III) as illustrated in Fig. 8(a). Thus, the adsorbate merges with area II. The EDL consists of areas I and II. In area IV above the adsorbate, cations and anions could coexist. Therefore, the negative potential above the adsorbate is small. Cations in area IV would affect the reaction activity depending on the cation size and the electrolyte concentration as discussed in previous experimental studies.11,14
The present EDL structure is remarkably different from the standard picture shown in Fig. 8(b). The adsorbate was assumed to be between the electrode and electrolyte solution. Therefore, the effect of the EDL has often been evaluated, for example, by adding an external electric field that is assumed to be generated between the electrode and electrolyte solution.100–102 However, our result shows that the adsorbates merge with the electrode surface (Fig. 8(a)); therefore, the EDL does not affect the stability of the adsorbates.
Our study indicates that the electrostatic potential distribution and accordingly the effect of the EDL formation on the reactivity will depend on the size of the adsorbate and the adsorption structure on the electrode. For example, as the adsorbate is away from the electrode surface, the standard EDL picture becomes appropriate as compared to the present EDL scenario because the adsorbate does not merge with the electrode. Indeed, the adsorption strength of physisorbed ions on an electrode depends on the electrode potential.65,103,104 Additionally, as the size of the adsorbate increases, it may longer merge with the electrode surface. In the case of the ORR, the OOH adsorbate in the associative mechanism would be influenced by the EDL because it is separated from the electrode surface compared with the O and OH adsorbates. Therefore, the energy profiles of electrochemical reactions are likely to depend on the atomic-scale details of the EDL structure.
Conclusions
This study investigated the ORR at the interface between a Pt electrode and a HClO4 aqueous solution. To elucidate the relationship between the EDL and the reaction energy profile, theoretical calculations were performed using our 3D-RISM-SCF method. Because of the grand canonical ensemble formulation, this method can give the ensemble average of the EDL structure at the atomic scale by explicitly considering the EDL charging depending on the electrode potential.Our calculation revealed that the solvation affects the reaction energy profile, whereas the electrode potential dependence of the dissociative mechanism was well reproduced with the simple estimation based on the classical electrochemistry. The charge analysis showed that the Pt electrode is positively charged whereas the O adsorbate remains negatively charged at the positive electrode potential. Accordingly, H3O+ locally distributes around the negatively charged adsorbates. The local solvation around the adsorbate could affect the dependence of the ORR activity on the cation size and on the electrolyte concentration, as reported in experimental studies. We further found that the charge distribution and solvation structure remarkably change depending on the electrode potential; nevertheless, these changes do not affect the energetics. Thus, we analyzed the electrostatic potential change owing to the EDL formation and revealed that the complex EDL structure results in the uniform electrostatic potential change that covers the adsorbate and Pt electrode. Therefore, the EDL has a negligible effect on the reaction energy profile.
The EDL investigated in this study has a complex structure, in which all the charged electrode, adsorbate, cations, anions, and solvent are indispensable as constituents. Previous studies showed that the EDL often governs the activity of electrochemical reactions. These studies suggest that the EDL has various influences on electrochemical reactions depending on the atomic-scale details of the EDL structure. Indeed, our detailed analysis also indicates that the atomic scale details of the adsorption structure on the electrode surface, e.g., the adsorbate–surface distance and the adsorbate size, will affect the dependence of electrochemical reactions on the electrode potential. This study provides a novel perspective on the EDL and its effect on electrochemical reactions.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
K. I. planned the study. K. I. and J. H. drafted the manuscript. S. K. performed the calculation using Quantum Espresso. K. I. performed the calculation using SALMON. All authors have approved the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was financially supported by JSPS KAKENHI (Grant No. JP23K17898, JP24K08346, and 25H01266) and the Collaborative Research Program of the Institute for Chemical Research, Kyoto University (Grant No. 2024-62). This work was also supported by the MEXT project, “Integrated Research Consortium on Chemical Sciences” and the Photo-excitonix Project and the Junior Scientist Promotion Project in Hokkaido University. Most of the theoretical computations were performed using the computational resources of the Grand Chariot supercomputer provided by Hokkaido University through the HPCI System Research Project (Project ID: hp230155 and hp240155). Some of the computations were performed at the RCCS (Okazaki, Japan; Project: 24-IMS-C002), Super Computer System, Institute for Chemical Research (Kyoto University).References
- J. O. Bockris and S. U. Khan, Surface Electrochemistry: A Molecular Level Approache, Springer Science & Business Media, 1993, vol. 2 Search PubMed.
- N. Marković and P. Ross Jr, Surf. Sci. Rep., 2002, 45, 117–229 CrossRef.
- M. Osawa, Bull. Chem. Soc. Jpn., 1997, 70, 2861–2880 CrossRef CAS.
- O. M. Magnussen, Chem. Rev., 2002, 102, 679–726 CrossRef CAS PubMed.
- K. Kneipp, M. Moskovits and H. Kneipp, Surface-enhanced Raman scattering: physics and applications, Springer Science & Business Media, 2006, vol. 103 Search PubMed.
- F. Zaera, Chem. Rev., 2012, 112, 2920–2986 CrossRef CAS PubMed.
- M. Saleheen and A. Heyden, ACS Catal., 2018, 8, 2188–2194 CrossRef CAS.
- J. Vatamanu and D. Bedrov, J. Phys. Chem. Lett., 2015, 6, 3594–3609 CrossRef CAS PubMed.
- J.-B. Le, X.-H. Yang, Y.-B. Zhuang, M. Jia and J. Cheng, J. Phys. Chem. Lett., 2021, 12, 8924–8931 CrossRef CAS PubMed.
- K. Schwarz and R. Sundararaman, Surf. Sci. Rep., 2020, 75, 100492 CrossRef CAS PubMed.
- T. Kumeda, H. Tajiri, O. Sakata, N. Hoshi and M. Nakamura, Nat. Commun., 2018, 9, 4378 CrossRef PubMed.
- B. Garlyyev, S. Xue, M. D. Pohl, D. Reinisch and A. S. Bandarenka, ACS Omega, 2018, 3, 15325–15331 CrossRef CAS PubMed.
- J. A. Z. Zeledón, G. A. Kamat, G. K. K. Gunasooriya, J. K. Nørskov, M. B. Stevens and T. F. Jaramillo, ChemElectroChem, 2021, 8, 2467–2478 CrossRef.
- M. Luo and M. T. Koper, Nat. Catal., 2022, 5, 615–623 CrossRef CAS.
- T. Kumeda, L. Laverdure, K. Honkala, M. M. Melander and K. Sakaushi, Angew. Chem., Int. Ed., 2023, 135, e202312841 CrossRef.
- X. Zhao and Y. Liu, J. Am. Chem. Soc., 2021, 143, 9423–9428 CrossRef CAS PubMed.
- S.-J. Qian, H. Cao, J.-W. Chen, J.-C. Chen, Y.-G. Wang and J. Li, ACS Catal., 2022, 12, 11530–11540 CrossRef CAS.
- H. N. Nong, L. J. Falling, A. Bergmann, M. Klingenhof, H. P. Tran, C. Spöri, R. Mom, J. Timoshenko, G. Zichittella and A. Knop-Gericke, et al. , Nature, 2020, 587, 408–413 CrossRef CAS PubMed.
- J. T. Mefford, A. R. Akbashev, M. Kang, C. L. Bentley, W. E. Gent, H. D. Deng, D. H. Alsem, Y.-S. Yu, N. J. Salmon and D. A. Shapiro, et al. , Nature, 2021, 593, 67–73 CrossRef CAS PubMed.
- R. G. Parr and Y. Weitao, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1989 Search PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms To Applications, Elsevier, 2001, vol. 1 Search PubMed.
- D. Marx and J. Hutter, Ab initio molecular dynamics: basic theory and advanced methods, Cambridge University Press, 2009 Search PubMed.
- D. Sholl and J. A. Steckel, Density functional theory: a practical introduction, John Wiley & Sons, 2011 Search PubMed.
- T. Helgaker, P. Jorgensen and J. Olsen, Molecular electronic-structure theory, John Wiley & Sons, 2014 Search PubMed.
- R. M. Martin, Electronic structure: basic theory and practical methods, Cambridge University Press, 2020 Search PubMed.
- H. Nakatsuji, J. Chem. Phys., 1987, 87, 4995 CrossRef CAS.
- A. B. Anderson and D. B. Kang, J. Phys. Chem. A, 1998, 102, 5993 CrossRef CAS.
- I. Tavernelli, R. Vuilleumier and M. Sprik, Phys. Rev. Lett., 2002, 88, 213002 CrossRef PubMed.
- J. Blumberger, L. Bernasconi, I. Tavernelli, R. Vuilleumier and M. Sprik, J. Am. Chem. Soc., 2004, 126, 3928 CrossRef CAS PubMed.
- Y. Cai and A. B. Anderson, J. Phys. Chem. B, 2004, 108, 9829 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886 CrossRef PubMed.
- C. D. Taylor, S. A. Wasileski, J.-S. Filhol and M. Neurock, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165402 CrossRef.
- N. D. Mermin, Phys. Rev., 1965, 137, A1441 CrossRef.
- C. Bureau and G. Lécayon, J. Chem. Phys., 1997, 106, 8821 CrossRef CAS.
- A. Y. Lozovoi, A. Alavi, J. Kohanoff and R. M. Lynden-Bell, J. Chem. Phys., 2001, 115, 1661 CrossRef CAS.
- K. Shiratori and K. Nobusada, Chem. Phys. Lett., 2008, 451, 158–162 CrossRef CAS.
- W. B. Schneider and A. A. Auer, Beilstein J. Nanotechnol., 2014, 5, 668 CrossRef PubMed.
- S. Jacobi and R. Baer, J. Chem. Phys., 2005, 123, 044112 CrossRef PubMed.
- M. Otani and O. Sugino, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115407 CrossRef.
- K. Iida, T. Yasuike and K. Nobusada, J. Chem. Phys., 2013, 139, 104101 CrossRef PubMed.
- R. Sundararaman and W. A. Goddard, J. Chem. Phys., 2015, 142, 064107 CrossRef PubMed.
- R. Sundararaman, W. A. Goddard and T. A. Arias, J. Chem. Phys., 2017, 146, 114104 CrossRef PubMed.
- M. M. Melander, M. J. Kuisma, T. E. K. Christensen and K. Honkala, J. Chem. Phys., 2019, 150, 041706 CrossRef PubMed.
- C. A. Rozzi, D. Varsano, A. Marini, E. K. Gross and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205119 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed.
- D. Chandler and H. C. Andersen, J. Chem. Phys., 1972, 57, 1930–1937 CrossRef CAS.
- F. Hirata and P. J. Rossky, Chem. Phys. Lett., 1981, 83, 329–334 CrossRef CAS.
- F. Hirata, Molecular theory of solvation, Springer Science & Business Media, 2003, vol. 24 Search PubMed.
- J. Perkyns and B. M. Pettitt, Chem. Phys. Lett., 1992, 190, 626–630 CrossRef CAS.
- A. Kovalenko and F. Hirata, J. Chem. Phys., 2000, 112, 10391–10402 CrossRef CAS.
- A. Kovalenko and F. Hirata, Chem. Phys. Lett., 1998, 290, 237–244 CrossRef CAS.
- A. Kovalenko and F. Hirata, J.Chem. Phys., 1999, 110, 10095–10112 CrossRef CAS.
- I. Vyalov and W. Rocchia, J. Chem. Phys., 2018, 148, 114106 CrossRef PubMed.
- S. Nishihara and M. Otani, Phys. Rev. B, 2017, 96, 115429 CrossRef.
- K. Iida, J. Phys. Chem. C, 2022, 126, 9466–9474 CrossRef CAS.
- M. Noda, S. A. Sato, Y. Hirokawa, M. Uemoto, T. Takeuchi, S. Yamada, A. Yamada, Y. Shinohara, M. Yamaguchi and K. Iida, et al. , Comput. Phys. Commun., 2019, 235, 356 CrossRef CAS.
- D. A. Case, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, A. Kovalenko, R. Krasny, T. Kurtzman, T. S. Lee, S. LeGrand, C. L. P. Li, J. Liu, T. Luchko, R. Luo, V. Man, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, A. Onufriev, F. Pan, S. Pantano, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, L. Wilson, R. M. Wolf, Y. X. X. Wu, Y. Xue, D. M. York and P. Kollman, Amber 20, University Of California Technical Report, 2020 Search PubMed.
- K. Yoshida, T. Yamaguchi, A. Kovalenko and F. Hirata, J. Phys. Chem. B, 2002, 106, 5042–5049 CrossRef CAS.
- H. Heinz, R. Vaia, B. Farmer and R. Naik, J. Phys. Chem. C, 2008, 112, 17281–17290 CrossRef CAS.
- B. Doherty, X. Zhong, S. Gathiaka, B. Li and O. Acevedo, J. Chem. Theory Comput., 2017, 13, 6131–6145 CrossRef CAS PubMed.
- A. Takamatsu, M. Higashi and H. Sato, Chem. Lett., 2022, 51, 791–795 CrossRef CAS.
- R. Gómez, J. M. Orts, B. Álvarez-Ruiz and J. M. Feliu, J. Phys. Chem. B, 2004, 108, 228–238 CrossRef.
- M. Teliska, V. S. Murthi, S. Mukerjee and D. E. Ramaker, J. Phys. Chem. C, 2007, 111, 9267–9274 CrossRef CAS.
- G. A. Kamat, J. A. Z. Zeledón, G. K. K. Gunasooriya, S. M. Dull, J. T. Perryman, J. K. Nørskov, M. B. Stevens and T. F. Jaramillo, Commun. Chem., 2022, 5, 20 CrossRef CAS PubMed.
- S. Phongphanphanee, N. Yoshida and F. Hirata, J. Mol. Liq., 2009, 147, 107–111 CrossRef CAS.
- R. Tesch, P. M. Kowalski and M. H. Eikerling, J. Phys.: Condens. Matter, 2021, 33, 444004 CrossRef CAS PubMed.
- T. Demeyere and C.-K. Skylaris, J. Phys. Chem. C, 2024, 128, 19586–19600 CrossRef CAS.
- M. Chen, H.-Y. Ko, R. C. Remsing, M. F. C. Andrade, B. Santra, Z. Sun, A. Selloni, R. Car, M. L. Klein and J. P. Perdew, et al. , Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10846–10851 CrossRef CAS PubMed.
- T. Fujita and T. Yamamoto, J. Chem. Phys., 2017, 147, 014110 CrossRef PubMed.
- T. Miyata, S. Ito, K. Hyodo and K. Shinmoto, Phys. A, 2024, 646, 129890 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- V. Barone, M. Casarin, D. Forrer, M. Pavone, M. Sambi and A. Vittadini, J. Comput. Chem., 2009, 30, 934–939 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- H. Nakai and A. Ishikawa, J. Chem. Phys., 2014, 141, 174106 CrossRef PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993 CrossRef CAS PubMed.
- M. Fuchs and M. Scheffler, Comput. Phys. Commun., 1999, 119, 67–98 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- A. M. Verma, L. Laverdure, M. M. Melander and K. Honkala, ACS Catal., 2021, 12, 662–675 CrossRef.
- Y. Sha, T. H. Yu, Y. Liu, B. V. Merinov and W. A. Goddard III, J. Phys. Chem. Lett., 2010, 1, 856–861 CrossRef CAS.
- A. Malek and M. H. Eikerling, Electrocatalysis, 2018, 9, 370–379 CrossRef CAS.
- E. Gileadi, S. Argade and J. O. Bockris, J. Phys. Chem., 1966, 70, 2044–2046 CrossRef CAS.
- T. Pajkossy and D. Kolb, Electrochim. Acta, 2001, 46, 3063–3071 CrossRef CAS.
- A. Cuesta, Surf. Sci., 2004, 572, 11–22 CrossRef CAS.
- R. Rizo, E. Sitta, E. Herrero, V. Climent and J. M. Feliu, Electrochim. Acta, 2015, 162, 138–145 CrossRef CAS.
- K. Ojha, N. Arulmozhi, D. Aranzales and M. T. Koper, Angew. Chem., 2020, 132, 721–725 CrossRef.
- S. Hagiwara, S. Nishihara, F. Kuroda and M. Otani, Phys. Rev. Mater., 2022, 6, 093802 CrossRef CAS.
- P. Xu, A. D. von Rueden, R. Schimmenti, M. Mavrikakis and J. Suntivich, Nat. Mater., 2023, 22, 503–510 CrossRef CAS PubMed.
- H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Appl. Catal., B, 2005, 56, 9–35 CrossRef CAS.
- K. Shinozaki, J. W. Zack, R. M. Richards, B. S. Pivovar and S. S. Kocha, J. Electrochem. Soc., 2015, 162, F1144 CrossRef CAS.
- T. Kawawaki, Y. Mitomi, N. Nishi, R. Kurosaki, K. Oiwa, T. Tanaka, H. Hirase, S. Miyajima, Y. Niihori and D. Osborn, et al. , Nanoscale, 2023, 15, 7272–7279 RSC.
- S. Sakong and A. Groß, Phys. Chem. Chem. Phys., 2020, 22, 10431–10437 RSC.
- H. Ogasawara, B. Brena, D. Nordlund, M. Nyberg, A. Pelmenschikov, L. Pettersson and A. Nilsson, Phys. Rev. Lett., 2002, 89, 276102 CrossRef CAS PubMed.
- G. Karlberg, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 5158 RSC.
- K.-Y. Yeh, S. A. Wasileski and M. J. Janik, Phys. Chem. Chem. Phys., 2009, 11, 10108–10117 RSC.
- S. R. Kelly, C. Kirk, K. Chan and J. K. Nørskov, J. Phys. Chem. C, 2020, 124, 14581–14591 CrossRef CAS.
- M. L. Foresti, M. Innocenti, F. Forni and R. Guidelli, Langmuir, 1998, 14, 7008–7016 CrossRef CAS.
- J. Mostany, E. Herrero, J. M. Feliu and J. Lipkowski, J. Phys. Chem. B, 2002, 106, 12787–12796 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The details of the theoretical method, the computational results of the homogeneous solution, the dependence of the free energy on the electrolyte concentration, the solvation structure, and the variation in the electrostatic potential depending on the electrode potential. See DOI: https://doi.org/10.1039/d5cy00369e |
| This journal is © The Royal Society of Chemistry 2025 |