Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Lowering the exponential wall: accelerating high-entropy alloy catalysts screening using local surface energy descriptors from neural network potentials
Tomoya
Shiota†
 *ab,
Kenji
Ishihara†
*ab,
Kenji
Ishihara†
 b and
Wataru
Mizukami
b and
Wataru
Mizukami
 *ab
*ab
aGraduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560-8531, Japan. E-mail: shiota.tomoya.ss@gmail.com; mizukami.wataru.qiqb@osaka-u.ac.jp
bCenter for Quantum Information and Quantum Biology, Osaka University, 1-2 Machikaneyama, Toyonaka 560-8531, Japan
First published on 29th January 2025
Abstract
Computational screening is indispensable for the efficient design of high-entropy alloys (HEAs), which hold considerable potential for catalytic applications. However, the chemical space of HEAs is exponentially vast with respect to the number of constituent elements, making even machine learning-based screening calculations time-intensive. To address this challenge, we propose a rapid method for predicting HEA properties using data from monometallic systems (or few-component alloys). Central to our approach is the newly introduced local surface energy (LSE) descriptor, which captures local surface reactivity at atomic resolution. We established a correlation between LSE and adsorption energies using monometallic systems. Using this correlation in a linear regression model, we successfully estimated molecular adsorption energies on HEAs with significantly higher accuracy than a conventional descriptor (i.e., generalized coordination numbers). Furthermore, we developed high-precision models by employing both classical and quantum machine learning. Our method enabled CO adsorption-energy calculations for 1000 quinary nanoparticles, comprising 201 atoms each, within a few days, considerably faster than density functional theory, which would require hundreds of years or neural network potentials, which would have taken hundreds of days. The proposed approach accelerates the exploration of the vast HEA chemical space, facilitating the design of novel catalysts.
1 Introduction
High-entropy alloys (HEAs), composed of five or more elemental species at concentrations ranging from 5 to 35 at%, have emerged as versatile materials with promising applications in catalysis and as functional materials.1–4 Their rich compositional diversity facilitates the way for the “cocktail effect”, resulting in unexpected properties that often surpass those of traditional single-element systems.3,5 Recent advancements have highlighted their superior catalytic performance;6–9 however, the vast array of potential combinations of elements poses a significant challenge for experimental exploration.To address this complexity, studies have focused on computational methods for efficient screening.9–13 First-principles calculations, such as density functional theory (DFT),14–17 coupled cluster (CC) theory18–20 and many-body perturbation theory (MBPT),21,22 describe chemical reactions on solid surfaces with high accuracy. Volcano plots, derived from first-principles calculations, illustrate the optimal adsorption energy range for catalytic activity, balancing between excessively strong and weak interactions.13,23,24 However, the heterogeneous surfaces of HEAs complicate the molecular adsorption characteristics, making first-principles approaches computationally intensive.
To circumvent these limitations, neural network potentials (NNPs) based on the Behler–Parrinello framework25–29 and graph neural networks,30–33 offer promising solutions. Universal NNPs can encompass extensive elemental diversity and achieve high computational efficiency while maintaining accuracy on par with that of DFT.31,32,34–47 Recently, NNPs specializing in HEAs have emerged, made more lightweight through knowledge distillation.48 These advances have accelerated the prediction of catalytic properties; however, computational challenges remain.
In contrast, descriptor-based machine learning models offer scalability by predicting adsorption energies through generalized coordination numbers (GCNs), d-band centers, surface microstructural features, and local atomic environments, bypassing direct energy assessments.10,11,49–56 These models have been proposed for predicting the adsorption energies of the remaining candidates by regressing the adsorption energies obtained from several first-principles calculations. Nonetheless, their applicability to HEAs is hampered by the complexity of alloy compositions and their dependence on extensive first-principles calculations.
To address these challenges, we propose a methodology for predicting the molecular adsorption energies on multi-element surfaces, such as HEAs, without direct adsorption-energy computations. Our approach focuses on a new descriptor that reflects the local reactivity of solid surfaces at atomic resolution. A key feature of the proposed method is its ability to predict the properties of multi-element systems using models constructed from data on single-element systems. We validated our method by comparing it with DFT for predicting the adsorption energies of CO on IrPdPtRhRu HEA NPs.
2 Methods
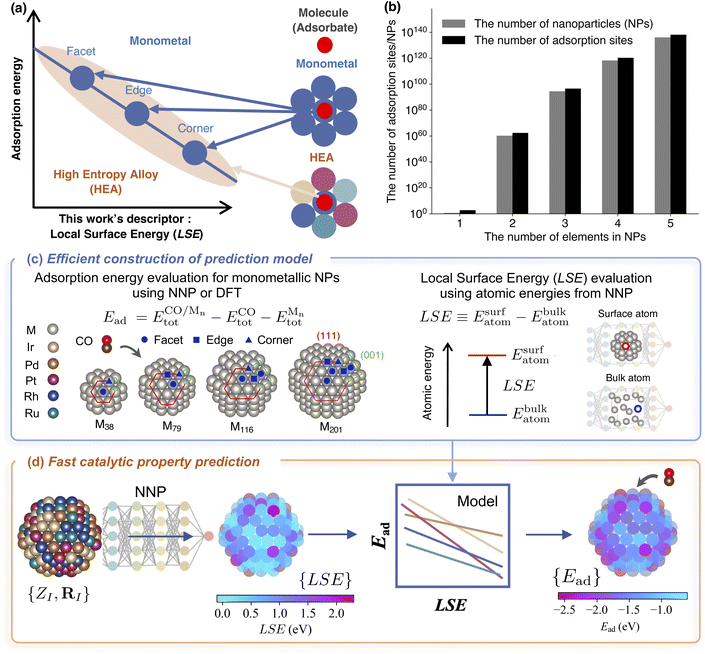
In this section, we introduce a novel model that employs data on monometallic surfaces to predict molecular adsorption energies on multimetallic surfaces. In Section 2.1, we clarify the target systems and the problems addressed in this study. In Section 2.2, we introduce the LSE—a scalar descriptor that captures the atomic-level surface stability—which is the foundation of our model construction and prediction. Section 2.3 outlines the methodologies employed to develop and refine the prediction model using the newly introduced LSE descriptor and data derived from monometallic surfaces.2.1 Target systems and problems
Designing new HEAs comprising five elements selected from a pool of approximately 40 different elemental candidates results in approximately 6.58 × 105 possible combinations. Moreover, even for a given set of five elements, an exponentially large degree of freedom exists in the distribution of these elements in the actual alloy. Furthermore, the catalysts synthesized in practice and use are NPs, which differ from ideal surfaces in that they contain sites with different coordination numbers, such as corners, edges, and facets (Fig. 1(b)). These diverse surface environments are the source of the cocktail effect, which contributes to the variability in catalytic properties. However, considering all these degrees of freedom when screening new catalyst candidates is not feasible. In this study, our objective was to identify the distribution of molecular adsorption energies, assuming that the elemental composition, size, and shape of the HEA NPs were predetermined.We made the following assumptions regarding the structure and composition of HEA NPs: the structure is a truncated octahedron NP with 201 atoms in a face-centered cubic (fcc) arrangement (see Fig. 1(d)), the elemental composition ratio is as uniform as possible, and the atomic arrangement is randomly determined following a uniform distribution. We also assumed that the molecule occupied only a single top site. In HEA201, there are 122 sites. Even with these assumptions, the number of adsorption sites on HEA NPs is approximately 1.3 × 10138 (Fig. 1(a)).
As a specific demonstration system, we measured the adsorption energies of CO molecules on IrPdPtRhRu NPs. In 2020, Wu et al. successfully synthesized IrPdPtRhRu NPs with nearly identical experimental composition ratios.6 The investigation of the adsorption characteristics of CO molecules is useful for evaluating the catalytic properties of HEAs.11,57 As precursor systems for developing predictive models for HEAs, the monometallic NPs are of the truncated octahedron type corresponding to Mnn = 38, 79, 116, 201. For the on-top adsorption of the CO molecule on monometallic NPs M201, only the irreducible adsorption sites are calculated as shown in Fig. 1(c). The adsorption energy Ead is calculated as follows:
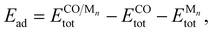 | (1) |
 , ECOtot, and
, ECOtot, and  denote the total energies of CO/Mn, CO, and Mn, respectively. The adsorption energies were computed using both the pretrained universal NNP M3GNet36 and DFT at the Perdew–Burke–Ernzerhof (PBE) level.
denote the total energies of CO/Mn, CO, and Mn, respectively. The adsorption energies were computed using both the pretrained universal NNP M3GNet36 and DFT at the Perdew–Burke–Ernzerhof (PBE) level.
2.2 Local surface energy (LSE) descriptor
The LSE descriptor is defined as follows:| LSE ≡ Esurfatom − Ebulkatom, | (2) |
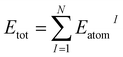 | (3) |
Yoo et al. demonstrated the ability to map the atomic energies obtained by NNPs onto NP and surface systems.64 Deringer et al. utilized the Gaussian approximation potential model to compute the atomic energies, which were then used to explore the configurational space and investigate the nature of defects in crystals.65,66 MLIPs such as NNPs enable efficient evaluation of LSEs because the atomic energies of all adsorption sites in one system can be obtained in a single calculation. Fig. 2 illustrates the workflow for evaluating the Local Surface Energy (LSE) using a pre-trained universal NNP.
2.3 Prediction model based on monometallic data
We introduce a predictive model for the adsorption energy of a molecule on a multi-element surface. This model is defined as a regression between the molecular adsorption energy on monometallic surfaces for each constituent element M of the multimetallic system and the LSE of the adsorption site prior to molecular adsorption. Fig. 1(c) illustrates the workflow for constructing the predictive model. As the simplest model, we adopted the least-squares linear regression model expressed as follows:| EMad(Predict.) = αM × LSE + βM. | (4) |
3 Results
In this section, we present the results for the prediction of the adsorption energy of HEA NPs using the proposed methods based on the LSE descriptor, focusing on the computational efficiency and precision. In Section 3.1, we demonstrate a strong correlation between the adsorption energy and the LSE descriptor, confirming that the LSE is a reliable descriptor of the adsorption energy between different sites in the NP. In Section 3.2, we verify the accuracy of LSE-based predictions by comparing them with DFT calculations, thereby proving the robustness of the prediction model. In Section 3.3, we analyze how the diverse surface structures and elemental compositions of 1000 different HEA NPs, comprising 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 environments, lead to a wide range of adsorption-energy distributions. Finally, in Section 3.4, we compare the computational efficiency of our LSE-based adsorption energy predictions with that of direct adsorption-energy predictions using the traditional NNP and DFT methods.
000 environments, lead to a wide range of adsorption-energy distributions. Finally, in Section 3.4, we compare the computational efficiency of our LSE-based adsorption energy predictions with that of direct adsorption-energy predictions using the traditional NNP and DFT methods.
3.1 Correlation between adsorption energy and LSE
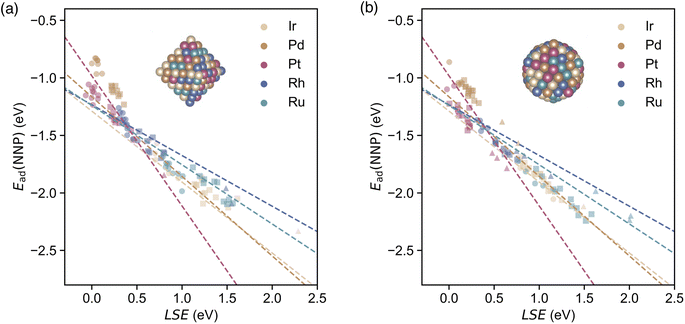
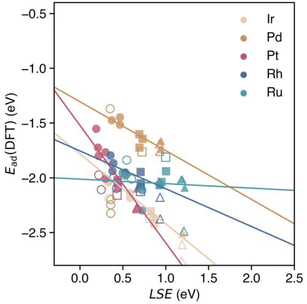
The correlation between the LSE and the CO adsorption energy Ead(NNP) of the monometallic NPs obtained using the NNP is shown in Fig. 3. The solid lines represent linear regressions of the adsorption energies of a CO molecule at the top sites of each monometallic system. For all the metal elements, the relationship between the adsorption energy Ead(NNP) of the CO molecule at the top site and the LSE is linear. The LSE values of all the adsorption sites for all elements range from approximately 0.2 to 1.2 eV. In other words, in all cases, the atomic energies are more unstable in the surface environment than in the bulk environment, which is reasonable given the lower coordination number in the surface environment. The adsorption energy Ead(NNP) ranges from approximately −1.2 to −2.0 eV. Next, we examined the adsorption sites on the NPs. For all elements, the adsorption energy decreased in the following order: facets, edges, and corners. In contrast, the LSE values increased in the order of facets, edges, and corners. The LSE values and adsorption energies were concentrated at the facets, edges, and corners, and energy gaps existed between each group of adsorption sites. The RMSE was 0.035 eV, revealing a strong correlation between the LSE and the adsorption energy (see Fig. 9 in the details of the LSE-based regression models in Appendix).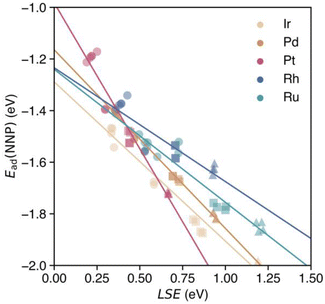 | ||
| Fig. 3 Adsorption energies of CO calculated using the NNP for each on-top adsorption site of monometallic NPs Mn with respect to the LSE. Solid lines represent the linear regressions of the adsorption energies of a CO molecule at the on-top sites of each monometallic NP according to eqn (4). Circles, squares, and triangles at each datapoint represent the facet, edge, and corner CO adsorption sites, respectively. | ||
Fig. 4 presents the adsorption energies calculated directly using the NNP and their predicted values (dashed lines). The RMSE was 0.150 eV, which exceeded that of the unitary system. However, a strong correlation was observed between the LSE and adsorption energy in the HEA, indicating that the adsorption energy in a multicomponent environment can be effectively predicted (Fig. 11(a) and (b) in the Appendix). This finding suggests that the LSE can efficiently and accurately predict the adsorption energies not only for unitary systems but also for complex systems such as HEAs. Notably, when we used the adsorption-energy range of −2.0 to −1.2 eV in the unitary system as the interpolation region for Ead(Predict.), the predictions were more reliable than those for other ranges. In the extrapolation region of Ead (Predict.), the difference from Ead(NNP) increased, and a maximum shift of approximately 0.5 eV was observed.
 | ||
| Fig. 4 Adsorption energies of CO calculated using the NNP for each on-top adsorption site of 20 HEA201 NPs with respect to the LSE. The inset presents a comparison of the distribution of adsorption energies for CO between the HEA NPs and monometallic NPs, with the x- and y-axes rescaled from Fig. 3 for consistency. Dashed lines represent the linear regressions of the adsorption energies of a CO molecule at the on-top sites of each monometallic NP based on eqn (4). Circles, squares, and triangles at each datapoint represent the facet, edge, and corner CO adsorption sites, respectively. | ||
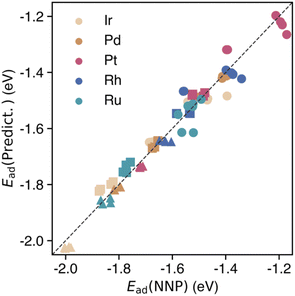
Next, we explored the trends for each elemental species. Fig. 4, 11(a) and (b) in the Appendix show that for all elemental species, the adsorption energies are nonlinearly estimated toward the unstable adsorption energy side. Additionally, the nonlinear region was dominated by adsorption at the facet sites. Pd atoms in HEA nanoparticles clearly show this non-linear behavior; unlike Pt atoms, they show a reversed pattern of adsorption energies. Compared to sites with low coordination numbers, such as corner and edge sites, the atoms on the facets were coordinated with eight or nine atoms. This increased coordination number renders them more sensitive to the surrounding environment than unitary systems. Consequently, the complex environment of HEAs may introduce unexpected nonlinearity into predictions. To show that this nonlinear trend can be captured by training the adsorption energies on HEA NPs, we applied kernel ridge regression (KRR) and quantum circuit learning (QCL) regression67 to construct an adsorption energy prediction model for each elemental species at the HEA NP adsorption sites. Fig. 11(c) and (d) in the Appendix show the correlation plots between the predicted and actual adsorption energies of CO on 14 HEA NP patterns generated by the regression model using KRR and QCL regression, respectively. The RMSEs of the adsorption energy predictions for all the adsorption sites provided by the KRR and QCL regression models were 0.0580 and 0.0579 eV, respectively, indicating comparable nonlinear regression performance. Compared with the uncorrected predictions based on the LSE, the RMSE values were reduced by a factor of approximately three.
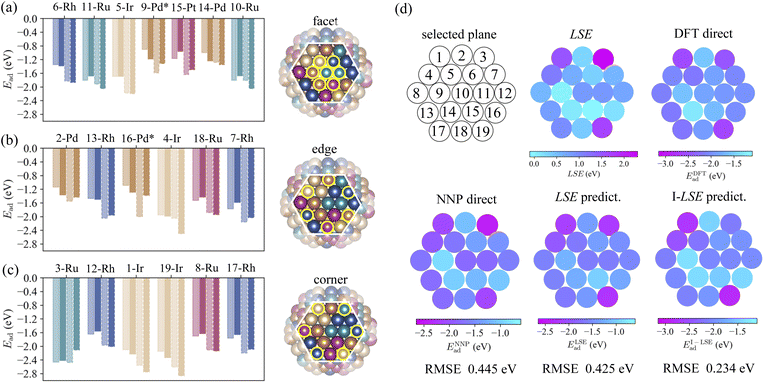
3.2 DFT verification of the LSE-based predictions
The accuracy of the adsorption energy predictions was verified using an NNP and the LSE with DFT calculations while seeking to increase the prediction accuracy. In our computing environment, the computation time for evaluating the adsorption energy via DFT was approximately 103 times that of the NNP, as indicated by Table 1. Therefore, we randomly selected one of the 20 structures of HEA201 discussed above and evaluated the adsorption energies for 19 sites on the (111) plane, as shown on the right side of Fig. 5. The selected HEA201 was Ir40Pd40Pt41Rh40Ru40. First, the prediction accuracy of the adsorption energies between the prediction based on the LSE and direct NNP calculation was compared with that of the DFT calculations. The RMSE of the adsorption energy for all sites obtained via the direct NNP calculation was 0.445 eV. The RMSE value of the prediction based on the LSE was 0.425 eV, corresponding to a slightly higher accuracy (0.020 eV) compared with the direct evaluation via the NNP. Thus, the accuracy of the prediction model using the LSE was close to that of the NNP. Although the RMSE of 0.445 eV for direct NNP calculations may appear large, the M3GNet NNP systematically overestimates CO adsorption energies, with a mean error (ME) of 0.388 eV relative to DFT as shown in Fig. 5. A similar overestimation trend is observed for monometallic NPs, where the RMSE and ME against DFT are 0.439 eV and 0.379 eV, respectively. As a result, the LSE-based prediction also displays a systematic overestimation of the CO adsorption energy in comparison with DFT. Notably, the adsorption energy range for the 19 HEA sites spans from 1.329 eV to 1.567 eV (by DFT and NNP, respectively), indicating a broad distribution of possible adsorption energies. Given this wide range, a constant shift between NNP and DFT remains comparatively tolerable for high-throughput screening of HEA catalysts.| Total time [sec.] | Total step [step] | sec./step | |
|---|---|---|---|
| a NNP calculations with M3GNet were performed using an AMD EPYC 7532 32-core processor with 64 CPUs. b DFT calculations with VASP were performed using 10 Intel(R) Xeon(R) Platinum 9242 CPUs each with 96 CPUs in an MPI parallel configuration, for 960 CPUs. | |||
| NNPa | 2314 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 480 |
0.22 |
| DFTb | 925![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 518 518 |
5008 | 184.81 |
While the M3GNet NNP has difficulty quantitatively describing CO-adsorbed states, it effectively captures the atomic-level stability of the NPs. This is supported by the small RMSD (0.09 Å) between the DFT-relaxed and NNP-relaxed HEA NP structures, as well as the LSE RMSE of 0.026 eV for the 19 target sites, indicating that M3GNet—trained on diverse crystal environments—can reliably describe complex HEA NP configurations despite their absence from its original training set. Consequently, by combining DFT-derived adsorption energies for monometallic NPs with M3GNet-derived LSE (i.e., the I-LSE method), the prediction error is halved to an RMSE of 0.234 eV. This improvement arises because the LSEs are calculated from the NPs before adsorption, thereby avoiding the systematic overestimation of adsorption energy found in direct NNP calculations, while retaining the efficiency of an LSE-based framework.
3.3 Distribution of the adsorption energy on HEA NPs
Fig. 6(a) shows the 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 LSE values of 1000 HEA NPs for each element and their total distribution. This distribution becomes smoother and converges as the number of NP patterns increases. The sum of all the elemental distributions shown in gray in Fig. 6(a) can be considered as an indicator of the reactivity of the entire HEA NP surface of the given elements. In the monometallic system, the LSE ranged from approximately 0.2 to 1.2 eV. However, in the quintic HEA environment, these values underwent significant changes and ranged from approximately −0.1 to 2.4 eV. The distribution of each element exhibited two prominent peaks. For Pt and Pd, the LSE exhibited a major peak near 0 eV (or a slightly lower energy), indicating improved stability compared with that in the monometallic environment. Second, the smaller peak remained nearly unchanged for Pd, whereas the LSE range expanded by approximately 0.3 eV for Pt. For Ir and Ru, the LSE values shifted toward higher energies compared with those in the monometallic systems. For Rh, a slight increase in the LSE range was observed, lying between those of the stable Pt and Pd groups and the less stable Ir and Ru groups.
000 LSE values of 1000 HEA NPs for each element and their total distribution. This distribution becomes smoother and converges as the number of NP patterns increases. The sum of all the elemental distributions shown in gray in Fig. 6(a) can be considered as an indicator of the reactivity of the entire HEA NP surface of the given elements. In the monometallic system, the LSE ranged from approximately 0.2 to 1.2 eV. However, in the quintic HEA environment, these values underwent significant changes and ranged from approximately −0.1 to 2.4 eV. The distribution of each element exhibited two prominent peaks. For Pt and Pd, the LSE exhibited a major peak near 0 eV (or a slightly lower energy), indicating improved stability compared with that in the monometallic environment. Second, the smaller peak remained nearly unchanged for Pd, whereas the LSE range expanded by approximately 0.3 eV for Pt. For Ir and Ru, the LSE values shifted toward higher energies compared with those in the monometallic systems. For Rh, a slight increase in the LSE range was observed, lying between those of the stable Pt and Pd groups and the less stable Ir and Ru groups.
 | ||
Fig. 6 (a) Distributions of 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 LSE values of all the topmost layer atoms of the 1000 structure-optimized HEA201 NPs for each element and their sum, respectively. (b) Distributions of adsorption energies of CO for all the on-top adsorption sites predicted using the LSEs in (a) and eqn (4). Solid lines represent the values for monometallic NP M201 (M = Ir, Pd, Pt, Rh, and Ru). 000 LSE values of all the topmost layer atoms of the 1000 structure-optimized HEA201 NPs for each element and their sum, respectively. (b) Distributions of adsorption energies of CO for all the on-top adsorption sites predicted using the LSEs in (a) and eqn (4). Solid lines represent the values for monometallic NP M201 (M = Ir, Pd, Pt, Rh, and Ru). | ||
Fig. 6(b) presents the predicted adsorption energies of CO on all the on-top sites of 1000 HEA201 NPs obtained using eqn (4) with LSE values. The range of the on-top adsorption energy Ead for CO in the monometallic system (Fig. 3) expanded by approximately 0.8 eV, from approximately −2.0 to −1.2 eV to −2.5 to −0.9 eV. This serves as an example of how adsorption characteristics diversify in a quintic HEA environment. The distribution of the adsorption energies for each element also exhibited two prominent peaks. Next, we examined the differences between the elemental species. For Pd and Pt, the LSE values were very close, but the range of adsorption energies was broader on the high-energy side by 0.2 eV for Pt. Similar trends were observed for Ir and Ru on the low-energy side. In the case of Rh, a slight extension in the range of both the high- and low-energy sides was observed compared with that of the monometallic system. In particular, the adsorption energy was concentrated in three adsorption site groups (corners, edges, and facets) in the monometallic NP environment, but these groups exhibited a broader range of values in the HEA NP environment. This representation as a distribution can help characterize and visualize the potential cocktail effect for efficient screening of novel HEAs across the periodic table.
3.4 Universality of the LSE-based method
In this section, we discuss the universality of the LSE-based prediction model constructed in this study. As described in Section 3.1, due to the vastness of the chemical space for HEA NPs, we restricted both the model construction and the target NP shape to truncated octahedra. However, the LSE-based model can be universally applied to any HEA NP shape, provided the structure is given. This is because the universal NNP is capable of evaluating atomic energies for the given structure and thus computing the LSEs. The resulting LSEs can then be fed into the LSE-based model—originally constructed using monometallic data—to predict adsorption energies for the given HEA NP.To verify the shape-independence of LSE-based prediction models, we evaluated its performance on two test sets: HEA146 in the form of a regular octahedron and HEA147 in the form of an icosahedron, as shown in the respective subsets in Fig. 7(a) and (b). These shapes were selected because they are among the most prevalent geometries for fcc NPs. Fig. 7(a) and (b) present the predicted CO adsorption energies from the NNP for all possible ontop sites on the regular octahedron and icosahedron, respectively. The corresponding LSE-based predictions are represented by the dashed lines as a function of LSE. For both NP shapes, we found clear correlations with the predictions obtained from the LSE-based model. The RMSE were 0.156 eV for the regular octahedron and 0.142 eV for the icosahedron, comparable to the RMSE of 0.150 eV achieved for truncated octahedra. These results demonstrate that our predictive framework exhibits universality with respect to NP shape within this scope.
It should be noted that while regular octahedra and icosahedra showcase the applicability of the LSE-based method for commonly explored fcc morphologies, many other potential NP shapes and surface reconstructions remain unexplored in this study. We focus here on the representative geometries to illustrate the applicability of the method, recognizing that a comprehensive proof of “universality” would require testing across more diverse crystal structures and potential defect sites of the HEA NPs. These aspects, along with extensions to other chemical compositions and surface features, are promising avenues for future research.
3.5 Comparison with GCN-based prediction model
In this section, we employ a GCN descriptor—a scalar descriptor similar to LSE—to construct a prediction model based on monometallic data and compare its predictive accuracy. The GCN descriptor quantifies the environment of the adsorption site by counting the coordination number of the nearest-neighbor atoms, and it is defined in ref. 49 Following the same approach used for the LSE-based predictive model of eqn (4), we examined the correlation between CO adsorption energies on monometallic surfaces and GCN values. Linear regression models were then constructed for each element type. As shown in Fig. 8(a), similar to LSE, a linear model accurately represents the relationship, achieving a precision of approximately 0.06 eV. The parameters of the linear regression models are summarized in Table 4 in Appendix section.Subsequently, we applied these linear models to predict the adsorption energies of the 20 HEA NPs presented in the Results section to evaluate the prediction accuracy. As depicted in Fig. 8(b), although the GCN-based predictions correlate with the directly computed adsorption energies, the discrete nature of GCN leads to variations of approximately from 1 to 1.5 eV even for identical GCN values. The resulting RMSE was 0.278 eV, approximately twice as large as that obtained using the LSE-based predictions, indicating that GCN alone is insufficient for capturing the environmental changes in multicomponent systems. This trend is consistent with findings reported by Nanba et al.51 Nonetheless, future improvements may be possible by combining GCN with other descriptors, such as LSE, to enhance the predictive capabilities of monometallic data-based adsorption energy prediction models.
3.6 Computational efficiency
Finally, we compared the computational performance of our method with that of conventional approaches for obtaining adsorption energy distributions. The time required to predict the adsorption energies of CO at 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sites across 1000 patterns of HEA201 using LSE was compared with the time required for direct calculations using the NNP and DFT. The use of the LSE eliminates the need for optimization of the adsorption structure for CO molecules. The computation times for the NNP and DFT are presented in Table 1. The computation time per structural optimization step with the NNP was approximately 1000 times shorter than that with DFT. However, as mentioned in Section 3.4, performing direct structural optimizations for 122
000 sites across 1000 patterns of HEA201 using LSE was compared with the time required for direct calculations using the NNP and DFT. The use of the LSE eliminates the need for optimization of the adsorption structure for CO molecules. The computation times for the NNP and DFT are presented in Table 1. The computation time per structural optimization step with the NNP was approximately 1000 times shorter than that with DFT. However, as mentioned in Section 3.4, performing direct structural optimizations for 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 adsorption sites requires approximately 171 days using the NNP and 188 years using DFT. These lengthy timescales were avoided by using the proposed method. The most time-consuming process in our approach is obtaining the LSE values through NNP structural optimization of 1000 HEA NPs, which was completed in just 1.4 days. The significant reduction in the execution time for adsorption energy predictions achievable with this method is expected to facilitate the screening of catalytic properties for HEAs with exponentially large combinations using the entire periodic table as candidates.
000 adsorption sites requires approximately 171 days using the NNP and 188 years using DFT. These lengthy timescales were avoided by using the proposed method. The most time-consuming process in our approach is obtaining the LSE values through NNP structural optimization of 1000 HEA NPs, which was completed in just 1.4 days. The significant reduction in the execution time for adsorption energy predictions achievable with this method is expected to facilitate the screening of catalytic properties for HEAs with exponentially large combinations using the entire periodic table as candidates.
4 Discussion
We utilized the atomic energy obtained from the NNPs and introduced a metric called the LSE, which represents the surface energy per atom. Using the LSE, we determined the adsorption energy of CO molecules on the top sites of IrPdPtRhRu HEA201 NPs with a large number of atomic combinations as a distribution (Fig. 6(b)). This approach offers a novel means of analyzing the atomic energies to evaluate various adsorption energies in multicomponent systems such as HEAs. The adsorption-energy distribution obtained via LSE prediction can help efficiently and effectively characterize and visualize unexpected cocktail effects induced by the vast chemical space of HEA NPs.Notably, our calculations solely considered the adsorption energies on monometallic NPs and isolated multicomponent NPs, without the need for a direct evaluation of the CO molecular adsorption energy on the HEA. This approach enables the evaluation of adsorption energies approximately 105 times faster than direct DFT calculations, facilitating the visualization of the cocktail effect. Regarding accuracy, a comparison with DFT calculations revealed that the predictions based on the LSE were nearly an order of magnitude larger than the chemical accuracy, although they were not quantitatively accurate. Nonetheless, the relative energies exhibited a similar trend, indicating that qualitative comparisons that consider the influence of the surrounding environment on each element are feasible. Consequently, this method can be employed as a screening tool prior to applying DFT calculations or high-level quantum chemical methods such as CC theory.
The LSE-predicted adsorption energies were highly accurate, with an RMSE of 0.150 eV relative to the correct values, despite their low cost compared with direct evaluations. However, nonlinearity relative to the correct values was observed, indicating nonlinear behavior with respect to the LSE. We introduced a naïve method to capture this nonlinearity: nonlinear regression between the directly evaluated CO adsorption energy and the LSE. We modeled nonlinear regression with KRR and the classical quantum hybrid algorithm QCL regression. Learning the adsorption energies for only 732 sites for NPs in six patterns of structures improved the resulting LSE predictions thrice for the remaining 14 patterns tested for 1708 sites. The constraint that the norm of the parameters in QCL regression must equal 1 is expected to act as regularization. The results of the KRR and QCL regression models indicated similar regularization capabilities. Although our adsorption-energy correction model does not inherently require quantum computing, its utility may be extended to a wider chemical space and the construction of models encompassing the entire periodic table. Furthermore, in this study, the adsorption energies of quintet systems were studied; it may be possible to systematically increase the accuracy by adding binary and ternary adsorption energies to the model.
Finally, we discuss potential applications of the proposed method for designing chemical reactions for catalyst and device development. Previous studies examined the role of atomic energy in increasing the accuracy and efficiency of NNPs and validated atomic-energy mapping results.64,68–71 Recently, studies have attempted to gain chemical insight from atomic energies.72 However, to the best of our knowledge, the proposed LSE prediction method is the first to demonstrate that atomic energy can serve as a descriptor for the efficient evaluation of catalytic properties. Moreover, in contrast to atomic energies, which are absolute quantities, LSEs are relative quantities and are thus expected to be less sensitive to differences in computational methods, such as the treatment of basis functions and inner-shell electrons. The proposed approach enhances chemical reaction design—a crucial component of machine learning-based material design—which has garnered significant attention in the scientific community over the past few years due to its promise to accelerate the discovery and development of useful materials.73,74
5 Conclusion
We developed a computational methodology for predicting the molecular adsorption energies on HEAs using the LSE descriptor derived from the NNPs calculated atomic energies. This method addresses the challenge of evaluating the vast chemical space of HEAs due to their compositional diversity and the computational expense associated with direct DFT and NNP calculations. The LSE descriptor efficiently captures the local reactivity of surface atoms, enabling rapid and accurate prediction of adsorption energies across a wide range of HEA configurations.Our approach significantly accelerates the computational process, reducing the computation time from hundreds of years with DFT and hundreds of days with the NNP to only a few hours, which makes it a practical tool for materials discovery and catalyst design. The adoption of nonlinear regression techniques combined with advanced machine learning models, such as KRR and QCL regression, has increased the accuracy of adsorption-energy predictions, even in the face of the nonlinearity inherent in multicomponent systems.
Building upon this work, future research can extend the application of the LSE descriptor to other molecular species and reaction systems, validating and enhancing its predictive accuracy across a broader spectrum of catalytic processes. Integrating the LSE descriptor with advanced machine learning algorithms could facilitate large-scale screening of HEA compositions, accelerating the discovery of optimal catalysts for specific reactions. Moreover, combining the LSE descriptor with additional descriptors, such as surface microstructural features or GCN, offers the potential to further refine predictive accuracy by accounting for local atomic environments in more detail.10,11,49–56
In this study, we assumed that the HEA NPs have random elemental configurations following a uniform distribution. However, short-range order is also important in high-entropy alloys.75–77 By combining our method with techniques for quantifying short-range order using E(3)-equivariant graph neural networks,78 we can potentially obtain more accurate distributions of reactivity. This integration would allow us to capture the effects of atomic arrangements more precisely, leading to improved predictions of catalytic properties.
Moreover, this approach holds the potential to consider more realistic environmental conditions, including the behavior of catalysts in solution or under operational settings. Incorporating factors such as solvent effects, temperature, and pressure into the screening process would enhance the relevance and applicability of the predictions, leading to more effective and practical catalyst designs. Furthermore, applying the LSE framework to other material systems, such as high-entropy nitrides, oxides, and carbides, could further expand its impact on materials design.
In conclusion, this research not only paves the way for rapid and accurate computational screening of catalytic materials but also sets the stage for developing computational tools capable of handling the complexities of modern materials science—particularly in the realm of high-entropy materials.
6 Computational details
6.1 Modeling
We modeled CO adsorption on the NPs, i.e., CO/Mn, using an atomic simulation environment (ASE).79,80 The initial lattice constants (LCs) of Mn were determined via bulk calculations. For HEA201, the largest bulk was used as the initial LC. A 15 Å vacuum region was inserted in all supercells to minimize cell-to-cell interactions. The initial structures of CO/Mn and CO/HEA201 were derived by placing CO on the on-top sites of the optimized structures of Mn and HEA201, respectively, with the distance between the C atom and the adsorption-site metal atom M set as 2 Å.6.2 NNP calculations
The NNP used was M3GNet, a universal NNP proposed by Chen and Ong.36 This M3GNet NNP was trained on approximately 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 crystal environments at the PBE or PBE+U levels of theory from the Materials Project,81 covering 89 elements. The crystal structures of the bulk M = Ir, Pd, Pt, Rh, Ru were assumed to be fcc. Although Ru exhibits a hexagonal close-packed form at room temperature, Ru with an fcc structure can be created using NPs.82 The atomic energy of the bulk fcc metal M was determined using the energy corresponding to the minimum value obtained when varying the LC of the material at intervals of approximately 0.01 Å. The resulting atomic-energy values and corresponding LCs are presented in Table 2. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm was used for structural optimizations, with a maximum step of 0.005 Å. In the CO/M and CO/HEA structural optimization calculations, the M and HEA structures were fixed as stable isolated systems. Only the CO and adsorption-site atoms were relaxed, with the constraint that the adsorbed molecules occupy the top site. Structural optimizations were performed until the force acting on each atom was 0.001 eV Å−1.
000 crystal environments at the PBE or PBE+U levels of theory from the Materials Project,81 covering 89 elements. The crystal structures of the bulk M = Ir, Pd, Pt, Rh, Ru were assumed to be fcc. Although Ru exhibits a hexagonal close-packed form at room temperature, Ru with an fcc structure can be created using NPs.82 The atomic energy of the bulk fcc metal M was determined using the energy corresponding to the minimum value obtained when varying the LC of the material at intervals of approximately 0.01 Å. The resulting atomic-energy values and corresponding LCs are presented in Table 2. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm was used for structural optimizations, with a maximum step of 0.005 Å. In the CO/M and CO/HEA structural optimization calculations, the M and HEA structures were fixed as stable isolated systems. Only the CO and adsorption-site atoms were relaxed, with the constraint that the adsorbed molecules occupy the top site. Structural optimizations were performed until the force acting on each atom was 0.001 eV Å−1.
| fcc bulk M | Ir | Pd | Pt | Rh | Ru |
|---|---|---|---|---|---|
| E bulkatom (eV) | −8.941 | −5.185 | −6.069 | −7.394 | −9.305 |
| LC (Å) | 3.875 | 3.957 | 3.977 | 3.850 | 3.815 |
6.3 DFT calculations
The DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP), version 5.4.4.83–85 We employed the PBE generalized gradient approximation functional as the exchange–correlation functional.86 The core electrons were treated using the projector-augmented wave method.87,88 Electronic structures were optimized using the blocked Davidson iteration scheme within a spin-restricted approximation. The cutoff energy for the plane-wave functions was set as 400 eV. Atomic coordinates were optimized using a conjugate-gradient algorithm with a convergence threshold of 0.01 eV Å−1.6.4 GCN evaluations
The GCN descriptor is evaluated according to the following equation, which is identical to the one defined in ref. 49. | (5) |
6.5 Nonlinear regressions
To capture the nonlinearity between LSE and CO adsorption energy, we trained a nonlinear regression model using all possible ontop adsorption sites (732 in total) from six randomly selected HEA nanoparticles out of the 20 used for validating the linear LSE-based model. For validation, all possible ontop adsorption sites on the remaining 14 HEA nanoparticles were utilized. KRRs were executed using scikit-learn version 1.2.2.89 A Gaussian kernel was selected as the kernel function of the KRR. The hyperparameters for each model were optimized over 100 iterations using a randomized search. QCL regressions were implemented using scikit-qulacs version 0.5.0.90 Qulacs version 0.5.6 was used as the quantum-circuit simulator.91 The number of qubits in the QCL regression model was 4. The number of iterations of the parameterized variational quantum circuit of the model corresponding to the weights of the neural network was 6. The timestep for the time evolution operator in parameterized variational quantum circuits was set as 0.5. The BFGS algorithm was used to update the parameters of the QCL model.Data availability
The data and code required to reproduce the figures and tables are publicly accessible on GitHub https://github.com/TShiotaSS/lse. The datasets for this study are available on Figshare at DOI: https://doi.org/10.6084/m9.figshare.26973409.v2. They contain structural and energetic information for both HEA and monometallic NPs. The datasets also include adsorption energy data from M3GNet and VASP calculations. The provided data includes relaxed structures and DFT calculations performed at the PBE level using VASP. Additionally, key descriptors such as GCN and LSE from M3GNet are included. We modified the code to extract the atomic energies from the pretrained M3GNet model on Github at https://github.com/materialsvirtuallab/m3gnet, which can be found at https://github.com/TShiotaSS/lse/tree/main/scripts/m3gnet_each_atom_energy. The implementation for QCL regression used in this study is available at https://github.com/Qulacs-Osaka/scikit-qulacs/tree/main.Conflicts of interest
There are no conflicts to declare.Appendix
Here, we summarize the parameters of the regression model for adsorption-energy prediction using the LSE descriptor as well as the results of the model accuracy validation. Fig. 9 shows the parity plot of the training data and prediction results for the LSE linear regression model presented in Fig. 2. The RMSE for predicting the training data was 0.035 eV. Fig. 10 presents the regression results for the linear regression model between the CO adsorption energies on monometallic NPs obtained via DFT calculations and the LSE. Two datapoints corresponding to the hollow sites that converged on the facets of Pd in 38- and 79-atom monometallic NPs were excluded from the regression model. For small NPs, the entire system tended to exhibit molecular characteristics upon adsorption, making it difficult for a simple regression model to capture these effects. However, for larger NPs, a linear relationship with the LSE, similar to that observed for the NNP, was confirmed. The parameters of the regression models constructed using the adsorption energies from both the NNP and DFT are presented in Table 3. Fig. 11 presents a parity plot of the prediction results for the data not included in the training data for the nonlinear regression model of HEA NP adsorption energies evaluated directly using the NNP. The prediction accuracies were 0.0580 and 0.0579 eV, respectively, indicating that, as demonstrated in this study, the regression models using KRR and QCL had comparable accuracy. Finally, the regression parameters of the GCN-based prediction model are summarized in Table 4.| Ir | Pd | Pt | Rh | Ru | |
|---|---|---|---|---|---|
| α (DFT) | −0.639 | −0.446 | −1.073 | −0.345 | −0.041 |
| α (NNP) | −0.617 | −0.692 | −1.131 | −0.441 | −0.515 |
| β (DFT) | −1.782 | −1.305 | −1.521 | −1.755 | −2.012 |
| β (NNP) | −1.289 | −1.165 | −0.983 | −1.234 | −1.240 |
| Ir | Pd | Pt | Rh | Ru | |
|---|---|---|---|---|---|
| α (NNP) | 0.185 | 0.139 | 0.173 | 0.078 | 0.121 |
| β (NNP) | −2.766 | −2.403 | −1.073 | −1.946 | −2.371 |
Acknowledgements
We thank Nobuki Inoue, Tuan Minh Do, and Ryo Watanabe for fruitful discussions. This project was supported by funding from the MEXT Quantum Leap Flagship Program (MEXTQLEAP) through Grant No. JPMXS0120319794, and the JST COI-NEXT Program through Grant No. JPMJPF2014. The completion of this research was partially facilitated by the JSPS Grants-in-Aid for Scientific Research (KAKENHI), specifically Grant No. JP23H03819 and JP21K18933. We thank the Supercomputer Center, the Institute for Solid State Physics, the University of Tokyo, for allowing us to use these facilities. This work was also achieved using SQUID at the Cybermedia Center, Osaka University.Notes and references
- B. Cantor, I. Chang, P. Knight and A. Vincent, J. Mater. Sci. Eng. A, 2004, 375, 213–218 CrossRef.
- J.-W. Yeh, S.-K. Chen, S.-J. Lin, J.-Y. Gan, T.-S. Chin, T.-T. Shun, C.-H. Tsau and S.-Y. Chang, Adv. Eng. Mater., 2004, 6, 299–303 CrossRef CAS.
- E. J. Pickering and N. G. Jones, Int. Mater. Rev., 2016, 61, 183–202 CrossRef CAS.
- E. P. George, D. Raabe and R. O. Ritchie, Nat. Rev. Mater., 2019, 4, 515–534 CrossRef CAS.
- B. Cao, C. Wang, T. Yang and C. Liu, Scr. Mater., 2020, 187, 250–255 CrossRef CAS.
- D. Wu, K. Kusada, T. Yamamoto, T. Toriyama, S. Matsumura, I. Gueye, O. Seo, J. Kim, S. Hiroi, O. Sakata, S. Kawaguchi, Y. Kubota and H. Kitagawa, Chem. Sci., 2020, 11, 12731–12736 RSC.
- D. Wu, K. Kusada, T. Yamamoto, T. Toriyama, S. Matsumura, S. Kawaguchi, Y. Kubota and H. Kitagawa, J. Am. Chem. Soc., 2020, 142, 13833–13838 CrossRef CAS PubMed.
- K. Kusada, D. Wu and H. Kitagawa, Chem.–Eur. J., 2020, 26, 5105–5130 CrossRef CAS PubMed.
- D. Wu, K. Kusada, Y. Nanba, M. Koyama, T. Yamamoto, T. Toriyama, S. Matsumura, O. Seo, I. Gueye and J. Kim, et al. , J. Am. Chem. Soc., 2022, 144, 3365–3369 CrossRef CAS PubMed.
- T. A. Batchelor, J. K. Pedersen, S. H. Winther, I. E. Castelli, K. W. Jacobsen and J. Rossmeisl, Joule, 2019, 3, 834–845 CrossRef CAS.
- J. K. Pedersen, T. A. Batchelor, A. Bagger and J. Rossmeisl, ACS Catal., 2020, 10, 2169–2176 CrossRef CAS.
- H. S. Oh, S. J. Kim, K. Odbadrakh, W. H. Ryu, K. N. Yoon, S. Mu, F. Körmann, Y. Ikeda, C. C. Tasan and D. Raabe, et al. , Nat. Commun., 2019, 10, 2090 CrossRef PubMed.
- W. Huo, S. Wang, F. J. Dominguez-Gutierrez, K. Ren, Ł. Kurpaska, F. Fang, S. Papanikolaou, H. S. Kim and J. Jiang, Mater. Res. Lett., 2023, 11, 713–732 CrossRef CAS.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- T. Shiota, W. Mizukami, H. Tochihara, K. Yagyu, T. Suzuki and Y. Aoki, J. Phys. Chem. C, 2020, 124, 24704–24712 CrossRef CAS.
- W. A. Saidi, npj Comput. Mater., 2022, 8, 86 CrossRef CAS.
- J. McClain, Q. Sun, G. K.-L. Chan and T. C. Berkelbach, J. Chem. Theory Comput., 2017, 13, 1209–1218 CrossRef CAS PubMed.
- T. Gruber, K. Liao, T. Tsatsoulis, F. Hummel and A. Grüneis, Phys. Rev. X, 2018, 8, 021043 CAS.
- I. Y. Zhang and A. Grüneis, Front. Mater., 2019, 6, 123 CrossRef.
- I. Shavitt and R. J. Bartlett, Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge University Press, 2009 Search PubMed.
- L. Schimka, J. Harl, A. Stroppa, A. Grüneis, M. Marsman, F. Mittendorfer and G. Kresse, Nat. Mater., 2010, 9, 741–744 CrossRef CAS PubMed.
- T. Bligaard, J. Nørskov, S. Dahl, J. Matthiesen, C. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- K. Lee, D. Yoo, W. Jeong and S. Han, Comput. Phys. Commun., 2019, 242, 95–103 CrossRef CAS.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural Message Passing for Quantum Chemistry, 2017 Search PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- C. L. Zitnick, A. Das, A. Kolluru, J. Lan, M. Shuaibi, A. Sriram, Z. Ulissi and B. Wood, Spherical Channels for Modeling Atomic Interactions, 2022 Search PubMed.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef PubMed.
- S. Takamoto, C. Shinagawa, D. Motoki, K. Nakago, W. Li, I. Kurata, T. Watanabe, Y. Yayama, H. Iriguchi and Y. Asano, et al. , Nat. Commun., 2022, 13, 2991 CrossRef CAS PubMed.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csányi, Adv. Neural Inf. Process. Syst., 2022, 35, 11423–11436 Search PubMed.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 1–11 Search PubMed.
- J. Gasteiger, M. Shuaibi, A. Sriram, S. Günnemann, Z. Ulissi, C. L. Zitnick and A. Das, arXiv, 2022, preprint, arXiv:2204.02782 Search PubMed.
- R. Tran, J. Lan, M. Shuaibi, B. M. Wood, S. Goyal, A. Das, J. Heras-Domingo, A. Kolluru, A. Rizvi and N. Shoghi, et al. , ACS Catal., 2023, 13, 3066–3084 CrossRef CAS.
- D. P. Kovács, J. H. Moore, N. J. Browning, I. Batatia, J. T. Horton, V. Kapil, I.-B. Magdău, D. J. Cole and G. Csányi, arXiv, 2023, preprint, arXiv:2312.15211 Search PubMed.
- I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell, X. R. Advincula, M. Asta, W. J. Baldwin, N. Bernstein, A. Bhowmik, S. M. Blau, V. Cărare, J. P. Darby, S. De, F. D. Pia, V. L. Deringer, R. Elijošius, Z. El-Machachi, E. Fako, A. C. Ferrari, A. Genreith-Schriever, J. George, R. E. A. Goodall, C. P. Grey, S. Han, W. Handley, H. H. Heenen, K. Hermansson, C. Holm, J. Jaafar, S. Hofmann, K. S. Jakob, H. Jung, V. Kapil, A. D. Kaplan, N. Karimitari, N. Kroupa, J. Kullgren, M. C. Kuner, D. Kuryla, G. Liepuoniute, J. T. Margraf, I.-B. Magdău, A. Michaelides, J. H. Moore, A. A. Naik, S. P. Niblett, S. W. Norwood, N. O'Neill, C. Ortner, K. A. Persson, K. Reuter, A. S. Rosen, L. L. Schaaf, C. Schran, E. Sivonxay, T. K. Stenczel, V. Svahn, C. Sutton, C. van der Oord, E. Varga-Umbrich, T. Vegge, M. Vondrák, Y. Wang, W. C. Witt, F. Zills and G. Csányi, A Foundation Model for Atomistic Materials Chemistry, 2023 Search PubMed.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Nat. Commun., 2023, 14, 579 CrossRef CAS PubMed.
- Y.-L. Liao, B. Wood, A. Das and T. Smidt, arXiv, 2023, preprint, arXiv:2306.12059 Search PubMed.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85 CrossRef CAS PubMed.
- T. Shiota, K. Ishihara, T. M. Do, T. Mori and W. Mizukami, arXiv, 2024, preprint, arXiv:2412.13088 Search PubMed.
- C. M. Clausen, J. Rossmeisl and Z. W. Ulissi, J. Phys. Chem. C, 2024, 128, 11190–11195 CrossRef CAS.
- F. Calle-Vallejo, J. Tymoczko, V. Colic, Q. H. Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Science, 2015, 350, 185–189 CrossRef CAS PubMed.
- J. Dean, M. G. Taylor and G. Mpourmpakis, Sci. Adv., 2019, 5, eaax5101 CrossRef CAS PubMed.
- Y. Nanba and M. Koyama, ACS Omega, 2021, 6, 3218–3226 CrossRef CAS PubMed.
- Z. Lu, Z. W. Chen and C. V. Singh, Matter, 2020, 3, 1318–1333 CrossRef.
- Z. Yang and W. Gao, Adv. Sci., 2022, 9, 2106043 CrossRef CAS PubMed.
- M. Tamtaji, S. Chen, Z. Hu, W. A. Goddard III and G. Chen, J. Phys. Chem. C, 2023, 127(21), 9992–10000 CrossRef CAS.
- D. Roy, S. C. Mandal and B. Pathak, ACS Appl. Mater. Interfaces, 2021, 13, 56151–56163 CrossRef CAS PubMed.
- D. Roy, S. Charan Mandal, A. Das and B. Pathak, Chem.–Eur. J., 2024, 30, e202302679 CrossRef CAS PubMed.
- M. P. Salinas-Quezada, J. K. Pedersen, P. Sebastián-Pascual, I. Chorkendorff, K. Biswas, J. Rossmeisl and M. Escudero-Escribano, EES Catal., 2024, 2, 941–952 RSC.
- H. Nakai, Chem. Phys. Lett., 2002, 363, 73–79 CrossRef CAS.
- Y. Kikuchi, Y. Imamura and H. Nakai, Int. J. Quantum Chem., 2009, 109, 2464–2473 CrossRef CAS.
- M. Yu, D. R. Trinkle and R. M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115113 CrossRef.
- Y. Huang, J. Kang, W. A. Goddard and L.-W. Wang, Phys. Rev. B, 2019, 99, 064103 CrossRef.
- J. J. Eriksen, J. Chem. Phys., 2020, 153, 214109 CrossRef CAS PubMed.
- T. Shiota, K. Ishihara and W. Mizukami, Digital Discovery, 2024, 3, 1714–1728 RSC.
- D. Yoo, K. Lee, W. Jeong, D. Lee, S. Watanabe and S. Han, Phys. Rev. Mater., 2019, 3, 093802 CrossRef CAS.
- Z. El-Machachi, M. Wilson and V. L. Deringer, Chem. Sci., 2022, 13, 13720–13731 RSC.
- J. D. Morrow, C. Ugwumadu, D. A. Drabold, S. R. Elliott, A. L. Goodwin and V. L. Deringer, Angew. Chem., 2024, e202403842 CAS.
- K. Mitarai, M. Negoro, M. Kitagawa and K. Fujii, Phys. Rev. A, 2018, 98, 032309 CrossRef CAS.
- W. Jeong, D. Yoo, K. Lee, J. Jung and S. Han, J. Phys. Chem. Lett., 2020, 11, 6090–6096 CrossRef CAS PubMed.
- S. Watanabe, W. Li, W. Jeong, D. Lee, K. Shimizu, E. Mimanitani, Y. Ando and S. Han, J. Phys.: Energy, 2020, 3, 012003 Search PubMed.
- H. A. Doan, C. Li, L. Ward, M. Zhou, L. A. Curtiss and R. S. Assary, Digital Discovery, 2023, 2, 59–68 RSC.
- S. Chong, F. Grasselli, C. B. Mahmoud, J. D. Morrow, V. L. Deringer and M. Ceriotti, Robustness of Local Predictions in Atomistic Machine Learning Models, 2023 Search PubMed.
- F. Ø. Kjeldal and J. J. Eriksen, J. Chem. Theory Comput., 2023, 19, 2029–2038 Search PubMed.
- M. Meuwly, Chem. Rev., 2021, 121, 10218–10239 CrossRef CAS PubMed.
- M. Wen, E. W. C. Spotte-Smith, S. M. Blau, M. J. McDermott, A. S. Krishnapriyan and K. A. Persson, Nat. Comput. Sci., 2023, 3, 12–24 CrossRef PubMed.
- P. Singh, A. V. Smirnov and D. D. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 224204 CrossRef.
- Z. Sun, C. Shi, C. Liu, H. Shi and J. Zhou, Mater. Des., 2022, 223, 111214 CrossRef CAS.
- K. Sheriff, Y. Cao, T. Smidt and R. Freitas, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2322962121 CrossRef CAS PubMed.
- K. Sheriff, Y. Cao and R. Freitas, npj Comput. Mater., 2024, 10, 215 Search PubMed.
- S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- K. Kusada, H. Kobayashi, T. Yamamoto, S. Matsumura, S. Naoya, K. Sato, K. Nagaoka, Y. Kubota and H. Kitagawa, J. Am. Chem. Soc., 2013, 135, 5493–5496 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 Search PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- https://github.com/Qulacs-Osaka/scikit-qulacs .
- Y. Suzuki, Y. Kawase, Y. Masumura, Y. Hiraga, M. Nakadai, J. Chen, K. M. Nakanishi, K. Mitarai, R. Imai, S. Tamiya, T. Yamamoto, T. Yan, T. Kawakubo, Y. O. Nakagawa, Y. Ibe, Y. Zhang, H. Yamashita, H. Yoshimura, A. Hayashi and K. Fujii, Quantum, 2021, 5, 559 CrossRef.
Footnote |
| † These two authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |